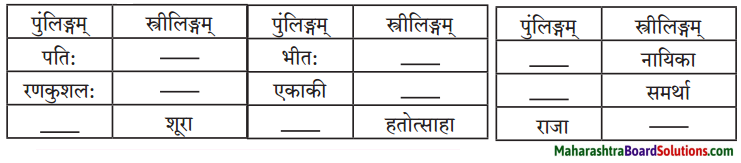
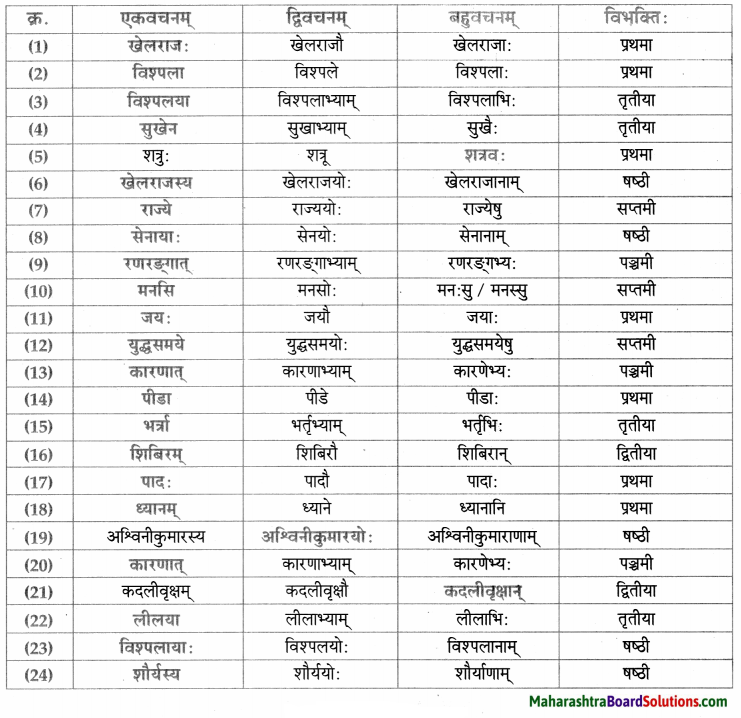
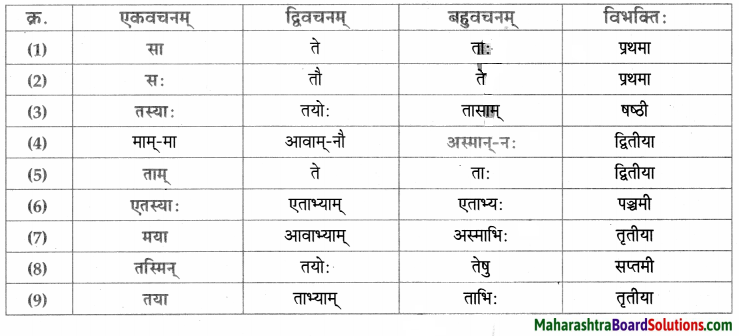
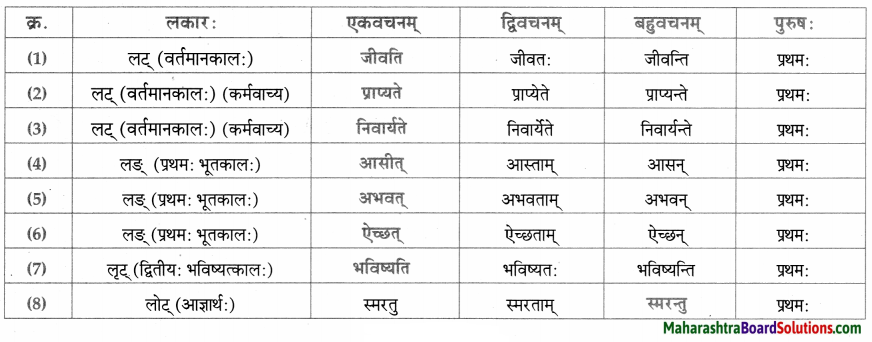
Balbharti Maharashtra State Board Class 9 Sanskrit Solutions Anand Chapter 11 मनोराज्यस्य फलम् Notes, Textbook Exercise Important Questions and Answers.
Maharashtra State Board Class 9 Sanskrit Anand Solutions Chapter 11 मनोराज्यस्य फलम्
Sanskrit Anand Std 9 Digest Chapter 11 मनोराज्यस्य फलम् Textbook Questions and Answers
भाषाभ्यास:
1. एकवाक्येन उत्तरत।
प्रश्न 1.
भिक्षुकस्य नाम किम् ?
उत्तरम् :
भिक्षुकस्य नाम स्वभावकृपणः।
प्रश्न 2.
स्वभावकृपणेन घट: कुत्र बद्धः?
उत्तरम् :
स्वभावकृपणेन घटः नागदन्ते बद्धः।
![]()
प्रश्न 3.
सोमशर्मा कस्मात् भीतः भविष्यति ?
उत्तरम् :
सोमशर्मा कुक्कुरात् भीतः भविष्यति।
प्रश्न 4.
सक्तुपिष्टेन पूर्णः घट: कस्मात् कारणात् भग्नः ?
उत्तरम् :
‘स्वप्नमग्न: ध्यानस्थित : भिक्षुकः लगुडप्रहारम् अकरोत्।’ तस्मात् घट: भग्नः।
प्रश्न 5.
सोमशर्मपितुः नाम किम् ?
उत्तरम् :
स्वभावकृपणः इति सोमशर्मपितुः नाम।
प्रश्न 6.
स्वभावकृपणेन कटः कुत्र प्रसारित: ?
उत्तरम् :
स्वभावकृपणेन कटः कलशस्य अधस्तात् प्रसारितः।
![]()
2. माध्यमभाषया उत्तरत।
प्रश्न 1.
स्वभावकृपणः किमर्थं पाण्डुरताम् अगच्छत्?
उत्तरम् :
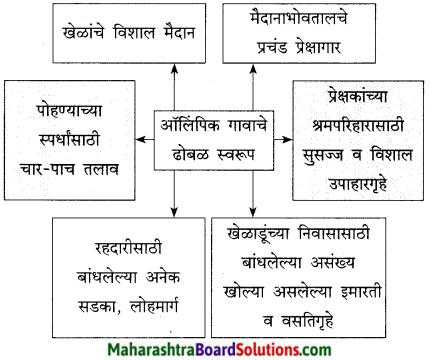
विष्णुशर्मा विरचित ‘पञ्चतन्त्र’ या जगप्रसिद्ध कथासंग्रहातील ‘अपरीक्षितकारकम्’ या तंत्रावर आधारित ‘मनोराज्यस्य फलम्’ ही कथा आहे. स्वभावकृपण नावाच्या भिक्षुकाच्या दिवास्वप्न पाहणाच्या स्वैर वृत्तीमुळे अंती त्याला नुकसान सोसावे लागते हे या कथेत मांडले आहे.
स्वभावकृपण नावाचा भिक्षुक भिक्षेतून मिळालेल्या सातूच्या पिठाने भरलेला घड़ा दोरीने खुंटीला अडकवून त्या खाली झोपला. तेव्हाच तो भविष्यात काय काय होईल याचा विचार करू लागला, ते पीठ विकून आपल्याला पैसे मिळतील त्यातून आपण दोन बकऱ्या विकत घेऊ पुढे आधिक श्रीमंत झाल्यावर, गायी त्यानतर म्हैस असे करत करत अनेक घोडेही विकत घेऊ असे दिवास्वप्नच जणू तो पाहू लागला.
त्यातही पुढे सोने मिळवून आपले रूपवती कन्येबरोबर लग्न होईल व आपल्याला सोमशर्मा नावाचा मुलगा असेल एवढे भविष्यातील सर्व विचार करत असताना त्याचा मुलगा सोमशर्मा कुत्र्याला घाबरतो म्हणून स्वभावकृपण कुत्र्याला काठीने मारतो हे सर्व स्वप्नात पाहत असताना, तंद्रीत असल्याने प्रत्यक्षातही स्वभावकृपणाने तीच कृती केली व त्यामुळे वर बांधून ठेवलेला पीठाचा घडा फुटला.
त्यातील पीठ स्वभावकृपणावर सांडल्यामुळे तो पांढरा झाला. जे घडलेलेच नाही त्या भविष्यातील गोष्टींचा सतत विचार करणे या अविवेकी वर्तनामुळे वर्तमानातील गोष्टीही भिक्षुक गमावून बसला.
The story ‘मनोराज्यस्य फलम् is based on the principle of ‘अपरीक्षितकारकम्’ from ‘पञ्चतन्त्र’ composed by विष्णुशर्मा, Amonk named स्वभावकृपण slept under a pot in which he had kept the flour of sattu. He started dreaming about his future.
He thought that he would sell the flour in the time of famine and earn hundred rupees. With those hundred rupees he would buy two goats. With those goats he would buy cows and with cows buffaloes. With them he would buy mares.
This is how he would earn a lot of gold with which he would build a mansion and get married to a beautiful girl. They would have a son whom he would name as सोमशर्मा, Once adog would come near his sons and he would hit that dog with wooden rod. Thinking this he actually hit and shattered the pot and got whitened. Day-dreaming always leads to losing what we actually have.
![]()
प्रश्न 2.
‘अपि दिवास्वप्नदर्शनं योग्यम् ?” इति कथायाः आधारेण लिखत ।
उत्तरम् :
विष्णुशर्मा विरचित ‘पञ्चतन्त्र’ या जगप्रसिद्ध कथासंग्रहातील ‘अपरीक्षितकारकम्’ या तंत्रावर आधारित ‘मनोराज्यस्य फलम्’ ही कथा आहे भिक्षुकाच्या दिवास्वप्न पाहण्याच्या वृत्तीचे कथेच्या अंती त्याला मिळालेले फळ अविवेकी वृत्तीने वर्तन केल्यास नुकसानच पदरी पडते हा उपदेश नकळतपणे मनावर बिंबवणारेच ठरते.
भिक्षेतून मिळालेले सातूचे पीठ एका घड्यात ठेवून तो घडा दोरीने खुंटीला अडकवून स्वभावकूपण त्या खालीच झोपला व तो भविष्यातील गोष्टींची दिवास्वप्ने रंगवू लागला. पीठ विकून पैसे मिळवेन इथपासून ते पुढे पशुपालनाचा व्यवसाय व त्यातून सोने प्राप्त करेन अशी गुंफण स्वभावकृपण स्वप्नात करू लागला, त्याही पुढे लग्नाचे, संसाराचे, अपत्याचे दिवास्वप्न तो रंगवू लागला.
त्याच स्वप्नात मग्न होऊन गेलेले असताना भानावर नसल्यामुळे स्वप्नातील कृती तो प्रत्यक्षातही केली व सातूच्या पिठाचा घडा काठीच्या प्रहाराने फुटला. यावरून हाच उपदेश मिळतो की, दिवास्वप्न पाहणे अयोग्य आहे. स्वप्न पूर्ण करण्यासाठी कार्य न करताच असलेल्या गोष्टीही हातातून निसटून जातात. त्यामुळे भविष्यात प्रगती साधायची असेल तर त्या ध्येयावर लक्ष केंद्रित करुन सतत त्यादृष्टीने कृती करणे आवश्यक आहे. ‘Preperation is a key to success’ म्हणूनच दिवास्वप्न न पाहता सतत प्रयत्न करत राहिल्यास वर्तमान व भविष्यकाळातही यश संपादन करता येते.
In the lesson ‘मनोराज्यस्य फलम्’ a message about day-dreaming is conveyed through a very interesting story. This story is based on one of the five principles of ‘पञ्चतन्त्र’ i.e ‘अपरीक्षितकारकम्’. A monk had a pot full of flour of sattu. He slept under that pot. He started dreaming how he would get rich after selling that flour in famine. Actually, there was no such situation of famine. He thought that he would sell flour of sattu and earn hundred rupees.
With that money, he would buy many animals and start a poultry business. In this way he would earn a lot of gold and build a mansion. He would get married to a beautiful girl and have a child whose name would beसोमशर्मा. Once when hthyref would be playing, a dog would come there and I would hit him with wooden rod.
While dreaming this he actually hit the pot and the pot got shattered. The flour on the basis of which the beggar was dreaming big things itself was vanished. The story tells us that a man should certainly dream big, but his dreams should be based on the reality.
![]()
3. अ. सन्धिविग्रहं कुरुत।
प्रश्न 1.
- तस्याधस्तात्
- सोमशर्मेति
- ततोऽहम् ।
उत्तरम् :
- तस्याधस्तात् – तस्य + अध: + तात्।
- सोमशमति – सोमशर्मा + इति।
- ततोऽहम् – तत: + अहम्।
![]()
आ. वर्णविग्रहं कुरुत।
प्रश्न 1.
- दुर्भिक्षम्
- रूपाढ्याम्
- ध्यानस्थितः
- स्वभावकृपणः
उत्तरम् :
- दुर्भिक्षम् – द् + उ + र + भ् + इ + क् + ष् + अ + म्।
- रूपाढ्याम् – र + ऊ + प् + आ + ढ् + य् + आ + म्।
- ध्यानस्थितः – ध् + य् + आ + न् + अ + स् + थ् + इ + त् + अः।
- स्वभावकृपणः – स् + व् + अ + भ + आ + व् + अ + क् + ऋ + प् + अ + ग् + अः।
![]()
4. समानार्थकशब्द लिखत।
कृपणः, दुर्भिक्षम्, अश्वः, धेनुः, सुवर्णम्, कुक्कुरः ।
प्रश्न 1.
समानार्थकशब्द लिखत।
कृपणः, दुर्भिक्षम्, अश्वः, धेनुः, सुवर्णम्, कुक्कुरः ।
उत्तरम् :
- कृपणः – कदर्यः, क्षुद्रः, किम्पचानः।
- दुर्भिक्षम् – वर्षाभावः।
- अश्वः – हयः, तुरगः, वाजी, घोटकः।
- धेनुः – गौः।
- सुवर्णम् – कनकम्, हेम, काञ्चनम्, हिरण्यम्।
- कुक्कुरः – सारमेयः, शुनकः, कौलेयकः।
Sanskrit Anand Class 9 Textbook Solutions Chapter 11 मनोराज्यस्य फलम् Additional Important Questions and Answers
उचितं पर्यायं चिनुत ।
प्रश्न 1.
कोऽपि भिक्षुकः ………… स्म।
(अ) प्रतिवसामि
(आ) प्रतिवसति
(इ) प्रत्यवसत्
(ई) प्रत्यवसन्
उत्तरम् :
(आ) प्रतिवसति।
![]()
प्रश्न 2.
कलशः ………… सम्पूरितः?
(अ) जलेन
(आ) धनेन
(इ) सक्तुपिष्टेन
(ई) रूप्यकेण
उत्तरम् :
(इ) सक्तुपिष्टेन।
प्रश्न 3.
भिक्षुक: अजाभिः प्रभूताः ………… ग्रहीष्यति।
(अ) अश्वाः
(आ) धेनूः
(इ) अश्वान्
(ई) महिषी:
उत्तरम् :
(आ) धेनूः
प्रश्न 4.
स्वभावकृपणस्य पुत्रस्य नाम …………।
(अ) सोमदेवः
(आ) विष्णुशर्मा
(इ) सोमशर्मा
(ई) देवदत्तः
उत्तरम् :
(इ) सोमशर्मा
![]()
प्रश्न 5.
कोपाविष्ट: भिक्षुकः काम् अभिधास्यति ?
(अ) सोमशर्माणम्
(आ) अजाम्
(इ) भार्याम्
(ई) बालकम्
उत्तरम् :
(इ) भार्याम्
प्रश्न 6.
स्वप्ने भिक्षुक: कं ताडयिष्यति?
(अ) महिषीम्
(आ) अश्वम्
(इ) अजाम्
(ई) कुक्कुरम्
उत्तरम् :
(ई) कुक्कुरम्
एकवाक्येन उत्तरत।
प्रश्न 1.
यदि दुर्भिक्षं भवति तर्हि कस्य विक्रयणेन भिक्षुक: रूप्यकाणां शतं प्राप्स्यति?
उत्तरम् :
यदि दुर्भिक्षं भवति तर्हि सक्तुपिष्टेन परिपूर्णघटस्य विक्रयेण रूप्यकाणां शतं प्राप्स्यति।
प्रश्न 2.
स्वप्ने भिक्षुक: कति अजा: केष्यति?
उत्तरम् :
स्वप्ने भिक्षुक; अजाद्वयं क्रेष्य
![]()
प्रश्न 3.
वडवापसवत: किं भविष्यति?
उत्तरम् :
वडवाप्रसवतः प्रभूताः अश्वाः भविष्यन्ति ।
प्रश्न 4.
भिक्षुकः कीदृशीं कन्याम् इच्छति?
उत्तरम् :
भिक्षुकः प्राप्तवयस्का रूपाझ्या कन्याम् इच्छति।
सत्यं वा असत्यं लिखत।
प्रश्न 1.
- भिक्षुकेन भिक्षया प्राप्तेन सक्तुपिष्टेन कलश: सम्पूरितः।
- भिक्षुकः भूमौ सुप्तः।
- भिक्षुकस्य नाम स्वभावकृपणः आसीत्।
- सोमशर्मा अन्धकारात् भीत: भविष्यति।
- लगुडप्रहारेण जलेन पूर्णः घट: भग्नः अभवत्।
- स्वभावकृपणः स्वप्नमग्नः आसीत् ।
- अश्वानां विक्रयणात्पभूतं सुवर्ण प्राप्स्यामि।
- स्वभावकृपणस्य पिता सोमशर्मा ।
- सुवर्णेन चतुःशालं गृहं सम्पत्स्यते।
उत्तरम् :
- सत्यम्
- असत्यम्
- सत्यम्
- असत्यम्
- असत्यम्
- सत्यम्
- सत्यम्
- असत्यम्
- सत्यम्
![]()
शब्दस्य वर्णविग्रहं कुरुत।
- कस्मिंश्चित् – क् + अ + स् + म् + इ + न् + श् + च् + ई + त्।
- सम्पूरितः – स् + अ + म् + प् + ऊ + र + इ + त् + अः।
- रज्ज्वा – र + अ + ज् + ज् + व् + आ।
- बद्ध्वा – ब + अ + द् + ध् + व् + आ।
- प्रसार्य – प् + र + अ + स् + आ + र + य् + अ।
- मत्समीपम् – म् + अ + त् + स् + अ + म् + ई + प् + अ + म्।
- कोपाविष्टः – क् + ओ + प् + आ + व् + ई + ष् + ट् + अः।
- स्वप्नमग्नः – स् + व् + अ + प् + न् + अ + म् + अ + ग् + न् + अः।
- षाण्मासिक – ष् + आ + ण + म् + आ + स् + इ + क + अ।
- ग्रहीष्यामि – ग् + र् + अ + ह् + ई + ष् + य् + आ + म् + इ।
प्रवनिर्माणं कुरुत।
प्रश्न 1.
- लगुडप्रहारेण: घट: भग्नः अभवत्।
- सोमशर्मा कुक्कुरात् भीत: भविष्यति।
- अश्वानां विक्रयणात्प्रभूतं सुवर्णं प्राप्स्यामि।
उत्तरम् :
- केन घट: भग्नः अभवत्?
- सोमशर्मा कस्मात् भीतः भविष्यति?
- केषां विक्रयणात्प्रभूतं सुवर्ण प्रास्यामि?
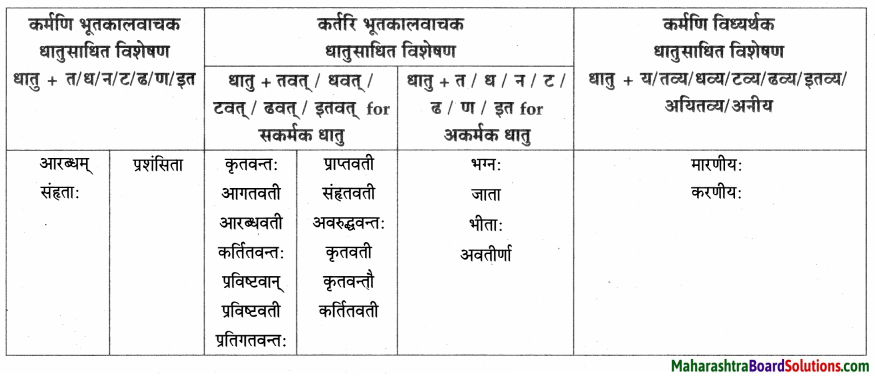
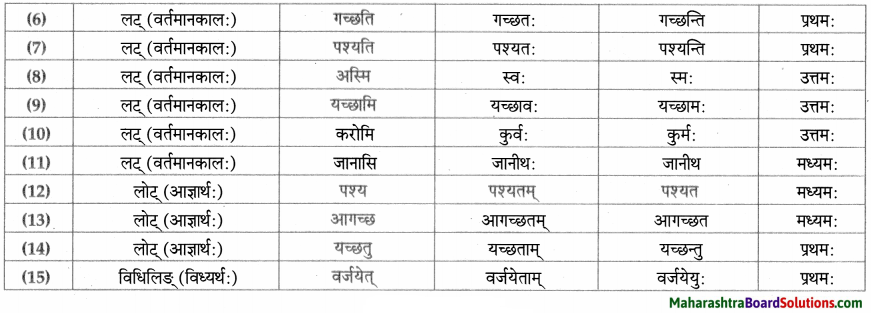
त्वान्त/ल्यबन्त/तुमन्त अव्ययानि।
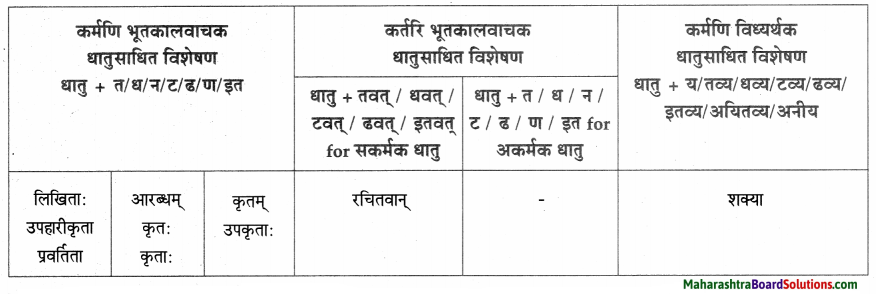
| त्वान्त अव्यय धातु + त्वा / ध्वा / ट्वा / ढ्वा / इत्वा अयित्वा | ल्यबन्त अव्यय उपसर्ग + धातु + य / त्य | तुमन्त अव्यय थातु + तुम् / धुम् / टुम् / ढुम् / इतुम् / अयितुम् |
| बद्ध्वा | प्रसार्य | – |
| दृष्ट्वा | समुत्थाय | – |
![]()
विभक्त्यन्तरूपाणि।
- प्रथमा – भिक्षुकः, कलश:, अयम्, परिपूर्णः, घटः, नाम, अहम्, अजा, वडवाः, अश्वाः, धनिकः, पुत्र:, सः, सोमशर्मा, अहम्, कुक्कुरः,सः, घटः, पाण्डुरः, सोमशमपिता, ध्यानस्थितः।
- द्वितीया – तम्, घटम्, कटम्, धेनूः, महिषी:, सुवर्णम्, गृहम, कन्याम, रूपाढ्याम्, बालकम, भार्याम्, कुक्कुरम्, लगुडप्रहारम्, चिन्ताम्, माम्।
- तृतीया – तेन, भिक्षया, सक्तुपिष्टेन, विक्रयणेन, रज्ज्वा, अजाभिः, धेनुभिः, महिषीभिः, सुवर्णेन, लगुडेन, प्रहारेण।
- चतुर्थी – महाम् पझमी – ताभ्याम्
- पञ्चमी – तस्मात्।
- षष्ठी – अस्य, तेषाम् , आवयोः, तस्य, मम।
- सप्तमी – नगरे, नागदन्ते, विषये।
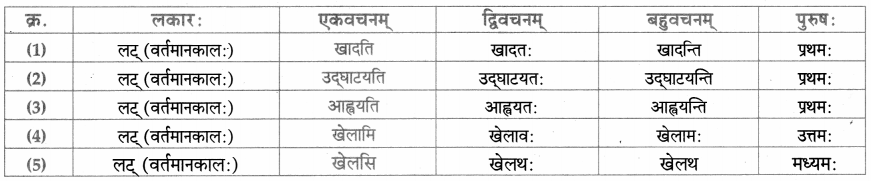
लकारं लिखत।
- प्रतिवसति – प्रति + वस् धातुः प्रथमगणः परस्मैपदं लट्लकार प्रथमपुरुष: बहुवचनम्।
- अचिन्तयत् – चिन्त् धातुः दशमगण: उभयपदम् अत्र परस्मैपदं लङ्लकारः प्रथमपुरुष: एकवचनम्।
- प्राप्स्यामि – प्र + आप् धातुः पञ्चमगण: परस्मैपदं लुट्लकार: उत्तमपुरुष: एकवचनम्।
- वेष्यामि – की धातुः नवमगणः परस्मैपदं लुट्लकार: उत्तमपुरुष: एकवचनम्।
- भविष्यति – भू धातुः प्रथमगणः परस्मैपदं लूट्लकार: प्रथमपुरुष: एकवचनम्।
- ग्रहीष्यामि – गृह धातुः नवमगण: उभयपदम् अत्र परस्मैपद लुट्लकार: उत्तमपुरुष: एकवचनम्।
- दास्यामि – दा धातः प्रथमगण:/तृतीयगण: उभयपदम् अत्र परस्मैपदं लट्लकार: उत्तमपुरुष: एकवचनम्।
- करिष्यामि – कृ धातुः अष्टमगण: उभयपदम् अत्र परस्मैपदं लुट्लकार: उत्तमपुरुष: एकवचनम्।
- आगमिष्यति – आ + गम् धातुः प्रथमगण: परस्मैपदं लुट्लकार: प्रथमपुरुष: एकवचनम्।
- अभिधास्यामि – अभि + धा धातु: तृतीयगणः परस्मैपदं लट्ल कार: उत्तमपुरुष: एकवचनम्।
- श्रोष्यति – शृ धातुः पञ्चमगण: परस्मैपदं लट्लकार: प्रथमपुरुष: एकवचनम्।
- ताडयिष्यामि – ताधातुः दशमगण: परस्मैपदं लुट्लकार: उत्तमपुरुष: एकवचनम्।
- ब्रवीमि – ब्रूधातुः द्वितीयगण: उभयपदम् अत्र परस्मैपदं लट्लकारः उत्तमपुरुष: एकवचनम्।
- शेते – शी धातु: द्वितीयगण: आत्मनेपदं लट्लकारः प्रथमपुरुष: एकवचनम्।
![]()
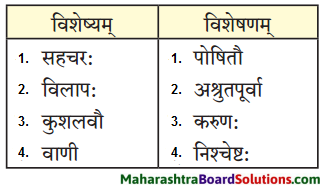
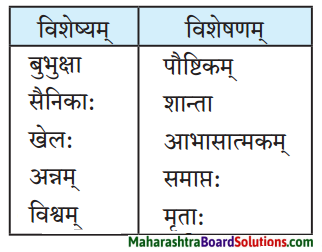
विशेषण-विशेष्य-सम्बन्ध: (स्तम्भमेलनं कुरुत)।
प्रश्न 1.
| विशेष्यम् | विशेषणम् |
| 1. जानुचलनयोग्यः | कन्या |
| 2. चतुःशालम् | सोमशर्मा |
| 3. प्राप्तवयस्का | गृहम् |
| 4. स्वप्नमग्नः | घट: |
| 5. भग्नः | चिन्ता |
| 6. अनागतवती | भिक्षुकः |
उत्तरम् :
| विशेष्यम् | विशेषणम् |
| 1. जानुचलनयोग्यः | सोमशर्मा |
| 2. चतुःशालम् | गृहम् |
| 3. प्राप्तवयस्का | कन्या |
| 4. स्वप्नमग्नः | भिक्षुकः |
| 5. भग्नः | घट: |
| 6. अनागतवती | चिन्ता |
कः कं वदति।
प्रश्न 1.
“गृह्मण बालकम्”।
उत्तरम् :
स्वभावकृपणः/ भिक्षुकः भार्या वदति।
उचितं कारणं चित्वा वाक्यं पुनर्लिखत।
![]()
प्रश्न 1.
सक्तुपिष्टेन पूर्ण: घट: भग्नः अभवत् यतः……….।
a. स्वप्नमग्न; ध्यानस्थितः भिक्षुक: लगुडप्रहारम् अकरोत्।
b. घट: भूमौ अपतत्।
उत्तरम् :
सक्तुपिष्टेन पूर्ण: घटः भग्नः अभवत् यतः स्वप्नमग्नः ध्यानस्थित : भिक्षुकः लगुडप्रहारम् अकरोत्।
सूचनानुसारं वाक्यपरिवर्तनं कुरुत।
प्रश्न 1.
स: अचिन्तयत्।
(लट्लकारं योजयत।)
उत्तरम् :
स: चिन्तयति।
प्रश्न 2.
घटस्य विक्रयणेन रूप्यकाणां शतं प्राप्स्यामि।
(लङ्लकारे परिवर्तयत।)
उत्तरम् :
घटस्य विक्रयणेन रूप्यकाणां शतं प्राप्नवम्।
![]()
प्रश्न 3.
अजाभिः प्रभूताः धेनू: ग्रहीष्यामि।
(बहुवचने परिवर्तयत।)
उत्तरम् :
अजाभिः प्रभूताः धेनूः ग्रहीष्यामः।
प्रश्न 4.
एकदा सोमशर्मा मां दृष्ट्वा मत्समीपम् आगमिष्यति।
(‘त्वान्त’ निष्कासयत।)
उत्तरम् :
एकदा सोमशर्मा मां दर्शविष्यति मत्समीपम् आगमिष्यति च।
प्रश्न 5.
स्वभावकृपणः सः पाण्डुरताम् अगच्छत्।
(‘स्म’ योजयत।)
उत्तरम् :
स्वभावकृपणः सः पाण्डुरतां गच्छति स्म।
समानार्थकशब्द योजयित्वा वाक्यं पुनर्लिखत।
- प्रभूता: – वडवाप्रसवतः प्रभूता: अश्वाः भविष्यन्ति। वडवाप्रसवत: बहवः/प्रचुराः अश्वा: भविष्यन्ति।
- पूर्णम् – यत्परिपूर्णोऽयं घटस्तावत् सक्तुपिष्टेन वर्तते। यत्परिसमग्र:/सकल:/अखण्डे ऽयं घटस्तावत् सक्तुपिष्टेन वर्तते।
- शोभनम् – बालस्य रूपं शोभनम् अस्ति। बालस्य रूपं सुन्दरं/रुचिरं/साधु अस्ति।
- कृपणः – कस्मिंश्चित् नगरे कश्चित् स्वभावकृपणो नाम कोऽपि भिक्षुकः प्रतिवसति स्म ।
कस्मिंशित् नगरे कश्चित् स्वभावकदर्य:/क्षुद्रः/किंपचान: नाम कोऽपि भिक्षुकः प्रतिवसति स्म।
![]()
व्याकरणम् :
शब्दानां पृथक्करणम्
| नाम | सर्वनाम | क्रियापदम् | विशेषणम् |
| स्वभावकृपणः, नगरे, भिक्षया, रज्ज्वा, नागदन्ते, कटम्, सक्तुपिष्टेन, अजा, धेनूः, धेनुभिः, महिषीभिः, वडवाः, भार्याम्, कुक्कुरम्, लगुडेन | तेन, तम्, तत्, सः, अयम् अस्यः, अहम्, ताभ्याम्, तेषाम् माम्-मा | प्रतिवसति, वर्तते, भवति, अचिन्तयत्, प्राप्स्यामि, भविष्यति, ग्रहीष्यामि, सम्पत्स्यते, दास्यति, करिष्यामि आगमिष्यति, अभिधास्यामि, श्रोष्यति, ताडयिष्यामि, क्रेष्यामि | सम्पूरित:, परिपूर्णः, प्रभूताः, प्रभूतम्, रूपाढ्याम्, पाण्डुर: |
समासाः।
| समस्तपदम् | अर्थ: | समासविग्रहः | समासनाम |
| स्वभावकृपणः | miser by nature | स्वभावेन कृपणः। | तृतीया तत्पुरुष समास। |
| कोपाविष्टः | overcome by anger | कोपेन आविष्टः। | तृतीया तत्पुरुष समास। |
| लगुडप्रहार: | blow of a stick | लगुडस्य प्रहारः। | षष्ठी तत्पुरुष समास। |
| जानुचलनम् | walking by the knees | जानुभ्याम् चलनम्। | तृतीया तत्पुरुष समास। |
| सक्तुपिष्टेन | with flour of sattu | सक्तो : पिष्टं, तेन। | षष्ठी तत्पुरुष समास। |
![]()
मनोराज्यस्य फलम् Summary in Marathi and English
प्रस्तावना :
भारतात कथाकथनाची परंपरा फार पूर्वीपासून आहे. शर्करावगुण्ठित उपदेश करून सहजपणे एखादे मूल्य पटविण्यासाठी गोष्ट हे प्रभावी माध्यम ठरते. विष्णुशर्मारचित पंचतंत्र या कथा संग्रहात पुढील 5 तंत्रे गोष्टीरूपाने मांडली आहेत.1) मित्रभेदः 2) मित्रसम्प्राप्तिः 3)काकोलुकीयम् 4)लब्धपणरा: 5) अपरीक्षितकारकम्. राजा अमरशक्तीच्या तीन मुलांना नीती व राज्यशास्त्राचे शिक्षण देण्यासाठी, व्यवहारज्ञानात चतुर बनविण्यासाठी विष्णुशर्माने हा ग्रंथ रचला.
विष्णुशर्मा विरचित ‘पंचतंत्र’ या जगप्रसिद्ध कथासंग्रहातील ‘अपरीक्षितकारकम्’ (अविचाराने केलेले काम) या तंत्रावर आधारित प्रस्तुत कथा आहे. आपल्या स्वप्नांच्या पूर्तीसाठी जिद्दीने झटणे आवश्यक असते. केवळ दिवास्वप्न पाहून, न घडलेल्या गोष्टींबद्दल विचार करत राहिल्यास वर्तमानात असलेल्या गोष्टीही हातातून निघून जातात, हा बोध भिक्षुकाच्या या कथेतून मिळतो.
India has a wide history of story literature. Stories have been a very strong and effective method of inculcating moral and ethical things since time immemorial A classical example of this is king Amarshakti whose sons could not be taught by any traditional means.
It uses only when the scholar Vishnusharma took them into this fold and narrated to them stories that could make them proficient in administration. It is these stories which form the basis of the five principles of पञ्चतन्त्र – 1) मित्रभेद: 2) मित्रसम्प्राप्ति: 3) काकोलूकीयम् 4) लब्धप्रणाश: 5) अपरीक्षितकारकम् The present story is taken from the अपरीक्षितकारकम् which deals with the effect of actions done without proper thinking. This story presents to us the ill-effects of daydreaming and building castles in air without proper action to follow it.
![]()
परिच्छेद : 1
कस्मिंश्चित् ………………. शतं प्राप्स्यामि।
कस्मिंश्चित् नगरे कश्चित् स्वभावकृपणो नाम कोऽपि भिक्षुकः प्रतिवसति स्म । तेन भिक्षया प्राप्तेन सक्तुपिष्टेन कलश: सम्पूरितः । तं च घट नागदन्ते रज्ज्वा बद्ध्वा तस्याधस्तात् कटं प्रसार्य सततं तद्विषये चिन्तयन् सः सुप्तः । स: अचिन्तयत् – “यत्परिपूर्णोऽयं घटस्तावत् सक्तुपिष्टेन वर्तते । यदि दुर्भिक्षं भवति तर्हि अस्य विक्रयणेन रूप्यकाणां शतं प्राप्स्यामि ।
अनुवादः
कोण्या एका नगरात कोणी एक स्वभावकृपण नावाचा भिक्षुक राहात असे. त्याने भिक्षा मागून मिळालेल्या सातूच्या पिठाने घडा पूर्ण भरला, आणि (त्याने) त्या घड्याला दोरीने खुंटीवर बांधून त्याच्या खालीच चटई पसरून सतत त्या विषयीच विचार करत तो (तिथे) झोपला. त्याने विचार केला – “हा घडा सातूच्या पिठाने पूर्ण भरलेला आहे. जर दुष्काळ पडला तर याच्या (सातूच्या पीठाच्या) विक्रीतून शंभर रूपये मिळवेन.
In certain city there lived a certain monk named स्वभावकृपण. He filled a pot with the flour of sattu which he obtained as alms. After hanging that pot with a rope to the nail, spreading a mat exactly below it, he fell asleep constantly thinking about it. He thought this pot is filled with sattu flour. If there is a famine, (scarcity of food) I’ll get hundred rupees by selling it.
![]()
परिच्छेद : 2
ततस्तेन ………….. जानुचलनयोग्यः भविष्यति।
ततस्तेन अहम् अजाद्वयं क्रेष्यामि। तत: पाण्मासिक-प्रसववशात् ताभ्यां यूथः भविष्यति। ततोऽजाभिः धेनू: ग्रहीष्यामि, धेनुभिः महिषी:, महिषीभिः वडवाः, वडवाप्रसवतः प्रभूता: अश्वाः भविष्यन्ति । तेषां विक्रयणात्प्रभूतं सुवर्ण प्राप्स्यमि। सुवर्णेन चतु:शालं गृहं सम्पत्स्यते। ततः कश्चित् धनिकः प्राप्तवयस्कां रूपाढ्यां कन्यां मां दास्यति । आवयोः पुत्रः भविष्यति । तस्याहं सोमशमति नाम करिष्यामि । तत: स: जानुचलनयोग्यः भविष्यति।
अनुवादः
त्यानंतर त्यातून मी दोन बकऱ्या विकत घेईन. त्यानंतर सहा महिन्यांनी त्यांच्या प्रजननातून त्यांचा कळप तयार होईल. त्यानंतर पुष्कळ बकऱ्या झाल्यावर गायी विकत घेईन. गाईंनंतर म्हशी, म्हशींनंतर घोड्या, घोड्यांच्या प्रजननातून पुष्कळ घोडे जन्माला येतील. त्यांच्या विक्रीतून पुष्कळ सोने मिळवेन.
त्या सोन्यामुळे चौसोपी घर होईल. तेव्हा कोणी एक धनिक वयात आलेली रूपवती कन्या मला देईल. आम्हां दोघांना मुलगा होईल. त्याचे मी सोमशर्मा असे नाव ठेवेन त्यानंतर तो रांगू लागेल.
Then, with that, I shall buy two goats. Then, after six month of their pro-creation, there will be a flock of them. Then with the goats, I shall get cows, with the cows buffaloes, with the buffaloes, many mares, from many mares there will be many horses.
I shall obtain lots of gold by selling them. With the gold there will be a mansion (four buildings enclosing a quadrangle). Then some rich man will give me his beautiful daughter of marriageable age. Then we will have a son. I will name him as Somasharma. Then he’ll be able crawl on knees.
![]()
परिच्छेद : 3
एकदा सोमशर्मा ………… यया ।।
एकदा सोमशर्मा मां दृष्ट्वा मत्समीपम् आगमिष्यति । ततोऽहं कोपाविष्टः अभिधास्यामि भार्याम्, “गृहाण बालकम्’ इति । साऽपि मम वचनं न श्रोष्यति । तावत्काले कश्चन कुक्कुरं तत्र आगमिष्यति । सोमशर्मा तस्मात् भीतः भविष्यति। ततोऽहं समुत्थाय लगुडेन तं कुक्कुर ताडयिष्यामि।” एवं स्वनमग्नः ध्यानस्थितः सः तथैव लगुडप्रहारम् अकरोत् । तेन लगुडपारेण सक्तुपिष्टेन पूर्णः सः घट: भग्नः अभवत् । स्वभावकृपणः सः पाण्डुरताम् अगच्छत् । अत: ब्रवीमि – अनागतवती चिन्तामसम्भाव्यां करोति यः । स एव पाण्डुर: शेते सोमशर्मपिता यथा ।।
अनुवादः
एकदा सोमशर्मा मला पाहून माझ्याजवळ येईल. तेव्हा रागावलेला मी पत्नीला म्हणेन, “मुलाला घे.” ती सुद्धा माझे बोलणे ऐकणार नाही. त्याचवेळी कोणी एक कुत्रा तेथे येईल. सोमशर्मा त्याला घाबरेल. तेव्हा मी उठून काठीने त्या कुत्र्याला मारेन, अशा प्रकारे स्वप्नात गढून गेल्याने विचारमग्न झालेल्या त्याने तशाच प्रकारे काठीचा प्रहार केला. त्या काठीच्या प्रहाराने सातूच्या पिठाने भरलेला तो घडा फुटला. तो स्वभावकृपण पांढरा झाला.
म्हणून म्हणतो – अद्याप न घडलेल्या गोष्टींची आणि अशक्य गोष्टींची जो उगाचच चिंता करतो (विचार करतो), तो झोपलेल्या सोमशाच्या पित्याप्रमाणेच पांढरा होतो.
Once after seeing me Heref will come to me. Then, I will angrily say to my wife ” Take the boy”. She too will not hear my words. By that time, a certain dog will come there. Somasharma will get scared of it. Then after getting up, I shall hit that dog with a stick.
Thus engrossed in the dream he who was thinking, struck a blow with the stick. Due to the blow of the stick, the pot filled with sattu flour was shattered (broke) and that स्वभावकृपण got all whitened. Hence I tell you, he who sleeps over (worries over) something yet to come, or something impossible, gets whitened (pale) just like Somasharma’s father who was sleeping.
![]()
सन्धिविग्रहः
- कश्चित् – क: + चित्।
- ततस्तेन – ततः + तेन। ततोऽजाभिः – ततः + अजाभिः।
- तस्याहम् – तस्य + अहम्।
- विक्रयणात्प्रभूतम् – विक्रयणात् + प्रभूतम्।
- तावत्काले – तावत् + काले।
- चिन्तामसम्भाव्याम् – चिन्ताम् + असम्भाव्याम्।
- साऽपि – सा + अपि।
- तथैव – तथा + एव।
- स्वभावकृपणो नाम – स्वभावकृपणः + नाम।
- कोऽपि – क: + अपि।
- तद्विषये – तत् + विषये।
- यत्परिपूर्णोऽयम् – यत् – परिपूर्ण: + अयम्।
- घटस्तावत् – घटः + तावत् ।
- कस्मिंचित् – कस्मिन् + चित् ।
![]()
समानार्थकशब्दाः
- भिक्षुकः – भिक्षुः, परिव्राजकः, परिव्राट्।
- रज्जुः – गुणः, सूत्रम्।
- नगरम् – पत्तनम्, पुरी।
- कलशः – घटः, कुम्भः ।
- वडवा – अश्वा, वामी।
- कन्या – तनया, पुत्री, दुहिता।
- पुत्रः – आत्मजः, सुतः, सुनः।
- प्रभूताः – बहुलाः, बहवः।
विरुद्धार्थकशब्दाः
- सुप्तः × जागरितः।
- पूर्णः × अपूर्णः ।
- प्रभूताः × स्तोकाः।
- समीपे × दूरे।
![]()
शब्दार्थाः
- स्वभावकृपणः – miserly by nature – स्वभावाने कंजूष
- सक्तुपिष्टम् – saktu flour – सातूचे पीठ
- नागदन्तः – bracket on the wall – खुंटी
- दुर्भिक्षम् – famine – दुष्काळ
- विक्रयणेन – by selling – विकून
- बद्ध्वा – having tied – बांधून
- प्रसार्य – having spread – पसरून
- अजा – goat – बकरी, शेळी
- महिषी – buffalo – म्हैस
- वडवा – mare – घोड़ी
- अश्वः – horse – घोडा
- प्रभूतम् – a lot – पुष्कळ
- प्राप्तवयस्का – of proper age – वयात आलेली
- जानुचलनयोग्य: – able to crawlon knees – रांगण्यायोग्य
- भ्यूथः – flock / shed – समूह, कळप
- ‘चतुःशालम् – quadrangle with four building (mansion) – वाडा
- मत्समीपम् – near me – माझ्याजवळ
- कोपाविष्टः – angry – अतिशय रागावलेला
- अभिधास्यामि – I will say – मी बोलेन
- गुहाण – you take – तू घे
- कुक्कुरः – dog – कुत्रा
- समुत्थाय – after getting up – उठून
- लगुडेन – with a stick – काठीने
- पाण्डुरः – white – पांढरा
- अनागतवती – not arrived – न आलेली
- असम्भाव्यम् – impossible – अशक्य
- शेते – sleeps – झोपतो