Balbharti Maharashtra State Board Class 9 Maths Solutions covers the Problem Set 2 Algebra 9th Class Maths Part 1 Answers Solutions Chapter 2 Real Numbers.
Problem Set 2 Algebra 9th Std Maths Part 1 Answers Chapter 2 Real Numbers
Question 1.
Choose the correct alternative answer for the questions given below. [1 Mark each]
i. Which one of the following is an irrational number?

Answer:
√5
ii. Which of the following is an irrational number?
(A) 0.17
(B) \(1.\overline { 513 }\)
(C) \(0.27\overline { 46 }\)
(D) 0.101001000……..
Answer:
(D) 0.101001000……..
iii. Decimal expansion of which of the following is non-terminating recurring?
![]()
Answer:
(C) \(\frac { 3 }{ 11 }\)
iv. Every point on the number line represents which of the following numbers?
(A) Natural numbers
(B) Irrational numbers
(C) Rational numbers
(D) Real numbers
Answer:
(D) Real numbers
v. The number [/latex]0.\dot { 4 }[/latex] in \(\frac { p }{ q }\) form is ……

Answer:
(A) \(\frac { 4 }{ 9 }\)
vi. What is √n , if n is not a perfect square number ?
(A) Natural number
(B) Rational number
(C) Irrational number
(D) Options A, B, C all are correct.
Answer:
(C) Irrational number
vii. Which of the following is not a surd ?

Answer:
(C) \(\sqrt [ 3 ]{ \sqrt { 64 } }\)
viii. What is the order of the surd \(\sqrt [ 3 ]{ \sqrt { 5 } }\) ?
(A) 3
(B) 2
(C) 6
(D) 5
Answer:
(C) 6
ix. Which one is the conjugate pair of 2√5 + √3 ?
(A) -2√5 + √3
(B) -2√5 – √3
(C) 2√3 – √5
(D) √3 + 2√5
Answer:
(A) -2√5 + √3
x. The value of |12 – (13 + 7) x 4| is ____ .
(A) – 68
(B) 68
(C) – 32
(D) 32
Answer:
(B) 68
Hints:
ii. Since the decimal expansion is neither terminating nor recurring, 0.101001000…. is an irrational number.
iii. \(\frac { 3 }{ 11 }\)
Denominator =11 = 1 x 11
Since, the denominator is other than prime factors 2 or 5.
∴ the decimal expansion of \(\frac { 3 }{ 11 }\) will be non terminating recurring.
v. Let x = [/latex]0.\dot { 4 }[/latex]
∴10 x = [/latex]0.\dot { 4 }[/latex]
∴10 – x = [/latex]4.\dot { 4 }[/latex] – [/latex]0.\dot { 4 }[/latex]
∴9x = 4
∴ x = \(\frac { 4 }{ 9 }\)
vii. \(\sqrt[3]{61}\) = 4, which is not an irrational number.
viii. \(\sqrt[3]{\sqrt{5}}=\sqrt[3 \times 2]{5}=\sqrt[6]{5}\)
∴ Order = 6
ix. The conjugate of 2√5 + √3 is 2√5 – √3 or -2√5 + √3
x. |12 – (13+7) x 4| = |12 – 20 x 4|
= |12 – 80|
= |-68|
= 68
Question 2.
Write the following numbers in \(\frac { p }{ q }\) form.
i. 0.555
ii. \(29.\overline { 568 }\)
iii. 9.315315…..
iv. 357.417417…..
v . \(30.\overline { 219 }\)
Solution:
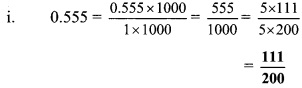
ii. Let x = \(29.\overline { 568 }\) …(i)
x = 29.568568…
Since, three numbers i.e. 5, 6 and 8 are repeating after the decimal point.
Thus, multiplying both sides by 1000,
1000x = 29568.568568…
1000 x= \(29568.\overline { 568 }\) …(ii)
Subtracting (i) from (ii),
1000x – x = \(29568.\overline { 568 }\) – \(29.\overline { 568 }\)
∴ 999x = 29539
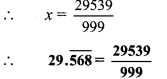
iii. Let x = 9.315315 … = \(9.\overline { 315 }\) …(i)
Since, three numbers i.e. 3, 1 and 5 are repeating after the decimal point.
Thus, multiplying both sides by 1000,
1000x = 9315.315315…
∴1000x = \(9315.\overline { 315 }\) …(ii)
Subtracting (i) from (ii),
1000x – x = \(9315.\overline { 315 }\) – \(9.\overline { 315 }\)
∴ 999x = 9306
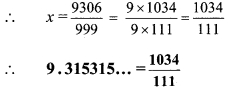
iv. Let x = 357.417417… = \(357.\overline { 417 }\) …(i)
Since, three numbers i.e. 4, 1 and 7 are repeating after the decimal point.
Thus, multiplying both sides by 1000,
1000x = 357417.417417…
∴ 1000x = 357417.417 …(ii)
Subtracting (i) from (ii),
1000x – x = \(357417.\overline { 417 }\) – \(357.\overline { 417 }\)
∴ 999x = 357060
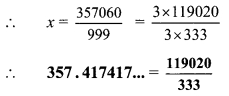
v. Let x = \(30.\overline { 219 }\) …(i)
∴ x = 30.219219
Since, three numbers i.e. 2, 1 and 9 are repeating after the decimal point.
Thus, multiplying both sides by 1000,
1000x= 30219.219219…
∴ 1000x = \(30219.\overline { 219 }\) …(ii)
Subtracting (i) from (ii),
1000x – x = \(30219.\overline { 219 }\) – \(30.\overline { 219 }\)
∴ 999x = 30189
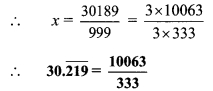
Question 3.
Write the following numbers in its decimal form.
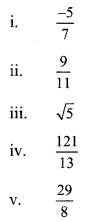
Solution:
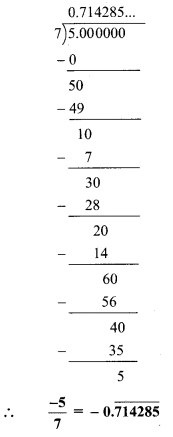
i. \(\frac { -5 }{ 7 }\)
ii. \(\frac { 9 }{ 11 }\)
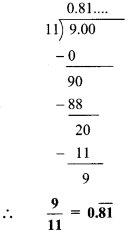
iii. √5

iv. \(\frac { 121 }{ 13 }\)
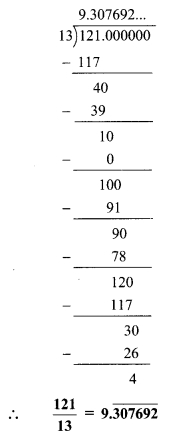
v. \(\frac { 29 }{ 8 }\)
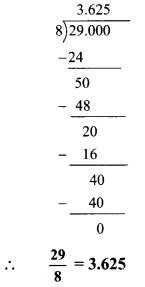
Question 4.
Show that 5 + √7 is an irrational number. [3 Marks]
Solution:
Let us assume that 5 + √7 is a rational number. So, we can find co-prime integers ‘a’ and ‘b’ (b ≠ 0) such that
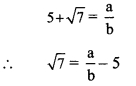
Since, ‘a’ and ‘b’ are integers, \(\sqrt [ a ]{ b }\) – 5 is a rational number and so √7 is a rational number.
∴ But this contradicts the fact that √7 is an irrational number.
Our assumption that 5 + √7 is a rational number is wrong.
∴ 5 + √7 is an irrational number.
Question 5.
Write the following surds in simplest form.
![]()
Solution:
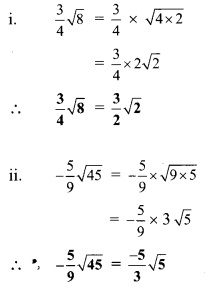
Question 6.
Write the simplest form of rationalising factor for the given surds.

Solution:
![]()
Now, 4√2 x √2 = 4 x 2 = 8, which is a rational number.
∴ √2 is the simplest form of the rationalising factor of √32 .
![]()
Now, 5√2 x √2 = 5 x 2 = 10, which is a rational number.
∴ √2 is the simplest form of the rationalising factor of √50 .
![]()
Now, 3√3 x √3 = 3 x 3 = 9, which is a rational number.
∴ √ 3 is the simplest form of the rationalising factor of √27 .
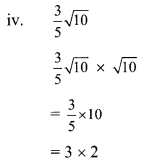
= 6, which is a rational number.
∴ √10 is the simplest form of the rationalising factor of \(\sqrt [ 3 ]{ 5 }\) √10 .
![]()
Now, 18√2 x √2 = 18 x 2 = 36, which is a rational number.
∴ √2 is the simplest form of the rationalising factor of 3√72.
vi. 4√11
4√11 x √11 = 4 x 11 = 44, which is a rational number.
∴ √11 is the simplest form of the rationalising factor of 4√11.
Question 7.
Simplify.
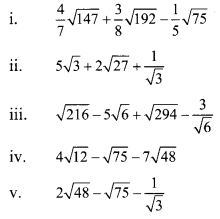
Solution:
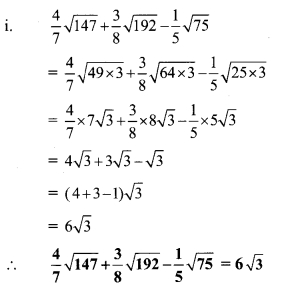
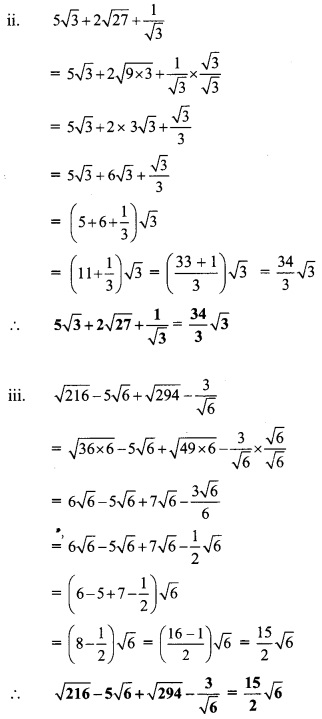
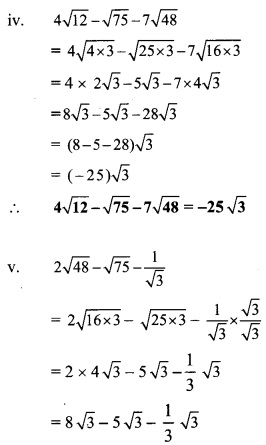
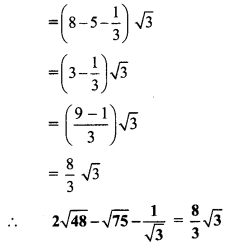
Question 8.
Rationalize the denominator.
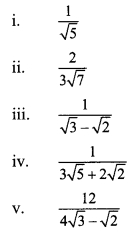
Solution:



Question 1.
Draw three or four circles of different radii on a card board. Cut these circles. Take a thread and measure the length of circumference and diameter of each of the circles. Note down the readings in the given table. (Textbook pg.no.23 )

Solution:
i. 14,44,3.1
ii. 16,50.3,3.1
iii. 11,34.6,3.1
From table, we observe that the ratio \(\sqrt [ c ]{ d }\) is nearly 3.1 which is constant. This ratio is denoted by π (pi).
Question 2.
To find the approximate value of π, take the wire of length 11 cm, 22 cm and 33 cm each. Make a circle from the wire. Measure the diameter and complete the following table.
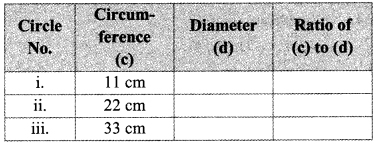
Verify that the ratio of circumference to the diameter of a circle is approximately \(\sqrt [ 22 ]{ 7 }\). (Textbook pg. no. 24)
Solution:
i. 3.5, \(\sqrt [ 22 ]{ 7 }\)
ii. 7, \(\sqrt [ 22 ]{ 7 }\)
iii. 10.5, \(\sqrt [ 22 ]{ 7 }\)
∴ The ratio of circumference to the diameter of each circle is \(\sqrt [ 22 ]{ 7 }\).