Balbharti Maharashtra State Board Class 9 Maths Solutions covers the Practice Set 6.1 Geometry 9th Class Maths Part 2 Answers Solutions Chapter 6 Circle.
Practice Set 6.1 Geometry 9th Std Maths Part 2 Answers Chapter 6 Circle
Question 1.
Distance of chord AB from the centre of a circle is 8 cm. Length of the chord AB is 12 cm. Find the diameter of a circle.
Given: In a circle with centre O,
OA is radius and AB is its chord,
seg OP ⊥ chord AB, A-P-B
AB = 12 cm, OP =8 cm
To Find: Diameter of the circle
Solution:
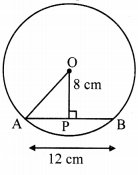
i. AP = \(\frac { 1 }{ 2 }\) AB [Perpendicular drawn from the centre of a circle to the chord bisects the chord.]
∴ AP = \(\frac { 1 }{ 2 }\) x 12 = 6 cm ….(i)
ii. In ∆OPA, ∠OPA = 90°
∴ OA2 = OP2 + AP2 [Pythagoras theorem]
= 82 + 62 [From (i)]
= 64 + 36
∴ OA2 = 100
∴ OA = \(\sqrt { 100 }\) [Taking square root on both sides]
= 10 cm
iii. Radius (r) = 10 cm
∴ Diameter = 2r = 2 x 10 = 20 cm
∴ The diameter of the circle is 20 cm.
Question 2.
Diameter of a circle is 26 cm and length of a chord of the circle is 24 cm. Find the distance of the chord from the centre.
Solution:
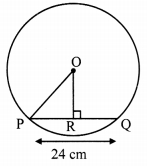
Given: In a circle with centre O,
PO is radius and PQ is its chord,
seg OR ⊥ chord PQ, P-R-Q
PQ = 24 cm, diameter (d) = 26 cm
To Find: Distance of the chord from the centre (OR)
Solution:
Radius (OP) = \(\frac { d }{ 2 }\) = \(\frac { 26 }{ 2 }\) = 13 cm ……(i)
∴ PR = \(\frac { 1 }{ 2 }\) PQ [Perpendicular drawn from the centre of a circle to the chord bisects the chord.]
= \(\frac { 1 }{ 2 }\) x 24 = 12 cm …..(ii)
ii. In ∆ORP, ∠ORP = 90°
∴ OP2= OR2 + PR2 [Pythagoras theorem]
∴ 132 = OR2 + 122 [From (i) and (ii)]
∴ 169 = OR2 + 144
∴ OR2 = 169 – 144
∴ OR2 = 25
∴ OR = √25 = 5 cm [Taking square root on both sides]
∴ The distance of the chord from the centre of the circle is 5 cm.
Question 3.
Radius of a circle is 34 cm and the distance of the chord from the centre is 30 cm, find the length of the chord.
Given: in a circle with centre A,
PA is radius and PQ is chord,
seg AM ⊥ chord PQ, P-M-Q
AP = 34 cm, AM = 30 cm
To Find: Length of the chord (PQ)
Solution:
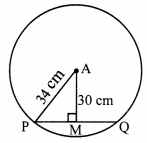
I. In ∆AMP, ∠AMP = 90°
∴ AP2 = AM2 + PM2 [Pythagoras theorem]
342 = 302 + PM2
∴ PM2 = 342 – 302
∴ PM2 (34 – 30)(34 + 30) [a2 – b2 = (a – b)(a + b)]
= 4 x 64
∴ PM = \(\sqrt { 4\times64 }\) ………(i) [Taking square root on both sides]
= 2 x 8 = 16cm
ii. Now, PM = \(\frac { 1 }{ 2 }\)(PQ) [Perpendicular drawn from the centre of a circle to the chord bisects the chord.]
16 = \(\frac { 1 }{ 2 }\)(PQ) [From (i)]
∴ PQ = 16 x 2
= 32cm
∴ The length of the chord of the circle is 32cm.
Question 4.
Radius of a circle with centre O is 41 units. Length of a chord PQ is 80 units, find the distance of the chord from the centre of the circle.
Given: In a circle with centre O,
OP is radius and PQ is its chord,
seg OM ⊥ chord PQ, P-M-Q
OP = 41 units, PQ = 80 units,
To Find: Distance of the chord from the centre of the circle(OM)
Solution:
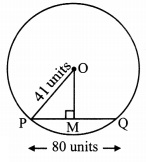
i. \(\frac { 1 }{ 2 }\)PM = (PQ) [Perpendicular drawn from the centre of a circle to the chord bisects the chord.]
= \(\frac { 1 }{ 2 }\)(80) = 40 Units ….(i)
ii. In ∆OMP, ∠OMP = 90°
∴ OP2 = OM2 + PM2 [Pythagoras theorem]
∴ 412 = OM2 + 402 [From (i)]
∴ OM2 = 412 – 402
= (41 -40) (41 +40) [a2 – b2 = (a – b) (a + b)]
= (1)(81)
∴ OM2 = 81 OM = √81 = 9 units [Taking square root on both sides] [From (i)]
∴ The distance of the chord from the centre of the circle is 9 units.
Question 5.
In the adjoining figure, centre of two circles is O. Chord AB of bigger circle intersects the smaller circle in points P and Q. Show that AP = BQ.
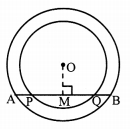
Given: Two concentric circles having centre O.
To prove: AP = BQ
Construction: Draw seg OM ⊥ chord AB, A-M-B
Solution:
Proof:
For smaller circle,
seg OM ⊥ chord PQ [Construction, A-P-M, M-Q-B]
∴ PM = MQ …..(i) [Perpendicular drawn from the centre of the circle to the chord bisects the chord.]
For bigger circle,
seg OM ⊥ chord AB [Construction]
∴ AM = MB [Perpendicular drawn from the centre of the circle to the chord bisects the chord.]
∴ AP + PM = MQ + QB [A-P-M, M-Q-B]
∴ AP + MQ = MQ + QB [From (i)]
∴ AP = BQ
Question 6.
Prove that, if a diameter of a circle bisects two chords of the circle then those two chords are parallel to each other.
Solution:
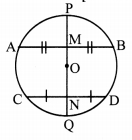
Given: O is the centre of the circle.
seg PQ is the diameter.
Diameter PQ bisects the chords AB and CD in points M and N respectively.
To prove: chord AB || chord CD.
Proof:
Diameter PQ bisects the chord AB in point M [Given]
∴ seg AM ≅ seg BM
∴ seg OM ⊥ chord AB [Segment joining the centre of a circle and the midpoint of its chord is perpendicular to the chord, P-M-O, O-N-Q]
∴ ∠OMA = 90° …..(i)
Also, diameter PQ bisects the chord CD in point N [Given]
∴ seg CN ≅ seg DN
seg ON ⊥ chord CD [Segment joining the centre of a circle and the midpoint of its chord is perpendicular to the chord, P-M-O, O-N-Q]
∴ ∠ONC = 90° …..(ii)
Now, ∠OMA + ∠ONC = 90° + 90° [From (i) and (ii)]
= 180°
But, ∠OMA and ∠ONC form a pair of interior angles on lines AB and CD when seg MN is their transversal.
∴ chord AB || chord CD [Interior angles test]