Balbharti Maharashtra State Board Class 9 Maths Solutions covers the Practice Set 9.1 Geometry 9th Class Maths Part 2 Answers Solutions Chapter 9 Surface Area and Volume.
Practice Set 9.1 Geometry 9th Std Maths Part 2 Answers Chapter 9 Surface Area and Volume
Question 1.
Length, breadth and height of a cuboid shape box of medicine is 20 cm, 12 cm and 10 cm respectively. Find the surface area of vertical faces and total surface area of this box.
Given: For cuboid shape box of medicine,
length (l) = 20 cm, breadth (b) = 12 cm and height (h) = 10 cm.
To find: Surface area of vertical faces and total surface area of the box
Solution:
i. Surface area of vertical faces of the box
= 2(l + b) x h
= 2(20+ 12) x 10
= 2 x 32 x 10
= 640 sq.cm.
ii. Total surface area of the box
= 2 (lb + bh + lh)
= 2(20 x 12+ 12 x 10 + 20 x 10)
= 2(240 + 120 + 200)
= 2 x 560
= 1120 sq.cm.
∴ The surface area of vertical faces and total surface area of the box are 640 sq.cm, and 1120 sq.cm, respectively.
Question 2.
Total surface area of a box of cuboid shape is 500 sq.unit. Its breadth and height is 6 unit and 5 unit respectively. What is the length of that box?
Given: For cuboid shape box,
breadth (b) = 6 unit, height (h) = 5 unit Total surface area = 500 sq. unit.
To find: Length of the box (l)
Solution:
Total surface area of the box = 2 (lb + bh + lh)
∴ 500 = 2 (6l + 6 x 5 + 5l)
∴ \(\frac { 500 }{ 2 }\) = (11l + 30)
∴ 250= 11l + 30
∴ 250 – 30= 11l
∴ 220 = 11l
∴ 220 = l
∴ \(\frac { 220 }{ 11 }\) = l
∴ l = 20 units
∴ The length of the box is 20 units.
Question 3.
Side of a cube is 4.5 cm. Find the surface area of all vertical faces and total surface area of the cube.
Given: Side of cube (l) = 4.5 cm
To find: Surface area of all vertical faces and the total surface area of the cube
Solution:
i. Area of vertical faces of cube = 4l2
= 4 (4.5)2 = 4 x 20.25 = 81 sq.cm.
ii. Total surface area of the cube = 6l2
= 6 (4.5)2
= 6 x 20.25
= 121.5 sq.cm.
∴ The surface area of all vertical faces and the total surface area of the cube are 81 sq.cm, and 121.5 sq.cm, respectively.
Question 4.
Total surface area of a cube is 5400 sq. cm. Find the surface area of all vertical faces of the cube.
Given: Total surface area of cube = 5400 sq.cm.
To find: Surface area of all vertical faces of the cube
Solution:
i. Total surface area of cube = 6l2
∴ 5400 = 6l2
∴ \(\frac { 5400 }{ 6 }\) = l2
∴ l2 = 900
ii. Area of vertical faces of cube = 4l2
= 4 x 900 = 3600 sq.cm.
∴ The surface area of all vertical faces of the cube is 3600 sq.cm.
Question 5.
Volume of a cuboid is 34.50 cubic metre. Breadth and height of the cuboid is 1.5 m and 1.15 m respectively. Find its length.
Given: Breadth (b) = 1.5 m, height (h) = 1.15 m
Volume of cuboid = 34.50 cubic metre
To find: Length of the cuboid (l)
Solution:
Volume of cuboid = l x b x h
∴ 34.50 = l x b x h
∴ 34.50 = l x 1.5 x 1.15
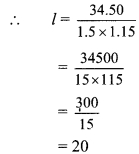
= 20
∴ The length of the cuboid is 20 m.
Question 6.
What will be the volume of a cube having length of edge 7.5 cm ?
Given: Length of edge of cube (l) = 7.5 cm
To find: Volume of a cube
Solution:
Volume of a cube = l2
= (7.5)3
= 421.875 ≈ 421.88 cubic cm
∴The volume of the cube is 421.88 cubic cm.
Question 7.
Radius of base of a cylinder is 20 cm and its height is 13 cm, find its curved surface area and total surface area, (π = 3.14)
Given: Radius (r) = 20 cm, height (h) = 13 cm
To find: Curved surface area and
the total surface area of the cylinder
Solution:
i. Curved surface area of cylinder = 2πrh
= 2 x 3.14 x 20 x 13
= 1632.8 sq.cm
ii. Total surface area of cylinder = 2πr(r + h)
= 2 x 3.14 x 20(20 + 13)
= 2 x 3.14 x 20 x 33 = 4144.8 sq.cm
∴ The curved surface area and the total surface area of the cylinder are 1632.8 sq.cm and 4144.8 sq.cm respectively.
Question 8.
Curved surface area of a cylinder is 1980 cm2 and radius of its base is 15 cm. Find the height of the cylinder. (π = \(\frac { 22 }{ 7 }\))
Given: Curved surface area of cylinder = 1980 sq.cm., radius (r) = 15 cm
To find: Height of the cylinder (h)
Solution:
Curved surface area of cylinder = 2πrh
∴ 1980 = 2 x \(\frac { 22 }{ 7 }\) x 15 x h
∴ \(h=\frac{1980 \times 7}{2 \times 22 \times 15}\)
∴ h = 21 cm
∴ The height of the cylinder is 21 cm.