Maharashtra Board 10th Class Maths Part 2 Practice Set 5.3 Solutions Chapter 5 Co-ordinate Geometry

Balbharti Maharashtra State Board Class 10 Maths Solutions covers the Practice Set 5.3 Geometry 10th Class Maths Part 2 Answers Solutions Chapter 5 Co-ordinate Geometry.

Practice Set 5.3 Geometry 10th Std Maths Part 2 Answers Chapter 5 Co-ordinate Geometry

Practice Set 5.3 Geometry Class 10 Question 1. Angles made by the line with the positive direction of X-axis are given. Find the slope of these lines.
i. 45°
ii. 60°
iii. 90°
Solution:
i. Angle made with the positive direction of
X-axis (θ) = 45°
Slope of the line (m) = tan θ
∴ m = tan 45° = 1
∴ The slope of the line is 1.

ii. Angle made with the positive direction of X-axis (θ) = 60°
Slope of the line (m) = tan θ
∴ m = tan 60° = \(\sqrt { 3 }\)
∴ The slope of the line is \(\sqrt { 3 }\).

iii. Angle made with the positive direction of
X-axis (θ) = 90°
Slope of the line (m) = tan θ
∴ m = tan 90°
But, the value of tan 90° is not defined.
∴ The slope of the line cannot be determined.

Practice Set 5.3 Geometry Question 2. Find the slopes of the lines passing through the given points.
i. A (2, 3), B (4, 7)
ii. P(-3, 1), Q (5, -2)
iii. C (5, -2), D (7, 3)
iv. L (-2, -3), M (-6, -8)
v. E (-4, -2), F (6, 3)
vi. T (0, -3), s (0,4)
Solution:
i. A (x₁, y₁) = A (2, 3) and B (x₂, y₂) = B (4, 7)
Here, x₁ = 2, x₂ = 4, y₁ = 3, y₂ = 7

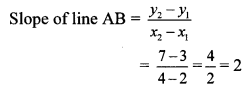
∴ The slope of line AB is 2.

ii. P (x₁, y₁) = P (-3, 1) and Q (x₂, y₂) = Q (5, -2)
Here, x₁ = -3, x₂ = 5, y₁ = 1, y₂ = -2

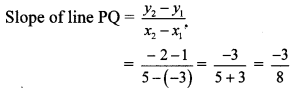
∴ The slope of line PQ is \(\frac { -3 }{ 8 } \)

iii. C (x₁, y₁) = C (5, -2) and D (x₂, y₂) = D (7, 3)
Here, x₁ = 5, x₂ = 7, y₁ = -2, y₂ = 3

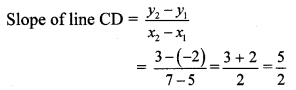
∴ The slope of line CD is \(\frac { 5 }{ 2 } \)

iv. L (x₁, y₁) = L (-2, -3) and M (x₂,y₂) = M (-6, -8)
Here, x₁ = -2, x₂ = – 6, y₁ = – 3, y₂ = – 8

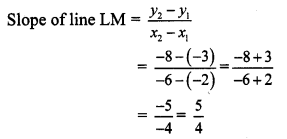
∴ The slope of line LM is \(\frac { 5 }{ 4 } \)

v. E (x₁, y₁) = E (-4, -2) and F (x₂, y₂) = F (6, 3)
Here,x₁ = -4, x₂ = 6, y₁ = -2, y₂ = 3

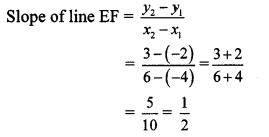
∴ The slope of line EF is \(\frac { 1 }{ 2 } \).

vi. T (x₁, y₁) = T (0, -3) and S (x₂, y₂) = S (0, 4)
Here, x₁ = 0, x₂ = 0, y₁ = -3, y₂ = 4

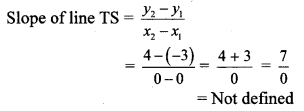
∴ The slope of line TS cannot be determined.

5.3.5 Practice Question 3. Determine whether the following points are collinear.
i. A (-1, -1), B (0, 1), C (1, 3)
ii. D (- 2, -3), E (1, 0), F (2, 1)
iii. L (2, 5), M (3, 3), N (5, 1)
iv. P (2, -5), Q (1, -3), R (-2, 3)
v. R (1, -4), S (-2, 2), T (-3,4)
vi. A(-4,4),K[-2,\(\frac { 5 }{ 2 } \)], N (4,-2)
Solution:


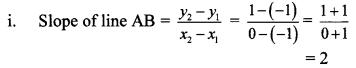
∴ slope of line AB = slope of line BC
∴ line AB || line BC
Also, point B is common to both the lines.
∴ Both lines are the same.
∴ Points A, B and C are collinear.

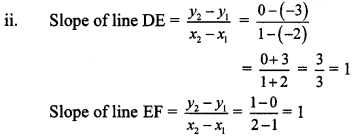
∴ slope of line DE = slope of line EF
∴ line DE || line EF
Also, point E is common to both the lines.
∴ Both lines are the same.
∴ Points D, E and F are collinear.

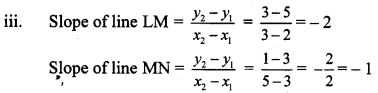
∴ slope of line LM ≠ slope of line MN
∴ Points L, M and N are not collinear.

∴ slope of line PQ = slope of line QR
∴ line PQ || line QR
Also, point Q is common to both the lines.
∴ Both lines are the same.
∴ Points P, Q and R are collinear.

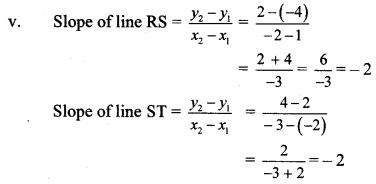
∴ slope of line RS = slope of line ST
∴ line RS || line ST
Also, point S is common to both the lines.
∴ Both lines are the same.
∴ Points R, S and T are collinear.

∴ slope of line AK = slope of line KN
∴ line AK || line KN
Also, point K is common to both the lines.
∴ Both lines are the same.
∴ Points A, K and N are collinear.

Practice Set 5.3 Geometry 9th Standard Question 4. If A (1, -1), B (0,4), C (-5,3) are vertices of a triangle, then find the slope of each side.
Solution:

∴ The slopes of the sides AB, BC and AC are -5, \(\frac { 1 }{ 5 } \) and \(\frac { -2 }{ 3 } \) respectively.

Geometry 5.3 Question 5. Show that A (-4, -7), B (-1, 2), C (8, 5) and D (5, -4) are the vertices of a parallelogram.
Proof:


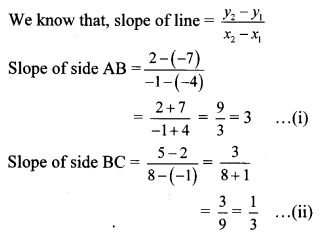
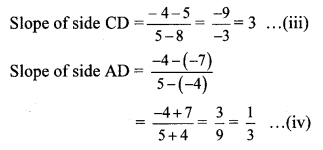
∴ Slope of side AB = Slope of side CD … [From (i) and (iii)]
∴ side AB || side CD
Slope of side BC = Slope of side AD … [From (ii) and (iv)]
∴ side BC || side AD
Both the pairs of opposite sides of ꠸ABCD are parallel.
꠸ABCD is a parallelogram.
Points A(-4, -7), B(-1, 2), C(8, 5) and D(5, -4) are the vertices of a parallelogram.

Question 6.
Find k, if R (1, -1), S (-2, k) and slope of line RS is -2.
Solution:
R(x₁, y₁) = R (1, -1), S (x₂, y₂) = S (-2, k)
Here, x₁ = 1, x₂ = -2, y₁ = -1, y₂ = k

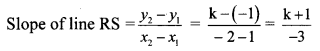
But, slope of line RS is -2. … [Given]
∴ -2 = \(\frac { k+1 }{ -3 } \)
∴ k + 1 = 6
∴ k = 6 – 1
∴ k = 5

5.3 Class 10 Question 7. Find k, if B (k, -5), C (1, 2) and slope of the line is 7.
Solution:
B(x₁, y₁) = B (k, -5), C (x₂, y₂) = C (1, 2)
Here, x₁ = k, x₂ = 1, y₁ = -5, y₂ = 2

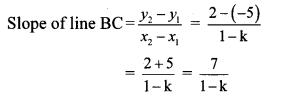
But, slope of line BC is 7. …[Given]
∴ 7 = \(\frac { 7 }{ 1-k } \)
∴ 7(1 – k) = 7
∴ 1 – k = \(\frac { 7 }{ 7 } \)
∴ 1 – k = 1
∴ k = 0

Question 8.
Find k, if PQ || RS and P (2, 4), Q (3, 6), R (3,1), S (5, k).
Solution:

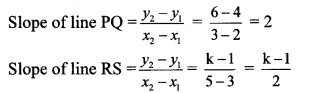
But, line PQ || line RS … [Given]
∴ Slope of line PQ = Slope of line RS
∴ 2 = \(\frac { k-1 }{ 2 } \)
∴ 4 = k – 1
∴ k = 4 + 1
∴ k = 5