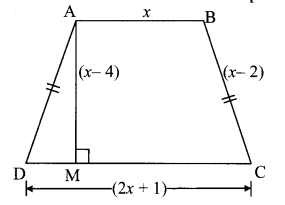
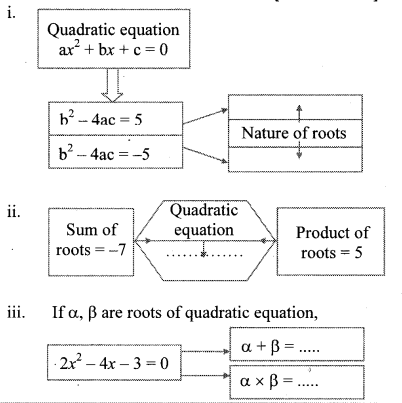
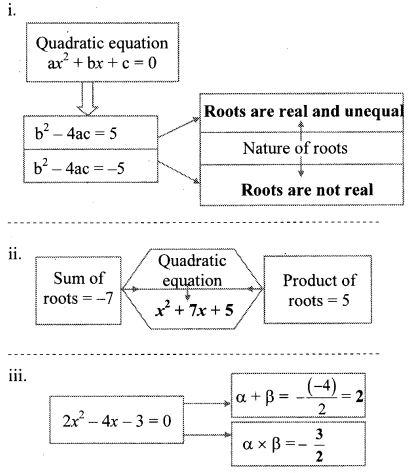
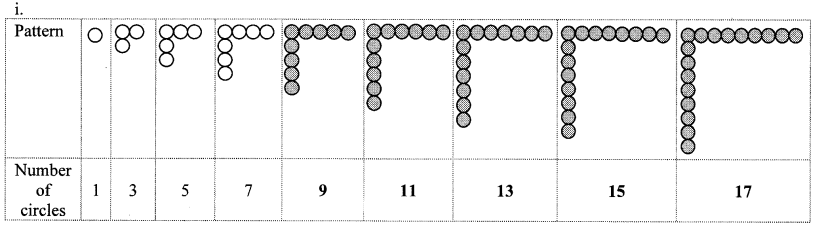
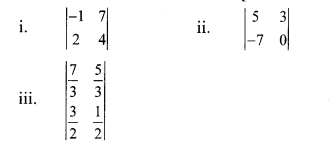
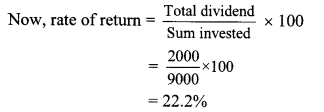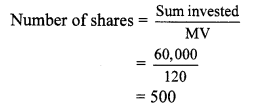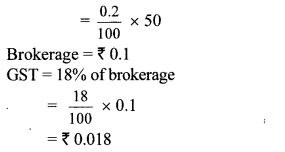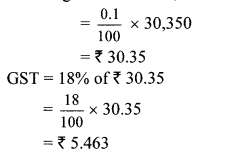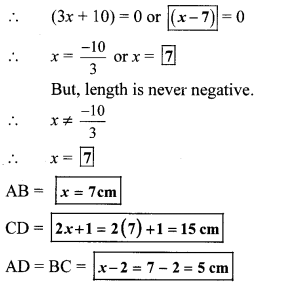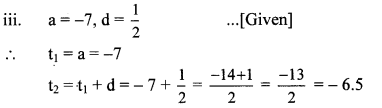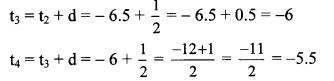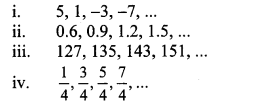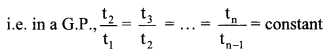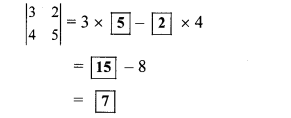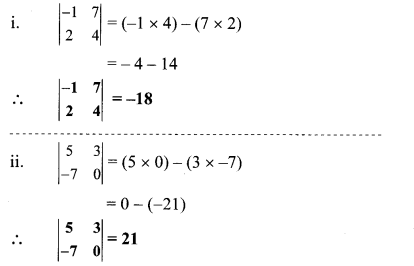Balbharati Maharashtra State Board 10th Std Textbook Solutions Answers Digest
- Maharashtra State Board Class 10 Maths Solutions
- Maharashtra State Board Class 10 Science Solutions
- Maharashtra State Board Class 10 History Solutions
- Maharashtra State Board Class 10 Political Science Solutions
- Maharashtra State Board Class 10 Geography Solutions
- Maharashtra State Board Class 10 English Solutions
- Maharashtra State Board Class 10 Hindi Solutions
- Maharashtra State Board Class 10 Marathi Solutions
- Maharashtra State Board Class 10 Sanskrit Solutions