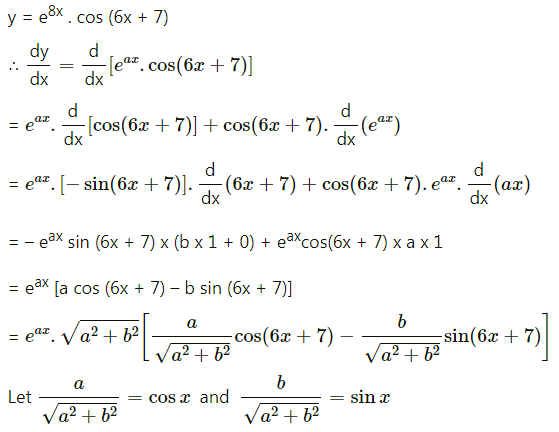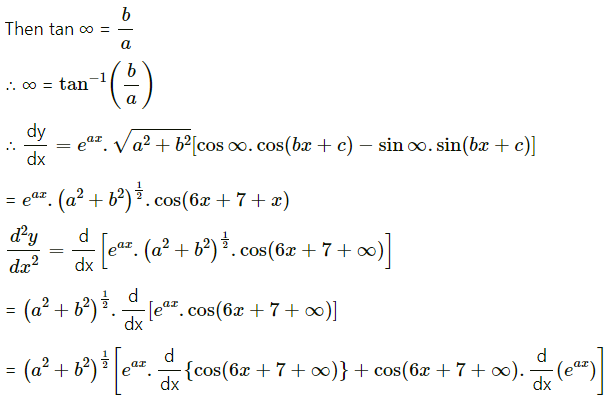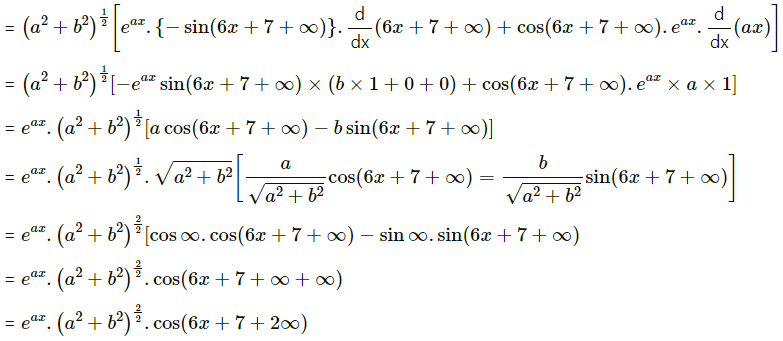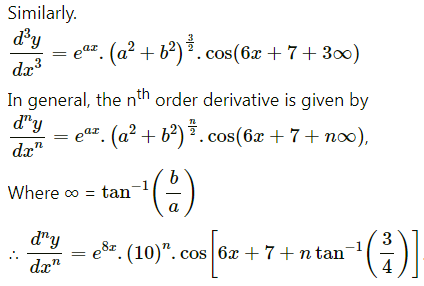Balbharti 12th Maharashtra State Board Maths Solutions Book Pdf Chapter 1 Differentiation Ex 1.5 Questions and Answers.
Maharashtra State Board 12th Maths Solutions Chapter 1 Differentiation Ex 1.5
Question 1.
Find the second order derivatives of the following:
(i) 2x5 – 4x3 – \(\frac{2}{x^{2}}\) – 9
Solution:
Let y = 2x5 – 4x3 – \(\frac{2}{x^{2}}\) – 9

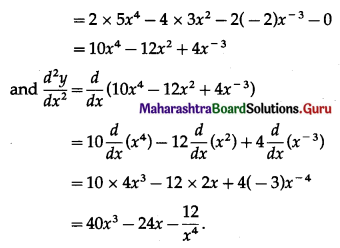
(ii) e2x . tan x
Solution:
Let y = e2x . tan x


![]()
(iii) e4x . cos 5x
Solution:
Let y = e4x . cos 5x
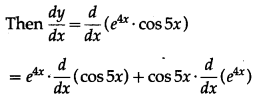

(iv) x3 . log x
Solution:
Let y = x3 . log x

(v) log(log x)
Solution:
Let y = log(log x)
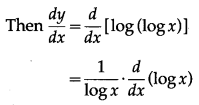

(vi) xx
Solution:
y = xx
log y = log xx = x log x
Differentiating both sides w.r.t. x, we get

Question 2.
Find \(\frac{d^{2} y}{d x^{2}}\) of the following:
(i) x = a(θ – sin θ), y = a (1 – cos θ)
Solution:
x = a(θ – sin θ), y = a (1 – cos θ)
Differentiating x and y w.r.t. θ, we get
\(\frac{d x}{d \theta}=a \frac{d}{d \theta}(\theta-\sin \theta)\) = a(1 – cos θ) …….(1)

(ii) x = 2at2, y = 4at
Solution:
x = 2at2, y = 4at
Differentiating x and y w.r.t. t, we get

![]()
(iii) x = sin θ, y = sin3θ at θ = \(\frac{\pi}{2}\)
Solution:
x = sin θ, y = sin3θ
Differentiating x and y w.r.t. θ, we get,


(iv) x = a cos θ, y = b sin θ at θ = \(\frac{\pi}{4}\)
Solution:
x = a cos θ, y = b sin θ
Differentiating x and y w.r.t. θ, we get
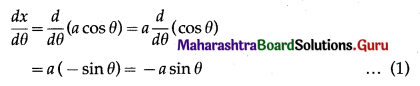


Question 3.
(i) If x = at2 and y = 2at, then show that \(x y \frac{d^{2} y}{d x^{2}}+a=0\)
Solution:
x = at2, y = 2at ………(1)
Differentiating x and y w.r.t. t, we get


(ii) If y = \(e^{m \tan ^{-1} x}\), show that \(\left(1+x^{2}\right) \frac{d^{2} y}{d x^{2}}+(2 x-m) \frac{d y}{d x}=0\)
Solution:
y = \(e^{m \tan ^{-1} x}\) ……..(1)

(iii) If x = cos t, y = emt, show that \(\left(1-x^{2}\right) \frac{d^{2} y}{d x^{2}}-x \frac{d y}{d x}-m^{2} y=0\)
Solution:
x = cos t, y = emt
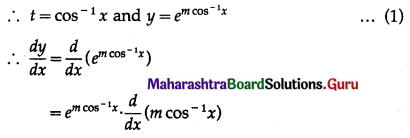

![]()
(iv) If y = x + tan x, show that \(\cos ^{2} x \cdot \frac{d^{2} y}{d x^{2}}-2 y+2 x=0\)
Solution:
y = x + tan x

(v) If y = eax . sin (bx), show that y2 – 2ay1 + (a2 + b2)y = 0.
Solution:
y = eax . sin (bx) ………(1)


(vi) If \(\sec ^{-1}\left(\frac{7 x^{3}-5 y^{3}}{7 x^{3}+5 y^{3}}\right)=m\), show that \(\frac{d^{2} y}{d x^{2}}=0\)
Solution:



(vii) If 2y = \(\sqrt{x+1}+\sqrt{x-1}\), show that 4(x2 – 1)y2 + 4xy1 – y = 0.
Solution:
2y = \(\sqrt{x+1}+\sqrt{x-1}\) …… (1)
Differentiating both sides w.r.t. x, we get


(viii) If y = \(\log \left(x+\sqrt{x^{2}+a^{2}}\right)^{m}\), show that \(\left(x^{2}+a^{2}\right) \frac{d^{2} y}{d x^{2}}+x \frac{d y}{d x}=0\)
Solution:
y = \(\log \left(x+\sqrt{x^{2}+a^{2}}\right)^{m}\) = \(m \log \left(x+\sqrt{x^{2}+a^{2}}\right)\)

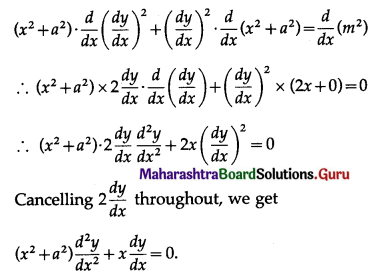
![]()
(ix) If y = sin(m cos-1x), then show that \(\left(1-x^{2}\right) \frac{d^{2} y}{d x^{2}}-x \frac{d y}{d x}+m^{2} y=0\)
Solution:
y = sin(m cos-1x)
sin-1y = m cos-1x
Differentiating both sides w.r.t. x, we get

(x) If y = log(log 2x), show that xy2 + y1(1 + xy1) = 0.
Solution:
y = log(log 2x)
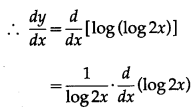

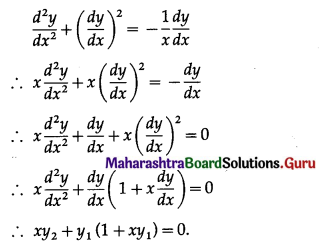
(xi) If x2 + 6xy + y2 = 10, show that \(\frac{d^{2} y}{d x^{2}}=\frac{80}{(3 x+y)^{3}}\)
Solution:
x2 + 6xy + y2 = 10 …… (1)
Differentiating both sides w.r.t. x, we get



(xii) If x = a sin t – b cos t, y = a cos t + b sin t, Show that \(\frac{d^{2} y}{d x^{2}}=-\frac{x^{2}+y^{2}}{y^{3}}\)
Solution:
x = a sin t – b cos t, y = a cos t + b sin t
Differentiating x and y w.r.t. t, we get
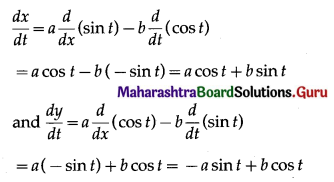

![]()
Question 4.
Find the nth derivative of the following:
(i) (ax + b)m
Solution:
Let y = (ax + b)m



(ii) \(\frac{1}{x}\)
Solution:
Let y = \(\frac{1}{x}\)

(iii) eax+b
Solution:
Let y = eax+b
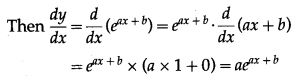

(iv) apx+q
Solution:
Let y = apx+q

![]()
(v) log(ax + b)
Solution:
Let y = log(ax + b)
Then \(\frac{d y}{d x}=\frac{d}{d x}[\log (a x+b)]\)

(vi) cos x
Solution:
Let y = cos x

(vii) sin(ax + b)
Solution:
Let y = sin(ax + b)


(viii) cos(3 – 2x)
Solution:
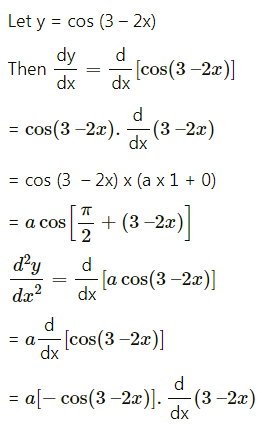
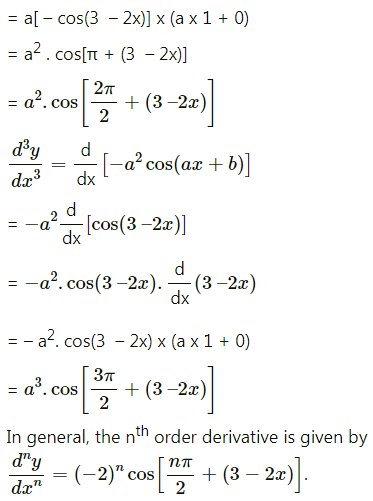
(ix) log(2x + 3)
Solution:
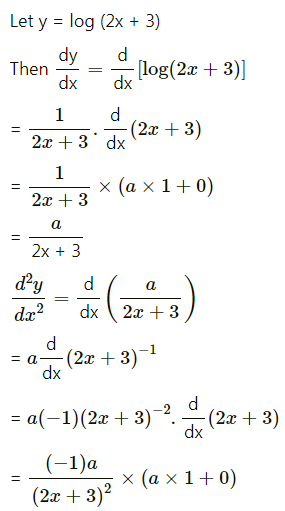

(x) \(\frac{1}{3 x-5}\)
Solution:
Let y = \(\frac{1}{3 x-5}\)


![]()
(xi) y = eax . cos (bx + c)
Solution:
y = eax . cos (bx + c)





(xii) y = e8x . cos (6x + 7)
Solution: