Category: Class 12

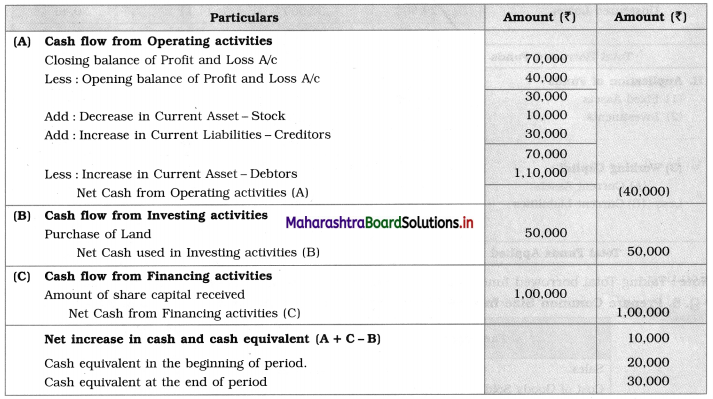
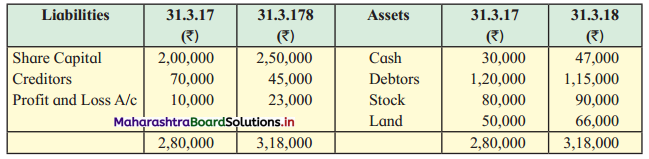
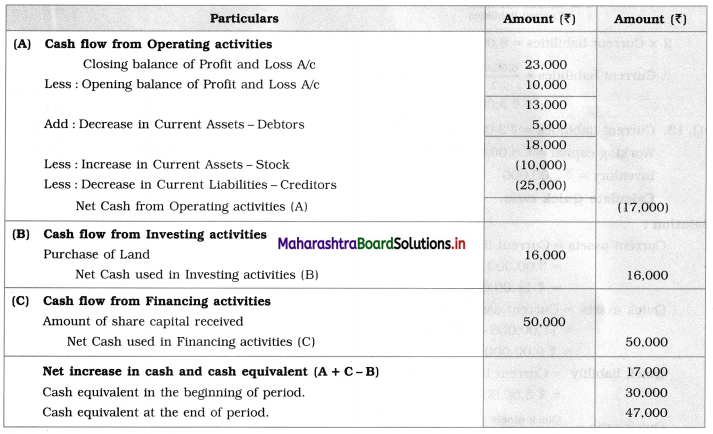
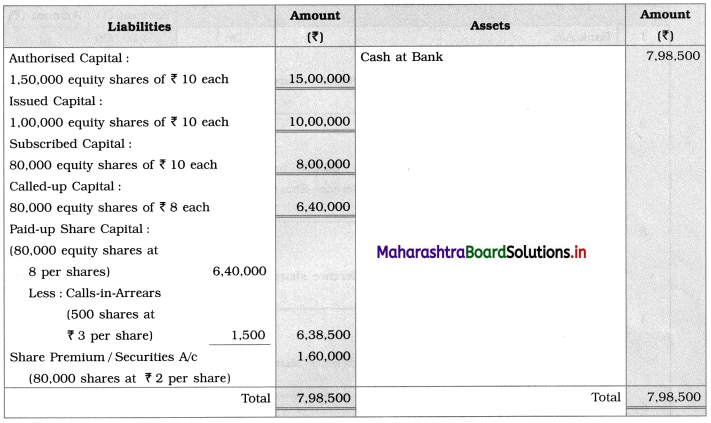
Balbharti Yuvakbharati English 12th Digest Chapter 3.1 Summary Writing Notes, Textbook Exercise Important Questions and Answers.

Maharashtra State Board Class 12 English Yuvakbharati Solutions Chapter 3.1 Summary Writing

12th English Digest Chapter 3.1 Summary Writing Textbook Questions and Answers

Discuss in pairs and guess the correct alternative for the following:

Question 1.
To summarize means …………… .
(a) Put information in chronological order.
(b) To recapitulate the main points in selection
(c) To introduce new information
(d) To write one’s opinion about selection
Answer:
(b) To recapitulate the main points in selection

Question 2.
The type of summary that consists of a paragraph to express the main idea is …………… .
(a) Outline
(b) Report
(c) Synopsis
(d) Written summary
Answer:
(d) Written summary

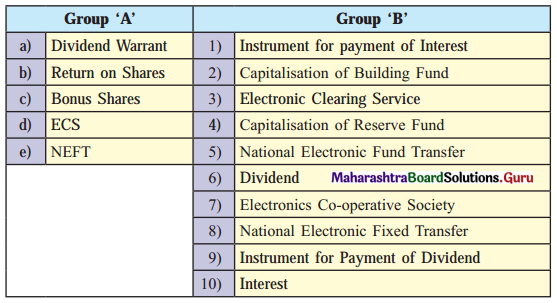
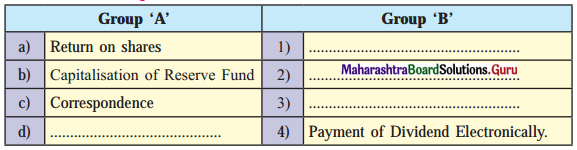
Question 3.
There are various ways of incorporating other writers’ works into your own writing. They differ according to the closeness of your writing to the source writing. Match the ways of writing in brief given in column (A) with their descriptions in column (B):

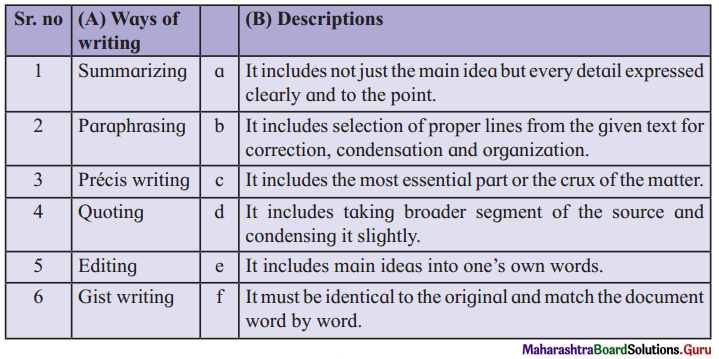
Answer:

1. Summarizing – (e) It includes main ideas into one’s own words.
2. Paraphrasing – (f) It must be identical to the original and match the document word by word.
3. Precis writing – (d) It includes taking broader segment of the source and condensing it slightly.
4. Quoting – (a) It includes not just the main idea but every detail expressed clearly and to the point.
5. Editing – (b) It includes selection of proper lines from the given text for correction, condensation and organization.
6. Gist writing – (c) It includes the most essential part or the crux of the matter.

(A1)

Question 1.
Complete the following as instructed:
Read the passage and write its summary according to the given steps:
Answer:
Use the following steps for summary writing:
Step 1: Read the article twice.
Step 2: The purpose of writing – To tell the reader about the interesting communication methods among birds and mammals.
Step 3: Identify the main idea – Surprising examples of communication methods among birds and mammals.
Steps 4 and 5: Write the first draft: Revise your first draft and edit it.
(Students may attempt this on their own.)
Step 5: Write the final draft (Given overleaf.)

(A2)

(ii) Avoid adverbs:
Delete the adverbs in italics and rewrite:

Question (a)
“That’s usually a good thing to do.”
Answer:
“That’s a good thing to do.”

Question (b)
“That’s fairly good coffee.”
Answer:
“That’s good coffee.”

Question (c)
“I totally agree.”
Answer:
“I agree.”

Question (d)
“Actually I disagree.”
Answer:
“I disagree.”

Question (iii)
One word substitution:
Find examples similar to those given in the textbook and make a list:
Answer:

1. friendly relationship in which people understand well : rapport (pronounced as ‘rappo’)
2. able to cause death: fatal
3. seize by way of penalty: confiscate
4. someone who goes into buildings in order to steal: burglar
5. the principal character in a play or a story: protagonist
6. the path described by an object moving in air: trajectory
7. a person regarded as a symbol: icon
8. a person who knows many languages: polyglot
9. a badly behaved child: brat
10. a period of ten years: decade
11. a persistent increase in the general level of prices: inflation
12. organisation of supplies and services for any, complex operation : logistics
13. extremely careful about details: meticulous
14. not harmful or offensive: innocuous
15. present, appearing or found everywhere: ubiquitous

(ii) Change the following sentences into simple:

Question (a)
Mr. Rohit is the member and he is also the director.
Answer:
Mr. Rohit is the member and also the director.

Question (b)
The room is so small that it cannot accommodate many people.
Answer:
The room is too small to accommodate many people.

Question (c)
You have to prove that you are innocent.
Answer:
You have to prove your innocence.

Question (d)
He was late so he walked in a great hurry.
Answer:
Being late, he walked in a great hurry.

(A4)

Question (i)
Read any book of your choice and write its summary according to the steps explained in the chapter.

Question (ii)
Find some professions that require the skill of summary writing and editing. Write them
in your notebook.

Yuvakbharati English 12th Digest Chapter 3.1 Summary Writing Additional Important Questions and Answers

Question (i)
Cut redundant words:
Write five examples of redundant words:
Answer:

1. puzzling mystery = ‘mystery’
2. connect together = ‘connect’
3. divide into two equal halves = ‘divide into halves
4. surrounded on all sides = ‘surrounded’
5. return back = ‘return’

Balbharti Yuvakbharati English 12th Digest Chapter 2.8 Small Towns and Rivers Notes, Textbook Exercise Important Questions and Answers.

Maharashtra State Board Class 12 English Yuvakbharati Solutions Chapter 2.8 Small Towns and Rivers

12th English Digest Chapter 2.8 Small Towns and Rivers Textbook Questions and Answers

Question (i)
Most of the civilizations have flourished on the banks of the rivers. Discuss the reasons in the class.
Points:
(a) Availability of water
(b) Fertile soil for agriculture
(c) Fishing ground
(d) Transport

Question (ii)
Write down the names of the famous cities that are situated on the banks of the rivers given below.
Answer:

River	City
Ganga	Varanasi
Yamuna	Mathura
Godavari	Rajahmundry
Varada	Sagara
Krishna	Vijayawada
Tapi	Surat

Question (iii)
Write down the names of the rivers on the banks of which following cities have prospered:
Answer:

City	River
London	Thames
Cairo	Nile
New York	Hudson
Paris	Siene

Question (iv)
Divide your class into groups and discuss the changes that might have taken place when the cities grow on the banks of the rivers.
Points: Dwellings are built – Population grows – Fishing flourishes – Outsiders come to settle – Trading takes place – Prosperity increases – Increased population, trade, traffic and fishing begin to harm the river system – River system shows damage – River starts to decay

Question (v)
Share your views in the class on the topic ‘Conservation of Rivers and Development of the Cities.’
(Students may list their own points of views.)

(A1)

Question 1.
State the importance of Nature in the lives of the people from the North-eastern part of India as expressed in the poem with reference to:
(a) Flowers
(b) River
(c) Bamboo
(d) East
Answer:
(a) Flowers – Tuberoses are woven into wreaths to be placed on the body of a departed as a mark of love and respect.
Sole: Most of the textual ‘Wh’ questions are converted to Activity Format.
(b) River: The people believe the river has a soul. They respect their rivers and even revere it as divine as its waters are immortal.
(c) Bamboo: The poet says ‘in the cool bamboo’. The colour is a cool green. The place where the bamboo grows is also cool.
(d) East: The direction of sunrise is very important for the people of Arunachal Pradesh. They ensure the dead are placed pointing west so that their soul directly enters the golden house of the sun. They believe that finally souls must attain the sun’s abode in the east.

(A2)

Question (i)
The poet has described her small town in Arunachal Pradesh. Pick out from the extract, the lines that describe the poet’s town.
Answer:
1. ‘My hometown lies calmly amidst the trees’,
2. ‘it is always the same In summer and winter With the dust flying Or the wind howling down the gorge’

Question (ii)
Make a list of natural elements mentioned in the extract.
Answer:
trees, winter, summer, wind, tuberoses, life, land, river, fish, stars

Question (iii)
‘The river has a soul.’ Elaborate the concept in your words as the poet has explained in the extract.
Answer:
When the poet says ‘The river has a soul’ she personifies the river. The river flows with great force – ‘like a torrent of grief. The river flowing with great force can be like a person pouring out grief in a storm of emotion. The river also seems to be holding its breath, maybe because it is choking with filth. There are no fishes. It is not clear and sparkling. So the poet says -‘I think it holds its breath seeking a land of fish and stars’.

Question (iv)
The poet is convinced with the thought of immortality of water. Pick out the relevant lines from the extract.
Answer:
‘The river has a soul’.

(v) The poet has used some unconventional expressions. Illustrate them in your words.

Question (a)
‘Torrent of grief.
Answer:
The poet describes the river flowing in summer with great speed. Just like someone becomes emotional in great sadness, the force of the water seems to be like the outpouring of sorrow of the river.

Question (vi)
The poet has connected the need to preserve Nature with the belief of particular community and her childhood memories. Write down the measures you would take to convince the people regarding the need to conserve the Nature.
Answer:
We have to make people at large realize that we are a part of the nature not apart from the nature. Saving nature is to save ourselves, To bring about this realization I can address my steps to two sections. The first would be the children. Saving water would be the first thing to teach children. Story-telling, poems, songs, games, cartoons and can easily bring the conservation ideas to young minds. I would take my ideas to schools, parks, malls and try to spread this to the young ones.

The other section is of course the adult public across economic and social levels. The well- off people must not be careless if they can afford to pay bills they can waste resources.

I will do everything possible. I will use social media to spread various messages/ mottos.

(A3)

Question (i)
Write down the expressions related to ‘the seasons’ from the extract.
Answer:
1. Summer or winter
2. ‘in the summer’

Question (ii)
Match column ‘A’ with column ‘B’.

A	B
1. cool 2. happy 3. dreadful 4. dry	(a) silence (b) earth (c) bamboo (d) pictures

Answer:

1. cool-bamboo
2. happy – pictures
3. dreadful – silence
4. dry-earth

(A4)

Question (i)
Read the expression ‘a sad wreath of tuberoses’.
‘Is the wreath sad?’ Explain the figure of speech.
Answer:
The figure of speech is transferred epithet. The sad mourners have placed the wreath of tuberoses on the dead. The emotion of sadness has been transferred to the flowers for effect.

Question (ii)
List and explain the metaphorical expressions from the extract.
Answer:
1. ‘torrent of grief’. The river sweeps along with great speed as if it is pouring out sorrow.
2. ‘Wind howling down the gorge’. The wind blowing through the narrow gorges creates a sound exactly like howling.
3. ‘The river has a soul’. The river is spoken of as a living being, a human.
4. ‘It holds its breath’. The river may be choking with debris and filth.

Question (iii)
‘The river has a soul.’
‘Life and death.’
These are the two expressions that are repeated in the poem; but both of them indicate different figures of speech. Find out and discuss.
Answer:
(a) ‘Life and death’
In the first usage it is used as antithesis, to emphasise the beginning and end.
In the second instance it is irony to indicate that neither life nor death is permanent. Ironically the rituals are permanent.
(b) ‘The river has a soul’
In the first instance it is used to personify the river. Several human-like qualities are attributed to the river,
= it cuts through the land
= it is cascading in grief
= it holds its breath
= it seeks a land

Question (iv)
Find out the beauty of the free verse reflected in this poem.
Answer:
“Small Towns and Rivers’ is written in free- verse. Since there are irregular lengths of lines and no rhyme, the reading of the poem is almost like a story-telling. Each stanza has a different number of lines and there is no order for mixing up the short and long lines.

The poem is not confined by an obvious rhythm so we feel there is a kind of freedom.We are free to imagine the widespread setting of the North-eastern terrain of mountains and rivers, mists, golden sunlight and the town by the river.

(A5)

Question (i)
Prepare the arguments for group discussion on the topic
‘A balanced progress never harms the Nature’.
For:

• Growth should be planned to take place in stages
• Planning vital for the growth
• Sustainability must be ensured
• Pros and cons of the damage to environment must be weighed
• Short-term gains in progress must not harm long-term eco-factors

Against:

• Growth must not be halted for issues of environment
• Costs will go up due to delays
• Delays in progress will slow down economy and employment
• Slowdown in economy will cause public to protest
• Sacrifices have to be made – one can’t have the cake and eat it too.

Question (ii)
Compose 4 to 6 lines on ‘Gift of the Seasons’.
Answer:
Gift of the Seasons
Each season brings a sweetly wrapt gift;
We can gift her back : no water pollution in
the season of the Sun.
No air pollution when
The rains come down.
And no degradation the rest of the year!

Question (iii)
Write an appreciation of the poem ‘Small Towns and Rivers’. Use the points given below:

• About the poem/poet/title
• Theme
• Poetic devices, language, style
• Special features – tone and type
• Values, message
• Your opinion about the poem

Answer:
The poem ‘Small Towns and Rivers’ written by Mamang Dai is a beautiful word-picture. It is also a lament of the poet about her beautiful native land of Arunachal Pradesh.

This theme shows in the way she begins the poem that small towns remind her of death. It is shocking. She implies the town is unchanging in all weathers, but development comes along and changes everything. There is irony in that the cycle of life and death shows that life is not permanent, but the rituals are permanent.

She uses metaphor that the rivers are not only alive like us humans, but actually immortal. She personifies the river by way the river ‘holds its breath’ because it is choking. It is flowing in search of a place where it will flow clean and clear. The poet uses metaphor of the water-cycle to illustrate the river has a soul and its waters are immortal.

The poet builds a climax with ‘shrine of happy’ childhood memories. This becomes growing up -‘grow with anxiety’. Then she speaks of how the dead are placed pointing west so the soul can ascend directly into the sun’s golden home in the east. This tells us about the traditions of her region.

The poem is in free verse and seems to be in easy language, but we can understand the full depth of meaning only after reading it more than once. The poem is a lament about the destruction of nature for development. We all will feel the sorrow of the poet when we read about how nature’s beauty is damaged for man’s greed called ‘progress’.

Question (iv)
Write a dialogue between two friends on ‘Importance of the rivers’
Answer:
Priya: Jai, it goes without saying that fresh, clean water is essential for humans and nature to survive. Rivers are precious sources of fresh drinking water for people across the world. And when rivers are so badly polluted by industry or by poor water management practices, it can be a case of life-or-death. This unfortunately happens across the world.

Jai: Yes Priya. Freshwater habitats account for some of the richest biodiversity in the world, and rivers are a vital, vibrant ecosystem for many species. Only those who live by the river know about this wealth of nature. Those who live far away and damaging the system with the poisons are not aware.

Priya: People depend on rivers for their way of life and their livelihoods. From fishing to agriculture, the way our waterways are managed has a direct impact on people’s lives. There are millions of people who follow their ancestors’ way of living and earning a livelihood. But modern technology has wrecked the very source of these.

Jai: Rivers are absolutely vital: for fresh drinking water, for people’s livelihoods and for nature. Unfortunately, they’re still threatened. We must commit to recovering freshwater biodiversity, restoring natural river flows and cleaning up polluted water for people and nature to thrive.
Priya: Yes Jai. I agree. It is the crying need of the day.

(A6)

Question (i)
Collect information about rivers in Maharashtra.

Question (ii)
Further reading:
‘The River Poems’ – Mamang Dai
‘The World Is Too Much With Us’ – William Wordsworth

Yuvakbharati English 12th Digest Chapter 2.8 Small Towns and Rivers Additional Important Questions and Answers

Read the extract and complete the activities given below:

Global Understanding:

Question 1.
Describe the river in the 3rd stanza.
Answer:
The river flows with great force -‘like a torrent’-. The river has life and soul. It breathes. But it seems as if the river is holding its breath. It seems to be in search of fishes which will live in it and stars which will be reflected in its waters.

Question 2.
What is meant by immortality?
Answer:
Immortality means the ability to live forever, without death.

Question 3.
Give reasons-The dead are placed pointing to the west.
Answer:
The people of Arunachal Pradesh believe that it will be possible for the soul of the departed person enter ‘the house of the sun’. They hope the soul will be able to ‘walk into the golden east’. So they place the dead (with feet) pointing to the west.

Question 4.
The poet has described her small town in Arunachal Pradesh. Pick out from the extract the lines that describe the poet’s town.
Answer:

1. The town has ‘A shrine of happy pictures’ to mark the days of childhood.
2. Small towns grow with anxiety for the future.
3. Like her town, ‘small towns’ are ‘by the river’.
4. Make a list of natural elements mentioned in the extract.

Question 5.
Make a list of natural elements mentioned in the extract.
Answer:
River, Earth, Mountaintops, Sun, Sunlight, Bamboo

Question 6.
The poet is convinced with the thought of immortality of water. Pick out the relevant lines from the extract.
Answer:
1. The river has a soul.
2. from the first drop of rain to dry earth
3. mist on the mountaintops
4. the immortality of water.

Interpretation/Inference/Analysis:

Question 1.
The land of fish and stars.
Answer:
The poet says she thinks the river is holding its breath. One has to hold one’s breath when he/she is unable to breathe or does not want to breathe. The river may be choking with garbage and is not able to breathe. The river may be stinking and may not be able to breathe.

As the river is so filthy there are no fish. It is dirty; the water is not sparkling in the day and cannot reflect the stars at night. So the river is in search of a land where there it can flow clean, it will have fish and where its clear water will sparkle in the sun and glitter with stars at night.

Question 2.
The river has a soul.’ Elaborate the concept in your words as the poet has explained in the extract.
Answer:
The poet states the river has a soul. The soul is deathless. The water that flows in the river came from the drops of rain. The water evaporated, rose as mist to the mountaintops. Then it formed clouds and poured down as rain to the dry earth and flowed again. Thus the river goes on, immortal, deathless.

Question 3.
The poet has used some unconventional expressions. Illustrate them in your words. Illustrate them in your words. Shrine of happy pictures
Answer:
There is a shrine probably in the town which has pictures inside. The pictures may be those of the happy moments experienced by the people in the town. Those memories are so sacred that it is a shrine to them. They protect and guard it because they have only sad and grim things happening at present.

Personal Response:

Question 1.
Rivers are our lifeline. They are an extremely important part of the eco-system and even considered sacred. Many major rivers and smaller ones have been misused and almost destroyed. Write down how we can restore our rivers to their original state.
Answer:
The condition of rivers worldwide is horrific. Everything from industrial chemical-waste to garbage is being thrown into rivers. Melted snow or the rainwater from springs come down from hills and mountains as sweet water for our survival. Polluting this is a crime against humanity.

Strict laws should be made and enforced to stop industrial activity near rivers. Wastes from industry, city, town or village must not reach the river. Only channels of rainwater must be allowed to reach the river. Awareness should be created for maintaining cleanliness along the banks.

In the olden days lakes, water bodies were considered precious and were guarded, Houses had wells. But people have lost the respect for water sources. Rivers are treated as sewage channels. Fines and punishments must be imposed and security put in for safeguarding our beautiful rivers.

Poetic Creativity:

Question 1.
Compose 4 to 6 lines on ‘River’.
Answer:
The River is our Mother

Like a mother the river soothes us.
When dying of thirst she revives us.
When tired and dirty she cleans us.
When growing our grain she waters the green.
Why! Oh why can’t we keep her clean!

Balbharti Yuvakbharati English 12th Digest Chapter 2.7 She Walks in Beauty Notes, Textbook Exercise Important Questions and Answers.

Maharashtra State Board Class 12 English Yuvakbharati Solutions Chapter 2.7 She Walks in Beauty

12th English Digest Chapter 2.7 She Walks in Beauty Textbook Questions and Answers

Question 1.
While judging any person you would consider certain aspects. Complete the diagram after carefully thinking what aspects you would consider:

Answer:

Question 2.
Make a list of proverbs and quotations related to ‘Beauty’.
Answer:
(a) Beauty is in the eye of the beholder.
(b) Beauty is only skin deep.
(c) Beauty is as beauty does.
(d) There is beauty in simplicity.
(e) Beauty is not in the face, it is a light in the heart.

Question 3.
Discuss your impressions about someone’s personality, and say what you like the most and why-
Answer:
The personality that captures the attention of all who meet her is Ms Murti.

1. Simplicity and warmth: She is a brilliant engineer, extremely wealthy yet is simple, and so cheerful and warm in her interaction with anyone she meets.
2. Humbleness: In spite her achievements, wealth and position she never mentions them, rather praises the efforts and achievements of others
3. Elegance: She is graceful and elegant and yet is never dressed expensively.
4. Motivational: She addresses young people and students in a way that is always encouraging and uplifting.
5. Generous: She is generous in giving those who are disadvantaged. She donates for the emancipation of women for making them economically independent.

(A1)

Question (i)
‘Beauty lies in the eyes of the beholder’ – you have probably heard this saying. Discuss in your class how far the statement is true.
Points:

• Outward appearance gives only an idea
• There may sometimes be an exception to the rule ‘first impression is the best
• The external look may be completely different if one looks deeper
• Henry Ford [founder of Ford Automobiles] dressed in the same old suit and said, ‘people who know me know who I am. People who don’t know me don’t matter, A very wealthy person may choose to appear very ordinary.

Question (ii)
Discuss with your partner about the most inspirational person you have come across. Also explain the reasons behind your opinion.
Points:

• Attended a lecture by A.P.J. Abdul Kalam, before he became President
• His views stayed in my mind
• He stressed on dreaming for high aims
• He stressed on the importance of hard work
• He came from very humble background
• He worked his way to achieve great things
• I also want to achieve something and I have a lot of support which Dr. Abdul Kalam may not have had.

(A2)

Question (i)
Match column A with column B:

Answer:

1. The lady’s beauty – a cloudless starry night
2. Her hair – wavy and black
3. Her eyes – a perfect blend of light and darkness
4. Her smile – soft, calm and eloquent
5. Her mind – at peace with all below a heart
6. Her face – expresses thoughts serenely and sweetly

Question (ii)
Complete the reasons:
The lady in the poem has a winning smile and a glowing skin. According to the poet she is blessed with these things. Explain why.
Answer:
The lady in the poem has a winning smile and a glowing skin. According to the poet she is blessed with these things because in the last stanza the poet says that lovely cheek, the calm brow, the delicate colouring, the glowing skin all are a result of her life spent without sin. She has a peaceful mind and an innocent heart. These come together to make her face glow with an inner beauty.

Question (iii)
The poet brings a perfect balance of outer beauty and inner beauty. Write a few lines from the poem on how the poet brings this balance in his description.
Answer:
One of the themes in the poem is harmony or balance. The poet does not directly call her beautiful, but she ‘walks in beauty’. The overall beauty is compared to a combination of cloudless (clear) climate and starry skies. He says the best of dark and light meet in her eyes and features, to be seen in the soft, dim light. The effect would not be so wonderful if it was even one shade darker or brighter. That balance of the light is important.

The poet says that her calm brow, sweet smile, the lovely colour of her skin, is the result of a peaceful mind, a loving heart and a pure life. Inner beauty is reflected in this ‘nameless grace’ – indescribable beauty.

Question (iv)
‘Beauty is skin deep.’ Do you agree with the statement? Or do you feel that beauty comes from within? Explain your views in a few sentences.
Answer:
I agree with the statement. Beauty is not about perfect features, clear skin, shining hair or smart clothes. Beauty is about the person’s heart. The helpful nature, a mind without guilt, a cheerful attitude, kind way of speaking will all be reflected in the person’s outward appearance.

The eyes are windows to a person’s soul, they say. If a person has wicked thoughts and bad intentions it shows in the eyes. The expression on the face will reflect the nasty mind. Harsh words will show their unkind nature. So beautiful features and perfect skin are not real indicators of beauty.

(A3)

Question (i)
Find out from the poem the words which are used to describe the lady.
Answer:

1. Raven tresses
2. Serene and sweet expression
3. Pure thoughts
4. Dearheart
5. Calm brow
6. Smiling face
7. Gowing skin
8. Innocent heart
9. Peaceful mind

Question (ii)
Find out the instances of contractions from the poem.
Answer:
The contractions in the poem are – ‘that’s’ – that is ‘o’er’ – over

(A4)

Question (i)
The poet creates imagery of light and darkness to bring out the beauty of the lady. Find out the lines with such imageries and complete the table:
Answer:

Lines with imagery	Reason for using
1. And all that’s best of dark and bright	To express the beauty of the eyes
2. Thus mellowed to that tender light – heaven to gaudy day denies	To convey the dim soft light of evening not the harsh brightness of the day
3. One shade the more, one ray the less	To stress the perfect balance between darkness of night and the glare of day

Question (ii)
Find out from the poem examples of:
(a) Simile
(b) Metaphor
(c) Alliteration
(d) Personification
(e) Antithesis.
Answer:

Figure of speech	Example	(Explanation)
1. Simile	like the night of cloudless climes and starry skies	(Her beauty Is directly compared to the cloudless starry skies.)
2. Metaphor	in every raven tress	(Her hair-tress – is shiny and jet black like a raven’s colour.)
3. Alliteration	Cloudless climes and starry skies	(The ‘c’ sound and ‘s’ occur in adjacent words for poetic effect.)
4. Personification	eloquent, The smiles that win	(The beautiful woman does the act of smiling, which wins hearts.)
5. Antithesis	1. best of dark and bright 2. One shade the more, one ray the less	(Words of opposite meanings are used for poetic effect.)

(A5)

Question (i)
Write an appreciation of the poem considering the following points :

• About the poem / poet / title
• Theme
• Poetic devices, language, style
• Special features – tone and type
• Values, message
• Your opinion about the poem

Answer:
Lord Byron’s poem opens with the same words that form the title: “She walks in beauty.” These four simple words quickly create an atmosphere of admiration and mystery. It is a short eighteen line poem having three sestets (six lines) in praise of an unnamed woman. The poet uses several poetic devices to express how deeply he is impressed.

There are several themes. One is of course beauty. Each feature of the woman – her eyes, her black (raven) tresses, her soft cheek, her calm brow and the lovely colour of skin is praised. The poet speaks of harmony. He speaks of the perfect blend of day and night, of light and dark. He speaks of the ‘mellowed’ or tender light which makes the beauty so rare, delicate and astonishing.

The other theme is the inner beauty which is what brings the outer beauty. He mentions ‘heaven’ [line 6] which may point to a divine side to the beauty. If a person is sinless their mind is pure and calm. There is no evil so the innocence inside causes the outer beauty which is indescribable – ‘nameless grace [line 8]

The poet uses simile [line 1] ‘like the night..’, alliteration – ‘cloudless climes’, ‘starry skies’. There is rhyme ababab in all the sestets. He uses metaphor -raven tress [line 9], and personification – ‘smiles that win’ [line 15]. There are many examples of antithesis through which the poet stresses on balance.

There is harmony of light – ‘dark and bright’, ‘tender light -gaudy day’, ‘one shade more, one ray less’. These are to emphasize that the beauty is not only physical and external, but actually because there is inner beauty. The mind is calm, the heart is innocent and this causes the outer beauty which is seen by him.

The poem is lyrical, has a steady rhythm and the language is rich with poetic devices. Though the poet does not name the woman, or give any details of her age, his admiration is felt in the tone. The message is about the importance of inner beauty, which is almost a divine thing that will make external beauty possible.

I feel the poem makes us realize that one should look deeper than just outward appearance. One should appreciate beauty in its entirety.

Question (ii)
Compose a poem of at least 4-6 lines on ‘Beauty of Nature’.
Answer:
Beauty of Nature

I look up at the majestic peaks I peer into the sapphire deeps I gaze at the endless shades of green My eyes drink the silver threads between.
In this life God I’m quite sure we can see Why? He’s everywhere in Nature’s beauty!

Question (iii)
Write at least one paragraph and expand the inherent idea of the saying ‘A Thing of Beauty is a Joy Forever’.
Answer:
A Thing of Beauty is a Joy Forever

We all love beauty. We are instantly attracted toward anything beautiful. Even children are drawn toward something pretty. We admire its qualities like lovely colour or soft texture. We admire something beautiful created by someone, like a painting or sculpture. We exclaim on the realistic appearance and the artist’s skill. We appreciate beauty in nature. Gorgeous flowers, majestic mountains, the green of hills and the charming waterfalls. We enjoy the sweetness of fruits.

To create something beautiful requires patience, effort and care. When all these come together the result is beautiful. We appreciate it whether it is in nature or is man-made. Our ears keenly listen to birds calling in the morning, melodious music, the rush of waves and the splashing of rain. Thus all our senses are attracted and we feel good when we see, hear or taste something. It brings us happiness.

Thus a thing of beauty is a joy forever.

(A6)

Question (i)
Browse the internet and find out different types of poems on ‘Beauty’.

Question (ii)
Byron’s name is often taken along with his two contemporaries – Shelley and Keats. Go to your school/college library and read some poems written by P. B. Shelley and John Keats to get a better idea about the Romantic Poets.

Yuvakbharati English 12th Digest Chapter 2.7 She Walks in Beauty Additional Important Questions and Answers

Read the poem and complete the given activities:

Global Understanding:

Question 1.
Complete the following:
The colour of the lady’s hair is
Answer:
The colour of the lady’s hair is shiny black (like a raven’s).

Interpretation/Inference/Analysis:

Question 1.
Complete the following:
Answer:
The phrase ‘dwelling – place’ refers to her mind. The poet says that her face sweetly expresses her thoughts and says that the dwelling place of those thoughts (expressed by the face) is very dear. The dwelling place of thoughts is the mind.

Balbharti Yuvakbharati English 12th Digest Chapter 2.6 Money Notes, Textbook Exercise Important Questions and Answers.

Maharashtra State Board Class 12 English Yuvakbharati Solutions Chapter 2.6 Money

12th English Digest Chapter 2.6 Money Textbook Questions and Answers

Question 1.
Discuss in the class about ‘Importance of money.’
Points :
(a) Money is used as capital in business.
(b) It is used by traders to Jill up stocks
(c) It is used by the common man for buying essentials/necessities.
(d) Everyone uses money for paying transport fare/ food-bill/wages and so on.

Question 2.
Complete the web:

Answer:

Question 3.
Make a list of the good qualities of your friend.
Answer:
(a) Calm and good tempered at all times
(b) Helpful and concerned about anyone in trouble
(c) Quick to intervene/calm down any situation that could become unpleasant
(d) Very simple and down to earth in spite of coming from an extremely wealthy background

Question 4.
Share your views on ‘Money is the root of all evils’.
Answer:
Points:

1. Money is a resource.
2. Resources should be available/ used in times of need
3. Money is accumulated by few people/others in need are deprived/some people are not paid fully/workers are paid less for their time and energy
4. Employer gets profit/ imbalance of resources
5. Imbalance in wealth causes discontent among disadvantaged sections of society.
6. Crime increases
7. Haves are targeted by have-nots
8. Normal life becomes unstable
9. Accumulation of money causes this upset in society
10. So important resource becomes reason for evil

Question 5.
Do you lend money to your friend? Give reasons:
Answer:

Yes	No
1. He/She comes from an economically disadvantaged background	1. I know that he/she gets enough money to spend
2. He/She is a very bright student, hopes to study well and find employment	2. He/She wastes time at movies and malls
3. He/She will fall sick if she does not have good nourishment	3. He/She has no intention of returning borrowed money
4. His/Her mother is the only bread winner. His/Her father very sick	4. He/She comes to college only to meet friends and socialize

(A1)

Question (i)
‘Money does not mean everything in life’. Justify the statement by giving examples. Take help of the following points:
(a) Money cannot give you eternal happiness.
(b) Art, music and literature can give you unending happiness.
(c) Money is short-lived.
(d) Money cannot purchase happiness and contentment.
Answer:
Happiness is in the mind. If a person is satisfied with what is on hand then he is happy. Rich clothes, gold, expensive food, servants may all be available. But the owner of these may still be sad and lonely.

Some are happy to make music another may create art or write. They may not have material possessions. But in their hearts they are happy to do what they love.

Money is only a medium to purchase our needs. One cannot give money and buy a bag of joy. Joy is in the heart. Money can be stolen. But joy cannot be stolen. One can earn money but not happiness. No amount of money will satisfy greed or buy happiness.

Question (ii)
Debate on the following topic in groups : Money is the solution for everything For: We need money for – Food-Clothes-Medicines- Education- Travel
Against: One cannot eat money itself/one must have food. We should not buy more than essential clothes/ no need to buy often-Good hygiene and food-habits will ensure health-Government schools are available- Travel is not needed for survival.

(A2)

(i) State whether the following statements are True or False. 

Question (a)
The poet knew no joy till he was rich.
Answer:
False. The poet had no joy as long as he was rich. He was happy when he was poor.

Question (b)
The poet felt that he should talk about his poverty.
Answer:
False. He could not talk about his money.

Question (c)
When the poet had money, he had many true friends.
Answer:
False. When the poet had money, all his friends were false ones.

Question (d)
When poet became poor he had very few real friends.
Answer:
True.

(ii) Write reasons for the following statements.

Question (a)
Friends came knocking all day at the poet’s door.
Answer:
When the poet was rich he had many callers. They claimed they were friends. They were being friendly because he had money. They were not true friends. Such people are called ‘fair-weather friends’.

Question (b)
Poor men’s wives hum like bees.
Answer:
Poor men have no worries. They do not have to safeguard their wealth from liars and cheats. They don’t have false friends who actually love his money and not him. When a man is satisfied with what he has he is happy. He is not chasing wealth and or pretending. The wives are busy and do not have the time to wish for fancy things or gossip. So a happy man has a happy busy wife.

Question (iii)
Money makes the world go round. Explain it in the light of the poet’s experience.
Answer:
Money makes the world go round is a popular saying. It means money is the most important thing in the world. But in ‘Money’, the poet does not accept this view. He had money but he could not say that he possessed it. There were many insincere men who said they were friends.

Contentment is the main thing for being happy, not worldly possessions. Lack of money is a problem. We need it for things like health or education. When all needs are taken care of, then excess money is not necessary. Money is needed in life but it is not the only important thing in life.

The poet repeats that money brought many false men to be near him. But in poverty only a few true friends were with him.

Question (iv)
Poor men need not go up so much as rich men should come down. Express your views regarding this statement.
Answer:
Poor men need not go up as rich men should come down. This statement is perfectly true. The poor will survive. Living a simple, real life, and working hard. They are happy with necessities which may not be expensive. They are content and that brings happiness. They do not have to worry about safeguarding the excess.

But the rich may not know how to live simply, just with basic necessities. They may have servants to do basic chores. They travel in style and sometimes for no reason. They spend unnecessarily. So the poor need not go up as much as the rich need to come down is true.

(A3)

Question (i)
Find out meanings of the phrases given below and use them in your own sentences:
Answer:
(a) Be in the money –
Meaning: to suddenly have a lot of money.
Sentence: It looks he is in the money, by the way he is giving everyone costly gifts.
(b) Win lots of money –
Meaning: get money in a lottery/ gambling/ get money through luck, not work.
Sentence: He bought a lottery ticket every week hoping to win lots of money.
(c) For my money –
Meaning: in exchange for. Worth the amount.
Sentence: The old man asked. ‘Is this all I’m getting for my money?’
(d) Money for old rope –
Meaning: money that is easily earned or gotten
Sentence: She got two thousand just for answering questions in the interview! Money for old rope!
(e) Put one’s money where one’s mouth is Meaning: to take appropriate action to support what one has said.
Sentence: The Municipal Commissioner promised he would put the money where his mouth is and immediately release funds for the school facilities as promised.

Question (ii)
Complete the crossword with the help of the clues from the poem :

Across:
1. A brass musical instrument – TRUMPET
2. A low steady continuous sound – HUM
3. False – UNTRUE
4. Say Something – SPEAK
Down :
5. Not imaginary – REAL
6. Ponder – THINK
7. Stinging insects – BEES
8. In large number – MANY
9. Strike a surface noisily – KNOCK

(A4)

Question (i)
Complete the following table:
Answer:

Figure of speech	Line from the poem	Explanation
1. Inversion	‘felt I like a child’”think I’ Much have I thought of life	The order of words – ‘I felt like a child’, ‘I think’ – is reversed for effect. ‘I have thought much of life’ is reversed to give effect.
2. Simile	‘Like a child. ‘wives do hum like bees about their work’.	The poet compares himself with a child The wives of poor men are as busy as bees in their work.
3. Repetition	‘When I had money, money, O! [line 1 and 17]	The line is repeated and the word money. The word is the theme and it is repeated to emphasize he was very rich.
4. Onomatopoeia	‘do hum like bees’	The word ‘hum’ imitates the humming of bees.
5. Antithesis	‘many a false man as a friend’ ‘many friends proved all untrue’ ‘poor ones laugh – rich ones frown’ ‘poor men need not go up-the rich men should come down’	The quality of friends is supposed to be sincere and loyal. But they are described as opposite – false and untrue. The poor smile and the rich frown. This is opposite of what we expect. The rich must know simplicity says the poet, the opposite of what we say that the poor must come up in life.

Question (ii)
Identify the rhyme scheme of all the stanzas of the poem.
Answer:
The rhyme scheme of the stanzas 1 to 4 is abcb.
The rhyme scheme of the 5th stanza is abab.

Question (iii)
Compose a short poem on ‘Friendship’.
Answer:
‘Friendship’
We knew playtime in the park
Study time in school.
We helped one another
Struggling for each difficult mark.
We grew up, and though we fought
We will meet years later
We fondly thought.

(A5)

Question 1.
Write an appreciation of the poem considering the following points:

• About the poem/poet/title
• Theme
• Poetic devices, language, style
• Special features-tone and type
• Values, message
• Your opinion about the poem

Answer:
William H. Davies – a Welsh poet and writer – in his poem ‘Money’ speaks of both times – when he had money and when he did not. Davies tramped through the United Kingdom and the United States.

So he actually led a poor simple life of a wanderer. He actually experienced the difference in the life of a rich man and a poor one. The theme of the poem is the effect of money on the behaviour of people. False friends are plenty when a man has money. The poet compares himself to a child with a trumpet. He is not allowed to blow it for there has been a death.

He uses simile again when the poor man’s wife is described as humming about busily like a bee. The poet also has seen that the lack of money does not mean lack of happiness. The poor man is able to laugh while a rich man frowns; he feels the rich must become poor to taste the simple joys of life – the use of antithesis helps to stress this point.

The poem has five stanzas of four lines each, The seven or eight syllable lines are short but rich ; in poetic devices. The rhyme scheme lends rhythm. Repetition of the word ‘money’ stresses the way man gives money too much importance when it actually takes away our happiness.

The message is that money does not bring happiness. The poor are cheerful while the rich are worried. The poem is very useful to remind us the value of money. It is a necessity. It is not the only thing to chase.

(A6)

Question (i)
Visit a library and read a few poems written by William H. Davies.

Question (ii)
There are many career opportunities related to finance and planning.

Question (iii)
Try to get information about the following careers by surfing the internet.
(a) Finance Management
(b) Banking and Finance
(c) Actuaries
(d) Economics
(e) Share Market
(f) Accountancy
(g) Company Secretary

Question (iv)
Economics is a very important subject in which you can pursue vour career. Browse the websites of these institutions and get information for various courses in Economics.
(a) Delhi School of Economics
(b) Indian Statistical Institute
(c) Gokhale Institute of Politics and Economics, Pune
(d) Madras School of Economics

Yuvakbharati English 12th Digest Chapter 2.6 Money Additional Important Questions and Answers

Interpretation/Inference/Analysis:

Question 1.
Complete the reasons:
Poor ones laugh because ………………
Answer:
Poor ones laugh because – poor people live a simple life. If the basic needs are fulfilled the poor man is happy. He has nothing to worry about or fear. When a man has wealth he has to safeguard it. The poor man is worry-free like health or education. When all needs are taken care of, then excess money is not necessary. Money is needed in life but it is not the only important thing in life. The poet repeats that money brought many false men to be near him. But in poverty, only a few true friends were with him.

Balbharti Yuvakbharati English 12th Digest Chapter 2.5 Father Returning Home Notes, Textbook Exercise Important Questions and Answers.

Maharashtra State Board Class 12 English Yuvakbharati Solutions Chapter 2.5 Father Returning Home

12th English Digest Chapter 2.5 Father Returning Home Textbook Questions and Answers

Question 1.
Discuss with your partner the difficulties that you face while commuting to and from the college by public transport.
Answer:
(a) crowded buses, trains
(b) are difficult to board in peak-hours
(c) have to miss a couple of trains/buses to board safely
(d) on such days miss an important lecture

Question 2.
The similar problems are faced by the other commuters on the way to their workplace. Imagine their plight and suggest three solutions.

Answer:

Question 3.
Complete the following table:
Answer:

A	B
The way our elders take care of us	The way you can take care of elders in your family.
1. Love and protect us. 2. Support, educate and guide us through childhood and youth until we are independent. 3. Provide us with pocket-money and gifts we ask for.	1. Help them in daily chores. 2. Help with errands to the bank, stores or other requirements. 3. Ensure good health with exercise/ social- engagement/doctor- visits/ meditation.

Question 4.
Write your duties towards the following:

Answer:

(A1)

Question (i)
Discuss with your friend the difficulties focused by the father in the poem.

Question (ii)
Discuss and write the character sketch of the father with the help of the given points.
(His pathetic condition, the treatment he receives at home, his solitude, the way he tries to overcome it)
Answer:
The father is on the late train. This shows he is hard-working. He does not spend any money on himself as his appearance is shown as shabby. He is uncaring about his appearance probably because he is lonely and heart-broken.

He is silent on the train-trip home. He does not speak to co-passengers. Perhaps the sadness in his heart prevents him from even small-talk. He has no travel-mates. He is silent through the trip, and gets off without waving goodbye to any passenger.

His family is cold, distant and uncaring. He is not greeted on arrival. He is given cold food which is not nourishing. He is left to eat the meal alone just reading his book. At the end of the work-day he reads a book, eats by himself, listens to the radio and dreams of the future all alone. Thus the father is a lonely old man, neglected by his own family in spite of working hard for them and heart-sick of his existence.

(A2)

Question (i)
Given below are the ideas conveyed through the poem. Match the pairs and draw out the hidden meaning from those expressions:


Answer:
1. The father hurries home crossing railway line – Father is so eager to meet family members that he doesn’t even bother about his safety.
2. Suburban area, visible through the train, is passed unnoticed – Because there is hardly anything enchanting/interesting in the monotonous routine journey to look out of the window
3. He is just as a small word, dropping from a sentence. – He has so little value in the society where his presence or absence might hardly make any difference
4. He doesn’t get a place in a crowded train. – Uncomfortable journey

(ii) Find the lines to prove the following facts from the extract:

Question (a)
Father is deprived of good food.
Answer:
‘Home again, I see him drinking weak tea Eating a stale chapati’

Question (b)
Children did not have a healthy relation with the father
Answer:
His sullen children have often refused to share
Jokes and secrets with him.

Question (iii)
The poet deals with the theme of man’s estrangement from a man-made world. Analyze it with the help of the extract.
Answer:
The father reaches home. He has a lonely poor meal, served without care. The stale cold food also indicates the coldness in relationships in the family. The weak tea is a metaphor for the fragile family bond. There is no bonding. Home is only a shelter for him and he is only a provider for them. The father is lonely among his own family as well. So the father is alone in the crowd of strangers and also among his own family.

Question (iv)
The father contemplates his past and peeps into his future. Give reasons.
Answer:
The father silently ponders on his past. There is no communication with his family members. He would have sat with family members together to recall happy memories and enjoy them again. Reliving the past would have been one way for the family to bond. But the father thinks of the past alone. Future plans could be also discussed with family members. A lot of discussions could have happened about money, savings, career, a wedding and so on.

Advice, suggestions are given, arguments and disagreements happen, and even anger sometimes. But the father has nothing like this happening in his presence. There is only a sullen silence. He remembers his past and thinks of possible grandchildren. No one shares his dreams. He spends the past, present and future alone and in silence.

(A3)

Question 1.
Complete the following using suitable describing words as they appear in the poem with the help of the words given in the brackets:
(weak, dim, muddy, soggy, stale)
Answer:
(a) Father’s attire – soggy
(b) Father’s tea – weak
(c) Father’s footwear – muddy
(d) Father’s food – stale
(e) Father’s eyesight – dim

(A4)

Question (i)
Identify and write the lines from the extract which expresses the following figures of speech:
Answer:

Figures of speech	Lines
1. Simile	‘Like a word dropped from a long sentence’ The father getting off the train is compared to a word dropped unnoticed as many others words are there.
2. Alliteration	1. ‘My father travels on the late evening train’ [1] The sound ‘t’ is repeated. 2. ’Suburbs slide past his unseeing eyes’ [3] the sound ‘s’ is repeated.

Question (ii)
I see him drinking weak tea, eating a stale chapati.
Here ‘stale chapati’ stands for stale food/ non-nourishing food or diet, where the part symbolizes the whole, i.e. food. Guess the name of the figure of speech.
Answer:
The figure of speech is ‘synecdoche’.

(A5)

Question (i)
Write a counterview on the following topic:
“Every day is a mother’s/ father’s day.”
(a) If you love them, you don’t need to wait for such days.
(b) Celebrating days is just a formality.
(c) Celebrations of the days condition your expression of emotions.
(d) It is a kind of a pretext to neglect your everyday responsibilities.
Answer:
We love and respect our parents. We must be sure to be loving and respectful in our everyday behaviour and actions. They work, laugh, sacrifice – all only for their children -US! When we behave respectfully and lovingly with elders, the cards or a special day in the year are just a formality.

Our feelings for our parents are unconditional. We don’t say ‘if they do something, only then will we do something in return, while interacting with elders in the family. We cannot be loving, caring, obedient and helpful only on a Father’s/Mother’s Day. We have to be all these towards our parents and elders EVERY DAY.

So ‘Every day is Mother’s/Father’s Day!’

Question (ii)
Write an appreciation of the poem considering the following points :

• About the poem/poet/title
• Theme
• Poetic devices, language, style
• Special features – tone and type
• Values, message
• Your opinion about the poem

Answer:
The poem ‘Father Returning Home’, by Dilip Chitre – a bilingual poet – is about a lonely old man’s coming home from a long day at work. The poet describes his silent and lonely journey home in the crowded Mumbai local train. It is a metaphor for the father’s isolated life even though he is among people.

The poet speaks of the ‘unseeing’ eyes on the scenery flashing past the train. The same thing the man sees daily when commuting has nothing new, just like his uninteresting life. The setting is dusk in monsoon. The man’s dress and appearance are also metaphorical.

His soggy clothes and mud stained raincoat symbolize his shabby appearance and also his sad life. The man carries a bag full of books. He is well-read maybe. Thus when the man gets off the train the poet compares it to a word falling from a sentence. He goes unnoticed as an unimportant word dropped from a long sentence – a simile. The ‘long sentence’ – imagery – makes us imagine the long train and the passenger is one word that is getting down.

The platform he crosses is grey, colour imagery for gloominess or dirty surroundings. The poet uses informal language and an easy style. The poet describes him ‘hurries’ along the platform and again ‘hurries’ on to his home. This repeated word shows his eagerness to reach his shelter and I get dry. The words create an imagery of a shabby, pitiable but scholarly man.

The second part of the poem is about the man in his home. The meal he eats shows the poor quality as well as the careless way it is served. He ‘ reads a book while he eats. That is a clear imagery for his loneliness at home also. The family offers no company after his long day and tiring commute.

In the toilet he is pondering on how he has been shut out of the world although he is in the crowd. He is a stranger among his family in his own home. His children don’t speak to him and won’t share any part of their life. They are not interested in his life also. He goes to sleep thinking of the past and future, listening to harsh sounds on the radio.

The message is how the elderly are used by their own children but neglected when they need care. The poem is about a man who may be misunderstood. He is lonely even in the middle of crowds. It teaches how we should not behave to j persons who are in the autumn of their life. I feel sorry for such people who have worked hard in their life but the younger relatives discard them once their use is over.

Question (iii)
Compose a short poem in about 4-6 lines on your father.
Answer:
My Father

He is unselfish, caring,
Honest and hard-working
Simple, strict and well-read
Upright, always respected
By family and every friend.
He tried to excel till the end.

Question (iv)
Write a character sketch of any one of your family member.
Answer:
My Mother
If anyone cannot believe angels walk on the earth they should come and meet my mother. My mother is the most affectionate and gentle human I have ever met. She has never spoken a harsh word to anyone as far as I recall. She is so very concerned for the comfort of every other person that she neglects herself.

She looks after her father-in-law who is in his eighties. He is a great scholar and gets many visitors. She attends cheerfully to them all apart from looking after us. My father, my sister and I help out with as much of the household chores as we can.

But the main load of running the home falls on her. She takes care of that responsibility so cheerfully as if it is very light. She is loving and jovial with our friends when my sister and I invite them home, She advises us not to overspend but always has a tasty meal when friends and relatives gather for a festival meal.

My father does not make any important decisions in my mother’s absence. She discusses everything till they arrive at the most suitable decision. Our grandfather will not eat anything which my mother has not made. After my grandmother passed, he relies on ‘Saru’ my mother, for his diet meals, medicine, his reference books, walking stick, shawl and everything to be in their place.

My mother is our world.

(A6)

Question (i)
Dilip Chitre has translated Sant Tukaram’s ‘Abhangas’ (devotional poems) for which he received Sahitya Akadeini Award. Browse the internet to collect more information about it.

Question (ii)
List various occupations related to services which can be rendered to senior citizens.
(a) To counsel patients of Alzheimers’ disease.
(b) (Students may attempt this on their own.)
(c) (Students may attempt this on their own.)

Yuvakbharati English 12th Digest Chapter 2.5 Father Returning Home Additional Important Questions and Answers

Read the extract and complete the given activities:

Global Understanding:

Question 1.
List the difficulties faced by the father in the extract.
Answer:

1. The father is returning late in the day.
2. He has to stand the entire trip home.
3. He is in wet clothes for a long time till he can reach home.
4. His sight is weak with age.
5. His cheap footwear is muddy and maybe inconvenient in the monsoon.

Question 2.
Find the lines to prove the following facts from the poem.
Father does not bother to buy anything new for himself and makes do with old, worn out possessions.
Answer:
‘His bag stuffed with books is falling apart’ (line 6)

Question 3.
Choose the correct option and give reasons for it:
Refusal of the children to share jokes and secrets indicates:
(a) They are angry
(b) Generation gap
(c) Lack of concern
Answer:
All three could be reasons.
The children are angry that the father is unable to earn more, provide better life for them.
The father is old and the youngsters cannot relate to him. They are selfish and don’t care for the man who is doing his best.
The children have no care, love or respect for the father. It might not be a close-knit family. So there is no concern for the hard-working breadwinner.

Question 4.
List the difficulties faced by the father in the extract.
Answer:

1. The father is not greeted on his arrival home at the end of the day; is not served any nourishing food – has weak tea and stale chapati.
2. The family does not interact with him. His book is his company.
3. His children are bad tempered sharing no details of their life or asking about his day.
4. He must be going to work like this, also returns silently, to a silent home to his unfriendly family for whom he works.
5. He is unnoticed, uncared for, unappreciated, almost like an outsider in his own home and family.

Inference/Interpretation/Analysis:

Question 1.
The poet deals with the theme of man’s estrangement from a man-made world. Analyze it with the help of the extract.
Answer:
There are two scenarios in the poem. The first part is about the father’s time spent time outside, and the second part describes his time in his home. The first line says he is travelling on the evening train. The Mumbai local trains are famously crowded. But among the crowds he does not speak to a fellow passenger. He stands silently through the commute till he gets down. He doesn’t take leave of any friend and no one waves to him. Among the crowds he is alone.

Question 2.
Given below are the ideas conveyed through the poem. Match the pairs and draw out the hidden meaning from those expressions:
Answer:

Expressions	Meaning
1. The father hurries home crossing railway line	(a) Uncomfortable journey
2. Suburban area, visible through the train, is passed unnoticed.	(b) Has least value in the society where his presence or absence might hardly make any difference
3. He is just as a small word, dropping from a sentence.	(c) Because there is hardly anything enchanting/ interesting in the monotonous routine journey to look out of the window
(4) He doesn’t get a place in a crowded train.	(d) Father is so eager to meet family members that he doesn’t even bother about his safety.

Answer:
1. Children avoid expressing themselves – Hostility of children
2. Father was deprived of refreshing hot beverages or nourishing diet – His basic daily requirements were also not catered to.
3. The father was destined to listen only to the crackling sounds on media – The father could not even have some entertainment by himself on the radio.
4. His sordid present is devoid of any hope – He could only indulge in imagination about his past and future.
5. The father’s endless commuting distance him from his children – Father is not less than any tribal wanderer, a modern nomad.

Personal Response:

Question 1.
Write a note on ‘the hard work faced by parents for the family’.
Answer:
Our parents love us from the moment we are born. They watch us grow up and give us everything they can. They try to fulfil our wishes to the maximum extent possible. They work hard. The father works outside the home and the mother in the home. They spend their time, energy and resources on the children.

The children should realize that their parents do so much for them. We must not take their sacrifice for granted. We can never repay them. We must at least try and give them comfort and joy. It is our first duty to obey and love our parents and look after them when they grow old and unable to take care of themselves.

Question 2.
Describe the nature of the family members, from the father’s behaviour in the extract.
Answer:
The family members seems selfish and uncaring. The father drinks weak tea and eats stale food on his return. It is possible to serve fresh food, to the bread-winner returning home even if it is the most simple or poorest of food. If he has a wife then she does not seem to care much about his wellbeing.

The poet clearly states that the children have refused to share any lighter moments or conversation with their father. Probably the mother’s behaviour has made the children also treat him this way. If it is poverty they are facing then the family seems selfish in demanding he work for them but not even offering their company or kindness in return.

Poetic Devices:

Question 1.
Find out the examples of transferred epithets from the extract.
Answer:
‘Suburbs slide past his unseeing eyes. The ‘unseeing’ is transferred to eyes. The eyes are seeing but his mind is not registering any sight. So the quality of ‘not seeing’ is given to the eyes.

Poetic Creativity:

Question 1.
Compose a few lines on ‘Distance’.
Answer:
Distance
I travel for an hour to work, and an hour back.
This is the exact distance of the track
Between myself and the people whom
I go to a place called home.

Maharashtra State Board HSC 12th Commerce Maths & Statistics Digest Pdf, 12th Commerce Maharashtra State Board Maths Solution Book Pdf Part 1 & 2 free download in English Medium and Marathi Medium 2021-2022.

Maharashtra State Board 12th Commerce Maths Digest Pdf

12th Commerce Maths Digest Pdf Part 1

Maharashtra State Board Std 12th Commerce Maths Textbook Solutions Chapter 1 Mathematical Logic

• Chapter 1 Mathematical Logic Ex 1.1
• Chapter 1 Mathematical Logic Ex 1.2
• Chapter 1 Mathematical Logic Ex 1.3
• Chapter 1 Mathematical Logic Ex 1.4
• Chapter 1 Mathematical Logic Ex 1.5
• Chapter 1 Mathematical Logic Ex 1.6
• Chapter 1 Mathematical Logic Ex 1.7
• Chapter 1 Mathematical Logic Ex 1.8
• Chapter 1 Mathematical Logic Ex 1.9
• Chapter 1 Mathematical Logic Ex 1.10
• Chapter 1 Mathematical Logic Miscellaneous Exercise 1

12th Commerce Maths Book Pdf Chapter 2 Matrices

• Chapter 2 Matrices Ex 2.1
• Chapter 2 Matrices Ex 2.2
• Chapter 2 Matrices Ex 2.3
• Chapter 2 Matrices Ex 2.4
• Chapter 2 Matrices Ex 2.5
• Chapter 2 Matrices Ex 2.6
• Chapter 2 Matrices Miscellaneous Exercise 2

Std 12 Commerce Statistics Part 1 Digest Pdf Chapter 3 Differentiation

• Chapter 3 Differentiation Ex 3.1
• Chapter 3 Differentiation Ex 3.2
• Chapter 3 Differentiation Ex 3.3
• Chapter 3 Differentiation Ex 3.4
• Chapter 3 Differentiation Ex 3.5
• Chapter 3 Differentiation Ex 3.6
• Chapter 3 Differentiation Miscellaneous Exercise 3

12th Commerce Maths Solution Book Pdf Chapter 4 Applications of Derivatives

• Chapter 4 Applications of Derivatives Ex 4.1
• Chapter 4 Applications of Derivatives Ex 4.2
• Chapter 4 Applications of Derivatives Ex 4.3
• Chapter 4 Applications of Derivatives Ex 4.4
• Chapter 4 Applications of Derivatives Miscellaneous Exercise 4

12th Commerce Maths Notes Chapter 5 Integration

• Chapter 5 Integration Ex 5.1
• Chapter 5 Integration Ex 5.2
• Chapter 5 Integration Ex 5.3
• Chapter 5 Integration Ex 5.4
• Chapter 5 Integration Ex 5.5
• Chapter 5 Integration Ex 5.6
• Chapter 5 Integration Miscellaneous Exercise 5

12th Commerce Maths Digest Pdf Chapter 6 Definite Integration

• Chapter 6 Definite Integration Ex 6.1
• Chapter 6 Definite Integration Ex 6.2
• Chapter 6 Definite Integration Miscellaneous Exercise 6

12th Maharashtra State Board Maths Solution Book Pdf Part 1 Chapter 7 Application of Definite Integration

• Chapter 7 Application of Definite Integration Ex 7.1
• Chapter 7 Application of Definite Integration Miscellaneous Exercise 7

12th Maths 1 Digest Pdf Chapter 8 Differential Equation and Applications

• Chapter 8 Differential Equation and Applications Ex 8.1
• Chapter 8 Differential Equation and Applications Ex 8.2
• Chapter 8 Differential Equation and Applications Ex 8.3
• Chapter 8 Differential Equation and Applications Ex 8.4
• Chapter 8 Differential Equation and Applications Ex 8.5
• Chapter 8 Differential Equation and Applications Ex 8.6
• Chapter 8 Differential Equation and Applications Miscellaneous Exercise 8

12th Commerce Maths Solution Book Pdf Part 2

HSC Maths Textbook Pdf Chapter 1 Commission, Brokerage and Discount

• Chapter 1 Commission, Brokerage and Discount Ex 1.1
• Chapter 1 Commission, Brokerage and Discount Ex 1.2
• Chapter 1 Commission, Brokerage and Discount Miscellaneous Exercise 1

12th Maths Digest Pdf Part 2 Chapter 2 Insurance and Annuity

• Chapter 2 Insurance and Annuity Ex 2.1
• Chapter 2 Insurance and Annuity Ex 2.2
• Chapter 2 Insurance and Annuity Miscellaneous Exercise 2

12 Maths Book Pdf State Board Chapter 3 Linear Regression

• Chapter 3 Linear Regression Ex 3.1
• Chapter 3 Linear Regression Ex 3.2
• Chapter 3 Linear Regression Ex 3.3
• Chapter 3 Linear Regression Miscellaneous Exercise 3

12th Maths 2 Digest Pdf Chapter 4 Time Series

• Chapter 4 Time Series Ex 4.1
• Chapter 4 Time Series Miscellaneous Exercise 4

12th Maths Part 2 Digest Pdf Chapter 5 Index Numbers

• Chapter 5 Index Numbers Ex 5.1
• Chapter 5 Index Numbers Ex 5.2
• Chapter 5 Index Numbers Ex 5.3
• Chapter 5 Index Numbers Miscellaneous Exercise 5

12th Statistics Book Chapter 6 Linear Programming

• Chapter 6 Linear Programming Ex 6.1
• Chapter 6 Linear Programming Ex 6.2
• Chapter 6 Linear Programming Miscellaneous Exercise 6

12th Commerce Maths Book Pdf Chapter 7 Assignment Problem and Sequencing

• Chapter 7 Assignment Problem and Sequencing Ex 7.1
• Chapter 7 Assignment Problem and Sequencing Ex 7.2
• Chapter 7 Assignment Problem and Sequencing Miscellaneous Exercise 7

12th Commerce Maths Solution Book Pdf Chapter 8 Probability Distributions

• Chapter 8 Probability Distributions Ex 8.1
• Chapter 8 Probability Distributions Ex 8.2
• Chapter 8 Probability Distributions Ex 8.3
• Chapter 8 Probability Distributions Ex 8.4
• Chapter 8 Probability Distributions Miscellaneous Exercise 8

Maharashtra State Board Class 12 Textbook Solutions

Maharashtra State Board Std 12th Commerce Book Keeping & Accountancy Textbook Solutions Digest

Book Keeping and Accountancy Class 12 Solutions | 12th BK Textbook Solutions

• Chapter 1 Introduction to Partnership and Partnership Final Accounts
• Chapter 2 Accounts of ‘Not for Profit’ Concerns
• Chapter 3 Reconstitution of Partnership (Admission of Partner)
• Chapter 4 Reconstitution of Partnership (Retirement of Partner)
• Chapter 5 Reconstitution of Partnership (Death of Partner)
• Chapter 6 Dissolution of Partnership Firm
• Chapter 7 Bills of Exchange
• Chapter 8 Company Accounts – Issue of Shares
• Chapter 9 Analysis of Financial Statements
• Chapter 10 Computer in Accounting

Maharashtra State Board Class 12 Textbook Solutions

Balbharti Maharashtra State Board Class 12 Psychology Solutions Chapter 8 Positive Psychology Textbook Exercise Questions and Answers.

Maharashtra State Board Class 12 Psychology Solutions Chapter 8 Positive Psychology

1. Choose the correct option and complete the following statements.

Question 1.
……………. is the father of positive psychology.
(a) Carver
(b) Masten
(c) Seligman
Answer:
(c) Seligman

Question 2.
Barbara Fredrickson introduced the Broaden and ………………. theory.
(a) Build
(b) Emotion
(c) Learning
Answer:
(a) Build

Question 3.
The belief that good things will happen is called as ………………..
(a) pessimism
(b) resilience
(c) optimism
Answer:
(c) optimism

Question 4.
The capacity to understand what the other person is experiencing is………………
(a) sympathy
(b) empathy
(c) emotion
Answer:
(b) empathy

2. Answer the following questions in 35 – 40 words each.

Question 1.
Explain the theories of happiness
Answer:
Happiness is a positive emotional state that is subjective to each person, for e.g., people feel happy when they are successful or surprised or loved, etc.
The main theories of happiness are-

1. Need/ goal satisfaction theories – Happiness is experienced when some need or goal is satisfied, e.g., Rohit feels happiness when he clears IIT-JEE exams.
2. Process/ activity theories – Happiness is experienced when one engages in a particular activity, e.g., Sumit enjoys trekking.
3. Genetic/ personality theories – Genetic and personality characteristics are involved in the experience of happiness.

Question 2.
What is mindfulness?
Answer:
Mindfulness is the basic human ability to be fully aware of where we are and what we are doing. It means that we should not be overly reactive or overwhelmed by what’s going on around us. Mindfulness refers to mental awareness that helps to focus on the ‘Here and Now’. It helps to increase self-regulation, which results in growth and happiness. Mindfulness is maintaining moment by moment awareness of our bodily sensations, environment, thoughts and feelings.

Question 3.
What is resilience?
Answer:
According to the American Psychological Association, resilience is the process of adapting well in the face of adversity, trauma, tragedy, threats or significant sources of stress such as family and relationships, health, work and finances, etc. It is the act of ‘bouncing back’ inspite of barriers or set backs.

Resilience helps the person to recover form setbacks with the least negative consequences. Individuals high on resilience exhibit the following characteristics-

1. they regain their confidence after a period of emotional disturbance
2. they are able to maintain their psychological well-being.

The types of resilience are physical, psychological, emotional and community resilience.

3. Write short notes on the following in 50 – 60 words each.

Question 1.
Life above zero
Answer:
Traditional psychology focused on life at and below zero. Zero is the line that divides illness form
health. Hence, life below zero indicates a life that is full of problems stress, diseases, etc. Positive psychology emphasizes the study of life above zero.

-1 to +1 indicates neutral charactristics while below 0 indicates disorders, dysfunction or illness. Life above zero covers a large area of positive aspects of behaviour such as mindfulness, resilience, happiness, hope, trust and empathy. It acknowledges elements of living that enrich and meaningfully sustain what is referred to as “the good life” in positive psychology.

Question 2.
Determinants of happiness
Answer:
Happiness is a positive emotional state. Factors like health, prestige, income, success, etc., contribute to only a small portion of our total happiness.
Some factors are predictors of long lasting happiness-

1. Strong, intimate social relationships, positive contacts and good support system.
2. Optimism leads to less of negative emotions like stress.
3. Self-esteem enhances our confidence level and ability to approach challenges in a constructive manner.
4. Achieving challenging goals- If the goals are too easy, it leads to boredom and if they are too difficult, it leads to frustration. Moderately challenging goals, increase the chance of success, leading to happiness.
5. Perceiving meaning and purpose in life, without which we will experience frustration, boredom, etc.
6. Looking at life’s challenges as an opportunity rather than a threat helps to develop our potential.

Question 3.
Characteristics of an optimist
Answer:
Optimism is a mental attitude that includes feelings of hopefulness and a belief that the future will be positive and favourable. It is the belief that negative events are merely setbacks that are temporary and can be overcome.
The characteristics of optimists are:

1. they try to choose the best options available
2. they tend to be high on self confidence
3. they face difficulties positively as they view them as a challenge for a person to become strong
4. they are hopeful about the future and do not generalize present failure to future events.

Question 4.
Methods to promote empathy
Answer:
Empathy is the capacity to understand and feel what another person is experiencing from within their frame of reference i.e. capacity to place oneself in another’s position.

According to Simon Baron-Cohen there are three components of empathy viz. cognitive empathy emotional reactivity and social skills. Empathy builds a sense of security and trust. It is closely related to emotional intelligence and is a key to successful relationships.
Empathy can be promoted by using the following methods-

1. Increase social interactions – Especially with people who need help in order to understand their perspectives and motives.
2. Connecting through similarities – With others, e.g., those having same hobbies/ work/ goals, etc.
3. Understanding what you are feeling – Those who are able to accurately judge their own motives, can empathize better.
4. Challenge yourself – Tasks that are challenging lead to the person struggling to achieve a goal. This lead to humility which enables empathy.
5. Cultivate a sense of curiosity – This leads to open-mindedness and a better understanding of those around us.
6. Widen our social circle – Contact with people of different races, cultures, viewpoints helps to increase empathy towards them at a neurological level.

4. Explain the Following concepts.

Question 1.
Positive Psychology
Answer:
Positive Psychology is a newly emerging branch of psychology. Martin Seligman officially introduced Positive Psychology as a subfield of psychology. It is the science of happiness, human strength and growth. Positive Psychology focuses on building of character strengths like courage, happiness, perseverance, etc., rather than on anxiety, conflict, avoidance, etc. According to Seligman, positive psychology is “the scientific study of positive human functioning and flourishing on multiple levels that include the biological, personal, relational, institutional, cultural and global dimensions of life.”

Question 2.
Half glass full and half glass empty.
Answer:
Optimism is a mental attitude that includes feelings of hopefulness. It is a belief that the future will be positive and favourable and that negative events are merely setbacks that are temporary and can be overcome. Seligman explained about optimism in the book ‘Learned Optimism’. Our perspective determines whether or not we will show optimism.

A glass which has water upto its mid level may be perceived as half full (optimism) or as half empty (pessimism). This is described as ‘Half glass full and half glass empty’.

Question 3.
Empathy
Answer:
Empathy is the capacity to understand and feel what another person is experiencing from within their frame of reference, i.e., capacity to place oneself in another’s position. According to Simon Baron-Cohen, there are three components of empathy viz. cognitive empathy i.e., perspective taking, emotional reactivity (connecting in an intimate bond with another person) and social skills (moved to help the other). Empathy builds a sense of security and trust. It is closely related to emotional intelligence and is a key to successful relationships.

Question 4.
Mindfulness
Answer:
Mindfulness is the basic human ability to be fully aware of where we are and what we are doing. It means that we should not be overly reactive or overwhelmed by what’s going on around us. Mindfulness refers to mental awareness that helps to focus on the ‘Here and Now’. It helps to increase self-regulation, which results in growth and happiness. Mindfulness is maintaining moment by moment awareness of our bodily sensations, environment, thoughts and feelings.

Question 5.
Social resilience
Answer:
According to the American Psychological Association, resilience is the process of adapting well in the face of adversity, trauma, tragedy, threats or significant sources of stress such as family, health, etc. It is the act of ‘bouncing back’ inspite of barriers or set backs.

Social resilience is also called community resilience. It is the ability of groups of people to respond to and recover from adverse situations such as natural disasters, epidemics, war and socio-economic challenges to their community. This is mainly due to strong connections or bonds that the community members have with each other.

5. Answer the following question in 150 – 200 words each.

Question 1.
What are the essential building blocks of resilience?
Answer:
According to the American Psychological Association, resilience is the process of adapting well in the face of adversity, trauma, tragedy, threats or significant sources of stress such as family, health, etc. It is the act of ‘bouncing back’ inspite of barriers or set backs. Resilience helps the person to recover form setbacks with the least negative consequences. Individuals who are resilience tend to-

1. regain their confidence after a period of emotional disturbance
2. they are able to maintain their psychological well-being.

6. The types of resilience are physical, psychological, emotional and community resilience.

According to Ann Masten, building blocks is ‘ordinary magic’, which involves behaviour that can be easily learnt. The 7 C’s of reilience are-

1. Competence – Competence is the ability or know-how to handle situations effectively. Competence is acquired through actual experience.
2. Confidence – True confidence is a strong belief in one’s own abilities. Confidence is gained by demonstrating competence in real life situations.
3. Connection – Family is the central force in an individual’s life. Connections with other people, schools and communities gives the individual a sense of security that allows him/her to be independent and develop creative solutions.
4. Character – It refers to a clear sense of right and wrong and a commitment to integrity. An individual with character has a strong sense of self-worth and confidence.
5. Contribution – An individual who understands the importance of personal contribution develops a sense of purpose that can motivate him/her, further leading to him/her psychological well-being.
6. Coping – A person who learns to cope effectively with stress is better prepared to overcome life’s challenges.
7. Control – When an individual realizes that he can control the outcomes of his decisions and actions, he is more likely to know that he has the ability to bounce back.

Question 2.
Recollect the most challenging situation you faced in your life till now and the way you dealt with it. With reference to the 7 C’s of Resilience, which qualities helped you to overcome the challenge? For each of the C’s write the process you adopted to deal with the situation.
Answer:
[Students are expected to answer this question by themselves.]

7. Find out the positive aspects of behaviour from the example given below and answer in one word.

Question 1.
Mahesh studies so attentively that he never gets distracted.
Answer:
Mindfulness

Question 2.
Sujata lost her hands in an accident. Now she has learned to write with her leg.
Answer:
Resilience

Question 3.
Vasanta’s daughter died by cancer. He has opened a rehabilitation center for cancer patients.
Answer:
Empathy

8. Case Study

Anurag was a software engineer working in one of the leading company’s in the USA for almost 5 years. He was in a stable relationship and he had plans to start a family and to settle there. Unfortunately due to the poor economy in USA he lost his job and had to return back to India. He felt distressed as he realized that he had lost everything he had worked so hard to build. This made him feel like a failure.

1. How do you think Anurag can apply the 7 C’s of resilience to overcome the difficult situation he is in?
2. As Anurag’s friend how will you empathise with him and help him deal with this challenge?
3. Anurag has developed a very pessimistic approach after these setbacks, how will you guide him to stay happy and optimistic?

Answer:
According to the American Psychological Association, resilience is the process of adapting well in the face of adversity, trauma, tragedy, threats or significant sources of stress such as family, health, etc. It is the act of ‘bouncing back’ inspite of barriers or set backs. Resilience helps the person to recover form setbacks. Individuals who are resilient tend to-
(i) regain their confidence after a period of emotional disturbance
(ii) maintain their psychological well-being.

Anurag can apply the 7 C’s of resilience as follows-
1. He has already worked in a reputed firm successfully. Hence he has the Competence and Confidence in his own abilities. Although he is feeling a sense of hopelessness and failure, he must live in the ‘Here and Now’ by taking stock of the situation. Character will provide Anurag self worth and provide a sense of purpose and motivation, i.e., Contribution. When he realizes that he can still succeed in life by applying for a similar job here and accepting the situation, i.e., Control he can use effective Coping mechanisms. Besides, he should not forget social support of family and friends, i.e., Connection.

2. As Anurag’s friend, I can understand and feel what he is going through, from his frame of reference. Since, he is feeling distressed and like a failure due to loss of job, I will empathize with him by being encouraging and supportive. I will try to make him understand that with his own competence and experience, he can easily find a well paying job in India. I will also encourage him to improve his professional skills and seek social support from family and friends.

3. It seems natural for a person who was in a good job, stable relationship and successful position to feel pessimistic and like a failure when all of these no longer exist in his life. I will help Anurag to have a positive approach towards the challenges and difficulties in his life, i.e., view all setbacks i.e. loss of job, being sent back from the USA, etc., as opportunities not as obstacles. This will help him to gain a better perspective.

Class 12 Psychology Chapter 8 Positive Psychology Intext Questions and Answers

ACTIVITY (Textbook Page. No. 99)

Activity 4

(a) Meera scored poor marks in the examination.
(b) Suresh’s scholarship application got rejected.
(c) Mahesh lost his job.
Imagine yourself in their position and answer the following questions-
(i) How does being in their situation make you feel?
(ii) What do you think about yourself and your future being in their position?
Answer:
(i) You may feel

• Hopeless and so you might think that your future is dark.
• Helpless and so you might think that you cannot do anything to get out of the situation.
• Worthless and so you might think that you are a failure.

(ii) In contrast you may also feel

• Hopeful and think that the current adverse situation can change in the future.
• Challenged and think that you have the ability to overcome the adversity.
• Confident and think that one failure does not define you

Activity 5 (Textbook Page. No. 100)

What would your feeling be in the following situations?
(i) After a long struggle your friend got a job.
(ii) You see a person who just met with an accident and is bleeding profusely.
(iii) Your cousin is awarded a PhD. degree.
Answer:
In all the above examples I would feel empathy i.e., feel what these persons are experiencing.
(i) I will also feel happy and hopeful.
(ii) I will also feel concerned and helpless,
(iii) I will feel elated and proud.

Activity 8 (Textbook Page. No. 104)

Think of someone you know who has faced a challenging situation in their life and were successfully able to deal with it. This situation may have been emotionally difficult to deal with like death of a loved one, loss of a job, dealing with chronic illness, failure etc. Answer the following questions and discuss the answers in class.

1. How did they handle the adverse situation?
2. Which obstacles did they have to overcome?
3. In your opinion which specific attitudes and skills helped them cope with the situation?
4. Do you think they received help and support from others?

Answer:
Sundari, a professor in a reputed college was diagnosed with cancer at age 35 years.

1. Initially, she was overcome by feelings of intense fear and hopelessness. However, she decided that she would not give up the fight against cancer.
2. She had to overcome obstacles such as intense pain, fear of chemotherapy, pity shown by some ‘well wishers’, financial constraints, etc.
3. Specific attitudes that helped her to cope with this trauma were Resilience, fighting spirit interacting with other cancer survivors and good coping skills.
4. Yes, she received immense support from family, colleagues, friends and support groups like CPAA and Cancer Aid Foundation.

Activity 9 (Textbook Page. No. 105)

Read about the life of Indian boxer Mary Kom. Discuss in class the struggles she faced and how she overcame them to win multiple medals for the country.
Answer:
Mary Kom was born in Kangathei in the north-east state of Manipur. She grew up in a humble surroundings in an agricultural family. She is the eldest of three siblings. Her father had been a keen wrestler. Since a young age, Mary exhibited an inclination towards sports, like athletics and football. She was inspired by Dingko Singh, (a fellow Manipur who won a gold medal in 1998 Asian games ) to take up boxing. She was unable to pass her matriculation exam but still cleared X Std., from NIOS, Imphal. When she was 15, she left home to study at the Sports Academy in Imphal.

Her first coach K. K. Meitei recalls her as being hard working, dedicated, a quick learner with a strong will power. She has won many accolades such as 6 World Championships, Bronze medal at London Olympics (2012), 1 gold medal each at Asian Games (2014) and at Commonwealth Games (2018). She has been awarded the Padma Shri, Padma Bhushan and Padam Vibushan.

Her life story exhibits how Mary overcome obstacles of poverty, family opposition, gender bias to become the undisputed Queen of Boxing. Even at age 37, she still has the hunger to compete and win medals for India. Mary showed resilience as she has returned to the very demanding sport of boxing, after the birth of each child and has exceeded all expectations.

Activities 1, 2, 3, and 6
Answer:
[These are personal response questions.]

Balbharti Maharashtra State Board Class 12 Psychology Solutions Chapter 7 First Aid in Mental Health Textbook Exercise Questions and Answers.

Maharashtra State Board Class 12 Psychology Solutions Chapter 7 First Aid in Mental Health

1. Choose the correct option and complete the following statements.

Question 1.
One of the major obstacles to getting help from a mental health professional is the ………………… attached to mental illness.
(a) policy
(b) stigma
(c) society
Answer:
(b) stigma

Question 2.
Friends and family are not a substitute for …………………..
(a) solving problems
(b) giving solutions
(c) professional help
Answer:
(c) professional help

Question 3.
In our culture the ………………….. of an individual is considered to be the reflection of one’s family.
(a) intelligence
(b) behaviour
(c) status
Answer:
(b) behaviour

Question 4.
Individuals who experience ………………… commonly have a negative thinking style.
(a) depression
(b) phobia
(c) acute stress
Answer:
(a) depression

2. Answer the following questions in 35 – 40 words each.

Question 1.
Describe the term Mental Health First Aid?
Answer:
Mental Health First Aid (MHFA) is an internationally recognized training programme designed to teach people how to identify the signs and symptoms of mental health problems and to provide assistance on a first aid basis. MHFA was originally developed by Betty Kitchener and Anthony Jorm.

First Aid in Mental Health is a concept based on the idea of ‘prevention is better than cure’. If the early signs of mental illness are recognized, it can help in the following ways.

1. Diagnosis – timely diagnosis at the onset of mental illness helps to prevent it from developing into a more severe form.
2. Intervention – early intervention helps to get professional help.
3. Relapse prevention – it prevent reoccurrence of symptom of the mental illness.

Question 2.
What are the stigmas attached to mental illness?
Answer:
One of the major obstacles to getting help from a mental health professional is the stigma that is attached to mental illness. We fear things that we do not understand. In the same way, our lack of understanding of mental illness makes us fear it.
This lack of knowledge and awareness makes us-

1. Blame the individual, i.e., think that mental illness is a personal failing or weakness.
2. Think that mental illness is caused as punishment for our sins.
3. Think that the person is intentionally behaving in an inappropriate way.

Question 3.
Anxiety disrupts day to day functioning of an individual : State two predispositional factors contributing to anxiety.
Answer:
Anxiety that is excessive or persists after the anxiety creating situation has subsided leads to anxiety disorders such as phobias, acute stress disorder, etc.
Predispositional factors in anxiety are-

1. Genetic factors – if anyone in the family has anxiety issues, then the person will be at a higher risk of exhibiting high levels of anxiety as compared to other persons.
2. Childhood trauma such as physical or mental neglect or abuse, death of a loved one, parental divorce, etc.

Question 4.
Your friend confided in you that he is suffering from anxiety.
Suggest two self- help strategies to help him deal with this issue.
Answer:
The self help strategies that can be suggested to help him deal with excessive anxiety are-

1. Engage in some activity that he always wanted to pursue for e.g., pottery, writing, sketching or voluntary social service.
2. Indulge in physical activity like exercise, outdoor games or trekking.
3. Relaxation techniques like laughter therapy, meditation and breathing techniques.

3. Answer the following in 80 – 100 words based on the given points.

Question 1.
Explain the reasons why First Aid in Mental Health is required.
(a) Stigma associated with mental health
(b) Shame
(c) People do not always know how to respond
(d) People may not always seek professional help
Answer:
MHFA is an internationally recognized training programme whose objective is to teach people how to identify the signs and symptoms of mental health problems and to provide assistance on a first aid basis.
(a) Stigma associated with mental health:
Lack of understanding about mental illness makes us fear it. This lack of awareness leads us to blame the person for behaving inappropriately or showing personal failing.

(b) Shame:
Often, a person who has been diagnosed with a mental illness is ridiculed or blamed. He/she experiences shame, withdraws from social interaction and does not reach out to others or seek help. Hence, it is beneficial to show understanding and provide support.

(c) People do not always know how to respond:
Most people may not respond in an adequate way to a mentally ill person who reaches out to them. Sometimes, their advice/help may do more harm than good. However, MHFA programme can help friends/family to identify early signs of mental illness and help the person to get professional help.

(d) People may not always seek professional help:
The main reasons for this is-

1. Culture – Stigma attached to mental illness prevents people from seeking professional help as it may hurt the reputation of the family.
2. Advice from elders – A mentally ill person may incorrectly believe that advice of elders alone is sufficient to cure his illness.
3. Superstitions – If the person is convinced that his//her mental illness is caused due to sins/curses etc., they will not want to visit a mental health professional. Hence, they will be deprived of the benefits of early intervention.

Question 2.
Explain the ALGEE Model in your own words.
(a) Approach, Assess and Assist in any crisis
(b) Listen non-judgmentally
(c) Give support and information
(d) Encourage the person to get professional help
(e) Encourage self-help and other support strategies
Answer:
ALGEE is an action plan to carry out First Aid in Mental Health.
(a) Approach, Assess and Assist in any crisis – An attempt is made to understand the situation and observe if there are behavioural changes in the person whom we are concerned about.

(b) Listen non-judgmentally – We should listen to the other person without letting our opinions influence us. We should not judge/ criticise but listen with acceptance and empathy. It does not imply that we agree with what the other person is saying but it ensures that the person feels supported.

(c) Give support and information – This helps the person to feel more in control of the situation since they have emotional and informational support.

(d) Encourage the person to get professional help – Persons suffering from mental illness may hesitate to seek help due to lack of knowledge or due to stigma attached. Others may not know how to respond to someone showing ‘red flags’ of mental illness and may do more harm than good. Mental health professionals are trained to help the person to identify the problem and cope with the situation.

(e) Encourage self-help and other support strategies – Self-help strategies are tasks that help to increase our resources to deal with stress and to maintain mental health such as exercise, adequate sleep, having hobbies, etc.

Question 3.
Enumerate the various symptoms that are exhibited by an individual with anxiety disorders.
(a) Physical Symptoms
(b) Psychological Symptoms
(c) Behavioural Symptoms
Answer:
Anxiety is an emotion characterised by feelings of tension, hopelessness, etc. Excessive level of anxiety which persists even after the anxiety producing situation has gone away, can lead to anxiety disorders.
(a) Physical Symptoms

1. Heart palpitations and rapid heart rate
2. Shortness of breath
3. Dizziness or headaches
4. Restlessness, tremors and shaking

(b) Psychological Symptoms

1. Mind racing or going blank
2. Difficulty in concentration
3. Forgetfulness
4. Problems in decision making
5. Irritability, impatience and anger

(c) Behavioural Symptoms

1. Avoiding people and situations
2. Repetitive checking
3. Strong urge to escape the situation

Question 4.
Explain excessive dependence on the internet.
(a) Meaning
(b) Four C’s to identify excessive internet usage
(c) Red flags that indicate internet addiction.
Answer:
(a) Meaning
The amount of time as well as reason for using the internet may become a matter of concern for e.g., online gambling, gaming, etc. The person may socialise more online with friends than real life socialising. Spending excess time online may cause the person to neglect family, relationships, work etc. Virtual world enables games/gambling almost continuously. This leads to the person neglecting personal hygiene, real life relationships and become withdrawn and irresponsible. The person may feel guilty or defensive about internet use. He/ she may panic in the absence of internet service. A growing dependence on internet refers to an inability to stop and down down.

(b) Four C’s to identify excessive internet usage
Excessive internet usage is characterised by extensive, problematic addiction to the use of computer and internet. It signifies poorly controlled preoccupations or behaviour regarding such usage. Excessive internet usage leads to personal distress and social impairment.
The four C’s to identify excessive internet usage are as follows-

1. Craving – Do you have an intense desire to use the internet?
2. Control – Do you have an inability to control your self using the internet?
3. Compulsion – Do you find it difficult to stop using the internet? Even though you know you should not spend so much time on it?
4. Consequence – Have you ever experienced any physical or psychological ill effects as a result of excessive use of the internet? If you answer a ‘yes’ for at least three of the C’s, it can be a matter of concern.

(c) Red flags that indicate internet addiction
The Red Flags that indicate over dependence on internet are-

1. Feelings of euphoria while using the internet.
2. Physical symptoms like headache, dry eyes, etc.
3. Inability to keep to schedules and boredom with routine tasks.
4. Poor personal hygiene and nutrition to remain online.

4. Analysis the following case study.

Sujata is now a sad and lonely girl. She has cut off herself from all her relatives and family friends. She doesn’t participate in any college programmes nor family functions. She is mostly found in the library all by herself. She has lost her self-confidence. At home she prefers eating in the bedroom and mostly indulges in television or mobile activities. Apply the ALGEE model and help Sujata to evolve in her mental health.
Answer:
Sujata is showing symptoms of depression and anxiety such as sadness, withdrawing from family/ friends and social activities. The ALGEE model can be used.

1. Approach, assess and assist in any crisis – Behavioural changes are very noticeable in Sujata. I can voice my concern to the teachers/ counsellor of the school or to her family members.
2. Listen in a non-judgemental manner -1 will try to meet Sujata in the library or any place where she feels comfortable. I will explain my concerns to her about not interacting with others and overuse of mobile phones. I will listen patiently and compassionately.
3. Give support and information – Let Sujata know that she has emotional support of her friends. There is nothing to feel guilty or ashamed of. She should hence be forthcoming about her problems.
4. Encourage her to get professional help – I will encourage her to meet the college counsellor who will be able to help her professionally.
5. Encourage self-help strategies – This will help Sujata to regain control over her life. Some positive measures include breathing exercises, yoga, laughter therapy, etc.

Balbharti Maharashtra State Board Class 12 Psychology Solutions Chapter 6 Psychological Disorders Textbook Exercise Questions and Answers.

Maharashtra State Board Class 12 Psychology Solutions Chapter 6 Psychological Disorders

1. (A) Choose the correct option and complete the following statements.

Question 1.
………………… is the present system for the classification of mental disorders.
(a) DSM-5
(b) WHO
(c) APA
Answer:
(a) DSM-5

Question 2.
Term Schizophrenia was first used by ………………
(a) Albert Ellis
(b) Eugene Bleuler
(c) John Travis
Answer:
(b) Eugene Bleuler

Question 3.
World Health Organization has developed …………….. for classification of all types of disorders.
(a) ICD
(b) DSM
(c) MCA
Answer:
(a) ICD

Question 4.
We find alternate phases of depression and mania in …………………. disorders.
(a) depressive
(b) bipolar
(c) anxiety
Answer:
(b) bipolar

(B). Match the pairs.

Question 1.

Group A	Group B
(1) Phobia	(a) 2013
(2) DSM-5	(b) Wellness
(3) ICD – 11	(c) Schizophrenia
(4) Eugen Bleuler	(d) 2019
(5) John Travis	(e) Illogical fear
(6) Depressive disorders	(f) Sad feelings for a long period of time

Answer:

Group A	Group B
(1) Phobia	(e) Illogical fear
(2) DSM-5	(a) 2013
(3) ICD – 11	(d) 2019
(4) Eugen Bleuler	(c) Schizophrenia
(5) John Travis	(b) Wellness
(6) Depressive disorders	(f) Sad feelings for a long period of time

(C) State whether the following statements are true or false.

Question 1.
Socially or culturally deviant behaviours are signs of psychological disorders.
Answer:
False

Question 2.
Schizophrenia is a serious psychological disorder.
Answer:
True

Question 3.
Feeling of hopelessness is one of the symptoms seen in depressive disorders.
Answer:
True

(D) Answer the following in one sentence each.

Question 1.
From which Latin word is the term anxiety derived?
Answer:
The word ‘anxiety’ is derived from the Latin word ‘Anxietas’ which means ‘uneasy or troubled mind’.

Question 2.
In which disorder does the person experience sadness and guilt for a long period of time?
Answer:
In a depressive disorder the person experiences sadness and guilt for a long period of time.

Question 3.
What do you call the fear that you experience unnecessarily in a non threatening situation?
Answer:
The fear that is experienced unnecessarily in a non threatening situation is called a phobia.

2. Answer the following questions Briefly.

Question 1.
Explain the nature of psychological disorder.
Answer:
The major criteria of abnormality or psychological disorders are deviance, personal distress and impaired functioning. Illness and absence of illness are not distinct categories but are on opposite poles of the continuum sequence as explained below.

Stage 1 – The person is physically and psychologically healthy. They are motivated and emotionally stable.
Stage 2 – The person may get affected by life stressors, feel anxious, lack energy, etc. For e.g., before an examination. It is possible to push oneself back towards positive health by adopting a healthy lifestyle.
Stage 3 – The person shows signs of psychological damage and experience negative feelings like sadness, lack of motivation, fear and may even indulge in addictive behaviour. However, even this stage is not irreversible.
Stage 4 – The person exhibits extreme distress, impairment in mental, emotional and social functioning. He/She needs professional treatment.

Question 2.
What is meant by Anxiety disorders?
Answer:
The word ‘anxiety’ is derived from the Latin word ‘Anxietas’ which means ‘uneasy or troubled mind’. Anxiety refers to a condition in which the person feels worried and uneasy for a long time for no obvious reasons. Anxiety disorders include disorders in which anxiety is the main symptom or is experienced when an attempt is made to modify some maladjustment. The main anxiety disorder are Generalised Anxiety disorder, Phobic disorder. Panic disorder, O. C. D, etc.

Question 3.
Narrate indicators of psychological disorders.
Answer:
According to DSM-5, there are five criteria (indicators) for psychological disorders.

1. Clinically significant syndrome – In psychological disorders, there should be a cluster of symptoms together i.e., a syndrome.
2. Distress and Impairment – There should be distress, i.e., psychological pain due to negative feelings and stress, as well as impairment, i.e., inability to perform appropriate roles in personal and social situations.
3. Dysfunction – If the symptoms lead to developmental or psychological dysfunctions, it signifies mental disorders.
4. Responses to stressors that are normally accepted responses e.g., sadness experienced at the loss of a loved one or culturally sanctioned responses are not considered as signs of mental disorders.
5. Behaviour which is only deviant but does not produce any disability/ distress/ dysfunction
   does not become a sign of mental disorder.

Question 4.
What is meant by bipolar disorder?
Answer:
Bipolar Disorder is also known as Manic Depressive disorder. The person experiences alternate phases of two states viz. mania and depression. Mania includes symptoms such as high energy, excitement, reduced need for sleep and loss of touch with reality, impulsivity, delusion, etc. Depressive state symptoms include low energy and motivation, loss of interest in daily activities, extreme sadness, apathy, feeling of hopelessness, fatigue, guilt, etc. Main causative factors are genetic factors, imbalance in neurotransmitters such as dopamine and epinephrine; environmental factors such as traumatic event.

Question 5.
Describe Post Traumatic Stress Disorders?
Answer:
If the symptoms of Acute Stress Disorder (ASD) continue for more than one month with the same intensity, the person is diagnosed with PTSD. A person who has suffered trauma goes through three stages viz-

1. Shock stage – the individual is in shock, i.e., extremely disturbed.
2. Suggestible stage – he/she may seek guidance from others and may either accept these suggestions unquestioningly or may get extra sensitive.
3. Recovery stage – the person shows signs of recovery.

However, some persons still show signs of mental illness i.e., PTSD.
The symptoms of PTSD include

1. nightmares, flashbacks, severe anxiety
2. hyper vigilance and avoidance of situations that bring back the trauma
3. irritability, social isolation
4. survivour’s guilt

3. Explain the Following concepts.

Question 1.
DSM-5
Answer:
Presently, the two major systems of classifying psychological disorders are DSM and ICD. Diagnostic and Statistical Manual for Mental Disorders (DSM) was published in its first version by the APA in 1952, i.e., DSM-I. In 2013, the DSM-5 was introduced which contains 22 broad categories of mental disorders with subcategories. It is the classification of officially recognized psychiatric disorders, for e.g., categories in DSM-5 include anxiety disorders, obsessive-compulsive and related disorders and personality disorders.

Question 2.
ICD 11
Answer:
Presently, the two major systems of classifying psychological disorders are DSM and ICD. The International Classification of Diseases and Related Health Problems (ICD) was created by the WHO for documenting all types of diagnoses, diseases, signs and symptoms and social circumstances. It contains a section on psychological disorders. The latest, 11th version of ICD was presented in 2019. According to the ICD-11, there are 19 broad categories of mental disorders, most of which overlap with DSM-5.

Question 3.
Phobia
Answer:
The main anxiety disorders include phobic disorders and generalized anxiety disorders. The word ‘phobia’ is derived from the Greek word ‘phobos’ which was used to refer to the God of Fear. A phobia is an intense, persistent but irrational and disproportionate fear of a specific object or situation. DSM classifies phobias as simple phobias, e.g., Acrophobia, Claustrophobia etc., and social phobias, e.g., fear of speaking or eating in public. The phobic object e.g., animals or situations e.g., elevators, almost always provide immediate anxiety.

Question 4.
Syndrome
Answer:
A syndrome refers to a cluster or collection of symptoms and signs that are characteristic of a diseases or disorder, e.g., Down’s syndrome. It is a group of symptoms which consistently occur together and indicate a particular condition. A syndrome refers to a set of symptoms that tend to occur together and can be associated with a particular physical or mental disorder. In psychological disorders, one of the criteria as suggested by DSM-5 is clinically significant syndrome.

Question 5.
Hallucination
Answer:
Hallucinations are false perceptions in the absence of appropriate stimuli. Hallucinations are a symptom of schizophrenia and other mental disorders. Commonly occurring hallucinations are visual, auditory, tactile, gustatory and olfactory in nature. For e.g., the person may hear voices telling him to do something. Hallucinations are also noticed due to substance abuse, medications, epilepsy, etc.

4. Write short notes on the following.

Question 1.
Nature of mental wellness
Answer:
According to the WHO, mental wellness refers to “a state of well-being in which the individual realizes his or her own abilities, can cope up with the normal stresses of life, can work productively and fruitfully, and is able to make a contribution to his or her community.”
The important aspects of mental wellness are –

1. Emotional aspect – There is a sense of well-being and contentment
2. Psychological aspect – There is high self esteem and tendency of self actualization.
3. Life philosophy – There are clear goals and objectives in life.

The Illness Wellness Continuum Model by John Travis

Quadrant 1 – The person is in an ideal state of functioning.
Quadrant 2 – Thepersonhasnomentalillnessbutexperiencessubjectivefeelingofunhappiness.
Quadrant 3 – The person suffers from mental illness yet he/she experiences a high sense of subjective well-being.
Quadrant 4 – This is the lowest level of functioning. The person has mental illness and also experiences distress.

Question 2.
Drug addiction
Answer:
Addictive disorders refer to the physical and psychological inability to stop consuming some substance or indulging in some activity although it is harmful. This includes dependence on drugs, nicotine, alcohol, etc., or activities like gambling, eating, gaming etc. Drug addiction refers to an inability to control the use of alcohol, nicotine, narcotics, marijuana, medications, etc.
Symptoms of addiction are-

1. Excessive consumption of drugs or alcohol and inability to reduce the dosage.
2. In case the person tries to stop the drug use, then withdrawal symptoms occur which include sweating, tremors, muscle pain, goosebumps, etc.
3. Physical and psychological dependence may lead to drug abuse or overdose of the addictive substance and even death of the person.
4. The person’s physical, emotional, social and financial well-being break down.

Alcoholics Anonymous (AA), Narcotics Anonymous (NA) are organizations that help addicts to overcome dependence.

Question 3.
Depressive disorders
Answer:
Depression is an emotional state typically marked by sadness and guilt, feelings of anxiety and hopelessness. Other symptoms include loss of appetite, interest and sleep, fatigue, sexual dysfunction and suicidal thoughts. Depression is associated with distractability, memory loss, neglect of personal hygiene, panic attacks and even substance abuse. Children may experience symptoms such as irritability, feelings of incompetence, difficulty in concentration, difficulty in sleeping, digestive problems etc.

Question 4.
Anxiety disorders
Answer:
The word ‘anxiety’ is derived from the Latin word ‘Anxietas’ which means ‘uneasy or troubled mind’. Anxiety refers to a condition in which the person feels worried and uneasy for a long time for no obvious reasons. The main anxiety disorders are.
(i) Generalized Anxiety Disorder – The person frequently experiences anxiety more intensely so that it starts interfering with the ability to perform daily tasks. Symptoms include irritability, headaches, insomnia, dizziness, breathlessness, etc.

(ii) Phobic disorders – The word ‘phobia’ is derived form the Greek word ‘phobos’ which was used to refer to the God of Fear. A phobia is an intense, persistent but irrational and disproportionate fear of a specific object or situation. DSM classifies phobias as simple phobias, e.g., Acrophobia, Claustrophobia etc., and social phobias, e.g., fear of speaking or eating in public.

5. Answer the following questions in 150 – 200 words.

Question 1.
Describe the criteria of psychological disorders.
Answer:
The major criteria of abnormality are deviance, personal distress and impaired functioning. Illness and absence of illness are not distinct categories but are on opposite poles of the continuum sequence as explained below.

Stage – 1: The person is physically and psychologically healthy. He/She are motivated and emotionally stable.
Stage – 2: The person may get affected by life stressors, feel anxious, lack energy, etc., for e.g., most students are tense before the exams. It is possible to push oneself back towards positive health by adopting a healthy lifestyle.
Stage – 3: The person shows signs of psychological damage and may experience negative feelings like sadness, lack of motivation, fear and may even indulge in addictive behaviour. However, even this stage is not irreversible.
Stage – 4: The person exhibits extreme distress, impairment in mental, emotional and social functioning. He/She needs professional treatment.

Psychological disorders are also called mental disorders. These are patterns of behavioural or psychological symptoms that impact multiple areas of life and create distress for the person.

According to DSM-5, there are five criteria for psychological disorders.

1. Clinically significant syndrome – In psychological disorders, there should be a cluster of symptoms together i.e., a syndrome.
2. Distress and Impairment – There should be distress, i.e., psychological pain due to negative feelings and stress, as well as impairment, i.e., inability to perform appropriate roles in personal and social situations.
3. Dysfunction – If the symptoms lead to developmental or psychological dysfunctions, it signifies mental disorders.
4. Responses to stressors that are normally accepted responses e.g., sadness experienced at the loss of a loved one or culturally sanctioned responses are not considered as signs of mental disorders.
5. Behaviour which is only deviant but does not produce any disability/ distress/ dysfunction does not become a sign of mental disorder.

Question 2.
Narrate any two psychological disorders in detail.
Answer:
Psychological disorders are also called mental disorders. These are patterns of behavioural or psychological symptoms that impact multiple areas of life and create distress for the person.
According to DSM-5, there are five criteria for psychological disorders are:

1. Clinically significant syndrome – In psychological disorders, there should be a cluster of symptoms together i.e., a syndrome.
2. Distress and Impairment – There should be distress, i.e., psychological pain due to negative feelings and stress, as well as impairment, i.e., inability to perform appropriate roles in personal and social situations.
3. Dysfunction – If the symptoms lead to developmental or psychological dysfunctions, it signifies mental disorders.
4. Responses to stressors that are normally accepted responses e.g., sadness experienced at the loss of a loved one or culturally sanctioned responses are not considered as signs of mental disorders.
5. Behaviour which is only deviant but does not produce any disability/ distress/ dysfunction does not become a sign of mental disorder.

(A) Anxiety Disorders – The word ‘anxiety’ is derived from the Latin word ‘Anxietas’ which means ‘uneasy or troubled mind’. Anxiety refers to a condition in which the person feels worried and uneasy for a long time for no obvious reasons.
The main anxiety disorders are-
(i) Generalized Anxiety Disorder – The person frequently experiences anxiety more intensely so that it starts interfering with the ability to perform daily tasks. Symptoms include irritability, headaches, insomnia, dizziness, breathlessness, etc.

(ii) Phobic disorders – The word ‘photjia’ is derived form the Greek word ‘phobos’ which was used to refer to the God of Fear. A phobia is an intense, persistent but irrational and disproportionate fear of a specific object or situation. DSM classifies phobias as simple phobias, e.g., Acrophobia, Claustrophobia etc., and social phobias, e.g., fear of speaking or eating in public.

(B) Trauma Trauma and Stress-Related Disorders
Stress is inevitable in life. Daily hassles, relationship issue, frustration, chronic illness, etc., lead to stress. If stress is in moderate intensity, it acts as a motivation. However, intense prolonged stress impairs normal functioning of the individual and may lead to stress disorders.
The two types of stress disorders are-
1. Acute Stress Disorder (ASD)
If a person (aged 6 years and above) has experienced extremely stressful situations like death of a loved one, serious disease or injury, sexual abuse, natural disasters, etc., then he/she may experience ASD. The symptoms of ASD include-

• emotional numbness and instability
• nightmares and sleep disturbances
• insomnia, lack of concentration, irritability and guilt feelings
• depression

2. Post Traumatic Stress Disorder (PTSD)
If symptoms of ASD continue for more than one month with the same intensity, the person is diagnosed with PTSD. A person who has suffered trauma goes through three stages viz.

• Shock stage – the individual is in shock, i.e., extremely disturbed.
• Suggestible stage – he/she may seek guidance from others and may either accept these suggestions unquestioningly or may get extra sensitive.
• Recovery stage – the person shows signs of recovery.

However, some persons still show signs of mental illness i.e., PTSD.

Question 3.
What is Schizophrenia? Describe the major symptoms of it.
Answer:
The term ‘Schizophrenia’ is derived from Greek words Schizein (to split) and phren (mind). Thus, the literal meaning of the word ‘schizophrenia’ is split mind. The term ‘schizophrenia’ was coined in 1911 by a Swiss psychologist, Paul Eugene Bleuler. Schizophrenia is a psychotic disorder.
According to DSM-5 the two types of symptoms for schizophrenia are-
(a) Positive symptoms are an excess addition to normal thoughts or behaviour of the period. Such symptoms are-

1. hallucinations – mainly auditory and visual hallucination
2. delusions – mainly of grandeur, reference and persecution
3. disorganized thought and speech
4. bizarre body movements and disorganized behaviour
5. incongruent affect.

(b) Negative symptoms are deficits of normal emotional responses or of thought processes. They lead to low level of functioning and may not improve much even with treatment. This includes-

1. emotional blunting – diminished emotional expression
2. anhedonia – inability to experience deep positive emotions
3. alogia – diminished speed
4. asociality – lack of desire to form relationships
5. avolition – lack of motivation
6. apathy.

Sometimes, a schizophrenic exhibits positive as well as negative symptoms.

Class 12 Psychology Chapter 6 Psychological Disorders Intext Questions and Answers

ACTIVITIES (Textbook Page. No. 62)

Activity 1

On the basis of your understanding of various criteria for abnormality, which of these would you consider as normal or abnormal behavior?

1. Hemant wears the same lucky blue shirt for all his major competitive exams.
2. Seema is not able to fall asleep easily.
3. Rakesh throws pillows and pounding fists on the wall during arguments if he finds himself losing ground.
4. Reena always experiences fear but is not able to specify what is so scary.

Answer:
All the stated examples show at least one of the five criteria for abnormality.

1. Hemant seems superstitious and lacks confidence. He appears moderately healthy.
2. Seema exhibits personal distress and signs of sleep disorders.
3. Rakesh exhibits clear symptoms of abnormal behaviour and seems extremely unhealthy mentally.
4. Reena seems to have anxiety disorder and may need professional help.

Activity 3 (Textbook Page. No. 67)

In which Quadrants of wellness illness continuum will you place Karan, Lalita, Pramila and Santosh?
Answer:
Karan – Quadrant 2, Pramila – Quadrant 3, Lalita – Quadrant 4, Santosh – Quadrant 3.

Activity 5 (Textbook Page. No. 68)

Collect information about Anxiety disorders and discuss this with your friends or parents.
Answer:
Anxiety disorders are characterised by feelings of worry and restlessness that tend to interfere with daily activities. Besides generalized anxiety disorder and phobia which are explained in the chapter, anxiety disorders includes Panic disorder, Obsessive-Compulsive disorder (OCD) and Social Anxiety disorders include disorders in which anxiety is the main symptom or is experienced. When an attempt is made to modify maladjustment.

Activity 6 (Textbook Page. No. 69)

Collect information about other types of phobia.
Answer:
A phobia is a persistent, irrational fear of a situation or object. Phobias are of three types viz. Social phobia (fear of social situations); specific phobias (fear of particular situations) and agoraphobia (fear of being alone in public places from which there is no easy escape). Some phobias are:

1. Claustrophobia (fear of enclose spaces)
2. Acrophobia (fear of heights)
3. Homophobia (fear of blood)
4. Zoophobia (fear of animals)
5. Arachnophobia (fear of spiders)
6. Pyrophobia (fear of fire)
7. Trypanophobia (fear of needles and injections)
8. Xenophobia (fear of foreigners or strangers)

Activity 7 (Textbook Page. No. 71)

We make use of various strategies to reduce our stress. Speak to five of your friends and make a list of atleast ten different strategies used by them to reduce stress. Share it with your group and discuss which are healthy and which are unhealthy.
Answer:
Some strategies to reduce stress are-

1. Negative coping such as use of alcohol/drugs, over eating, agression, etc.
2. Exercise
3. Developing a hobby
4. Indulging in some constructive activity
5. Following relaxation/meditation techniques
6. Seeking social support, i.e., of friends/ family, etc.
7. Having proper time management
8. Developing rational thinking and positive attitude
9. Indulging in self care, e.g., proper diet, rest, etc.
10. Seeking professional help if needed

Activity 9 (Textbook Page. No. 74)

Identify from the internet the red flags (signaling symptoms) for various disorders that you have already studied.
Answer:
Red flags for the following disorders.
(1) Phobias

• Displaying extreme nervousness or distress when in the presence of the source of the phobia
• Avoidance behaviour
• Refusal to face certain situations

(2) Depression

• Irritability, moodiness and agitation.
• Inability to concentrate
• Unexplained aches and pains
• Disruptions in sleep habits
• Changes in appetite and eating habits
• Suicidal thoughts.

(3) Bipolar disorder

• Change in thought processes, and concentration
• Change in sleep patterns
• Change is social interaction
• Uncharacteristic moodiness

(4) PTSD

• Persistent negative thoughts
• Trouble in concentration
• Irritability and aggression
• Engaging in reckless behaviour
• Changes in sleep and appetite
• Loss of interest in friends/family/favourite activities.