Balbharti 12th Maharashtra State Board Maths Solutions Book Pdf Chapter 6 Differential Equations Ex 6.6 Questions and Answers.
Maharashtra State Board 12th Maths Solutions Chapter 6 Differential Equations Ex 6.6
Question 1.
In a certain culture of bacteria, the rate of increase is proportional to the number present. If it is found that the number doubles in 4 hours, find the number of times the bacteria are increased in 12 hours.
Solution:
Let x be the number of bacteria in the culture at time t.
Then the rate of increase is \(\frac{d x}{d t}\) which is proportional to x.
∴ \(\frac{d x}{d t}\) ∝ x
∴ \(\frac{d x}{d t}\) = kx, where k is a constant
∴ \(\frac{d x}{x}\) = k dt
On integrating, we get
\(\int \frac{d x}{x}\) = k∫dt + c
∴ log x = kt + c
Initially, i.e. when t = 0, let x = x0
log x0 = k × 0 + c
∴ c = log x0
∴ log x = kt + log x0
∴ log x – log x0 = kt
∴ log(\(\frac{x}{x_{0}}\)) = kt ………(1)
Since the number doubles in 4 hours, i.e. when t = 4, x = 2x0
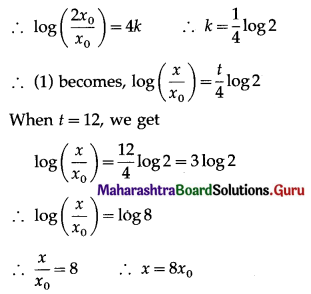
∴ the number of bacteria will be 8 times the original number in 12 hours.
![]()
Question 2.
If the population of a country doubles in 60 years; in how many years will it be triple (treble) under the assumption that the rate of increase is proportional to the number of inhabitants?
[Given log 2 = 0.6912, log 3 = 1.0986]
Solution:
Let P be the population at time t years.
Then \(\frac{d P}{d t}\), the rate of increase of population is proportional to P.
∴ \(\frac{d P}{d t}\) ∝ P
∴ \(\frac{d P}{d t}\) = kP, where k is a constant
∴ \(\frac{d P}{P}\) = k dt
On integrating, we get
\(\int \frac{d P}{P}\) = k∫dt + c
∴ log P = kt + c
Initially i.e. when t = 0, let P = P0
∴ log P0 = k x 0 + c
∴ c = log P0
∴ log P = kt + log P0
∴ log P – log P0 = kt
∴ log(\(\frac{P}{P_{0}}\)) = kt ……(1)
Since, the population doubles in 60 years, i.e. when t = 60, P = 2P0
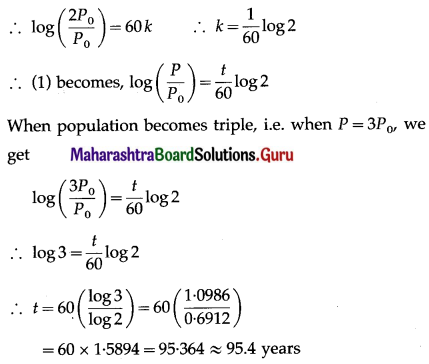
∴ the population becomes triple in 95.4 years (approximately).
Question 3.
If a body cools from 80°C to 50°C at room temperature of 25°C in 30 minutes, find the temperature of the body after 1 hour.
Solution:
Let θ°C be the temperature of the body at time t minutes.
The room temperature is given to be 25°C.
Then by Newton’s law of cooling, \(\frac{d \theta}{d t}\), the rate of change of temperature, is proportional to (θ – 25).


∴ the temperature of the body will be 36.36°C after 1 hour.
![]()
Question 4.
The rate of growth of bacteria is proportional to the number present. If initially, there were 1000 bacteria and the number doubles in 1 hour, find the number of bacteria after 2½ hours. [Take √2 = 1.414]
Solution:
Let x be the number of bacteria at time t.
Then the rate of increase is \(\frac{d x}{d t}\) which is proportional to x.
∴ \(\frac{d x}{d t}\) ∝ x
∴ \(\frac{d x}{d t}\) = kx, where k is a constant
∴ \(\frac{d x}{x}\) = k dt
On integrating, we get
\(\int \frac{d x}{x}\) = k∫dt + c
∴ log x = kt + c
Initially, i.e. when t = 0, x = 1000
∴ log 1000 = k × 0 + c
∴ c = log 1000
∴ log x = kt + log 1000
∴ log x – log 1000 = kt
∴ log(\(\frac{x}{1000}\)) = kt ……(1)
Now, when t = 1, x = 2 × 1000 = 2000
∴ log(\(\frac{2000}{1000}\)) = k
∴ k = log 2
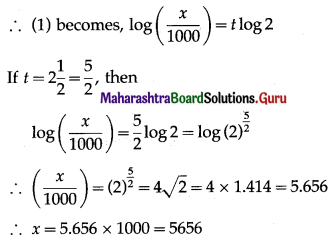
∴ the number of bacteria after 2½ hours = 5656.
Question 5.
The rate of disintegration of a radioactive element at any time t is proportional to its mass at that time. Find the time during which the original mass of 1.5 gm will disintegrate into its mass of 0.5 gm.
Solution:
Let m be the mass of the radioactive element at time t.
Then the rate of disintegration is \(\frac{d m}{d t}\) which is proportional to m.

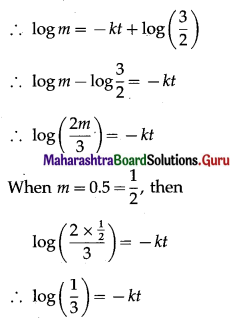
∴ log(3)-1 = -kt
∴ -log 3 = -kt
∴ t = \(\frac{1}{k}\) log 3
∴ the original mass will disintegrate to 0.5 gm when t = \(\frac{1}{k}\) log 3
![]()
Question 6.
The rate of decay of certain substances is directly proportional to the amount present at that instant. Initially, there is 25 gm of certain substance and two hours later it is found that 9 gm are left. Find the amount left after one more hour.
Solution:
Let x gm be the amount of the substance left at time t.
Then the rate of decay is \(\frac{d x}{d t}\), which is proportional to x.


∴ \(\frac{x}{25}=\frac{27}{125}\)
∴ x = \(\frac{27}{5}\)
∴ the amount left after 3 hours \(\frac{27}{5}\) gm.
Question 7.
Find the population of a city at any time t, given that the rate of increase of population is proportional to the population at that instant and that in a period of 40 years, the population increased from 30,000 to 40,000.
Solution:
Let P be the population of the city at time t.
Then \(\frac{d P}{d t}\), the rate of increase of population is proportional to P.
∴ \(\frac{d P}{d t}\) ∝ P
∴ \(\frac{d P}{d t}\) = kP, where k is a constant.
∴ \(\frac{d P}{P}\) = k dt
On integrating, we get
\(\int \frac{1}{P} d P\) = k∫dt + c
∴ log P = kt + c
Initially, i.e. when t = 0, P = 30000
∴ log 30000 = k × 0 + c
∴ c = log 30000
∴ log P = kt + log 30000
∴ log P – log 30000 = kt
∴ log(\(\frac{P}{30000}\)) = kt …….(1)
Now, when t = 40, P = 40000
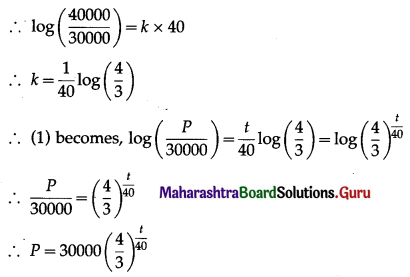
∴ the population of the city at time t = 30000\(\left(\frac{4}{3}\right)^{\frac{t}{40}}\).
![]()
Question 8.
A body cools according to Newton’s law from 100°C to 60°C in 20 minutes. The temperature of the surroundings is 20°C. How long will it take to cool down to 30°C?
Solution:
Let θ°C be the temperature of the body at time t.
The temperature of the surrounding is given to be 20°C.
According to Newton’s law of cooling


∴ the body will cool down to 30°C in 60 minutes, i.e. in 1 hour.
Question 9.
A right circular cone has a height of 9 cm and a radius of the base of 5 cm. It is inverted and water is poured into it. If at any instant the water level rises at the rate of \(\left(\frac{\pi}{A}\right)\) cm/sec, where A is the area of the water surface
at that instant, show that the vessel will be full in 75 seconds.
Solution:
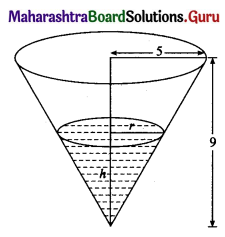
Let r be the radius of the water surface and h be the height of the water at time t.
∴ area of the water surface A = πr2 sq cm.
Since height of the right circular cone is 9 cm and radius of the base is 5 cm.
\(\frac{r}{h}=\frac{5}{9}\)
∴ r = \(\frac{5}{9} h\)
∴ area of water surface, i.e. A = \(\pi\left(\frac{5}{9} h\right)^{2}\)
∴ A = \(\frac{25 \pi h^{2}}{81}\) ……..(1)
The water level, i.e. the rate of change of h is \(\frac{d h}{d t}\) rises at the rate of \(\left(\frac{\pi}{A}\right)\) cm/sec.

∴ t = \(\frac{81 \times 9 \times 25}{3 \times 81}\) = 75
Hence, the vessel will be full in 75 seconds.
![]()
Question 10.
Assume that a spherical raindrop evaporates at a rate proportional to its surface area. If its radius originally is 3 mm and 1 hour later has been reduced to 2 mm, find an expression for the radius of the raindrop at any time t.
Solution:
Let r be the radius, V be the volume and S be the surface area of the spherical raindrop at time t.
Then V = \(\frac{4}{3}\)πr3 and S = 4πr2
The rate at which the raindrop evaporates is \(\frac{d V}{d t}\) which is proportional to the surface area.
∴ \(\frac{d V}{d t}\) ∝ S
∴ \(\frac{d V}{d t}\) = -kS, where k > 0 ………(1)
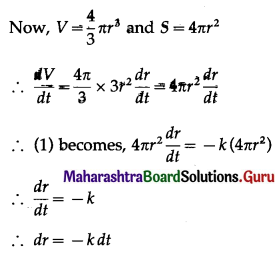
On integrating, we get
∫dr = -k∫dt + c
∴ r = -kt + c
Initially, i.e. when t = 0, r = 3
∴ 3 = -k × 0 + c
∴ c = 3
∴ r = -kt + 3
When t = 1, r = 2
∴ 2 = -k × 1 + 3
∴ k = 1
∴ r = -t + 3
∴ r = 3 – t, where 0 ≤ t ≤ 3.
This is the required expression for the radius of the raindrop at any time t.
Question 11.
The rate of growth of the population of a city at any time t is proportional to the size of the population. For a certain city, it is found that the constant of proportionality is 0.04. Find the population of the city after 25 years, if the initial population is 10,000. [Take e = 2.7182]
Solution:
Let P be the population of the city at time t.
Then the rate of growth of population is \(\frac{d P}{d t}\) which is proportional to P.
∴ \(\frac{d P}{d t}\) ∝ P
∴ \(\frac{d P}{d t}\) = kP, where k = 0.04
∴ \(\frac{d P}{d t}\) = (0.04)P
∴ \(\frac{1}{P}\) dP = (0.04)dt
On integrating, we get
\(\int \frac{1}{P} d P\) = (0.04) ∫dt + c
∴ log P = (0.04)t + c
Initially, i.e., when t = 0, P = 10000
∴ log 10000 = (0.04) × 0 + c
∴ c = log 10000
∴ log P = (0.04)t + log 10000
∴ log P – log 10000 = (0.04)t
∴ log(\(\frac{P}{10000}\)) = (0.04)t
When t = 25, then
∴ log(\(\frac{P}{10000}\)) = 0.04 × 25 = 1
∴ log(\(\frac{P}{10000}\)) = log e ……[∵ log e = 1]
∴ \(\frac{P}{10000}\) = e = 2.7182
∴ P = 2.7182 × 10000 = 27182
∴ the population of the city after 25 years will be 27,182.
![]()
Question 12.
Radium decomposes at a rate proportional to the amount present at any time. If p percent of the amount disappears in one year, what percent of the amount of radium will be left after 2 years?
Solution:
Let x be the amount of the radium at time t.
Then the rate of decomposition is \(\frac{d x}{d t}\) which is proportional to x.

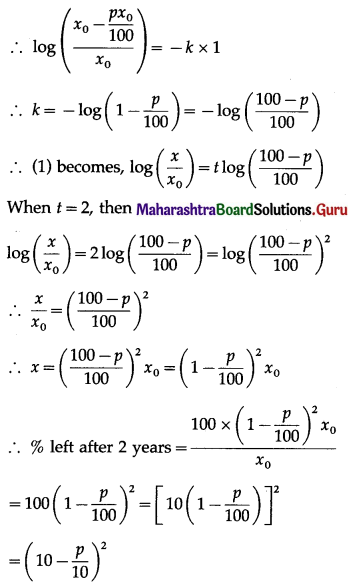
Hence, \(\left(10-\frac{p}{10}\right)^{2} \%\) of the amount will be left after 2 years.