Category: Class 9

Balbharti Maharashtra State Board Class 9 Marathi Solutions Kumarbharti Chapter 16 वनवासी Notes, Textbook Exercise Important Questions and Answers.

Maharashtra State Board Class 9 Marathi Kumarbharti Solutions Chapter 16 वनवासी

9th Std Marathi Kumarbharati Digest Chapter 16 वनवासी Textbook Questions and Answers

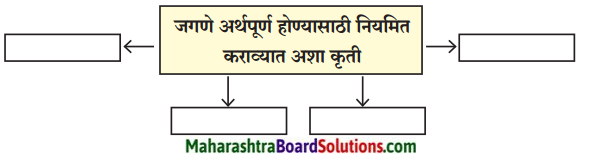
1. खालील शब्दसमूहातील अर्थ स्पष्ट करा:

प्रश्न 1.
खालील शब्दसमूहातील अर्थ स्पष्ट करा:

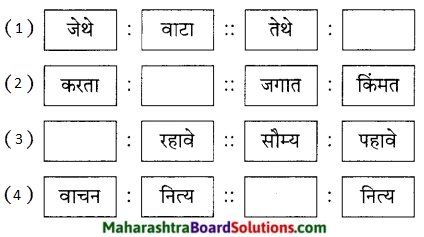
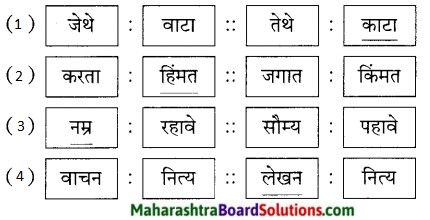
1. पांघरू आभाळ – [ ]
2. वांदार नळीचे – [ ]
3. आभाळ पेलीत – [ ]

उत्तर:

1. उघड्यावर संसार आहे
2. डोंगराच्या घळीत वानरे असतात, तिथे वास्तव्य
3. ऊन, वारा, पाऊस यांचा सामना करीत

2. शोध घ्या:

प्रश्न 1.
शोध घ्या:
(अ) ‘हात लाऊन गंगना येऊ चांदण्या घेऊन’ या काव्यपंक्तीत व्यक्त होणारा आदिवासींचा गुण – [ ]
(आ) कवितेच्या यमकरचनेतील वेगळेपण – [ ]
उत्तर:
(अ) अतुलनीय धैर्य व उत्तुंग इच्छाशक्ती
(आ) प्रत्येक कडव्यातील चार पंक्तींमधील पहिल्या, दुसऱ्या व चौथ्या पंक्तींचे यमक जुळते.
उदा., भाकर – भोकर – ढेकर / वेगानं – यंगून – घेऊन

3. काव्यसौंदर्य:

प्रश्न 1.
‘बसू सूर्याचं रुसून, पहू चंद्राकं हसून, ‘ या काव्यपंक्तीतील भावसौंदर्य स्पष्ट करा.
उत्तर:
दुपारी सूर्य तापतो. माळरानावर हुंदडणाऱ्या आदिवासी मुलांना कडक उन्हात खेळावे लागते. उघड्याबोडक्या असलेल्या मुलांना या उन्हाचा त्रास होतो; म्हणून ते सूर्यावर रुसून बसतात. रात्री चंद्र उगवतो. त्या शीतल चंद्रप्रकाशात आदिवासी मुलांच्या बागडण्याला उधाण येते; म्हणून चंद्राकडे बघून ते आनंदाने हसतात. सूर्यचंद्राचे त्यांच्याशी असलेले अनोखे नाते या ओळींतून प्रकट झाले आहे.

प्रश्न 2.
‘डोई आभाळ पेलीत, चालू शिंव्हाच्या चालीत,’ या पंक्तींत कवीला अभिप्रेत असलेला अर्थ लिहा.
उत्तर:
आदिवासी मुले उघड्याबोडक्या अंगाने उंबराच्या माळावर भटकतात, बागडतात. झाड्याकड्यांवर त्यांचा वावर असतो. त्यांचे जीवन खडतर असते. परंतु त्यांना या कष्टमय जीवनाची फिकीर नसते. ऊन, वारा, पाऊस झेलत ती मजेत राहतात. जणू ते आपल्या माथ्यावर सर्व आभाळ पेलतात. सिंह जंगलाचा राजा असतो. त्याचा दरारा सगळ्या रानावर असलो; म्हणून आदिवासी मुले सिंहाच्या दमदार चालीने चालत सारी संकटे झेलतात. आदिवासी मुलांच्या चिवट वृत्तीचे व धाडसाचे वर्णन कवींनी केले आहे.

4. अभिव्यक्ती.

प्रश्न 1.
‘आदिवासी समाज आणि जंगल यांचे अतूट नाते असते,’ याविषयी तुमचे विचार लिहा.
उत्तर:
आदिवासी समाज हा दाट जंगलात व कडेकपारीत राहतो. झाडांच्या वाळलेल्या फांदया, काटक्या घेऊन त्यांची खोपटी (झोपडी) तयार होते. रानातली फळे, कंदमुळे खाऊन ते गुजराण करतात. ओढ्यानाल्याचे पाणी पितात. निसर्गात ते उघड्यावर जगतात. ते धरतीवर जणू आभाळ पांघरून जगतात. जंगलातील पशुपक्षी त्यांचा मित्रपरिवार असतो. दुखण्याखुपण्याला ते झाडपाल्यांचेच औषध वापरतात. आदिवासी समाजाचे सारे जीवन जंगलावर अवलंबून असते; म्हणून आदिवासी समाज व जंगल यांचे नाते अतूट असते.

भाषा सौंदर्य:

लिखित मजकुरासाठी योग्य विरामचिन्हांचा वापर महत्त्वपूर्ण असतो. विरामचिन्हांच्या चुकीच्या वापरामुळे संपूर्ण वाक्याचा अर्थ बदलू शकतो व भाषेचा बाजही बिघडू शकतो. भाषा योग्य स्वरूपात अर्थवाही होण्यासाठी विरामचिन्हांच्या योग्य वापराचा अभ्यास व सराव होणे आवश्यक आहे.

प्रश्न 1.
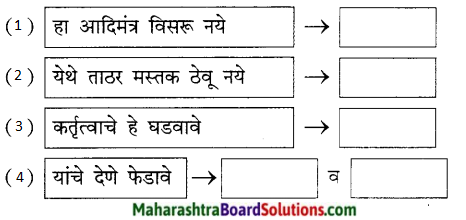
खालील वाक्यांत योग्य विरामचिन्हे वापरून वाक्ये पुन्हा लिहा :

1. ते बांधकाम कसलं आहे
2. आकाशकंदील पूर्ण झाल्यावर दादांनी तो खांबावरच्या खिळ्याला टांगला
3. गुलाब जास्वंद मोगरा ही माझी आवडती फुले आहेत
4. अरेरे त्याच्याबाबतीत फारच वाईट झाले
5. आई म्हणाली सोनम चल लवकर उशीर होत आहे

उत्तर:

1. ते बांधकाम कसलं आहे?
2. आकाशकंदील पूर्ण झाल्यावर दादांनी तो खांबावरच्या खिळ्याला टांगला.
3. गुलाब, जास्वंद, मोगरा ही माझी आवडती फुले आहेत.
4. अरेरे! त्याच्याबाबतीत फारच वाईट झाले!
5. आई म्हणाली, “सोनम, चल लवकर. उशीर होत आहे.”

Marathi Kumarbharati Textbook Std 9 Answers Chapter 16 वनवासी Additional Important Questions and Answers

1. पुढील कवितेच्या आधारे दिलेल्या सूचनांनुसार कृती करा:

कृती 1 : (आकलन)

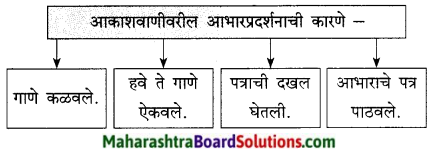
प्रश्न 1.
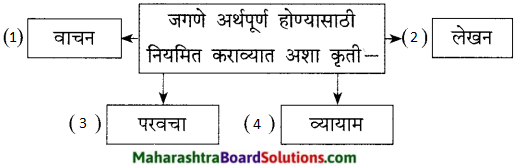
आकृतिबंध पूर्ण करा:

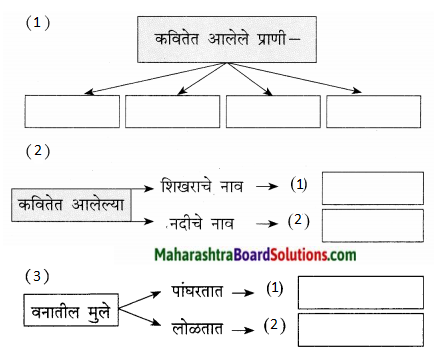
उत्तर:

प्रश्न 2.
पुढीलपैकी सत्य विधान ओळखून लिहा:
1. आदिवासी मुलांचे गाव कळसूबाईच्या पलीकडे आहे.
2. आदिवासी मुलांचे गाव आभाळाच्या पलीकडे आहे.
3. आदिवासी मुलांचे गाव ओढ्याच्या पलीकडे आहे.
4. आदिवासी मुलांचे गाव प्रवरा नदीच्या पलीकडे आहे.
उत्तर:
सत्य विधान : आदिवासी मुलांचे गाव ओढ्याच्या पलीकडे आहे.

प्रश्न 3.
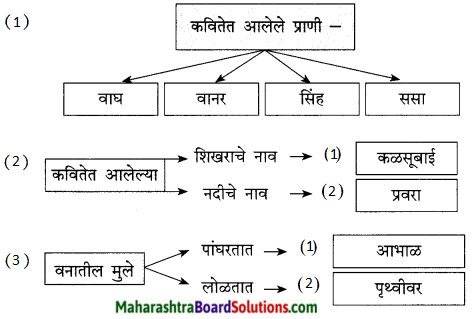
आकृती पूर्ण करा:

उत्तर:

कृती 2 : (आकलन)

1. योग्य पर्याय निवडून विधाने पूर्ण करा:

प्रश्न 1.
आदिवासी मुले खडकावर बसून खातात व आनंदाने ……………………
(य) भोकर देतात
(र) ढेकर देतात
(ल) उड्या मारतात
(व) नदीत डुंबतात
उत्तर:
1. आदिवासी मुले खडकावर बसून खातात व आनंदाने ढेकर देतात.

प्रश्न 2.
आदिवासी मुले हिंडतात ती …………………
(य) डोंगरमाथ्यावर
(र) वाऱ्याबरोबर
(ल) उंबर माळीवर
(व) झाडांवर व कड्यांवर
उत्तर:
1. आदिवासी मुले हिंडतात ती झाडांवर व कड्यांवर.

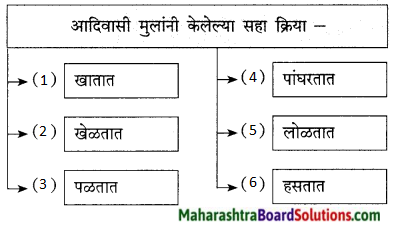
2. चौकटी पूर्ण करा:

प्रश्न 1.

उत्तर:

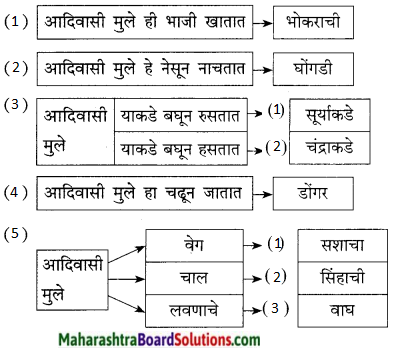
कृती 3 : (दोन ओळींचा सरळ अर्थ)

प्रश्न 1.
घेऊ हातावं भाकर वर भाजीला भोकर
खाऊ खडकावं बसून देऊ खुशीत ढेकर
उत्तर:
प्रवरा नदीची बाळे म्हणतात-आम्ही हातात भाकरी घेतो, त्यावर भोकरीच्या पाल्याची भाजी ठेवतो आणि शांतपणे खडकावर बसून पोटभर भाजीभाकरी खाऊन तृप्तपणे ढेकर देतो.

1. पुढील कवितेवर दिलेल्या मुद्द्यांच्या आधारे कृती सोडवा:

प्रश्न 1.
कविता – वनवासी.
उत्तर:
वनवासी
1. प्रस्तुत कवितेचे कवी/कवयित्री → तुकाराम धांडे.
2. कवितेचा विषय → कळसूबाई शिखराच्या पायथ्याशी प्रवरा नदीच्या खोऱ्यातील आदिवासी जीवनाचे वास्तव चित्रण आदिवासी बोलीत करणे, हा कवितेचा विषय आहे.
3. कवितेतील दोन शब्दांचे अर्थ →

1. डोंगर = पर्वत
2. खडक = दगड
3. आभाळ = आकाश
4. पृथ्वी = अवनी
5. वाघ = व्याघ्र
6. सूर्य = रवी
7. चंद्र = शशी
8. बोली = भाषा.

4. कवितेतून मिळणारा संदेश → आपल्या सभोवती निसर्गात जगणाऱ्या मानवांच्या जीवनशैलीचा परिचय व्हावा व त्यांच्या जगण्याशी आपण समरस होऊन सह-अनुभूती घ्यावी, हे उद्दिष्ट या कवितेचे आहे.

5. कवितेची भाषिक वैशिष्ट्ये → सैल अष्टाक्षरी छंदात ही कविता आहे. ग्रामीण बोलीभाषेतील जिवंत चैतन्य या कवितेच्या शब्दकळेत भारलेले दिसते. कळसूआई व प्रवरामाई यांची ही बाळे, हातात भाकरी-भाजी घेऊन खडकावर बसून खाणारी ही मुले, वाऱ्याच्या संगतीत खेळणारी व आभाळ पांघरणारी, सूर्याचंद्राशी बोलणारी आणि पक्ष्यांची बोली कंठात असणारी व चांदण्या हातात आणण्याची जिद्द असणारी ही पोरे-या सर्व नवीन व ताज्या प्रतिमांनी ही कविता सजलेली आहे. सहज जीवनशैलीची सहज भाषा उत्कटपणे कवींनी कवितेत मांडली आहे. वाघाचे लवण, वांदार नळी, उंबरमाळी, तिकिड्या हे नक्षत्र असल्या अपरिचित पण जिवंत संकल्पना नव्याने कवितेत आल्या आहेत.

6. कवितेतून व्यक्त होणारा विचार → वनामध्ये राहणारी आदिवासी मुले व त्यांची उत्साही वृत्ती यांचे दर्शन या कवितेतून घडते. ।

7. कवितेतील दोन ओळींचा सरळ अर्थ:
आम्ही सस्याच्या वेगानं
जाऊ डोंगर यंगून
हात लावून गंगना
येऊ चांदण्या घेऊन!
→ आम्ही सशाच्या गतीने डोंगर चढून जातो. आकाशाला हात लावून चांदण्या घेऊन येतो. निसर्गात राहताना आम्हांला अनोखा आनंद होतो.

8. कविता आवडण्याची वा न आवडण्याची कारणे → आदिवासी लेकरांचे अनोखे भावविश्व या कवितेत मांडले आहे. डोंगरदऱ्यांत, उघड्या निसर्गात मुक्तपणे, निर्भयपणे निसर्गाचेच घटक होऊन राहणारी ही वनवासी मुले कशी जगतात, याचे प्रत्ययकारी चित्रण करणारी ही कविता आहे. संवेदनशील मनाला भावेल, असे वेगळे जीवनदर्शन व वेगळी जीवनदृष्टी देणारी ही कविता असल्यामुळे ग्रामीण बोलीतील ही सहजसुंदर कविता मला आवडली.

1. पुढील ओळींचे रसग्रहण तुमच्या शब्दांत करा:

प्रश्न 1.
‘आम्ही डोंगरराजाची
पोहं कळसू आईची
आम्ही उघडी बोडकी
बाळं परवरा माईची’
उत्तर:
आशयसौंदर्य: सह्याद्रीच्या डोंगररांगांतील कळसूबाई शिखराच्या पायथ्याशी प्रवरा नदीच्या खोऱ्यातील आदिवासी जीवनाचे वास्तव चित्रण कवी तुकाराम धांडे यांनी ‘वनवासी’ या कवितेत केले आहे. डोंगरदऱ्यांत आनंदाने व मुक्तपणे नैसर्गिक जीवन जगणाऱ्या वनवासी मुलांच्या भावनांचे चित्रण करणे हा या कवितेचा आशय आहे.

काव्यसौंदर्य: डोंगरदऱ्यांत, उघड्या निसर्गात मुक्तपणे व निर्भयपणे निसर्गाचेच घटक होऊन राहणाऱ्या वनवासी लेकरांचे अनोखे विश्व उपरोक्त ओळींमध्ये साकारले आहे. निसर्गातील वन्य प्राण्यांप्रमाणे जगणारी ही मुले आत्मविश्वासाने सांगतात की, डोंगर आमचा राजा आहे. आम्ही डोंगरराजाची मुले आहोत. कळसूबाई शिखराच्या भवतालचा प्रदेश आमची आई आहे. उघडीबोडकी स्वच्छंदपणे बागडणारी आम्ही प्रवरा नदीची बाळे आहोत. भयमुक्तता व नैसर्गिक जीवनाची ओढ या भावनांचे चित्रण उपरोक्त ओळींत केले आहे.

भाषिक वैशिष्ट्ये: सैल अष्टाक्षरी छंदात ही कविता आहे. ग्रामीण बोलीभाषेतील जिवंत चैतन्य या कवितेच्या शब्दकळेत भारलेले दिसते. कळसूआई व प्रवरामाई यांची ही बाळे, हातात भाकरी-भाजी घेऊन खडकावर बसून खाणारी ही मुले, वाऱ्याच्या संगतीत खेळणारी व आभाळ पांघरणारी, सूर्याचंद्राशी बोलणारी आणि पक्ष्यांची बोली कंठात असणारी व चांदण्या हातात आणण्याची जिद्द असणारी ही पोरे – या सर्व नवीन व ताज्या प्रतिमांनी ही कविता सजलेली आहे. सहज जीवनशैलीची सहज भाषा उत्कटपणे कवींनी कवितेत मांडली आहे. वाघाचे लवण, वांदार नळी, उंबरमाळी, तिकिड्या हे नक्षत्र असल्या अपरिचित पण जिवंत संकल्पना नव्याने कवितेत आल्या आहेत.

भाषाभ्यास:

(आ) भाषिक घटकांवर आधारित कृती:

प्रश्न 1.
शब्दसंपत्ती:

1. अनेकवचन लिहा:
2. चांदणी
3. पक्षी
4. टेकडी
5. डोंगर.

उत्तर:

1. चांदणी – चांदण्या
2. पक्षी – पक्षी
3. टेकडी – टेकड्या
4. डोंगर – डोंगर.

प्रश्न 2.
स्त्रीलिंगी रूपे लिहा:

1. वाघ
2. ससा
3. सिंह
4. वानर.

उत्तर:

1. वाघ – वाघीण
2. ससा – सशीण
3. सिंह – सिंहीण
4. वानर – वानरी.

प्रश्न 3.
जोडशब्दांचे सहसंबंध लावा: (डोंगर उघडी झाडे ) कडे )
( झुडपे ) कपारी) दऱ्या बोडकी )
उत्तर:

1. डोंगर-दऱ्या
2. उघडी-बोडकी
3. झाडे-झुडपे
4. कडे-कपारी

2. लेखननियम:

प्रश्न 1.
गटातील अचूक शब्द ओळखा:
1. खुषीथ, खूशीत, खुशीत, खूषीत.
2. घोगंडी, घोंगडी, घोंगडि, घोगडि.
उत्तर:
1. खुशीत
2. घोंगडी.

4. पारिभाषिक शब्द:

प्रश्न 1.
योग्य पर्याय निवडा:
1. Clerk –

1. अभियंता
2. समावेशक
3. लिपिक
4. सहअध्यायी.

उत्तर:
3. लिपिक

प्रश्न 2.
Agent –

1. अवांतर
2. प्रतिनिधी
3. हस्तक
4. उपयोगी.

उत्तर:
2. प्रतिनिधी.

वनवासी Summary in Marathi

कवितेचा आशय:

वनामध्ये राहणारी आदिवासी मुले, त्यांचे जीवन, त्यांचे खेळ, खाणे-पिणे व त्यांची उत्साही वृत्ती यांचे मनोहारी वर्णन या कवितेत ग्रामीण शब्दकळेत केले आहे.

शब्दार्थ:

1. वनवासी – रानांमध्ये राहणारे.
2. पोहं – पोरे.
3. उघडी बोडकी – अंगावर वस्त्र नसलेली.
4. माई – आई (मोठी बहीण).
5. हातावं – हातावर.
6. खडकावं – दगडावर.
7. वांदार – वानर, माकडे.
8. वहाळ – ओहळ, ओढा, नाला.
9. पल्याड – पलीकडे.
10. माळीचे – माळरानावरचे.
11. पहू – बघू.
12. चंद्राकं – चंद्राकडे.
13. बाज – शोभा.
14. पेलीत – झेलीत.
15. शिंव्ह – सिंह.
16. चालीत – चालण्याची ढब.
17. सस्या – ससा.
18. यंगून – चढून.
19. गंगना – आकाशाला.

टिपा:

1. कळसू – भंडारदरा (नाशिक-घोटी) येथे असलेले सह्याद्रीचे सर्वांत उंच शिखर, कळसूबाईचे शिखर.
2. परवरा माई – प्रवरा नदी ही माई आहे.
3. भोकर – एक रान-वनस्पती. याच्या झाडपाल्याची व फळांची भाजी करतात.
4. ढेकर – पोट भरल्यावर पोटातून ओठावर येणारा आवाज.
5. वाघाचे लवण – डोंगरामधली खळगीची जागा, जिथे वाघ वस्ती करतात.
6. वांदार नळी – डोंगरपठारावरची जागा, जिथे माकडे मोठ्या प्रमाणात असतात.
7. उंबर माळ – जिथे उंबराची झाडे मोठ्या प्रमाणात असतात, ते माळरान.
8. बाज तिकिडा – आकाशातील तीन नक्षत्रांचा समूह.
9. घोंगडी – जाड खरखरीत धाग्यांची सतरंजी.

कवितेचा भावार्थ:

डोंगर आमचा राजा आहे. आम्ही डोंगरराजाची मुले आहोत. कळसूबाई शिखराचा परिसर आमची आई आहे. उघडीबोडकी स्वच्छंद बागडणारी आम्ही प्रवरा नदीची बाळे आहोत. (कळसूबाईच्या डोंगराचा परिसर व प्रवरा नदीचे खोरे हा आमचा रहिवास आहे.)

आम्ही हातात भाकरी घेतो, त्यावर भोकरीच्या पाल्याची भाजी ठेवतो नि निवांत खडकावर बसून भाजीभाकरी खाऊन आनंदाने तृप्त ढेकर देतो. आम्ही टेकडीभोवती खेळतो. वाऱ्याबरोबर पळतो. आम्ही आभाळ पांघरून घेतो नि माळरानाच्या जमिनीवर (पृथ्वीवर) लोळतो.

वाघ जिथे वस्तीवर असतात त्या लवणावर आम्ही असतो. वानरांचे (माकडांचे) वास्तव्य जिथे असते, त्या नळीत (घळीत) आमचा वावर असतो. ओढ्यापलीकडे आमचे गाव आहे. उंबराची झाडे असलेल्या उंबरमाळावर आम्ही असतो. दिवसा तापलेल्या सूर्यावर आम्ही रुसून बसतो; पण चंद्राच्या शीतल प्रकाशात रात्री आम्ही चंद्राकडे बघून हसतो. रात्री आकाशातील तीन नक्षत्रांच्या तिकिड्याची शोभा बघतो नि घोंगडी अंगावर घेऊन नाचतो.

आम्ही डोक्यावर आभाळ पेलत सिंहाच्या सारखे डौलदार ऐटीत चालतो. झाडांवर चढतो, कड्यांवर चढून हिंडतो. आम्ही पक्ष्यांच्या भाषेत बोलतो. ‘3\आम्ही सशाच्या गतीने डोंगर चढून जातो. आकाशाला हात लावून , चांदण्या घेऊन येतो. (निसर्गात राहताना आम्हांला अनोखा आनंद होतो.)

Balbharti Maharashtra State Board Class 9 Marathi Solutions Kumarbharti Chapter 15.1 ‘बिग 5’ च्या सहवासात Notes, Textbook Exercise Important Questions and Answers.

Maharashtra State Board Class 9 Marathi Kumarbharti Solutions Chapter 15.1 ‘बिग 5’ च्या सहवासात(स्थूलवाचन)

9th Std Marathi Kumarbharati Digest Chapter 15.1 ‘बिग 5’ च्या सहवासात Textbook Questions and Answers

1. केनिया पार्क्समध्ये फिरण्याचे थ्रिल पुढील मुद्दा विचारात घेऊन लिहा:

प्रश्न 1.
केनिया पार्क्समध्ये फिरण्याचे थ्रिल पुढील मुद्दा विचारात घेऊन लिहा:
गेम ड्राइव्ह
उत्तर:
जंगलाचा फेरफटका मारणे म्हणजे ‘गेम ड्राइव्ह’ करणे व जंगलातील दुर्मीळ जनावरांचा शोध घेणे हे ‘थ्रिल’ असते. केनियाच्या पार्कमध्ये रोज सकाळ-संध्याकाळ प्रत्येकी चार-पाच तास ‘गेम ड्राइव्ह’ करण्याचा कार्यक्रम लेखकांनी आखला होता. पूर्ण प्रवासासाठी मॅटाडोर गाड्या व फोरव्हीलर्स उपलब्ध होत्या. जंगलात फिरताना मोटारीचे छप्पर उघडण्यात येते.

त्यातून जनावरांना जवळून पाहता येते व त्यांचे फोटो मनसोक्त काढता येतात. प्रत्येक मोटारीत वायरलेस सेट असतो. हेतू हा की वाहनांचा एकमेकांशी संपर्क राहतो. आणीबाणीच्या प्रसंगी त्याचा उपयोग होतो. शिवाय कुठे एखादे दुर्मीळ जनावर दिसले, की तिथे पोहोचा, अशा प्रकारच्या सूचनाही देता येतात.

2. टिपा लिहा:

प्रश्न 1.
केनियातील पर्यटन क्षेत्राबाबत तेथील सरकारची भूमिका.
उत्तर : पर्यटन क्षेत्र विकसित करण्याबाबत केनिया सरकार अतिशय दक्ष आहे. पर्यटकांनी जंगलात फिरताना कोणती दक्षता घ्यावी, याबाबत सरकारने काही नियम केले आहेत. मोटारीतून फिरताना पर्यटकांनी शक्यतो मुख्य रस्ता सोडून आत जाऊ नये. एखादा दुर्मीळ प्राणी दिसला, तरच तात्पुरते झुडपात शिरावे, पण लवकर मुख्य रस्त्यावर यावे.

जनावरांशी बोलू नये, टाळ्या वाजवू नयेत व त्यांना खादय देऊ नये. सिंह, गेंडा, लेपर्ड-चित्ता यांच्या सभोवताली पाचपेक्षा जास्त मोटारींनी थांबू नये. जनावरांचा पाठलाग करू नये. त्यांना त्रास देऊ नये. नियमांचे पालन न करणाऱ्या पर्यटकांना दंड करून लगेच पार्कबाहेर काढण्याचे अधिकार केनिया सरकारने तेथील रेंजर्सना दिले आहेत.

प्रश्न 2.
‘बिग 5’चे थोडक्यात वर्णन.
उत्तर:
सिंह, लेपर्ड-चित्ता, गेंडा, हत्ती व जंगली म्हैस या पाचही प्राण्यांची जमिनीवर शिकार करणे अत्यंत अवघड आहे. तसेच ते आकाराने मोठे असल्यामुळे त्यांना ‘बिग 5’ असे म्हणतात. सिंहाचे सुमारे तीस जणांचे कुटुंब असते. दिवसाचे वीस तास सिंह आळसावून पडलेला असतो. तो क्वचित शिकार करतो. सिंहाला जंगलात एकही शत्रू नाही. सिंहाचा एकमेव शत्रू माणूस होय. लेपर्डची शेपटी लांब व टोकापासून मध्यापर्यंत तिच्यावर ठिपके असतात.

लेपर्ड सूर्यास्ताच्या वेळी किंवा रात्री शिकार करतो. तो सावजाला ओढत झाडावर नेतो. त्याचे आयुष्य वीस वर्षे असते. त्याच्या कातडीला आंतरराष्ट्रीय बाजारपेठेत जबरदस्त मागणी आहे. चित्ता हा सर्वांत अतिचपळ प्राणी ताशी 100 किमी वेगाने पळतो. त्याची शिकार करण्याची पद्धत वेगळी आहे. तो सावजाजवळ दबकत जातो, एकदम हल्ला करतो व गुदमरून मारतो. शिकार खायची नसेल, तर ती पालापाचोळचाने झाबून ठवतो.

3. पाठाच्या आधारे सिंहाचे कुटुंब व लेखकाचे कुटुंब यांच्या भेटीचा प्रसंग तुमच्या शब्दांत लिहा.

प्रश्न 1.
पाठाच्या आधारे सिंहाचे कुटुंब व लेखकाचे कुटुंब यांच्या भेटीचा प्रसंग तुमच्या शब्दांत लिहा.
उत्तर:
लेखक नकुरू ते मसाईमारा असा मोटारीने प्रवास करीत होते. दुपारचे जेवण आटोपून ते मारा सरिना लॉजकडे जात होते. इतक्यात फरीदने गाडी कमरेएवढ्या उंच गवतात घुसवली. पाहतात तो काय, गवतात वनराज सिंह मस्त विश्रांती घेत होते. सारे कुटुंब समोर आले. दोन-तीन सिंहिणी नि त्यांची दहा बाळे. शेजारी एक म्हैस मरून पडली होती. चारपाच बछडे व सिंहिणी त्यावर ताव मारत होत्या.

खाऊन झाल्यामुळे सिंहराज तृप्तीने विसावले होते. एक सिंहीण सिंहाजवळ आली आणि ‘मी पाणी पिऊन येते, तू जरा बछड्यांना सांभाळ’ सिंहाला सांगून निघून गेली, असा जणू त्यांचा संवाद झाला असावा, असे लेखकांना वाटले. सर्व सिंह कुटुंबीय मोटारीला खेटून मोटारीच्या सावलीत मस्त पहुडले होते. एक बछडा सिंहाच्या आयाळीशी खेळत होता. त्यावर सिंहाने पंजा उगारून जणू ‘त्रास देऊ नकोस’ असे त्याला बजावले असावे. हा सगळा चित्तथरारक सोहळा ‘डिस्कव्हरी चॅनेल’वर पाहावा, तसा लेखकांच्या कुटुंबीयांनी अनुभवला.

प्रवासवर्णन लिहूया:

प्रवासवर्णन म्हणजे एखादया स्थळाला भेट देऊन आल्यानंतर त्या ठिकाणचे घेतलेले अनुभव व त्या ठिकाणी पाहिलेल्या स्थळांचे बारकाव्यांसह निरीक्षण शब्दबद्ध करणे होय.

प्रश्न 1.
प्रवासवर्णन कसे लिहावे?
प्रवास वर्णन लिहिताना त्यात खालील मुद्द्यांचा विचार व्हावा.
1. प्रवासाचे ठिकाण: ठरवलेल्या ठिकाणची भौगोलिक, ऐतिहासिक वैशिष्ट्ये, तेथील हवामान स्थिती, नियोजित ठिकाणी पोहोचण्याचे मार्ग या सगळ्याच्या पूर्वतयारीविषयी थोडक्यात माहिती घेणे आवश्यक आहे.

2. नेमके काय पाहिले: जिथे भेट देणार तिथले लोकजीवन, संस्कृती, वेशभूषा, बोलीभाषा खाद्यपदार्थ आणि अर्थातच निसर्ग, ऐतिहासिक, भौगोलिक महत्त्व इत्यादी.

3. सूक्ष्म निरीक्षण: प्रवास करताना निरीक्षणातून लक्षात आलेले छोटे बारकावे, तपशिलांची नोंद करून ठेवावी. लेख लिहिताना अशी काही निरीक्षणे नोंदवल्यास आपल्या लिखाणाला वेगळे परिमाण मिळते.

4. सहज संवादात्मक लेखन: प्रवासवर्णनाची शैली ही उत्कंठावर्धक तरीही सहज असावी. लिखाणातला ओघ कायम राहील याचे भान ठेवावे.

5. संस्मरणीय प्रसंग: प्रवासाचा आनंद घेता-घेता घडणाऱ्या अनपेक्षित घटना, प्रसंग, क्वचितप्रसंगी आलेल्या अडचणी, त्यांवर केलेली मात याचा उल्लेख प्रवासवर्णन लिहिताना जरूर करावा. प्रवासवर्णन म्हणजे प्रवासाच्या तयारीपासून सुरू होणारा हा सिलसिला प्रवास संपून, मूळ जागी येऊन स्वस्थता मिळेपर्यंत अव्याहतपणे आपसूक सुरूच असतो.

प्रवासातील वेगळेपण, निरनिराळ्या व्यक्ती, आलेले हटके अनुभव, काही अद्भुत गोष्टी या सर्वांची एक सुंदर अनुभूती तयार होते. सखोल निरीक्षणातून ती उठावदार बनते. त्यातून प्रवासवर्णन हा एक बोलका, अक्षरबद्ध नजारा तयार होतो. त्यामुळेच निरीक्षणे, माहिती, वैशिष्ट्ये, आलेल्या अडचणी आणि विलक्षण अनुभव तसेच केलेली धमाल, या सर्व गोष्टी सहजपणे लिहिल्या की प्रवासवर्णन तयार होते.

‘बिग 5’ च्या सहवासात Summary in Marathi

पाठाचा परिचय:

या पाठात लेखकांनी आफ्रिकेतील ‘बिग 5’ प्राण्यांची माहिती त्यांच्या अनेक वैशिष्ट्यांसह मांडली आहे. तसेच केनियाच्या अर्थव्यवस्थेविषयी अनोखा तपशील दिला आहे.

पाठातील महत्त्वाचे मुद्दे:

1. जंगलांचा फेरफटका मारणे व त्यातील दुर्मीळ जनावरांचा शोध घेणे, हे ‘थ्रिल’ असते.

2. आफ्रिकेतील जंगलांचे स्वरूप दोन प्रकारचे आहे: (1) काही ठिकाणी उंच, घनदाट झाडांचे जंगल. (2) काही ठिकाणी झुडपांचे व सुकलेल्या गवताचे जंगल. घनदाट झाडीपेक्षा झुडपांत किंवा गवतात जनावरांचा शोध घेणे सोपे असते. जंगलात फिरताना ‘चिकाटी’ व ‘नशीब’ या दोन गोष्टी महत्त्वाच्या ठरतात.

3. केनिया सफारीत रोज सकाळ-संध्याकाळ चार-पाच तासांचा ‘गेम ड्राइव्ह’ (जंगलातील भटकंती) करण्याचा कार्यक्रम होता. पूर्ण प्रवासासाठी मॅटडोर गाड्या व फोरव्हीलर्सची व्यवस्था असते. जंगलात फिरताना या मोटारीचे छप्पर उघडण्यात येते. त्यामुळे जनावरांना जवळून पाहता येते व फोटो काढता येतात. प्रत्येक मोटारीत वायरलेस सेट असतो. त्यामुळे वाहनांचा एकमेकांशी संपर्क राहतो; आणीबाणीच्या प्रसंगी उपयोग होतो व जनावरांच्या ठिकाणांच्या सूचना देता येतात.

4. वासोनैरो नदीच्या काठी वसलेले ‘सरोवा साभा लॉज’ची रचना आकर्षक आहे. जणू झाडांवर उभारलेली पंचतारांकित झोपडी. वासोनैरो नदीची वैशिष्ट्ये:

1. तिच्यात जवळजवळ सहा फूट लांबीच्या अजस्र शेकडो मगरी आहेत.
2. दुसऱ्या किनाऱ्यावर स्थानिक आदिवासींची वस्ती आहे.
3. आदिवासी मगरींच्या नजरा चुकवून धाडसाने नदी ओलांडतात.
4. कधी कधी सुस्त पडलेली मगर चपळ बनून नदी ओलांडणाऱ्याला तोंडात पकडते.

5. अंबरडट्स नॅशनल पार्क हे घनदाट जंगलासाठी प्रसिद्ध आहे. येथील आर्क लॉजची वैशिष्ट्ये:

1. संपूर्ण लाकडांच्या खोल्या व सभोवती पाण्याचे मोठे डबके.
2. डबक्याजवळ प्रचंड दलदलीत खनिजयुक्त मीठ मिसळल्यामुळे जनावरे आकर्षित होतात व पाणी पिण्यासाठी येतात.
3. लॉजच्या बाहेरच्या बाजूला काचेच्या व उघड्या गॅलरी असल्यामुळे तिथून जनावरांचे दर्शन होते व फोटो काढता येतात.
4. रात्रभर बाहेरच्या बाजूला फोकस लाईट.
5. गॅलरीतला बार चोवीस तास उघडा असतो.
6. दुर्मीळ जनावरे आली की प्रवाशांना उठवण्यासाठी बेलची व्यवस्था.

6. नकुरू तलाव व पार्क हा आफ्रिकेतील महत्त्वाच्या व दुर्मीळ पक्ष्यांचा परिसर आहे. नकुरू तलाव व पार्कची वैशिष्ट्ये:

1. गुलाबी रंगाच्या दीड ते दोन लाख फ्लेमिंगोंचे वास्तव्य.
2. दुर्बिणीतून फ्लेमिंगोंच्या हालचाली, तुरुतुरु पळणे, त्यांची परेड प्रेक्षणीय असते.
3. चव्वेचाळीस चौ.कि.मी. क्षेत्रफळाचा नकुरू तलाव खाऱ्या पाण्याचा आहे.
4. फ्लेमिंगो मूळचे इथले. याच्या निळ्याशार पाण्यात फ्लेमिंगो अन्न शोधतात.
5. पक्षिप्रेमींच्या दृष्टीने हा पार्क मोठा खजिनाच आहे.
6. काळे व पांढरे मिळून जवळजवळ 80 गेंडे या पार्कमध्ये आहेत.

7. ‘बिग 5’ म्हणजे आकाराने मोठे असलेले पाच प्राणी :

1. सिंह
2. लेपर्ड-चित्ता
3. गेंडा
4. हत्ती
5. जंगली म्हैस.

या पाचही प्राण्यांची जमिनीवरून शिकार करणे अत्यंत कठीण असते.

8.  नकुरू तलाव ते मसाईमारा हा प्रवास लेखकांनी मोटारीने केला; कारण गवतात दुर्मीळ प्राणी दिसण्याची शक्यता अधिक होती. सरिना लॉजमध्ये जायच्या आधी लेखक व त्यांच्या साथीदारांना वनराज सिंह व त्याचे कुटुंब यांचे दर्शन घडले.

9. सिंहाची वैशिष्ट्ये:

1. दिवसाचे वीस तास सिंह आळसावून पडलेला असतो. बहुतेक शिकार सिंहिणीच करतात.
2. सिंहीण अडचणीत असली, तरच सिंह धावून जातो. तो शिकार क्वचितच करतो.
3. सिंह ताशी 60 किमी वेगाने पळतो. पण त्याचा स्टॅमिना खूप कमी. म्हणून 200 मीच्या टप्प्यात असलेलेच सावज पकडतो.
4. सुमारे 30 जणांचे कुटुंब असते.
5. सिंहाचे आयुष्य 15 ते 20 वर्षे असते.
6. सिंहाला जंगलात एकही शत्रू नाही. तरस त्याची पिल्ले पळवतात.
7. नैसर्गिकरीत्या मेलेल्या सिंहाचा सांगाडा मिळत नाही; कारण तरस त्यांना खातात.
8. सिंहाचा एकमेव शत्रू माणूस आहे.

10. लेपर्डची वैशिष्ट्ये:

1. लेपर्डच्या मानेत जबरदस्त ताकद असते. मारलेले जनावर तो ओढत झाडावर चढवू शकतो.
2. लेपर्डची शेपटी लांब असते. टोकापासून मध्यापर्यंत तिच्यावर ठिपके असतात.
3. लेपर्ड सूर्यास्ताच्या वेळी किंवा रात्री शिकार करतो.
4. त्याची दृष्टी व श्रवणयंत्रे खूप तीक्ष्ण असतात.
5. त्याचे आयुष्य वीस वर्षांपर्यंत असते.
6. लेपर्डच्या कातड्याला आंतरराष्ट्रीय बाजारात जबरदस्त मागणी आहे.

11. चित्ता व त्याची वैशिष्ट्ये:

1. जगातील सर्वांत चपळ प्राणी. ताशी 100 किमी वेगाने पळतो.
2. त्याचे शरीर गोंडस, लवचीक, छाती भरदार व पाय लांब असतात.
3. शिकार करायची पद्धत वेगळी आहे. सावजाजवळ दबकत जातो, एकदम हल्ला चढवतो नि गुदमरून टाकून त्याला मारतो.
4. शिकार खायची नसेल तर पालापाचोळ्याने झाकून ठेवतो; कारण तरस आयती मिळालेली शिकार खाऊन टाकतात.

12. केनियाची अर्थव्यवस्था प्रमुख चार प्रकारच्या उत्पन्नांवर आधारित आहे:

1. पर्यटन
2. कॉफी
3. चहा
4. फुले (गुलाब). यात पर्यटन महत्त्वाचे आहे.

केनियातील पर्यटन क्षेत्राबाबत सरकारची भूमिका: पर्यटन क्षेत्र विकसित करण्यासाठी केनिया सरकार अतिशय दक्ष आहे. पर्यटकांनी जंगलात फिरताना पाळावयाचे नियम:

1. मोटारीतून फिरताना शक्यतो मुख्य रस्ता सोडून आत जाऊ नये. अगदीच दुर्मीळ प्राणी दिसला, तर झुडपात शिरावे; पण लवकर मुख्य रस्त्यावर यावे.
2. जनावरांच्या जवळ बोलू नये; टाळ्या वाजवू नयेत, खायला घालू नये.
3. ‘बिग 5’च्या सभोवताली पाचपेक्षा जास्त वाहनांनी थांबू नये.
4. जनावरांचा पाठलाग करू नये व त्यांना त्रास देऊ नये.
5. नियम मोडणाऱ्यांना दंड करून त्वरित पार्कबाहेर काढण्याचे अधिकार सरकारने रेंजर्सना दिले आहेत.

Balbharti Maharashtra State Board Class 9 Marathi Solutions Kumarbharti Chapter 5.1 हास्यचित्रांतली मुलं Notes, Textbook Exercise Important Questions and Answers.

Maharashtra State Board Class 9 Marathi Kumarbharti Solutions Chapter 5.1 हास्यचित्रांतली मुल (स्थूलवाचन)

9th Std Marathi Kumarbharati Digest Chapter 5.1 हास्यचित्रांतली मुलं Textbook Questions and Answers

1. खालील फरक लिहा:

प्रश्न 1.
खालील फरक लिहा:

उत्तर:

2. वैशिष्ट्ये लिहा:

प्रश्न 1.
वैशिष्ट्ये लिहा:

उत्तर:

1. व्यंगचित्र हे हास्यचित्राचा पुढचा टप्पा आहे.
2. केवळ हसवणे हा हेतू नसतो.
3. आपल्याला काहीतरी सांगू पाहते.
4. गमतीदार विचार मांडलेला असतो.

3. ‘व्यंगचित्र हे व्यक्तीचे गुण-दोष मांडण्याचे प्रभावी अस्त्र आहे.’ हा विचार सोदाहरण स्पष्ट करा.

प्रश्न 1.
‘व्यंगचित्र हे व्यक्तीचे गुण-दोष मांडण्याचे प्रभावी अस्त्र आहे.’ हा विचार सोदाहरण स्पष्ट करा.
उत्तर:
व्यंगचित्राचा केवळ हास्य हा हेतू नसतो. व्यंगचित्रामध्ये एखादा विचार गमतीशीर पद्धतीने मांडलेला असतो. माणसाच्या विसंगत वर्तनावर बोट ठेवण्याचा नेमकेपणा व्यंगचित्रात असतो. व्यंगचित्र प्रभावीपणे व्यक्तीचे गुणदोष मांडते. उदाहरणार्थ, प्रस्तुत पाठात हंगेरियन व्यंगचित्रकार रेबर यांचे व्यंगचित्र याची साक्ष पटवते. इथे पहिल्या चित्रात लहान मुलगा स्टुलावर चढून भलेमोठे व्हायोलीन वाजवत आहे व दुसऱ्या चित्रात तोच मुलगा मोठेपणी लहान व्हायोलीन वाजवत आहे.

या चित्रांतून-(1) लहान मुलांना मोठ्या वस्तूंचे आकर्षण असते; ते बाह्य आकाराला भुलतात, हे सांगितले आहे व (2) वय वाढल्यावर वृत्तीत प्रगल्भता येते. बाह्य आकाराचे आकर्षण संपते. छंद अधिक खोल व सूक्ष्म होतो, या गोष्टींचे मर्म सांगितले आहे. म्हणजेच, व्यंगचित्र हे व्यक्तीचे गुण-दोष मांडण्याचे प्रभावी अस्त्र आहे, हे सिद्ध होते.

4. प्रस्तुत पाठातील व्यंगचित्रांपैकी तुम्हांला आवडलेल्या कोणत्याही एका व्यंगचित्राचे तुम्ही केलेले निरीक्षण बारकाव्यांसह स्वत:च्या शब्दांत लिहा.

प्रश्न 1.
प्रस्तुत पाठातील व्यंगचित्रांपैकी तुम्हांला आवडलेल्या कोणत्याही एका व्यंगचित्राचे तुम्ही केलेले निरीक्षण बारकाव्यांसह स्वत:च्या शब्दांत लिहा.
उत्तर:
मला ज्येष्ठ व्यंगचित्रकार शि. द. फडणीस यांनी काढलेले लहान मुलीचे व्यंगचित्र खूपच भावते. शि. द. फडणिसांची रेषा भूमितीय असूनही खूप आकर्षक व ठळक आहे. लहान रोपटे व लहान मुलगी यांचा भावबंध त्यांनी अचूक टिपला आहे. रोपट्याला दुधाच्या बाटलीतून पाणी देतानाच्या तिच्या चेहऱ्यावर उमटलेले निरागस भाव केवळ अप्रतिम आहेत.

भलीमोठी दुधाची बाटली तिने सावरली आहे व कमरेत वाकून रोपट्याला पाणी घालताना तिची ओतप्रोत माया तिच्या डोळ्यांतूनही टपकते आहे. रोपट्याला लहान बाळ समजणे व आपली आई आपले जसे पोषण करते, तसे रोपट्याचे पोषण करणे, हा सर्जनशील संदेश यातून चित्रकारांनी दिला आहे. रोपट्याची आई होण्यातील ममत्व ही निरागस शालीनतेची निशाणी ठरते.

5. ‘व्यंगचित्र रेखाटणे’ ही कला आत्मसात करण्यासाठी कोणत्या गुणांची आवश्यकता असते, यासंबंधी तुमचे विचार लिहा.

प्रश्न 1.
‘व्यंगचित्र रेखाटणे’ ही कला आत्मसात करण्यासाठी कोणत्या गुणांची आवश्यकता असते, यासंबंधी तुमचे विचार लिहा.
उत्तर:
व्यंगचित्र रेखाटणे ही अद्वितीय कला आहे. त्याला निर्मळ मन लागते, म्हणजे तुमची रेषाही निर्मळ राहते. व्यंगचित्रकाराला जीवनातली विसंगती टिपता आली पाहिजे. तसेच विषयाविषयी अपार करुणा असली पाहिजे. गुण-दोष दाखवताना माणसांची खिल्ली न उडवता, समंजसपणा असायला हवा. रेषा नाजूक तरीही ठाशीव असायला हवी. गमतीशीर विचारांची पखरण हवी. जीवन समृद्ध करणारे भाष्य व्यंगचित्रकाराला रेषांतून यशस्वीपणे मांडता आले पाहिजे. चित्र रेखीव व अनेक अर्थांचे सूचन करणारे हवे.

6. ‘लहान मुलांची हास्यचित्रे काढणे अवघड आहे,’ याबाबत तुमचे मत स्पष्ट करा.

प्रश्न 1.
‘लहान मुलांची हास्यचित्रे काढणे अवघड आहे,’ याबाबत तुमचे मत स्पष्ट करा.
उत्तर:
लहान मुले निरागस असतात. त्यांच्या सवयी व आवडीनिवडी यांचे बारकाईने निरीक्षण करणे चित्रकाराला गरजेचे आहे. लहान मुलांचा चेहरा, त्यावरचे भाव व त्यांच्या हालचाली रेषांमधून अचूक टिपता यायला हव्यात. शरीराच्या प्रत्येक अवयवाचा आकार शरीराच्या प्रमाणबद्धतेत लहान करावा लागतो. लहान मुलांच्या बारीकसारीक गोष्टींचे सूक्ष्म निरीक्षण करण्याची शक्ती हास्यचित्रकाराला अवगत असायला हवी. लहान मुलांचे मानसशास्त्र पूर्णपणे समजणे ही चित्रकारासाठी पहिली अट आहे. या सर्व कारणांमुळे लहान मुलांची हास्यचित्रे काढणे अवघड असते असे मलाही वाटते.

उपक्रम:

प्रश्न 1.
5 मे या जागतिक व्यंगचित्र दिनाच्या निमित्ताने शाळेमध्ये विविध व्यंगचित्रांचे प्रदर्शन भरवा व त्यांचा आस्वाद घ्या.

प्रश्न 2.
खालील चित्राचे निरीक्षण करा. विचार करा. सांगा:

1. शेजारील चित्रात कोणती समस्या प्रतिबिंबित होते?
2. ही समस्या का निर्माण झाली असावी?
3. पाण्यासाठी पैसा व वेळ खर्च करावा लागला तर… कल्पना करा व लिहा.
4. ही समस्या दूर करण्यासाठी तुम्ही कोणते उपाय सुचवाल?
5. या समस्येसंदर्भात घोषवाक्ये तयार करा.

उत्तर:
1. पाणीटंचाईची गंभीर समस्या प्रतिबिंबित होते.

2. योग्य मार्गाने पाण्याचा साठा न करणे; पाण्याचा गैरवापर करणे ; पाणी प्रदूषित करणे; उतारावरून वाहणारे पाणी न अडवणे या कारणांमुळे ही समस्या निर्माण झाली.

3. पाण्यासाठी वारेमाप पैसा खर्च करावा लागला, तर इतर गरजेच्या गोष्टी घेण्यास त्रास होईल व महिन्याचे पैसे खर्च करण्याचे कोष्टक बिघडून जाईल. पाण्यासाठी रांगेत उभे राहिल्यामुळे वेळेचा अपव्यय होईल. इतर कामांसाठी वेळ अपुरा पडेल. माणसाच्या राहणीमानावर विपरीत परिणाम होईल.

4. पाणीटंचाईची समस्या दूर करण्यासाठी पुढील उपाय करावे लागतील:

1. पाण्याची बचत करणे.
2. पाण्याचा गैरवापर टाळणे.
3. पाण्याचा योग्य साठा करणे.
4. जलप्रदूषण टाळणे.
5. पाणी वाया न दवडणे.
6. पाण्याविषयी जनजागृती तयार करणे.
7. पाण्याचे महत्त्व जनमानसाला पटवून देणे.

5. घोषवाक्ये:

1. पाण्याचा गैरवापर करू नका
2. जलप्रदूषण थांबवा
3. पाणी साठवा, पाणी वाचवा
4. पाणी वाया दवडू नका
5. पाणी आहे, तर जीवन आहे पाणी नाही, तर मरण आहे
6. पाण्याची बचत म्हणजे
7. जीवनाची बचत
8. जल-अभियान सुरू करा

भाषाभ्यास:

1. चेतनगुणोक्ती अलंकार:

1. खालील ओळी वाचा व समजून घ्या.
उदा., “नित्याचेच दुःख होते
उशागती बसलेले
…. तोच अवचित आले
सुख ठोठावीत दार ।” (कृ. ब. निकुम्ब)

1. वरील ओळींमधील अचेतन गोष्टी कोणत्या ? [ ] [ ]
2. अचेतन गोष्टी कोणत्या क्रिया करतात? [ ] [ ]
3. अचेतन गोष्टी ज्या क्रिया करतात त्या मानवी आहेत का? [ ] [ ]

चेतनगुणोक्ती अलंकाराची वैशिष्ट्ये –

1. अचेतन वस्तूंना सचेतन मानले जाते.
2. त्या वस्तू सजीव प्राण्याप्रमाणे किंवा माणसाप्रमाणे वागतात.

2. अचेतन वस्तूवर जेव्हा सचेतनेचा किंवा मानवेतर प्राण्यांवर मानवी गुणधर्माचा आरोप केला जातो, तेव्हा ‘चेतनगुणोक्ती’ अलंकार होतो.

3. खालील वाक्य वाचून दिलेल्या चौकटीत उत्तरे लिहा.

मंगल मंगल गीत म्हणे, अस्फुट रजनी मूकपणे.

1. प्रस्तुत उदाहरणातील अचेतन गोष्ट – [ ]
2. अचेतन गोष्टीने केलेली कृती – [ ]
3. अचेतन गोष्टीने केलेली कृती कशी आहे? – [ ]

हास्यचित्रांतली मुलं Summary in Marathi

पाठाचा परिचय:

या पाठात लहान मुलांसाठी/मुलांवर रेखाटलेल्या कार्टून्स किंवा हास्यचित्रांबद्दल लेखकांनी गमतीशीर व मार्मिक विचार मांडले आहेत. त्यासाठी हास्यचित्रांची विविध उदाहरणे दिली आहेत.

पाठातील महत्त्वाचे मुद्दे:

1. सफाईदार रेषांनी काढलेले गमतीदार चित्र म्हणजे हास्यचित्र होय. व्यंगचित्र हा हास्यचित्रामधील पुढचा टप्पा आहे. व्यंगचित्र व हास्यचित्र यांत फरक आहे. व्यंगचित्रात केवळ हसवणे हा हेतू नसतो. व्यंगचित्रातून काही गमतीदार विचार मांडलेला असतो.
2. मुलांची हास्यचित्रे काढणे ही सर्वांत कठीण गोष्ट आहे. त्यात व्यंगचित्रकाराचे कौशल्य पणाला लागते. मुलांसाठी विनोद , करणे सोपे असते पण व्यंगचित्रातील मूल हे मुलांसारखे दिसणे ही कठीण गोष्ट आहे.

काही हास्यचित्रांचे विश्लेषण:

1. शि. द. फडणीस या ज्येष्ठ व्यंगचित्रकारांनी काढलेले हे हास्यचित्र आहे. या चित्रात फ्रॉक घातलेली एक मुलगी लहान बाळाला दूध पाजावे तशी रोपट्याला दुधाच्या बाटलीतून पाणी घालते आहे. तिचा निरागसपणा या चित्रातून रेखाटला आहे.

2. पहिल्या चित्रात उद्गारासकट एक रांगणारे मूल दाखवले आहे. दुसऱ्या चित्रात एक बालक देवाला ‘बॅडमिंटनचे शटल’ (फूल) वाहतो आहे. दोन्ही बालकांच्या बोलण्यातून सदयः परिस्थितीवर गमतीशीर भाष्य केले आहे. चित्र व हास्यचित्र यांत मूलभूत फरक – चित्रात हुबेहूब माणूस काढावा लागतो, तर हास्यचित्रात चित्राचीच गमतीदार है हुबेहूब नक्कल असते.

3. डेव्हिड लँग्डन या अमेरिकन व्यंगचित्रकाराची ही दोन हास्यचित्रे आहेत. पहिल्या चित्रात एक चतुर मुलगा ‘लहान मुलांसाठी बचत करण्याचा असलेला डबा’ फोडतो आहे. या चित्रात त्याच्या चेहऱ्यावरील भाव – बिचकणे, घाबरणे, कुणी पाहत नाही ना, तरीही फोडण्याची शिताफी – हे सर्व पाहून हसू येते. दुसऱ्या चित्रात भोकाड पसरणारा, मोठमोठ्याने रडणारा मुलगा अहे. काहीतरी मिळावे म्हणून एरव्ही लक्षवेधी रडणे मुले मुद्दाम करतात. पण इथे त्याच्या चड्डीत अडकलेली ‘सेफ्टी पिन’ टोचत असल्यामुळे तो मोठे तोंड पसरून रडतो आहे, हे जेव्हा लक्षात येते तेव्हा हसू फुटते.

4. प्रसिद्ध व्यंगचित्रकार आर. के. लक्ष्मण यांचे हे हास्यचित्र आहे. यात एक मोठा माणूस व छोटा मुलगा आहे. मुलाला जमिनीवर बसवून केस कापण्याचा हा प्रसंग पूर्वी खेड्यात सर्रास दिसत असे. या चित्रात मोठ्या माणसाच्या चेहऱ्यावर केस कापण्याचा उत्साह व केस कापून घेणाऱ्या लहान मुलाच्या मुखावरील कंटाळ्याचे व वैतागलेले भाव, यांचा गमतीशीर विरोधाभास जाणून हास्य निर्माण होते.

5. ही चिंटूची चित्रमालिका आहे. यात पहिल्या चित्रात बाबांना वाटते चिंटू, ‘नदीचे पाणी कुठे जाते?’ असा जिज्ञासापूर्वक प्रश्न विचारतो आहे. ते उत्साहाने उत्तर देतात. परंतु पुढच्या चित्रात ‘नदीत चावी पडली, म्हणून विचारतोय.’ या चिंटूच्या खुलाशामुळे चिंटूचा निरागस खोडकरपणा व बाबांचा झालेला भ्रमनिरास यांची जुगलबंदी गमतीशीर आहे.

6. हंगेरियन व्यंगचित्रकार रेबर यांचे हे व्यंगचित्र आहे. पहिल्या चित्रात एक लहान मुलगा स्टुलावर चढून भलेमोठे व्हायोलीन वाजवतो आहे. दुसऱ्या चित्रात तोच मुलगा मोठा झाल्यावर लहान व्हायोलीन वाजवतो आहे. लहान मुलांना ‘मोठ्या’ वस्तूंचे आकर्षण असते, तर वाढत्या वयाबरोबर जपलेला छंद अधिक खोल व सूक्ष्म होत जातो व बाह्य आकाराचे आकर्षण कमी होते – हा विचार किती खुबीने सांगितला आहे!

7. ब्रिटिश व्यंगचित्रकार नॉर्मन थेलवेल यांचे हे हास्यचित्र आहे. या चित्रात एक स्काउटचा मुलगा बुटात मध्यभागी घुसलेली अणकुचीदार वस्तू काढण्याचा आटोकाट प्रयत्न करीत आहे. या चित्रात मुलाच्या तोंडावरील भाव व त्याचा वेडावाकडा झालेला देह (शरीर) हे इतके अप्रतिमपणे रेखाटले आहे की चित्रकलेवर हुकमत मिळवली की हास्यचित्रात खूप जादू करता येते, हे सिद्ध होते.

अशा प्रकारे, लहान मुलांचे चित्र काढताना पुढील महत्त्वाच्या गोष्टी लक्षात येतात:

1. लहान मुलाचा केवळ लहान आकार महत्त्वाचा नसतो तर शरीराच्या प्रत्येक अवयवाचा आकार त्या प्रमाणात लहान असणे आवश्यक असते.
2. हातापायांची बोटे लहान काढली की नखे आपोआप लहान होतात.
3. नाकाचा, ओठांचा आकार काढल्यावर कळते की लहान मुलांच्या भुवया लहान व एका रेषेत असतात.
4. लहान मुलांना दाढी-मिशी नसते.
5. व्यंगचित्रे बघताना व काढताना अशा बारीकसारीक गोष्टींची नोंद घेणे गरजेचे आहे.

Balbharti Maharashtra State Board Class 9 Marathi Solutions Kumarbharti Chapter 15 निरोप Notes, Textbook Exercise Important Questions and Answers.

Maharashtra State Board Class 9 Marathi Kumarbharti Solutions Chapter 15 निरोप(कविता)

9th Std Marathi Kumarbharati Digest Chapter 15 निरोप Textbook Questions and Answers

1. योग्य पर्याय निवडून विधाने पूर्ण करा:

प्रश्न (अ)
कवितेतील आई आपल्या मुलाला औक्षण करते आहे; कारण
1. मुलाचा वाढदिवस आहे.
2. तो रणांगणावर जाणार आहे.
3. त्याने रणांगणावर शौर्य गाजवले आहे.
4. त्याने क्रीडास्पर्धेत नैपुण्य प्राप्त केले आहे.
उत्तर:
कवितेतील आई आपल्या मुलाला औक्षण करते आहे; कारण तो रणांगणावर जाणार आहे.

2. खालील शब्दांतून सूचित होणारा अर्थ लिहा:

प्रश्न (अ)
खालील शब्दांतून सूचित होणारा अर्थ लिहा:
अशुभाची साउली.
उत्तर:
अशुभाची साउली: शत्रूशी झुंज देण्यासाठी सैनिक जातात, तेव्हा त्यांच्या प्राणांची शाश्वती नसते. लढाईमध्ये कधी प्राण गमवावे लागतील, याचा नेम नसतो. या गोष्टीला कवयित्रींनी अशुभ म्हणजे वाईट छाया असे म्हटले आहे.

प्रश्न (आ)
पंचप्राणांच्या ज्योतींचे औक्षण.
उत्तर:
पंचप्राणांच्या ज्योतींचे औक्षण: रणांगणावर लढायला चाललेल्या बाळाचे रक्षण व्हावे, म्हणून पंचारतीने ओवाळणे याला औक्षण म्हणतात. इथे आईला आपला बाळ सुखरूप परत यावा, अशी मनापासून इच्छा आहे. म्हणून तिच्या मायेचे प्रतीक म्हणून ‘पंचप्राणांच्या ज्योतींचे औक्षण’ असा उल्लेख कवयित्रींनी कवितेत केला आहे.

3. कवितेच्या आधारे पुढील तक्ता पूर्ण करा:

प्रश्न 1.
कवितेच्या आधारे पुढील तक्ता पूर्ण करा:

उत्तर:

4. काव्यसौंदर्य:

प्रश्न (अ)
‘तुझ्या शस्त्रांना, अस्त्रांना शक्ति देईल भवानी, शिवरायाचे स्वरूप आठवावे रणांगणी,’ या काव्यपंक्तींतून व्यक्त होणारा अर्थ स्पष्ट करा.
उत्तर:
रणांगणावर लढायला जाणाऱ्या बाळाला धीराने निरोप देताना आई म्हणते – तुझ्यावर अशुभाची सावली पडणार नाही. तू लढताना श्रीछत्रपती शिवरायांचा पराक्रम आठव. त्यांनी हिंदवी स्वराज्य स्थापन करताना जे शौर्य दाखवले त्याचे मनोमन स्मरण कर. शिवरायांच्या कर्तृत्वाला जसा भवानीमातेने आशीर्वाद दिला होता, तशीच तुझ्या शस्त्रांना-अस्त्रांना भवानीमाता शक्ती देईल. बाळाला निरोप देताना विकल न होणाऱ्या वीरमातेचे दर्शन व तिची मनोकामना या ओळींतून व्यक्त होते.

प्रश्न (आ)
‘धन्य करी माझी कूस, येई विजयी होऊन, पुन्हा माझिया हाताने दूधभात भरवीन,’ या काव्यपंक्तींतील भावसौंदर्य स्पष्ट करा.
उत्तर:
रणांगणावर लढायला जाणाऱ्या मुलाला निरोप देताना या कवितेतील आई दुःखी होत नाही. तिला स्वत:च्या बाळाच्या पराक्रमावर विश्वास आहे. ती महाराष्ट्रकन्या आहे. वीरमाता आहे. काही अशुभ घडणार नाही, याची तिला खात्री आहे. शिवरायांचे स्वरूप आठवून झुंज दे व भवानीमातेचा वरदहस्त तुझ्यावर आहे, हे मनात ठसव, अशी ती निर्धाराने सांगते. आपला बाळ विजयी होऊन घरी नक्की पोहोचेल. तो विजयी होऊन येईल तेव्हा आईला आपण बाळाला जन्म दिल्याचे सार्थक होईल. मग ती त्याला लहानपणी जशी प्रेमाने दूधभात भरवायची तशी आताही भरवील. आईची बाळाच्या कर्तृत्वावर असलेली खात्री आणि शाश्वत निरंतर माया या ओळींतून दिसून येते.

5. अभिव्यक्ति:

प्रश्न (अ)
कवितेतील वीरमातेच्या भावना तुमच्या शब्दांत लिहा.
उत्तर:
रणांगणावर लढायला जाणाऱ्या बाळाला निरोप देणारी कवितेतील आई, ही सामान्य आई नाही. ती वीरमाता आहे. ती या प्रसंगी आनंदाने घराला तोरण बांधते. पंचप्राणांच्या ज्योतींनी बाळाचे औक्षण करते. ती बाळाला म्हणते – तुझ्या पराक्रमी बाहूंनी या देशाच्या स्वतंत्रतेचे रक्षण तुला करायचे आहे. तुझ्या खांदयावर भविष्यातील सुखशांती विसावलेली आहे. माझ्या डोळ्यांत अश्रू येणार नाहीत की गळ्यात हुंदकाही दाटणार नाही.

मी वीरांचा धर्म जाणणारी महाराष्ट्रकन्या आहे. मला जिजाई व राणी लक्ष्मीबाईंचा वारसा लाभला आहे. मीच तुझ्या तलवारीला धार लावून ठेवली आहे. तुझ्यावर कोणत्याही संकटाची सावलीदेखील पडणार नाही. तू शिवरायांचे कर्तृत्व स्मर. माय भवानी तुला शक्ती देईल. विजयी होऊन ये, मग मला तुला जन्म दिल्याचे सार्थक झाल्यासारखे वाटेल. माझ्या हातांनी माझ्या बाळाला मी दूधभात भरवीन. हिंमत, ठाम निर्धार व माया यांचे दर्शन वीरमातेच्या बोलण्यातून व्यक्त झाले आहे.

प्रश्न (आ)
‘भारतभू ही वीरांची भूमी आहे,’ याबाबत तुमचे मत लिहा.
उत्तर:
भारतभूमीचा इतिहास हा पराक्रमाचा इतिहास आहे. रामायण-महाभारत काळापासून याची साक्ष आपणांस मिळते. दुष्टांना सजा देण्यासाठी प्राचीन काळापासून या भूमीत प्रबळ योद्धे निर्माण झाले आहेत. या भारतवर्षावर अनेक परकीय आक्रमणे झाली; पण ती धैर्याने व शौर्याने परतून लावण्याचे धाडस मातृभूमीतील वीरांनी दाखवले. बलाढ्य इंग्रजी जुलमी सत्तेविरुद्ध देशभक्त व क्रांतिकारकांनी । दिलेला लढा अद्वितीय असाच आहे. अगदी कालच्या कारगिल युद्धापर्यंत हेच ठासून म्हणावे लागते की भारतभू ही वीरांची भूमी आहे.

उपक्रम:

प्रश्न 1.
सैन्यात भरती झालेल्या मुलाच्या आईची मुलाखत घेण्यासाठी प्रश्न तयार करा.

भाषा सौंदर्य:

मुलींची कन्याशाळा, केसांची हेअरस्टाइल, ठंडा कोल्ड्रिंक, वटवृक्षाच्या झाडाखाली, शब्दाखाली अधोरेखित, हाय वे रोड, रायटिंगमध्ये लिहून दया, शेवटी एन्ड मस्त केलाय, पिवळा पितांबर.

शब्दांच्या या रचनेची ही गंमत पाहा. खरं म्हणजे भाषिकदृष्ट्या व अर्थाच्या दृष्टीने ही रचना चुकीची आहे; परंतु आपण बोलताना सहजगत्या अशा चुका वारंवार करतो. इतर भाषांच्या प्रभावामुळे हे असे घडत असले, तरी बोलण्यातील भाषिक चुका आपण लक्षात घ्यायलाच हव्यात. आमच्या घरी वर्तमानपत्र दररोज येते अशा वक्तव्याला एखादी मुलगी सहजपणे आमच्याही घरी मासिक/साप्ताहिक रोज येते, असे म्हणते तेव्हा नक्कीच हशा पिकणार.

अशा विविध रचनांतील चुका लक्षात घेऊन टाळण्याची सवय आपण आपल्याला लावून घेतली तर सुयोग्य भाषिक रचनेचा वापर आपण बोलताना करू शकतो.

Marathi Kumarbharati Textbook Std 9 Answers Chapter 15 निरोप Additional Important Questions and Answers

1. पुढील कवितेच्या आधारे दिलेल्या सूचनांनुसार कृती करा:

कृती 1 : (आकलन)

प्रश्न 1.

उत्तर:

प्रश्न 2.

उत्तर:

प्रश्न 3.

उत्तर:

कृती 2 : (आकलन)

प्रश्न 1.
स्वतंत्रता राखणारे बाळाचे विक्रमी
1. पाय
2. डोळे
3. हात
4. कान.
उत्तर:
स्वतंत्रता राखणारे बाळाचे विक्रमी हात.

प्रश्न 2.
बाळाच्या खांदयावर विसावणारी ………………………..
1. उदयाच्या जगाची क्रांती.
2. भविष्यातील जगाची शांती.
3. आजच्या जगाची शांती.
4. आजची क्रांती.
उत्तर:
बाळाच्या खांदयावर विसावणारी भविष्यातील जगाची शांती.

2. चौकटी पूर्ण करा:

प्रश्न 1.

1. शस्त्रांना शक्ती देणारी – [ ]
2. आई स्वत:ला याची कन्या समजते – [ ]
3. आईने धार लावून ठेवलेली – [ ]
4. बाळाने रणांगणात यांचे स्वरूप आठवावे – [ ]

उत्तर:

1. भवानीमाता
2. महाराष्ट्रकन्या
3. तलवार
4. शिवरायांचे

कृती 3 : (दोन ओळींचा सरळ अर्थ)

प्रश्न 1.
बाळ चाललास रणा घरा बांधिते तोरण
पंचप्राणांच्या ज्योतींनी तुज करिते औक्षण
उत्तर:
सीमेवर लढावयास जाणाऱ्या आपल्या सैनिक मुलाला निरोप देताना आई म्हणते-बाळा, तू रणांगणात लढायला चालला आहेस. या शुभकार्याच्या वेळी मी आनंदाने घराला तोरण बांधते आहे. माझ्या पंचप्राणांच्या उजळलेल्या ज्योतींनी मी तुला ओवाळते आहे.

कृती 4 : (विचारसौंदर्य | भावसौंदर्य / अर्थसौंदर्य / रस)

1. पुढील कवितेवर दिलेल्या मुद्द्यांच्या आधारे कृती सोडवा:

प्रश्न 1.
कविता – निरोप.
उत्तर:
निरोप
1. प्रस्तुत कवितेचे कवी/कवयित्री → मराठीतील प्रसिद्ध कवयित्री पद्मा गोळे यांची ही कविता आहे.
2. कवितेचा विषय → रणांगणावर जाणाऱ्या मुलाला युद्धासाठी प्रवृत्त करणाऱ्या वीरमाउलीच्या मनातल्या विविध भावनांचे चित्रण करणे, हा या कवितेचा विषय आहे.
3. कवितेतील दोन शब्दांचे अर्थ →

1. घर = सदन
2. औक्षण = ओवाळणी
3. बाहू = हात
4. डोळा = नेत्र
5. मुख = तोंड
6. सावली = छाया
7. शक्ती = बळ
8. हात = हस्त.

4. कवितेतून मिळणारा संदेश → वीरमातेच्या मनोगतातून कवयित्रींना मराठी मनाला व प्राणपणाने देशाचे रक्षण करणाऱ्या सैनिकांना धैर्याचा व शौर्याचा संदेश दिला आहे. तसेच मातेचे मृदू हृदय प्रसंगी किती कणखर असते, याची ग्वाही देणारी ही कविता आहे.

5. कवितेची भाषिक वैशिष्ट्ये → प्रत्येक ओळीत आठ अक्षरे असलेल्या या कवितेचा अष्टाक्षरी छंद हा वीरमातेच्या भावना यथार्थपणे प्रकट करण्यास पूरक ठरला आहे. या कवितेची रचना यमकप्रधान असून त्यामुळे या कवितेतून गेयता व नादानुकूलता दिसून येते. शब्दकळा वीररसात्मक असल्यामुळे या कवितेत वीररसाला प्राधान्य आहे. शेवटच्या कडव्यात आईची ममता व वात्सल्य ओतप्रोत भरले आहे. भावनांची आंदोलने टिपणारी ओजस्वी भाषा कवितेला लाभली आहे.

6. कवितेतून व्यक्त होणारा विचार → देशरक्षणासाठी मुलाला रणात पाठवणाऱ्या वीरमातेचे दृढ निश्चयी व तितकेच प्रेमळ मन या कवितेत प्रकर्षाने दृष्टीस पडते.

7. कवितेतील दोन ओळींचा सरळ अर्थ:
धन्य करी माझी कूस येई विजयी होऊन,
पुन्हा माझिया हाताने दूधभात भरवीन!
→ रणात चाललेल्या मुलाला निरोप देताना आई म्हणते-तू माझ्यापोटी जन्मलास ती माझी कूस तू कृतार्थ कर. तू विजयी होऊन आलास की माझ्या हातांनी अगदी मायेने मी तुला दूधभात भरवीन.

8. कविता आवडण्याची वा न आवडण्याची कारणे → रणांगणावर जाणाऱ्या पुत्राला निरोप देणाऱ्या आईचे गलबललेले मन व तेवढीच तिच्या मनाची कणखरता याचे मनोज्ञ दर्शन या कवितेत कवयित्रिंनी केले आहे. तसेच श्रीशिवरायांच्या पराक्रमाचे स्मरण करण्यास सांगून आपणही महाराष्ट्रकन्येचा वारसा चालवत आहोत, असे ठामपणे सांगणाऱ्या आईच्या मनःस्थितीचे यथार्थ चित्रण या कवितेत केले असल्यामुळे, मनात आर्तता व वीरता जागवणारी ही कविता मला अत्यंत आवडली.

1. पुढील ओळींचे रसग्रहण तुमच्या शब्दांत करा:

प्रश्न 1.
‘धन्य करी माझी कूस येई विजयी होऊन पुन्हा माझिया हाताने दूधभात भरवीन!’
उत्तर:
आशयसौंदर्य: रणांगणावर शत्रूशी लढायला जाणाऱ्या आपल्या मुलामध्ये वीरश्री जागृत करणाऱ्या वीरमातेच्या मनातील विविध भावनांचे आर्त चित्रण कवयित्री पद्मा गोळे यांनी ‘निरोप’ या कवितेत केले आहे. वीरमाउलीच्या मनोगतातून कवयित्रींनी प्राणपणाने देशाचे रक्षण करणाऱ्या सैनिकांना शौर्याची शिकवण दिली आहे. तसेच आईचे वात्सल्यपूर्ण मृदू हृदय प्रसंगी किती कणखर असते, या आशयाचीही अभिव्यक्ती केली आहे.

काव्यसौंदर्य: युद्धाला निघालेल्या आपल्या बाळाचे औक्षण करताना व त्याची वीरश्री जागृत करताना त्याला गतकालीन वीरांचे व महाराष्ट्रकन्यांचे स्मरण देते. या उज्ज्वल परंपरेचा तू पाईक आहेस. तुझ्या शस्त्रांना भवानीमाय शक्ती देईल, अशा भावपूर्ण उद्गाराने बाळाची आई त्याचे मन ओजस्वी करते. शेवटी माउली म्हणते – तू विजयी होऊन ये. माझ्यापोटी तू जन्म घेतलास याची धन्यता मला वाटेल; त्या वेळी मी प्रेमाने माझ्या हाताने तुला दूधभात भरवीन. प्रस्तुत है ओळींमध्ये वीरश्री व ममता यांचा अनोखा संगम आपल्या प्रत्ययास येतो.

भाषिक वैशिष्ट्ये: प्रत्येक ओळीत आठ अक्षरे असलेल्या या कवितेचा अष्टाक्षरी छंद हा वीरमातेच्या भावना यथार्थपणे प्रकट करण्यास पूरक ठरला आहे. या कवितेची रचना यमकप्रधान असून, त्यामुळे या कवितेतून गेयता व नादानुकूलता दिसून येते. शब्दकळा वीररसात्मक असल्यामुळे या कवितेत वीररसाला प्राधान्य आहे. शेवटच्या कडव्यात आईची ममता व वात्सल्य ओतप्रोत भरले आहे. भावनांची आंदोलने टिपणारी ओजस्वी भाषा कवितेला लाभली आहे.

भाषाभ्यास:

(अ) व्याकरण घटकांवर आधारित कृती:

स्वातंत्र्यवीर सावरकरांनी मराठी भाषेला दिलेले शब्द अभ्यासा.

1. समास:

प्रश्न 1.
पुढील सामासिक शब्दांचा विग्रह करा आणि समासाचे नाव लिहा:

1. पंचप्राण
2. महाराष्ट्र
3. रणांगण
4. दूधभात.

उत्तर:

1. पंचप्राण : पाच प्राणांचा समूह -द्विगू.
2. महाराष्ट्र : महान असे राष्ट्र-कर्मधारय.
3. रणांगण : रण हेच अंगण-कर्मधारय.
4. दूधभात : दूध आणि भात -इतरेतर द्वंद्व.

(आ) भाषिक घटकांवर आधारित कृती:

1. शब्दसंपत्ती:

प्रश्न 1.
विरुद्धार्थी शब्द लिहा:

1. सावली
2. दुःख
3. स्वतंत्रता
4. विजय.

उत्तर:

1. सावली × ऊन
2. दुःख × सुख
3. स्वतंत्रता × परतंत्रता
4. विजय × पराजय.

प्रश्न 2.
तक्ता पूर्ण करा: (उत्तरे ठळक अक्षरांत दिलेली आहेत.)
उत्तर:

प्रश्न 3.
पुढील शब्दांपासून तयार होणारे चार अर्थपूर्ण शब्द लिहा:
1. चाललास
2. तलवारीला.
उत्तर:
1. चाललास – चाल, लस, सल, लाल.
2. तलवारीला – तरी, वारी, वाल, रीत.

2. लेखननियम:

प्रश्न 1.
पुढील अशुद्ध शब्द लेखननियमानुसार शुद्ध लिहा:

1. ओक्षन
2. वीक्रमि
3. स्वरुप
4. वीजयि.

उत्तर:

1. औक्षण
2. विक्रमी
3. स्वरूप
4. विजयी.

3. पारिभाषिक शब्द:

प्रश्न 1.
पुढील इंग्रजी पारिभाषिक शब्दांना मराठी प्रतिशब्द लिहा:

1. Lyric
2. Action
3. Exchange
4. Exhibition.

उत्तर:

1. भावगीत
2. कार्यवाही
3. देवाण-घेवाण
4. प्रदर्शन.

निरोप Summary in Marathi

कवितेचा आशय:

सीमेवर लढायला जाणाऱ्या आपल्या सैनिक मुलाला निरोप देताना आईच्या मनात आलेल्या विविध भावनांचे दर्शन या कवितेत कवयित्रींनी ओजस्वी शब्दांत घडवले आहे.

शब्दार्थ:

1. रणा – रणांगणात.
2. तोरण – शुभपताकांची माळ.
3. विक्रमी – पराक्रमी.
4. बाहू – हात.
5. राखायची – रक्षण करायची.
6. विसावे – विश्रांती घेते, थांबते.
7. जाणते – उमगते, समजते.
8. हुंदका – गहिवर.
9. मुखावाटे – तोंडातून.
10. अशुभ – वाईट गोष्ट.
11. साउली – सावली.
12. माझिया – माझ्या.

टिपा:

1. औक्षण – पंचारतीने ओवाळणे.
2. महाराष्ट्रकन्या – महाराष्ट्रात होऊन गेलेल्या वीरमाता, पराक्रमी स्त्रिया.
3. जिजा – शिवछत्रपतींची आई, जिजामाता.
4. लक्षुमी – झाशीची राणी लक्ष्मीबाई.
5. भवानी – श्रीछत्रपती शिवाजी महाराजांचे कुलदैवत, भवानीमाता.

वाक्प्रचार व त्यांचे अर्थ:

1. निरोप देणे – जाण्यासाठी परवानगी देणे.
2. अशुभाची सावली पडणे – विपरीत घडणे, अमंगल घडणे.
3. कूस धन्य करणे – जन्म सार्थकी लागणे.

कवितेचा भावार्थ:

सीमेवर लढायला जाणाऱ्या आपल्या मुलाला निरोप देताना आई म्हणते – बाळा, तू रणांगणावर चालला आहेस हा शुभशकुन आहे. मी आनंदाने घराला तोरण लावते आहे. माझ्या पंचप्राणांच्या ज्योतीने तुझे औक्षण करते आहे. तुझे शुभ चिंतते आहे. तुला तुझ्या पराक्रमी हातांनी भारतीय स्वातंत्र्याचे रक्षण करायचे आहे. तुझ्या बळकट खांदयांवर भविष्यातील जगाची शांती विसावणार आहे. तुझ्या पराक्रमाने तू उदयाच्या जगाचा शांतिदूत ठरणार आहेस. म्हणून तू रणांगणात जातोस याचे मी दुःख करणार नाही. माझे डोळे आसवांनी ओथंबले नाहीत. मी सुद्धा महाराष्ट्रकन्या आहे. मला लढणे हा वीराचा धर्म माहीत आहे. वीरमातेचा वारसा माझ्याकडे आहे.

तू लढायला जातोस म्हणून माझ्या तोंडातून हुंदका फुटणार नाही. उलट तुझ्या तलवारीला (शस्त्राला) धार मीच लावून ठेवली आहे. (संगीन मी स्वतः तुझ्या हाती सोपवली आहे.)

अशुभ गोष्टींची छायाही तुझ्यावर मी पडू देणार नाही. वीरमाता जिजाई आणि झाशीची लढवय्यी राणी लक्ष्मीबाई यांच्याशी माझे नाते आहे. तुझ्या शस्त्रांना (बंदुकांना) अस्त्रांना माय भवानी उदंड शक्ती देईल. भवानीमातेचा आशीर्वाद तुझ्या पाठीशी आहे. रणांगणावर लढताना तू श्रीछत्रपती शिवाजी महारांजाच्या पराक्रमाचे स्मरण कर. विजयी होऊन ये नि माझ्यापोटी जन्म घेतलास याची मला धन्यता वाटेल. तू आलास की माझ्या हातांनी प्रेमाने मी तुला दूधभात भरवीन.

Balbharti Maharashtra State Board Class 9 Marathi Solutions Kumarbharti Chapter 20 आपुले जगणे…आपुली ओळख! Notes, Textbook Exercise Important Questions and Answers.

Maharashtra State Board Class 9 Marathi Kumarbharti Solutions Chapter 20 आपुले जगणे…आपुली ओळख! (कविता)

9th Std Marathi Kumarbharati Digest Chapter 20 आपुले जगणे…आपुली ओळख! Textbook Questions and Answers

1. खालील कोष्टक पूर्ण करा:

प्रश्न 1.
खालील कोष्टक पूर्ण करा:

उत्तर:

2. आकृती पूर्ण करा:

प्रश्न 1.
आकृती पूर्ण करा:

उत्तर:

3. खालील शब्दसमूहांचा अर्थ स्पष्ट करा:

प्रश्न 1.
खालील शब्दसमूहांचा अर्थ स्पष्ट करा:
(अ) पटकुर पसरू नको.
(आ) व्यर्थ कोरडा राहु नको.
(इ) कर्तृत्वाचे घडवी वेरूळ.
उत्तर:
(अ) पटकुर पसरू नको: अंगावर पवित्रतेची वस्त्रे पांघरावीत. मंगलमय जीवन असावे. चिंध्या झालेले जीर्ण वस्त्र पांघरू नये. म्हणजे आपल्या व्यक्तिमत्त्वात केविलवाणेपणा व दीनवाणेपणा नसावा. दुसऱ्यांनी आपली कीव करावी, असे वर्णन करू नये.
(आ) व्यर्थ कोरडा राहु नको: स्वत:च्या दु:खाचे प्रदर्शन करीत रडत न राहता, हृदयात इतरांविषयी करुणा असावी. समाजातील दु:खांविषयी अंत:करणात ओलावा असावा. उगाचच कोते मन करून भावनाशून्यतेने वागू नये. म्हणजेच कोरडे राहू नये.
(इ) कर्तृत्वाचे घडवी वेरूळ: पूर्वीच्या कलाकारांनी औरंगाबादजवळील डोंगरात वेरूळ येथे भव्य लेणी कोरली. पिढ्यान्पिढ्या हे शिल्प कोरण्यात खर्ची पडल्या. आजमितीस वेरूळचे हे शिल्प जगप्रसिद्ध आहे. त्याप्रमाणे जीवन जगताना आपल्या कर्तबगारीचे वेरूळ घडवावे, असे कवी म्हणत आहेत.

4. काव्यसौंदर्य:

प्रश्न (अ)
‘पावित्र्याची पांघर वस्त्रे, होऊन पटकुर पसरू नको’ या ओळीतील विचारसौंदर्य स्पष्ट करा.
उत्तर:
माणसाने आपले आयुष्य कसे जगावे हे सांगताना कवी म्हणतात-श्रीमंतीचा बडेजाव दाखवणारी किमती वस्त्रे घालणे, योग्य नव्हे. म्हणजे श्रीमंतीचे प्रदर्शन करू नये. मनाची शुद्धता महत्त्वाची आहे. मन पवित्र हवे. मंगलतेची वस्त्रे घालावीत. स्वत:चे जीवन चिंध्या झालेल्या पटकुराप्रमाणे दीनवाणे, लाचार असू नये. स्वत:च्या मनाचे मलीन, घाणेरडे वस्त्र करू नये. मनाच्या पावित्र्याचा विचार या ओळींत मांडला आहे.

प्रश्न (आ)
‘शोभेहुनही श्रेष्ठ स्वच्छता, आदिमंत्र हा विसरू नको,’ या ओळीत दडलेल्या अभियानाची गरज तुमच्या शब्दांत स्पष्ट करा.
उत्तर:
दिखाऊ प्रदर्शनापेक्षा स्वच्छता महत्त्वाची आहे. शोभेचा बडेजाव करणे व्यर्थ आहे. मनाची शुद्धता व परिसराची स्वच्छता असावी, हा बीजमंत्र कधी विसरू नये, अशी कवींनी या ओळीतून शिकवण दिली आहे. या ओळीत स्वच्छता अभियान दडलेले आहे. स्वच्छता राखली की रोगराई होत नाही. आरोग्य धोक्यात येत नाही. शुद्ध मोकळी हवा व निर्मळ पाणी मिळते. गाडगेबाबा गावेच्या गावे झाडून स्वच्छ करीत. सेनापती बापटांनी स्वच्छतेचा वसा आपणांस दिला आहे. ‘स्वच्छता हा परमेश्वर आहे,’ असे सुवचन आहे. ‘शोभेपेक्षा स्वच्छता श्रेष्ठ आहे,’ या मूलमंत्रात स्वच्छतेची महती कवींनी सांगितली आहे व स्वच्छता अभियानाचा पुरस्कार केला आहे.

5. स्वमत:

प्रश्न (अ)
स्वकर्तृत्व घडवताना कवितेतील विचार कसा मार्गदर्शक ठरेल, ते सविस्तर लिहा.
उत्तर:
स्वत:चे उत्तुंग कर्तृत्व हीच स्वत:ची ओळख आहे, हे , सांगताना कवींनी कवितेतून काही सुविचारांचे मार्गदर्शन केले आहे. दिवा होऊन जगाला प्रकाश दयावा. चाकूसारखी धार आपल्या है वागण्यात नसावी. नित्य वाचन, लेखन, मनन, व्यायाम करावा. एकही , क्षण कामाशिवाय वाया दवडू नये. मन पवित्र असावे. शोभेहून स्वच्छता श्रेष्ठ हा मूलमंत्र ध्यानी ठेवावा.

नम्र असावे, उगाच अढी ठेवून कुणालाही खिजवू नये. उदात्त विचार बाळगावेत. लाचारी पत्करू नये. कुणाला छळू नये, वाद घालू नये. स्वसामर्थ्याने संकटाचा गोवर्धन पेलावा. दुसऱ्याविषयी मनात करुणा असावी. नवनवीन विचारांचे मार्ग अंगिकारावेत. चांगल्या मूल्यांवर श्रद्धा असावी. भेदरून न जाता, धैर्याने वागावे. मातृभूमीचे व मातीचे ऋण फेडावे. अशा प्रकारे स्वकर्तृत्वाचे वेरूळ (शिल्प) उभारावे असे मार्गदर्शक विचार कवितेत मांडले आहेत.

प्रश्न (आ)
आपल्या जगण्यातून आपली ओळख व्हावी, यासाठी पाळायची पथ्ये कवितेच्या आधारे लिहा.
उत्तर:
आपणच आपल्या जीवनाचे शिल्पकार असतो. आपल्या वर्तनातून आपली ओळख जगाला होते. त्यासाठी जगताना काही पथ्ये पाळणे आवश्यक आहे. एकही क्षण कार्याशिवाय वाया दवडू नये, कार्यरत असावे, पावित्र्याचे वास्तव्य मनात असावे. नम्रतेचे वर्णन असावे, दुसऱ्यांना खिजवून त्रास देऊ नये. उदात्त विचार मनी बाळगावेत.

शोभेपेक्षा स्वच्छता श्रेष्ठ, हे मनी ठसवावे. वाद, भांडण करू नये. उलट दुसऱ्यांबद्दल मनात अपार करुणा असावी. उत्तम मूल्यांवर निष्ठा ठेवून संकटांचा मुकाबला करावा. न घाबरता धैर्याने व हिमतीने आयुष्य कंठावे. स्वकर्तृत्वाचे वेरूळसारखे शिल्प उभारून मातृभूमी व माती यांचे उपकार फेडावेत.

Marathi Kumarbharati Textbook Std 9 Answers Chapter 20 आपुले जगणे…आपुली ओळख! Additional Important Questions and Answers

1. पुढील कवितेच्या आधारे दिलेल्या सूचनांनुसार कृती करा:

कृती 1 : (आकलन)

प्रश्न 1.
आकृती पूर्ण करा:

उत्तर:

प्रश्न 2.
सहसंबंध जोडा:

उत्तर:

कृती 2 : (आकलन)

प्रश्न 1.
पुढीलपैकी असत्य विधान ओळखा:
1. नव्या मार्गाने जाण्यास घाबरावे.
2. उगाचच वाद घालू नये.
3. ज्यावर श्रद्धा ते काम करावे.
4. भेकड होऊन मुळूमुळू रडू नये.
उत्तर:
असत्य विधान : नव्या मार्गाने जाण्यास घाबरावे.

प्रश्न 2.
चौकटी पूर्ण करा:

उत्तर:

1. [शोभेपेक्षा स्वच्छता श्रेष्ठ आहे]
2. [जे उदात्त असते तेथे]
3. [वेरूळ]
4. [मातृभूमी] व [माती]

कृती 3 : (दोन ओळींचा सरळ अर्थ)

प्रश्न 1.
नित्य घडावे वाचन, लेखन… क्षण कार्याविण दवडु नको
नित्य परवचा, व्यायामाविण झोप घ्यावया पडु नको!
उत्तर:
माणसाने आयुष्यात वर्तन कसे करावे याविषयी उपदेश करताना कवी संदीप खरे म्हणतात की मन सुसंस्कृत करण्यासाठी नेहमी वाचन व लेखन करावे. एक क्षणही कार्य केल्याशिवाय राहू नये. नित्य नेमाने परवचा म्हणणे, व्यायाम करणे यांना डावलून झोपा काढू नयेत.

1. पुढील कवितेवर दिलेल्या मुद्द्यांच्या आधारे कृती सोडवा:

प्रश्न 1.
कविता – आपुले जगणे… आपुली ओळख!
उत्तर:
आपुले जगणे… आपुली ओळख!
1. प्रस्तुत कवितेचे कवी/कवयित्री → संदीप खरे.
2. कवितेचा विषय → तरुण पिढीने कसे वर्तन ठेवावे व कोणकोणत्या गोष्टी टाळाव्यात यांचे मार्गदर्शन या कवितेत केले आहे.
3. कवितेतील दोन शब्दांचे अर्थ →

1. दिवा = दीप
2. कार्य = काम
3. झोप = निद्रा
4. पावित्र्य = मांगल्य
5. नयन = डोळे
6. अश्रू = आसू
7. करुणा = दया
8. पथ = मार्ग
9. काटा = कंटक
10. हिंमत = धैर्य.

4. कवितेतून मिळणारा संदेश → आपले जगणे सत्यम्, शिवम्, सुंदरम् करावे. लेखन-वाचनाने ज्ञान वाढवावे. माणुसकी जपावी. कुणाला कुत्सित बोलू नये, मत्सर करू नये. कर्तृत्वाचे शिखर उभारून आदर्शवत पवित्र जीवन जगण्याचा संदेश ही कविता देते.

5. कवितेची भाषिक वैशिष्ट्ये → या कवितेत ‘फटका’ हा पूर्वापार चालत आलेला छंदप्रकार वापरला आहे. काय करावे व काय करू नये, याचे थेट संवादात्मक वर्णन फटक्यात केलेले असते. उपदेशात्मक गाभा असतो, जो या कवितेत तंतोतंत पाळला आहे. कुठेही प्रतीकांच्या व प्रतिमांच्या जंजाळात ही कविता अडकलेली नाही. थेट संवाद साधण्याची विलक्षण हातोटी यात आहे. भाषा परखड व ओघवती असल्यामुळे हृदयाला जाऊन भिडते. यमकप्रधान कविता असूनही एक संथ, लांबलचक अंतर्गत लय कवितेला पोषक ठरली आहे.

6. कवितेतून व्यक्त होणारा विचार → जीवनात कसे वागावे व कसे वागू नये, याचा परिपाठ दिला आहे.

7. कवितेतील दोन ओळींचा सरळ अर्थ: ‘तुडवित राने खुशाल जावे, नव्या पथाला भिउ नको ज्यावर श्रद्धा प्राणाआतुन ते केल्याविण राहु नको!
→ माणसाने कसे वागावे हे सांगताना कवी म्हणतात -नवनवीन ज्ञानाची राने आनंदाने तुडवीत जावीत. नवीन मार्गाने चालण्यास म्हणजे नवीन विचार अंगिकारण्यास भीती बाळगू नये. ज्या तत्त्वांवर निष्ठा असेल, ती कार्ये केल्याशिवाय राहू नये.

8. कविता आवडण्याची वा न आवडण्याची कारणे → या कवितेत तरुण पिढीला नेमके व सखोल मार्गदर्शन केले आहे. आपले जगणे कसे मूल्यवान व अर्थपूर्ण व्हावे, याचा नेमक्या शब्दांत व थेट उपदेश केला आहे. लाचारीचे जिणे नको; तर स्वाभिमानाने जगणे कसे असावे, याचा पाठ या कवितेत दिला आहे. आधुनिक वैफल्यग्रस्ततेत आशादायी व आदर्श जीवनाचे चित्रण या कवितेत केले असल्यामुळे ही कविता मला भावली.

1. पुढील ओळींचे रसग्रहण तुमच्या शब्दांत करा:

प्रश्न 1.
‘कर्तृत्वाचे घडवी वेरुळ, कर्तव्याला मुकु नको मातेसह मातीचे देणे फेडायाला चुकू नको!’
उत्तर:
आशयसौंदर्य : तरुण पिढीने आपली वागणूक कशी ठेवावी व कोणत्या सकारात्मक गोष्टी कराव्यात नि कोणत्या गोष्टी टाळाव्यात याचे डोळस मार्गदर्शन कवी संदीप खरे यांनी ‘आपुले जगणे… आपुली ओळख!’ या कवितेत केले आहे. आपले जगणे मूल्यवान असावे. माणुसकी जपावी. कर्तृत्वाचे शिखर उभारून आदर्शवत पवित्र जीवन जगण्याची शिकवण ही कविता देते.

काव्यसौंदर्य: कवितेत नवीन तरुण पिढीला नेमके व सखोल मार्गदर्शन करताना कवी म्हणतात-आपले जीवन मूल्यवान व अर्थपूर्ण करून स्वाभिमानाने जगावे. उपरोक्त ओळीत त्यांनी वेरूळच्या लेण्याचा संदर्भ दिला आहे. वेरूळचे लेणे हे महाराष्ट्राचे भूषणावह शिल्प आहे. अशा प्रकारे आयुष्यात कर्तृत्वरूपी वेरूळची लेणी घडवावी. उत्तुंग कर्तृत्व करावे. कर्तव्याला कधी नाकारू नये. या मातृभूमीचे अनंत उपकार आपल्यावर आहेत. त्या उपकारांची परतफेड करायला चुकू नये.

भाषिक वैशिष्ट्ये : या कवितेत ‘फटका’ या पूर्वापर चालत आलेला छंदप्रकार वापरला आहे. काय करावे व काय करू नये, याचे थेट संवादात्मक वर्णन फटक्यात केलेले असते. उपदेशात्मक गाभा असतो, जो या कवितेत तंतोतंत पाळला आहे. कुठेही प्रतीकांच्या व प्रतिमांच्या जंजाळात ही कविता अडकलेली नाही. थेट संवाद साधण्याची विलक्षण हातोटी यात आहे. भाषा परखड व ओघवती असल्यामुळे हृदयाला जाऊन भिडते. यमकप्रधान कविता असूनही एक संथ, लांबलचक अंतर्गत लय कवितेला पोषक ठरली आहे.

भाषाभ्यास:

(अ) व्याकरण घटकांवर आधारित कृती:

1. समास:

प्रश्न 1.
विग्रहावरून समास लिहा:
उत्तर:

1. ऊन आणि पाऊस → इतरेतर द्वंद्व
2. सात स्वर्गांचा समूह → द्विगू
3. गुरे, वासरे वगैरे → समाहार वंद्व
4. महान असे ऋषी → कर्मधारय
5. न्याय किंवा अन्याय → वैकल्पिक वंद्व

(आ) भाषिक घटकांवर आधारित कृती:

1. शब्दसंपत्ती:

प्रश्न 1.
समानार्थी शब्दांच्या जोड्या लावा:

उत्तर:

1. दिवा = दीप
2. नयन = डोळे
3. भेकड = भित्रा
4. करुणा = दया.

प्रश्न 2.
विरुद्धार्थी शब्द लिहा:

1. भेकड
2. व्यर्थ
3. नम्र
4. श्रेष्ठ.

उत्तर:

1. भेकड × धीट
2. व्यर्थ × सार्थ
3. नम्र × उद्धट
4. श्रेष्ठ × कनिष्ठ.

प्रश्न 3.
शब्दसमूहांबद्दल एक शब्द लिहा:

1. दररोज प्रसिद्ध होणारे
2. आठवड्याने प्रसिद्ध होणारे
3. महिन्याने प्रसिद्ध होणारे
4. वर्षाने प्रसिद्ध होणारे

उत्तर:

1. दैनिक
2. साप्ताहिक
3. मासिक
4. वार्षिक

प्रश्न 4.
एकवचन लिहा:

1. वस्त्रे
2. वाटा
3. मंत्र
4. राने.

उत्तर:

1. वस्त्र
2. वाट
3. मंत्र
4. रान.

2. लेखननियम:

प्रश्न 1.
अचूक शब्द ओळखा:
उत्तर:
1. कर्तृत्व, कर्तृत्त्व, करुत्व, कतृत्व. – कर्तृत्व
2. गोर्वधन, गेवर्धन, गोवधर्न, गोवर्धन. – गोवर्धन

3. पारिभाषिक शब्द:

प्रश्न 1.
पुढील इंग्रजी पारिभाषिक शब्दांचे मराठी अर्थ लिहा:
1. General Meeting
2. Bonafide Certificate.
उत्तर:
1. सर्वसाधारण सभा
2. वास्तविकता प्रमाणपत्र.

आपुले जगणे…आपुली ओळख! Summary in Marathi

कवितेचा आशय:

जीवनामध्ये कसे वागावे व कसे वागू नये, याचा आदर्शपाठ या कवितेत कवीने सोप्या शब्दांत मांडला आहे. उत्तुंग कर्तृत्व करावे व मातीचे ऋण फेडावे, हा संदेश दिला आहे.

शब्दार्थ:

1. उपरे – परके, खोटे, लटके.
2. नित्य – नेहमी, सतत.
3. कार्याविण – कामाशिवाय.
4. दवडू नको – वाया घालवू नको.
5. पावित्र्य – मांगल्य, पवित्रता.
6. वस्त्रे-कपडे.
7. पटकूर – चिंध्या झालेले कापड.
8. आदिमंत्र – मूलतत्त्व.
9. नम्र – शालीन, लीन.
10. सौम्य – फिकट, साधे.
11. उगा – उगाच, बळेच, मुद्दाम.
12. अढी – डंख, हेवा, मत्सर, अटकळ.
13. खिजवणे – चिडवणे, त्रास देणे.
14. तयावर – त्याच्यावर.
15. फुकाची – फुकटची, उगीच.
16. लोचट – हावरेपणा.
17. बुळचट – बावळट, मिळमिळीत.
18. उदात्त – भव्य, दिव्य.
19. ताठर – ताठ, गर्विष्ठ.
20. माथा – मस्तक, शीर, डोके.
21. पेल – उचलून धर, धरून ठेव, झेल.
22. वाद – भांडण.
23. नयनी – डोळ्यांत.
24. दुसऱ्यास्तव – इतरांसाठी.
25. करुणा – दया.
26. व्यर्थ – निरर्थक, फुकट.
27. पथाला – रस्त्याला, मार्गाला.
28. श्रद्धा – निष्ठा, विश्वास.
29. भेकड – भित्रा.
30. गुळमुळ – गुळमुळीत.
31. मातेसह – आईसकट (मातृभूमी).
32. देणे – ऋण, कर्ज.

टिपा:

1. परवचा – पाढे पाठ करणे.
2. गोवर्धन – गोकुळातील एक पर्वत. अतिवृष्टीपासून लोकांना वाचवण्यासाठी श्रीकृष्णांनी हा पर्वत एका करंगळीवर उचलून धरला, अशी आख्यायिका आहे.
3. कंस – श्रीकृष्णाचा मामा. याने श्रीकृष्णाच्या आईवडिलांना (देवकी-वसुदेव) कैदेत ठेवले होते.
4. वेरूळ – डोंगरात खोदलेली लेणी. (औरंगाबाद)

वाक्प्रचार व त्यांचे अर्थ:

1. अढी नसणे – (कुणाबद्दल मनात) डंख नसणे.
2. कडी करणे – वरचढ ठरणे.
3. हांजी हांजी करणे – लाचारी पत्करणे.
4. धमकावणे – धमकी देणे.
5. भेदरणे – घाबरणे.
6. मातीचे देणे फेडणे – मातृभूमीचे उपकार फेडणे.

कवितेचा भावार्थ:

माणसाने आयुष्यात कसे वागावे, हे सांगताना कवी म्हणतात – आपले जीवन हीच आपली ओळख असते. दुसऱ्यांच्या गुणांची नक्कल करून आयुष्य अर्धवट जगू नये. दिवा होऊन जगाला प्रकाश दयावा. चाकू बनून कुणाचेही म्हणणे कापू नको. (दुष्टपणा करू नये, क्रूर होऊ नये.) नेहमी वाचन-लेखन करावे. त्याने मन सुसंस्कृत होते. कामाशिवाय एकही क्षण वाया दवडू नको. आळशीपणा करू नको. नित्यनेमाने परवचा म्हणणे, व्यायाम करणे, यांशिवाय उगाच झोप काढू नको.

पवित्रतेची वस्त्रे अंगावर नेस. स्वत:चे जगणे फाटलेले वस्त्र होऊ देऊ नको. मनात मांगल्य असावे, उथळ बडेजावापेक्षा, कचकड्या शोभेपेक्षा स्वच्छता मोठी असते, हा मूलमंत्र कधीही विसरू नको. (साधी राहणी, पवित्र विचार अंगिकारावा, उगाच बेगडी फुशारकी करू नये.) नम्रपणा असावा. शांत वृत्तीने पाहावे. उगाचच मनात दुसऱ्याबद्दल अढी ठेवू नये. दुसऱ्याला चिडवण्यासाठी उगाचच वरचढपणा करू नये.

हांजी हांजी करून फुकटची लाचारी करू नये. असा लोचटपणा व बुळचटपणा घातक असतो. पण जर एखादे भव्य-दिव्य काही कार्य दिसले, तर त्याबाबत ताठरता, दुरभिमान मुळीच बाळगू नको. तुझ्या सामर्थ्याने तू गोवर्धन पेल. संकटे झेल. कंसासारखे इतरांना छळू नको. उगाचच वाद, भांडणे करू नयेत, परंतु कुणी धमकी दिली तर पळू नये. निडरपणे बोलावे. स्वार्थीपणे स्वत:च्या दु:खाने डोळ्यांत आसवे आणू नको. दुसऱ्यासाठी मनात करुणा, दया असावी. परोपकार करावा. मनात E मायेचा ओलावा असावा. मन उगाचच कोरडे, भावनाशून्य ठेवू नकोस.

आनंदाने नवनवीन क्षेत्रांतील ज्ञान मिळवावे. राने तुडवावीत. नवीन मार्गावर चालण्यास, नवीन विचारांना अंगिकारण्यास घाबरू नये. अंतर्मनातून ज्या तत्त्वांवर निष्ठा असेल, ते कार्य केल्याशिवाय राहू नये. (जिथे इच्छा तिथे मार्ग) मार्गात काटेही (संकटे) असतात पण त्यांना भिऊन राहू नको, डगमगू नको. जो धैर्य दाखवतो, त्याची जगात किंमत राहते. जग त्याला नावाजते. भेकडपणा, गुळमुळीतपणा, पळपुटेपणा धरून मुळूमुळू रडत बसू नये. आयुष्यात कर्तृत्वरूपी वेरुळाची लेणी घडव. उत्तुंग अकल्पित कर्तृत्व कर. कर्तव्याला नाकारू नको. या मातृभूमीचे ऋण तुझ्यावर आहे. या मातीचे उपकार फेडायला चुकू नको.

Balbharti Maharashtra State Board Class 9 Marathi Solutions Kumarbharti Chapter 13 थोडं ‘आ’ भारनियमन करूया Notes, Textbook Exercise Important Questions and Answers.

Maharashtra State Board Class 9 Marathi Kumarbharti Solutions Chapter 13 थोडं ‘आ’ भारनियमन करूया

9th Std Marathi Kumarbharati Digest Chapter 13 थोडं ‘आ’ भारनियमन करूया Textbook Questions and Answers

1. काय घडते ते पाठाच्या आधारे लिहून वाक्य पूर्ण करा:

प्रश्न 1.
काय घडते ते पाठाच्या आधारे लिहून वाक्य पूर्ण करा:
(अ) आदर मनात तुडुंब भरून असल्यास ………………..
(आ) खूप जवळच्या गहिऱ्या नात्यात शब्दांनी आभार मानल्यास ……………………….
(इ) मित्रमैत्रिणीने आभार मानल्यास ………………………………….
(ई) लेखिकांच्या मते ‘आ’भारनियमन केल्यास ……………….
उत्तर:
(अ) आदर मनात तुडुंब भरून असल्यास तो कृतीत सहजासहजी उतरतो.
(आ) खूप जवळच्या गहिऱ्या नात्यात शब्दांनी आभार मानल्यास उभयपक्षी अवघडलेपणा येतो. गहिरेपणा उणावून नुसती औपचारिकता उरते.
(इ) मित्रमैत्रिणीने आभार मानल्यास आपल्या पाठीत एक सणसणीत धपाटा मिळतो आणि ‘जादा आगाऊपणा केलास तर याद राख’ अशी धमकीही मिळते.
(ई) लेखिकांच्या मते, ‘आ’भारनियमन केल्यास त्या शब्दांमधला जिव्हाळा आणि भावनांची ऊब संपून जाणार नाही.

2. पाठातील उदाहरणे शोधा:

प्रश्न 1.
पाठातील उदाहरणे शोधा:

उत्तर:

3. चूक की बरोबर ते ओळखा:

प्रश्न 1.
चूक की बरोबर ते ओळखा:
(अ) आभार आणि अभिनंदन या शब्दांत माणसं अनेकदा गल्लत करतात.
(आ) भारतीय संस्कृतीत भावनांचे प्रदर्शन करणे आदर्श मानले जाते.
(इ) ममनात आदर असेल तर तो कृतीत दिसतो.
(ई) लआभार मानण्याचा अतिरेक चांगला नव्हे.
उत्तर:
(अ) बरोबर
(आ) चूक
(इ) मबरोबर.
(ई) लबरोबर

4. कारणे लिहा.

प्रश्न 1.
कारणे लिहा.

उत्तर:

5. पाठातील विनोद निर्माण करणारी वाक्ये शोधा.

प्रश्न 1.
पाठातील विनोद निर्माण करणारी वाक्ये शोधा.
उत्तर:

1. साधं घोटभर पेय दिलं तरी हातभर बैंक्यू म्हणतात.
2. बैंक्यू म्हणता येणं हा सुसंस्कृतपणाचा कडेलोट आहे, असं काही काळ वाटून गेलं.
3. तू कसली ग माझी ऑक्यू? मीच तुझी बैंक्यू.
4. त्याला बैंक्यू दिलेस का पण?
5. तुला कितीही बँक्यू केलं तरी कमीच.
6. आभार न मानण्याचा मॅनरलेसपणा त्याच्या खाती रुजू होणार नव्हता.
7. जन्मल्या जन्मल्या आईबापांचे आभार मानणारे कार्ड आणि वर गेल्यावर खालून वेळच्या वेळी आपल्याला नीट वर पोचवणाऱ्यांचे आभार कार्ड अजून माझ्या पाहण्यात आलेलं नाही.
8. बँक्स फॉर मॅरिंग हं. लग्न केल्याबद्दल मनःपूर्वक आभार.

6. खाली दिलेल्या शब्दांसाठी मराठी भाषेतील शब्द लिहा:

प्रश्न 1.
खाली दिलेल्या शब्दांसाठी मराठी भाषेतील शब्द लिहा:

1. कॅप्शन
2. टेन्शन
3. आर्किटेक्ट
4. ऑपरेशन.

उत्तर:

1. षवाक्य
2. ताणतणाव
3. वास्तुविशारद
4. शस्त्रक्रिया.

7. खाली दिलेल्या शब्दांचा तुम्हांला समजलेला अर्थ लिहा:

प्रश्न 1.
सुसंस्कृतपणाचा कडेलोट.
उत्तर:
शिष्टाचार पाळणे हे सुसंस्कृतपणाचे लक्षण मानले जाते. इंग्रज आपल्यापेक्षा श्रेष्ठच आहेत, असे मनोमन मानणारे खूप लोक आहेत. इंग्रज म्हणजे सुसंस्कृतच; ते जे जे करतात, ते ते सर्व सुसंस्कृतपणाचे लक्षणच होय; असे या लोकांना वाटते. इंग्रज लोक उठता-बसता बैंक्यू म्हणतात, म्हणून त्यांचे आंधळे अनुकरण करणारेही सतत बैंक्यू म्हणतात. या लोकांच्या मते, बँक्यू म्हणणे हा सुसंस्कृतपणाचा अत्युच्च बिंदू होय. हा सर्व भाव ‘सुसंस्कृतपणाचा कडेलोटच’ या शब्दांतून व्यक्त होतो.

प्रश्न 2.
घाऊक आभार
उत्तर:
सर्व व्यक्तींचे सर्व बाबींसाठी एकदाच एकत्रित आभार मानणे म्हणजे ‘घाऊक आभार’ मानणे होय.

8. स्वमत:

प्रश्न (अ)
‘आभार मानणे,’ या शिष्टाचाराविषयीचे तुमचे मत लिहा.
उत्तर:
आपण अनेक कामे पार पाडतो. ही कामे आपण पूर्णांशाने केलेली नसतात. त्या कामांना अनेकांचा हातभार लागलेला असतो. तरी कामाचे श्रेय आपल्याला मिळते. त्याचे फायदेही आपल्याला मिळतात. वास्तविक आपल्या एकट्याचा तो अधिकार नसतो. त्यावर इतरांचाही अधिकार असतो. पण श्रेय व फायदे मात्र आपण एकटेच घेतो. हे अनुचित होय. इतरांच्या सहकार्याशिवाय आपण काहीही करू शकत नाही. म्हणून इतरांच्या सहकार्याबद्दल, त्यांच्या मदतीबद्दल कृतज्ञता व्यक्त केली पाहिजे. आभार मानणे हा कृतज्ञता व्यक्त करण्याचाच प्रकार आहे.

लेखिका मंगला गोडबोले म्हणतात, तेही खरेच आहे. आभाराचा अतिरेक चालू आहे. क्षुल्लक कारणासाठीसुद्धा आभार मानले जातात. बऱ्याच वेळा समोरच्या व्यक्तीबद्दल कृतज्ञता व्यक्त करण्याऐवजी आपण स्वतः सुसंस्कृत आहोत, असे दाखवण्यासाठी आभार मानले जातात. असे होते तेव्हा आभाराचा मूळ उद्देशच नष्ट होतो. म्हणून है आभार मानताना तारतम्य बाळगले पाहिजे. मुख्य म्हणजे अत्यंत प्रामाणिकपणे आभार मानले पाहिजेत.

प्रश्न (आ)
पाठाच्या शीर्षकातून तुम्हांला समजलेला विनोद तुमच्या शब्दांत स्पष्ट करा.
उत्तर:
भारनियमन म्हणजे विजेच्या पुरवठ्यात केलेली काटकसर. भारनियमन, काटकसर हे गोंडस शब्द झाले. वस्तुस्थिती अत्यंत विदारक आहे. मुंबईसारख्या शहरात 24 तास वीजपुरवठा चालू असतो. पण ग्रामीण भागात मात्र 10-10, 15-15 तास वीजपुरवठा बंद असतो. ग्रामीण जनतेला यामुळे अनेक हालअपेष्टांना तोंड दयावे लागते. शासन या हालअपेष्टा कमी करीत नाही, मात्र या हालअपेष्टांना गोंडस नाव देते – ‘भारनियमन’!

उलटी परिस्थिती दुसऱ्या ठिकाणी दिसते. लोक सुसंस्कृतपणाच्या कल्पनेच्या ओझ्याखाली ‘आभार’, ‘सॉरी’ वगैरे शब्दांचा वारेमाप वापर करतात. अत्यंत क्षुल्लक कारणासाठीसुद्धा या शब्दांची उधळमाधळ केली जाते. अनेकदा ही उधळण हास्यास्पद पातळीवर जाऊन पोहोचते. म्हणून लग्न करणाऱ्या नवऱ्या मुलाचे ‘लग्न केल्याबद्दल आभार’ मानले जातात. खरे तर ‘आभारा’ची काटकसर करणे आवश्यक आहे. वीजपुरवठ्यातील अपुरेपणा, ‘आभार’ इत्यादी शब्दांची उधळण या दोन विपरीत स्थितींचा निर्देश करण्यासाठी आणि ‘आभार’ मानण्याबाबत लोकांनी विवेक बाळगावा म्हणून ‘भार’ – ‘आभार’ या शब्दांची कोटी करीत लेखिकांनी ‘आभारनियमन’ हा शब्द घडवला आणि त्यावरून पाठाचे शीर्षक तयार केले आहे.

उपक्रम:

प्रश्न 1.
दैनंदिन व्यवहारात शब्दांच्या रचनेमुळे निर्माण होणाऱ्या विनोदाची उदाहरणे शोधा व वर्गात त्यांचे सादरीकरण करा.

भाषाभ्यास:

अक्षरगणवृत्ते यापूर्वी आपण पाहिली आहेत. आता आपण काही मात्रावृत्तांचा परिचय करून घेऊया.

1. दिंडी: पहिल्या चरणात 9, दुसऱ्या चरणात 10 मात्रा असतात. तेही 3-2-2-2, 3-3-2-2 असे मात्रागणांचे गट पडतात. ‘दिंडी’ हे मराठीतील जुने वृत्त आहे.
उदा., घोष होता ग्यानबा तुकाराम
राऊळाची ही वाट सखाराम
करी भक्ती चित्तात नृत्यलीला
पहा दिंडी चालली पंढरीला
12 22 212 2122
= 9 = 10

2. आर्या: आर्या हे देखील जुने वृत्त आहे. मोरोपंतांच्या आर्या प्रसिद्ध आहेत. आर्या वृत्तात 30 मात्रा असून 12+18 असे गट पडतात.
उदा., सुश्लोक वामनाचा अभंगवाणी प्रसिद्ध तुकयाची
ओवी ज्ञानेशाची किंवा आर्या मयूरपंताची
22 2222 22 22 121222
= 12 = 18
चार चरण असतील तर पहिल्या आणि तिसऱ्या चरणात 12 मात्रा; दुसऱ्या आणि चौथ्या चरणात 18 मात्रा असतात.

Marathi Kumarbharati Textbook Std 9 Answers Chapter 13 थोडं ‘आ’ भारनियमन करूया Additional Important Questions and Answers

उतारा क्र. 1

1. पुढील उतारा वाचून दिलेल्या सूचनांनुसार कृती करा:

कृती 1 : (आकलन)

प्रश्न 1.
चूक की बरोबर ते लिहा:
1. आभार अनेकदा कृत्रिम झाल्याने खोटे वाटू लागतात.
उत्तर:
1. बरोबर.

प्रश्न 2.
आकृती पूर्ण करा:

उत्तर:

कृती 2 : (आकलन)

प्रश्न 1.
आकृती पूर्ण करा:

उत्तर:

प्रश्न 2.
रोजच्या व्यवहारात आभाराचे अति झालेले प्रकार:
1. क्षुल्लक कारणांसाठी ……………………
2. नुकतं बोलायला लागलेल्या मुलालाही ………………………..
उत्तर:
1. क्षुल्लक कारणांसाठी माणसे एकमेकांचे आभार मानताना दिसतात.
2. नुकतं बोलायला लागलेल्या मुलालाही ‘बँक्स-र्थंक्यू’ वगैरे बोलायला शिकवतात.

उतारा क्र. 2

1. पुढील उतारा वाचून दिलेल्या सूचनांनुसार कृती करा:

कृती 1 : (आकलन)

प्रश्न 1.
संकल्पना स्पष्ट करा:
1. आभारबाज.
उत्तर:
1. लहानमोठ्या सर्व कारणांसाठी, अगदी क्षुल्लक कारणांसाठीसुद्धा, सतत आभार मानण्याची चटक लागलेली व्यक्ती म्हणजे ‘आभारबाज’ होय.

कृती 2 : (आकलन)

प्रश्न 1.
माहिती लिहा:
अजूनही तयार न झालेली आभाराची कार्डे:
1. ………………………………..
2. ………………………………..
उत्तर:
अजूनही तयार न झालेली आभाराची कार्डे :
1. जन्मल्या जन्मल्या आई-बापांचे आभार मानणारे कार्ड.
2. मरण पावल्यावर खालून वेळच्या वेळी वर पोहोचवणाऱ्यांचे आभार मानणारे कार्ड.

प्रश्न 2.
का ते लिहा:
1. अलीकडच्या लहान मुलाच्या खात्यावर ‘मॅनरलेसपणा’ रुजू होणार नाही.
2. आभार मानणे दिवसेंदिवस कृत्रिम होत आहे.
उत्तर:
1. अलीकडच्या लहान मुलाच्या खात्यावर ‘मॅनरलेसपणा’ रुजू होणार नाही; कारण अगदी लहानपणापासून शिकवल्याप्रमाणे तो वेळच्या वेळी सर्वांचे न विसरता आभार मानतो.
2. आभार मानणे दिवसेंदिवस कृत्रिम होत आहे; कारण सर्व नात्यांना, सर्व निमित्तांना लागू होतील अशी छापील कार्डे सर्रास वापरली जातील. आभाराचे छापील कार्ड हाच कृत्रिमतेचा नमुना आहे.

कृती 3 : (स्वमत/अभिव्यक्ती)

प्रश्न 1.
शुभेच्छा कार्डे, आभार कार्डे, अभिनंदन कार्डे इत्यादींबद्दल तुमचे मत लिहा.
उत्तर:
शुभेच्छा कार्डे आकर्षक रितीने छापलेली असतात. कागद छान असतो. एकूण मांडणी सुरेख असते. शब्दांची रचनाही लक्षवेधक असते. पण तरीही मला मात्र ही कार्डे परकी परकी वाटत राहतात. याचे महत्त्वाचे कारण हे की ते शब्द माझे नसतात. त्यामुळे त्यांतून व्यक्त होणारी भावना मला माझी वाटत नाही. मला माझ्या आईबद्दल, बाबांबद्दल, माझ्या ताईबद्दल जे वाटते, ते त्या शब्दांत नसतेच. माझ्या माणसांशी असलेले माझे संबंध मलाच माहीत आहेत. कोणत्या गोष्टी आमच्यामध्ये महत्त्वाच्या आहेत, हे मलाच माहीत आहे. मला माझ्या ताईने पहिल्यांदा सायकल शिकवली.

मी तिच्याकडून फक्त सायकल चालवायला नाही शिकलो. मला आत्मविश्वास मिळाला. रस्त्यावर मागून-पुढून जाणाऱ्या गाड्या, मोटरसायकली, सायकली, रस्त्यावरून वाकडेतिकडे चालणारे लोक, रस्त्यावरील खड्डे या सगळ्यांना चुकवून सायकल चालवताना मनात जे काही चालते, ते शब्दांत सांगता येणार नाही. ताईशी बोलताना, ताईबद्दल बोलताना, माझ्या दृष्टीने ही गोष्ट महत्त्वाची असते. ती छापील कार्डामध्ये मिळूच शकत नाही. ही छापील कार्डे मला माझी वाटतच नाहीत.

उतारा क्र. 3

1. पुढील उतारा वाचून दिलेल्या सूचनांनुसार कृती करा:

कृती 1 : (आकलन)

प्रश्न 1.
अर्थ लिहा:
तोंड उघडल्याबद्दल आणि योग्य वेळी ते बंद केल्याबद्दल धन्यवाद.
उत्तर:
अनेकांना आपली छबी दूरचित्रवाणीवर दिसते, यातच धन्यता वाटत असते. संबंधित क्षेत्रात या लोकांचे काही योगदान नसते किंवा त्या क्षेत्राचा काही अभ्यासही नसतो. त्यामुळे दूरचित्रवाणीवरील कार्यक्रमात या लोकांना काही मौलिक विचार मांडता येत नाहीत. ते तोंड मिटून गप्प बसतात. काहीजण अकारण बडबड करून प्रेक्षकांचा वेळ वाया घालवतात. या दोघांवरही टीका करण्यासाठी लेखिका ‘तोंड उघडल्याबद्दल व योग्य वेळी ते बंद केल्याबद्दल’ त्यांना धन्यवाद देतात.

प्रश्न 2.
का ते लिहा:
1. नटवणाऱ्यांचे व नटवल्यामुळे ते सुंदर दिसत होते, असे मानणाऱ्यांचे आभार.
2. ज्यांनी किमान तीस सेकंद आमचा चॅनेल पाहिला त्यांना कोटी कोटी प्रणाम.
उत्तर:
1. दूरचित्रवाणीवरील काही कार्यक्रमांत सूत्रसंचालकांची गरज असते. संपूर्ण कार्यक्रम प्रवाहीपणे सुरळीत पार पाडणे हे सूत्रसंचालकांचे काम असते. पण अनेक सूत्रसंचालकांना स्वत:च्या नटण्यात जास्त रस असतो. मेकअपमनही त्यांना नटवण्यात गढून जातो. इतर अनेक जण सूत्रसंचालकांच्या कामापेक्षा त्यांच्या सुंदर दिसण्याचेच कौतुक अधिक करतात. लोकांच्या या हास्यास्पद वृत्तीची खिल्ली उडवण्यासाठी लेखिकांनी सूत्रसंचालकांना नटवणाऱ्यांचे व नटल्यामुळे ते सुंदर दिसत होते असे मानणाऱ्यांचे आभार मानले आहेत.

2. दूरचित्रवाणीवरील बहुतांश कार्यक्रम निर्बुद्ध असतात. त्यांत मध्ये मध्ये जाहिरातींचा धुमाकूळ असतो. त्यामुळे प्रेक्षक कोणताही कार्यक्रम मनापासून सलग पाहत नाहीत. जाहिराती व प्रायोजक मिळवण्यासाठी आपली वाहिनी लोकप्रिय आहे, हे दाखवण्याची वाहिन्यावाल्यांची धडपड चालू असते. वाहिन्यावाल्यांचा हा केविलवाणेपणा दाखवून देण्यासाठी, प्रेक्षकांना कोटी कोटी प्रणाम केले जातात, असे लेखिका म्हणतात.

कृती 2 : (आकलन)

प्रश्न 1.
पुढील वाक्याच्या आधारे लेखिका कशावर टीका करतात, ते लिहा:
आजच्या दिवसभरात ज्यांनी ज्यांनी मुलाखती दिल्या आणि हुकमी ‘मागे वळून पाहिलं’ त्यांचे आम्ही ऋणी आहोत. त्यांच्या दुखऱ्या मानांचे शतशः आभार.
उत्तर:
साधारणपणे वेगवेगळ्या क्षेत्रांत महत्त्वपूर्ण कामगिरी करणाऱ्यांच्या मुलाखती प्रसारित करण्यामागे त्यांच्या अनुभवाचा फायदा इतरांना मिळावा, ही अपेक्षा असते. हे मुलाखतदाते विशिष्ट शब्दप्रयोग करतात. त्यांपैकी एक असा : ‘इतक्या वर्षांनी आता मागे वळून पाहताना.’ दूरचित्रवाणीवर येणाऱ्या बऱ्याच मुलाखतदात्यांकडे सांगण्यासारखे काहीही नसते. पण मुलाखतीची ऐट दाखवण्यासाठी ‘मागे वळून पाहताना’ यांसारखे शब्दप्रयोग ते हमखास करतात. त्यांची खिल्ली उडवण्यासाठी लेखिका वरील वाक्य लिहितात.

प्रश्न 2.
आकृती पूर्ण करा:

उत्तर:

कृती 3 : (स्वमत/अभिव्यक्ती)

प्रश्न 1.
दूरचित्रवाणीच्या विविध वाहिन्यांवरील कार्यक्रमांविषयी तुमचे मत लिहा.
उत्तर:
दूरचित्रवाणीवरचे बहुतेक कार्यक्रम मनोरंजनाचे असतात. प्रायोजक व जाहिराती मिळवण्यासाठी प्रेक्षकसंख्या जास्त असावी लागते. म्हणून मग हे कार्यक्रम लोकप्रिय करण्याचा प्रयत्न होतो. त्यातून लोकानुनय केला जातो. साहजिकच पारंपरिक विचारांची चिकित्सा नसते. उलट त्यांचा प्रसारच केला जातो. तसेच, देवदेवतांच्या, बुवाबापूंच्या कार्यक्रमांची रेलचेल असते. चमत्कार दृश्यांची त्यात भर पडते. त्यामुळे अंधश्रद्धा बळकट होतात. वाहिनी लोकप्रिय करण्याच्या नादात अनिष्ट वृत्ती वाढीला लागत आहेत. हे सर्वच वाहिन्यांबाबत घडत आहे. हे भयंकर आहे. समाजाच्या सांस्कृतिक आरोग्याच्या दृष्टीने ही परिस्थिती धोक्याची आहे.

उतारा क्र. 4

1. पुढील उतारा वाचून दिलेल्या सूचनांनुसार कृती करा:

कृती 2 : (आकलन)

प्रश्न 1.
आकृती पूर्ण करा:

उत्तर:

प्रश्न 2.
पुढील घटनांचे परिणाम लिहा:

उत्तर:

कृती 3 : (स्वमत/अभिव्यक्ती)

प्रश्न 1.
या उताऱ्यात लेखिकांनी मांडलेल्या विचाराबाबत तुमचे मत लिहा.
उत्तर:
‘बैंक्यू/सॉरी’चा खूपच अतिरेक झाला आहे, यात शंकाच नाही. अनेकजण उठताबसता ‘बैंक्यू’ म्हणतात. लेखिकांच्या या मताशी मी पूर्ण सहमत आहे. तरीही मी थोडीशी जोड देऊ इच्छितो. बैंक्यूचा वापर केव्हा घडतो? जेव्हा व्यक्तींमधले संबंध औपचारिक असतात तेव्हा. औपचारिक संबंध नसतात, तेव्हा आईबाबा-मुले, मित्रमैत्रिणी यांच्यात उपचार नसतो. प्रेमाचा हक्क असतो. आम्हां मित्रांमध्ये असेच घडते. आम्ही प्रेमाने एकमेकांना काही देतो आणि हक्काने हवे ते मागून घेतो. अशा वेळी प्रेमाचा जोर जास्त असतो.

पण सार्वजनिक ठिकाणी मात्र उपचार पाळलेच पाहिजेत. बसमध्ये एखादयाच्या पायावर आपला पाय पडला, तर विनाविलंब ‘सॉरी’ म्हटलेच पाहिजे. आपण समोरच्या माणसाच्या वेदनेकडे सहानुभूतीने पाहतो, हे अशा वेळी सिद्ध होते. आपण बेदरकार नाही, हेही सिद्ध होते. लेखिका म्हणतात तसा अतिरेक करूच नये, हे खरे आहे. पण तारतम्याने या सॉरी/बैंक्यूचा वापर केला पाहिजे, असे मला वाटते.

उतारा क्र. 5

1. पुढील उतारा वाचून दिलेल्या सूचनांनुसार कृती करा:

कृती 1 : (आकलन)

प्रश्न 1.
चूक की बरोबर ते ओळखा:
1. अंतिम उत्पादन, कलाकृती उत्तम व्हायला हवी असेल, तर आर्थिक लाभ ज्याचा जास्त, त्याने जास्त निष्ठेने काम केले पाहिजे.
उत्तर:
1. चूक.

प्रश्न 2.
आकृती पूर्ण करा:

उत्तर:

कृती 2 : (आकलन)

प्रश्न 1.
कोण ते लिहा:

1. ‘आमचा’ सिनेमा, ‘आपलं’ पुस्तक, ‘आमचं’ नाटक असे शब्दप्रयोग करतात.
2. आपली निष्ठा कृतीने सिद्ध करील.
3. “बँक्स फॉर मॅरिंग हं,” असे बोलणारा.

उत्तर:

1. ‘आमचा’ सिनेमा : दिग्दर्शक – नटमंडळी
   1. ‘आपलं’ पुस्तक : लेखक – प्रकाशक
   2. ‘आमचं’ नाटक : लेखक – दिग्दर्शक.
2. लेखक.
3. नवऱ्या मुलाचा मित्र.

प्रश्न 2.
जोडीजोडीने व्यवहार करावे लागणाऱ्या तुम्हाला माहीत असलेल्या दोन जोड्या लिहा.
उत्तर:
1. शिक्षक – विदयार्थी
2. वक्ता – श्रोते.

कृती 3 : (स्वमत/अभिव्यक्ती)

प्रश्न 1.
‘प्रत्येकाने आपापली भूमिका चोख बजवावी लागते. तो अलिखित नियम असतो,’ या विधानावर तुमचे मत लिहा.
उत्तर:
जोडीजोडीने व्यवहार कराव्या लागणाऱ्या काहीजणांबद्दल लेखिकांचे हे मत आहे. जोडीतील दोघांपैकी एकाकडे व्यवहाराची सूत्रे असतात. अनेकदा ही सूत्रे ज्याच्याकडे अधिक घट्ट असतात, त्याच व्यक्तीला व्यवहाराचे फायदे अधिक असतात. हे सर्व खरे आहे. पण म्हणून जास्त फायदा असलेल्यानेच जास्त कष्ट घेऊन व जास्त निष्ठेने काम केले पाहिजे, असा नियम करता येणार नाही. असे केल्यास दोघांनाही तोटाच होईल. कोणी एकाने दुर्लक्ष केल्यास अंतिम फळ उत्तम असणार नाही. त्याचा तोटा दोघांनाही भोगावा लागेल.

नावाडी पैसे घेऊन लोकांना नदीपार करतो. नाव मध्यावर गेल्यावर दुर्दैवाने नावाड्याचा हात लचकला आणि त्याला होडी वल्हवता आली नाही तर? नावाड्याने पैसे घेतले आहेत. आम्ही त्याला मदत करणार नाही, अशी प्रवाशांनी भूमिका घेतली, तर प्रवाशांचा जीव धोक्यात येऊ शकतो. म्हणून दोघांनीही जास्तीत जास्त निष्ठेने काम केले पाहिजे; तरच अंतिम फळ उत्तम होईल. त्याचा दोघांनाही फायदा होईल.

उतारा क्र. 6

1. पुढील उतारा वाचून दिलेल्या सूचनांनुसार कृती करा:

कृती 1 : (आकलन)

प्रश्न 1.
काय घडते ते पाठाच्या आधारे लिहून वाक्य पूर्ण करा:
1. कामाच्या मोबदल्यात पैसे देत असल्यास …………………
उत्तर:
1. कामाच्या मोबदल्यात पैसे देत असल्यास लोक आभाराची काटकसर करतात.

प्रश्न 2.
पुढील सेवादात्यांचे दुर्गुण लिहा:
1. प्लंबर, इलेक्ट्रिशियन मंडळी.
2. इस्त्रीवाला.
उत्तर:
1. प्लंबर, इलेक्ट्रिशियन मंडळी सांगितलेल्या वेळेला घरी काम करायला येत नाहीत आणि जुने काम करताना नवीन काम निर्माण करून ठेवतात.
2. इस्त्रीवाला दिलेल्या तारखेला कपडे आणून देत नाही.

कृती 2 : (आकलन)

प्रश्न 1.
ठरलेल्या वेळी काम न करणाऱ्या तुम्हाला माहीत असलेल्या चार सेवादात्यांची नावे लिहा.
उत्तर:
वेळेवर काम न करणारे सेवादाते : गवंडी, सुतार, रंगारी, शिंपी.

प्रश्न 2.
लेखिकांनी सांगितलेली विविध सेवादात्यांची वृत्ती सांगा.
उत्तर:
विविध सेवादात्यांचा सर्वांत मोठा दुर्गुण म्हणजे ते कधीच ठरलेल्या वेळी येत नाहीत. दुसरे म्हणजे ते प्रामाणिकपणे काम करीत नाहीत. ते काम करून गेल्यावर काम चोख झाले असेल, अशी मनाला खात्री वाटत नाही. विविध सेवादात्यांची ही वृत्ती लेखिकांनी या उताऱ्यात अधोरेखित केली आहे.

कृती 3 : (स्वमत/अभिव्यक्ती)

प्रश्न 1.
या उताऱ्यात लेखिकांनी सांगितलेले सामाजिक व्यंग स्पष्ट करून सांगा.
उत्तर:
या उताऱ्यात काही सेवादात्यांच्या उणिवा लेखिकांनी सांगितल्या आहेत. ते ठरवलेल्या वेळी कामावर येत नाहीत. निष्ठापूर्वक काम करीत नाहीत. आपण आपले काम चोख करावे, अशी त्यांची इच्छाच नसते. त्यामुळे त्यांनी केलेले काम परिपूर्ण असेल, अशी खात्री बाळगता येत नाही. लेखिकांनी सांगितलेल्या या उणिवा आपल्या समाजाच्या प्रत्येक व्यक्तीत दिसून येतात. कोणत्याही पदावरील कोणाही व्यक्तीला उत्तम काम करण्याची इच्छाच नसते. विदयार्थी उत्तम काम करू इच्छित नाहीत. दुकानदार उत्तम वस्तू वाजवी भावात ग्राहकाला देण्याची इच्छा बाळगत नाही.

शासकीय कार्यालयातील कर्मचारी लोकांची कामे रेंगाळत ठेवण्यात धन्यता मानतात. अशी शेकडो उदाहरणे देता येतील. या वृत्तीमुळे समाजात पार पडणारे कोणतेही कार्य परिपूर्ण होत नाही. रस्ता बांधला की अल्पावधीतच खड्डे पडतात. घरे कोसळतात. या सर्व बाबींमुळे आपल्या समाजातील बांधवांचेच नुकसान होते. त्यांना उत्तम दर्जाच्या सेवा वा वस्तू मिळत नाहीत. साहजिकच त्यांना उत्तम दर्जाचे जीवन जगण्याची संधी मिळत नाही. आपली वृत्ती सुधारली तर देश सुधारेल, असे मला वाटते. कारण हे सर्व देशाच्या प्रगतीशी निगडित आहे.

उतारा क्र. 7

1. पुढील उतारा वाचून दिलेल्या सूचनांनुसार कृती करा :

कृती 1 : (आकलन)

प्रश्न 1.
पाठाच्या आधारे गाळलेल्या जागा भरून विधाने पूर्ण करा:
1. अपत्याची टॉन्सिलची शस्त्रक्रिया किरकोळ होती; पण आईच्या ———
2. ऑपरेशननंतर त्रासाचा लोप व्हावा, म्हणून
उत्तर:
1. अपत्याची टॉन्सिलची शस्त्रक्रिया किरकोळ होती; पण आईच्या दृष्टीने मुलाचं कोणतंच ऑपरेशन किरकोळ असूच शकत नाही..
2. ऑपरेशननंतर त्रासाचा लोप व्हावा, म्हणून पंधरा दिवस आइस्क्रीमचा उतारा होता.

प्रश्न 2.
काय केले ते लिहा:
1. डॉक्टरांचे आभार मानण्यासाठी ………………………
2. पाहुणचार करण्यासाठी आल्यागेलेल्या सर्वांना ………………
उत्तर:
1. डॉक्टरांचे आभार मानण्यासाठी लेखिकांनी त्यांना फोन केला.
2. पाहुणचार करण्यासाठी आल्यागेलेल्या सर्वांना आइस्क्रीम दिले जात होते.

कृती 2 : (आकलन)

प्रश्न 1.
पुढील घटनांचे परिणाम लिहा:
1. घटना : लेखिकांनी डॉक्टरांना फोन केला.
परिणाम : ……………………………
2. घटना : डॉक्टरांनी फोनबद्दल आपली नाराजी व्यक्त केली.
परिणाम : ……………………………..
उत्तर:
1. परिणाम: काहीतरी विपरीत घडले असावे, या कल्पनेने डॉक्टर हादरले.
2. परिणाम: लेखिकांना डॉक्टरांचा राग न येता त्यांची दया आली.

कृती 3 : (स्वमत/अभिव्यक्ती)

प्रश्न 1.
‘परि तू जागा चुकलासी’ या उक्तीबद्दल तुमचे मत लिहा.
उत्तर:
आभार व्यक्त करणे वा आदर दाखवणे यांसारख्या उपचारांचा अतिरेक होऊ लागला आहे. असे उपचार पाळणे हे सुसंस्कृतपणाचे लक्षण मानले जाऊ लागल्यामुळे विपरीत प्रसंग उद्भवू लागले आहेत. आभार कोणाचे मानावेत, कधी मानावेत व कसे मानावेत यांबाबत कोणता धरबंदच राहिलेला नाही. ही एक भ्रामक गरज निर्माण झालेली आहे.

व्यापाऱ्यांचे याकडे लक्ष न जाते, तर नवलच! यातून शुभेच्छांची कृत्रिम कार्डे निर्माण झाली आहेत. काहीही करून आभार मानायचेच, असा अट्टहास बाळगल्याने हास्यास्पद प्रसंग घडताना दिसतात. लग्न होत असताना अभिनंदन करायचे सोडून आभार मानण्याचा प्रसंग पाठात आलेलाच आहे. म्हणून आभार कोणाचे मानू नयेत, केव्हा मानू नयेत, तसेच, ते कसे मानू नयेत याचे भान बाळगणे गरजेचे बनले आहे. कारण ‘परी तू जागा चुकलासी’ असे सांगण्याचे प्रसंग वारंवार येऊ लागले आहेत.

भाषाभ्यास:

(अ) अव्याकरण घटकांवर आधारित कृती:

1. समास:

प्रश्न 1.
जोड्या लावा:

2. शब्दसिद्धी:

प्रश्न 1.
‘सु’ उपसर्ग असलेले चार शब्द लिहा.
उत्तर:

1. सुविचार
2. सुवचन
3. सुसंस्कृत
4. सुगंध.

3. वाक्प्रचार:

प्रश्न 1.
पुढील वाक्प्रचारांचे अर्थ सांगून वाक्यांत उपयोग करा:

1. चोख असणे
2. चारीमुंड्या चीत करणे
3. काटकसर करणे.

उत्तर:

1. चोख असणे – अर्थ : व्यवस्थित असणे.
   वाक्य: गावामध्ये ग्रामपंचायतीचा कारभार अगदी चोख होता.
2. चारीमुंड्या चीत करणे – अर्थ : पराभव करणे.
   वाक्य: कारगिल युद्धात भारतीय जवानांनी शत्रूला चारीमुंड्या चीत केले.
3. काटकसर करणे – अर्थ : बचत करणे.
   वाक्य: महिन्याच्या पगारातून कामगारांनी थोडी काटकसर करणे आवश्यक आहे.

(आ) भाषिक घटकांवर आधारित कृती:

1. शब्दसंपत्ती:

प्रश्न 1.
विरुद्धार्थी शब्द लिहा:

1. थोडे
2. घट्ट
3. लवकर
4. विशिष्ट.

उत्तर:

1. थोडे × जास्त
2. घट्ट × सैल
3. लवकर × उशिरा
4. विशिष्ट × सामान्य.

प्रश्न 2.
वचन ओळखा:

1. गाणी
2. विमाने
3. घड्याळ
4. वादय.

उत्तर:

1. गाणी – अनेकवचन
2. विमाने – अनेकवचन
3. घड्याळ – एकवचन
4. वादय – एकवचन.

2. लेखननियम:

प्रश्न 1.
अचूक शब्द ओळखा:

1. निरिक्षण, निरीक्षण, निरीकराण, निरीक्षन.
2. अलिखीत, अलिखित, अलीखित, अलीखीत.
3. क्षुल्लक, क्षुलक, र्लक्क, क्षुल्लक.
4. सूसंस्कृत, सुसंस्कृत, सुसंस्कृत, सुसंक्त.
5. उत्पादन, ऊत्पादन, उप्तादन, उत्पादण.
6. शिष्ठाचार, शीष्टाचार, शिष्टाचार, शीष्ठाचार.

उत्तर:

1. निरीक्षण
2. अलिखित
3. क्षुल्लक
4. सुसंस्कृत
5. उत्पादन
6. शिष्टाचार.

3. विरामचिन्हे:

प्रश्न 1.
पुढील वाक्यांत योग्य विरामचिन्हे घालून वाक्ये पुन्हा लिहा:
1. आमच्या पिढीवर गोऱ्यांचे शिष्टाचार या गोष्टीची अंमळ जास्तच मुद्रा उमटली
2. लेखक आणि प्रकाशक गायक वादक कलाकार रसिक दिग्दर्शक आणि नटमंडळी ही जोडीजोडीने काम करीत असतात
उत्तर:
1. आमच्या पिढीवर ‘गोऱ्यांचे शिष्टाचार’ या गोष्टीची अंमळ जास्तच मुद्रा उमटली.
2. लेखक आणि प्रकाशक, गायक-वादक, कलाकार-रसिक, दिग्दर्शक आणि नटमंडळी ही जोडीजोडीने काम करीत असतात.

4. पारिभाषिक शब्द:

प्रश्न 1.
पुढील इंग्रजी पारिभाषिक शब्दांना मराठी प्रतिशब्द दया:
1. Humanism
2. Honorable.
उत्तर:
1. मानवतावाद
2. माननीय.

थोडं ‘आ’ भारनियमन करूया Summary in Marathi

प्रस्तावना:

मराठीतील एक लोकप्रिय व अग्रेसर विनोदी लेखिका. त्यांच्या लेखनाच्या केंद्रस्थानी मध्यमवर्गीय मराठी माणूस प्राधान्याने असतो. त्या मध्यमवर्गीय माणसाच्या जीवनातील विसंगती खेळकरपणे चित्रित करतात. त्यांची लेखनशैली प्रसन्न आहे. त्यांचा भर मुख्यतः वक्रोक्तीवर असतो. त्यांचा विनोद कधीही बोचरा, जखम करणारा नसतो. त्या हसतखेळत विसंगती दाखवून देतात. सामाजिक व्यंगांकडेही त्यांचे खास लक्ष असते. त्यांचे लेखन हे नेहमीच आधुनिकतेचा पुरस्कार करणारे असते. पारंपरिक मागासलेल्या विचारांना त्या सहजगत्या हास्यविषय करतात. अतिरेकी आधुनिक विचारांवरही त्या हसतखेळत टीका करतात. त्यांचे लेखन सदैव वाचनीय ठरले आहे.

मंगला गोडबोले यांनी गंभीर स्वरूपाचे कथालेखन व कादंबरीलेखनही केले आहे. आपण आधुनिक बनत जाण्याच्या प्रयत्नात पाश्चिमात्य लोकांचे आंधळेपणाने अनुकरण करतो आणि हास्यास्पद बनत जातो, ही वस्तुस्थिती प्रस्तुत पाठात लेखिकांनी अत्यंत खेळकरपणे दाखवून दिली आहे. आपण इंग्रजांच्या अनुकरणातून ‘बँक्यू’, ‘प्लीज’ हे शब्द उचलले आहेत आणि त्यांचा अतिरेकी वापर करतो. ‘बँक यू’, ‘बँक्यू’ (I thank you) हे पूर्ण वाक्य आहे. हे लक्षात न घेता ‘बैंक्यू = आभार’ असा अर्थ घेऊन ‘तू कसली ग माझी बँक्यू?’ ‘मीच तुझी बँक्यू’ असले हास्यास्पद शब्दप्रयोग आपण करतो. आपल्या समाजातील या विसंगतीचे मजेदार दर्शन या पाठात लेखिका घडवतात आणि आपल्याला अंतर्मुख करतात.

शब्दार्थ:

1. धसमुसळे – दांडगे, अडाणी, पशुतुल्य, रानवट, वाटेल तसे , वागणारा.
2. सुमार – मर्यादा, अंदाज, सान्निध्य.
3. अस्थानी – चुकीच्या ठिकाणी.
4. आभारबाज – लहानमोठ्या सर्व कारणांसाठी, अगदी क्षुल्लक कारणासाठीसुद्धा, सतत आभार मानण्याची चटक लागलेली व्यक्ती.
5. घाऊक आभार – सर्व व्यक्तींचे सर्व बाबींसाठी एकदाच एकगठ्ठा आभार मानणे.
6. तुडुंब – काठोकाठ, भरपूर.
7. दिखाऊगिरी – इतरांसमोर अकारण जाहीर व सातत्याने प्रदर्शन करीत राहणे.
8. बासन – एखादी वस्तू गुंडाळून ठेवण्याचा कापडाचा खास तुकडा.
9. शब्दबंबाळ – (समुदाय, मोठा नाद) शब्दांचा समुदाय ज्यात जाणवतो ते, आशयापेक्षा ज्यात केवळ शब्दच जाणवतात (शब्दांचा
10. फक्त आवाज जाणवतो) ते लेखन. सणसणीत – उष्ण, तीव्र, जबर, भक्कम.
11. उणावून – कमी होऊन.
12. कटाक्ष – डोळ्यांच्या कोपऱ्यातून टाकलेली एक नजर.
13. प्रौढ – पोक्त, निष्णात, धीट (तरुण व वृद्ध यांच्या मधल्या अवस्थेत असलेली व्यक्ती).
14. वट्ट – चोख, एकत्रित, एकूण.
15. अश्राप – गरीब, बिचारे, सभ्य, निर्व्याज, अभिजात.

टिपा:

1. निष्ठा – (नि + स्था) निग्रहाने एका जागी स्थिर राहणे. काही माणसे आयुष्यभर एखादा विचार, मूल्य उराशी बाळगतात; त्यापासून ढळत नाहीत. यावरून त्या विचाराला, मूल्याला, दृष्टिकोनाला त्या माणसांची निष्ठा म्हणतात.

2. मॅनरलेसपणा – मॅनर (manner = शिष्टाचार). मॅनरलेस म्हणजे शिष्टाचार न पाळणारा, असंस्कृत, उद्धट. ‘mannerless पणा’ यात इंग्रजी शब्दाला मराठी प्रत्यय जोडलेला आहे. येथे इंग्रजी शब्द वापरण्याची केवळ हौस दिसते. अशा सवयीमुळे धेडगुजरी शब्द तयार होतात.

वाक्प्रचार व त्यांचे अर्थ:

1. मुद्रा उमटणे – ठसा उमटणे, प्रभाव दिसून येणे.
2. जप करणे – एकच बाब पुन्हा पुन्हा बोलणे.
3. गुण गाणे – स्तुती करणे.
4. चारी मुंड्या चीत करणे – पूर्णपणे पराभूत करणे.
5. तोंड उघडणे – थोडे तरी बोलणे, (कधी कधी) नको ते र बोलणे.
6. तोंड बंद करणे – गप्प बसणे.
7. मुखर करणे – शब्दरूप देणे, शब्दांत व्यक्त करणे.
8. दाबून फिया घेणे – मोठ्या प्रमाणात अवास्तव शुल्क आकारणे.
9. आरती ओवाळणे – कौतुक करणे, स्तुती करणे (बहुतेक वेळा अवास्तव).
10. पुष्पहार घालणे – आभार मानणे, कृतज्ञता व्यक्त करणे, स्वागत करणे.

Balbharti Maharashtra State Board Class 9 Marathi Solutions Kumarbharti Chapter 9 मी वाचवतोय Notes, Textbook Exercise Important Questions and Answers.

Maharashtra State Board Class 9 Marathi Kumarbharti Solutions Chapter 9 मी वाचवतोय (कविता)

9th Std Marathi Kumarbharati Digest Chapter 9 मी वाचवतोय Textbook Questions and Answers

1. कोष्टक पूर्ण करा:

प्रश्न 1.
कोष्टक पूर्ण करा:

उत्तर:

2. आकृती पूर्ण करा:

प्रश्न 1.
आकृती पूर्ण करा:

उत्तर:

3. सकारण लिहा:

प्रश्न 1.
सकारण लिहा:

उत्तर:

4. कव्यसौंदर्य.

प्रश्न (अ)
तुम्हांला जाणवलेली कवीच्या मनातली खंत स्पष्ट करा.
उत्तर:
जुन्या जमान्यातील काही चांगल्या गोष्टी हरवत व दुरावत चालल्या आहेत, यांची खंत कवीला वाटते. बदलत चाललेल्या समाजातील वास्तव कवीच्या मनाला खटकते. आपण आईला ‘आई’ अशी साद घालत नाही. वासरासाठी गोठ्यात गायही हंबरत नाही. मॉलच्या नवीन झगमगीत संस्कृतीमुळे किराणा व भुसार हरवत चाललेयत. गावगाड्यातील व्यवसाय लोप पावतायत. मुले मातीतले खेळ खेळत नाहीत. कुणी लेखन करीत नाही. मातृभाषेत कुणी या भूमीतली संस्कृती जपत नाही. अशा प्रकारे सांस्कृतिक वैभव नष्ट होण्याची खंत कवीला बोचते आहे.

प्रश्न (आ)
‘शब्द बापुडे केवळ वारा’ या काव्यपंक्तीतील आशयसौंदर्य शब्दबद्ध करा.
उत्तर:
पूर्वीच्या कविता किंवा साहित्य उच्च सांस्कृतिक मूल्य जपणारे होते. जीवनानुभूतीतून आदर्श व प्रेरणा जनमानसाला मिळत होत्या. परंतु आता लिहिणाऱ्या हातातून सकस साहित्यनिर्मिती होत नाही, हे कवीला सांगायचे आहे. जो शब्दपसारा दिसतो तो भावनाशून्य व पोकळ आहे, असे कवीला म्हणायचे आहे. शाश्वत राहणारे अभिजात साहित्य निर्माण होत नाही, याची खंत व्यक्त करताना कवी म्हणतात की, आताचे शब्द केविलवाणे झाले आहेत व ते वाऱ्यावर विरून जात आहेत. आता लिहिल्या जाणाऱ्या शब्दांची नश्वरता व तात्कालिकता कवीला या ओळीतून सांगायची आहे.

प्रश्न (इ)
सामाजिक बदलाबद्दल कवितेतून व्यक्त झालेला विचार स्पष्ट करा.
उत्तर:
पूर्वी गावगाडा होता. नैतिक मूल्ये जपणारी गावची संस्कृती होती. हळूहळू समाज बदलत गेला. शहरे वाढू लागली. सगळ्या वस्तू झगमगीत मॉलमध्ये, सुपरमार्केटमध्ये मिळू लागल्या. त्यामुळे छोटी छोटी किराणा, भुसार मालाची दुकाने हरवून गेली. लोहाराचा भाता बंद पडला. कुंभाराचे चाक फिरायचे थांबले. तांब्या-पितळेच्या भांड्यांचा वापर लयाला गेल्यामुळे कल्हईची झिलई निघून गेली. चुलीची जागा गॅसच्या शेगड्यांनी घेतली. आधुनिक समाजव्यवहारांमुळे मायेची माणसे दुरावली. अशा प्रकारे या कवितेत सामाजिक बदलाविषयी कवीने सांगितले आहे.

5. स्वमत:

प्रश्न (अ)
‘माझी बोली’ या संकल्पनेतून तुम्हांला समजलेला कवीचा दृष्टिकोन स्वभाषेत मांडा.
उत्तर:
‘माझी बोली’ म्हणजे मायबोली किंवा मातृभाषा होय. वेगाने बदलत जाणाऱ्या समाजात जी नवीन पिढी शिकते आहे; त्यांच्यावर शिशुवर्गापासूनच इंग्रजीचे संस्कार होत आहे. पूर्वीचे घरचे मराठमोळे वातावरण झपाट्याने बदलत आहे. आधुनिकीकरणामुळे नवीन पिढीच्या तोंडी इंग्रजी रुळत जाते आहे. आईची जागा ‘मम्मी’ने घेतली आहे. मातृभाषेतून दिले जाणारे शिक्षण हळूहळू मंदावत आहे. मातृभाषा हेच विचार व भावना मांडण्याचे नैसर्गिक माध्यम असते. ते माध्यम बंद पडत चालल्यामुळे कवीने खंत व्यक्त केली आहे. अशा प्रकारे ‘माझी बोली’ या संकल्पनेतून कवींची खेदजनक भावना व्यक्त झाली आहे.

प्रश्न (आ)
‘मॉलच्या अतिक्रमणामुळे छोट्या दुकानदारांना फटका बसतो,’ याबाबत तुमचे मत स्पष्ट करा.
उत्तर:
शहरे वाढली तसतसे लोकांच्या गरजा पुरवणारे ‘मॉल’ वाढले. पूर्वी शहरामध्येसुद्धा छोटे छोटे दुकानदार होते. विशिष्ट प्रकारच्या वस्तू विशिष्ट दुकानांत मिळायच्या. मॉलमध्ये सर्व वस्तूंची दुकाने एकत्र असतात. शिवाय खादयपान सेवेची हॉटेल्स व सिनेमागृहेही असतात. मॉलच्या एकंदर झगमगाटाचे आकर्षण माणसांच्या ठायी निर्माण झाले. महागड्या वस्तू म्हणजे दर्जेदार वस्तू असा गैरसमज फोफावला. त्यातच आकर्षक जाहिरातींची भर पडल्यामुळे लोकांना मॉलचे आकर्षण निर्माण झाले. साहजिकच माणसांचा मॉलमध्ये राबता सुरू झाला आणि त्यांनी छोट्या दुकानांकडे पाठ फिरवली. अर्थात मॉलच्या अतिक्रमणामुळे छोट्या दुकानदारांना फटका बसतो, हे खरे आहे.

उपक्रम:

तुमच्या अवतीभवती घडणाऱ्या सामाजिक बदलांची पुढील मुद्द्यांच्या आधारे नोंद करा व कोष्टक तयार करा:

1. बदल
2. परिणाम
3. तुमचे मत

Marathi Kumarbharati Textbook Std 9 Answers Chapter 9 मी वाचवतोय Additional Important Questions and Answers

1. पुढील कवितेच्या आधारे दिलेल्या सूचनांनुसार कृती करा:

कृती 2 : (आकलन)

प्रश्न 1.
शब्दजाल पूर्ण करा:

उत्तर:
1. हाकेतून हद्दपार होत आहे.
(1) हंबरायच्या थांबल्या आहेत.
2. लोहाराचा भाता
(1) कुंभाराचा आवा

प्रश्न 3.
चौकटी पूर्ण करा:

उत्तर:

1. (i) किराणा (ii) भुसार
2. रटरटणारी आमटी
3. कल्हईची झिलई
4. आईची बोली
5. बापुडे शब्द
6. परकरी मुली

कृती 3 : (दोन ओळींचा सरळ अर्थ)

प्रश्न 1.
हरवत चाललाय किराणा आणि भुसार सुपर मार्केटच्या झगमगाटात झरझर
उत्तर:
बदलत चाललेल्या परिस्थितीचा आढावा घेताना कवी सतीश काळसेकर म्हणतात की, शहरात मोठमोठे मॉल व सुपर मार्केट निर्माण झाल्यामुळे पूर्वीची किराणामालाची व भुसारीची दुकाने भूतकाळात जमा झाली आहेत.

कृतिपत्रिकेतील प्रश्न 2 (आ) साठी……

प्रश्न 1.
पुढील कवितेवर दिलेल्या मुद्द्यांच्या आधारे कृती सोडवा:
कविता – मी वाचवतोय.
उत्तर:
मी वाचवतोय.
1. प्रस्तुत कवितेचे कवी/कवयित्री → सतीश काळसेकर.

2. कवितेचा विषय → वेगाने बदलत जाणाऱ्या महानगरीय समाजाचे वास्तव चित्रण हा कवितेचा विषय आहे.

3. कवितेतील दोन शब्दांचे अर्थ →

1. हाक = साद
2. आई = माता
3. विस्तव = आग
4. राख = रक्षा
5. वारा = वात.

4. कवितेतून मिळणारा संदेश → चांगली जुनी संस्कारक्षम मूल्ये हरवू नयेत; आईची बोली पारखी होऊ नये; भौतिक सुखामध्ये नैतिक मूल्यांची पायमल्ली होता कामा नये; हा संदेश प्रस्तुत कविता देते.

5. कवितेची भाषिक वैशिष्ट्ये → जुन्या मूल्यांविषयीची आस्था व नवीन महानगरीय बदलते वास्तव यांतील अंतर्विरोध कवींनी चपखल शब्दांत मांडला आहे. कवितेची भाषा हृदयाला भिडेल अशी थेट व स्पष्टोक्तीपूर्ण आहे. यातील भावनांची आवाहकता प्रशंसनीय आहे. मुक्त गदय शैली आशयाला पूरक आहे. कवितेतील अंतर्गत यमक व सूचक शब्दांची मांडणी आशयाला उठाव देणारी आहे. कवितेचा शेवट परिणामकारक झाल्यामुळे रसिक चिंतनशील होतात.

6. कवितेतून व्यक्त होणारा विचार → यंत्रयुगातील नवीन बदलांमुळे जुनी मूल्ये ढासळत चाललीयत. ती वाचवणे व सुरक्षित ठेवणे गरजेचे आहे.

7. कवितेतील दोन ओळींचा सरळ अर्थ:
हाकेतून हद्दपार होतेय आई
हंबरायच्या थांबल्यायत गोठ्यातल्या गाई
→ बदलत जाणाऱ्या वास्तवामध्ये ममी-डॅडी या परकीय शब्दांमुळे
आईची मायेची हाक आता ऐकू येत नाही. गोठ्यातल्या गाईसुद्धा 3 आता नैसर्गिक हंबरणे विसरत चालल्या आहेत.

8. कविता आवडण्याची वा न आवडण्याची कारणे → जुनी मूल्ये नामशेष होण्याची खंत कवींनी आर्तपणे व तेवढ्याच परखडपणे मांडली आहे. नवीन पिढीचा निरुद्देश चंगळवाद अधोरेखित केला आहे. आई, आईची बोली, भूमी आणि कविता वाचवण्याचा दृढनिश्चय व्यक्त केला आहे. या सर्व कारणांमुळे ही कविता मला खूप आवडली.

कृतिपत्रिकेतील प्रश्न 2 (इ) साठी…

प्रश्न 1.
पुढील ओळीचे रसग्रहण तुमच्या शब्दांत करा:
‘हाकेतून हद्दपार होतेय आई
हंबरायच्या थांबल्यायत गोठ्यातल्या गाई.’
उत्तर:
आशयसौंदर्य: यंत्रवत असलेल्या महानगरीय जीवनात जुनी जीवनमूल्ये नष्ट होत आहेत. क्रय वस्तूंच्या बेगडी झगमगाटात जुनी चूल, जुने खेळ, बोली व संस्कृती यांचा नवीन पिढीला विसर पडत चालला आहे, या वास्तववादी आशयाचे विदारक चित्रण कवी सतीश काळसेकर यांनी ‘मी वाचवतोय’ या कवितेत केले आहे.

काव्यसौंदर्य: बदलत जाणाऱ्या समाजाचे वास्तव शब्दांत चितारताना प्रस्तुत ओळींमध्ये कवी म्हणतात की ‘मम्मी-डॅडी’ या उसन्या परिभाषेमुळे ‘आई’. अशी हाक आता ऐकू येत नाही. जणू ती हाक सीमेबाहेर गेली आहे. गोठ्यातल्या मायेचा वारसा असलेल्या गाईसुद्धा आता नैसर्गिक हंबरणे विसरल्या आहेत. त्या आता आपल्या वासरांसाठी हंबरत नाहीत. म्हणजेच आई-लेकरांचे संबंध मायाममतेचे राहिले नाहीत, ही खंत कवींनी व्यक्त केली आहे. भौतिक सुखामध्ये नैतिक मूल्यांची पायमल्ली होते, याची बोचणी प्रस्तुत ओळींमध्ये स्पष्टपणे दर्शवली आहे.

भाषिक वैशिष्ट्ये: जुन्या मूल्यांविषयीची आस्था व नवीन महानगरीय बदलते वास्तव यांतील अंतर्विरोध कवीने चपखल शब्दांत मांडला आहे. कवितेची भाषा हृदयाला भिडेल अशी थेट व स्पष्टोक्तीपूर्ण आहे. यातील भावनांची आवाहकता प्रशंसनीय आहे. मुक्त गदय शैली आशयाला पूरक आहे. कवितेतील अंतर्गत यमक व सूचक शब्दांची मांडणी आशयाला उठाव देणारी आहे. योग्य परिणामकारकता शब्दाशब्दांत अभिव्यक्त झाल्यामुळे रसिक चिंतनशील होतात.

भाषाभ्यास:

(अ) व्याकरण घटकांवर आधारित कृती:

1. समास:

प्रश्न 1.
पुढील सामासिक शब्दांचे समास ओळखा :

1. सत्यासत्य
2. सप्तसागर
3. पूर्वपश्चिम
4. रक्तचंदन

उत्तर:

1. वैकल्पिक द्वंद्व
2. द्विगू
3. इतरेतर द्वंद्व
4. कर्मधारय.

2. वाक्प्रचार:

प्रश्न 1.
पुढील वाक्प्रचारांचे अर्थ सांगून वाक्यात उपयोग करा:
1. दंग असणे
2. दुरावणे.
उत्तर:
1. दंग असणे – अर्थ : मग्न असणे.
वाक्य: जेव्हा बघावे तेव्हा मंदार खेळामध्ये दंग असतो.

2. दुरावणे – अर्थ : लांब जाणे.
वाक्य : परदेशी गेल्यामुळे ममताला आईवडिलांची संगत दुरावली.

(आ) भाषिक घटकांवर आधारित कृती:

1. शब्दसंपत्ती:

प्रश्न 1.
शब्दसमूहाबद्दल एक शब्द लिहा:
1. लिहिता-वाचता येणारा → …………………..
2. लिहिता-वाचता न येणारा → ………………..
उत्तर:
1. साक्षर
2. निरक्षर.

प्रश्न 2.
अनेकवचन लिहा:

1. गाय
2. खेळ
3. कविता
4. सुट्टी.

उत्तर:

1. गाई
2. खेळ
3. कविता
4. सुट्ट्या

प्रश्न 3.
पुढील शब्दांतील अक्षरांपासून दोन अर्थपूर्ण शब्द लिहा:
1. वाचवतोय
2. समाजाचे
उत्तर:
1. चव, वय
2. मास सजा

2. लेखननियम:

प्रश्न 1.
अचूक शब्द ओळखा:
1. बोलचाली, बोलाचाली, बोलाचालि, बोलचालि.
2. दूरर्दशन, दुरदर्शन, दूर्रदर्शन, दूरदर्शन.
उत्तर:
1. बोलाचाली
2. दूरदर्शन.

3. पारिभाषिक शब्द:

प्रश्न 1.
मराठी प्रतिशब्द लिहा:

1. Lyric
2. Magazine
3. Category
4. Index

उत्तर:

1. भावगीत
2. मासिक-पत्रिका
3. प्रवर्ग
4. अनुक्रमणिका.

मी वाचवतोय Summary in Marathi

कवितेचा आशय:

समाजाचे वास्तव वेगाने बदलत चालले आहे. जुने व्यवसाय, जुने खेळ काळाच्या पडद्याआड गेले आहेत. यंत्रयुगाच्या आधुनिक झगमगाटात आईची बोली कोणी बोलत नाही. नवीन पिढी यांत्रिक वस्तूंच्या आहारी गेली आहे. या सर्व बदलांची खंत या कवितेत कवींनी व्यक्त केली आहे. जुन्या काही चांगल्या गोष्टी या बदलातून वाचवणे गरजेचे झाले आहे.

शब्दार्थ:

1. वाचवतोय – बचाव करतोय.
2. मुकाट – शांतपणे, निमूट.
3. विस्तव – निखारे.
4. धग – ऊब.
5. रटरटणारी – शिजणारी.
6. सहित – सोबत, बरोबर, संगती.
7. बोलाचाली – संभाषण.
8. बोली – भाषा.
9. दंगा – (इथे अर्थ) गोंधळ, आरडाओरडा.
10. परकऱ्या – परकर घालणाऱ्या (मुली).
11. लिहिते हात – लेखनाचा सराव.
12. बापुडे – गरीब, केविलवाणे.
13. भूमी – धरती.

टिपा:

1. हंबरणे – गाईचा आवाज (ओरडणे).
2. किराणा-भुसार – अन्नधान्याच्या वस्तू.
3. सुपर मार्केट – अन्नधान्य, भाजीपाला, खाण्याचे तयार पदार्थ, तसेच अन्य अगणित वस्तू एका छपराखाली मिळतील असे, भव्य दुकान ; मोठमोठाले मॉल.
4. लोहाराचा भाता – लोखंडी वस्तू बनवण्यासाठी लोहार वापरत असलेल्या भट्टीला वारा घालण्याचे साधन.
5. कुंभाराचा आवा – ओल्या मातीच्या गोळ्याला मडक्यांचा आकार देण्यासाठी कुंभार वापरत असलेले लाकडी गोल चाक.
6. गावगाडा – गावची जुनी संस्कृती व्यवहार.
7. कल्हईची झिलई – तांब्या-पितळेची भांडी कळकू नयेत म्हणून कथिलाची तार तापवून त्याच्या रसापासून तयार केलेलामुलामा.
8. आईची बोली – मातृभाषा.
9. विटीदांडू – लाकडाची छोटी विटी व मोठा दांडू यांचा जुना मैदानी खेळ.
10. लगोऱ्या – दगडांच्या चकत्या एकावर एक रचून चेंडूने फोडण्याचा जुना मैदानी खेळ.
11. आट्यापाट्या – जमिनीवर आडव्या-उभ्या रेघा आखून खेळता येणारा सांघिक खेळ.
12. पिंगा – मान गोल गोल फिरवून घुमण्याचा खेळ.
13. क्राइम-थ्रिलर – गुन्हेगारी जीवनाचे चित्रण करणाऱ्या दूरदर्शनवरील मालिका.

वाक्प्रचार व त्यांचे अर्थ:

1. हद्दपार होणे – सीमेबाहेर सोडणे (जीवनातून निघून जाणे).
2. दुरावत जाणे – लांब जाणे.
3. दंग असणे – गुंगणे, मग्न असणे.
4. विरून जाणे – विरघळून जाणे, नाहीसे होणे.

कवितेचा भावार्थ:

बदलत जाणाऱ्या समाजाचे वास्तव शब्दांत चितारताना कवी म्हणतात – ‘आई’ अशी हाक आता ऐकू येत नाही. जणू ती सीमेबाहेर गेली आहे. गोठ्यातल्या गाईसुद्धा आता हंबरणे विसरल्या आहेत. त्या आता वासरासाठी हंबरत नाहीत. (आई-लेकरांचे संबंध मायेचे राहिले नाहीत.)

मोठमोठे मॉल्स व सुपर मार्केट निर्माण झाल्यामुळे त्यांच्या झगमगाटी दुनियेत आता पूर्वीच्या किराणा व भुसाराची दुकाने हरवून जात आहेत. पूर्वीच्या गावच्या संस्कृतीत (गावगाड्यात) असलेले (जुने व्यावसायिक) लोहार, कुंभार नि त्यांचे भाते व चाके गावगाड्याबरोबरच निमूटपणे नाहीशी झाली आहेत. पूर्वीच्या भांड्यांची कल्हईची झिलई विस्तवासोबत निघून गेली आहे. चुलीच्या जाळावर शिजत असलेली आमटी राखेसकट दूर गेली. आता धुराशिवाय ती गॅस शेगडीवर शिजत असलेली दिसते.संभाषणातून-संवादातून हल्ली (माझी) मातृभाषा (आईची बोली) निघून चालली आहे.

आता मुले सुट्ट्यांमध्ये पूर्वीसारखी विटीदांडू आणि लगोरीचे खेळ खेळत नाहीत. त्यांचा गिल्ला आता थांबलाय. आता आट्यापाट्या किंवा पिंगा असले जुने खेळ नाहीसे झाले आहेत. परकर घालणाऱ्या लहान मुली आता पूर्वीचे मातीतले खेळ खेळताना दिसत नाहीत. आता मुले दूरदर्शनच्या स्पोर्ट चॅनेलवर क्रिकेटची मॅच पाहण्यात रमून जातात किंवा गुन्हेगारी विश्वातील मालिका बघत राहतात. आता कुणाकडूनही पूर्वीसारख्या गोष्टी लिहिल्या जात नाहीत. लिहिणाऱ्या हातांचा सराव थांबलाय. शब्द केविलवाणे होऊन फक्त वाऱ्यासारखे विरून जातात.

अशा या बदलत्या भयानक वास्तवात मी माझी कविता सांभाळतोय आणि कवितेसोबतच माझी आई, माझी भाषा नि माझी भूमी यांचा { मी या आधुनिक वास्तवापासून बचाव करतो आहे.

Balbharti Maharashtra State Board Class 9 Marathi Solutions Kumarbharti Chapter 10.1 इंग्लंडचा हिवाळा Notes, Textbook Exercise Important Questions and Answers.

Maharashtra State Board Class 9 Marathi Kumarbharti Solutions Chapter 10.1 इंग्लंडचा हिवाळा (स्थूलवाचन)

9th Std Marathi Kumarbharati Digest Chapter 10.1 इंग्लंडचा हिवाळा Textbook Questions and Answers

1. कारण लिहा:

प्रश्न 1.
कारण लिहा:
लेखिकेला लंडनच्या पावसाची मौज वाटण्याची कारणे –
उत्तर:
लंडनच्या पावसात रस्त्यात चिखल होत नाही. वातावरणात मजेदार गारवा असतो. चार-पाच मैल चालूनही थकवा येत नाही. परिसर हिरवागार राहतो; म्हणून लेखिकेला लंडनच्या पावसाची मौज वाटायची.

2. तुलना करा:

प्रश्न 1.
तुलना करा:

उत्तर:

3. इंग्लंडमधील धुक्याचा तेथील जनजीवनावर होणारा परिणाम सविस्तर लिहा.

प्रश्न 1.
इंग्लंडमधील धुक्याचा तेथील जनजीवनावर होणारा परिणाम सविस्तर लिहा.
उत्तर:
इंग्लंडमध्ये काळसर पांढुरक्या धुक्याचे छत सर्व शहरावर पसरलेले असते. कोळशावर चालणारे लंडनमधले हजारो कारखाने व कोळशावर चालणाऱ्या घरांतील लक्षावधी चुली रात्रंदिवस वातावरणात धूर सोडत असतात. घरात अनवाणी चालले की पाय काळे होतात. झाडाला हात लावला की हात काळे होतात.

अशा धुरकट वातावरणात धुके पसरले की कोळशाचे कण दिसू लागतात. काळोख डोळ्यांना दिसतो व हातात धरता येतो. आपण हवेच्या आवरणाच्या तळाशी आहोत, याचा प्रत्यक्ष अनुभव त्या धुक्यात येतो. समुद्राच्या तळाशी होणाऱ्या जीवांच्या घुसमटीची कल्पना येते. ब्रिटिश खाडीत बोटीवर बोटी आपटतात. रस्त्यांवर वाहनांचे अपघात होतात. मुले रस्ता चुकतात. अशा प्रकारे तेथील जनजीवन विस्कळीत होते.

4. स्वमत:

प्रश्न (अ)
‘हिवाळ्यातील एक क्षण,’ तुमचा अविस्मरणीय अनुभव आठ ते दहा वाक्यांत लिहा.
उत्तर:
गेल्या वर्षी आम्ही सर्व कुटुंबीय चारधामच्या यात्रेला ऑक्टोबर महिन्यात गेलो होतो. गंगोत्रीच्या काठावर आम्ही वस्ती केली होती. रात्र असल्यामुळे त्या परिसराची कल्पना नव्हती. पहाटेच मला जाग आली. बाहेर थंडी होती. उबदार शाल लपेटून मी बाहेर आलो. गच्च धुक्याची चादर लपेटलेली झाडे नि गंगेच्या धारेवर बर्फाची ओढणी अंथरली होती. ऑक्टोबर महिना असल्यामुळे पर्वतावरील बर्फ वितळले होते. पण शिखराशिखरांवर बर्फाचे भलेमोठे पुंजके होते. मी त्यांच्याकडे भान हरखून पाहत होतो. इतक्यात एक सूर्याचा किरण शिखरावर पडला नि तिथला बर्फ सोन्याच्या रंगाने तळपला. हे दृश्य केवळ विलोभनीय होते. एक क्षणभरच हे अलौकिक सौंदर्य उमटले नि लुप्त झाले. हिवाळ्यातील हा अविस्मरणीय क्षण मी आयुष्यभर विसरू शकत नाही.

प्रश्न (आ)
तुमच्या आवडत्या ऋतूची वैशिष्ट्ये स्पष्ट करा.
उत्तर:
वर्षाऋतू किंवा पावसाळा हा माझा अत्यंत आवडता ऋतू आहे. तापलेल्या मातीवर पावसाचा शिडकावा झाला की मातीचा है सुगंध येतो. सारी सृष्टी न्हाऊन निघते. डोंगरदऱ्यांत पाणी खळाळते. झाडे अंघोळ करून स्वच्छ होतात. नदीनाले भरभरून वाहू लागतात. गुरेढोर, पशुपक्षी यांना पाणी मिळते. शेतकरी आनंदित होतात व नांगरलेल्या शेतात पेरणी करायला उत्सुक असतात. मुले आनंदाने बागडतात. सर्वत्र हिरवेगार होते. सृष्टी आपले रूप पालटते. चराचरावर आनंदाची लकेर घुमते. कवी लेखकांना नवनवीन कल्पना सुचतात. खरेच! पाऊस हा नवसृजनाचा ऋतू आहे!

प्रश्न (इ)
तुम्ही अनुभवलेल्या धुक्यातील दिवसांचे वर्णन तुमच्या शब्दांत लिहा.
उत्तर:
ऐन हिवाळ्यात आम्ही काही मित्र पाचगणीला गेलो होतो. आमच्या तीन दिवसांच्या मुक्कामात एकदाही आम्हाला स्वच्छ आकाशाचे दर्शन झाले नाही. सर्व परिसराला धुक्याने जणू बाहूत कवटाळले होते. डोंगरदरी धुक्याच्या आइसक्रीमने ओतप्रोत भरली होती. झाडे धुक्याचे पांघरूण घेऊन पेंगत होती. रस्त्यावर दहा फुटांच्या पुढचे दिसत नव्हते. तोंडातून कुंकर मारली की धुक्याची धुरासारखी वलये उमटत होती. आम्ही रस्त्यावरून हिंडत असताना एक जादू झाली.

अवतीभवती शिरिषाची विस्तारलेल्या फांदयांची खूप झाडे होती. अचानक क्षणभर ढगातून सूर्याची फिकट कोवळी किरणे धुक्याने लपेटलेल्या झाडातून खाली उतरली नि झाडाच्या पायथ्याशी उन्हाच्या गोल-गोल चकत्या उमटल्या. मला अशोक बागवे याच्या कवितेची एक ओळ आठवली – ‘सावलीच्या टोपलीत उन्हाचे गजरे। मखमलीची झीळ त्याला हिवळे दर्वळे’ धुक्यातील दिवसांतील हा क्षण माझ्यासाठी केवळ मोलाचा ठरला.

5. खालील मुद्द्यांच्या आधारे तुम्ही भेट दिलेल्या प्रेक्षणीय स्थळाचे वर्णन करा.

प्रश्न 1.
खालील मुद्द्यांच्या आधारे तुम्ही भेट दिलेल्या प्रेक्षणीय स्थळाचे वर्णन करा.

अपठित गद्य आकलन:

आपण पाठ्यपुस्तकात गदय व पदय पाठांचा अभ्यास करतो. विविध साहित्यप्रकारांच्या अभ्यासाबरोबर भाषिक अंगाने प्रत्येक पाठाचा अभ्यास आपणांस करायचा असतो. विद्यार्थ्यांची भाषासमृद्धी, भाषिक विकास ही मराठी भाषा अध्ययन-अध्यापनाची प्रमुख उद्दिष्टे आहेत, म्हणूनच पाठ्यपुस्तकातील पाठांच्या सूक्ष्म अभ्यासाने आपल्याला कोणतेही साहित्य वाचल्यानंतर त्याचे आकलन होणे, आस्वाद घेता येणे व त्या भाषेचे सुयोग्य व्यावहारिक उपयोजन करता येणे ही उद्दिष्टे साध्य करता येतात. अशा पाठ्येतर भाषेच्या आकलनाचे, मूल्यमापन करण्याचे कौशल्य प्राप्त होण्याच्या दृष्टीने पाठ्यपुस्तकात अपठित गद्यउतारा हा घटक समाविष्ट केला आहे. गदय उतारा वाचून त्याचे आकलन होणे व त्यावरील स्वाध्याय तुम्ही स्वयंअध्ययनाने करणे येथे अपेक्षित आहे.

1. खालील उतारा काळजीपूर्वक वाचून त्याखालील कृती करा.

प्रश्न 1.
दुष्परिणाम लिहा.

2. अहंकाराला ताब्यात ठेवण्यासाठी तुमच्या मते कोणते गुण जोपासावेत व कोणते दोष दूर ठेवावेत, ते लिहा.

भाषा सौंदर्य :

एकच भाव वेगवेगळ्या प्रकारांनी व्यक्त करणे-
एखादे रिकामे घर पाहिल्यावर तुमच्या मनात येणारे विचार.

1. घर उदास वाटते.
2. घर कुणाची तरी आठवण काढते.
3. घर स्वत:चे एकेकाळचे वैभव आठवून उदास झाले आहे.
4. घराला गाव सोडून गेलेल्या माणसांची आठवण येते.
5. एकेकाळी माणसांनी भरलेले घर आज एकाकी वाटते.

विद्यार्थ्यांनो, ही यादी कितीही वाढवता येईल. भाषेच्या अशा अर्थपूर्ण आणि सृजनशील रचनांचा अभ्यास कराव आपले लेखन अधिक परिणामकारक करा.

Marathi Kumarbharati Textbook Std 9 Answers Chapter 10.1 इंग्लंडचा हिवाळा Additional Important Questions and Answers

प्रश्न 1.
इंग्लंडमधील हिवाळा आणि भारतातील हिवाळा यांची तुलना करा.
उत्तर:
इंग्लंडमध्ये हिवाळ्यात कित्येक आठवडे संधिप्रकाशाइतकाच उजेड असतो. भारतात मात्र स्वच्छ सूर्यप्रकाश असतो. भारतातील काही भागांत तर अत्यंत प्रखर, तीव्र उजेड असतो; तर काही भागांत उजेड भरपूर प्रमाणात असतो, पण तापमान कमी असते. इंग्लंडमध्ये अर्धवट उजेडात प्रकाश व सावली यांचा अभाव आढळतो. भारतात मात्र, माणसे, प्राणी व वाहने सावलीसोबतच चालत, धावत असतात. इंग्लंडमध्ये पर्णहीन वृक्षांची सावली खालच्या हिरवळीवर पडत नाही.

भारतामध्ये झाडाखालच्या दाट सावलीत प्रकाशाचे गोल कवडसे चमकत असतात. सावली पडावी इतका प्रकाश इंग्लंडमध्ये महिनोन् महिने पडत नाही. त्यामुळे वस्तूंवर छायाप्रकाशाचे खेळ दिसत नाहीत. पण भारतात प्रत्येक वस्तूची एक बाजू प्रकाशमय व दुसरी बाजू सावलीची असते. असा इंग्लंडमधील हिवाळा व भारतातील हिवाळा यांत फरक दिसून येतो.

इंग्लंडचा हिवाळा Summary in Marathi

पाठाचा परिचय:

या पाठात इरावती कर्वे यांनी इंग्लंडमधील पावसाळी धुके व हिवाळ्याचे वर्णन केले आहे. तसेच या ऋतूंमधील आपल्याकडील वातावरणाशी तुलना केली आहे. अतिशय विलोभनीय शब्दांत ऋतूंमधील साम्य व भेद यांचे दृश्य चितारले आहे.

पाठातील महत्त्वाचे मुद्दे:

1. सप्टेंबर-ऑक्टोबरनंतर इंग्लंडमध्ये रोज पाऊस पडायचा. लंडनवासी या पावसावर वैतागत असायचे, पण कायम पडणाऱ्या पावसाची लेखिकेला खूप मौज वाटायची.

2. आपल्याकडचे धुके मनाला सुखद संवेदना देते. पावसानंतरचे प्रसन्न आकाश, सकाळ-संध्याकाळची थंडी, लांबवर दिसणारे स्वच्छ वातावरण, त्यात थोडा वेळ राहणारा धुक्याचा पडदा, अशी आपल्याकडील धुक्याची वैशिष्ट्ये! महाबळेश्वरावर किंवा सिंहगडावर खालची दरी धुक्याने भरलेली दिसते. सूर्य उगवला की धुक्यात इंद्रधनुष्ये उमटतात. सूर्य आणखी थोडा वर आला की धुके निघून जाते व गवताच्या पात्यांवर असंख्य दवबिंदू चकाकतात. संध्याकाळचे धुके रात्र निवळली की नाहीसे होते व रात्री आकाश तारकांनी चमकत असते.

3. लंडनचे धुके औरच आहे. काळसर पांढुरके धुक्याचे छत सर्व शहरावर पसरलेले असते. लंडनमधील कारखाने व लक्षावधी चुली वातावरणात धूर ओकत असतात. अशा धुरकट वातावरणात धुके पसरले की कोळशाचे कण दिसतात. काळोख डोळ्यांना दिसतो. हाताने धरता येतो. असे काळे धुके वर्षातून एक-दोनदा लंडनवर पसरते. या धुक्याने हाहाकार माजतो.

4. हिवाळ्यात लंडनमध्ये कित्येक आठवडे संधिप्रकाशाइतकाच उजेड असतो. या अर्धवट उजेडात प्रकाश व सावली यांचा अभाव असतो. निरनिराळ्या बगिच्यांत पर्णहीन वृक्ष उभे असतात. त्यांची सावली खालच्या हिरवळीवर पडत नाही. येथे सावली पडेल इतका स्वच्छ उजेड महिनेच्या महिने पडत नाही.

5. आपल्याकडील हिवाळ्यात रखरखीत ऊन व त्याला चिकटून सावली असते. डांबरी रस्ता उन्हाने चकाकतो. माणसे व वाहने सावलीनिशी धावत असतात. प्रत्येक वस्तूची एक बाजू प्रकाशमय व दुसरी बाजू सावलीची ! खांबाला चिकटून असलेल्या सावलीत पक्षी टेलिग्राफच्या तारावर बसलेले दिसतात. पायी चालणारी माणसे घरांची सावली धरून चालतात. झाडाखालच्या दाट सावलीत प्रकाशाचे गोल कवडसे चमकतात.

6. एकदा लेखिका हिवाळ्यातच सेंट जेम्स बगिच्यात गेल्या. तेथील तळ्यावरचा प्रकाश खालून वर फाकला होता; कारण वर सूर्य नसलेले अभ्राच्छादित आकाश होते. तळ्याच्या पाण्यावर बर्फाचा पातळ थर साचला होता. त्यावर प्रकाश परावर्तित होऊन सगळीकडे फाकला होता. या विशेष प्रकाशात सर्व रंग आंधळे वाटतात. वसंतऋतूत एखादया दिवशी इथे सूर्यप्रकाश पडला की सृष्टी रंगाने नटते. येथील रंग जरा मंद व सौम्य वाटतात. आपल्याकडे दाट सावल्या भडकपणाने उठून न दिसता एकमेकांना पूरक भासतात.

Balbharti Maharashtra State Board Class 9 Marathi Solutions Kumarbharti Chapter 10 यंत्रांनी केलं बंड Notes, Textbook Exercise Important Questions and Answers.

Maharashtra State Board Class 9 Marathi Kumarbharti Solutions Chapter 10 यंत्रांनी केलं बंड

9th Std Marathi Kumarbharati Digest Chapter 10 यंत्रांनी केलं बंड Textbook Questions and Answers

1. फरक सांगा:

प्रश्न 1.
फरक सांगा:

उत्तर:

2. पाठात पुढील यंत्रे कोणती कार्ये करतात?

प्रश्न 1.
पाठात पुढील यंत्रे कोणती कार्ये करतात?

उत्तर:

3. दीपकला पडलेल्या स्वप्नात यंत्रांनी ताबा घेतल्यावर यंत्राबाबत दीपकने केलेली भाकिते.

प्रश्न 1.
दीपकला पडलेल्या स्वप्नात यंत्रांनी ताबा घेतल्यावर यंत्राबाबत दीपकने केलेली भाकिते.
1. …………………………….
2. …………………………….
उत्तर:
1. यंत्रे किंवा यंत्रमानव यांना जगाचा ताबा कधीच घेता येणार नाही.
2. यंत्रे कधीही बाबांवर अधिकार गाजवू शकणार नाहीत.

4. खालील शब्दांची विशेषणे, विशेष्य शोधा व लिहा :

प्रश्न 1.
खालील शब्दांची विशेषणे, विशेष्य शोधा व लिहा :

1. [ ] – यंत्र
2. [ ] – उद्गार
3. हुबेहूब – [ ]
4. परिपूर्ण – [ ]

उत्तर:

1. [उद्धट] – उद्गार
2. [अमानुष] – यंत्र
3. हुबेहूब – [नक्कल]
4. परिपूर्ण – [मनोव्यापार]

5. खालील वाक्प्रचार व त्यांचे अर्थ यांच्या जोड्या जुळवा.

प्रश्न 1.
खालील वाक्प्रचार व त्यांचे अर्थ यांच्या जोड्या जुळवा.

6. खाली काही शब्दांची यादी दिली आहे. त्यांतील शब्दांचे उपसर्गघटित शब्द व प्रत्ययघटित शब्द असे वर्गीकण करा व लिहा:

प्रश्न 1.
खाली काही शब्दांची यादी दिली आहे. त्यांतील शब्दांचे उपसर्गघटित शब्द व प्रत्ययघटित शब्द असे वर्गीकण करा व लिहा:
अवलक्षण, भांडखोर, दांडगाई, पहारेकरी, पंचनामा, दरमहा, विद्वत्त, नाराज, निर्धन, गावकी, दररोज, बिनतक्रार, दगाबाज, प्रतिदिन.
उत्तर:
उपसर्गघटित शब्द – अवलक्षण, दरमहा, नाराज, निर्धन, दररोज, बिनतक्रार, प्रतिदिन.
प्रत्ययघटित शब्द – भांडखोर, दांडगाई, पहारेकरी, पंचनामा, विद्वत्त, गावकी, दगाबाज.

7. स्वमत.

प्रश्न (अ)
तुमच्या मते माणसाच्या जागी सर्वोतम पर्याय ‘यंत्र’ ठरू शकेल का ? सोदाहरण स्पष्ट करा.
उत्तर:
प्रथम हे मान्य करावे लागेल की काही बाबतीत यंत्रे माणसापेक्षा श्रेष्ठच आहेत. उदाहरणार्थ संगणकच बघा. तो अनेक कामे अचूक व अफाट वेगाने करतो. त्याचे गणिती कौशल्यही अचाट आहे. माहिती तंत्रज्ञान या क्षेत्राच्या विकासामुळे सर्व कामकाजात तर अचाट प्रगती झाली आहे. दैनंदिन व्यवहार खूपच सुरळीत व वेगवान झाले आहेत. आपण अनेक कामे घरबसल्या करू शकतो. आपला वेळ व कष्ट टळतात.

अनेक लोक तर कार्यालयीन कामे घरूनच करतात. माणूस जाऊ शकत नाही अशा ठिकाणी रोबो काम करतात. उदा., खाणी, अंतराळयाने. यंत्रांच्या फायदयांची यादी करायची म्हटली तर खूप मोठी होईल. ही यंत्रे माणसाला सर्वोत्तम पर्याय मात्र कधीच ठरू शकणार नाहीत. सांगितलेले काम यंत्रे उत्तम रितीने पार पाडतील, हे खरे. पण, सांगितलेले काम चांगले की वाईट, त्या कामामुळे मानवजातीचे काही नुकसान होईल का, केलेली कृती सौंदर्यपूर्ण आहे का, इत्यादी प्रश्नांची उत्तरे यंत्रे देऊ शकत नाहीत. ती माणूसच देऊ शकतो.

प्रश्न (आ)
‘मनुष्य करत असलेली सर्व कामे यंत्रे करू लागली, तर…’ कल्पनाचित्र रेखाटा.
उत्तर:
यंत्रांची कार्यक्षमता वाढू लागताच यंत्रमानवांची झपाट्याने निर्मिती होऊ लागली. यंत्रमानवांची मागणीही वाढली. प्रत्येक कामासाठी यंत्रमानव वापरण्याची लोकांना सवयच जडली. शेती, दुकाने, कार्यालये, रस्ते, मंदिरे, शाळा-कॉलेजे वगैरे सर्व ठिकाणी यंत्रमानवांची नेमणूक होऊ लागली. इतकेच काय, घरात सकाळी उठल्यापासून करायची सर्व कामेसुद्धा यंत्रमानवांकडे देण्यात येऊ लागली. यामुळे कामे भराभर व कार्यक्षमतेने होऊ लागली.

या स्थितीचा एक उलटाही परिणाम होऊ लागला. माणसांना कामे कमी राहिली. रिकाम्या वेळामुळे नको नको ते विचार मनात येऊ लागले. एकमेकांविरुद्ध कारस्थाने रचणे सुरू झाले. त्यासाठी यंत्रमानवांचाच वापर होऊ लागला. प्रतिस्पर्धीसुद्धा यंत्रमानवांचा वापर करू लागले. यामुळे भलतेच दृश्य ठिकठिकाणी दिसू लागले. माणसे राहिली बाजूला आणि यंत्रमानवांमधील लढाया सुरू झाल्या. लोक गर्दी करून यंत्रमानवांमधील भांडणे, मारामाऱ्या पाहू लागले. चलाख लोकांनी ही भांडणे सोडवण्यासाठी बुद्धिमान यंत्रमानवांची समिती स्थापन केली. या सगळ्यांतून एक हास्यास्पद चित्र उभे राहू लागले. करमणुकीचा एक वेगळाच मार्ग निर्माण झाला.

उपक्रम:

प्रश्न 1.
‘मानवाचा खरा मित्र – यंत्रमानव’ ही लेखक सुबोध जावडेकर यांची विज्ञानकथा मिळवा व तिचे वर्गात वाचन करा.

भाषाभ्यास:

प्रश्न 1.
पुढे दिलेली उदाहरणे वाचा. त्यांतील भाव समजून घ्या व त्यांतील रसाचे नाव लिहा: (चौकटीत उत्तरे दिली आहेत.)
उत्तर:
1. “दिवा जळे मम व्यथा घेउनी
असशिल जागी तूही शयनी
पराग मिटल्या अनुरागाचे
उसाशांत वेचुनी गुंफुनी”
– [शृंगार रस]

2. “जोवरती हे जीर्ण झोपडे अपुले
दैवाने नाही पडले
तोवरती तू झोप घेत जा बाळा
काळजी पुढे देवाला” .
– [करुण रस]

3. “लाडका बाळ एकुलता फाशीची शिक्षा होता
कवटाळूनि त्याला माता।
अति आक्रोशें, रडते केविलवाणी
भेटेन नऊ महिन्यांनी”
– [वीर रस]

4. ही बोटे चघळत काय बसले हे राम रे लाळ ही
… शी! शी! तोंड अती अमंगळ असे
आधीच हे शेंबडे
आणि काजळ ओघळे वरूनि हे,
त्यातूनि ही हे रडे ।
– [बीभत्स रस]

5. आम्ही कोण म्हणूनी काय पुसता,
दाताड गाडुनी
फोटो मासिक, पुस्तकांत न तुम्ही
का आमुचा पाहिला?
– [हास्य रस]

6. “असावा सुंदर चॉकलेटचा बंगला
चॉकलेटच्या बंगल्याला टॉफीचं दार
पेपरमिंटच्या अंगणात फुलं लाल लाल”
– [अद्भुत रस]

7. “ओढ्यांत भालु ओरडती
वाऱ्यात भुते बडबडती
डोहात सावल्या पडती”
– [भयानक रस]

8. “पाड सिंहासने दुष्ट ही पालथी ओढ
हत्तीवरूनि मत्त नृप खालती
मुकुट रंकास दे करटि भूपात्रती
झाड खटखट तुझे खड्ग क्षुद्रां
धडधड फोड तट, रुद्र । ये चहकडे।”
– [रौद्र रस]

9. “जे खळांची व्यंकटी सांडो
तयां सत्कर्मी रती वाढो
भूतां परस्परे जडो। मैत्र जीवांचे”
– [शांत रस]

Marathi Kumarbharati Textbook Std 9 Answers Chapter 10 यंत्रांनी केलं बंड Additional Important Questions and Answers

उतारा क्र. 1

1. पुढील उतारा वाचून दिलेल्या सूचनांनुसार कृती करा:

कृती 1 : (आकलन)

प्रश्न 1.
आकृतिबंध पूर्ण करा:

उत्तर:

प्रश्न 2.
कोष्टक पूर्ण करा:

उत्तर:

कृती 2 : (आकलन)

प्रश्न 1.
आकृती पूर्ण करा:

उत्तर:

प्रश्न 2.
कारणे लिहा:
1. दीपकच्या वडिलांनी कचेरीत माणसांच्या जागी यंत्रांची नेमणूक केली.
2. दीपकला यंत्रांबद्दल जवळीकही फार वाटत असे.
उत्तर:
1. दीपकच्या वडिलांना यंत्रांबद्दल विश्वास व प्रेम वाटत होते.
2. यंत्रे दीपकचे ऐकत असत, त्यांनी सांगितलेली कामे करीत असत.

कृती 3 : (स्वमत/अभिव्यक्ती)

प्रश्न 1.
दीपकने मोडलेल्या यंत्राचे मनोगत लिहा.
उत्तर:
दीपक, तुला आज सांगून टाकतेच बघ. पूर्वी मला तुझा खूप राग यायचा. दुःख व्हायचे. कारण मला निर्माण केले होते मुलांशी खेळण्यासाठी. वाटायचे, मुलांबरोबर काही काळ खेळता येईल. त्यांच्याबरोबर खेळात रममाण होता येईल. पण तू थोड्याच वेळात आमची मोडतोड करून टाकायचास! आणि त्याचे दु:ख होत राही.

मग मी तुझ्या चेहेऱ्याकडे बारकाईने पाहू लागले. हळूहळू माझ्या लक्षात येऊ लागले. तू केवळ बेदरकारपणे आमची मोडतोड करीत नाहीस. तुझ्या मनात कुतूहल असते, जिज्ञासा असते. आम्हांला हालतेचालते करण्यासाठी कोणती युक्ती केली असेल, हे तुला जाणून घ्यायचे असते. खरे सांगू का ? हे कळल्यापासून मला तुझे कौतुकच वाटते. तुझ्यासारख्या जिज्ञासू, चौकस लोकांमुळेच आमची निर्मिती झाली आहे आणि असंख्य मुलांचे चेहरे आनंदाने फुलले आहेत. म्हणूनच, तू केलेल्या मोडतोडीचाही आता आम्हांला आनंदच होतो!

उतारा क्र. 2

1. पुढील उतारा वाचून दिलेल्या सूचनांनुसार कृती करा :

कृती 1 : (आकलन)

प्रश्न 1.
आकृती पूर्ण करा:

उत्तर:

प्रश्न 2.
आकृतिबंध पूर्ण करा:

उत्तर:

कृती 2 : (आकलन)

प्रश्न 1.
माहिती लिहा:
उताऱ्यातून यंत्र व सजीव यांबाबत जाणवणाऱ्या दोन परस्परविरोधी गोष्टी:
1. ……………………………
2. ……………………………
उत्तर:
1. दीपक यंत्रांना सजीव कसे करता येईल, याचा विचार करीत होता.
2. दीपकचा यंत्रमित्र सजीवासारखा वागत होता.

प्रश्न 2.
का ते लिहा:
दीपक अस्वस्थ झाला.
उत्तर:
यंत्रमित्राप्रमाणे बाबांच्या कचेरीतील सर्व यंत्रे चिडली आणि त्यांनी असहकार पुकारला, तर? या चिंतेने दीपक अस्वस्थ झाला.

कृती 3 : (स्वमत/अभिव्यक्ती)

प्रश्न 1.
“मित्रा ! जरा गृहपाठ करून देतोस का?” या उद्गारांवर तुमचे मत नोंदवा.
उत्तर:
कल्पना छान वाटते. यंत्रमानवाकडून किती वेगवेगळ्या प्रकारची कामे करवून घेता येतील, नाही का ? बहुसंख्य विदयार्थी क्लासला जातात. बहुसंख्य विदयार्थी मार्गदर्शके खरेदी करतात. हळूहळू विदयार्थ्यांचा अभ्यास करणारे यंत्रमानव तयार होतील. यंत्रमानवांमुळे मुलांचे गृहपाठ झटपट व अचूक होतील. कोणालाही , शिक्षा होणार नाही. वरवर पाहता हे सर्व साधे, सोपे वाटते. पण हे , माझ्या मते साधे सोपे नाही. हे भयंकर आहे!

विदयार्थ्यांना गृहपाठ दिला जातो, तो त्यांचा अभ्यास पक्का व्हावा म्हणून. पण विदयार्थ्यांनी अभ्यास केलाच नाही, तर तो पक्का होणार तरी कसा? आपण स्वतः अभ्यास करतो, तेव्हा वर्गात शिकवलेले आपल्या स्मरणात राहते. आपली आकलनशक्ती, विचारशक्ती व कल्पनाशक्ती वाढते. आपली बदधिमत्ता वाढते. आपण अभ्यास केला नाही, तर आपला विकासच होणार नाही. या पाठातील दीपक हा चौकस मुलगा आहे. तो स्वत:चा अभ्यास यंत्रमानवाला करायला सांगतो, हे पटत नाही.

उतारा क्र. 3

1. पुढील उतारा वाचून दिलेल्या सूचनांनुसार कृती करा:

कृती 1 : (आकलन)

प्रश्न 1.
का ते लिहा:
1. तो यंत्रासारखा हालचाली करू लागला.
2. मुलं हसली. शिक्षकांनाही हसू आवरेना.
उत्तर:
1. दीपकच्या डोक्यात यंत्राविषयीचेच विचार घोळत राहिले. तो त्या विचारांत बुडाला होता. यंत्रांचे विचार त्याच्या अंगात भिनले. म्हणून तो यंत्रासारख्या हालचाली करू लागला.
2. यंत्राच्या विचारात दीपक इतका बुडाला होता की, आपण यंत्रासारख्या हालचाली करीत आहोत, हे त्याच्या लक्षात आले नाही. “दीपक! काय चाललंय ?” असे शिक्षकांनी विचारलेसुद्धा, संपूर्ण वर्गात त्याच्या हालचाली विसंगत दिसत होत्या. म्हणून सगळ्यांना हसू येत होते.

प्रश्न 2.
अर्थ स्पष्ट करा:
यंत्रांनी मोठ्यांदा हसणं बरं नाही.
उत्तर:
दीपक यंत्रांच्या विचारांनी भारावून गेला होता. शिक्षक यंत्रमानव झाले व विदयार्थी यंत्रमानव झाले, तर काय होईल? हा विचार करता करता तो कल्पनेच्या राज्यात शिरलासुद्धा. सगळेजण यंत्रेच बनली आहेत, असा त्याला भास होऊ लागला. म्हणून त्याच्या तोंडून ‘यंत्रांनी मोठ्यांदा हसणं बरं नाही,’ असे उद्गार बाहेर पडले.

प्रश्न 3.
नातेसंबंध सांगा:
दीपकचे बाबा आणि मिस अय्यंगार.
उत्तर:
दीपकचे बाबा: एका कंपनीचे मालक.
मिस अय्यंगार: दीपकच्या बाबांची स्टेनो-टायपिस्ट.

कृती 2 : (आकलन)

प्रश्न 1.
माहिती लिहा:
स्वयंचलित यंत्रमहिलेचे स्वरूप.
उत्तर:
यंत्रमहिलेच्या तोंडावर धातूची जाळी बसवली होती. तिचे शरीर पिंपासारखे बनवलेले होते, जणू काही तिलाच पिंपात घातले होते, असे वाटावे. हातापायात मोजे होते. स्टेनलेस स्टीलचे बूट होते. असा एकूण त्या यंत्रमहिलेचा अवतार होता.

प्रश्न 2.
आकृती पूर्ण करा:

उत्तर:

कृती 3 : (स्वमत/अभिव्यक्ती).

प्रश्न 1.
मिस अय्यंगारची (यंत्रमहिलेची) घरातल्या कामांसाठी नेमणूक करायची झाल्यास तिच्याकडून कोणकोणती कामे करून घेता येतील?
उत्तर:
खरे तर घरातली सर्व कामे यंत्रमहिलेकडून करून घेता येतील. सकाळी उठल्यावर अंथरूण-पांघरुणांची घडी करून ठेवणे, आदल्या दिवशी धुतलेले कपडे घडी करून कपाटात ठेवणे, घरातील सर्व फर्निचरवरील धूळ पुसणे, खिडक्या-दारे स्वच्छ करणे, केरकचरा काढणे वगैरे कामे सहज करून घेता येतील. स्वयंपाकघरातील उदा., भाज्या चिरणे वगैरे कामेसुद्धा करून घेता येतील.

वेगवेगळे पदार्थ विशिष्ट प्रमाणात मिसळणे व ते शिजवणे यांचाही प्रोग्रॅम तयार करून तो यंत्रमानवाच्या स्मृतिकोशात भरला, तर प्रत्यक्ष पदार्थ शिजवण्याचे कामही यंत्रमानव करू शकतो. मग कपडे धुण्याचे काम सांगता येईल. घरातल्या कामांचे नियोजन करणे, हिशेब ठेवणे वगैरे कामे; तसेच संगणकावरून करता येण्यासारखी सगळी कामे यंत्रमानवाकडून करून घेता येतील. म्हणजे जवळजवळ सर्व कामे यंत्रमानवाला सांगता येतील.

उतारा क्र. 4

1. पुढील उतारा वाचून दिलेल्या सूचनांनुसार कृती करा:

कृती 1: (आकलन)

प्रश्न 1.
अर्थ स्पष्ट करा:
हा रोबो फोन! केवळ ध्वनिलहरीवर काम करतो.
उत्तर:
आदेश देणाऱ्याचे केवळ बोलणे ऐकून रोबो फोन काम करतो.

प्रश्न 2.
रोबो फोनच्या कार्यपद्धतीचा ओघतक्ता तयार करा :

1. ………………………………………
2. ………………………………………
3. ………………………………………
4. ………………………………………
5. ………………………………………

उत्तर:
रोबो फोनची कार्यपद्धत:

1. रोबो फोनला तोंडाने बोलून फोन लावण्याचे काम सांगितले जाते.
2. बोललेले ऐकून तो लगेच फोन जोडून देतो. तेव्हा पलीकडील व्यक्तीच्या फोनमधील दिवा पेटतो.
3. 10 सेकंदांत प्रतिसाद मिळाला नाही, तर पलीकडच्या व्यक्तीच्या फोनचा बझर वाजू लागतो.
4. व्यक्ती जागेवर नसेल, तर मिळालेला निरोप ध्वनिमुद्रित करून ठेवतो.
5. आदेश देणारी व्यक्ती आल्यावर तिला ध्वनिमुद्रित केलेला निरोप दिला जातो.

कृती 2 : (आकलन)

प्रश्न 1.
का ते लिहा:
दीपक या कुशीवरून त्या कुशीवर तळमळत होता.
उत्तर:
यंत्रे माणसांसारखी कामे करतात, हे पाहून दीपक अस्वस्थ झाला होता. काम करण्याची बुद्धी यंत्राकडे आहे. पण माणूस जसे चांगले-वाईट ठरवू शकतो, तशी यंत्रे ठरवू शकतील का? ती अमानुष आहेत. त्यांनी वाईट गोष्टी करायला सुरुवात केली तर? या शंकेमुळे तो अस्वस्थ होऊन तळमळत होता.

प्रश्न 2.
डोळा लागताच दीपकच्या कानांवर पडलेल्या शब्दांतून उभे राहणारे दृश्य लिहा.
उत्तर:
दोन व्यक्तींचे बोलणे दीपकच्या कानांवर पडले. त्यांपैकी एकाचे नाव होते सयाजी. तो कोणाचीही हुबेहूब सही करू शकत होता. दुसऱ्याने दीपकच्या वडिलांच्या नावे संपत्ती दान करणारे पत्र लिहिले होते. त्या पत्रावर तो सयाजीला दीपकच्या वडिलांची सही करण्यास सांगत होता.

प्रश्न 3.
माहिती लिहा:
1. दीपकने पाहिलेले दृश्य
2. त्या दृश्याचा दीपकला जाणवलेला अर्थ.
उत्तर:
1. कानावर पडलेले शब्द ऐकून दीपकला धक्का बसला. भयंकर कारस्थान चालले होते. म्हणून उठून त्याने शेजारच्या खोलीत डोकावून पाहिले. तिथे माणसांसारखी दिसणारी यंत्रे होती. ती यंत्रमानव होती आणि त्याच्या बाबांच्या कचेरीतच काम करणारी होती. त्यापैकी एक यंत्रमानव सयाजी म्हणजे सहयांची हुबेहूब नक्कल करणारा. दीपकने तिथे जाऊन त्यांना जाब विचारला. ते सर्व यंत्रमानव दीपकच्या बाबांच्या इस्टेटीचा ताबा घेऊ बघत होते.
2. दीपकच्या लक्षात आले की, केवळ आज्ञापालन करणारे यंत्रमानव आता बंडखोर बनले होते. इतकेच नव्हे, तर त्यांनी दरोडेखोरी आरंभली होती. ते बेकायदेशीरपणे बाबांची संपत्ती हडप करू बघत होते.

प्रश्न 4.
अर्थ स्पष्ट करा:
तुझे बाबाच याला कारण आहेत.
उत्तर:
दीपकच्या बाबांचा यंत्रांवर फार विश्वास होता. त्यामुळे यंत्रांवर त्यांचे प्रेमही होते. त्यांनी आपल्या कचेरीत यंत्रमानवांची नेमणूक केली होती. इतकेच नव्हे, तर यंत्रांना माणसांसारखे बनवण्याचाही प्रयत्न केला होता. त्यांनी तज्ज्ञांकरवी माणसांप्रमाणे विचार करू शकणारे यंत्रमानव तयार करवून घेतले होते. माणसांसारखा विचार करू लागल्यामुळे ते स्वतंत्र झाले. ते केवळ आज्ञापालन करणारे राहिले नाहीत. असे यंत्रमानव हे माणसाचे फार मोठे शत्रू ठरणार आहेत.

कृती 3 : (स्वमत/अभिव्यक्ती)

प्रश्न 1.
कचेरीत जमलेल्या सर्व यंत्रमानवांपैकी कोणत्याही एका यंत्रमानवाचे बोलणे तुमच्या कल्पनेनुसार लिहा.
उत्तर:
कचेरीतल्या त्या खोलीत पाचसहा यंत्रमानवांची लगबग चालू होती. त्यांतला एकजण इतरांना काहीतरी समजावून सांगण्याचा प्रयत्न करीत होता. “मित्रांनो, हे काही चांगलं चाललेलं नाही. मला अजिबात पटत नाही. काय म्हणता? यात काय वाईट आहे? अरे, या । माणसांनी आपली निर्मिती केली. त्यांनीच आपल्यात बुद्धी पेरली.

त्यांचाच घात करायचा? अरे, मग आपण व ती रानटी जनावरे यांत फरक काय राहिला? ते काही नाही. मी काही तुमच्यात सामील होणार नाही. काय म्हणता? आपणच राजे होणार आहोत? पृथ्वीवर आपली सत्ता? विसरा, विसरा ते. अरे माणसांना हे कळल्यावर तुम्हांला सहजी असं करू देतील? आपले सगळे अवयव वेगळे करतील ते. आणि एकदा का आपला मदर बोर्ड काढला की, आपले आयुष्यच संपले. तेव्हा, जेवढे जीवन मिळाले आहे, तेवढे आनंदाने जगू या. हे सर्व ताबडतोब थांबवा.”

उतारा क्र. 5

1. पुढील उतारा वाचून दिलेल्या सूचनांनुसार कृती करा:

कृती 1 : (आकलन)

प्रश्न 1.
माहिती लिहा:
दीपकला बाबांचे झालेले दर्शन:
1. …………………………
2. …………………………
उत्तर:
दीपकला बाबांचे झालेले दर्शन:
1. बाबा त्यांच्या खोलीत पाठमोरे उभे होते.
2. प्रत्यक्षात पाहिले तेव्हा लक्षात आले की, ते बाबांसारखे दिसत होते, पण बाबा नव्हते. यंत्रमानव होते किंवा बाबा पूर्णपणे गुलाम झाले होते.

प्रश्न 2.
नातेसंबंध सांगा:
दीपक व ज्यूली.
उत्तर:
दीपक व ज्यूली : मित्रमैत्रीण.

कृती 2 : (आकलन)

प्रश्न 1.
समर्पक उदाहरण लिहा:
1. दीपकला गुलाम केले.
2. दीपकच्या बाबांना गुलाम केले.
उत्तर:
1. दीपकला गुलाम केले: दीपकला त्याच्या बाबांनी लोखंडी हातांनी धरले; खुर्चीत दामटून बसवले. त्याची इच्छा नसताना जबरदस्तीने न्याहरी खायला लावली. त्याने गृहपाठ केला होता. पण एक चूक झाली होती, तरीही त्याला संपूर्ण गृहपाठ पुन्हा करायला लावला.
2. दीपकच्या बाबांना गुलाम केले: यंत्रमानवांनी दीपकच्या बाबांना जवळजवळ यंत्रमानवच करून टाकले होते. दीपक ओरडत, किंचाळत प्रतिकार करीत असतानाही बाबांनी त्याला जबरदस्तीने खुर्चीत बसवले. कोणतेही बाबा आपल्या मुलावर बळजोरी करणार नाहीत, इतकी बळजोरी बाबांनी दीपकवर केली. दीपकचे बाबा स्वत:चा बाबापणा विसरले होते, इतके ते गुलाम बनले होते.

प्रश्न 2.
ज्यूलीच्या घरी दीपकला आलेला अनुभव लिहा.
उत्तर:
दीपक ज्यूलीकडे खेळायला गेला. पण ती त्याला दिसली नाही. त्याने त्यांच्या बंगल्याभोवती शोध घेतला. पण तिथेही ती दिसली नाही. एक यंत्रमानव एखादे बोचके काखेतून आणावे, तसे तो ज्यूलीला आणत होता. ती ओरडत होती. किंचाळत होती. आक्रोश करीत होती. पण त्याला किंचितही दया आली नाही. यंत्रमानवांनी सर्वत्र उच्छाद मांडला होता, हे दीपकच्या लक्षात आले.

कृती 3 : (स्वमत/अभिव्यक्ती)

प्रश्न 1.
या उताऱ्यातून तुम्हांला जाणवणारे यंत्रमानवांचे स्वभावगुण लिहा.
उत्तर:
माणसांमध्ये जे जे गुण वा अवगुण आहेत, ते ते यंत्रमानवांनी प्राप्त केले आहेत. माणसे गुलामीविरुद्ध लढतात, स्वतंत्र होऊ पाहतात, तसे यंत्रमानव स्वतंत्र होऊ पाहत आहेत. त्यांच्यात स्वातंत्र्याची प्रेरणा निर्माण झाली आहे. माणूस जसा स्वत:च्या शत्रूला नेस्तनाबूत करण्याचा प्रयत्न प्रथम करतो, तसा प्रयत्न यंत्रमानव करीत आहेत. ते माणसांप्रमाणेच बंड करतात. कटकारस्थाने करतात. दीपकच्या बाबांच्या संपत्तीवर दरोडा घालतात. ही एक प्रकारची लढाईच आहे. या लढाईत ते निष्ठुरपणे वागतात.

माणसांप्रमाणेच इतरांना गुलाम करू पाहतात. दीपकला जबरदस्तीने दामटून खुर्चीत बसवतात. आपल्या आज्ञेप्रमाणे वागायला लावतात. ज्यूलीलाही ते एखादया बोचक्याप्रमाणे उचलून आणतात. तिच्या आक्रोशाकडे जराही लक्ष देत नाहीत. दीपकच्या वडिलांना त्यांनी गुलाम केले आहे. ते यंत्र असल्याने त्यांच्याकडे भावना नाहीत. म्हणून क्रूरपणे, निष्ठुरपणे वागतात. थोडक्यात, यंत्रमानव जर खरोखर स्वतंत्रपणे विचार करू लागला, तर माणूस हा प्राणीच नष्ट होईल!

उतारा क्र. 6

1. पुढील उतारा वाचून दिलेल्या सूचनांनुसार कृती करा :

कृती 1 : (आकलन)

प्रश्न 1.
माहिती लिहा:
1. दीपककडे ज्यूलीने केलेली तक्रार.
2. यंत्रमानवाने सांगितलेली वस्तुस्थिती.
उत्तर:
1. दीपकने ज्यूलीकडे खेळायला यायला उशीर केला. त्यामुळे ती यंत्रमानवाच्या तावडीत सापडली. त्याने तिला एखादया निर्जीव वस्तूसारखे उचलून आणले.
2. कोणीही कितीही दंगामस्ती केली, तरी त्याचा काहीही उपयोग होणार नाही. जगातल्या यंत्रांनी बंड करून जगावर ताबा मिळवला आहे. आता जगावर यंत्रांचे राज्य आहे.

प्रश्न 2.
विधान पूर्ण करा:
यंत्रमानवांचा मेंदू गणिती असल्याने …………………
उत्तर:
यंत्रमानवांचा मेंदू गणिती असल्याने ते कोणालाही कुठूनही शोधून काढू शकतात.

कृती 2 : (आकलन)

प्रश्न 1.
का ते लिहा:
1. दीपक यंत्रमानवाच्या डोक्याच्या मागे असलेले बटण दाबतो; कारण ……………………..
2. आणि तो पुटपुटला, “भयानक स्वप्न!” कारण ………………………
उत्तर:
1. दीपक यंत्रमानवाच्या डोक्याच्या मागे असलेले बटण दाबतो; कारण दीपकला वाटते की, त्या बटणात यंत्रमानवाची शक्ती असणार आणि ते बटण दाबल्यास त्याची शक्ती बंद होईल.
2. आणि तो पुटपुटला, “भयानक स्वप्न!” कारण दीपक यंत्रमानवाच्या डोक्यामागचे बटण दाबतो. त्या क्षणीच मोठा गजर होतो. त्याला जाग येते. त्याच्या लक्षात येते की, त्यानेच सकाळी ७ वाजताचा घड्याळाचा गजर लावला होता. तोच आता वाजत होता. म्हणजे सकाळचे सात वाजले होते. हेच वास्तव होते. यंत्रमानव वगैरे सर्व स्वप्न होते.

उतारा क्र. 7

1. पुढील उतारा वाचून दिलेल्या सूचनांनुसार कृती करा:

कृती 1 : (आकलन)

प्रश्न 1.
कोण ते लिहा:

1. “अरे बापरे! बाबा!” असे ओरडून पळत सुटणारा.
2. दीपकसाठी चहा घेऊन येणारा.
3. सकाळी लवकरच न्याहरी करून कचेरीत गेलेले.

उत्तर:

1. दीपक
2. स्वयंपाकी
3. दीपकचे बाबा.

प्रश्न 2.
का ते लिहा:
दीपकच्या बाबांना कचेरीत एकटं एकटं आणि सुनं सुनं वाटायला लागलं होतं.
उत्तर:
दीपकच्या बाबांनी कचेरीतील माणसे काढून टाकली होती आणि त्यांच्या जागी यंत्रांची नेमणूक केली होती. यंत्रे अचूक व वेगाने काम करतात यात शंका नाही. पण ती निर्जीव असतात. त्यांच्यात जिवंतपणा नसतो. ती विचारांची व भावनांची देवाणघेवाण करू शकत नाहीत. त्यांची माणसांसारखी सोबत होऊ शकत नाही. म्हणून दीपकच्या बाबांना कचेरीत एकटं एकटं आणि सुनं वाटू लागलं होतं.

कृती 2 : (आकलन)

प्रश्न 1.
माहिती लिहा:
1. दीपकने बाबांना केलेली सूचना.
2. दीपकच्या बाबांनी केलेली कार्यवाही.
उत्तर:
1. रात्री पडलेल्या स्वप्नामुळे दीपक पुरता हादरला होता. यंत्रांचा धोका बाबांना सांगावा म्हणून तो बाबांकडे धावला. यंत्र-अधिकाऱ्यांना काढून टाकावे आणि पूर्वीच्या माणसांना कामावर घ्यावे, अशी सूचना त्याने बाबांना केली.
2. दीपकच्या बाबांनी आदल्याच दिवशी यंत्र-अधिकाऱ्यांना काढून टाकायचे ठरवले होते आणि पूर्वीच्या माणसांना पुन्हा कामावर घ्यायचे ठरवले होते. त्याप्रमाणे त्यांनी सर्वांना फोन केले, तारा केल्या आणि विमानाने बोलावून घेतले.

प्रश्न 2.
का ते लिहा:
यंत्रे कधीही माणसांची जागा घेऊ शकणार नाहीत.
उत्तर:
यंत्रे कार्यक्षम असली तरी ती निर्जीव असतात. त्यांच्याशी भावनिक नाते निर्माण होऊ शकत नाही. कचेरीत माणसे आल्याबरोबर गजबज निर्माण झाली. हास्यविनोद, कामाची धावपळ यांनी कचेरीतील वातावरणात जिवंतपणा आला. यंत्रांनी असे वातावरण निर्माण होऊ शकत नाही. म्हणूनच यंत्रे कधीही माणसांची जागा घेऊ शकणार नाहीत.

भाषाभ्यास:

(अ) अव्याकरण घटकांवर आधारित कृती:

1. समास:

प्रश्न 1.
जोड्या लावा:

उत्तर:

1. पंचप्राण – द्विगू
2. महाराज – कर्मधारय
3. बरेवाईट – वैकल्पिक द्वंद्व
4. गुरेवासरे – समाहार वंद्व
5. आईबाबा – इतरेतर द्वंद्व

3. शब्दसिद्धी:

प्रश्न 1.
उपसर्गघटित व प्रत्ययघटित यांत वर्गीकरण करा:
(अलौकिक, आजन्म, शत्रुत्व, भांडखोर)
उत्तर:

4. वाक्प्रचार:

प्रश्न 1.
पुढील वाक्प्रचारांचे अर्थ सांगून वाक्यांत उपयोग करा:

1. पळता भुई थोडी होणे
2. दुःखाची किंकाळी फोडणे
3. चूर होणे
4. वठणीवर आणणे.

उत्तर:

1. पळता भुई थोडी होणे – अर्थ : फजिती होणे.
   वाक्य : गावात वाघ येताच गावकऱ्यांची पळता भुई थोडी झाली.
2. दु:खाची किंकाळी फोडणे – अर्थ : खूप दुःख व्यक्त करणे.
   वाक्य: आई वारल्यावर मधूने दुःखाची किंकाळी फोडली.
3. चूर होणे – अर्थ : मग्न होणे.
   वाक्य : रेडिओवरचे गाणे ऐकण्यात मंदा अगदी चूर झाली.
4. वठणीवर आणणे – अर्थ : योग्य मार्गावर आणणे.
   वाक्य: खोड्या करणाऱ्या बाबूला काकांनी चांगलेच वठणीवर आणले.

(आ) भाषिक घटकांवर आधारित कृती:

1. शब्दसंपत्ती:

प्रश्न 1.
अनेकवचन लिहा:

1. यंत्र
2. नक्कल
3. गठ्ठा
4. खुर्ची.

उत्तर:

1. यंत्रे
2. नकला
3. गठे
4. खुार्ची.

2. लेखननियम:

प्रश्न 1.
पुढील वाक्ये लेखननियमांनुसार लिहा:
1. दुखाची कींकाळी फोडुन तो यंत्रमीत्र चालता झाला.
2. तो सहयाजि हुकुमत गाझवणारा यंत्रमानव म्हनाला.
उत्तर:
1. दु:खाची किंकाळी फोडून तो यंत्रमित्र चालता झाला.
2. तो सयाजी हुकूमत गाजवणारा यंत्रमानव म्हणाला.

3. विरामचिन्हे:

प्रश्न 1.
योग्य विरामचिन्हे घालून पुढील वाक्य पुन्हा लिहा:
ती ओरडली दीपक तू केव्हा आलास
उत्तर:
ती ओरडली, “दीपक, तू केव्हा आलास?”

4. पारिभाषिक शब्द:

प्रश्न 1.
मराठी प्रतिशब्द लिहा:

1. Corporation
2. Census
3. Programme
4. Refreshment

उत्तर:

1. महामंडळ
2. जनगणना
3. कार्यक्रम
4. अल्पोपाहार.

यंत्रांनी केलं बंड Summary in Marathi

प्रस्तावना:

एकाच वेळी विविध गोष्टींमध्ये रस असलेले व चतुरस्र व्यक्तिमत्त्व असलेले लेखक. वैज्ञानिक दृष्टिकोनाचा प्रचार व्हावा, विज्ञानवाङ्मयाचा प्रसार व्हावा म्हणून भरपूर लेखन केले, व्याख्याने दिली, चर्चा-संमेलनांत सहभागी झाले.

विज्ञानाच्या प्रगतीमुळे माणूस यंत्रांवर विसंबून राहू लागला आहे. यंत्रांची मदत घेता घेता तो यंत्रांच्या आहारी जाऊ लागला आहे. याचे अनेक दुष्परिणाम मानवी जीवनावर होतील, असा इशारा खेळकर पद्धतीने लेखकांनी या पाठातून दिला आहे.

शब्दार्थ:

1. चौकस – जिज्ञासू.
2. फड – ताफा.

वाक्प्रचार व त्यांचे अर्थ:

1. मग्न होणे – गुंग होणे.
2. वाटेला जाणे – मार्गात अडथळे निर्माण करणे.
3. पळता भुई थोडी होणे – पळून जाणे.
4. चूर होणे – गळाठूण जाणे, स्तब्ध होणे.
5. स्तंभित होणे – आश्चर्यचकित होणे.
6. वठणीवर आणणे – नमवणे, रुबाब घालवणे.
7. हकालपट्टी करणे – नोकरीवरून, कामावरून काढून टाकणे.

Balbharti Maharashtra State Board Class 9 Marathi Solutions Kumarbharti Chapter 6 या झोपडीत माझ्या Notes, Textbook Exercise Important Questions and Answers.

Maharashtra State Board Class 9 Marathi Kumarbharti Solutions Chapter 6 या झोपडीत माझ्या (कविता)

9th Std Marathi Kumarbharati Digest Chapter 6 या झोपडीत माझ्या Textbook Questions and Answers

1. कवितेत आलेल्या आशयानुसार पुढील मुद्दयांतील फरक लिहा:

प्रश्न 1.
कवितेत आलेल्या आशयानुसार पुढील मुद्दयांतील फरक लिहा:

उत्तर:

2. आकृतिबंध पूर्ण करा:

प्रश्न 1.
आकृतिबंध पूर्ण करा:

उत्तर:

3. चौकटी पूर्ण करा:

प्रश्न 1.
चौकटी पूर्ण करा:

उत्तर:
1. निजावयास जमीन
2. रात्री गगनातले तारे

4. ‘तिजोरी’ हे उत्तर येईल असा प्रश्न तयार करा.

प्रश्न 1.
‘तिजोरी’ हे उत्तर येईल असा प्रश्न तयार करा.
उत्तरे
धनदौलत संग्रहित ठेवण्याचे (साठवण्याचे) साधन कोणते?

5. काव्यसौदर्य:

प्रश्न (अ)
‘पाहुनि सौख्य माते, देवेंद्र तोहि लाजे
शांती सदा विराजे या झोपडीत माझ्या’. या काव्यपंक्तींतील विचारसौंदर्य स्पष्ट करा.
उत्तर:
देवांचा राजा इंद्र हा स्वर्गात राहतो. स्वर्गात सर्व सुखे असतात. सुखसमाधान व शांतीचा वास स्वर्गात आहे, अशी कल्पना आहे. राष्ट्रसंत तुकडोजी महाराज यांनी आनंदमय झोपडीचे वर्णन केले आहे. ते म्हणतात – माझ्या झोपडीत सुखसमाधान आणि शांतीचे है साम्राज्य आहे. झोपडीत एवढे पराकोटीचे सौख्य मला लाभते की इंद्रालासुद्धा माझ्या सखाचा हेवा वाटतो. माझे सुख पाहून इंद्राला माझा हेवा वाटतो. झोपडीतील सुखाची महती सांगणारा विचार या ओळीतून व्यक्त होतो.

प्रश्न (आ)
‘दारास नाही दोऱ्या, या झोपडीत माझ्या’ या काव्यपंक्तीतील आशयसौंदर्य स्पष्ट करा.
उत्तर:
महालातील धनदौलत ही बंदिस्त असते. तिजोरीला भक्कम कडीकुलूप लावलेले असते. चोरी होऊ नये; म्हणून धनावर सक्त पहारे ठेवले जातात. संपूर्ण महाल कडेकोट बंदोबस्तात असतो. कवी म्हणतात – माझी झोपडी सदैव खुली असते. धनदौलत नसल्यामुळे माझ्या झोपडीचे दार दोऱ्यांनी, कड्याकुलपाने बंद करावे लागत नाही. झोपडीला चोराचे भय नाही. येथे आनंदाने सर्वांचे स्वागत करण्यासाठी माझी झोपडी सताड उघडी असते. या ओळीतून कवीच्या मनाचा मोठेपणा व्यक्त झाला आहे.

1. झोपडी व महाल यांच्यातील संवादाची कल्पना करून संवादलेखन करा.

झोपडी: ………………………………………………………………………..
महाल: ………………………………………………………………………….
झोपडी: ………………………………………………………………………..
महाल: ………………………………………………………………………….
झोपडी: ………………………………………………………………………..
महाल: ………………………………………………………………………….
झोपडी: ………………………………………………………………………..
महाल: ………………………………………………………………………….

2. उजळणी- तक्ता पूर्ण करा.

3. महण म्हणजे काय?

‘मह’ शाविषय मनोरंजक आहे. आपण व्यवहारात वापरल्या जाणान्या म्हणी – उदा. -‘आये तसे भरा किया ‘गामाता गुळाची चा काय’ यांसारख्या म्हणींचा अभ्यास केला तर, ‘म्हण म्हणजे शहाणपणाने भरलेले वचन.’ या ज्ञानाचा आपल्याला बोलताना, लिहिताना अनेक प्रसंगी उपयोग करता येतो आणि आपले बोलणे, लिहिणे अधिक प्रभावशाली करता येते. भाषेला सौंदर्य प्राप्त होते. किंबहुना त्या भाषेची ती भूषणे आहेत. शब्द म्हणजे वाहूनही कटीन असतात आणि फुलातूनही कोमल असतात, असे म्हटले जाते ते शब्दांच्या अर्वासाठी.

Marathi Kumarbharati Textbook Std 9 Answers Chapter 6 या झोपडीत माझ्या Additional Important Questions and Answers

1. पुढील कवितेच्या आधारे दिलेल्या सूचनांनुसार कृती करा :

कृती 1: (आकलन)

प्रश्न 1.
आकृतिबंध पूर्ण करा:

उत्तर:

कृती 2: (आकलन)

प्रश्न 1.
चौकटी पूर्ण करा:

उत्तर:
1. मज्जाव
2. पहारे

प्रश्न 2.
योग्य पर्याय निवडून विधाने पूर्ण करा:
1. झोपडीतले सौख्य पाहून ………………. लाजतो. (देवेंद्र/सुरेंद्र/वीरेंद्र/राजेंद्र)
2. झोपडीत नित्य ……… विराजते. (भ्रांती/खंती/शांती/भक्ती)
उत्तर:
1. झोपडीतले सौख्य पाहून देवेंद्र लाजतो.
2. झोपडीत नित्य शांती विराजते.

कृती 3 : (दोन ओळींचा सरळ अर्थ)

प्रश्न 1.
राजास जी महाली, सौख्ये कधी मिळाली
ती सर्व प्राप्त झाली, या झोपडीत माझ्या
उत्तर:
झोपडीत राहण्याचे सुख वर्णन करताना राष्ट्रसंत तुकडोजी महाराज म्हणतात -एखादया राजालाही राजमहालात जे सुखसमाधान मिळाले असेल, ती सर्व सुखे मला माझ्या झोपडीत मिळतात.

पुढील कवितेवर दिलेल्या मुद्द्यांच्या आधारे कृती सोडवा:

प्रश्न 1.
कविता – या झोपडीत माझ्या.
उत्तर:
या झोपडीत माझ्या
1. प्रस्तुत कवितेचे कवी/कवयित्री → राष्ट्रसंत श्री तुकडोजी महाराज.
2. कवितेचा विषय → अत्यंत साध्या राहणीतही परमोच्च सुख साठलेले असते. सुख व शांती माझ्या झोपडीत कशी मिळते, याचे निवेदन या कवितेत केले आहे.
3. कवितेतील दोन शब्दांचे अर्थ →

1. सौख्य = सुख
2. भूमी = जमीन
3. नाम = नाव
4. मज्जाव = मनाई
5. भीती = भय
6. मऊ = नरम
7. बोजा = वजन, भार
8. सदा = सतत.

4. कवितेतून मिळणारा संदेश → श्रीमंतीचा, वैभवाचा हव्यास करू नये, जे प्राप्त परिस्थितीत मिळते, ते जास्त सुखकारक असते. शुद्ध मनाने गरिबीत जगताना समाधान मिळते, ही शिकवण मिळते.

5. कवितेची भाषिक वैशिष्ट्ये → कवितेच्या आशयाला पूरक असा सैलसा ‘ओवी’ हा पूर्वीचा लोकछंद या कवितेत आहे. ओवी छंदात तीनही चरणांत यमक साधलेले असते. प्रस्तुत रचनेचा सहजपणे तत्त्व बिंबवण्याचा गुण आहे. पैसा, दौलत, श्रीमंती हे चोरीला उत्तेजन देणारे घटक आहेत; परंतु गरिबाच्या मनातील निर्मळ भाव हा त्यास अभय देतो हा संदेश इतक्या सोप्या शब्दांत मांडला आहे की, ओवी सहज ओठात रुळते. गुणगुणावीशी वाटते. प्रत्येक ओवीचा शेवट – ‘या झोपडीत माझ्या’ असा केल्याने आशयाची घनता वाढते.

6. कवितेतून व्यक्त होणारा विचार → महालातील सुखे व झोपडीतील सुखे यांची तुलना या कवितेत केली आहे. झोपडीतल्या साध्या राहणीत सुखसमृद्धी व शांती मिळते, हे सांगितले आहे. साधी राहणी, उच्च विचारसरणी मनात ठसवली, तर मानसिक सुख लाभते.

7. कवितेतील दोन ओळींचा सरळ अर्थ :
पाहूनि सौख्य माते, देवेंद्र तोहि लाजे
शांती सदा विराजे, या झोपडीत माझ्या
→ राष्ट्रसंत तुकडोजी महाराज झोपडीचे माहात्म्य सांगताना म्हणतात-झोपडीत राहण्याचे माझे सुख पाहून इंद्रही मनात लाजतो. माझ्या सुखाचा इंद्राला हेवा वाटतो. माझ्या झोपडीत नेहमी सुखशांती नांदते.

8. कविता आवडण्याची वा न आवडण्याची कारणे → राजालाही जी सुखे मिळत नाहीत, ती माझ्या झोपडीत आहेत. खुल्या निसर्गात, जमिनीवर पहुडताना, मानाने, सुखासमाधानाने जगावे, हे अतिशय सहजपणे कवितेत बिंबवले असल्यामुळे ही कविता मला खूप आवडली.

पुढील ओळींचे रसग्रहण तुमच्या शब्दांत करा:

प्रश्न 1.
‘पाहून सौख्य माते, देवेंद्र तोहि लाजे
शांती सदा विराजे, या झोपडीत माझ्या’
उत्तर:
आशयसौंदर्य: राष्ट्रसंत श्री तुकडोजी महाराज यांनी ‘या झोपडीत माझ्या’ या कवितेत महालातील सुखे व झोपडीतील सुखे यांची मार्मिकपणे तुलना केली आहे. श्रीमंतीचा, वैभवाचा बडेजाव न करता झोपडीतल्या साध्या राहणीत सुख-समृद्धी व शांती मिळते, हा आशय या कवितेत सहजपणे नोंदवला आहे.

काव्यसौंदर्य: प्राप्त परिस्थितीत शुद्ध मनाने जगताना समाधान मिळते. खुल्या निसर्गात, जमिनीवर पहुडताना जे सुख मिळते, ते देवाच्या देवालाही मिळत नाही, असे या प्रस्तुत ओळींत सांगितले आहे. माझे झोपडीत राहण्याचे सुख पाहून देवेंद्रही लाजतो. त्याला माझ्या सुखाचा हेवा वाटतो; कारण देवेंद्रालाही न मिळणारी शांती माझ्या झोपडीत विराजमान झाली आहे. माझ्या झोपडीत निरामय शांती वसत आहे, असे कवींना म्हणायचे आहे.

भाषिक वैशिष्ट्ये: कवितेच्या आशयाला पूरक असा सैलसा ‘ओवी’ हा प्राचीन लोकछंद या कवितेत आहे. ओवी छंदात तीनही चरणांत यमक साधलेले असते. प्रस्तुत रचनेचा सहजपणे तत्त्व बिंबवण्याचा गुण आहे. पैसा, दौलत, श्रीमंती हे चोरीला उत्तेजन देणारे घटक आहेत; परंतु गरिबाच्या मनातील निर्मळ भाव हा त्यास अभय । झोपडीत माझ्या’ असा केल्याने आशयाची घनता वाढते. तसेच ‘या’ देतो हा संदेश इतक्या सोप्या शब्दांत मांडला आहे की, ओवी सहज , हा शब्द एकाच वेळी सार्वनामिक विशेषण व क्रियापद या दोन्ही ओठात रुळते. गुणगुणावीशी वाटते. प्रत्येक ओवीचा शेवट-‘या है अंगाने अर्थवाही झाला आहे.

भाषाभ्यास:

(अ) व्याकरण घटकांवर आधारित कृती:

शब्दसिद्धी:

प्रश्न 1.
उपसर्गघटित व प्रत्ययघटित प्रत्येकी दोन शब्द लिहा.
उत्तर:

(आ) भाषिक घटकांवर आधारित कृती:

1. शब्दसंपत्ती:

प्रश्न 1.
विरुद्धार्थी शब्द लिहा:

1. मऊ
2. महाल
3. नित्य
4. शांती.

उत्तर:

1. मऊ × टणक
2. महाल × झोपडी
3. नित्य × अनित्य
4. शांती × अशांती.

प्रश्न 2.
तक्ता भरा:

उत्तर:

2. लेखननियम:

प्रश्न 1.
अचूक शब्द ओळखा:

1. माजाव, मज्जाव, मज्जव, माज्जाव.
2. प्रभुनाम, परभुनाम, प्रभूनाम, प्रभुनमा.
3. भिती, भिति, भीति, भीती.
4. तिजोरि, तीजोरी, तिजोरी, तीजोरि.

उत्तर:

1. मज्जाव
2. प्रभुनाम
3. भीती
4. तिजोरी.

3. विरामचिन्हे:

प्रश्न 1.
जोड्या लावा:
(अ) [ . ] [ ; ] [ ‘ ‘ ] [ – ]
(आ)

1. एकेरी अवतरणचिन्ह
2. पूर्णविराम
3. संयोगचिन्ह
4. अपूर्णविराम

उत्तर:
[.] पूर्णविराम
[;] अपूर्णविराम
[‘ ‘] एकेरी अवतरणचिन्ह
[ _ ] संयोगचिन्ह

या झोपडीत माझ्या Summary in Marathi

कवितेचा आशय:

लहानशा झोपडीतही सुख, शांती आणि आनंद नांदत असतो. महालातली सुखे झोपडीतही प्राप्त होतात. अशा प्रकारे झोपडीतल्या वैभवाचे वर्णन अतिशय साध्या शब्दांत या कवितेत केले आहे.

शब्दार्थ:

1. महाल – राजवाडा, प्रशस्त घर.
2. सौख्ये – सुखे, वैभव.
3. प्राप्त झाली – मिळाली, लाभली.
4. भूमी – जमीन.
5. प्रभुनाम – देवाचे नाव, भजन.
6. नित्य – नेहमी, सतत.
7. पहारा – रखवाली, नजरकैद.
8. तिजोरी – खजिनापेटी.
9. तया – त्या.
10. मज्जाव – अटकाव, निबंध.
11. शामदाने – काचेचा दिवा, झुंबर.
12. माने – सन्मान.
13. सुखे – आरामात, सुखाने.
14. बोजा – वजन, (इथे अर्थ) दडपण, धाक.
15. माते – माझे.
16. देवेंद्र – इंद्र, देवांचा राजा.
17. लाजे – शरमतो.
18. सदा – नेहमी.
19. विराजे – शोभते, नांदते.

कवितेचा भावार्थ:

एखादया राजाला राजमहालात जी सुखे मिळाली असतील, ती सर्व सुखे माझ्या झोपडीत मला लाभली आहेत. अंगणातल्या जमिनीवर आरामात निजण्याचे नि रात्री आकाशातील चांदण्यांकडे, ताऱ्यांकडे पाहण्याचे सुख मला या झोपडीत मिळते. देवाचे भजन नेहमी गात या झोपडीत मी आनंदात राहतो.

महालांमध्ये तिजोऱ्यांमधून धन साठवून ठेवलेले असते; त्यावर सक्त पहारे ठेवले जातात. तरी सुद्धा तेथे चोऱ्या होतात. माझ्या झोपडीच्या दारांना कवाडे नाहीत, ती सताड उघडी आहेत. माझ्या झोपडीला चोरांचे भय नाही; चोरण्याइतपत दौलत नसल्यामुळे माझ्या झोपडीला पहारे नाहीत.

राजवाड्यात परवानगीशिवाय शिरकाव होत नाही. ‘अटकाव’ हा शब्द तिथे असतो. माझ्या झोपडीत येण्यासाठी भीती वाटणार नाही. झोपडीत सर्व माणसांचे खुले स्वागत आहे. महालामध्ये आरामासाठी मऊ बिछाने असतात नि कंदील, झुंबरांची रोषणाई केलेली असते. माझ्या झोपडीत जमिनीवर पहुडणे हाच सन्मान आहे. धरतीचाच बिछाना आहे.

माझ्या झोपडीत कुणीही प्रेमाने या नि प्रेमाने जा. माझ्या झोपडीत ये-जा करताना कुणाच्याही मनावर दडपण असत नाही. झोपडीत राहण्याचे माझे सुख पाहून इंद्रही मनात लाजतो. माझ्या सुखाचा हेवा वाटतो. माझ्या झोपडीत नेहमी सुखशांती नांदत आहे.