10th Standard Maths 2 Practice Set 5.2 Chapter 5 Co-ordinate Geometry Textbook Answers Maharashtra Board

Balbharti Maharashtra State Board Class 10 Maths Solutions covers the Practice Set 5.2 Geometry 10th Class Maths Part 2 Answers Solutions Chapter 5 Co-ordinate Geometry.

Class 10 Maths Part 2 Practice Set 5.2 Chapter 5 Co-ordinate Geometry Questions With Answers Maharashtra Board

Question 1.
Find the co-ordinates of point P if P divides the line segment joining the points A (-1, 7) and B (4, -3) in the ratio 2:3.
Solution:
Let the co-ordinates of point P be (x, y) and A (x1, y1) B (x2, y2) be the given points.
Here, x1 = -1, y1 = 7, x2 = 4, y2 = -3, m = 2, n = 3
∴ By section formula,
Maharashtra Board Class 10 Maths Solutions Chapter 5 Co-ordinate Geometry Practice Set 5.2 1
∴ The co-ordinates of point P are (1,3).

Question 2.
In each of the following examples find the co-ordinates of point A which divides segment PQ in the ratio a : b.
i. P (-3, 7), Q (1, -4), a : b = 2 : 1
ii. P (-2, -5), Q (4, 3), a : b = 3 : 4
iii. P (2, 6), Q (-4, 1), a : b = 1 : 2
Solution:
Let the co-ordinates of point A be (x, y).
i. Let P (x1, y1), Q (x2, y2) be the given points.
Here, x1 = -3, y1 = 7, x2 = 1, y2 = -4, a = 2, b = 1
∴ By section formula,
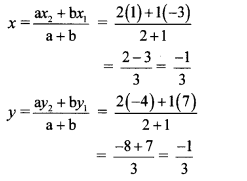
Maharashtra Board Class 10 Maths Solutions Chapter 5 Co-ordinate Geometry Practice Set 5.2 2
∴ The co-ordinates of point A are (\(\frac { -1 }{ 3 } \),\(\frac { -1 }{ 3 } \)).

ii. Let P (x1,y1), Q (x2, y2) be the given points.
Here, x1 = -2, y1 = -5, x2 = 4, y2 = 3, a = 3, b = 4
By section formula,
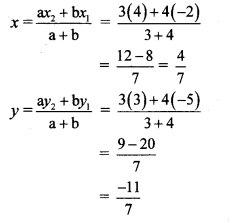
Maharashtra Board Class 10 Maths Solutions Chapter 5 Co-ordinate Geometry Practice Set 5.2 3
∴ The co-ordinates of point A are (\(\frac { 4 }{ 7 } \),\(\frac { -11 }{ 7 } \))

iii. Let P (x1, y1), Q (x2, y2) be the given points.
Here,x1 = 2,y1 = 6, x2 = -4, y2 = 1, a = 1,b = 2
∴ By section formula,
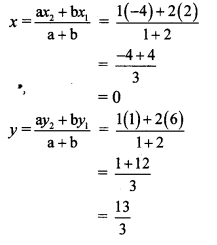
Maharashtra Board Class 10 Maths Solutions Chapter 5 Co-ordinate Geometry Practice Set 5.2 4
∴ The co-ordinates of point A are (0,\(\frac { 13 }{ 3 } \))

Question 3.
Find the ratio in which point T (-1, 6) divides the line segment joining the points P (-3,10) and Q (6, -8).
Solution:
Let P (x1, y1), Q (x2, y2) and T (x, y) be the given points.
Here, x1 = -3, y1 = 10, x2 = 6, y2 = -8, x = -1, y = 6
∴ By section formula,
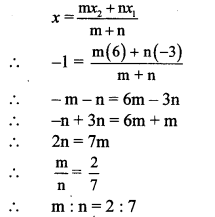
Maharashtra Board Class 10 Maths Solutions Chapter 5 Co-ordinate Geometry Practice Set 5.2 5
∴ Point T divides seg PQ in the ratio 2 : 7.

Question 4.
Point P is the centre of the circle and AB is a diameter. Find the co-ordinates of point B if co-ordinates of point A and P are (2, -3) and (-2,0) respectively.
Solution:
Let A (x1, y1), B (x2, y2) and P (x, y) be the given points.
Here, x1 = 2, y1 =-3,
x = -2, y = 0
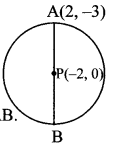
Maharashtra Board Class 10 Maths Solutions Chapter 5 Co-ordinate Geometry Practice Set 5.2 6
Point P is the midpoint of seg AB.
∴ By midpoint formula,
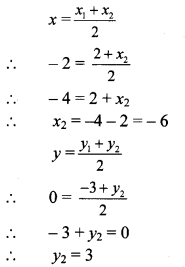
Maharashtra Board Class 10 Maths Solutions Chapter 5 Co-ordinate Geometry Practice Set 5.2 7
∴ The co-ordinates of point B are (-6,3).

Question 5.
Find the ratio in which point P (k, 7) divides the segment joining A (8, 9) and B (1,2). Also find k.
Solution:
Let A (x1, y1), B (x2, y2) and P (x, y) be the given points.
Here, x1 = 8, y1 = 9, x2 = 1, y2 = 2, x = k, y = 7
∴ By section formula,
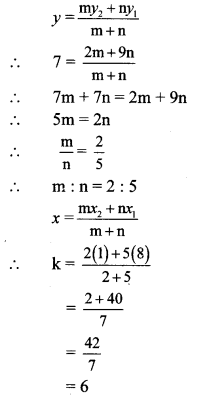
Maharashtra Board Class 10 Maths Solutions Chapter 5 Co-ordinate Geometry Practice Set 5.2 8
∴ Point P divides seg AB in the ratio 2 : 5, and the value of k is 6.

Question 6.
Find the co-ordinates of midpoint of the segment joining the points (22, 20) and (0,16).
Solution:
Let A (x1, y1) = A (22, 20),
B (x2,y2) = B (0, 16)
Let the co-ordinates of the midpoint be P (x,y).
∴ By midpoint formula,
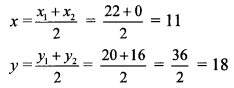
Maharashtra Board Class 10 Maths Solutions Chapter 5 Co-ordinate Geometry Practice Set 5.2 9
The co-ordinates of the midpoint of the segment joining (22, 20) and (0, 16) are (11,18).

Question 7.
Find the centroids of the triangles whose vertices are given below.
i. (-7, 6), (2,-2), (8, 5)
ii. (3, -5), (4, 3), (11,-4)
iii. (4, 7), (8, 4), (7, 11)
Solution:
i. Let A (x1, y1) = A (-7, 6),
B (x2, y2) = B (2, -2),
C (x3, y3) = C(8, 5)
∴ By centroid formula,
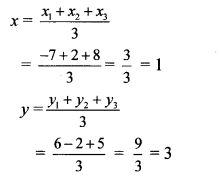
Maharashtra Board Class 10 Maths Solutions Chapter 5 Co-ordinate Geometry Practice Set 5.2 10
∴ The co-ordinates of the centroid are (1,3).

ii. Let A (x1 y1) = A (3, -5),
B (x2, y2) = B (4, 3),
C(x3, y3) = C(11,-4)
∴ By centroid formula,
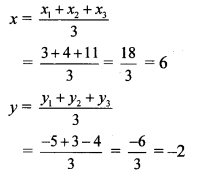
Maharashtra Board Class 10 Maths Solutions Chapter 5 Co-ordinate Geometry Practice Set 5.2 11
∴ The co-ordinates of the centroid are (6, -2).

iii. Let A (x1, y1) = A (4, 7),
B (x2, y2) = B (8,4),
C (x3, y3) = C(7,11)
∴ By centroid formula,
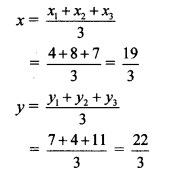
Maharashtra Board Class 10 Maths Solutions Chapter 5 Co-ordinate Geometry Practice Set 5.2 12
∴ The co-ordinates of the centroid are (\(\frac { 19 }{ 3 } \),\(\frac { 22 }{ 3 } \))

Question 8.
In ∆ABC, G (-4, -7) is the centroid. If A (-14, -19) and B (3, 5), then find the co-ordinates of C.
Solution:
G (x, y) = G (-4, -7),
A (x1, y1) = A (-14, -19),
B(x2, y2) = B(3,5)
Let the co-ordinates of point C be (x3, y3).
G is the centroid.
By centroid formula,
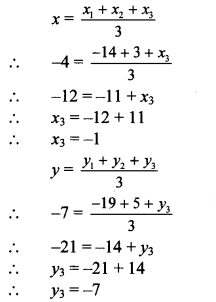
Maharashtra Board Class 10 Maths Solutions Chapter 5 Co-ordinate Geometry Practice Set 5.2 13
∴ The co-ordinates of point C are (-1, – 7).

Question 9.
A (h, -6), B (2, 3) and C (-6, k) are the co-ordinates of vertices of a triangle whose centroid is G (1,5). Find h and k.
Solution:
A(x1,y1) = A(h, -6),
B (x2, y2) = B(2, 3),
C (x3, y3) = C (-6, k)
∴ centroid G (x, y) = G (1, 5)
G is the centroid.
By centroid formula,
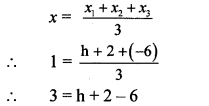
Maharashtra Board Class 10 Maths Solutions Chapter 5 Co-ordinate Geometry Practice Set 5.2 14
∴ 3 = h – 4
∴ h = 3 + 4
∴ h = 7
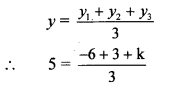
Maharashtra Board Class 10 Maths Solutions Chapter 5 Co-ordinate Geometry Practice Set 5.2 15
∴ 15 = -3 + k
∴ k = 15 + 3
∴ k = 18
∴ h = 7 and k = 18

Question 10.
Find the co-ordinates of the points of trisection of the line segment AB with A (2,7) and B (-4, -8).
Solution:
A (2, 7), B H,-8)
Suppose the points P and Q trisect seg AB.
∴ AP = PQ = QB
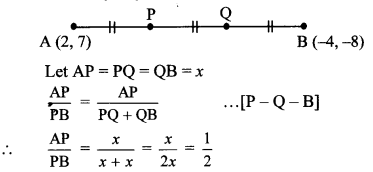
Maharashtra Board Class 10 Maths Solutions Chapter 5 Co-ordinate Geometry Practice Set 5.2 16
∴ Point P divides seg AB in the ratio 1:2.
∴ By section formula,
Maharashtra Board Class 10 Maths Solutions Chapter 5 Co-ordinate Geometry Practice Set 5.2 17
Co-ordinates of P are (0, 2).
Point Q is the midpoint of PB.
By midpoint formula,
Maharashtra Board Class 10 Maths Solutions Chapter 5 Co-ordinate Geometry Practice Set 5.2 18
Co-ordinates of Q are (-2, -3).
∴ The co-ordinates of the points of trisection seg AB are (0,2) and (-2, -3).

Question 11.
If A (-14, -10), B (6, -2) are given, find the co-ordinates of the points which divide segment AB into four equal parts.
Solution:
Let the points C, D and E divide seg AB in four equal parts.
Maharashtra Board Class 10 Maths Solutions Chapter 5 Co-ordinate Geometry Practice Set 5.2 19
Point D is the midpoint of seg AB.
∴ By midpoint formula,
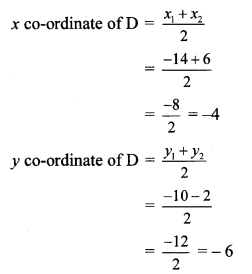
Maharashtra Board Class 10 Maths Solutions Chapter 5 Co-ordinate Geometry Practice Set 5.2 20
∴ Co-ordinates of D are (-4, -6).
Point C is the midpoint of seg AD.
∴ By midpoint formula,
Maharashtra Board Class 10 Maths Solutions Chapter 5 Co-ordinate Geometry Practice Set 5.2 21
∴ Co-ordinates of C are (-9, -8).
Point E is the midpoint of seg DB.
∴ By midpoint formula,
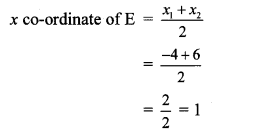
Maharashtra Board Class 10 Maths Solutions Chapter 5 Co-ordinate Geometry Practice Set 5.2 22
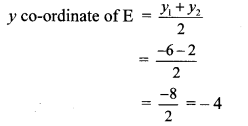
Maharashtra Board Class 10 Maths Solutions Chapter 5 Co-ordinate Geometry Practice Set 5.2 23
∴ Co-ordinates of E are (1,-4).
∴ The co-ordinates of the points dividing seg AB in four equal parts are C(-9, -8), D(-4, -6) and E(1, – 4).

Question 12.
If A (20, 10), B (0, 20) are given, find the co-ordinates of the points which divide segment AB into five congruent parts.
Solution:
Suppose the points C, D, E and F divide seg AB in five congruent parts.
∴ AC = CD = DE = EF = FB
Maharashtra Board Class 10 Maths Solutions Chapter 5 Co-ordinate Geometry Practice Set 5.2 24
∴ co-ordinates of C are (16, 12).
E is the midpoint of seg CB.
By midpoint formula,
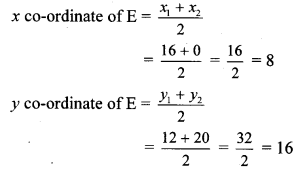
Maharashtra Board Class 10 Maths Solutions Chapter 5 Co-ordinate Geometry Practice Set 5.2 25
∴ co-ordinates of E are (8, 16).
D is the midpoint of seg CE.
Maharashtra Board Class 10 Maths Solutions Chapter 5 Co-ordinate Geometry Practice Set 5.2 26
∴ co-ordinates of F are (4, 18).
∴ The co-ordinates of the points dividing seg AB in five congruent parts are C (16, 12), D (12, 14), E (8, 16) and F (4, 18).

Maharashtra Board Class 10 Maths Chapter 5 Co-ordinate Geometry Intext Questions and Activities

Question 1.
A (15, 5), B (9, 20) and A-P-B. Find the ratio in which point P (11, 15) divides segment AB. Find the ratio using x and y co-ordinates. Write the conclusion. (Textbook pg. no. 113)
Solution:
Suppose point P (11,15) divides segment AB in the ratio m : n.
By section formula,
Maharashtra Board Class 10 Maths Solutions Chapter 5 Co-ordinate Geometry Practice Set 5.2 27
∴ Point P divides seg AB in the ratio 2 : 1.
The ratio obtained by using x and y co-ordinates is the same.

Question 2.
External division: (Textbook pg. no. 115)
Suppose point R divides seg PQ externally in the ratio 3:1.
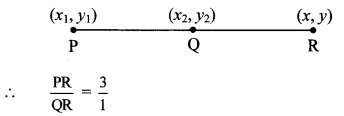
Maharashtra Board Class 10 Maths Solutions Chapter 5 Co-ordinate Geometry Practice Set 5.2 28
Let the common multiple be k.
Let PR = 3k and QR = k
Now, PR = PQ + QR … [P – Q – R]
∴ 3k = PQ + k
∴ \(\frac { PQ }{ QR } \) = \(\frac { 2k }{ k } \) = \(\frac { 2 }{ 1 } \)
∴ Point Q divides seg PR in the ratio 2 : 1 internally.
Thus, we can find the co-ordinates of point R, when co-ordinates of points P and Q are given.

Maharashtra State Board Class 10 Maths Solutions Part 2