Practice Set 6.1 Geometry 10th Standard Maths Part 2 Chapter 6 Trigonometry Solutions Maharashtra Board

10th Standard Maths 2 Practice Set 6.1 Chapter 6 Trigonometry Textbook Answers Maharashtra Board

Balbharti Maharashtra State Board Class 10 Maths Solutions covers the Practice Set 6.1 Geometry 10th Class Maths Part 2 Answers Solutions Chapter 6 Trigonometry.

Class 10 Maths Part 2 Practice Set 6.1 Chapter 6 Trigonometry Questions With Answers Maharashtra Board

Question 1.
If sin θ = \(\frac { 7 }{ 25 } \), find the values of cos θ and tan θ.
Solution:
sin θ = \(\frac { 7 }{ 25 } \) … [Given]
We know that,
sin² θ + cos² θ = 1

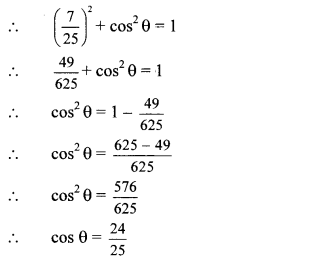
…[Taking square root of both sides] Now, tan θ = \(\frac{\sin \theta}{\cos \theta}\)

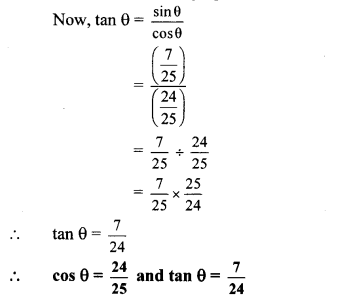
Alternate Method:
sin θ = \(\frac { 7 }{ 25 } \) …(i) [Given]
Consider ∆ABC, where ∠ABC 90° and ∠ACB = θ.
sin θ = \(\frac { AB }{ AC } \) … (ii) [By definition]
∴ \(\frac { AB }{ AC } \) = \(\frac { 7 }{ 25 } \) … [From (i) and (ii)]

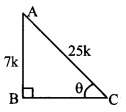
LetAB = 7k and AC = 25k
In ∆ABC, ∠B = 90°
∴ AB² + BC² = AC² … [Pythagoras theorem]
∴ (7k)² + BC² = (25k)²
∴ 49k² + BC² = 625k²
∴ BC² = 625k² – 49k²
∴ BC² = 576k²
∴ BC = 24k …[Taking square root of both sides]

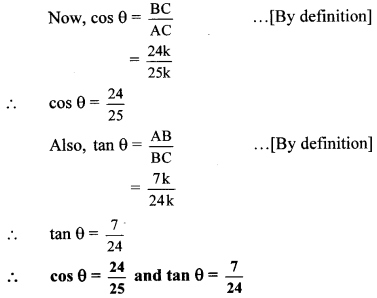
Question 2.
If tan θ = \(\frac { 3 }{ 4 } \), find the values of sec θ and cos θ.
Solution:

Alternate Method:
tan θ = \(\frac { 3 }{ 4 } \) …(i)[Given]
Consider ∆ABC, where ∠ABC 90° and ∠ACB = θ.
tan θ = \(\frac { AB }{ BC } \) … (ii) [By definition]
∴ \(\frac { AB }{ BC } \) = \(\frac { 3 }{ 4 } \) … [From (i) and (ii)]

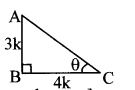
Let AB = 3k and BC 4k
In ∆ABC,∠B = 90°
∴ AB² + BC² = AC² …[Pythagoras theorem]
∴ (3k)² + (4k)² = AC²
∴ 9k² + 16k² = AC²
∴ AC² = 25k²
∴ AC = 5k …[Taking square root of both sides]

Question 3.
If cot θ = \(\frac { 40 }{ 9 } \), find the values of cosec θ and sin θ
Solution:

..[Taking square root of both sides]

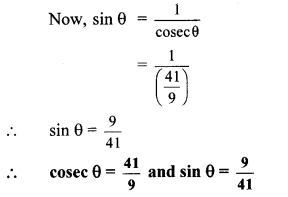
Alternate Method:
cot θ = \(\frac { 40 }{ 9 } \) ….(i) [Given]
Consider ∆ABC, where ∠ABC = 90° and
∠ACB = θ
cot θ = \(\frac { BC }{ AB } \) …(ii) [By defnition]
∴ \(\frac { BC }{ AB } \) = \(\frac { 40 }{ 9 } \) ….. [From (i) and (ii)]
Let BC = 40k and AB = 9k

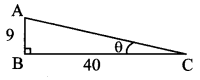
In ∆ABC, ∠B = 90°
∴ AB² + BC² = AC² … [Pythagoras theorem]
∴ (9k)² + (40k)² = AC²
∴ 81k² + 1600k² = AC²
∴ AC² = 1681k²
∴ AC = 41k … [Taking square root of both sides]

Question 4.
If 5 sec θ – 12 cosec θ = θ, find the values of sec θ, cos θ and sin θ.
Solution:
5 sec θ – 12 cosec θ = 0 …[Given]
∴ 5 sec θ = 12 cosec θ

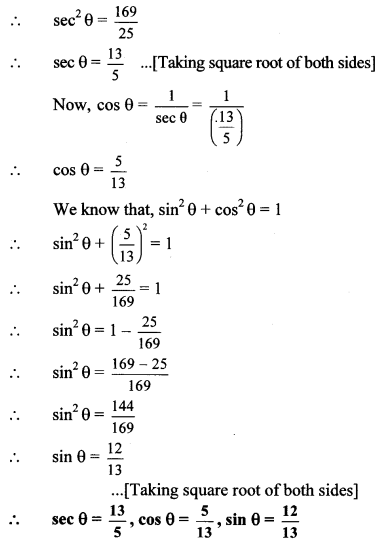
Question 5.
If tan θ = 1, then find the value of

Solution:
tan θ = 1 … [Given]
We know that, tan 45° = 1
∴ tan θ = tan 45°
∴ θ = 45°

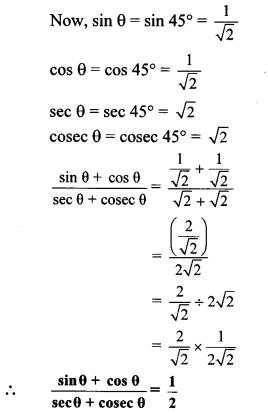
Question 6.
Prove that:
i. \(\frac{\sin ^{2} \theta}{\cos \theta}+\cos \theta=\sec \theta\)
ii. cos² θ (1+ tan² θ) = 1
iii. \(\sqrt{\frac{1-\sin \theta}{1+\sin \theta}}=\sec \theta-\tan \theta\)
iv. (sec θ – cos θ) (cot θ + tan θ) tan θ. sec θ
v. cot θ + tan θ cosec θ. sec θ
vi. \(\frac{1}{\sec \theta-\tan \theta}=\sec \theta+\tan \theta\)
vii. sin⁴ θ – cos⁴ θ = 1 – 2 cos² θ
viii. \(\sec \theta+\tan \theta=\frac{\cos \theta}{1-\sin \theta}\)

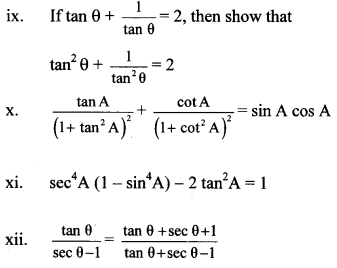
Proof:
i. L.H.S. = \(\frac{\sin ^{2} \theta}{\cos \theta}+\cos \theta\)

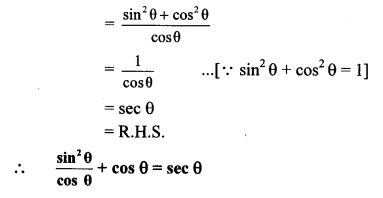
ii. L.H.S. = cos² θ(1 + tan² θ)
= cos² θ sec² θ …[∵ 1 + tan² θ = sec² θ]

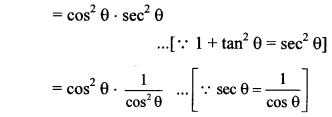
= 1
= R.H.S.
∴ cos² θ (1 + tan² θ) = 1

iv. L.H.S. = (sec θ – cos θ) (cot θ + tan θ)

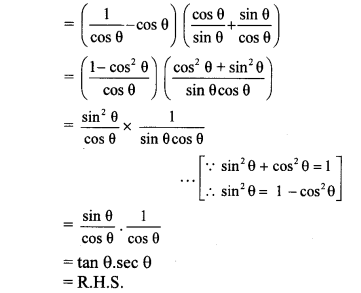
∴ (sec θ – cos θ) (cot θ + tan θ) = tan θ. sec θ

v. L.H.S. = cot θ + tan θ

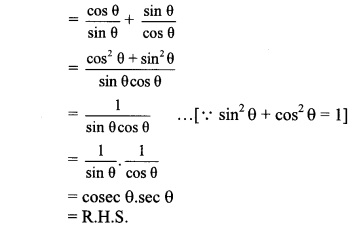
∴ cot θ + tan θ = cosec θ.sec θ

vii. L.H.S. = sin⁴ θ – cos⁴ θ
= (sin² θ)² – (cos² θ)²
= (sin² θ + cos² θ) (sin² θ – cos² θ)
= (1) (sin² θ – cos² θ) ….[∵ sin² θ + cos² θ = 1]
= sin² θ – cos² θ
= (1 – cos² θ) – cos² θ …[θ sin² θ = 1 – cos² θ]
= 1 – 2 cos² θ
= R.H.S.
∴ sin⁴ θ – cos⁴ θ = 1 – 2 cos² θ

viii. L.H.S. = sec θ + tan θ

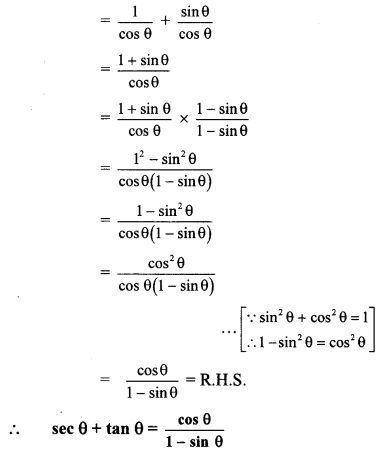
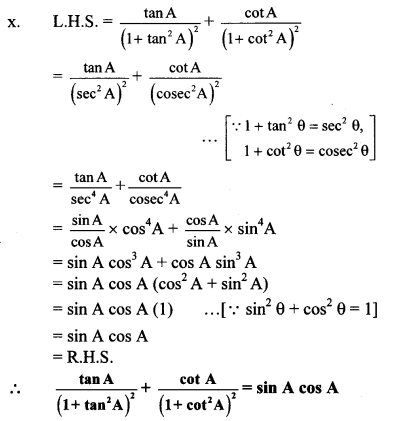
xi. L.H.S. = sec⁴ A (1 – sin⁴ A) – 2 tan² A
= sec⁴ A [1² – (sin² A)²] – 2 tan² A
= sec⁴ A (1 – sin²A) (1 + sin² A) – 2 tan² A
= sec⁴ A cos²A (1 + sin² A) – 2 tan²A
[ ∵ sin² θ + cos² θ = 1 ,∵ 1 – sin² θ = cos² θ]

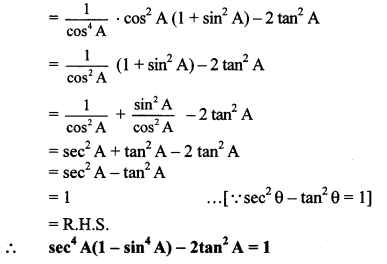
Maharashtra Board Class 10 Maths Chapter 6 Trigonometry Intext Questions and Activities

Question 1.
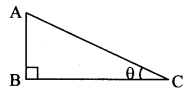
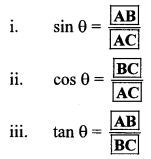
Fill in the blanks with reference to the figure given below. (Textbook pg. no. 124)

Solution:

Question 2.
Complete the relations in ratios given below. (Textbook pg, no. 124)

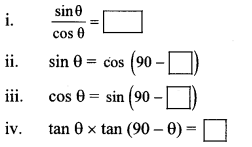
Solution:
i. \(\frac{\sin \theta}{\cos \theta}\) = [tan θ]
ii. sin θ = cos (90 – θ)
iii. cos θ = (90 – θ)
iv. tan θ × tan (90 – θ) = 1

Question 3.
Complete the equation. (Textbook pg. no, 124)
sin² θ + cos² θ = [______]
Solution:
sin² θ + cos² θ = [1]

Question 4.
Write the values of the following trigonometric ratios. (Textbook pg. no. 124)

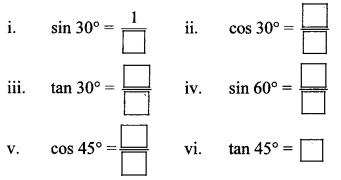
Solution:

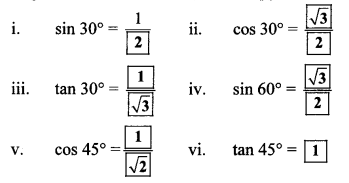
Maharashtra Board Class 10 Maths Solutions

Maharashtra State Board Class 10 Maths Solutions Part 2

• Co-ordinate Geometry Practice Set 5.1 Class 10 Maths Solutions
• Co-ordinate Geometry Practice Set 5.2 Class 10 Maths Solutions
• Co-ordinate Geometry Practice Set 5.3 Class 10 Maths Solutions
• Co-ordinate Geometry Problem Set 5 Class 10 Maths Solutions
• Trigonometry Practice Set 6.1 Class 10 Maths Solutions
• Trigonometry Practice Set 6.2 Class 10 Maths Solutions
• Trigonometry Problem Set 6 Class 10 Maths Solutions
• Mensuration Practice Set 7.1 Class 10 Maths Solutions
• Mensuration Practice Set 7.2 Class 10 Maths Solutions
• Mensuration Practice Set 7.3 Class 10 Maths Solutions
• Mensuration Practice Set 7.4 Class 10 Maths Solutions
• Mensuration Problem Set 7 Class 10 Maths Solutions