Problem Set 7 Geometry 10th Standard Maths Part 2 Chapter 7 Mensuration Solutions Maharashtra Board

10th Standard Maths 2 Problem Set 7 Chapter 7 Mensuration Textbook Answers Maharashtra Board

Balbharti Maharashtra State Board Class 10 Maths Solutions covers the Problem Set 7 Geometry 10th Class Maths Part 2 Answers Solutions Chapter 7 Mensuration.

Class 10 Maths Part 2 Problem Set 7 Chapter 7 Mensuration Questions With Answers Maharashtra Board

Problem Set 7 Question 1. Choose the correct alternative answer for each of the following questions.

i. The ratio of circumference and area of a circle is 2 : 7. Find its circumference.
(A) 14 π
(B) \(\frac{7}{\pi}\)
(C) 7π
(D) \(\frac{14}{\pi}\)
Answer:

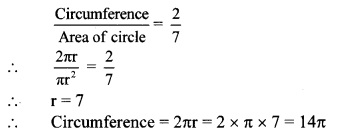
(A)

ii. If measure of an arc of a circle is 160° and its length is 44 cm, find the circumference of the circle.
(A) 66 cm
(B) 44 cm
(C) 160 cm
(D) 99 cm
Answer:

(D)

iii. Find the perimeter of a sector of a circle if its measure is 90° and radius is 7 cm.
(A) 44 cm
(B) 25 cm
(C) 36 cm
(D) 56 cm
Answer:

(B)

iv. Find the curved surface area of a cone of radius 7 cm and height 24 cm.
(A) 440 cm²
(B) 550 cm²
(C) 330 cm²
(D) 110 cm²
Answer:

(B)

v. The curved surface area of a cylinder is 440 cm² and its radius is 5 cm. Find its height.
(A) \(\frac{44}{\pi}\) cm
(B) 22π cm
(C) 44π cm
(D) \(\frac{22}{\pi}\)
Answer:

(A)

vi. A cone was melted and cast into a cylinder of the same radius as that of the base of the cone. If the height of the cylinder is 5 cm, find the height of the cone.
(A) 15 cm
(B) 10 cm
(C) 18 cm
(D) 5 cm
Answer:

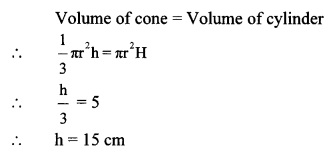
(A)

vii. Find the volume of a cube of side 0.01 cm.
(A) 1 cm
(B) 0.001 cm³
(C) 0.0001 cm³
(D) 0.000001 cm³
Answer:
Volume of cube = (side)³
= (0.01)³ = 0.000001 cm³
(D)

viii. Find the side of a cube of volume 1 m³
(A) 1 cm
(B) 10 cm
(C) 100 cm
(D) 1000 cm
Answer:
Volume of cube = (side)³
∴ 1 = (side)³
∴ Side = 1 m
= 100 cm
(C)

Problem Set 7 Geometry Class 10 Question 2. A washing tub in the shape of a frustum of a cone has height 21 cm. The radii of the circular top and bottom are 20 cm and 15 cm respectively. What is the capacity of the tub? = (π = \(\frac { 22 }{ 7 } \))
Given: For the frustum shaped tub,
height (h) = 21 cm,
radii (r₁) = 20 cm, and (r₂) = 15 cm
To find: Capacity (volume) of the tub.
Solution:
Volume of frustum = \(\frac { 1 }{ 3 } \) πh (r₁² + r₂² + r₁ × r₂)

∴ The capacity of the tub is 20.35 litres.

10th Geometry Problem Set 7 Question 3. Some plastic balls of radius 1 cm were melted and cast into a tube. The thickness, length and outer radius of the tube were 2 cm, 90 cm and 30 cm respectively. How many balls were melted to make the tube?
Given: For the cylindrical tube,
height (h) = 90 cm,
outer radius (R) = 30 cm,
thickness = 2 cm
For the plastic spherical ball,
radius (r₁) = 1 cm
To find: Number of balls melted.
Solution:

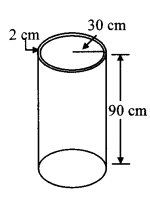
Inner radius of tube (r)
= outer radius – thickness of tube
= 30 – 2
= 28 cm
Volume of plastic required for the tube = Outer volume of tube – Inner volume of hollow tube
= πR²h – πr²h
= πh(R² – r²)
= π × 90 (30² – 28²)
= π × 90 (30 + 28) (30 – 28) …[∵ a² – b² = (a + b)(a – b)]
= 90 × 58 × 2π cm³

∴ 7830 plastic balls were melted to make the tube.

Problem Set 7 Geometry Question 4.
A metal parallelopiped of measures 16 cm × 11cm × 10cm was melted to make coins. How many coins were made if the thickness and diameter of each coin was 2 mm and 2 cm respectively?
Given: For the parallelopiped.,
length (l) = 16 cm, breadth (b) = 11 cm,
height (h) = 10 cm
For the cylindrical coin,
thickness (H) = 2 mm,
diameter (D) 2 cm
To find: Number of coins made.
Solution:
Volume of parallelopiped = l × b × h
= 16 × 11 × 10
= 1760 cm³
Thickness of coin (H) = 2 mm
= 0.2 cm …[∵ 1 cm = 10 mm]
Diameter of coin (D) = 2 cm

∴ 2800 coins were made by melting the parallelopiped.

Mensuration Problem Question 5.  The diameter and length of a roller is 120 cm and 84 cm respectively. To level the ground, 200 rotations of the roller are required. Find the expenditure to level the ground at the rate of ₹ 10 per sq.m.
Given: For the cylindrical roller,
diameter (d) =120 cm,
length = height (h) = 84 cm
To find: Expenditure of levelling the ground.
Solution:
Diameter of roller (d) = 120 cm

Now, area of ground levelled in one rotation = curved surface area of roller
= 3.168 m²
∴ Area of ground levelled in 200 rotations
= 3.168 × 200 =
633.6 m²
Rate of levelling = ₹ 10 per m²
∴ Expenditure of levelling the ground
= 633.6 × 10 = ₹ 6336
∴ The expenditure of levelling the ground is ₹ 6336.

Question 6.
The diameter and thickness of a hollow metal sphere are 12 cm and 0.01 m respectively. The density of the metal is 8.88 gm per cm3. Find the outer surface area and mass of the sphere, [π = 3.14]
Given: For the hollow sphere,
diameter (D) =12 cm, thickness = 0.01 m
density of the metal = 8.88 gm per cm³
To find: i. Outer surface area of the sphere
ii. Mass of the sphere.

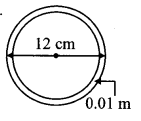
Solution:
Diameter of the sphere (D)
= 12 cm
∴ Radius of sphere (R)
= \(\frac { d }{ 2 } \) = \(\frac { 12 }{ 2 } \) = 6 cm
∴ Surface area of sphere = 4πR²
= 4 × 3.14 × 6²
= 452.16 cm²
Thickness of sphere = 0.01 m
= 0.01 × 100 cm …[∵ 1 m = 100 cm]
= 1 cm
∴ Inner radius of the sphere (r)
= Outer radius – thickness of sphere
= 6 – 1 = 5 cm
∴ Volume of hollow sphere
= Volume of outer sphere – Volume of inner sphere

∴ The outer surface area and the mass of the sphere are 452.16 cm² and 3383.19 gm respectively.

Question 7.
A cylindrical bucket of diameter 28 cm and height 20 cm was full of sand. When the sand in the bucket was poured on the ground, the sand got converted into a shape of a cone. If the height of the cone was 14 cm, what was the base area of the cone?
Given: For the cylindrical bucket,
diameter (d) = 28 cm, height (h) = 20 cm
For the conical heap of sand,
height (H) = 14 cm
To find: Base area of the cone (πR²).
Solution:
Diameter of the bucket (d) = 28 cm


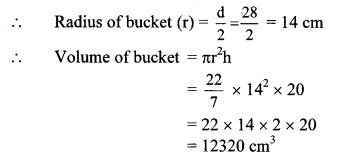
The base area of the cone is 2640 cm².

Question 8.
The radius of a metallic sphere is 9 cm. It was melted to make a wire of diameter 4 mm. Find the length of the wire.
Given: For metallic sphere,
radius (R) = 9 cm
For the cylindrical wire,
diameter (d) = 4 mm
To find: Length of wire (h).
Solution:

∴ The length of the wire is 243 m.

Question 9.
The area of a sector of a circle of 6 cm radius is 157t sq.cm. Find the measure of the arc and length of the arc corresponding to the sector.
Given: Radius (r) = 6 cm,
area of sector = 15 π cm²
To find: i. Measure of the arc (θ),
ii. Length of the arc (l)
Solution:

∴ The measure of the arc and the length of the arc are 150° and 5π cm respectively.

Question 10.
In the adjoining figure, seg AB is a chord of a circle with centre P. If PA = 8 cm and distance of chord AB from the centre P is 4 cm, find the area of the shaded portion.

(π = 3.14, \(\sqrt { 3 }\) = 1.73)
Given: Radius (r) = PA = 8 cm,
PC = 4 cm
To find: Area of shaded region.
Solution:

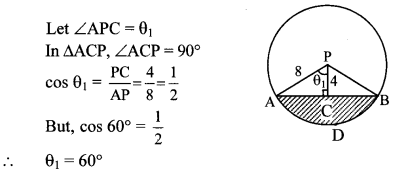
Similarly, we can show that, ∠BPC = 60°
∠APB = ∠APC + ∠BPC …[Angle sum property]
∴ θ = 60° + 60° = 120°


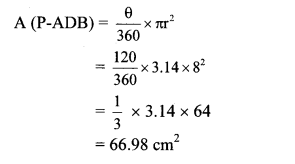
Area of shaded region = A(P-ADB) – A(∆APB)
= 66.98 – 27.68
= 39.30 cm²
∴ The area of the shaded region is 39.30 cm².

Question 11.
In the adjoining figure, square ABCD is inscribed in the sector A-PCQ. The radius of sector C-BXD is 20 cm. Complete the following activity to find the area of shaded region.

Solution:
Side of square ABCD
= radius of sector C-BXD = [20] cm
Area of square = (side)² = 20² = 400 cm² ….(i)
Area of shaded region inside the square = Area of square ABCD – Area of sector C-BXD

Radius of bigger sector
= Length of diagonal of square ABCD
= \(\sqrt { 2 }\) × side
= 20 \(\sqrt { 2 }\) cm
Area of the shaded regions outside the square
= Area of sector A-PCQ – Area of square ABCD
= A(A – PCQ) – A(꠸ABCD)

Alternate method:

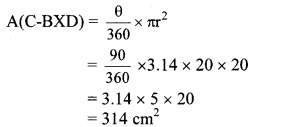
□ABCD is a square. … [Given]
Side of □ABCD = radius of sector (C-BXD)
= 20 cm
Radius of sector (A-PCQ) = Diagonal
= \(\sqrt { 2 }\) × side
= \(\sqrt { 2 }\) × 20
= 20 \(\sqrt { 2 }\) cm

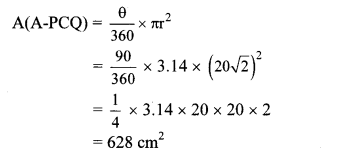
Now, Area of shaded region
= A(A-PCQ) – A(C-BXD)
= 628 – 314
= 314 cm²
∴ The area of the shaded region is 314 cm².

Question 12.
In the adjoining figure, two circles with centres O and P are touching internally at point A. If BQ = 9, DE = 5, complete the following activity to find the radii of the circles.

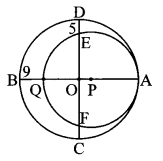
Solution:
Let the radius of the bigger circle be R and that of smaller circle be r.
OA, OB, OC and OD are the radii of the bigger circle.
∴ OA = OB = OC = OD = R
PQ = PA = r
OQ + BQ = OB … [B – Q – O]
OQ = OB – BQ = R – 9
OE + DE = OD ….[D – E – O]
OE = OD – DE = [R – 5]
As the chords QA and EF of the circle with centre P intersect in the interior of the circle, so by the property of internal division of two chords of a circle,
OQ × OA = OE × OF
∴ (R – 9) × R = (R – 5) × (R – 5) …[∵ OE = OF]
∴ R² – 9R = R² – 10R + 25
∴ -9R + 10R = 25
∴ R = [25units]
AQ = AB – BQ = 2r ….[B-Q-A]
∴ 2r = 50 – 9 = 41
∴ r = \(\frac { 41 }{ 2 } \) = 20.5 units

Maharashtra State Board Class 10 Maths Solutions Part 2

• Co-ordinate Geometry Practice Set 5.1 Class 10 Maths Solutions
• Co-ordinate Geometry Practice Set 5.2 Class 10 Maths Solutions
• Co-ordinate Geometry Practice Set 5.3 Class 10 Maths Solutions
• Co-ordinate Geometry Problem Set 5 Class 10 Maths Solutions
• Trigonometry Practice Set 6.1 Class 10 Maths Solutions
• Trigonometry Practice Set 6.2 Class 10 Maths Solutions
• Trigonometry Problem Set 6 Class 10 Maths Solutions
• Mensuration Practice Set 7.1 Class 10 Maths Solutions
• Mensuration Practice Set 7.2 Class 10 Maths Solutions
• Mensuration Practice Set 7.3 Class 10 Maths Solutions
• Mensuration Practice Set 7.4 Class 10 Maths Solutions
• Mensuration Problem Set 7 Class 10 Maths Solutions