Balbharati Maharashtra State Board 11th Commerce Maths Solution Book Pdf Chapter 3 Skewness Ex 3.1 Questions and Answers.
Maharashtra State Board 11th Commerce Maths Solutions Chapter 3 Skewness Ex 3.1
Question 1.
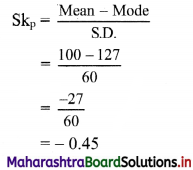
For a distribution, mean = 100, mode = 127 and S.D. = 60. Find the Pearson coefficient of skewness Skp.
Solution:
Given, Mean = 100, Mode = 127, S.D. = 60
Question 2.
The mean and variance of a distribution are 60 and 100 respectively. Find the mode and the median of the distribution if Skp = -0.3.
Solution:
Given, Mean = 60, Variance = 100, Skp = -0.3
∴ S.D. = √Variance = √100 = 10
Skp = \(\frac{\text { Mean }-\text { Mode }}{\text { S.D. }}\)
∴ -0.3 = \(\frac{60-\text { Mode }}{10}\)
∴ -3 = 60 – Mode
∴ Mode = 60 + 3 = 63
Mean – Mode = 3 (Mean – Median)
∴ 60 – 63 = 3(60 – Median)
∴ -3 = 180 – 3Median
∴ 3Median = 180 + 3 = 183
∴ Median = \(\frac{183}{3}\)
∴ Median = 61
![]()
Question 3.
For a data set, sum of upper and lower quartiles is 100, difference between upper and lower quartiles is 40 and the median is 30. Find the coefficient of skewness.
Solution:
Given, Q3 + Q1 = 100 ……(i)
Q3 – Q1 = 40 …..(ii)
Median = Q2 = 30
Adding (i) and (ii), we get
2Q3 = 140
∴ Q3 = 70
Substituting the value of Q3 in (i), we get
70 + Q1 = 100
∴ Q1 = 100 – 70 = 30
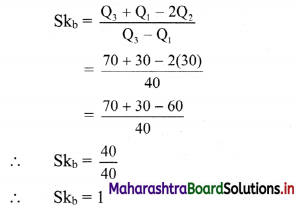
Question 4.
For a data set with an upper quartile equal to 55 and median equal to 42, if the distribution is symmetric, find the value of the lower quartile.
Solution:
Upper quartile = Q3 = 55
Median = Q2 = 42
Since, the distribution is symmetric.
∴ Skb = 0
Skb = \(\frac{Q_{3}+Q_{1}-2 Q_{2}}{Q_{3}-Q_{1}}\)
∴ 0 = \(\frac{Q_{3}+Q_{1}-2 Q_{2}}{Q_{3}-Q_{1}}\)
∴ 0 = Q3 + Q1 – 2Q2
∴ Q1 = 2Q2 – Q3
∴ Q1 = 2(42) – 55
∴ Q1 = 84 – 55
∴ Q1 = 29
Question 5.
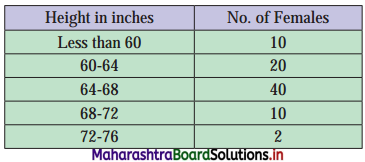
Obtain coefficient of skewness by formula and comment on the nature of the distribution.
Solution:
We construct the less than cumulative frequency table as given below.

Q1 class = class containing \(\left(\frac{\mathrm{N}}{4}\right)^{\mathrm{th}}\) observation
∴ \(\frac{\mathrm{N}}{4}=\frac{82}{4}\) = 20.5
Cumulative frequency which is just greater than (or equal) to 20.5 is 30.
∴ Q1 lies in the class 60 – 64.
∴ L = 60, h = 4, f = 20, c.f. = 10
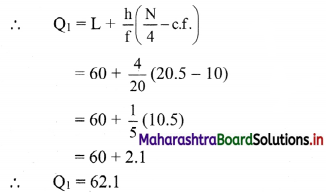
Q2 class = class containing \(\left(\frac{\mathrm{N}}{2}\right)^{\mathrm{th}}\) observation
∴ \(\frac{\mathrm{N}}{2}=\frac{82}{2}\) = 41
Cumulative frequency which is just greater than (or equal) to 41 is 70.
∴ Q2 lies in the class 64 – 68.
∴ L = 64, h = 4, f = 40, c.f. = 30
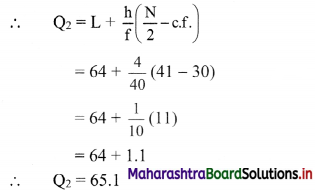
Q3 class = class containing \(\left(\frac{3 \mathrm{~N}}{4}\right)^{\text {th }}\) observation
∴ \(\frac{3 \mathrm{~N}}{4}=\frac{3 \times 82}{4}\) = 61.5
Cumulative frequency which is just greater than (or equal) to 61.5 is 70.
∴ Q3 lies in the class 64 – 68.
∴ L = 64, h = 4, f = 40, c.f. = 30
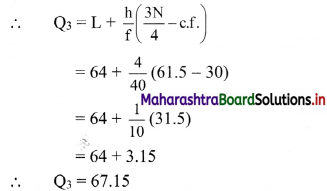

∴ Skb = -0.1881
Since, Skb < 0, the distribution is negatively skewed.
![]()
Question 6.
Find Skp for the following set of observations.
17, 17, 21, 14, 15, 20, 19, 16, 13, 17, 18
Solution:
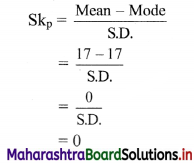
Σxi = 17 + 17 + 21 + 14 + 15 + 20 + 19 + 16 + 13 + 17 + 18 = 187
Mean = \(\frac{\sum x_{i}}{n}=\frac{187}{11}\) = 17
Mode = Observation that occurs most frequently in the data = 17
Question 7.
Calculate Skb for the following set of observations of the yield of wheat in kg from 13 plots:
4.6, 3.5, 4.8, 5.1, 4.7, 5.5, 4.7, 3.6, 3.5, 4.2, 3.5, 3.6, 5.2
Solution:
The given data can be arranged in ascending order as follows:
3.5, 3.5, 3.5, 3.6, 3.6, 4.2, 4.6, 4.7, 4.7, 4.8, 5.1, 5.2, 5.5
Here, n = 13
Q1 = value of \(\left(\frac{n+1}{4}\right)^{\text {th }}\) observation
= value of \(\left(\frac{13+1}{4}\right)^{\text {th }}\) observation
= value of (3.50)th observation
= value of 3rd observation + 0.50(value of 4th observation – value of 3rd observation)
= 3.5 + 0.50(3.6 – 3.5)
= 3.5 + 0.50(0.1)
= 3.5 + 0.05
∴ Q1 = 3.55
Q2 = value of 2\(\left(\frac{n+1}{4}\right)^{\text {th }}\) observation
= value of 2\(\left(\frac{13+1}{4}\right)^{\text {th }}\) observation
= value of (2 × 3.50)th observation
= value of 7th observation
∴ Q2 = 4.6
Q3 = value of 3\(\left(\frac{n+1}{4}\right)^{\text {th }}\) observation
= value of 3\(\left(\frac{13+1}{4}\right)^{\text {th }}\) observation
= value of (3 × 3.50)th observation
= value of (10.50)th observation
= value of 10th observation + 0.50 (value of 11th obseration – value of 10th observation)
= 4.8 + 0.50(5.1 – 4.8)
= 4.8 + 0.50(0.3)
∴ Q3 = 4.95
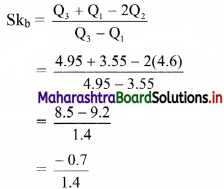
∴ Skb = -0.5
![]()
Question 8.
For a frequency distribution Q3 – Q2 = 90 and Q2 – Q1 = 120. Find Skb.
Solution:
Given, Q2 – Q1 = 90, Q2 – Q1 = 120
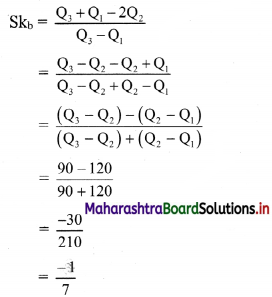
∴ Skb = -0.1429