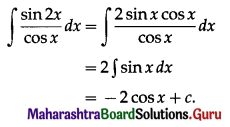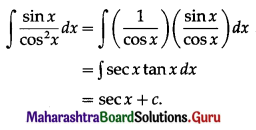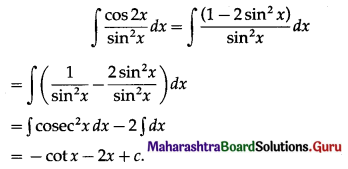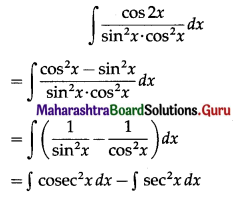Category: Class 11

Balbharati Maharashtra State Board 11th Commerce Maths Solution Book Pdf Chapter 9 Commercial Mathematics Ex 9.3 Questions and Answers.

Maharashtra State Board 11th Commerce Maths Solutions Chapter 9 Commercial Mathematics Ex 9.3

Question 1.
What would be the simple interest on an amount of ₹ 9,600 at the rate of 6% per annum after 3 years?
Solution:
Given Principal P = ₹ 9600
Rate of interest R = 6% p.a.
Number of years = T = 3
Simple Interest I = \(\frac{\text { PRT }}{100}\)
= \(\frac{9600 \times 3 \times 6}{100}\)
= 96 × 18
= 1728
∴ Simple interest after 3 years would be ₹ 1728

Question 2.
What would be the simple interest at the rate of 9\(\frac{1}{2}\)% per annum on ₹ 6,000 for 2\(\frac{1}{2}\) years?
Solution:
Rate of interest per annum R = 9\(\frac{1}{2}\)% = \(\frac{19}{2}\)%
Principal P = ₹ 6000
Duration T = 2\(\frac{1}{2}\) = \(\frac{5}{2}\) years
∴ Simple Interest, I = \(\frac{\text { PRT }}{100}\)
= 6000 × \(\frac{19}{2} \times \frac{5}{2} \times \frac{1}{100}\)
= 15 × 19 × 5
= 1425
∴ Simple interest would be ₹ 1425.

Question 3.
What would be the simple interest on ₹ 8,400 in 9 months at the rate of 8.25 percent per annum?
Solution:
Principal P = ₹ 8400
Rate of interest R = 8.25%
Duration T = 9 months = \(\frac{3}{4}\) years

∴ Simple interest would be ₹ 519.75.

Question 4.
What would be the compound interest on ₹ 4200 for 18 months at 10% per annum compounded half yearly?
Solution:
Principal P = ₹ 4200
Rate of interest R = 10%
Duration T = 18 months = 1.5 years
compounding is done half yearly

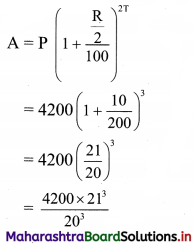
= \(\frac{4200 \times 9261}{2000}\)
= 4862.025
I = A – P
= 4862.025 – 4200
= 662.025
∴ Compound interest would be ₹ 662.025.

Question 5.
Find compound interest on ₹ 10,000 for 2 years at 8% per annum compounded half yearly.
Solution:
Principal P = ₹ 10,000
Rate of interest R = 8% p.a. compounded half yearly
Duration T = 2 years

I = A – P
= 11648.58 – 10000
= 1698.58
∴ Compound interest is ₹ 1698.58.

Question 6.
In how many years ₹ 1,00,000 will become ₹ 1,33,100 at compound interest rate of 10% per annum?
Solution:
Principal P = ₹ 1,00,000
Amount A = ₹ 1,33,100
Rate of interest R = 10% p.a.

∴ ₹ 1,00,000 will become ₹ 1,33,100 after 3 years.

Question 7.
A certain sum of money becomes three times of itself in 20 years at simple interest. In how many does it become double of itself at the same rate of simple interest?
Solution:
Given that, sum of money triples itself in 20 years
∴ P + I = 3P
∴ I = 2P
and T = 20 years
Now simple interest I = \(\frac{\text { PRT }}{100}\)
∴ 2P = \(\frac{\mathrm{P} \times \mathrm{R} \times 20}{100}\)
∴ R = 10
∴ Rate of interest = 10% per annum
The time period is to be calculated for the condition that the sum doubles itself i.e. for the condition
P + I = 2P
i.e. I = P
\(\frac{\mathrm{P} \times \mathrm{R} \times \mathrm{T}}{100}\) = P
∴ \(\frac{10 \times T}{100}\) = 1
∴ T = 10
∴ The sum will become double of itself in 10 years.

Question 8.
A person borrows 10,000 for 2 year at 4% p.a. simple interest he immediately lends it to another person at 6.5% p.a. for 2 years. Find his total gain in the transaction.
Solution:
Person borrows money at 4% per annum and lends it at 6.5% per annum.
∴ His gain is (6.5 – 4) = 2.5% on ₹ 10000 for 2 years
i.e. gain = \(\frac{1000 \times 2.5 \times 2}{100}\)
= 100 × 5
= ₹ 500
∴ The person will gain ₹ 500 in this transaction.

Question 9.
A man deposits X 200 at the end of each year in recurring account at 5% compound interest. How much will it become at the end of 3 years?
Solution:
At end of 1st year, 2nd year and 3rd year ₹ 200 were deposited.
Rate of interest R = 5% p.a.
At end of 3 years, amount
= 200 + \(200\left[1+\frac{5}{100}\right]+200\left[1+\frac{5}{100}\right]^{2}\)
= 200 [1 + 1.05 + (1.05)2]
= 200 [2.05 + 1.1025]
= 200 [3.1525]
= 630.5
At end of 3 years, the account will have a balance of ₹ 630.5.

Question 10.
A man gets a simple interest of ₹ 2,000 on a certain principal at the rate of 5% p.a. in 4 years. What compound interest will the man get on twice the principal in 2 years at the same rate.
Solution:
Let Principal amount = P
Simple Interest I = ₹ 2000
Rate of interest R = 5% p.a.
Time duration T = 4 years
I = \(\frac{\text { PRT }}{100}\)
∴ 2000 = \(\frac{\mathrm{P} \times 5 \times 4}{100}\)
∴ P = 10000
Twice the principal was invested for compound interest with the same rate of interest for 2 years.
Here, P = 2 × 10,000 = ₹ 20,000
∴ Amount received,

I = A – P = 22050 – 20000 = 2050
The man will receive ₹ 2050 as compound interest.

Question 11.
The difference between simple interest and compound interest on a certain sum of money is ₹ 32 at 8% per annum for 2 years. Find the amount.
Solution:
Compound Interest = A – P = \(\mathrm{P}\left(1+\frac{\mathrm{R}}{100}\right)^{\mathrm{T}}-\mathrm{P}\)
Simple interest = \(\frac{\text { PRT }}{100}\)
Given R = 8%, T = 2 years and
compound interest – simple interest = ₹ 32

∴ The man will receive a compound interest of ₹ 5000.

Balbharti 12th Maharashtra State Board Maths Solutions Book Pdf Chapter 3 Indefinite Integration Ex 3.1 Questions and Answers.

Maharashtra State Board 12th Maths Solutions Chapter 3 Indefinite Integration Ex 3.1

I. Integrate the following functions w.r.t. x:

(i) x³ + x² – x + 1
Solution:

(ii) \(x^{2}\left(1-\frac{2}{x}\right)^{2}\)
Solution:

(iii) \(3 \sec ^{2} x-\frac{4}{x}+\frac{1}{x \sqrt{x}}-7\)
Solution:

(iv) \(2 x^{3}-5 x+\frac{3}{x}+\frac{4}{x^{5}}\)
Solution:

(v) \(\frac{3 x^{3}-2 x+5}{x \sqrt{x}}\)
Solution:

II. Evaluate:

(i) ∫tan² x . dx
Solution:

(ii) \(\int \frac{\sin 2 x}{\cos x} \cdot d x\)
Solution:

(iii) \(\int \frac{\sin x}{\cos ^{2} x} \cdot d x\)
Solution:

(iv) \(\int \frac{\cos 2 x}{\sin ^{2} x} \cdot d x\)
Solution:

(v) \(\int \frac{\cos 2 x}{\sin ^{2} x \cdot \cos ^{2} x} \cdot d x\)
Solution:

= -cot x – tan x + c

(vi) \(\int \frac{\sin x}{1+\sin x} \cdot d x\)
Solution:

(vii) \(\int \frac{\tan x}{\sec x+\tan x} \cdot d x\)
Solution:

(viii) \(\int \sqrt{1+\sin 2 x} \cdot d x\)
Solution:

(ix) \(\int \sqrt{1-\cos 2 x} \cdot d x\)
Solution:

(x) ∫sin 4x cos 3x dx
Solution:

III. Evaluate:

(i) \(\int \frac{x}{x+2} \cdot d x\)
Solution:

(ii) \(\int \frac{4 x+3}{2 x+1} \cdot d x\)
Solution:

(iii) \(\int \frac{5 x+2}{3 x-4} \cdot d x\)
Solution:

(iv) \(\int \frac{x-2}{\sqrt{x+5}} \cdot d x\)
Solution:

(v) \(\int \frac{2 x-7}{\sqrt{4 x-1}} \cdot d x\)
Solution:

(vi) \(\int \frac{\sin 4 x}{\cos 2 x} \cdot d x\)
Solution:

(vii) \(\int \sqrt{1+\sin 5 x} \cdot d x\)
Solution:

(viii) ∫cos² x . dx
Solution:

(ix) \(\int \frac{2}{\sqrt{x}-\sqrt{x+3}} \cdot d x\)
Solution:

(x) \(\int \frac{3}{\sqrt{7 x-2}-\sqrt{7 x-5}} \cdot d x\)
Solution:

IV.

Question 1.
If f'(x) = x – \(\frac{3}{x^{3}}\), f(1) = \(\frac{11}{2}\), find f(x).
Solution:
By the definition of integral,

Balbharti Maharashtra State Board Class 11 Psychology Solutions Chapter 8 Memory Textbook Exercise Questions and Answers.

Maharashtra State Board Class 11 Psychology Solutions Chapter 8 Memory

1A. Complete the following statements.

Question 1.
One of the important processes for storage of information in the LTM is _____________
a. perception
b. elaborative rehearsal
c. encoding
Answer:
b. elaborative rehearsal

Question 2.
Memory is a/an _____________
a. activity
b. process
c. performance
Answer:
b. process

Question 3.
_____________ memory has the shortest duration.
a. Sensory
b. Short Term
c. Long Term
Answer:
c. Long Term

Question 4.
_____________ memory is also known as Working Memory.
a. Long Term
b. Accidental
c. Short Term
Answer:
c. Short Term

Question 5.
_____________ memory has unlimited capacity.
a. Sensory
b. Short Term
c. Long Term
Answer:
a. Sensory

Question 6.
The span of Short-Term Memory is _____________
a. 5+/-2
b. 7+/-2
c. 9+/-2
Answer:
b. 7+/-2

1B. State whether the following statements are true or false. If false, correct them. If true, explain why.

Question 1.
Our sense organs also have memory.
Answer:
True
Explanation: Our sense organs have the capacity to retain the sensory impression received through the five senses for a very short time even after the source stimulus is withdrawn. It is known as sensory memory.

Question 2.
Short-term memory has an unlimited capacity.
Answer:
False
Reason: STM holds the information between 15 to 30 seconds and the capacity of STM is about seven items at a time. Fleece, has limited capacity.

Question 3.
Conscious memory of facts and events is called explicit memory.
Answer:
True
Explanation: Explicit memory is a type of LTM that contains conscious memories of facts and events.

Question 4.
Implicit memory is the memory of skills.
Answer:
True
Explanation: Implicit memory is the unconscious memory of skills and how we do things, regarding the use of objects or movements of the body.

Question 5.
When we memorize meanings, concepts, and principles, it is called episodic memory.
Answer:
False
Reason: Episodic memory is a memory of experiences and specific events which we recall step by step to reconstruct actual events.

Question 6.
The method of relearning is also known as the saving method.
Answer:
True
Explanation: In relearning method, there is a saving of time taken to learn the same material. Fleece, this method is also known as the saving method.

Question 7.
The most vivid memory is flashbulb memory.
Answer:
True
Explanation: Flashbulb memories are vivid memories of what we were doing at the time of an emotion-provoking event.

1C. Identify the odd item from the following.

Question 1.
Encoding, Storage, Tip of the tongue (TOT), Retrieval
Answer:
Tip of the tongue (TOT)

Question 2.
Keyword method, Method of Loci, Chunking, Rote learning, First letter technique
Answer:
Rote learning

Question 3.
Sensory register, STM, Flashbulb memory, LTM
Answer:
Sensory register

Question 4.
Recall, Recognition, Relearning, Trace decay
Answer:
Trace decay

1D. Match the following pairs.

Question 1.

A	B
1. A technique to improve memory	a. Short-term memory
2. The most vivid memory	b. Declarative memory
3. Working memory	c. Implicit memory
4. Most organized memory	d. Flashbulb memory
5. Playing the harmonium after a long time	e. Method of Loci
6. Writing an essay on perceptual process	f. LTM
	g. Recall method
	h. Relearning method

Answer:

A	B
1. A technique to improve memory	e. Method of Loci
2. The most vivid memory	d. Flashbulb memory
3. Working memory	a. Short-term memory
4. Most organized memory	f. LTM
5. Playing the harmonium after a long time	c. Implicit memory
6. Writing an essay on perceptual process	g. Recall method

2. Answer the following questions in around 35-40 words each.

Question 1.
Explain any one example of Flashbulb memory from your life.
Answer:

• I clearly remember the day when my grandmother passed away.
• On that day, I had an omelet for breakfast and went to college around 10.30 a.m. I attended only two lectures and then received a call about this bad news. After that, my best friend accompanied me home.

Question 2.
Explain the model of working memory proposed by Baddeley.
Answer:

• Baddeley called STM a working bench of memory.
• In the working memory model given by him, a central executive is responsible for the coordination between sub-systems of the phonological loop, episodic buffer, and the visuospatial sketchpad.
• Both phonological loop and visuospatial sketchpad have two components.

Question 3.
Explain the Tip of the tongue (TOT) phenomenon with an example.
Answer:

• Sometimes, when we search through our library of experiences to retrieve information from LTM, we cannot recall it even when we have that information on the tip of the tongue.
• e.g. you want to recall the name of your cousin’s favourite clothing brand. Instead of that name, you recall all similar names.

Question 4.
Give an example of episodic memory.
Answer:

• I remember a four-day-long celebration of my sister’s wedding.
• It started with Haldi followed by Mehendi and the sangeet ceremony. After that, there was a grand wedding followed by a reception ceremony.
• I also remember all preparations, outfits that I wore, and the food that we had in those four days.

Question 5.
What is motivated forgetting?
Answer:

• Motivated forgetting is a behaviour in which people may forget unwanted memories either consciously or unconsciously.
• It is also called a conscious coping strategy but it should not be confused with defense mechanisms.
• There are two levels of motivated forgetting, viz. Repression and Thought suppression.

3. Compare and contrast.

Question 1.
STM and LTM
Answer:

• Only the significant sensory inputs enter the Short-Term Memory (STM) through maintenance rehearsal. On the other hand, some items in STM enter the Long-Term Memory (LTM) after elaborative rehearsal which makes information meaningful and connects the same with already existing information in the LTM.
• STM holds the information between 15 to 30 seconds and the capacity of STM is about seven items at a time. Conversely, once information enters LTM, it is retained more or less permanently and the amount of information stored in LTM is unlimited.

Question 2.
Implicit Memory and Explicit Memory
Answer:

• Implicit memory is the unconscious memory of skills and how we do things while explicit memory is conscious memory of facts and events.
• Implicit memory is also known as procedural memory while explicit memory is also known as declarative memory.

Question 3.
Semantic memory and Episodic memory
Answer:

• Semantic memory is a more structured record of facts, meanings, concepts, and knowledge. On the other hand, episodic memory is a memory of experiences and specific events which we recall step by step to reconstruct the actual events.
• Semantic memories have personal context which includes vocabulary, mathematics, rules of logic while episodic memory is the memory of autobiographical events with times, places, and associated emotions.

Question 4.
Storage failure and Retrieval failure
Answer:

• In case of storage, failure acquired and encoded information is not stored properly while in case of retrieval failure, problems arise while recalling the stored information for its actual use.
• Both storage failure and retrieval failure make it difficult to use the retained information in the future.

Question 5.
Recall method and Recognition method
Answer:

• The recall method involves remembering a fact, event, or object that is not currently physically present and requires the direct uncovering of information from memory, (e.g. long essay-type answers). In the recognition method, already learned material is present and the learner has to recognize it. (e.g. MCQs).
• Recognition is relatively easier than recall. So, a score of memory by recognition method is usually more than the recall method.

4. What will you do if…

Question 1.
You have to prepare a long speech covering all the activities in your college and present at the annual function
Answer:

• I will make a list of all the activities and rehearse it a number of times so as to ensure better retention.
• I may also make a note with all points in brief which I can refer to if I forget something in the middle of a speech.

Question 2.
How will you apply ‘POWER’ to prepare for the final exam of Psychology?
Answer:

• Prepare: Before starting to study, I would prepare myself for it by setting goals. I will make myself aware of why am I studying Psychology, e.g. for acquiring good marks in the final exam.
• Organize: I will organize the study material properly and make a schedule for each chapter. I will allot less time for chapters that are easy and familiar. I may study these chapters when I am a bit tired. Conversely, I will allot more hours to chapters that are unfamiliar, complicated, or technical. I will also ensure to study these complex chapters when I am fresh.
• Work: I know that I have to work hard to achieve the goal of acquiring good marks. So, I will learn with the motive to understand and remember. I will try to associate new information with something that I have already learned.
• Evaluate: I will try to evaluate my progress by solving practice papers. It will enable me to know how much I have learned and the quality of my knowledge.
• Rethink: I will reanalyze, review, question, and challenge myself. I will also rethink whether I need to change my method of studying so as to achieve the goal of acquiring good marks in the final exam.

5. Short Notes.

Question 1.
Characteristics of Memory
Answer:

• Memory is an ability by which information is encoded, stored, and retrieved when needed.
• Three basic processes or characteristics of memory are Acquisition, Storage, and Retrieval.
• The acquisition is the process of acquiring information from our sense organs. The information acquired and encoded is stored over a period of time. In retrieval, the stored information is recalled for the purpose of its actual use.
• There are three stages of memory, viz. Sensory information store, short-term memory, and long-term memory.

Question 2.
Techniques to improve memory
Answer:
Some techniques to improve memory are as follows:

• Keyword method: In the keyword method, any two different pieces of information can be linked together. It is an effective method for remembering definitions and learning foreign language vocabulary.
• Encoding specificity: According to encoding specificity, memory is improved when information is available while learning is also available at the time to recall.
• Method of loci: It involves creating an imaginary route so that things can be remembered in a better way. e.g. steps to solve mathematical problems.
• Mnemonic devices: Mnemonics will include acronyms or first letter techniques (e.g. VIBGYOR includes colours of the rainbow). It will also include visualization. Another technique is chunking where one can place large information into small chunks.
• Practice and rehearsal: Relearning the same material a number of times lead to better retention and better recall. For small size or easy material, it is effective to optimally utilize our time and learn the entire material. For large size or difficult material, we must take breaks and learn the material in parts.
• Minimizing interference: We should not learn similar subjects together as they might interfere with each other. Also, one must take a rest for minimising such interference.
• POWER method: One can also use the POWER method for improving memory. Here, P stands for Preparation, 0 stands for Organisation, W stands for Work, E stands for Evaluation and R stands for Rethinking.

Question 3.
Motivated forgetting
Answer:

• Motivated forgetting is a behaviour in which people may forget unwanted memories either consciously or unconsciously.
• It is also called a conscious coping strategy but it should not be confused with defense mechanisms.
• There are two levels of motivated forgetting, viz. Repression and Thought suppression.
• Repression: Sigmund Freud’s Psychoanalytic model states that we subconsciously push unwanted thoughts and memories into our unconsciousness. People think that such repressed memories are completely forgotten.
• e.g. a girl who had experienced sexual abuse during childhood may completely forget about it. But she may have difficulty while forming a romantic relationship.
• Thought suppression: It is a conscious effort where we forget the memories of unwanted incidents and experiences of our lives, e.g. a person will avoid talking about his breakup.
• Thought suppression can be time-consuming and also quite difficult as such suppressed thoughts tend to reoccur, e.g. a person may try to suppress the thoughts about his ex but he may not be successful in doing so.

Question 4.
Causes of forgetting
Answer:

• Trace decay: Our memories fade out when we don’t use them for a longer period, i.e., traces of memory get decayed over time if they are not used.
• Trace distortion: Some researchers believe that memory traces are not decayed but are distorted over a period of time and forgetting occurs.
• Interference: Some researchers believe that we forget when materials that we learn one after the other interfere with each other. There are two types of interference, viz. retroactive interference and proactive interference.
• Motivated forgetting: It is a behaviour in which people may forget unwanted memories either consciously or unconsciously. There are two levels of motivated forgetting, viz. Repression and Thought suppression.

6. Answer the following questions in 150-200 words.

Question 1.
Explain the process of human memory in detail.
Answer:

• Memory is an ability by which information is encoded, stored, and retrieved when needed.
• The basic processes of memory include acquisition (encoding), storage, and retrieval.
  
• Acquisition/Encoding: Acquisition is the process of acquiring information from sense organs. Encoding is the process of transforming the information received into suitable symbols like pictures, figures, words, numbers.
• Storage: The information acquired and encoded is preserved over a period of time. The process of storage is essential for using that information in the future.
• Retrieval: It is the process of recalling the stored information for the purpose of its actual use. We tend to retrieve mobile numbers, names, etc. in our daily life.
• We can think of these processes as analogous to the functions of a computer.

Question 2.
Explain the theories of forgetting in detail.
Answer:

• Forgetting is the failure to retrieve the material from our long-term memory which we had already stored.
• Researchers have put forward various theories of forgetting. Each theory highlights different reasons behind forgetting.
• The various theories of forgetting are: Trace decay theory, Trace distortion theory, and Interference theory.
  • Trace decay: Our memories fade out when we don’t use them for a longer period, i.e., traces of memory get decayed over time if they are not used.
  • Trace distortion: Some researchers believe that memory traces are not decayed but are distorted over a period of time and forgetting occurs.
  • Interference: Some researchers believe that we forget when materials that we learn one after the other interfere with each other. There are two types of interference, viz. retroactive interference and proactive interference.

7. Arrange the following elements in concepts of memory in ascending order.

Question 1.
Elaborative rehearsal, Short Term Memory, Receiving information from the environment, Long Term Memory, Retrieval
Answer:

• Receiving information from the environment
• Short Term Memory
• Elaborative rehearsal
• Long Term Memory
• Retrieval

Activities

Activity 1 (Textbook Page No. 87)

Do you remember your first picnic at your school? Do you remember your primary school teacher? Now can you remember what food you ate last Monday? Why you can remember some incidents from the past clearly while you cannot remember some things which happened yesterday?
Answer:
We remember some incidents from the past clearly when they are a part of our long-term memory. Similarly, we cannot remember certain incidents from the recent past whey they form a part of our sensory or short-term memory.

Activity 2 (Textbook Page No. 87)

Why does this happen? 25 workers used to work in Thomas Edison’s Bulb and Phonogram unit of industries. There was a huge tree near his company. After 6 months, Edison asked his workers about the huge tree but not a single worker could give information about that tree. Why do you think this happened despite seeing the tree every day?
Answer:
I feel the none of the workers could give information about the tree near their company since it was a part of their sensory memory, i.e., they perceived the stimulus (tree) with sense organs but did not rehearse it enough for it to become a part of their long term memory.

Balbharti Maharashtra State Board Class 11 Psychology Solutions Chapter 7 Nervous System Textbook Exercise Questions and Answers.

Maharashtra State Board Class 11 Psychology Solutions Chapter 7 Nervous System

1A. Complete the following statements with appropriate options.

Question 1.
Brain is a part of _________ nervous system.
a. central
b. peripheral
c. somatic
Answer:
a. central

Question 2.
_________ are the building blocks of the nervous system.
a. Cells
b. Neurons
c. Tissues
Answer:
b. Neurons

Question 3.
_________ nervous system prepares us for the fight or flight responses.
a. Somatic
b. Parasympathetic
c. Sympathetic
Answer:
c. Sympathetic

Question 4.
The gap between two neurons is called _________
a. synapse
b. joint
c. vacuum
Answer:
a. synapse

1B. Match the following pairs.

Question 1.

A	B
1. Thyroxin	a. Pituitary
2. Epinephrine	b. Parathyroid
3. Parathormone	c. Thyroid
4. Androgen	d. Adrenal gland
5. Somatotropin hormones	e. Salivary gland
	f. Sex glands

Answer:

A	B
1. Thyroxin	c. Thyroid
2. Epinephrine	d. Adrenal gland
3. Parathormone	b. Parathyroid
4. Androgen	f. Sex glands
5. Somatotropin hormones	a. Pituitary

1C. Identify the odd item following series of words.

Question 1.
The frontal lobe, Parietal lobe, Thalamus, Occipital lobe
Answer:
Thalamus

Question 2.
Dopamine, Serotonin, Norepinephrine, Uric acid, GABA
Answer:
Uric acid

Question 3.
Dendrite, Nucleus, Tectum, Axon, Synapse
Answer:
Tectum

Question 4.
Knee jerk, Sneezing, Thinking, Blinking of eyes
Answer:
Thinking

Question 5.
Thyroid, Sweat glands, Adrenal gland, Gonads, Pituitary gland
Answer:
Sweat glands

1D. Identify which hormones with hyposecretion or hypersecretion would lead to the following conditions.

Question 1.
Abnormal height, gigantism
Answer:
Hypersecretion – Somatotropin

Question 2.
Hyperactivity, speedy metabolism.
Answer:
Hypersecretion – Thyroxin

Question 3.
Cretinism
Answer:
Hyposecretion – Thyroxin

Question 4.
Stunted growth, dwarfism
Answer:
Hyposecretion – Somatotropin

Question 5.
Myxedema, fatigue, sluggishness, depression
Answer:
Hyposecretion – Thyroxin

Question 6.
Increased appetite, overactivity, restlessness, lack of concentration
Answer:
Hyposecretion – Insulin, and glycogen

2. Which part of the brain is involved in processing the following information?

Question 1.
Smelling a flower
Answer:
Occipital lobe

Question 2.
Maintaining balance while standing upright
Answer:
Cerebellum

Question 3.
Comprehending a speech
Answer:
Temporal Lobe

Question 4.
Memorizing a childhood experience
Answer:
Frontal lobe

Question 5.
Feeling touch
Answer:
Parietal lobe

Question 6.
Seeing a picture
Answer:
Occipital lobe

Question 7.
Feeling hungry
Answer:
Hypothalamus

Question 8.
Feeling afraid
Answer:
Amygdala

3. Answer the following questions in 35 to 40 words.

Question 1.
Explain the functions of the hypothalamus.
Answer:

• Hypothalamus controls major bodily needs i.e., primary needs of an individual like hunger, thirst, sex as well as temperature regulation, and sleep.
• It is also called the pleasure center of our body.

Question 2.
Describe the functions of each of the four lobes.
Answer:

• Frontal lobe: It controls motor actions, thinking, memory and reasoning. It has Broca’s area which helps in speech production.
• Parietal lobe: It helps in understanding information regarding skin-like touch, pressure, pain, and temperature.
• Occipital lobe: It is the visual processing center. It controls the sense of hearing, smell, and taste. It has Wernicke’s area which helps in language understanding.
• Temporal Lobe: Hearing, understanding language, memory for language take place because of the temporal lobe.

Question 3.
Explain the functions of the Amygdala and Hippocampus.
Answer:

• Amygdala: It stores emotional memories of experiences. We experience emotions, especially fear due to the amygdala.
• Hippocampus: It is the storage of long-term memories. If a person gets Alzheimer’s disease, his hippocampus is. mainly affected.

Question 4.
What is a synapse? How does a nerve impulse travel from one to another neuron?
Answer:

• A synapse is a gap between two neurons.
• The nerve impulse or neural message jumps across the synapse in order to reach the dendrite of another neuron.
• When the neural message is passing through, it excites or inhibits the neurotransmitter in it. This chemical reaction decides our reaction to various situations.

Question 5.
Which are the important parts of the hindbrain? Explain their functions.
Answer:
Important parts of the hindbrain and their functions are as follows:

• Cerebellum: It helps in maintaining body posture and body balance. It also helps in the coordination of the movements.
• Brain stem: Medulla oblongata controls the breathing rate, pulse rate, blood pressure, and digestion. Pons sends and receives information from the lower parts of the brain. It helps to transmit messages between the cerebellum and cortex.
• Reticular activation system: Its main function is to maintain wakefulness, concentration, and alertness.

Question 6.
How do endocrine glands affect our behaviour?
Answer:

• Endocrine glands secrete chemical substances called hormones.
• Hormones are like messengers that are responsible for certain behaviours or the absence of reactions.
• e.g. Thyroid gland secretes the thyroxin hormone. Its hypersecretion leads to Grave’s disease while hyposecretion results in cretinism or myxedema.

4. Write short notes.

Question 1.
Autonomic Nervous System
Answer:

• The autonomic nervous system controls the internal activities of the human body including heart rate, breathing, digestion, disposal of waste products, and toxins.
• It is divided into the sympathetic and parasympathetic nervous systems.
• The sympathetic nervous system prepares our body to face stressful and threatening situations. It prepares us for a ‘flight or fight reaction. The job of the system is just opposite to its name.
• The parasympathetic nervous system takes over when the situation becomes normal. It directs our body to store energy for emergencies.

Question 2.
Limbic System
Answer:
One of the important parts of the brain is the limbic system.

• Hippocampus, amygdala, thalamus, and hypothalamus are parts of the limbic system.
• Hippocampus is responsible for the storage of long-term memories.
• Amygdala stores emotional memories of our experiences.
• Thalamus is called a relay station of the brain. It receives all information from the body and sends it to various parts of the brain.
• Hypothalamus controls major bodily needs like hunger, thirst, sex as well as temperature regulation, and sleep.

Question 3.
Neurotransmitters
Answer:
Neurotransmitters are chemical messengers. The important neurotransmitters are:

• Acetylcholine: It is a chemical released by motor neurons of the nervous system to activate muscles.
• Dopamine: It is released by the brain. If the level of dopamine is normal, we experience happy, pleasant feelings. It also plays an important role in the motivational process.
• Norepinephrine: It increases the force of skeletal muscles, especially during fight or flight response.
• Serotonin: It plays a role mainly in cognition, reward, learning, and memory. It also controls wakefulness, sleep, hunger, thirst, and liking.
• Glutamate: It helps in learning, memory, and maintaining sugar levels.
• GABA (Gama Amino Butyric Acid): It is the chief inhibitory neurotransmitter i.e. its principal role is to reduce the excitability of neurons throughout the nervous system. If it is less, it leads to convulsions and we cannot control body movements.

Question 4.
Pituitary gland
Answer:

• The pituitary gland is one of the endocrine glands, i.e., glands that secrete chemical substances into the bloodstream.
• It is also called as master gland as it helps other glands to produce their secretions and secretes the majority of hormones.
• It consists of the anterior lobe and posterior lobe.
• Anterior lobe: It secretes somatotropin, growth hormone, and adrenocorticotropic hormone. It helps the growth of the body and aids the adrenal gland. The hormones secreted by this gland are also vital for the nourishment of foetus.
• Hypo or hypersecretion in the anterior lobe: Hyposecretion leads to dwarfism, wherein a person is very short (two-three feet tall). On the other hand, hypersecretion can lead to gigantism, wherein a person becomes very huge and is eight-nine feet tall. Hypersecretion can also result in acromegaly, wherein a person has the features of a chimpanzee.
• Posterior lobe: It secretes oxytocin (which creates a feeling of happiness), pituitrin (which helps smooth muscle functioning of the stomach), thyrotrophic follicle-stimulating luteinizing hormone (which helps in the nourishment of foetus), and endorphins (which help to create neurotransmitters).

5. Compare and contrast

Question 1.
Sympathetic nervous system and Parasympathetic nervous system
Answer:

• The sympathetic nervous system prepares our body to face stressful and threatening situations. It prepares us for a ‘flight or fight reaction. On the other hand, the parasympathetic nervous system takes over when the situation becomes normal,
• Example:
  • Situation: Suppose you are chased by a dog.
  • Sympathetic nervous system: Due to the functioning of this system, your heartbeat and palpitation increase. You also start to sweat.
  • Parasympathetic nervous system: When PNS takes over, your heart rate, palpitation, and sweating become normal. You regain a cool and composed state due to the functioning of this system.

Question 2.
Exocrine glands and Endocrine glands
Answer:

• Exocrine glands directly release their secretions into the organ or tissue while endocrine glands secrete chemical substances into the bloodstream.
• Exocrine glands have separate ducts for their secretion and so, they are also called duct glands, e.g. sweat glands and tear glands. On the other hand, endocrine glands are called ductless glands as they don’t have a separate duct. e.g. pituitary gland and thyroid gland.

6. Answer in 150-200 words.

Question 1.
Explain the functions of various parts of the human brain.
Answer:
The brain consists of three major parts, viz. hindbrain, midbrain, and forebrain. Its functions are as follows:
i. Hindbrain

• Cerebellum: It helps in maintaining body posture and balance as well as aids in the coordination of movements.
• Brain stem: Medulla oblongata controls the breathing rate, pulse rate, blood pressure, and digestion. Pons helps to transmit messages between the cerebellum and cortex.
• Reticular activation system: It is the ‘Alarm clock’ of the body. It maintains wakefulness, concentration, and alertness.

ii. Midbrain: It sends information to the upper part of the brain and controls eye movements.

iii. Forebrain

• Cerebrum: Cerebral cortex controls higher-order mental processes such as attention, perception, learning, memory. The surface of the cerebral cortex is divided into right and left hemispheres. Neurons from the right hemisphere control the left side of the body and vice versa. Left hemisphere controls language, spatial relation, and pattern recognition.
• Four lobes: Frontal lobe controls motor actions, thinking, memory and reasoning. The parietal lobe helps us in understanding information regarding skin. The occipital lobe controls our vision. The temporal lobe is responsible for hearing, understanding language, and memory for language.

Question 2.
Explain the significance of endocrine glands in human behaviour. State the functions of any five endocrine glands in detail.
Answer:

• Endocrine glands secrete vital chemical substances called hormones. There is a strong impact of hormones upon human behavior.
• Hormones are responsible for certain behaviours or the absence of reactions.
• Over (hyper) or under (hypo) secretion of hormones may lead to a variety of problems.
• e.g. Hypersecretion of insulin and glycogen hormones by the pancreas reduces blood sugar levels. It results in hyperglycemia, wherein a person lacks energy and motivation, may faint and go to coma. Conversely, in the case of hyposecretion, a person gets diabetes. He becomes quite hungry and feels very tired and restless. He also shows irritated behaviour and faces frequent and uncontrolled urination.

The functions of the five endocrine glands are as follows:

• Thyroid gland: It secretes thyroxin which maintains the rate of metabolism.
• Parathyroid gland: It secretes parathyroxin which maintains calcium as well as phosphate balance.
• Pancreas: It secretes insulin and glycogen that is responsible for maintaining blood sugar levels.
• Adrenal gland: Cortex secretes cortin or cortisone which maintains the level of water, sugar, and sodium. The medulla secretes adrenalin (which is associated with fear) and noradrenaline (which is associated with anger). Medulla plays important role in emotional excitement.
• Gonads (sex gland): Testes in males secrete androgen and testosterone. These hormones are responsible for secondary sex characteristics in males. Their voice becomes hoarse. They also get mustaches and beards. Ovaries in females secrete estrogen and progesterone. These hormones are responsible for secondary sex characteristics in females. As a result, feminine looks develop and menarche begins.

Activities

Activity 1 (Textbook Page No. 76)

Few activities are given below. Identify the system which dominates during these activities.

1. Picking up an object from the ground
2. Shivering when we sense danger
3. Feeling composed when we feel safe
4. Increase in heart rate when we sense that we are going to meet with an accident

Answer:

1. Central nervous system
2. Sympathetic nervous system
3. Parasympathetic nervous system
4. Sympathetic nervous system

Activity 2 (Textbook Page No. 80)

Think of the following actions. Which of them would be reflex actions and which of them will not be reflex actions?

• Throwing a ball in a cricket match
• Closing the eyes if someone brings a finger too close to them.
• Removing the hand when you accidentally touch a thorn.
• Immediate movement of the knee when tapped just below it.
• Touching a hot object and pulling back your hand.

Answer:
Reflex actions:

• Closing the eyes if someone brings a finger too close to them.
• Removing the hand when you accidentally touch a thorn.
• Immediate movement of the knee when tapped just below it.
• Touching a hot object and pulling back your hand.

Non-reflex actions:

• Throwing a ball in a cricket match

Balbharti Maharashtra State Board Class 11 History Solutions Chapter 5 Janapadas and Republics Textbook Exercise Questions and Answers.

Maharashtra State Board Class 11 History Solutions Chapter 5 Janapadas and Republics

1A. Choose the correct alternative and write the complete sentences.

Question 1.
A region occupied by the ‘janas’ was called as __________
(a) Ganarajya
(b) Janapada
(c) Mahajanapada
(d) Gotra
Answer:
(b) Janapada

Question 2.
The principal functionary of a Ganasangha was known as __________
(a) Senapati
(b) Bhandagarika
(c) Raja
(d) Uparaja
Answer:
(c) Raja

Question 3.
The author of the ‘Ashtadhyayi’ which mentions ‘Janapadin’ was __________
(a) Kautilya
(b) Panini
(c) Chanakya
(d) Vyas
Answer:
(b) Panini

Question 4.
The sense of territoriality and the ensuing awareness __________ were the main factors responsible for the formation of ancient Janapadas in India.
(a) of unity
(b) of authority
(c) of autonomy
(d) of public authority
Answer:
(c) of autonomy

1B. Find the incorrect pairs from set ‘B’ and write the correct ones.

Question 1.

Set ‘A’	Set ‘B’
(a) Praachya	of the east
(b) Praatichya	of the west
(c) Udichya	of the north
(d) Aparanta	the region to the north of Vindhya ranges

Answer:
(d) Aparanta – the region to the south of Vindhya ranges

2. Choose the correct reason and complete the sentence.

Question 1.
The Ganasangha of the Youdhey, Malav, Kshudraka were mentioned as Ayudhajivi. Because-
(a) it was in the northeast region of the Indian Subcontinent.
(b) these people were skilled warriors and warfare was the means of their livelihood.
(c) they were skilled in trade and commerce.
(d) these were the ganasanghas dependent on agriculture and animal husbandry.
Answer:
(b) these people were skilled warriors and warfare was the means of their livelihood.

3. Complete the concept map.

Question 1.

Answer:

4. Explain the concepts with examples.

Question 1.
Ganarajya and Sangharajya
Answer:

• ‘Gana’ means the ruling class comprising members of equal social status.
• Similarly, ‘sangha’ means a state formed by many kulas or janapadas by coming together.
• By the 6th century B.C.E. many sangharajyas had come into existence.
• There were three main types of the ancient federation of states in India:
• Ganarajya of the members of the same kula. For example, Malava and Shibi.
• Ganarajya was created by more than one kulas coming together. For example, Vajji Ganasangha. It included eight kulas. Vajji, Lichchhavi, Dnyatruk, and Videha were the important ganas among them.
• More than one ganrajyas coming together to create a sangharajya. For example, Yaudheya- Kshudrak Sangh.

Question 2.
Vartashastarpajivi Ganasnagh
Answer:

• Ancient Indian literature mentions two more types of ganasanghas.
• ‘Ayudhjivi’ sangh and ‘Varta-Shastropajivi’ sangh.
• ‘Varta’ means trade and commerce.
• The people in the Varta-Shastropajivi ganasanghas lived by trade and commerce, agriculture and animal husbandry, as well as their skills in warfare.
• People in the Kamboj and Saurashtra ganasanghas earned their livelihood by these means.

Question 3.
‘Jana’ and ‘Janapada’
Answer:

• Vedic people used the term Jana to designate a group of people, united under a common bond of singular kinship structure.
• Their settlement was known as ‘Grama’.
• A cluster of gramas consisting of the same Jana was known by the name of that particular Jana.
• A region occupied by a Janas was called Janapada.
• Gradually the Janapadas had more formal administrative structures transforming them into independent states.
• These were the first well-established states of ancient India.
• However, this does not necessarily mean that every Janapada evolved into an independent state.

5. Answer the following questions in detail.

Question 1.
Describe the democratic and oligarchic states in ancient India.
Answer:
Democratic States:

• Some of the ganasanghas were divided into regional zones called ‘Khanda’.
• They functioned through a group of elected individuals, who were found capable.
• Each of the elected members represented his respective khanda.
• These elected members were installed with collective authority for the smooth running of the ganasangha.
• This was a democratic system. Ganasanghas which functioned in this democratic way existed in Punjab and Sindh at the time of Alexander’s invasion.
• Each elective representative of the respective regional zone was designated as ‘Ganamukhya’.
• Every ganamukhya was a member of the assembly known as ‘ganaparishada’.
• The decisions made by the ganaparishada were implemented by designated functionaries of various cadres.
• He was known as the ‘Adhyaksha’ or ‘Raja’.

Oligarchic States:

• In this type the elite class in the society held all the powers of decision-making and administration,
• Panini and Kautilya mention them as ‘Rajshabdopajivi’ Sangh.
• Panini includes Vajji, Andhaka, Vrishni, Yaudheya in the Rajashabdopjivi type.
• Kautilya includes the Vrijji or Vajji, Madrak, Kuru, Panchala, etc. in this type.
• This type of ganasanghas was more prevalent in the eastern region of Uttar Pradesh and Bihar.

Activity

Present an act in the class based on the simulation of the administrative system of an oligarchic state.
Answer:
Students have to make the presentation in class.

Balbharti Maharashtra State Board Class 11 History Solutions Chapter 4 Vedic Period Textbook Exercise Questions and Answers.

Maharashtra State Board Class 11 History Solutions Chapter 4 Vedic Period

1A. Choose the correct alternative and write the complete sentences.

Question 1.
The importance of agriculture is clearly emphasised in the ______________ mandala of the Rigveda.
(a) 4th
(b) 10th
(c) 8th
(d) 6th
Answer:
(b) 10th

Question 2.
A potter is mentioned as an artisan in the ______________ for the first time.
(a) Rigveda
(b) Yajurveda
(c) Samaveda
(d) Atharvaveda
Answer:
(b) Yajurveda

Question 3.
The god who protected the animals was known as ______________
(a) Indra
(b) Pushan
(c) Ashwin
(d) Varun
Answer:
(b) Pushan

1B. Find the incorrect pair from set ‘B’ and write the correct ones.

Question 1.

Set ‘A’	Set ‘B’
(a) Nishka	Gold ornament
(b) Barley	Maincrop of the Vedic people
(c) Krishtya	The apparatus of drawing water from the well
(d) Navya	River transport

Answer:
(c) Krishtya – Tribal settlements

1C. Write the names.

Question 1.
A branch of linguistics.
Answer:
Philology

Question 2.
A battle was fought among the ten tribal chiefs.
Answer:
Dasharajnya Yuddha

Question 3.
Cultivable land prepared by ploughing.
Answer:
Urvara

2. Complete the concept map given below:

Question 1.

Answer:

3. Choose the correct reason and complete the sentence.

Question 1.
Panis were looked upon as enemies by the Vedic people because-
(a) they belonged to a different tribe.
(b) their language was impure.
(c) Panis used to steal the cattle of the Vedic people.
(d) Panis did not obey the orders of the Vedic people.
Answer:
(c) Panis used to steal the cattle of the Vedic people.

4. State your opinion.

Question 1.
There is a debate about the original home of the Aryans.
Answer:

• The debate began in the 16th Century. Till then the concept of the ‘Aryans’ was not known.
• The European academics became aware of the similarities between Sanskrit and Latin-Greek languages.
• This resulted in the notion of the Indo-European language family which gave momentum to the search for a Mother language from which developed the Indo-European languages.

Question 2.
The Rigvedic people subsisted on agriculture.
Answer:

• The Rigvedic tribal settlements have been mentioned as ‘Krishtya’ in the Rigveda. ‘Krish’ means ploughing.
• Hence the people who ploughed and also their settlements were mentioned as ‘Krishtya’.
• The importance of agriculture is clearly emphasised in the 10th mandala of Rigveda.
• It states that for the farmer his ploughshare is the means of obtaining.

5. Explain the following concepts.

Question 1.
Origin of Aryan people.
Answer:

• There are multiple unanswered questions, such as, who were the Aryans, did they arrive in India from a distant place or were they natives of India, which are the archaeological sites where the remains of their culture are found, how to identify those remains, etc.
• Most of the information about their culture is derived from Vedic literature. There are various v opinions about the chronology of the Vedic culture.
• However, there is a general agreement that the Vedic people composed Rigveda in India around 1500 B.C.E.
• However, Lokmanya Tilak calculated this date as 6000 B.C.E. on the basis of astronomical events.
• He was also of the opinion that the original home of the Aryans was in the Arctic region.
• This debate began in the 16th century. Till then the concept of the ‘Aryans’ was not known.

Question 2.
Indo-European family of languages.
Answer:

• In the year 1583, an Italian merchant by the name of Filippo Sassetti came to Kochi (Cochin) the port city in Kerala.
• He never returned to his motherland. He stayed in Kerala and Goa. During his stay, he wrote detailed letters to his family members about Indian life, language and culture. He happens to be the first European who wrote about his observations of Indian society.
• He also studied Sanskrit. He was the first one who observed the similarities between Sanskrit and Latin.
• His observations could be said to be the first, to give impetus to the notion of a family of Indo-European languages.

Balbharti Maharashtra State Board Class 11 History Solutions Chapter 3 Chalcolithic Villages in India Textbook Exercise Questions and Answers.

Maharashtra State Board Class 11 History Solutions Chapter 3 Chalcolithic Villages in India

1A. Choose the correct alternative and write the complete sentences.

Question 1.
On one of the cemetery H pots, dead humans are seen carried by ____________ in their stomach.
(a) deer
(b) peacock
(c) fish
(d) bull
Answer:
(b) peacock

Question 2.
The archaeological evidence shows that Balathal was a center of mass production of ____________
(a) stone pots
(b) copper pots
(c) earthen pots
(d) glassware
Answer:
(c) earthen pots

Question 3.
Permanent villages of farmers were first established in Maharashtra by ____________ people.
(a) Savalda
(b) Malwa
(c) Harappa
(d) Kayatha
Answer:
(b) Malwa

1B. Find the incorrect pair from set ‘B’ and write the correct ones.

Question 1.

Set ‘A’	Set ‘A’
1. Savalda Culture	Daimadabad
2. Malwa Culture	Navadatoli
3. Ahar Culture	Sonpur
4. Jorwe Culture	Inamgaon

Answer:
3. Ahar Culture – Balathal

2A. Explain the statements with reasons.

Question 1.
Harappan people had to migrate.
Answer:

• When the Mature (urban) Harappan civilisation collapsed completely, the people of Late Harappan cultures who had settled on the ruins of Mature Harappan cities had to migrate elsewhere.
• The urban Harappans and the Late Harappans dispersed. Wherever these people reached, new rural cultures came into being.
• Thus, as the Harappan civilisation collapsed, Harappan people had to migrate.

Question 2.
People of ‘Malwa’ culture were the first farmers of Maharashtra.
Answer:

• The people of Malwa culture reached Maharashtra around 1600 B.C.E. Permanent villages of farmers were first established in Maharashtra by the Malwa people.
• After arriving in Maharashtra, they came into contact with the neolithic people in Karnataka.
• It resulted in a few changes in the pot-making technology of Malwa people as far as shapes of the pots and designs are concerned.
• Thus, they were considered the first farmers of Maharashtra as they were the first to establish in Maharashtra.

3. State your opinion.

Question 1.
It seems that the Harappan people had gone as far as Bihar.
Answer:

• Chalcolithic sites have been discovered in Bihar, Bengal, Odisha, and Madhya Pradesh.
• The excavations at sites like Chirand, Sonpur, etc. yielded earthen pots of black-and-red ware.
• The shapes of these pots are similar to those of Harappan culture.
• Thus, it seems that the Harappan people had gone as far as Bihar, and the local cultures were influenced by them.

4. Write short notes.

Question 1.
Banas Culture
Answer:

• The chalcolithic culture in India generally belongs to, the Post-Harappan period.
• However, the ‘Ahar’ or ‘Banas’ culture in the Mewad region of Rajasthan was contemporary to the Harappan civilisation.
• Balathal and Gilund are important sites of Ahar culture.
• It was first discovered at Ahar near Udaipur, so it was named as ‘Ahar’ culture.
• Ahar is a tributary of the river Banas, so it is also known as ‘Banas culture’.

Question 2.
Malwa Culture
Answer:

• The name ‘Malwa’ tells us that this culture originated and spread first in the Malwa region.
• It flourished in Madhya Pradesh during 1800 B.C.E. – 1200 B.C.E. Navadatoli, situated on the bank of Narmada is an important site of Malwa culture.
• The people of Malwa culture reached Maharashtra around 1600 B.C.E.
• Permanent villages of farmers were first established in Maharashtra by the Malwa people. They were the first farmers of Maharashtra.

Question 3.
Kayatha Culture
Answer:

• Kayatha is a chalcolithic site situated on the banks of the river known as Chhoti Kali Sindh at a distance of 25 km from Ujjain in Madhya Pradesh.
• Kayatha culture was contemporary to the Harappan civilisation.
• The Kayatha people followed agriculture and animal husbandry.
• They mainly used handmade pots and microliths.

5. Write about the chalcolithic cultures in Gujarat with the help of the given points.

Question 1.
(a) Period
(b) Means of livelihood
(c) Geographical spread
(d) Evidence of cultural contact with other people.
Answer:
(a) Period: The chalcolithic settlements in Gujarat coincide with the following phases of the Harappan culture:

• Early Harappan phase (3950-2600 B.C.E.)
• Mature (urban) phase (2600-1900 B.C.E.)
• Post-Harappan phase (1900-900 B.C.E.)

(b) Means of livelihood: There are ample sources of semi-precious stones in Gujarat. Making beads of these stones was a big industry during Harappan times. The Neolithic settlements in Gujarat played a major role in procuring these stones. People residing in the neolithic settlements of Gujarat were mainly pastoral, that is people whose primary occupation was animal husbandry. Thus, making beads, animal husbandry, pottery making were some of the means of livelihood.

(c) Geographical spread: There are regional variations in the characteristics of the chalcolithic cultures of Gujarat. The chalcolithic pottery of Kutch – Saurashtra and Northern Gujarat are distinct from each other. The chalcolithic villages in Kutch-Saurashtra were abandoned by 1900 B.C.E.

(d) Evidence of cultural contact with other people: In the post-Harappan period there were two chalcolithic cultures in Gujarat. The culture in south Gujarat was known as ‘Prabhas’ culture and the one in northeastern Gujarat was known as ‘Rangpur’ culture. These cultures existed till 1800-1200 B.C.E.

Activity

With the help of the Internet, reference books, field trips, newspaper articles, etc. obtain pictures of excavated artifacts and architectural remains and arrange an exhibition under the guidance of your teachers.
Answer:
To be done by students.

Balbharti Maharashtra State Board Class 11 History Solutions Chapter 2 First Cities of India Textbook Exercise Questions and Answers.

Maharashtra State Board Class 11 History Solutions Chapter 2 First Cities of India

1. Choose the correct alternative and write the complete sentences.

Question 1.
In the early phase of agriculture, making __________ pots and farming were the jobs of women.
(a) copper
(b) bronze
(c) earthen
(d) stone
Answer:
(c) earthen

Question 2.
Lothal is known for its ancient __________
(a) agriculture
(b) dock
(c) textiles
(d) tools
Answer:
(b) dock

Question 3.
A general impression prevailed that the Harappan seals had some connection with the __________ civilisation.
(a) Chinese
(b) Greek
(c) Mesopotamian
(d) Egyptian
Answer:
(c) Mesopotamian

Question 4.
The bodies (mummies) of dead royalties in Egypt were wrapped in __________ coloured cloth.
(a) white
(b) black
(c) red
(d) blue
Answer:
(d) blue

2A. Choose the correct reason and complete the sentence.

Question 1.
The major reason for the decline of the Mesopotamian civilisation was __________
(a) foreign invasion
(b) deteriorating environment
(c) loss in trade
(d) migration
Answer:
(b) deteriorating environment

2B. Find the incorrect pair from set ‘B’ and write the correct ones.

Question 1.

Set ‘A’	Set ‘B’
(a) Dilmun	Bahrain
(b) Makan	Oman-Iran-Baluchistan Coastal region
(c) Shortugai	Mesopotamia
(d) Meluhha	Region of Harappa civilisation

Answer:
(c) Shortugai – Badakshan province of Afghanistan

3. Explain the statements with reasons.

Question 1.
The remains found in cities like Harappa, Mohenjodaro, Kalibangan, Lothal, Dholavira, Rakhigarhi, etc. are evidence of the past glory of this civilization.
Answer:

• A well-developed and rich civilisation flourished in the Indian subcontinent in the period from 3500-3000 B.C.E.
• This period is characterised by systematic town planning, with houses of baked brick, granaries, excellent drainage systems, public baths, and impressive public movements.
• Good administrative control over the distribution of water and other resources.
• Remains also prove a good social organisation, a proper social hierarchy based on the position of power.
• Flourishing internal and distant trade, mass production of goods, and craft specialisation developed writing system of script on Harappan seals give evidence of the past glory of the civilisation.

Question 2.
Lapis lazuli had a very important place in the Harappan trade.
Answer:

• A network of small towns, big and small villages, and campsites of semi-nomadic people functioned to cater to the needs of major urban centres of the Harappan civilisation.
• The Harappan settlement of ‘Shortugai’ in the Badakshan province of Afghanistan, is rich with mines of lapis lazuli, a semi-precious stone in Mesopotamia.
• The Mesopotamian epics describe Goddess Inanna’s palace, the walls of which were embedded with this stone, lapis lazuli.
• This stone was a very important commodity in the Harappan trade with Mesopotamia.

Question 3.
Harappan civilisation declined.
Answer:

• Sir Mortimer Wheeler in his study has concluded that the Harappan civilisation was destroyed by Indra, who destroyed the fortified cities.
• Vedic Aryans destroyed the Harappan cities under the leadership of Indra.
• The civilisation also declined due to the cumulative effects of factors such as the decline in trade, climatic changes, and the weakening of the economy.

4. State your opinion.

Question 1.
The Harappan cities and villages in the vicinity were interdependent.
Answer:

• The interrelationship between Harappan cities and villages was dependent on the mechanism of making available food grains and raw materials.
• A network of small towns, big and small villages, and campsites of semi-nomadic people, functioned to cater to the needs of major urban centres of Harappan civilisation.
• The city people were dependent on natural sources and villages in their vicinity, to meet the needs of urban lifestyle and urban administration.

Question 2.
The Harappan cities seem to have a well-organised administrative system.
Answer:

• The Harappan cities had a well organised administrative system to manage industrial production, import-export, the interrelationship between cities managing trading operations and villages around them.
• The town planning, standardization of bricks, weights, seals, shapes, and ornamentation of various objects, confirm the presence of an efficient administrative system.
• Cities like Harappa and Mohenjodaro were perhaps regional capitals.
• Lothal and Kalibangan were important religious centres.
• However, the nature of Harappan polity, whether it was a single state or a federation of small states, is not yet known.

5. Answer the following questions with the help of given points.

Question 1.
Write about the characteristics of Harappan cities with the help of the given points:
(a) Town planning
(b) Social organisation
(c) Administration
(d) Economy
Answer:
(a) Town planning:

• The town planning of Harappan cities was very systematic.
• Houses were of baked bricks, which included bathrooms, toilets, wells.
• Granaries existed, with impressive public monuments.
• The excellent drainage systems, public baths, and independent fortification walls are highlights.
• The grid pattern was used, where streets crossed each other in right angles, and the resulted blocks were used for building houses.
• The English bond masonry method was used with two headers and two stretchers to build a wall, which was especially useful for earthquake-prone areas.

(b) Social organisation:

• Social hierarchy was based on the position of power.
• Classes of skilled artisans and individuals were based on craft specialisation.
• Belief systems existed, with evidence of burials indicating rituals after death.
• Artifacts and architecture also indicate belief systems.

(c) Administration:

• Administrative control existed over the distribution of water and other resources.
• The size of bricks indicates the use of standardisation and ratio.
• Weights, set style of shapes and painted designs of pottery, majestic and non-residential buildings for public administrative offices are also seen.

(d) Economy:

• Harappan civilisation practiced mass production of goods for trade purposes.
• The concentration of factories and residences of artisans in a particular area of the city indicates the purpose of convenience of production, flourishing internal and distant trade, and administrative control over trade transactions.
• Well-shaped, beautiful earthen pots, statues, metal objects of gold, silver, copper, and bronze were made.
• Various types of beads were prepared, indicating a sound economy.

Activity

Collect information and illustrations with the help of the internet about the town planning of the Harappan cities and Chandigarh. Compare them.
Answer:
The town planning of the Harappan Cities:

• The Harappans were the first to build planned cities with a scientific drainage system.
• Their cities were built on a uniform plan.
• The people of Indus valley lived a highly civilized and developed life.
• This highly developed and scientific plan can be seen in the following areas.

Streets:

• The streets were straight and cut each other at right angles
• They were 13 to 34 feet wide and were well lined.
• The streets and roads divided the city into rectangular blocks.
• Lamp posts were provided at regular intervals.
• Dust bins were also provided on the streets which proves the presence of a good municipal administration.

Drainage System:

• The city was provided with an excellent closed drainage system.
• Each house had its own drainage and soak pit which was connected to the public drainage.
• Brick-laid channels were found through every street.
• The drains were covered and had manholes at regular intervals for cleaning and clearing.
• Large brick culverts were constructed on the outskirts of the city to carry excess water.
• The Indus valley civilization had a perfect underground drainage system.

The Great Bath:

• The most striking feature of Mohenjo Daro is the Great Bath.
• It consists of a large quadrangle. In the center, there is a large swimming pool approx. 39 ft long, 23 ft wide, and 8 ft deep.
• This swimming pool had rooms and galleries on all four sides.
• It had a flight of steps at either end and a well in one of the adjoining rooms. The water was discharged by a huge drain.
• The Great Bath had 8ft thick outer walls.

Granaries:

• The largest building in Mohenjo Daro is the granary which is 45.71 m long and 15.23 m wide.
• Granaries have also been found in Harappa and the southern parts of Kalibangan.
• These granaries were used to store grains which were probably collected as revenue or storehouses to be used in emergencies.

Buildings:

• People of the Indus valley civilization built houses and other buildings on the side streets.
• Built terraced houses of burnt bricks.
• Every house had two or more rooms, there were also more than one-storied houses.

The town planning of Chandigarh City:

• Chandigarh, the capital of the northern Indian states of Punjab and Haryana was designed by the Swiss-French modernist architect, Le Corbusier.
• Buildings include the Capitol Complex with its High Court, Secretariat, and Legislative Assembly.

Balbharti Maharashtra State Board Class 11 Sociology Solutions Chapter 7 Social Stratification Textbook Exercise Questions and Answers.

Maharashtra State Board Class 11 Sociology Solutions Chapter 7 Social Stratification

1. (A) Choose the correct alternative and complete the statements.

Question 1.
Social stratification is ……………….
(local / national / universal)
Answer:
universal

Question 2.
Class is a ………………. form of stratification.
(open / closed / rigid)
Answer:
open

Question 3.
Gender based stratification has led to ………………. in society.
(justice / exploitation / equality)
Answer:
exploitation

Question 4.
Social stratification of ………………. is based on the principle of purity and pollution.
(class / gender / caste)
Answer:
caste

1. (B) Correct the incorrect pair.

Question 1.
(a) Ownership of wealth – Economic Capital
(b) Membership and involvement in social network – Social Capital
(c) Gained through education – Cultural Capital
(d) Prestige, status and social honour – Economic Capital
Answer:
(d) Prestige, status, social honour – Symbolic Capital

1. (C) Correct underlined words and complete the sentence.

Question 1.
Caste is based on wealth.
Answer:
Class is based on wealth.

Question 2.
A hierarchical system where women are given a lower social status is stratification based on class.
Answer:
A hierarchical system where women are given a lower social status is stratification based on gender.

2. Write short notes.

Question 1.
Principles of social stratification.
Answer:

1. Stratification is social: Social stratification is not determined by biological differences but it is governed by social norms and sanctions.
2. Social stratification persists over generations : In all society’s parents confer their social status on their children. Thus, the pattern of inequality stays same from generation to generation.
3. Social stratification is universal but variable : Social stratification is found everywhere. At the same time the nature of inequality varies. ‘What’ is unequal and ‘how’ unequal, changes within the context of a society.
4. Social stratification involves inequality : Any stratified system not only gives people more resources but also justifies this arrangement and defines them as fair.
5. Social stratification is consequential : Stratification affects every aspect of life of all individuals. Social life is affected because of the position of an individual in the social hierarchy. Some experience positive consequences, while others face negative consequence of the hierarchy in a particular society.

Question 2.
Characteristics of caste according to Dr. G.S. Ghurye.
Answer:
Dr. G.S. Ghurye a well known Sociologist and Indologist defines caste in terms of its essential characteristics. They are as follows:
1.Segmental division by society : Society is divided into various castes. The membership of castes are determined by birth. Therefore, mobility from one caste to another is impossible.

2. Hierarchy: Castes or segments are arranged in terms of hierarchy. According to Dr. Ghurye, castes are graded and arranged into a hierarchy on the basis of the concept of ‘purity and pollution’.

3. Restriction on feeding and social intercourse : This fact of separation is reinforced by the notion of ‘purity and pollution’. Each caste imposes restrictions on its members with regard to food and social intercourse.

4. Differential civil and religious privileges and disabilities : In a caste society there is an unequal distribution of privileges and disabilities among its members. The higher castes enjoy all privileges and lower caste suffer from all kinds of disabilities.

5. Lack of unrestricted choice of occupation : Choice of occupation is not free under caste system. Occupations are hereditary and the members of the caste are expected to follow their traditional occupation.

6. Endogamy : Endogamy is the essence of caste system. Every caste of sub-caste insists that its member should marry within the group.

Question 3.
Types of mobility.
Answer:
1. Horizontal Mobility : It refers to change of residence or job without status change. Under this type of social mobility, a person changes one’s occupation but the overall social standing remains the same. Certain occupation like doctor, engineer and teacher may enjoy the same status but when an engineer changes one’s occupation from engineer to teaching engineering there is a horizontal shift from one occupational category to another but no change has taken place in the system of social stratification.

2. Vertical Mobility : Vertical mobility refers to any change in the occupational, economic, political status of an individual or a group which leads to change of their position. Vertical Mobility stands for change of social position, either upward or downward.

3. Intergenerational Mobility : This type of mobility means that one generation changes its social status in contrast to the previous generation. However, this mobility may be upward or downward. For e.g., people of lower caste or class may provide facilities to their children to get higher education, training and skills, with the help of which the younger generation may get employment in higher position.

4. Intragenerational Mobility : This type of mobility takes place in the lifespan of one generation. A person may start one’s career as a clerk and after acquiring more education, becomes an IFS Officer. Here the individual moves up and occupies a higher social position than previously.

3. Differentiate between.

Question 1.
Caste and Class.
Answer:

Caste	Class
(i) Different castes form a hierarchy of social preference and each position in the caste structure is defined in terms of its ‘purity and pollution’.	(i) A social class is made up of similar social status who regard one another as social equals.
(ii) In a caste stratification system, an individual’s position depends on the status attributes ascribed by birth.	(ii) In a class stratification system and individual’s position depends on the possession of substantial amounts of wealth, occupation, education and prestige which is achieved.
(iii) Caste is an example of closed stratification.	(iii) Class system is an example of open stratification.
(iv) In this type of social stratification there is no scope for social mobility.	(iv) In this type of social stratification there is scope for social mobility.

Question 2.
Intragenerational Mobility and Intergenerational Mobility.
Answer:

Intragenerational Mobility	Intergenerational Mobility
(i) This type of mobility takes place in the lifespan of one generation.	(i) This type of mobility means that one generation changes its social status in contrast to the previous generation.
(ii) This mobility is upward.	(ii) The mobility may be upward or downward.
(iii) A person may start one’s own career as a clerk. He / she acquires more education and over a period of time becomes an IFS Officer. Here the individual moves up and occupies a higher social position than previously.	(iii) People of lower caste or class may provide facilities to their children to get higher education, training and skills. With the help of these skills the younger generation may get employment in higher position.
(iv) It refers to advancement in one’s social level during the course of one’s lifetime.	(iv) It refers to a change in the status of family members, one generation to the next.

4. Explain the following concept with suitable examples.

Question 1.
Vertical Mobility
Answer:

1. Vertical mobility refers to any change in the occupational economic or political status of an individual or a group which leads to change of their position.
2. Vertical mobility stands for change of social position either upward or downward, which can be labelled as ascending or descending type of mobility.

Example : A person who works as a customer assistant, works hard and starts his own business successfully. In such a position there is a clear change in the position of the individual.

Question 2.
Intergenerational Mobility
Answer:

1. This type of mobility means that one generation changes its social status in contrast to the previous generation.
2. However, this mobility may be upward or downward.

Example : People of lower caste or class may provide facilities to their children to get higher education, training and skills, with the help of which the younger generation may get employment in higher position.

5. (A) Complete the concept maps.

Question 1.

Answer:

5. (B) State whether the following statements are true or false with reasons.

Question 1.
There is no mobility in the class system.
Answer:
This statement is False.

1. Class system is an example of open stratification in which individuals or groups enjoy the freedom of changing their social strata, i.e., in class system there is scope for social mobility. Individuals or groups move from one strata to another.
2. The class system in modern industrial society (Upper class, middle class and lower class) is an example of open stratification.
3. The criteria of open stratification i.e., class system are power, property, intelligence, skills, etc.

Question 2.
Education had led to women’s empowerment.
Answer:
This statement is True.

1. Education is a milestone of women empowerment because it enables them to respond to challenges, to confront their traditional role and change their life.
2. Education creates occupational achievement, self-awareness, satisfaction etc.
3. Education is one of the main levers of social class which has helped women empower and change their status in society.

6. Answer the following in detail (About 150-200 words).

Question 1.
Discuss class and gender as forms of social stratification with suitable examples of your own.
Answer:
Class as a form of social stratification:
A social class is made up of people of similar social status who regard one another as social equals.
Each class has a set of values, attitudes, beliefs and behaviour norms which differ from those of the other classes. A social class is essentially a status group which is achieved. Class is almost a universal phenomenon. Each social class has its own status in the society. Status is associated with prestige. A social class is relatively a stable group. Social class represent an open social system. An open class system in one in which vertical social mobility is possible.

Example : Within this system, individuals can move from one class to another through hard work, education and skills. Ownership of wealth and occupation are the chief criteria of class differences but education, hereditary, prestige, group participation, self identification and recognition by others, also play an important role in class distinction.

Gender as a form of social stratification:
Gender stratification refers to social ranking, where men typically inhabit higher statuses than women. A common general definition of gender stratification refers to the unequal distribution of wealth, power and privilege between the two sexes. Throughout the world, most societies allocate fewer resources to women than men. Almost all societies are characterized by sexism. Sexism is the belief that one sex is superior than the other. Although, societies have been believing in the superiority of men over women and therefore have been dominating women. This male dominance is supported further by patriarchy. The process of socialization is gendered and creates gender hierarchy. Example : Boys are given toy cars or lego sets or bat and ball to play whereas girls are given household sets, medical sets, dolls, etc.

11th Sociology Digest Chapter 7 Social Stratification Intext Questions and Answers

ACTIVITY (Textbook Page No. 75)

Question 1.
Watch the Marathi movie, ‘Fandry’ and write a film review describing the social, cultural and economic obstacles created by caste barriers.
Answer:
Review of the Marathi Movie ‘Fandry’. The film powerfully busts the myth of individual merit in a caste-decided society. In a small village in Maharashtra Jabya portrays friend Pirya are the only two boys from a so-called untouchable caste. Jabya doesn’t want to consider his caste an obstacle to his aspirations. These hopes of wanting to move out of the confines of his caste are shown through Jabya’s love for his classmate Shalu, an upper caste by birth. Jabya and Pirya, meanwhile want to hunt down the exclusive black sparrow which Jabya believes would help him to win Shalu’s love. His father Kachru wants him to continue their tradition. From being called blacky to being made to feel ashamed of his mother’s occupation. When she comes to school Jabya’s trials indicate the prejudices that make the promise of equality sound like unreal.

In theory, Jabya’s school is supposed to uplift him to a modern and caste-less society where he should be able to choose the work he wants to do. Yet we see how modern education itself is not free from caste. In caste system social set up everything is pre-decided by one’s caste, whom one can love and be friends with, the occupation he has to choose etc. Fandry makes visible the way in which caste is so central to all our relatives.

Question 2.
In today’s world the characteristics of caste are changing. Find out which of the characteristics are changing and which are remaining constant. Conduct a group discussion on the same. (Textbook Page No. 75)
Answer:
In the modern age, many changes happen in the features and functions of caste system. A group discussion can be conducted on the following changes within the caste system.

1. Decline in the superiority of upper caste.
2. Changes in the restrictions regarding social habits.
3. Changes in the restrictions regarding marriage.
4. Changes in the restrictions regarding occupation.
5. Changes in the disabilities of lower castes.
6. Loss of faith in the ascribed status.
7. Changes in lifestyle.
8. Changes in inter-caste relations.
9. Changes in the lower of caste Panchayats.
10. Restrictions on education removed
11. Changes in the philosophical basis.

Question 3.
Divide the class into groups. Each group can select one of the issue mentioned and collect information on it. The group should present their findings to the class. (Textbook Page No. 78)
Answer:
Present findings on any one of the issues to the class.
1. The Economy : Explains how women are being paid low for some amount of work done by men in various unorganized sectors. Also, dual role played by women and unpaid work.

2. The Polity : Explains about women exercising the power of right to vote, in spite of reservation for women, the number of women in official positions of power are less as world leaders, less number of women at war and peace movements.

3. Crime : Explains the crime committed by women, increase in number of women coming in conflict with the law; women prisons in India are relatively less crowded, women commit fewer and different crimes compared to men.

4. Religion : Most religions elevate the status of men over women and have striker sanctions against women and require them to be submissive.

5. Family : In spite of women sharing the economic role, the role of men in raising children is still minimum or negligible. Traditional sexual division of labour where women looked after the house and men played the role of economic provider is still prevalent in the society. Women are expected to balance between home and work.

6. Health : Women neglect their health and nutrition. The frequency of women to visit a doctor is very less as most of the time they manage with home remedies.

Question 4.
Find out examples of intergenerational and intragenerational mobility from your surroundings and present it in your classroom.
Answer:
1. Intergenerational mobility means one generation changes its social status in contrast to the previous generation.
Example : Eminent personality like Dr. B. R. Ambedkar.

2. Intragenerational mobility this type of mobility takes place in the life span of one generation. Example : A person may start one’s career as a clerk and after acquiring more education over a period of time he becomes an IAS officer. Students should find out similar examples of intergenerational and intragenerational mobility from their surroundings.

Question 5.
Arrange the group reading of any two of the following books and conduct a group discussion on the caste and gender discrimination/inequality Baburao Bagul-Jevha Mi Jaat chorli Hoti, Daya Pawar- Baluta, Urmila Pawar- Aaydaan, Omprakash Valmiki- Jhootan, Kishor Shantabai Kale- Against all Odds. (Textbook Page No. 81)
Answer:
Baburao Bagul – ‘Jevha Mi Jaat Chorli Hoti’: This most poignant story recites about an educated Dalit trying to escape his caste profession of scavenging, is an ethnography of caste oppression, description of gender roles shaped by caste, the way Dalit women are oppressed, critique of the political economy of a caste society.

Daya Pawar – ‘Baluta’ : It generalizes the status of rural untouchables. Baluta is a collection of memories of life trapped within the framework of India’s caste system. The frustration and helplessness of being born as a Dalit and the inner conflict in the writer’s mind. He thinks of education as a means to escape from his downtrodden life but ends up being the agent of his lifelong distress.

Urmila Pawar – ‘Aaydaan’: The lives of different members of the family are woven together in a narrative that gradually reveals different aspects of the everyday life of Dalits the manifold ways in which caste assets itself and grinds them down.

Omprakash Valmiki – ‘Jhootan’ : An autobiography by Omprakash Valmiki in which he has explored the issues of Dalits. Being socially segregated for centuries the Dalits are obliged to live a helpless life.

Kishor Shantabai Kale – ‘Against all Odds: The book raises many questions about the exploitation life of women in Kolhati community.

Balbharti Maharashtra State Board Class 11 Sociology Solutions Chapter 1 Introduction to Sociology Textbook Exercise Questions and Answers.

Maharashtra State Board Class 11 Sociology Solutions Chapter 1 Introduction to Sociology

1. (A) Choose the correct alternative and complete the statements.

Question 1.
The term ‘Socius’ means ………………..
(science / companion / social)
Answer:
companion

Question 2.
The term ‘logos’ means ………………..
(associate / science / methodology)
Answer:
science

Question 3.
…………………. is often regarded as the ‘Father of Sociology’.
(Durkheim / Weber/ Comte)
Answer:
Comte

Question 4.
When sociologist make an effort to understand practical problems of daily life it is a/an …………….. science.
(pure / application / theoretical)
Answer:
application

1. (B) Correct the incorrect pair.

Question 1.
(a) Study of role of biology in human life – Bio-Sociology
(b) Study of social words of Art and Aesthetics – Sociology of Art
(c) Theoretical of knowledge in sociology in marketing segmental division of customers, Needs analysis etc. – Sociology of Market Research
(d) Study of visual dimensions of social life – Diaspora Studies
Answer:
(d) Study of visual dimensions of social life – Visual Sociology

1. (C) Identify the appropriate term from the given options.

(Diaspora Studies, The Positive Philosophy, Theoretical Science)
Question 1.
Comte coined the term sociology in this book.
Answer:
Positive Philosophy

Question 2.
Sociology is concerned with developing sociological theory.
Answer:
Theoretical Science

1. (D) Correct underlined words and complete the sentence.

Question 1.
When sociological research is done for its own sake it makes sociology a/an applied science.
Answer:
When sociological research is done for its own sake it makes sociology a pure as well as a social science.

Question 2.
Rape, hate, crimes and terrorism are examples of social institutions.
Answer:
Rape, hate, crimes and terrorism are examples of social problems/ pathology.

2. Write short notes.

Question 1.
Nature of sociology
Answer:

1. Sociology is an empirical science : Sociology studies and analyses social facts on the basis of scientific method. Empiricism is it’s central feature as a science.
2. Sociology is a theoretical and applied science : Verification and formulation of new theories is a constant process in sociology. Also, many branches of sociology are based on the application of sociological knowledge to the field. Hence, it is a ‘pure’ as well as an ‘applied’ social science.
3. Sociology is a factual science : The aim of sociology of to find out the reality of society hence sociology studies the constructive part ans destructive elements in society.
4. Sociology is a holistic science : Sociology does not limit itself to the study of any specific or particular aspect of society. It studies society as a whole.

Question 2.
New emerging areas in sociology
Answer:
The subject matter of sociology is very wide. Hence, new areas emerging in sociology are:

1. Bio-sociology : Studies the role of biology in human social life.
2. Sociology of art : Helps to understand the social world of art and aesthetics.
3. Sociology of market research : It deals with the theoretical knowledge of sociology in marketing, segmental division of customers, needs analysis etc.
4. Visual sociology : Based on visual dimensions of social life.
5. Diaspora studies : Studies migration and its cultural, literacy, social, demographic, anthropological, political, economic impact and international of relations.

Question 3.
Enlightenment period
Answer:

1. The Europe produced a ‘Scientific Revolution’ in the Renaissance period. There was increased emphasis on science in society as a whole. The technological advancement influenced every sector of life.
2. The ideas and discoveries contributed by science led to emergence of sociology. This era is known as the enlightenment period.
3. The Enlightenment period saw the beginning of the scientific revolution. Science was considered in the social context and looked at as a tool for satisfying the needs of humanity.
4. New scientific discoveries helped in the eradication of blind beliefs. This period has made a significant contribution to shaping a scientific attitude in Sociology.

3. Differentiate between.

Question 1.
Natural Science and Social Science.
Answer:

Natural Science	Social Science
(i) A study of natural Sciences includes physical, chemical and biological factors of nature.	(i) Social sciences like economics, political science, sociology studies different aspects of society with major concerns of human beings.
(ii) It studies objectively and in very scientific manner because experimentation in the laboratory is possible.	(ii) It also studies objectively and adopts certain scientific methods but to conduct experiment in the laboratory is not possible at all times.
(iii) Results and findings are more accurate and exact.	(iii) Difficult to maintain accuracy and exact predictions about human behaviour.
(iv) Example : Biology, Chemistry, Physics, Botany etc.	(iv) Example : Sociology, Geography, History etc.

Question 2.
Theoretical Science and Applied Science.
Answer:

Theoretical Science	Applied Science
(i) Theoretical research is explanatory and leads to the advancement of knowledge.	(i) Applied science is for development purposes and solves practical problems of society.
(ii) Theoretical framework is the structure that can hold the theory.	(ii) Applied science means practical application of sociological theory.
(iii) The purpose of theoretical science is to increase understanding.	(iii) The purpose of applied science is to bring about social change.
(iv) Example – A study of the social structure of a slum.	(iv) Example – A study, to prevent delinquency in a slum.

4. Explain the following concept with suitable examples.

Question 1.
Diaspora
Answer:

1. Diaspora is he movement of the people from their original place to other geographical area.
2. Though people migrate they maintain their originality in the migrated area.
3. The people though they have migrated from their original place, follow their rituals, customs and maintain their original existence in areas where they have been migrated.
   Example: Migration of rural people to urban area.

Question 2.
Bio-Sociology
Answer:

1. Bio-Sociology is a subject that has emerged relatively recently in Sociology.
2. Researchers in the area use a variety of sociological methodologies to study the role of biology in human social life.
3. Biologically male and female are different. Both have different strength and capacity because of their body structure. But in society culture plays different role in nurturing them.
4. These discrimination and differences affected the society in a great way. Bio-Sociology helps to understand this concept.
   Example : Gender differences and discrimination.

5. (A) Complete the concept maps.

Answer:

5. (B) State whether the following statements are true or false with reasons.

Question 1.
The French revolution led to changes in society.
Answer:
This statement is True.

1. French Revolution was one of the best examples of struggle for freedom and equality.
2. Through this revolution feudal system had been overthrown. The new system came into existence which was based on the principles of liberty, fraternity and equality.
3. French revolution brought tremendous changes in the life of the people not only in France but all over Europe. Hence, French revolution led to changes in society.

Question 2.
The development in natural sciences has had an impact on sociology as a discipline.
Answer:
This statement is True.

1. Natural sciences are differentiated from other modes of knowledge, by method, not by subject matter.
2. The revolutionary concept that social phenomena are natural phenomena and therefore can be studied by natural – science methodology is being rapidly accepted.
3. Sociology uses scientific methods and research to solve the many problems of society like poverty unemployment etc. Hence, the development in natural science has had an impact on sociology as a discipline.

6. Give your personal response.

Question 1.
Is India in the ‘scientific’ stage of growth? Explain why you hold the view that you do.
Answer:
Yes, India is in the ‘scientific’ stage of growth.
During ancient period India faced many social problems like blind faith, illiteracy, child-infanticide etc. Many cultural, political differences etc., were followed. By adopting scientific method, sociologist have been trying to minimize the problems. They have suggested some measures to the government to find out certain solutions to solve the problems.

The technological and scientific advancement influenced every sector of life. India’s scientific stage of growth includes technical development, which have resulted in technological inventions for scientific growth.

Question 2.
Explain in brief the link between cinema and society.
Answer:
Cinema is one of the means of mass media. Cinema and society are inter related and inter connected with each other. Society influences the cinema and vice versa. But cinema has both positive and negative influences on the society. As far as India is concerned one can find diversity in each and every aspect of society. In such situations cinema plays important role in integrating the society. It also helps to inculcate certain values like honesty, hard work, sympathy, charity, brotherhood etc.

Society influences the cinema and its subject matter. Film makers give special attention on the interest and demand of the people of the society.

7. Answer the following in detail (About 150-200 words).

Question 1.
Discuss with suitable examples, the scope of sociology in today’s world.
Answer:
The following points explains the scope of sociology in today’s world.
1. Bio-Sociology – Example : Gender differences and discrimination. Researchers in the area* use a variety of sociological methodologies to study the role of biology in human social life.

2. Sociology of Art – Example : Warli paintings depicts their lifestyle or paintings related with Mohenjo Daro and Harappan Civilization. This area helps to understand the social world of art and aesthetics. This field seeks to understand the social context of the production and consumption of art.

3. Sociology of Market Research – Example : Advertising of bathing soap by convincing the people that they have used river Ganga’s water in that. This is an applied field that connects marketing and sociological strategies to understand the market in a meaningful way.

4. Visual Sociology – Example: A researcher takes help of newspaper, film, movie, photographs for their study or for the study of a particular society. Visual sociology is concerned with visual dimension of social life. With the help of film, movie, pictures one can visualize or imagine a particular problem, on the basis of which valid and relevant data can be collected.

5. Diaspora Studies – Example : Migration of rural people to urban area. Diaspora is one of the movements of the people from their original place to other geographical area. Though people migrate they maintain their originality in the migrated area. The people though they have migrated from their original place, follow their rituals, customs and maintain their original existence in areas where they have been migrated.

11th Sociology Digest Chapter 1 Introduction to Sociology Intext Questions and Answers

ACTIVITY (Textbook Page No. 6)

Question 1.
You have read about commercial, scientific, industrial and French revolutions which were responsible for the emergence of Sociology as a discipline. Identify the effects of industrial development on Indian society.
Answer:
The effects of industrial development on Indian society are:

1. The use of new tools, machinery and techniques have increased the production speed of goods.
2. Development of trade, new institutions like, banks, credit /debit card facilities emerged.
3. Industrialization lead to Urbanization leading to migration of people from rural to the urban areas.
4. Rise in the factory system of production which provided many new job opportunities in small and large scale industries.
5. Emergences of new organisation and industrial policy.
6. Increase in national income.
7. Improved living standards of the people.
8. Stimulation of progress in other sectors of the economy.
9. Promotes specialization of labour.
10. Provides large scope for technological progress.

Question 2.
Interview two people from your local area, who have migrated from another place. Find out the reasons for shifting and ask about their experiences and problems. (Textbook Page No. 8)
Answer:
Following is a case of inter-state migration in India.
Interview name : Mr. XYZ
Migrated from : Bihar
Migrated to : Mumbai.
Reasons : Advanced economic and social life. Advanced / better quality of education. Faster access to facilities and services like healthcare, education, etc. Higher job opportunities and better standard of living.

Experience : As time passes, a house on rent. Good education to children. Happy urban life.
Problems : Language barriers
Discrimination and inequality
Less paid
Difficulties in job hunting
Exploitation housing problems

Question 3.
Visit any nearby NGO and collect information about their work. Prepare a PPT and present it in your class. (Textbook Page No. 9)
Answer:
Akshara : Empowering Women and Girls.
Akshara is a society helping women live a violent free dignified life without discrimination. It focuses on empowering women and girls through education, productive works and resistance to violence in their lives, so they can be strong and independent contributing members to society.

Akshara has a three-dimensional vision for change:

1. Changing hearts and minds of young women and men.
2. Transforming public attitudes
3. Reforming systems that deny gender justice

Work – (a) Akshara provides scholarships for education, training in life and technical skills and job placements for socially, economically disadvantaged young women.
(b) Akshara trains young men to become support gender equality and take up personal and social action.
(c) Akshara caters gender oriented educational stuff, online a training material videos and documentaries.
(d) Akshara lobbies with the state.

Vision – To establish a gender equality and violence free society
Goods – (a) Enhance societal consciousness on gender inequality.
(b) Employment of women and youth.
(c) Prevent violence towards women.

Question 4.
Discuss the statement listed
(i) Sociology is practical and related to life
(ii) Careers in Sociology. (Textbook Page No. 11)
Answer:
(i) Sociology is practical and related to life : Practical sociology refers to a form of sociological practice that is concerned with using sociological theories and research to understand on going activities. It is the task of sociology to study the social problems through the methods of scientific research and to find out solutions to them.

Sociology studies everyday social life, human interaction, institutions, behaviour and its origins. Sociology helps us to understand our and other people’s culture and environment.

(ii) Careers in Sociology.

1. Human Resources
2. Journalism
3. Social Work / Public services
4. Academics
5. Consumers Relations
6. Lawyer
7. Guidance Counsellor (Guidance counsellor use knowledge of the Sociology of learning to help students navigate the academic world.)