Balbharati Maharashtra State Board 11th Commerce Maths Solution Book Pdf Chapter 8 Continuity Ex 8.1 Questions and Answers.
Maharashtra State Board 11th Commerce Maths Solutions Chapter 8 Continuity Ex 8.1
Question 1.
Examine the continuity of
(i) f(x) = x3 + 2x2 – x – 2 at x = -2
Solution:
f(x) = x3 + 2x2 – x – 2
Here f(x) is a polynomial function and hence it is continuous for all x ∈ R.
∴ f(x) is continuous at x = -2
(ii) f(x) = \(\frac{x^{2}-9}{x-3}\) on R
Solution:
f(x) = \(\frac{x^{2}-9}{x-3}\); x ∈ R
f(x) is a rational function and is continuous for all x ∈ R, except at the points where denominator becomes zero.
Here, denominator x – 3 = 0 when x = 3.
∴ Function f is continuous for all x ∈ R, except at x = 3, where it is not defined.
![]()
Question 2.
Examine whether the function is continuous at the points indicated against them.
(i) f(x) = x3 – 2x + 1, for x ≤ 2
= 3x – 2, for x > 2, at x = 2
Solution:
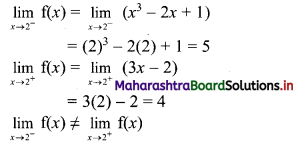
∴ Function f is discontinuous at x = 2
(ii) f(x) = \(\frac{x^{2}+18 x-19}{x-1}\) for x ≠ 1
= 20, for x = 1, at x = 1
Solution:

∴ f(x) is continuous at x = 1
Question 3.
Test the continuity of the following functions at the points indicated against them.
(i) f(x) = \(\frac{\sqrt{x-1}-(x-1)^{\frac{1}{3}}}{x-2}\) for x ≠ 2
= \(\frac{1}{5}\) for x = 2, at x = 2
Solution:

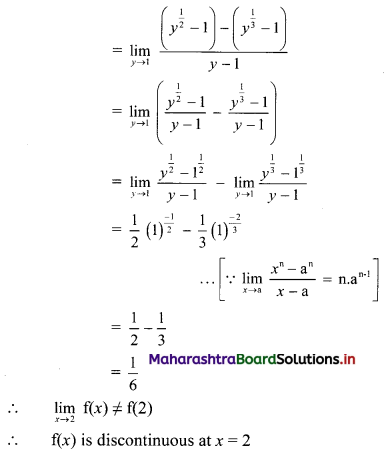
(ii) f(x) = \(\frac{x^{3}-8}{\sqrt{x+2}-\sqrt{3 x-2}}\) for x ≠ 2
= -24 for x = 2, at x = 2
Solution:


(iii) f(x) = 4x + 1 for x ≤ \(\frac{8}{3}\)
= \(\frac{59-9 x}{3}\), for x > \(\frac{8}{3}\), at x = \(\frac{8}{3}\)
Solution:


![]()
(iv) f(x) = \(\frac{x^{3}-27}{x^{2}-9}\) for 0 ≤ x < 3
= \(\frac{9}{2}\), for 3 ≤ x ≤ 6, at x = 3
Solution:

Question 4.
(i) If f(x) = \(\frac{24^{x}-8^{x}-3^{x}+1}{12^{x}-4^{x}-3^{x}+1}\), for x ≠ 0
= k, for x = 0
is continuous at x = 0, find k.
Solution:
Function f is continuous at x = 0

(ii) If f(x) = \(\frac{5^{x}+5^{-x}-2}{x^{2}}\), for x ≠ 0
= k for x = 0
is continuous at x = 0, find k.
Solution:
Function f is continuous at x = 0

(iii) For what values of a and b is the function
f(x) = ax + 2b + 18 for x ≤ 0
= x2 + 3a – b for 0 < x ≤ 2 = 8x – 2 for x > 2,
continuous for every x?
Solution:
Function f is continuous for every x.
∴ Function f is continuous at x = 0 and x = 2
As f is continuous at x = 0.
∴ \(\lim _{x \rightarrow 0^{-}} \mathrm{f}(x)=\lim _{x \rightarrow 0^{+}} \mathrm{f}(x)\)
∴ \(\lim _{x \rightarrow 0^{-}}(a x+2 b+18)=\lim _{x \rightarrow 0^{+}}\left(x^{2}+3 a-b\right)\)
∴ a(0) + 2b + 18 = (0)2 + 3a – b
∴ 3a – 3b = 18
∴ a – b = 6 …..(i)
Also, Function f is continous at x = 2
∴ \(\lim _{x \rightarrow 2^{-}} \mathrm{f}(x)=\lim _{x \rightarrow 2^{-}} \mathrm{f}(x)\)
∴ \(\lim _{x \rightarrow 2^{-}}\left(x^{2}+3 a-b\right)=\lim _{x \rightarrow 2^{-}}(8 x-2)\)
∴ (2)2 + 3a – b = 8(2) – 2
∴ 4 + 3a – b = 14
∴ 3a – b = 10 …..(ii)
Subtracting (i) from (ii), we get
2a = 4
∴ a = 2
Substituting a = 2 in (i), we get
2 – b = 6
∴ b = -4
∴ a = 2 and b = -4
![]()
(iv) For what values of a and b is the function
f(x) = \(\frac{x^{2}-4}{x-2}\) for x < 2
= ax2 – bx + 3 for 2 ≤ x < 3
= 2x – a + b for x ≥ 3
continuous in its domain.
Solution:
Function f is continuous for every x on R.
∴ Function f is continuous at x = 2 and x = 3.
As f is continuous at x = 2.
∴ \(\lim _{x \rightarrow 2^{-}} f(x)=\lim _{x \rightarrow 2^{+}} f(x)\)

∴ 2 + 2 = a(2)2 – b(2) + 3
∴ 4 = 4a – 2b + 3
∴ 4a – 2b = 1 …..(i)
Also function f is continuous at x = 3
∴ \(\lim _{x \rightarrow 3^{-}} f(x)=\lim _{x \rightarrow 3^{+}} f(x)\)
∴ \(\lim _{x \rightarrow 3^{-}}\left(a x^{2}-b x+3\right)=\lim _{x \rightarrow 3^{+}}(2 x-a+b)\)
∴ a(3)2 – b(3) + 3 = 2(3) – a + b
∴ 9a – 3b + 3 = 6 – a + b
∴ 10a – 4b = 3 …..(ii)
Multiplying (i) by 2, we get
8a – 4b = 2 …..(iii)
Subtracting (iii) from (ii), we get
2a = 1
∴ a = \(\frac{1}{2}\)
Substituting a = \(\frac{1}{2}\) in (i), we get
4(\(\frac{1}{2}\)) – 2b = 1
∴ 2 – 2b = 1
∴ 1 = 2b
∴ b = \(\frac{1}{2}\)
∴ a = \(\frac{1}{2}\) and b = \(\frac{1}{2}\)