Balbharati Maharashtra State Board 11th Commerce Maths Solution Book Pdf Chapter 9 Commercial Mathematics Ex 9.5 Questions and Answers.
Maharashtra State Board 11th Commerce Maths Solutions Chapter 9 Commercial Mathematics Ex 9.5
Question 1.
Three partners shared the profit in a business in the ratio 5 : 6 : 7. They had partnered for 12 months, 10 months, and 8 months respectively. What was the ratio of their investments?
Solution:
Let the ratio of investments of the three partners be p : q : r.
They partnered for 12 months, 10 months, and 8 months respectively.
∴ The profit shared by the partners will be in proportion to the product of capital invested and their respective time periods.
∴ 12 × p : 10 × q : 8 × r = 5 : 6 : 7

From (i) & (ii), we have
p : q : r = 50 : 72 : 105
∴ The ratio of their investments was 50 : 72 : 105.
Question 2.
Kamala, Vimala and Pramila enter into a partnership. They invest ₹ 40,000, ₹ 80,000 and ₹ 1,20,000 respectively. At the end of the first year, Vimala withdraws ₹ 40,000, while at the end of the second year, Pramila withdraws ₹ 80,000. In what ratio will the profit be shared at the end of 3 years?
Solution:
Given that, Kamala, Vimala, and Pramila invest ₹ 40,000, ₹ 80,000, and ₹ 1,20,000 respectively.
The ratio of profits is to be calculated at the end of 3 years.
Vimala withdraws ₹ 40,000 at the end of the first year.
∴ Vimala invested ₹ 80,000 for one year and 40,000 for 2 years.
Pramila withdraws ₹ 80,000 at the end of the second year.
∴ Pramila invested ₹ 1,20,000 for two years and 40,000 for one year.
Kamala invested ₹ 40,000 for all the 3 years.
∴ The ratio of profits to be shared at the end of 3 years will be
= 40,000 × 3 : 80,000 × 1 + 40,000 × 2 : 1,20,000 × 2 + 40,000 × 1
= 1,20,000 : 1,60,000 : 2,80,000
= 12 : 16 : 28
= 3 : 4 : 7
Alternate Method:
Given that, Kamala, Vimala and Pramila invest ₹ 40,000, ₹ 80,000 & ₹ 1,20,000 respectively.
Given, information can be tabulated as:
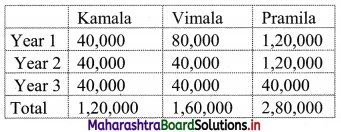
∴ The profits to be shared at the end of 3 years will be
= 1,20,000 : 1,60,000 : 2,80,000
= 12 : 16 : 28
= 3 : 4 : 7
![]()
Question 3.
Sanjeev started a business investing ₹ 25,000 in 1999. In 2000, he invested an additional amount of ₹ 10,000 and Rajeev joined him with an amount of ₹ 35,000. In 2001, Sanjeev invested another additional amount of ₹ 10,000 and Pawan joined them with an amount of ₹ 35,000. What will be Rajeev’s share in the profit of ₹ 1,50,000 earned at the end of 3rd year from the start of the business in 1999?
Solution:
The given information can be tabulated as:
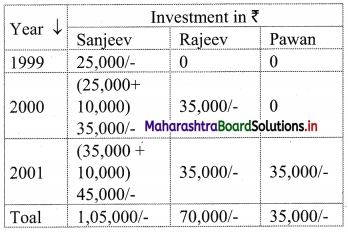
∴ The ratio of profits to be shared at the end of 3 years will be 1,05,000 : 70,000 : 35,000
i.e. in the proportion 3 : 2 : 1
Given, profit earned ₹ 1,50,000/-
∴ Rajeev’s share in the profit = \(\frac{2}{6}\) × 1,50,000 = ₹ 50,000/-
Question 4.
Teena, Leena, and Meena invest in a partnership in the ratio: 7/2, 4/3, 6/5. After 4 months, Teena increases her share by 50%. If the total profit at the end of one year is ₹ 21,600, then what is Leena’s share in the profit?
Solution:
Investment of Teena, Leena and Meena are in the ratio \(\frac{7}{2}: \frac{4}{3}: \frac{6}{5}\)
After 4 months, Teena’s share increases by 50%.
i.e. \(\frac{7}{2}+\left(\frac{7}{2} \times \frac{50}{100}\right)=\frac{7}{2}+\frac{7}{4}\)
i.e. \(\frac{21}{4}\)
The profit will be shared in the proportion of product of capitals and respective time periods in months.
i.e. \(\frac{7}{2} \times 4+\frac{21}{4} \times 8: \frac{4}{3} \times 12: \frac{6}{5} \times 12\)
i.e. 56 : 16 : \(\frac{72}{5}\)
i.e. 7 : 2 : \(\frac{9}{5}\)
i.e. in the proportion 35 : 10 : 9 …..[Multiplying throughout by 5]
Given that profit at the end of one year = ₹ 21,600/-
∴ Leena’s share in the profit = \(\frac{10}{54}\) × 21,600
= 5 × 800
= 4000
∴ Leena’s share in the profit is ₹ 4000/-.
Question 5.
Dilip and Pradeep invested amounts in the ratio 2 : 1, whereas the ratio between amounts invested by Dilip and Sudip was 3 : 2. If ₹ 1,49,500 was their profit, how much amount did Sudip receive?
Solution:
Let the amounts invested by Dilip, Pradeep and Sudip be ₹ ‘d’, ₹ ‘p’ and ₹ ‘s’ respectively.
Given that, d : p = 2 : 1
∴ d : p = 6 : 3 …..(i)
and d : s = 3 : 2
∴ d : s = 6 : 4 …..(ii)
From (i) and (ii),
d : p : s = 6 : 3 : 4
∴ The ratio of profits to be shared among Dilip, Pradeep and Sudip will be 6 : 3 : 4.
Given, profit earned = ₹ 1,49,500/-
∴ Sudip’s share in the profit = \(\frac{4}{13}\) × 1,49,500
= 4 × 11,500
= ₹ 46,000/-
![]()
Question 6.
The ratio of investments of two partners Jatin and Lalit is 11 : 12 and the ratio of their profits is 2 : 3. If Jatin invested the money for 8 months, find for how much time Lalit invested his money.
Solution:
Let ‘x’ be the time in months for which Lalit invested his money
Jatin and Lalit invested their money in the ratio 11 : 12.
Jatin invested his money for 8 months and the ratio of their profits is 2 : 3.
∴ 11 × 8 : 12 × x = 2 : 3
∴ \(\frac{88}{12 x}=\frac{2}{3}\)
∴ x = \(\frac{88 \times 3}{2 \times 12}\)
∴ x = 11
∴ Lalit invested his money for 11 months.
Question 7.
Three friends had dinner at a restaurant. When the bill was received, Alpana paid \(\frac{2}{3}\) as much as Beena paid and Beena paid \(\frac{1}{2}\) as much as Catherin paid. What fraction of the bill did Beena pay?
Solution:
Let ‘T’ be the total bill amount at the restaurant and ‘a’, ‘b’, and ‘c’ be the share of Alpana, Beena, and Catherin respectively.
Given, that Alpana paid \(\frac{2}{3}\) as much as Beena paid
∴ a = \(\frac{2}{3}\) b …..(i)
Also, Beena paid \(\frac{1}{2}\) as much as Catherin paid.
∴ b = \(\frac{1}{2}\) c
∴ c = 2b …….(ii)
∴ Three friends paid the total bill amount.
∴ a + b + c = T …..(iii)
Using (i) and (ii) in (iii), we get

Thus, Beena paid \(\left(\frac{3}{11}\right)^{\text {th }}\) fraction of the total bill amount.
Question 8.
Roy starts a business with ₹ 10,000, Shikha joins him after 2 months with 20% more investment than Roy, after 2 months Tariq joins him with 40% less than Shikha. If the profit earned by them at the end of the year is equal to twice the difference between the investment of Roy and ten times the investment of Tariq. Find the profit of Roy?
Solution:
Given that, Roy starts the business with ₹ 10,000.
Shikha joins him after 2 months with 20% more investment than Roy.
∴ Shikha’s investment = 10,000 + (10,000 × \(\frac{20}{100}\)) = ₹ 12,000
Tariq joins after two more months with an investment 40% less than Shikha.
∴ Tariq’s investment = 12,000 – (12,000 × \(\frac{40}{100}\)) = ₹ 7,200
Now, the profit will be shared in the proportion of product of capitals and respective periods in months.
i.e. 10,000 × 12 : 12,000 × 10 : 7,200 × 8
i.e. in the proportion, 25 : 25 : 12 …..(i) [Dividing throughout by 4,800]
Given that, profit at the end of the year = twice of the difference between investment of Roy and ten times the investment of Tariq.
∴ Profit = 2 [(10 × 7,200) – 10,000]
= 2[72,000 – 10,000]
= 2 × 62,000
= ₹ 1,24,000
∴ Roy’s share of profit = \(\frac{25}{62}\) × 1,24,000 …..[From (i)]
= ₹ 50,000/-
![]()
Question 9.
If 4(P’s Capital) = 6(Q’s Capital) = 10 (R’s Capital), then out of the total profit of ₹ 5,580, what is R’s share?
Solution:
Let ‘p’, ‘q’ and ‘r’ be P, Q and R’s Capital for the business respectively.
∴ 4p = 6q = 10r
L.C.M of 4, 6, 10 = 60
∴ We take 4p = 6q = 10r = 60x
∴ p = 15x, q = 10x, r = 6x
∴ p : q : r = 15 : 10 : 6
Given that total profit = ₹ 5580
R’s share in the profit = \(\frac{6}{31}\) × 5580 = ₹ 1080/-
Question 10.
A and B start a business, with A investing the total capital of ₹ 50,000, on the condition that B pays interest at the rate of 10% per annum on his half of the capital. A is a working partner and receives ₹ 1,500 per month from the total profit and any profit remaining is equally shared by both of them. At the end of the year, it was found that the income of A is twice that of B. Find the total profit for the year?
Solution:
Let ‘x’ and ‘y’ be the profits earned by A and B respectively and let ‘z’ be the total profit for the year.
A is the working partner and receives ₹ 1500 per month from the total profit.
i.e. 12 × 1500 = ₹ 18,000 at the end of the year.
The remaining profit is shared between A and B equally.
∴ y = \(\frac{z-18000}{2}\) …..(i)
Thus, profit earned by A at the end of that year is given by
x = 18000 + \(\left(\frac{z-18000}{2}\right)\)
∴ x = \(\frac{z+18000}{2}\) ……(ii)
A invests the entire capital on the condition that B pays A interest at the rate of 10% per annum on his half of the capital.
∴ At the end of the first year,
A will receive \(\frac{10}{100}\) × 25,000 i.e. ₹ 2500/- over and above his share of profit.
∴ A’s income = Profit of A + 2500 = x + 2500
Given that,
income of A = twice the income of B
∴ x + 2500 = 2y …..(iii)
Using (i) and (ii) in (iii), we get
\(\frac{z+18000}{2}\) + 2500 = 2\(\left(\frac{z-18000}{2}\right)\)
z + 18000 + 5000 = 2(z – 18000)
z + 23000 = 2z – 36000
∴ z = 59,000
∴ The total profit for the year = ₹ 59,000/-