Balbharati Maharashtra State Board 11th Commerce Maths Solution Book Pdf Chapter 9 Commercial Mathematics Ex 9.7 Questions and Answers.
Maharashtra State Board 11th Commerce Maths Solutions Chapter 9 Commercial Mathematics Ex 9.7
Question 1.
Shantanu has a choice to invest in ₹ 10 shares of two firms at ₹ 13 or at ₹ 16. If the first firm pays a 5% dividend and the second firm pays a 6% dividend per annum, find:
(i) Which firm is paying better?
(ii) If Shantanu invests equally in both the firms and the difference between the return from them is ₹ 30. Find how much, in all, does he invest.
Solution:
(i) For firm 1:
Face value of the share (F.V.) = ₹ 10
Market value of the share (M.V.) = ₹ 13
Dividend = 5%
∴ Annual income from the share = \(\frac{5}{100}\) × 10 = ₹ 0.5

For firm 2:
Face value of the share (F.V.) = ₹ 10
Market value of the share (M.V.) = ₹ 16
Dividend = 5%
∴ Annual income from the share = \(\frac{6}{100}\) × 10 = ₹ 0.6
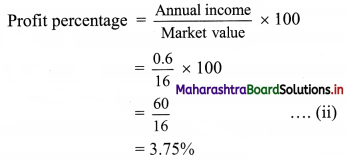
Since, the profit percentage from firm 1 > profit percentage from firm 2, the first firm is paying better.
(ii) Let ‘X’ be the amount Shantanu invests in each of the firms.
Given that difference between the return from them is ₹ 30, we have

In all, Shantanu invests = 2X
= 2 × 31,200
= ₹ 62,400/-
![]()
Question 2.
A dividend of 9% was declared on ₹ 100 shares selling at a certain price in the stock market. If the rate of return is 7.5% calculate
(i) The market price of each share, and
(ii) The amount to be invested to obtain an annual dividend of ₹ 630.
Solution:
(i) Given that,
Face value of the share (F.V) = ₹ 100
Dividend = 9%
Rate of return = 7.5%
Annual income from the share = \(\frac{9}{100}\) × 100 = ₹ 9

∴ The market price of the share is ₹ 120.
(ii) Let ‘X’ be the amount to be invested to obtain an annual dividend of ₹ 630.
∴ 7.5% of X is ₹ 630
∴ \(\frac{7.5}{100}\) × X = 630
∴ X = \(\frac{630 \times 100}{7.5}\)
∴ X = 8400
∴ ₹ 8400 need to be invested to obtain an annual dividend of ₹ 630.
Question 3.
Nilesh has the option of investing his money in 8% ₹ 10 shares at a premium of ₹ 3.50 or 7% ₹ 100 shares at a premium of 20%. Which of the two investments will be more profitable for him?
Solution:
For share 1:
Face value of the share (F.V.) = ₹ 10
Premium = ₹ 3.5
∴ Market value of the share (M.V.) = 10 + 3.5 = ₹ 13.5
Dividend = 8 %
∴ Annual income from the share = \(\frac{8}{100}\) × 10 = ₹ 0.8
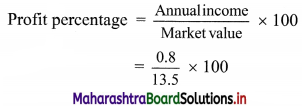
= \(\frac{800}{135}\)
= 5.93%
For share 2:
Face value of the share (F.V.) = ₹ 100
Premium = 20%
∴ Market value of the share (M.V.) = 100 + (\(\frac{20}{100}\) × 100) = ₹ 120
Dividend = 7%
Annual income from the share = \(\frac{7}{100}\) × 100 = ₹ 7

Since, profit percentage from share 1 > profit percentage from share 2, investing in the first kind of shares will be more profitable for Nilesh.
![]()
Question 4.
Sudhakar invests ₹ 1344 in buying shares of face value ₹ 24 selling at a 12% premium. The dividend on the shares is 15% per annum. Calculate
(i) The number of shares Sudhakar buys, and
(ii) The dividend he receives annually.
Solution:
Given that,
Face value of the share (F.V.) = ₹ 24
Premium = 12%
∴ Market value of the share (M.V.) = 24 + (\(\frac{12}{100}\) × 24) = ₹ 26.88
(i) Sudhakar invests ₹ 1344 in the shares
∴ Number of shares purchased by Sudhakar = \(\frac{1344}{26.88}\) = 50
∴ Sudhakar buys 50 shares.
(ii) Dividend on the share = 15%
Annual income on one share = \(\frac{15}{100}\) × 24 = ₹ 3.6
∴ The total dividend he receives annually = 50 × 3.6 = ₹ 180
∴ Sudhakar receives ₹ 180 as his annual dividend.
Question 5.
Sameer invests ₹ 5625 in a company paying 7% per annum when the share of ₹ 10 stands for ₹ 12.50. Find Sameer’s income from this investment. If he sells 60% of these shares of ₹ 10 each, find his gain or loss in this transaction.
Solution:
Given:
Face value of the share (F.V.) = ₹ 10
Market value of the share (M.V.) = ₹ 12.5
Amount invested in shares = ₹ 5625
∴ Number of shares purchased by Sameer = \(\frac{5625}{12.5}\) = 450
Dividend = 7%
Annual income from one share = \(\frac{7}{100}\) × 10 = ₹ 0.7
∴ Sameer’s income from this investment = number of shares × annual income from one share
= 450 × 0.7
= ₹ 315
Sameer sells 60 % of these shares = \(\frac{60}{100}\) × 450 = 270 shares
Sameer purchased these shares at ₹ 12.5 per share.
∴ Purchase price for these shares = 270 × 12.5 = ₹ 3375
If he sells these shares at ₹ 10 per share, he would receive 270 × 10 = ₹ 2700
∴ In this transaction, Sameer would incur a loss of 3375 – 2700 = ₹ 675
![]()
Question 6.
Geeta buys ₹ 100 shares of a company that pays a 15% dividend. She buys the shares at a price from the market that gives her a 10% return on her investment. At what price did she buy each share?
Solution:
Given that,
Face value of the share (F.V.) = ₹ 100
Dividend = 15%
∴ Annual income from the share = \(\frac{15}{100}\) × 100 = ₹ 15
Rate of return on investment = 10%
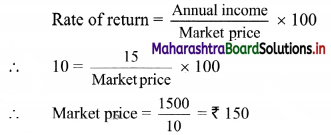
∴ Geeta bought each share from the market at ₹ 150.
Question 7.
Tejas invests in 9% ₹ 100 shares at ₹ 145 but Shail invests in 7% ₹ 100 shares at ₹ 116. Whose investment is better?
Solution:
Investment of Tejas:
Given that, the Face value of the share (F.V.) = ₹ 100
The market value of the share (M.V.) = ₹ 145
Dividend = 9%
Annual income from the share = \(\frac{9}{100}\) × 100 = ₹ 9
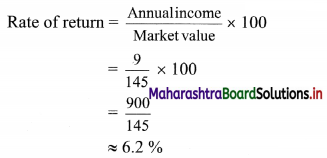
Investment of Shail:
Face value of the share (F.V.) = ₹ 100
Market value of the share (M.V.) = ₹ 116
Dividend = 7%
Annual income from the share = \(\frac{7}{100}\) × 100 = ₹ 7
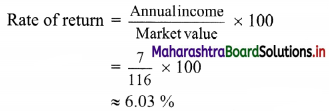
Since the rate of return for Tejas’s investment is greater than that for Shail’s, Tejas’s investment is better.
Question 8.
A 6% share yields 8%. Find the market value of a ₹ 100 share.
Solution:
Given that,
Face value of the share = ₹ 100
Dividend = 6%
Yield = 8%
Annual income on the share = \(\frac{6}{100}\) × 100 = ₹ 6
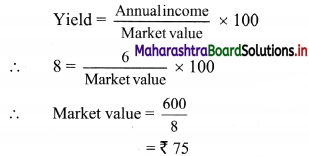
∴ The market value of the share = ₹ 75
Question 9.
Ashwini bought ₹ 40 shares at a premium of 40%. Find the income, if Ashwini invests ₹ 14,000 in these shares and receives a dividend at the rate of 8% on the nominal value of the shares.
Solution:
Given,
Face value of the shares (F.V.) = ₹ 40
Premium = 40%
Market value of the shares (M.V.) = 40 + (40 × \(\frac{40}{100}\))
= 40 + 16
= ₹ 56
Ashwini invests ₹ 14000 in these shares
∴ Number of shares bought by Ashwini = \(\frac{Amount Invested}{Market value of one share}\)
= \(\frac{14000}{56}\)
= 250
Dividend = 8%
∴ Annual income on one share = \(\frac{8}{100}\) × 40 = ₹ 3.2
∴ Income of Ashwini on 250 shares = 250 × 3.2 = ₹ 800
∴ Ashwini earns ₹ 800 on her investment.
![]()
Question 10.
Mr. Rutvik invests ₹ 30,000 in buying shares of a company that pays a 12% dividend annually on ₹ 100 shares selling at a premium of ₹ 50. Find
(i) The number of shares bought Mr. Rutvik and
(ii) His annual income from the shares.
Solution:
Given that,
Face value of a share (F.V.) = ₹ 100
Premium = ₹ 50
∴ Market value of a share (M.V.) = 100 + 50 = ₹ 150
Dividend =12%
Mr. Rutvik invests ₹ 30,000 in the shares.
(i) Number of shares bought by Mr. Rutvik = \(\frac{Amount invested}{Market value}\)
= \(\frac{30000}{150}\)
= 200
(ii) Dividend on the share = 12%
∴ Annual income from one share = \(\frac{12}{100}\) × 100 = ₹ 12
∴ His annual income from shares = number of shares × income from one share
= 200 × 12
= ₹ 2400
Question 11.
Rasika bought ₹ 40 shares at a discount of 40%. Find the income, if she invests ₹ 12,000 in these shares and receives a dividend at the rate of 11% on the nominal value of the shares.
Solution:
Given,
Face value of the shares (F.V.) = ₹ 40
Discount = 40%
∴ Market value of the shares (M.V.) = 40 – (40 × \(\frac{40}{100}\))
= 40 – 16
= ₹ 24
Rasika invests ₹ 12,000 in these shares.
∴ Number of shares bought by Rasika = \(\frac{Amount invested}{Market value of one share}\)
= \(\frac{12000}{24}\)
= 500
Dividend = 11%
∴ Annual income on one share = \(\frac{11}{100}\) × 40 = ₹ 4.4
∴ Rasika’s income on 200 such shares = 500 × 4.4 = ₹ 2200
∴ Rasika earns ₹ 2200 from her investment.
Question 12.
Nisha invests ₹ 15,840 in buying shares of nominal value ₹ 24 selling at a premium of 10%. The company pays a 15% dividend annually. Find
(i) The dividend she receives annually, and
(ii) The rate of return from her investment.
Solution:
Given that,
Face value of the share (F.V.) = ₹ 24
Premium = 10%
∴ Market value of the share (M.V.) = 24 + (24 × \(\frac{10}{100}\))
= 24 + 2.4
= ₹ 26.4
Dividend = 15%
∴ Annual income on the share = \(\frac{15}{100}\) × 24 = ₹ 3.6
Nisha invests ₹ 15,840 in these shares.
∴ Number of shares bought by Nisha

(i) Annual dividend received by Nisha = Number of shares × annual income from one share
= 600 × 3.6
= ₹ 2160
(ii) Rate of return from the investment

Question 13.
Ashutosh buys 80, ₹ 100 shares at a discount of 20% and receives a return of 12% on his money. Calculate
(i) The amount invested by Ashutosh.
(ii) The rate of dividend paid by the company.
Solution:
Given
Face value of the shares (F.V.) = ₹ 100
Discount = 20%
∴ Market value of the shares (M.V.) = 100 – (100 × \(\frac{20}{100}\)) = ₹ 80
(i) Amount invested by Ashutosh = number of shares × market value of the shares
= 80 × 80
= ₹ 6400
(ii) Ashutosh receives a return of 12% on his money.
∴ Ashutosh’s income from shares = \(\frac{12}{100}\) × 6400 = ₹ 768
∴ Ashutosh’s annual income from one share = \(\frac{768}{80}\) = ₹ 9.6
Annual income from one share = \(\frac{\text { Dividend }}{100} \times \text { Face value }\)
∴ 9 6 = \(\frac{\text { Dividend }}{100} \times 100\)
∴ Rate of dividend = 9.6%
![]()
Question 14.
Vaishnavi bought 1000, ₹ 100 shares from the stock market carrying 8% dividend quoted at ₹ 130. A few days later the market value of the shares went up by 10%. Vaishnavi sold all her shares. What was her total income from this transaction?
Solution:
Given that,
Face value of the shares (F.V.) = ₹ 100
The market value of the shares (M.V.) = ₹ 130
Dividend = 8%
Income from the each share = \(\frac{8}{100}\) × 100 = ₹ 8
Number of shares bought by Vaishnavi = 1000
∴ Vaishnavi’s income from dividend = 1000 × 8 = ₹ 8000
The price of the shares went up by 10%
New market value of the shares = 130 + (130 × \(\frac{10}{100}\)) = ₹ 143
Vaishnavi sold the shares at ₹ 143 which she bought at ₹ 130 each.
∴ Vaishnavi’s profit on one share =143 – 130 = ₹ 13
∴ Vaishnavi’s profit after selling all her shares =1000 × 13 = ₹ 13,000
Vaishnavi’s total income from this transaction = Income from dividend + income from sale of shares
= 8,000 + 13,000
= ₹ 21,000
∴ Vaishnavi’s total income from this transaction was ₹ 21,000.
Question 15.
Mr. Dinesh invests ₹ 20,800 in 6% ₹ 100 shares at ₹ 104, and ₹ 14,300 in 10.5% ₹ 100 shares at ₹ 143. What will be his annual income from the shares?
Solution:
For 1st kind of shares,
Face value of shares (F.V.) = ₹ 100
Dividend = 6%
∴ Annual income from one share = \(\frac{6}{100}\) × 100 = ₹ 6
Market value of the share (M.V.) = ₹ 104
Total amount invested = ₹ 20,800
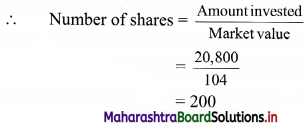
∴ Total income from 1st kind of shares = 200 × 6 = ₹ 1200
For 2nd kind of shares,
Face value of shares (F.V.) = ₹ 100
Dividend = 10.5%
∴ Annual income from one share = \(\frac{10.5}{100}\) × 100 = ₹ 10.5
Market value of the share (M.V.) = ₹ 143
Total amount invested = ₹ 14300
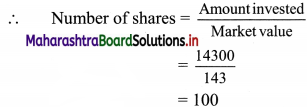
∴ Total income from 2nd kind of shares = 100 × 10.5 = ₹ 1050
∴ Total annual income of Dinesh from both these shares = 1200 + 1050 = ₹ 2250
Question 16.
A company declares a semi-annual dividend of 5%. Daniel has 400 shares of the company. If Daniel’s annual income from the shares is ₹ 1,000, find the face value of each share.
Solution:
Given that,
Semi-annual dividend = 5%
∴ Annual dividend = 10%
Number of shares with Daniel = 400
Daniel’s annual income from the shares = ₹ 1000
∴ Annual income from one share = \(\frac{1000}{400}\) = ₹ 2.5
But annual income from one share = \(\frac{\text { Annualdividend }}{100} \times \text { Face value }\)
∴ 2.5 = \(\frac{10}{100}\) × Face value of the share
∴ Face value of the share = ₹ 25
![]()
Question 17.
Bhargav buys 400, ₹ 20 shares at a premium of ₹ 4 each and receives a dividend of 12%. Find
(i) The amount invested by Bhargav.
(ii) His total income from the shares.
(iii) Percentage return on his money.
Solution:
Given that,
Face value of the shares (F.V.) = ₹ 20
Premium = ₹ 4
∴ Market value of the shares (M.V.) = ₹ 24
Dividend = 12%
∴ Annual income from the share = \(\frac{12}{100}\) × 20 = ₹ 2.4
Bhargav buys 400 shares
(i) The amount invested by Bhargav = number of shares × market value
= 400 × 24
= ₹ 9600
(ii) Bhargav’s income from the shares = number of shares × annual income from one share
= 400 × 2.4
= ₹ 960
(iii) Percentage return on Bhargav’s money

∴ Bhargav gets 10% as the rate of return on his money.
Question 18.
Anil buys 350 ₹ 100 shares of a company at a premium of 20% from the market. The company pays 12% dividend annually. Find
(i) the investment made by Anil,
(ii) his annual income from the shares, and
(iii) the rate of return from the shares.
Solution:
Given that,
Face value of shares (F.V.) = ₹ 100
Premium = 20%
∴ Market value of shares (M.V.) = 100 + (\(\frac{20}{100}\) × 100) = ₹ 120
Dividend = 12%
∴ Annual income from one share = \(\frac{12}{100}\) × 100 = ₹ 12
Anil buys 350 shares.
(i) Amount invested by Anil = number of shares × market value
= 350 × 120
= ₹ 42,000
![]()
(ii) Anil’s annual income from the shares = number of shares × annual income from one share
= 350 × 12
= ₹ 4200
(iii) Rate of return from shares
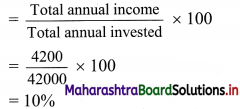
∴ The rate of return from Anil’s shares is 10%.