Balbharati Maharashtra State Board 12th Commerce Maths Digest Pdf Chapter 3 Linear Regression Ex 3.2 Questions and Answers.
Maharashtra State Board 12th Commerce Maths Solutions Chapter 3 Linear Regression Ex 3.2
Question 1.
For bivariate data.
\(\bar{x}\) = 53, \(\bar{x}\) = 28, byx = -1.2, bxy = -0.3
Find,
(i) Correlation coefficient between X and Y.
(ii) Estimate Y for X = 50
(iii) Estimate X for Y = 25
Solution:
(i) r2 = byx . bxy
r2 = (-1.2)(-0.3)
r2 = 0.36
r = ±0.6
Since, byx and bxy are negative, r = -0.6
(ii) Regression equation of Y on X is
(Y – \(\bar{y}\)) = byx (X – \(\bar{x}\))
Y – 28 = -1.2(50 – 53)
Y – 28 = -1.2(-3)
Y – 28 = 3.6
Y = 31.6
(iii) Regression equation of X on Y is
(X – \(\bar{x}\)) = bxy (Y – \(\bar{y}\))
(X – 53) = -0.3(25 – 28)
X – 53 = -0.3(-3)
X – 53 = 0.9
X = 53.9
![]()
Question 2.
From the data of 20 pairs of observation on X and Y, following result are obtained \(\bar{x}\) = 199, \(\bar{y}\) = 94, \(\sum\left(x_{i}-\bar{x}\right)^{2}\) = 1200, \(\sum\left(y_{i}-\bar{y}\right)^{2}\) = 300
\(\sum\left(x_{i}-\bar{x}\right)\left(y_{i}-\bar{y}\right)\) = -250
Find
(i) The line of regression of Y on X.
(ii) The line of regression of X on Y.
(iii) Correlation coefficient between X on Y.
Solution:
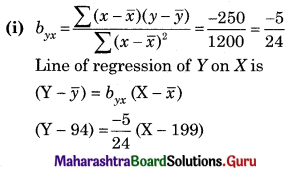

Question 3.
From the data of 7 pairs of observations on X and Y following results are obtained.
Σ(xi – 70 ) = -35, Σ(yi – 60) = -7, Σ(xi – 70)2 = 2989, Σ(yi – 60)2 = 476, Σ(xi – 70) (yi – 60) = 1064 [Given √0.7884 = 0.8879]
Obtain
(i) The line of regression of Y on X.
(ii) The line of regression of X on Y.
(iii) The correlation coefficient between X and Y.
Solution:


(i) Line of regression Y on X is
(Y – \(\bar{y}\)) = byx (X – \(\bar{x}\))
(Y – 59) = 0.36(x – 65)
(Y – 59) = 0.36x – 23.4
Y = 0.36x + 35.6
(ii) Line of regression X on Y is
(X – \(\bar{x}\)) = bxy (Y – \(\bar{y}\))
(X – 65) = 2.19(y – 59)
(X – 65) = 2.19y – 129.21
X = 2.19y – 64.21
(iii) r2 = byx . bxy
r2 = (0.36) (2.19)
r2 = 0.7884
r = ±√0.7884 = ±0.8879
Since byx and bxy are positive.
∴ r = 0.8879
![]()
Question 4.
You are given the following information about advertising expenditure and sales.
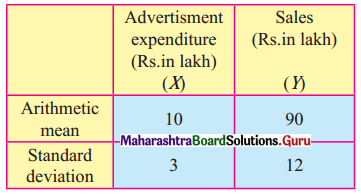
Correlation coefficient between X and Y is 0.8
(i) Obtain two regression equations.
(ii) What is the likely sales when the advertising budget is ₹ 15 lakh?
(iii) What should be the advertising budget if the company wants to attain sales target of ₹ 120 lakh?
Solution:
Given, \(\bar{x}\) = 10, \(\bar{y}\) = 90, σx = 3, σy = 12, r = 0.8
byx = \(\frac{r \sigma_{y}}{\sigma_{x}}=0.8 \times \frac{12}{3}\) = 3.2
bxy = \(\frac{r \sigma_{x}}{\sigma_{y}}=0.8 \times \frac{3}{12}\) = 0.2
(i) Regression equation of Y on X is
(Y – \(\bar{y}\)) = byx (X – \(\bar{x}\))
(Y – 90) = 3.2(x – 10)
Y – 90 = 3.2x – 32
Y = 3.2x + 58
Regression equation of X on Y is
(X – \(\bar{x}\)) = bxy (Y – \(\bar{y}\))
(X – 10) = 0.2(y – 90)
X – 10 = 0.2y + 18
X = 0.2y – 8
(ii) When x = 15,
Y = 3.2(15) + 58
= 48 + 58
= 106 lakh
(iii) When y = 120
X = 0.2(120) – 8
= 24 – 8
= 16 lakh
Question 5.
Bring out inconsistency if any, in the following:
(i) byx + bxy = 1.30 and r = 0.75
(ii) byx = bxy = 1.50 and r = -0.9
(iii) byx = 1.9 and bxy = -0.25
(iv) byx = 2.6 and bxy = \(\frac{1}{2.6}\)
Solution:
(i) Given, byx + bxy = 1.30 and r = 0.75
\(\frac{b_{y x}+b_{x y}}{2}=\frac{1.30}{2}\) = 0.65
But for regression coefficients byx and bxy
\(\left|\frac{b_{y x}+b_{x y}}{2}\right| \geq r\)
Here, 0.65 < r = 0.75
∴ The data is inconsistent
(ii) The signs of byx, bxy and r must be same (all three positive or all three negative)
∴ The data is inconsistent.
(iii) The signs of byx and bxy should be same (either both positive or both negative)
∴ The data is consistent.
(iv) byx . bxy = 2.6 × \(\frac{1}{2.6}\) = 1
∴ 0 ≤ r2 ≤ 1
∴ The data is consistent.
![]()
Question 6.
Two sample from bivariate populations have 15 observation each. The sample means of X and Y are 25 and 18 respectively. The corresponding sum of square of deviations from respective means are 136 and 150. The sum of product of deviations from respective means is 123. Obtain the equation of line of regression of X on Y.
Solution:
Given, n = 15, \(\bar{x}\) = 25, \(\bar{y}\) = 18, Σ(x – \(\bar{x}\)) = 136, Σ(y – \(\bar{y}\)) = 150, Σ(x – \(\bar{x}\)) (y – \(\bar{y}\)) = 123
Regression equation of X on Y is (X – \(\bar{x}\)) = bxy (Y – \(\bar{y}\))
(X – 25) = 0.82(y – 18)
(X – 25) = 082y – 14.76
X = 0.82y + 10.24
Question 7.
For a certain bivariate data
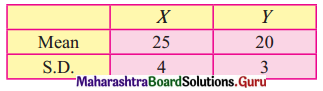
And r = 0.5 estimate y when x = 10 and estimate x when y = 16
Solution:
Given, \(\bar{x}\) = 25, \(\bar{y}\) = 20, σx = 4, σy = 3, r = 0.5
byx = \(\frac{r \sigma_{y}}{\sigma_{y}}=0.5 \times \frac{3}{4}\) = 0.375
Regression equation of Y on X is
(Y – \(\bar{y}\)) = byx (X – \(\bar{x}\))
(Y – 20) = 0.375(x – 25)
Y – 20 = 0.375x – 9.375
Y = 0.375x + 10.625
When, x = 10
Y = 0.375(10) + 10.625
= 3.75 + 10.625
= 14.375
bxy = \(\frac{r \sigma_{x}}{\sigma_{y}}=0.5 \times \frac{4}{3}\) = 0.67
Regression equation of X on Y is
(X – \(\bar{x}\)) = byx (Y – \(\bar{y}\))
(X – 25) = 0.67(y – 20)
(X – 25) = 0.67y – 13.4
X = 0.67y + 11.6
When, Y = 16
x = 0.67(16) + 11.6
= 10.72 + 11.6
= 22.32
Question 8.
Given the following information about the production and demand of a commodity obtain the two regression lines:
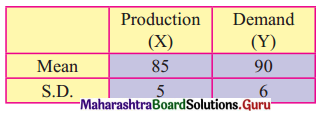
Coefficient of correlation between X and Y is 0.6. Also estimate the problem when demand is 100.
Solution:
Given \(\bar{x}\) = 85, \(\bar{y}\) = 90, σx = 5, σy = 6 and r = 0.6
bxy = \(\frac{r \sigma_{x}}{\sigma_{y}}=0.6 \times \frac{5}{6}\) = 0.5
byx = \(\frac{r \sigma_{y}}{\sigma_{x}}=0.6 \times \frac{6}{5}\) = 0.72
Regression equation of X on Y is
(X – \(\bar{x}\)) = bxy (Y – \(\bar{y}\))
(X – 85) = 0.5(y – 90)
(X – 85 ) = 0.5y – 45
X = 0.5y + 40
When y = 100,
x = 0.5 (100) + 40
= 50 + 40
= 90
Regression equation of Y on X is
(Y – \(\bar{y}\)) = byx (X – \(\bar{x}\))
(Y – 90) = 0.72(x – 85)
(Y – 90) = 0.72x – 61.2
Y = 0.72x + 28.8
![]()
Question 9.
Given the following data, obtain linear regression estimate of X for Y = 10
Solution:
\(\bar{x}\) = 7.6, \(\bar{y}\) = 14.8, σx = 3.2, σy = 16 and r = 0.7
bxy = \(\frac{r \sigma_{x}}{\sigma_{y}}=0.7 \times \frac{3.2}{16}\) = 0.14
Regression equation of X on Y is
(X – \(\bar{y}\)) = bxy (Y – \(\bar{y}\))
(X – 7.6) = 0.14(y – 14.8)
X – 7.6 = 0.14y – 2.072
X = 0.14y + 5.528
When y = 10
x = 0.14(10) + 5.528
= 1.4 + 5.528
= 6.928
Question 10.
An inquiry of 50 families to study the relationship between expenditure on accommodation (₹ x) and expenditure on food and entertainment (₹ y) gave the following result:
Σx = 8500, Σy = 9600, σx = 60, σy = 20, r = 0.6
Estimate the expenditure on food and entertainment when expenditure on accommodation is ₹ 200
Solution:
n = 50 (given)

Regression equation of Y on X is
Y – \(\bar{y}\) = byx (X – \(\bar{x}\))
(Y – 192) = 0.2(200 – 170)
Y – 192 = 0.2(30)
Y = 192 + 6
Y = 198
Question 11.
The following data about the sales and advertisement expenditure of a firms is given below (in ₹ crores)
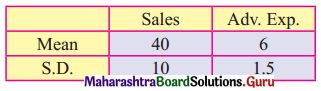
Also correlation coefficient between X and Y is 0.9
(i) Estimate the likely sales for a proposed advertisement expenditure of ₹ 10 crores.
(ii) What should be the advertisement expenditure if the firm proposes a sales target ₹ 60 crores
Let the sales be X and advertisement expenditure be Y
Solution:
Given, \(\bar{x}\) = 40, \(\bar{y}\) = 6, σx = 10, σy = 1.5, r = 0.9
byx = \(\frac{r \sigma_{y}}{\sigma_{x}}=0.9 \times \frac{1.5}{10}\) = 0.135
bxy = \(\frac{r \sigma_{x}}{\sigma_{y}}=0.9 \times \frac{10}{1.5}\) = 6
(i) Regression equation of X on Y is
(X – \(\bar{x}\)) = bxy (Y – \(\bar{y}\))
(X – 40) = 6(y – 6)
X – 40 = 6y – 36
X = 6y + 4
When y = 10
x = 6 (10) + 4
= 60 + 4
= 64 crores
(ii) Regression equation Y on X is
(Y – \(\bar{y}\)) = byx (X – \(\bar{x}\))
(Y – 6) = 0.135 (x – 40)
Y – 6 = 0.135x – 5.4
Y = 0.135x + 0.6
When x = 60
Y = 0.135 (60) + 0.6
= 8.1 + 0.6
= 8.7 crores
![]()
Question 12.
For certain bivariate data the following information are available
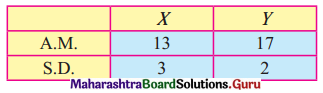
Correlation coefficient between x and y is 0.6, estimate x when y = 15 and estimate y when x = 10.
Solution:
Given, \(\bar{x}\) = 13, \(\bar{y}\) = 17, σx = 3, σy = 2, r = 0.6
byx = \(\frac{r \sigma_{y}}{\sigma_{x}}=0.6 \times \frac{2}{3}\) = 0.4
bxy = \(\frac{r \sigma_{x}}{\sigma_{y}}=0.6 \times \frac{3}{2}\) = 0.9
Regression equation of Y on X
(Y – \(\bar{y}\)) = byx (X – \(\bar{x}\))
Y – 17 = 0.4(x – 13)
Y = 0.4x + 11.8
When x = 10
Y = 0.4(10) + 11.8
= 4 + 11.8
= 15.8
Regression equation of X on Y
(X – \(\bar{x}\)) = bxy (Y – \(\bar{y}\))
(X – 13) = 0.9(y – 17)
X – 13 = 0.9y – 15.3
X = 0.9y – 2.3
When y = 15
X = 0.9(15) – 2.3
= 13.5 – 2.3
= 11.2