Differentiation Class 12 Commerce Maths 1 Chapter 3 Miscellaneous Exercise 3 Answers Maharashtra Board
Balbharati Maharashtra State Board 12th Commerce Maths Solution Book Pdf Chapter 3 Differentiation Miscellaneous Exercise 3 Questions and Answers.
Std 12 Maths 1 Miscellaneous Exercise 3 Solutions Commerce Maths
(I) Choose the correct alternative:
Question 1.
If y = (5x3 – 4x2 – 8x)9, then \(\frac{d y}{d x}\) = ___________
(a) 9(5x3 – 4x2 – 8x)8 (15x2 – 8x – 8)
(b) 9(5x3 – 4x2 – 8x)9 (15x2 – 8x – 8)
(c) 9(5x3 – 4x2 – 8x)8 (5x2 – 8x – 8)
(d) 9(5x3 – 4x2 – 8x)9 (5x2 – 8x – 8)
Answer:
(a) 9(5x3 – 4x2 – 8x)8 (15x2 – 8x – 8)
Question 2.
If y = \(\sqrt{x+\frac{1}{x}}\), then \(\frac{d y}{d x}\) = ?
(a) \(\frac{x^{2}-1}{2 x^{2} \sqrt{x^{2}+1}}\)
(b) \(\frac{1-x^{2}}{2 x^{2} \sqrt{x^{2}+1}}\)
(c) \(\frac{x^{2}-1}{2 x \sqrt{x} \sqrt{x^{2}+1}}\)
(d) \(\frac{1-x^{2}}{2 x \sqrt{x} \sqrt{x^{2}+1}}\)
Answer:
(c) \(\frac{x^{2}-1}{2 x \sqrt{x} \sqrt{x^{2}+1}}\)
Hint:

Question 3.
If y = \(e^{\log x}\) then \(\frac{d y}{d x}\) = ?
(a) \(\frac{e^{\log x}}{x}\)
(b) \(\frac{1}{x}\)
(c) 0
(d) \(\frac{1}{2}\)
Answer:
(a) \(\frac{e^{\log x}}{x}\)
![]()
Question 4.
If y = 2x2 + 22 + a2, then \(\frac{d y}{d x}\) = ?
(a) x
(b) 4x
(c) 2x
(d) -2x
Answer:
(b) 4x
Question 5.
If y = 5x . x5, then \(\frac{d y}{d x}\) = ?
(a) 5x . x4(5 + log 5)
(b) 5x . x5(5 + log 5)
(c) 5x . x4(5 + x log 5)
(d) 5x . x5(5 + x log 5)
Answer:
(c) 5x . x4(5 + x log 5)
Question 6.
If y = \(\log \left(\frac{e^{x}}{x^{2}}\right)\) then \(\frac{d y}{d x}\) = ?
(a) \(\frac{2-x}{x}\)
(b) \(\frac{x-2}{x}\)
(c) \(\frac{e-x}{ex}\)
(d) \(\frac{x-e}{ex}\)
Answer:
(b) \(\frac{x-2}{x}\)
Hint:
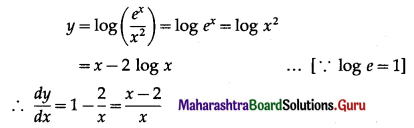
Question 7.
If ax2 + 2hxy + by2 = 0, then \(\frac{d y}{d x}\) = ?
(a) \(\frac{(a x+h y)}{(h x+b y)}\)
(b) \(\frac{-(a x+h y)}{(h x+b y)}\)
(c) \(\frac{(a x-h y)}{(h x+b y)}\)
(d) \(\frac{(2 a x+h y)}{(h x+3 b y)}\)
Answer:
(b) \(\frac{-(a x+h y)}{(h x+b y)}\)
Question 8.
If x4 . y5 = (x + y)(m+1) and \(\frac{d y}{d x}=\frac{y}{x}\) then m = ?
(a) 8
(b) 4
(c) 5
(d) 20
Answer:
(a) 8
Hint:
If xp . yq = (x + y)p+q, then \(\frac{d y}{d x}=\frac{y}{x}\)
∴ m + 1 = 4 + 5 = 9
∴ m = 8.
![]()
Question 9.
If x = \(\frac{e^{t}+e^{-t}}{2}\), y = \(\frac{e^{t}-e^{-t}}{2}\) then \(\frac{d y}{d x}\) = ?
(a) \(\frac{-y}{x}\)
(b) \(\frac{y}{x}\)
(c) \(\frac{-x}{y}\)
(d) \(\frac{x}{y}\)
Answer:
(d) \(\frac{x}{y}\)
Hint:

Question 10.
If x = 2at2, y = 4at, then \(\frac{d y}{d x}\) = ?
(a) \(-\frac{1}{2 a t^{2}}\)
(b) \(\frac{1}{2 a t^{3}}\)
(c) \(\frac{1}{t}\)
(d) \(\frac{1}{4 a t^{3}}\)
Answer:
(c) \(\frac{1}{t}\)
(II) Fill in the blanks:
Question 1.
If 3x2y + 3xy2 = 0 then \(\frac{d y}{d x}\) = …………
Answer:
-1
Hint:
3x2y + 3xy2 = 0
∴ 3xy(x + y) = 0
∴ x + y = 0
∴ y = -x
∴ \(\frac{d y}{d x}\) = -1
Question 2.
If xm . yn = (x+y)(m+n) then \(\frac{d y}{d x}=\frac{\ldots \ldots}{x}\)
Answer:
y
Question 3.
If 0 = log(xy) + a then \(\frac{d y}{d x}=\frac{-y}{\ldots . .}\)
Answer:
x
![]()
Question 4.
If x = t log t and y = tt then \(\frac{d y}{d x}\) = …………
Answer:
y
Hint:
x = t log t = log tt = log y
∴ 1 = \(\frac{1}{y} \cdot \frac{d y}{d x}\)
∴ \(\frac{d y}{d x}\) = y
Question 5.
If y = x . log x then \(\frac{d^{2} y}{d x^{2}}\) = …………..
Answer:
\(\frac{1}{x}\)
Question 6.
If y = [log(x)]2 then \(\frac{d^{2} y}{d x^{2}}\) = …………..
Answer:
\(\frac{2(1-\log x)}{x^{2}}\)
Hint:

Question 7.
If x = y + \(\frac{1}{y}\) then \(\frac{d y}{d x}\) = …………
Answer:
\(\frac{y^{2}}{y^{2}-1}\)
Hint:

Question 8.
If y = eax, then x.\(\frac{d y}{d x}\) = …………
Answer:
axy
Question 9.
If x = t . log t, y = tt then \(\frac{d y}{d x}\) = …………
Answer:
y
![]()
Question 10.
If y = \(\left(x+\sqrt{x^{2}-1}\right)^{m}\) then \(\sqrt{\left(x^{2}-1\right)} \frac{d y}{d x}\) = ………
Answer:
my
Hint:

(III) State whether each of the following is True or False:
Question 1.
If f’ is the derivative of f, then the derivative of the inverse of f is the inverse of f’.
Answer:
False
Question 2.
The derivative of loga x, where a is constant is \(\frac{1}{x \cdot \log a}\).
Answer:
True
Question 3.
The derivative of f(x) = ax, where a is constant is x . ax-1
Answer:
False
Question 4.
The derivative of a polynomial is polynomial.
Answer:
True
![]()
Question 5.
\(\frac{d}{d x}\left(10^{x}\right)=x \cdot 10^{x-1}\)
Answer:
False
Question 6.
If y = log x, then \(\frac{d y}{d x}=\frac{1}{x}\).
Answer:
True
Question 7.
If y = e2, then \(\frac{d y}{d x}\) = 2e.
Answer:
False
Question 8.
The derivative of ax is ax. log a.
Answer:
True
Question 9.
The derivative of xm . yn = (x + y)(m+n) is \(\frac{x}{y}\)
Answer:
False
(IV) Solve the following:
Question 1.
If y = (6x3 – 3x2 – 9x)10, find \(\frac{d y}{d x}\)
Solution:
Given y = (6x3 – 3x2 – 9x)10

Question 2.
If y = \(\sqrt[5]{\left(3 x^{2}+8 x+5\right)^{4}}\), find \(\frac{d y}{d x}\).
Solution:
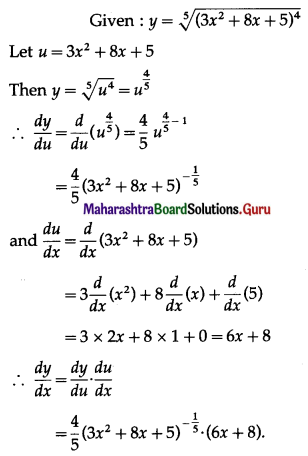
![]()
Question 3.
If y = [log(log(log x))]2, find \(\frac{d y}{d x}\).
Solution:


Question 4.
Find the rate of change of demand (x) of a commodity with respect to its price (y) if y = 25 + 30x – x2.
Solution:

Question 5.
Find the rate of change of demand (x) of a commodity with respect to its price (y) if y = \(\frac{5 x+7}{2 x-13}\)
Solution:

Question 6.
Find \(\frac{d y}{d x}\) if y = xx.
Solution:
y = xx
∴ log y = log xx = x log x
Differentiating both sides w.r.t. x, we get
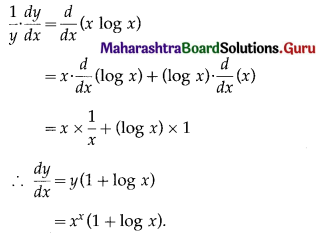
![]()
Question 7.
Find \(\frac{d y}{d x}\) if y = \(2^{x^{x}}\).
Solution:

Question 8.
Find \(\frac{d y}{d x}\), if y = \(\sqrt{\frac{(3 x-4)^{3}}{(x+1)^{4}(x+2)}}\)
Solution:
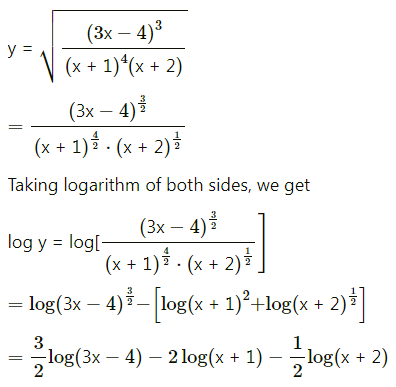
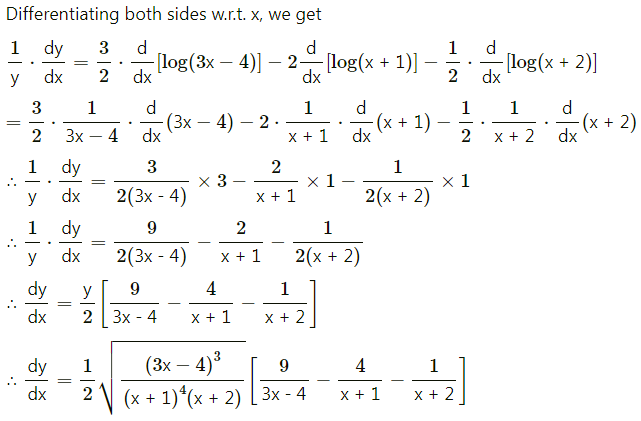
Question 9.
Find \(\frac{d y}{d x}\) if y = xx + (7x – 1)x
Solution:


Question 10.
If y = x3 + 3xy2 + 3x2y, find \(\frac{d y}{d x}\).
Solution:
y = x3 + 3xy2 + 3x2y
Differentiating both sides w.r.t. x, we get

Question 11.
If x3 + y2 + xy = 7, find \(\frac{d y}{d x}\).
Solution:
x3 + y2 + xy = 7
Differentiating both sides w.r.t. x, we get

![]()
Question 12.
If x3y3 = x2 – y2, find \(\frac{d y}{d x}\).
Solution:
x3y3 = x2 – y2
Differentiating both sides w.r.t. x, we get

Question 13.
If x7 . y9 = (x + y)16, then show that \(\frac{d y}{d x}=\frac{y}{x}\).
Solution:
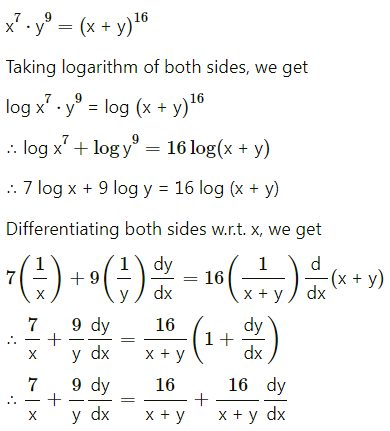
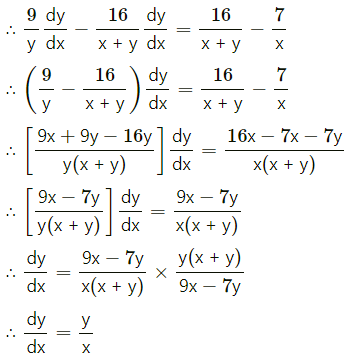
Question 14.
If xa . yb = (x + y)a+b, then show that \(\frac{d y}{d x}=\frac{y}{x}\).
Solution:

Question 15.
Find \(\frac{d y}{d x}\) if x = 5t2, y = 10t.
Solution:
x = 5t2, y = 10t
Differentiating x and y w.r.t. t, we get
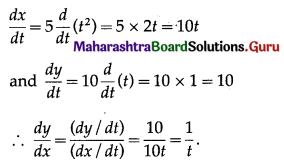
Question 16.
Find \(\frac{d y}{d x}\) if x = e3t, y = \(e^{\sqrt{t}}\).
Solution:
x = e3t, y = \(e^{\sqrt{t}}\)
Differentiating x and y w.r.t. t, we get

Question 17.
Differentiate log(1 + x2) with respect to ax.
Solution:
Let u = log(1 + x2) and v = ax
Then we want to find \(\frac{d u}{d v}\)
Differentiating u and v w.r.t. x, we get

![]()
Question 18.
Differentiate e(4x+5) with resepct to 104x.
Solution:
Let u = e(4x+5) and v = 104x
Then we want to find \(\frac{d u}{d v}\)
Differentiating u and v w.r.t. x, we get

Question 19.
Find \(\frac{d^{2} y}{d x^{2}}\), if y = log x.
Solution:
y = log x
Differentiating w.r.t. x, we get
\(\frac{d y}{d x}=\frac{d}{d x}(\log x)=\frac{1}{x}\)
Differentiating again w.r.t. x, we get
\(\frac{d^{2} y}{d x^{2}}=\frac{d}{d x}\left(\frac{1}{x}\right)=-\frac{1}{x^{2}}\)
Question 20.
Find \(\frac{d^{2} y}{d x^{2}}\), if y = 2at, x = at2.
Solution:
x = at2, y = 2at
Differentiating x and y w.r.t. t, we get

Question 21.
Find \(\frac{d^{2} y}{d x^{2}}\), if y = x2 . ex
Solution:
y = x2 . ex
Differentiating w.r.t. x, we get

= ex (2x + 2 + x2 + 2x)
= ex (x2 + 4x + 2).
![]()
Question 22.
If x2 + 6xy + y2 = 10, then show that \(\frac{d^{2} y}{d x^{2}}=\frac{80}{(3 x+y)^{3}}\).
Solution:
x2 + 6xy + y2 = 10 ……..(1)
Differentiating both sides w.r.t. a, we get



Question 23.
If ax2 + 2hxy + by2 = 0, then show that \(\frac{d^{2} y}{d x^{2}}\) = 0.
Solution:
ax2 + 2hxy + by2 = 0 ……..(1)
∴ ax2 + hxy + hxy + by2 = 0
∴ x(ax + hy) + y(hx + by) = 0
∴ x(ax + hy) = -y(hx + by)
∴ \(\frac{a x+h y}{h x+b y}=-\frac{y}{x}\) …….(2)
Differentiating (1) w.r.t. x, we get

Std 12 Commerce Statistics Part 1 Digest Pdf
- Differentiation Ex 3.1 Class 12 Commerce Maths Textbook Solutions
- Differentiation Ex 3.2 Class 12 Commerce Maths Textbook Solutions
- Differentiation Ex 3.3 Class 12 Commerce Maths Textbook Solutions
- Differentiation Ex 3.4 Class 12 Commerce Maths Textbook Solutions
- Differentiation Ex 3.5 Class 12 Commerce Maths Textbook Solutions
- Differentiation Ex 3.6 Class 12 Commerce Maths Textbook Solutions
- Differentiation Miscellaneous Exercise 3 Class 12 Commerce Maths Textbook Solutions