Balbharti 12th Maharashtra State Board Maths Solutions Book Pdf Chapter 3 Trigonometric Functions Ex 3.2 Questions and Answers.
Maharashtra State Board 12th Maths Solutions Chapter 3 Trigonometric Functions Ex 3.2
Question 1.
Find the Cartesian co-ordinates of the point whose polar co-ordinates are :
(i) \(\left(\sqrt{2}, \frac{\pi}{4}\right)\)
Solution:
Here, r = \(\sqrt {2}\) and θ = \(\frac{\pi}{4}\)
Let the cartesian coordinates be (x, y)
Then, x = rcosθ = \(\sqrt {2}\)cos\(\frac{\pi}{4}\) = \(\sqrt{2}\left(\frac{1}{\sqrt{2}}\right)\) = 1
y = rsinθ = \(\sqrt {2}\)sin\(\frac{\pi}{4}\) = \(\sqrt{2}\left(\frac{1}{\sqrt{2}}\right)\) = 1
∴ the cartesian coordinates of the given point are (1, 1).
(ii) \(\left(4, \frac{\pi}{2}\right)\)
Solution:
(iii) \(\left(\frac{3}{4}, \frac{3 \pi}{4}\right)\)
Solution:
Here, r = \(\frac{3}{4}\) and θ = \(\frac{3 \pi}{4}\)
Let the cartesian coordinates be (x, y)

![]()
(iv) \(\left(\frac{1}{2}, \frac{7 \pi}{3}\right)\)
Solution:
Here, r = \(\frac{1}{2}\) and θ = \(\frac{7 \pi}{4}\)
Let the cartesian coordinates be (x, y)
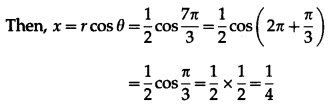
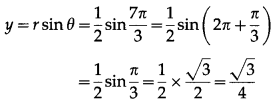
∴ the cartesian coordinates of the given point are \(\left(\frac{1}{4}, \frac{\sqrt{3}}{4}\right)\)
Question 2.
Find the of the polar co-ordinates point whose Cartesian co-ordinates are.
(i) \((\sqrt{2}, \sqrt{2})\)
Solution:
Here x = \(\sqrt {2}\) and y = \(\sqrt {2}\)
∴ the point lies in the first quadrant.
Let the polar coordinates be (r, θ)
Then, r2 = x2 + y2 = (\(\sqrt {2}\) )2 + (\(\sqrt {2}\) )2 = 2 + 2 = 4
∴ r = 2 … [∵ r > 0]
cos θ = \(\frac{x}{r}=\frac{\sqrt{2}}{2}=\frac{1}{\sqrt{2}}\)
and sin θ = \(\frac{y}{r}=\frac{\sqrt{2}}{2}=\frac{1}{\sqrt{2}}\)
∴ tan θ = 1
Since the point lies in the first quadrant and
0 ≤ θ ≤ 2π, tan θ = 1 = tan\(\frac{\pi}{4}\)
∴ θ = \(\frac{\pi}{4}\)
∴ the polar coordinates of the given point are \(\left(2, \frac{\pi}{4}\right)\).
![]()
(ii) \(\left(0, \frac{1}{2}\right)\)
Solution:
Here x = 0 and y = \(\frac{1}{2}\)
the point lies on the positive side of Y-axis. Let the polar coordinates be (r, θ)
Then, r2 = x2 + y2 = (0)2 + \(\left(\frac{1}{2}\right)^{2}=0+\frac{1}{4}=\frac{1}{4}\)
∴ r = \(\frac{1}{2}\) …[∵ r > 0]
cosθ = \(\frac{x}{r}=\frac{0}{(1 / 2)}\) = 0
and sin θ = \(\frac{y}{r}=\frac{(1 / 2)}{(1 / 2)}\) = 1
Since, the point lies on the positive side of Y-axis and 0 ≤ θ ≤ 2π
cosθ = 0 = cos\(\frac{\pi}{2}\) and sinθ = 1 = sin\(\frac{\pi}{2}\)
∴ θ = \(\frac{\pi}{2}\)
∴ the polar coordinates of the given point are \(\left(\frac{1}{2}, \frac{\pi}{2}\right)\).
(iii) \((1,-\sqrt{3})\)
Solution:
Here x = 1 and y = \(-\sqrt{3}\)
∴ the point lies in the fourth quadrant.
Let the polar coordinates be (r, θ).
Then, r2 = x2 + y2 = (1)2 + (\(-\sqrt {3}\) )2 = 1 + 3 = 4
∴ r = 2 … [∵ r > 0]

∴ the polar coordinates of the given point are \(\left(2, \frac{5 \pi}{3}\right)\).
![]()
(iv) \(\left(\frac{3}{2}, \frac{3 \sqrt{3}}{2}\right)\)
Solution:
Question 3.
In ∆ABC, if ∠A = 45º, ∠B = 60º then find the ratio of its sides.
Solution:
By the sine rule,
\(\frac{a}{\sin \mathrm{A}}\) = \(\frac{b}{\sin \mathrm{B}}\) = \(\frac{c}{\sin \mathrm{C}}\)
∴ \(\frac{a}{b}=\frac{\sin A}{\sin B}\) and \(\frac{b}{c}=\frac{\sin B}{\sin C}\)
∴ a : b : c = sinA : sinB : sinC
Given ∠A = 45° and ∠B = 60°
∵ ∠A + ∠B + ∠C = 180°
∴ 45° + 60° + ∠C = 180°
∴ ∠C = 180° – 105° = 75°
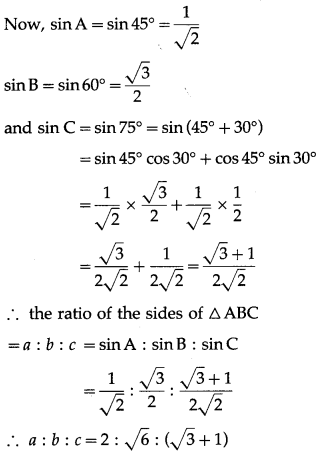
![]()
Question 4.
In ∆ABC, prove that sin \(\left(\frac{\mathbf{B}-\mathbf{C}}{2}\right)=\left(\frac{\boldsymbol{b}-\boldsymbol{c}}{a}\right)\) cos \(\frac{A}{2}\).
Solution:
By the sine rule,

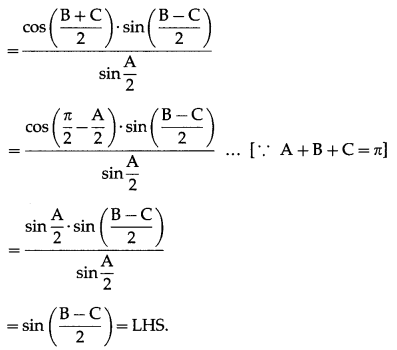
Question 5.
With usual notations prove that 2 \(\left\{a \sin ^{2} \frac{C}{2}+c \sin ^{2} \frac{A}{2}\right\}\) = a – b + c.
Solution:

![]()
Question 6.
In ∆ABC, prove that a3sin(B – C) + b3sin(C – A) + c3sin(A – B) = 0
Solution:
By the sine rule,
\(\frac{a}{\sin A}\) = \(\frac{b}{\sin B}\) = \(\frac{c}{\sin C}\) = k
∴ a = k sin A, b = k sin B, c = k sin C
LHS = a3sin (B – C) + b3sin (C – A) + c3sin (A – B)
= a3(sin B cos C – cos B sin C) + b3(sinCcos A – cos C sin A) + c3(sinAcosB – cos A sin B)
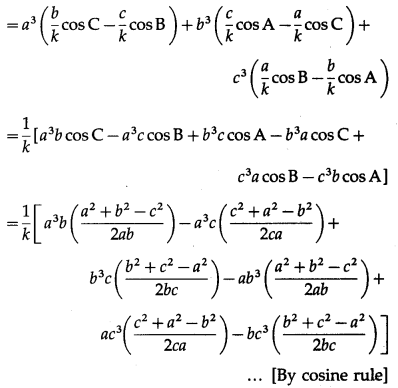
= \(\frac{1}{2 k}\) [a2(a2 + b2 – c2) – a2(a2 + c2 – b2) + b2(b2 + c2 – a2) – b2(a2 + b2 – c2) + c2(c2 + a2 – b2) – c2(b2 + c2 – a2)]
= \(\frac{1}{2 k}\) [a4 + a2b2 – a2c2 – a4 – a2c2 + a2b2 + b4 + b2c2 – a2b2 – a2b2 – b4 + b2c2 + c4 + a2c2 – b2c2 – b2c2 – c4 + a2c2]
= \(\frac{1}{2 k}\)(0) = 0 = RHS.
Question 7.
In ∆ABC, if cot A, cot B, cot C are in A.P. then show that a2, b2, c2 are also in A.P
Solution:
By the sine rule,
\(\frac{\sin \mathrm{A}}{a}\) = \(\frac{\sin \mathrm{B}}{b}\) =\(\frac{\sin \mathrm{C}}{c}\) = k
∴ sin A = ka, sin B = kb, sin C = kc …(1)
Now, cot A, cotB, cotC are in A.P.
∴ cotC – cotB = cotB – cot A
∴ cotA + cotC = 2cotB

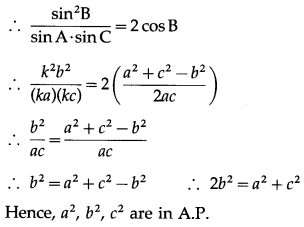
![]()
Question 8.
In ∆ABC, if a cos A = b cos B then prove that the triangle is right angled or an isosceles traingle.
Solution:
By the sine rule,
\(\frac{a}{\sin \mathrm{A}}\) = \(\frac{b}{\sin \mathrm{B}}\) = k
a = k sin A and b = k sin B
∴ a cos A = b cos B gives
k sin A cos A = k sin B cos B
∴ 2 sin A cos A = 2 sin B cos B
∴ sin 2A = sin 2B ∴ sin 2A – sin 2B = 0
∴ 2 cos (A + B)∙sin (A -B) = 0
∴ 2cos (π – C)∙sin(A – B) = 0 … [∵ A + B + C = π]
∴ -2 cos C∙sin (A – B) = 0
∴ cos C = 0 OR sin(A -B) = 0
∴ C = 90° OR A – B = 0
∴ C = 90° OR A = B
∴ the triangle is either rightangled or an isosceles triangle.
Question 9.
With usual notations prove that 2(bc cos A + ac cos B + ab cos C) = a2 + b2 + c2.
Solution:
LHS = 2 (bc cos A + ac cos B + ab cos C)
= 2bc cos A + 2ac cos B + 2ab cos C
= 2bc \(\left(\frac{b^{2}+c^{2}-a^{2}}{2 b c}\right)\) + 2ac\(\left(\frac{c^{2}+a^{2}-b^{2}}{2 c a}\right)\) + 2ab\(\left(\frac{a^{2}+b^{2}-c^{2}}{2 a b}\right)\) …(By cosine rule]
= b2 + c2 – a2 + c2 + a2 – b2 + a2 + b2 – c2 = a2 + b2 + c2 = RHS.
![]()
Question 10.
In △ABC, if a = 18, b = 24, c = 30 then find the values of
(i) cos A
Solution:
Given : a = 18, b = 24 and c = 30
∴ 2s = a + b + c = 18 + 24 + 30 = 72 ∴ s = 36
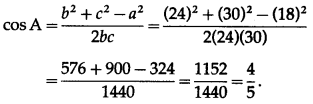
(ii) sin\(\frac{A}{2}\)
Solution:
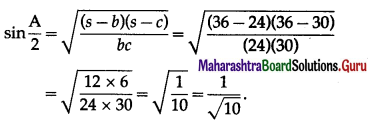
(iii) cos\(\frac{A}{2}\)
Solution:
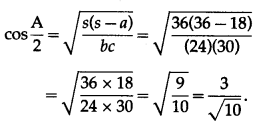
![]()
(iv) tan\(\frac{A}{2}\)
Solution:
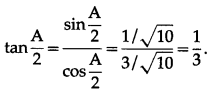
(v) A(△ABC)
Solution:

(iv) sin A.
Solution:
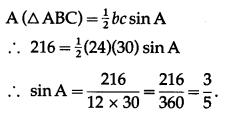
Question 11.
In △ABC prove that (b + c – a) tan \(\frac{A}{2}\) = (c + a – b) tan\(\frac{B}{2}\) = (a + b – c) tan\(\frac{C}{2}\).
Solution:
(b + c – a) tan \(\frac{A}{2}\)
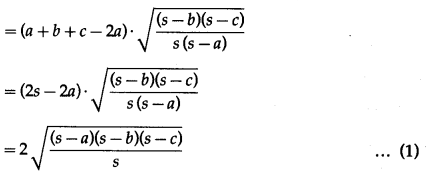

![]()
Question 12.
In △ABC prove that sin \(\frac{A}{2}\)∙sin \(\frac{A}{2}\)∙sin \(\frac{A}{2}\) = \(\frac{[A(\triangle A B C)]^{2}}{a b c s}\)
Solution:
LHS = sin \(\frac{A}{2}\)∙sin \(\frac{B}{2}\)∙sin \(\frac{C}{2}\)