Maharashtra Board Class 11 Chemistry Solutions Chapter 10 States of Matter

Balbharti Maharashtra State Board 11th Chemistry Textbook Solutions Chapter 10 States of Matter Textbook Exercise Questions and Answers.

Maharashtra State Board 11th Chemistry Solutions Chapter 10 States of Matter

1. Select and write the most appropriate alternatives from the given choices.

Question A.
The unit of viscosity is
a. dynes
b. newton
c. gram
d. poise
Answer:
d. poise

Question B.
Which of the following is true for 2 moles of an ideal gas?
a. PV = nRT
b. PV = RT
c. PV = 2RT
d. PV = T
Answer:
c. PV = 2RT

Question C.
Intermolecular forces in liquid are
a. greater than gases
b. less than solids
c. both a and b
d. greater than solids
Answer:
c. both a and b

Question D.
Interactive forces are ………. in ideal gas.
a. nil
b. small
c. large
d. same as that of real gases
Answer:
a. nil

Question E.
At constant temperature the pressure of 22.4 dm³ volume of an ideal gas was increased from 10⁵ kPa to 210 kPa, New volume could be-
a. 44.8 dm³
b. 11.2 dm³
c. 22.4 dm³
d. 5.6 dm³
Answer:
b. 11.2 dm³

2. Answer in one sentence.

Question A.
Name the term used for mixing of different gases by random molecular motion and ferquent collision.
Answer:
The mixing of different gases by random molecular motion and frequent collision is called diffusion.

Question B.
The pressure that each individual gas would exert if it were alone in the container, what do we call it as ?
Answer:
The pressure that each individual gas would exert if it were alone in the container is called as partial pressure.

Question C.
When a gas is heated the particles move more quickly. What is the change in volume of a heated gas if the pressure is kept constant ?
Answer:
The volume of the gas increases on heating if pressure is kept constant.

Question D.
A bubble of methane gas rises from the bottom of the North sea. What will happen to the size of the bubble as it rises to the surface ?
Answer:
According to Boyle’s law, the size of the bubble of methane gas increases as it rises to the surface.

Question E.
Convert the following temperatures from degree celcius to kelvin.
a. -15° C
b. 25° C
c. -197° C
d. 273° C
Answer:
a. T(K) = t°C +273.15
∴ T(K) = -15 °C + 273.15 = 258.15 K
b. T(K) = t°C +273.15
∴ T(K) = 25 °C + 273.15 = 298.15 K
c. T(K) = t°C + 273.15
∴ T(K) = -197 °C + 273.15 = 76.15 K
d. T(K) = t°C + 273.15
∴ T(K) = 273 °C + 273.15 = 546.15 K

Question F.
Convert the following pressure values into Pascals.
a. 10 atmosphere
b. 1 kPa.
c. 107000 Nm^-2
d. 1 atmosphere
Answer:
a. 10 atmosphere:
1 atm = 101325 Pa
∴ 10 atm = 1013250 Pa
= 1.01325 × 10⁶ Pa

b. 1 kPa:
1 kPa = 1000 Pa

c. 107000 N m^-2:
1 N m^-2 = 1 Pa
∴ 107000 Nm^-2 = 107000 Pa
= 1.07 × 10⁵ Pa

d. 1 atmosphere:
1 atm = 101325 Pa
= 1.01325 × 10⁵ Pa

Question G.
Convert:
a. Exactly 1.5 atm to pascals
b. 89 kPa to newton per square metre (N m^-2)
c. 101.325 kPa to bar
d. -100 °C to Kelvin
e. 0.124 torr to standard atmosphere
Answer:
a. Exactly 1.5 atm to pascals:
1 atm = 101325 Pa
∴ 1.5 atm = 1.5 × 101325
= 151987.5 Pa

b. 89 kPa to newton per square metre (N m^-2):
1 Pa = 1 N m^-2 and 1 Pa = 10^-3 kPa
∴ 10^-3 kPa = 1 N m^-2
∴ 89 kPa = \(\frac{1 \times 89}{10^{-3}}\) N m^-2 = 89000 N m^-2

c. 101.325 kPa to bar:
1 bar = 1.0 × 10⁵ Pa
= 1.0 × 10² k Pa
∴ 100 kPa = 1 bar
∴ 101.325 kPa = \(\frac{1 \times 101.325}{100}\)
= 1.01325 bar

d. -100 °C to Kelvin:
T(K) = t °C + 273.15
∴ T(K) = (- 100 °C) + 273.15 = 173.15 K

e. 0.124 torr to standard atmosphere:
1 atm = 760 torr
∴ 1 torr = \(\frac {1}{760}\)atm
∴ 0.124 torr = 0.124 × \(\frac {1}{760}\)
= 1.632 × 10^-4 atm

Question H.
If density of a gas is measured at constant temperature and pressure then which of the following statement is correct ?
a. Density is directly proportional to molar mass of the gas.
b. Greater the density greater is the molar mass of the gas.
c. If density, temperature and pressure is given ideal gas equation can be used to find molar mass.
d. All the above statements are correct.
Answer:
d. All the above statements are correct.

Question I.
Observe the following conversions.

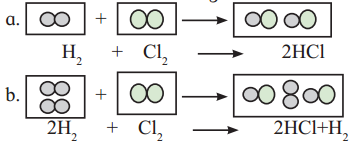
Which of the above reactions is in accordance with the priciple of stoichiometry ?
Answer:
Both the reactions are in accordance with the principle of stoichiometry.
In the first reaction, both the reactants are completely consumed to form product according to reaction stoichiometry.
1 mol hydrogen + 1 mol chlorine → 2 mol hydrogen chloride
In the second reaction, chlorine is the limiting reagent and it is completely consumed to form hydrogen chloride. Excess hydrogen remains unreacted at the end of the reaction. This reaction also follows principle of stoichiometry.
2 mol hydrogen + 1 mol chlorine → 2 mol hydrogen chloride + 1 mol hydrogen

Question J.
Hot air balloons float in air because of the low density of the air inside the balloon. Explain this with the help of an appropriate gas law.

Answer:
The working of hot air balloon can be explained with the help of Charles’ law. According to Charles’ law, at constant pressure, the volume of a fixed amount of a gas varies directly with the temperature. This means that as the temperature increases, the air inside the balloon expands and occupies more volume. Thus, hot air inside the balloon is less dense than the surrounding cold air. This causes the hot air balloon to float in air.

3. Answer the following questions.

Question A.
Identify the gas laws from the following diagrams.

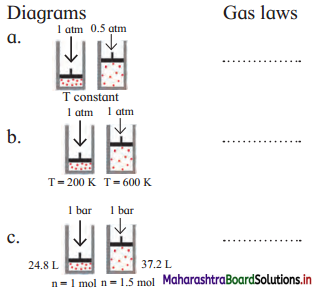
Answer:
a. Boyle’s law
b. Charles’ law
c. Avogadro’s law [Note: Assuming, T constant]

Question B.
Consider a sample of a gas in a cylinder with a movable piston.

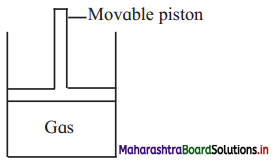
Show digramatically the changes in the position of piston, if
a. Pressure is increased from 1.0 bar to 2.0 bar at constant temperature.
b. Temperature is decreased from 300 K to 150 K at constant pressure
c. Temperature is decreased from 400 K to 300 K and pressure is decreased from 4 bar to 3 bar.
Answer:

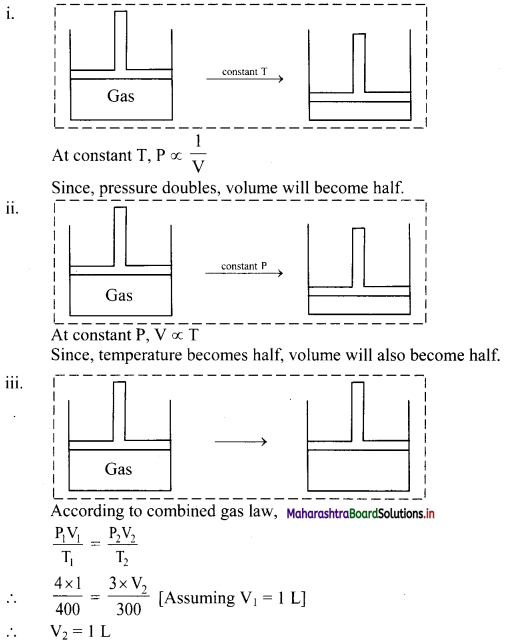
Thus, the volume of the gas remains the same.
Hence, there will be no change in the position of the piston.

Question D.
List the characteristic physical properties of the gases.
Answer:
Characteristic physical properties of the gases:

• Gases are lighter than solids and liquids (i.e., possess lower density).
• Gases do not possess a fixed volume and shape. They occupy entire space available and take the shape of the container.
• Gas molecules are widely separated and are in continuous, random motion. Therefore, gases exert pressure equally in all directions due to collision of gas molecules, on the walls of the container.
• In case of gases, intermolecular forces are weakest.
• Gases possess the property of diffusion, which is a spontaneous homogeneous inter mixing of two or more gases.
• Gases are highly compressible.

Question E.
Define the terms:
a. Polarizability
b. Hydrogen bond
c. Aqueous tension
d. Dipole moment
Answer:
a. Polarizability is defined as the ability of an atom or a molecule to form momentary dipoles, that means, the ability of the atom or molecule to become polar by redistributing its electrons.

b. The electrostatic force of attraction between positively polarised hydrogen atom of one molecule and a highly electronegative atom (which may be negatively charged) of other molecule is called as hydrogen bond.

c. The pressure exerted by saturated water vapour is called aqueous tension.

d. Dipole moment (p) is the product of the magnitude of the charge (Q) and the distance between the centres of positive and negative charge (r). It is designated by a Greek Letter (p) and its unit is Debye (D).

Question F.
Would it be easier to drink water with a straw on the top of the Mount Everest or at the base ? Explain.
Answer:
When you drink through a straw, the pressure inside the straw reduces (as the air is withdraw by mouth) and the liquid is pushed up to your mouth by atmospheric pressure. Thus, drinking with a straw makes use of pressure difference to force the liquid into your mouth. So, if the pressure difference is less it will be difficult to drink through a straw. On the top of the Mount Everest, atmospheric pressure is very low. Hence, it will be difficult to drink water with a straw on the top of Mount Everest as compared to at the base.

Question G.
Identify type of the intermolecular forces in the following compounds.
a. CH₃ – OH
b. CH₂ = CH₂
c. CHCl₃
d. CH₂Cl₂
Answer:
a. Hydrogen bonding (dipole-dipole attraction) and London dispersion forces
b. London dispersion forces
c. Dipole-dipole interactions and London dispersion forces
d. Dipole-dipole interactions and London dispersion forces

Question H.
Name the types of intermolecular forces present in Ar, Cl₂, CCl₄ and HNO₃.
Answer:
a. Ar: London dispersion forces
b. Cl₂: London dispersion forces
c. CCl₄: London dispersion forces
d. HNO₃: Flydrogen bonding (dipole-dipole attraction) and London dispersion forces.

Question I.
Match the pairs of the following :

	A		B
a.	Boyle’s law	i.	At constant pressure and volume
b.	Charles’ law	ii.	At constant temperature
		iii.	At constant pressure

Answer:
a – ii,
b – iii

Question J.
Write the statement for :
(a) Boyle’s law
(b) Charles’ law
Answer:
a. Statement of Boyle’s law: For a fixed mass (number of moles ‘n’) of a gas at constant temperature, the pressure (P) of the gas is inversely proportional to the volume (V) of the gas.
OR
At constant temperature, the pressure of fixed amount (number of moles) of a gas varies inversely with its volume.

b. Statement for Charles’ law:
‘At constant pressure, the volume of a fixed mass of a gas is directly proportional to its temperature in Kelvin.

Question K.
Differentiate between Real gas and Ideal gas.
Answer:
Ideal gas:

1. Strictly obeys Boyle’s and Charles’ law.
   \(\frac{\mathrm{PV}}{\mathrm{nRT}}\) = 1
2. Molecules are perfectly elastic.
3. No attraction or repulsion between the gas molecules i.e. collision without loss of kinetic energy (K.E.)
4. Actual volume of the gas molecules is negligible as compared to total volume of the gas.
5. Ideal gases cannot be liquified even at low temperature but continues to obey Charles’ law and finally occupies zero volume at 0 K.
6. Practically, ideal gas does not exist.

Real gas:

1. Shows deviation from Boyle’s and Charles’ law at high pressure and temperature, i.e. obeys Boyle’s law and Charles’ law at low pressure and high temperature. \(\frac{\mathrm{PV}}{\mathrm{nRT}}\) ≠ 1
2. Molecules are not perfectly elastic.
3. Intermolecular attraction is present, hence collision takes place with loss of kinetic energy.
4. Actual volume of individual gas molecule is significant at high pressure and low- temperature.
5. Real gases undergo liquefaction at low’ temperature when cooled and compressed.
6. Gases that exist in nature like H₂, O₂, CO₂, N₂, He, etc. are real gases.

4. Answer the following questions

Question A.
State and write mathematical expression for Dalton’s law of partial pressure and explain it with suitable example.
Answer:
i. Statement: The total pressure of a mixture of two or more non-reactive gases is the sum of the partial pressures of the individual gases in the mixture.
ii. Explanation:
Dalton’s law can be mathematically expressed as:
P_Total = P₁ + P₂ + P₃ …(at constant T and V)
where, P_Total is the total pressure of the mixture and P₁, P₂, P₃, … are the partial pressures of individual gases 1, 2, 3, … in the mixture.
For example, consider two non-reactive gases A and B. On mixing the two gases, pressure exerted by individual gas A in the mixture of both the gases is called partial pressure of gas A (say P₁). Likewise, partial pressure of gas B is P₂. According to Dalton’s law, total pressure of the mixture of gas A and B at constant T and V will be given as:
P_Total = P₁ + P₂

iii. Schematic illustration of Dalton’s law of partial pressures:

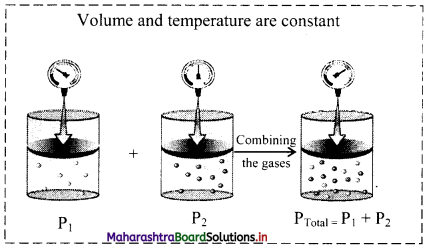
Question B.
Derive an Ideal gas equation. Mention the terms involved in it. Also write how it is utilised to obtain combined gas law.
Answer:
According to Boyle’s law,
V ∝ \(\frac{1}{\mathrm{P}}\) (at constant T and n) ……….(1)
According to Charles’ law,
V ∝ T (at constant P and n) ……(2)
According to Avogadro’s law,
V ∝ n (at constant P and T) ……(3)
Combining relations (1), (2) and (3), we get
V ∝ \(\frac{\mathrm{nT}}{\mathrm{P}}\)
Converting this proportionality into an equation by introducing a constant of proportionality (‘R’ known as gas constant), we get
∴ V = \(\frac{\mathrm{nRT}}{\mathrm{P}}\)
On rearranging the above equation, we get
PV = nRT
where,
P = Pressure of gas,
V = Volume of gas,
n = number of moles of gas,
R = Gas constant,
T = Absolute temperature of gas.
This is the ideal gas equation or equation of state.
[Note: In the ideal gas equation, R is called gas constant or universal gas constant, whose value is same for all the gases. In this equation, if three variables are known, fourth can be calculated. The equation describes the state of an ideal gas. Hence, it is also called as equation of state.]

The ideal gas equation is written as PV = nRT …(1)
On rearranging equation (1), we get,

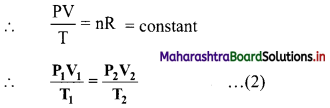
The ideal gas equation used in this form is called combined gas law.

Question C.
With the help of graph answer the following –

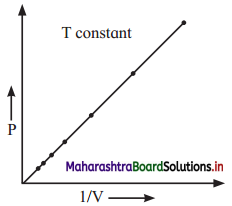
At constant temperature,
a. Graph shows relation between pressure and volume. Represent the relation mathematically.
b. Identify the law.
c. Write the statement of law.
Answer:
a. P ∝ \(\frac{1}{\mathrm{~V}}\)
b. The graph represents Boyle’s law as it gives relation between pressure and volume at constant temperature.
c. Statement of Boyle’s law: For a fixed mass (number of moles ‘n’) of a gas at constant temperature, the pressure (P) of the gas is inversely proportional to the volume (V) of the gas.
OR
At constant temperature, the pressure of fixed amount (number of moles) of a gas varies inversely with its volume.

Question D.
Write Postulates of kinetic theory of gases.
Answer:
Postulates of kinetic theory of gases:

• Gases consist of tiny particles (molecules or atoms).
• On an average, gas molecules remain far apart from each other. Therefore, the actual volume of the gas molecules is negligible as compared to the volume of the container. Hence, gases are highly compressible.
• The attractive forces between the gas molecules are negligible at ordinary temperature and pressure. As a result, gas expands to occupy entire volume of the container.
• Gas molecules are in constant random motion and move in all possible directions in straight lines. They collide with each other and with the walls of the container.
• Pressure of the gas is due to the collision of gas molecules with the walls of the container.
• The collisions of the gas molecules are perfectly elastic in nature, which means that the total energy of the gaseous particle remains unchanged after collision.
• The different gas molecules move with different velocities at any instant and hence have different kinetic energies. However, the average kinetic energy of the gas molecules is directly proportional to the absolute temperature.

Question E.
Write a short note on
a. Vapour pressure.
b. Surface tension
c. Viscosity.
Answer:
a. Vapour pressure:

• Molecules of liquid have tendency to escape from its surface to form vapour above it. This called evaporation.
• When a liquid is placed in a closed container, the liquid undergoes evaporation and vapours formed undergo condensation.
• At equilibrium, the rate of evaporation and rate of condensation are equal.
• The pressure exerted by the vapour in equilibrium with the liquid is known as saturated vapour pressure or simply vapour pressure.
• Vapour pressure is measured by means of a manometer.
• The most common unit for vapour pressure is torr. 1 torr = 1 mm Hg.

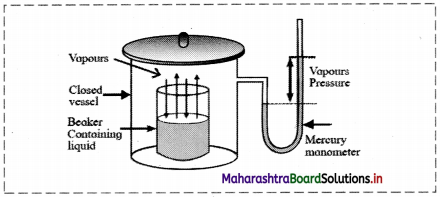
[Note: i. The vapour pressure of water is also called aqueous tension.
ii. Water has a vapour pressure of approximately 20 torr at room temperature.]

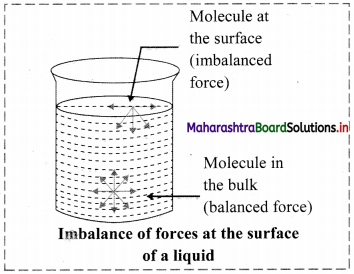
b. Surface tension:

• The particles in the bulk of liquid are uniformly attracted in all directions and the net force acting on the molecules present inside the bulk is zero.
• But the molecules at the surface experience a net attractive force towards the interior of the liquid, or the forces acting on the molecules on the surface are imbalanced.
• Therefore, liquids have tendency to minimize their surface area and the surface acts as a stretched membrane.
• The force acting per unit length perpendicular to the line drawn on the surface of liquid is called surface tension.
• Unit: Surface tension is measured in SI unit, N m^-1 and is denoted by Greek letter ‘γ’

c. Viscosity:
i. Liquids (fluids) have tendency to flow.
ii. Viscosity measures the magnitude of internal friction in a liquid or fluid to flow as measured by the force per unit area resisting uniform flow.
iii. Different layers of a liquid flow with different velocity. This called laminar flow. Here, the layers of molecules in the immediate contact of the fixed surface remains stationary. The subsequent layers slip over one another. Strong intermolecular forces obstruct the layers from slipping over one another, resulting in a friction between the layers.
iv. Viscosity is defined as the force of friction between the successive layers of a flowing liquid. It is also the resistance to the flow of a liquid.
v. When a liquid flow through a tube, the central layer has the highest velocity, whereas the layer along the inner wall in the tube remains stationary. This is a result of the viscosity of a liquid. Hence, a velocity gradient exists across the cross-section of the tube.

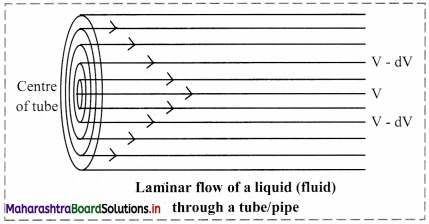
vi. Viscosity is expressed in terms of coefficient of viscosity, ‘η’ (Eta). The SI unit of viscosity coefficient is N s m^-2 (newton second per square meter). In CGS system, the unit (η) is measured in poise.
1 poise = 1 g cm^-1 s^-1 = 10^-1 kg m^-1 s^-1

5. Solve the following

Question A.
A balloon is inflated with helium gas at room temperature of 25 °C and at 1 bar pressure when its initial volume is 2.27L and allowed to rise in air. As it rises in the air external pressure decreases and the volume of the gas increases till finally it bursts when external pressure is 0.3bar. What is the limit at which volume of the balloon can stay inflated ?
Answer:
Given: P₁ = Initial pressure = 1 bar
V₁ = Initial volume = 2.27 L
P₂ = Final pressure = 0.3 bar
To find: V₂ = Final volume
Formula: P₁V₁ = P₂V₂ (at constant n and T)
Calculation: According to Boyle’s law,
P₁V₁ = P₂V₂ (at constant n and T)
∴ V₂ = \(\frac{P_{1} V_{1}}{P_{2}}=\frac{1 \times 2.27}{0.3}\) = 7.566667 L ≈ 7.567 L
Ans: The balloon can stay inflated below the volume of 7.567 L.

Question B.
A syringe has a volume of 10.0 cm³ at pressure 1 atm. If you plug the end so that no gas can escape and push the plunger down, what must be the final volume to change the pressure to 3.5 atm?

Answer:
Given: P₁ = Initial pressure = 1 atm
V₁ = Initial volume = 10.0 cm³
P₂ = Final pressure = 3.5 atm
To find: V₂ = Final volume
Formula: P₁V₁ = P₂V₂ (at constant n and T)
Calculation: According to Boyle’s law,
P₁V₁ = P₂V₂ (at constant n and T)
∴ V₂ = \(\frac{\mathrm{P}_{1} \mathrm{~V}_{1}}{\mathrm{P}_{2}}=\frac{1 \times 10.0}{3.5}\)
= 2.857 L
Ans: The final volume of the gas in the syringe is 2.857 L.

Question C.
The volume of a given mass of a gas at 0°C is 2 dm³. Calculate the new volume of the gas at constant pressure when
a. The temperature is increased by 10°C.
b.The temperature is decreased by 10°C.
Answer:
Given: T₁ = Initial temperature = 0 °C = 0 + 273.15 = 273.15 K,
V₁ = Initial volume = 2 dm³
a. T₂ = Final temperature = 273.15 K + 10 = 283.15 K
b. T₂ = Final temperature = 273.15 K – 10 = 263.15 K
To find: V₂ = Final volume in both the cases
Formula: \(\frac{\mathrm{V}_{\mathrm{l}}}{\mathrm{T}_{1}}=\frac{\mathrm{V}_{2}}{\mathrm{~T}_{2}}\) (at constant n and P)
Calculation: According to Charles’ law,

Ans: The new volume of a given mass of gas is:
a. 2.073 dm³
b. 1.927 dm³

Question D.
A hot air balloon has a volume of 2800 m³ at 99 °C. What is the volume if the air cools to 80 °C?

Answer:
Given: V₁ = Initial volume = 2800 m³, T₁ = Initial temperature = 99 °C = 99 + 273.15 = 372.15 K,
T₂ = Final temperature = 80 °C = 80 + 273.15 K = 353.15 K
To find: V₂ = Final volume
Formula: = \(\frac{\mathrm{V}_{1}}{\mathrm{~T}_{1}}=\frac{\mathrm{V}_{2}}{\mathrm{~T}_{2}}\) (at constant n and P)
Calculation: According to Charles’ law,
\(\frac{\mathrm{V}_{1}}{\mathrm{~T}_{1}}=\frac{\mathrm{V}_{2}}{\mathrm{~T}_{2}}\) (at constant n and P)
∴ \(\mathrm{V}_{2}=\frac{\mathrm{V}_{1} \mathrm{~T}_{2}}{\mathrm{~T}_{1}}=\frac{2800 \times 353.15}{372.15}=\mathbf{2 6 5 7 \mathrm { m } ^ { 3 }}\)
Ans: The volume of the balloon when the air cools to 80 °C is 2657 m³.

Question E.
At 0 °C, a gas occupies 22.4 liters. How nuch hot must be the gas in celsius and in kelvin to reach volume of 25.0 literes?
Answer:
V₁ = Initial volume of the gas = 22.4 L,
T₁ = Initial temperature = 0 + 273.15 = 273.15 K,
V₂ = Final volume = 25.0 L
To find: T₂ = Final temperature in Celsius and in Kelvin

Ans: The temperature of the gas must be 31.7 °C or 304.9 K.

Question F.
A 20 L container holds 0.650 mol of He gas at 37 °C at a pressure of 628.3 bar. What will be new pressure inside the container if the volume is reduced to 12 L. The temperature is increased to 177 °C and 1.25 mol of additional He gas was added to it?
Answer:
Given: V₁ = Initial volume = 20 L, n₁ = Initial number of moles = 0.650 mol
P₁ = Initial pressure = 628.3 bar
T₁ = Initial temperature = 37 °C = 37 + 273.15 K = 310.15 K
n₂ = Final number of moles = 0.650 + 1.25 = 1.90 mol, V₂ = Final volume = 12 L
T₂ = Final temperature = 177 °C = 177 + 273.15 K = 450.15 K, R = 0.0821 L atm K^-1 mol^-1
To find: P₂ = Final pressure
Formula: PV = nRT
Calculation: According to ideal gas equation,
P₂V₂ = n₂RT₂.
∴ \(\mathrm{P}_{2}=\frac{\mathrm{n}_{2} \mathrm{RT}_{2}}{\mathrm{~V}_{2}}=\frac{1.90 \times 0.0821 \times 450.15}{12}=\mathbf{5 . 8 5 2} \mathrm{atm}\)
Ans: The final pressure of the gas is 5.852 atm.
[Note: In the above numerical, converting the pressure value to different units, we get: 5.852 atm = 4447.52 torr = 5.928 bar]

Question G.
Nitrogen gas is filled in a container of volume 2.32 L at 32 °C and 4.7 atm pressure. Calculate the number of moles of the gas.
Answer:
Given: V = 2.32 L, P = 4.7 atm, T = 32 °C = 32 + 273.15 K = 305.15 K
R = 0.0821 L atm K^-1 mol^-1
To find: n = number of moles of gas
Formula: PV = nRT
Calculation: According to ideal gas equation,
PV = nRT
∴ \(\mathrm{n}=\frac{\mathrm{PV}}{\mathrm{RT}}=\frac{4.7 \times 2.32}{0.0821 \times 305.15}=\mathbf{0 . 4 3 5} \mathrm{moles}\)
Ans: Number of moles of N₂ gas in the given volume is 0.435 moles.

Question H.
At 25 °C and 760 mm of Hg pressure a gas occupies 600 mL volume. What will be its pressure at the height where temperature is 10 °C and volume of the gas 640 mL ?
Answer:
Given: V₁ = Initial volume = 600 mL, V₂ = Final volume = 640 mL
P₁ = Initial pressure = 760 mm Hg
T₁ = Initial temperature = 25 °C = 25 + 273.15 K = 298.15 K
T₂ = Final temperature = 10 °C = 10 + 273.15 K = 283.15 K
P₂ = Final pressure
Formula: \(\frac{\mathrm{P}_{1} \mathrm{~V}_{1}}{\mathrm{~T}_{1}}=\frac{\mathrm{P}_{2} \mathrm{~V}_{2}}{\mathrm{~T}_{2}}\)
Calculation: According to combined gas law.

Ans: The final pressure of a gas is 676.654 mm Hg.

Question I.
A neon-dioxygen mixture contains 70.6 g dioxygen and 167.5g neon. If pressure of the mixture of the gases in the cylinder is 25 bar. What is the partial pressure of dioxygen and neon in the mixture?
Answer:
Given: m_O2 = 70.6 g, m_Ne = 167.5 g,
P_Total = 25 bar
To find: Partial pressure of each gas
Formula: P₁ = x₁ × P_Total
Calculation: Determine number of moles (n) of each gas using formula: n = \(\frac{\mathrm{m}}{\mathrm{M}}\)

Ans: The partial pressure of dioxygen and neon are 5.2 bar and 19.8 bar respectively.

Question J.
Calculate the pressure in atm of 1.0 mole of helium in a 2.0 dm³ container at 20.0 °C.
Answer:
Given: n = number of moles = 1.0 mol, V = volume = 2.0 dm³
T = Temperature = 20.0 °C = 20.0 + 273.15 K = 293.15 K
R = 0.0821 L atm K^-1 mol^-1
To find: Pressure (P)
Formula: PV = nRT
Calculation: According to ideal gas equation,

Ans: The pressure of the given helium gas is 12.03 atm.

Question K.
Calculate the volume of 1 mole of a gas at exactly 20 °C at a pressure of 101.35 kPa.
Answer:
Given: n = number of moles = 1 mol, P = pressure = 101.35 kPa = 1.00025 atm ≈ 1 atm
T = Temperature = 20 °C = 20 + 273.15 K = 293.15 K
R = 0.0821 dm³ atm K^-1 mol^-1
To find: Volume (V)
Formula: PV = nRT
Calculation: According to ideal gas equation,
PV = nRT

Ans: The volume of the given gas is 24.07 dm³.

Question L.
Calculate the number of molecules of methane in 0.50 m³ of the gas at a pressure of 2.0 × 10² kPa and a temperature of exactly 300 K.
Answer:
V = 0.5 m³, P = 2.0 × 10² kPa = 2.0 × 10⁵ Pa
T = 300 K, R = 8.314 J K^-1 mol^-1
To find: Number of molecules of methane gas
Formula: PV = nRT
Calculation: According to ideal gas equation,
n = \(\frac{\mathrm{PV}}{\mathrm{RT}}=\frac{2.0 \times 10^{5} \times 0.5}{8.314 \times 300}=40 \mathrm{~mol}\)
Number of molecules = n × NA = 40 × 6.022 × 10²³ = 2.4088 × 10²³ ≈ 2.409 × 10²⁵
Ans: The number of molecules of methane gas present is 2.409 × 10²⁵ molecules.

11th Chemistry Digest Chapter 10 States of Matter Intext Questions and Answers

Do you know? (Textbook Page No. 140)

Question 1.
Consider three compounds: H₂S, H₂Se and H₂O. Identify which has the highest boiling point. Justify.
Answer:
Among the three compounds H₂O, H₂S and H₂Se, the first one, H₂O has the smallest molecular mass. But it has the highest B.P. of 100 °C. B.P. of H₂S is -60 °C and of H₂Se is -41.25 °C. The extraordinary high B.P. of H₂O is due to very strong hydrogen bonding even though it has the lowest molecular mass.

Can you tell? (Textbook Page No. 140)

Question i.
What are the various components present in the atmosphere?
Answer:
Various components present in the atmosphere are as follows:
a. Nitrogen (78%)
b. Oxygen (21%)
c. Carbon dioxide and other gases (0.03%)
d. Inert gases (mainly argon) (0.97%)
e. Traces of water vapour

Question ii.
Name five elements and five compounds those exist as gases at room temperature.
Answer:
Five elements and five compounds that exist as gases at room temperature are as follows:

No.	Elements
a.	Nitrogen
b.	Oxygen
c.	Hydrogen
d.	Chlorine
e.	Argon

No.	Compounds
a.	Carbon dioxide
b.	Carbon monoxide
c.	Nitrogen dioxide
d.	Sulphur dioxide
e.	Methane

Just think. (Textbook Page No. 140)

Question 1.
What is air?
Answer:

• Air is a mixture of various gases.
• One cannot see air but can feel the cool breeze.
• The composition of air by volume is around 78 percent N₂, 21 percent O₂ and 1 percent other gases including CO₂.

Use your brainpower. (Textbook Page No. 141)

Question 1.
Find the unit in which car-tyre pressure is measured.
Answer:
Car-tyre pressure is measured in the units of pounds per square inch (psi) or Newton per metre square (N m^-2).

Do you know? (Textbook Page No. 142)

Question 1.
How does a bicycle pump work?
Answer:
A bicycle pump works on Boyle’s law. Pushing a bicycle pump squashes the same number of particles into a smaller volume. This squashing means particles hit the walls of the pump more often, increasing the pressure. The increased pressure of a gas can be felt on palm by pushing in the piston of a bicycle pump.

Internet my friend (Textbook Page No. 143)

Question 1.
i. Watch Boyle’s law experiment.
ii. Find applications of Boyle’s law.
iii. Try to study how Boyle’s law helps in ‘scuba-diving’ i.e., importance of Boyle’s law in scuba diving an exhilarating sport.
Answer:
i. Students can refer to ‘Boyle’s law experiment’ on YouTube channel of ‘Socratica’.
ii. a. Syringes: When the plunger of a syringe is pulled back out, it causes the volume of the gas inside it to increase due to the reduction of pressure. This creates a vacuum in the syringe, which is constantly trying to adjust the pressure back to normal. However, since the only substance available, such as the blood or medication, is on the other side of the needle, this liquid is sucked into the vacuum, increasing the pressure and decreasing the volume of the gas. When we push the plunger back down, the pressure again increases, lowering the volume inside the syringe, and pushing the fluid out.

b. Respiration: Boyle’s law is essential for the human breathing process. When person breathes in, his/her lung volume increases and the pressure within decreases. Since air always moves from areas of high pressure to areas of low pressure, air is drawn into the lungs. The opposite happens when person exhales. Since the lung volume decreases, the pressure within increases, forcing the air out of the lungs

c. Storage of Gases: Many industries store gases under high pressure. This allows the gas to be stored at a low volume, saving plenty of storage space.
[Note: Students are expected to search more on the internet about various other applications of Boyle’s law on their own.]

iii. Importance of Boyle’s law in scuba diving:
a. Boyle’s law affects scuba diving in many ways.
b. It explains the role of pressure in the aquatic environment.
c. As divers descend, the water pressure surrounding them increases, causing air in their body and equipment to have a smaller volume. As the divers ascend, water pressure decreases, causing their body and equipment to expand to acquire a greater volume.
d. Furthermore, it is crucial that scuba divers never attempt to hold their breath when immersed in water.
e. According to Boyle’s law, if divers attempt this when they ascend to a body of water of less pressure, then the air that is trapped in their lungs will over-expand and rupture. This is known as Pulmonary Barotrauma. Thus, it is important for scuba divers to exhale as they ascend because the external pressure increases.
f. Also, if a diver returns to the surface too quickly, dissolved gases in the blood expand and form bubbles, which can get stuck in capillaries and organs (causing the ‘bends’).
[Note: Students are expected to collect additional information their own.]

Just think. (Textbook Page No. 144)

Question i.
Why does bicycle tyre burst during summer?
Answer:

• According to Charles’ law, at constant pressure, the volume of a fixed amount of a gas varies directly with the temperature. This means that as the temperature increases, the volume also increases.
• During summer, the temperature of the surrounding air is high. Due to the high temperature, the air inside the tyre gets heated. This will increase the volume of the tyres and it will burst.

Question ii.
Why do the hot air balloons fly high?
Answer:

• According to Charles’ law, at constant pressure, gases expand on heating and become less dense. Thus, hot air is less dense than cold air.
• In a hot air balloon, the air inside it is heated by a burner. Upon heating, the air inside the balloon expands and becomes lighter (less dense) than the cooler air on the outside. This causes the hot air balloon to fly high in air.

Just think. (Textbook Page No. 145)

Question 1.
i. List out various real-life examples of Charles’ law.
ii. Refer and watch Charles’ law experiments.
Answer:
i. Few real-life examples of Charles’ law:
a. Helium balloon: If we fill a helium balloon in a warm or hot room, and then take it into a cold room, it shrinks up and will look like it has lost some of the air inside it. This shows that gases expand on heating and contract on cooling.
b. A bottle of deodorant: If we expose a bottle of deodorant to sunlight and high temperatures, the air molecules inside the bottle will expand which can lead to the bursting of the deodorant bottle. This is another example of Charles’ law.
c. Basketball: You may have noticed that a basketball has less responsive bounce during winter than in summer. This yet another example of Charles’ law. When a basketball is inflated, the air pressure inside it is set to a fixed value. As the temperature falls, the volume of the gas inside the ball also decreases proportionally.
[Note: Students are expected to collect additional real-life examples on their own,]

ii. pi [Note: Students can scan the adjacent QR code to visualize Charles’ law with the aid of a relevant video.]

Use your brainpower. (Textbook Page No. 146)

Question 1.
Why does the pressure in the automobile tyres change during hot summer or winter season?
Answer:

• According to Gay-Lussac’s law, at constant volume, pressure of a fixed amount of a gas is directly proportional to its absolute temperature.
• During hot summer, the temperature of automobile tyre increases faster. Consequently, the air inside the tyre gets heated and the gas molecules starts moving faster.
• As the volume of the tyre remains constant, the pressure inside it increases.
• During winter, the temperature of automobile tyre decreases. Consequently, the air inside the tyre gets cooled and the gas molecules starts moving much slower and the pressure inside the tyre decreases.

Just think. (Textbook Page No. 149)

Question 1.
Do all pure gases and mixtures of gases obey the gas laws?
Answer:
Yes, the gas laws are also applicable to the mixtures of gases. The measurable properties of a mixture of the gases such as pressure, temperature, volume, and amount of gaseous mixture are all related by an ideal gas law.

Just think. (Textbook Page No. 150)

Question 1.
Where is Dalton’s law applicable?
Answer:
Air is a gaseous mixture of different gases. Dalton’s law is useful for the study of various phenomena in air, for example, air pollution.

Just think. (Textbook Page No. 155)

Question 1.
What makes the oil rise through the wick in an oil lamp?
Answer:
In an oil lamp, oil rises through the wick due to the capillary action. Such a capillary rise of oil is due to the surface tension of oil. The wick acts as a capillary tube. When the wick is placed in oil, the attractive forces between the oil and the inner wall of the capillary (wick) pull the oil up through the wick.