Balbharti Maharashtra State Board 11th Physics Textbook Solutions Chapter 11 Electric Current Through Conductors Textbook Exercise Questions and Answers.
Maharashtra State Board 11th Physics Solutions Chapter 11 Electric Current Through Conductors
1. Choose the correct Alternative.
Question 1.
You are given four bulbs of 25 W, 40 W, 60 W, and 100 W of power, all operating at 230 V. Which of them has the lowest resistance?
(A) 25 W
(B) 40 W
(C) 60 W
(D) 100 W
Answer:
(D) 100 W
Question 2.
Which of the following is an ohmic conductor?
(A) transistor
(B) vacuum tube
(C) electrolyte
(D) nichrome wire
Answer:
(D) nichrome wire
![]()
Question 3.
A rheostat is used
(A) to bring on a known change of resistance in the circuit to alter the current.
(B) to continuously change the resistance in any arbitrary manner and there by alter the current.
(C) to make and break the circuit at any instant.
(D) neither to alter the resistance nor the current.
Answer:
(B) to continuously change the resistance in any arbitrary manner and there by alter the current.
Question 4.
The wire of length L and resistance R is stretched so that its radius of cross-section is halved. What is its new resistance?
(A) 5R
(B) 8R
(C) 4R
(D) 16R
Answer:
(D) 16R
Question 5.
Masses of three pieces of wires made of the same metal are in the ratio 1 : 3 : 5 and their lengths are in the ratio 5 : 3 : 1. The ratios of their resistances are
(A) 1 : 3 : 5
(B) 5 : 3 : 1
(C) 1 : 15 : 125
(D) 125 : 15 : 1
Answer:
(D) 125 : 15 : 1
Question 6.
The internal resistance of a cell of emf 2 V is 0.1 Ω, it is connected to a resistance of 0.9 Ω. The voltage across the cell will be
(A) 0.5 V
(B) 1.8 V
(C) 1.95 V
(D) 3V
Answer:
(B) 1.8 V
Question 7.
100 cells each of emf 5 V and internal resistance 1 Ω are to be arranged so as to produce maximum current in a 25 Ω resistance. Each row contains equal number of cells. The number of rows should be
(A) 2
(B) 4
(C) 5
(D) 100
Answer:
(A) 2
Question 8.
Five dry cells each of voltage 1.5 V are connected as shown in diagram
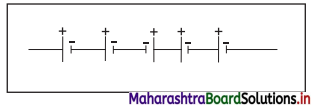
What is the overall voltage with this arrangement?
(A) 0 V
(B) 4.5 V
(C) 6.0 V
(D) 7.5 V
Answer:
(B) 4.5 V
2. Give reasons / short answers
Question 1.
In given circuit diagram two resistors are connected to a 5V supply.
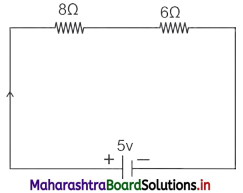
i. Calculate potential difference across the 8Q resistor.
ii. A third resistor is now connected in parallel with 6 Ω resistor. Will the potential difference across the 8 Ω resistor be larger, smaller or same as before? Explain the reason for your answer.
Answer:
Total current flowing through the circuit,
I = \(\frac {V}{R_s}\)
= \(\frac {5}{8+6}\)
= \(\frac {5}{14}\) = 0.36 A
∴ Potential difference across 8 f2 (Vi) = 0.36 × 8
= 2.88 V
![]()
ii. Potential difference across 8 Ω resistor will be larger.
Reason: As per question, the new circuit diagram will be
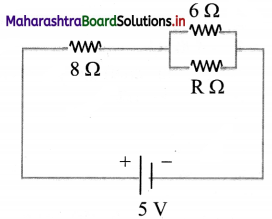
When any resistor is connected parallel to 6 Ω resistance. Then the resistance across that branch (6 Ω and R Ω) will become less than 6 Ω. i.e., equivalent resistance of the entire circuit will decrease and hence current will increase. Since, V = IR, the potential difference across 8 Ω resistor will be larger.
Question 2.
Prove that the current density of a metallic conductor is directly proportional to the drift speed of electrons.
Answer:
i. Consider a part of conducting wire with its free electrons having the drift speed vd in the direction opposite to the electric field \(\vec{E}\).
ii. All the electrons move with the same drift speed vd and the current I is the same throughout the cross section (A) of the wire.
iii. Let L be the length of the wire and n be the number of free electrons per unit volume of the wire. Then the total number of free electrons in the length L of the conducting wire is nAL.
iv. The total charge in the length L is,
q = nALe ………….. (1)
where, e is the charge of electron.
v. Equation (1) is total charge that moves through any cross section of the wire in a certain time interval t.
∴ t = \(\frac {L}{v_d}\) ………….. (2)
vi. Current is given by,
I = \(\frac {q}{t}\) = \(\frac {nALe}{L/v_d}\) ……………. [From Equations (1) and (2)]
= n Avde
Hence
vd = \(\frac {1}{nAe}\)
= \(\frac {J}{ne}\) …………. (∵ J = \(\frac {1}{A}\))
Hence for constant ‘ne’, current density of a metallic conductor is directly proportional to the drift speed of electrons, J ∝ vd.
3. Answer the following questions.
Question 1.
Distinguish between ohmic and non ohmic substances; explain with the help of example.
Answer:
| Ohmic substances | Non-ohmic substances |
| 1. Substances which obey ohm’s law are called ohmic substances. | Substances which do not obey ohm’s law are called non-ohmic substances. |
| 2. Potential difference (V) versus current (I) curve is a straight line. | Potential difference (V) versus current (I) curve is not a straight line. |
| 3. Resistance of these substances is constant i.e. they follow linear I-V characteristic. | Resistance of these substances |
| Expression for resistance is, R = \(\frac {V}{I}\) | Expression for resistance is, R = \(\lim _{\Delta I \rightarrow 0} \frac{\Delta V}{\Delta I}=\frac{d V}{d I}\) |
| Examples: Gold, silver, copper etc. | Examples: Liquid electrolytes, vacuum tubes, junction diodes, thermistors etc. |
![]()
Question 2.
DC current flows in a metal piece of non uniform cross-section. Which of these quantities remains constant along the conductor: current, current density or drift speed?
Answer:
Drift velocity and current density will change as it depends upon area of cross-section whereas current will remain constant.
4. Solve the following problems.
Question 1.
What is the resistance of one of the rails of a railway track 20 km long at 20°C? The cross-section area of rail is 25 cm² and the rail is made of steel having resistivity at 20°C as 6 × 10-8 Ω m.
Answer:
Given: l = 20 km = 20 × 10³ m,
A = 25 cm² = 25 × 10-4 m²,
ρ = 6 × 10-8 Ω m
To find: Resistance of rail (R)
Formula: ρ = \(\frac {RA}{l}\)
Calculation: From formula.
R = ρ\(\frac {l}{A}\)
∴ R = \(\frac {6×10^{-8}×20×10^3}{A}\) = \(\frac {6×4}{5}\) × 10-1
= 0.48 Ω
Question 2.
A battery after a long use has an emf 24 V and an internal resistance 380 Ω. Calculate the maximum current drawn from the battery. Can this battery drive starting motor of car?
Answer:
E = 24 V, r = 380 Ω
i. Maximum current (Imax)
ii. Can battery start the motor?
Formula: Imax = \(\frac {E}{r}\)
Calculation:
From formula,
Imax = \(\frac {24}{380}\) = 0,063 A
As, the value of current is very small compared to required current to run a starting motor of a car, this battery cannot be used to drive the motor.
Question 3.
A battery of emf 12 V and internal resistance 3 O is connected to a resistor. If the current in the circuit is 0.5 A,
i. Calculate resistance of resistor.
ii. Calculate terminal voltage of the battery when the circuit is closed.
Answer:
Given: E = 12 V, r = 3 Ω, I = 0.5 A
To find:
i. Resistance (R)
ii. Terminal voltage (V)
Formulae:
i. E = I (r + R)
ii. V = IR
Calculation: From formula (i),
E = Ir + IR
∴ R = \(\frac {E-Ir}{l}\)
= \(\frac {12-0.5×3}{0.5}\)
= 21 Ω
From formula (ii),
V = 0.5 × 21
= 10.5 V
![]()
Question 4.
The magnitude of current density in a copper wire is 500 A/cm². If the number of free electrons per cm³ of copper is 8.47 × 1022, calculate the drift velocity of the electrons through the copper wire (charge on an e = 1.6 × 10-19 C)
Answer:
Given: J = 500 A/cm² = 500 × 104 A/m²,
n = 8.47 × 1022 electrons/cm³
= 8.47 × 1028 electrons/m³
e = 1.6 × 10-19 C
To Find: Drift velocity (vd)
Formula: vd = \(\frac {J}{ne}\)
Calculation:
From formula,
vd = \(\frac {500×10^4}{8.47×10^{28}×1.6×10^{-19}}\)
= \(\frac {500}{8.47×1.6}\) × 10-5
= {antilog [log 500 – log 8.47 – log 1.6]} × 10-5
= {antilog [2.6990 – 0.9279 -0.2041]} × 10-5
= {antilog [1.5670]} × 10-5
= 3.690 × 101 × 10-5
= 3.69 × 10-4 m/s
Question 5.
Three resistors 10 Ω, 20 Ω and 30 Ω are connected in series combination.
i. Find equivalent resistance of series combination.
ii. When this series combination is connected to 12 V supply, by neglecting the value of internal resistance, obtain potential difference across each resistor.
Answer:
Given: R1 = 10 Ω, R2 = 20 Ω,
R3 = 30 Ω, V = 12 V
To Find: i. Series equivalent resistance(Rs)
ii. Potential difference across each resistor (V1, V2, V3)
Formula: i. Rs = R1 + R2 + R3
ii. V = IR
Calculation:
From formula (i),
Rs = 10 + 20 + 30 = 60 Ω
From formula (ii),
I = \(\frac {V}{R}\) = \(\frac {12}{60}\) = 0.2 A
∴ Potential difference across R1,
V1 = I × R1 = 0.2 × 10 = 2 V
∴ Potential difference across R2,
V2 = 0.2 × 20 = 4 V
∴ Potential difference across R3,
V3 = 0.2 × 30 = 6 V
Question 6.
Two resistors 1 Ω and 2 Ω are connected in parallel combination.
i. Find equivalent resistance of parallel combination.
ii. When this parallel combination is connected to 9 V supply, by neglecting internal resistance, calculate current through each resistor.
Answer:
R1 = 1 kΩ = 10³ Ω,
R2 = 2 kΩ = 2 × 10³ Ω, V = 9 V
To find:
i. Parallel equivalent resistance (Rp)
ii. Current through 1 kΩ and 2 kΩ (I1 and I2)
Formula:
i. \(\frac {1}{R_p}\) = \(\frac {1}{R_1}\) + \(\frac {1}{R_2}\)
ii. V = IR
Calculation: From formula (i),
\(\frac {1}{R_p}\) = \(\frac {1}{10^3}\) + \(\frac {1}{2×10^3}\)
= \(\frac {3}{2×10^3}\)
∴ Rp = \(\frac {2×10^3}{3}\) = 0.66 kΩ
From formula (ii),
I1 = \(\frac {V}{R_1}\) + \(\frac {9}{10^3}\)
= 9 × 10-3 A
= 3 mA
I2 = \(\frac {V}{R_2}\) + \(\frac {9}{2×10^3}\)
= 4.5 × 10-3 A
= 4.5 mA
Question 7.
A silver wire has a resistance of 4.2 Ω at 27°C and resistance 5.4 Ω at 100°C. Determine the temperature coefficient of resistance.
Answer:
Given: R1 =4.2 Ω, R2 = 5.4 Ω,
T, = 27° C, T2= 100 °C
To find: Temperature coefficient of resistance (α)
Formula: α = \(\frac {R_2-R_1}{R_1(T_2-T_1)}\)
Calculation:
From Formula
α = \(\frac {5.4-4.2}{4.2(100-27)}\) = 3.91 × 10-3/°C
![]()
Question 8.
A 6 m long wire has diameter 0.5 mm. Its resistance is 50 Ω. Find the resistivity and conductivity.
Answer:
Given: l = 6 m, D = 0.5 mm,
r = 0.25 mm = 0.25 × 10-3 m, R = 50 Ω
To find:
i. Resistivity (ρ)
ii. Conductivity (σ)
Formulae:
i. ρ = \(\frac {RA}{l}\) = \(\frac {Rπr^2}{l}\)
ii. σ = \(\frac {1}{ρ}\)
Calculation:
From formula (i),
ρ = \(\frac {50×3.142×(0.25×10^{-3})^2}{6}\)
= {antilog [log 50 + log 3.142 + 21og 0.25 -log 6]} × 10-6
= {antilog [ 1.6990 + 0.4972 + 2(1.3979) -0.7782]} × 10-6
= {antilog [2.1962 + 2 .7958 – 0.7782]} × 10-6
= {antilog [0.9920 – 0.7782]} × 10-6
= {antilog [0.2138]} × 10-6
= 1.636 × 10-6 Ω/m
From formula (ii),
σ = \(\frac {1}{1.636×10^{-6}}\)
= 0.6157 × 106
….(Using reciprocal from log table)
= 6.157 × 105 m/Ω
Question 9.
Find the value of resistances for the following colour code.
i. Blue Green Red Gold
ii. Brown Black Red Silver
iii. Red Red Orange Gold
iv. Orange White Red Gold
v. Yellow Violet Brown Silver
Answer:
i. Given: Blue – Green – Red – Gold
To find: Value of resistance
Formula: Value of resistance
= (xy × 10z ± T%)Ω
Calculation:
| Colour | Blue (x) | Green (y) | Red (z) | Gold (T%) |
| Code | 6 | 5 | 2 | ± 5 |
From formula,
Value of resistance = (65 × 10² ± 5%) Ω
Value of resistance = 6.5 kΩ ± 5%
ii. Given: Brown – Black – Red – Silver
To find: Value of resistance
Formula: Value of resistance
= (xy × 10z + T%) Ω
Calculation:
| Colour | Brown (x) | Black (y) | Red (z) | sliver (T%) |
| Code | 1 | 0 | 2 | ± 10 |
From formula,
Value of resistance = (10 × 10² ± 10%) Ω
Value of resistance = 1.0 kΩ ± 10%
iii. Given: Red – Red – Orange – Gold
To find: Value of the resistance
Formula: Value of the resistance
= (xy × 10z ± T%)
Calculation:
| Colour | Red (x) | Red (y) | Orange (z) | Gold (T%) |
| Code | 2 | 2 | 3 | ± 5 |
From formula,
Value of resistance = (22 × 10³ ± 5%)Ω
Value of resistance = 22 kΩ ± 5%
[Note: The answer given above is presented considering correct order of magnitude.]
iv. Given: Orange – White – Red – Gold
To find: Value of the resistance
Formula: Value of the resistance
= (xy × 10z ± T%)
Calculation:
| Colour | Ornage (x) | White (y) | Red (z) | Gold (T%) |
| Code | 3 | 9 | 2 | ± 5 |
From formula,
Value of resistance = (39 × 10² ± 5%) Ω
Value of resistance = 3.9 kΩ ± 5%
v. Given: Yellow-Violet-Brown-Silver
To find: Value of the resistance
Formula: Value of the resistance
= (xy × 10z ± T%)
Calculation:
| Colour | Yellow (x) | violet (y) | Brown (z) | Sliver (T%) |
| Code | 4 | 7 | 1 | ± 10 |
From formula,
Value of resistance = (47 × 10 ± 10%) Ω
Value of resistance = 470 Ω ± 10%
[Note: The answer given above is presented considering correct order of magnitude.]
Question 10.
Find the colour code for the following value of resistor having tolerance ± 10%.
i. 330 Ω
ii. 100 Ω
iii. 47 kΩ
iv. 160 Ω
v. 1 kΩ
Answer:
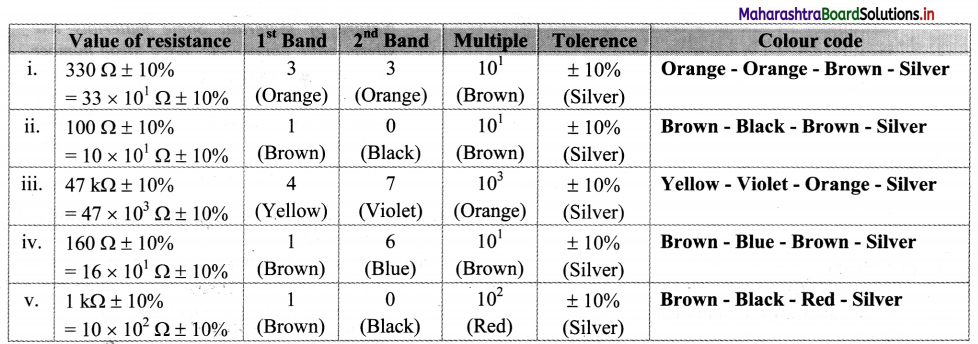
![]()
Question 11.
A current of 4 A flows through an automobile headlight. How many electrons flow through the headlight in a time of 2 hrs?
Answer:
Given: I = 4 A, t = 2 hrs = 2 × 60 × 60 s
To find: Number of electrons (N)
Formula: I = \(\frac {q}{t}\) = \(\frac {Ne}{t}\)
Calculation: As we know, e = 1.6 × 10-19 C
From formula,
N = \(\frac {It}{e}\) = \(\frac {4×2×60×60}{1.6×10^{-19}}\) = 18 × 10-23
Question 12.
The heating element connected to 230 V draws a current of 5 A. Determine the amount of heat dissipated in 1 hour (J = 4.2 J/cal).
Answer:
Given: V = 230 V, I = 5 A,
At = 1 hour = 60 × 60 sec
To find: Heat dissipated (H)
Formula: H = ∆U = I∆tV
Calculation: From formula,
H = 5 × 60 × 60 × 230
= 4.14 × 106 J
Heat dissipated in calorie,
H = \(\frac {4.14×10^6}{4.2}\) = 985.7 × 10³ cal
= 985.7 kcal
11th Physics Digest Chapter 11 Electric Current Through Conductors Intext Questions and Answers
Can you recall? (Textbookpage no. 207)
An electric current in a metallic conductor such as a wire is due to the flow of electrons, the negatively charged particles in the wire. What is the role of the valence electrons which are the outermost electrons of an atom?
Answer:
i. The valence electrons become de-localized when a large number of atoms come together in a metal.
ii. These electrons become conduction electrons or free electrons constituting an electric current when a potential difference is applied across the conductor.
![]()
Internet my friend (Textbook page no. 218)
https://www.britannica.com/science/supercond activity physics
[Students are expected to visit the above-mentioned website and Collect more information about superconductivity.]