Balbharti Maharashtra State Board 11th Physics Textbook Solutions Chapter 6 Mechanical Properties of Solids Textbook Exercise Questions and Answers.
Maharashtra State Board 11th Physics Solutions Chapter 6 Mechanical Properties of Solids
1. Choose the correct answer:
Question 1.
Change in dimensions is known as …………..
(A) deformation
(B) formation
(C) contraction
(D) strain.
Answer:
(A) deformation
Question 2.
The point on stress-strain curve at which strain begins to increase even without increase in stress is called…………
(A) elastic point
(B) yield point
(C) breaking point
(D) neck point
Answer:
(B) yield point
![]()
Question 3.
Strain energy of a stretched wire is 18 × 10-3 J and strain energy per unit volume of the same wire and same cross section is 6 × 10-3 J/m3. Its volume will be………….
(A) 3cm3
(B) 3 m3
(C) 6 m3
(D) 6 cm3
Answer:
(B) 3 m3
Question 4.
……………. is the property of a material which enables it to resist plastic deformation.
(A) elasticity
(B) plasticity
(C) hardness
(D) ductility
Answer:
(C) hardness
Question 5.
The ability of a material to resist fracturing when a force is applied to it, is called……………
(A) toughness
(B) hardness
(C) elasticity
(D) plasticity.
Answer:
(A) toughness
2. Answer in one sentence:
Question 1.
Define elasticity.
Answer:
If a body regains its original shape and size after removal of the deforming force, it is called an elastic body and the property is called elasticity.
Question 2.
What do you mean by deformation?
Answer:
The change in shape or size or both of u body due to an external force is called deformation.
Question 3.
State the SI unit and dimensions of stress.
Answer:
- SI unit: N m-2 or pascal (Pa)
- Dimensions: [L-1M1T-2]
Question 4.
Define strain.
Answer:
Strain:
- Strain is defined as the ratio of change in dimensions of the body to its original dimensions.
Strain = \(\frac{\text { change in dimensions }}{\text { original dimensions }}\) - Types of strain:
- Longitudinal strain,
- Volume strain,
- Shearing strain.
Question 5.
What is Young’s modulus of a rigid body?
Answer:
Young’s modulus (Y): It is the modulus of elasticity related to change in length of an object like a metal wire, rod, beam, etc., due to the applied deforming force.
Question 6.
Why bridges are unsafe after a very long use?
Answer:
A bridge during its use undergoes recurring stress depending upon the movement of vehicles on it. When bridge is used for long time, it loses its elastic strength and ultimately may collapse. Hence, the bridges are declared unsafe after long use.
Question 7.
How should be a force applied on a body to produce shearing stress?
Answer:
A tangential force which is parallel to the top and the bottom surface of the body should be applied to produce shearing stress.
Question 8.
State the conditions under which Hooke’s law holds good.
Answer:
Hooke’s Taw holds good only when a wire/body is loaded within its elastic limit.
Question 9.
Define Poisson’s ratio.
Answer:
Within elastic limit, the ratio of lateral strain to the linear strain is called the Poisson‘s ratio.
![]()
Question 10.
What is an elastomer?
Answer:
A material that can be elastically stretched to a larger value of strain is called an elastomer.
Question 11.
What do you mean by elastic hysteresis?
Answer:
- In case of some materials like vulcanized rubber, when the stress applied on a body decreases to zero, the strain does not return to zero immediately. The strain lags behind the stress. This lagging of strain behind the stress is called elastic hysteresis.
- Below figure shows the stress-strain curve for increasing and decreasing load. It encloses a loop. Area of loop gives the energy dissipated during deformation of a material.
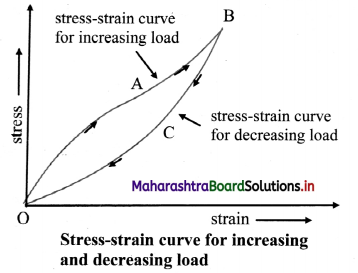
Question 12.
State the names of the hardest material and the softest material.
Answer:
Hardest material: Diamond
Softest material: Aluminium
[Note: Material with highest strength is steel whereas material with lowest strength is plasticine clay.]
Question 13.
Define friction.
Answer:
The property which resists the relative motion between two surfaces in contact is called friction.
Question 14.
Why force of static friction is known as ‘self-adjusting force?
Answer:
The force of static friction varies in accordance with applied force. Hence, it is called as self adjusting force.
Question 15.
Name two factors on which the coefficient of friction depends.
Answer:
Coefficient of friction depends upon:
- the materials of the surfaces in contact.
- the nature of the surfaces.
3. Answer in short:
Question 1.
Distinguish between elasticity and plasticity.
Answer:
| No. | Elasticity | Plasticity |
| i. | Body regains its original shape or size after removal of deforming force. | Body does not regain its original shape or size after removal of deforming force. |
| ii. | Restoring forces are strong enough to bring the displaced molecules to their original positions. | Restoring forces are not strong enough to bring the molecules back to their original positions. |
| Examples of elastic materials: metals, rubber, quartz, etc | Examples of plastic materials: clay, putty, plasticine, thick mud, etc |
Question 2.
State any four methods to reduce friction.
Answer:
Friction can be reduced by using polished surfaces, using lubricants, using grease and using ball bearings.
Question 3.
What is rolling friction? How does it arise?
Answer:
- Friction between two bodies in contact when one body is rolling over the other, is called rolling friction.
- Rolling friction arises as the point of contact of the body with the surface keep changing continuously.
![]()
Question 4.
Explain how lubricants help in reducing friction?
Answer:
- The friction between lubricant to surface is much less than the friction between two same surfaces. Hence using lubricants reduces the friction between the two surfaces.
- When lubricant is applied to machine parts, it fills the depression present on the surface in contact. Thus, less friction is occurred between machine parts.
- Application of lubricants also reduces wear and tear of machine parts which in turn reduces friction.
- Advantage: Reduction in function reduces dissipation of energy in machines due to which efficiency of machines increases.
Question 5.
State the laws of static friction.
Answer:
Laws of static friction:
- First law: The limiting force of static friction (FL) is directly proportional to the normal reaction (N) between the two surfaces in contact.
FL ∝ N
∴ FL = µs N
where, µs = constant called coefficient of static friction. - Second law: The limiting force of friction is
independent of the apparent area between the surfaces in contact, so long as the normal reaction remains the same. - Third law: The limiting force of friction depends upon materials in contact and the nature of their surfaces.
Question 6.
State the laws of kinetic friction.
Answer:
Laws of kinetic friction:
- First law: The force of kinetic friction (Fk) is directly proportional to the normal reaction (N) between two surfaces in contact.
Fk ∝ N
∴ Fk = µkN
where, µk = constant called coefficient of kinetic friction. - Second law: Force of kinetic friction is independent of shape and apparent area of the surfaces in contact.
- Third law: Force of kinetic friction depends upon the nature and material of the surfaces in contact.
- Fourth law: The magnitude of the force of kinetic friction is independent of the relative velocity between the object and the surface provided that the relative velocity is neither too large nor too small.
Question 7.
State advantages of friction.
Answer:
Advantages of friction:
- We can walk due to friction between ground and feet.
- We can hold object in hand due to static friction.
- Brakes of vehicles work due to friction; hence we can reduce speed or stop vehicles.
- Climbing on a tree is possible due to friction.
Question 8.
State disadvantages of friction.
Answer:
Disadvantages of friction:
- Friction opposes motion.
- Friction produces heat in different parts of machines. It also produces noise.
- Automobile engines consume more fuel due to friction.
Question 9.
What do you mean by a brittle substance? Give any two examples.
Answer:
- Substances which breaks within the elastic limit are called brittle substances.
- Examples: Glass, ceramics.
4. Long answer type questions:
Question 1.
Distinguish between Young’s modulus, bulk modulus and modulus of rigidity.
Answer:
| No | Young’s modulus | Bulk modulus | Modulus of rigidity |
| i. | It is the ratio of longitudinal stress to longitudinal strain. | It is the ratio of volume stress to volume strain. | It is the ratio of shearing stress to shearing strain. |
| ii. | It is given by, Y = \(\frac{\mathrm{MgL}}{\pi \mathrm{r}^{2} l}\) | It is given by, K = \(\frac{V d P}{d V}\) | It is given by, \(\eta=\frac{F}{A \theta}\) |
| iii. | It exists in solids. | It exists in solid, liquid and gases. | It exists in solids. |
| iv. | It relates to change in
length of a body. |
It relates to change in volume of a body. | It relates to change in shape of a body. |
Question 2.
Define stress and strain. What are their different types?
Answer:
i) Stress:
- The internal restoring force per unit area of a both is called stress.
Stress = \(\frac{\text { deforming force }}{\text { area }}=\frac{|\vec{F}|}{\mathrm{A}}\)
where \(\vec{F}\) is internal restoring force or external applied deforming force. - Types of stress:
- Longitudinal stress,
- Volume stress,
- Shearing stress.
ii. Strain:
- Strain is defined as the ratio of change in dimensions of the body to its original dimensions.
Strain = \(\frac{\text { change in dimensions }}{\text { original dimensions }}\) - Types of strain:
- Longitudinal strain,
- Volume strain,
- Shearing strain.
![]()
Question 3.
What is Young’s modulus? Describe an experiment to find out Young’s modulus of material in the form of a long straight wire.
Answer:
Definition: Young ‘s modulus is the ratio of longitudinal stress to longitudinal strain.
It is denoted by Y.
Unit: N/m2 or Pa in SI system.
Dimensions: [L-1M1T-2]
Experimental description to find Young’s modulus:
i. Consider a metal wire suspended from a rigid support. A load is attached to the free end of the wire. Due to this, deforming force gets applied to the free end of wire in downward direction and it produces a change in length.
Let,
L = original length of wire,
Mg = weight suspended to wire,
l = extension or elongation,
(L + l) = new length of wire.
r = radius of the cross section of wire
ii. In its equilibrium position,

Question 4.
Derive an expression for strain energy per unit volume of the material of a wire.
Answer:
Expression for strain energy per unit volume;
i. Consider a wire of original length L and cross sectional area A stretched by a force F acting along its length. The wire gets stretched and elongation l is produced in it
ii. If the wire is perfectly elastic then,
Longitudinal stress = \(\frac{F}{A}\)
Longitudinal strain = \(\frac{l}{L}\)

iii. The magnitude of stretching force increases from zero to F during elongation of wire.
Let ‘f’ be the restoring force and ‘x’ be its corresponding extension at certain instant during the process of extension.
∴ f = \(\frac{\text { YAx }}{\mathrm{L}}\) ……………. (2)
iv. Let ‘dW’ be the work done for the further small extension ‘dx’.
Work = force × displacement
∴ dW = fdx
∴ dW= \(\frac{\text { YAx }}{L}\) dx …………..(3) [From (2)]
v. The total amount of work done in stretching the wire from x = 0 to x = l can be found out by integrating equation (3).

∴ Work done in stretching a wire,
W = \(\frac{1}{2}\) × load × extension
vi. Work done by stretching force is equal to strain energy gained by the wire.
∴ Strain energy = \(\frac{1}{2}\) × load × extension
vii. Work done per unit volume
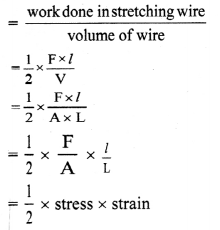
∴ Strain energy per unit volume = \(\frac{1}{2}\) × stress × strain
viii. Other forms:

Question 5.
What is friction? Define coefficient of static friction and coefficient of kinetic friction. Give the necessary formula for each.
Answer:
- The property which resists the relative motion between two surfaces in contact is called friction.
- The coefficient of static friction is defined as the ratio of limiting force of friction to the normal reaction.
Formula: \(\mu_{\mathrm{S}}=\frac{\mathrm{F}_{\mathrm{L}}}{\mathrm{N}}\) - The coefficient of kinetic friction is defined as the ratio of force of kinetic friction to the normal reaction between the two surfaces in contact.
Formula: \(\mu_{\mathrm{k}}=\frac{\mathrm{F}_{\mathrm{K}}}{\mathrm{N}}\)
![]()
Question 6.
State Hooke’s law. Draw a labelled graph of tensile stress against tensile strain for a metal wire up to the breaking point. In this graph show the region in which Hooke’s law is obeyed.
Answer:
i) Statement: Within elastic limit, stress is directly proportional to strain.
Explanation;
- According to Hooke’s law,
Stress ∝ Strain

This constant of proportionality is called modulus of elasticity. - Modulus of elasticity of a material is the slope of stress-strain curve in elastic deformation region and depends on the nature of the material.
- The graph of strain (on X-axis) and stress (on Y-axis) within elastic limit is shown in the figure.
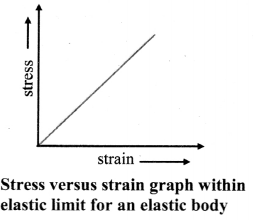
ii)
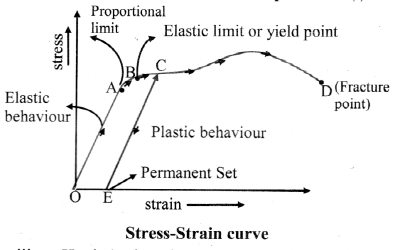
iii) Hooke’s law is completely obeyed in the region OA.
5. Answer the following
Question 1.
Calculate the coefficient of static friction for an object of mass 50 kg placed on horizontal table pulled by attaching a spring balance. The force is increased gradually it is observed that the object just moves when spring balance shows 50N.
[Answer: µs = 0.102]
Solution:
Given: m = 50 kg, FL = 50 N, g = 9.8 m/s2
To find: Coefficient of static friction (µs)
Formula: µs = \(\frac{\mathrm{F}_{\mathrm{L}}}{\mathrm{N}}=\frac{\mathrm{F}_{\mathrm{L}}}{\mathrm{mg}}\)
µs = \(\frac{50}{50 \times 9.8}\) = 0.102
Answer:
The coefficient of static friction is 0.102.
Question 2.
A block of mass 37 kg rests on a rough horizontal plane having coefficient of static friction 0.3. Find out the least force required to just move the block horizontally.
[Answer: F= 108.8N]
Solution:
Given: m = 37 kg, µs = 0.3, g = 9.8 m /s2
To find: Limiting force (FL)
Formula: FL = µSN = µS mg
Calculation: From formula,
FL = 0.3 × 37 × 9.8 = 108.8 N
Answer:
The force required to move the block is 108.8 N.
Question 3.
A body of mass 37 kg rests on a rough horizontal surface. The minimum horizontal force required to just start the motion is 68.5 N. In order to keep the body moving with constant velocity, a force of 43 N is needed. What is the value of
a) coefficient of static friction? and
b) coefficient of kinetic friction?
Asw:
a) µs = 0.188
b) µk = 0.118]
Solution:
Given:
FL = 68.5 N, Fk = 43 N,
m = 37 kg, g = 9.8 m/s2
To find:
i. Coefficient of static friction (µs)
ii. Coefficient of kinetic friction (µk)
Formulae:
i. µs = \(\frac{F_{L}}{N}\) = \(\frac{F_{L}}{m g}\)
ii. µk = \(\frac{F_{k}}{N}\) = \(\frac{\mathrm{F}_{\mathrm{k}}}{\mathrm{mg}}\)
Calculation:
From formula (i),
∴ µs = \(\frac{F_{S}}{N}=\frac{68.5}{37 \times 9.8}\) = 0.1889
From formula (ii),
∴ µk = \(\frac{F_{k}}{N}=\frac{43}{37 \times 9.8}\) = 0.1186
Answer:
- The coefficient of static friction is 0.1889.
- The coefficient of kinetic friction is 0.1186.
[Note: Answers calculated above are in accordance with textual methods of calculation.]
Question 4.
A wire gets stretched by 4mm due to a certain load. If the same load is applied to a wire of same material with half the length and double the diameter of the first wire. What will be the change in its length?
Solution:
Given. l1 = 4mm = 4 × 10-3 m
L2 = \(\frac{\mathrm{L}_{1}}{2}\), D2 = 2D, r2 = 2r1
To find: Change in length (l2)
Formula: Y = \(\frac{\mathrm{FL}}{\mathrm{Al}}=\frac{\mathrm{FL}}{\pi \mathrm{r}^{2} l}\)
Calculation: From formula,

= 0.5 × 10-3 m
= 0.5 mm
The new change in length of the wire is 0.5 mm.
![]()
Question 5.
Calculate the work done in stretching a steel wire of length 2m and cross sectional area 0.0225mm2 when a load of 100 N is slowly applied to its free end. [Young’s modulus of steel= 2 × 1011 N/m2]
Solution:
Given. L = 2m, F = 100 N,
A = 0.0225 mm2 = 2.25 × 10-8 m2,
Y = 2 × 10-11 N/m2,
To find: Work (W)
Formula: W = \(\frac{1}{2}\) × F × l
Claculation:

= antilog [log 10 – log 4.5]
= antilog [1.0000 – 0.6532 ]
= antilog [0.3468]
∴ W = 2.222 J
Answer:
The work done in stretching the steel wire is 2.222 J.
Question 6.
A solid metal sphere of volume 0.31m3 is dropped in an ocean where water pressure is 2 × 107 N/m2. Calculate change in volume of the sphere if bulk modulus of the metal is 6.1 × 1010 N/m2
Solution:
Given: V= 0.31 m3, dP = 2 × 107 N/m2,
K = 6.1 × 1010 N/m2
To find: Change in volume (dV)
Formula: K = V × \(\frac{\mathrm{dP}}{\mathrm{dV}}\)
Calculation: From formula,
dV = \(\frac{\mathrm{V} \times \mathrm{dP}}{\mathrm{K}}\)
∴ dV = \(\frac{0.31 \times 2 \times 10^{7}}{6.1 \times 10^{10}}\) ≈ 10-4 m3
The change in volume of the sphere is 10-4 m3.
Question 7.
A wire of mild steel has initial length 1.5 m and diameter 0.60 mm is extended by 6.3 mm when a certain force is applied to it. If Young’s modulus of mild steel is 2.1 × 1011 N/m2, calculate the force applied.
Solution:
Given:
L = 1.5m, d = 0.60 mm,
r = \(\frac{d}{2}\) = 0.30 mm = 3 × 10-4 m,
Y = 2.1 × 1011 N/m2,
l = 6.3 mm = 6.3 × 10-3 m
To find: Force (F)
Calculation:
From formula,
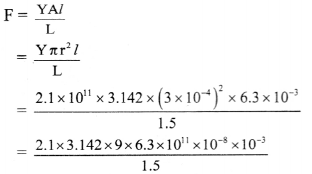
= 2.1 × 3.142 × 6 × 6.3
= antilog [log 2.1 + log 3.142 + log 6 + log 6.3]
= antilog [0.3222 + 0.4972 + 0.7782 + 0.7993]
= antilog [2.3969]
= 2.494 × 102
≈ 250 N
The force applied on wire is 250 N.
Question 8.
A composite wire is prepared by joining a tungsten wire and steel wire end to end. Both the wires are of the same length and the same area of cross section. If this composite wire is suspended to a rigid support and a force is applied to its free end, it gets extended by 3.25mm. Calculate the increase in length of tungsten wire and steel wire separately.
[Given: Ysteel = 2 × 1011 Pa, YTungsten = 4.11 × 1011 Pa]
Solution:
Given: ls + lT = 3.25 mm,
YT = 4.11 × 1011 Pa
Ys = 2 × 1011 Pa
To find: Extension in tungsten wire (lT)
Extension in steel wire (ls)

But ls + lT = 3.25
ls + 0.487 ls = 3.25
ls(1 + 0.487) = 3.25
ls = 2.186 mm
∴ lT = 3.25 – 2.186
= 1.064 mm
The extension in tungsten wire is 1.064 mm and the extension in steel wire is 2.186 mm.
[Note: Values of Young’s modulus of tungsten and steel considered above are standard values. Using them, calculation is carried out ¡n accordance with textual method.]
Question 9.
A steel wire having cross sectional area 1.2 mm2 is stretched by a force of 120 N. If a lateral strain of 1.455 mm is produced in the wire, calculate the Poisson’s ratio.
Solution:
Given: A = 1.2 mm2 = 1.2 × 10-6 m2,
F = 120 N, Ysteel = 2 × 1011 N/m2,
Lateral strain = 1.455 × 10-4
To find: Poisson’s ratio (σ)

The Poisson’s ratio of steel is 0.291.
[Note: Lateral strain being ratio of two same physical quantities, is unitless. hence, value given in question ¡s modified to 1.455 × 10-4 to reach the answer given in textbook.]
Question 10.
A telephone wire 125m long and 1mm in radius is stretched to a length 125.25m when a force of 800N is applied. What is the value of Young’s modulus for material of wire?
Solution:
Given: L = 125m,
r = 1 mm= 1 × 10-3 m
l = 125.25 – 125 = 0.25 m,
F = 800N
To find: Young’s modulus (Y)
Formula: Y \(\frac{\mathrm{FL}}{\mathrm{Al}}=\frac{\mathrm{FL}}{\pi \mathrm{r}^{2} l}\)
Calculation: From formula,
Y = \(\frac{800 \times 125}{3.142 \times 10^{-6} \times 0.25}\)
= {antilog [log 800 + log 125 – log 3.142 – log 0.25 ]} × 106
= {antilog [2.9031 + 2.0969 – 0.4972 – \(\overline{1}\) .3979]} × 106
= {antilog[5.1049]} × 106
= 1.274 × 105
= 1.274 × 1011 N/m2
The Young’s modulus of telephone wire is 1.274 × 1011 N/m2.
Question 11.
A rubber band originally 30cm long is stretched to a length of 32cm by certain load. What is the strain produced?
Solution:
Given: L = 30 cm = 30 × 10 -2 m,
∆l = 32 cm – 30 cm = 2cm = 2 × 10 -2 m
To find. Strain
Formula: Strain = \(\frac{\Delta l}{\mathrm{~L}}\)
Calculation: From formula,
Strain = \(\frac{2 \times 10^{-2}}{30 \times 10^{-2}}\) = 6.667 × 10 -2
The strain produced in the wire is 6.667 × 10 -2.
![]()
Question 12.
What is the stress in a wire which is 50m long and 0.01cm2 in cross section, if the wire bears a load of 100kg?
Solution:
Given: M = 100 kg, L 50 m, A = 0.01 × 10-4 m
To find: Stress
Formula: Stress = \(\frac{\mathrm{F}}{\mathrm{A}}=\frac{\mathrm{Mg}}{\mathrm{A}}\)
Calculation: From formula,
Stress = \(\frac{100 \times 9.8}{0.01 \times 10^{-4}}\) = 9.8 × 108 N/m2
The stress in the wire is 9.8 × 108 N/m2.
Question 13.
What is the strain in a cable of original length 50m whose length increases by 2.5cm when a load is lifted?
Solution:
Given: L = 50m, ∆l = 2.5cm = 2.5 × 10 -2 m
To find: Strain
Formula: Strain = \(\frac{\Delta l}{\mathrm{~L}}\)
Calculation: From formula,
Strain = \(\frac{2.5 \times 10^{-2}}{50}\) = 5 × 10-4
The Strain produced in wire is 5 × 10-4 .
11th Physics Digest Chapter 6 Mechanical Properties of Solids Intext Questions and Answers
Can you recall? (Textbook Page No. 100)
Question 1.
- Can you name a few objects which change their shape and size on application of a force and regain their original shape and size when the force is removed?
- Can you name objects which do not regain their original shape and size when the external force is removed?
Answer:
- Objects such as rubber, metals, quartz, etc. change their shape and size on application of a force (within specific limit) and regain their original shape and size when the force is removed.
- Objects such as putty, clay, thick mud. etc. do not regain their original shape and size when the external force is removed.
![]()
Can you tell? (Textbook Page No. 107)
Question 1.
Why does a rubber band become loose after repeated use?
Answer:
- After repeated use of rubber band, its stress-strain curve does not remain linear.
- In such case, since rubber crosses its elastic limit, there is a permanent set formed on the rubber due to which it becomes loose.
Can you tell? (Textbook Page No.111)
Question 1.
i. It is difficult to run fast on sand.
ii. It is easy to roll than pull a barrel along a road.
iii. An inflated tyre rolls easily than a flat tyre.
iv. Friction is a necessary evil.
Answer:
i.
- The intermolecular space between crystals of sand is very large as compared to that in a rigid surface.
- Thus, there are number of depressions at the points of contact of feet and sand surface.
- Projections and depressions between sand and feet are not completely interlocked.
- Thus, action and reaction force become unbalanced. The horizontal component of force helps to move forward and vertical component of the force resist to move.
Hence, it becomes difficult to run fast on sand.
ii.
- When a barrel is pulled along a road, the friction between the tyres and road is kinetic friction, but when its rolls along the road it undergoes rolling friction.
- The force of kinetic friction is greater than force of rolling friction.
Hence, it is easy to roll than pull a barrel along a road.
iii.
- When the tyre is inflated, the pressure inside the tyre is reducing the normal force between tyre and the ground, and thus reducing the friction between the tyre and the road.
- When the tyre gets deflated, it gets deformed during rolling, the supplied energy is used up in changing the shape and not overcoming the friction, and thus due to deformation, friction increases.
Hence, an inflated tyre rolls easily than a flat tyre.
iv.
- Friction helps us to walk, hold objects in hand, lift objects and without friction we cannot walk, we cannot grip or hold objects with our hands,
- Friction is responsible for wear and tear of various part of machines, it produces heat in different parts of machine and also produces noise but it also helps in ball bearing or connecting screws.
Hence, friction is said to be a necessary evil because it is useful as well as harmful.
Internet my friend (Textbook Page No. 111)
Question 1.
i. https ://opentextbc. ca/physicstestbook2/ chapter/friction/
ii. https://www.livescience.com/
iii. https://www.khanacademy.org/science/physics
iv. https://courses.lumenleaming.com/physics/ chapter/5-3-elasticity-stress-and-strain/
v. https://www.toppr.com/guides/physics/
Answer:
[Students are expected to visit the above mentioned websites and collect more information about mechanical properties of solid.]