Maharashtra Board 12th Maths Solutions Chapter 3 Trigonometric Functions Ex 3.3

Balbharti 12th Maharashtra State Board Maths Solutions Book Pdf Chapter 3 Trigonometric Functions Ex 3.3 Questions and Answers.

Maharashtra State Board 12th Maths Solutions Chapter 3 Trigonometric Functions Ex 3.3

Question 1.
Find the principal values of the following :
(i) sin^-1\(\left(\frac{1}{2}\right)\)
Solution:
The principal value branch of sin^-1x is \(\left[-\frac{\pi}{2}, \frac{\pi}{2}\right]\).
Let sin^-1\(\left(\frac{1}{2}\right)\) = ∝, where \(\frac{-\pi}{2}\) ≤ ∝ ≤ \(\frac{\pi}{2}\)
∴ sin∝ = \(\frac{1}{2}\) = sin\(\frac{\pi}{6}\)
∴ ∝ = \(\frac{\pi}{6}\) …[∵ – \(\frac{\pi}{2}\) ≤ \(\frac{\pi}{6}\) ≤ \(\frac{\pi}{2}\)]
∴ the principal value of sin^-1\(\left(\frac{1}{2}\right)\) is \(\frac{\pi}{6}\).

(ii) cosec^-1(2)
Solution:
The principal value branch of cosec^-1x is \(\left[-\frac{\pi}{2}, \frac{\pi}{2}\right]\) – {0}.
Let cosec^-1(2) = ∝, where \(\frac{-\pi}{2}\) ≤ ∝ ≤ \(\frac{\pi}{2}\), ∝ ≠ 0
∴ cosec^-1 ∝ = 2 = cosec\(\frac{\pi}{6}\)
∴ ∝ = \(\frac{\pi}{6}\) …[∵ –\(\frac{\pi}{2}\) ≤ \(\frac{\pi}{6}\) ≤ \(\frac{\pi}{2}\)]
∴ the principal value of cosec^-1(2) is \(\frac{\pi}{6}\).

(iii) tan^-1(-1)
Solution:
The principal value branch of tan^-1x is \(\left(-\frac{\pi}{2}, \frac{\pi}{2}\right)\)
Let tan^-1(-1) = ∝, where \(\frac{-\pi}{2}\) < ∝ < \(\frac{\pi}{2}\)
∴ tan∝ = -1 = -tan\(\frac{\pi}{4}\)
∴ tan∝ = tan\(\left(-\frac{\pi}{4}\right)\) …[∵ tan(-θ) = -tanθ]
∴ ∝ = –\(\frac{\pi}{4}\) …[∵ –\(\frac{\pi}{2}\) < \(\frac{-\pi}{4}\) < \(\frac{\pi}{2}\)]
∴ the principal value of tan^-1(-1) is –\(\frac{\pi}{4}\).

(iv) tan^-1(-\(\sqrt {3}\))
Solution:
The principal value branch of tan^-1x is \(\left(-\frac{\pi}{2}, \frac{\pi}{2}\right)\).
Let tan^-1(-\(\sqrt {3}\)) = ∝, where \(\frac{-\pi}{2}\) < ∝ < \(\frac{\pi}{2}\)
∴ tan∝ = –\(\sqrt {3}\) = -tan\(\frac{\pi}{3}\)
∴ tan∝ = tan\(\left(-\frac{\pi}{3}\right)\) …[∵ tan(-θ) = -tanθ]
∴ ∝ = –\(\frac{\pi}{3}\) …[∵ –\(\frac{\pi}{2}\) < \(\frac{-\pi}{3}\) < \(\frac{\pi}{2}\)]
∴ the principal value of tan^-1(-\(\sqrt {3}\)) is –\(\frac{\pi}{3}\).

(v) sin^-1 \(\left(\frac{1}{\sqrt{2}}\right)\)
Solution:
The principal value branch of sin^-1x is \(\left[-\frac{\pi}{2}, \frac{\pi}{2}\right]\).
Let sin^-1 \(\left(\frac{1}{\sqrt{2}}\right)\) = ∝, where \(\frac{-\pi}{2}\) < ∝ < \(\frac{\pi}{2}\)
∴ sin∝ = \(\left(\frac{1}{\sqrt{2}}\right)\) = sin\(\frac{\pi}{4}\)
∴ ∝ = \(\frac{\pi}{4}\) …[∵ –\(\frac{\pi}{2}\) ≤ \(\frac{\pi}{4}\) ≤ \(\frac{\pi}{2}\)]
∴ the principal value of sin^-1 \(\left(\frac{1}{\sqrt{2}}\right)\) is \(\frac{\pi}{4}\).

(vi) cos^-1\(\left(-\frac{1}{2}\right)\)
Solution:
The principal value branch of cos^-1x is (0, π).
Let cos^-1\(\left(-\frac{1}{2}\right)\) = ∝, where 0 ≤ ∝ ≤ π
∴ cos∝ = \(-\frac{1}{2}\) = -cos\(\frac{\pi}{3}\)
∴ cos∝ = cos\(\left(\pi-\frac{\pi}{3}\right)\) …[∵ cos(π – θ) = -cosθ)
∴ cos∝ = cos\(\frac{2 \pi}{3}\)
∴ ∝ = \(\frac{2 \pi}{3}\) …[∵ 0 ≤ \(\frac{2 \pi}{3}\) ≤ π]
∴ the principal value of cos^-1\(\left(-\frac{1}{2}\right)\) is \(\frac{2 \pi}{3}\).

Question 2.
Evaluate the following :
(i) tan^-1(1) + cos^-1\(\left(\frac{1}{2}\right)\) + sin^-1\(\left(\frac{1}{2}\right)\)
Solution:

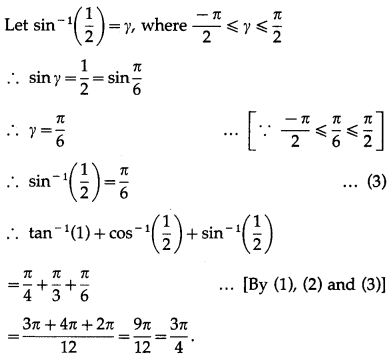
(ii) cos^-1\(\left(\frac{1}{2}\right)\) + 2 sin^-1\(\left(\frac{1}{2}\right)\)
Solution:

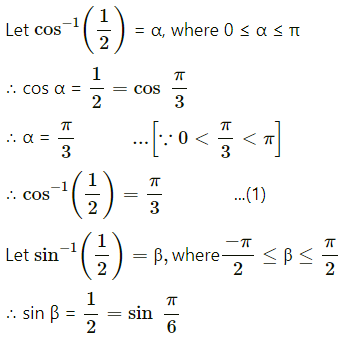
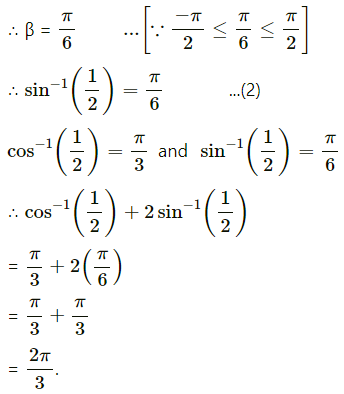
(iii) tan^-1\(\sqrt {3}\) – sec^-1(-2)
Solution:

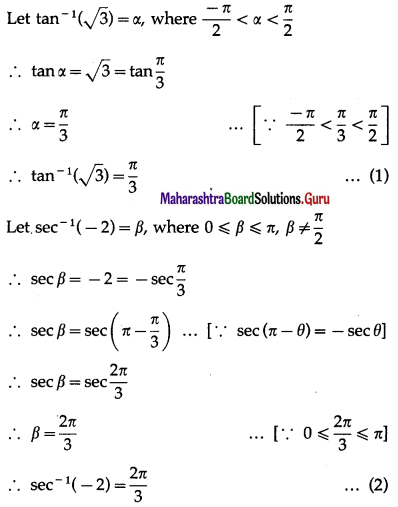
∴ tan^-1\(\sqrt {3}\) – sec^-1(-2)
= \(\frac{\pi}{3}-\frac{2 \pi}{3}\) …[By (1) and (2)]
= –\(\frac{\pi}{3}\).

(iv) cosec^-1( \(-\sqrt{2}\)) + cot^-1(\(\sqrt{3}\))
Solution:

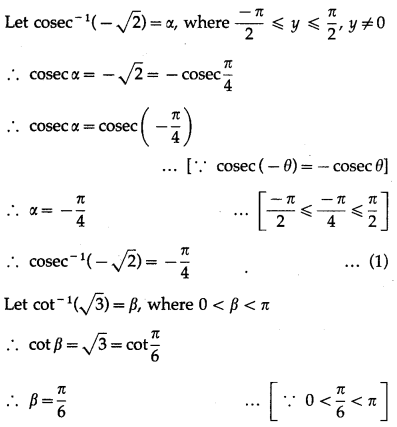
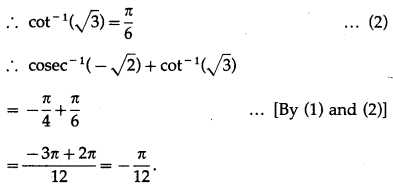
Question 3.
Prove the following :
(i) sin^-1\(\left(\frac{1}{\sqrt{2}}\right)\) – 3sin^-1\(\left(\frac{\sqrt{3}}{2}\right)\) = –\(-\frac{3 \pi}{4}\)
Question is modified.
sin^-1\(\left(\frac{1}{\sqrt{2}}\right)\) – 3sin^-1\(\left(\frac{\sqrt{3}}{2}\right)\) = –\(\frac{3 \pi}{4}\)
Solution:

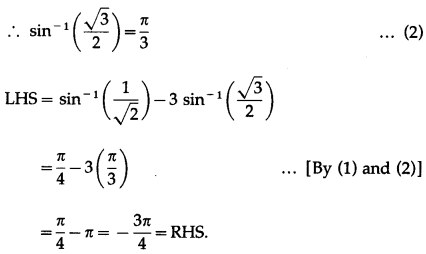
(ii) sin^-1\(\left(-\frac{1}{2}\right)\) + cos^-1\(\left(-\frac{\sqrt{3}}{2}\right)\) = cos^-1\(\left(-\frac{1}{2}\right)\)
Solution:

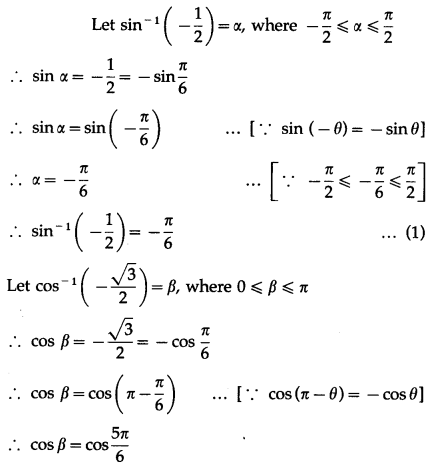
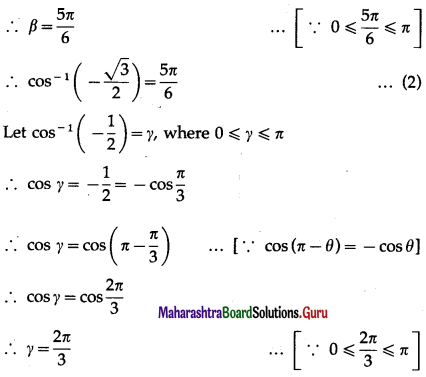
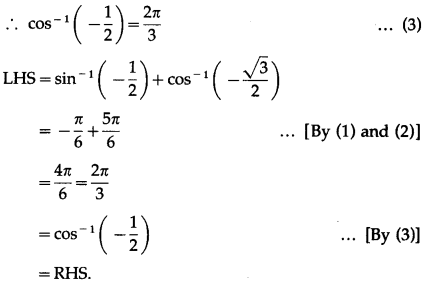
(iii) sin^-1\(\left(\frac{3}{5}\right)\) + cos^-1\(\left(\frac{12}{13}\right)\) = sin^-1\(\left(\frac{56}{65}\right)\)
Solution:

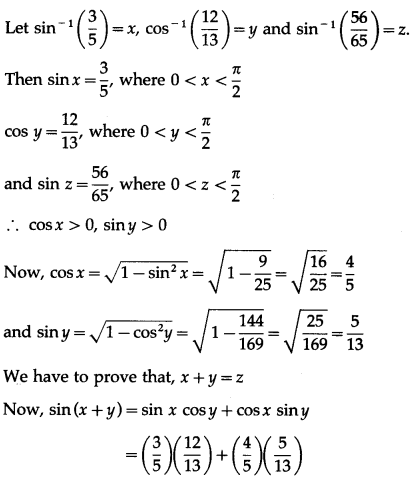
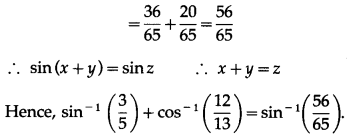
(iv) cos^-1\(\left(\frac{3}{5}\right)\) + cos^-1\(\left(\frac{4}{5}\right)\) = \(\frac{\pi}{2}\)
Solution:
Let cos^-1\(\left(\frac{3}{5}\right)\) = x
∴ cosx = \(\left(\frac{3}{5}\right)\), where 0 < x < \(\frac{\pi}{2}\) ∴ sinx > 0

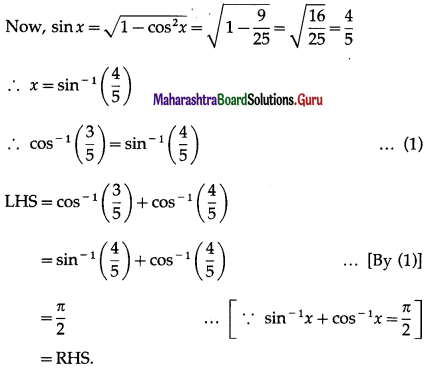
(v) tan^-1\(\left(\frac{1}{2}\right)\) + tan^-1\(\left(\frac{1}{3}\right)\) = \(\frac{\pi}{4}\)
Solution:
LHS = tan^-1\(\left(\frac{1}{2}\right)\) + tan^-1\(\left(\frac{1}{3}\right)\)
= tan^-1\(\left(\frac{\frac{1}{2}+\frac{1}{3}}{1-\frac{1}{2} \times \frac{1}{3}}\right)\)
= tan^-1\(\left(\frac{3+2}{6-1}\right)\) = tan^-1(1)
= tan^-1\(\left(\tan \frac{\pi}{4}\right)\) = \(\frac{\pi}{4}\)
= RHS.

(vi) 2 tan^-1\(\left(\frac{1}{3}\right)\) = tan^-1\(\left(\frac{3}{4}\right)\)
Solution:

(vii) tan^-1\(\left[\frac{\cos \theta+\sin \theta}{\cos \theta-\sin \theta}\right]\) = \(\frac{\pi}{4}\) + θ if θ ∈ \(\left(-\frac{\pi}{4}, \frac{\pi}{4}\right)\)
Solution:

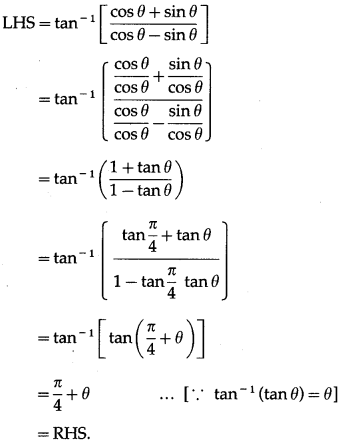
(viii) tan^-1\(\sqrt{\frac{1-\cos \theta}{1+\cos \theta}}=\frac{\theta}{2}\), if θ ∈ (0, π)
Solution:

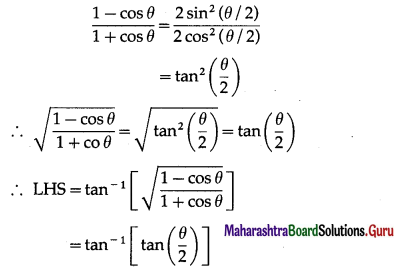
= \(\frac{\theta}{2}\) …[∵ tan^-1(tanθ) = θ]
= RHS.