Category: Class 12

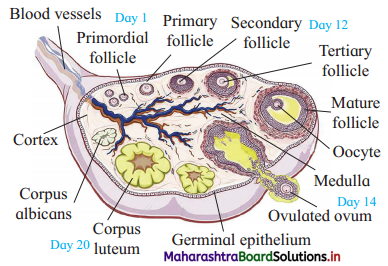
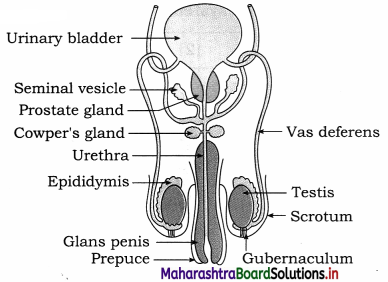
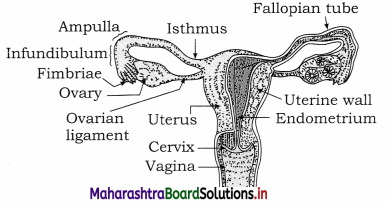
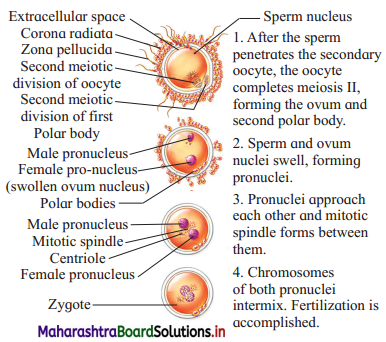
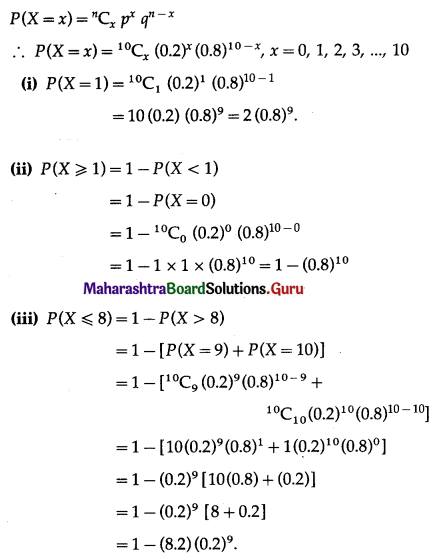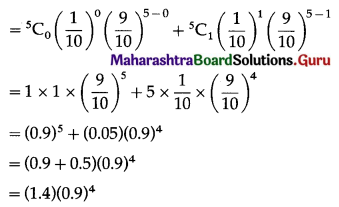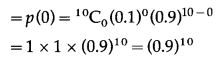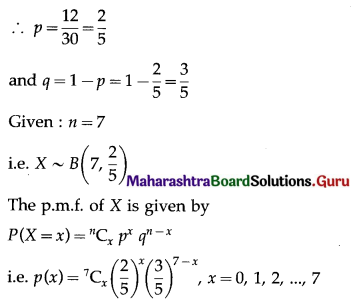Enhancement of Food Production Class 12 Exercise Question Answers Solutions Maharashtra Board

Balbharti Maharashtra State Board 12th Biology Textbook Solutions Chapter 11 Enhancement of Food Production Textbook Exercise Questions and Answers.

Class 12 Biology Chapter 11 Exercise Solutions Maharashtra Board

Biology Class 12 Chapter 11 Exercise Solutions

1. Multiple choice questions

Question 1.
Antibiotic Chloromycetin is obtained from ………………….
(a) Streptomyces erythreus
(b) Penicillium chrysogenum
(c) Streptomyces venezuelae
(d) Streptomyces griseus
Answer:
(c) Streptomyces venezuelae

Question 2.
Removal of large pieces of floating debris, oily substances, etc. during sewage treatment is called ………………….
(a) primary treatment
(b) secondary treatment
(c) final treatment
(d) amplification
Answer:
(a) primary treatment

Question 3.
Which one of the following is free living bacterial biofertilizer?
(a) Azotobacter
(b) Rhizobium
(c) Nostoc
(d) Bacillus thuringiensis
Answer:
(a) Azotobacter

Question 4.
Most commonly used substrate for industrial production of beer is ………………….
(a) barley
(b) wheat
(c) corn
(d) sugar cane molasses
Answer:
(a) barley

Question 5.
Ethanol is commercially produced through a particular species of ………………….
(a) Aspergillus
(b) Saccharomyces
(c) Clostridium
(d) Trichoderma
Answer:
(b) Saccharomyces

Question 6.
One of the free-living anaerobic nitrogen- fixers is ………………….
(a) Azotobacter
(b) Beijerinckia
(c) Rhodospirillum
(d) Rhizobium
Answer:
(c) Rhodospirillum

Question 7.
Microorganisms also help in production of food like ………………….
(a) bread
(b) alcoholic beverages
(c) vegetables
(d) pulses
Answer:
(a) bread

Question 8.
MOET technique is used for ………………….
(a) production of hybrids
(b) inbreeding
(c) outbreeding
(d) outcrossing
Answer:
(a) production of hybrids

Question 9.
Mule is the outcome of ………………….
(a) inbreeding
(b) artificial insemination
(c) interspecific hybridization
(d) outbreeding
Answer:
(c) interspecific hybridization

2. Very Short Answer Questions

Question 1.
What makes idlis puffy?
Answer:
During preparation of idlis, rice and black gram flour is fermented by air borne Leuconostoc and Streptococcus bacteria. CO₂ produced during fermentation makes them puffy.

Question 2.
Bacterial biofertilizers.
Answer:
Rhizobium, Frankia, Pseudomonas striata, Bacillus polymyxa, Agrobacterium, Microccocus, Azotobacter, Costridium, Beijerinkia, Klebsiella.

Question 3.
What is the microbial source of vitamin B₁₂?
Answer:
The microbial source of vitamin B₁₂ is Pseudomonas denitrificans.

Question 4.
What is the microbial source of enzyme invertase?
Answer:
The microbial source of enzyme invertase is Saccharomyces cerevisiae.

Question 5.
Milk starts to coagulate when Lactic Acid Bacteria (LAB) are added to warm milk as a starter. Mention any two other benefits of LAB.
Answer:
Lactic Acid Bacteria (LAB) check the growth of disease causing microbes and produce vitamin B.

Question 6.
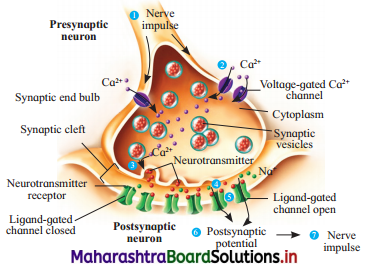
Name the enzyme produced by Streptococcus bacterium. Explain its importance in medical sciences.
Answer:
The enzyme produced by Streptococcus spp. is streptokinase. It is used as a ‘clot buster’ for clearing blood clots in the blood vessels in heart patients.

Question 7.
What is breed?
Answer:
Breed is a group of animals related by descent and similar in most characters like general appearance, features, size, configuration, etc.

Question 8.
Estuary
Answer:
Estuary is a place where river meets the sea.

Question 9.
What is shellac?
Answer:
Shellac is the pure form of lac obtained by washing and filtering.

3. Short Answer Questions.

Question 1.
Many microbes are used at home during preparation of food items. Comment on such useful ones with examples.
Answer:

1. Many food preparations made at home involves the use of microorganisms.
2. The microbes Lactobacilli are used in the preparation of dhokla from gram flour and buttermilk by the process of fermentation.
3. Dosa and idlis are prepared by using batter of rice and black gram which is fermented by air borne Leuconostoc and Streptococcus bacteria.
4. Large, fleshy fruiting bodies of some mushrooms and truffles are directly used as food. It is sugar free, fat free food rich in proteins, vitamins, minerals and amino acids. It is food with low calories.
5. Curd is prepared by inoculating milk with Lactobacillus acidophilus. Lactic acid produced during fermentation causes coagulation and partial digestion of milk protein casein and milk turns into curd.
6. Buttermilk is the acidulated liquid left after churning of butter from curd, is called buttermilk.

Question 2.
What is biogas? Write in brief about the production process.
Answer:
Biogas is a mixture of methane CH₄ (50-60%), CO₂ (30-40%), H₂S (0-3%) and other gases (CO, N₂, H₂) in traces.

Biogas production process:
a. A typical biogas plant consists of digester (made up of concrete bricks and cement or steel and is partly buried in the soil) and gas holder (a cylindrical gas tank to collect gases).
b. Raw materials like cow dung is mixed with water in equal proportion to make slurry which is fed into the digester’ through a side opening (charge pit).

Anaerobic digestion involves following processes:
i. Hydrolysis or solubilization:
Anaerobic hydrolyzing bacteria like Clostridium and Pseudomonas hydrolyse carbohydrates into simple sugars, proteins into amino acids and lipids into fatty acids.

ii. Acidogenesis:
Facultative and obligate anaerobic, acidogenic bacteria convert simple organic substances into acids like formic acid, acetic acid, H₂ and CO₂

iii. Methanogenesis:
Anaerobic methanogenic bacteria like Methanobacterium, Methanococcus convert acetate, H₂ and CO₂ into Methane, CO₂ and H₂O and other products.
12 mol CH₃COOH → 12CH₄ + 12CO₂ 4mol H.COOH → CH₄ + 3CO₂ + 2H₂O CO₂ + 4H₂ → CH₄ + 2H₂O

Question 3.
Biocontrol agents.
Answer:
(1) Biocontrol agents are the organisms like (bacteria, fungi, viruses and protozoans) act which are employed for controlling pathogens, pests and weeds.

(2) They cause the disease to the pest or compete or kill them.

(3) The use of biocontrol measures greatly reduces use of toxic chemicals and pesticides that are harmful to human beings and also pollute our environment.

(4) Biocontrol agents and their hosts.

• Bacteria (Bacillus thuringiensis, B. papilliae and B. lentimorbus Hosts : Caterpillars, cabbage worms, adult beetles
• Fungi (Beauveria bassiana, Entomophothora, pallidaroseum, Zoophthora radicans) Host : Aphid crocci, A. unguicilata, mealy bugs, mites, white flies, etc.
• Protozoans (Nosema locustae) Host: Grasshoppers, caterpillars, crickets
• Viruses (Nucleopolyhedro virus-NPV, Granulovirus-GV) Host : Caterpillars, Gypsy moth, ants and beetles.

(5) Some examples:

• Bacillus thuringiensis (Bt) is a microbiai pesticide used to get rid of butterfly, caterpillars.
• Trichoderma fungus is an effective biocontrol agent against soil borne fungal plant pathogens which infect roots and rhizomes.
• Phytophthora palmiuora is a mycoherbicide that controls milk weed in orchards.
• Pseudomonas spp. is a bacterial herbicide that attacks several weeds.
• Tyrea moth controls the weed Senecio jacobeac.

Question 4.
Name any two enzymes and antibiotics with their microbial source.
Answer:

1. Microbial source of Chloromycetin. – Streptomyces venezuelae
2. Microbial source of Erythromycin. – Streptomyces erythreus
3. Microbial source of Penicillin. – Penicillium chrysogenum
4. Microbial source of Streptomycin. – Streptomyces griseus
5. Microbial source of Griseofulvin. – Penicillium griseojulvum
6. Microbial source of Bacitracin. – Bacillus licheniformis
7. Microbial source of Oxytetracyclin / Terramycin. – Streptomyces aurifaciens
8. The enzyme produced by Streptococcus bacterium. – Streptokinase
9. Microbial source of Invertase. – Saccharomyces cerevisiae
10. Microbial source of Pectinase. – Sclerotinia libertine, Aspergillus niger
11. Microbial source of Lipase. – Candida lipolytica
12. Microbial source of Cellulase. – Trichoderma konigii

Question 5.
Write the principles of farm management.
Answer:
The principles of farm management are as follows:

1. Selection of high-yielding breeds.
2. Understanding the feed requirements of farm animals.
3. Supply of adequate nutritional sources for the animals.
4. Maintaining the cleanliness of environment.
5. Maintenance of health with the help of veterinary supervision.
6. Undertaking vaccination programmes.
7. Development of high-yielding cross-bred varieties.
8. Making various products and their preservation.
9. Distribution and marketing of the farm produce.

Question 6.
Give the economic importance of fisheries.
Answer:
Economic importance of fisheries is as follows:

1. Fish is a nutritious food and thus is a source of many vitamins, minerals and nutrients.
2. Commercial products such as fish oil, fish meal and fertilizers, fish guano, fish glue, isinglass are prepared from fish.
3. These by-products are used in paints, soaps, oils and medicines.
4. Some organisms like prawns and lobsters have high export value and market price.
5. Fish farming and other fishery trades provide job opportunity and self-employment
6. Productivity and national economy is improved through fishery practices.

Question 7.
Enlist the species of honey bee mentioning their specific uses.
Answer:
(1) The four species of honey bees commonly found in India : Apis dorsata (rock bee, or wild bee), Apis jlorea (little bee), Apis mellifera (European bee) and Apis indica (Indian bee).

(2) Uses:

• Rock bee : They produce 36 kg of honey per comb per year. They produce bee wax.
• Little bee : They produce half kg of honey per hive per year.
• European bee : The average production per colony per year is 25 to 40 kg.
• Indian bee : The average production per colony per year is 6 to 8 kg.

Question 8.
What are A, B, C, D in the table given below.

Answer:
A : Penicillium chrysogenum
B : Vinegar (Acetic acid)
C : Fungus
D : Sachharomyces cerevisiae var. ellipsoidis

4. Long Answer Questions.

Question 1.
Explain the process of sewage water treatment before it can be discharged into natural bodies. Why is this treatment essential?
Answer:
Sewage treatment includes following steps:
(1) Preliminary Treatment:

• Screening: The larger suspended or floating objects are filtered and removed in screening chambers by passing the sewage through screens or net in the chambers.
• Grit Chamber : Filtered sewage is passed into series of grit chambers which contain large stones (pebbles) and brick-ballast. Coarse particles which settle down by gravity are removed.

(2) Primary treatment (physical treatment):

• The sewage water is pumped into the primary sedimentation tank where 50-70% of the suspended solid or organic matter get sedimented and about 30-40% (in number) of coliform organisms are removed.
• The organic matter which is settled down is called primary sludge.
• Primary sludge is removed by mechanically operated devices.
• Dissolved organic matter and micro-organisms in the supernatant (effluent) are then removed by the secondary treatment.

(3) Secondary treatment (biological treatment):

• The primary effluent is passed into large aeration tanks where it is constantly agitated mechanically and air is pumped into it.
• The mesh like masses of aerobic bacteria, slime and fungal hyphae, known as floes are formed.
• Aerobic microbes consume most of the organic matter and this reduces BOD (Biochemical Oxygen Demand) of the effluent.

(4) Tertiary treatment:

• Once the BOD is sufficiently reduced, waste water is passed into a settling tank where the floes are allowed to sediment.
• The sediment is called activated sludge.
• Small part of activated sludge is transferred to aeration tank and the major part is pumped in to large anaerobic sludge digesters.
• In these tanks, anaerobic bacteria grow and digest the bacteria and fungi in the sludge and gases like methane, hydrogen sulphide, CO₂, etc. are released.
• Effluents from these digesters are released in natural water bodies like rivers and streams after chlorination which kills pathogenic bacteria.
• Digested sludge is then disposed.

Question 2.
Lac culture.
Answer:

1. Lac is a pink coloured resin secreted by dermal glands of female lac insect (Trachardia lacca) that hardens on coming in contact with air forming lac.
2. Lac is a complex substance having resin, sugar, water, minerals and alkaline substances.
3. Lac insect is colonial in habit and it feeds on succulent twigs like ber, peepal, palas, kusum, babool,
4. These plants are artificially inoculated in order to get better and regular supply of good quality and quantity of lac.
5. Natural lac is always contaminated and pure form of lac obtained by washing and filtering is called as shellac.
6. Lac is used to make bangles, toys, woodwork, inks, mirrors, etc.
7. India’s share is 85% of total lac produced in the world.

Question 3.
Describe various methods of fish preservation.
Answer:

1. Fish is a highly perishable commodity.
2. After catching the fish it immediately starts spoilage process.
3. In order to prevent this process, the fish preservation is done.

The different methods of fish preservation are as follows:

1. Chilling : This involves covering the fish with layers of ice. Ice is effective for short term preservation. It inhibits the activity of autolytic enzymes.
2. Freezing : It is a long duration preservation method. Fish are freezed at 0°C to -20°C. This also inhibit autolytic enzyme activities and slows down bacterial growth.
3. Freeze drying : The deep frozen -fish at -20°C are dried by direct sublimation of ice to water vapour with any melting into liquid water. This is achieved by exposing the frozen fish to 140°C in a vacuum chamber. The fish is then packed or canned in dried condition.
4. Sun drying : This inhibits the growth of microorganisms that spoil the fish.
5. Smoke drying : Smoke is prepared by burning woods with less resinous matter. Bacteria are destroyed by the acid content of the smoke. Smoking also give the characteristic colour, taste and odour to fish.
6. Salting : Salt removes the moisture from the fish tissues by osmosis. High salt concentration destroys autolytic enzymes and halts bacterial activity.
7. Canning : Canning involves sealing the food in a container, heat ‘sterilising’ the sealed unit and cooling it to ambient temperature for subsequent storage.

Question 4.
Give an account of poultry diseases.
Answer:
Various poultry diseases are as follows:

1. Viral diseases : Ranikhet, Bronchitis, Avian influenza (bird flu), etc. Bird flu had serious impact on poultry farming and also caused human infection.
2. Bacterial diseases : Pullorum, Cholera, Typhoid, TB, CRD (chronic respiratory disease), Enteritis, etc.
3. Fungal diseases : Aspergillosis, Favus and Thrush.
4. Parasitic diseases : Lice infection, round worm, caecal worm infections, etc.
5. Protozoan diseases : Coccidiosis.

Question 5.
Give an account of mutation breeding with examples.
Answer:

1. Mutations are sudden heritable changes in the genotype.
2. Natural mutations occur at a very slow rate.
3. Natural physical mutagens include exposure to high temperature, high concentration of C02, X-rays, UV rays.
4. Mutations can be induced by using various mutagens.
5. Mutagens cause gene mutations and chromosomal aberrations.
6. Chemical mutagens include nitrous acid, EMS (Ethyl – Methyl – Sulphonate), mustard gas, colchicine, etc.
7. Seedlings or seeds are irradiated by using CO60 or UV bulbs or X-ray machines.
8. The mutated seedlings are then screened for resistance to diseases/pests, high yield, etc.
9. Examples of mutant varieties in different crops are Jagannath (rice), NP 836 (rust resistant wheat variety), Indore-2 (cotton variety resistant to bollworm), Regina-II (cabbage variety resistant to bacterial rot).

Question 6.
Describe briefly various steps of plant breeding methods.
Answer:
The main steps of the plant breeding program (Hybridization) are as follows:

(1) Collection of variability:

• Germplasm collection is the entire collection of all the diverse alleles for all genes in a given crop.
• Wild species and relatives of the cultivated species having desired traits are collected and preserved.
• Forests and natural reserves are the means of in situ conservation of germplasm.
• Botanical gardens, seed banks, etc. are means of ex situ conservation of germplasm.

(2) Evaluation and selection of parents:

• The collected germplasm is evaluated to identify healthy and vigorous plants with desirable and complementary characters.
• Selected parents are selfed for three to four generations to increase homozygosity.
• Only pure lines are selected, multiplied and used in the hybridization.

(3) Hybridization:

• The variety showing maximum desirable features is selected as female (recurrent) parent and the other variety which lacks good characters found in recurrent parent is selected as male parent (donor).
• The pollen grains from anthers of male parent are artificially dusted over stigmas of emasculated flowers of female parent.
• Hybrid seeds are collected and sown to grow F₁ geneartion.

(4) Selection and Testing of Superior Recombinants:

• The F₁ hybrid plants which are superior to both the parents and having high hybrid vigour, are selected and selfed for few generations to make them homozygous for the said desirable characters.
• This ensures that there is no further segregation of the characters.

(5) Testing, release and commercialization of new cultivars:

• The newly selected lines are evaluated for the productivity and desirable features like disease resistance, pest resistance, quality, etc.
• They are initially grown under controlled conditions of water, fertilizers, etc. and their performance is recorded.
• The selected lines are then grown for at least three generations in natural field, in different agroclimatic zones.
• Finally variety is released as new variety for use by the farmers.

Maharashtra State Board 12th Std Biology Textbook Solutions 

• Control and Co-ordination Class 12 Biology Textbook Solutions
• Human Health and Diseases Class 12 Biology Textbook Solutions
• Enhancement of Food Production Class 12 Biology Textbook Solutions
• Biotechnology Class 12 Biology Textbook Solutions
• Organisms and Populations Class 12 Biology Textbook Solutions
• Ecosystems and Energy Flow Class 12 Biology Textbook Solutions
• Biodiversity, Conservation and Environmental Issues Class 12 Biology Textbook Solutions

Human Health and Diseases Class 12 Exercise Question Answers Solutions Maharashtra Board

Balbharti Maharashtra State Board 12th Biology Textbook Solutions Chapter 10 Human Health and Diseases Textbook Exercise Questions and Answers.

Class 12 Biology Chapter 10 Exercise Solutions Maharashtra Board

Biology Class 12 Chapter 10 Exercise Solutions

1. Multiple Choice Questions

Question 1.
Which of the following is NOT caused by unsterilized needles?
(a) Elephantiasis
(b) AIDS
(e) Malaria
(d) Hepatitis
Answer:
(a) Elephantiasis

Question 2.
Opium derivative is …………………
(a) Codeine
(b) Caffeine
(c) Heroin
(d) Psilocybin
Answer:
(c) Heroin

Question 3.
The stimulant present in tea is …………………
(a) tannin
(b) cocaine
(C) caffeine
(d) crack
Answer:
(c) caffeine

Question 4.
WhIch of the following Is caused by smoking?
(a) Liver cirrhosis
(b) Pulmonary tuberculosis
(c) Emphysema
(d) Malaria
Answer:
(c) Emphysema

Question 5.
An antibody is …………………
(a) molecuic that binds specifically an antigen
(b) WBC which invades bacteria
(c) secretion of mammalian RBC
(d) cellular component of blood
Answer:
(a) molecule that binds specifically an antigen

Question 6.
The antiviral proteins released by a virus-infected cell are called …………………
(a) histamines
(b) interferons
(c) pyrogens
(d) allergens
Answer:
(b) interferons

Question 7.
Both B-cells and T-cells are derived from …………………
(a) lymph nodes
(b) thymus glands
(c) liver
(d) stem cells in bone marrow
Answer:
(b) thymus glands

Question 8.
Which of the following diseases can be contracted by droplet infection?
(a) Malaria
(b) Chicken pox
(c) Pneumonia
(d) Rabies
Answer:
(c) Pneumonia

Question 9.
Confirmatory test used for detecting HIV infection is …………………
(a) ELISA
(b) Western blot
(c) Widal test
(d) Eastern blot
Answer:
(b) Western blot

Question 10.
Elephantiasis is caused by …………………
(a) W. barterofti
(b) P. vivax
(c) Bedbug
(d) Elephant
Answer:
(a) W. bancrofti

Question 11.
Innate immunity is provided by …………………
(a) phagocytes
(b) antibody
(c) T-lymphocytes
(d) B-lymphocytes
Answer:
(c) T-lymphocytes

2. Short Answer Questions

Question 1.
What is the source of cocaine?
Answer:
Source of cocaine is coca plant – Erythroxylum coca.

Question 2.
Name one disease caused by smoking.
Answer:
Emphysema. (Damaged and enlarged lungs causing breathlessness)

Question 3.
Which cells stimulate B-cells to form antibodies ?
Answer:
Helper T-cells stimulate B-cells to form antibodies.

Question 4.
What does the abbreviation AIDS stand for?
Answer:
AIDS stands for Acquired Immuno Deficiency Syndrome.

Question 5.
Name the causative agent of typhoid fever.
Answer:
Salmonella typhi

Question 6.
What is Rh factor?
Answer:
Antigen ‘D’ present on the surface of RBCs is known as Rh factor.

Question 7
What is schizont?
Answer:
Schizont is a ring-like form produced from merozoites inside the erythrocytes of human beings, infected by Plasmodium, which again forms new merozoites.

Question 8.
Name the addicting component found in tobacco.
Answer:
Nicotine

Question 9.
Name the pathogen causing Malaria.
Answer:
Plasmodium vivax

Question 10.
Name the vector of Filariasis.
Answer:
Female Culex mosquito

Question 11.
Name of the causative agent of ringworm.
Answer:
Trichophyton

Question 12.
Health
Answer:
Health is defined as the state of complete physical, mental and social well¬being and not merely the absence of disease or infirmity.

3. Short Answer Questions

Question 1.
What are acquired diseases?
Answer:
Diseases which are developed after the birth of an individual are called acquired diseases. These are of two types, viz. (a) Communicable or infectious diseases and (b) Non- communicable or Non-infectious diseases. Communicable or infectious diseases are transmitted from infected person to another healthy person either directly or indirectly. They are caused due to pathogens like viruses, bacteria, fungi, helminth worms, etc. Non-communicable or Non-infectious diseases cannot be transmitted from infected person to another healthy one either directly or indirectly.

Question 2.
Antigen and antibody.
Answer:

Question 3.
Name the infective stage of Plasmodium. Give Symptoms of malaria
Answer:
Sporozoite
I. Symptoms of malaria:

1. Fever accompanied by shivering.
2. Joint pain or arthralgia.
3. Vomiting.
4. Anaemia caused due to rupture of RBCs or haemolysis.
5. Haemoglobinuria.
6. Retinal damage.
7. Convulsions.
8. Cyclical occurrence of sudden coldness followed by rigor and then fever and sweating lasting for four to six hours. This is called a classic symptom of malaria.
9. Splenomegaly or enlarged spleen, severe headache, cerebral ischemia, hepatomegaly, i. e. enlarged liver, hypoglycaemia and haemoglobinuria with renal failure may occur in severe infections.

II. Spread / Transmission of malaria:

1. Malaria parasite is transmitted through the female Anopheles mosquito and hence it is known as mosquito-borne disease. Mosquito acts as a vector.
2. There are four species of Plasmodium, viz., P. vivax, P. falciparum, P. ovale and P. malariae which transmit malaria.

Question 4.
Explain the mode of infection and cause of elephantiasis.
Answer:
Mode of infection, i.e. transmission:

1. The parasite Wuchereria bancrofti is transmitted from a patient to other normal human being by female Culex mosquito.
2. The filarial larvae leave mosquito body and arrive on the human skin where they penetrate the skin and enter inside.
3. They undergo two moultings to become adults. Later they settle in the lymphatic system. They incubate for about 8-16 months.
4. When they settle in lymphatic system, this infection is called lymphatic filariasis.
5. The worms start infecting lymphatic circulation resulting into enlargement of lymph vessels and lymph nodes. The extremities like legs or limbs become swollen which resembles elephant legs. Therefore it is called elephantiasis.
6. This condition is lymphoedema, i.e. accumulation of lymph fluid in tissue causing swelling.

Question 5.
Why is smoking a bad habit?
Answer:

1. Smoking involves inhaling the cigarette smoke which contains nicotine and other toxic substances like N-nitrosodimethlene. There is some amount of carbon monoxide.
   All these substances affect the normal respiratory health.
2. Smoking invites problems like asthma, hypertension, heart disease, stroke, lung damage.
3. The worst impact is that these substances are carcinogenic and hence can cause cancer of larynx, trachea, lung, etc.
4. Smoking not only affects the smokers but also has bad effect on others due to passive smokers.
5. In women, smoking is still hazardous as their ovaries can undergo mutations due to mutagenic chemicals found in smoke.
6. Therefore, smoking is a very bad habit.

Question 6.
What do the abbreviations AMIS and CMIS denote?
Answer:
AMIS is Antibody-mediated immune system or humoral immunity and CMIS is cell- mediated immune system.

Question 7.
What is a carcinogen? Name one chemical carcinogen with its target tissue.
Answer:

1. Carcinogen is the substance or agent that causes cancer.
2. Urinary bladder cancer caused by 2-naphthylamine and 4-aminobiphenyl.

Question 8.
Active immunity and passive immunity.
Answer:

4. Short Answer Questions

Question 1.
B-cells and T-cells.
Answer:

Question 2.
What are the symptoms of malaria? How does malaria spread?
Answer:
Symptoms of malaria:

1. Fever accompanied by shivering.
2. Joint pain or arthralgia.
3. Vomiting.
4. Anaemia caused due to rupture of RBCs or haemolysis.
5. Haemoglobinuria.

Question 3.
AIDS.
Answer:
(1) AIDS or the acquired immuno deficiency syndrome, is fatal viral disease caused by a retrovirus (ss RNA) known as the human immuno deficiency virus (HIV) which weakens the body’s immune system. It is called a modern pandemic.

(2) The HIV attacks the immune system which in turn causes many opportunistic infections, neurological disorders and unusual malignancies ultimately leading to death.

(3) AIDS was first noticed in USA in 1981 whereas in India, first confirmed case of AIDS was in April 1986 from Tamil Nadu.

(4) HIV is transmitted through body fluids such as saliva, tears, nervous system tissue, spinal fluid, blood, semen, vaginal fluid and breast milk. However, only blood, semen, vaginal secretions and breast milk generally transmit infection to others.

(5) The transmission of HIV occurs by sexual contact, through blood and blood products and by contaminated syringes, needles, etc. There is also transplacental transmission or through breast milk at the time of nursing.

(6) Accidental needle injury, artificial insemination with infected donated semen and transplantation with infected organs are some of the rare occasions of transmission of HIV.

(7) HIV infection is not spread by casual contact such as hugging, bite of mosquitoes or using other objects touched by a patient.

(8) Acute HIV infection progresses over time to asymptomatic HIV infection and then to early symptomatic HIV infection. Later, it progresses to full blown AIDS when patient shows advanced HIV infection with CD4 T-cell count below 200 cells/mm.

Question 4.
Give the symptoms of cancer.
Answer:
Symptoms of cancer:

1. Presence of lump or tumour.
2. White patches in the mouth.
3. Change in a wart or mole on the skin.
4. Swollen or enlarged lymph nodes.
5. Vertigo, headaches or seizures if cancer affect the brain.
6. Coughing and shortness of breath if lungs are affected due to cancer.

Question 5.
Antigens on blood cells.
Answer:

1. There are about 30 known antigens on the surface of human red blood cells. They decide the type of blood group such as ABO, Rh, Duffy, Kidd, Lewis, P MNS, Bombay.
2. The different blood groups are determined genetically due to presence of a particular antigen.
3. Landsteiner found two antigens or agglutinogens on the surface of human red blood cells which are named as antigen A and antigen B.
4. There is another antigen called Antigen D which decides the Rh status of the blood. If Antigen D is present, the person is said to be RH positive and when it is lacking, the person is Rh negative.
5. These antigens are responsible for types of blood group and the specific transfusions.
6. Antigens present on the RBCs and antibodies present in the serum can cause agglutination reactions if they are non-compatible. Therefore, at the time of transfusion blood groups are checked properly.

Question 6.
Antigen-antibody complex:
Img 1
Answer:

1. Between antigen and antibody there is specificity.
2. Each antibody is specific for a particular antigen.
3. On the antigens there are combining sites which are called antigenic determinants or epitopes.
4. Epitopes react with the corresponding antigen binding sites of antibodies which are called paratopes.
5. The antigen binding sites are located on the variable regions of the antibody. Variable regions have small variations which make each antibody highly specific for a particular antigen.
6. Owing to variable region the antibody can recognize the specific antigen.
7. Antibody thus binds to specific antigen in a lock and key manner, forming an antigen- antibody complex.

Question 7.
What are the various public health measures, which you would suggest as safeguard against infectious diseases?
Answer:
Infectious diseases spread through pathogens, therefore, it is an important duty of each person to decrease the risk of infecting our own self or others. This can be achieved by

1. Washing hands often, especially whenever, we are in contact with food and water. Before and after preparing food, before eating and after using the toilet, hand wash is a must.
2. Vaccinations : Immunization helps us to protect against contracting many diseases. Therefore, timely vaccination should be taken. Especially at the time of epidemic, one must keep distance from infected area or get vaccinated.
3. One must be at home if there are signs and symptoms of an infection. By going out, we may infect other healthy persons.
4. Proper diet and exercise should be followed to improve one’s own immunity.
5. Hygiene should be utmost in the kitchen and dining area. One must take care while eating uncovered and leftover food.
6. Bathroom and toilet should be cleaned daily as there can be a high concentration of bacteria or other infectious agents in these areas.
7. One should have responsible sexual behaviour to avoid sexually transmitted diseases.
8. Personal items such as toothbrush, comb, towel, undergarments or razor blade should never be shared.
9. Travelling should be avoided because we may infect other passengers during travel. Moreover, our illness can be aggravated. Some special immunizations are needed during certain travels, such as anti-cholera vaccine while going to Pandharpur during Ashadhi.

Question 8.
How does the transmission of each of the following diseases take place?
(a) Amoebiasis:
Answer:
Amoebiasis is usually transmitted by the following ways:

1. The faecal-oral route.
2. Through contact with dirty hands or objects.
3. By anal-oral contact.
4. Through contaminated food and water.

(b) Malaria:
Answer:
Symptoms of malaria:

1. Fever accompanied by shivering.
2. Joint pain or arthralgia.
3. Vomiting.
4. Anaemia caused due to rupture of RBCs or haemolysis.
5. Haemoglobinuria.

(c) Ascariasis:
Answer:

1. Unsafe and unhygienic food and drinks contaminated with the eggs of Ascaris are the main mode of transmission.
2. Eggs hatch inside the intestine of the new host.
3. The larvae pass through various organs and settle as adults in the digestive system.

(d) Pneumonia:
Answer:

1. Pneumonia usually spreads by direct person to person contact.
2. It is also spread via droplet infection, i.e. droplets released by infected person.
3. Using clothes and utensils of the patient.

Question 9.
What measures would you take to prevent water-borne diseases?
Answer:

1. To prevent water-borne diseases, use of safe, clean and potable water is a must. Water should be filtered, then boiled and stored in covered container. If possible water purifier systems should be installed at home.
2. One should preferably use bottled water or carry our own water container while travelling.
3. Cleaning of water containers and maintaining personal hygiene near water storage is a must.
4. Megacities offer chlorinated and purified water for citizens. But villages and smaller rural set ups use river water which may be highly contaminated with pathogens. Such water should be purified before consumption to prevent water-borne diseases.

Question 10.
Typhoid.
Answer:
Typhoid is an infective disease caused by Gram-ve bacterium, Salmonella typhi.
(1) It is food and water-borne infection. In the intestinal lumen of infected person this bacteria is found.

(2) The bacterium has “O” – antigen, which is a lipopolysaccharide (LPS), present on surface coat and its flagella has “H” – antigen. Thus it becomes pathogenic.

(3) Signs and Symptoms of typhoid are as follows:
Prolonged and high fever with nausea, fatigue, headache.
Abdominal pain, constipation or diarrhoea. In severe cases rose-coloured rash is seen on skin. Tongue shows white coating and there is cough. Anorexia or loss of appetite is seen. In chronic cases there is breathlessness, irregular heartbeats and haemorrhage.

(4) Poor hygiene habits and poor sanitation and insects like houseflies and cockroaches spread typhoid.

(5) Typhoid is diagnosed by Widal test.

(6) Antibiotics like Chloromycetin can cure typhoid. Preventive vaccines such as oral Ty21a vaccine and injectable typhim vi and typherix against typhoid are also available. Chronic cases need surgical removal of gall bladder.

5. Match the following.

Answer:

6. Long Answer Questions

Question 1.
Describe the structure of antibody.
Answer:
Img 2

1. Antibodies are highly specific to specific antigens. They are glycoprotein called immunoglobulins (Igs.).
2. They are produced by plasma cells. Plasma cells are in turn formed by B-lymphocytes.
3. About 2000 molecules of antibodies are formed per second by the plasma cells.
4. Antibody is a ‘Y’-shaped molecule. It has four polypeptide chains, two heavy or H-chains and two light or L-chains.
5. Disulfide bonds (-s-s-) hold the polypeptide chains together to form a ‘Y’-shaped structure.
6. The region holding arms and stem of antibody is termed as hinge. Each chain of the antibody has two distinct regions, the variable region and the constant region.
7. Variable regions have a paratope which is an antigen-binding site. This part of antibody recognizes and binds to the specific antigen forming an antigen-antibody complex.
8. Antibodies are called bivalent as they carry two antigen binding sites.

Question 2.
Vaccination.
Answer:

1. Vaccines are prepared from inactivated pathogen, in the form of protein or sugar from pathogen or dead form of pathogen or toxoid from pathogens or attenuated pathogen.
2. These when they are administered to a person to protect against a particular pathogen, it is called vaccination.
3. Vaccination ’teaches’ the immune system to recognize and eliminate pathogenic organism. Because, already in the body the vaccine is injected and body has made antibodies in response to it. Thus, body is prepared before the attack, if at all it is exposed to pathogen.
4. Thus, it is an important form of primary prevention, which reduces the chances of illness by protecting people. It works by exposing the pathogen in a safe form.
5. Vaccinations control spread of diseases like measles, polio, tetanus and whooping cough that once threatened many lives.
6. Vaccination controls the epidemic outbreak of diseases, if all the people Eire pre-vaccinated.
7. Some hazardous diseases like small, pox and polio have been completely eradicated by the vaccination.

Question 3.
What is cancer? Differentiate between benign tumour and malignant tumour. The main five types of cancer
Answer:
I. Cancer : Cancer is a disease caused by uncontrolled cell division due to disturbed cell cycle.

II. Difference between benign tumour and malignant tumour:

III. The main five types of cancer:

Types of Cancer : According to the tissue affected, the cancers are classified into five main types. These are as follows:

1. Carcinoma : Cancer of epithelial tissue covering or lining the body organs is known as carcinoma. E.g. breast cancer, lung cancer, cancer of stomach, skin cancer, etc.
2. Sarcoma : Cancer of connective tissue is called sarcoma. Following are the types of sarcoma osteosarcoma (bone cancer), myosarcoma (muscle cancer),
   chondrosarcoma (cancer of cartilage) and liposarcoma (cancer of adipose tissue).
3. Lymphoma : Cancer of lymphatic tissue is called lymphoma. Lymphatic nodes, spleen and tissues of immune system are affected due to lymphoma.
4. Leukaemia : Leukaemia is blood cancer. In this condition, excessive formation of leucocytes take place in the bone marrow. There are millions of abnormal immature leucocytes which cannot fight infections. Monocytic leukaemia, lymphoblastic leukaemia, etc. are the types of leukaemia.
5. Adenocarcinoma : Cancer of glandular tissues such as thyroid, pituitary, adrenal, etc. is called adenocarcinoma.

Question 4.
Describe the different type of immunity.
Answer: There are two basic types of immunity, viz. innate immunity and acquired immunity.
(A) Innate immunity:

1. Innate immunity is natural, inborn immunity, which helps the body to fight against the invasion of microorganisms.
2. Innate immunity is non-specific because it does not depend on previous exposure to foreign substances.
3. Innate immunity mechanisms consist of various types of barriers such as anatomical barriers, physiological barriers, phagocytic barriers and inflammatory barriers. They prevent entry of foreign agents into the body.

(B) Acquired immunity:

1. The immunity that an individual acquires during his life is called acquired immunity or adaptive immunity or specific immunity. It helps the body to adapt by fighting against specific antigens hence it is called adaptive immunity. Since it is produced specifically against an antigen, it is called specific immunity.
2. Acquired immunity takes long time for its activation.
3. This type of immunity is seen only in vertebrates.
4. Due to acquired immunity, the body is able to defend against any invading foreign agent.

Question 5.
Describe the ill-effects of alcoholism on health.
Answer:

1. Alcohol in any form is toxic for the body. Hence as soon as alcohol is consumed, the liver tries to detoxify it.
2. In low doses it acts as a stimulant but in high dose, it acts on central nervous system, especially the cerebrum and cerebellum. Still higher dose can induce a comatose condition.
3. Alcohol affect the gastrointestinal tract by causing inflammation and damage to gastric 4 mucosa. Ulceration and painful condition arises in alcoholics.
4. Excessive doses of alcohol induce vomiting.
5. The worst effect of alcohol is on liver causing diseases like cirrhosis.
6. Alcohol induces hypertension and cardiac problems.
7. Apart from physical effect, it causes deterioration of mental health and emotional well-being.
8. Alcoholic person cannot think due to numbness in his/her cerebrum.
9. The social health is greatly affected as the alcoholic can cause problems to his family, friends and society in general.

Question 6.
In your view, what motivates the youngsters to take to alcohol or drugs and how can this be avoided?
Answer:
I. Taking drugs or alcohol:

1. Youngsters are at the vulnerable age, where they lack the planning about their future.
2. If they fall into bad company or are facing parental neglect, they get hooked on to alcohol or drugs.
3. Some common causes for addiction among youngsters are insufficient parental supervision and monitoring or excessive pressure and expectations from them. Lack of communication between an adolescent and parents.
4. Poorly defined rules for the family. Continuous family conflicts.
5. Favourable parental attitudes towards alcohol and drug uses. Many a times, at home children are exposed to such habits.
6. Inability to cope up with present and hence switching to the addictions. Risk taking behaviour which is common among youngsters.

II. Methods/measures to avoid drug abuse:

1. There should be complete acceptance for the child, because the adolescent phase is the most crucial phase when the children should be treated with love, care and respect.
2. Many physical, hormonal and psychological transformations are taking place in this phase. Therefore child suffers from stressful situation.
3. Wrong company and bad influence of peer group can trap the child in bad addictive habits. Thus, family should be supportive and communicative to help such children.
4. The sexual thoughts should be sublimed by channelizing energy into healthy pursuits like sports, reading, music, yoga and other extracurricular activities.
5. Ill-effects of drugs or alcohol should be told to youngsters.
6. Education and counselling can control the children from getting hooked on to the addictions.

Question 7.
Do you think that friends can influence one to take alcohol/drugs? If yes, how may one protect himself/herself from such an influence?
Answer:
Friends can influence one to take alcohol and drugs, if a boy or girl is timid and non-communicative with his or her parents and teachers. It also depends on the personality of the indtvidual. In the adolescent age, many fall in trap due to such peer pressure. The confusion in the mind and role of hormones playing on the psyche and thought process makes one unable to understand the hazards of such habits. Also there is curiosity to do these experimentations due to bad influence of media.

If there is complete trust and friendship with sensible parents, then such influence does not work. One should protect himself or herself by a strong denial. Communicating such incidents to an elder in whom a boy or girl can confide, is very important. One should tell his or her friends about the ill-effects of alcohol and drugs. He should be made aware of these aspects that he or she has learnt in this lesson.

Maharashtra State Board 12th Std Biology Textbook Solutions 

• Control and Co-ordination Class 12 Biology Textbook Solutions
• Human Health and Diseases Class 12 Biology Textbook Solutions
• Enhancement of Food Production Class 12 Biology Textbook Solutions
• Biotechnology Class 12 Biology Textbook Solutions
• Organisms and Populations Class 12 Biology Textbook Solutions
• Ecosystems and Energy Flow Class 12 Biology Textbook Solutions
• Biodiversity, Conservation and Environmental Issues Class 12 Biology Textbook Solutions

Control and Co-ordination Class 12 Exercise Question Answers Solutions Maharashtra Board

Balbharti Maharashtra State Board 12th Biology Textbook Solutions Chapter 9 Control and Co-ordination Textbook Exercise Questions and Answers.

Class 12 Biology Chapter 9 Exercise Solutions Maharashtra Board

Biology Class 12 Chapter 9 Exercise Solutions

1. Multiple choice questions

Question 1.
The nervous system of mammals uses both electrical and chemical means to send signals via neurons. Which part of the neuron receives impulse?
(a) Axon
(b) Dendron
(c) Nodes of Ranvier
(d) Neurilemma
Answer:
(b) Dendron

Question 2.
……………. is a neurotransmitter.
(a) ADH
(b) Acetyl CoA
(c) Acetyl choline
(d) Inositol
Answer:
(c) Acetyl choline

Question 3.
The supporting cells that produce myelin sheath in the PNS are …………….
(a) Oligodendrocytes
(b) Satellite cells
(c) Astrocytes
(d) Schwann cells
Answer:
(d) Schwann cells

Question 4.
A collection of neuron cell bodies located outside the CNS is called …………….
(a) tract
(b) nucleus
(c) nerve
(d) ganglion
Answer:
(d) ganglion

Question 5.
Receptors for protein hormones are located …………….
(a) in cytoplasm
(b) on cell surface
(c) in nucleus
(d) on Golgi complex
Answer:
(b) on cell surface

Question 6.
If parathyroid gland of man Eire removed, the specific result will be …………….
(a) onset of aging
(b) disturbance of Ca⁺⁺
(c) onset of myxoedema
(d) elevation of blood pressure
Answer:
(b) disturbance of Ca⁺⁺

Question 7.
Hormone thyroxine, adrenaline and non¬adrenaline are formed from ……………
(a) Glycine
(b) Arginine
(c) Ornithine
(d) Tyrosine
Answer:
(d) Tyrosine

Question 8.
Pheromones are chemical messengers produced by animals and released outside the body. The odour of these substance affects …………….
(a) skin colour
(b) excretion
(c) digestion
(d) behaviour
Answer:
(d) behaviour

Question 9.
Which one of the following is a set of discrete endocrine gland?
(a) Salivary glands, thyroid, adrenal, ovary
(b) Adrenal, testis, ovary, liver
(c) Pituitary, thyroid, adrenal, thymus
(d) Pituitary, pancreas, adrenal, thymus
Answer:
(c) Pituitary, thyroid, adrenal, thymus

Question 10.
After ovulation, Graafian follicle changes into …………….
(a) corpus luteum
(b) corpus albicans
(c) corpus spongiosum
(d) corpus callosum
Answer:
(a) corpus luteum

Question 11.
Which one of the following pairs correctly matches a hormone with a disease resulting from its deficiency?
(a) Parathyroid hormone – Diabetes insipidus
(b) Luteinising hormone – Diabetes mellitus
(c) Insulin – Hyperglycaemia
(d) Thyroxine – Tetany
Answer:
(c) Insulin – Hyperglycaemia

Question 12.
……………. is in direct contact of brain in humans.
(a) Cranium
(b) Dura mater
(c) Arachnoid
(d) Pia mater
Answer:
(d) Pia mater

2. Very very short answer questions.

Question 1.
What is the function of red nucleus?
Answer:
Red nucleus plays an important role in controlling posture and muscle tone, modifying some motor activities and motor coordination.

Question 2.
What is the importance of corpora quadrigemina?
Answer:
Corpora quadrigemina consists of 4 solid rounded structures, viz. superior and inferior colliculi. Superior colliculi control visual reflexes while inferior colliculi control auditory reflexes.

Question 3.
What does the cerebellum of brain control?
Answer:
Cerebellum of brain is an important centre which maintains equilibrium of body, posture, balancing orientation, moderation of voluntary movements and maintenance of muscle tone.

Question 4.
Name the three ear ossicles.
Answer:
Malleus [hammer], incus [anvil] and stapes [stirrup].

Question 5.
Name the anti abortion hormone.
Answer:
Progesterone.

Question 6.
Name an organ which acts as temporary endocrine gland.
Answer:
Placenta. Corpus luteum in ovary.

Question 7.
Name the type of hormones which bind to the DNA and alter the gene expression.
Answer:
Steroid hormones.

Question 8.
What is the cause of abnormal elongation of long bones of arms and legs and of lower jaw.
Answer:
Hypersecretion of growth hormones in adults causes abnormal elongation of long bones of arms and legs and of lower jaw i.e. acromegaly.

Question 9.
Name the hormone secreted by the pineal gland.
Answer:
Melatonin.

Question 10.
Which endocrine gland plays important, role in improving immunity?
Answer:
The endocrine gland, thymus plays an important role in improving immunity.

3. Match the organism with the type of nervous system found in them.

Answer:

4. Very short answer questions.

Question 1.
Describe the endocrine role of islets of Langerhans.
OR
Islets of Langerhans.
Answer:
Endocrine cells of pancreas form groups of cells called Islets of Langerhans. There are four kinds of cells in islets of Langerhans which secrete hormones.

1. Alpha (α) cells : They are 20% and secrete glucagon. Glucagon is a hyperglycemic hormone. It stimulates liver for glucogenolysis and increases the blood glucose level.
2. Beta (β) cells : They are 70% and secrete insulin. Insulin is a hypoglycemic hormone. It stimulates liver and muscles for glycogenesis. This lowers blood glucose level.
3. Delta (δ) cells : They are 5% and secrete somatostatin. Somatostatin inhibits the secretion of glucagon and insulin. It also decreases the gastric secretions, motility and absorption in digestive tract. In general it is a growth inhibiting factor.
4. PP cells or F cells : They form 5%. They secrete pancreatic polypeptide (PP) which inhibits the release of pancreatic juice.

Question 2.
Mention the function of testosterone?
Answer:
Testosterone is a steroid sex hormone secreted by testes and cortex of adrenal glands. It controls the secondary sexual characters in males.

Question 3.
Give symptoms of the disease caused by hyposecretion of ADH.
Answer:
Polydipsia, i.e. frequent thirst and polyuria, i.e. frequent urination are the symptoms of the disease caused by hyposecretion of ADH.

5. Short answer questions

Question 1.
Rakesh got hurt on his head when he fell down from his motorbike. Which inner membranes must have protected his brain? What other roles do they have to play
Answer:

1. When Rakesh fell down from his motorbike, the inner membranes that protected his brain were meninges, viz. dura mater, arachnoid membrane and pia mater. Morevover, CSF must have also acted as a shock absorber.
2. Dura mater : It is the outer tough membrane protective in function.
3. Arachnoid membrane : It is the middle web-like membrane which communicates with fluids of upper sub dural space and lower sub arachnoid space.
4. Pia mater : It is the innermost highly vascularised nutritive membrane in close contact with brain and spinal cord.

Question 2.
Injury to medulla oblongata may prove fatal.
OR
Injury to medulla oblongata causes sudden death. Explain.
Answer:

1. Medulla oblongata is the region of the brain that controls all the involuntary activities.
2. Vital activities such as heartbeats, respiration, vasomotor activities, peristalsis, etc. are under the control of medulla oblongata.
3. When medulla oblongata is injured, all these vital functions are instantly stopped.
4. Therefore, injury to medulla oblongata causes sudden death.

Question 3.
Distinguish between the sympathetic and parasympathetic nervous system on the basis of the effect they have on:
Heartbeat andUrinary Bladder.
Answer:

Question 4.
While holding a tea cup Mr. Kothari’s hands rattle. Which disorder he may be suffering from and what is the reason for this?
Answer:

1. This condition is due to Parkinson’s disease.
2. It is due to degeneration of dopamine- producing neurons in the CNS.
3. 80% of the patients develop this condition along with stiffness, difficulty in walking, balance and coordination.

Question 5.
List the properties of the nerve fibres.
Answer:

1. Excitability / irritability
2. Conductivity
3. Stimulus
4. Summation
5. All or none
6. Refractory period
7. Synaptic delay
8. Synaptic fatigue
9. Velocity.

Question 6.
How does tongue detect the sensation of taste?
Answer:

1. The surface of tongue is with gustatoreceptors.
2. These receptors are sensitive to the chemicals [sweet, salt, sour, bitter and umami (savory)] present in the food.
3. The receptor cells get stimulated, generate the impulse which is given to the sensory neuron.

Question 7.
State the site of production and function of Secretin, Gastrin and Cholecystokinin.
Answer:

Question 8.
An adult patient suffers from low heart rate, low metabolic rate and low body temperature. He also lacks alertness, intelligence and initiative. What can be this disease? What can be its cause and cure ?
Answer:

1. The above symptoms indicate that the person is suffering from Myxoedema.
2. Myxoedema is condition caused due to hypothyroidism.
3. Hypothyroidism causes deficiency of thyroid hormones like T₃ and T₄ (thyroxine). This results in low BMR.
4. This condition can be cured by giving injections of thyroxine or tablets containing hormone preparation.

Question 9.
Where is the pituitary gland located? Enlist the hormones secreted by anterior pituitary.
Answer:
The pituitary gland is attached to hypothalamus on the ventral surface of brain. It is lodged in a bony depression called sella turcica of sphenoid bone.
For names of hormones:

1. GH : [Growth Hormone/STH : Somatotropic Hormone]
2. TSH/TTH – [Thyroid Stimulating Hormone/ Thyrotropic Hormone]
3. ACTH – [adrenocorticotropic hormone]
4. PRL – [prolactin]

Gonadotropins-

1. FSH [follicle stimulating hormone]
2. LH/ICSH – [leutinizing hormone/ interstitial cells stimulating hormone]

Question 10.
Explain how the adrenal medulla and sympathetic nervous system function as a closely integrated system.
Answer:

1. Adrenal medulla originates from embryonic neuro – ectoderm.
2. It consists of rounded group of large granular cells called chromaffin cells. They are modified post-ganglionic cells of sympathetic nervous system which have lost normal processes and acquired glandular function.
3. These cells are connected with pre-ganglionic fibres of sympathetic nervous system.
4. Hence adrenal medulla is an extension of sympathetic nervous system.
5. Thus adrenal medulla and sympathetic nervous system functions as a closely integrated system.

Question 11.
Name the secretion of alpha, beta and delta cells of islets of Langerhans. Explain their role.
Answer:

Question 12.
Which are the two types of goitre? What are their causes?
Answer:
(1) Goitre is the enlargement of thyroid gland. It is easily visible at the base of neck when a person is suffering from it.

(2) Goitre is of two types.

1. Simple goitre : It is also called endemic goitre. This is due to iodine deficiency in the food. This causes iodine deficit in blood. In an attempt to take more iodine from blood, the blood supply to the gland increases. This results in swelling on the thyroid.
2. Exophthalmic goitre : It is also called toxic goitre. This is due to hyperactive thyroid gland. This can happen if there is overstimulation of thyroid due to excess of ACTH. This disorder is also called Grave’s disease or hyperthyroidism.

Question 13.
Name the ovarian hormone and give their functions.
Answer:

6. Answer the following.

Complete the table.

Answer:

7. Long answer questions.

Question 1.
Explain the process of conduction of nerve impulses up to development of action potential.
Answer:

1. The origin and maintenance of resting potential depends on the original state of no stimulation.
2. Any stimulus or disturbance to the membrane will make the membrane permeable to Na⁺ ions. This causes rapid influx of Na⁺ ions.
3. The voltage gated Na⁺/K⁺ channels are unique. They can change the potential difference of the membrane as per the stimulus received and also the gates operate separately and are self closing.
4. During resting potential, both gates are closed and resting potential is maintained.
5. However during depolarization, the Na⁺ channels open but not the K⁺ channels. This causes Na⁺ to rush into the axon and bring about a depolarisation. This condition is called action potential.
6. Extra cellular fluid (ECF) becomes electronegative with respect to the inner membrane which becomes electropositive.

Question 2.
Draw the neat labelled diagrams.
a. Human ear.
Answer:

b. Sectional view of human eye.
Answer:

c. Draw the neat labelled diagram of sagittal section or L.S. of human brain
Answer:

d. Draw the neat labelled diagram of Multipolar Neuron.
Answer:

Question 3.
Answer the questions after observing the diagram given below.

a. What do the synaptic vesicles contain?
Answer:
Synaptic vesicles contain a neurotransmitter – acetyl choline.

b. What process is used to release the neurotransmitter ?
Answer:
Exocytosis.

c. What should be the reason for the next impulse to be conducted?
Answer:
Removal of neurotransmitter by the action of acetyl cholinesterase.

d. Will the impulse be carried by post synaptic membrane even if one pre-synaptic neuron is there?
Answer:
As far as impulse is transmitted by pre-synaptic neuron, it will be received by post-synaptic neuron.

e. Can you name the channel responsible for their transmission?
Answer:
Ca⁺⁺ channel

Question 4.
Explain the Reflex Pathway with the help of a neat labelled diagram.
OR
With the help of a neat and labelled diagram, describe reflex arc.
Answer:

I. Reflex action : Reflex action Is defined as a quick, automatic involuntary and often unconscious action brought about when the receptors are stimulated by external or internal stimuli.

II. Reflex arc : Reflex actions are controlled by CNS. Reflex arc is the structural or functional unit of reflex action. Simple reflex arc is formed of the following five components.
(1) Receptor organ : The sensory part that receives the stimulus is called receptor organ. It can be any sense organ that receives the stimulus and converts it into the impulse, e.g. skin, eye, ear, tongue, nasal epithelium, etc.

(2) Sensory neuron or afferent neuron:
Sensory part carrying impulse from receptor organ to CNS is called sensory neuron. Its cyton is located in dorsal root ganglion. Its dendron is long and connected to receptor while the axon enters in the grey matter of spinal cord to form a synapse.

(3) Association, adjustor or intermediate neuron : It is present in the grey matter of spinal cord. Receiving impulse from sensory neuron, interpreting it and generating motor impulse are done by association neuron.
(4) Motor neuron (effector) : The cyton of motor neuron is present in the ventral horn of grey matter and axon travels through ventral root. It conducts motor impulse from spinal cord to effector organ.

(5) Effector organ : Effector organ is a specialized part of the body which is excited by receiving the motor impulse. It gives proper response to the stimulus, e.g. muscles or glands. The path of reflex action is followed by the unidirectional impulse. It originates in the receptor organ and ends in effector organ through CNS.

Question 5.
Krishna was going to school and on the way he saw a major bus accident. His heartbeat increased and hands and feet become cold. Name the part of the nervous system that had a role to play in this reaction.
Answer:

1. The symptoms observed in Krishna were due to sympathetic nervous system. Emergency conditions trigger sympathetic nervous system to stimulate adrenal medulla.
2. The cells of adrenal medulla secrete catecholamines like adrenaline and nor¬adrenaline.
3. These hormones have direct effect on the pacemaker of the heart which causes increase in the heart rate and other associated symptoms.
4. This is a typical fright reaction caused by intervention of sympathetic nervous system.

Question 6.
What will be the effect of thyroid gland atrophy on the human body?
Answer:

1. Atrophy means degeneration. Atrophy of thyroid gland will result in deficient secretion of thyroid hormones leading to hypothyroidism. Deficiency of thyroid hormones [T₃ and T₄] and thyrocalcitonin will cause following effects on the body.
2. Decrease in BMR i.e. basal metabolic rate, decrease in the blood pressure, heart beat, body temperature, etc.
3. Occurrence of myxoedema in which there is abnormal deposition of fats under the skin giving puffy appearance in adults.
4. Irregularities in menstrual cycle in case of female patients.
5. Hair become brittle and fall.
6. Calcium metabolism also disturbs due to lack of thyrocalcitonin.

Question 7.
Write the names of hormones and the glands secreting them for the regulation of following functions
(a) Growth of thyroid and secretion of thyroxine.
Answer:
TSH by adenohypophysis.

(b) Helps in relaxing pubic ligaments to facilitate easy birth of young ones.
Answer:
Relaxin by degenerating corpus luteum of the ovary.

(c) Stimulate intestinal glands to secrete intestinal juice.
Answer:
Secretin by duodenal mucosa.

(d) Controls calcium level in the blood.
Answer:
Calcitonin [hypocalcemic hormone] by thyroid and parathormone [ hypercalcemic hormone] by parathyroid glands.

(e) Controls tubular absorption of water in kidneys.
Answer:
ADH by hypothalamus.

(f) Urinary elimination of water.
Answer:
Atrial natriuretic factor by atria of heart.

(g) Sodium and potassium ion metabolism.
Answer:
Aldosterone by adrenal cortex.

(h) Basal Metabolic rate.
Answer:
T₃ and T₄ by thyroid gland.

(I) Uterine contraction.
Answer:
Oxytocin by hypothalamus.

(j) Heartbeat and blood pressure.
Answer:
Adrenaline, non-adrenaline [stimulation] and acetylcholine [inhibition] by adrenal medulla.

(k) Secretion of growth hormone.
Answer:
GHRF by hypothalamus.

(l) Maturation of Graafian follicle.
Answer:
FSH by anterior pituitary.

Question 8.
Explain the role of hypothalamus and pituitary as a coordinated unit in maintaining homeostasis.
Answer:

1. Homeostasis is maintenance of constant internal environment of the body.
2. When certain hormones from any endocrine glands are secreted in excess quantity, the : inhibiting factors from hypothalamus, automatically exert negative feedback and stop the production of stimulating hormones from pituitary.
3. Similarly, if any hormone is in deficit, then j the concerned gland is given message through releasing factor. This way the hormone production remains in a balanced state or homeostasis.
4. E.g. If thyroxine from thyroid gland is secreted in excess, the secretion of TSH from pituitary is stopped by stopping the production of TRF from hypothalamus.
5. Though most of the endocrine glands are under the influence of pituitary gland, it is in turn controlled by hypothalamus.
6. Hypothalamus secretes releasing factors and inhibiting factors and hence regulate the secretions of pituitary (hypophysis).
7. There is negative feedback mechanism in controlling the secretions of the endocrine glands.
8. Hypothalamus forms the hypothalamo- hypophyseal axis through which transportation of neurohormones take place.

Following are the releasing and inhibiting factors produced by hypothalamus:

1. Somatotropin/GHRF : It stimulates release of growth hormone.
2. Somatostatin/GHRIF : It inhibits the release of growth hormone.
3. Adrenocorticotropin Releasing Hormone / CRF : It stimulates the release of ACTH by the anterior pituitary gland.
4. Thyrotropin Releasing Hormone /TRF : It stimulates the release of TSH by anterior pituitary gland.
5. Gonadotropin Releasing Hormone (GnRH) : It stimulates pituitary to secrete gonadotropins.
6. Prolactin Inhibiting Hormone (Prolactostatin) : It inhibits prolactin released by anterior pituitary gland.
7. Gastrin Releasing Peptide (GRP).
8. Gastric Inhibitory Polypeptide (GIP).

Question 9.
What is adenohypophysis ? Name the hormones secreted by it.
Answer:

1. Adenohypophysis is the large anterior lobe of pituitary gland.
2. It is derived from embryonic ectoderm in the form of Rathke’s pouch which is a small outgrowth from the roof of embryonic stomodaeum.
3. It is made up of epitheloid secretory cells.

It secretes following hormones:

1. GH : [Growth Hormone/STH : Somatotropic Hormone]
2. TSH/TTH – [Thyroid Stimulating Hormone/ Thyrotropic Hormone]
3. ACTH – [adrenocorticotropic hormone]
4. PRL – [prolactin]

Gonadotropins-

1. FSH [follicle stimulating hormone]
2. LH/ICSH – [leutinizing hormone/ interstitial cells stimulating hormone]

Question 10.
Describe, in brief, an account of disorders of adrenal gland.
Answer:
(1) Disorders of adrenal cortical secretions are caused due to hyposecretion and hypersecretion of adrenal corcoid hormones.

(2) Hyposecretion of corticosteroids causes Addison’s disease.

(3) The symptoms of Addison’s disease are low blood sugar, low body temperature, feeble heart action, low BR acidosis, low Na⁺ and K⁺ concentration in plasma, excessive loss of Na⁺ and water in urine, impaired kidney functioning and kidney failure, etc. it leads to weight loss, general weakness, nausea, vomiting and diarrhoea.

(4) Hypersecretion of corticoids causes Cushing’s disease.

(5) The symptoms of Cushing’s disease are high blood sugar level, glucosuria, alkalosis, enhancement of total quantity of electrolytes in extracellular fluid, polydipsia, increased BR muscle paralysis, obesity, wasting of limb muscles, etc.

Question 11.
Explain action of steroid hormones and proteinous hormones.
OR
Explain the mode of action of steroid hormones.
Answer:
The hormones always act on their target organs or tissues to induce their effects. The target tissues have specific binding sites or receptor sites which contain hormone receptors.
I. Steroid hormones:

1. The steroid hormones are lipid soluble and can easily cross the lipoproteinous plasma membrane.
2. The hormone receptors for steroid hormones are present in cytoplasm or in nucleus.
3. Hormone-receptor complex formed in cytoplasm enters the nucleus and regulate the gene expression or chromosome function.
4. In some cases the receptors are present inside the nucleus where hormone receptor complex is formed.
5. These complexes interact with the genome to evoke biochemical changes that result in physiological and developmental functions.

II. Protein hormones:

1. The hormone receptors for protein hormones are present on the cell membrane (i.e. membrane bound receptors).
2. When the hormone binds to its receptor, it forms hormone-receptor complex. Each receptor is specific to a specific hormone.
3. The hormones which interact with membrane bound receptors normally do not enter the target cell but generate second messengers. Such as cyclic AMP Ca⁺⁺ or IP (Inositol triphosphate), etc.
4. This leads to certain biochemical changes : in the target tissue.
5. Thus, the tissue metabolism and consequently the physiological functions are regulated by hormones.

Question 12.
Describe in brief an account of disorders of the thyroid.
OR
What are the functional disorders of thyroid gland? Describe in brief.
Answer:
Disorders of thyroid gland are of three types, viz. hypothyroidism, hyperthyroidism and simple goitre.
(1) Hypothyroidism : Hypothyroidism is deficient secretion of thyroxine. This hyposecretion causes two types of disorders, viz. cretinism in children and myoxedema in adults.
(i) Cretinism : Hyposecretion of thyroxine in childhood causes cretinism. The symptoms of cretinism are retardation of physical and mental growth.

(ii) Myxoedema : Deficiency of thyroxine in adults causes this disorder. It is also referred to as Gull’s disease. Symptoms are thickening and puffiness of the skin and subcutaneous tissue particularly of face and extremities. Patients with low BMR. It also causes mental dullness, loss of memory, slow action.

(2) Hyperthyroidism : Excessive secretion of thyroxine causes exophthalmic goitre or Grave’s disease. There is slight enlargement of thyroid gland. It increases BMR, heart rate, pulse rate and BE Reduction in body weight due to rapid oxidation, nervousness, irritability. Peculiar symptom is exophthalmos, i.e. bulging of eyeballs with staring look and less blinking. This is caused by deposition of fats behind the eye balls in eye sockets. There is muscular weakness and loss of weight.

(3) Simple goitre (Iodine deficiency goitre) : Simple goitre occurs due to deficiency of iodine in diet or drinking water. Simple goitre causes enlargement of thyroid gland. Thyroid gland in an attempt to get more iodine from the blood, swells due to increased blood supply. Prevention of goitre can be done by administering iodized table salt. It is also called endemic goitre as it is common in hilly areas.

Maharashtra State Board 12th Std Biology Textbook Solutions 

• Control and Co-ordination Class 12 Biology Textbook Solutions
• Human Health and Diseases Class 12 Biology Textbook Solutions
• Enhancement of Food Production Class 12 Biology Textbook Solutions
• Biotechnology Class 12 Biology Textbook Solutions
• Organisms and Populations Class 12 Biology Textbook Solutions
• Ecosystems and Energy Flow Class 12 Biology Textbook Solutions
• Biodiversity, Conservation and Environmental Issues Class 12 Biology Textbook Solutions

Plant Growth and Mineral Nutrition Class 12 Exercise Question Answers Solutions Maharashtra Board

Balbharti Maharashtra State Board 12th Biology Textbook Solutions Chapter 7 Plant Growth and Mineral Nutrition Textbook Exercise Questions and Answers.

Class 12 Biology Chapter 7 Exercise Solutions Maharashtra Board

Biology Class 12 Chapter 7 Exercise Solutions

1. Multiple choice questions

Question 1.
Which of the hormone can replace vernalization?
(a) Auxin
(b) Cytokinin
(c) Gibberellins
(d) Ethylene
Answer:
(c) Gibberellins

Question 2.
The principle pathway of water translocation in angiosperms is ………………..
(a) Sieve cells
(b) Sieve tube elements
(c) Xylem
(d) Xylem and phloem
Answer:
(c) Xylem

Question 3.
Abscissic acid controls ………………..
(a) cell division
(b) leaf fall and dormancy
(c) shoot elongation
(d) cell elongation and wall formation
Answer:
(b) leaf fall and dormancy

Question 4.
Which is employed for artificial ripening of banana fruits?
(a) Auxin
(b) Ethylene
(c) Cytokinin
(d) Gibberellin
Answer:
(b) Ethylene

Question 5.
Which of the following is required for stimulation of flowering in plants?
(a) Adequate oxygen
(b) Definite photoperiod
(c) Adequate water
(d) Water and minerals
Answer:
(b) Definite photoperiod

Question 6.
For short day plants, the critical period is ………………..
(a) light
(b) dark/night
(c) UV rays
(d) Both (a) and (c)
Answer:
(b) dark/night

Question 7.
Which of the following is NOT day neutral plant?
(a) Tomato
(b) Cotton
(c) Sunflower
(d) Soybean
Answer:
(d) Soybean

Question 8.
Essential macro elements are ………………..
(a) manufactured during photosynthesis
(b) produced by enzymes
(c) obtained from soil
(d) produced by growth hormones
Answer:
(c) obtained from soil

Question 9.
Function of Zinc is ………………..
(a) closing of stomata
(b) biosynthesis of 3-IAA
(c) synthesis of chlorophyll
(d) oxidation of carbohydrates
Answer:
(b) biosynthesis of 3-LAA

Question 10.
Necrosis means ………………..
(a) yellow spot on the leaves
(b) death of tissue
(c) darkening of green colour in leaves
(d) wilting of leaves
Answer:
(b) death of tissue

Question 11.
Conversion of nitrates to nitrogen is called ………………..
(a) ammonification
(b) nitrification
(c) nitrogen fixation
(d) denitrification
Answer:
(d) denitrification

Question 12.
How many molecules of ATP are required to fix one molecule of nitrogen?
(a) 12
(b) 20
(c) 6
(d) 16
Answer:
(d) 16

2. Very short answer questions

Question 1.
Enlist the phases of growth in plants.
Answer:
The three phases of growth are phase of cell division, phase of cell enlargement and phase of cell maturation.

Question 2.
Give full form of IAA.
Answer:
Full form is Indole Acetic Acid.

Question 3.
What does it mean by ‘open growth’?
Answer:
In plants the growth is indeterminate and takes place throughout the life at specific regions having meristems.

Question 4.
Plant stress hormone.
Answer:
Abscissic acid.

Question 5.
What is denitrification?
Answer:
Anaerobic bacteria can convert nitrates of soil back into nitrogen gas. That process performed by denitrifying bacteria is denitrification.

Question 6.
Bacteria responsible for conversion of nitrite to nitrate.
Answer:
Nitrobacter.

Question 7.
What is the role of gibberellins in rosette plants?
Answer:
In rosette plants like beet and cabbage, bolting, i.e. elongation of internodes before flowering is observed due to effect of gibberellins.

Question 8.
Vernalization
Answer:
The response of plant to the influence of low temperature on flowering in plants is called vernalization.

Question 9.
Photoperiodism
Answer:
The response of plant to the influence of light for initiation of flowering is known as photoperiodism.

Question 10.
What is grand period of growth?
Answer:
There are three phases of growth and the total time required for all phases to occur is called grand period of growth.

3. Short Answer Questions

Question 1.
(i) Differentiation
Answer:

1. It is a process of maturation of cells derived from apical meristems.
2. Differentiation is a permanent change in structure and function of cells that leads to its maturation.
3. Cell undergoes major anatomical and physiological change during differentiation process.
4. In hydrophytic plants parenchyma cells develop large schizogenous cavities which help them in aeration, buoyancy and mechanical support.

(ii) Redifferentiation
Answer:

1. It is a process in which cells produced by de-differentiation lose their capacity of division and become mature.
2. The cells mature to perform specific function.
3. Interfascicular cambium is formed by process of dedifferentiation loses its capacity to divide.
4. Secondary xylem and secondary phloem is formed form this cambium in vascular cylinder.

Question 2.
Arithmetic growth and Geometric growth
Answer:

Question 3.
Enlist the role and deficiency symptoms of: (a) nitrogen (b) phosphorus (c) potassium.
Answer:
(a) Nitrogen:
Role : Constituent of proteins as amino acids, nucleic acids, vitamins, hormones, coenzymes, ATP and chlorophyll molecule.
Deficiency symptoms : stunted growth and chlorosis.

(b) Phosphorus:
Role : Constituent of cell membrane, certain proteins, nucleic acids and nucleotides, required for all phosphorylation reactions.
Deficiency symptoms : Poor growth, leaves dull green

(c) Potassium :
Role : Determination of anion – cation balance in cell, necessary for protein synthesis, involved in formation of cell membrane, opening and closing of stomata, activates enzymes, helps in maintenance of turgidity of cells.
Deficiency symptom : Yellow edges in leaves, premature death.

Question 4.
What is short day plant? Give any two examples.
Answer:
The plants which flower when the day length or light period is shorter than the critical photoperiod are called short day plants or SDP
SDPs usually flower during winter and late summer.
Examples – Dahlia, Aster, Tobacco, Chrysanthemum, Soybean (Glycine max) and Cocklebur (Xanthium).

Question 5.
What is vernalization? Give its significance.
Answer:
A low temperature or chilling treatment that induces early flowering in plants is known as vernalization.

Significance:

1. Due to chilling treatment crops can be produced earlier.
2. Crops can be grown in areas where they do not grow naturally.

4. Long answer questions

Question 1.
Explain sigmoid growth curve with the help of diagram.
Answer:

1. When growth occurs in plants three distinct phases of growth are noticed.
2. Phase of cell formation is first phase where meristematic cells divide and new cells added.
3. In phase of cell enlargement newly formed cells elongate and with turgidity there is cell enlargement.
4. In phase of cell maturation cells get differentiated.
5. When we compare the growth rate it differs in these three phases.
6. In first phase or lag phase it is slow, while in log phase or exponential phase, growth rate accelerates and it reaches maximum.
7. In stationary phase of maturation growth rate slows down and comes to steady state.
8. When this changing rate of growth is plotted against time duration in a graph a sigmoid or S-shaped growth curve is obtained.

Question 2.
Describe the types of plants on the basis of photoperiod required, with the help of suitable examples.
Answer:

1. Effect of light duration on flowering of plants is known as photoperiodism.
2. Depending on photoperiodic response, plants are categorised into three types – Short day plants, long day plants and day neutral plants.

1. Short day plants : Plants that flower under short day length conditions are called short day plants. Plants such as Dahlia, Xanthium, Soybean, Aster, Tobacco and Chrysanthemum are short day plants or SDR. Short day plants require a long uninterrupted dark period for flowering. Therefore, they are also called long night plants.

2. Long day plants : Plants that flower only when they are exposed to light period longer than their critical photoperiod are called long day plants or LDP Long day plants require a short dark or night period for flowering. Hence, they are also called short night plants. Plants such as radish, spinach, wheat, poppy, cabbage, pea, sugar beet, etc. are long day plants.

3. Day neutral plants : Plants in which the flowering is not affected by the day length period are called day neutral plants or DNP or photoneutral plants. Plants such as cucumber, sunflower, cotton, balsam, maize, tomato, etc. are day neutral plants.

Question 3.
Explain biological nitrogen fixation with example.
Answer:

1. Conversion of atmospheric nitrogen into nitrogenous salts to make it available to plants for its update is described as nitrogen fixation.
2. When living organisms are involved in nitrogen fixation process it is known as biological nitrogen fixation.
3. The process is mainly carried out by prokaryotic organisms, i.e. different kinds of bacteria present in soil.
4. The nitrogen fixing organisms are known as diazotrophs or nitrogen fixers and about 70% nitrogen is fixed by them.
5. The nitrogen fixers are either free living bacteria or symbiotic associated with other higher plants e.g. Rhizobium.
6. The cyanobacteria have specialized cells heterocysts which help in process of nitrogen fixation.
7. Nitrogen fixation is high energy requiring process and 16 ATP molecules are needed for fixation of one molecule of nitrogen to ammonia.
8. Soil bacteria like Nitrosomonas, Nitrosocyccus convert ammonia to nitrate and the Nitrobacter convert nitrite to nitrate. This is known as nitrification, biological oxidation.
9. These bacteria are chemoautotrophic and utilize these processes for their metabolism.
10. Fabaceae plants like pea, bean have root nodules which harbour symbiotic bacterium Rhizobium which fixes nitrogen. It is host specific, soil bacterium, Nitrogen is made available to host plant.

Question 4.
Write on macro and micro nutrients required for plant growth.
Answer:

1. Plants absorb mineral nutrients from their surroundings.
2. For a proper growth of plants about 35 to 40 different elements are required.
3. Plants absorb these nutrients in ionic or dissolved form from soil with their root system e.g. Phosphorus as PO₄^–, Sulphur as SO₄^2- etc.
4. Based on their requirement in quantity, they are classified as major nutrients or macronutrients and those needed in small amounts Eire minor or micronutrients.
5. Macroelements are required in large amounts, as they play nutritive and structural roles e.g. C, H, O, R Mg, N, K, S and Ca. – Ca pectate cell wall component, Mg component of chlorophyll.
6. C, H, O are non-mineral major elements obtained from air and water e.g. CO₂ is source of carbon, Hydrogen from water.
7. Microelements are required in traces as they mainly have catalytic role as co-factors or activators of enzymes.
8. Microelements may be needed for certain activity in life cycle of plant e.g. B for pollen germination, Si has protective role during stress conditions and fungal attacks, Al enhances availability of phosphorus.
9. The important micronutrients for plant growth are Mn, B, Cu, Zn, Cl.

Maharashtra State Board 12th Std Biology Textbook Solutions

• Reproduction in Lower and Higher Plants Class 12 Biology Textbook Solutions
• Reproduction in Lower and Higher Animals Class 12 Biology Textbook Solutions
• Inheritance and Variation Class 12 Biology Textbook Solutions
• Molecular Basis of Inheritance Class 12 Biology Textbook Solutions
• Origin and Evolution of Life Class 12 Biology Textbook Solutions
• Plant Water Relation Class 12 Biology Textbook Solutions
• Plant Growth and Mineral Nutrition Class 12 Biology Textbook Solutions
• Respiration and Circulation Class 12 Biology Textbook Solutions

Plant Water Relation Class 12 Exercise Question Answers Solutions Maharashtra Board

Balbharti Maharashtra State Board 12th Biology Textbook Solutions Chapter 6 Plant Water Relation Textbook Exercise Questions and Answers.

Class 12 Biology Chapter 6 Exercise Solutions Maharashtra Board

Biology Class 12 Chapter 6 Exercise Solutions

1. Multiple Choice Questions

Question 1.
In soil, water available for absorption by root is ……………..
(a) gravitational water
(b) capillary water
(c) hygroscopic water
(d) combined water
Answer:
(b) capillary water

Question 2.
The most widely accepted theory for ascent of sap is ……………..
(a) capillarity theory
(b) root pressure theory
(c) diffusion
(d) transpiration pull theory
Answer:
(d) transpiration pull theory

Question 3.
Water movement between the cells is due to ……………..
(a) T.E
(b) W.P
(c) D.P.D.
(d) incipient plasmolysis
Answer:
(c) D.P.D.

Question 4.
In guard cells, when sugar is converted into starch, the stomata pore ……………..
(a) closes almost completely
(b) opens partially
(c) opens fully
(d) remains unchanged
Answer:
(a) closes almost completely

Question 5.
Surface tension is due to ……………..
(a) diffusion
(b) osmosis
(c) gravitational force
(d) cohesion
Answer:
(d) cohesion

Question 6.
Which of the following type of solution has lower level of solutes than the solution?
(a) Isotonic
(b) Hypotonic
(c) Hypertonic
(d) Anisotonic
Answer:
(b) Hypotonie

Question 7.
During rainy season wooden doors warp and become difficult to open or to close because of ……………..
(a) plasmolysis
(b) imbibition
(c) osmosis
(d) diffusion
Answer:
(b) imbibition

Question 8.
Water absorption takes place through ……………..
(a) lateral root
(b) root cap
(c) root hair
(d) primary root
Answer:
(c) root hair

Question 9.
Due to low atmospheric pressure the rate of transpiration will ……………..
(a) increase
(b) decrease rapidly
(c) decrease slowly
(d) remain unaffected
Answer:
(a) increase

Question 10.
Osmosis is a property of ……………..
(a) solute
(b) solvent
(c) solution
(d) membrane
Answer:
(c) solution

2. Very short answer question

Question 1.
What is osmotic pressure?
Answer:
The pressure exerted due to osmosis is osmotic pressure.

Question 2.
Name the condition in which protoplasm of the plant cell shrinks.
Answer:
Plasmolysis

Question 3.
What happens when a pressure greater than the atmospheric pressure is applied to pure water or a solution?
Answer:
When a pressure greater than the atmospheric pressure is applied to pure water or a solution then water potential of pure water or solution increases.

Question 4.
Which type of solution will bring about deplasmolysis ?
Answer:
Placing a plasmolysed cell in hypotonic solution will bring about deplasmolysis.

Question 5.
Which type of plants have negative root pressure?
Answer:
Plants showing excessive transpiration have negative root pressure.

Question 6.
In which conditions transpiration pull will be affected?
Answer:
Due to temperature fluctuations during day and night gas bubbles may be formed which affects transpiration pull.

Question 7.
Mention the shape of guard cells in Cyperus.
Answer:
Kidney shaped and dumbbell shaped guard cells are seen.

Question 8.
Why do diurnal changes occur in osmotic potential of guard cells?
Answer:
Enzyme activity of phosphorylase converts starch into sugar during daytime and sugar is converted to starch during night. This causes changes in osmotic potential of guard cells.

Question 9.
What is symplast pathway?
Answer:
When water is absorbed by root hair it passes across from one living cell to other living cell through the plasmodesmatal connections between them, then it is called symplast pathway across the root.

3. Answer the Following Questions

Question 1.
Describe mechanism of absorption of water.
Answer:

1. The absorption of water takes place by two modes, i.e. active absorption and passive absorption.
2. Passive absorption is the chief method of absorption (98%).
3. There is no expenditure of energy in passive absorption.
4. Transpiration pull is a driving force and water moves depending upon concentration gradient. Water is pulled upwards.
5. It occurs during daytime when there is active transpiration.
6. Active absorption occurs usually during night time as due to closure of stomata transpiration stops.
7. Water absorption is against D.ED. gradient, A.T.R energy is required which is available from respiration.
8. Active absorption may be osmotic or non- osmotic type.
9. For osmotic absorption root pressure has a role.

Question 2.
Discuss theories of water translocation.
Answer:

1. Translocation of water is transport of water along with dissolved minerals from roots to aerial parts.
2. The movement is against the gravity and described as ascent of sap.
3. The translocation occurs through lumen of water conducting tissue xylem mainly vessels and tracheids.
4. Different theories have been discussed for translocation mechanism like vital force theory (Root pressure), relay pump, physical force (capillary), etc.
5. Cohesion tension theory or transpiration pull theory is most widely accepted theory.

Question 3.
What is transpiration? Describe mechanism of opening and closing of stomata.
Answer:

1. The loss of water in the form of vapour is called transpiration.
2. Stomatal transpiration is a main type of transpiration where minute pores are concerned with it.
3. Stomata are bounded by two guard cells which in turn are surrounded by accessory cells.
4. Opening and closing of stomata is controlled by turgidity of guard cells.
5. When guard cells become turgid due to endosmosis their lateral thin and elastic wall bulges or stretch out.
6. The inner thick and inelastic wall is pulled apart, thus the stoma opens during daytime.
7. At night when guard cells become flaccid due to exosmosis the wall relaxes and stoma closes.
8. Endosmosis and exosmosis takes place due to changes in osmotic potential of guard cells.

Question 4.
What is transpiration? Explain role of transpiration.
Answer:
Transpiration : The loss of water from plant body in the form of vapour is called transpiration.

Role of transpiration:

1. Removal of excess of water
2. Helps in passive absorption of water and minerals
3. Helps in ascent of sap – transpiration pull
4. Maintains turgor of cells
5. Imparts cooling effect by reducing temperature 90% – 93% is stomatal transpiration and hence when stomata are open gaseous exchange takes place.

Question 5.
Explain root pressure theory and its limitations.
Answer:

1. Root pressure theory is proposed by J. Pristley.
2. For translocation of water, activity of living cells of root is responsible.
3. Absorption of water by root hair is a constant and continuous process and due to this a hydrostatic pressure is developed in cortical cells.
4. Owing to this hydrostatic pressure i.e. root pressure, water is forced into xylem and further conducted upwards.
5. Root pressure is an osmotic phenomenon.

Limitation of this theory:

1. Not applicable to tall plants above 20 metres.
2. Even in absence of root pressure ascent of sap is noticed.
3. In actively transpiring plants, root pressure is not developed.
4. In taller gymnosperms, root pressure is zero.
5. Xylem sap is under tension and shows negative hydrostatic pressure.

Question 6.
Explain capillarity theory of water translocation.
Answer:

1. Capillarity theory of water translocation is proposed by Bohem.
2. Capillarity is because of surface tension and cohesive forces and adhesive forces of water molecules.
3. Xylem vessels and tracheids are tubular elements having their lumen.
4. In these elements water column exists due to combined action of cohesive and adhesive forces of water and lignified wall.
5. As a result of this capillarity water is raised upwards.

Question 7.
Why is transpiration called ‘a necessary evil’?
Answer:

1. The loss of water in the form of water vapour is called transpiration.
2. About 90 – 93% of transpiration occurs through stomata, small apertures located in the epidermis of leaves.
3. For this process stomata must remain open and then only gaseous exchange by diffusion takes places.
4. Gaseous exchange is necessary for respiration and photosynthesis. If stomata remain closed then it will affect productivity of plant.
5. The process is necessary evil because water which is important for plant is lost in the process.
6. At the same time it helps in absorption of water and its translocation. Hence it cannot be avoided.
   So Curtis has rightly called it as necessary evil.

Question 8.
Explain movement of water in the root.
Answer:

1. Root hairs absorb water by imbibition then diffusion which is followed by osmosis.
2. As water is taken inside the root hair cell it becomes turgid i.e. increase in turgor pressure (T.E)
3. Root hair cell has less D.ED. but adjacent cortical cell has more D.PD.
4. The inner cortical cell has more osmotic potential so it will suck water from root hair cell.
5. Root hair cell becomes flaccid and ready to absorb soil water.
6. Water is passed on similarly in inner cortical cells.
7. Water moves rapidly through loose cortical cells up to endodermis and through passage cells in pericycle.
8. From pericycle due to hydrostatic pressure developed it is forced into protoxylem.

Question 9.
(i) Osmosis
Answer:
It is a special type of diffusion of solvent through a semipermeable membrane.

(ii) Diffusion
Answer:
It is the movement of ions/ atoms/molecules of a substance from the region of higher concentration to the region of their lower concentration.

(iii) Plasmolysis
Answer:
Exo-osmosis in a living cell when placed in hypertonic solution is called plasmolysis.

(iv) Imbibition
Answer:
It is swelling up of hydrophilic colloids due to adsorption of water.

(v) Guttation
Answer:
The loss of water in the form of liquid is called guttation.

(vi) Transpiration
Answer:
The loss of water from plant body in the form of vapour is called transpiration.

(vii) Ascent of sap
Answer:
The transport of water with dissolved minerals in it from root to other aerial parts of plant against the gravity is called ascent of sap.

(viii) Active absorption
Answer:
Water absorption by activity of root which is against the D.PD. gradient along with expenditure of A.T.E energy generated by respiration is the process of active absorption.

(ix) Diffusion Pressure Deficit (D.P.D.)
Answer:
The difference in the diffusion pressures of pure solvent and the solvent in a solution is called diffusion pressure deficit.

(x) Turgor pressure
Answer:
It is the pressure exerted by turgid cell sap on to the cell membrane and cell wall.

(xi) Water potential
Answer:
Chemical potential of water is called water potential.

(xii) Wall pressure
Answer:
Thick and rigid cell wall exerts a counter pressure to turgor pressure developed on the cell sap is called wall pressure that operates in opposite direction.

(xiii) Root pressure
Answer:
As absorption of water by root hair being a continuous process, a sort of hydrostatic pressure is developed in living cells of root, this is called root pressure.

Question 10.
Osmotic Pressure (O.P) and Turgor Pressure (T.P)
Answer:

Question 11.
How are the minerals absorbed by the plants ?
Answer:

1. Soil is the chief source of minerals for the plants.
2. Minerals get dissolved in the soil water.
3. Minerals are absorbed by the plants in the ionic form mainly through roots.
4. Absorption of minerals is independent of water.
5. Absorbed minerals are pulled upwards along with xylem sap.
6. Mineral ions can be remobilized in the plant body form older parts to young plants E.g. Ions of S, P and N.

4. Long answer questions

Question 1.
Describe structure of root hair.
Answer:

1. Water from soil is absorbed by plants with the help of root hairs.
2. Root hairs are present in zone of absorption.
3. Epidermal cells form unicellular extensions which are short lived (ephemeral) structures i.e. root hairs.
4. Root hairs are nothing but cytoplasmic extensions of epiblema cell.
5. Root hairs are long tube like structures of about 1 to 10 mm.
6. They are colourless, unbranched and very delicate structures.
7. A large central vacuole is surrounded by thin layer of cytoplasm, plasma membrane and outer cell wall.
8. The cell wall of root hair is thin and double layered with outer layer of pectin and inner layer of cellulose which is freely permeable.

Question 2.
Write on journey of water from soil to xylem in roots.
Answer:

1. Unicellular root hairs which are tubular extensions of epiblema cells absorb readily available capillary water from soil.
2. The three physical processes imbibition, diffusion and osmosis are concerned with absorption of water.
3. Water molecules get adsorbed on cell wall of root hair (imbibition).
4. They enter the root hair cell by diffusion through cell wall which is freely permeable.
5. By process of osmosis they enter through plasma membrane which is semipermeable.
6. The root hair cell becomes turgid and hence its turgor pressure increases and D.ED. value decreases.
7. The adjacent cell of cortex has more D.ED. value as its osmotic potential is more.
8. The cortical cell thus takes water from epidermal cell which is turgid. This process goes on due to gradient of suction pressure developed from cell to cell till thin walled passage cells of endodermis.
9. From endodermis it will enter pericycle and then due to hydrostatic pressure it is forced in protoxylem cell.
10. The pathway of water is by apoplast and symplast.
11. When water passes through cell wall and intercellular spaces of cortex it is apoplast pathway.
12. When water passes across living cells through their plasmodesmatal connections it is symplast pathway.

Question 3.
Explain cohesion theory of translocation of water.
Answer:

1. This is very widely accepted theory of ascent of sap proposed by Dixon and Joly.
2. It is based on principles of adhesion and cohesion of water molecules and transpiration by plants.
3. A strong force of attraction existing between water molecules is cohesion and the force of attraction between water molecules and lignified walls of xylem elements is adhesion.
4. Ascent of sap occurs through lumen of xylem elements.
5. Owing to cohesive and adhesive forces a continuous water column is maintained in xylem from root to aerial parts i.e. leaves.
6. Transpiration occurs through stomata and transpiration pull is developed in leaf vessels.
7. This tension or pull is transmitted downwards through vein to roots which triggers ascent of sap.
8. In transpiration, water is lost in vapour form and this increases D.PD. of mesophyll cells that are near guard cells.
9. Mesophyll cells absorb water from xylem in leaf and a gradient of D.PD. or suction pressure (S. E) is set.
10. Owing to this gradient from guard cell to xylem in leaf, a transpiration pull or tension is created in xylem.
11. Hence water column is pulled upward passively against gravity.

Question 4.
Write on mechanism of opening and closing of stomata.
Answer:

1. Transpiration takes place through stomata. Turgidity of guard cells controls opening and closing of stomata
2. Turgor pressure exerted on unevenly thickened wall of guard cell is responsible for the movement.
3. The outer thin wall which is elastic is stretched out which pulls inner thick inelastic wall and thus stomata open.
4. When guard cells are flaccid that results in closure of stomata.
5. According to starch-sugar in ter conversion theory enzyme phosphorylase converts starch to sugar during daytime.
6. Sugar being osmotically active, the O.E of guard cells is increased. The water is absorbed from subsidiary cells. Due to turgidity walls are stretched and stoma opens.
7. During night-time sugar is converted to starch and hence guard cells loose water and become flaccid. Hence there is closure of stomata.
8. According to proton transport theory, the movement is due to transport of H⁺ and K⁺ ions.
9. Subsidiary cells are reservoirs of K⁺ ions. Starch is converted to malic acid which dissociate into malate and proton (H⁺) during day.
10. Proton transported to subsidiary cells and K⁺ ions are taken from it. This forms potassium malate in guard cells.
11. Potassium malate increases osmotic potential and endo osmosis occurs hence turgidity of guard cells. → stomata opens,
12. The uptake of K⁺ and Cl^– ions is stopped by abscissic acid formed during night. This changes permeability. Guard cells become hypotonic and loose water as they become flaccid stomata close.

Question 5.
What is hydroponics? How is it useful in identifying the role of nutrients?
Answer:
(1) Growing plants in aqueous (soilless) medium is known as hydroponics. [Greek word hudor = water and ponos = work]

(2) It is technique of growing plants by supplying all necessary nutrients in the water supply given to plant.

(3) A nutrient medium is prepared by dissolving necessary salts of micronutrients and macronutricnts In desired quantity and roots of plants are suspended in this liquid with appropriate support.

(4) Hydroponics is of great use in studying the deficiency symptoms of different mineral nutrients.

(5) The plants uptake mineral nutrients in the form of dissolved ions with the help of root hairs from the surrounding medium or nutrient solution supplied.

(6) While preparing the required nutricnt medium particular nutrient can be totally avoided and then the effect of lack of that nutrient can be studied in variation of plant growth.

(7) Any visible change noticed from normal structure and function of the plant is the symptom or hunger sign considered.

(8) For e.g. Yellowing of leaf is observed due to loss of chlorophyll pigments or Chiorosis is noticed if Magnesium is lacking as it is a structural componen of chlorophyll pigment.

Question 6.
Explain the active absorption of minerals.
Answer:

1. Plants absorb minerals from the soil with their root system.
2. MInerals are absorbed from the soil In the form of charged particles, positively charged cations and negatively charged anions.
3. The absorption of minerals against the concentration gradient which requires expenditure of metabolic energy is called active absorption.
4. The ATP energy derived from resp’ration in root cells Is utilized for active absrption.
5. Ions get accumulated in the root hair against the concentration gradient.
6. These ions pass into cortical cells and finally reach xylem of roots.
7. Along with the water these minerals are carried to other parts of plant.

Maharashtra State Board 12th Std Biology Textbook Solutions

• Reproduction in Lower and Higher Plants Class 12 Biology Textbook Solutions
• Reproduction in Lower and Higher Animals Class 12 Biology Textbook Solutions
• Inheritance and Variation Class 12 Biology Textbook Solutions
• Molecular Basis of Inheritance Class 12 Biology Textbook Solutions
• Origin and Evolution of Life Class 12 Biology Textbook Solutions
• Plant Water Relation Class 12 Biology Textbook Solutions
• Plant Growth and Mineral Nutrition Class 12 Biology Textbook Solutions
• Respiration and Circulation Class 12 Biology Textbook Solutions

Origin and Evolution of Life Class 12 Exercise Question Answers Solutions Maharashtra Board

Balbharti Maharashtra State Board 12th Biology Textbook Solutions Chapter 5 Origin and Evolution of Life Textbook Exercise Questions and Answers.

Class 12 Biology Chapter 5 Exercise Solutions Maharashtra Board

Biology Class 12 Chapter 5 Exercise Solutions

1. Multiple Choice Questions

Question 1.
Who proposed that the first form of life could have come from pre-existing non-living organic molecules?
(a) Alfred Wallace
(b) Oparin and Haldane
(c) Charles Darwin
(d) Louis Pasteur
Answer:
(b) Oparin and Haldane

Question 2.
The sequence of origin of life may be
(a) Organic materials – inorganic materials – Eobiont – colloidal aggregates – cell.
(b) Inorganic materials – organic materials – colloidal aggregates – Eobiont – cell.
(c) Organic materials – inorganic materials – colloidal aggregates – cell.
(d) Inorganic materials – organic materials – Eobiont – colloidal aggregates – cell.
Answer:
(b) Inorganic materials – organic materials- colloidal aggregates – Eobiont – cell.

Question 3.
In Hardy-Weinberg equation, the frequency of homozygous recessive individual is represented by-
(a) p²
(b) pq
(c) q²
(d) 2pq
Answer:
(c) q²

Question 4.
Select the analogous organs.
(a) Forelimbs of whale and bat
(b) Flippers of dolphins and penguin
(c) Thorn and tendrils of bougainvillea and Cucurbita
(d) Vertebrate hearts or brains
Answer:
(b) Flippers of dolphins and penguin

Question 5.
Archaeopteryx is known as missing link because it is a fossil and share characters of both
(a) Fishes and amphibians
(b) Annelida and Arthropoda
(c) Reptiles and birds
(d) Chordates and non-chordates
Answer:
(c) Reptiles and birds

Question 6.
Identify the wrong statement regarding evolution.
(a) Darwin’s variations are small and directional.
(b) Mutations are random and non- directional.
(c) Adaptive radiations leads to divergent evolution.
(d) Mutations are non-random and directional.
Answer:
(d) Mutations are non-random and directional

Question 7.
Gene frequency in a population remain constant due to ……………….
(a) Mutation
(b) Migration
(c) Random mating
(d) Non-random mating
Answer:
(c) Random mating

Question 8.
Which of the following characteristic is not : shown by the ape?
(a) Prognathous face
(b) Tail is present
(c) Chin is absent
(d) Forelimbs are longer than hind limbs
Answer:
(b) Tail is present

Question 9.
………………. can be considered as connecting link between ape and man.
(a) Australopithecus
(b) Homo habilis
(c) Homo erectus
(d) Neanderthal man
Answer:
(a) Australopithecus

Question 10.
The Cranial capacity of Neanderthal man was ……………….
(a) 600 cc
(b) 940 cc
(c) 1400 cc
(d) 1600 cc
Answer:
(c) 1400 cc

2. Very short answer questions

Question 1.
Define
(i) Gene pool
Answer:
The sum total of genes of all individuals of interbreeding population or Mendelian population is called gene pool.

(ii) Gene frequency
Answer:
The proportion of an allele in the gene pool as compared with other alleles at the same locus is termed as gene frequency.

(iii) Organic evolution
Answer:
Organic evolution can be defined as slow, gradual, continuous and irreversible changes through which the present-day complex forms of the life developed (or evolved) from their simple pre-existing forms.

(iv) Population
Answer:
All individuals of the same species form a group which is called a population.

(v) Speciation
Answer:
Formation of new species from the pre-existing single group of organisms is called speciation.

Question 2.
What is adaptive radiation?
Answer:
The process of evolution which results in transformation of original species to many different varieties is called adaptive radiation.

Question 3.
If the variation occurs in population by chance alone and not by natural selection and bring change in frequencies of an allele, what is it called?
Answer:
If the variation occurs in population by chance alone and not by natural selection to bring change in frequencies of an allele, it is called genetic drift.

Question 4.
State the Hardy-Weinberg equilibrium law.
Answer:
The Hardy-Weinberg equilibrium law states that at equilibrium point both the allelic frequency and genotypic frequency remain constant from generation to generation, in the diploid, sexually reproducing, large, free interbreeding population in which mating is random and there is absence of any other factors that change the allele frequency.

Question 5.
What is homologous organs?
Answer:
Homologous organs are those organs, which are structurally similar but perform different functions.

Question 6.
What is vestigial organ?
Answer:
Vestigial organs are imperfectly developed and non-functional organs which are in degenerate form, they may be functional in some related and other animals or in ancestor.

Question 7.
What is the scientific name of modern man?
Answer:
Homo sapiens sapiens is the scientific name of modern man.

Question 8.
What is coacervate?
Answer:
Coacervates are colloidal aggregations of hydrophobic proteins and lipids which grew in size by taking up material from surrounding aqueous medium.

Question 9.
Which period is known as ‘age of Reptilia’?
Answer:
Jurassic period from Mesozoic era is known as age of Reptilia.

Question 10.
Name the ancestor of human which is described as man with ape brain.
Answer:
Australopithecus, the ancestor of human which is described as man with ape brain.

Short Answer Questions

Question 1.
Genetic drift.
Answer:

1. Genetic drift is random, directionless fluctuation that takes place in allele frequency.
2. It occurs by pure chance, in small sized population.
3. Genetic drift becomes an evolutional factor as it can change the gene frequency.
4. Sewall wright has given this concept and hence it is also known as Sewall wright effect.
5. Due to genetic drift, some alleles of a population are lost or reduced by chance and some others may be increased.
6. Some time, a few individuals become isolated from the large population and they produce new population in new geographical area.
7. Genetic drift is also called founders’ effect because original drifted population becomes ‘founders’ in the new area.
   E.g. Non-adaptive character of huge horns in Antelope is fixed due to genetic drift.

Question 2.
Enlist the different factors that are responsible for changing gene frequency.
Answer:
Gene flow, genetic drift, gene mutations, chromosomal aberrations such as deletion, duplication, inversion and translocation, genetic recombinations, natural selection, isolation are some of the factors which are responsible for changing the gene frequency.

Question 3.
Draw a graph to show that natural selection leads to disruptive change.
Answer:

Question 4.
Significance of fossils
Answer:

1. Fossils are studied under palaeontology. They are used in reconstruction of phylogeny.
2. Fossil study helps in studying various forms and structures of extinct animals.
3. By understanding the structure of fossil, record of missing link between two groups of organisms can be deduced.
4. By studying fossils various body forms and their evolution can be understood. They also help to understand the habit and habitat.
5. Some fossils provide the evolutionary evidences such a connecting links.

Question 5.
Write the objections to Mutation theory of Hugo de Vries.
Answer:
Objections to Mutation Theory:

1. Hugo de Vries observed the large and discontinuous variation. But these were chromosomal aberrations. Only gene mutations usually bring about minor changes.
2. Rate by which mutations take place is very slow as compared to the requirement of evolution.
3. Chromosomal aberrations are very unstable.
4. The organisms with chromosomal aberration are usually sterile and thus chromosomal aberrations have little significance in evolution.

Question 6.
What is disruptive selection? Give example.
Answer:
Disruptive selection:

1. The natural selection that disrupts the mean characters of the population, is called disruptive selection.
2. Greater number of individuals acquire peripheral character value at both ends of the distribution curve. E.g. Finches with large size or small size, both will be selected.
3. Extreme phenotypes are selected in evolutionary process and intermediate forms are eliminated.
4. When distribution curve is plotted it shows two peaks for two extremes.
5. Disruptive selection is rare because, nature always tries to balance the characters.
6. It ensures the effect on the entire gene pool of a population, considering all mating types or systems.

Example of disruptive selection:
African seed cracker finches are types of seed-feeder birds which have different sizes of beak. The seeds available to them were of small and large sized. Large beak sized birds feeds on large seeds while small beak sized birds feed on small seeds.

Such large and small birds thus thrive well. However, intermediate beak sized birds are unable to feed on either type of seeds so they starve and their population was decreased gradually. Natural selection eliminated them and thus the population of finches appear disrupted.

4. Match the columns

Question 1.

Answer:

5. Long Answer Questions

Question 1.
Would you consider wings of butterfly and bat as homologous or analogous and why?
Answer:
Wings of butterfly are made up of chitin. They neither have bones, nor muscles in the wings. The bat’s wings are actually patagium. They have muscles and bones just as those seen in all vertebrate limb series. Therefore, these two examples cannot be homologous. However, both the animals use the wings for flight. This is an indication that their function is similar but structure is different, hence they are analogous organs.

Question 2.
What is adaptive radiation? Explain with suitable example.
Answer:

1. Adaptive radiation is the process of evolution which results in transformation of original species to many different varieties.
2. The well-known example of adaptive radiation is Darwin’s Finches. When Charles Darwin went on his voyage to Galapagos islands, he noticed finches which is a variety of small birds.
3. According to Darwin’s observations, the American main land species of finches was the original one which must have migrated to the different islands of Galapagos.
4. Since environmental conditions here were different, they adapted in various ways to the differing environmental conditions of these islands.
5. Original bird had a beak suited for eating seeds, but the changed feeding pattern has changed the shape of beaks too. Some birds also show altered beaks for insectivorous mode. Thus, this demonstrated adaptive radiation.
6. Adaptive radiation in Australian Marsupials is also well studied. In Australia, there are many marsupial mammals who evolved from common ancestor.
7. Adaptive radiation leads to divergent evolution.

Question 3.
By talking industrial melanism as one example, explain the concept of natural selection.
OR
Explain natural selection in action by quoting the example of industrial melanism.
Answer:
1. Industrial melanism is the best example of natural selection which was studied by Kettlewell. In U.K. there are two varieties of peppered moths, Biston betularia and Biston carbonaria.

2. Before industrialisation, in Great Britain, Biston betularia were more in number than Biston carbonaria. B. Betularia is greyish white while B.carbonaria is melanic form.

3. These nocturnal moths rest on tree trunk during day. White-winged moth can camouflage well with the lichen covered whitish barks of trees. They thus escaped the attention of the predatory birds. But at the same time melanic forms were visible due to white barks of the trees. Their number was thus reduced as they were preyed upon by birds.

4. Later there was an industrial revolution, which ultimately resulted in air pollution causing dark soot to settle on the barks of the trees. Lichens too were destroyed and the melanic forms were now at advantage. Melanic forms could camouflage with black tree trunks and their number increased. White-winged moth become clearly seen in changed colours of the trees and thus they were easily caught by predatory birds. This caused decrease in their number.

5. Natural selection thus acted in changed environmental conditions and helped in the establishment of a phenotypic traits. The changed traits were more adaptive and hence were selected. Natural selection encourages those genes or traits that assure highest degree of adaptive efficiency between population and its environment.

Question 4.
Describe the Urey and Miller’s experiment.
Answer:

1. Urey and Miller performed an experiment to prove Oparin’s theory of chemical evolution.

2. They selected a spark discharge apparatus that consisted of closed system of glass having tungsten electrodes, flask for water boiling, a side tube connected to a vacuum pump, a cooling jacket and U-shaped trap.

3. The entire apparatus was first evacuated and made sterile and pre-biotic atmosphere was created in it.

4. The flask was filled with some water and mixture of methane, ammonia and hydrogen in the ratio of 1 : 2 : 2 were slowly passed through the stopcock, without allowing air.

5. Heat was supplied to the flask at very low temperature causing water to boil. The flask simulated the ocean present on primitive earth. Process of evaporation and precipitation was simulated by using heating mantle and condenser respectively.

6. Water vapours along with other gases were circulated continuously through continuous electric sparks. These sparks were given to the mixture for several days causing the gases to interact. This too simulated lightning.

7. Mixture of CH₄, NH₃ and H₂ gases passed through a condenser and was condensed to liquid.

8. The liquefied mixture was collected in the U-shaped trap, present at the bottom of the apparatus. It was found that variety of simple organic compounds (urea, amino acids, lactic acid and sugars) were formed in the apparatus.

This experiment provides the evidence in support to the fact that simple molecules present in the earth’s early atmosphere combined to form the organic building blocks of life.

Question 5.
What is Isolation? Describe the different types of reproductive isolations.
Answer:
1. Isolation means separation of the population of a particular species into smaller units. The organisms belonging to these subunits are prevented from interbreeding due to some barrier. These barriers are called isolating mechanisms.

2. They prevent the genetic exchange and gene flow.

3. Due to isolating mechanisms in nature the divergence among organisms takes place gradually leading to speciation. The isolating mechanisms are of two types namely, geographical isolation and reproductive isolation.

I. Geographical Isolation : The barrier in the form of physical distance or geographical barrier is called geographical isolation. The original population gets divided into two or more groups by geographical barriers such as river, ocean, mountain, glacier, etc. Organisms cannot cross the barriers on their own and hence interbreeding is prevented between isolated groups.

The separated groups experience different environmental factors and they acquire new traits by mutations. The separated populations develop distinct gene pool and they do not interbreed. Each subgroup then evolves differently which results into formation of new species. E.g. Darwin’s Finches, African elephant, Loxodonta and Indian elephant, Elephas.

II. Reproductive Isolation : Two populations may be occupying the same area, they may not be separated by geographical barrier, but then also they are reproductively isolated. Such reproductive isolation occurs due to change in genetic material, gene pool and structure of genital organs. Such differences prevent interbreeding between population. Such isolation later leads to speciation.

III. Different types of reproductive isolations : Reproductive isolation is of two types, viz. pre-zygotic and post-zygotic isolating mechanisms.

1. Pre-zygotic or pre-mating isolating mechanisms do not allow individuals to mate with each other at all.
2. By various mechanisms the two groups remain isolated.
3. In post-zygotic or post-mating isolating mechanisms, the two individuals can mate but the result of mating is not favourable.
4. Thus the populations remain isolated without the actual genetic exchange.

Question 6.
What is Genetic variations? Explain the different factors responsible for genetic variations.
Answer:
Genetic variations : The change in gene and gene frequencies is known as genetic variation. Genetic variations are caused by following factors:
(i) Mutations : Sudden permanent heritable change is called mutation. Mutation can occur in the gene, in the chromosome structure and in chromosome number. Mutation that occurs within the single gene is called point mutation or gene mutation. This leads to the change in the phenotype of the organism, causing variations.

(ii) Genetic recombination : In sexually reproducing organisms, during gamete formation, exchange of genetic material occurs between non-sister chromatids of homologous chromosomes. This is called crossing over. It produces new genetic combinations which result in variation. Fertilization between opposite mating gametes leads to various recombinations resulting into the phenotypic variations. These result in change in the frequencies of alleles.

(iii) Gene flow : Gene flow is movement of genes into or out of a population. Gene movement may be in the form of migration of organism, or gametes (dispersal of pollens) or segments of DNA (transformation). Gene flow also alters gene frequency causing evolutionary changes.

(iv) Genetic drift : Any random fluctuation (alteration) in allele frequency, occurring in the natural population by pure chance, is called genetic drift. For example, when the size of a population is severely reduced due to natural disasters like earthquakes, floods, fires, etc. elimination of particular alleles from a population becomes possible. Smaller populations have greater chances for genetic drift. It results in the change in the gene frequency. Genetic drift is also an important factor for evolutionary change.

(v) Chromosomal aberrations : The structural, morphological change in chromosome due to rearrangement of genes is called chromosomal aberrations. Due to changes in the gene arrangement or gene sequence variations are caused.

6. Complete the chart

Answer:

Maharashtra State Board 12th Std Biology Textbook Solutions

• Reproduction in Lower and Higher Plants Class 12 Biology Textbook Solutions
• Reproduction in Lower and Higher Animals Class 12 Biology Textbook Solutions
• Inheritance and Variation Class 12 Biology Textbook Solutions
• Molecular Basis of Inheritance Class 12 Biology Textbook Solutions
• Origin and Evolution of Life Class 12 Biology Textbook Solutions
• Plant Water Relation Class 12 Biology Textbook Solutions
• Plant Growth and Mineral Nutrition Class 12 Biology Textbook Solutions
• Respiration and Circulation Class 12 Biology Textbook Solutions

Molecular Basis of Inheritance Class 12 Exercise Question Answers Solutions Maharashtra Board

Balbharti Maharashtra State Board 12th Biology Textbook Solutions Chapter 4 Molecular Basis of Inheritance Textbook Exercise Questions and Answers.

Class 12 Biology Chapter 4 Exercise Solutions Maharashtra Board

Biology Class 12 Chapter 4 Exercise Solutions

1. Multiple Choice Questions

Question 1.
Griffith worked on ………………..
(a) Bacteriophage
(b) Drosophila
(c) Frog eggs
(d) Streptococci
Answer:
(d) Streptococci

Question 2.
The molecular knives of DNA are ………………..
(a) Ligases
(b) Polymerases
(c) Endonucleases
(d) Transcriptase
Answer:
(c) Endonucleases

Question 3.
Translation occurs in the ………………..
(a) Nucleus
(b) Cytoplasm
(c) Nucleolus
(d) Lysosomes
Answer:
(b) Cytoplasm

Question 4.
The enzyme required for transcription is ………………..
(a) DNA polymerase
(b) RNApolymerase
(c) Restriction enzyme
(d) RNase
Answer:
(b) RNA polymerase

Question 5.
Transcription is the transfer of genetic information from ………………..
(a) DNA to RNA
(b) t-RNA to m-RNA
(c) DNA to m-RNA
(d) m-RNA to t-RNA
Answer:
(a) DNA to RNA

Question 6.
Which of the following is NOT part of protein synthesis?
(a) Replication
(b) Translation
(c) Transcription
(d) All of these
Answer:
(a) Replication

Question 7.
In the RNA molecule, which nitrogen base is found in place of thymine?
(a) Guanine
(b) Cytosine
(c) Thymine
(d) Uracil
Answer:
(d) Uracil

Question 8.
How many codons are needed to specify three amino acids?
(a) 3
(b) 6
(c) 9
(d) 12
Answer:
(a) 3

Question 9.
Which out of the following is NOT an example of inducible operon?
(a) Lactose operon
(b) Histidine operon
(c) Arabinose operon
(d) Tryptophan operon
Answer:
(d) Tryptophan operon

Question 10.
Place the following event of translation in the correct sequence ………………..
i. Binding of met-t-RNA to the start codon.
ii. Covalent bonding between two amino acids.
iii. Binding of second t-RNA.
iv. Joining of small and large ribosome subunits.
(a) iii, iv, i, ii
(b) i, iv, iii, ii
(c) iv, iii, ii, i
(d) ii, iii, iv, i
Answer:
(b) i, iv, iii, ii

2. Very Short Answer Questions

Question 1.
What is the function of an RNA primer during protein synthesis?
Answer:
During DNA replication, RNA primer provides 3’ OH to which DNA polymerase enzyme can add nucleotides to synthesize new strand using parental strand of DNA as template.
[Note : RNA primer has no direct role in protein synthesis.]

Question 2.
Why is the genetic code considered as commaless?
Answer:
The triplet codon are arranged one after the other on m-RNA molecule without any gap or space and therefore genetic code is considered as commaless.

Question 3
Genome
Answer:
Genome is the total genetic constitution of an organism or a complete copy of genetic information (DNA) or one complete set of chromosomes (monoploid or haploid) of an organism.

Question 4.
Which enzyme does remove supercoils from replicating DNA?
Answer:
Super-helix relaxing enzyme (Topoisomerase) removes supercoils from replicating DNA.

Question 5.
Why are Okazaki fragments formed on lagging strand only?
Answer:
Okazaki fragments are formed only on lagging template as only short stretch of lagging template becomes available for replication at one time.

Question 6.
When does DNA replication take place?
Answer:
In eukaryotes DNA-replication takes place during S-phase of interphase of cell cycle and in prokaryotes. DNA replicates prior to cell division.

Question 7.
Define term Codogen and Codon
Answer:
Codogen is a triplet of nucleotides present on the DNA which specifies one particular amino acid.
Codon is a triplet of nucleotides present on the m-RNA which specifies one particular amino acid.

Question 8.
What is degeneracy of genetic code?
Answer:
Genetic code is degenerate as 61 codons code for 20 amino acids, that is two or more codons can specify the same amino acid. E.g. Cysteine has two codons, while isoleucine has three codons.

Question 9.
Which are the nucleosomal ‘core’ histones?
Answer:
Two molecules each of histone proteins, viz. H₂A. H₂B, H₃ and H₄ are the nucleosomal ‘core’ histones.

3. Short Answer Questions

Question 1.
DNA packaging in eukaryotic cell.
Answer:

1. In eukaryotic cells, DNA (2.2 metres) is condensed, coiled and supercoiled to be packaged efficiently in the nucleus (10^-16 m).
2. DNA is associated with histone and non-histone proteins.
3. Histones are a set of positively charged, basic proteins, rich in basic amino acid residues lysine and arginine.
4. Nucleosome consists of nucleosome core (two molecules of each of histone proteins viz. H₂A, H₂B, H₃ and H₄ forming histone octamer) and negatively charged DNA (146 bps) that wraps around the histone octamer by 1 3/4 turns.
5. H₁ protein binds the DNA thread where it enters and leaves the nucleosome.
6. Adjacent nucleosomes are linked with linker DNA (varies in length from 8 to 114 bp, average length of linker DNA is about 54 bp).
7. Each nucleosome contains 200 bp of DNA.
8. Packaging involves formation of – Beads on string (10 nm diameter), Solenoid fibre (looks like coiled telephone wire, 30 nm diameter/300Å), Chromatin fibre and Chromosome.
9. Non-Histone Chromosomal Proteins (NHC) contribute to the packaging of chromatin at a higher level.

Question 2.
Enlist the characteristics of genetic code.
Answer:
The characteristics of genetic code are

1. Genetic code is triplet, commaless and non-overlapping.
2. It is degenerate and non-ambiguous.
3. It is universal
4. It has polarity.

Question 3.
Applications of DNA fingerprinting.
Answer:
Applications of DNA fingerprinting are as follows:

1. In forensic science to solve rape and murder cases.
2. Finds out the biological father or mother or both, of the child, in case of disputed parentage.
3. Used in pedigree analysis in cats, dogs, horses and humans.

Question 4.
Explain the role of lactose in ‘Lac Operon’.
Answer:

1. A small amount of beta-galactoside permease enzyme is present in cell even when Lac operon is switched off and it allows a few molecules of lactose to enter into the cell.
2. Lactose binds to repressor and inactivates it.
3. Repressor – lactose complex cannot bind with the operator gene, which is then turned on.
4. RNA polymerase transcribes all the structural genes to produce lac m-RNA which is then translated to produce all enzymes.
5. Thus, lactose acts as an inducer.
6. When the inducer level falls, the operator is blocked again by repressor and structural genes are repressed again. This is negative feedback.

4. Short Answer Questions

Question 1.
Human genome project.
Answer:
1. Human Genome Project (HGP) was initiated in 1990 under the International administration of the Human Genome Organization (HUGO) and it was completed r in 2003.

2. The main aims:

• To sequence 3 billion base pairs of DNA in human genome and to map an estimated 33000 genes.
• To store the information collected from the project in databases.
• To develop tools and techniques for analysis of the data.
• Transfer of the related technologies to the private sectors, such as industries.
• Taking care of the legal, ethical and social issues which may arise from project.
• To sequence the genomes of several other organisms such as bacteria e.g. E.coli, Caenorhabditis elegans, Saccharomyces cerevisiae, Drosophil, rice, Arabidopsis), Mus musculus, etc.

3. Significance:

1. HGP has a major impact in the fields like Medicine, Biotechnology, Bioinformatics and the Life sciences.
2. More understanding of functions of genes, proteins and human evolution.

Question 2.
Describe the structure of operon.
Answer:

1. An operon is a unit of gene expression and regulation.
2. It includes the structural genes and their control elements. Control elements are promoters and operators.
3. The structural genes code for proteins, r-RNA and t-RNA that are necessary for all the cells.
4. Promoters are signal sequences in DNA. They start the RNA synthesis. They also act as sites where the RNA polymerases are bound during transcription.
5. Operators are present between the promoters and structural genes.
6. There is repressor protein that binds to the operator region of the operon.
7. There are regulatory genes which are responsible for the formation of repressors which interact with operators.

Question 3.
In the figure below A, B and C are three types of

Answer:
Answer: A, B and C are A : m-RNA, B : r-RNA, C : t-RNA

Question 4.
Identify the labelled structures on the following diagram of translation.

Part A is the ………………
Part B is the ………………
Part C is the ………………
Answer:
Part A is the anti-codon.
Part B is the amino acid.
Part C is the larger subunit of ribosome.

Question 5.
Match the entries in Column I with those of Column II and choose the correct answer.

Answer:

5. Long Answer Questions

Question 1.
Explain the process of DNA replication.
Answer:

DNA replication is semi-conservative replication. It involves following steps:
Activation of Nucleotides:

1. Nucleotides (dAMP dGMR dCMP and dTMP) present in the nucleoplasm, are activated by ATP in presence of an enzyme phosphorylase.
2. This phosphorylation results in the formation of deoxyribonucleotide triphosphates i.e. dATE dGTR dCTP and dTTE

Point of Origin or Initiation point:

1. Replication begins at specific point ‘O- Origin and terminates at point ‘T’.
2. At the point ‘O’, enzyme endonuclease nicks (breaks the sugar-phosphate backbone or the phosphodiester bond) one of the strands of DNA, temporarily.

Unwinding of DNA molecule:

1. Enzyme DNA helices breaks weak hydrogen bonds in the vicinity of ‘O’.
2. The strands of DNA separate and unwind. This unwinding is bidirectional.
3. SSBP (Single strand binding proteins) remains attached to both the separated strands and prevent them from recoiling (rejoining).

Replicating fork:

1. Y-shape replication fork is formed due to unwinding and separation of two strands.
2. The unwinding of strands results in strain which is released by super-helix relaxing enzyme.

Synthesis of new strands:

1. Each separated strand acts as a template for the synthesis of new complementary strand.
2. A small RNA primer (synthesized by activity of enzyme RNA primase) get attached to the 3′ end of template strand and attracts complementary nucleotides from surrounding nucleoplasm.
3. These nucleotides bind to the complementary nucleotides on the template strand by hydrogen bonds (i.e. A = T or T = A; G = C or C = G, CEG).
4. The phosphodiester bonds are formed between nucleotides of new strand to form a polynucleotide strand.
5. The enzyme DNA polymerase catalyses synthesis of new complementary strand always in 5′ – 3′ direction.

Leading and Lagging strand:

1. The template strand with free 3′ is called the leading template.
2. The template strand with free 5′ end is called the lagging template.
3. The replication always starts at C-3 end of template strand and proceeds towards C-5 end.
4. New strands are always formed in 5′ → 3′ direction.
5. The new strand which develops continuously towards replicating fork is called the leading strand.
6. The new strand which develops discontinuously away from the replicating fork is called the lagging strand.
7. Maturation of Okazaki fragments : The lagging strand is synthesized in the form of small Okazaki fragments which are joined by enzyme DNA ligase.
8. Later RNA primers are removed by the combined action of RNase H, an enzyme that degrades the RNA strand of RNA-DNA hybrids, and polymerase I.
9. Gaps formed are filled by complementary DNA sequence with the help of DNA polymerase-I in prokaryotes and DNA polymerase-a in eukaryotes.
10. Finally, DNA gyrase (topoisomerase) enzyme forms double helix to form daughter DNA molecules.

Formation of two daughter DNA molecules:

1. In each daughter DNA molecule, one strand is parental and the other one is newly synthesized.
2. Thus, 50% part (i.e. one strand of the helix) is contributed by mother DNA. Hence, it is described as semiconservative replication.

Question 2.
Describe the process of transcription in protein synthesis.
Answer:

Transcription involves three stages, viz. Initiation, Elongation and Termination.
(1) Initiation:

1. RNA polymerase binds to promoter site.
2. It then moves along the DNA and causes local unwinding of DNA duplex into two strands in the region of the gene.
3. Only antisense strand functions as template.

(2) Elongation:

• The complementary ribonucleoside tri-phosphates get attached to exposed bases of DNA template chain.
• As transcription proceeds, the hybrid DNA-RNA molecule dissociates and makes m-RNA molecule free.
• As the m-RNA grows, the transcribed region of DNA molecule becomes spirally coiled and regains double helical form.

(3) Termination:
When RNA polymerase reaches the terminator site on the DNA, both enzyme and newly formed m-RNA (primary transcript) gets released.

Question 3.
Describe the process of translation in protein synthesis.
Answer:

Translation involves the following steps:
1. Activation of amino acids and formation of charged t-RNA (t-RNA – amino acid complex):
i. In the presence of an enzyme amino acyl t-RNA synthetase, the amino acid is activated and then attached to the specific t-RNA molecule at 3’ end to form charged t-RNA (t-RNA – amino acid complex).

ii. ATP is essential for the reaction.

2. Initiation of Polypeptide chain:

• Small subunit of ribosome binds to the m-RNA at 5’ end.
• Start codon is positioned properly at P-site.
• Initiator t-RNA, (carrying amino acid methionine in eukaryotes or formyl methionine in prokaryotes) binds with initiation codon (AUG) of m-RNA, by its anticodon (UAC) through hydrogen bonds.
• The large subunit of ribosome joins with the smaller subunit in the presence of Mg⁺⁺.
• Thus, initiator charged t-RNA occupies the P-site and A – site is vacant.

3. Elongations of polypeptide chain:
Addition of amino acid occurs in 3 Step cycle-
i. Codon recognition.
Anticodon of second (and subsequent) amino acyl t-RNA molecule recognizes and binds with codon at A-site by hydrogen bonds.

ii. Peptide bond formation.

1. Ribozyme catalyzes the peptide bond formation between amino acids on the initiator t-RNA at P-site and t-RNA at A-site.
2. It takes less than 0.1 second for formation of peptide bond.
3. Initiator t-RNA at ‘P’ site is then released from E-site.

iii. Translocation.

1. Translocation is the process in which sequence of codons on m-RNA is decoded and accordingly amino acids are added in specific sequence to form a polypeptide on ribosomes.
2. Due to this A’-site becomes vacant to receive next charged t-RNA molecule.
3. The events like arrival of t-RNA – amino acid complex, formation of peptide bond, ribosomal translocation and release of previous t-RNA, are repeated.
4. As ribosome move over the m-RNA, all the codons on m-RNA are exposed oiie by one for translation.

4. Termination and release of polypeptide:
When stop codon (UAA, UAG, UGA) gets exposed at the A-site, the release factor binds to the stop codon, thereby terminating the translation process
The polypeptide gets released in the cytoplasm.
Two subunits of ribosome dissociate and last t-RNA and m-RNA are released in the cytoplasm.
m-RNA gets denatured by nucleases immediately.

Question 4.
Describe Lac ‘Operon’.
Answer:

Lac operon consists of the following components:
(1) Regulator gene:

• Regulator gene precedes the promoter gene.
• It may not be present immediately adjacent to operator gene.
• Regulator gene codes for a repressor protein which binds with operator gene and represses (stops) its action.

(2) Promoter gene:

• It precedes the operator gene.
• It is present adjacent to operator gene.
• RNA Polymerase enzyme binds at promoter site.
• Promoter gene base sequence determines which strand of DNA acts a template.

(3) Operator gene:

• It precedes the structural genes.
• When operator gene is turned on by an inducer, the structural genes get transcribed to form m-RNA.

(4) Structural gene:

• There are 3 structural genes in the sequence lac-Z, lac-Y and lac-A.
• Enzymes produced are β-galactosidase, β-galactoside permease and transacetylase respectively.
  Inducer Allolactose acts as an inducer. It inactivates the repressor by binding with it.

Question 5.
Justify the statements. If the answer is false, change the underlined word(s) to make the statement true.
(i) The DNA molecule is double stranded and the RNA molecule is single stranded.
Answer:

1. DNA as the genetic material has to be chemically and structurally stable.
2. It should be able to generate its replica.
3. Sugar-phosphate backbone and complementary base pairing between the two strands, give stability to DNA.
4. Both the strands of DNA act as template for synthesis of their complementary strands. This allows accurate replication of DNA.
5. Single stranded RNA can be folded to form complex structures and perform specific functions such as synthesis of proteins.

(ii) The process of translation occurs at the ribosome.
Answer:

1. Translation is the process in which sequence of codons of m-RNA is decoded and accordingly amino acids are added in specific sequence to form a polypeptide on ribosomes.
2. Ribosome has one binding site for m-RNA. It orients m-RNA molecule in such a way that all the codons are properly read.
3. Ribosome has three binding sites for t-RNA : P-site (peptidyl t-RNA-site), A-site (aminoacyl t-RNA-site) and E-site (exit site).
4. t-RNAs place the required amino acids in correct sequence and translate the coded message of RNA.
5. In eukaryotes, a groove which is present between two subunits of ribosomes, protects the polypeptide chain from the action of cellular enzymes and also protects m-RNA from the action of nucleases.
6. Thus ribosome plays an important role in translation.

(iii) The job of m-RNA is to pick up amino acids and transport them to the ribosomes.
Answer:
The job of t-RNA is to pick up amino acids and transport them to ribosomes. t-RNA is an adapter molecule. It reads the codons of m-RNA and also simultaneously transfer specific amino acid to m-RNA Ribosome complex. It binds with amino acid at its 3′ end.

(iv) Transcription must occur before translation may occur.
Answer:
In prokaryotes, translation can start before transcription is complete, as both these processes occur in the same compartment, i.e. cytoplasm. But in eukaryotes, transcription and processing of hnRNA occurs in nucleus. hnRNA then comes out of the nucleus through nuclear pores and then it is translated at ribosomes in the cytoplasm.

Question 6.
Guess
(i) the possible locations of DNA on the collected evidence from a crime scene and
(ii) the possible sources of DNA.

Answer:

Maharashtra State Board 12th Std Biology Textbook Solutions

• Reproduction in Lower and Higher Plants Class 12 Biology Textbook Solutions
• Reproduction in Lower and Higher Animals Class 12 Biology Textbook Solutions
• Inheritance and Variation Class 12 Biology Textbook Solutions
• Molecular Basis of Inheritance Class 12 Biology Textbook Solutions
• Origin and Evolution of Life Class 12 Biology Textbook Solutions
• Plant Water Relation Class 12 Biology Textbook Solutions
• Plant Growth and Mineral Nutrition Class 12 Biology Textbook Solutions
• Respiration and Circulation Class 12 Biology Textbook Solutions

Inheritance and Variation Class 12 Exercise Question Answers Solutions Maharashtra Board

Balbharti Maharashtra State Board 12th Biology Textbook Solutions Chapter 3 Inheritance and Variation Textbook Exercise Questions and Answers.

Class 12 Biology Chapter 3 Exercise Solutions Maharashtra Board

Biology Class 12 Chapter 3 Exercise Solutions

1. Multiple Choice Questions

Question 1.
Phenotypic ratio of incomplete dominance in Mirabilis jalapa.
(a) 2 : 1 : 1
(b) 1 : 2 : 1
(c) 3 : 1
(d) 2 : 2
Answer:
(b) 1 : 2 : 1

Question 2.
In dihybrid cross, F₂ generation offspring show four different phenotypes while the genotypes are ……………….
(a) six
(b) nine
(c) eight
(d) sixteen
Answer:
(b) nine

Question 3.
A cross between an individual with unknown genotype for a trait with recessive plant for that trait is ……………….
(a) back cross
(b) reciprocal cross
(C) monohybrid cross
(d) test cross
Answer:
(d) test cross

Question 4.
When phenotypic and genotypic ratios are the same, then it is an example of ……………….
(a) incomplete dominance
(b) complete dominance
(c) multiple alleles
(d) cytoplasmic inheritance
Answer:
(a) incomplete dominance

Question 5.
If the centromere is situated near the end of the chromosome, the chromosome is called ……………….
(a) Metacentric
(b) Acrocentric
(c) Sub-Metacentric
(d) Telocentric
Answer:
(d) Telocentric

Question 6.
Chromosomal theory of inheritance was proposed by ……………….
(a) Sutton and Boveri
(b) Watson and Crick
(c) Miller and Urey
(d) Oparin and Halden
Answer:
(a) Sutton and Boveri

Question 7.
If the genes are located in a chromosome as p-q-r-s-t, which of the following gene pairs will have least probability of being inherited together ?
(a) p and q
(b) r and s
(c) s and t
(d) p and s
Answer:
(d) p and s

Question 8.
Find the mismatched pair:
(a) Down’s syndrome = 44 + XY
(b) Turner’s syndrome = 44 + XO
(c) Klinefelter’s syndrome = 44 + XXY
(d) Super female = 44 + XXX
Answer:
(a) Down’s syndrome = 44 + XY

Question 9.
A colourblind man marries a woman, who is homozygous for normal colour vision, the probability of their son being colour blind is ……………….
(a) 0%
(b) 25%
(c) 50%
(d) 100%
Answer:
(a) 0%

2. Very Short Answer Questions

Question 1.
Explain the statements
a. Test cross is back cross but back cross is not necessarily a test cross.
b. Law of dominance is not universal.
Answer:
a. (1) Test cross is the cross between F₁ hybrid and its homozygous recessive parent.
(2) Back cross is the cross of offspring with any one of the parents, either dominant or recessive.
(3) Therefore, test cross can be a back cross – but back cross cannot be a test cross.

b. (1) There are many traits in many organisms which show dominance. For example, widow’s peak in human beings is a dominant trait. Yellow seed colour and round seed shape are dominant traits in pea plant.
(2) However, there are characters which are either co-dominant, such as genes for human blood group A and B or incompletely dominant as in flower colour of Mirabilis jalapa.
(3) Therefore the law of dominance is not universally applicable.

Question 2.
Define the following terms:
a. Dihybrid cross
b. Homozygous
c. Heterozygous
d. Test cross
Answer:
a. A cross between parents differing in two heritable traits is called dihybrid cross.
b. An individual possessing identical alleles for a particular trait is called homozygous or pure for that trait. E.g. TT for tallness and tt for dwarfness.
c. An individual possessing contrasting allele for a particular trait is called heterozygous. E.g. Tt showing tallness.
d. The cross of F₁ progeny with homozygous recessive parent is called a test cross.

Question 3.
What are allosomes?
Answer:
Allosomes are the chromosomes which decide the sex of an organism.

Question 4.
What is crossing over?
Answer:
Crossing over is the process of forming new recombinations by interchanging and exchanging non-sister chromatid arms of the homologous chromosomes.

Question 5.
Give one example of autosomal recessive disorder.
Answer:
Thalassemia is an example of autosomal recessive disorder.

Question 6.
What are X-linked genes?
Answer:
Genes located on the non-homologous region of X chromosome are called X-linked genes.

Question 7.
What are holandric traits?
Answer:
Genes located on the non-homologous region of Y chromosome are called Y-linked genes. The traits due to such genes are called holandric traits which are seen only in male sex.

Question 8.
Give an example of chromosomal disorder caused due to non-disjunction of autosomes.
Answer:
Down’s syndrome is an example of chromosomal disorder caused due to non-disjunction of autosomes.

Question 9.
Give one example of complete sex linkage.
Answer:
Sex linkage can be complete X linkage and complete Y linkage. X linkage is haemophilia and Y linkage is hypertrichosis.

3. Short Answer Questions

Question 1.
Enlist seven traits of pea plant selected / studied by Mendel.
Answer:
Seven traits in pea selected by Mendel:

1. Tall habit versus dwarf habit (Height of the plant).
2. Purple flowers versus white flowers. (Colour of flowers)
3. Yellow seeds versus green seeds. (Colour of seeds)
4. Round seeds versus wrinkled seeds. (Shape of seeds)
5. Green pods versus yellow pods. (Colour of pods)
6. Inflated pods versus constricted pods. (Shape of pods)
7. Axial flower versus terminal flower. (Position of a flower)

Question 2.
Why law of segregation is also called the law of purity of gametes?
Answer:
(1) Mendel’s law of segregation is also called Law of purity of gametes because, during formation of gametes, the alleles separate/ segregate from each other and only one allele enters a gamete.

(2) The separation of one allele does not affect other. Since single allele enters a gamete means gametes will be pure for a trait.
E.g. The contrasting characters such as tall (T) and dwarf (t) present in F₁ hybrid (Tt) segregate during the formation of gametes.

(3) Owing to this, two types of gametes i.e. T and t are formed which are pure for the characters which they carry.
(4) Thus for example:

Question 3.
Pleiotropy.
Answer:

1. When a single gene controls two or more different traits, it is called a pleiotropic gene and the phenomenon is known as pleiotropy or pleiotropism.
2. The pleiotropic ratio is always 1 : 2 instead . of normal 3 : 1.
3. Sickle-cell anaemia is caused by the gene HbS. The healthy or normal gene which is dominant is HbA. The heterozygotes or carriers i.e., HbA/Hbs show anaemia as there is deficiency of haemoglobin due to sickling of RBCs. Abnormally low concentration of oxygen can cause sickling of RBCs.
4. The homozygotes possessing the recessive gene HbS die because of fatal anaemia because the gene for sickle-cell anaemia is lethal in homozygous condition and causes sickle-cell trait in heterozygous carrier.
5. Thus a single gene produces two different expressions.
6. When two carriers are married they will produce normal carriers and Sickle-cell anaemic children in the ratio of 1 : 2 : 1. Out of these three children sickle-cell anaemic child will die leaving the ratio 1 : 2 instead of 3 : 1.

Question 4.
What are the reasons of Mendel’s success?
Answer:
Reasons for Mendel’s success:

1. Mendel planned his experiments carefully and these experiments consisted of large sample.
2. He always recorded the results of number of plants of each type and their ratios.
3. The contrasting characters that he chose were easily recognizable.
4. The seven pairs of contrasting characters that he selected were under control of a single factor each. They were present on separate chromosomes and were transmitted from one generation to the next.
5. Mendel studied and introduced concept of dominance and recessiveness.

Question 5.
“Father is responsible for determination of sex of child and not the mother”. Justify.
Answer:

1. Human made is heterogame tic, i.e. he produces two different types of sperms. One is bearing X chromosome along with 22 autosomes and the other is Y bearing sperm with 22 autosomes.
2. Mother, on the other hand, is homogametic, producing all similar types of ova, i.e 22 + X chromosomal combination.
3. If 22+X bearing sperm fertilise an egg, female child is formed while if Y bearing sperm fertilizes an egg, male child is formed.
4. Thus the sex of the child is dependent upon type of sperm that father gives, therefore, it is said that father is responsible for determination of sex of a child and not the mother.

Question 6.
What is linkage? How many linkage groups do occur in human being and maize?
Answer:

1. Linkage is defined as the tendency of the genes to be inherited together because they are present in the same chromosome. Linkage group is group of genes situated on a chromosome.
2. Humans have 23 linkage groups because they have 23 pairs of chromosomes.
3. Maize plant has 10 linkage groups because they have 10 pairs of chromosomes.

Question 7.
PKU.
Answer:

1. PKU means phenylketonuria which is an autosomal recessive inborn error.
2. In this disorder the metabolism of phenylalanine does not occur due to deficiency of phenylalanine hydroxylase (PAH) enzyme.
3. This enzyme is necessary to metabolize the amino acid phenylalanine to the amino acid tyrosine.
4. When PAH activity is reduced, phenylalanine accumulates in blood and cerebrospinal fluid and is converted into phenylpyruvate or phenyl-ketone which is a toxic compound. This may cause mental retardation. Excess phenylalanine is excreted in urine, hence this disease is called phenylketonuria.
5. PKU is caused by mutations in the PAH gene on chromosome no. 12.
6. Untreated PKU causes abnormal phenotype which includes growth failure, poor skin pigmentation, microcephaly, seizures, global developmental delay and severe intellectual impairment. However, at birth if an infant is checked for PKU, the further abnormalities can be avoided.

Question 8.
Compare X-chromosome and Y-chromosome.
Answer:

Question 9.
Explain the chromosomal theory of inheritance.
Answer:
Chromosomal theory of inheritance was put forth by Sutton and Boveri after studying paraillel behaviour of genes and chromosomes during meiotic division. This theory states following points:

1. Chromosomal theory identifies chromosomes as the carrier of genetic material.
2. All the hereditary characters are transmitted by gametes. Nucleus of gametes, i.e. sperms and ova of the parents contain chromosomes which transmit the heredity to offspring.
3. Chromosomes are found in pairs in somatic or diploid cells.
4. During gamete formation, homologous chromosomes pair and segregate independently at meiosis. The diploid condition is converted into haploid condition. Thus each gamete contains only one chromosome of a pair.
5. During fertilization, the union of sperm and egg restores the diploid number of chromosomes.

Question 10.
Observe the given pedigree chart and answer the following questions

(a) Identify whether the trait is sex-linked or autosomal.
(b) Give an example of a trait in human beings which shows such a pattern of inheritance.
Answer:
Pedigree given above shows:

1. First Generation : Carrier woman marrying a sufferer man. Their three children are in following birth order.
2. Second generation : First son is normal, second daughter is carrier and third daughter is sufferer.
3. Third generation : The sufferer daughter marries a normal man. Her children are normal daughter and sufferer son.

(a) The above pedigree show sex-linked (X-linked) trait. Since criss-cross inheritance is seen in the trait, it must be sex-linked inheritance.
(b) Such trait and its inheritance can be seen in colour blindness.

4. Match the Columns

rewrite the matching pairs.

Answer:

5. Long Answer Questions

Question 1.
What is dihybrid cross? Explain with suitable example and checker board method.
Answer:
1. A cross which involves two pairs of alleles is called a dihybrid cross. A phenotypic ratio of 9 : 3 : 3 : 1 obtained in the F₂ generation of a dihybrid cross is called a dihybrid ratio.

(2) Thus for example, when we cross a true breeding pea plant bearing round and yellow seeds with a true breeding pea plant bearing wrinkled and green seeds we get pea plants bearing round and yellow seeds in the F₁ generation.

(3) When F₁ plants are selfed, we get a ratio of 9 : 3 : 3 : 1 in the F₂ generation, where 9 plants bear yellow round seeds, 3 plants bear yellow wrinkled seeds, 3 plants bear green round seeds and 1 plant bears green wrinkled seeds.

(4) Parents (P₁) : RRYY × rryy
Gametes of P₁ RY and ry
F₁ generation : RrYy(Yellow round)
On selfing F₁ : RrYy × RrYy
Gametes of F₁ : RY, Ry, rY, ry

P₂ generation:

Round Yellow : 9 Round green : 3 Wrinkled yellow : 3 Wrinkled green : 1
Phenotypic ratio : 9 : 3 : 3 : 1
Genotypic ratio : 1 : 2 : 1 : 2 : 4 : 2 : 1 : 2 : 1

Question 2.
Explain with suitable example an independent assortment.
Answer:
(1) The law of independent assortment states that when hybrid possessing two or more pairs of contrasting characters bearing alleles form gametes, the alleles in each pair segregate independently of the other pair. Therefore, the inheritance of one pair of characters is independent of that of the other pair of characters.
(2) For example, when we cross a pea plant which is tall and having purple flowers with dwarf plant having white flowers we obtain all tall plants with purple flowers in F₁ generation. When F₁ generation are selfed, 9 : 3 : 3 : 1 ratio was obtained in F₂ generation with 9 tall and purple flower, 3 tall with white flowers, 3 dwarf with purple flowers and 1 which was dwarf and white. Tallness and purple colour are dominant traits while dwarfness and white colour are recessive traits.

(i) Homozygous tall purple – TTPP
(ii) Homozygous dwarf white – ttpp

Tall purple = 9. Tall white = 3
Dwarf purple = 3, Dwarf white = 1,
Phenotypic ratio = 9 : 3 : 3 : 1
Results : The offspring of F₁ generation will be in the proportion of 9 : 3 : 3 : 1, where 9 are tall purple, 3 are tall white, 3 are dwarf purple and 1 is dwarf white.

Question 3.
Define test cross and explain its significance.
Answer:
1. Definition of test cross : A cross between F₁ offspring and its homozygous recessive parent is called a test cross.
2. Significance of test cross:

• Test cross can be used to find out the genotype of any plant which shows dominant characters.
• Whether the plant is homozygous or heterozygous can be understood by performing test cross.
• Test cross is used to introduce useful recessive traits in the hybrids of self- pollinated plants.
• Test cross is quicker method to improve the variety of crop plants and thus it is useful for breeders and geneticists.
• Test cross can be used for verifying the laws of inheritance.

Question 4.
What is parthenogenesis? Explain the haplodiploid method of sex determination in honey bee.
Answer:
I. Parthenogenesis is a natural form of asexual reproduction in which growth and development of embryos occur without fertilization by sperm. In some insects like honey bees, parthenogenesis means development of an embryo from an unfertilized egg cell.

II. In honey bee:

1. Sex determination is by haplodiploid system.
2. Sex is determined by the number of sets of chromosomes received by an individual.
3. The egg which is fertilized by sperm, becomes diploid and develops into female.
4. The egg which is not fertilized develops by parthenogenesis and develops into a male.
5. The queen and worker bee therefore contain 32 chromosomes. The drone, i.e. male bears 16 chromosomes.
6. The sperms are produced by mitosis while eggs are produced by meiosis.

Question 5.
In the answer for inheritance of X-linked. genes, Madhav had shown carrier male. His answer was marked incorrect. Madhav was wondering why his marks were cut. Explain the reason.
Answer:
Males can never be carriers. They have single X and other Y chromosome. In X linked inheritance, the genes are present on the non-homologous region of X chromosome. Males do not have other X and hence if the genes are present on his X chromosome, they will not be suppressed in them. The Y chromosome does not have dominant gene to hide this expression as there is no homolorous region too. But in case of females, there are double X chromosomes and hence if X-linked gene is recessive, the other X can hide the expression of such X-linked gene.

Thus she becomes a carrier without showing any physical characters. She is physically normal and does not suffer from such X-linked recessive disorder. Thus, Madhav will get his answer wrong due to incorrect concept.

Question 6.
With the help of neat labelled diagram, describe the structure of chromosome.
Answer:

(1) A chromosome is best visible during metaphase, when it is highly condensed.

(2) Chromosome shows two identical halves, called sister chromatids. Chromatids are held together at centromere which is also called primary constriction.

(3) Primary constriction has disc shaped plate called kinetochore. This plate is useful for attachment of spindle fibres at the time of cell division.

(4) Additional narrow areas called secondary constrictions are seen in some chromosomes which are known as nucleolar organizers. They help in the formation of nucleolus. At secondary constriction (i) there is nucleolar organising region. Secondary constriction (ii) shows attachment of satellite body or SAT body.

(5) Each chromatid is made up of sub¬chromatids called chromonemata. Each chromonema consists of a long, unbranched, slender, highly coiled DNA thread. This double stranded DNA molecule extends throughout the length of the chromosome.

(6) The ends of the chromatid arms are called telomeres.

Question 7.
What is criss-cross inheritance? Explain with suitable example.
Answer:
Criss-cross inheritance is the type of inheritance in which the genes are passed on from father to daughter and then to her son, i.e. from male to female and from female to male (grandson). In other words, it is also said that the transmission is from the grandfather to his grandson through his daughter.

I. Inheritance of Colour blindness show criss-cross pattern.
(1) Colour blindness is a sex-linked disorder in which the person concerned cannot distinguish between red and green colours.

(2) It is recessively X-linked disorder, which is expressed in males. It is rarely seen in females.

(3) The genes for normal vision are dominant whereas those for colour blindness are recessive.

(4)

• Gene for normal vision : X^C
• Gene for colour blindness : X^c
• Normal female : X^CX^C
• Normal male : X^CY
• Colour blind female : X^cX^c
• Carrier female : X^CX^c
• Colour blind male : X^c Y

II. Crosses showing the inheritance of colour blindness:
(i) A cross between normal female and colour-blind male.

(ii) A cross of carrier female with normal male.

(1) Normal female with Colour blind male. Such cross produces 50% carrier daughters and 50% normal sons.

(2) Carrier female with normal male. Such a cross produces 25% normal daughters, 25% normal sons, 25% carrier daughters and 25% colour blind sons.

(3) Colour blind father transmits the disorder to his grandson through his carrier daughter. The inheritance of characters from the father to his grandson through his daughter is called criss-cross inheritance.

Question 8.
Describe the different types of chromosomes.
Answer:
I. Chromosomes are classified into the following four types according to the position of the centromere in them:
(1) Metacentric : In metacentric chromosome, the centromere is situated in the middle of the chromosome. The two arms of the chromosome are nearly equal. It appears ‘V’-shaped during anaphase.

(2) Sub-metacentric : In sub-metacentric chromosome, the centromere is situated some distance away from the middle. Due to this, one arm of the chromosome is shorter than the other. It appears T-shaped during anaphase.

(3) Acrocentric : In acrocentric chromosome, the centromere is situated near the end of the chromosome. One arm of the acrocentric chromosome is very short while the other is long making it appear like ‘J’-shaped during anaphase.

(4) Telocentric : In telocentric chromosome, the centromere is situated at the tip of the chromosome. Telocentric chromosome has only one arm thus it appears rod-shaped.

II. Based on the functions, chromosomes are divided into autosomes and allosomes. Autosomes are somatic chromosomes which decide the body characters. Allosomes are sex chromosomes which decide the sex of the individual.

Maharashtra State Board 12th Std Biology Textbook Solutions

• Reproduction in Lower and Higher Plants Class 12 Biology Textbook Solutions
• Reproduction in Lower and Higher Animals Class 12 Biology Textbook Solutions
• Inheritance and Variation Class 12 Biology Textbook Solutions
• Molecular Basis of Inheritance Class 12 Biology Textbook Solutions
• Origin and Evolution of Life Class 12 Biology Textbook Solutions
• Plant Water Relation Class 12 Biology Textbook Solutions
• Plant Growth and Mineral Nutrition Class 12 Biology Textbook Solutions
• Respiration and Circulation Class 12 Biology Textbook Solutions

Reproduction in Lower and Higher Animals Class 12 Exercise Question Answers Solutions Maharashtra Board

Balbharti Maharashtra State Board 12th Biology Textbook Solutions Chapter 2 Reproduction in Lower and Higher Animals Textbook Exercise Questions and Answers.

Class 12 Biology Chapter 2 Exercise Solutions Maharashtra Board

Biology Class 12 Chapter 2 Exercise Solutions

1. Multiple choice questions

Question 1.
The number of nuclei present in a zygote is ……………….
(a) two
(b) one
(c) four
(d) eight
Answer:
(b) one

Question 2.
Which of these is the male reproductive organ in human?
(a) Sperm
(b) Seminal fluid
(c) Testes
(d) Ovary
Answer:
(c) Testes

Question 3.
Attachment of embryo to the wall of the uterus is known as ……………….
(a) fertilization
(b) gestation
(c) cleavage
(d) implantation
Answer:
(d) implantation

Question 4.
Rupturing of follicles and discharge of ova is known as ……………….
(a) capacitation
(b) gestation
(c) ovulation
(d) copulation
Answer:
(c) ovulation

Question 5.
In human females, the fertilized egg gets implanted in uterus ……………….
(a) after about 7 days of fertilization
(b) after about 30 days of fertilization
(c) after about two months of fertilization
(d) after about 3 weeks of fertilization
Answer:
(a) after about 7 days of fertilization

Question 6.
Test tube baby technique is called ……………….
(a) In vivo fertilization
(b) In situ fertilization
(c) In Vitro Fertilization
(d) Artificial Insemination
Answer:
(c) In Vitro Fertilization

Question 7.

The given figure shows a human sperm. Various parts of it are labelled as A, B, C, and D. Which labelled part represents acrosome?
(a) B.
(b) C
(c) D
(d) A
Answer:
(d) A

Question 8.
Presence of beard in boys is a ……………….
(a) primary sex organ
(b) secondary sexual character
(c) secondary sex organ
(d) primary sexual character
Answer:
(b) secondary sexual character

2. Very short answer questions

Question 1.
What is the difference between a foetus and an embryo?
Answer:
Embryo is a growing egg after fertilization until the main parts of the body and the internal organs have started to take shape while foetus is a stage which has the appearance of a fully developed offspring.

Question 2.
Outline the path of sperm up to the urethra.
Answer:
The path of sperm up to the urethra in male is as follows :
Seminiferous tubules → Rete testis → Vasa efferentia → Epididymis → Vas deferens → Ejaculatory ducts Urethra.

Question 3.
Which glands contribute fluids to the semen?
Answer:
The glands which contribute fluids to the semen are seminal vesicles, prostate gland.

Question 4.
Name the endocrine glands involved in maintaining the sexual characteristics of males.
Answer:
Interstitial cells of Leydig which lie in between the seminiferous tubules are involved in maintaining the sexual characteristics of male by secreting the male hormone androgen or testosterone. Adenohypophysis also regulates this secretion from the testis.

Question 5.
Where does fertilization and implantation occur?
Answer:
Fertilization of ovum takes place in the ampulla region of fallopian tube whereas implantation occur in the endometrium of uterus.

Question 6.
Enlist the external genital organs in female.
Answer:
The external genital organs in female include the following parts such as vestibule, labia minora, clitoris, labia majora and mons Veneris.

Question 8.
What is the difference between embryo and zygote?
Answer:
Zygote is the unicellular diploid structure formed as a result of fusion of sperm and ovum whereas embryo is a multicellular structure formed from zygote in the uterus 3 weeks after fertilization.

3. Fill in the blanks

Question 1.
The primary sex organ in human male is ……………….
Answer:
testis

Question 2.
The ……………… is also called the womb.
Answer:
uterus

Question 3.
Sperm fertilizes ovum in the ……………….. of fallopian tube.
Answer:
ampulla

Question 4.
The disc like structure which helps in the transfer of substances to and from the foetus’s body is called ………………..
Answer:
placenta

Question 5.
Gonorrhoea is caused by ……………….. bacteria.
Answer:
Neisseria gonorrhoeae

Question 6.
The hormone produced by the testis is ……………………
Answer:
testosterone / androgen.

4. Short Answer Questions

Question 1.
Budding in Hydra.
Answer:

1. Budding is a type of asexual reproduction method seen in Hydra.
2. Budding takes place during favourable period.
3. Towards the basal end of the body, small outgrowth is produced which is called a bud.
4. It grows and forms tentacles and gradually forms a new individual.
5. The young Hydra after complete development detaches from the parent and becomes an independent new organism.

Question 2.
Explain the different methods of reproduction occurring in sponges.
Answer:

1. Sponges reproduce both asexually and sexually and they also possess the power of regeneration. Their sexual reproduction is similar to higher animals even though their body organization is primitive type.
2. Asexual reproduction in sponges takes place by regeneration, budding and gemmule formation.
3. In sponges, during unfavourable period, gemmule is produced. It is an internal bud.
4. Archaeocytes which are dormant cells are seen in the aggregation in gemmule. These cells are capable of developing into a new organism.
5. Amoebocytes are other cells which secrete thick resistant layer of secretion which is coated around archaeocytes.
6. When favourable conditions of water and temperature return back, the gemmules can develop into new individuals by hatching, e.g. Spongilla.

Question 3.
IVF.
Answer:

1. In laboratory under sterile conditions, oocyte and sperms are placed in a test tube or glass plate to form a zygote. This process is called In Vitro Fertilization.
2. The zygote with 8 blastomeres is then transferred into the fallopian tube for further development.
3. IVF technique is used when childless couple wants to have a baby, but there are issues of sterility.
4. IVF is also called test tube baby technique.

Question 4.
Comment on any two mechanical contraceptive methods.
Answer:
Two mechanical contraceptive methods are as follows:
A. Condom or Nirodh:

1. It is a protective barrier in the form of thin rubber sheath which is used by male partner during the sexual coitus. It covers the penis and does not allow semen to flow during copulation.
2. Thus the entry of ejaculated semen into the female reproductive tract is obstructed. This can prevent conception. It is a simple and effective method and has no side effects.
3. “Nirodh” is a condom, most widely used in India as a contraceptive by males.
4. Condom also protects both the partners against sexually transmitted diseases such as AIDS and others.

B. Diaphragm, cervical caps and vaults:

1. Diaphragm and cervical caps are to be used by females as mechanical contraceptive measures.
2. They are made up of rubber. They are fitted on the cervix in vagina so that they prevent the entry of sperms into the uterus.
3. They are kept at least six hours after sexual intercourse in order to inhibit sperms from entering female genital tract.

Question 5.
Tubectomy.
Answer:

1. The permanent birth control method in women, is called tubectomy.
2. It is a surgical method, also called sterilization.
3. In tubectomy, a small part of the fallopian tube is tied and cut.
4. Tubectomy blocks transport of oocytes and also blocks sperms, thus preventing fertilization from reaching the oocyte.

Question 6.
Give the name of causal organism of Syphilis and write on its symptoms.
Answer:
1. Syphilis is a sexually transmitted veneral disease caused by a Spirochaete bacterium Treponema pallidum.

2. The site of infection is the mucous membrane in genital, rectal and oral region.

3. Symptoms of syphilis:

• Primary lesion known as chancre at the site of infection.
• They are seen on the external genitalia in males and inside the vagina in females.
• Skin rashes accompanied by fever, inflammed joints and loss of hair.
• Paralysis
• Degenerative changes in the heart and brain.

Question 7.
What is colostrum?
Answer:

1. The fluid secreted by the mammary glands soon after childbirth is called colostrum.
2. Colostrum is the sticky and yellow fluid. It contains proteins, lactose and mother’s antibodies, e.g. IgA.
3. The fat content in colostrum is low.
4. The antibodies present in colostrum helps in developing resistance for the newborn baby at a time when its own immune response is not fully developed.

5. Answer the Following Questions

Question 1.
Describe the phases of menstrual cycle and their hormonal control.
Answer:
Menstrual cycle (Ovarian cycle):
i. Menstrual cycle involves a series of cyclic, changes in the ovary and uterus. The cyclic events are regulated by gonadotropins from pituitary and the hormones from ovary.
ii. The cyclic events in woman are repeated within approximately 28 days.
iii. Menstrual cycle is divided into following phases, viz.

1. Menstrual phase (Day 1-5)
2. Follicular phase in ovary that coincides with proliferative phase in uterus. Post menstrual phase (Day 5-14)
3. Ovulatory phase (Day 14-15)
4. Luteal phase in ovary which coincides with secretory phase in uterus (Day 16 to 28).

1. Menstrual Phase:

• Menstrual phase occurs in the absence of fertilization.
• During menstruation, uterine endometrium is sloughed off. Level of progesterone and estrogen decrease during this phase resulting into release of prostaglandins which cause this rupture.
• Blood about 45-100 ml, tissue fluid, mucus, endometrial lining and unfertilized oocyte and other cellular debris is discharged through vagina as a menstrual flow. The endometrial lining becomes about 1 mm thin.
• Fibrinolysin does not allow blood to clot during this period.
• Pituitary starts secreting FSH, which further makes many primordial follicles to develop into primary and few of them into secondary follicles.

2. Proliferative phase/Follicular phase/Post menstrual phase:

• During this phase in the ovary the follicles develop while in uterus the endometrium starts proliferating. 6 to 12 secondary follicles start developing but usually only one of them becomes Graafian follicle due to action of FSH.
• Developing secondary follicles secrete the hormone estrogen.
• Estrogen brings about regeneration of endometrium. Further proliferation of endometrium causes formation of endothelial cells, endometrial or uterine glands and network of blood vessels. Endometrium’s thickness becomes 3-5 mm.

(3) Ovulatory phase:

• Ovulation occurs in this phase. Mature Graafian follicle ruptures and secondary oocyte is released into the pelvic region of abdomen.
• Ovulation occurs due to surging quantity of LH from pituitary.

(4) Luteal phase/Secretary phase :
(i) Since the empty Graafian follicle converts itself into corpus luteum under the influence of LH, this phase is called luteal phase in ovary. At the same time, the uterine endometrium thickens and becomes more secretory and hence it is called secretory phase in uterus.

(ii) Corpus luteum secretes progesterone, some amount of estrogens and inhibin. These hormones stimulate the growth of endometrial glands which later start uterine secretions.

(iii) Endometrium becomes more vascularized becomes 8-10 mm. in thickness. These changes are the preparation for the implantation of the ovum if fertilization occurs.

(iv) In absence of fertilization, corpus luteum can survive for only two weeks and then degenerate into a non-secretory white scar called corpus albicans.

(v) If ovum is fertilized, woman becomes pregnant and hormone hCG (human Chorionic Gonadotropin) is secreted by chorionic membrane of embryo which keeps corpus luteum active till the formation of placenta.

Question 2.
Explain the steps of parturition.
Answer:
Parturition involves the following three steps:
1. Dilation stage:

• Dilation stage means dilating the birth canal or passage though which baby is pushed out. In the beginning uterine contractions start from top and baby is moved to cervix. Due to compression of blood vessels and movements of flexible joints in pelvic girdle, mother experiences labour pains.
• Oxytocin is secreted later in more amount causing severe uterine contractions. This pushes baby in a head down position and closer to cervix.
• Cervix and vagina both are dilated.
• This stage lasts for about 12 hours.
• At the end, amniotic sac ruptures and amniotic fluid is passed out.

2. Expulsion stage:

• During second stage of about 20 to 60 minutes, the uterine and abdominal contractions become stronger.
• Foetus moves out with head down position through cervix and vagina.
• The umbilical cord which connects the baby to placenta is tied and cut off close to the baby’s navel.

3. After birth or placental stage : In the last stage of 10 to 45 minutes, once the baby is out then the placenta is also separated from uterine wall and is expelled out as “after birth”. This is accompanied by severe contractions of the uterus.

Question 3.
Explain the histological structure of testis.
Answer:
Histological structure of testis:

1. The external covering of testis is a fibrous connective tissue called tunica albuginea.
2. Then there is an incomplete peritoneal covering called tunica vaginalis.
3. Interior to this there is a covering called tunica vascularis formed by capillaries.
4. The testis is composed of many seminiferous tubules that are lined by cuboidal germinal epithelial cells.
5. In the seminiferous tubules various stages of developing sperms are seen as spermatogenesis takes place here. These stages are spermatogonia, primary and secondary spermatocytes, spermatids and sperms.
6. Large, pyramidal sub tentacular cells, nurse cells or Sertoli cells are present between germinal epithelium. Sperm bundles remain attached to Sertoli cells with their heads.
7. Seminiferous tubules form sperms whereas Sertoli cells provide nourishment to the sperms till maturation.
8. In between the seminiferous tubules there are interstitial cells of Leydig which are endocrine in nature. They secrete testosterone.

Question 4.
Describe the structure of blastocyst or blastulation
Answer:

1. The outer layer of cells of the morula is called trophoblast or trophoectoderm. This layer absorbs the nutritive fluid secreted by uterine endometrial membrane.
2. As more and more fluid is absorbed by trophoblast cells, the cells become flat and a cavity called blastocyst cavity or blastocoel or segmentation cavity is formed.
3. This causes trophoblast cells to get separated from inner cell mass except at one side.
4. The trophoblast cells in contact with embryonal knob are known as cells of Rauber. As the quantity of fluid increases, the morula enlarges rapidly and assumes the shape of a cyst. This stage is called blastocyst.
5. The side of the blastocyst to which embryonal knob is attached is known as the embryonic or animal pole and the opposite side as abembryonic pole.
6. The trophoblast produces extra embryonic membranes and does not participate in the formation of embryo proper.
7. Zona pellucida disappears allowing the blastula to increase in size and volume. The blastocyst stage is reached in about five days after fertilization.
8. Blastocyst depends on mother for nutrition which it obtained through placenta.

Question 5.
Explain the histological structure of ovary in human.
Answer:
Histological structure of ovary:
(1) Each ovary is a compact structure differentiated into a central part called medulla and the outer part called cortex.

(2) The cortex is covered externally by a layer of germinal epithelium while the medulla contains the stroma or loose connective tissue with blood vessels, lymph vessels and nerve fibres.

(3) Different stages of developing ovarian follicles are seen in the cortex. Each primordial follicle has at its centre a large primary oocyte (2n) surrounded by a single layer of flat follicular cells, then gradually it matures.

(4) In the ovary during each menstrual cycle there is a maturation of primordial follicles into multilayered primary, secondary and Graafian follicles.

(5) Every Graafian follicle has three layers, viz. theca externa, theca interna and membrana granulosa which are from outer to inner side. A space called antrum filled with liquor folliculi is present inside the follicle. There is a small hillock of cells called cumulus oophours or discus proligerus over which the ovum is lodged. The ovum in turn is covered by vitelline membrane, zona pellucida and corona radiata from inner side to outer surface.

(6) Ovarian cortex also shows corpus luteum, or yellow body formed from empty Graafian follicle after ovulation. Corpus luteum is converted into corpus albicans or white body in case of absence of conception.

Question 6.
Describe the various methods of birth control to avoid pregnancy.
Answer:
Birth control/Contraceptive methods are of two main types, viz. temporary and permanent.
A. Temporary methods:
(1) Natural method/Safe period/Rhythm method : A week before and a week after menstrual bleeding is considered the safe period for sexual intercourse. It is based on the fact that ovulation occurs on the 14th day of menstrual cycle.

(2) Coitus Interruptus or withdrawal : In this method, the male partner withdraws his penis from the vagina before ejaculation, so as to avoid insemination. This method also has some drawbacks, as the pre-ejaculation fluid may contain sperms and this can cause fertilization.

(3) Lactational amenorrhoea (absence of menstruation) : This method is based on the fact that ovulation does not occur during the period of intense lactation following parturition so chances of conception are almost negligible. However, this method also has high chances of failure.

(4) Chemical means (spermicides) : In this method chemicals like foam, tablets, jellies and creams are introduced into the vagina before sexual intercourse, they adhere to the mucous membrane, immobilize and kill the sperms.

(5) Mechanical means/Barrier methods:
(i) Condom : It is a thin rubber sheath that is used to cover the penis of the male. Condom should be used before starting coital activity. It also prevents STDs and AIDS.

(ii) Diaphragm, cervical caps and vaults : These devices made of rubber are inserted into the female reproductive tract to cover the cervix diming copulation. They prevent conception by blocking the entry of sperms through the cervix.

(iii) Intra-uterine devices (IUDs) : These are plastic or metal objects placed in the uterus by a doctor. These include Lippes loop, copper releasing IUDs (Cu-T, Cu 7, multiload 375) and hormone releasing IUDs (LNG-20, progestasert). They prevent fertilization of the egg or implantation of the embryo.

(6) Physiological (Oral) Devices : Birth control pills (oral contraceptive pills) check ovulation as they inhibit the secretion of follicle stimulating hormone (FSH) and luteinizing hormone (LH) that are necessary for ovulation. The pill ‘Saheli’ is taken weekly.

(7) Other contraceptives : The birth control implant is similar to that of pills in their mode of action. It is implanted under the skin of the upper arm of the female.

B. Permanent methods surgical operations : In men surgical operation is called vasectomy and in women it is called tubectomy. This method blocks gamete transport and prevent pregnancy.

Question 7.
What are the goals of RCH programmes?
Answer:
Goals of RCH programmes are as follows:

1. Various aspects related to reproduction are made aware to general public.
2. Facilities are provided to people to understand and build up reproductive health.
3. Support is given for building up a reproductively healthy society.
4. Three critical health indicators, i.e. reducing total infertility rate, infant mortality rate and maternal mortality rate are well looked after.

Question 8.
What is parturition? Which hormones are involved in parturition?
Answer:

1. Parturition is the act of expelling out the mature foetus from the uterus of mother via the vagina.
2. When the foetus is fully mature, it starts secreting ACTH (Adreno Cortico Trophic Hormone) from its pituitary.
3. ACTH stimulates adrenal glands of foetus to produce corticosteroids.
4. These corticosteroids diffuse from foetal blood to mother’s blood across the placenta. Corticosteroids accumulate in mother’s blood that results in decreased amount of progesterone. Corticosteroids also increase secretion of prostaglandins.
5. Simultaneously estrogen levels rise bringing about initation of contractions of uterine muscular wall.
6. Reduced progesterone level and increased estrogen level cause secretion of oxytocin from mother’s pituitary. This causes greater stimulation of myometrium of uterus.
7. Prostaglandins cause increased forceful contraction of uterus which expels the foetus out of the uterus.
8. Hormone relaxin secreted by the placenta makes the pubic ligaments and sacroiliac joints of the mother loosen. This causes widening of birth canal which facilitates the normal birth of the baby.

Question 9.
What are the functions of male accessory glands?
OR
Write a brief account of accessory sex glands associated with human male reproductive system.
Answer:
Seminal Vesicles, prostate gland and Cowper’s glands are associated with human male reproductive system.
(i) Seminal Vesicles:

1. Seminal vesicles occur in pair present on the posterior side of urinary bladder. Its secretion consists about 60% of the total volume of the semen. The secretion is an alkaline seminal fluid containing fructose, fibrinogen and prostaglandins.
2. Fructose helps in the movement of sperms by providing energy to them.
3. Semen is coagulated in bolus by fibrinogen. This helps in faster movements of sperms in vagina after insemination.
4. Reverse peristalsis in vagina and uterus for faster movement of sperms towards the egg in the female body is elided by prostaglandins.

(ii) Prostate gland:

1. It is a single gland located under the urinary bladder. It has about 20 to 30 separate lobes which open separately into the urethra.
2. Prostatic fluid secreted by this gland is milky white and slightly acidic. It forms 30 % of the semen and is secreted in urethra.
3. Its contents are citric acid, acid phosphatase and various other enzymes.
4. The sperms are protected from the acidic environment of vagina by acid phosphatase.

(iii) Cowper’s glands (Bulbo-urethral glands):

1. Cowper’s glands occur in pair on either side of urethra. They are small and pea shaped.
2. Cowper’s glands secrete an alkaline, viscous, mucous-like fluid. It helps as lubricant during copulation.

Question 10.
What is capacitation? Give its importance.
Answer:

1. Capacitation is the process by which the sperms are made capable to swim up to the fallopian tubes. This process takes place in 5-6 hours.
2. 50% of ejaculated sperms die due to unfavourable vaginal and uterine conditions.
3. The remaining sperms are capacitated with the help of prostaglandin and vestibular secretions of female tract. It involves the changes in the membrane covering the acrosome.
4. Due to capacitation, acrosome membrane becomes thin, Calcium ions enters the sperm and their tail begin to show rapid whiplash movements.
5. Sperms become extra active and then they ascend upwards to reach fallopian tubes.
6. After capacitation the sperms swim through the vagina and uterus and reach ampulla of fallopian tube within 5 minutes.

Long answer questions

Question 1.
Explain the following parts of male reproductive system along with labelled diagram showing these parts – Testis, vasa deferentia, epididymis, seminal vesicle, prostate gland and penis.
OR
With the help of a neat, labelled diagram, describe the human male reproductive system.
Answer:

(i) Testis, the male gonad, the accessory ducts and glands along with external genitalia form the male reproductive system.

(ii) Testes:

1. Testes are male gonads with dimensions of about 4.5. cm length, 2.5 cm width and 3 cm thickness.
2. There are about 200 to 300 lobules in each testis in which there are seminiferous tubules that form rete testis.
3. Testes produce sperms and secrete male sex hormone, androgen or testosterone.

(iii) Accessory ducts : Rete testis, vasa efferentia, epididymis, vas deferens, ejaculatory duct and urethra together form the accessory ducts of male reproductive system.
1. Vasa efferentia : Vasa efferentia are 12-20 fine tubules. They arise from rete testis and end into the epididymis. The sperms from the testis are carried by these ducts to the epididymis.

2. Epididymis : Epididymis are long and coiled tubes having three parts, viz. caput, corpus and cauda epididymis. They are located on the posterior border of each testis. The sperms undergo maturation in epididymis.

3. Vasa deferentia:

• Vasa deferentia are a pair of 40 cm long tubular structures that arise from cauda epididymis.
• Each vas deferens enters the abdominal cavity through the inguinal canal and then ascends in the form of spermatic cord.
• Vas deferens of each side is joined by the duct from seminal vesicle to form ejaculatory duct.

4. Ejaculatory duct : About 2 cm long pair of ducts formed by joining of vas deferens and a duct of seminal vesicle are the ejaculatory ducts. Both ejaculatory ducts open into urethra near the prostate gland. Seminal fluid containing spermatozoa are carried by ejaculatory duct to the urethra.

5. Urethra : The male urethra provides a common passage for the urine and semen hence is also called urinogenital duct.

(iv) Accessory glands : Associated with male reproductive system are : (a) Seminal vesicles (b) Prostate gland and (c) Cowper’s or Bulbourethral glands. Every accessory gland has secretion which helps in functions of reproductive system.

(v) External genitalia : External genitalia consists of penis and scrotum.
1. Penis:

• Penis is the copulatory organ used for insemination or deposition of sperms in female genital tract.
• It is cylindrical, erectile and pendulous organ through which passes the urethra.
• It contains three columns of erectile tissues which has abundant blood sinuses.
• The tip is called glans penis while the retractible fold of skin on penis is called prepuce.

2. Scrotum : The scrotum is a pouch of pigmented skin arising from lower abdominal wall. It protects testes within it. Scrotum acts as thermoregulator. Testis are suspended in scrotum by spermatic cord.

Question 2.
Describe female reproductive system of human
Answer:

The female reproductive system consists of internal organs and external genitalia.

Internal organs are pair of ovaries and pair of fallopian ducts or oviducts, single median uterus and vagina. External genitalia is called vulva. There are a pair of vestibular glands in external genitalia. Mammary glands or breasts are also associated with reproductive system of female.

(1) Ovaries:

• Ovaries are situated in the abdomen in upper lateral part of the pelvis near the kidneys. Their dimensions are about 3 cm in length, 1.5 cm in breadth and 1.0 cm thick. They are solid, oval or almond shaped organs.
• Ovaries produce ova and they are also endocrine in nature as they produce estrogen, progesterone, relaxin, activin and inhibin.
• Ovarian hormones bring about secondary sexual characters. They also control menstrual cycle, pregnancy and parturition.

(2) Fallopian tubes/oviducts:
(i) Fallopian tubes lie horizontally over peritoneal cavity. These are about 10 to 12 cm long, narrow, muscular structure lined by ciliated epithelium.
(ii) They transport the ovum after ovulation from the ovary to the uterus.
(iii) Fallopian tube can be subdivided into the following three parts:

• The infundibulum which bears a number of finger-like processes called fimbriae at its free border.
• Infundibulum is funnel-shaped having ostium which receives ova released from the ovary.
• The second part is the ampulla where the fertilization takes place.
• The last part is short cornua or isthmus which opens into the uterus.

(3) Uterus/Womb:
(i) Uterus is a pear-shaped, highly muscular, thick walled, hollow organ measuring about 8 cm in length, 5 cm in width and 2 cm in thickness.

(ii) Uterus has the following three parts : Fundus, Body or corpus and Cervix.

(iii) The cervix communicates above with the body of the uterus by an aperture, the internal os and with vagina below by an opening the external os.

(iv) Uterus has three-layered wall. These layers are:

• Perimetrium : An outer serous layer.
• Myometrium : The middle thick muscular layer of smooth muscles.
• Endometrium : The inner highly vascular mucosa that has many uterine glands.

(v) Uterus receives the ovum from fallopian tube. It develops placenta during pregnancy for the nourishment of foetus. At the time of parturition, it expels the young one at birth.

(4) Vagina:

• Vagina is a highly distensible fibro-muscular tube that lies between the cervix and the vestibule.
• It is about 7 to 9 cm in length and is internally lined by stratified and non- keratinised epithelium. The vaginal wall has inner mucous lining.
• Vagina acts as a birth canal as well as copulatory passage. It also allows passage of menstrual flow.
• Vagina opens into vestibule by vaginal orifice which may be covered with hymen which is also a mucous membrane.

(5) External genitalia or vulva or pudendum : The external genitalia consists of five parts; viz. labia majora, labia minora, mons veneris, clitoris and vestibule.

(6) A pair of vestibular glands / Bartholin’s glands : These glands open into the vestibule and release a lubricating fluid.

(7) A pair of mammary glands/breasts : These are the accessory organs of female reproductive system for production and release of milk after parturition.

Question 3.
Describe the process of fertilization.
Answer:
(1) Fertilization is the process of fusion of the haploid male and female gametes which results in the formation of a diploid zygote (2n).

(2) In human beings fertilization is internal. Sperms deposited in vagina, swim across the uterus and fertilize the ovum in ampulla of the fallopian tube.

(3) Fertilization involves the following events:
(i) Insemination : Discharge of semen into the vagina at the time of copulation is called insemination.

(ii) Movement of sperm towards egg : Sperms reaching the vagina undergo capacitation process for 5-6 hours. During capacitation acrosomal membrane of sperm becomes thin and Ca⁺⁺ enters the sperm making it extra active. Sperms reach up to the ampulla by swimming aided with contraction of uterus and fallopian tubes. These contractions are stimulated by oxytocin of female. By capacitation sperm can reach ampulla within 5 minutes, they remain 5 viable for 24 to 48 hours, whereas ovum remains viable for 24 hours.

(iii) Entry of sperm into the egg : Though many sperms reach the ampulla, only a single sperm fertilizes the ovum. The acrosome of sperm after coming in contact with the ovum, releases lysins; hyaluronidase and corona penetrating enzymes. Due to these enzymes cells of corona radiata are separated and dissolved. The sperm head then passes through zona pellucida of egg. The zona pellucida has glycoprotein fertilizin receptor proteins. These bind to specific acid protein-antifertilizin of sperm. This makes sperm and ovum to come together. Fertilizin-Antifertilizin interaction is species- specific.

(iv) Acrosome reaction : When the sperm head comes in contact with the zona pellucida, its acrosome covering ruptures to release lytic enzymes, acrosin or zona lysin. These enzymes dissolve plasma membrane of egg so that the sperm nucleus and the centrioles enter the egg, while other parts remain outside. Now the vitelline membrane of egg changes into fertilization membrane which prevents any further entry of other sperms into the egg, thus polyspermy is prevented.

(v) Activation of ovum : After the entry of sperm head into ovum, it gets activated to resume and complete its meiosis-II. With this it gives out the second polar body. The germinal vesicle organises into female pronucleus. At this stage, it is true ovum.

(vi) Fusion of egg and sperm : The coverings of male and female pronuclei degenerate results in the formation of a synkaryon by a process called syngamy or karyogamy. The zygote is thus formed.

Question 4.
Explain the process by which zygote divides and redivides to form the morula.
Answer:
(1) Cleavage is a rapid mitotic division to form a blastula. These divisions takes place immediately after fertilization. The cells formed by cleavage are called blastomeres.

(2) The type of cleavage in human is holoblastic, i.e. the whole zygote gets divided, radial and indeterminate, i.e. fate of each blastomere is not predetermined.

(3) Cleavage show faster synthesis of DNA and high consumption of oxygen.

(4) Since there is no growth phase between the cleavages, the size of blastomeres will be reduced with every successive cleavage.

(5) The cleavages occur as follows:

(6) Successive divisions produce a solid ball of cells called morula of 16 cells. It consists of an outer layer of smaller clearer cells and an inner mass of larger cells.

(7) Morula reaches the uterus about 4-6 days after fertilization.

Maharashtra State Board 12th Std Biology Textbook Solutions

• Reproduction in Lower and Higher Plants Class 12 Biology Textbook Solutions
• Reproduction in Lower and Higher Animals Class 12 Biology Textbook Solutions
• Inheritance and Variation Class 12 Biology Textbook Solutions
• Molecular Basis of Inheritance Class 12 Biology Textbook Solutions
• Origin and Evolution of Life Class 12 Biology Textbook Solutions
• Plant Water Relation Class 12 Biology Textbook Solutions
• Plant Growth and Mineral Nutrition Class 12 Biology Textbook Solutions
• Respiration and Circulation Class 12 Biology Textbook Solutions

Balbharti 12th Maharashtra State Board Maths Solutions Book Pdf Chapter 8 Binomial Distribution Miscellaneous Exercise 8 Questions and Answers.

12th Maths Part 2 Binomial Distribution Miscellaneous Exercise 8 Questions And Answers Maharashtra Board

(I) Choose the correct option from the given alternatives:

Question 1.
The mean and the variance of a binomial distribution are 4 and 2 respectively. Then the probability of 2 successes is
(a) √50
(b) 5
(c) 25
(d) 10
Answer:
(b) 5

Question 2.
The mean and the variance of a binomial distribution are 4 and 2 respectively. Then the probablity of 2 successes is
(a) \(\frac{128}{256}\)
(b) \(\frac{219}{256}\)
(c) \(\frac{37}{256}\)
(d) \(\frac{28}{256}\)
Answer:
(d) \(\frac{28}{256}\)

Question 3.
For a binomial distribution, n = 5. If P(X = 4) = P(X = 3) then p = ___________
(a) \(\frac{1}{3}\)
(b) \(\frac{3}{4}\)
(c) 1
(d) \(\frac{2}{3}\)
Answer:
(d) \(\frac{2}{3}\)

Question 4.
In a binomial distribution, n = 4. If 2 P(X = 3) = 3 P(X = 2) then p = ___________
(a) \(\frac{4}{13}\)
(b) \(\frac{5}{13}\)
(c) \(\frac{9}{13}\)
(d) \(\frac{6}{13}\)
Answer:
(c) \(\frac{9}{13}\)

Question 5.
If X ~ B (4, p) and P (X = 0) = \(\frac{16}{81}\), then P (X = 4) = ___________
(a) \(\frac{1}{16}\)
(b) \(\frac{1}{81}\)
(c) \(\frac{1}{27}\)
(d) \(\frac{1}{8}\)
Answer:
(b) \(\frac{1}{81}\)

Question 6.
The probability of a shooter hitting a target is \(\frac{3}{4}\). How many minimum numbers of times must he fie so that the probability of hitting the target at least once is more than 0·99?
(a) 2
(b) 3
(c) 4
(d) 5
Answer:
(c) 4

Question 7.
If the mean and variance of a binomial distribution are 18 and 12 respectively, then n = ___________
(a) 36
(b) 54
(c) 18
(d) 27
Answer:
(b) 54

(II) Solve the following:

Question 1.
Let X ~ B(10, 0.2). Find
(i) P(X = 1)
(ii) P(X ≥ 1)
(iii) P(X ≤ 8).
Solution:
X ~ B(10, 0.2)
∴ n = 10, p = 0.2
∴ q = 1 – p = 1 – 0.2 = 0.8
The p,m.f. of X is given by

Question 2.
Let X ~ B(n, p).
(i) If n = 10, E(X) = 5, find p and Var(X).
(ii) If E(X) = 5 and Var(X) = 2.5, find n and p.
Solution:
X ~ B(n, p)
(i) Given: n = 10 and E(X) = 5
But E(X) = np
∴ np = 5.
∴ 10p = 5
∴ p = \(\frac{1}{2}\)
∴ q = 1 – p = 1 – \(\frac{1}{2}\) = \(\frac{1}{2}\)
Var(X) = npq = 10(\(\frac{1}{2}\))(\(\frac{1}{2}\)) = 2.5.
Hence, p = \(\frac{1}{2}\) and Var(X) = 2.5

(ii) Given: E(X) = 5 and Var(X) = 2.5
∴ np = 5 and npq = 2.5
∴ \(\frac{n p q}{n p}=\frac{2.5}{5}\)
∴ q = 0.5 = \(\frac{5}{10}=\frac{1}{2}\)
∴ p = 1 – q = 1 – \(\frac{1}{2}\) = \(\frac{1}{2}\)
Substituting p = \(\frac{1}{2}\) in np = 5, we get
n(\(\frac{1}{2}\)) = 5
∴ n = 10
Hence, n = 10 and p = \(\frac{1}{2}\)

Question 3.
If a fair coin is tossed 10 times and the probability that it shows heads (i) 5 times (ii) in the first four tosses and tail in the last six tosses.
Solution:
Let X = number of heads.
p = probability that coin tossed shows a head
∴ p = \(\frac{1}{2}\)
q = 1 – p = 1 – \(\frac{1}{2}\) = \(\frac{1}{2}\)
Given: n = 10
∴ X ~ B(10, \(\frac{1}{2}\))
The p.m.f. of X is given by
P(X = x) = \({ }^{n} C_{x} P^{x} q^{n-x}\)

(i) P(coin shows heads 5 times) = P[X = 5]

Hence, the probability that can shows heads exactly 5 times = \(\frac{63}{256}\)

(ii) P(getting heads in first four tosses and tails in last six tosses) = P(X = 4)

Hence, the probability that getting heads in first four tosses and tails in last six tosses = \(\frac{105}{512}\).

Question 4.
The probability that a bomb will hit a target is 0.8. Find the probability that out of 10 bombs dropped, exactly 2 will miss the target.
Solution:
Let X = the number of bombs hitting the target.
p = probability that bomb will hit the target
∴ p = 0.8 = \(\frac{8}{10}=\frac{4}{5}\)
∴ q = 1 – p = 1 – \(\frac{4}{5}\) = \(\frac{1}{5}\)
Given: n = 10
∴ X ~ B(10, \(\frac{4}{5}\))
The p.m.f. of X is given as:
P[X = x] = \({ }^{n} \mathrm{C}_{x} p^{x} q^{n-x}\)
i.e.p(x) = \({ }^{10} \mathrm{C}_{x}\left(\frac{4}{5}\right)^{x}\left(\frac{1}{5}\right)^{10-x}\)
P(exactly 2 bombs will miss the target) = P(exactly 8 bombs will hit the target)
= P[X = 8]
= p(8)

Hence, the probability that exactly 2 bombs will miss the target = 45\(\left(\frac{2^{16}}{5^{10}}\right)\)

Question 5.
The probability that a mountain bike travelling along a certain track will have a tire burst is 0.05. Find the probability that among 17 riders:
(i) exactly one has a burst tyre
(ii) at most three have a burst tyre
(iii) two or more have burst tyres.
Solution:
Let X = number of burst tyres.
p = probability that a mountain bike travelling along a certain track will have a tyre burst.
∴ p = 0.05
∴ q = 1 – p = 1 – 0.05 = 0.95
Given: n = 17
∴ X ~ B(17, 0.05)
The p.m.f. of X is given by
P(X = x) = \({ }^{n} \mathrm{C}_{x} P^{x} q^{n-x}\)
i.e.(x) = \({ }^{17} \mathrm{C}_{x}(0.05)^{x}(0.95)^{17-x}\), x = 0, 1, 2, ……, 17
(i) P(exactly one has a burst tyre)
P(X = 1) = p(1) = \({ }^{17} \mathrm{C}_{1}\) (0.05)¹ (0.95)^17-1
= 17(0.05) (0.95)¹⁶
= 0.85(0.95)¹⁶
Hence, the probability that riders has exactly one burst tyre = (0.85)(0.95)¹⁶

(ii) P(at most three have a burst tyre) = P(X ≤ 3)
= P(X = 0) + P(X = 1) + P(X = 2) + P(X = 3)
= p(0) + p(1) + p(2) + p(3)


Hence, the probability that at most three riders have burst tyre = (2.0325)(0.95)¹⁴.

(iii) P(two or more have tyre burst) = P(X ≥ 2)
= 1 – P(X < 2)
= 1 – [P(X = 0) + P(X = 1)]
= 1 – [p(0) + p(1)]
= 1 – [\({ }^{17} \mathrm{C}_{0}\) (0.05)⁰ (0.95)¹⁷ + \({ }^{17} \mathrm{C}_{1}\) (0.05)(0.95)¹⁶]
= 1 – [1(1)(0.95)¹⁷ + 17(0.05)(0.95)¹⁶]
= 1 – (0.95)¹⁶[0.95 + 0.85]
= 1 – (1.80)(0.95)¹⁶
= 1 – (1.8)(0.95)¹⁶
Hence, the probability that two or more riders have tyre burst = 1 – (1.8)(0.95)¹⁶.

Question 6.
The probability that a lamp in a classroom will be burnt out is 0.3. Six such lamps are fitted in the classroom. If it is known that the classroom is unusable if the number of lamps burning in it is less than four, find the probability that the classroom cannot be used on a random occasion.
Solution:
Let X = number of lamps burnt out in the classroom.
p = probability of a lamp in a classroom will be burnt
∴ p = 0.3 = \(\frac{3}{10}\)
∴ q = 1 – p = 1 – \(\frac{3}{10}\) = \(\frac{7}{10}\)
Given: n = 6
∴ X ~ B(6, \(\frac{3}{10}\))
The p.m.f. of X is given as:
P[X = x] = \({ }^{n} \mathrm{C}_{x} p^{x} q^{n-x}\)
i.e., p(x) = \({ }^{6} \mathrm{C}_{x}\left(\frac{3}{10}\right)^{x}\left(\frac{7}{10}\right)^{6-x}\)
Since the classroom is unusable if the number of lamps burning in it is less than four, therefore
P(classroom cannot be used) = P[X < 4]
= P[X = 0] + P[X = 1] + P[X = 2] + P[X = 3]
= p(0) + p(1) + p(2) + p(3)

Hence, the probability that the classroom cannot be used on a random occasion is 0.92953.

Question 7.
A lot of 100 items contain 10 defective items. Five items are selected at random from the lot and sent to the retail store. What is the probability that the store will receive at most one defective item?
Solution:
Let X = number of defective items.
p = probability that item is defective
∴ p = \(\frac{10}{100}=\frac{1}{10}\)
∴ q = 1 – p = 1 – \(\frac{1}{10}\) = \(\frac{9}{10}\)
Given: n = 5
∴ X ~ B(5, \(\frac{1}{10}\))
The p.m.f. of X is given as:
P[X = x] = \({ }^{n} \mathrm{C}_{x} p^{x} q^{n-x}\)
i.e., p(x) = \({ }^{5} C_{x}\left(\frac{1}{10}\right)^{x}\left(\frac{9}{10}\right)^{5-x}\)
P (store will receive at most one defective item) = P[X ≤ 1]
=P[X = 0] + P[X = 1]
= p(0) + p(1)

Hence, the probability that the store will receive at most one defective item is (1.4)(0.9)⁴.

Question 8.
A large chain retailer purchases a certain kind of electronic device from a manufacturer. The manufacturer indicates that the defective rate of the device is 3%. The inspector of the retailer picks 20 items from a shipment. What is the probability that the store will receive at most one defective item?
Solution:
Let X = number of defective electronic devices.
p = probability that device is defective
∴ p = 3% = \(\frac{3}{100}\)
∴ q = 1 – p = 1 – \(\frac{3}{100}\) = \(\frac{97}{100}\)
Given: n = 20
∴ X ~ B(20, \(\frac{3}{100}\))
The p.m.f. of X is given as:

Hence, the probability that the store will receive at most one defective item = (1.57)(0.97)¹⁹.

Question 9.
The probability that a certain kind of component will survive a check test is 0.6. Find the probability that exactly 2 of the next 4 tested components tested survive.
Solution:
Let X = number of tested components survive.
p = probability that the component survives the check test

Hence, the probability that exactly 2 of the 4 tested components survive is 0.3456.

Question 10.
An examination consists of 10 multiple choice questions, in each of which a candidate has to deduce which one of five suggested answers is correct. A completely unprepared student guesses each answer completely randomly. What is the probability that this student gets 8 or more questions correct? Draw the appropriate moral.
Solution:
Let X = number of correct answers.
p = probability that student gets correct answer
∴ p = \(\frac{1}{5}\)
∴ q = 1 – p = 1 – \(\frac{1}{5}\) = \(\frac{4}{5}\)
Given: n = 10 (number of total questions)
∴ X ~ B(10, \(\frac{1}{5}\))
The p.m.f. of X is given by

Hence, the probability that student gets 8 or more questions correct = \(\frac{30.44}{5^{8}}\)

Question 11.
The probability that a machine will produce all bolts in a production run within specification is 0.998. A sample of 8 machines is taken at random. Calculate the probability that (i) all 8 machines (ii) 7 or 8 machines (iii) at most 6 machines will produce all bolts within specification.
Solution:
Let X = number of machines which produce the bolts within specification.
p = probability that a machine produce bolts within specification
p = 0.998 and q = 1 – p = 1 – 0.998 = 0.002
Given: n = 8
∴ X ~ B(8, 0.998)
The p.m.f. of X is given by
P(X = x) = \({ }^{n} \mathrm{C}_{x} p^{x} q^{n-x}\)
i.e. p(x) = \({ }^{8} \mathrm{C}_{x}(0.998)^{x}(0.002)^{8-x}\), x = 0, 1, 2, …, 8
(i) P(all 8 machines will produce all bolts within specification) = P[X = 8]
= p(8)
= \({ }^{8} \mathrm{C}_{8}\) (0.998)⁸ (0.002)^8-8
= 1(0.998)⁸ . (1)
= (0.998)⁸
Hence, the probability that all 8 machines produce all bolts with specification = (0.998)⁸.

(ii) P(7 or 8 machines will produce all bolts within i specification) = P (X = 7) + P (X = 8)

Hence, the probability that 7 or 8 machines produce all bolts within specification = (1.014)(0.998)⁷.

(iii) P(at most 6 machines will produce all bolts with specification) = P[X ≤ 6]
= 1 – P[x > 6]
= 1 – [P(X = 7) + P(X = 8)]
= 1 – [P(7) + P(8)]
= 1 – (1.014)(0.998)⁷
Hence, the probability that at most 6 machines will produce all bolts with specification = 1 – (1.014)(0.998)⁷.

Question 12.
The probability that a machine develops a fault within the first 3 years of use is 0.003. If 40 machines are selected at random, calculate the probability that 38 or more will develop any faults within the first 3 years of use.
Solution:
Let X = the number of machines who develop a fault.
p = probability that a machine develops a fait within the first 3 years of use
∴ p = 0.003 and q = 1 – p = 1 – 0.003 = 0.997
Given: n = 40
∴ X ~ B(40, 0.003)
The p.m.f. of X is given by

Hence, the probability that 38 or more machines will develop the fault within 3 years of use = (775.44)(0.003)³⁸.

Question 13.
A computer installation has 10 terminals. Independently, the probability that anyone terminal will require attention during a week is 0.1. Find the probabilities that (i) 0 (ii) 1 (iii) 2 (iv) 3 or more, terminals will require attention during the next week.
Solution:
Let X = number of terminals which required attention during a week.
p = probability that any terminal will require attention during a week
∴ p = 0.1 and q = 1 – p = 1 – 0.1 = 0.9
Given: n = 10
∴ X ~ B(10, 0.1)
The p.m.f. of X is given by
P(X = x) = \({ }^{n} \mathrm{C}_{x} p^{x} q^{n-x}\)
i.e. p(x) = \({ }^{10} C_{x}(0.1)^{x}(0.9)^{10-x}\), x = 0, 1, 2, …, 10
(i) P(no terminal will require attention) = P(X = 0)

Hence, the probability that no terminal requires attention = (0.9)¹⁰

(ii) P(1 terminal will require attention)

Hence, the probability that 1 terminal requires attention = (0.9)⁹.

(iii) P(2 terminals will require attention)

Hence, the probability that 2 terminals require attention = (0.45)(0.9)⁸.

(iv) P(3 or more terminals will require attention)

Hence, the probability that 3 or more terminals require attention = 1 – (2.16) × (0.9)⁸.

Question 14.
In a large school, 80% of the pupil like Mathematics. A visitor to the school asks each of 4 pupils, chosen at random, whether they like Mathematics.
(i) Calculate the probabilities of obtaining an answer yes from 0, 1, 2, 3, 4 of the pupils.
(ii) Find the probability that the visitor obtains answer yes from at least 2 pupils:
(a) when the number of pupils questioned remains at 4.
(b) when the number of pupils questioned is increased to 8.
Solution:
Let X = number of pupils like Mathematics.
p = probability that pupils like Mathematics

(i) The probabilities of obtaining an answer yes from 0, 1, 2, 3, 4 of pupils are P(X = 0), P(X = 1), P(X = 2), P(X = 3) and P(X = 4) respectively

(ii) (a) P(visitor obtains the answer yes from at least 2 pupils when the number of pupils questioned remains at 4) = P(X ≥ 2)
= P(X = 2) + P(X = 3) + P(X = 4)

(b) P(the visitor obtains the answer yes from at least 2 pupils when number of pupils questioned is increased to 8)

Question 15.
It is observed that it rains 12 days out of 30 days. Find the probability that
(i) it rains exactly 3 days of the week.
(ii) it will rain at least 2 days of a given week.
Solution:
Let X = the number of days it rains in a week.
p = probability that it rains

(i) P(it rains exactly 3 days of week) = P(X = 3)

Hence, the probability that it rains exactly 3 days of week = 0.2903.

(ii) P(it will rain at least 2 days of the given week)

Hence, the probability that it rains at least 2 days of a given week = 0.8414

Question 16.
If the probability of success in a single trial is 0.01. How many trials are required in order to have a probability greater than 0.5 of getting at least one success?
Solution:
Let X = number of successes.
p = probability of success in a single trial
∴ p = 0.01
and q = 1 – p = 1 – 0.01 = 0.99
∴ X ~ B(n, 0.01)
The p.m.f. of X is given by
P(X = x) = \({ }^{n} \mathrm{C}_{x} p^{x} q^{n-x}\)

Hence, the number of trials required in order to have a probability greater than 0.5 of getting at least one success is \(\frac{\log 0.5}{\log 0.99}\) or 68.

Question 17.
In binomial distribution with five Bernoulli’s trials, the probability of one and two success are 0.4096 and 0.2048 respectively. Find the probability of success.
Solution:
Given: X ~ B(n = 5, p)
The probability of X success is


Hence, the probability of success is \(\frac{1}{5}\).

12th Maharashtra State Board Maths Solutions Pdf Part 2

• Probability Distributions Ex 7.1 Class 12 Maths Solutions
• Probability Distributions Ex 7.2 Class 12 Maths Solutions
• Probability Distributions Miscellaneous Exercise 7 Class 12 Maths Solutions
• Binomial Distribution Ex 8.1 Class 12 Maths Solutions
• Binomial Distribution Miscellaneous Exercise 8 Class 12 Maths Solutions