Category: Class 12

Class 12 English Chapter 4.3 Around the World in Eighty Days Question Answer Maharashtra Board

Balbharti Yuvakbharati English 12th Digest Chapter 4.3 Around the World in Eighty Days Notes, Textbook Exercise Important Questions and Answers.

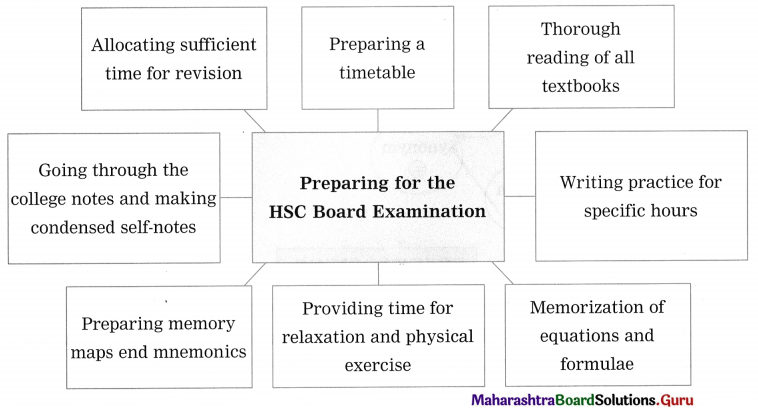
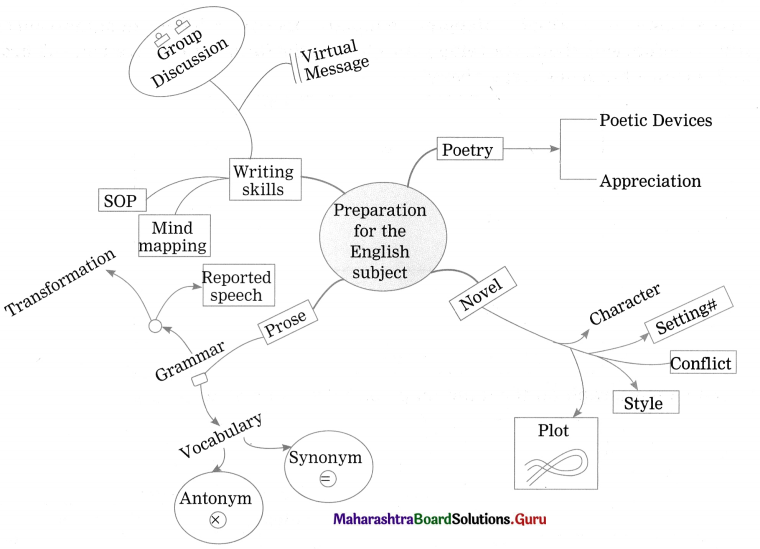
12th Std English Chapter 4.3 Brainstorming Question Answer

12th English Digest Chapter 4.3 Around the World in Eighty Days Textbook Questions and Answers

CHARACTER:

(A1)

Question (i)
One of the following is not a major character of the novel. Choose the correct one and justify.
(Select the correct one.)
(a) Phileas Fogg
(b) Aouda
(c) James Strand
(d) Jean Passepartout
Answer:
James Strand is not a major character of the novel. He was the real bank robber whom Fix was searching for.

Question (ii)
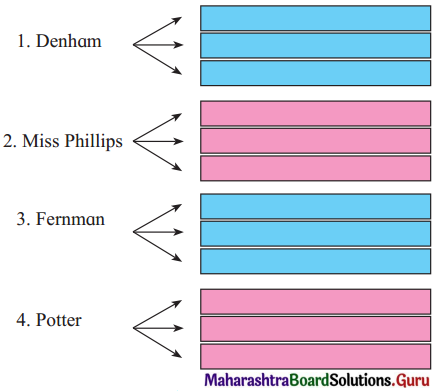
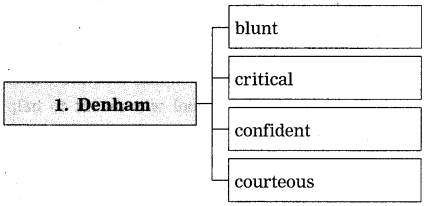
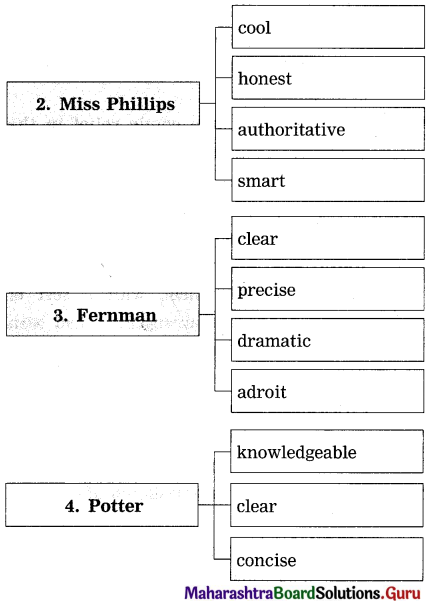
Complete the table highlighting the various traits of the major characters in the extract.
Answer:

Question (iii)
Phileas Fogg is as cool as a cucumber whereas Passepartout is as crazy as a loon. Explain the statement by citing some references from the extract.
Answer:
Phileas Fogg was always cool except when he hit the detective Fix. He was cool and calm in prison. Even when he felt that he had lost the wager, he shut himself up in his house quietly without any noise. He was cool when dealing with Passepartout, and also when dealing with Aouda. He could control his emotions and appear to be expressionless. Passepartout, on the other hand was a very emotional and excitable person. He was very repentant when he realized that he could have prevented Fogg’s arrest; he was thrilled when he knew that Fogg was marrying Aouda.

He was tremendously worried about Fogg when he thought that Fogg had lost the wager. Finally, when he came to know that they had reached earlier than they had thought and there was a chance that they could reach the Reform Club in time to win the bet, he became very excited. He rushed back breathlessly to inform Fogg of the fact that it was Saturday and not Sunday.

Question (iv)
Detective Fix tried hard but could not fix the charge of robbery on Fogg. Explain the statement from the point of view of Fix.
Answer:
From the point of view of Detective Fix : Scotland Yard had given only a vague description of the man who had robbed a great sum from the bank of England. I thought that Fogg fitted the description and he was the bank robber. I put obstacles in Fogg’s path just so that I could arrest him whenever I got the warrant from England. The moment we reached Liverpool, I arrested him. However, after arresting him, I found that he was not the guilty person, and the robber had already been arrested in Edinburgh some days earlier.

Fogg was a respectable gentleman living at Saville Row. There was no proof and no evidence against him except that he had been travelling all over the world apparently without any purpose. I was sorry that I arrested him wrongly and I apologized to him.

Question (v)
Describe the character sketch of Aouda from Fogg’s point of view.
Answer:
From Fogg’s point of view: Aouda has had a very difficult time in India. She was nearly killed by her persecutors, but I, Fogg, managed to save her and bring her to England with me. She is a wonderful person and so grateful for what I did. She was even apologetic for having delayed my return – she did not think about the danger she was in from her persecutors! She is very loving. She is not at all money-minded and was ready to marry me even though I did not have a penny to my name. How many will do this? What a compassionate, kind-hearted and generous person! An admirable woman, indeed, and one whom I am proud to have as my wife.

PLOT:

(A2)

Question (i)
Arrange the incidents in correct sequence as per their occurrence in the extract.
(a) Aouda accepted Fogg’s proposal of marriage.
(b) When set free, the first thing that Fogg did was he knocked Fix down.
(c) As a part of duty, Fix arrested Fogg.
(d) At the fifty-seventh second, Fogg entered the Reform Club Saloon.
Answer:
(c) As a part of duty, Fix arrested Fogg.
(b) When set free, the first thing that Fogg did was he knocked Fix down.
(d) At the fifty-seventh second, Fogg entered the Reform Club Saloon.
(a) Aouda accepted Fogg’s proposal of marriage.

Question (ii)
There is a sudden twist in the climax of the novel. Explain by citing some lines and relevant examples from the extract.
Answer:
Fogg and the reader first think that Fogg has lost not only the wager, but also the money and honour that went with it. The following lines tell us this : ‘After having steadily traversed that long journey, overcome a hundred obstacles, braved many dangers, and still found time to do some good on his way, to fail near the goal by a sudden event which he could not have foreseen, and against which he was unarmed; it was terrible!’ The unforeseen event was his arrest and imprisonment by detective Fix, who mistakenly thought he was the bank robber.

However, the twist comes when Passepartout finds out that it is not Sunday but Saturday, and perhaps they can just make it to the Reform Club in time. Just as Fogg’s antagonists are counting the seconds to their win,, Fogg manages to reach the Club and win the wager, giving a happy and thrilling ending to the novel. The following lines tell us this : ‘At the fifty-seventh second the door of the saloon opened; and the pendulum had not beat the sixtieth second when Phileas Fogg appeared, followed by an excited crowd who had forced their way through the club doors, and in his calm voice, said, “Here I am, gentlemen!”’

Question (iii)
Which of the following is an appropriate reason for Phileas Fogg starting his journey around the world?
(a) Fellow members bet Fogg
(b) Fogg bets his fellow members
(c) Fogg wants to marry Aouda
(d) Fogg committed robbery
Ans.
(a) Fellow members bet Fogg

SETTING:

(A3)

Question (i)
Choose from the following options, the means of transport used in the novel and explain the way they help the characters.
(a) Elephant
(b) Horse
(c) Train
(d) Steamer
Answer:
Elephants, trains and steamers were used as a means of transport in the novel. They help the characters go around the world in the allotted time. After overcoming a number of obstacles, they reach London in time to win the wager.

Question (ii)
The beginning of the extract is a scene in the prison at the custom house. From there the novel moves further from one place/spot to another. Pick and explain all the places/spots where the incidents took place.
Answer:
From the prison at the custom house, Fogg and his companions go to Liverpool station to catch a train back to London, where Fogg lives and where the Reform Club is located. Once they reach London, thinking that they had lost the wager, they go to Saville Row, which is Fogg’s residence. The next location is the preacher’s house where Passepartout goes to make arrangements for Fogg’s wedding. The last location is the Reform Club, which Fogg reaches in time to win his wager.

Question (iii)
Most of the setting in the extract is in London. Explain how this is suited to the theme of the novel.
Answer:
Fogg’s residence was in London. The Reform Club, which Fogg frequented on a regular basis and where the all-important wager took place, is also in London. Fogg’s journey starts from London and ends in London. Hence, London is the central place in the novel, and thus this setting is suited to the theme.

(iv) Describe the importance of the following places in the development of the plot and behaviour of the characters.

Question (a)
Liverpool.
Answer:
Liverpool is the place where Fogg disembarks from his steamer, and from where he has to catch a train to London. Liverpool is also the place where he is arrested by Fix and thus misses his train. He arranges a special train in an attempt to reach London on time.

Question (b)
London.
Answer:
Fogg lives in London. The Reform Club, which Fogg frequented on a regular basis, is also in London. Fogg’s accepts the wager in London; his journey starts from London and ends in London. Hence, London is the central place in the novel.

Question (c)
Reform Club.
Answer:
Reform Club is the place which Fogg frequented on a regular basis. It is at the Reform Club that Fogg gets involved in an argument over an article, and where the wager with his fellow club members takes place. It is the place where Fogg was supposed to return before 8.45 p.m. on 21 December, 80 days later. It is the place where his antagonists are waiting anxiously for him, and which he reaches at practically the last second to win his wager.

Question (d)
Saville Row.
Answer:
Phileas Fogg’s residence is in Saville Row.
This is also the place where he takes Aouda.
Fogg has always stayed quietly at this place.
When he returned from his trip around the world and thought he had lost the wager, he remained there so quietly that no one even knew he had returned.

Question (e)
Edinburgh.
Answer:
Detective Fix arrested Phileas Fogg in Liverpool thinking that he was a bank robber. However, the real bank robber, James Strand, had been arrested on 17th December at Edinburgh.

Question (iv)
Select the correct options:
Find from the options, the place which are not mentioned in the extract:
(a) Bombay (Now, Mumbai)
(b) Allahabad
(c) Chennai
(d) Calcutta (Now, Kolkata)
Answer:
Allahabad, Chennai

THEME:

(A4)

Question (i)
Find and explain the significance of various exciting incidents in the extract.
Answer:
The first exciting incident was when Fogg was arrested by Detective Fix and imprisoned in the Custom House. This meant that his return to London would be delayed, for he would have missed his train.

The second exciting incident was his release. This meant that he could perhaps still reach London on time.

The third exciting incident was when he tried to organize a train to London but had problems.

The fourth exciting incident was Aouda’s marriage proposal and Fogg’s acceptance of it. This showed that Aouda was not at all materialistic and extremely grateful to Fogg for what he had done. She was willing to marry Fogg even after knowing that he was penniless.
The fifth exciting incident was when Passepartout, on reaching the clergyman’s house, discovers that it is not Sunday as they had thought but Saturday, and there was a chance that they could still win the wager. The sixth most exciting incident was Fogg’s reaching the Reform Club at the last moment and winning the wager. All the twists and turns and the climax at the end keeps the reader glued to the novel right till the end.

Question (ii)
Write 4-5 sentences on the ‘Time’ theme of the extract.
Answer:
Phileas Fogg has to go around the world in eighty days if he has to win the wager. As he and his companions struggle to do this, time foils their plans in many cases. Fogg gets arrested for no fault of his and loses precious time. He is unable to catch the train from Liverpool, and the special train he arranged too gets delayed. Fogg is afraid that he has lost the bet. However, in the end, Fogg wins the bet with seconds to spare as he gained a day when crossing the International Date Line. His journey through the time zones had gained him a day. The ultimate message is that no one can control time; time will work the way it wants to work, and humans are at its mercy.

Question (iii)
Write 4-5 sentences on the ‘Morality’ theme of the extract.
Answer:
Fogg embarks on his journey to preserve his honour and prove his worth to the men at the Reform Club. He spends nearly all of his money along the way, showing that riches are not what he is truly out for. He is honourable – when he thinks he is penniless, he does not want Aouda to marry him. Aouda, by proposing to him, shows that she is not materialistic. He forgives Passepartout his mistakes. Passepartout shows his loyalty and love for his master at every step.

In the end, when he wins the bet, he divides whatever money is left between Passepartout and Detective Fix, showing that he had no grudges against him. The writer shows that with human effort and willpower enormous obstacles can be overcome. The writer also tells us in the end that Fogg had won something more important than money, by travelling around the world. He had won a charming woman, who made him the happiest of men. The moral at the end is that love and its attainment is more important than all the challenges and money in the world.

Question (iv)
Write the central idea of the given extract of the novel, ‘Around the World in Eighty Days’.
Answer:
The central idea of the given extract is how Fogg ultimately wins the bet even though there are unexpected delays and missed trains. He had unknowingly gained a day when crossing the International Date Line, and hence he was still in time to meet the deadline. The final statement is that love and its attainment is more important than all the challenges and money in the world.

Question (v)
Justice is served/done in the end. Explain.
Answer:
Phileas Fogg is an honourable and compassionate person. He wants to win his wager of going around the world in eighty S days. He struggles against time, as well as the obstacles and delays that come his way. Finally, when he reaches Liverpool and is about to go to London to win his wager, he is arrested because he is wrongly thought to be a bank robber. Throughout this ordeal, Fogg is calm and unshakeable. Even though he thinks he has lost the wager, he does not blame anyone or lose his temper.

He tells Aouda that he cannot marry her and make her live in poverty. Justice is done unexpectedly in the end when he wins the wager. He had unknowingly gained a day when crossing the International Date Line, and hence he was still in time to meet the deadline. In the end, the writer tells us that Fogg had won something more important than money, by travelling around the world. He had won a charming woman, who made him the happiest of men. Thus, justice was done to the quiet and honourable Phileas Fogg.

LANGUAGE:

(A5)

(i) Elaborate the following quotes in the light of the extract of the novel, ‘Around the World in Eighty Days’.

Question (a)
‘Quitters never win and winners never quit’.
Answer:
Even though Fogg loses time due to being wrongly arrested and imprisoned, he makes every effort to reach London on time. He arranges a special train from Liverpool. He does not quit when he feels that there is some faint chance of a win. Later, when Passepartout discovers that it is Saturday and not Sunday, and that there is still a chance of winning, Fogg puts aside everything and rushes headlong to the Reform Club. He does not give up in spite of all the obstacles, and comes out a winner, both in winning the bet and the love of a good woman.

Question (b)
‘Time is the only solution to problems’.
Answer:
The most important theme in the extract is time. Fogg’s wager is a race against time, and his adventures illustrate repeatedly that time is fickle, and either works for or against them. In many cases, time foils their plans, when the delays build up and the train to Liverpool leaves without them. In the end, though, it is time that helps wins Fogg his bet, since they gained a day when crossing the International Date Line. The ultimate message is that no one can control time; time will work the way it wants to work, and humans are at its mercy. Time is the only solution to problems.

Question (ii)
Following are some dialogues of the major characters in the extract. Find out who the speaker is, his/her tone, style, significance, etc., of the dialogue.
Answer:

Yuvakbharati English 12th Textbook Answers Solutions Section 4 (Genre-Drama)

• History of Novel Class 11 English Solutions
• To Sir, with Love Class 11 English Solutions
• Around the World in Eighty Days Class 11 English Solutions
• The Sign of Four Class 11 English Solutions

Class 12 English Chapter 4.2 To Sir, with Love Question Answer Maharashtra Board

Balbharti Yuvakbharati English 12th Digest Chapter 4.2 To Sir, with Love Notes, Textbook Exercise Important Questions and Answers.

12th Std English Chapter 4.2 Brainstorming Question Answer

12th English Digest Chapter 4.2 To Sir, with Love Textbook Questions and Answers

Character:

(A1)

Question (i)
From the options given below, choose the name of the teacher and write a couple of lines from the extract in support of your answer.
(a) Denham
(b) Miss Joseph
(c) Sapiano
(d) Dale-Evans
Answer:
Dale-Evans is the teacher. The lines to support this are: The names were called Mr. Weston, Mrs. Dale-Evans, Miss Phillips. Denham and Miss Joseph led the others off the stage and the teachers took their seats.

Question (ii)
Complete the table highlighting the various traits of the major characters in the extract.

Answer:

Question (iii)
The narrator played a crucial role in bringing a significant change in the students. Discuss the statement by citing some references from the extract.
Answer:
The narrator initially had a very difficult time with the students who were disrespectful, ill- mannered and mischievous. They considered him to be an arrogant outsider, unfamiliar with the social environment in which they I have grown up. They harass him from day one; however, they come around after only a few weeks, completely changing both their hygiene and their attitudes towards one another.

This marks the success of the narrator in handling the students in a very amicable way. This is proved on the day of the half-yearly report of the Students’ Council. The narrator’s students allocate tasks in a business-like way. They present their reports confidently and clearly. They are cool and efficient in their work. They are courteous towards each other and the teachers, and they accept the verdict of the teachers. This shows the significant and crucial change brought about by the narrator in his students.

Question (iv)
Femman brought a comic relief in the Students’ Council programme. Explain with an incident.
Answer:
In order to explain a point, Fernman made a signal to someone off-stage. Two students, Welsh and Alison, appeared bearing a skeleton between them, with a sort of gallows. When this arrangement had been set up there was the skeleton hanging from a hook screwed into the top of its skull, gently revolving at the end of a cord. This brought some comic relief to the proceedings, and the students laughed uproariously.

(v) Give a brief character-sketch of –

Question (a)
Denham.
Answer:
Denham is business-like and confident while allocating tasks and fitting in the j programme. He is an important official for the function and sits confidently beside the Head. He courteously addresses the girls as ‘Miss’. While discussing P.T. and Games, he shocks the audience with his views. He is a trained boxer and does not want to do P.T. exercises which he feels are unnecessary for him. His tone is initially blunt, critical and argumentative. However, when Miss Phillips gently replies to his arguments and outwits him, he graciously and politely accepts his defeat.

Question (b)
Miss Joseph.
Answer:
Miss Joseph is business-like and confident while allocating tasks and fitting in the programme. She is an important official for the function. She sits on the stage beside Mr. Florian with composure. She also addresses the audience with confidence.

Question (c)
The Narrator.
Answer:
Ricky Braithwaite, the narrator, is a very sensitive person. He is very upset at the racism that he has to face after serving in the army. He gets a job in a school, and initially has a very difficult time with the students who are disrespectful, ill-mannered and mischievous. They harass him from day one. However, his novel and creative ideas, innovative techniques and understanding of the students’ psychology, ultimately wins their hearts.

Though he was bullied, harassed, mentally and physically tortured many times, he didn’t lose his patience and continued implementing his novel ideas and techniques that helped him to bring a significant change in his students’ lives. On the day of the half-yearly report of the Students’ Council, he is very anxious to see how they behave. When they are business-like, confident, cool and courteous, he feels proud of them.

Question (d)
Miss Dare.
Answer:
Miss Dare spoke about the problems which all humanity has to face in terms of sickness and disease, and of the advantages gained by interchange of knowledge, advice and assistance. Her contribution was something of an anticlimax after Femman’s performance, and she seemed to realise it, but continued with her speech.

Question (e)
Miss Phillips.
Answer:
Miss Phillips, whom everyone had thought to be frilly and brainless, proves while answering Denham’s questions that she is the best-informed of the three teachers on the stage. She intervenes skilfully when the other two teachers are at a loss, without embarrassing them. She speaks coolly, honestly and with authority.

She is very slightly built but she controls her class very well. She tells Denham that the whole timetable in the school was meant to help the students in the world after they left school, and doing what one was told in spite of not liking it, is part of the training. She confidently asserts that she was sure that Denham saw the importance of what she had said, and why he had to do P.T. Thus, she put ‘ Denham in his place very coolly.

Question (vi)
Compare the following characters:
Answer:
Miss Joseph and Denham:
Miss Joseph and Denham are both business-like and efficient while allocating tasks and fitting in the programme. They are important officials for the function and sit on the stage confidently beside Mr. Florian. Both address the audience with confidence.

However, Denham is blunt, critical and argumentative while discussing the P.T. exercises that everyone has to do in school. He argues with Miss Phillips, but when Miss Phillips pleasantly and coolly puts him in his place, he graciously accepts defeat. He is also courteous in his dealing with the ladies.

Miss Phillips, whom everyone had thought to be frilly and brainless, proved while answering Denham’s questions that she was the best-informed of the three teachers on the stage. She intervened skilfully when the other two teachers were at a loss, without embarrassing them. She spoke coolly, honestly and with authority.

When Denham is blunt, critical and argumentative while discussing the P.T. exercises that everyone has to do in school, she tells Denham that the whole timetable in the school was meant to help the students in the world after they left school, and doing what one was told in spite of not liking it, is part of the training. She gives her views confidently and puts Denham in his place very coolly. Denham accepts his defeat courteously.

Fernman and Miss Dare:

Fernman is clear, precise and dramatic. He keeps the audience spell-bound by his speech. Miss Dare and Fernman discuss the subject of physiology, with Fernman stealing the show by exhibiting a model of a human skeleton and stressing the class conclusion that “basically all people were the same.” Miss Dare speaks about the problems which all humanity has to face in terms of sickness and disease, and of the advantages gained by interchange of knowledge, advice and assistance.

Her contribution was something of an anticlimax after Fernman’s performance, and she seemed to realise it, but continued with her speech. Fernman was also adroit while questioning the teachers.

The narrator, a teacher, is sensitive, and upset about racism, which has affected him directly. He initially had a very difficult time with the students who were disrespectful, ill-mannered and mischievous. However, he didn’t lose his patience and continued implementing his novel ideas and techniques. This helped him to bring a significant change in his students’ lives. He is very anxious about the students and later proud of their confidence, understanding and behaviour.

The Head of the school, Mr. Florian, addressed the school on the day of the half-yearly report of the Students’ Council. He spoke about the aims and policy of the school and of the important contribution each child could make. He gave praise wherever necessary, but insisted that there was yet a great deal to be done. His remarks showed that he identified himself with the school and everyone in it. At the end he expressed his pride in all the children and his deep appreciation of their efforts.

PLOT:

(A2)

Question (i)
Arrange the incidents in correct sequence as per their occurrence in the extract.
(a) Denham was outwitted by Miss Phillips.
(b) The head of the school closed the proceedings.
(c) Denham asserted that P.T. periods were a waste of time.
(d) The slips were folded and placed in a hat.
(e) Fernman was as usual a trump card.
(f) Denham called out the names of the representatives.
(g) Students’ Council was held every year on November 15th.
Answer:
(g) Students’ Council was held every year on November 15th.
(f) Denham called out the names of the representatives.
(e) Fernman was as usual a trump card.
(d) The slips were folded and placed in a hat.
(c) Denham asserted that P.T. periods were a waste of time.
(a) Denham was outwitted by Miss Phillips.
(b) The head of the school closed the proceedings.

Question (ii)
Describe in brief the purpose of organising the half-yearly report programme of Students’ Council.
Answer:
During the half-yearly report programme of Students’ Council, each class would report, through its representatives, on the studies pursued during the half year which began after Easter. A representative was chosen for each subject. When all the classes had completed their reports a panel of teachers would be invited to occupy the stage and answer questions from the body of the hall on matters arising out of the various reports. Throughout all the reports, the emphasis was on what they understood rather than on what they were expected to learn.

Question (iii)
Write in your words the entire half- yearly report programme of Students’ Council.
Answer:
In the half-yearly report of the Students’ Council, the students report to the faculty and other students on what they have been studying thus far. The representatives of the narrator’s class spoke knowledgeably about their coursework and placed a considerable amount of emphasis on how much they had learnt about different people, cultures, customs, and the importance of international and interracial cooperation.

Miss Joseph and Denham, both students of the narrator’s class, presided over the meeting. Mr. Florian, the headmaster, addressed the meeting with a lengthy presentation. After this, one after another, each class gave a brief report of their progress, through their chosen representatives, on what they had been studying in each subject so far. A panel of teachers was then chosen to answer any questions put by the students.

The lowest class began first; the narrator’s class, being the oldest, was the last to present their report. Miss Joseph began the highest class’s proceedings by clarifying that the common theme underlying all their studies that term was the interdependency of mankind. Potter spoke in the field of math, focusing on how greater understanding in the world is fostered by the use of common weights and measures.

Miss Pegg and Jackson spoke on geography, and Miss Dare and Fernman discussed the subject of physiology, with Fernman stealing the show by exhibiting a model of a human skeleton and stressing the class conclusion that “basically all people are the same.” Miss Dodd reported on history, and Miss Joseph on domestic science. Denham created a stir by speaking on the subject of P.T. and games, complaining that the class ‘was ill-conceived and pointless.’

Mr. Weston, Mrs. Dale-Evans, and Miss Phillips were chosen at random to answer students’ questions. When Denham pursued his inquiry on the necessity of requiring all students to take P.T., Mr. Weston responded quite ridiculously, trying to bluster his way out of the subject, and offering no sensible argument. Unexpectedly, the quiet and hesitant Miss Phillips stepped in and gave a strong defence of the practice. Finally, Denham, knowing that he had been outwitted, had no choice but to respectfully accept his defeat. The narrator was immensely satisfied with the progress of the students of his class.

Question (iv)
Describe the question-answer session that took place at the end of the extract.
Answer:
The questions were mostly from the two top classes. The teachers had no briefing, and were often caught out stammering in their indecision. One of the teachers, Miss Euphemia Phillips proved to be the coolest and best informed of the three teachers on the stage. She dealt with questions put to her with honesty and with authority, and would often intervene skilfully to assist one of the others without causing embarrassment.

While Femman was skillful in his questioning, Denham was blunt in his criticism. He severely criticised the general pattern of P.T. and games. Denham was a trained boxer, and insisted that such exercises were only advantageous if practised daily and for more sustained periods; P.T. twice weekly for twenty minutes was a waste of time, he asserted.

Miss Phillips reminded the school that every subject, including P.T. and games, , had been carefully considered and fitted into the teaching timetable so that each student received maximum benefit from it. The school considered it in terms of the greatest good for the greatest number. She added, hinting at Denham, that while some were fortunate in their own fine physical development and did not really need the few meagre helpings of P.T. and games which the school could offer, there were others for whom the programme was ideally suited. It would be beyond anyone’s powers to please everybody.

She suggested that some of the older boys might even be able to help in that respect. Denham, not put off by these sugary remarks, replied that only the kids who needed it could take it, while the others could have a game of football or something, instead of doing something useless.

This was a difficult question to answer, but Miss Phillips replied pleasantly that it should be considered as much an exercise of the mind as it is of the body. The whole timetable in the school was meant to help them in the world after they left the school, and doing what one was told in spite of not liking it, was part of the training. That answer defeated Denham and he accepted his defeat gracefully.

Question (v)
Describe the discussion that took place between Miss Joseph and Denham.
(There is no discussion between Miss Joseph and Denham.)

SETTING:

(A3)

Question (i)
Identify the event that took place in the extract. Give reason/s to support your answer:
(a) Annual Sports Day on November 15th
(b) Annual Social and Cultural Gathering on November 15th
(c) Half-yearly report of Students’ Council on November 15th
(d) Farewell Programme on November 15th
Answer:
(c) Half-yearly report of Students’ Council on November 15th
The following lines support this:
The half-yearly report of the Students’ Council was on November 15th, and was one of the important days in the calendar of Greenslade School.

Question (ii)
The event in the extract was held at the Choose the correct alternative. Give reason/s to support your answer.
(a) author’s house
(b) auditorium of the school
(c) market
(d) garden
Answer:
(b) auditorium of the school
The following lines support this:
A bell was rung at 10.00 a.m. and everyone trooped into the auditorium to sit together in classes.

Question (iii)
The incidents in the extract occurred at a particular place. Explain the significance of that place in your own words.
Answer:
The extract confines itself to narrating the incidents that take place on the important day of the half-yearly report of the Students’ s Council. This report takes place in the presence of the Head of the school, the teachers and the students. It is a serious and formal programme, and the setting is the auditorium, with a stage and a formal atmosphere. This is just right.

Question (iv)
Explain how the setting of the extract contributes to the theme of the novel.
Answer:
One of the themes of the novel is the teacher- student relationship, and the change in the behaviour of the students after the narrator’s patient dealing. The narrator initially had a very difficult time with the students who were disrespectful, ill- mannered and mischievous. He finds that the students belong to a background that is not suitable for learning and for their overall development and progress.

They are in no mood to change their attitude and behaviour. The narrator, with his novel and creative ideas, innovative techniques and understanding of the students’ psychology, ultimately wins their hearts. The narrator is now anxious to see how far his teaching has been effective.

He can judge it from the behaviour and attitude of his students on the important day of the half-yearly report of the Students’ Council. This report takes place in the presence of the Head of the school, the teachers and the students. It is a serious and formal programme, and the setting of the auditorium, a stage and a formal atmosphere, is just right. The discussion and the question . and answer session also contributes to the theme.

THEME:

(A4)

Question (i)
‘When the turn of my class came I sat up anxiously’.
Explain the reasons of the narrator’s anxiety hy citing suitable references from the extract.
Answer:
The narrator initially had a very difficult time with the students who were disrespectful, ill-mannered and mischievous. They were in no mood to change their attitude and behaviour. The narrator with his novel and creative ideas, innovative techniques and understanding of the students’ psychology, ultimately wins their hearts. The narrator later grew very fond of his students and wanted them to do well in their lives. He wanted them to shine. He is now anxious to see how far his teaching has been effective.

He can judge it from their behaviour, conduct and attitude on the important day of the half-yearly report of the Students’ Council. He also wanted to see how they would express themselves and how much they had understood during the given period. The programme takes place in the presence of the Head of the school, the teachers and the students. It is a serious and formal one. Hence he sat up anxiously when the turn of his class came.

Question (ii)
Select two statements that describe the theme of the extract:
(a) Half-yearly report of the Students’ Council was not an important event for the students and teachers of school.
(b) The writer was immensely pleased to notice the progress of his students.
(c) The students showed a remarkable change in their behaviour and were progressing in all the subjects.
(d) The head of the institution was against I conducting such activities in the school.
Answer:
(b) The writer was immensely pleased to notice the progress of his students.
(c) The students showed a remarkable change in their behaviour and were j progressing in all the subjects.

Question (iii)
The relationship between the teacher and the students is highlighted in the extract. Illustrate with suitable examples from the extract.
Answer:
In the extract, the narrator describes the day on which the half-yearly report of the Students’ Council takes place. It is entirely the students’ affair; the students are given full freedom. Denham and Miss Joseph conduct the whole programme and preside over it. The students and teachers all listen attentively to the reports made by the student representatives on what they have been studying till then. At the end of the students’ presentation, three teachers are chosen at random to answer the students’ questions. They have to answer whatever questions are put to them by the students. Fernman questions them adroitly; Denham is blunt, critical and argumentative.

Two of the teachers are flustered by the questions, which they find difficult to answer. However, Miss Phillips intervenes skilfully when the other two teachers are at a loss without embarrassing them. She speaks coolly, honestly and with authority. Denham counter-questions her; she is cool and pleasant. The programme is serious, formal and frank. It is a democratic set up. There is freedom of expression, fearlessness on the part of students, honesty and analysis of issues.

Question (iv)
Explain in brief the theme of the extract.
Answer:
The theme of the extract is the student- teacher relationship and the proceedings of the half-yearly report of the Students’ Council. The extract shows the improvement in the conduct of the students, the increase in their level of confidence and courtesy. It also shows the freedom and candour in student-teacher interaction in the school.

Question (v)
Describe the atmosphere of the school described in the extract.
Answer:
In the extract, the narrator describes the day on which the half-yearly report of the Students’ Council takes place. Here, the students of the school report to the faculty and other students on what they have been studying thus far. It is entirely the students’ affair; the students conduct the whole programme and preside over it. At the end of the students’ presentation, three teachers are chosen at random to answer the students’ questions.

The programme is serious, formal and frank. The students honestly give their reports and ask questions fearlessly. The selected teachers do their best to answer the critical and blunt questions put to them. It is a democratic set up. There is freedom of expression, honesty, and analysis of issues on that day.

LANGUAGE:

(A4)

(i) Explain the following statements that enrich the language and create a powerful impact.

Question (a)
Miss Phillips is transformed into a very convincing personality.
Answer:
Miss Phillips is earlier considered as ‘frilly and brainless’; but she was the best- informed of the three teachers on the stage, She intervened skilfully when the other two I teachers were at a loss without embarrassing them. She spoke coolly, honestly and with authority. When Denham is blunt, critical and argumentative while discussing the P.T. exercises, she tells Denham that the whole timetable in the school was meant to help the students in the world after they left school, and doing what one was told in spite of not liking it, is part of the training.

She confidently asserted that she was sure that Denham saw the importance of what she had said, and why he had to do P.T. Thus, she put Denham in his place very coolly and pleasantly, and Denham accepted his defeat courteously. The teacher who was considered brainless is transformed into a s . very convincing personality at the end.

Question (b)
There are many features of language that contribute to the smooth sailing of ) the plot.
Answer:
With reference to the extract, the words used by the narrator contribute to the smooth sailing of the plot. Expressions and sentences like ‘the school showed its approval by laughing uproariously’, ‘Fernman was wonderful; he had them eating out of his hand’, ‘frilly and seemingly brainless’ ‘Miss Phillips took the reins and her stock promptly shot up a hundredfold’, ‘sugary remarks’, ‘her baby-blue eyes twinkling in her delight at this crossing of staves’, ‘this frilly, innocent-looking puss had gobbled her canary without leaving the tiniest feather’ lend beauty and interest to the writing. Apt words and expressions have been used to give the reader a compete idea of the situation. The programme has also been described clearly.

(ii) Following are some dialogues of the major characters in the extract. Find out who the speaker is, his/her tone, the style, significance etc. of the dialogues:

Question 1.
“Then why do we have to do P.T.? Why don’t they take only the kids who need it?”
Answer:
The speaker is Denham. His tone is initially blunt, critical and argumentative. He is a trained boxer and does not want to do P.T exercises which he feels are unnecessary for him. However, when Miss Phillips gently replies to his arguments and outwits him, he has the grace to accept his defeat. The blunt and critical Denham turns into a gracious loser.

Question 2.
“Let’s say it is as much an exercise of the mind as it is of the body, Denham.”
Answer:
The speaker is Miss Phillips. She answers Denham’s questions coolly, honestly and with authority. She tells him that the whole timetable in the school was meant to help the students in the world after they left school, and doing what one was told in spite of not liking it, is part of the training. She confidently asserted that she was sure that Denham saw the importance of what she had said, and why he had to do P.T. This piece of advice was not meant only for Denham but for the whole school and the reader as well.

Yuvakbharati English 12th Textbook Answers Solutions Section 4 (Genre-Drama)

• History of Novel Class 11 English Solutions
• To Sir, with Love Class 11 English Solutions
• Around the World in Eighty Days Class 11 English Solutions
• The Sign of Four Class 11 English Solutions

Class 12 English Chapter 4.1 History of Novel Question Answer Maharashtra Board

Balbharti Yuvakbharati English 12th Digest Chapter 4.1 History of Novel Notes, Textbook Exercise Important Questions and Answers.

12th Std English Chapter 4.1 Brainstorming Question Answer

12th English Digest Chapter 4.1 History of Novel Textbook Questions and Answers

1. Match the columns:

Question 1.
Match the columns:

Answer:

2. Pick out the odd element from each group:

Question (i)
Arun Joshi, Vikram Seth, Graham Greene, Kiran Nagarkar
Answer:
Graham Greene (Graham Greene was an English novelist; the others are Indian writers)

Question (ii)
Place, Period, Theme, Climate, Lifestyle
Answer:
Theme (the others are aspects of the setting)

Question (iii)
Theme, Plot, Character, Novella
Answer:
Novella (‘Novella’ is a ‘novel’; the others are the elements of a novel)

3. Complete the following statements:

Question 1.
Complete the following statements:
Answer:
(i) The two types of conflicts that the plot may have are internal (inside the mind of the character) or external (with other characters or entities).
(ii) The word ‘picaresque’ is originated from the Spanish word ‘picaro,’ which means a rogue.
(iii) The epistolary novel presents the narrative through a series of correspondence or other documents like letters or diary entries.
(iv) In the eighteenth century, the middle class could get the time for reading and discussing the novels because the spread of machines helped them in their work and could provide them with some spare time.

4. Write short notes on:

Question 1.
Write short notes on:
(i) Style of the novel
(ii) Stream of consciousness novel
(iii) Novella
(iv) Indian tradition of novels.
Answer:
(i) Style of the novel: The language and the techniques used by the author for the narration of the course of events is known as the ‘style’. An author can use extensive vocabulary and difficult phrases or he may be brief and could write only to the point or he may mix both according to the requirement of his story. He may use linguistic devices like figures of speech to make the narrative effective. All these factors decide the ‘texture’ of the narration and create an impact on the readers.

(ii) Stream of consciousness novel: The phrase ‘Stream of consciousness’ means the flow of thoughts in the minds of the characters. This phrase was coined by William James in his treatise ‘Principles of Psychology.’ (1890). In such a novel, incidents in the plot are in the sequence of their occurrence. The novelist narrates them just as they occur in the minds of the characters. Sometimes they do not make sense; but they truthfully represent the thoughts without any censoring or editing.

(iii) Novella: The word ‘Novella’ which means new is originated from the Italian word ‘novelle’. A Novella is a type of prose fiction which is shorter than a full length novel and longer than short stories. It is a well-structured yet short narrative, often satiric or realistic in tone. Novella usually focuses on one incident or issue with one or two main characters and takes place at a single location. Given below are some of the famous novellas in English:

1. ‘The Heart of Darkness’ by Joseph Conrad
2. ‘The Turn of the Screw’ by Henry James
3. ‘Billy Budd’ by Hermann Melville
4. ‘Death in Venice’ by Thomas Mann
5. ‘Seize The Day’ by Saul Bellow
6. ‘Pearl’ by John Steinbeck

(iv) Indian tradition of novels: Indians have also played a major role in the writing of English Novels. ‘Rajmohan’s Wife’, by Bankim Chandra Chattopadhyaya was the first novel in English written by an Indian. The period after that is marked by a few more navels written by Indian writers. These novels were based on either nationalistic virtues or social issues. Mulkraj Anand, R.K. Narayan and Raja Rao were the major trio who prevailed in the period after that.

Novelists like Anita Desai, Nayantara Sahgal, Arun Joshi and Manohar Malgaonkar changed the current of Indian English novel through their works. Amitav Ghosh, Vikram Seth and Upamanyu Chatterjee improved upon the Indian novel in English by adding new features to it. In recent years, Indian novelists like Salman Rushdie, Arvind Adiga, Arundhati Roy, Kiran Desai and Kiran Nagarkar have come into the limelight. The tradition of the Indian English novel has undergone a vital change since its birth and has undoubtedly a very bright future.

Yuvakbharati English 12th Digest Chapter 4.1 History of Novel Additional Important Questions and Answers

Question 1.
Pick out the statements that are False. Rewrite them correctly:
1. Setting describes the behaviour of the characters in the story.
2. The main character in the story is referred to as the ‘novella’.
3. The struggle between the opposite forces in the story is called ‘conflict.’
4. Theme is the central idea in the novel which can be expressed in a nutshell.
5. The plot and character are affected due to the setting.
6. ‘Plot’ is the narrative style of the author.
Answer:
False statements:
1. Setting describes the behaviour of the characters in the story.
2. The main character in the story is referred to as the ‘novella’.
6. ‘Plot’ is the narrative style of the author.

Corrected statements:
1. Characterization describes the behaviour of the characters in the story.
2. The main character in the story is referred to as the ‘protagonist’.
6. Plot is the course of events that make up the theme.

Question 2.
Rewrite the following statements in chronological order:
1. Mulkraj Anand, R.K. Narayan and Raja Rao were the major trio who prevailed in the period after that.
2. The novel originated as the literary form in England.
3. Indian novelists like Arvind Adiga, Arundhati Roy and Kiran Desai have dazzled with their writing.
4. Many stalwart novelists such as Charles Dickens, Walter Scott became famous.
Answer:
2. The novel originated as the literary form in England.
4. Many stalwart novelists such as Charles Dickens, Walter Scott became famous.
1. Mulkraj Anand, R.K. Narayan and Raja Rao were the major trio who prevailed in the period after that.
3. Indian novelists like Arvind Adiga, Arundhati Roy and Kiran Desai have dazzled with their writing.

Question 3.
List the types of novels.
Answer:
The types of novels are: Realistic
Novel, Picaresque Novel, Historical
Novel, Epistolary Novel, Gothic Novel, Autobiographical Novel, Allegorical Novel, Utopian/Dystopian Novel, Psychological Novel, Stream of Consciousness Novel, Bildungsroman Novel.

Question 4.
Choose the correct options from the brackets and fill in the blanks :
Answer:
1. The characters in the Realistic novel interact with other characters and undergo plausible and everyday experiences. (Realistic/Utopian)
2. A Picaresque novel narrates the adventures of the protagonist, who is an eccentric or a disreputable person, in an episodic form. (Picaresque/Realistic)
3. The Dystopian novel is about an imaginary community or society possessing the ideal qualities. (Dystopian/Picaresque)
4. In the Stream of Consciousness novel, the novelist narrates the character’s thoughts as they enter the mind of the character. (Stream of Consciousness/ Utopian)
5. The Bildungsroman novel is a fictional biography or autobiography which is concerned with the growth of the protagonist’s mind, spirit and character from childhood to adulthood. (Bildungsroman/Gothic)
6. The Gothic novel includes terror, mystery, horror, thriller, supernatural, doom, death or decay or haunted buildings. (Dystopian/Gothic)

Glossary:

1. genre – a style, especially in the arts, that involves a particular set of characteristics,
2. embellishing – decorating.
3. adopted – followed,
4. precursor – something that happened or existed before another thing,
5. profoundly – deeply,
6. elite – upper class.
7. aspirations – ambitions, desires,
8. encompass – include,
9. plenteous – plentiful,
10. stalwart – (here) a person who has achieved great recognition and appreciation,
11. innovative – new and original,
12. pageant – a colourful or impressive procession of people.
13. ameliorate – to make something better,
14. dazzling – shining.
15. satiric – sharp or sarcastic.
16. interweaving – combining; twisting together,
17. thumbnail sketch – brief description,
18. antagonist – a person who is opposed to the hero,
19. laconic – short and crisp.
20. plausible – believable,
21. eccentric – peculiar; crazy; out-of-the-way.
22. disreputable – not respectable.
23. speculative – unproven, unreal,
24. extraterrestrial – of or from outside the earth or its atmosphere.
25. amateur – inexperienced; unprofessional.

Yuvakbharati English 12th Textbook Answers Solutions Section 4 (Genre-Drama)

• History of Novel Class 11 English Solutions
• To Sir, with Love Class 11 English Solutions
• Around the World in Eighty Days Class 11 English Solutions
• The Sign of Four Class 11 English Solutions

Class 12 English Chapter 3.6 Group Discussion Question Answer Maharashtra Board

Balbharti Yuvakbharati English 12th Digest Chapter 3.6 Group Discussion Notes, Textbook Exercise Important Questions and Answers.

12th Std English Chapter 3.6 Brainstorming Question Answer

12th English Digest Chapter 3.6 Group Discussion Textbook Questions and Answers

You must have discussed many things with your friends, classmates in a group. It might be about going on a picnic or selecting a gift for your teacher:

Question (i)
What do you think are the benefits of a group discussion?
Answer:
(a) A Group Discussion allows the participants to share their views and opinions.
(b) It allows each participant to analyse the topic or case.
(c) A Group Discussion allows the participants to reach a general consensus.

Question (ii)
Do you think some people are right and some are wrong in a group discussion? Why?
Answer:
Yes, I do think so. Generally, we hold a view on a topic or a situation. This view is either strengthened or weakened by the ongoing arguments in a Group Discussion. Due to j confirmation bias, we tend to think that the participants who strengthen our views j are right. Similarly, we think of those who go against our views are wrong. (The ideal situation is that we keep an open mind and assess each argument on its own merit but this is easier said than done.)

Question (iii)
People have different views and opinions because:

Answer:

Question (iv)
Complete the web highlighting the uses of ‘Group Discussion’. One is done for you.

Answer:

(A1)

Question 1.
Rama, Asif, Rachana and Aarav are participating in a group discussion. The evaluator has given them a topic. ‘Teenagers are more inclined towards junk food nowadays.’ Write suitable dialogues for each participant giving his/her opinion on the topic.
Evaluator: You’ve all been given a few minutes to think on your topic for today’s group discussion, which is ‘Teenagers are more inclined towards junk food.’ You may now begin the discussion. Who would like to start?
Rama: ………………………………………………. .
Asif: ………………………………………………….. .
Aarav: ……………………………………………….. .
Rachana: ……………………………………………. .
Evaluator: Please conclude.
Aarav: ………………………………………………… .
Answer:
Rama: I think I will. In my opinion it is very true. Junk food leads to obesity and we find more obese teenagers around nowadays.
Asif: I am afraid I can’t agree with that statement. Most of the teenagers in our college look quite fit and active.
Aarav: I think we must see the issue in a wider perspective. The inclination towards junk food among teenagers is a worldwide phenomenon. One can’t jump to a conclusion by just looking around and citing a few examples in our college.
Rachana: It seems to me that Rama made a valid point. Teenagers world over are inclined towards junk food and it poses a great threat. I suggest the teenagers change their food habit and resort more to healthy snacks. Our tradition offers a wide variety of such snacks.
Evaluator: Please conclude.
Aarav: We can conclude by saying that our teenagers are inclined to junk food. They must change their food habit. It is high time they switched to healthy snacks. We need healthy citizens to take our country forward.

(A2)

Question 1.
Read the following statements, if you agree say ‘Yes’ and if you don’t agree, say ‘No’. State the reason for your opinion.
Answer:

Reason: Group discussion helps us realize that there are other possible views and opinions. A receptive and accommodative mind is a prerequisite for anyone who participate in a group discussion. Moreover, the candidate must be able to feel the pulse of the discussion. This, in turn, will help to reach a consensus.

(A3)

Question (i)
Group discussion helps to unravel the following personality traits in a person.

Answer:

Question (ii)
Match the following:

Answer:

(A4)

Question (i)
Write the following sentences in reported/indirect speech:
(a) He said, “If you find my answers satisfactory, will you give me five rupees?”
(b) The astrologer said, “You were left for dead. Am I right?”
(c) “I should have been dead if some passerby had not chanced to peep into the well,” exclaimed Guru Nayak.
(d) He told her, “Do you know a great load is gone from me today.”
Answer:
(a) He asked me whether I would give him five rupees if I found his answers satisfactory.
(b) The astrologer asked whether he was right in saying that I had been left for dead.
(c) Guru Nayak exclaimed that he would have been dead unless some passerby had chanced to peep into the well.
(d) He asked her whether she knew that a great load was gone from him that day.

Question (ii)
Read a part of a conversation between Neha and Nidhi.
Answer:
Neha: Where are you going, Nidhi?
Nidhi: I am going for my music lessons.
The above conversation is written in exact words spoken. If this conversation was to be reported by a third person then it would be written as:

Neha asked Nidhi where she was going. Nidhi replied that she was going for her music lessons. Notice the changes in the reported sentence.
Note the changes in pronouns, tenses, reporting and reported verbs and other changes.
Answer:
1. Table showing tense change:
Simple Present → Simple Past
Present Continuous → Past Continuous
Simple Past → Past Perfect
Past Continuous → Past Perfect Continuous
Simple Future → Conditional

2. Table showing change in Place and Time

1. here – there
2. now – then
3. today – that day
4. tomorrow – the next day
5. yesterday – the day before
6. next week – the following week
7. last night- the previous night

3. Table showing the changes in Pronoun.

Question (iii)
Now find sentences from the text in the direct speech and convert them into the reported speech.
(Students may attempt this on their own.)
Read the following sentences given in the indirect speech and convert them into the direct speech.
(a) Shirish said that he would not be able to solve the problem.
(b) Lata told me to give her a glass of water.
(c) Ananya exclaimed with joy that she had received the Ph.D. degree.
(d) Shilpa asked us if there was any other Rian document to be typed.
(e) Swati said that she would not get the money.
Answer:
(a) Shirish said, “I will not be able to solve the problem.”
(b) Lata said, “Give me a glass of water.”
(c) Ananya said, “Hurrah! I have received the Ph.D. degree.”
(d) Shilpa said, “Is there any other document to be typed?”
(e) Swati said, “I will not get the money.”

(A5)

Question (i)
An economically deprived girl student in your class who has received admission in a reputed college abroad needs monetary help to pursue further studies there. Have a group discussion amongst your friends to seek solutions to help her. Write four/five views in the form of dialogues.
Answer:

• Rian: Well, folks! we need to do something urgently in Tejaswini’s case. Money shouldn’t come in her way to pursue a course abroad. My parents offered 50,000/- right away!
• Eugine: I managed to get a loan of rupees one lakh from my parents. I should take up some part-time job and repay it within three years. I hope I will be able to do it. Anyway, I am quite happy to be of some help to our dear friend.
• Kanika: Only way before me was to ask for an advance from my music troupe. We don’t get much programmes of late. Still they agreed to pay me 75,000. Will that be okay?
• Tabu: We thought you would raise a hefty sum, being ‘a great singer’ and all. Okay, jokes apart, I will present my case. My brother offered a donation of rupees two lakh right away. No conditions! No strings attached!!
• Rian: Okay, folks! Now we have pooled 4.25 lakhs.

That will bankroll Tejaswini’s fee, travel, initial expenses, etc, etc. She can very well take up a summer job and the like to meet her further expenses. Let’s now congratulate ourselves for being such thick friends!

Question (ii)
There is an inter-school cricket match and your school is losing. As you are the captain, have a group discussion with your teammates in the tea-break about the strategy to be followed to save your school from losing the match. Give at least four /five suggestions.
Answer:

• Captain: See, we must break this partnership anyhow. Both the batsmen appear very much settled and they are hitting all over the place.
• Spinner: The pitch doesn’t support many turns. I suggest we bring back the fast bowlers.
• Captain: You have a point there. What we need most now is a wicket. Right now. Otherwise, the game is as good as lost.
• Fast bowler (1): I agree that we resume pace bowling. But remember: it’s a gamble. I think I will need a slip-in position. I will attack, outside the off-stump. Hope I get the right line.
• Captain: What do you think, Sonu?
• Sonu (Fast bowler) (2): Okay then. I will take up from the pavilion end. Think the wind is in favour.
• Captain: Attempt yorkers.
• Sonu: Sure. I suggest you keep a deep third man.
• Captain: Done. Now, guys-no sloppy fielding-no dropped catches. And nothing short of a win. (All go into a huddle.)

Question (iii)
Form four groups in your class and have a group discussion on the following topics.
(a) Role of ICT in education
(b) Clean India

Yuvakbharati English 12th Digest Chapter 3.6 Group Discussion Additional Important Questions and Answers

Other writing skills:

Dos and Don’ts associated with ‘Expansion of Ideas’:

Expand the idea inherent in the following:

Question 1.
Charity begins at home Ans. Charity is the noble deed of giving money, food or other help to people who are in need of these things. The given proverb is a warning to those who seek fame in the name of charity. The proverb reminds us that we must first help the needy people around us – our family and friends. Any deed of charity that forgets this principle goes against the spirit of this high ideal.

Our deeds of charity must begin from the centre and then radiate to the periphery. Or else, it would prove to be a selfish pursuit of chasing fame or other favour. We must first open our eyes to the miseries around us. We must first cater to the needs of these people. Then we can spread our work of charity farther afield.

We see that many people treat their family members and servants very shabbily. But when it comes to a photo opportunity to pose as a philanthropist, they jump at it. This is sheer hypocrisy and the saying serves as an eye opener to these hypocrites.

Question 2.
Make hay while the sun shines
Answer:
Hay making, that is the process of cutting and drying grass, must be done while the sun shines. Rain would spoil everything and the farmer knows it well. In other words, we should make the best use of opportunities and favourable conditions while they last.

When life presents opportunities, we must seize them and not let them go. Everyone in their lifetime gets a chance to move ahead in life. If we miss that opportunity, it may never come our way again. We will live all our life to regret the missed chance. In short, we should seize the chance while it exists. We must always be alert to notice the opportune moment. Grab it and move further in life. To put it in another way : “We must strike while the iron is hot”.

Question 3.
Prevention is better than cure.
Answer:
The proverb stresses the need for foresight and precaution in dealing with any possible eventuality in life. We often ignore the signs of trouble and when the trouble finally, occurs, we regret our neglect.

We must make it a practice to guard ourselves against diseases by taking adequate preventive measures. This will save us the trouble of undergoing costly treatments. Strangely, certain epidemics offer no cure or vaccine for a long time, then prevention becomes the only option before us. Wearing of masks, keeping social distance and maintaining hand-hygiene are the only ways to save us from such a threatening situation.

Metaphorically, the idea can be extended to fields other than disease and medicine. Proper maintenance of machines, roads and bridges can prevent their deterioration and thus forestall disaster. At the political and economical level too, many problems that we face today would not have existed had the authorities acted promptly, firmly and boldly at the very start.

Examples for Practice:

1. Unity is Strength,
2. Books – Our best friends,
3. Honesty is the Best Policy
4. Perseverance is the Key to Success
5. Pollution: Earth’s enemy number one.

Formal Letters:

General Format for a Formal Letter:

1. Sender’s Address
2. Pin Code
3. Date
4. Name and address of the addressee
5. Subject (a phrase about the general content of the letter)
6. Reference (referring to a letter previously received/advertisement etc.)
7. Salutation (Dear Sir/Madam or simply Sir/ Madam)
8. Body of the letter (in 3 or 4 paragraphs)
9. Subscription (Complimentary Close like Yours faithfully, Yours truly, etc.)
10. The name given in the Activity Sheet/XYZ

Write the letters as instructed:

Question 1.
Write a letter to the editor of a newspaper drawing attention to the increasing noise pollution in your area.
Answer:
3 A, Ravikiran,
Chikuwadi,
Borivali (West),
Mumbai – 400 092.
1st September, 2020

The Editor,
The Indian Express,
Nariman Point,
Mumbai – 400 021.

Sir,

I wish to draw the attention of the authorities to the terrible noise pollution in our neighbourhood. There is deafening noise created by heavy traffic on the narrow roads of our locality throughout the day and night. The drivers honk continuously, and the vehicles emit poisonous fumes. The hawkers who sell their goods on the roads and footpaths shout at the top of their voices.

All this is literally making the people sick. With the approaching festival season, the beat of drums and the loud music accompanying it are bound to make life all the more unbearable for all of us who reside here.

I hope the authorities concerned wake up in time to the hazards of noise pollution and take prompt action to stop this menace.

Yours truly,
ABC

Question 2.
You want to visit a sugar factory to know more about the sugar production process. Write a letter to the Manager of the sugar factory near your college seeking permission. Give details about the intended visit.
Answer:
Ideal College,
Vidyapeeth Marg,
Beed – 431 122.
5th February 2020

The Manager,
Sakhar Factory Ltd.,
Beed – 431 122.
Sub: Request to visit your factory.

Dear Sir,

As part of our science project, 10 students of Std. XII (Ideal College) would like to visit your factory during the latter half of this month. We will be accompanied by our Chemistry Professor, Dr Ahirwal. It is our desire to have first hand information about the production of sugar. We believe that a visit to the factory will give us more valuable information than we can ever get out of textbooks.

Do let us know what would be the most suitable day and time for our visit. Since we now have study leave, any day and any time will be suitable for us. Also let us know if there are any special rules or conditions we need to follow during the visit. We do hope that you will not say no to our request.

Yours faithfully,
XYZ

Question 3.
Write a letter to a celebrity who supports a meaningful and innovative campaign and thus has become your idol.
Answer:
7, Vicky Apartments,
J.T. Road,
Nashik – 422 001.
17th September, 2020

Ms. Nandita Das,
Actor and Activist.
Dear Ms. Das,

Your support to the campaign ‘Black is Beautiful’ made a real impact on me. Honestly, I now look upon you as my guide, mentor, pathfinder and idol.

I have always found the discrimination based on colour really disgusting. It is nothing short of racial bias. I wish to join this campaign. I want to fight against the revolting obsession with the skin colour.

As you are a person who lived and proved this bias wrong, I take courage from you. You are a pathfinder and idol for today’s youth. I wish all those who are involved in the campaign the very best.

Yours sincerely,
RST

Question 4.
The New Arts, Science and Commerce College, Karad- 415 101, needs a librarian, They have advertised in the Indian Express, dated 17th October 2020. Write a letter of application to the Principal, with the help of the CV given below:

Curriculum Vitae (cv)
Name: Ms Deepali Rane
Address: A-303, Munir Apartments, Valkumbh, Karad – 415 110.
Email: [email protected]
Nationality: Indian
Date of Birth: 16-5-1990
Qualifications: B.Com., B. Lib. Sc.
Experience: Working as an Associate Librarian at the Karad Public Library.
Languages known: Marathi, English, Hindi
Interests: Reading, painting, music
Answer:
A-303, Munir Apartments,
Valkumbh,
Karad- 415 110.
17th October 2020

The Principal,
The New Arts, Science and Commerce College,
Karad – 415 101.
Sub: Application for the post of Librarian.
Ref: Your advertisement in the ‘Indian Express’, dated 17 October 2020.

Sir/Madam,

This is with reference to your advertisement in the ‘Indian Express’, dated 17 October 2020 for the post of librarian in your college.

I am a qualified librarian. I passed my B.Com. in 2011. I also passed the degree in library science in 2013, from Pune University, with First Class. Since then, I have been working at the Karad Public Library as an Associate Librarian. I can speak English, Hindi and Marathi fluently.

I am applying for the job in your renowned college as I feel that I now have sufficient experience to take up independently the job of a librarian. I get along well with the younger generation, and I can assure you that I will do my best to give you satisfaction, should you appoint me for the post. I enclose photocopies of the necessary certificates.

Thanking you,
Yours faithfully,
Deepali Rane
Enel. : Photocopies of B.Com, B. Lib. Sc. Certificates

Report Writing:

Write the reports as instructed:

Question 1.
During a global pandemic, a nationwide lockdown was announced. Write a newspaper report on this with the help of the following points :

• Declaration of the lockdown
• All movements stopped
• Essential services allowed
• Guidelines for safety laid down

Answer:
Biggest Lockdown Ever

Staff Reporter

New Delhi, March 25: Nation went into a lockdown at the stroke of midnight amidst the ongoing threat of COVID-19 pandemic. Though the scare of the pandemic has been in the air for some time, the lockdown came as a bolt from the blue to citizens all over.

The Prime Minister declared the step of lockdown in a live telecast on TV at 8:00 o’clock last night. The PM in his speech appealed to the citizens to maintain the lockdown rules fully and effectively. “There is no better option before us than going into this strict but painful measure,” he told the country during the telecast.

Flights, domestic as well as international, are now grounded. Railways suspended all services. Public transport came to a halt. Only essential services are allowed and the police are on the streets to ensure that everyone complies with the lockdown measures. Detailed guidelines for the lockdown have been laid down and citizens are advised to venture out only for emergencies. The message of social distancing and hand-hygiene are put across through various media.

“Stay Home and Stay Safe” is the new mantra. As normal life has been hit unlike anything that happened in the past, the citizens are grappling with the new norms. “We must sacrifice our liberty for a greater common good,” a senior citizen told this reporter.

Question 2.
Write a report of Republic Day Celebrations in your college.
Answer:
Republic Day at Model College Malegaon, January 28: This year, Republic Day was celebrated with great fanfare on the campus. It was a special occasion because Narendra Jain of the NCC was to be felicitated for winning the target-shooting gold medal by the Police Academy. The National Flag was unfurled at 7-30 a.m. by the Chairman of the College Management Trust.

The National Anthem was played by the college band while everyone stood respectfully to attention. Meera Pandit of Std. XII recited a poem composed by her, ‘Majha Desh Mahaan’. This was well appreciated by one and all. The Chief Guest spoke to us about our duties as citizens of the Republic of India. Then Narendra Jain was given the award by Senior Inspector Kale of the Police Academy. This was a solemn ceremony. Sweets were distributed and the gathering then dispersed.

Question 3.
Read the following headline of a news item “Cold Wave Sweeps North India”. Write a suitable dateline, lead paragraph and conclusion. Use a byline as well.
Answer:
Cold Wave Sweeps North India By A Special Correspondent Delhi, December 12 : Winter continued to send shivers across northern India, claiming another life in Uttar Pradesh. Delhi recorded the coldest day in the past fifty years on Monday.

A four-month-old boy died in Kanpur. The winter chill also swept through Punjab, x Haryana, Rajasthan, and Himachal Pradesh and minimum temperatures hovered between minus and plus five. The mercury dipped to a record low in many northern cities. In New Delhi, the air traffic has been severely hit by the fog.

Question 4.
Read the following headline of a news item “Milk for Millions” scheme inaugurated. Write a suitable dateline, lead paragraph and conclusion. Add a byline.
Answer:
‘Milk for Millions’ Scheme Inaugurated
By Sonali Mazumdar

New Delhi, August 29: Inaugurating the ‘Milk for Millions’ scheme of the National Dairy Development Board (NDDB) here, the Prime Minister called for a second white revolution to provide milk to the millions of undernourished infants of the country. “We must ensure at all costs that our infants get the basic nourishment, which is their right by birth,” he declared amidst loud applause.

The NDDB chairman said the projected 300 million output for 2020-21 would suffice to support the scheme. “A detailed plan with Panchayat-level participation has been already chalked out for the execution of the scheme,” he added.

Question 5.
Mumbai School Sports Association’s (MSSA) under-14 interschool football championship final was held on 17th November. Write a newspaper report on this with the help of following points :

• Don Bosco School vs Gokuldham School
• Don Bosco won by 3-1
• Goals scored after the half time
• Venue: Brabourne stadium
• Shield awarded

Answer:

Don Bosco Bags Mssa Shield
By Sports Reporter

MUMBAI, November 18: In the Mumbai School Sports Association’s (MSSA) Under-14 interschool football championship final, Don Bosco beat Gokuldham 3-1 at Brabourne here today.

The clash of the old rivals was a sheer delight to the crowd. Till half time, it was anybody’s game. Expectedly, in the second half, Don Bosco went on the offensive hook, line and sinker. Their ace striker Vipul Shetty shot two marvellous goals within the span of six minutes. Later, Mukul Vanik’s header off a corner kick came as the saving grace for Gokuldham. Don Bosco’s captain Melvin D’sa received the shield amidst loud cheering.

Question 6.
An auto driver returns a bag of cash to a passenger who had forgotten the bag in the auto. Write a newspaper report on this with the help of following points :

• Notices the bag after dropping the passenger
• Began the search for the owner
• Ultimately traced the passenger
• Refuses reward
• Honesty is the best policy.

Answer:
Auto Driver Shows The Way – By Aarohi Bokil
PUNE, March 12: Setting yet another example to prove ‘honesty is the best policy’, an auto driver here returned a bag containing two lakhs to its owner.

“I was queuing at the petrol pump after dropping my last passenger when I noticed a leather bag on the back seat. Opening it I found wads of notes; and then my hunt for the owner began,” Abdul Latif – the auto driver – said.

It took Latif two hours and two hundred rupees worth of fuel to trace the owner. “It is nothing short of a miracle that he traced me following such vague leads,” Hiten Vora – the bag’s owner- said with a voice breaking with emotion. Abdul Latif, however, refused to take any reward. When asked about the loss he incurred in the process, the youngster dismissed the issue with a hearty laugh.

Speech Writing

Draft the following speeches as instructed:

Question 1.
Prepare a short speech to be delivered by you in class on the occasion of the send off for students of Std. XII.
Answer:
A Hearty Farewell

Honourable Principal, Respected Professors and dear friends,

Today is an important day for us because it is the day we take leave of you in order to study for the coming HSC examinations. We hope that all of us will pass the examination with resounding success. Some of us may continue with higher education, some of us may seek employment hereafter. But we shall never forget these two years that we spent on this campus. These were years not only of great fun and freedom, but also of successful learning.

We got our first lessons in democracy here. We learnt to live in harmony with all kinds of people. Our professors were patient with us and were always there to clear our doubts. We are grateful to them. We are also grateful to all of you who made these years such a rich experience for us. A heartfelt thanks to you once again, and may God bless our efforts in the coming examinations.

Thank you.

Question 2.
Prepare a short speech to be delivered by you in class on the occasion of the Independence Day.
Answer:
India of My Dreams

Respected Sir/Madam and dear friends,

This is a very special and important day for us. On this day we remember those who fought for our freedom. On this day our National Flag flies atop all important buildings and institutions. I believe that Independence Day is a day when we need to pledge ourselves to the nation anew. It is a day when we need to make fresh commitments to all the ideals of our Constitution; ideals such as freedom, justice, equality and brotherhood. It is a day when we need to put to test whether we truly follow these ideals.

Let us carry forward the torch of freedom. Let us in fact be soldiers who will fight against the evils that this nation now faces; evils such as terrorism, corruption, inequality and superstition. Only when these evils are overcome, will our nation be truly free.

Jai Hind!

Question 3.
Write a speech on ‘Democracy’.
Answer:
Ideal Democracy

Honourable Judges, Respected Teachers and dear friends,

Unfortunately, democracy in India today does not work the way it should. It is limited to the day when the masses go to the polling booths and cast their votes. Then they return to their routine lives.

Most people do not actively participate in serious social issues. They do not react to the injustice happening around. Many among us do not bother to raise our voice against the corrupt practices going on around us. Casting our votes once in five years or so is not the sole idea of being a responsible citizen. A citizen should be always vigilant. Likewise, we also need a responsible media to expose those who are corrupt. Further, the people’s representatives should realize that they are accountable to the voters. If all these things work together then only can we reap the real fruits of democracy.

Thank you!

Dialogue Writing:

Write the dialogues as instructed:

Question 1.
You wish to open a postal savings account in the post office in your locality. Write the conversation between you and the Postmaster in the form of a dialogue.
Answer:

• Myself: Good morning sir. I wish to open a I postal savings account. How do I go about it?
• Postmaster: Just fill this form giving proper details about your name and address and sign on the dotted line there at the bottom.
• Myself: What is the minimum amount that I can put in?
• Postmaster: Oh, you can put in any amount you want. How much do you want to deposit right now?
• Myself: I would like to open the account with 500.
• Postmaster: Then hand over the money to me and I will give you a receipt for it.
• Myself: Here is the form and the money. Postmaster : Here is your receipt. Now you have a postal savings account. You can collect your passbook after half an hour.
• Myself: Thank you sir.
• Postmaster: You’re welcome.

Question 2.
Write a conversation between you and your mother about ‘domestic duties’:
Answer:

• Myself: Mother, do I have to do the dishes every day?
• Mother: Well, dear, you’ve got to learn sometime. You can never tell when the need may arise.
• Myself: But I have so much to study. And I have projects to complete.
• Mother: I understand. But this work has also to be done.
• Myself: Can’t the servant do it?
• Mother: Oh, she will be coming late today and the dishes are all cluttered up. In the future it will be very difficult to get a domestic help. Then you will thank me for training you.
• Myself: Mother, I plan to get a good job and earn a lot of money. I will employ a housemaid permanently in my house to look after everything, including looking after the children.
• Mother: You can never be so sure about the future. So just get down to the dishes, and don’t argue.
• Myself: Ok mother, if you say so.

Question 3.
You are in Std. XII in your college. On the first day of the new academic year you meet a student of Std. XI. Write a conversation you have with the ‘fresher’ :
Answer:

• Myself: Hello. You’re new, aren’t you? What’s your name?
• Fresher: Hello, I’m Nitin.
• Myself: Which school are you from?
• Fresher: I’m from Ideal School.
• Myself: I guess you’ve taken Commerce. Right?
• Fresher: Yes.
• Myself: I’m in Commerce too. Have you found your class? You seem nervous.
• Fresher: Yah. It’s the first day. And they say that the seniors rag the freshers.
• Myself: Oh, nothing. Just a little teasing, that’s all. You don’t have to be scared. It’s only to make you feel at home.
• Fresher: Will you be there?
• Myself: Yes, I’ll be there. Don’t worry. My name is Ketan. I’ll say you’re my friend. No one will do anything to you.
• Fresher: Hey, thanks a lot. You’re a real pal! I have to go and find my class. See you later. Bye.
• Myself: Bye.

View-Counterview

Write the counterviews as instructed:

Question 1.
Write a Counterview for the topic: ‘The Cellphone has given us social networking- not society’. You may consider the following points for the View section of the topic and then write the Counterview. The cellphone has given us social networking – not society View:
– cellphone did not bring in any social change, except instant communication
– instead of being a means of social bonding (e.g. the railways or the loudspeaker earlier), the cellphones make the people live in their own individual islands
– cellphones have just succeeded in making too many people talk for too long a time on matters too silly.
Answer:
Cellphones did usher in a new society (Counterview)

Bringing instant communication to the poor itself is a social revolution. The poor was earlier deprived of both – speedy transport and quick communication. Speedy communication saves time, and time is money for the poor as it is to the rich. More so for the poor who sell their labour by hours and days. In addition, the availability of affordable handsets brought in a sort of socialism. Now even the unlettered can talk directly to his near and dear ones he needn’t pester a ‘babu’ to get his letters written.

When it comes to social bonding, the cellphones have played a major role of late in organizing protest rallies and morchas. It has become so much easier to connect people using cellphones. And about talking too long on things too silly – this is not a new phenomenon. Such people were there in the past, and will be there till the end of the world. For them, if not the cellphone, a pair of apparently listening ears will do. They will chat and chat. We cannot blame it on the cellphones.

Question 2.
Write a Counterview for the topic ‘Junk food should be replaced with organic food’. You may consider the following points for the View section of the topic and then write the Counterview. Junk food should be replaced with organic food (View Section)
– Junk food lacks nutrients
– it leads to obesity
– leads to many diseases
– organic food is a better option always
Answer:
Attacking fast food is the new fad (Counterview)
First of all, I object to the umbrella term ‘junk food’ which we indiscriminately use to brand a variety of food items. The dictionary defines ‘junk food’ as something ‘that is quick and easy to prepare and eat but that is thought to be bad for your health’. Yes, it is thought to be bad. There is no conclusive evidence to prove that the so called junk food is bad beyond doubt. Then again, such one-size-fits- all definition overlooks the fact that many fast food joints sell a variety of salads and greens, One can understand if someone brings out a list of items with their respective nutritional values and says that these are perfectly ‘junk’, But that is not happening. One has also to take into account’ the age and lifestyle of the eater, If you eat organic food and lead a sedentary life, obesity and diseases are assured results.

Moreover, I think, the passion for organic food is just another fad. People attach a sort of sophistication to organic food. To me, organic food is just the ordinary food with a university education socially more acceptable and stylish – nothing much different in essence.

Question 3.
Write a Counterview for the topic: ‘Sports should be optional in colleges’. You may consider the following points for the View section of the topic and then write the Counterview:
Sports should be optional in colleges (view section)
– Difficult syllabus; students need to prepare for entrance tests to competitive examinations
– Very little time for activities other than study -Not enough infrastructure to accommodate
all students
– Students have little sports background in schools
Answer:
Every student in college should take up some kind of sport (Counterview)
The College is the last chance that the student has to learn some game or sport that will stand him or her in good stead for the rest of his or her life. If a student hasn’t already played some sport during his or her school days, he or she should be encouraged to take up some activity during his or her college days. This will have the effect of bringing discipline into the campus, and providing students at that age with the much needed vent for their energies.

College campuses are usually large and can accommodate many games such as badminton, table tennis, squash, boxing and lawn tennis. Football, cricket and hockey are usually encouraged as a rule. Colleges can allot more funds to sports. This will help in the long run and will give to the nation citizens who have developed an all-round personality. It will reduce the time spent by students on undesirable activities such as eve-teasing, smoking and indulging in campus violence. Sports is never a waste, and the more students are encouraged to take part, the better.

Leaflet

Write the following leaflets as instructed:

Question 1.
Prepare a leaflet about a Tree Plantation Ceremony that your class is organizing. Give details about the venue and time. You may ask for help by way of manure, saplings, ideas, etc. Give details about whom the students should contact.
Answer:

Question 2.
Prepare a leaflet on ‘Save the Earth’. Make use of the foUowing points:
– make the slogan attractive
– make a persuasive appeal
– give information about the programmes to be undertaken
– ask for contributions
– explain the need to save the environment
– add other ideas of your own
Answer:

Question 2.
Prepare a short tourist leaflet on any seaside resort you have visited with the help of points given below :
1. How to reach there?
2. Accommodation.
3. Places worth-seeing.
4. Specialities.
5. Add your own points.
Answer:
Devbagh

Devbagh, a seaside resort, is a tiny island off the west coast of Karwar, in Karnataka. It is near the confluence of the Kali river and the sea.

1. Ways to reach: Devbagh is well- connected to Mumbai and Bengaluru by road. It is 2 hours by road from Goa and a 20-minute boat ride from Karwar.
2. Accommodation available : Devbagh forest beach resort offers cozily furnished tents and log cabins.
3. Sight-seeing : Shivganga Falls, Magod Falls, Lalguli Falls, Dandeli Wildlife Sanctuary, Temples, Historical spots, Beautiful beaches, etc.
4. Specialities : Spicy crab curry is the region’s speciality. Most food preparations are liberally garnished with coconut.
5. Most suitable time for visits : Throughout the year, though the best season is from October to May.
6. Additional information: Plenty of interesting activities for the adventurous – water sports, cruises to neighbouring uninhabited islands, snorkelling trips, sea kayaking, rafting trips, etc.

Appeal

Write the following appeals as instructed:

Question 1.
A student in your college seeks immediate medical help. His parents are unable to afford the huge amount needed for the operation. Prepare an appeal to be put on the college noticeboard requesting the students to donate generously. Take the help of the following points:
– the name of the illness
– the cost of the operation
– how the contributions can be made
Answer:

Question 2.
Prepare an appeal based on the information given below:
The Khadi and Village Industries Commission proposes to promote Khadi wear. They would like people to buy and wear Khadi for natural feel and elegant texture. The cloth also promotes good health and ensures quality. They propose to give a special discount on cotton, silk (spun), silk (reeled), woollen and polyvastra varieties of Khadi. Every metre of Khadi purchased by each of you will help provide employment to many.
Answer:

Interview

Write interview questions based on the given situation:

Question 1.
Imagine that you have to interview a social campaigner of your choice. Frame a set of 8-10 questions to interview him/ her as per the following points :

• Introducing the guest
• Background of the campaign
• Setbacks/Criticism
• Support/Achievements
• Dreams/Message

Answer:
Good morning, Ms. Nandita Das! Glad to have you on our show. Your ‘Black is Beautiful’ campaign has been a great success and I think our viewers would like to know something more about it.

1. Let me begin by asking you the most relevant question first: What had prompted you to take up such a radical campaign?
2. What were the initial setbacks that you had faced?
3. Were you apprehensive of the reaction from traditional society?
4. How do you explain our deep-rooted obsession with skin colour?
5. Has the Western World changed their attitude of “White supremacy” over the years?
6. Does this “colour bias” affect the boys as much as the girls?
7. Who supported you most during the campaign?
8. Certain print media groups and television channels stopped accepting advertisements for the so called ‘fairness creams’ after your campaign. Do you expect many more such positive initiatives?
9. Many people, especially young girls, look up to you as their idol. How do you hope to live up to their expectations?
10. Is there any special message for our youth?

Question 2.
Imagine that yon have to interview the District Medical Officer during the outbreak of a serious epidemic. Frame a set of 8-10 questions to interview him/her as per the following points:

• introduction
• the gravity of the situation
• briefing on technical terms
• importance of precautions
• preparedness to combat the disease

Answer:
Today we have with us our DMO to reassure us about the safety measures taken by the district authorities. Good morning Madam! Could you spare a few moments to enlighten our viewers about the unprecedented situation we face now.

1. Thank you. Let me first ask you how grave is the situation as of now?
2. There are many new term in currency now as quarantine, self-isolation, tracing contacts, etc. Could you briefly explain these terms for the benefit of our general viewers?
3. How important is social-distancing in the present scenario?
4. Should masks to be preserved for the frontline workers or is it a must for each and everyone?
5. Do we have enough testing kits now?
6. What is the difference between rapid test and RT-PCR test?
7. What are the elementary precaution to be taken other than social-distancing and hand- hygiene?
8. Do you have enough medical staff to tide over such an emergency?
9. Do we have enough ventilators and ICU beds?
10. How is the coordination between the various departments of the district administration?

Question 3.
Imagine that you have to interview a “Save the Trees” campaigner. Frame a set of 8-10 questions to interview him/her as per the following points:

• introduction
• success so far
• forest conservation laws
• attitude of people to climate change
• factors working for and against the campaign

Answer:
Good evening Sir! I think it is the need of the time that our young generation realize the importance of your campaign. I am very glad to have you on our special “Environment Day” programme.

1. How do you evaluate the success of your campaign so far?
2. Do you think that people still show a callous disregard towards the threat of climate change?
3. Why is there a lack of awareness among our countrymen about the importance of trees?
4. Why doesn’t the government enforce the forest conservation laws effectively?
5. What are the substitutes for timber in the construction industry?
6. Have you ever felt that you are defending a lost cause?
7. How far does the Indian tradition of worshipping trees help you in your campaign?
8. Do you get enough funds to carry on your campaign?
9. Is the younger generation more receptive to environmental issues?
10. What piece of advice would you like to give to the school children?

Question 4.
Imagine that you have to interview a teacher who has received the President’s award. Prepare a set of 8-10 questions to interview him/her as per the following points:

• Introducing the guest
• Feeling during the moment
• Reason for taking up teaching
• Contentment/Satisfaction
• Opinion about young teachers
• Setback and reward of the profession

Answer:
Good morning Madam! I take it as a great privilege to be with you and have a chat. Thank you very much for sparing your valuable time.

1. How did you feel during those brief moments with the President?
2. Do you think that you have lived a complete life and it is time to retire?
3. At what point of time in your life did you find that teaching is your calling?
4. Many teachers find teaching a thankless job : What is your opinion about that?
5. Was there any conflict between your personal life and professional life?
6. Do you think teaching attracts real talent in this materialistic world?
7. What, in your view, are the most essential qualities of a teacher?
8. Do you find the young cro0p of teachers as great promise?
9. What were the setbacks that you faced in your long career?
10. How did your students, who are spread far and wide, react to this honour?

E-Mails:

Question 1.
Read the following advertisement and prepare a letter of application to be sent by email. (Do not give your bio-data.)
Situation Vacant
Wanted: A Computer Engineer
Candidate must have passed B.E. in
Computer Engineering.
Experience holder will be preferred.
Write giving details to:
Email: [email protected]

Sir/Madam,I have recently passed my B.E. in Computer Engineering from J L M Engineering College, Ratnagiri with a pass percentage of 61.1 also have three months of experience developing software for Pragati Electronics in Ratnagiri. The project was for the maintenance of accounts of MHEL Pvt. Ltd.

I do hope that you will consider me for appointment in your esteemed company. I shall be able to arrange my own accommodation in Pune. I anticipate an early call for an interview. My details are in the CV that I have attached.

I assure you of dedicated service, should I be considered for the post.

Yours truly,
XYZ

Blog Writing

A List of Blogging Sites/Apps.
Given below is a list of blogging sites/ apps from where you can begin blogging.

1. https://zapier.com/blog/best-blog-sites/
2. https://www.wpbeginner.com/beginners- guide/how-to-clioose-the-best-blogging- platform/
3. https: / /www. say ansamanta. com/best- android-apps-blogger.html
4. https://www.excellentwebworld.com/latest- blogging-trend/
5. https://www.livejournal.com
6. https:// www.wordpress.com
7. https://www.blogger.com
8. https://www.blogs.myspace.com.

Question 1.
Write blogs on the following topics
Say no to tobacco.
Answer:

Question 2.
Man v/s Nature.
Answer:

Film Review:

Students are advised to read film reviews that appear in periodicals and online. This will familiarize them with the technical terms and expressions used in reviews.

After viewing a film, attempt to write your own review based on the guidelines given above. It is always a good practice to make a first draft and revise it after some time. This will help you eliminate any personal bias that has distorted the review. Revising the text also enables you to write comprehensive but concise reviews.

The Art of Compering

Imagine that you are a compere of the ‘Annual Day Celebrations’ of your college. Write a script for the same. You can take the help of the following points.

• Brief introduction
• Lighting of the Lamp
• Welcome Speech
• Speech of the Chief Guest
• Entertainments
• Vote of thanks

Answer:
1. Introduction and lighting the lamp: Good evening to all present here today on this special occasion. We have been awaiting this day with great anticipation. And finally here we are gathered to usher in that great day! Let’s begin the function with the lighting of the traditional lamp and I request our honourable Chief Guest Shri Ganesh Narvekar to inaugurate the function by lighting the lamp. [The chief guest together with certain other dignitaries on the dais lit the lamp.]
2. Welcome speech: Next we go to the Welcome Speech. Our respected Principal will now address the audience and welcome the Chief Guest. [Principal’s speech – 8-10 minutes.]
3. Speech of the Chief Guest: Now I request the honourable Chief Guest to take the podium.
[Chief Guest comes to the podium and delivers his speech – about 10 minutes.]
4. Entertainments: Now the curtains will be down for a few moments in preparation for the entertainment programme.
[Curtains down. The chief guest and other dignitaries are ushered to their seats in the audience. Stage is cleared. Curtain raises.]

(a) Now the college orchestra will delight you with their musical programme.
/Musical programme for 45 minutes]
(b) Yes, that was a big round of applause and a greatly deserved one! Let’s move on to our next item. Students of Std. XI will now perform a fusion dance. Welcome them with a warm applause!
[Dance lasts about 30 minutes.]
5. Vote of thanks: Now I call upon our Vice-principal to propose a vote of thanks. [About 2-3 minutes]
Now I thank you all once again. Special thanks to our talented artist-friends who made this evening a memorable one.

Yuvakbharati English 12th Digest Guide Section 3 (Writing Skills)

• Summary Writing Class 11 English Solutions
• Do Schools Really Kill Creativity? (Mind-Mapping) Class 11 English Solutions
• Note–Making Class 11 English Solutions
• Statement of Purpose Class 11 English Solutions
• Drafting a Virtual Message Class 11 English Solutions
• Group Discussion Class 11 English Solutions

Class 12 English Chapter 3.5 Drafting a Virtual Message Question Answer Maharashtra Board

Balbharti Yuvakbharati English 12th Digest Chapter 3.5 Drafting a Virtual Message Notes, Textbook Exercise Important Questions and Answers.

12th Std English Chapter 3.5 Brainstorming Question Answer

12th English Digest Chapter 3.5 Drafting a Virtual Message Textbook Questions and Answers

(i) Given below is a two-way communication cycle or the process of communication.

(a) Can you guess the role of the sender and the receiver in this process? What do we encode? What do we decode?

Question 1.
Can you guess the role of the sender and the receiver in this process?

Answer:
The role of the sender is to transcribe what he/she wants to convey to the receiver in a message. The role of the receiver is to interpret the conveyed message and to grasp its meaning. As messages use commonly accepted components like words, symbols and signs, the receiver generally finds no difficulty in interpreting them. However, the sender must be careful to create a clear message so as to avoid any kind of misinterpretation or misreading.

Question 2.
What do we encode?
Answer:
We encode what we want to convey to the I receiver in the form of an unambiguous (clear in meaning) message.

Question 3.
What do we decode?
Answer:
We decode from the message the idea that it conveys by way of interpreting it. A clear message is easy to interpret.

Question (b)
People send messages to others for different purposes. Mention at least five purposes/reasons for which messages are generally sent.
Answer:
1. To inform the receiver about the facts, events, etc.
2. To express feelings like sympathy, solidarity etc.

Question (ii)
Given below is a tree-diagram explaining two major types of messages. Complete the blank boxes in the diagram. One is done for you.
Answer:

(A1)

Question (i)
In pairs, enact the given conversation between Rakesh and Mrs Sarkar.
Answer:

• Rakesh: Hello, may I speak to Dr Sarkar?
• Mrs. Sarkar: He has gone to the hospital to attend the OPD. May I know who is speaking? ‘
• Rakesh: Yes, I am Rakesh Sood. My wife has been having a severe headache since yesterday. Since this morning she has also developed a high temperature. I would be very grateful if the doctor could come over to our place to examine her.
• Mrs. Sarkar: Of course. Please let me note down your address.
• Rakesh: It is B-49, New Colony.
• Mrs. Sarkar: I will give him your message as soon as he returns.
• Rakesh: Thank you.

Question (ii)
Mrs Sarkar had to leave for the school where she teaches. So she wrote a message for her husband. Draft the message in not more than 50 words.
(Students can enact the conversation in class.)
Answer:
22/06 – 9 am
Sumit

One Rakesh Sood staying at B-49, New Colony rang up this morning to say his wife has not been keeping well. She had headache yesterday and has been running a high temperature since this morning. He wanted you to go over their place and attend her at the earliest.

Sunita

Question (iii)
Using information from the dialogue given below, write the message which Amrita left for her brother, Sourajit. (Do not leave out any vital information or add any new information).
Answer:

• Shekhar: Is this 28473892?
• Amrita: Yes, May I know who is speaking?
• Shekhar: I am Shekhar, I want to speak to Sourajit. I am his friend from IHM, Goa.
• Amrita: I am his sister. Sourajit is not at home at the moment. Can you ring up a little later?
• Shekhar: I shall be a little busy. Actually, I have got a placement at the Hotel Mumbai, and will have to join with immediate effect.

So right now I am trying to get all the formalities completed. This is the news that I wanted to give Sourajit. Will you do that for me? Also tell him that I will let him know my new cell phone number as soon as I get one.
Amrita: I’ll do that. Bye and all the best. Amrita had to leave for office. So she wrote a note for Sourajit. Draft her message in not more than 50 words.

Question (iv)
You are Priyanka, a personal assistant to Ms Sen. She was away attending a meeting when Mr Garg rang up. You spoke to him and jotted down his message in your notepad.
Draft the message for Ms Sen using the information in your notes given below.
Mr Garg – rang up – 5 pm – has received the CDs and the posters – coming tomorrow – to thank Ms Sen and to personally hand over the cheque.
Answer:
5.15 pm [30th Sept.]
Madam,

Mr. Garg rang up at five in the evening while you were away attending the meeting. He said he had received the CDs and posters and would come tomorrow to express his thanks to you. He said he would also hand over the cheque to you personally.

Priyanka
(P.A)

Question (v)
Read the following conversation between Aashna and Mr. Singh.
Answer:
Aashna: Hello, may I speak to Ranajit, please?
I would like to see the notes which our biology teacher gave to the class during my absence.
Mr Singh: I will definitely do that.

Question (vi)
Since Mr Singh had to go for his morning walk he left a message for Ranajit. Draft that message in 50 words.
Answer:
Raj at comes home from school and finds the door locked. Since he has a duplicate key he enters and finds a note from his mother kept on the table. In it she explains that she had to rush to the hospital with Mrs Manohar, their neighbour, who had met with an accident. She has also written that he should have the rice and curry kept on the dining table for lunch. He could heat the food in the microwave oven if he wanted to, but he should be very careful while handling the switch.

Question (vii)
Using the information given below, write biology notebook to school today. I was absent from school due to illness. a message which Manu left for his sister. Renu. (Do not add any new information.

The message should not exceed 50 words). Ruhaan rang up – book – reading session – ‘Children Ask Kalam’ – Dr A.P.J. Abdul Kalam – compilation of letters received by him from children and his answers – Oxford Book Store – 8 pm, this evening, – pick you up – 6:30 pm attend reading session together.
Answer:
28th Nov. 2 pm
Renu

Ruhaan rang up to say that there is a book reading session at Oxford Book Store this evening at 8 o’clock. The book is “Children Ask Kalam” – a compilation of letters received by Dr. Kalam and his answers. I will pick you up at 6:30 pm sharp. We will attend it together.

Manu

Question (viii)
Given below is a template tor a message. Imagine you are working as a receptionist in a company and you are supposed to maintain the call record.
Complete the details given in the template for a particular message

Answer:

Explore:

(a) Browse the net and prepare a tabular column to explain the ‘Dos and Don’ts’ while drafting messages.
(b) Browse the net to find innovative ‘Message Templates’.
(c) Prepare a collection of short messages that are usually drafted and exchanged within the family members to keep them well informed and updated in case of different situations.
(d) Prepare a project titled, ‘The Importance of Messages in Everyday Life’.
(Students may attempt the above on their own.)

Yuvakbharati English 12th Digest Guide Section 3 (Writing Skills)

• Summary Writing Class 11 English Solutions
• Do Schools Really Kill Creativity? (Mind-Mapping) Class 11 English Solutions
• Note–Making Class 11 English Solutions
• Statement of Purpose Class 11 English Solutions
• Drafting a Virtual Message Class 11 English Solutions
• Group Discussion Class 11 English Solutions

Class 12 English Chapter 3.4 Statement of Purpose Question Answer Maharashtra Board

Balbharti Yuvakbharati English 12th Digest Chapter 3.4 Statement of Purpose Notes, Textbook Exercise Important Questions and Answers.

12th Std English Chapter 3.4 Brainstorming Question Answer

12th English Digest Chapter 3.4 Statement of Purpose Textbook Questions and Answers

Question 1.
Match the professions with the desired qualities: (The answers are given directly.)
Answer:

1. Businessman – c. convincing, selling, risk-taking
2. Artist – d. imaginative, creative, thinking out of
3. Advocate – e. logical reasoning, oratory, critical thinking.
4. Police – b. alert, investigative, love for physical activity
5. Scientist – a. reading, experimenting, researching

Question 2.
What is your career goal?
Answer:
My career goal is to be an astronaut.

Question 3.
Which of your qualities would help you in achieving your career goal?

Answer:

Question 4.
List the obstacles which might hamper in achieving your goals in life. One is done for you.
Answer:

1. Lack of proper guidance.
2. Opposition from family for choosing a strange career.
3. Lack of knowledge about the career prospects.
4. Lack of training centres in our country at present.

(A1)

Question 1.
Discuss and exchange your views with your partner about your career plan
Answer:

• My Partner: I think I should now think of a definite career plan. Have you ever thought of a career plan?
• Myself: Of course! I have a definite plan and I am quite focused on it.
• My Partner: Would you mind sharing your goals with me?
• Myself: Why not? You are my friend and you have every right to know it.
• Myself: I want to be a doctor. It is not that primary school ambition when every one wants to be an engineer or a doctor.
• My Partner: I wanted to be an airline pilot during those days.
• Myself: There could be many like you. Those were just fleeting fancies. You just can’t call them career goals.
• My Partner: Do you think your plan is real and practical?
• Myself: Surely I do! That’s why I call it my career plan. My whole focus is on it. I work hard to achieve my goal.
• My Partner: There are many doctors around and I don’t find any particular charm to be one among those ‘white coats’.
• Myself: Oh, yes! You are free to have your opinions, but whatever I do will have my personal stamp on it. I am unique and I am going to be a unique doctor.
• My Partner: Is that something like going to the villages barefoot?
• Myself: Could be that. Perhaps much more than that. You will see it yourself sometime in the future. I am quite steadfast in my resolve.
• My Partner: Okay, okay. I wish you all the best. I wish I had your will to win.

(A2)

Question 1.
You must have decided your aim in life. Which institute/university would you like to join for your diploma/ graduation. Write a Statement of Purpose as a part of your application to the institute/university.
Answer:
I would like to graduate in history from Birkbeck College under the University of London. Given below is my Statement of Purpose attached as part of my application.

Statement of Purpose:

For me, history was just a list of monarchs, a catalogue of wars and a chronicle of dynasties. All this changed when I reached the VUIth standard. I was, then, fortunate to study history under a dynamic teacher. He changed my perspectives. I realized that there is social history and economic history. There is history of science and ideas. The tipping point came when my teacher introduced me to the Bhakti Movement.

I realized that I belong to the land of Saints – Maharashtra. The lives of saints fascinated me. I delved deep into books to know more about their work and time. I read about Sant Namdeo, Sant Dynaneshwar, Sant Eknath, Sant Tukaram and Ramdas Swami. What I gained, of course, was very precious. My fascination with the subject grew by each passing day.

My aim in seeking admission to your college is that you have a very good department in South Asian History. I know that the late eminent historian Eric Hobsbawm taught in your college throughout his career. Likewise, the famous R. J. Evans and Roy Foster were once members among your faculty. So I am hopeful that I would get a chance to learn under world class teachers once I get into your esteemed institution.

My broad plan is to have a sound grounding in the medieval socio-economic history of India during my graduation years and then move on to the Bhakti Movement during my post-graduate studies. Doctoral and post-doctoral research would be focused on the life and work of a single saint.

I am an avid reader. I hope my exposure to saint literature in Marathi would stand me in good stead. I am a state-level chess player. Chess, as per the game theory, is a full information game. Your opponent see on the board as much as you see. However, the patient search for possibilities pay the dividend. The player processes the various permutations and combinations and finally makes that unique move – the winning move! I am sure that I have it in me.

I worked as an amateur research assistant to Dr. Pendse while he was working on his monumental work on the Bhakti Movement. I also have a diploma in “Indexing Books in Humanities”. I earnestly hope that an exposure to the excellent academic atmosphere prevailing in your prestigious institution would bring forth the best in me and thus allow me to contribute my mite to the rich cultural heritage of my land!

(A3)

Question 1.
Enrich your vocabulary.
Match the job terms with their meanings.

Answer:

1. to be your own boss – (g) to have your own business
2. a dead-end job – (f) a job with no promotional opportunities
3. a good team player – (j) someone who can work well with other people
4. a heavy workload – (h) to have a lot of work to do
5. a high-powered job – (b) an important/ powerful job
6. job satisfaction – (i) enjoying your job
7. manual work – (a) work that requires physical activity
8. to be stuck in a rut – (e) to be in a boring job that is hard to leave
9. to be stuck behind a desk – (c) to be unhappy in an office job
10. a nine-to-five job – (d) a normal job having a duty of 8 hours

(A4)

Question 1.
Read the dialogue given below and fill in the blanks with the appropriate job terms given above.
(The answer parts are underlined.)
Answer:
Varsha: Vivek, what kind of a job are you looking for?
Vivek: Varsha, I want to be my own boss. I don’t like a nine-to-five job. My present job is not challenging. I am stuck behind a desk. I am not afraid of a heavy workload and I am a good team player. Moreover, this is a dead-end job. I am looking for an opportunity to try new winds.

A5. Read the personal details given below and prepare a suitable Statement of Purpose:

Question (i)
University of Bath, UK is one of the leading Universities for Business Studies. You belong to a business family – wish to start your own business, carry forward your family business in future. In your junior college you have opted for commerce, scored well in your Std. X Board examination – You made profit in the stall you had put up in the business fair organized by your school/ college. Your hobbies are playing cricket/ hockey – you get along well with people.
Answer:
I belong to a family which had a long tradition in business. My father is a third generation businessman. I grew up meeting relatives who are in some business or the other. Naturally, I have never thought of any pursuit other than business.

My family business is doing quite well but the world of business is changing rapidly. To keep up with the changing times, I must keep abreast of the new developments in the world of business. Hence I aspire for a degree in business studies from an institution of high standing as yours.

I did exceedingly well in my Standard X Board Examination scoring impressive marks in Maths and English. For the junior college I opted commerce as my main stream. Accountancy is my favourite area of study. I feel quite comfortable with the subject because balance sheet analysis, stocks, trade, tariff, etc. have always been the words in currency during any of the family gatherings.

A cool head on his shoulders is a must for a businessman. With an agitated mind you can’t ever take the right decisions. I am cool by nature. I assess the pros and cons with a dispassionate mind. No wonder that I was always made the captain of our cricket team. Cricket being a mind game as well, one needs to make quick and effective decisions. Moreover, one needs to make one’s team mates believe that the decision is theirs! There lies the magic of a team player and leader and so far I have been a great hit at it.

As they say, the proof of the pudding is in the eating. Just thinking that I am endowed with great business acumen would remain a mere boast until I prove it with an example. Luckily I had a great chance coming my way during the business fair organized by our college.

What I proposed was a stall selling helmets. The principal flatly rejected the idea saying that in a college where most of the students are under-18 and are not eligible for a driving licence, it was preposterous to come out with such a bizarre idea. I persisted and somehow got the permission. It was a three-day fair.

On the first day, just as I had expected, many students told me that their siblings and parents do have helmets at home – but they don’t wear it. This was the tipping point. I asked them to bring those unworn helmets the next day. I would compensate for the old ones – they need to pay only the difference for the new ones. (I had already made a tie-up with a second-hand helmet dealer. I offered an environment-friendly bag as well to each prospective buyer.)

Students, especially girls, warmed towards the idea greatly. Being a gift, their brothers or parents just won’t be able to neglect the helmets. The magic word here was ‘gift’; and the sentimental aura surrounding the gesture. The venture clicked. I made a handsome profit. The satisfaction of being instrumental in saving many lives was a bonus.

I know for sure that the case narrated above is not a path-breaking event. But for me, it was an eye-opener. I realized that business is mainly a game based on human psychology. Reading a bit of behavioural economics taught me that not all economic demands stem from rational thought.

Yes, your prestigious institution can offer me what I seek. I seek something more than a degree in business studies. Your esteemed faculty, I hope, will provide me the right exposure I need. I look forward to novel ventures. I want to tread on an unbeaten path. For me, business is not just about making money. It is the thrill of living every moment in the exhilaration of weighing choices and making decisions. For that I need to learn new things. For that I need to get into an institution like yours.

Question (ii)
You are an avid animal lover. You have a pet dog and some lovebirds at home. You are extremely fond of them. You have been a member of bird watcher’s club. You have loved going on a safari. You have taken care of orphan animals, or animals who are hurt. In school you loved Biology. You wish to make a career in this field. The University of Cambridge offers an excellent course/ programme which would boost your career. Make a Statement of Purpose which will help you to get admission to this University.
Answer:
Statement of Purpose

I was captivated by the world of animals much early in my life. There are of course, many people around who love animals; but I doubt whether they share the same intensity which I have. I love animals of all softs. I care for animals big and small. I equally love the ones who fly and the ones who crawl.

My parents have been quite supportive of my passion. My collection of lovebirds and the pet dog which I have now are their gifts. I observe my pets and all other animals around me with undiminishing curiosity. Their behaviour fascinates me: Though ‘biology’ has been my favourite subject all along, I never knew that there are courses catering to my specific need. So your biology graduation course with focus on animal behaviour is “the one” I sought after.

I very well know that observation and study of animals demand infinite patience. Many senior members of our “Bird watchers’ club’ usually appreciate my great patience. I also have an eye for detail. Each time I go for a safari, I notice something new. Each time there seems to be a revelation of sort.

If I say I care for my pets that would be just stating the obvious. My love for animals goes beyond boundaries. Any animal suffering or struggling anywhere is my concern. There have been umpteen cases where I took care of and tended orphaned animals; but each case was unique and every one of them is etched in my memory in its vivid detail.

Though my interaction with animals has a long record, my theoretical studies about animals are not much to boast of. I have read the works of Nikolaas Tinbergin, Konrad Lorenz. Karl Von Frich and Ivan Pavlov – all pioneers in the field of animal behaviour. Nevertheless, I know that a lot has been happening of late. Moreover, I wish to learn the discipline in an organized way. And your esteemed institution is “the place” for it. I am hopeful that I will be able to contribute something significant to the field I love most.

(A6)

Question 1.
Browse different websites and find out the universities offering best courses in life Sciences, Arts, Sports, Music, Engineering and medicine. Collect and share any other additional information related to the course which seems important.
(Students may attempt this on their own.)

Yuvakbharati English 12th Digest Guide Section 3 (Writing Skills)

• Summary Writing Class 11 English Solutions
• Do Schools Really Kill Creativity? (Mind-Mapping) Class 11 English Solutions
• Note–Making Class 11 English Solutions
• Statement of Purpose Class 11 English Solutions
• Drafting a Virtual Message Class 11 English Solutions
• Group Discussion Class 11 English Solutions

Class 12 English Chapter 3.3 Note-Making Question Answer Maharashtra Board

Balbharti Yuvakbharati English 12th Digest Chapter 3.3 Note-Making Notes, Textbook Exercise Important Questions and Answers.

12th Std English Chapter 3.3 Brainstorming Question Answer

12th English Digest Chapter 3.3 Note-Making Textbook Questions and Answers

Question 1.
Complete the web.

Answer:

Question 2.
Discuss in groups why you take notes.

Answer:

Better notes will help you remember concepts, develop meaningful learning skills and gain better understanding of a topic. Discuss in groups different styles or methods you use in your note-making/taking. For example, to underlining iportant facts.
(We have given here a few of the methods employed in Note-making/Note-taking in blank formats. Students may experiment and find out the most useful method/ methods on their own. The selection of method largely depends upon the personal trait, taste and talent of j each individual student.)

Question 3.
Now let’s complete the following diagram that represents Prana and its elements: (The answers are given directly. For the relevant article, refer to page 149 of the textbook.)

Answer:

Example: Transfer the above information in the form of a table:
(Answers are given directly and underlined)
Bodily process

(A1)

Question 1.
Read the following passage carefully and complete the activities.

(A2)

Question 1.
Read the passage given on page 151 of the textbook and complete the following points with the help of the above text. (Give a suitable title.)
The Perils of self-medication
Answer:

Yuvakbharati English 12th Digest Chapter 3.3 Note-Making Additional Important Questions and Answers

Question 1.
Cornell Two-column notes
Answer:
(Blank format)

Outlining method:

Question 1.
In Outlining method, you put the main idea/topic closest to the left side of your page as headers. Then use indentations (i.e. to leave space as if you begin a new paragraph and moving to the right each time) to arrange the related points one after the other.

Blank format:
Keyword:
• This is the main division.
• This is a sub-division.
• This is a supporting fact.
Keyword :
• This is the main topic.
• This is a sub-topic.
• This is an argument in support.

Box and Bullet method:

In this, a box is drawn for every main idea. Under each box are supporting points written against bullet points.
Blank format:
Title:
Author:
Central idea -1
______________
______________
______________

Central idea – 2
______________
______________
______________

Question 2.
Table:
Answer:

Pie Chart:

Question 1.
Pie Chart showing the land use in India.
Answer:

Bar Graph:

Question 1.
Bar Graph showing the Organ Donation Pattern in India (By a Study Group)
Answer:

Line Graph:

Question 1.
Line Graph showing the price of motorbikes and the corresponding sales
Answer:

Conclusion:

Organizing the notes is an essential component of Note-making or Note-taking. Students must remember that the ‘notes’ are for further use. If you fail to make any sense of your ‘notes’ later, the very purpose of Note-taking and Note-making is defeated. So the use of proper headings and sub-headings are very important. You must judiciously use numbers and letters for the sub-topics and derived points. Underlining and using an asterisk (*) will help you to identify the main points at a glance. Above all, the method and style of Note-taking/Note-making should be in tune with your personal propensity of ordering things.

Yuvakbharati English 12th Digest Guide Section 3 (Writing Skills)

• Summary Writing Class 11 English Solutions
• Do Schools Really Kill Creativity? (Mind-Mapping) Class 11 English Solutions
• Note–Making Class 11 English Solutions
• Statement of Purpose Class 11 English Solutions
• Drafting a Virtual Message Class 11 English Solutions
• Group Discussion Class 11 English Solutions

Class 12 English Chapter 3.2 Do Schools Really Kill Creativity? (Mind-Mapping) Question Answer Maharashtra Board

Balbharti Yuvakbharati English 12th Digest Chapter 3.2 Do Schools Really Kill Creativity? (Mind-Mapping) Notes, Textbook Exercise Important Questions and Answers.

12th Std English Chapter 3.2 Brainstorming Question Answer

12th English Digest Chapter 3.2 Do Schools Really Kill Creativity? Textbook Questions and Answers

Question 1.
Observe the given figure and complete the activities that follow:

(a) Replace the ‘main idea’ by any other thought or title of your own.
(b) Add three supporting ideas to the main idea as their branches.
(c) Add two ideas to one of the branches that explains the meaning of the branch.
Answer:

Question 2.
Complete the given blank spaces/balloons with your ideas in the figure that describes your basic preparation for the HSC Board Examination. Also complete the activities that follows:

Answer:

Activity:

Complete a similar type of detailed graphical figure in your own style showing the thoughts/ ideas/concepts that keep on generating in your mind and then you choose a particular style/design or a graphical representation to describe the same idea/facts/situations – then this type of presentation can be called ‘Mind – Mapping.’
Use different shapes, arrows, lines, connectors, balloons, boxes, curved arrows, callouts, scribbles, scrolls, explosions, etc. to describe your point of view.

For example:

(A1)

Question 1.
Study the tabular column given on page 141 of the Textbook. In pairs, tell your partner the importance of each one: (The first one is given here as an example. Students may attempt 2 to 8 on their own in a manner akin to the one given below.) Enhance activities with Mind-Mapping.

Answer:

• Student A: How does mind – mapping help us?
• Student B: It helps us see an overall picture.
• Student A: Would you kindly explain it a bit more?
• Student B: See, as one would expect, mind – mapping conveys the whole idea through hierarchy and relationships.
• Student A: By the way, what is ‘hierarchy’?
• Student B: Hierarchy is a system in which classes, status, authority, etc. are ranked one above the other.
• Student A: I think I’ve got it. With the help of mind – mapping we ‘maps out’ the points beginning from the more important ones and going on to the less important ones.
• Student B: Exactly! It is a sort of branching out. What I find exciting is that the ‘mapping out’ originates from our brain quite spontaneously.
• Student A: Being the creators we grasp it fully, don’t we?
• Student B: Yes, we do. Now you got it fully right!

(A2)

Question 1.
Given below is a ‘Mind – Mapping’ template. Use your ideas/thoughts/concepts to illustrate/develop them. (Develop your ideas in the form of main branch, sub-branches and tertiary branches respectively).

Also, write a paragraph on the mind map you have completed.
Answer:

The above given figure is my Mind Map about infectious diseases. The four main ideas are the Spread, Precautions, Treatment and Containment of such infectious diseases. The best way to check the spread of infection is the practice of personal hygiene and social distancing. Maintenance of proper civic sense is called upon from each citizen. Containing the disease becomes a challenge when diseases like COVID-19 breaks out. Lack of vaccine or specific medicine makes the situation very grave. Self-isolation, quarantine, and in extreme situations, Lockdown, etc. are practised to curtail the community spread of the contagion.

A sudden spike in the cases put great strain on the health care system. Authorities try to circumvent the spike by flattening the curve of the spike. Whenever there is a pandemic, it is the duty of the citizens to help the authorities by obeying all the directives.

(A3)

Question 1.
Develop a ‘Mind – Mapping’ frame/design to show the development in your personality seen with yourself in the last 5 years. You can take the help of the following points in order to develop each of them into further branches:
(Development in Physique, Self-learning Process, Communication Skills, Social Awareness, Family Responsibility)
Answer:

(A4)

Question 1.
Develop a ‘Mind – Mapping’ frame/design to show the ‘Benefits of games and sports’ to the students. You can take the help of the following points in order to develop each of them into further branches:
(Fitness and stamina, team spirit and sportsmanship, group behaviour, killer’s instinct, will to win)
Answer:

(A5)

Browse the internet to know the following:

Question 1.
Different Frames/Designs on Mind – Mapping :
(One example is given below. Students may browse the internet to find more.)
Answer:
Spidergram.

Question 2.
Benefits of Mind – Mapping:
Answer:
Mind – Mapping is an effective tool that helps us capture the logical thinking process that goes on in our mind. It enables us to put pieces of information in the proper slots. The gathered pieces of information then assume a compact and condensed format which can be committed to memory with vividness and clarity. Mind – Mapping also helps generate a stream of creative ideas. The speed and spontaneity of Mind – Mapping proves to be a great advantage during brainstorming sessions.

Question 3.
Uses of Mind – Mapping in note-taking:
Answer:
Mind – Mapping is a creative way of note-taking. We do not remain just passive listeners noting down points mechanically. On the contrary, Mind – Mapping helps us put our creative selves in the process. Thus, we become the co-producers of the information. Using Mind-Mapping in note-taking also enables us to structure the information to suit our natural inclinations of arrangement.

Question 4.
Difference between Mind – Mapping and Concept Mapping:
Answer:
A Concept map is a diagram that shows the suggested relationships among concepts. Concept maps, unlike Mind maps, allow more divergence due to their multiple hubs and clusters. Mind maps are often restricted to radial hierarchies and tree structures. Another feature that distinguishes a Mind map from a Concept map is that in a Mind map the basic idea is embodied in the centre image and the main themes radiate from the centre as branches. This, then branches off further as twigs.

Yuvakbharati English 12th Digest Guide Section 3 (Writing Skills)

• Summary Writing Class 11 English Solutions
• Do Schools Really Kill Creativity? (Mind-Mapping) Class 11 English Solutions
• Note–Making Class 11 English Solutions
• Statement of Purpose Class 11 English Solutions
• Drafting a Virtual Message Class 11 English Solutions
• Group Discussion Class 11 English Solutions

Class 12 English Chapter 3.1 Summary Writing Question Answer Maharashtra Board

Balbharti Yuvakbharati English 12th Digest Chapter 3.1 Summary Writing Notes, Textbook Exercise Important Questions and Answers.

12th Std English Chapter 3.1 Brainstorming Question Answer

12th English Digest Chapter 3.1 Summary Writing Textbook Questions and Answers

Discuss in pairs and guess the correct alternative for the following:

Question 1.
To summarize means …………… .
(a) Put information in chronological order.
(b) To recapitulate the main points in selection
(c) To introduce new information
(d) To write one’s opinion about selection
Answer:
(b) To recapitulate the main points in selection

Question 2.
The type of summary that consists of a paragraph to express the main idea is …………… .
(a) Outline
(b) Report
(c) Synopsis
(d) Written summary
Answer:
(d) Written summary

Question 3.
There are various ways of incorporating other writers’ works into your own writing. They differ according to the closeness of your writing to the source writing. Match the ways of writing in brief given in column (A) with their descriptions in column (B):

Answer:

1. Summarizing – (e) It includes main ideas into one’s own words.
2. Paraphrasing – (f) It must be identical to the original and match the document word by word.
3. Precis writing – (d) It includes taking broader segment of the source and condensing it slightly.
4. Quoting – (a) It includes not just the main idea but every detail expressed clearly and to the point.
5. Editing – (b) It includes selection of proper lines from the given text for correction, condensation and organization.
6. Gist writing – (c) It includes the most essential part or the crux of the matter.

(A1)

Question 1.
Complete the following as instructed:
Read the passage and write its summary according to the given steps:
Answer:
Use the following steps for summary writing:
Step 1: Read the article twice.
Step 2: The purpose of writing – To tell the reader about the interesting communication methods among birds and mammals.
Step 3: Identify the main idea – Surprising examples of communication methods among birds and mammals.
Steps 4 and 5: Write the first draft: Revise your first draft and edit it.
(Students may attempt this on their own.)
Step 5: Write the final draft (Given overleaf.)

(A2)

(ii) Avoid adverbs:
Delete the adverbs in italics and rewrite:

Question (a)
“That’s usually a good thing to do.”
Answer:
“That’s a good thing to do.”

Question (b)
“That’s fairly good coffee.”
Answer:
“That’s good coffee.”

Question (c)
“I totally agree.”
Answer:
“I agree.”

Question (d)
“Actually I disagree.”
Answer:
“I disagree.”

Question (iii)
One word substitution:
Find examples similar to those given in the textbook and make a list:
Answer:

1. friendly relationship in which people understand well : rapport (pronounced as ‘rappo’)
2. able to cause death: fatal
3. seize by way of penalty: confiscate
4. someone who goes into buildings in order to steal: burglar
5. the principal character in a play or a story: protagonist
6. the path described by an object moving in air: trajectory
7. a person regarded as a symbol: icon
8. a person who knows many languages: polyglot
9. a badly behaved child: brat
10. a period of ten years: decade
11. a persistent increase in the general level of prices: inflation
12. organisation of supplies and services for any, complex operation : logistics
13. extremely careful about details: meticulous
14. not harmful or offensive: innocuous
15. present, appearing or found everywhere: ubiquitous

(ii) Change the following sentences into simple:

Question (a)
Mr. Rohit is the member and he is also the director.
Answer:
Mr. Rohit is the member and also the director.

Question (b)
The room is so small that it cannot accommodate many people.
Answer:
The room is too small to accommodate many people.

Question (c)
You have to prove that you are innocent.
Answer:
You have to prove your innocence.

Question (d)
He was late so he walked in a great hurry.
Answer:
Being late, he walked in a great hurry.

(A4)

Question (i)
Read any book of your choice and write its summary according to the steps explained in the chapter.

Question (ii)
Find some professions that require the skill of summary writing and editing. Write them
in your notebook.

Yuvakbharati English 12th Digest Chapter 3.1 Summary Writing Additional Important Questions and Answers

Question (i)
Cut redundant words:
Write five examples of redundant words:
Answer:

1. puzzling mystery = ‘mystery’
2. connect together = ‘connect’
3. divide into two equal halves = ‘divide into halves
4. surrounded on all sides = ‘surrounded’
5. return back = ‘return’

Yuvakbharati English 12th Digest Guide Section 3 (Writing Skills)

• Summary Writing Class 11 English Solutions
• Do Schools Really Kill Creativity? (Mind-Mapping) Class 11 English Solutions
• Note–Making Class 11 English Solutions
• Statement of Purpose Class 11 English Solutions
• Drafting a Virtual Message Class 11 English Solutions
• Group Discussion Class 11 English Solutions

Class 12 English Chapter 2.8 Small Towns and Rivers Question Answer Maharashtra Board

Balbharti Yuvakbharati English 12th Digest Chapter 2.8 Small Towns and Rivers Notes, Textbook Exercise Important Questions and Answers.

12th Std English Chapter 2.8 Brainstorming Question Answer

12th English Digest Chapter 2.8 Small Towns and Rivers Textbook Questions and Answers

Question (i)
Most of the civilizations have flourished on the banks of the rivers. Discuss the reasons in the class.
Points:
(a) Availability of water
(b) Fertile soil for agriculture
(c) Fishing ground
(d) Transport

Question (ii)
Write down the names of the famous cities that are situated on the banks of the rivers given below.
Answer:

Question (iii)
Write down the names of the rivers on the banks of which following cities have prospered:
Answer:

Question (iv)
Divide your class into groups and discuss the changes that might have taken place when the cities grow on the banks of the rivers.
Points: Dwellings are built – Population grows – Fishing flourishes – Outsiders come to settle – Trading takes place – Prosperity increases – Increased population, trade, traffic and fishing begin to harm the river system – River system shows damage – River starts to decay

Question (v)
Share your views in the class on the topic ‘Conservation of Rivers and Development of the Cities.’
(Students may list their own points of views.)

(A1)

Question 1.
State the importance of Nature in the lives of the people from the North-eastern part of India as expressed in the poem with reference to:
(a) Flowers
(b) River
(c) Bamboo
(d) East
Answer:
(a) Flowers – Tuberoses are woven into wreaths to be placed on the body of a departed as a mark of love and respect.
Sole: Most of the textual ‘Wh’ questions are converted to Activity Format.
(b) River: The people believe the river has a soul. They respect their rivers and even revere it as divine as its waters are immortal.
(c) Bamboo: The poet says ‘in the cool bamboo’. The colour is a cool green. The place where the bamboo grows is also cool.
(d) East: The direction of sunrise is very important for the people of Arunachal Pradesh. They ensure the dead are placed pointing west so that their soul directly enters the golden house of the sun. They believe that finally souls must attain the sun’s abode in the east.

(A2)

Question (i)
The poet has described her small town in Arunachal Pradesh. Pick out from the extract, the lines that describe the poet’s town.
Answer:
1. ‘My hometown lies calmly amidst the trees’,
2. ‘it is always the same In summer and winter With the dust flying Or the wind howling down the gorge’

Question (ii)
Make a list of natural elements mentioned in the extract.
Answer:
trees, winter, summer, wind, tuberoses, life, land, river, fish, stars

Question (iii)
‘The river has a soul.’ Elaborate the concept in your words as the poet has explained in the extract.
Answer:
When the poet says ‘The river has a soul’ she personifies the river. The river flows with great force – ‘like a torrent of grief. The river flowing with great force can be like a person pouring out grief in a storm of emotion. The river also seems to be holding its breath, maybe because it is choking with filth. There are no fishes. It is not clear and sparkling. So the poet says -‘I think it holds its breath seeking a land of fish and stars’.

Question (iv)
The poet is convinced with the thought of immortality of water. Pick out the relevant lines from the extract.
Answer:
‘The river has a soul’.

(v) The poet has used some unconventional expressions. Illustrate them in your words.

Question (a)
‘Torrent of grief.
Answer:
The poet describes the river flowing in summer with great speed. Just like someone becomes emotional in great sadness, the force of the water seems to be like the outpouring of sorrow of the river.

Question (vi)
The poet has connected the need to preserve Nature with the belief of particular community and her childhood memories. Write down the measures you would take to convince the people regarding the need to conserve the Nature.
Answer:
We have to make people at large realize that we are a part of the nature not apart from the nature. Saving nature is to save ourselves, To bring about this realization I can address my steps to two sections. The first would be the children. Saving water would be the first thing to teach children. Story-telling, poems, songs, games, cartoons and can easily bring the conservation ideas to young minds. I would take my ideas to schools, parks, malls and try to spread this to the young ones.

The other section is of course the adult public across economic and social levels. The well- off people must not be careless if they can afford to pay bills they can waste resources.

I will do everything possible. I will use social media to spread various messages/ mottos.

(A3)

Question (i)
Write down the expressions related to ‘the seasons’ from the extract.
Answer:
1. Summer or winter
2. ‘in the summer’

Question (ii)
Match column ‘A’ with column ‘B’.

Answer:

1. cool-bamboo
2. happy – pictures
3. dreadful – silence
4. dry-earth

(A4)

Question (i)
Read the expression ‘a sad wreath of tuberoses’.
‘Is the wreath sad?’ Explain the figure of speech.
Answer:
The figure of speech is transferred epithet. The sad mourners have placed the wreath of tuberoses on the dead. The emotion of sadness has been transferred to the flowers for effect.

Question (ii)
List and explain the metaphorical expressions from the extract.
Answer:
1. ‘torrent of grief’. The river sweeps along with great speed as if it is pouring out sorrow.
2. ‘Wind howling down the gorge’. The wind blowing through the narrow gorges creates a sound exactly like howling.
3. ‘The river has a soul’. The river is spoken of as a living being, a human.
4. ‘It holds its breath’. The river may be choking with debris and filth.

Question (iii)
‘The river has a soul.’
‘Life and death.’
These are the two expressions that are repeated in the poem; but both of them indicate different figures of speech. Find out and discuss.
Answer:
(a) ‘Life and death’
In the first usage it is used as antithesis, to emphasise the beginning and end.
In the second instance it is irony to indicate that neither life nor death is permanent. Ironically the rituals are permanent.
(b) ‘The river has a soul’
In the first instance it is used to personify the river. Several human-like qualities are attributed to the river,
= it cuts through the land
= it is cascading in grief
= it holds its breath
= it seeks a land

Question (iv)
Find out the beauty of the free verse reflected in this poem.
Answer:
“Small Towns and Rivers’ is written in free- verse. Since there are irregular lengths of lines and no rhyme, the reading of the poem is almost like a story-telling. Each stanza has a different number of lines and there is no order for mixing up the short and long lines.

The poem is not confined by an obvious rhythm so we feel there is a kind of freedom.We are free to imagine the widespread setting of the North-eastern terrain of mountains and rivers, mists, golden sunlight and the town by the river.

(A5)

Question (i)
Prepare the arguments for group discussion on the topic
‘A balanced progress never harms the Nature’.
For:

• Growth should be planned to take place in stages
• Planning vital for the growth
• Sustainability must be ensured
• Pros and cons of the damage to environment must be weighed
• Short-term gains in progress must not harm long-term eco-factors

Against:

• Growth must not be halted for issues of environment
• Costs will go up due to delays
• Delays in progress will slow down economy and employment
• Slowdown in economy will cause public to protest
• Sacrifices have to be made – one can’t have the cake and eat it too.

Question (ii)
Compose 4 to 6 lines on ‘Gift of the Seasons’.
Answer:
Gift of the Seasons
Each season brings a sweetly wrapt gift;
We can gift her back : no water pollution in
the season of the Sun.
No air pollution when
The rains come down.
And no degradation the rest of the year!

Question (iii)
Write an appreciation of the poem ‘Small Towns and Rivers’. Use the points given below:

• About the poem/poet/title
• Theme
• Poetic devices, language, style
• Special features – tone and type
• Values, message
• Your opinion about the poem

Answer:
The poem ‘Small Towns and Rivers’ written by Mamang Dai is a beautiful word-picture. It is also a lament of the poet about her beautiful native land of Arunachal Pradesh.

This theme shows in the way she begins the poem that small towns remind her of death. It is shocking. She implies the town is unchanging in all weathers, but development comes along and changes everything. There is irony in that the cycle of life and death shows that life is not permanent, but the rituals are permanent.

She uses metaphor that the rivers are not only alive like us humans, but actually immortal. She personifies the river by way the river ‘holds its breath’ because it is choking. It is flowing in search of a place where it will flow clean and clear. The poet uses metaphor of the water-cycle to illustrate the river has a soul and its waters are immortal.

The poet builds a climax with ‘shrine of happy’ childhood memories. This becomes growing up -‘grow with anxiety’. Then she speaks of how the dead are placed pointing west so the soul can ascend directly into the sun’s golden home in the east. This tells us about the traditions of her region.

The poem is in free verse and seems to be in easy language, but we can understand the full depth of meaning only after reading it more than once. The poem is a lament about the destruction of nature for development. We all will feel the sorrow of the poet when we read about how nature’s beauty is damaged for man’s greed called ‘progress’.

Question (iv)
Write a dialogue between two friends on ‘Importance of the rivers’
Answer:
Priya: Jai, it goes without saying that fresh, clean water is essential for humans and nature to survive. Rivers are precious sources of fresh drinking water for people across the world. And when rivers are so badly polluted by industry or by poor water management practices, it can be a case of life-or-death. This unfortunately happens across the world.

Jai: Yes Priya. Freshwater habitats account for some of the richest biodiversity in the world, and rivers are a vital, vibrant ecosystem for many species. Only those who live by the river know about this wealth of nature. Those who live far away and damaging the system with the poisons are not aware.

Priya: People depend on rivers for their way of life and their livelihoods. From fishing to agriculture, the way our waterways are managed has a direct impact on people’s lives. There are millions of people who follow their ancestors’ way of living and earning a livelihood. But modern technology has wrecked the very source of these.

Jai: Rivers are absolutely vital: for fresh drinking water, for people’s livelihoods and for nature. Unfortunately, they’re still threatened. We must commit to recovering freshwater biodiversity, restoring natural river flows and cleaning up polluted water for people and nature to thrive.
Priya: Yes Jai. I agree. It is the crying need of the day.

(A6)

Question (i)
Collect information about rivers in Maharashtra.

Question (ii)
Further reading:
‘The River Poems’ – Mamang Dai
‘The World Is Too Much With Us’ – William Wordsworth

Yuvakbharati English 12th Digest Chapter 2.8 Small Towns and Rivers Additional Important Questions and Answers

Read the extract and complete the activities given below:

Global Understanding:

Question 1.
Describe the river in the 3rd stanza.
Answer:
The river flows with great force -‘like a torrent’-. The river has life and soul. It breathes. But it seems as if the river is holding its breath. It seems to be in search of fishes which will live in it and stars which will be reflected in its waters.

Question 2.
What is meant by immortality?
Answer:
Immortality means the ability to live forever, without death.

Question 3.
Give reasons-The dead are placed pointing to the west.
Answer:
The people of Arunachal Pradesh believe that it will be possible for the soul of the departed person enter ‘the house of the sun’. They hope the soul will be able to ‘walk into the golden east’. So they place the dead (with feet) pointing to the west.

Question 4.
The poet has described her small town in Arunachal Pradesh. Pick out from the extract the lines that describe the poet’s town.
Answer:

1. The town has ‘A shrine of happy pictures’ to mark the days of childhood.
2. Small towns grow with anxiety for the future.
3. Like her town, ‘small towns’ are ‘by the river’.
4. Make a list of natural elements mentioned in the extract.

Question 5.
Make a list of natural elements mentioned in the extract.
Answer:
River, Earth, Mountaintops, Sun, Sunlight, Bamboo

Question 6.
The poet is convinced with the thought of immortality of water. Pick out the relevant lines from the extract.
Answer:
1. The river has a soul.
2. from the first drop of rain to dry earth
3. mist on the mountaintops
4. the immortality of water.

Interpretation/Inference/Analysis:

Question 1.
The land of fish and stars.
Answer:
The poet says she thinks the river is holding its breath. One has to hold one’s breath when he/she is unable to breathe or does not want to breathe. The river may be choking with garbage and is not able to breathe. The river may be stinking and may not be able to breathe.

As the river is so filthy there are no fish. It is dirty; the water is not sparkling in the day and cannot reflect the stars at night. So the river is in search of a land where there it can flow clean, it will have fish and where its clear water will sparkle in the sun and glitter with stars at night.

Question 2.
The river has a soul.’ Elaborate the concept in your words as the poet has explained in the extract.
Answer:
The poet states the river has a soul. The soul is deathless. The water that flows in the river came from the drops of rain. The water evaporated, rose as mist to the mountaintops. Then it formed clouds and poured down as rain to the dry earth and flowed again. Thus the river goes on, immortal, deathless.

Question 3.
The poet has used some unconventional expressions. Illustrate them in your words. Illustrate them in your words. Shrine of happy pictures
Answer:
There is a shrine probably in the town which has pictures inside. The pictures may be those of the happy moments experienced by the people in the town. Those memories are so sacred that it is a shrine to them. They protect and guard it because they have only sad and grim things happening at present.

Personal Response:

Question 1.
Rivers are our lifeline. They are an extremely important part of the eco-system and even considered sacred. Many major rivers and smaller ones have been misused and almost destroyed. Write down how we can restore our rivers to their original state.
Answer:
The condition of rivers worldwide is horrific. Everything from industrial chemical-waste to garbage is being thrown into rivers. Melted snow or the rainwater from springs come down from hills and mountains as sweet water for our survival. Polluting this is a crime against humanity.

Strict laws should be made and enforced to stop industrial activity near rivers. Wastes from industry, city, town or village must not reach the river. Only channels of rainwater must be allowed to reach the river. Awareness should be created for maintaining cleanliness along the banks.

In the olden days lakes, water bodies were considered precious and were guarded, Houses had wells. But people have lost the respect for water sources. Rivers are treated as sewage channels. Fines and punishments must be imposed and security put in for safeguarding our beautiful rivers.

Poetic Creativity:

Question 1.
Compose 4 to 6 lines on ‘River’.
Answer:
The River is our Mother

Like a mother the river soothes us.
When dying of thirst she revives us.
When tired and dirty she cleans us.
When growing our grain she waters the green.
Why! Oh why can’t we keep her clean!

English Yuvakbharati 12th Full Digest Section 2 (Poetry)

• Song of the Open Road Class 11 English Solutions
• Indian Weavers Class 11 English Solutions
• The Inchcape Rock Class 11 English Solutions
• Have you Earned Your Tomorrow Class 11 English Solutions
• Father Returning Home Class 11 English Solutions
• Money Class 11 English Solutions
• She Walks in Beauty Class 11 English Solutions
• Small Towns and Rivers Class 11 English Solutions