Category: Class 12

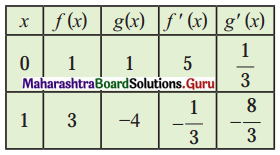
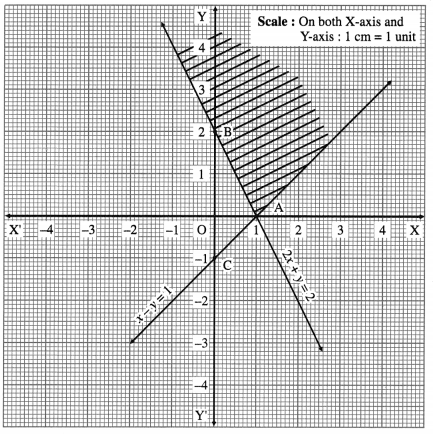
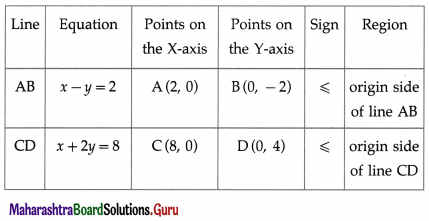
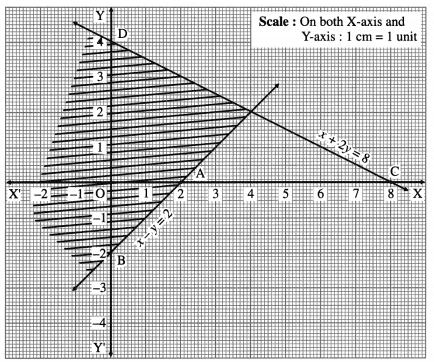
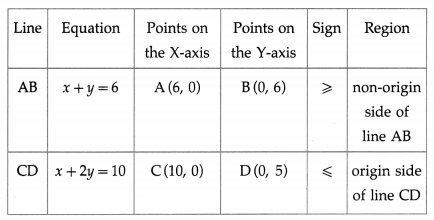
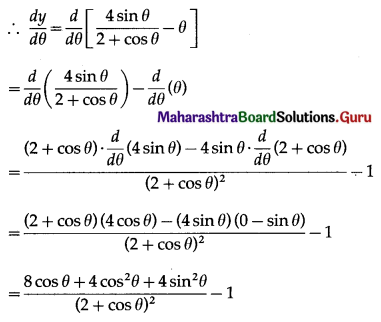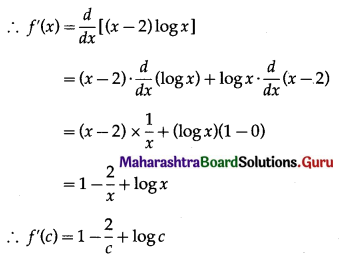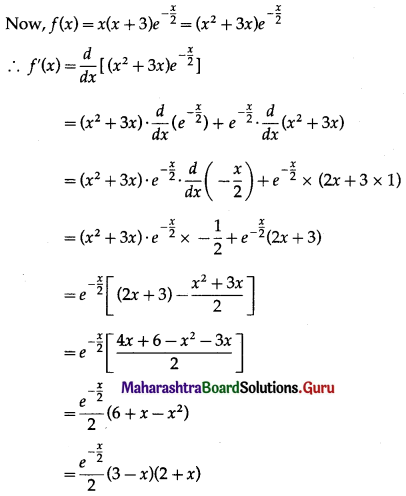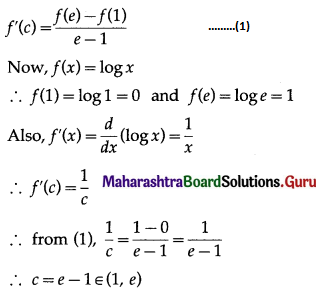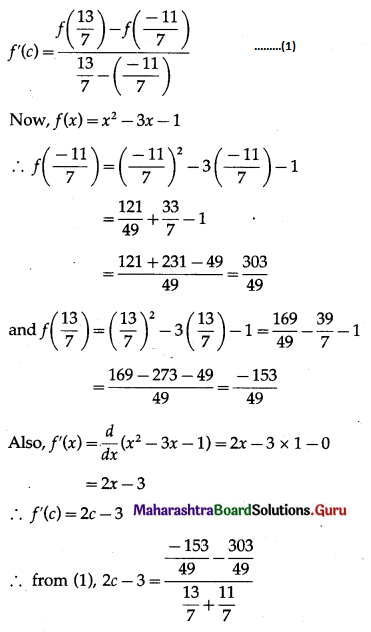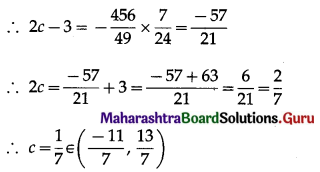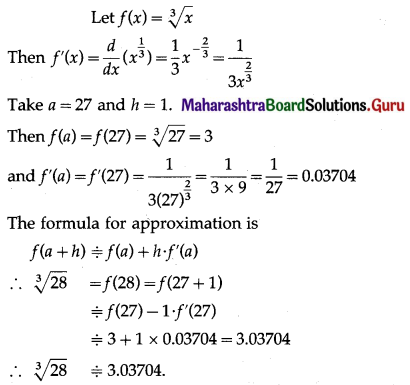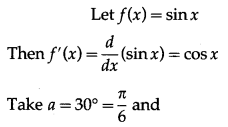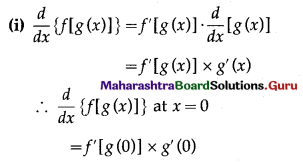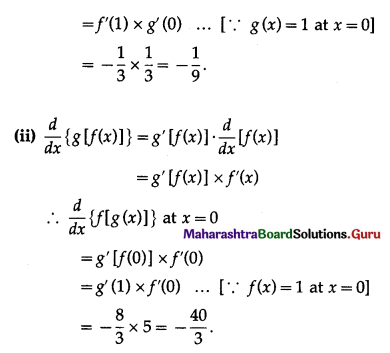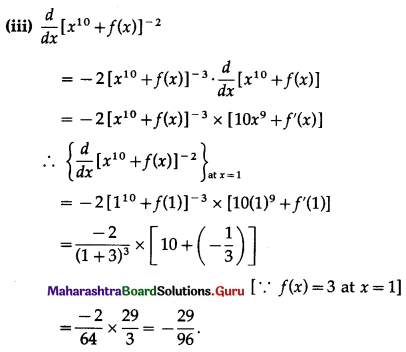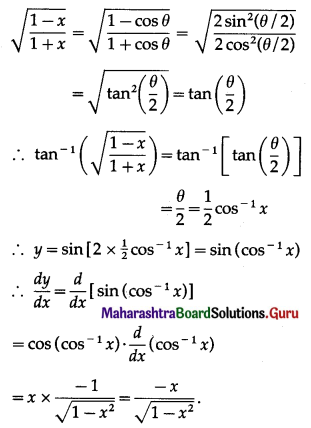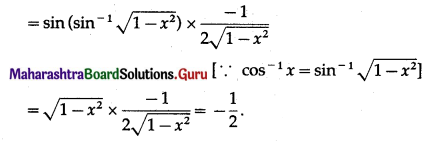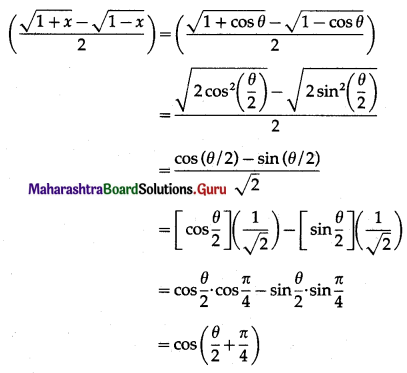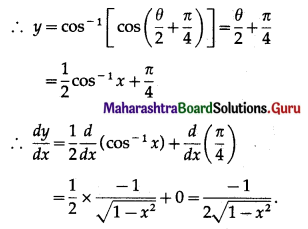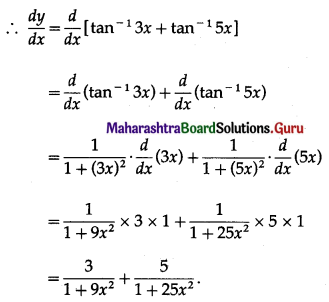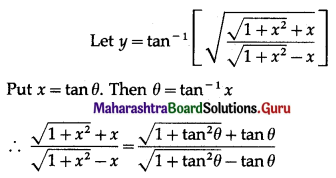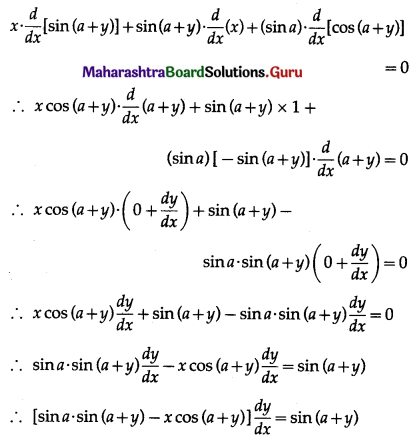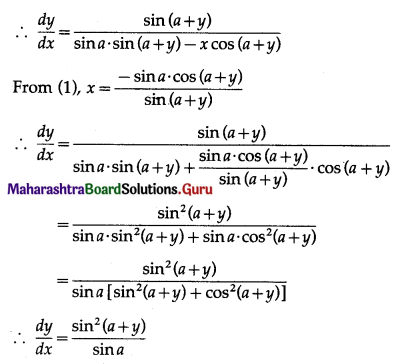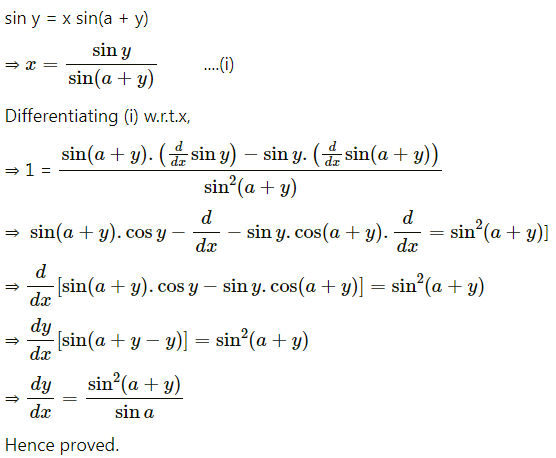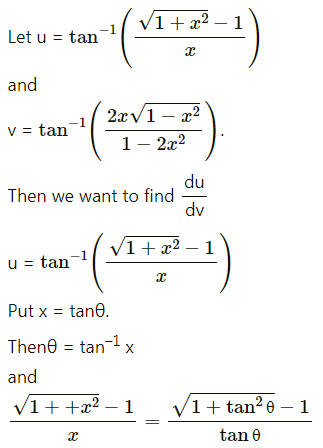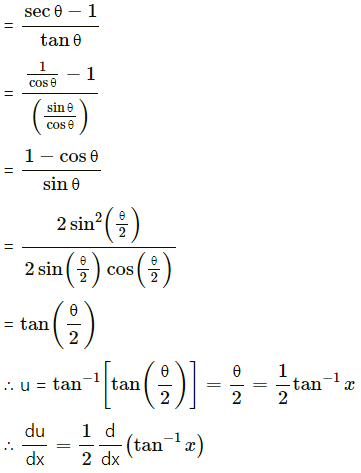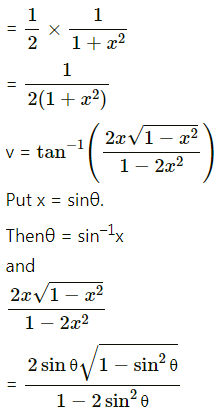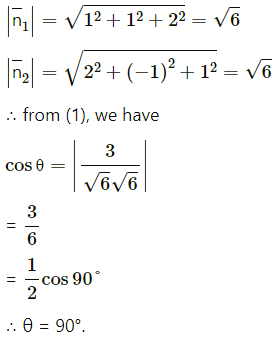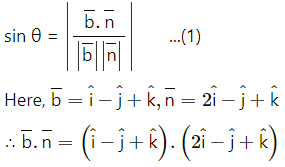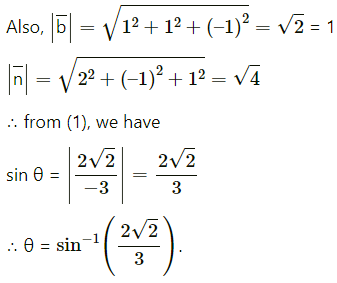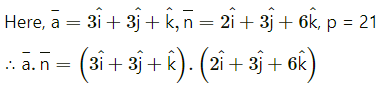Balbharti 12th Maharashtra State Board Maths Solutions Book Pdf Chapter 2 Applications of Derivatives Ex 2.4 Questions and Answers.

Maharashtra State Board 12th Maths Solutions Chapter 2 Applications of Derivatives Ex 2.4

Question 1.
Test whether the following functions are increasing or decreasing.
(i) f(x) = x³ – 6x² + 12x – 16, x ∈ R.
Solution:
f(x) = x³ – 6x² + 12x – 16
∴ f'(x) = \(\frac{d}{d x}\) (x³ – 6x² + 12x – 16)
= 3x² – 6 × 2x + 12 × 1 – 0
= 3x² – 12x + 12
= 3(x² – 4x + 4)
= 3(x – 2)² ≥ 0 for all x ∈ R
∴ f(x) ≥ 0 for all x ∈ R
∴ f is increasing for all x ∈ R.

(ii) f(x) = 2 – 3x + 3x² – x³, x ∈ R.
Solution:
f(x) = 2 – 3x + 3x² – x³
∴ f'(x) = \(\frac{d}{d x}\) (2 – 3x + 3x² – x³)
= 0 – 3 × 1 + 3 × 2x – 3x²
= -3 + 6x – 3x²
= -3(x² – 2x + 1)
= -3(x – 1)² ≤ 0 for all x ∈ R
∴ f'(x) ≤ 0 for all x ∈ R
∴ f is decreasing for all x ∈ R.

(iii) f(x) = x – \(\frac{1}{x}\), x ∈ R, x ≠ 0.
Solution:
f(x) = x – \(\frac{1}{x}\)
f'(x) = \(\frac{d}{d x}\left(x-\frac{1}{x}\right)=1-\left(\frac{-1}{x^{2}}\right)\)
= \(1+\frac{1}{x^{2}}\) > 0 for all x ∈ R, x ≠ 0
∴ f'(x) > 0 for all x ∈ R, where x ≠ 0
∴ f is increasing for all x ∈ R, where x ≠ 0.

Question 2.
Find the values of x for which the following functions are strictly increasing:
(i) f(x) = 2x³ – 3x² – 12x + 6
Solution:
f(x) = 2x³ – 3x² – 12x + 6
∴ f'(x) = \(\frac{d}{d x}\) (2x³ – 3x² – 12x + 6)
= 2 × 3x² – 3 × 2x – 12 × 1 + 0
= 6x² – 6x – 12
= 6(x² – x – 2)
f is strictly increasing if f'(x) > 0
i.e. if 6(x² – x – 2) > 0
i.e. if x² – x – 2 > 0
i.e. if x² – x > 2
i.e. if x² – x + \(\frac{1}{4}\) > 2 + \(\frac{1}{4}\)
i.e. if \(\left(x-\frac{1}{2}\right)^{2}>\frac{9}{4}\)
i.e. if x – \(\frac{1}{2}\) > \(\frac{3}{2}\) or x – \(\frac{1}{2}\) < \(\frac{-3}{2}\) i.e. if x > 2 or x < -1
∴ f is strictly increasing if x < -1 or x > 2.

(ii) f(x) = 3 + 3x – 3x² + x³
Solution:
f(x) = 3 + 3x – 3x² + x³
∴ f'(x) = \(\frac{d}{d x}\) (3 + 3x – 3x² + x³)
= 0 + 3 × 1 – 3 × 2x + 3x²
= 3 – 6x + 3x²
= 3(x² – 2x + 1)
f is strictly increasing if f'(x) > 0
i.e. if 3(x² – 2x + 1) > 0
i.e. if x² – 2x + 1 > 0
i.e. if (x – 1)² > 0
This is possible if x ∈ R and x ≠ 1
i.e. x ∈ R – {1}
∴ f is strictly increasing if x ∈ R – {1}.

(iii) f(x) = x³ – 6x² – 36x + 7
Solution:
f(x) = x³ – 6x² – 36x + 7
∴ f'(x) = \(\frac{d}{d x}\) (x³ – 6x² – 36x + 7)
= 3x² – 6 × 2x – 36 × 1 + 0
= 3x² – 12x – 36
= 3(x² – 4x – 12)
f is strictly increasing if f'(x) > 0
i.e. if 3(x² – 4x – 12) > 0
i.e. if x² – 4x – 12 > 0
i.e. if x² – 4x > 12
i.e. if x² – 4x + 4 > 12 + 4
i.e. if (x – 2)² > 16
i.e. if x – 2 > 4 or x – 2 < -4 i.e. if x > 6 or x < -2
∴ f is strictly increasing if x < -2 or x > 6.

Question 3.
Find the values of x for which the following functions are strictly decreasiong:
(i) f(x) = 2x³ – 3x² – 12x + 6
Solution:
f(x) = 2x³ – 3x² – 12x + 6
∴ f'(x) = \(\frac{d}{d x}\) (2x³ – 3x² – 12x + 6)
= 2 × 3x² – 3 × 2x – 12 × 1 + 0
= 6x² – 6x – 12
= 6(x² – x – 2)
f is strictly decreasing if f'(x) < 0
i.e. if 6(x² – x – 2) < 0
i.e. if x² – x – 2 < 0
i.e. if x² – x < 2
i.e. if x² – x + \(\frac{1}{4}\) < 2 + \(\frac{1}{4}\)
i.e. if \(\left(x-\frac{1}{2}\right)^{2}<\frac{9}{4}\)
i.e. if \(-\frac{3}{2}<x-\frac{1}{2}<\frac{3}{2}\)
i.e. if \(-\frac{3}{2}+\frac{1}{2}<x-\frac{1}{2}+\frac{1}{2}<\frac{3}{2}+\frac{1}{2}\)
i.e. if -1 < x < 2
∴ f is strictly decreasing if -1 < x < 2.

(ii) f(x) = x + \(\frac{25}{x}\)
Solution:
f(x) = x + \(\frac{25}{x}\), x ≠ 0
∴ f'(x) = \(\frac{d}{d x}\left(x+\frac{25}{x}\right)\)
= 1 + 25(-1) x^-2
= 1 – \(\frac{25}{x^{2}}\)
f is is strictly decreasing if f'(x) < 0
i.e. if 1 – \(\frac{25}{x^{2}}\) < 0
i.e. if 1 < \(\frac{25}{x^{2}}\)
i.e. if x² < 25
i.e. if -5 < x < 5, x ≠ 0
i.e. if x ∈ (-5, 5) – {0}
∴ f is strictly decreasing if x ∈ (-5, 5) – {0}.

(iii) f(x) = x³ – 9x² + 24x + 12
Solution:
f(x) = x³ – 9x² + 24x + 12
∴ f'(x) = \(\frac{d}{d x}\) (x³ – 9x² + 24x + 12)
= 3x² – 9 × 2x + 24 × 1 + 0
= 3x² – 18x + 24
= 3(x² – 6x + 8)
f is strictly decreasing if f'(x) < 0
i.e. if 3(x² – 6x + 8) < 0
i.e. if x² – 6x + 8 < 0
i.e. if x² – 6x < -8
i.e. if x² – 6x + 9 < -8 + 9
i.e. if (x – 3)² < 1
i.e. if -1 < x – 3 < 1
i.e. if -1 + 3 < x – 3 + 3 < 1 + 3
i.e. if 2 < x < 4
i.e., if x ∈ (2, 4)
∴ f is strictly decreasing if x ∈ (2, 4)

Question 4.
Find the values of x for which the function f(x) = x³ – 12x² – 144x + 13
(a) increasing
(b) decreasing.
Solution:
f(x) = x³ – 12x² – 144x + 13
∴ f'(x) = \(\frac{d}{d x}\) (x³ – 12x² – 144x + 13)
= 3x² – 12 × 2x – 144 × 1 + 0
= 3x² – 24x – 144
= 3(x² – 8x – 48)

(a) f is increasing if f'(x) ≥ 0
i.e. if 3(x² – 8x – 48) ≥ 0
i.e. if x² – 8x – 48 ≥ 0
i.e. if x² – 8x ≥ 48
i.e. if x² – 8x + 16 ≥ 48 + 16
i.e. if (x – 4)² ≥ 64
i.e. if x – 4 ≥ 8 or x – 4 ≤ -8
i.e. if x > 12 or x ≤ -4
∴ f is increasing if x ≤ -4 or x ≥ 12,
i.e. x ∈ (-∞, -4] ∪ [12, ∞).

(b) f is decreasing if f'(x) ≤ 0
i.e. if 3(x² – 8x – 48) ≤ 0
i.e. if x² – 8x – 48 ≤ 0
i.e. if x² – 8x ≤ 48
i.e. if x² – 8x + 16 ≤ 48 + 16
i.e. if (x – 4)² ≤ 64
i.e. if -8 ≤ x – 4 ≤ 8
i.e. if -4 ≤ x ≤ 12
∴ f is decreasing if -4 ≤ x ≤ 12, i.e. x ∈ [-4, 12].

Question 5.
Find the values of x for which f(x) = 2x³ – 15x² – 144x – 7 is
(a) strictly increasing
(b) strictly decreasing.
Solution:
f(x) = 2x³ – 15x² – 144x – 7
f'(x) = \(\frac{d}{d x}\) (2x³ – 15x² – 144x – 7)
= 2 × 3x² – 15 × 2x – 144 × 1 – 0
= 6x² – 30x – 144
= 6(x² – 5x – 24)
(a) f is strictly increasing if f'(x) > 0
i.e. if 6(x² – 5x – 24) > 0
i.e. if x² – 5x – 24 > 0
i.e. if x² – 5x > 24
i.e. if x² – 5x + \(\frac{25}{4}\) > 24 + \(\frac{25}{4}\)
i.e. if \(\left(x-\frac{5}{2}\right)^{2}>\frac{121}{4}\)
i.e. if \(x-\frac{5}{2}>\frac{11}{2} \text { or } x-\frac{5}{2}<-\frac{11}{2}\) i.e. if x > 8 or x < -3
∴ f is strictly increasing, if x < -3 or x > 8.

(b) f is strictly decreasing if f'(x) < 0
i.e. if 6(x² – 5x – 24) < 0
i.e. if x² – 5x – 24 < 0
i.e. if x² – 5x < 24
i.e. if x² – 5x + \(\frac{25}{4}\) < 24 + \(\frac{25}{4}\)
i.e. if \(\left(x-\frac{5}{2}\right)^{2}<\frac{121}{4}\)
i.e. if \(-\frac{11}{2}<x-\frac{5}{2}<\frac{11}{2}\)
i.e. if \(-\frac{11}{2}+\frac{5}{2}<x-\frac{5}{2}+\frac{5}{2}<\frac{11}{2}+\frac{5}{2}\)
i.e. if -3 < x < 8
∴ f is strictly decreasing, if -3 < x < 8.

Question 6.
Find the values of x for which f(x) = \(\frac{\boldsymbol{x}}{x^{2}+1}\) is
(a) strictly increasing
(b) strictly decreasing.
Solution:
f(x) = \(\frac{\boldsymbol{x}}{x^{2}+1}\)

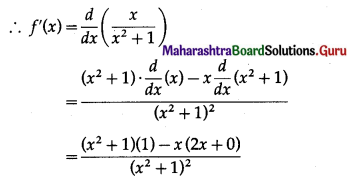
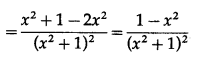
(a) f is strictly increasing if f'(x) > 0
i.e. if \(\frac{1-x^{2}}{\left(x^{2}+1\right)^{2}}\) > 0
i.e. if 1 – x² > 0 ……..[∵ (x² + 1)² > 0]
i.e. if 1 > x²
i.e. if x² < 1
i.e. if -1 < x < 1
∴ f is strictly increasing if -1 < x < 1

(b) f is strictly decreasing if f'(x) < 0
i.e. if \(\frac{1-x^{2}}{\left(x^{2}+1\right)^{2}}\) < 0
i.e. if 1 – x² < 0 ……..[∵ (x² + 1)² > 0]
i.e. if 1 < x² i.e. if x² > 1
i.e. if x > 1 or x < -1
∴ f is strictly decreasing if x < -1 or x > 1
i.e. x ∈ (-∞, -1) ∪ (1, ∞).

Question 7.
Show that f(x) = 3x + \(\frac{1}{3 x}\) is increasing in (\(\frac{1}{3}\), 1) and decreasing in (\(\frac{1}{9}\), \(\frac{1}{3}\))
Solution:
f(x) = 3x + \(\frac{1}{3 x}\)

Question 8.
Show that f(x) = x – cos x is increasing for all x.
Solution:
f(x) = x – cos x
∴ f'(x) = \(\frac{d}{d x}\) (x – cos x)
= 1 – (-sin x)
= 1 + sin x
Now, -1 ≤ sin x ≤ 1 for all x ∈ R
∴ -1 + 1 ≤ 1 + sin x ≤ 1 for all x ∈ R
∴ 0 ≤ f'(x) ≤ 1 for all x ∈ R
∴ f'(x) ≥ 0 for all x ∈ R
∴ f is increasing for all x.

Question 9.
Find the maximum and minimum of the following functions:
(i) y = 5x³ + 2x² – 3x
Solution:

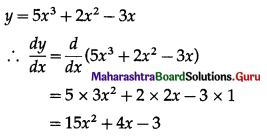
(ii) f(x) = 2x³ – 21x² + 36x – 20
Solution:
f(x) = 2x³ – 21x² + 36x – 20
∴ f'(x) = \(\frac{d}{d x}\) (2x³ – 21x² + 36x – 20)
= 2 × 3x² – 21 × 2x + 36 × 1 – 0
= 6x² – 42x + 36
and f”(x) = \(\frac{d}{d x}\) (6x² – 42x + 36)
= 6 × 2x – 42 × 1 + 0
= 12x – 42
f'(x) = 0 gives 6x² – 42x + 36 = 0
∴ x² – 7x + 6 = 0
∴ (x – 1)(x – 6) = 0
the roots of f'(x) = 0 are x₁ = 1 and x₂ = 6.

Method 1 (Second Derivative Test):
(a) f”(1) = 12(1) – 42 = -30 < 0
∴ by the second derivative test, f has maximum at x = 1
and maximum value of f at x = 1
f(1) = 2(1)³ – 21(1)² + 36(1) – 20
= 2 – 21 + 36 – 20
= -3

(b) f”(6) = 12(6) – 42 = 30 > 0
∴ by the second derivative test, f has minimum at x = 6
and minimum value of f at x = 6
f(6) = 2(6)³ – 21(6)² + 36(6) – 20
= 432 – 756 + 216 – 20
= -128.
Hence, the function f has maximum value -3 at x = 1 and minimum value -128 at x = 6.

Method 2 (First Derivative Test):
(a) f'(x) = 6(x – 1)(x – 6)
Consider x = 1
Let h be a small positive number. Then
f'(1 – h) = 6(1 – h – 1)(1 – h – 6)
= 6(-h)(-5 – h)
= 6h(5 + h)> 0
and f'(1 + h) = 6(1 + h – 1)(1 + h – 6)
= 6h(h – 5) < 0, as h is small positive number.
∴ by the first derivative test, f has maximum at x = 1 and maximum value of f at x = 1
f(1) = 2(1)³ – 21(1)² + 36(1) – 20
= 2 – 21 + 36 – 20
= -3

(b) f'(x) = 6(x – 1)(x – 6)
Consider x = 6
Let h be a small positive number. Then
f'(6 – h) = 6(6 – h – 1)(6 – h – 6)
= 6(5 – h)(-h)
= -6h(5 – h) < 0, as h is small positive number
and f'(6 + h) = 6(6 + h – 1)(6 + h – 6) = 6(5 + h)(h) > 0
∴ by the first derivative test, f has minimum at x = 6
and minimum value of f at x = 6
f(6) = 2(6)³ – 21(6)² + 36(6) – 20
= 432 – 756 + 216 – 20
= -128
Hence, the function f has maximum value -3 at x = 1
and minimum value -128 at x = 6.

(iii) f(x) = x³ – 9x² + 24x
Solution:
f(x) = x³ – 9x² + 24x
∴ f'(x) = \(\frac{d}{d x}\) (x³ – 9x² + 24x)
= 3x² – 9 × 2x + 24 × 1
= 3x² – 18x + 24
and f”(x) = \(\frac{d}{d x}\) (3x² – 18x + 24)
= 3 × 2x – 18 × 1 + 0
= 6x – 18
f'(x) = 0 gives 3x² – 18x + 24 = 0
∴ x² – 6x + 8 = 0
∴ (x – 2)(x – 4) = 0
∴ the roots of f'(x) = 0 are x₁ = 2 and x₂ = 4.

(a) f”(2) = 6(2) – 18 = -6 < 0
∴ by the second derivative test, f has maximum at x = 2
and maximum value of f at x = 2
f(2) = (2)³ – 9(2)² + 24(2)
= 8 – 36 + 48
= 20

(b) f”(4) = 6(4) – 18 = 6 > 0
∴ by the second derivative test, f has minimum at x = 4
and minimum value of f at x = 4
f(4) = (4)³ – 9(4)² + 24(4)
= 64 – 144 + 96
= 16
Hence, the function f has maximum value 20 at x = 2 and minimum value 16 at x = 4.

(iv) f(x) = x² + \(\frac{16}{x^{2}}\)
Solution:

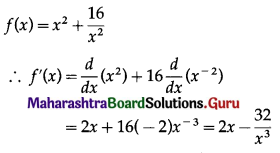
(v) f(x) = x log x
Solution:

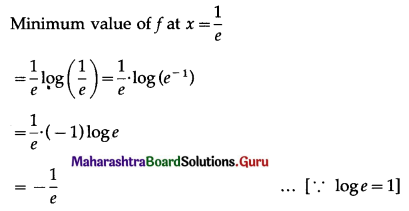
(vi) f(x) = \(\frac{\log x}{x}\)
Solution:

Question 10.
Divide the number 30 into two parts such that their product is maximum.
Solution:
Let the first part of 30 be x.
Then the second part is 30 – x.
∴ their product = x(30 – x) = 30x – x² = f(x) ……(Say)
∴ f'(x) = \(\frac{d}{d x}\) (30x – x²)
= 30 × 1 – 2x
= 30 – 2x
and f”(x) = \(\frac{d}{d x}\) (30 – 2x)
= 0 – 2 × 1
= -2
The root of the equation f(x) = 0,
i.e. 30 – 2x = 0 is x = 15 and f”(15) = -2 < 0
∴ by the second derivative test, f is maximum at x = 15.
Hence, the required parts of 30 are 15 and 15.

Question 11.
Divide the number 20 into two parts such that the sum of their squares is minimum.
Solution:
Let the first part of 20 be x.
Then the second part is 20 – x.
∴ sum of their squares = x² + (20 – x)² = f(x) …… (Say)
∴ f'(x) = \(\frac{d}{d x}\) [x² + (20 – x)²]
= 2x + 2(20 – x) . \(\frac{d}{d x}\) (20 – x)
= 2x + 2(20 – x) × (0 – 1)
= 2x – 40 + 2x
= 4x – 40
and f”(x) = \(\frac{d}{d x}\) (4x – 40)
= 4 × 1 – 0
= 4
The root of the equation f'(x) = 0,
i.e. 4x – 40 = 0 is x = 10 and f”(10) = 4 > 0
∴ by the second derivative test, f is minimum at x = 10.
Hence, the required parts of 20 are 10 and 10.

Question 12.
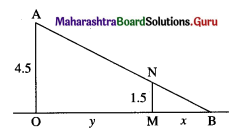
A wire of length 36 meters is bent in the form of a rectangle. Find its dimensions if the area of the rectangle is maximum.
Solution:
Let x metres and y metres be the length and breadth of the rectangle.
Then its perimeter is 2(x + y) = 36
x + y = 18
y = 18 – x
Area of the rectangle = xy = x (18 – x)
Let f(x) = x(18 – x) = 18x – x²
∴ f'(x) = \(\frac{d}{d x}\) (18x – x²) = 18 – 2x
and f”(x) = \(\frac{d}{d x}\) (18 – 2x) = 0 – 2 × 1 = -2
Now, f'(x) = 0, if 18 – 2x = 0
i.e. if x = 9
and f”(9) = -2 < 0
∴ by the second derivative test, f has maximum value at x = 9.
When x = 9, y = 18 – 9 = 9
∴ x = 9 cm, y = 9 cm
∴ the rectangle is a square of side 9 metres.

Question 13.
A ball is thrown in the air. Its height at any time t is given by h = 3 + 14t – 5t². Find the maximum height it can reach.
Solution:
The height h at any t is given by h = 3 + 14t – 5t²


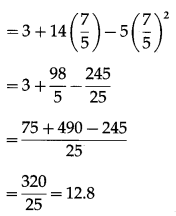
Hence, the maximum height the ball can reach = 12.8 units.

Question 14.
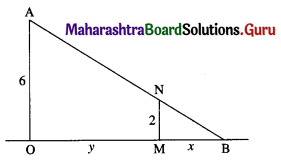
Find the largest size of a rectangle that can be inscribed in a semicircle of radius 1 unit, so that two vertices lie on the diameter.
Solution:

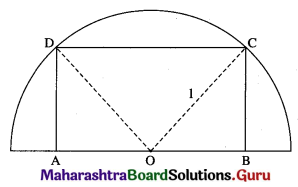
Let ABCD be the rectangle inscribed in a semicircle of radius 1 unit such that the vertices A and B lie on the diameter.
Let AB = DC = x and BC = AD = y.
Let O be the centre of the semicircle.
Join OC and OD. Then OC = OD = radius = 1.
Also, AD = BC and m∠A = m∠B = 90°.
∴ OA = OB
∴ OB = \(\frac{1}{2}\) AB = \(\frac{x}{2}\)
In right angled triangle OBC,
OB² + BC² = OC²




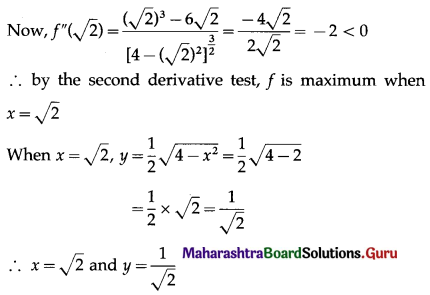
Hence, the area of the rectangle is maximum (i.e. rectangle has the largest size) when its length is √2 units and breadth is \(\frac{1}{\sqrt{2}}\) unit.

Question 15.
An open cylindrical tank whose base is a circle is to be constructed of metal sheet so as to contain a volume of πa³ cu cm of water. Find the dimensions so that the quantity of the metal sheet required is minimum.
Solution:
Let x be the radius of the base, h be the height, V be the volume and S be the total surface area of the cylindrical tank.
Then V = πa³ … (Given)
∴ πx²h = πa³
∴ h = \(\frac{a^{3}}{x^{2}}\) ……..(1)
Now, S = 2πxh + πx²

∴ by the second derivative test, S is minimum when x = a
When x = a, from (1)
h = \(\frac{a^{3}}{a^{2}}\) = a
Hence, the quantity of metal sheet is minimum when radius height = a cm.

Question 16.
The perimeter of a triangle is 10 cm. If one of the sides is 4 cm. What are the other two sides of the triangle for its maximum area?
Solution:

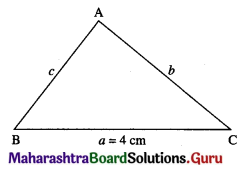
Let ABC be the triangle such that the side BC = a = 4 cm.
Also, the perimeter of the triangle is 10 cm.
i.e. a + b + c = 10
∴ 2s = 10
∴ s = 5
Also, 4 + b + c = 10
∴ b + c = 6
∴ b = 6 – c
Let ∆ be the area of the triangle.



∴ by the second derivative test, ∆ is maximum when c = 3.
When c = 3, b = 6 – c = 6 – 3 = 3
Hence, the area of the triangle is maximum when the other two sides are 3 cm and 3 cm.

Question 17.
A box with a square base is to have an open top. The surface area of the box is 192 sq cm. What should be its dimensions in order that the volume is largest?
Solution:
Let x cm be the side of square base and h cm be its height.
Then x² + 4xh = 192
∴ h = \(\frac{192-x^{2}}{4 x}\) …… (1)
Let V be the volume of the box.

∴ by the second derivative test, V is maximum at x = 8.
If x = 8, h = \(\frac{192-64}{4(8)}=\frac{128}{32}\) = 4
Hence, the volume of the box is largest, when the side of square base is 8 cm and its height is 4 cm.

Question 18.
The profit function P (x) of a firm, selling x items per day is given by P(x) = (150 – x)x – 1625. Find the number of items the firm should manufacture to get maximum profit. Find the maximum profit.
Solution:
Profit function P (x) is given by
P(x) = (150 – x)x – 1625 = 150x – x² -1625
∴ P'(x) = \(\frac{d}{d x}\) (150x – x² – 1625)
= 150 × 1 – 2x – 0
= 150 – 2x
and P”(x) = \(\frac{d}{d x}\) (150 – 2x)
= 0 – 2 × 1
= -2
Now, P'(x) = 0 gives, 150 – 2x = 0
∴ x = 75
and P”(75) = -2 < 0
∴ by the second derivative test, P(x) is maximum when x = 75
Maximum profit = P(75)
= (150 – 75)75 – 1625
= 75 × 75 – 1625
= 4000
Hence, the profit will be maximum, if the manufacturer manufactures 75 items and the maximum profit is 4000.

Question 19.
Find two numbers whose sum is 15 and when the square of one multiplied by the cube of the other is maximum.
Solution:
Let the two numbers be x and y.
Then x + y = 15
∴ y = 15 – x
Let P is the product of square of y and cube of x.
Then P = x³y²
= x³(15 – x)²
= x³(225 – 30x + x²)
= x⁵ – 30x⁴ + 225x³
∴ \(\frac{d P}{d x}\) = \(\frac{d}{d x}\) (x⁵ – 30x⁴ + 225x³)
= 5x⁴ – 30 × 4x³ + 225 × 3x²
= 5x⁴ – 120x³ + 675x²
and \(\frac{d^{2} P}{d x^{2}}\) = \(\frac{d}{d x}\) (5x⁴ – 120x³ + 675x²)
= 5 × 4x³ – 120 × 3x² + 675 × 2x
= 20x³ – 360x² + 1350x
= 10x(2x² – 36x + 135)
Now, \(\frac{d P}{d x}\) = 0 gives 5x⁴ – 120x³ + 675x² = 0
∴ 5x²(x² – 24x +135) = 0
∴ 5x²(x² – 15x – 9x + 135) = 0
∴ 5x²[x(x – 15) – 9(x – 35)] = 0
∴ 5x²(x – 15)(x – 9) = 0
∴ the roots of \(\frac{d P}{d x}\) = 0 are x₁ = 0, x₂ = 15 and x₃ = 9
If x = 0, then y = 15 – 0 = 15
If x = 15, then y = 15 – 15 = 0
In both cases, product x³y² is zero, which is not maximum.
∴ x ≠ 0 and x ≠ 15
∴ x = 6
Now, \(\left(\frac{d^{2} P}{d x^{2}}\right)_{\text {at } x=6}\) = 10(6)[2(6)² – 36 × 6 + 135]
= 60[72 – 216 + 135]
= 60(-9)
= -540 < 0
∴ P is maximum when x = 6
If x = 6, then y = 15 – 6 = 9
Hence, the required numbers are 6 and 9.

Question 20.
Show that among rectangles of given area, the square has least perimeter.
Solution:
Let x be the length and y be the breadth of the rectangle whose area is A sq units (which is given as constant).
Then xy = A
∴ y = \(\frac{A}{x}\) ………(1)
Let P be the perimeter of the rectangle.

x = y
∴ rectangle is a square.
Hence, among rectangles of given area, the square has least perimeter.

Question 21.
Show that the height of a closed right circular cylinder of given volume and least surface area is equal to its diameter.
Solution:
Let x be the radius of base, h be the height and S be the surface area of the closed right circular cylinder whose volume is V which is given to be constant.
Then πr²h = V
∴ h = \(\frac{V}{\pi r^{2}}=\frac{A}{x^{2}}\) …….(1)
where A = \(\frac{V}{\pi}\), which is constant.


Hence, the surface area is least when height of the closed right circular cylinder is equal to its diameter.

Question 22.
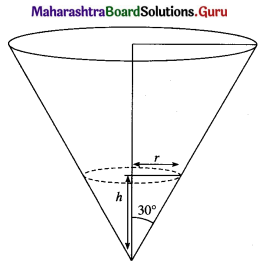
Find the volume of the largest cylinder that can be inscribed in a sphere of radius ‘r’ cm.
Solution:
Let R be the radius and h be the height of the cylinder which is inscribed in a sphere of radius r cm.
Then from the figure,


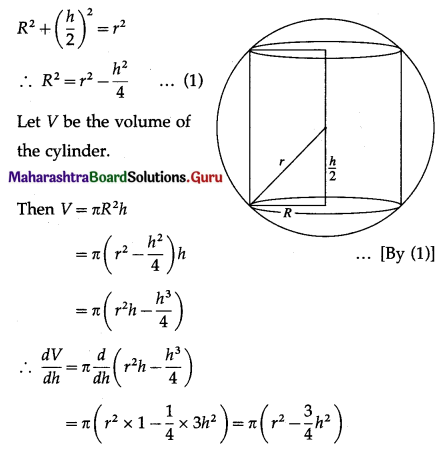
Hence, the volume of the largest cylinder inscribed in a sphere of radius ‘r’ cm = \(\frac{4 \pi r^{3}}{3 \sqrt{3}}\) cu cm.

Question 23.
Show that y = log(1 + x) – \(\frac{2 x}{2+x}\), x > -1 is an increasing function on its domain.
Solution:
y = log(1 + x) – \(\frac{2 x}{2+x}\), x > -1

Hence, the given function is increasing function on its domain.

Question 24.
Prove that y = \(\frac{4 \sin \theta}{2+\cos \theta}\) – θ is an increasing function if θ ∈ [0, \(\frac{\pi}{2}\)]
Solution:
y = \(\frac{4 \sin \theta}{2+\cos \theta}\) – θ

Balbharti 12th Maharashtra State Board Maths Solutions Book Pdf Chapter 2 Applications of Derivatives Ex 2.3 Questions and Answers.

Maharashtra State Board 12th Maths Solutions Chapter 2 Applications of Derivatives Ex 2.3

Question 1.
Check the validity of the Rolle’s theorem for the following functions.
(i) f(x) = x² – 4x + 3, x ∈ [1, 3]
Solution:
The function f given as f(x) = x² – 4x + 3 is polynomial function.
Hence, it is continuous on [1, 3] and differentiable on (1, 3).
Now, f(1) = 1² – 4(1) + 3 = 1 – 4 + 3 = 0
and f(3) = 3² – 4(3) + 3 = 9 – 12 + 3 = 0
∴ f(1) = f(3)
Thus, the function f satisfies all the conditions of Rolle’s theorem.

(ii) f(x) = e^-x sin x, x ∈ [0, π].
Solution:
The functions e^-x and sin x are continuous and differentiable on their domains.
∴ f(x) = e^-x sin x is continuous on [0, π] and differentiable on (0, π).
Now, f(0) = e⁰ sin 0 = 1 × 0 = 0
and f(π) = e^-π sin π = e^-π × 0 = 0
∴ f(0) = f(π)
Thus, the function f satisfies all the conditions of the Rolle’s theorem.

(iii) f(x) = 2x² – 5x + 3, x ∈ [1, 3].
Solution:
The function f given as f(x) = 2x² – 5x + 3 is a polynomial function.
Hence, it is continuous on [1, 3] and differentiable on (1, 3).
Now, f(1) = 2(1)² – 5(1) + 3 = 2 – 5 + 3 = 0
and f(3) = 2(3)² – 5(3) + 3 = 18 – 15 + 3 = 6
∴ f(1) ≠ f(3)
Hence, the conditions of Rolle’s theorem are not satisfied.

(iv) f(x) = sin x – cos x + 3, x ∈ [0, 2π].
Solution:
The functions sin x, cos x and 3 are continuous and differentiable on their domains.
∴ f(x) = sin x – cos x + 3 is continuous on [0, 2π] and differentiable on (0, 2π).
Now, f(0) = sin 0 – cos 0 + 3 = 0 – 1 + 3 = 2
and f(2π) = sin 2π – cos 2π + 3 = 0 – 1 + 3 = 2
∴ f(0) = f(2π)
Thus, the function f satisfies all the conditions of the Rolle’s theorem.

(v) f(x) = x², if 0 ≤ x ≤ 2
= 6 – x, if 2 < x ≤ 6.
Solution:
f(x) = x², if 0 ≤ x ≤ 2
= 6 – x, if 2 < x ≤ 6
∴ f(x) = \(\frac{d}{d x}\left(x^{2}\right)\) = 2x, if 0 ≤ x ≤ 2
= \(\frac{d}{d x}(6-x)\) = -1, if 2 < x ≤ 6
∴ Lf'(2) = 2(2) = 4 and Rf'(2) = -1
∴ Lf'(2) ≠ Rf'(2)
∴ f is not differentiable at x = 2 and 2 ∈ (0, 6).
∴ f is not differentiable at all the points on (0, 6).
Hence, the conditions of Rolle’s theorem are not satisfied.

(vi) f(x) = \(x^{\frac{2}{3}}\), x ∈ [-1, 1].
Solution:
f(x) = \(x^{\frac{2}{3}}\)
∴ \(f^{\prime}(x)=\frac{d}{d x}\left(x^{\frac{2}{3}}\right)=\frac{2}{3} x^{-\frac{1}{3}}\) = \(\frac{2}{3 \sqrt[3]{x}}\)
This does not exist at x = 0 and 0 ∈ (-1, 1)
∴ f is not differentiable on the interval (-1, 1).
Hence, the conditions of Rolle’s theorem are not satisfied.

Question 2.
Given an interval [a, b] that satisfies hypothesis of Rolle’s theorem for the function f(x) = x⁴ + x² – 2. It is known that a = -1. Find the value of b.
Solution:
f(x) = x⁴ + x² – 2
Since the hypothesis of Rolle’s theorem are satisfied by f in the interval [a, b], we have
f(a) = f(b), where a = -1
Now, f(a) = f(-1) = (-1)⁴ + (-1)² – 2 = 1 + 1 – 2 = 0
and f(b) = b⁴ + b² – 2
∴ f(a) = f(b) gives
0 = b⁴ + b² – 2 i.e. b⁴ + b² – 2 = 0.
Since, b = 1 satisfies this equation, b = 1 is one of the roots of this equation.
Hence, b = 1.

Question 3.
Verify Rolle’s theorem for the following functions.
(i) f(x) = sin x + cos x + 7, x ∈ [0, 2π]
Solution:
The functions sin x, cos x and 7 are continuous and differentiable on their domains.
∴ f(x) = sin x + cos x + 7 is continuous on [0, 2π] and differentiable on (0, 2π)
Now, f(0) = sin 0 + cos 0 + 7 = 0 + 1 + 7 = 8
and f(2π) = sin 2π + cos 2π + 7 = 0 + 1 + 7 = 8
∴ f(0) = f(2π)
Thus, the function f satisfies all the conditions of Rolle’s theorem.
∴ there exists c ∈ (0, 2π) such that f'(c) = 0.
Now, f(x) = sin x + cos x + 7
∴ f'(x) = \(\frac{d}{d x}\) (sin x + cos x + 7)
= cos x – sin x + 0
= cos x – sin x
∴ f'(c) = cos c – sin c
∴ f'(c) = 0 gives, cos c – sin c = 0
∴ cos c = sin c
∴ c = \(\frac{\pi}{4}, \frac{5 \pi}{4}, \frac{9 \pi}{4}, \ldots\)
But \(\frac{\pi}{4}, \frac{5 \pi}{4}\) ∈ (0, 2π)
∴ c = \(\frac{\pi}{4} \text { or } \frac{5 \pi}{4}\)
Hence, the Rolle’s theorem is verified.

(ii) f(x) = sin(\(\frac{x}{2}\)), x ∈ [0, 2π]
Solution:
The function f(x) = sin(\(\frac{x}{2}\)) is continuous on [0, 2π] and differentiable on (0, 2π).
Now, f(0) = sin 0 = 0
and f(2π) = sin π = 0
∴ f(0) = f(2π)
Thus, the function f satisfies all the conditions of Rolle’s theorem.
∴ there exists c ∈ (0, 2π) such that f'(c) = 0.


Hence, Rolle’s theorem is verified.

(iii) f(x) = x² – 5x + 9, x ∈ [1, 4].
Solution:
The function f given as f(x) = x² – 5x + 9 is a polynomial function.
Hence it is continuous on [1, 4] and differentiable on (1, 4).
Now, f(1) = 1² – 5(1) + 9 = 1 – 5 + 9 = 5
and f(4) = 4² – 5(4) + 9 = 16 – 20+ 9 = 5
∴ f(1) = f(4)
Thus, the function f satisfies all the conditions of the Rolle’s theorem.
∴ there exists c ∈ (1, 4) such that f'(c) = 0.
Now, f(x) = x2 – 5x + 9
∴ f'(x) = \(\frac{d}{d x}\) (x² – 5x + 9)
= 2x – 5 × 1 + 0
= 2x – 5
∴ f'(c) = 2c – 5
∴ f'(c) = 0 gives, 2c – 5 = 0
∴ c = 5/2 ∈ (1, 4)
Hence, the Rolle’s theorem is verified.

Question 4.
If Rolle’s theorem holds for the function f(x) = x³ + px² + qx + 5, x ∈ [1, 3] with c = 2 + \(\frac{1}{\sqrt{3}}\), find the values of p and q.
Solution:
The Rolle’s theorem holds for the function f(x) = x³ + px² + qx + 5, x ∈ [1, 3]
∴ f(1) = f(3)
∴ 1³ + p(1)² + q(1) + 5 = 3³ + p (3)² + q(3) + 5
∴ 1 + p + q + 5 = 27 + 9p + 3q + 5
∴ 8p + 2q = -26
∴ 4p + q = -13 ….. (1)
Also, there exists at least one point c ∈ (1, 3) such that f'(c) = 0.
Now, f'(x) = \(\frac{d}{d x}\) (x³ + px² + qx + 5)
= 3x² + p × 2x + q × 1 + 0
= 3x² + 2px + q

But f'(c) = 0
∴ \(4 p+\frac{2 p}{\sqrt{3}}+q+13+\frac{12}{\sqrt{3}}=0\)
∴ (4√3 + 2)p + √3q + (13√3 + 12) = 0
∴ (4√3 + 2)p + √3q = -13√3 – 12 ……. (2)
Multiplying equation (1) by √3, we get
4√3p + √3q= -13√3
Subtracting this equation from (2), we get
2p = -12 ⇒ p= -6
∴ from (1), 4(-6) + q = -13 ⇒ q = 11
Hence, p = -6 and q = 11.

Question 5.
If Rolle’s theorem holds for the function f(x) = (x – 2) log x, x ∈ [1, 2], show that the equation x log x = 2 – x is satisfied by at least one value of x in (1, 2).
Solution:
The Rolle’s theorem holds for the function f(x) = (x – 2) log x, x ∈ [1, 2].
∴ there exists at least one real number c ∈ (1, 2) such that f'(c) = 0.
Now, f(x) = (x – 2) log x

∴ f'(c) = 0 gives 1 – \(\frac{2}{c}\) + log c = 0
∴ c – 2 + c log c = 0
∴ c log c = 2 – c, where c ∈ (1, 2)
∴ c satisfies the equation x log x = 2 – x, c ∈ (1, 2).
Hence, the equation x log x = 2 – x is satisfied by at least one value of x in (1, 2).

Question 6.
The function f(x) = \(x(x+3) e^{-\frac{x}{2}}\) satisfies all the conditions of Rolle’s theorem on [-3, 0]. Find the value of c such that f'(c) = 0.
Solution:
The function f(x) satisfies all the conditions of Rolle’s theorem, therefore there exist c ∈ (-3, 0) such that f'(c) = 0.

Question 7.
Verify Lagrange’s mean value theorem for the following functions:
(i) f(x) = log x on [1, e].
Solution:
The function f given as f(x) = log x is a logarithmic function that is continuous for all positive real numbers.
Hence, it is continuous on [1, e] and differentiable on (1, e).
Thus, the function f satisfies the conditions of Lagrange’s mean value theorem.
∴ there exists c ∈ (1, e) such that

Hence, Lagrange’s mean value theorem is verified.

(ii) f(x) = (x – 1)(x – 2)(x – 3) on [0, 4].
Solution:
The function f given as
f(x) = (x – 1)(x – 2)(x – 3)
= (x – 1)(x² – 5x + 6)
= x³ – 5x² + 6x – x² + 5x – 6
= x³ – 6x² + 11x – 6 is a polynomial function.
Hence, it is continuous on [0, 4] and differentiable on (0, 4).
Thus, the function f satisfies the conditions of Lagrange’s, mean value theorem.
∴ there exists c ∈ (0, 4) such that


Hence, Lagrange’s mean value theorem is verified.

(iii) f(x) = x² – 3x – 1, x ∈ \(\left[\frac{-11}{7}, \frac{13}{7}\right]\)
Solution:
The function f given as f(x) = x² – 3x – 1 is a polynomial function.
Hence, it is continuous on \(\left[\frac{-11}{7}, \frac{13}{7}\right]\) and differentiable on \(\left(\frac{-11}{7}, \frac{13}{7}\right)\).
Thus, the function f satisfies the conditions of LMVT.
∴ there exists c ∈ \(\left(\frac{-11}{7}, \frac{13}{7}\right)\) such that


Hence, Lagrange’s mean value theorem is verified.

(iv) f(x) = 2x – x², x ∈ [0, 1].
Solution:
The function f given as f(x) = 2x – x² is a polynomial function.
Hence, it is continuous on [0, 1] and differentiable on (0, 1).
Thus, the function f satisfies the conditions of Lagrange’s mean value theorem.
∴ there exists c ∈ (0, 1) such that

Hence, Lagrange’s mean value theorem is verified.

(v) f(x) = \(\frac{x-1}{x-3}\) on [4, 5].
Solution:
The function f given as
f(x) = \(\frac{x-1}{x-3}\) is a rational function which is continuous except at x = 3.
But 3 ∉ [4, 5]
Hence, it is continuous on [4, 5] and differentiable on (4, 5).
Thus, the function f satisfies the conditions of Lagrange’s mean value theorem.
∴ there exists c ∈ (4, 5) such that
f'(c) = \(\frac{f(5)-f(4)}{5-4}\) ……..(1)

Hence, Lagrange’s mean value theorem is verified.

Balbharti 12th Maharashtra State Board Maths Solutions Book Pdf Chapter 2 Applications of Derivatives Ex 2.2 Questions and Answers.

Maharashtra State Board 12th Maths Solutions Chapter 2 Applications of Derivatives Ex 2.2

Question 1.
Find the approximate value of given functions, at required points.
(i) √8.95
Solution:

√8.95 = 2.9917

(ii) \(\sqrt[3]{28}\)
Solution:

(iii) \(\sqrt[5]{31.98}\)
Solution:

(iv) (3.97)⁴
Solution:

(v) (4.01)³
Solution:

Question 2.
Find the approximate values of:
(i) sin 61°, given that 1° = 0.0174^c, √3 = 1.732.
Solution:

(ii) sin(29° 30′), given that 1° = 0.0175^c, √3 = 1.732.
Solution:

(iii) cos(60° 30′), given that 1° = 0.0175^c, √3 = 1.732.
Solution:

(iv) tan (45° 40′), given that 1° = 0.0175^c.
Solution:

Question 3.
Find the approximate values of
(i) tan^-1(0.999).
Solution:

(ii) cot^-1(0.999).
Solution:

(iii) tan^-1(1.001).
Solution:

Question 4.
Find the approximate values of:
(i) e^0.995, given that e = 2.7183.
Solution:

(ii) e^2.1, given that e² = 7.389.
Solution:

(iii) 3^2.01, given that log 3 = 1.0986.
Solution:

Question 5.
Find the approximate values of:
(i) log_e(101), given that log_e10 = 2.3026.
Solution:

(ii) log_e(9.01), given that log 3 = 1.0986.
Solution:

(iii) log₁₀(1016), given that log₁₀e = 0.4343.
Solution:

Question 6.
Find the approximate values of:
(i) f(x) = x³ – 3x + 5 at x = 1.99
Solution:

(ii) f(x) = x³ + 5x² – 7x +10 at x = 1.12
Solution:

Balbharti 12th Maharashtra State Board Maths Solutions Book Pdf Chapter 2 Applications of Derivatives Ex 2.1 Questions and Answers.

Maharashtra State Board 12th Maths Solutions Chapter 2 Applications of Derivatives Ex 2.1

Question 1.
Find the equations of tangents and normals to the curve at the point on it.
(i) y = x² + 2e^x + 2 at (0, 4)
Solution:

(ii) x³ + y³ – 9xy = 0 at (2, 4)
Solution:
x³ + y³ – 9xy = 0
Differentiating both sides w.r.t. x, we get


Hence, the equations of tangent and normal are 4x – 5y + 12 = 0 and 5x + 4y – 26 = 0 respectively.

(iii) x² – √3xy + 2y² = 5 at (√3, 2)
Solution:
x² – √3xy + 2y² = 5
Differentiating both sides w.r.t. x, we get

the slope of normal at (√3, 2) does not exist.
normal is parallel to Y-axis.
equation of the normal is of the form x = k
Since, it passes through the point (√3, 2), k = √3
equation of the normal is x = √3.
Hence, the equations of tangent and normal are y = 2 and x = √3 respectively.

(iv) 2xy + π sin y = 2π at (1, \(\frac{\pi}{2}\))
Solution:
2xy + π sin y = 2π
Differentiating both sides w.r.t. x, we get


Hence, the equations of tangent and normal are πx + 2y – 2π = 0 and 4x – 2πy + π² – 4 = 0 respectively.

(v) x sin 2y = y cos 2x at (\(\frac{\pi}{4}\), \(\frac{\pi}{2}\))
Solution:
x sin 2y = y cos 2x
Differentiating both sides w.r.t. x, we get



Hence, the equations of the tangent and normal are 2x – y = 0 and 4x + 8y – 5π = 0 respectively.

(vi) x = sin θ and y = cos 2θ at θ = \(\frac{\pi}{6}\)
Solution:
When θ = \(\frac{\pi}{6}\), x = sin\(\frac{\pi}{6}\) and y = cos\(\frac{\pi}{3}\)
∴ x = \(\frac{1}{2}\) and y = \(\frac{1}{2}\)
Hence, the point at which we want to find the equations of tangent and normal is (\(\frac{1}{2}\), \(\frac{1}{2}\))
Now, x = sin θ, y = cos 2θ
Differentiating x and y w.r.t. θ, we get


2y – 1 = x – \(\frac{1}{2}\)
4y – 2 = 2x – 1
2x – 4y + 1 = 0
Hence, equations of the tangent and normal are 4x + 2y – 3 = 0 and 2x – 4y + 1 = 0 respectively.

(vii) x = √t, y = t – \(\frac{1}{\sqrt{t}}\), at t = 4.
Solution:
When t = 4, x = √4 and y = 4 – \(\frac{1}{\sqrt{4}}\)
∴ x = 2 and y = 4 – \(\frac{1}{2}\) = \(\frac{7}{2}\)
Hence, the point at which we want to find the equations of tangent and normal is (2, \(\frac{7}{2}\)).
Now, x = √t, y = t – \(\frac{1}{\sqrt{t}}\)
Differentiating x and y w.r.t. t, we get



Hence, the equations of tangent and normal are 17x – 4y – 20 = 0 and 8x + 34y – 135 = 0 respectively.

Question 2.
Find the point of the curve y = \(\sqrt{x-3}\) where the tangent is perpendicular to the line 6x + 3y – 5 = 0.
Solution:
Let the required point on the curve y = \(\sqrt{x-3}\) be P(x₁, y₁).
Differentiating y = \(\sqrt{x-3}\) w.r.t. x, we get

Hence, the required points are (4, 1) and (4, -1).

Question 3.
Find the points on the curve y = x³ – 2x² – x where the tangents are parallel to 3x – y + 1 = 0.
Solution:
Let the required point on the curve y = x³ – 2x² – x be P(x₁, y₁).

Question 4.
Find the equations of the tangents to the curve x² + y² – 2x – 4y + 1 = 0 which are parallel to the X-axis.
Solution:
Let P (x₁, y₁) be the point on the curve x² + y² – 2x – 4y + 1 = 0 where the tangent is parallel to X-axis.
Differentiating x² + y² – 2x – 4y + 1 = 0 w.r.t. x, we get


the coordinates of the points are (1, 0) or (1, 4)
Since the tangents are parallel to X-axis, their equations are of the form y = k
If it passes through the point (1, 0), k = 0, and if it passes through the point (1, 4), k = 4
Hence, the equations of the tangents are y = 0 and y = 4.

Question 5.
Find the equations of the normals to the curve 3x² – y² = 8, which are parallel to the line x + 3y = 4.
Solution:
Let P(x₁, y₁) be the foot of the required normal to the curve 3x² – y² = 8.
Differentiating 3x² – y² = 8 w.r.t. x, we get


Hence, the equations of the normals are x + 3y – 8 = 0 and x + 3y + 8 = 0.

Question 6.
If the line y = 4x – 5 touches the curve y² = ax³ + b at the point (2, 3), find a and b.
Solution:
y² = ax³ + b
Differentiating both sides w.r.t. x, we get

= slope of the tangent at (2, 3)
Since, the line y = 4x – 5 touches the curve at the point (2, 3), slope of the tangent at (2, 3) is 4.
2a = 4 ⇒ a = 2
Since (2, 3) lies on the curve y² = ax³ + b
(3)² = a(2)³ + b
9 = 8a + b
9 = 8(2) + b …… [∵ a = 2]
b = -7
Hence, a = 2 and b = -7.

Question 7.
A particle moves along the curve 6y = x³ + 2. Find the points on the curve at which y-coordinate is changing 8 times as fast as the x-coordinate.
Solution:
Let P(x₁, y₁) be the point on the curve 6y = x³ + 2 whose y-coordinate is changing 8 times as fast as the x-coordinate.

Question 8.
A spherical soap bubble is expanding so that its radius is increasing at the rate of 0.02 cm/sec. At what rate is the surface area increasing, when its radius is 5 cm?
Solution:
Let r be the radius and S be the surface area of the soap bubble at any time t.
Then S = 4πr²
Differentiating w.r.t. t, we get

Hence, the surface area of the soap bubble is increasing at the rate of 0.87c cm² / sec.

Question 9.
The surface area of a spherical balloon is increasing at the rate of 2 cm²/sec. At what rate is the volume of the balloon is increasing, when the radius of the balloon is 6 cm?
Solution:
Let r be the radius, S be the surface area and V be the volume of the spherical balloon at any time t.
Then S = 4πr² and V = \(\frac{4}{3} \pi r^{3}\)
Differentiating w.r.t. t, we get

Hence, the volume of the spherical balloon is increasing at the rate of 6 cm³ / sec.

Question 10.
If each side of an equilateral triangle increases at the rate of √2 cm/sec, find the rate of increase of its area when its side of length is 3 cm.
Solution:
If x cm is the side of the equilateral triangle and A is its area, then \(A=\frac{\sqrt{3}}{4} x^{2}\)
Differentiating w.r.t. f, we get

Hence, rate of increase of the area of equilateral triangle = \(\frac{3 \sqrt{6}}{2}\) cm² / sec.

Question 11.
The volume of a sphere increases at the rate of 20 cm³/sec. Find the rate of change of its surface area, when its radius is 5 cm.
Solution:
Let r be the radius, S be the surface area and V be the volume of the sphere at any time t.
Then S = 4πr² and V = \(\frac{4}{3} \pi r^{3}\)
Differentiating w.r.t. t, we get

Hence, the surface area of the sphere is changing at the rate of 8 cm²/sec.

Question 12.
The edge of a cube is decreasing at the rate of 0.6 cm/sec. Find the rate at which its volume is decreasing, when the edge of the cube is 2 cm.
Solution:
Let x be the edge of the cube and V be its volume at any time t.
Then V = x³
Differentiating both sides w.r.t. t, we get

Hence, the volume of the cube is decreasing at the rate of 7.2 cm³/sec.

Question 13.
A man of height 2 meters walks at a uniform speed of 6 km/hr away from a lamp post of 6 meters high. Find the rate at which the length of the shadow is increasing.
Solution:
Let OA be the lamp post, MN the man, MB = x, his shadow, and OM = y, the distance of the man from the lamp post at time t.

Then \(\frac{d y}{d t}\) = 6 km/hr is the rate at which the man is moving at away from the lamp post.
\(\frac{d x}{d t}\) is the rate at which his shadow is increasing.
From the figure,
\(\frac{x}{2}=\frac{x+y}{6}\)
6x = 2x + 2y
4x = 2y
x = \(\frac{1}{2}\) y
\(\frac{d x}{d t}=\frac{1}{2} \frac{d y}{d t}=\frac{1}{2} \times 6=3 \mathrm{~km} / \mathrm{hr}\)
Hence, the length of the shadow is increasing at the rate of 3 km/hr.

Question 14.
A man of height 1.5 meters walks towards a lamp post of height 4.5 meters, at the rate of (\(\frac{3}{4}\)) meter/sec.
Find the rate at which
(i) his shadow is shortening
(ii) the tip of the shadow is moving.
Solution:

Let OA be the lamp post, MN the man, MB = x his shadow and OM = y the distance of the man from lamp post at time t.
Then \(\frac{d y}{d t}=\frac{3}{4}\) is the rate at which the man is moving towards the lamp post.
\(\frac{d x}{d t}\) is the rate at which his shadow is shortening.
B is the tip of the shadow and it is at a distance of x + y from the post.
\(\frac{d}{d t}(x+y)=\frac{d x}{d t}+\frac{d y}{d t}\) is the rate at which the tip of the shadow is moving.
From the figure,
\(\frac{x}{1.5}=\frac{x+y}{4.5}\)
45x = 15x + 15y
30x = 15y
x = \(\frac{1}{2}\)y
\(\frac{d x}{d t}=\frac{1}{2} \cdot \frac{d y}{d t}=\frac{1}{2}\left(\frac{3}{4}\right)=\left(\frac{3}{8}\right) \text { metre/sec }\)
and \(\frac{d x}{d t}+\frac{d y}{d t}=\frac{3}{8}+\frac{3}{4}=\left(\frac{9}{8}\right) \text { metres } / \mathrm{sec}\)
Hence (i) the shadow is shortening at the rate of (\(\frac{3}{8}\)) metre/sec, and
(ii) the tip of shadow is moving at the rate of (\(\frac{9}{8}\)) metres/sec.

Question 15.
A ladder 10 metres long is leaning against a vertical wall. If the bottom of the ladder is pulled horizontally away from the wall at the rate of 1.2 metres per second, find how fast the top of the ladder is sliding down the wall, when the bottom is 6 metres away from the wall.
Solution:

Let AB be the ladder, where AB = 10 metres.
Let at time t seconds, the end A of the ladder be x metres from the wall and the end B be y metres from the ground.
Since, OAB is a right angled triangle, by Pythagoras’ theorem
x² + y² = 10² i.e. y² = 100 – x²
Differentiating w.r.t. t, we get
2y \(\frac{d y}{d t}\) = 0 – 2x \(\frac{d x}{d t}\)
∴ \(\frac{d y}{d t}=-\frac{x}{y} \cdot \frac{d x}{d t}\) ……..(1)
Now, \(\frac{d x}{d t}\) = 1.2 metres/sec is the rate at which the bottom at of the ladder is pulled horizontally and \(\frac{d y}{d t}\) is the rate at which the top of ladder B is sliding.
When x = 6, y² = 100 – 36 = 64
y = 8
(1) gives \(\frac{d y}{d t}=-\frac{6}{8}(1.2)=-\frac{6}{8} \times \frac{12}{10}\)
\(=-\frac{9}{10}=-0.9\)
Hence, the top of the ladder is sliding down the wall, at the rate of 0.9 metre/sec.

Question 16.
If water is poured into an inverted hollow cone whose semi-vertical angle is 30° so that its depth (measured along the axis) increases at the rate of 1 cm/sec. Find the rate at which the volume of water increases when the depth is 2 cm.
Solution:

Let r be the radius, h be the height, θ be the semi-vertical angle and V be the volume of the water at any time t.

Hence, the volume of water is increasing at the rate of \(\left(\frac{4 \pi}{3}\right)\) cm3/sec.

Balbharti 12th Maharashtra State Board Maths Solutions Book Pdf Chapter 1 Differentiation Miscellaneous Exercise 1 Questions and Answers.

Maharashtra State Board 12th Maths Solutions Chapter 1 Differentiation Miscellaneous Exercise 1

(I) Choose the correct option from the given alternatives:

Question 1.
Let f(1) = 3, f'(1) = \(-\frac{1}{3}\), g(1) = -4 and g'(1) = \(-\frac{8}{3}\). The derivative of \(\sqrt{[f(x)]^{2}+[g(x)]^{2}}\) w.r.t. x at x = 1 is
(a) \(-\frac{29}{15}\)
(b) \(\frac{7}{3}\)
(c) \(\frac{31}{15}\)
(d) \(\frac{29}{15}\)
Answer:
(d) \(\frac{29}{15}\)

Question 2.
If y = sec(tan^-1 x), then \(\frac{d y}{d x}\) at x = 1, is equal to
(a) \(\frac{1}{2}\)
(b) 1
(c) \(\frac{1}{\sqrt{2}}\)
(d) 2
Answer:
(c) \(\frac{1}{\sqrt{2}}\)

Question 3.
If f(x) = \(\sin ^{-1}\left(\frac{4^{x+\frac{1}{2}}}{1+2^{4 x}}\right)\), which of the following is not the derivative of f(x)?
(a) \(\frac{2 \cdot 4^{x} \log 4}{1+4^{2 x}}\)
(b) \(\frac{4^{x+1} \log 2}{1+4^{2 x}}\)
(c) \(\frac{4^{x+1} \log 4}{1+4^{4 x}}\)
(d) \(\frac{2^{2(x+1)} \log 2}{1+2^{4 x}}\)
Answer:
(c) \(\frac{4^{x+1} \log 4}{1+4^{4 x}}\)

Question 4.
If x^y = y^x, then\(\frac{d y}{d x}\) = _______
(a) \(\frac{x(x \log y-y)}{y(y \log x-x)}\)
(b) \(\frac{y(y \log x-x)}{x(x \log y-y)}\)
(c) \(\frac{y^{2}(1-\log x)}{x^{2}(1-\log y)}\)
(d) \(\frac{y(1-\log x)}{x(1-\log y)}\)
Answer:
(b) \(\frac{y(y \log x-x)}{x(x \log y-y)}\)

Question 5.
If y = sin (2 sin^-1 x), then \(\frac{d y}{d x}\) = _______
(a) \(\frac{2-4 x^{2}}{\sqrt{1-x^{2}}}\)
(b) \(\frac{2+4 x^{2}}{\sqrt{1-x^{2}}}\)
(c) \(\frac{4 x^{2}-1}{\sqrt{1-x^{2}}}\)
(d) \(\frac{1-2 x^{2}}{\sqrt{1-x^{2}}}\)
Answer:
(a) \(\frac{2-4 x^{2}}{\sqrt{1-x^{2}}}\)

Question 6.
If y = \(\tan ^{-1}\left(\frac{x}{1+\sqrt{1-x^{2}}}\right)+\sin \left[2 \tan ^{-1}\left(\sqrt{\frac{1-x}{1+x}}\right)\right]\), then \(\frac{d y}{d x}\) = _______
(a) \(\frac{x}{\sqrt{1-x^{2}}}\)
(b) \(\frac{1-2 x}{\sqrt{1-x^{2}}}\)
(c) \(\frac{1-2 x}{2 \sqrt{1-x^{2}}}\)
(d) \(\frac{1-2 x^{2}}{\sqrt{1-x^{2}}}\)
Answer:
(c) \(\frac{1-2 x}{2 \sqrt{1-x^{2}}}\)

Question 7.
If y is a function of x and log(x + y) = 2xy, then the value of y'(0) = _______
(a) 2
(b) 0
(c) -1
(d) 1
Answer:
(d) 1

Question 8.
If g is the inverse of function f and f'(x) = \(\frac{1}{1+x^{7}}\), then the value of g'(x) is equal to:
(a) 1 + x⁷
(b) \(\frac{1}{1+[g(x)]^{7}}\)
(c) 1 + [g(x)]⁷
(d) 7x⁶
Answer:
(c) 1 + [g(x)]⁷

Question 9.
If \(x \sqrt{y+1}+y \sqrt{x+1}=0\) and x ≠ y, then \(\frac{d y}{d x}\) = _______
(a) \(\frac{1}{(1+x)^{2}}\)
(b) \(-\frac{1}{(1+x)^{2}}\)
(c) (1 + x)²
(d) \(-\frac{x}{x+1}\)
Answer:
(b) \(-\frac{1}{(1+x)^{2}}\)

Question 10.
If y = \(\tan ^{-1}\left(\sqrt{\frac{a-x}{a+x}}\right)\), where -a < x < a, then \(\frac{d y}{d x}\) = _______
(a) \(\frac{x}{\sqrt{a^{2}-x^{2}}}\)
(b) \(\frac{a}{\sqrt{a^{2}-x^{2}}}\)
(c) \(-\frac{1}{2 \sqrt{a^{2}-x^{2}}}\)
(d) \(\frac{1}{2 \sqrt{a^{2}-x^{2}}}\)
Answer:
(c) \(-\frac{1}{2 \sqrt{a^{2}-x^{2}}}\)
[Hint: Put x = a cos θ]

Question 11.
If x = a (cos θ + θ sin θ), y = a (sin θ – θ cos θ), then \(\left[\frac{d^{2} y}{d x^{2}}\right]_{\theta=\frac{\pi}{4}}\) = _______
(a) \(\frac{8 \sqrt{2}}{a \pi}\)
(b) \(-\frac{8 \sqrt{2}}{a \pi}\)
(c) \(\frac{a \pi}{8 \sqrt{2}}\)
(d) \(\frac{4 \sqrt{2}}{a \pi}\)
Answer:
(a) \(\frac{8 \sqrt{2}}{a \pi}\)

Question 12.
If y = a cos (log x) and \(A \frac{d^{2} y}{d x^{2}}+B \frac{d y}{d x}+C=0\), then the values of A, B, C are _______
(a) x², -x, -y
(b) x², x, y
(c) x², x, -y
(d) x², -x, y
Answer:
(b) x², x, y

(II) Solve the following:

Question 1.


Let u(x) = f[g(x)], v(x) = g[f(x)] and w(x) = g[g(x)]. Find each derivative at x = 1, if it exists i.e. find u'(1), v'(1) and w'(1). if it doesn’t exist then explain why?
Solution:

Question 2.
The values of f(x), g(x), f'(x) and g'(x) are given in the following table:

Match the following:

Solution:

Question 3.
Suppose that the functions f and g and their derivatives with respect to x have the following values at x = 0 and x = 1.

(i) The derivative of f[g(x)] w.r.t. x at x = 0 is _______
(ii) The derivative of g[f(x)] w.r.t. x at x = 0 is _______
(iii) The value of \(\left[\frac{d}{d x}\left[x^{10}+f(x)\right]^{-2}\right]_{x=1}\) is _______
(iv) The derivative of f[(x+g(x))] w.r.t. x at x = 0 is _______
Solution:

Question 4.
Differentiate the following w.r.t. x:
(i) \(\sin \left[2 \tan ^{-1}\left(\sqrt{\frac{1-x}{1+x}}\right)\right]\)
Solution:
Let y = \(\sin \left[2 \tan ^{-1}\left(\sqrt{\frac{1-x}{1+x}}\right)\right]\)
Put x = cos θ, Then θ = cos^-1 x and

(ii) \(\sin ^{2}\left[\cot ^{-1}\left(\sqrt{\frac{1+x}{1-x}}\right)\right]\)
Solution:
Let y = \(\sin ^{2}\left[\cot ^{-1}\left(\sqrt{\frac{1+x}{1-x}}\right)\right]\)
Put x = cos θ. Then θ = cos^-1 x and

(iii) \(\tan ^{-1}\left[\frac{\sqrt{x}(3-x)}{1-3 x}\right]\)
Solution:

(iv) \(\cos ^{-1}\left(\frac{\sqrt{1+x}-\sqrt{1-x}}{2}\right)\)
Solution:
Let y = \(\cos ^{-1}\left(\frac{\sqrt{1+x}-\sqrt{1-x}}{2}\right)\)
Put x = cos θ. Then θ = cos^-1 x and

(v) \(\tan ^{-1}\left(\frac{x}{1+6 x^{2}}\right)+\cot ^{-1}\left(\frac{1-10 x^{2}}{7 x}\right)\)
Solution:

(vi) \(\tan ^{-1}\left[\sqrt{\frac{\sqrt{1+x^{2}+x}}{\sqrt{1+x^{2}}-x}}\right]\)
Solution:

Question 5.
(i) If \(\sqrt{y+x}+\sqrt{y-x}=c\), show that \(\frac{d y}{d x}=\frac{y}{x}-\sqrt{\frac{y^{2}}{x^{2}}-1}\)
Solution:
\(\sqrt{y+x}+\sqrt{y-x}=c\)
Differentiating both sides w.r.t. x, we get

(ii) If \(x \sqrt{1-y^{2}}+y \sqrt{1-x^{2}}=1\), then show that \(\frac{d y}{d x}=-\sqrt{\frac{1-y^{2}}{1-x^{2}}}\)
Solution:
\(x \sqrt{1-y^{2}}+y \sqrt{1-x^{2}}=1\)
\(y \sqrt{1-x^{2}}+x \sqrt{1-y^{2}}=1\)
Differentiating both sides w.r.t. x, we get

(iii) If x sin(a + y) + sin a cos(a + y) = 0, then show \(\frac{d y}{d x}=\frac{\sin ^{2}(a+y)}{\sin a}\)
Solution:
x sin(a + y) + sin a . cos (a + y) = 0 ….. (1)
Differentiating w.r.t. x, we get

(iv) If sin y = x sin(a + y), then show that \(\frac{d y}{d x}=\frac{\sin ^{2}(a+y)}{\sin a}\)
Solution:

(v) If x = \(e^{\frac{x}{y}}\), then show that \(\frac{d y}{d x}=\frac{x-y}{x \log x}\)
Solution:
x = \(e^{\frac{x}{y}}\)
\(\frac{x}{y}\) = log x …..(1)
y = \(\frac{x}{\log x}\)

(vi) If y = f(x) is a differentiable function of x, then show that \(\frac{d^{2} x}{d y^{2}}=-\left(\frac{d y}{d x}\right)^{-3} \cdot \frac{d^{2} y}{d x^{2}}\)
Solution:
If y = f(x) is a differentiable function of x such that inverse function x = f^-1(y) exists,

Question 6.
(i) Differentiate \(\tan ^{-1}\left(\frac{\sqrt{1+x^{2}}-1}{x}\right)\) w.r.t. \(\tan ^{-1}\left(\frac{2 x \sqrt{1-x^{2}}}{1-2 x^{2}}\right)\)
Solution:

(ii) Differentiate \(\log \left[\frac{\sqrt{1+x^{2}}+x}{\sqrt{1+x^{2}}-x}\right]\) w.r.t. cos(log x)
Solution:

(iii) Differentiate \(\tan ^{-1}\left(\frac{\sqrt{1+x^{2}}-1}{x}\right)\) w.r.t. \(\cos ^{-1}\left(\sqrt{\frac{1+\sqrt{1+x^{2}}}{2 \sqrt{1+x^{2}}}}\right)\)
Solution:

Question 7.
(i) If y² = a² cos²x + b² sin²x, show that \(y+\frac{d^{2} y}{d x^{2}}=\frac{a^{2} b^{2}}{y^{3}}\)
Solution:
y² = a² cos²x + b² sin²x …… (1)
Differentiating both sides w.r.t. x, we get

(ii) If log y = log(sin x) – x², show that \(\frac{d^{2} y}{d x^{2}}+4 x \frac{d y}{d x}+\left(4 x^{2}+3\right) y=0\)
Solution:

(iii) If x = a cos θ, y = b sin θ, show that \(a^{2}\left[y \frac{d^{2} y}{d x^{2}}+\left(\frac{d y}{d x}\right)^{2}\right]+b^{2}=0\)
Solution:
x = a cos θ, y = b sin θ
Differentiating x and y w.r.t. θ, we get

(iv) If y = A cos(log x) + B sin(log x), show that x²y₂ + xy₁ + y = o.
Solution:
y = A cos (log x) + B sin (log x) …… (1)
Differentiating both sides w.r.t. x, we get

(v) If y = A e^mx + B e^nx, show that y₂ – (m + n) y₁ + (mn) y = 0.
Solution:
y = A e^mx + B e^nx
Differentiating w.r.t. x, we get

Balbharti 12th Maharashtra State Board Maths Solutions Book Pdf Chapter 7 Linear Programming Ex 7.4 Questions and Answers.

Maharashtra State Board 12th Maths Solutions Chapter 7 Linear Programming Ex 7.4

Question 1.
Maximize : z = 11x + 8y subject to x ≤ 4, y ≤ 6,
x + y ≤ 6, x ≥ 0, y ≥ 0.
Solution:
First we draw the lines AB, CD and ED whose equations are x = 4, y = 6 and x + y = 6 respectively.


The feasible region is shaded portion OAPDO in the graph.
The vertices of the feasible region are O (0, 0), A (4, 0), P and D (0, 6)
P is point of intersection of lines x + y = 6 and x = 4.
Substituting x = 4 in x + y = 6, we get
4 + y = 6 ∴ y = 2 ∴ P is (4, 2).
∴ the corner points of feasible region are O (0, 0), A (4, 0), P(4, 2) and D(0 ,6).
The values of the objective function z = 11x + 8y at these vertices are
z (O) = 11(0) + 8(0) = 0 + 0 = 0
z(a) = 11(4) + 8(0) = 44 + 0 = 44
z (P) = 11(4) + 8(2) = 44 + 16 = 60
z (D) = 11(0) + 8(2) = 0 + 16 = 16
∴ z has maximum value 60, when x = 4 and y = 2.

Question 2.
Maximize : z = 4x + 6y subject to 3x + 2y ≤ 12,
x + y ≥ 4, x, y ≥ 0.
Solution:
First we draw the lines AB and AC whose equations are 3x + 2y = 12 and x + y = 4 respectively.


The feasible region is the ∆ABC which is shaded in the graph.
The vertices of the feasible region (i.e. corner points) are A (4, 0), B (0, 6) and C (0, 4).
The values of the objective function z = 4x + 6y at these vertices are
z(a) = 4(4) + 6(0) = 16 + 0 = 16
z(B) = 4(0)+ 6(6) = 0 + 36 = 36
z(C) = 4(0) + 6(4) = 0 + 24 = 24
∴ has maximum value 36, when x = 0, y = 6.

Question 3.
Maximize : z = 7x + 11y subject to 3x + 5y ≤ 26
5x + 3y ≤ 30, x ≥ 0, y ≥ 0.
Solution:
First we draw the lines AB and CD whose equations are 3x + 5y = 26 and 5x + 3y = 30 respectively.


The feasible region is OCPBO which is shaded in the graph.
The vertices of the feasible region are O (0, 0), C (6, 0), p and B(0, \(\frac{26}{5}\))
The vertex P is the point of intersection of the lines
3x + 5y = 26 … (1)
and 5x + 3y = 30 … (2)
Multiplying equation (1) by 3 and equation (2) by 5, we get
9x + 15y = 78
and 25x + 15y = 150
On subtracting, we get
16x = 72 ∴ x = \(\frac{72}{16}=\frac{9}{2}\) = 4.5
Substituting x = 4.5 in equation (2), we get
5(4.5) + 3y = 30
22.5 + 3y = 30
∴ 3y = 7.5 ∴ y = 2.5
∴ P is (4.5, 2.5)
The values of the objective function z = 7x + 11y at these corner points are
z (O) = 7(0) + 11(0) = 0 + 0 = 0
z (C) = 7(6) + 11(0) = 42 + 0 = 42
z (P) = 7(4.5) + 11 (2.5) = 31.5 + 27.5 = 59.0 = 59
z(B) = 7(0) + 11\(\left(\frac{26}{5}\right)=\frac{286}{5}\) = 57.2
∴ z has maximum value 59, when x = 4.5 and y = 2.5.

Question 4.
Maximize : z = 10x + 25y subject to 0 ≤ x ≤ 3,
0 ≤ y ≤ 3, x + y ≤ 5 also find maximum value of z.
Solution:
First we draw the lines AB, CD and EF whose equations are x = 3, y = 3 and x + y = 5 respectively.


The feasible region is OAPQDO which is shaded in the i graph.
The vertices of the feasible region are O (0, 0), A (3, 0), P, Q and D(0, 3).
t P is the point of intersection of the lines x + y = 5 and x = 3.
Substituting x = 3 in x + y = 5, we get
3 + y = 5 ∴ y = 2
∴ P is (3, 2)
Q is the point of intersection of the lines x + y = 5 and y = 3
Substituting y = 3 in x + y = 5, we get
x + 3 = 5 ∴ x = 2
∴ Q is (2, 3)
The values of the objective function z = 10x + 25y at these vertices are
z(O) = 10(0) + 25(0) = 0 + 0 = 0
z(a) = 10(3) + 25(0) = 30 + 0 = 30
z(P) = 10(3) + 25(2) = 30 + 50 = 80
z(Q) = 10(2) + 25(3) = 20 + 75 = 95
z(D) = 10(0)+ 25(3) = 0 + 75 = 75
∴ z has maximum value 95, when x = 2 and y = 3.

Question 5.
Maximize : z = 3x + 5y subject to x + 4y ≤ 24, 3x + y ≤ 21,
x + y ≤ 9, x ≥ 0, y ≥ 0 also find maximum value of z.
Solution:
First we draw the lines AB, CD and EF whose equations are x + 4y = 24, 3x + y = 21 and x + y = 9 respectively.


The feasible region is OCPQBO which is shaded in the graph.
The vertices of the feasible region are O (0, 0), C (7, 0), P, Q and B (0, 6).
P is the point of intersection of the lines
3x + y = 21 … (1)
and x + y = 9 … (2)
On subtracting, we get 2x = 12 ∴ x = 6
Substituting x = 6 in equation (2), we get
6 + y = 9 ∴ y = 3
∴ P = (6, 3)
Q is the point of intersection of the lines
x + 4y = 24 … (3)
and x + y = 9 … (2)
On subtracting, we get
3y = 15 ∴ y = 5
Substituting y = 5 in equation (2), we get
x + 5= 9 ∴ x = 4
∴ Q = (4, 5)
∴ the corner points of the feasible region are 0(0,0), C(7, 0), P (6, 3), Q (4, 5) and B (0, 6).
The values of the objective function 2 = 3x + 5y at these corner points are
z(O) = 3(0)+ 5(0) = 0 + 0 = 0
z(C) = 3(7) + 5(0) = 21 + 0 = 21
z(P) = 3(6) + 5(3) = 18 + 15 = 33
z(Q) = 3(4) + 5(5) = 12 + 25 = 37
z(B) = 3(0)+ 5(6) = 0 + 30 = 30
∴ z has maximum value 37, when x = 4 and y = 5.

Question 6.
Minimize : z = 7x + y subject to 5x + y ≥ 5, x + y ≥ 3,
x ≥ 0, y ≥ 0.
Solution:
First we draw the lines AB and CD whose equations are 5x + y = 5 and x + y = 3 respectively.


The feasible region is XCPBY which is shaded in the graph.
The vertices of the feasible region are C (3, 0), P and B (0, 5).
P is the point of the intersection of the lines
5x + y = 5
and x + y = 3
On subtracting, we get
4x = 2 ∴ x = \(\frac{1}{2}\)
Substituting x = \(\frac{1}{2}\) in x + y = 3, we get
\(\frac{1}{2}\) + y = 3
∴ y = \(\frac{5}{2}\) ∴ P = \(\left(\frac{1}{2}, \frac{5}{2}\right)\)
The values of the objective function z = 7x + y at these vertices are
z(C) = 7(3) + 0 = 21
z(B) = 7(0) + 5 = 5
∴ z has minimum value 5, when x = 0 and y = 5.

Question 7.
Minimize : z = 8x + 10y subject to 2x + y ≥ 7, 2x + 3y ≥ 15,
y ≥ 2, x ≥ 0, y ≥ 0.
Solution:
First we draw the lines AB, CD and EF whose equations are 2x + y = 7, 2x + 3y = 15 and y = 2 respectively.


The feasible region is EPQBY which is shaded in the graph. The vertices of the feasible region are P, Q and B(0,7). P is the point of intersection of the lines 2x + 3y = 15 and y = 2.
Substituting y – 2 in 2x + 3y = 15, we get 2x + 3(2) = 15
∴ 2x = 9 ∴ x = 4.5 ∴ P = (4.5, 2)
Q is the point of intersection of the lines
2x + 3y = 15 … (1)
and 2x + y = 7 … (2)
On subtracting, we get
2y = 8 ∴ y = 4
∴ from (2), 2x + 4 = 7
∴ 2x = 3 ∴ x = 1.5
∴ Q = (1.5, 4)
The values of the objective function z = 8x + 10y at these vertices are
z(P) = 8(4.5) + 10(2) = 36 + 20 = 56
z(Q) = 8(1.5) + 10(4) = 12 + 40 = 52
z(B) = 8(0) +10(7) = 70
∴ z has minimum value 52, when x = 1.5 and y = 4

Question 8.
Minimize : z = 6x + 21y subject to x + 2y ≥ 3, x + 4y ≥ 4,
3x + y ≥ 3, x ≥ 0, y ≥ 0.
Solution:
First we draw the lines AB, CD and EF whose equations are x + 2y = 3, x + 4y = 4 and 3x + y = 3 respectively.


The feasible region is XCPQFY which is shaded in the graph.
The vertices of the feasible region are C (4, 0), P, Q and F(0, 3).
P is the point of intersection of the lines x + 4y = 4 and x + 2y = 3
On subtracting, we get
2y = 1 ∴ y = \(\frac{1}{2}\)
Substituting y = \(\frac{1}{2}\) in x + 2y = 3, we get
x + 2\(\left(\frac{1}{2}\right)\) = 3
∴ x = 2
∴ P = (2, \(\frac{1}{2}\))
Q is the point of intersection of the lines
x + 2y = 3 … (1)
and 3x + y = 3 ….(2)
Multiplying equation (1) by 3, we get 3x + 6y = 9
Subtracting equation (2) from this equation, we get
5y = 6
∴ y = \(\frac{6}{5}\)
∴ from (1), x + 2\(\left(\frac{6}{5}\right)\) = 3
∴ x = 3 – \(\frac{12}{5}=\frac{3}{5}\)
Q ≡ \(\left(\frac{3}{5}, \frac{6}{5}\right)\)
The values of the objective function z = 6x + 21y at these vertices are
z(C) = 6(4) + 21(0) = 24
z(P) = 6(2) + 21\(\left(\frac{1}{2}\right)\)
= 12 + 10.5 = 22.5
z(Q)= 6\(\left(\frac{3}{5}\right)\) + 21\(\left(\frac{6}{5}\right)\)
= \(\frac{18}{5}+\frac{126}{5}=\frac{144}{5}\) = 28.8
2 (F) = 6(0) + 21(3) = 63
∴ z has minimum value 22.5, when x = 2 and y = \(\frac{1}{2}\).

Balbharti 12th Maharashtra State Board Maths Solutions Book Pdf Chapter 7 Linear Programming Ex 7.3 Questions and Answers.

Maharashtra State Board 12th Maths Solutions Chapter 7 Linear Programming Ex 7.3

Question 1.
A manufacturing firm produces two types of gadgets A and B, which are first processed in the foundry and then sent to the machine shop for finishing. The number of man-hours of labour required in each shop for production of A and B per unit and the number of man-hours available for the firm are as follows :

Profit on the sale of A is ₹ 30 and B is ₹ 20 per units. Formulate the L.P.P. to have maximum profit.
Solution:
Let the number of gadgets A produced by the firm be x and the number of gadgets B produced by the firm be y.
The profit on the sale of A is ₹ 30 per unit and on the sale of B is ₹ 20 per unit.
∴ total profit is z = 30x + 20y.
This is a linear function which is to be maximized. Hence it is the objective function.
The constraints are as per the following table :

From the table total man hours of labour required for x units of gadget A and y units of gadget B in foundry is (10x + 6y) hours and total man hours of labour required in machine shop is (5x + 4y) hours.
Since, maximum time avilable in foundry and machine shops are 60 hours and 35 hours respectively.
Therefore, the constraints are 10x + 6y ≤ 60, 5x + 4y ≤ 35. Since, x and y cannot be negative, we have x ≥ 0, y ≥ 0. Hence, the given LPP can be formulated as :
Maximize z = 30x + 20y, subject to 10x + 6y ≤ 60, 5x + 4y ≤ 35, x ≥ 0, y ≥ 0.

Question 2.
In a cattle breading firm, it is prescribed that the food ration for one animal must contain 14, 22 and 1 units of nutrients A, B and C respectively. Two different kinds of fodder are available. Each unit of these two contains the following amounts of these three nutrients :

The cost of fodder 1 is ₹3 per unit and that of fodder ₹ 2, Formulate the L.P.P. to minimize the cost.
Solution:
Let x units of fodder 1 and y units of fodder 2 be prescribed.
The cost of fodder 1 is ₹ 3 per unit and cost of fodder 2 is ₹ 2 per unit.
∴ total cost is z = 3x + 2y
This is the linear function which is to be minimized. Hence it is the objective function. The constraints are as per the following table :

From table fodder contains (2x + y) units of nutrients A, (2x + 3y) units of nutrients B and (x + y) units of nutrients C. The minimum requirements of these nutrients are 14 units, 22 units and 1 unit respectively.
Therefore, the constraints are
2x + y ≥ 14, 2x + 3y ≥ 22, x + y ≥ 1
Since, number of units (i.e. x and y) cannot be negative, we have, x ≥ 0, y ≥ 0.
Hence, the given LPP can be formulated as
Minimize z = 3x + 2y, subject to
2x + y ≥ 14, 2x + 3y ≥ 22, x + y ≥ 1, x ≥ 0, y ≥ 0.

Question 3.
A company manufactures two types of chemicals A and B. Each chemical requires two types of raw material P and Q. The table below shows number of units of P and Q required to manufacture one unit of A and one unit of B and the total availability of P and Q.

The company gets profits of ₹350 and ₹400 by selling one unit of A and one unit of B respectively. (Assume that the entire production of A and B can be sold). How many units of the chemicals A and B should be manufactured so that the company get maximum profit? Formulate the problem as L.P.P. to maximize the profit.
Solution:
Let the company manufactures x units of chemical A and y units of chemical B. Then the total profit f to the company is p = ₹ (350x + 400y).
This is a linear function which is to be maximized.
Hence, it is the objective function.
The constraints are as per the following table:

The raw material P required for x units of chemical A and y units of chemical B is 3x + 2y. Since, the maximum availability of P is 120, we have the first constraint as 3x + 2y ≤ 120.
Similarly, considering the raw material Q, we have : 2x + 5y ≤ 160.
Since, x and y cannot be negative, we have, x ≥ 0, y ≥ 0.
Hence, the given LPP can be formulated as :
Maximize p = 350x + 400y, subject to
3x + 2y ≤ 120, 2x + 5y ≤ 160, x ≥ 0, y ≥ 0.

Question 4.
A printing company prints two types of magazines A and B. The company earns ₹ 10 and ₹ 15 on magazines A and B per copy. These are processed on three machines I, II, III. Magazine A requires 2 hours on Machine I, 5 hours on Machine II and 2 hours on Machine III. Magazine B requires 3 hours on Machine I, 2 hours on Machine II and 6 hours on Machine III. Machines I, II, III are available for 36, 50, 60 hours per week respectively. Formulate the L.P.P. to determine weekly production of A and B, so that the total profit is maximum.
Solution:
Let the company prints x magazine of type A and y magazine of type B.
Profit on sale of magazine A is ₹ 10 per copy and magazine B is ₹ 15 per copy.
Therefore, the total earning z of the company is
z = ₹ (10x + 15y).
This is a linear function which is to be maximized.
Hence, it is the objective function.
The constraints are as per the following table:

From the table, the total time required for Machine I is (2x + 3y) hours, for Machine II is (5x + 2y) hours and for Machine III is (2x + 6y) hours. The machines I, II, III are available for 36,50 and 60 hours per week. Therefore, the constraints are 2x + 3y ≤ 36, 5x + 2y ≤ 50, 2x + 6y ≤ 60.
Since x and y cannot be negative. We have, x ≥ 0, y ≥ 0. Hence, the given LPP can be formulated as :
Maximize z = 10x + 15y, subject to
2x + 3y ≤ 36, 5x + 2y ≤ 50, 2x + 6y ≤ 60, x ≥ 0, y ≥ 0.

Question 5.
A manufacture produces bulbs and tubes. Each of these must be processed through two machines M₁ and M₂. A package of bulbs require 1 hour of work on Machine M₁ and 3 hours of work on M₂. A package of tubes require 2 hours on Machine M₁ and 4 hours on Machine M₂. He earns a profit of ₹ 13.5 per package of bulbs and ₹ 55 per package of tubes. Formulate the LLP to maximize the profit, if he operates the machine M₁, for atmost 10 hours a day and machine M₂ for atmost 12 hours a day.
Solution:
Let the number of packages of bulbs produced by manufacturer be x and packages of tubes be y. The manufacturer earns a profit of ₹ 13.5 per package of bulbs and ₹ 55 per package of tubes.
Therefore, his total profit is p = ₹ (13.5x + 55y)
This is a linear function which is to be maximized.
Hence, it is the objective function.
The constraints are as per the following table :

From the table, the total time required for Machine M₁ is (x + 2y) hours and for Machine M₂ is (3x + 4y) hours.
Given Machine M₁ and M₂ are available for atmost 10 hours and 12 hours a day respectively.
Therefore, the constraints are x + 2y ≤ 10, 3x + 4y ≤ 12. Since, x and y cannot be negative, we have, x ≥ 0, y ≥ 0. Hence, the given LPP can be formulated as :
Maximize p = 13.5x + 55y, subject to x + 2y ≤ 10, 3x + 4y ≤ 12, x ≥ 0, y ≥ 0.

Question 6.
A company manufactures two types of fertilizers F₁ and F₂. Each type of fertilizer requires
two raw materials A and B. The number of units of A and B required to manufacture one unit of fertilizer F₁ and F₂ and availability of the raw materials A and B per day are given in the
table below :

By selling one unit of F₁ and one unit of F₂, company gets a profit of ₹ 500 and ₹ 750
respectively. Formulate the problem as L.P.P. to maximize the profit.
Solution:
Let the company manufactures x units of fertilizers F₁ and y units of fertilizers F₁. Then the total profit to the company is
z = ₹(500x + 750y).
This is a linear function that is to be maximized. Hence, it is an objective function.

The raw material A required for x units of Fertilizers F₁ and y units of Fertilizers F₂ is 2x + Since the maximum availability of A is 40, we have the first constraint as 2x + 3y ≤ 40.
Similarly, considering the raw material B, we have x + 4y ≤ 70.
Since, x and y cannot be negative, we have, x ≥ 0, y ≥ 0.
Hence, the given LPP can be formulated as:
Maximize z = 500x + 750y, subject to
2x + 3y ≤ 40, x + 4y ≤ 70, x ≥ 0, y ≥ 0.

Question 7.
A doctor has prescribed two different units of foods A and B to form a weekly diet for a sick person. The minimum requirements of fats, carbohydrates and proteins are 18, 28, 14 units respectively. One unit of food A has 4 units of fats. 14 units of carbohydrates and 8 units of protein. One unit of food B has 6 units of fat, 12 units of carbohydrates and 8 units of protein. The price of food A is ₹ 4.5 per unit and that of food B is ₹ 3.5 per unit. Form the L.P.P. so that the sick person’s diet meets the requirements at a minimum cost.
Solution:
Let the diet of sick person include x units of food A and y units of food B.
Then x ≥ 0, y ≥ 0.
The prices of food A and B are ₹ 4.5 and ₹ 3.5 per unit respectively.
Therefore, the total cost is z = ₹ (4.5x + 3.5y)
This is the linear function which is to be minimized.
Hence, it is objective function.
The constraints are as per the following table :

From the table, the sick person’s diet will include (4x + 6y) units of fats, (14x + 12y) units of carbohydrates and (8x + 8y) units of proteins. The minimum requirements of these ingredients are 18 units, 28 units and 14 units respectively.
Therefore, the constraints are
4x + 6y ≥ 18, 14x + 12y ≥ 28, 8x + 8y ≥ 14.
Hence, the given LPP can be formulated as
Minimize z = 4.5x + 3.5y, subject to
4x + 6y ≥ 18, 14x + 12y ≥ 28, 8x + 8y ≥ 14, x ≥ 0, y ≥ 0.

Question 8.
If John drives a car at a speed of 60 kms/hour he has to spend ₹ 5 per km on petrol. If he drives at a faster speed of 90 kms/hour, the cost of petrol increases to ₹ 8 per km. He has ₹ 600 to spend on petrol and wishes to travel the maximum distance within an hour. Formulate the above problem as L.P.P.
Solution:
Let John travel xl km at a speed of 60 km/ hour and x₁ km at a speed of 90 km/hour.
Therefore, time required to travel a distance of x₁ km is \(\frac{x_{1}}{60}\) hours and the time required to travel a distance of
x₂ km is \(\frac{x_{2}}{90}\) hours.
∴ total time required to travel is \(\left(\frac{x_{1}}{60}+\frac{x_{2}}{90}\right)\) hours.
Since he wishes to travel the maximum distance within an hour,
\(\frac{x_{1}}{60}+\frac{x_{2}}{90}\) ≤ 1
He has to spend ₹ 5 per km on petrol at a speed of 60 km/hour and ₹ 8 per km at a speed of 90 km/hour.
∴ the total cost of travelling is ₹ (5x₁ + 8x₂)
Since he has ₹ 600 to spend on petrol,
5x₁ + 8x₂ ≤ 600
Since distance is never negative, x₁ ≥ 0, x₂ ≥ 0.
Total distance travelled by John is z. = (x₁ + x₂) km.
This is the linear function which is to be maximized.
Hence, it is objective function.
Hence, the given LPP can be formulated as :
Maximize z = x₁ + x₂, subject to
\(\frac{x_{1}}{60}+\frac{x_{2}}{90}\) ≤ 1, 5x₁ + 8x₂ ≤ 600, x₁ ≥ 0, x₂ ≥ 0.

Question 9.
The company makes concrete bricks made up of cement and sand. The weight of a concrete brick has to be least 5 kg. Cement costs ₹ 20 per kg. and sand costs of ₹ 6 per kg. strength consideration dictate that a concrete brick should contain minimum 4 kg. of cement and not more than 2 kg. of sand. Form the L.P.P. for the cost to be minimum.
Solution:
Let the company use x₁ kg of cement and x₂ kg of sand to make concrete bricks.
Cement costs ₹ 20 per kg and sand costs ₹ 6 per kg.
∴ the total cost c = ₹ (20x₁ + 6x₂)
This is a linear function which is to be minimized.
Hence, it is the objective function.
Total weight of brick = (x₁ + x₂) kg
Since the weight of concrete brick has to be at least 5 kg,
∴ x₁ + x₂ ≥ 5.
Since concrete brick should contain minimum 4 kg of cement and not more than 2 kg of sand,
x₁ ≥ 4 and 0 ≤ x₂ ≤ 2
Hence, the given LPP can be formulated as :
Minimize c = 20x₁ + 6x₂, subject to
x₁ + x₂ ≥ 5, x₁ ≥ 4, 0 ≤ x₂ ≤ 2.

Balbharti 12th Maharashtra State Board Maths Solutions Book Pdf Chapter 7 Linear Programming Ex 7.2 Questions and Answers.

Maharashtra State Board 12th Maths Solutions Chapter 7 Linear Programming Ex 7.2

I) Find the feasible solution of the following inequations graphically.
Question 1.
3x + 2y ≤ 18, 2x + y ≤ 10, x ≥ 0, y ≥ 0
Solution:
First we draw the lines AB and CD whose equations are 3x + 2y = 18 and 2x + y = 10 respectively.


The feasible solution is OCPBO which is shaded in the graph.

Question 2.
2x + 3y ≤ 6, x + y ≥ 2, x ≥ 0, y ≥ 0
Solution:
First we draw the lines AB and CB whose equations are 2x + 3y = 6 and x + y = 2 respectively.


The feasible solution is ∆ABC which is shaded in the graph.

Question 3.
3x + 4y ≥ 12, 4x + 7y ≤ 28, y ≥ 1, x ≥ 0
Solution:
First we draw the lines AB, CD and EF whose equations are 3x + 4 y = 12, 4x + 7y = 28 and y = 1 respectively.


The feasible solution is PQDBP. which is shaded in the graph.

Question 4.
x + 4y ≤ 24, 3x + y ≤ 21, x + y ≤ 9, x ≥ 0, y ≥ 0.
Solution:
First we draw the lines AB, CD and EF whose equations are x + 4y = 24, 3x + y = 21 and x + y = 9 respectively.


The feasible solution is OCPQBO. which is shaded in the graph.

Question 5.
0 ≤ x ≤ 3, 0 ≤ y ≤ 3, x + y ≤ 5, 2x + y ≥ 4
Solution:
First we draw the lines AB, CD, EF and GH whose equations are x + y = 5, 2x + y = 4, x = 3 and y = 3 respectively.


The feasible solution is CEPQRC. which is shaded in the graph.

Question 6.
x – 2y ≤ 2, x + y ≥ 3, -2x + y ≤ 4, x ≥ 0, y ≥ 0
Solution:
First we draw the lines AB, CD and EF whose equations are x – 2y = 2, x + y = 3 and -2x + y = 4 respectively.


The feasible solution is shaded in the graph.

Question 7.
A company produces two types of articles A and B which requires silver and gold. Each unit of A requires 3 gm of silver and 1 gm of gold, while each unit of B requires 2 gm of silver and 2 gm of gold. The company has 6 gm of silver and 4 gm of gold. Construct the inequations and find the feasible solution graphically.
Solution:
Let the company produces x units of article A and y units of article B.
The given data can be tabulated as:

Inequations are :
x + 2y ≤ 4 and 3x + 2y ≤ 6
x and y are number of items, x ≥ 0, y ≥ 0
First we draw the lines AB and CD whose equations are x + 2y = 4 and 3x + 2y = 6 respectively.


The feasible solution is OCPBO. which is shaded in the graph.

Question 8.
A furniture dealer deals in tables and chairs. He has Rs.1,50,000 to invest and a space to store at most 60 pieces. A table costs him Rs.1500 and a chair Rs.750. Construct the inequations and find the feasible solution.
Question is modified
A furniture dealer deals in tables and chairs. He has ₹ 15,000 to invest and a space to store at most 60 pieces. A table costs him ₹ 150 and a chair ₹ 750. Construct the inequations and find the feasible solution.
Solution:
Let x be the number of tables and y be the number of chairs. Then x ≥ 0, y ≥ 0.
The dealer has a space to store at most 60 pieces.
∴ x + y ≤ 60
Since, the cost of each table is ₹ 150 and that of each chair is ₹ 750, the total cost of x tables and y chairs is 150x + 750y. Since the dealer has ₹ 15,000 to invest, 150x + 750y ≤ 15,000
Hence the system of inequations are
x + y ≤ 60, 150x + 750y ≤ 15000, x ≥ 0, y ≥ 0.
First we draw the lines AB and CD whose equations are x + y = 60 and 150x + 750y = 15,000 respectively.


The feasible solution is OAPDO. which is shaded in the graph.

Balbharti 12th Maharashtra State Board Maths Solutions Book Pdf Chapter 7 Linear Programming Ex 7.1 Questions and Answers.

Maharashtra State Board 12th Maths Solutions Chapter 7 Linear Programming Ex 7.1

Question 1.
Solve graphically :
(i) x ≥ 0
Solution:
Consider the line whose equation is x = 0. This represents the Y-axis.
To find the solution set, we have to check any point other than origin.
Let us check the point (1, 1)
When x = 1, x ≥ 0
∴ (1, 1) lies in the required region
Therefore, the solution set is the Y-axis and the right
side of the Y-axis which is shaded in the graph.

(ii) x ≤ 0
Solution:
Consider the line whose equation is x = 0.
This represents the Y-axis.
To find the solution set, we have to check any point other than origin.
Let us check the point (1, 1).
When x = 1, x ≰ 0
∴ (1, 1) does not lie in the required region.
Therefore, the solution set is the Y-axis and the left side of the Y-axis which is shaded in the graph.

(iii) y ≥ 0
Solution:
Consider the line whose equation is y = 0. This represents the X-axis. To find the solution set, we have to check any point other than origin. Let us check the point (1, 1).
When y = 1, y ≥ 0
∴ (1, 1) lies in the required region.
Therefore, the solution set is the X-axis and above the X-axis which is shaded in the graph.

(iv) y ≤ 0
Solution:
(iv) Consider the line whose equation is y = 0. This represents the X-axis.
To find the solution set, we have to check any point other than origin.
Let us check the point (1, 1).
When y = 1, y ≰ 0.
∴ (1, 1) does not lie in the required region.
Therefore, the solution set is the X-axis and below the X-axis which is shaded in the graph.

Question 2.
Solve graphically :
(i) x ≥ 0 and y ≥ 0
Solution:
Consider the lines whose equations are x = 0, y = 0.
These represents the equations of Y-axis and X-axis respectively, which divide the plane into four parts.
(i) Since x ≥ 0, y ≥ 0, the solution set is in the first quadrant which is shaded in the graph.

(ii) x ≤ 0 and y ≥ 0
Solution:
Since x ≤ 0, y ≥ 0, the solution set is in the second quadrant which is shaded in the graph.

(iii) x ≤ 0 and y ≤ 0
Solution:
Since x ≤ 0, y ≤ 0, the solution set is in the third quadrant which is shaded in the graph.

(iv) x ≥ 0 and y ≤ 0
Solution:
Since x ≥ 0, y ≤ 0, the solution set is in the fourth ! quadrant which is shaded in the graph.

Question 3.
Solve graphically :
(i) 2x – 3 ≥ 0
Solution:
Consider the line whose equation is 2x – 3 = 0,
i.e. x = \(\frac{3}{2}\)
This represents a line parallel to Y-axis passing through the point (\(\frac{3}{2}\), 0)
Draw the line x =\(\frac{3}{2}\).
To find the solution set, we have to check the position of the origin (0, 0).
When x = 0, 2x – 3 = 2 × 0 – 3 = -3 ≱ 0
∴ the coordinates of the origin does not satisfy the given inequality.
∴ the solution set consists of the line x = \(\frac{3}{2}\) and the non-origin side of the line which is shaded in the graph.

(ii) 2y – 5 ≥ 0
Solution:
Consider the line whose equation is 2y – 5 = 0, i.e. y = \(\frac{5}{2}\)
This represents a line parallel to X-axis passing through the point (0, \(\frac{5}{2}\)).
Draw the line y = \(\frac{5}{2}\).
To find the solution set, we have to check the position of the origin (0, 0).
When y = 0, 2y – 5 = 2 × 0 – 5 = -5 ≱ 0
∴ the coordinates of the origin does not satisfy the given inequality.
∴ the solution set consists of the line y = \(\frac{5}{2}\) and the non-origin side of the line which is shaded in the graph.

(iii) 3x + 4 ≤ 0
Solution:
(iii) Consider the line whose equation is 3x + 4 = 0,
i.e. x = \(-\frac{4}{3}\)
This represents a line parallel to Y-axis passing through the point (\(-\frac{4}{3}\), 0).
Draw the line x = \(-\frac{4}{3}\).
To find the solution set, we have to check the position of the origin (0, 0).
When x = 0, 3x + 4 = 3 × 0 + 4= 4 ≰ 0
∴ the coordinates of the origin does not satisfy the given inequality.
∴ the solution set consists of the line x = \(-\frac{4}{3}\) and the non-origin side of the line which is shaded in the graph.

(iv) 5y + 3 ≤ 0
Solution:
(iv) Consider the line whose equation is 5y + 3 = 0,
i.e. y = \(\frac{-3}{5}\)
This represents a line parallel to X-axis passing through the point (0, \(\frac{-3}{5}\))
Draw the line y = \(\frac{-3}{5}\).
To find the solution set, we have to check the position of the origin (0, 0).
When y = 0, 5y + 3 = 5 × 0 + 3 = 3 ≰ 0
∴ the coordinates of the origin does not satisfy the given inequality.
∴ the solution set consists of the line y = \(\frac{-3}{5}\) and the non-origin side of the line which is shaded in the graph.

Question 4.
Solve graphically :
(i) x + 2y ≤ 6
Solution:
Consider the line whose equation is x + 2y = 6.
To find the points of intersection of this line with the coordinate axes.
Put y = 0, we get x = 6.
∴ A = (6, 0) is a point on the line.
Put x = 0, we get 2y = 6, i.e. y = 3
∴ B = (0, 3) is another point on the line.

Draw the line AB joining these points. This line divide the line into two parts.
1. Origin side 2. Non-origin side
To find the solution set, we have to check the position of the origin (0, 0) with respect to the line.
When x = 0, y = 0, then x + 2y = 0 which is less than 6.
∴ x + 2y ≤ 6 in this case.
Hence, origin lies in the required region. Therefore, the given inequality is the origin side which is
shaded in the graph.
This is the solution set of x + 2y ≤ 6.

(ii) 2x – 5y ≥ 10
Solution:
Consider the line whose equation is 2x – 5y = 10.
To find the points of intersection of this line with the coordinate axes.
Put y = 0, we get 2x = 10, i.e. x = 5.
∴ A = (5, 0) is a point on the line.
Put x = 0, we get -5y = 10, i.e. y = -2
∴ B = (0, -2) is another point on the line.

Draw the line AB joining these points. This line J divide the plane in two parts.
1. Origin side 2. Non-origin side
To find the solution set, we have to check the position of the origin (0, 0) with respect to the line. When x = 0, y = 0, then 2x – 5y = 0 which is neither greater nor equal to 10.
∴ 2x – 5y ≱ 10 in this case.
Hence (0, 0) will not lie in the required region.
Therefore, the given inequality is the non-origin side, which is shaded in the graph.
This is the solution set of 2x – 5y ≥ 10.

(iii) 3x + 2y ≥ 0
Solution:
Consider the line whose equation is 3x + 2y = 0.
The constant term is zero, therefore this line is passing through the origin.
∴ one point on the line is O ≡ (0, 0).
To find the another point, we can give any value of x and get the corresponding value of y.
Put x = 2, we get 6 + 2y = 0 i.e. y = – 3
∴ A = (2, -3) is another point on the line.
Draw the line OA.
To find the solution set, we cannot check (0, 0) as it is already on the line.
We can check any other point which is not on the line.
Let us check the point (1, 1)

When x = 1, y = 1, then 3x + 2y = 3 + 2 = 5 which is greater than zero.
∴ 3x + 2y > 0 in this case.
Hence (1, 1) lies in the required region. Therefore, the required region is the upper side which is shaded in the graph.
This is the solution set of 3x + 2y ≥ 0.

(iv) 5x – 3y ≤ 0
Solution:
Consider the line whose equation is 5x – 3y = 0. The constant term is zero, therefore this line is passing through the origin.
∴ one point on the line is the origin O = (0, 0).
To find the other point, we can give any value of x and get the corresponding value of y.
Put x = 3, we get 15 – 3y = 0, i.e. y = 5
∴ A ≡ (3, 5) is another point on the line.
Draw the line OA.
To find the solution set, we cannot check 0(0, 0), as it is already on the line. We can check any other point which is not on the line.
Let us check the point (1, -1).
When x = 1, y = -1 then 5x – 3y = 5 + 3 = 8
which is neither less nor equal to zero.
∴ 5x – 3y ≰ 0 in this case.
Hence (1, -1) will not lie in the required region. Therefore, the required region is the upper side which is shaded in the graph.

This is the solution set of 5x – 3y ≤ 0.

Question 5.
Solve graphically :
(i) 2x + y ≥ 2 and x – y ≤ 1
Solution:
First we draw the lines AB and AC whose equations are 2x + y = 2 and x – y = 1 respectively.


The solution set of the given system of inequalities is shaded in the graph.

(ii) x – y ≤ 2 and x + 2y ≤ 8
Solution:
First we draw the lines AB and CD whose equations are x – y = 2 and x + 2y = 8 respectively.


The solution set of the given system of inequalities is shaded in the graph.

(iii) x + y ≥ 6 and x + 2y ≤ 10
Solution:
First we draw the lines AB and CD whose equations are x + y = 6 and x + 2y = 10 respectively.


The solution set of the given system of inequalities is shaded in the graph.

(iv) 2x + 3y ≤ 6 and x + 4y ≥ 4
Solution:
First we draw the lines AB and CD whose equations are 2x + 3y = 6 and x + 4y = 4 respectively.

The solution set of the given system of inequalities is shaded in the graph.

(v) 2x + y ≥ 5 and x – y ≤ 1
Solution:
First we draw the lines AB and CD whose equations are 2x + y = 5 and x – y = 1 respectively.


The solution set of the given system of inequations is shaded in the graph.

Balbharti 12th Maharashtra State Board Maths Solutions Book Pdf Chapter 6 Line and Plane Miscellaneous Exercise 6B Questions and Answers.

Maharashtra State Board 12th Maths Solutions Chapter 6 Line and Plane Miscellaneous Exercise 6B

Question 1.
If the line \(\frac{x}{3}=\frac{y}{4}\) = z is perpendicular to the line \(\frac{x-1}{k}=\frac{y+2}{3}=\frac{z-3}{k-1}\) then the value of k is:

Solution:
(b) \(-\frac{11}{4}\)

Question 2.
The vector equation of line 2x – 1 = 3y + 2 = z – 2 is

Solution:
(a) \(\bar{r}=\left(\frac{1}{2} \hat{i}-\frac{2}{3} \hat{j}+2 \hat{k}\right)+\lambda(3 \hat{i}+2 \hat{j}+6 \hat{k})\)

Question 3.
The direction ratios of the line which is perpendicular to the two lines \(\frac{x-7}{2}=\frac{y+17}{-3}=\frac{z-6}{1}\) and \(\frac{x+5}{1}=\frac{y+3}{2}=\frac{z-6}{-2}\) are
(A) 4, 5, 7
(B) 4, -5, 7
(C) 4, -5, -7
(D) -4, 5, 8
Solution:
(A) 4, 5, 7

Question 4.
The length of the perpendicular from (1, 6, 3) to the line \(\frac{x}{1}=\frac{y-1}{2}=\frac{z-2}{3}\)
(A) 3
(B) \(\sqrt {11}\)
(C) \(\sqrt {13}\)
(D) 5
Solution:
(C ) \(\sqrt {13}\)

Question 5.
The shortest distance between the lines \(\bar{r}=(\hat{i}+2 \hat{j}+\hat{k})+\lambda(\hat{i}-\hat{j}-\hat{k})\) and \(\bar{r}=(2 \hat{i}-\hat{j}-\hat{k})+\mu(2 \hat{i}+\hat{j}+2 \hat{k})\) is
Question is modified.
The shortest distance between the lines \(\bar{r}=(\hat{i}+2 \hat{j}+\hat{k})+\lambda(\hat{i}-\hat{j}+\hat{k})\) and \(\bar{r}=(2 \hat{i}-\hat{j}-\hat{k})+\mu(2 \hat{i}+\hat{j}+2 \hat{k})\) is

Solution:
(c) \(\frac{3}{\sqrt{2}}\)

Question 6.
The lines \(\frac{x-2}{1}=\frac{y-3}{1}=\frac{z-4}{-k}\) and \(\frac{x-1}{k}=\frac{y-4}{2}=\frac{z-5}{1}\). and coplanar if
(A) k = 1 or -1
(B) k = 0 or -3
(C) k = + 3
(D) k = 0 or -1
Solution:
(B ) k = 0 or -3

Question 7.
The lines \(\frac{x}{1}=\frac{y}{2}=\frac{z}{3}\) and \(\frac{x-1}{-2}=\frac{y-2}{-4}=\frac{z-3}{6}\) and are
(A) perpendicular
(B) inrersecting
(C) skew
(D) coincident
Solution:
(B) inrersecting

Question 8.
Equation of X-axis is
(A) x = y = z
(B) y = z
(C) y = 0, z = 0
(D) x = 0, y = 0
Solution:
(C) y = 0, z = 0

Question 9.
The angle between the lines 2x = 3y = -z and 6x = -y = -4z is
(A ) 45º
(B ) 30º
(C ) 0º
(D ) 90º
Solution:
(D ) 90º

Question 10.
The direction ratios of the line 3x + 1 = 6y – 2 = 1 – z are
(A ) 2, 1, 6
(B ) 2, 1, -6
(C ) 2, -1, 6
(D ) -2, 1, 6
Solution:
(B ) 2, 1, -6

Question 11.
The perpendicular distance of the plane 2x + 3y – z = k from the origin is \(\sqrt {14}\) units, the value
of k is
(A ) 14
(B ) 196
(C ) \(2\sqrt {14}\)
(D ) \(\frac{\sqrt{14}}{2}\)
Solution:
(A ) 14

Question 12.
The angle between the planes and \(\bar{r} \cdot(\bar{i}-2 \bar{j}+3 \bar{k})+4=0\) and \(\bar{r} \cdot(2 \bar{i}+\bar{j}-3 \bar{k})+7=0\) is

Solution:
(d) cos^-1\(\left(\frac{9}{14}\right)\)

Question 13.
If the planes \(\bar{r} \cdot(2 \bar{i}-\lambda \bar{j}+\bar{k})=3\) and \(\bar{r} \cdot(4 \bar{i}-\bar{j}+\mu \bar{k})=5\) are parallel, then the values of λ and μ are respectively.

Solution:
(d) \(\frac{1}{2}\), 2

Question 14.
The equation of the plane passing through (2, -1, 3) and making equal intercepts on the coordinate axes is
(A ) x + y + z =1
(B ) x + y + z = 2
(C ) x + y + z = 3
(D ) x + y + z = 4
Solution:
(D ) x + y + z = 4

Question 15.
Measure of angle between the planes 5x – 2y + 3z – 7 = 0 and 15x – 6y + 9z + 5 = 0 is
(A ) 0º
(B ) 30º
(C ) 45º
(D ) 90º
Solution:
(A ) 0º

Question 16.
The direction cosines of the normal to the plane 2x – y + 2z = 3 are

Solution:
(a) \(\frac{2}{3}, \frac{-1}{3}, \frac{2}{3}\)

Question 17.
The equation of the plane passing through the points (1, -1, 1), (3, 2, 4) and parallel to Y-axis is :
(A ) 3x + 2z – 1 = 0
(B ) 3x – 2z = 1
(C ) 3x + 2z + 1 = 0
(D ) 3x + 2z = 2
Solution:
(B ) 3x – 2z = 1

Question 18.
The equation of the plane in which the line \(\frac{x-5}{4}=\frac{y-7}{4}=\frac{z+3}{-5}\) and \(\frac{x-8}{7}=\frac{y-4}{1}=\frac{z+5}{3}\) lie, is
(A ) 17x – 47y – 24z + 172 = 0
(B ) 17x + 47y – 24z + 172 = 0
(C ) 17x + 47y + 24z +172 = 0
(D ) 17x – 47y + 24z + 172 = 0
Solution:
(A ) 17x – 47y – 24z + 172 = 0

Question 19.
If the line \(\frac{x+1}{2}=\frac{y-m}{3}=\frac{z-4}{6}\) lies in the plane 3x – 14y + 6z + 49 = 0, then the value of m is:
(A ) 5
(B ) 3
(C ) 2
(D ) -5
Solution:
(A ) 5

Question 20.
The foot of perpendicular drawn from the point (0,0,0) to the plane is (4, -2, -5) then the equation of the plane is
(A ) 4x + y + 5z = 14
(B ) 4x – 2y – 5z = 45
(C ) x – 2y – 5z = 10
(D ) 4x + y + 6z = 11
Solution:
(B ) 4x – 2y – 5z = 45

II. Solve the following :
Question 1.
Find the vector equation of the plane which is at a distance of 5 unit from the origin and which is normal to the vector \(2 \hat{i}+\hat{j}+2 \hat{k}\)
Solution:
If \(\hat{n}\) is a unit vector along the normal and p i the length of the perpendicular from origin to the plane, then the vector equation of the plane \(\bar{r} \cdot \hat{n}\) = p
Here, \(\overline{\mathrm{n}}=2 \hat{\mathrm{i}}+\hat{\mathrm{j}}+2 \hat{\mathrm{k}}\) and p = 5

Question 2.
Find the perpendicular distance of the origin from the plane 6x + 2y + 3z – 7 = 0
Solution:
The distance of the point (x₁, y₁, z₁) from the plane ax + by + cz + d is \(\left|\frac{a x_{1}+b y_{1}+c z_{1}+d}{\sqrt{a^{2}+b^{2}+c^{2}}}\right|\)
∴ the distance of the point (1, 1, -1) from the plane 6x + 2y + 3z – 7 = 0 is

= 1units.

Question 3.
Find the coordinates of the foot of the perpendicular drawn from the origin to the plane 2x + 3y + 6z = 49.
Solution:
The equation of the plane is 2x + 3y + 6z = 49
Dividing each term by
\(\sqrt{2^{2}+3^{2}+(-6)^{2}}\)
= \(\sqrt{49}\)
= 7
we get
\(\frac{2}{7}\)x + \(\frac{3}{7}\)y – \(\frac{6}{7}\)z = \(\frac{49}{7}\) = 7
This is the normal form of the equation of plane.
∴ the direction cosines of the perpendicular drawn from the origin to the plane are
l = \(\frac{2}{7}\), m = \(\frac{3}{7}\), n = \(\frac{6}{7}\)
and length of perpendicular from origin to the plane is p = 7.
the coordinates of the foot of the perpendicular from the origin to the plane are
(lp, ∓, np)i.e.(2, 3, 6)

Question 4.
Reduce the equation \(\bar{r} \cdot(\hat{i}+8 \hat{j}+24 \hat{k})=13\) to normal form and hence find
(i) the length of the perpendicular from the origin to the plane
(ii) direction cosines of the normal.
Solution:
The normal form of equation of a plane is \(\bar{r} \cdot \hat{n}\) = p where \(\hat{n}\) is unit vector along the normal and p is the length of perpendicular drawn from origin to the plane.
Given pane is \(\text { r. }(6 \hat{\mathrm{i}}+8 \hat{\mathrm{j}}+24 \hat{\mathrm{k}})=13\) …(1)

This is the normal form of the equation of plane.
Comparing with \(\bar{r} \cdot \hat{n}\) = p,
(i) the length of the perpendicular from the origin to plane is \(\frac{1}{2}\).
(ii) direction cosines of the normal are \(\frac{3}{13}, \frac{4}{13}, \frac{12}{13}\)

Question 5.
Find the vector equation of the plane passing through the points A(1, -2, 1), B (2, -1, -3) and C (0, 1, 5).
Solution:
The vector equation of the plane passing through three non-collinear points A(\(\bar{a}\)), B(\(\bar{b}\)) and C(\(\bar{c}\)) is \(\bar{r} \cdot(\overline{\mathrm{AB}} \times \overline{\mathrm{AC}})=\bar{a} \cdot(\overline{\mathrm{AB}} \times \overline{\mathrm{AC}})\) … (1)

Question 6.
Find the Cartesian equation of the plane passing through A(1, -2, 3) and the direction ratios of whose normal are 0, 2, 0.
Solution:
The Cartesian equation of the plane passing through (x₁, y₁, z₁), the direction ratios of whose normal are a, b, c, is
a(x – x₁) + b(y – y₁) + c(z – z₁) = 0
∴ the cartesian equation of the required plane is
o(x + 1) + 2(y + 2) + 5(z – 3) = 0
i.e. 0 + 2y – 4 + 10z – 15 = 0
i.e. y + 2 = 0.

Question 7.
Find the Cartesian equation of the plane passing through A(7, 8, 6) and parallel to the plane \(\bar{r} \cdot(6 \hat{i}+8 \hat{j}+7 \hat{k})=0\)
Solution:
The cartesian equation of the plane \(\bar{r} \cdot(6 \hat{i}+8 \hat{j}+7 \hat{k})=0\) is 6x + 8y + 7z = 0 The required plane is parallel to it
∴ its cartesian equation is
6x + 8y + 7z = p …(1)
A (7, 8, 6) lies on it and hence satisfies its equation
∴ (6)(7) + (8)(8) + (7)(6) = p
i.e., p = 42 + 64 + 42 = 148.
∴ from (1), the cartesian equation of the required plane is 6x + 8y + 7z = 148.

Question 8.
The foot of the perpendicular drawn from the origin to a plane is M(1, 2,0). Find the vector equation of the plane.
Solution:
The vector equation of the plane passing through A(\(\bar{a}\)) and perpendicular to \(\bar{n}\) is \(\bar{r} \cdot \bar{n}=\bar{a} \cdot \bar{n}\).
M(1, 2, 0) is the foot of the perpendicular drawn from origin to the plane. Then the plane is passing through M and is
perpendicular to OM.
If \(\bar{m}\) is the position vector of M, then \(\bar{m}\) = \(\hat{\mathrm{i}}\).
Normal to the plane is
\(\bar{n}\) = \(\overline{\mathrm{OM}}\) = \(\hat{\mathrm{i}}\)
\(\overline{\mathrm{m}} \cdot \overline{\mathrm{n}}\) = \(\hat{\mathrm{i}}, \hat{i}\) = 5
∴ the vector equation of the required plane is
\(\bar{r} \cdot(\hat{i}+2 \hat{j})\) = 5

Question 9.
A plane makes non zero intercepts a, b, c on the co-ordinates axes. Show that the vector equation of the plane is \(\bar{r} \cdot(b c \hat{i}+c a \hat{j}+a b \hat{k})\) = abc
Solution:
The vector equation of the plane passing through A(\(\bar{a}\)), B(\(\bar{b}\)).. C(\(\bar{c}\)), where A, B, C are non collinear is
\(\overline{\mathrm{r}} \cdot(\overline{\mathrm{AB}} \times \overline{\mathrm{AC}})=\overline{\mathrm{a}} \cdot(\overline{\mathrm{AB}} \times \overline{\mathrm{AC}})\) …(1)
The required plane makes intercepts 1, 1, 1 on the coordinate axes.
∴ it passes through the three non collinear points A = (1, 0, 0), B = (0, 1, 0), C = (0, , 1)

Question 10.
Find the vector equation of the plane passing through the pointA(-2, 3, 5) and parallel to vectors \(4 \hat{i}+3 \hat{k}\) and \(\hat{i}+\hat{j}\)
Solution:
The vector equation of the plane passing through the point A(\(\bar{a}\)) and parallel to the vectors \(\bar{b}\) and \(\bar{c}\) is


= (-2)(-4) + (7)(-1) + (5)(4)
= 8 – 7 + 8
= 35
∴ From (1), the vector equation of the required plane is \(\overline{\mathrm{r}} \cdot(-3 \hat{\mathrm{i}}-3 a t \mathrm{j}+4 \hat{\mathrm{k}})\) = 35.

Question 11.
Find the Cartesian equation of the plane \(\bar{r}=\lambda(\hat{i}+\hat{j}-\hat{k})+\mu(\hat{i}+2 \hat{j}+3 \hat{k})\)
Solution:
The equation \(\bar{r}=\bar{a}+\lambda \bar{b}+\mu \bar{c}\) represents a plane passing through a point having position vector \(\overline{\mathrm{a}}\) and parallel to vectors \(\overline{\mathrm{b}}\) and \(\overline{\mathrm{c}}\).
Here,

Question 12.
Find the vector equations of planes which pass through A(1, 2, 3), B (3, 2, 1) and make equal intercepts on the co-ordinates axes.
Question is modified
Find the cartesian equations of the planes which pass through A(1, 2, 3), B(3, 2, 1) and make equal intercepts on the coordinate axes.
Solution:
Case 1 : Let all the intercepts be 0.
Then the plane passes through the origin.
Then the cartesian equation of the plane is
ax + by + cz = 0 …..(1)
(1, 2, 3) and (3, 2, 1) lie on the plane.
∴ a + 2b + 3c = 0 and 3a + 2b + c = 0

∴ a, b, c are proportional to 1, -2, 1
∴ from (1), the required cartesian equation is x – 2y + z = 0.
Case 2 : Let the plane make non zero intercept p on each axis.
then its equation is \(\frac{x}{p}+\frac{y}{p}+\frac{z}{p}\) = 1
i.e. x + y + z = p …(2)
Since this plane pass through (1, 2, 3) and (3, 2, 1)
∴ 1 + 2 + 3 = p and 3 + 2 + 1 = p
∴ p = 6
∴ from (2), the required cartesian equation is
x + y + z = 6
Hence, the cartesian equations of required planes are x + y + z = 6 and x – 2y + z = 0.

Question 13.
Find the vector equation of the plane which makes equal non-zero intercepts on the co-ordinates axes and passes through (1, 1, 1).
Solution:
Case 1 : Let all the intercepts be 0.
Then the plane passes through the origin.
Then the vector equation of the plane is ax + by + cz …(1)
(1, 1, 1) lie on the plane.
∴ 1a + 1b + 1c = 0

∴ from (1), the required cartesian equation is x – y + z = 0
Case 2 : Let he plane make non zero intercept p on each axis.
then its equation is \(\frac{\hat{\mathrm{i}}}{p}+\frac{\hat{\mathrm{j}}}{p}+\frac{\hat{\mathrm{k}}}{p}=1\) = 1
i.e. \(\hat{i}+\hat{j}+\hat{k}=p\) = p ….(2)
Since this plane pass through (1, 1, 1)
∴ 1 + 1 + 1 = p
∴ p = 3
∴ from (2), the required cartesian equation is \(\hat{i}+\hat{j}+\hat{k}\) = 3
Hence, the cartesian equations of required planes are \(\bar{r} \cdot(\hat{i}+\hat{j}+\hat{k})=3\)

Question 14.
Find the angle between planes \(\bar{r} \cdot(-2 \hat{i}+\hat{j}+2 \hat{k})=17\) and \(\bar{r} \cdot(2 \hat{i}+2 \hat{j}+\hat{k})=71\).
Solution:
The acute angle between the planes

= (1)(2) + (1)(1) + (2)(1)
= 2 + 1 + 2
= 5
Also,

Question 15.
Find the acute angle between the line \(\bar{r}=\lambda(\hat{i}-\hat{j}+\hat{k})\) and the plane \(\bar{r} \cdot(2 \hat{i}-\hat{j}+\hat{k})=23\)
Solution:
The acute angle θ between the line \(\overline{\mathrm{r}}=\overline{\mathrm{a}}+\lambda \overline{\mathrm{b}}\) and the plane \(\overline{\mathrm{r}} \cdot \overline{\mathrm{n}}\) = d is given by

= (2)(2) + (3)(-1) + (-6)(1)
= 4 – 3 – 6
= -5

Question 16.
Show that lines \(\bar{r}=(\hat{i}+4 \hat{j})+\lambda(\hat{i}+2 \hat{j}+3 \hat{k})\) and \(\bar{r}=(3 \hat{j}-\hat{k})+\mu(2 \hat{i}+3 \hat{j}+4 \hat{k})\)
Solution:

Question 17.
Find the distance of the point \(3 \hat{i}+3 \hat{j}+\hat{k}\) from the plane \(\bar{r} \cdot(2 \hat{i}+3 \hat{j}+6 \hat{k})=21\)
Solution:
The distance of the point A(\(\bar{a}\)) from the plane \(\bar{r} \cdot \bar{n}\) = p is given by d = \(\frac{|\bar{a} \cdot \bar{n}-p|}{|\bar{n}|}\) ……(1)

= (3)(2) + (3)(3) + (1)(-6)
= 6 + 9 – 6
= 9

Question 18.
Find the distance of the point (13, 13, -13) from the plane 3x + 4y – 12z = 0.
Solution:

= 19units.

Question 19.
Find the vector equation of the plane passing through the origln and containing the line \(\bar{r}=(\hat{i}+4 \hat{j}+\hat{k})+\lambda(\hat{i}+2 \hat{j}+\hat{k})\).
Solution:
The vector equation of the plane passing through A(\(\bar{a}\)) and perpendicular to the vector \(\bar{n}\) is \(\bar{r} \cdot \bar{n}=\bar{a} \cdot \bar{n}\) … (1)
We can take \(\bar{a}\) = \(\bar{0}\) since the plane passes through the origin.
The point M with position vector \(\bar{m}\) =\(\hat{i}+4 \hat{j}+\hat{k}\) lies on the line and hence it lies on the plane.
.’. \(\overline{\mathrm{OM}}=\bar{m}=\hat{i}+4 \hat{j}+\hat{k}\) lies on the plane.
The plane contains the given line which is parallel to \(\bar{b}=\hat{i}+2 \hat{j}+\hat{k}\)
Let \(\bar{n}\) be normal to the plane. Then \(\bar{n}\) is perpendicular to \(\overline{\mathrm{OM}}\) as well as \(\bar{b}\)

Question 20.
Find the vector equation of the plane which bisects the segment joining A(2, 3, 6) and B( 4, 3, -2) at right angle.
Solution:
The vector equation of the plane passing through A(\(\bar{a}\)) and perpendicular to the vector \(\bar{n}\) is \(\bar{r} \cdot \bar{n}=\bar{a} \cdot \bar{n}\) ….(1)
The position vectors \(\bar{a}\) and \(\bar{b}\) of the given points A and B are \(\bar{a}=2 \hat{i}+3 \hat{j}+6 \hat{k}\) and \(\bar{b}=4 \hat{i}+3 \hat{j}-2 \hat{k}\)
If M is the midpoint of segment AB, the position vector \(\bar{m}\) of M is given by

Question 21.
Show thatlines x = y, z = 0 and x + y = 0, z = 0 intersect each other. Find the vector equation of the plane determined by them.
Solution:
Given lines are x = y, z = 0 and x + y = 0, z = 0.
It is clear that (0, 0, 0) satisfies both the equations.
∴ the lines intersect at O whose position vector is \(\overline{0}\)
Since z = 0 for both the lines, both the lines lie in XY- plane.
Hence, we have to find equation of XY-plane.
Z-axis is perpendicular to XY-plane.
∴ normal to XY plane is \(\hat{k}\).
0(\(\overline{0}\)) lies on the plane.
By using \(\bar{r} \cdot \bar{n}=\bar{a} \cdot \bar{n}\), the vector equation of the required plane is \(\bar{r} \cdot \hat{k}=\overline{0} \cdot \bar{k}\)
i.e. \(\bar{r} \cdot \hat{k}=0\).
Hence, the given lines intersect each other and the vector equation of the plane determine by them is \(\bar{r} \cdot \hat{k}=0\).