Balbharti 12th Maharashtra State Board Maths Solutions Book Pdf Chapter 1 Differentiation Miscellaneous Exercise 1 Questions and Answers.
Maharashtra State Board 12th Maths Solutions Chapter 1 Differentiation Miscellaneous Exercise 1
(I) Choose the correct option from the given alternatives:
Question 1.
Let f(1) = 3, f'(1) = \(-\frac{1}{3}\), g(1) = -4 and g'(1) = \(-\frac{8}{3}\). The derivative of \(\sqrt{[f(x)]^{2}+[g(x)]^{2}}\) w.r.t. x at x = 1 is
(a) \(-\frac{29}{15}\)
(b) \(\frac{7}{3}\)
(c) \(\frac{31}{15}\)
(d) \(\frac{29}{15}\)
Answer:
(d) \(\frac{29}{15}\)

Question 2.
If y = sec(tan-1 x), then \(\frac{d y}{d x}\) at x = 1, is equal to
(a) \(\frac{1}{2}\)
(b) 1
(c) \(\frac{1}{\sqrt{2}}\)
(d) 2
Answer:
(c) \(\frac{1}{\sqrt{2}}\)
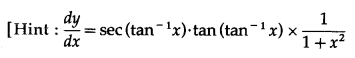

![]()
Question 3.
If f(x) = \(\sin ^{-1}\left(\frac{4^{x+\frac{1}{2}}}{1+2^{4 x}}\right)\), which of the following is not the derivative of f(x)?
(a) \(\frac{2 \cdot 4^{x} \log 4}{1+4^{2 x}}\)
(b) \(\frac{4^{x+1} \log 2}{1+4^{2 x}}\)
(c) \(\frac{4^{x+1} \log 4}{1+4^{4 x}}\)
(d) \(\frac{2^{2(x+1)} \log 2}{1+2^{4 x}}\)
Answer:
(c) \(\frac{4^{x+1} \log 4}{1+4^{4 x}}\)

Question 4.
If xy = yx, then\(\frac{d y}{d x}\) = _______
(a) \(\frac{x(x \log y-y)}{y(y \log x-x)}\)
(b) \(\frac{y(y \log x-x)}{x(x \log y-y)}\)
(c) \(\frac{y^{2}(1-\log x)}{x^{2}(1-\log y)}\)
(d) \(\frac{y(1-\log x)}{x(1-\log y)}\)
Answer:
(b) \(\frac{y(y \log x-x)}{x(x \log y-y)}\)

Question 5.
If y = sin (2 sin-1 x), then \(\frac{d y}{d x}\) = _______
(a) \(\frac{2-4 x^{2}}{\sqrt{1-x^{2}}}\)
(b) \(\frac{2+4 x^{2}}{\sqrt{1-x^{2}}}\)
(c) \(\frac{4 x^{2}-1}{\sqrt{1-x^{2}}}\)
(d) \(\frac{1-2 x^{2}}{\sqrt{1-x^{2}}}\)
Answer:
(a) \(\frac{2-4 x^{2}}{\sqrt{1-x^{2}}}\)
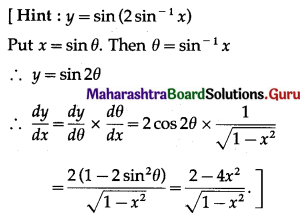
Question 6.
If y = \(\tan ^{-1}\left(\frac{x}{1+\sqrt{1-x^{2}}}\right)+\sin \left[2 \tan ^{-1}\left(\sqrt{\frac{1-x}{1+x}}\right)\right]\), then \(\frac{d y}{d x}\) = _______
(a) \(\frac{x}{\sqrt{1-x^{2}}}\)
(b) \(\frac{1-2 x}{\sqrt{1-x^{2}}}\)
(c) \(\frac{1-2 x}{2 \sqrt{1-x^{2}}}\)
(d) \(\frac{1-2 x^{2}}{\sqrt{1-x^{2}}}\)
Answer:
(c) \(\frac{1-2 x}{2 \sqrt{1-x^{2}}}\)


Question 7.
If y is a function of x and log(x + y) = 2xy, then the value of y'(0) = _______
(a) 2
(b) 0
(c) -1
(d) 1
Answer:
(d) 1

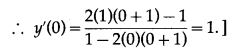
![]()
Question 8.
If g is the inverse of function f and f'(x) = \(\frac{1}{1+x^{7}}\), then the value of g'(x) is equal to:
(a) 1 + x7
(b) \(\frac{1}{1+[g(x)]^{7}}\)
(c) 1 + [g(x)]7
(d) 7x6
Answer:
(c) 1 + [g(x)]7

Question 9.
If \(x \sqrt{y+1}+y \sqrt{x+1}=0\) and x ≠ y, then \(\frac{d y}{d x}\) = _______
(a) \(\frac{1}{(1+x)^{2}}\)
(b) \(-\frac{1}{(1+x)^{2}}\)
(c) (1 + x)2
(d) \(-\frac{x}{x+1}\)
Answer:
(b) \(-\frac{1}{(1+x)^{2}}\)

Question 10.
If y = \(\tan ^{-1}\left(\sqrt{\frac{a-x}{a+x}}\right)\), where -a < x < a, then \(\frac{d y}{d x}\) = _______
(a) \(\frac{x}{\sqrt{a^{2}-x^{2}}}\)
(b) \(\frac{a}{\sqrt{a^{2}-x^{2}}}\)
(c) \(-\frac{1}{2 \sqrt{a^{2}-x^{2}}}\)
(d) \(\frac{1}{2 \sqrt{a^{2}-x^{2}}}\)
Answer:
(c) \(-\frac{1}{2 \sqrt{a^{2}-x^{2}}}\)
[Hint: Put x = a cos θ]
Question 11.
If x = a (cos θ + θ sin θ), y = a (sin θ – θ cos θ), then \(\left[\frac{d^{2} y}{d x^{2}}\right]_{\theta=\frac{\pi}{4}}\) = _______
(a) \(\frac{8 \sqrt{2}}{a \pi}\)
(b) \(-\frac{8 \sqrt{2}}{a \pi}\)
(c) \(\frac{a \pi}{8 \sqrt{2}}\)
(d) \(\frac{4 \sqrt{2}}{a \pi}\)
Answer:
(a) \(\frac{8 \sqrt{2}}{a \pi}\)
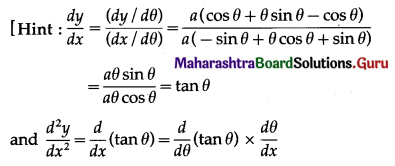

Question 12.
If y = a cos (log x) and \(A \frac{d^{2} y}{d x^{2}}+B \frac{d y}{d x}+C=0\), then the values of A, B, C are _______
(a) x2, -x, -y
(b) x2, x, y
(c) x2, x, -y
(d) x2, -x, y
Answer:
(b) x2, x, y

(II) Solve the following:
Question 1.
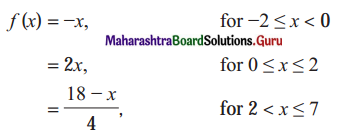
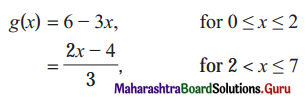
Let u(x) = f[g(x)], v(x) = g[f(x)] and w(x) = g[g(x)]. Find each derivative at x = 1, if it exists i.e. find u'(1), v'(1) and w'(1). if it doesn’t exist then explain why?
Solution:



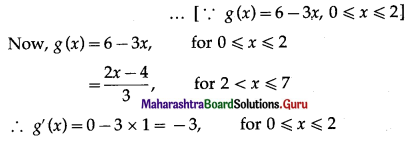

![]()
Question 2.
The values of f(x), g(x), f'(x) and g'(x) are given in the following table:
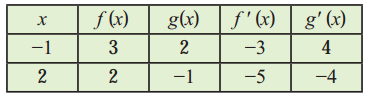
Match the following:
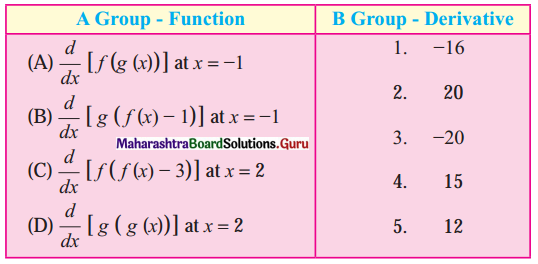
Solution:


Question 3.
Suppose that the functions f and g and their derivatives with respect to x have the following values at x = 0 and x = 1.
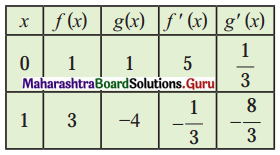
(i) The derivative of f[g(x)] w.r.t. x at x = 0 is _______
(ii) The derivative of g[f(x)] w.r.t. x at x = 0 is _______
(iii) The value of \(\left[\frac{d}{d x}\left[x^{10}+f(x)\right]^{-2}\right]_{x=1}\) is _______
(iv) The derivative of f[(x+g(x))] w.r.t. x at x = 0 is _______
Solution:
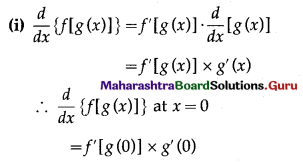
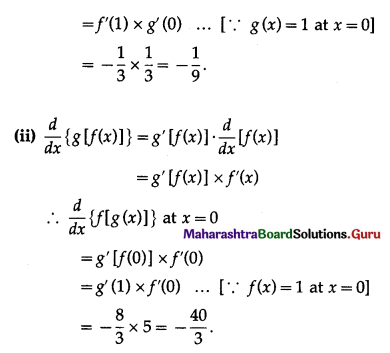
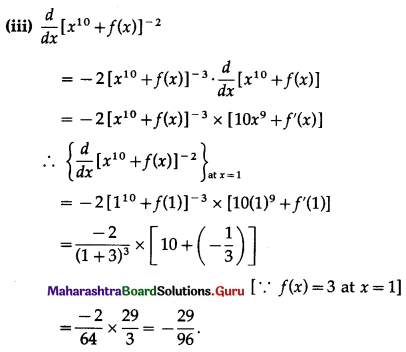

Question 4.
Differentiate the following w.r.t. x:
(i) \(\sin \left[2 \tan ^{-1}\left(\sqrt{\frac{1-x}{1+x}}\right)\right]\)
Solution:
Let y = \(\sin \left[2 \tan ^{-1}\left(\sqrt{\frac{1-x}{1+x}}\right)\right]\)
Put x = cos θ, Then θ = cos-1 x and
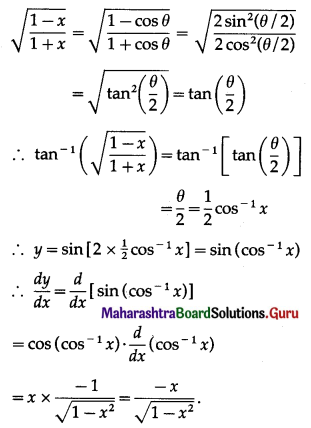
(ii) \(\sin ^{2}\left[\cot ^{-1}\left(\sqrt{\frac{1+x}{1-x}}\right)\right]\)
Solution:
Let y = \(\sin ^{2}\left[\cot ^{-1}\left(\sqrt{\frac{1+x}{1-x}}\right)\right]\)
Put x = cos θ. Then θ = cos-1 x and

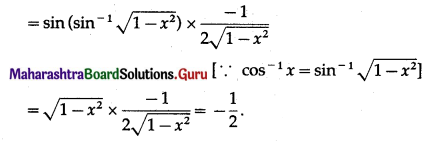
(iii) \(\tan ^{-1}\left[\frac{\sqrt{x}(3-x)}{1-3 x}\right]\)
Solution:

(iv) \(\cos ^{-1}\left(\frac{\sqrt{1+x}-\sqrt{1-x}}{2}\right)\)
Solution:
Let y = \(\cos ^{-1}\left(\frac{\sqrt{1+x}-\sqrt{1-x}}{2}\right)\)
Put x = cos θ. Then θ = cos-1 x and
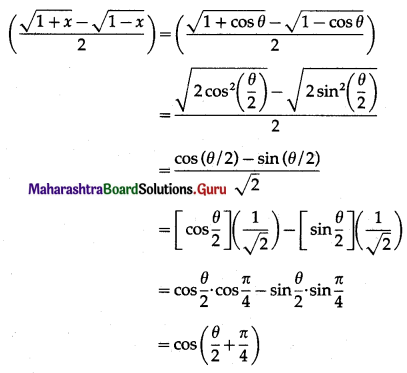
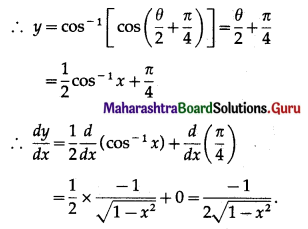
![]()
(v) \(\tan ^{-1}\left(\frac{x}{1+6 x^{2}}\right)+\cot ^{-1}\left(\frac{1-10 x^{2}}{7 x}\right)\)
Solution:

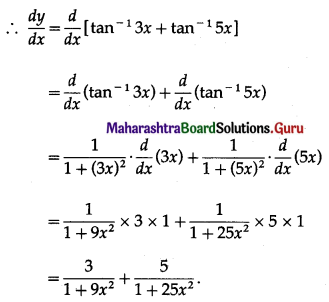
(vi) \(\tan ^{-1}\left[\sqrt{\frac{\sqrt{1+x^{2}+x}}{\sqrt{1+x^{2}}-x}}\right]\)
Solution:
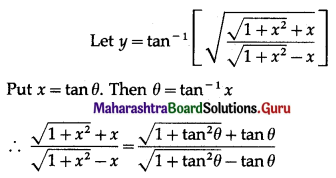


Question 5.
(i) If \(\sqrt{y+x}+\sqrt{y-x}=c\), show that \(\frac{d y}{d x}=\frac{y}{x}-\sqrt{\frac{y^{2}}{x^{2}}-1}\)
Solution:
\(\sqrt{y+x}+\sqrt{y-x}=c\)
Differentiating both sides w.r.t. x, we get


(ii) If \(x \sqrt{1-y^{2}}+y \sqrt{1-x^{2}}=1\), then show that \(\frac{d y}{d x}=-\sqrt{\frac{1-y^{2}}{1-x^{2}}}\)
Solution:
\(x \sqrt{1-y^{2}}+y \sqrt{1-x^{2}}=1\)
\(y \sqrt{1-x^{2}}+x \sqrt{1-y^{2}}=1\)
Differentiating both sides w.r.t. x, we get


(iii) If x sin(a + y) + sin a cos(a + y) = 0, then show \(\frac{d y}{d x}=\frac{\sin ^{2}(a+y)}{\sin a}\)
Solution:
x sin(a + y) + sin a . cos (a + y) = 0 ….. (1)
Differentiating w.r.t. x, we get
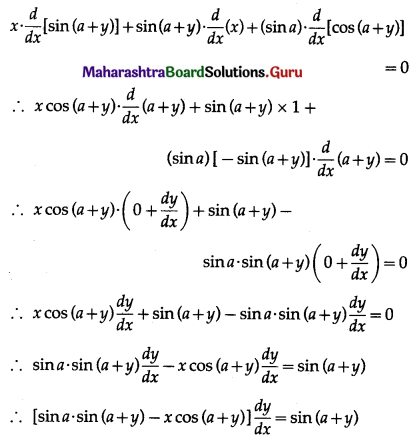
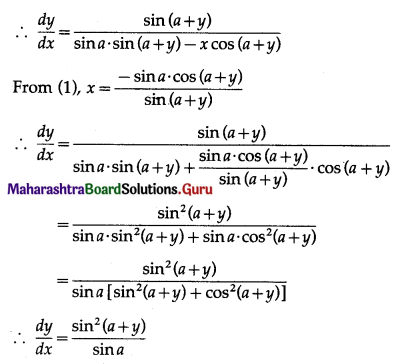

(iv) If sin y = x sin(a + y), then show that \(\frac{d y}{d x}=\frac{\sin ^{2}(a+y)}{\sin a}\)
Solution:
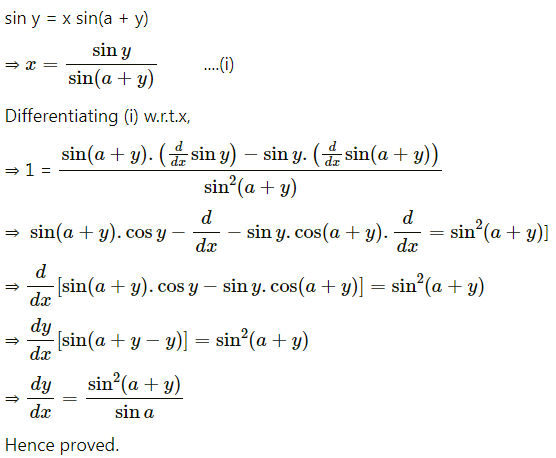
(v) If x = \(e^{\frac{x}{y}}\), then show that \(\frac{d y}{d x}=\frac{x-y}{x \log x}\)
Solution:
x = \(e^{\frac{x}{y}}\)
\(\frac{x}{y}\) = log x …..(1)
y = \(\frac{x}{\log x}\)

![]()
(vi) If y = f(x) is a differentiable function of x, then show that \(\frac{d^{2} x}{d y^{2}}=-\left(\frac{d y}{d x}\right)^{-3} \cdot \frac{d^{2} y}{d x^{2}}\)
Solution:
If y = f(x) is a differentiable function of x such that inverse function x = f-1(y) exists,

Question 6.
(i) Differentiate \(\tan ^{-1}\left(\frac{\sqrt{1+x^{2}}-1}{x}\right)\) w.r.t. \(\tan ^{-1}\left(\frac{2 x \sqrt{1-x^{2}}}{1-2 x^{2}}\right)\)
Solution:
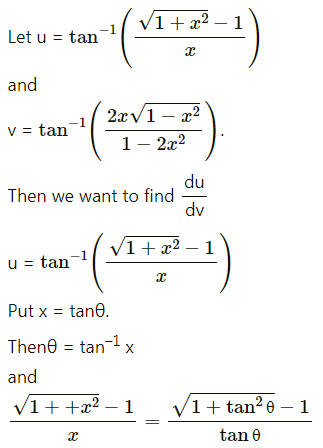
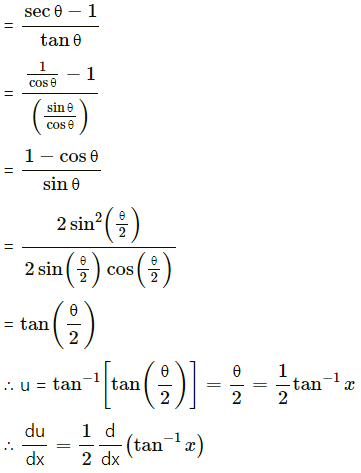
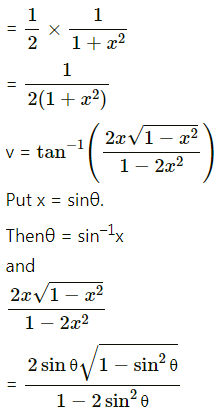
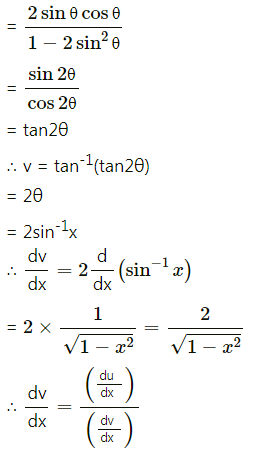
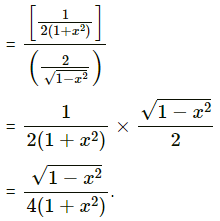
(ii) Differentiate \(\log \left[\frac{\sqrt{1+x^{2}}+x}{\sqrt{1+x^{2}}-x}\right]\) w.r.t. cos(log x)
Solution:



(iii) Differentiate \(\tan ^{-1}\left(\frac{\sqrt{1+x^{2}}-1}{x}\right)\) w.r.t. \(\cos ^{-1}\left(\sqrt{\frac{1+\sqrt{1+x^{2}}}{2 \sqrt{1+x^{2}}}}\right)\)
Solution:



Question 7.
(i) If y2 = a2 cos2x + b2 sin2x, show that \(y+\frac{d^{2} y}{d x^{2}}=\frac{a^{2} b^{2}}{y^{3}}\)
Solution:
y2 = a2 cos2x + b2 sin2x …… (1)
Differentiating both sides w.r.t. x, we get
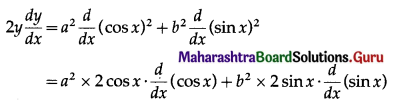


(ii) If log y = log(sin x) – x2, show that \(\frac{d^{2} y}{d x^{2}}+4 x \frac{d y}{d x}+\left(4 x^{2}+3\right) y=0\)
Solution:


![]()
(iii) If x = a cos θ, y = b sin θ, show that \(a^{2}\left[y \frac{d^{2} y}{d x^{2}}+\left(\frac{d y}{d x}\right)^{2}\right]+b^{2}=0\)
Solution:
x = a cos θ, y = b sin θ
Differentiating x and y w.r.t. θ, we get


(iv) If y = A cos(log x) + B sin(log x), show that x2y2 + xy1 + y = o.
Solution:
y = A cos (log x) + B sin (log x) …… (1)
Differentiating both sides w.r.t. x, we get


(v) If y = A emx + B enx, show that y2 – (m + n) y1 + (mn) y = 0.
Solution:
y = A emx + B enx
Differentiating w.r.t. x, we get
