Category: Class 12

Class 12 English Chapter 2.7 She Walks in Beauty Question Answer Maharashtra Board

Balbharti Yuvakbharati English 12th Digest Chapter 2.7 She Walks in Beauty Notes, Textbook Exercise Important Questions and Answers.

12th Std English Chapter 2.7 Brainstorming Question Answer

12th English Digest Chapter 2.7 She Walks in Beauty Textbook Questions and Answers

Question 1.
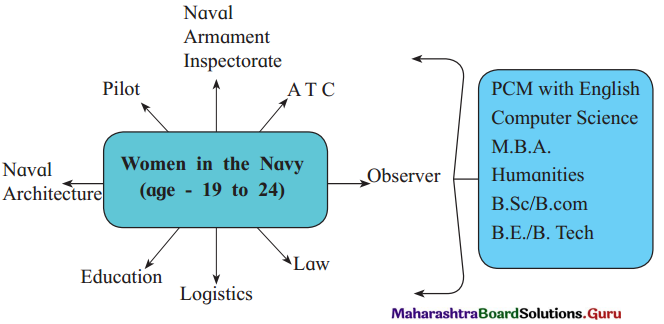
While judging any person you would consider certain aspects. Complete the diagram after carefully thinking what aspects you would consider:

Answer:

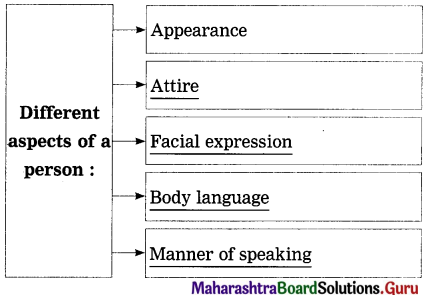
Question 2.
Make a list of proverbs and quotations related to ‘Beauty’.
Answer:
(a) Beauty is in the eye of the beholder.
(b) Beauty is only skin deep.
(c) Beauty is as beauty does.
(d) There is beauty in simplicity.
(e) Beauty is not in the face, it is a light in the heart.

Question 3.
Discuss your impressions about someone’s personality, and say what you like the most and why-
Answer:
The personality that captures the attention of all who meet her is Ms Murti.

1. Simplicity and warmth: She is a brilliant engineer, extremely wealthy yet is simple, and so cheerful and warm in her interaction with anyone she meets.
2. Humbleness: In spite her achievements, wealth and position she never mentions them, rather praises the efforts and achievements of others
3. Elegance: She is graceful and elegant and yet is never dressed expensively.
4. Motivational: She addresses young people and students in a way that is always encouraging and uplifting.
5. Generous: She is generous in giving those who are disadvantaged. She donates for the emancipation of women for making them economically independent.

(A1)

Question (i)
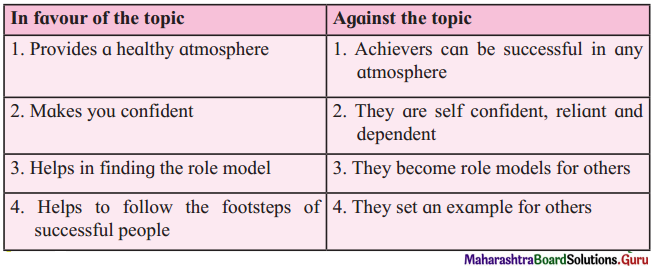
‘Beauty lies in the eyes of the beholder’ – you have probably heard this saying. Discuss in your class how far the statement is true.
Points:

• Outward appearance gives only an idea
• There may sometimes be an exception to the rule ‘first impression is the best
• The external look may be completely different if one looks deeper
• Henry Ford [founder of Ford Automobiles] dressed in the same old suit and said, ‘people who know me know who I am. People who don’t know me don’t matter, A very wealthy person may choose to appear very ordinary.

Question (ii)
Discuss with your partner about the most inspirational person you have come across. Also explain the reasons behind your opinion.
Points:

• Attended a lecture by A.P.J. Abdul Kalam, before he became President
• His views stayed in my mind
• He stressed on dreaming for high aims
• He stressed on the importance of hard work
• He came from very humble background
• He worked his way to achieve great things
• I also want to achieve something and I have a lot of support which Dr. Abdul Kalam may not have had.

(A2)

Question (i)
Match column A with column B:

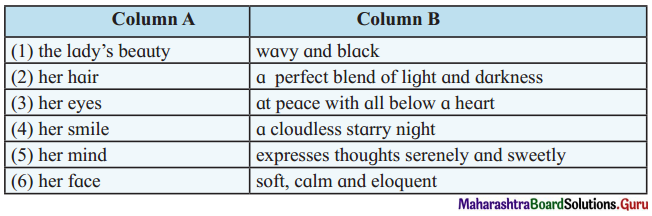
Answer:

1. The lady’s beauty – a cloudless starry night
2. Her hair – wavy and black
3. Her eyes – a perfect blend of light and darkness
4. Her smile – soft, calm and eloquent
5. Her mind – at peace with all below a heart
6. Her face – expresses thoughts serenely and sweetly

Question (ii)
Complete the reasons:
The lady in the poem has a winning smile and a glowing skin. According to the poet she is blessed with these things. Explain why.
Answer:
The lady in the poem has a winning smile and a glowing skin. According to the poet she is blessed with these things because in the last stanza the poet says that lovely cheek, the calm brow, the delicate colouring, the glowing skin all are a result of her life spent without sin. She has a peaceful mind and an innocent heart. These come together to make her face glow with an inner beauty.

Question (iii)
The poet brings a perfect balance of outer beauty and inner beauty. Write a few lines from the poem on how the poet brings this balance in his description.
Answer:
One of the themes in the poem is harmony or balance. The poet does not directly call her beautiful, but she ‘walks in beauty’. The overall beauty is compared to a combination of cloudless (clear) climate and starry skies. He says the best of dark and light meet in her eyes and features, to be seen in the soft, dim light. The effect would not be so wonderful if it was even one shade darker or brighter. That balance of the light is important.

The poet says that her calm brow, sweet smile, the lovely colour of her skin, is the result of a peaceful mind, a loving heart and a pure life. Inner beauty is reflected in this ‘nameless grace’ – indescribable beauty.

Question (iv)
‘Beauty is skin deep.’ Do you agree with the statement? Or do you feel that beauty comes from within? Explain your views in a few sentences.
Answer:
I agree with the statement. Beauty is not about perfect features, clear skin, shining hair or smart clothes. Beauty is about the person’s heart. The helpful nature, a mind without guilt, a cheerful attitude, kind way of speaking will all be reflected in the person’s outward appearance.

The eyes are windows to a person’s soul, they say. If a person has wicked thoughts and bad intentions it shows in the eyes. The expression on the face will reflect the nasty mind. Harsh words will show their unkind nature. So beautiful features and perfect skin are not real indicators of beauty.

(A3)

Question (i)
Find out from the poem the words which are used to describe the lady.
Answer:

1. Raven tresses
2. Serene and sweet expression
3. Pure thoughts
4. Dearheart
5. Calm brow
6. Smiling face
7. Gowing skin
8. Innocent heart
9. Peaceful mind

Question (ii)
Find out the instances of contractions from the poem.
Answer:
The contractions in the poem are – ‘that’s’ – that is ‘o’er’ – over

(A4)

Question (i)
The poet creates imagery of light and darkness to bring out the beauty of the lady. Find out the lines with such imageries and complete the table:
Answer:

Question (ii)
Find out from the poem examples of:
(a) Simile
(b) Metaphor
(c) Alliteration
(d) Personification
(e) Antithesis.
Answer:

(A5)

Question (i)
Write an appreciation of the poem considering the following points :

• About the poem / poet / title
• Theme
• Poetic devices, language, style
• Special features – tone and type
• Values, message
• Your opinion about the poem

Answer:
Lord Byron’s poem opens with the same words that form the title: “She walks in beauty.” These four simple words quickly create an atmosphere of admiration and mystery. It is a short eighteen line poem having three sestets (six lines) in praise of an unnamed woman. The poet uses several poetic devices to express how deeply he is impressed.

There are several themes. One is of course beauty. Each feature of the woman – her eyes, her black (raven) tresses, her soft cheek, her calm brow and the lovely colour of skin is praised. The poet speaks of harmony. He speaks of the perfect blend of day and night, of light and dark. He speaks of the ‘mellowed’ or tender light which makes the beauty so rare, delicate and astonishing.

The other theme is the inner beauty which is what brings the outer beauty. He mentions ‘heaven’ [line 6] which may point to a divine side to the beauty. If a person is sinless their mind is pure and calm. There is no evil so the innocence inside causes the outer beauty which is indescribable – ‘nameless grace [line 8]

The poet uses simile [line 1] ‘like the night..’, alliteration – ‘cloudless climes’, ‘starry skies’. There is rhyme ababab in all the sestets. He uses metaphor -raven tress [line 9], and personification – ‘smiles that win’ [line 15]. There are many examples of antithesis through which the poet stresses on balance.

There is harmony of light – ‘dark and bright’, ‘tender light -gaudy day’, ‘one shade more, one ray less’. These are to emphasize that the beauty is not only physical and external, but actually because there is inner beauty. The mind is calm, the heart is innocent and this causes the outer beauty which is seen by him.

The poem is lyrical, has a steady rhythm and the language is rich with poetic devices. Though the poet does not name the woman, or give any details of her age, his admiration is felt in the tone. The message is about the importance of inner beauty, which is almost a divine thing that will make external beauty possible.

I feel the poem makes us realize that one should look deeper than just outward appearance. One should appreciate beauty in its entirety.

Question (ii)
Compose a poem of at least 4-6 lines on ‘Beauty of Nature’.
Answer:
Beauty of Nature

I look up at the majestic peaks I peer into the sapphire deeps I gaze at the endless shades of green My eyes drink the silver threads between.
In this life God I’m quite sure we can see Why? He’s everywhere in Nature’s beauty!

Question (iii)
Write at least one paragraph and expand the inherent idea of the saying ‘A Thing of Beauty is a Joy Forever’.
Answer:
A Thing of Beauty is a Joy Forever

We all love beauty. We are instantly attracted toward anything beautiful. Even children are drawn toward something pretty. We admire its qualities like lovely colour or soft texture. We admire something beautiful created by someone, like a painting or sculpture. We exclaim on the realistic appearance and the artist’s skill. We appreciate beauty in nature. Gorgeous flowers, majestic mountains, the green of hills and the charming waterfalls. We enjoy the sweetness of fruits.

To create something beautiful requires patience, effort and care. When all these come together the result is beautiful. We appreciate it whether it is in nature or is man-made. Our ears keenly listen to birds calling in the morning, melodious music, the rush of waves and the splashing of rain. Thus all our senses are attracted and we feel good when we see, hear or taste something. It brings us happiness.

Thus a thing of beauty is a joy forever.

(A6)

Question (i)
Browse the internet and find out different types of poems on ‘Beauty’.

Question (ii)
Byron’s name is often taken along with his two contemporaries – Shelley and Keats. Go to your school/college library and read some poems written by P. B. Shelley and John Keats to get a better idea about the Romantic Poets.

Yuvakbharati English 12th Digest Chapter 2.7 She Walks in Beauty Additional Important Questions and Answers

Read the poem and complete the given activities:

Global Understanding:

Question 1.
Complete the following:
The colour of the lady’s hair is
Answer:
The colour of the lady’s hair is shiny black (like a raven’s).

Interpretation/Inference/Analysis:

Question 1.
Complete the following:
Answer:
The phrase ‘dwelling – place’ refers to her mind. The poet says that her face sweetly expresses her thoughts and says that the dwelling place of those thoughts (expressed by the face) is very dear. The dwelling place of thoughts is the mind.

English Yuvakbharati 12th Full Digest Section 2 (Poetry)

• Song of the Open Road Class 11 English Solutions
• Indian Weavers Class 11 English Solutions
• The Inchcape Rock Class 11 English Solutions
• Have you Earned Your Tomorrow Class 11 English Solutions
• Father Returning Home Class 11 English Solutions
• Money Class 11 English Solutions
• She Walks in Beauty Class 11 English Solutions
• Small Towns and Rivers Class 11 English Solutions

Class 12 English Chapter 2.6 Money Question Answer Maharashtra Board

Balbharti Yuvakbharati English 12th Digest Chapter 2.6 Money Notes, Textbook Exercise Important Questions and Answers.

12th Std English Chapter 2.6 Brainstorming Question Answer

12th English Digest Chapter 2.6 Money Textbook Questions and Answers

Question 1.
Discuss in the class about ‘Importance of money.’
Points :
(a) Money is used as capital in business.
(b) It is used by traders to Jill up stocks
(c) It is used by the common man for buying essentials/necessities.
(d) Everyone uses money for paying transport fare/ food-bill/wages and so on.

Question 2.
Complete the web:

Answer:

Question 3.
Make a list of the good qualities of your friend.
Answer:
(a) Calm and good tempered at all times
(b) Helpful and concerned about anyone in trouble
(c) Quick to intervene/calm down any situation that could become unpleasant
(d) Very simple and down to earth in spite of coming from an extremely wealthy background

Question 4.
Share your views on ‘Money is the root of all evils’.
Answer:
Points:

1. Money is a resource.
2. Resources should be available/ used in times of need
3. Money is accumulated by few people/others in need are deprived/some people are not paid fully/workers are paid less for their time and energy
4. Employer gets profit/ imbalance of resources
5. Imbalance in wealth causes discontent among disadvantaged sections of society.
6. Crime increases
7. Haves are targeted by have-nots
8. Normal life becomes unstable
9. Accumulation of money causes this upset in society
10. So important resource becomes reason for evil

Question 5.
Do you lend money to your friend? Give reasons:
Answer:

(A1)

Question (i)
‘Money does not mean everything in life’. Justify the statement by giving examples. Take help of the following points:
(a) Money cannot give you eternal happiness.
(b) Art, music and literature can give you unending happiness.
(c) Money is short-lived.
(d) Money cannot purchase happiness and contentment.
Answer:
Happiness is in the mind. If a person is satisfied with what is on hand then he is happy. Rich clothes, gold, expensive food, servants may all be available. But the owner of these may still be sad and lonely.

Some are happy to make music another may create art or write. They may not have material possessions. But in their hearts they are happy to do what they love.

Money is only a medium to purchase our needs. One cannot give money and buy a bag of joy. Joy is in the heart. Money can be stolen. But joy cannot be stolen. One can earn money but not happiness. No amount of money will satisfy greed or buy happiness.

Question (ii)
Debate on the following topic in groups : Money is the solution for everything For: We need money for – Food-Clothes-Medicines- Education- Travel
Against: One cannot eat money itself/one must have food. We should not buy more than essential clothes/ no need to buy often-Good hygiene and food-habits will ensure health-Government schools are available- Travel is not needed for survival.

(A2)

(i) State whether the following statements are True or False. 

Question (a)
The poet knew no joy till he was rich.
Answer:
False. The poet had no joy as long as he was rich. He was happy when he was poor.

Question (b)
The poet felt that he should talk about his poverty.
Answer:
False. He could not talk about his money.

Question (c)
When the poet had money, he had many true friends.
Answer:
False. When the poet had money, all his friends were false ones.

Question (d)
When poet became poor he had very few real friends.
Answer:
True.

(ii) Write reasons for the following statements.

Question (a)
Friends came knocking all day at the poet’s door.
Answer:
When the poet was rich he had many callers. They claimed they were friends. They were being friendly because he had money. They were not true friends. Such people are called ‘fair-weather friends’.

Question (b)
Poor men’s wives hum like bees.
Answer:
Poor men have no worries. They do not have to safeguard their wealth from liars and cheats. They don’t have false friends who actually love his money and not him. When a man is satisfied with what he has he is happy. He is not chasing wealth and or pretending. The wives are busy and do not have the time to wish for fancy things or gossip. So a happy man has a happy busy wife.

Question (iii)
Money makes the world go round. Explain it in the light of the poet’s experience.
Answer:
Money makes the world go round is a popular saying. It means money is the most important thing in the world. But in ‘Money’, the poet does not accept this view. He had money but he could not say that he possessed it. There were many insincere men who said they were friends.

Contentment is the main thing for being happy, not worldly possessions. Lack of money is a problem. We need it for things like health or education. When all needs are taken care of, then excess money is not necessary. Money is needed in life but it is not the only important thing in life.

The poet repeats that money brought many false men to be near him. But in poverty only a few true friends were with him.

Question (iv)
Poor men need not go up so much as rich men should come down. Express your views regarding this statement.
Answer:
Poor men need not go up as rich men should come down. This statement is perfectly true. The poor will survive. Living a simple, real life, and working hard. They are happy with necessities which may not be expensive. They are content and that brings happiness. They do not have to worry about safeguarding the excess.

But the rich may not know how to live simply, just with basic necessities. They may have servants to do basic chores. They travel in style and sometimes for no reason. They spend unnecessarily. So the poor need not go up as much as the rich need to come down is true.

(A3)

Question (i)
Find out meanings of the phrases given below and use them in your own sentences:
Answer:
(a) Be in the money –
Meaning: to suddenly have a lot of money.
Sentence: It looks he is in the money, by the way he is giving everyone costly gifts.
(b) Win lots of money –
Meaning: get money in a lottery/ gambling/ get money through luck, not work.
Sentence: He bought a lottery ticket every week hoping to win lots of money.
(c) For my money –
Meaning: in exchange for. Worth the amount.
Sentence: The old man asked. ‘Is this all I’m getting for my money?’
(d) Money for old rope –
Meaning: money that is easily earned or gotten
Sentence: She got two thousand just for answering questions in the interview! Money for old rope!
(e) Put one’s money where one’s mouth is Meaning: to take appropriate action to support what one has said.
Sentence: The Municipal Commissioner promised he would put the money where his mouth is and immediately release funds for the school facilities as promised.

Question (ii)
Complete the crossword with the help of the clues from the poem :

Across:
1. A brass musical instrument – TRUMPET
2. A low steady continuous sound – HUM
3. False – UNTRUE
4. Say Something – SPEAK
Down :
5. Not imaginary – REAL
6. Ponder – THINK
7. Stinging insects – BEES
8. In large number – MANY
9. Strike a surface noisily – KNOCK

(A4)

Question (i)
Complete the following table:
Answer:

Question (ii)
Identify the rhyme scheme of all the stanzas of the poem.
Answer:
The rhyme scheme of the stanzas 1 to 4 is abcb.
The rhyme scheme of the 5th stanza is abab.

Question (iii)
Compose a short poem on ‘Friendship’.
Answer:
‘Friendship’
We knew playtime in the park
Study time in school.
We helped one another
Struggling for each difficult mark.
We grew up, and though we fought
We will meet years later
We fondly thought.

(A5)

Question 1.
Write an appreciation of the poem considering the following points:

• About the poem/poet/title
• Theme
• Poetic devices, language, style
• Special features-tone and type
• Values, message
• Your opinion about the poem

Answer:
William H. Davies – a Welsh poet and writer – in his poem ‘Money’ speaks of both times – when he had money and when he did not. Davies tramped through the United Kingdom and the United States.

So he actually led a poor simple life of a wanderer. He actually experienced the difference in the life of a rich man and a poor one. The theme of the poem is the effect of money on the behaviour of people. False friends are plenty when a man has money. The poet compares himself to a child with a trumpet. He is not allowed to blow it for there has been a death.

He uses simile again when the poor man’s wife is described as humming about busily like a bee. The poet also has seen that the lack of money does not mean lack of happiness. The poor man is able to laugh while a rich man frowns; he feels the rich must become poor to taste the simple joys of life – the use of antithesis helps to stress this point.

The poem has five stanzas of four lines each, The seven or eight syllable lines are short but rich ; in poetic devices. The rhyme scheme lends rhythm. Repetition of the word ‘money’ stresses the way man gives money too much importance when it actually takes away our happiness.

The message is that money does not bring happiness. The poor are cheerful while the rich are worried. The poem is very useful to remind us the value of money. It is a necessity. It is not the only thing to chase.

(A6)

Question (i)
Visit a library and read a few poems written by William H. Davies.

Question (ii)
There are many career opportunities related to finance and planning.

Question (iii)
Try to get information about the following careers by surfing the internet.
(a) Finance Management
(b) Banking and Finance
(c) Actuaries
(d) Economics
(e) Share Market
(f) Accountancy
(g) Company Secretary

Question (iv)
Economics is a very important subject in which you can pursue vour career. Browse the websites of these institutions and get information for various courses in Economics.
(a) Delhi School of Economics
(b) Indian Statistical Institute
(c) Gokhale Institute of Politics and Economics, Pune
(d) Madras School of Economics

Yuvakbharati English 12th Digest Chapter 2.6 Money Additional Important Questions and Answers

Interpretation/Inference/Analysis:

Question 1.
Complete the reasons:
Poor ones laugh because ………………
Answer:
Poor ones laugh because – poor people live a simple life. If the basic needs are fulfilled the poor man is happy. He has nothing to worry about or fear. When a man has wealth he has to safeguard it. The poor man is worry-free like health or education. When all needs are taken care of, then excess money is not necessary. Money is needed in life but it is not the only important thing in life. The poet repeats that money brought many false men to be near him. But in poverty, only a few true friends were with him.

English Yuvakbharati 12th Full Digest Section 2 (Poetry)

• Song of the Open Road Class 11 English Solutions
• Indian Weavers Class 11 English Solutions
• The Inchcape Rock Class 11 English Solutions
• Have you Earned Your Tomorrow Class 11 English Solutions
• Father Returning Home Class 11 English Solutions
• Money Class 11 English Solutions
• She Walks in Beauty Class 11 English Solutions
• Small Towns and Rivers Class 11 English Solutions

Class 12 English Chapter 2.5 Father Returning Home Question Answer Maharashtra Board

Balbharti Yuvakbharati English 12th Digest Chapter 2.5 Father Returning Home Notes, Textbook Exercise Important Questions and Answers.

12th Std English Chapter 2.5 Brainstorming Question Answer

12th English Digest Chapter 2.5 Father Returning Home Textbook Questions and Answers

Question 1.
Discuss with your partner the difficulties that you face while commuting to and from the college by public transport.
Answer:
(a) crowded buses, trains
(b) are difficult to board in peak-hours
(c) have to miss a couple of trains/buses to board safely
(d) on such days miss an important lecture

Question 2.
The similar problems are faced by the other commuters on the way to their workplace. Imagine their plight and suggest three solutions.

Answer:

Question 3.
Complete the following table:
Answer:

Question 4.
Write your duties towards the following:

Answer:

(A1)

Question (i)
Discuss with your friend the difficulties focused by the father in the poem.

Question (ii)
Discuss and write the character sketch of the father with the help of the given points.
(His pathetic condition, the treatment he receives at home, his solitude, the way he tries to overcome it)
Answer:
The father is on the late train. This shows he is hard-working. He does not spend any money on himself as his appearance is shown as shabby. He is uncaring about his appearance probably because he is lonely and heart-broken.

He is silent on the train-trip home. He does not speak to co-passengers. Perhaps the sadness in his heart prevents him from even small-talk. He has no travel-mates. He is silent through the trip, and gets off without waving goodbye to any passenger.

His family is cold, distant and uncaring. He is not greeted on arrival. He is given cold food which is not nourishing. He is left to eat the meal alone just reading his book. At the end of the work-day he reads a book, eats by himself, listens to the radio and dreams of the future all alone. Thus the father is a lonely old man, neglected by his own family in spite of working hard for them and heart-sick of his existence.

(A2)

Question (i)
Given below are the ideas conveyed through the poem. Match the pairs and draw out the hidden meaning from those expressions:


Answer:
1. The father hurries home crossing railway line – Father is so eager to meet family members that he doesn’t even bother about his safety.
2. Suburban area, visible through the train, is passed unnoticed – Because there is hardly anything enchanting/interesting in the monotonous routine journey to look out of the window
3. He is just as a small word, dropping from a sentence. – He has so little value in the society where his presence or absence might hardly make any difference
4. He doesn’t get a place in a crowded train. – Uncomfortable journey

(ii) Find the lines to prove the following facts from the extract:

Question (a)
Father is deprived of good food.
Answer:
‘Home again, I see him drinking weak tea Eating a stale chapati’

Question (b)
Children did not have a healthy relation with the father
Answer:
His sullen children have often refused to share
Jokes and secrets with him.

Question (iii)
The poet deals with the theme of man’s estrangement from a man-made world. Analyze it with the help of the extract.
Answer:
The father reaches home. He has a lonely poor meal, served without care. The stale cold food also indicates the coldness in relationships in the family. The weak tea is a metaphor for the fragile family bond. There is no bonding. Home is only a shelter for him and he is only a provider for them. The father is lonely among his own family as well. So the father is alone in the crowd of strangers and also among his own family.

Question (iv)
The father contemplates his past and peeps into his future. Give reasons.
Answer:
The father silently ponders on his past. There is no communication with his family members. He would have sat with family members together to recall happy memories and enjoy them again. Reliving the past would have been one way for the family to bond. But the father thinks of the past alone. Future plans could be also discussed with family members. A lot of discussions could have happened about money, savings, career, a wedding and so on.

Advice, suggestions are given, arguments and disagreements happen, and even anger sometimes. But the father has nothing like this happening in his presence. There is only a sullen silence. He remembers his past and thinks of possible grandchildren. No one shares his dreams. He spends the past, present and future alone and in silence.

(A3)

Question 1.
Complete the following using suitable describing words as they appear in the poem with the help of the words given in the brackets:
(weak, dim, muddy, soggy, stale)
Answer:
(a) Father’s attire – soggy
(b) Father’s tea – weak
(c) Father’s footwear – muddy
(d) Father’s food – stale
(e) Father’s eyesight – dim

(A4)

Question (i)
Identify and write the lines from the extract which expresses the following figures of speech:
Answer:

Question (ii)
I see him drinking weak tea, eating a stale chapati.
Here ‘stale chapati’ stands for stale food/ non-nourishing food or diet, where the part symbolizes the whole, i.e. food. Guess the name of the figure of speech.
Answer:
The figure of speech is ‘synecdoche’.

(A5)

Question (i)
Write a counterview on the following topic:
“Every day is a mother’s/ father’s day.”
(a) If you love them, you don’t need to wait for such days.
(b) Celebrating days is just a formality.
(c) Celebrations of the days condition your expression of emotions.
(d) It is a kind of a pretext to neglect your everyday responsibilities.
Answer:
We love and respect our parents. We must be sure to be loving and respectful in our everyday behaviour and actions. They work, laugh, sacrifice – all only for their children -US! When we behave respectfully and lovingly with elders, the cards or a special day in the year are just a formality.

Our feelings for our parents are unconditional. We don’t say ‘if they do something, only then will we do something in return, while interacting with elders in the family. We cannot be loving, caring, obedient and helpful only on a Father’s/Mother’s Day. We have to be all these towards our parents and elders EVERY DAY.

So ‘Every day is Mother’s/Father’s Day!’

Question (ii)
Write an appreciation of the poem considering the following points :

• About the poem/poet/title
• Theme
• Poetic devices, language, style
• Special features – tone and type
• Values, message
• Your opinion about the poem

Answer:
The poem ‘Father Returning Home’, by Dilip Chitre – a bilingual poet – is about a lonely old man’s coming home from a long day at work. The poet describes his silent and lonely journey home in the crowded Mumbai local train. It is a metaphor for the father’s isolated life even though he is among people.

The poet speaks of the ‘unseeing’ eyes on the scenery flashing past the train. The same thing the man sees daily when commuting has nothing new, just like his uninteresting life. The setting is dusk in monsoon. The man’s dress and appearance are also metaphorical.

His soggy clothes and mud stained raincoat symbolize his shabby appearance and also his sad life. The man carries a bag full of books. He is well-read maybe. Thus when the man gets off the train the poet compares it to a word falling from a sentence. He goes unnoticed as an unimportant word dropped from a long sentence – a simile. The ‘long sentence’ – imagery – makes us imagine the long train and the passenger is one word that is getting down.

The platform he crosses is grey, colour imagery for gloominess or dirty surroundings. The poet uses informal language and an easy style. The poet describes him ‘hurries’ along the platform and again ‘hurries’ on to his home. This repeated word shows his eagerness to reach his shelter and I get dry. The words create an imagery of a shabby, pitiable but scholarly man.

The second part of the poem is about the man in his home. The meal he eats shows the poor quality as well as the careless way it is served. He ‘ reads a book while he eats. That is a clear imagery for his loneliness at home also. The family offers no company after his long day and tiring commute.

In the toilet he is pondering on how he has been shut out of the world although he is in the crowd. He is a stranger among his family in his own home. His children don’t speak to him and won’t share any part of their life. They are not interested in his life also. He goes to sleep thinking of the past and future, listening to harsh sounds on the radio.

The message is how the elderly are used by their own children but neglected when they need care. The poem is about a man who may be misunderstood. He is lonely even in the middle of crowds. It teaches how we should not behave to j persons who are in the autumn of their life. I feel sorry for such people who have worked hard in their life but the younger relatives discard them once their use is over.

Question (iii)
Compose a short poem in about 4-6 lines on your father.
Answer:
My Father

He is unselfish, caring,
Honest and hard-working
Simple, strict and well-read
Upright, always respected
By family and every friend.
He tried to excel till the end.

Question (iv)
Write a character sketch of any one of your family member.
Answer:
My Mother
If anyone cannot believe angels walk on the earth they should come and meet my mother. My mother is the most affectionate and gentle human I have ever met. She has never spoken a harsh word to anyone as far as I recall. She is so very concerned for the comfort of every other person that she neglects herself.

She looks after her father-in-law who is in his eighties. He is a great scholar and gets many visitors. She attends cheerfully to them all apart from looking after us. My father, my sister and I help out with as much of the household chores as we can.

But the main load of running the home falls on her. She takes care of that responsibility so cheerfully as if it is very light. She is loving and jovial with our friends when my sister and I invite them home, She advises us not to overspend but always has a tasty meal when friends and relatives gather for a festival meal.

My father does not make any important decisions in my mother’s absence. She discusses everything till they arrive at the most suitable decision. Our grandfather will not eat anything which my mother has not made. After my grandmother passed, he relies on ‘Saru’ my mother, for his diet meals, medicine, his reference books, walking stick, shawl and everything to be in their place.

My mother is our world.

(A6)

Question (i)
Dilip Chitre has translated Sant Tukaram’s ‘Abhangas’ (devotional poems) for which he received Sahitya Akadeini Award. Browse the internet to collect more information about it.

Question (ii)
List various occupations related to services which can be rendered to senior citizens.
(a) To counsel patients of Alzheimers’ disease.
(b) (Students may attempt this on their own.)
(c) (Students may attempt this on their own.)

Yuvakbharati English 12th Digest Chapter 2.5 Father Returning Home Additional Important Questions and Answers

Read the extract and complete the given activities:

Global Understanding:

Question 1.
List the difficulties faced by the father in the extract.
Answer:

1. The father is returning late in the day.
2. He has to stand the entire trip home.
3. He is in wet clothes for a long time till he can reach home.
4. His sight is weak with age.
5. His cheap footwear is muddy and maybe inconvenient in the monsoon.

Question 2.
Find the lines to prove the following facts from the poem.
Father does not bother to buy anything new for himself and makes do with old, worn out possessions.
Answer:
‘His bag stuffed with books is falling apart’ (line 6)

Question 3.
Choose the correct option and give reasons for it:
Refusal of the children to share jokes and secrets indicates:
(a) They are angry
(b) Generation gap
(c) Lack of concern
Answer:
All three could be reasons.
The children are angry that the father is unable to earn more, provide better life for them.
The father is old and the youngsters cannot relate to him. They are selfish and don’t care for the man who is doing his best.
The children have no care, love or respect for the father. It might not be a close-knit family. So there is no concern for the hard-working breadwinner.

Question 4.
List the difficulties faced by the father in the extract.
Answer:

1. The father is not greeted on his arrival home at the end of the day; is not served any nourishing food – has weak tea and stale chapati.
2. The family does not interact with him. His book is his company.
3. His children are bad tempered sharing no details of their life or asking about his day.
4. He must be going to work like this, also returns silently, to a silent home to his unfriendly family for whom he works.
5. He is unnoticed, uncared for, unappreciated, almost like an outsider in his own home and family.

Inference/Interpretation/Analysis:

Question 1.
The poet deals with the theme of man’s estrangement from a man-made world. Analyze it with the help of the extract.
Answer:
There are two scenarios in the poem. The first part is about the father’s time spent time outside, and the second part describes his time in his home. The first line says he is travelling on the evening train. The Mumbai local trains are famously crowded. But among the crowds he does not speak to a fellow passenger. He stands silently through the commute till he gets down. He doesn’t take leave of any friend and no one waves to him. Among the crowds he is alone.

Question 2.
Given below are the ideas conveyed through the poem. Match the pairs and draw out the hidden meaning from those expressions:
Answer:

Answer:
1. Children avoid expressing themselves – Hostility of children
2. Father was deprived of refreshing hot beverages or nourishing diet – His basic daily requirements were also not catered to.
3. The father was destined to listen only to the crackling sounds on media – The father could not even have some entertainment by himself on the radio.
4. His sordid present is devoid of any hope – He could only indulge in imagination about his past and future.
5. The father’s endless commuting distance him from his children – Father is not less than any tribal wanderer, a modern nomad.

Personal Response:

Question 1.
Write a note on ‘the hard work faced by parents for the family’.
Answer:
Our parents love us from the moment we are born. They watch us grow up and give us everything they can. They try to fulfil our wishes to the maximum extent possible. They work hard. The father works outside the home and the mother in the home. They spend their time, energy and resources on the children.

The children should realize that their parents do so much for them. We must not take their sacrifice for granted. We can never repay them. We must at least try and give them comfort and joy. It is our first duty to obey and love our parents and look after them when they grow old and unable to take care of themselves.

Question 2.
Describe the nature of the family members, from the father’s behaviour in the extract.
Answer:
The family members seems selfish and uncaring. The father drinks weak tea and eats stale food on his return. It is possible to serve fresh food, to the bread-winner returning home even if it is the most simple or poorest of food. If he has a wife then she does not seem to care much about his wellbeing.

The poet clearly states that the children have refused to share any lighter moments or conversation with their father. Probably the mother’s behaviour has made the children also treat him this way. If it is poverty they are facing then the family seems selfish in demanding he work for them but not even offering their company or kindness in return.

Poetic Devices:

Question 1.
Find out the examples of transferred epithets from the extract.
Answer:
‘Suburbs slide past his unseeing eyes. The ‘unseeing’ is transferred to eyes. The eyes are seeing but his mind is not registering any sight. So the quality of ‘not seeing’ is given to the eyes.

Poetic Creativity:

Question 1.
Compose a few lines on ‘Distance’.
Answer:
Distance
I travel for an hour to work, and an hour back.
This is the exact distance of the track
Between myself and the people whom
I go to a place called home.

English Yuvakbharati 12th Full Digest Section 2 (Poetry)

• Song of the Open Road Class 11 English Solutions
• Indian Weavers Class 11 English Solutions
• The Inchcape Rock Class 11 English Solutions
• Have you Earned Your Tomorrow Class 11 English Solutions
• Father Returning Home Class 11 English Solutions
• Money Class 11 English Solutions
• She Walks in Beauty Class 11 English Solutions
• Small Towns and Rivers Class 11 English Solutions

Class 12 English Chapter 2.4 Have you Earned Your Tomorrow Question Answer Maharashtra Board

Balbharti Yuvakbharati English 12th Digest Chapter 2.4 Have you Earned Your Tomorrow Notes, Textbook Exercise Important Questions and Answers.

12th Std English Chapter 2.4 Brainstorming Question Answer

12th English Digest Chapter 2.4 Have you Earned Your Tomorrow Textbook Questions and Answers

Question 1.
Complete the following web

Answer:

Question 2.
Discuss with your paitner about the different idioms/proverbs related to word ‘tomorrow’.
Answer:
(a) Never put off until tomorrow what you can do today.
(b) Tomorrow’s battle is won during today’s practice. (Japanese Proverb)
(c) Today must not borrow from tomorrow. [German Proverb]
(d) Yesterday, today and tomorrow – these are the three days of man.. [Chinese Proverb]

Question 3.
When you make your future plans you think of:
Answer:

1. Career
2. Higher studies
3. Retirement-plans/Financial security
4. Family life
5. Goal in life to be accomplished

Question 4.
‘Plan your tomorrow’ by completing the table given below.
Answer:

(A1)

Question 1.
Discuss with your friend how she/he spent the whole day that was beneficial for others.
Points:
(a) visited retirement home/time spent with elderly residents
(b) spent time conversing about their children/ grandchildren/ looking at photos,
(c) taught some of them how to use the internet to communicate/learned some traditional recipes
(d) promised to visit often regularly

(A2)

Question (i)
……..’was it well or sorely spent’? Explain the meaning and give illustrations.
Answer:
The poet asks the reader again and again if he/she spent each day well or wasted it -‘sorely spent’. We all are busy with our own lives, acting for our own benefit. The poet inspires us to be mindful and must be of use to the world around us. The poet prompts us to speak kindly and unselfishly help, at least one fellow human everyday. The message is implied throughout the poem.

He asks if you have made one person happy, some stranger who had lost all hope, to find some hope again. So he will speak well of you. Is someone grateful to you at the end of (each) the day?

Question (ii)
‘As you close your eyes in slumber do you think that God would say,
You have earned one more tomorrow by the work you did today?’
Elaborate the idea expressed in these lines.
Answer:
The poet indirectly means that each day we exist we must make our living useful. We are not sure if we shall wake in the morning. We pray we do. But for God to grant us one more day -tomorrow – we have to justify our existence today. Did we put today to use? Did we help at least one fellow-human? Did we extend the help without expecting any returns?

Did at least one person feel grateful for your act of help? If nothing, we can make the effort to speak a kind word to a stranger we may pass by in our daily hurry. So one has live mindfully, unselfishly and look for ways to be of help to someone in need. That is the minimum expected by God. Or to have lived as a human would be futile.

Question (iii)
The poet suggests that one should do good to others. Complete the table by giving examples of doing good to following people.
Answer:

(A3)

Question (i)
Pick out the describing words from the poem and add a noun of your own.
Answer:

Question (ii)
Match the words given in column A with their meaning in column B:

Answer:

1. Cheerful – happy
2. Selfish – concerned with one’s own pleasure
3. Sorely – with the feeling of disappointment
4. Discontent – lack of satisfaction

Question (iii)
There are a few examples of homonyms in the poem. For example ‘spoke’. List homonyms from the poem and give their meanings.
Answer:
Passed:

1. (of a candidate) be successful in (an examination, test, or course).
2. went past/left behind Deed:
3. an action that is performed intentionally or consciously.
4. a legal document that is signed and delivered, especially one regarding the ownership of property or legal rights.

Waste:
1. use or expend carelessly, extravagantly, or to no purpose.
(of a person or a part of the body) become progressively weaker and more emaciated.
2. (of a material, substance, or by-product) eliminated or discarded as no longer useful or required after the completion of a process.

Question (iv)
Find out expressions/phrases which denote, ‘going away’ from each stanza.
Answer:

1. Stanza 1: “is almost over”
2. Stanza 1: “passed his way”
3. Stanza 1: “is almost over”
4. Stanza 2: “vanish in the throng”
5. Stanza 2: “rushed along”
6. Stanza 3: “were fading now”

(A4)

Question (i)
The poet has used different poetic devices like Alliteration and Interrrogation in the poem. Identify them and pick out the lines.
Answer:

Question (ii)
The rhyme scheme of the first stanza is ‘aabb’. Find the rhyme scheme of other stanzas.
Answer:
The rhyme scheme of all the stanzas is ‘aabb’.

(A5)

Question (i)
Write the appreciation of this poem based on the points given below :

• About the poem/ poet and the title
• The theme
• Poetic style
• The language/poetic devices used in the poem
• Special features
• Message, Values, Morals in the poem
• Your opinion about the poem

Answer:
The poet, Edgar Guest’s “Have you Earned your Tomorrow”, is a thought provoking composition. The title itself pushes our mind to wonder if today we have done something useful.

It Urges the reader to be thoughtful in everyday life about the people around them. The poet puts forward questions. Each question forces us to ask ourselves if we are kind, unselfish, patient and thoughtful. In our everyday rush, to live our life only for our own benefit, we forget to consider the people nearby who may be less fortunate.

There is interrogation in eleven lines of the sixteen-line poem. The language is simple. There is alliteration and rhyme. The poem has four stanzas of four lines each. The first stanza has four lines, each having fourteen syllables. The second, third and fourth stanzas also with four lines, have fifteen syllables each.

The clear message of the poem is one’s life is meaningful only if it is useful for humanity at large. The poet says one’s conscience has to know that your existence is justified. Or one cannot feel he has the right to ask for one more day of life. It is an uplifting poem. We can take the message and begin implementing it in our life immediately and every day.

Question (ii)
Prepare a mind map on ‘How to plan a goal for tomorrow’ or ‘My future goal’. Take the help of points given in ‘Writing Skills Section’ for preparing a mind map.
Answer:

Question (iii)
Write a set of 8 to 10 interview questions to be asked to a social worker. Take the help of the following points:

• Childhood
• Education
• Service
• Difficulties
• Future plans
• Achievements
• Message

Answer:

1. Good evening Rima ma’am. I would like to know a bit about your life. Could we begin with a walk down memory lane to your childhood?
2. What was your hobby/past-time in your childhood?
3. Which is the best memory during your school/high school/college years? Which phase did you enjoy the most?
4. You have moved to different cities due to your father’s job. Which is the city/town which you loved living in the most?
5. How did you get into social service? Who was your role model or inspiration?
6. What were the challenges and difficulties that caused any setback in your life?
7. What plans do you have for the future? Would you mind sharing a little of those with your fans?
8. There are many achievements you have seen. Which is the most important according to you?
9. What is the message you want to give to those in this noble field? What would be your tip especially for youngsters?

Question (iv)
Compose 4-6 lines on your own on ‘Good deeds’.
Answer:
‘Good deeds’
The tree gives shade and fruits it does not eat
The river flows cool and sweet of water it doesn’t drink.
When a stranger sad or in need you may meet
Be sure you lift him up, not let him into despair sink.

(A6)

Question (i)
Find out different career opportunities in the field of social work.

Question (ii)
Collect information of the NGOs working for the underprivileged section of the society.

Yuvakbharati English 12th Digest Chapter 2.4 Have you Earned Your Tomorrow Additional Important Questions and Answers

Read the poem and complete the activities given below:

Personal Response:

Question 1.
Describe the various ways you use to greet your elder.
Answer:
Whenever we meet our elders we greet them with great respect and love. Through the length and breadth of our country touching the feet of elders is the tradition. We also fold our palms in the very Indian greeting of ‘Namaste’. This comes from the word ‘Namaskaar’. In south India touching people is not a normal custom. Younger people prostrate full length before elders such as parents, uncles-aunts, gurus and even older siblings. In north India the younger bend before the elders and ladies cover their head with the shawl or sari edge. Age is a very significant factor. The greeting is always a gesture of respect and the elders respond affectionately by showering blessings.

Poetic Devices:

Question 1.
Identify an example of synecdoche from the poem.
Answer:
‘Is a single heart rejoicing over what you did or said;’
The word ‘heart’, 3rd line of the 3rd stanza is an example of synecdoche.
The word heart – a part – refers to a whole or the person who is rejoicing.

English Yuvakbharati 12th Full Digest Section 2 (Poetry)

• Song of the Open Road Class 11 English Solutions
• Indian Weavers Class 11 English Solutions
• The Inchcape Rock Class 11 English Solutions
• Have you Earned Your Tomorrow Class 11 English Solutions
• Father Returning Home Class 11 English Solutions
• Money Class 11 English Solutions
• She Walks in Beauty Class 11 English Solutions
• Small Towns and Rivers Class 11 English Solutions

Class 12 English Chapter 2.3 The Inchcape Rock Road Question Answer Maharashtra Board

Balbharti Yuvakbharati English 12th Digest Chapter 2.3 The Inchcape Rock Notes, Textbook Exercise Important Questions and Answers.

12th Std English Chapter 2.3 Brainstorming Question Answer

12th English Digest Chapter 2.3 The Inchcape Rock Textbook Questions and Answers

Question 1.
Prepare a word register related to marine life:
Answer:
sailors; ship; tides; winds; seabed; anchor; captain; submarine; international-waters; port; harbour; shipyard; patrol; trawler; sail; port; starboard; deep-sea.

Question 2.
The functions of a lighthouse are:

Answer:

Question 3.
Discuss in pairs the various famous rocks in the world and mention the places where they are.
Answer:

Question 4.
Narrate in the class a story about someone who destroyed or spoilt someone else’s good work.
(Points: A bright Student-Punctual, cheerful, intelligent-Helpful to classmates, explains and lends notes-Tutored junior class students- Jealous group tears up notes before exams-Is able to study with the friends whom he/she helped-The jealous group is outwitted)

Question 5.
Discuss the following expressions in pairs/groups. Take the help of your teacher.
(a) As you sow so shall you reap.
(b) Crime gets its own punishment
(c) What goes around comes around
(d) Tit for tat
(e) Evil digs a pit for others but falls into the same.
Answer:
All the above are idioms and proverbs. They all convey the same meaning. They all mean that when a person acts with a certain intention, the results will be the same as the action. If the intentions are good the person will benefit from rewards. If the intentions are evil he will be punished.

(A1)

Question 1.
Narrate in groups the scene described in the beginning of the poem.
Points:
A clear calm day at sea
The sea was quiet – the ship is still
The wind is not blowing – the sails unmoving
The waves do not move the Bell
All these point fin first 3 stanzas] to a quiet sea and
calm weather one morning in spring.

(A2)

Question (i)
Complete the following statement:
The Abbot of Aberbrothok placed a bell on the Inchcape Rock because
Answer:
The Abbot of Aberbrothok placed a bell on the Inchcape Rock because there were dangerous rocks near the coast which would wreck ships.

Question (ii)
Given below are the events that give the theme of the poem in a jumbled form. Arrange in a proper sequence as per their occurrence.
(a) The waves were so small that they did not move enough to ring the bell at the Inchcape Rock.
(b) The Abbot of Aberbrothok had placed the bell on a buoy on the rock.
(c) There was a thick haze spread over the atmosphere.
(d) Ralph bent over from the boat.
(e) Sir Ralph cursed himself in despair and in his frustration tore his hair.
Answer:
(b) The Abbot of Aberbrothok had placed the bell on a buoy on the rock.
(a) The waves were so small that they did not move enough to ring the bell at the Inchcape Rock.
(d) Ralph bent over from the boat.
(c) There was a thick haze spread over the atmosphere.
(e) Sir Ralph cursed himself in despair and in his frustration tore his hair.

Question (iii)
Describe the qualities of the Abbot of Aberbrothok in your own words.

Answer:

Question (iv)
‘Jealousy’ is the most incurable defect, Justify.
Answer:
When someone is in a better position of money or success or fame, there are people who feel that they should destroy that. This is jealousy. We can see people who have more, and we can also work hard to reach that position. But when someone wants to destroy that person who has reached the better position that is wickedness. The jealous person is not willing to work for that state. They will not accept a lesser place also. So a jealous mind-set slowly becomes completely evil.

Question (v)
‘But the Rover’s mirth was wickedness’. Explain this line in your own words with the help of the extract.
Answer:
The season of spring made everyone feel happy and light-hearted. The Rover was whistling and singing. But this joyful mood made him reckless. He wanted to trouble the Abbot. The Abbot had put a Bell there as a warning about the Inchcape Rock. Ralph rashly decided to undo his good work. The Rover was jealous of the Abbot who was blessed by grateful sailors. He wanted to trouble the Abbot of Aberbrothok.

(A3)

Question 1.
Some words in the poem are related to different parts of a ship or a mariner’s life. Given below are the meanings of those terms. Identify the word.
Answer:
(a) Helps in steering the ship-wheel
(b) The lowest part of the ship – keel
(c) Floating object that shows direction- buoy
(d) Another name for a ship-vessel
(e) Sinking – gurgling

(A4)

Question 1.
Select the appropriate figure of speech from the box given below and complete the table.
Answer:

(A5)

Question (i)
Write the appreciation of this poem based on the points given below :

• About the poem/poet and the title
• The theme
• Poetic style
• The language/poetic devices used in the poem
• Special features
• Message, Values, Morals in the poem
• Your opinion about the poem

Answer:
The Poem “The Inchcape Rock’ is about a real stretch of treacherous rocks near the Scottish coast. I Robert Southey wrote prose and other poems too. But this poem is well-liked. The title gives the clue that the rock is a part of an interesting story.

The theme is about an Abbot and a pirate. The Abbot is concerned for his fellow humans and helps to save sailors. He put the Inchcape Bell on a buoy to warn ships day and night of the terrible Inchcape Rock, during storms. [According to records, warning bell was placed.]

But the Rover in a fit of madness, on a spring day, cut the bell just to trouble the Abbot. Many months later, when the pirate was sailing towards Scotland, the weather was different. As the frightened sailors were caught in the dark stormy sea the pirate realised he had not troubled the Abbot but brought ruin for himself and his sailors.

The poem is a ballad. The story is told in stanzas of four lines, with aabb rhyme. The story is told in easy language. The poet uses many Old English words like ‘blest’, ‘Quoth’, and ‘canst’. The poet begins with spring, a metaphor for the pleasant mood, with a calm sea, still air and the ship in quiet waters. Repetition emphasizes the gladness in the heart.

The mood changes from mischief to wickedness. When the mist blocks the sun, metaphor makes the story gloomy, suspenseful. The nightfall is the metaphor for the dark situation for the ship, its sailors. They finally meet a violent end. There is alliteration which adds to the beauty of the poem.

The poem is a didactic one with a clear message – “When we try to trouble others, trouble first comes to the doer.” The story has a moral and is useful even in these times.

Question (ii)
Compose 4 to 6 lines on ‘Sea’ :
Answer:
Sea
I meet the sky far away, brothers of the same colour.
I mirror his white woolly sheep and birds.
I pull and push; deep down or sometimes upwards
In my cool-world, small and big creatures, softly slither.

(A6)

Question (i)
Expand the ideas on your own on the following topics:
(a) Pride goes before a fall.
(b) Time and tide wait for none.
(c) Man proposes, God disposes.
(d) Look before you leap.

Question (a)
Pride goes before a fall.
Answer:
There is a saying in Sanskrit that translates as “Knowledge brings humility.” The opposite would be that only an ignorant person would be proud or arrogant. A person becomes overconfident about himself or what he has. He starts thinking lowly of others. Only a harsh experience makes him see his stupidity.

There is a story about the God of riches who was drunk on his wealth. He invited all the other gods to a grand feast so that his wealth would be seen by them. He also invited Shiva and Parvati. They gently told him they would not be able to come, They said their son Ganesha would come instead. The host welcomed his guests.

Ganesha also arrived. The guests seated in a dazzling hall ate their fill of the lavish food. They praised the food, the hospitality and took leave impressed by the grandeur of everything there. But Ganesha was still being served. The host was stunned to see the servants running frantically to serve at the little boy’s speed of eating. The cooks were preparing more food. The puzzled King saw to it that Ganesha was served what he wanted.

Then word came from the kitchen that supplies were needed. Soon the supplies in adjacent villages were empty. Ganesha in anger chased the King till he ran to Shiva’s abode. Ganesha complained he was not fed. The King realized his foolishness trying jto impress the Lord and Mother with his riches. He went humbled, not able to feed one child.

Hence how much ever one possesses one must not think lowly of others. The right kind of knowledge makes a person more and more humble. Like the tree full of fruits bends lower and lower.

Question (ii)
The poem begins with:
‘Without either sign or sound of their shock, The waves flowed over the Inchcape Rock.’
It ends with:
On the basis of these lines explain the change in mood of the poem.
Answer:
At the beginning of the poem the season is spring, the weather is mild and the sea-waters are calm. The waves pour softly over the Inchcape Bell. The Heavy Bell on a buoy would ring due to strong waves only in stormy weather.

When the Rover cut the Bell it was spring season. The mood was happy, light-hearted. He was up to mischief in a rash, jolly mood on a lovely spring day. He wanted to only trouble the Abbot.

After undoing the Abbot’s good work the Rover went away on his criminal voyages. But when he was returning the sea was stormy. Wild winds threw the ship off course. The mood is of confusion and fear because a thick fog covered them from the sun. The mood is of suspense, the sailors are lost.

By nightfall they did not still know where they were. They are really and metaphorically in the dark. They could hear the waves crashing yet they did not know which land was near. There is fear. There was no wild wind but the rough sea was pulling their ship along. They desperately wanted some clue to help them to know their location. The ship shattered onto the rocks as the Rover yelled and cursed. The dramatic end is violent and filled with despair.

(A7)

Question (i)
Read the tree diagrams and information given on pages 109-110 of the textbook and find out more information about opportunities in ‘on and off the shore’ the Indian Navy.

Question (ii)
Required qualifications and various fields/opportunities for women to join in the Navy.

Question (iii)
Colleges that provide education in oceanography-
National Institute of Oceanography, Goa
National Institute of Oceanography, Mumbai
MBA (Logistic Shipping Management), IIKM Business School, Calicut, Kerala
Indira Gandhi College of Distance Education IGCDE, Tamil Nadu

Yuvakbharati English 12th Digest Chapter 2.3 The Inchcape Rock Additional Important Questions and Answers

Read the extract and complete the activities given below:

Global Understanding:

Question 1.
Give reasons for the sailors’ appreciation of the Abbot.
Answer:
There were some dangerous rocks near the Scottish coast. The Abbot of Aberbrothok had placed a buoy and fixed a bell on it, near those rocks. If the sea was rough sailors could spot the buoy. Even in the darkness the rough seas made the bell ring. So by day or night the Abbot’s bell saved the sailors and their ships from the rocks, and they blessed him.

Question 2.
Complete the following:
‘Wheel’d round’ here implies
Answer:
Wheel’d around here implies a flock of birds flying round in circles, which looks like a wheel.

Question 3.
Describe the state of mind of Ralph.
Answer:
Ralph the Rover also felt the effects of the season of spring. He felt very cheerful; he whistled and sang as he walked about on the deck. He was in an extremely happy state of mind but his joy was evil in intentions.

Question 4.
Complete the following:
Answer:
The pirate asked his men to row him over to the Inchcape Bell. He then bent over and cut the Bell from the buoy. He did so that the sailors of the next ship would no longer bless the Abbot for placing the warning Bell.

Question 5.
Choose the words and phrases that could describe Sir Ralph the Rover.
(a) Criminal
(b) Jealous
(c) Arrogant
(d) Vicious
(e) Spiteful
Answer:
All of the above

Question 6.
Choose the correct option:
On spotting the bell, Rover cut the bell from the buoy. This was an act of:
(a) Hatred
(b) Anger
(c) Jealousy
(d) Frustration
Answer:
(c) Jealousy

Question 7.
‘O Christ! It is the Inchcape Rock’ – Give reasons for Ralph’s Exclaimation.
Answer:
The Rover’s ship had struck the terrible rocks feared by sailors. Some time ago he himself had cut off the Bell put there by the blessed Abbot. Now his own ship had hit the Inchcape Rock and was going to sink with all his riches. He too was sure about to die.

Question 8.
Complete the following statements:
Answer:
1. The result of the thick haze that covered the sky was that the sailors had no way of knowing in which direction they were sailing.
2. The Rover in frustration pulled his hair and cursed himself because he himself had cut the Bell which would have rang and the sound would have helped them to save themselves from those killer-rocks.

Inference/Interpretation/Analysis:

Question 1.
The pirate is given the title ‘Sir’ though he was a feared criminal. He is called a ‘rover’. Give reasons for the same.
Answer:
Though he was a feared criminal Ralph was the captain of his ship. The crew may have addressed him ‘Sir’ which explains it attached to his name. A rover is a person, animal, or thing that roves, or wanders, Ralph the pirate roamed around on the seas looking for ships to attack and loot. Maybe that is why he was called Ralph the Rover.

Question 2.
The poet gives hints to the reader in the second stanza of the extract. Find the significant line from the extract and give reason for your answer.
Answer:
The second stanza of this extract tells about what the pirate did after removing the Bell. He roamed the seas and carried on his evil activities, killing and looting.

The last line is the hint of what is to happen later. ‘He steers his course for Scotland’s shore.’ The rover set the course ‘for Scotland’s shores’. This is significant because the treacherous Inchcape Rock was on the Scottish shores. So we get an idea that something may happen there.

Question 3.
Read the following lines and say what the situation was:
‘For me thinks we should be near the shore’. ‘Now where we are I cannot tell,’
Answer:
The sailors could hear the waves crashing on the shore. But they had been blown about by wild winds all day and so did not where they had reached. They did not know which land or shore was near. The situation was that danger was near.

Question 4.
Explain the danger implied in the two lines:
‘They hear no sound, the swell is strong; Though the wind hath fallen they drift along,’
Answer:
There was no sound except the breakers crashing on a nearby shore. There was no wind. But the sea was rough and the strong sea pulled the helpless ship along. The sailors were confused and could not make out which was the safe direction.

Personal Response:

Question 1.
Write an account of something which you did out of concern for others.
Answer:
In our colony there is a young couple living with twin toddlers and elderly parents. The young man is a doctor and his working hours are sometimes unpredictable.

My family is aware of this and we help in small ways. I help the elderly lady to take a walk on the street and my brother helps the gentleman. I also help the young mother to mind the small children if she has to go out shopping. I sometimes run errands for them too.

Question 2.
Give your opinion on the following line and explain its significance.
‘Quoth Sir Ralph, ‘The next who comes to the Rock
Won’t bless the Abbot of Aberbrothok.’
Answer:
The Pirate says these words after he cut the Bell placed by the Abbot. The Abbot had placed it for saving others. This act had brought fame for the Abbot and also the blessings of the many sailors that were saved. But the pirate was jealous of the fame. He cut the Bell thinking to harm the Abbot. When someone is concerned about others they are not looking for fame. But a selfish person is blinded by jealousy. They behave foolishly and cause trouble only for themselves.

Question 3.
‘Now where we are I cannot tell,
But I wish I could hear the Inchcape Bell’ From these lines describe the thoughts of
(a) ……… the sailors in the Rover’s ship.
(b) ……. the Rover’s.
Answer:
(a) The sailors must have been terrified. They may have been feeling angry with their Captain for his senseless act of cutting off the Inchcape Bell. It would be useful now to save them.
(b) The captain of the pirates must have been going mad with fear of the possible crash and sure death of everyone on board. He did not know where his ship was located. He was wondering if they were going to Crash on the Inchcape Rock. He had ensured his own destruction and death by cutting the Bell.

Poetic Devices:

Question 1.
Pick out the examples of imagery from the extract, state what kind it is and explain.
Answer:
Example of Visual imagery from the extract:
1. ‘The ship was as still as she could be’.
2. ‘Her keel was steady in the ocean’. Both the lines depict how the ship was on the sea, almost unmoving.
3. ‘The waves flow’d over the Inchcape Rock;
So little they rose, so little they fell,
They did not move the Inchcape Bell.’
These lines in the second stanza describe the very mild sea and the small waves.

Examples of Sound imagery from the extract:

1. And over the waves its warning rung. The line describes the loud warning sounded by the Inchcape Bell in a storm,
2. ‘And there was joyance in their sound.’ These lines show an air of joy in that scene. Even the birds seemed to be flying round and round – like a wheel – ‘wheel’d round’, ‘joyance in their sound’.

Question 2.
Pick out the examples of imagery from the extract, state what kind it is and explain.
Answer:
The lines with Visual imagery:
1. The Sun in heaven was shining gay,
The Sun shone bright and made the morning cheerful.
2. The sea birds screamed as they wheel’d round,
The birds seemed to be flying round and round in joy, like a wheel.

Examples of Sound imagery from the extract:
1. And over the waves its warning rung. The line describes the loud warning sounded by the Inchcape Bell in a storm.
2. ‘The sea-birds scream’d as they wheel’d round
And there was joyance in their sound.’
These lines show an air of joy in that scene. Even the birds seemed to be happy as their calls seemed like they were screaming in joy, ‘joyance in their sound’.

Question 3.
‘Gurgling sound’. Find the figure of speech.
Answer:
This is onomatopoeia. The pronunciation of the word resembles the meaning – the sound of an object sinking and bubbles rising and bursting.

Question 4.
Pick out an example of imagery from the extract.
Answer:
‘So thick a haze o’erspreads the sky,
They cannot see the Sun on high.’
The reader is able to imagine the fog so dense that the sun is blocked out. This is visual imagery.

Poetic Creativity:

Question 1.
Compose 2-4 lines using “A Song in the Air” as the theme. You could begin with…
‘The leaves rustle gently….’
Answer:
‘The leaves rustle gently and flowers nod. The droplets gather into a bigger drop The birds shake their plumes, bright-eyed. A song is in the air, the new day, a pretty bride.’

Question 2.
Compose 2-4 lines with one of the following as the theme : anger/ hatred/jealousy
Answer:
The Enemy Inside

I don’t know where he hides everyday He flashes in my eyes, in some words I say
To elders, family, friends. I am surprised
By my own words, my actions, only later I cried.

Question 3.
Compose 2-4 lines with one of the following as the theme:
Answer:
I Regret

I think of the harsh remark
The careless action I threw
I vow not to repeat anymore
As I begin this day new.

Writing Skills:

Question (a)
Time and tide wait for none Points:
There is a time for doing each thing

• Postponing action is laziness
• If the time for the action is lost the opportunity is lost for ever.
• Only regret remains.

Question (b)
Man proposes, God disposes

Points:

• It is in one’s power to plan a way of doing things
• It is a smart thing to prepare in advance
• In spite of planning we may not be able to carry on with the plan due to circumstances
• We must accept the unexpected circumstances and yet go ahead by some other method
• We must be flexible and find an alternative way
• It is smart to always have a Plan B ready

Question (c)
Look before you leap Points:

• Before we act one must think of the results
• only a fool will act without thinking of the future consequences of the present action
• if we think the results are going to harm someone, one must not do that
• It is also a good thing to take the advice of experienced or elders when making important decisions.

English Yuvakbharati 12th Full Digest Section 2 (Poetry)

• Song of the Open Road Class 11 English Solutions
• Indian Weavers Class 11 English Solutions
• The Inchcape Rock Class 11 English Solutions
• Have you Earned Your Tomorrow Class 11 English Solutions
• Father Returning Home Class 11 English Solutions
• Money Class 11 English Solutions
• She Walks in Beauty Class 11 English Solutions
• Small Towns and Rivers Class 11 English Solutions

Class 12 English Chapter 2.2 Indian Weavers Question Answer Maharashtra Board

Balbharti Yuvakbharati English 12th Digest Chapter 2.2 Indian Weavers Notes, Textbook Exercise Important Questions and Answers.

12th Std English Chapter 2.2 Brainstorming Question Answer

12th English Digest Chapter 2.2 Indian Weavers Textbook Questions and Answers

Question 1.
Artisans are also called craftsmen. They are creators of diverse goods and use their hands to create unique, functional and also decorative items using traditional techniques. Now complete the web given below:

Answer:

Question 2.
Discuss with your partner the seasons/ occasions when we need:
Answer:
(a) Woollen clothes – in winter
(b) Casual clothes – when at home
(c) Rich silk clothes – festivals, weddings
(d) Colourful, comfortable clothes – travel, socializing

Question 3.
Let’s play a game. The teacher will ask the students some questions. Students will understand that there are some exceptions to the general rules. Let’s start:
Answer:
(a) One who weaves is a – weaver
(b) One who plays a game is a – sportsman
(c) One who sings is a – singer
(d) One who dances is a – dancer
(e) One who teaches is a – teacher
(f) One who cooks is a – cook/chef

Question 4.
We have often seen the picture of Gandhiji spinning on his charkha. Discuss the reasons behind this.
(a) To give rural people an opportunity to earn their livelihood.
(b) To give the message to wear hand-spun clothes.
(c) To convey the message of simple living.
(d) To be self-reliant.

Question 5.
Name some tools used by the weavers.
(a) Loom
(b) Shuttle
(c) Bobbin
(d) Scissors

Question 6.
Name some types of yarns used by the weavers.
(a) Linen
(b) Cotton
(c) Jute
(d) Flax
(e) Silk

(A1)

Question 1.
Discuss with your partner the following vocations:
(a) Weaving:
[Points:
India has rich heritage of weaving.

• Handloom weaving the second most widespread occupation next to agriculture.
• Each region of India has its typical yarn, style and fabric.
• India is tropical – people like to wear cotton
• Silks from different regions of India are prized by women worldwide.]

(b) Tailoring:
[Points:

• A tailor can make someone a star with style and fitting.
• Can have own machines, and stitch clothes according to client’s needs.
• Could be under a designer creating high fashion garments.
• Could be under a fashion-house label, working at computerized machines.
• hey create the trending fashions world- wide.]

(c) Knitting:
[Points:

• Knitting is weaving with two needles with woollen yarn.
• Many women are skilled.
• Women in cold regions do knitting to make warm clothes for the family.
• Knitting is done on machines too.]

(d) Embroidering:
[Points:

• Embroidery needs skilful fingers and patience.
• From hankies to wall-hangings are laboriously made with silk threads and tiny needles.
• Many other beautiful things like tablecloths, dress-collars, sari-edges, bedcovers and cushion sleeves.
• Machine embroidery also is done.]

(A2)

Question (i)
Discuss the various products made by the weavers in the poem.
Answer:
The poet asks the weavers what they are weaving at daybreak. It is a brightly coloured cloth and she asks the reason. The weavers reply that the robes, in the gay colour of the wild kingfisher, are for a newborn.

The poet next asks the weavers at dusk, for what they are weaving that bright cloth. The purple and green shaded fabric is for a queen’s wedding veil, reply the weavers. The poet asks what they are making in the chill night in the moonlight. The weavers are weaving a cloth as white as a feather, as a cloud. They say they are weaving a shroud for a dead man’s funeral.

Question (ii)
The words in the three stanzas of the poem mention different times of a day. Complete the table.
Answer:

Question (iii)
The poem reveals three phases of life. Fill in the blanks with feelings and colours appropriate to the phase of life.
Answer:

Question (iv)
Complete the sentence:
The weavers weave in the chill moonlight ……………….. .
Answer:
The weavers weave in the chill moonlight a cloth as white as a feather, as a cloud, a shroud, for a dead man’s funeral.

Question (v)
Pick out two words used to describe the weavers in the last stanza. Also state their importance.
Answer:
‘Solemn’ and ‘still’ are the two words used in the last stanza to describe the weavers. The words describe the occasion for which the craftsmen are working. A shroud is being woven for a funeral. The workers’ mood is also serious and unsmiling because of the occasion.

Question (vi)
Express your views about the present conditions of weavers.
Answer:
Weaving has existed for thousands of years in India. It was second only to agriculture. The weaves and fabrics from various regions were known around the world. From the Bengal muslin, to Kashmiri, Banarasi and Kancheevaram silks the cloth from India was renowned for the quality and fineness, the designs and richness.

Industrialization then brought problems for them. Power-looms are faster and manufacture large quantities in short time, Fashion-houses buy fabric from the weavers, put their labels and sell off the cloth at a very high price compared to the price paid to the craftsmen.

The craftsmen remain unknown, their craft under-valued and their life is in poverty. Ancient skills are lost and some take loans to somehow struggle. When debts are too much they commit suicide. Master weavers send away sons to cities to take up jobs.

They do not want the sons to struggle. Parents will not give girls in marriage to weavers. They lack facilities like lighting and water supply. Though the government has given subsidies for weavers most of it is lost to bribes and the weavers receive negligible sums.

Question (vii)
Describe in your own words the steps or measures that can be taken to solve the problems of the weavers.
Answer:
Weavers are unorganized. Buyers offer very low prices and if one weaver refuses, they go to another weaver. So the prices are at lowest. The government allocates crores for Handloom Promotion Council, but the weavers get nothing. Weavers’ organization can help the situation.

The weavers are forced to sell their creations to designers at low rates. No one helps to update weavers of the latest fashions trends. Also their creations are not commercially advertised. Handloom industry is eco-friendly in every way. It should be promoted by the Government, designers and supported by the public.

Subsidies for buying yarns and dyes should be given to the craftsmen. Clean water and proper lighting facilities are needed for the craftsmen. Some designers and activists for the weaver communities have begun working for the upliftment of the community and marketing the product.

The buyer can buy directly from the weavers and cut out corrupt middlemen. Exhibitions for selling wares to the public will bring the craftsmen and buyer closer. We can hope that soon the craftsmen of handloom will regain the lost glory which they deserve.

Question (viii)
Express your own views and opinions from the weavers point of view and complete the following table:
Answer:

(A3)

Question (i)
Pick out the rhyming words from the poem.
Answer:
1st stanza: day – gaywild – child
2nd stanza: night – bright; green – queen
3rd stanza: still – chill; cloud – shroud

Question (ii)
Give antonyms and synonyms of the following and make sentences –
Answer:

Question (iii)
Make a word register for clothes/attire/ dress:
Answer:
garments, togs, outfit, wardrobe, raiment, apparel, get-up, gear.

(A4)

Question (i)
Complete the following table:
Answer:

Question (ii)
The rhyme scheme in the first stanza is ‘aabb’. Find rhyme schemes in the second and third stanzas:
Answer:
The rhyme scheme in the second stanza is – aabb.
The rhyme scheme for the third stanza is – aabb.

(A5)

Question (i)
The poet has asked a question at the beginning of every stanza. Explain the effect it creates on the reader.
Answer:
Each stanza of the poem begins with a question to the weaver. The first is at dawn as the poet asks why they are working so early. The second question asks why they make the bright coloured garment at dusk. The third stanza begins asking them why they are working so late, in the cold darkness.

In the question the reader knows about the time of day, the colour of the cloth. The reply gives information about the purpose of the new cloth and why that colour is chosen. The poem is like a conversation between the poet and craftsmen. It conveys the metaphor using time of day and stage of life, the colour and cloth suited for that stage. The mood of the weavers matches the time and purpose of their work. The poem thus flows easily.

Question (ii)
Write an appreciation of the poem with the help of following points:

• About the poem/poet and the title
• The theme
• Poetic style
• The language/poetic devices used in the poem
• Special features
• Message, values, morals in the poem
• Your opinion about the poem

Answer:
The poet Sarojini Naidu’s poem ‘Indian Weavers’ tells about the work of India’s famous handloom craftsmen. The three stanzas mark the three stages of life itself. The weavers reply to questions about why they are weaving that particular piece of cloth, of a certain colour at that time of day.

The theme is cycle of life. The weavers use colours associated with birth, marriage and death through weaving cloths for a newborn, a queen- bride and a dead man. Three stanzas of four line each in the form of questions & answers. The conversational tone gives a flow like life, one stage moving into the next.

The poem is a metaphor for the cycle of life: new life-dawn, marriage-dusk, and death-night. Simile compares the woven garments to objects in colours apt for that stage of life. The sound of ‘w’ occurs a total of 20 times, at least once in all lines except one. This alliteration gives a musical quality.

The poem is dedicated to the talented weavers and the fabrics of India which were world famous. It shows the hard work of craftsmen and how we use their products in every occasion of our life. This poem is a beautiful way of the poet to salute the weavers of India. I find that the weavers are not only skillful but also talented. They combine colours and create patterns that are eye-catching. They know which colours are apt for occasions. The poet brings out their talent as well their hard-working nature.

Question (iii)
Compose four lines on ‘Importance of clothes’.
Answer:
The attire indicates the man he is
His coat brings him confidence and protects too
The colour indicates her mood and occasion The weaver makes the christening, wedding and celebration.

Question (iv)
Write an appeal to use handloom products in our daily life.
Answer:
An Appeal

THREADS -The Handloom Research And Development Society, Maharashtra is proud to present to you the wonderful creations of THREADS for the first-time.
The weaves come directly from the craftsmen to you, the customer.
The range of products includes Pure silk Silk-cotton Cotton Linen Jute
Come and see, appreciate the skills and support the craftsmen who practice our ancient art.
There are wedding saris and Punjabi suits in pure silk, casual wear in all the materials, bed linen, towels, door mats, carpets, hand towels, handkerchiefs, scarves to suit every budget.
Come support our artisans and appreciate the fine quality of our finest Indian weaves!!
Come. Support us. You will Love our Indian fabrics. We need your support.

Contact: Incharge Mrs. Das.
99123 xxxx Email: MrsDas@xxx.

Question (v)
Visit a handloom factory near your locality and write a report of it.
Answer:
Weavers Of Dreams
– by Team A, SYJC -Com. 25/02/2020. The SYJC students of the S.K.Nayak Junior College went on an educational tour to Moinbad village to take a tour of the handloom factory there.

The students viewed many of the processes involved in the weaving of a saree. The students were taken on a guided tour by a local who is a family member of one of the weaver – households of the village. In the first stage the bundles of white yarn were strung on iron frames. The frames held by two men were dipped into hot iron vats of boiling dye.

The yarn is dipped several times, thoroughly drenched for the colour to coat the yarn evenly. After several minutes the men transfer each bundle on to short thick wooden rods. They twist the sticks to wring the bundle dry. A third man takes the hot bundle on another stick and lays the bundles to dry.

The next stage the students saw was coloured yarn stretched on frames several metres long. This was outside in the open. The guide told us it was for a sari. It was a blue yarn in the middle with purple yarn on both sides lengthwise, for borders. Each yarn is stretched, the number of threads for each colour counted.

There were long buildings which are the workshops. Here are frames, looms and the weavers seated before each loom. Each weaver was working on a saree. The guide told us that one saree averagely takes four to seven days. If the design is complicated and in different colours it takes longer.

The finished products are folded and packaged for the market. The tour ended with the students speaking to the weavers at the looms and craftsmen dyeing the yarns. The craftsmen spoke to the visitors giving interesting details about the popular colour combinations. They told us about auspicious colours for special occasions. The artisans also spoke about a different place where traditional nine-yard long are woven. Those are mostly for weddings. The students took photographs of the various processes and the artisans happily posed for them.

Question (vi)
A handicraft exhibition is being organized in your college. You are given the task to compere the inaugural function. Write the script for compering.
Answer:
1. Introduction: A very Good evening and warm welcome to all. This is for a very special kind of occasion we have gathered here this morning. We want to bring the spotlight on that section of our nation’s citizenry who are carrying thousands of years of our heritage on their shoulders! No in their skilful fingers!! Yes our very talented craftsmen. We have our craftsmen with their various talents to showcase their beautiful creations.

We have the weavers of the rich Paithani silks, the Warli painters, the makers of the famous Kolhapur Leather – Footwear, the intricate Bidri brassware, the Dhurrie Weavers, Banjara Embroidery…. all these from Maharashtra. We have men and women with magic in their hands from other states too. Craftsmen have come from distant Meghalaya and Nagaland, from neighbouring Gujarat. We have the makers of the amazing Kashmiri embroidery to the wooden toymakers from Andhra. And so any more.

2. Welcome speech: Our Respected Principal, Sri. Harsh Nayak, our beloved teachers, staff and all my friends join me in welcoming the Honourable Chief Guest, the textile Minister, Shrimati Mandakini Gadge, to this exciting and colourful programme. A very warm welcome to you Madam! It is a great pleasure and an honour to have you here. And a warm welcome to all the parents and all guests.

3. Inaugural Ceremony – Lighting of the Lamp: I request our Chief Guest Shrimati Mandakini Gadge and our Principal to kindly come to the dais. We request you to light the ceremonial lamp, in the traditional Indian way, to declare the exhibition open.

4. Prayer song: And now kindly take your seats for a short programme before we go around viewing the exhibition. Music is such a positive influence. So starting on a note of gratitude we have the prayer song by the stars of our music-club, Nandini, Sonia, Bhaskar, Jay and Kavita. Manjeet is accompanying them on the violin.

5. Welcome Programme: Thank you for that lovely song to begin the programme my friends. Now for a unique performance! We have a Fashion-show!! It is unique because the students of our college and our participating craftsmen-guests worked together for the last few days. This is a first! A big round of applause for our models on the catwalk!

6. Concluding Remarks: Thank you for your encouragement! Wasn’t that wonderful? You may have noticed for yourself, but let me clarify. The stylish saris, salwar suits, elegant kurtas, those shawls, the stunning neck-pieces, the baskets on the ladies’ arms, the wooden screens in the backdrop, the lampshades on the stage, the carpet on the catwalk… and all the decor you can see on the stage are all creations of the masters who are displaying their creations in the exhibition! You now have an idea of what is in store for dressing stylishly, or doing up your home elegantly. That was only starters! The main course is still waiting for you. And there is dessert as well…!!

1. I now request our Chief Guest Shrimati Gadge to address the audience.
2. Thank you, for those words of praise and appreciation of the craftsmen Madam. They richly deserve them.
3. This is the first time a college is hosting such an exhibition. We welcome you all to go around and view the stunning collection of handicraft products. There are master workers who will show you how some of their handicraft is created. They will happily demonstrate their ancient skills. You can watch how the lovely designs we wear are made at the loom.

There are demos to show the yarn being dyed and informative presentations showing the stages in the process. The beadwork artists can help guests to select stones and make them into elegant neck-pieces. There are stalls selling numerous stunning products. Apparel, Decor pieces for your homes, gifts for the festival season.

I invite our Honourable Chief Guest to formally declare the exhibition open and take a leisurely round of the displays.
4. Thank you all for making this festival of crafts a resounding success.

(A6)

Question 1.
Go to your college library and collect and read the poems written by Sarojini Naidu.

Question 2.
Find various career opportunities in Small Scale Industries like Handloom, Art and Craft, Block Printing, etc.

Question 3.
Find out information about the Mahavastra of Maharashtra – Paithani

Yuvakbharati English 12th Digest Chapter 2.2 Indian Weavers Additional Important Questions and Answers

Read the poem and complete the activities given below:

Global Understanding:

Question 1.
The weavers reply to the poet’s questions in each stanza. What is the common factor? What do you understand from that?
1st stanza: ‘Blue as the wing of a halcyon wild’
2nd stanza: ‘Like the plumes of a peacock, purple and green,’
3rd stanza: ‘White as a feather ..’
Answer:
We find reference to a bird in all the three comparisons. In all of them the weavers refer to the colour of the birds’ feathers. We could take it not only refers to the brightness but also to the lightness of the cloth. The fabric is as soft and light as feathers for the tender newborn, or for the transparent veil of the queen. The pure white shroud for the dead is soft too.

English Yuvakbharati 12th Full Digest Section 2 (Poetry)

• Song of the Open Road Class 11 English Solutions
• Indian Weavers Class 11 English Solutions
• The Inchcape Rock Class 11 English Solutions
• Have you Earned Your Tomorrow Class 11 English Solutions
• Father Returning Home Class 11 English Solutions
• Money Class 11 English Solutions
• She Walks in Beauty Class 11 English Solutions
• Small Towns and Rivers Class 11 English Solutions

Class 12 English Chapter 2.1 Song of the Open Road Question Answer Maharashtra Board

Balbharti Yuvakbharati English 12th Digest Chapter 2.1 Song of the Open Road Notes, Textbook Exercise Important Questions and Answers.

12th Std English Chapter 2.1 Brainstorming Question Answer

12th English Digest Chapter 2.1 Song of the Open Road Textbook Questions and Answers

Question 1.
Choose the mode of travel that you would like the most, for a journey.
(a) Airways
(b) Waterways
(c) Railways
(d) Roadways.
Give reasons for your preference.
Answer:
(a) Airways:

• Time-saving even if costly
• Affordable nowadays due to economy airlines
• Useful to go all over the world if one can afford
• Qan enjoy birds’- eye view of different places

(b) Waterways:

• Enjoyable way to travel
• Commuting on waterways is not common all over India.
• In Kerala people use boats on canals and creeks for daily commute
• Long-distance travel by cruise-ship would offer new experiences on the oceans
• Can experience peace of mind and relaxation on long journey by waterway

(c) Railways:

• safe, quick and cheap way to travel long distances
• convenient for overnight journeys – no extra cost for night stay and rest
• comfortable for individuals, families, large groups
• view of the passing landscape and communities living along the route
• opportunity to meet people and even make new friends
• work, family trips, pilgrimage, touring – all kinds ofjourneys are possible and affordable.

(d) Roadways:

• can travel through remote areas
• travel by own vehicle gives more freedom.
• can enjoy the natural beauty -greenery, mountains, water-bodies
• see various geographical features, flora, and styles of clothing, food and even language.

Question 2.
Discuss with your partner, the preparations you would like to make for the journey chosen.
Answer:
(a) A journey by road will need a (virtual) map for the route to take. Road trips are unpredictable. Except for highways we do not know where food, water and facilities like restrooms or pharmacy may be available. One has to carry food, drinks and emergency medicines for unexpected situations. Umbrella or other rainwear, flashlight, spare tyre, tool box and jack are a must. Also when travelling by one’s own vehicle we must have the vehicle serviced and in perfect shape for long distance travel.

(b) All documents related to the vehicle – driver’s licence, registration- papers and insurance papers must be updated and ready to be shown. All journeys require the traveller to wear suitable comfortable clothes. So one would have to wear and pack clothes and accessories accordingly. One also has to foresee what weather conditions maybe along the journey and carry suitable items for that.

(c) Since all of us own mobile phones and our family will want to know about our well-being, one must remember to carry the phone charger and even a power- bank if possible. One must carry a list of emergency contact numbers on paper, in case one’s phone is lost or does not work.

(d) If one decides to travel alone one must be in touch with their loved ones daily, at least once at a particular time. If one has company then the travellers should also discuss the budget, schedule, how to tackle emergencies.and also what to do in unexpected situations.

Question 3.
Discuss the ways in which you would overcome the problems/hindrances/ difficulties you face during the journey.
Answer:
(a) In case of a problem or difficulty, I would go to the nearest place where I can try and resolve the problem.
(b) I would inform my family about the problem.
(c) I would take any steps needed to see that the problem does not become worse.
(d) I would ensure that I am safe till the problem is resolved and I can continue the journey/return home.

Question 4.
During every journey we have to observe certain rules. Discuss your ideas of the journey without any restrictions.
Answer:
(a) I would go with my friends since we work well as a team even though we have I varied interests and skills. We are like-minded about most things. We will share the costs and all of us drive well.
(b) My friends and I love to have fun but none of us is ever unruly. We do, always will, respect the law and are particular about others’ safety and our own.
(c) We will be. sure to never speed or drive rashly. None of us smokes nor consumes forbidden substances like alcohol.
(d) We will ensure that each gets some rest. We will also make sure we keep a log book to record our road trip for memories as well as a guide for later trips, so we can avoid the mistakes and fill in loopholes.

(A1)

Question (i)
Pick out the lines showing that the poet is prepared to enjoy every moment of his journey.
Answer:

• ‘Afoot and light-hearted I take to the open road,..’
• ‘Healthy, free, the world before me.’
• ‘The long brown path before me leading wherever I choose.’
• ‘Henceforth I ask not good-fortune, I myself am good-fortune,’
• ‘Strong and content I travel the open road.’
• ‘The earth, that is sufficient,’

Question (ii)
By ‘old delicious burdens’ the poet means
(a) the luggage
(b) the food he carries
(c) sweet memories of the past
Answer:
(c) sweet memories of the past

Question (iii)
The poet is a person who is free from all inhibitions. Discuss how the concept is expressed in the poem.
Answer:
The poet is about to embark on a trip. He j does not consider anything can restrict him, even his own hesitation or doubts. He says he is prepared -‘afoot ’and ‘light-hearted’, He is physically fit and mentally without any dilemma. He is all set to follow the road to his dream/destination. ‘Healthy and free’ He does not (want to) depend on good luck or fortune to be kind to him. He has his life, his destiny, in his own hands and is. confident that is enough. ‘I ask not good-fortune, I myself am good-fortune’.

He is no longer going to delay his journey with complaints, criticising that everything is not perfect. What is there is enough for him. ‘I whimper no more, postpone no more, need nothing,’ ‘The earth, that is sufficient’. His determination is strong and he has decided to progress on his path in life. ‘Strong and content I travel the open road.’

(A2)

Question (i)
Following are the activities of the poet related to his journey on the road. Divide them into two parts as ‘activities the poet will practise’ and ‘activities he will not practise’.
1. Walking along the road though he does not know where it reaches
2. Complaining about the discomforts during the journey
3. Postponing the journey
4. Praying for good fortune
5. Carrying the fond memories of the good people
6. Creating contacts with famous and influential people
7. Striving to achieve high and bright success
8. Reflecting and developing his own ‘self Activities he will practise’.
Answer:
Activities he will practise:
1. Walking along the road though he does not know where it reaches
5. Carrying the fond memories of good people
7. Striving to achieve high and bright success
8. Reflecting and developing his own ‘self Activities he will not practise

Activities he will not practise:
2. Complaining about discomforts during the journey
3. Postponing the journey
4. Praying for good fortune
6. Creating contacts with famous and influential people

(ii) Write down the traits the poet exhibits through the following lines.

Question (a)
Henceforth, I ask for no good fortune –
Answer:
I myself am good fortune – Self-confidence

Question (b)
Henceforth I whimper no more, postpone no more, need nothing –
Answer:
Positive and self-reliant

Question (c)
I do not want the constellations any nearer –
Answer:
self-assured and independent

Question (d)
I swear it is impossible for me to get rid of them –
Answer:
clear-thinking and knowing his mind

Question (e)
I am filled with them – I will fill them in return –
Answer:
aware and honest about himself

Question (iii)
‘Healthy, free, the world before me.’ Express your views regarding the above line.
Answer:
The poet is about to set out on life’s journey. He is of healthy body and mind. He feels strong enough to meet challenges he may have to face on the way. His attitude seems positive, hopeful and determined – he says ‘the world before me’ – showing this.

Hence we can say he is ready to make use of every opportunity the world can provide and he will not delay or complain, postpone or criticize, blaming others. He can make any dream come true.

(A3)

Question 1.
The poet has used many describing words like ‘healthy’ in the poem. Make a list and classify them as
(a) For the world: ……………
(b) For himself: ………………
(c) For the road: ………………
Answer:
(a) For the world: sufficient
(b) For himself: light-hearted, healthy, free, good-fortune, strong, content,
(c) For the road: open, long brown path

(A4)

Question (i)
The road in the poem does not mean only the road to travel. The poet wants to suggest the road of life. Explain the metaphor with the help of the poem.
Answer:
In a journey we may go on, we plan on the mode of travel, and hope to have an enjoyable trip. We want to admire the scenes passing by. We may meet new people. Sometimes we may come across some difficulties, yet we complete the trip and return home to our normal routine.

For a trip, we make travel plans decide the destination and so on. But life itself is a long journey. In our life we have family and friends. We don’t know what will happen in future. We remember pleasant as well as sad situations of the past. We work hard, find success, face failure, and attain glory and defeat. So life goes on.

In both, a trip or in life, the attitude is important in how we make the journey. One must go ahead with a positive and flexible mind-set. Unexpected situations will come up. We may have pleasant as well as unpleasant situations. But if we have self-belief, any difficulty can be faced. One must just be strong.

The poem also tells we have memories. We are held back by attachments. But we can carry the beautiful past as happy memories, We should always go forward in the journey of life.

Question (ii)
There are certain words that are repeated in the poem. For example, ‘no more’ (Line 7) Find out other similar expressions. Explain the I effect they have created in the poem.
Answer:
There are several words that are repeated.
1. ‘open road’ – lines 1 and 7. Indicates the path in life is open wide for the poet/ person to make any choice he wants. The opportunities are unlimited.
2. ‘before me’ – the poet is looking at the road ahead, his future life, his outlook for the upcoming journey (of life).
3. ‘Henceforth I’ – lines 4 and 5. The poet conveys ‘from that point onwards’ he has decided to do or not do certain things.
4. ‘good-fortune’ – he believes good fortune or destiny is not external. It is within one’s power, in one’s own hands.
5. ‘I know’ – lines 11 and 12. This shows his full awareness.
6. I carry’ – lines 12, and twice in 13, I indicate the weight of the burdens though they may be delicious.
7. ‘they are’ – line 10 emphasizes that entity (constellations or people with power) belongs where it is.

Question (iii)
The use of personal pronoun ‘I’ is evident and prominent in this poem. Give reasons.
Answer:
The repetition of the pronoun ‘I’ occurs fifteen times in as many lines of the poem. This shows us how fully in charge the poet is of his life, his destiny, his actions, his decisions and the consequences.
The repeated use of T shows that he is confident of himself and is able to take his life forward independent of other’s support. He is going to stop complaining, criticizing.
He will approach the future on his own strengths. Ready to use the opportunities that he comes across, the poet is quite sure he does not need either luck or influential friends to help his attempts. He seems assured of his own capabilities.

(A5)

Question (i)
With the help of the following points, write a poetic appreciation of the poem ‘Song of the Open Road’.

• the poem
• title
• theme
• style
• poetic devices
• message
• your opinion.

Answer:
‘The Song of the Open Road’ by American poet, Walt Whitman is about optimism, energy j and confidence. The world offers opportunities to anyone who wants to use them.

Walt Whitman’s works were a powerful influence on other writers. The poet himself struggled as a child of twelve. He dropped out of school to take up some job to help the family income. He worked as lawyer’s assistant, printer’s assistant, as a teacher and journalist. He helped look after the wounded in the American Civil War.

Question (ii)
Write four to six lines of Free Verse on the topic ‘The road that leads to my college’. Express that it is the road to knowledge and bright future. You may begin like this: Evlery day I tread with the bag of books
Answer:
‘The Road That Leads to My College’ Every day I tread with the bag of books And a hopeful step, Into the space of light and hope, Lean look for myself. I go to become more ready For tomorrow and the day after. Every day, every way I Grow and grow thankful and wise, strongly hopeful.

Question (iii)
Write a blog on the following topic.
(a) Man is Free by Birth.
Answer:
Man is Free by Birth

The statement is true in every sense of the word ‘free’. If someone does not have physical freedom, it is visible. But the freedom of the mind, thoughts, emotions, the spirit, the soul, is also vital for one to fully find satisfaction in life.

I remember an advertisement to bring up boys to be sensitive. Usually boys are discouraged from showing tears. It is thought tears of fear, anxiety, pain, loss are signs of weakness when a boy cries. There should be no external signs of these emotions and parents compare the boy to a girl. They make fun of their sons to stop him crying. In this way they take away the child’s freedom to express emotions. They take away his sensitivity!

Taking away of freedom is often done by adults to their children. The parents give guidance for the future but parents impose their own expectations on the kids and take away their freedom to choose a life-goal. The child’s natural liking or strength is not considered. The herd mentality makes parents force their children to follow a field which other students are doing. They earn lots of money. But they don’t notice their child does not like or is not good at it. So the child grows up leaving his passion.

Adults teach children that out of respect and good manners they must not question them. Children will grow up seeing injustice being done. They will notice bad things happening. But their desire to question is silent. They keep quiet and accept even bad things as normal.

I could go on. But let us ensure that freedom is alive and well. Let us allow everyone to be themselves, to follow their heart, to speak out when necessary, to fulfil their dreams. But we must ensure that this freedom never injures another or interferes with other people’s freedom.

The poem says ‘open’ road. It is about freedom. The poet wants to go out from restrictions and comforts. The poet wants to be self-reliant. He is confident. The poem is in free verse. There are many poetic devices but no metre or rhyme, We immediately notice repetition. There is also Transferred epithet.

The poem is a dramatic monologue. The poem inspires us to explore the world using our abilities. Comfort, complaints, criticisms and fate are not excuses for one’s inaction.

Question (iv)
Expand the ideas suggested in the following lines:
(a) All roads lead to Rome.
Answer:
The road system in the Roman Empire was built in a way that a person could take a road from anywhere and he would reach Rome. This means that every matter can be approached differently. Everyone has their own way to approach a matter. It could be doing some work or solving a problem. Each person has their way of doing things.

It means that we should agree not to be narrow minded. We should appreciate the other person’s way of doing things also. We should not expect everyone to think exactly the same way as we do. We should allow individuals to follow their method. Sometimes some work is given. That person will complete the work in his way. When giving the task the method of doing it need not be forced. Even if it is completely new then the person may do it himself. If he is not able to do it he can ask for help.

When there is a problem many people may be trying to find a solution. We can discuss ideas. Many ideas may be put forward. There can be so many ideas that are useful for solving the problem. One may be quicker. Another may be cheaper. One may need more people. So all ideas can be pooled to finally solve the problem.

Even the head of the country has a team of ministers. The leader discusses and consults with the team for running the country. All of them play a role for successful running of the government. This is true of teamwork and cooperation. We can all work for the same goal. The work may be so big that many are required to work together. It is not necessary for everyone to do exactly the same thing. But all work together in different methods so that we reach the desired goal.

Question (b)
A man without liberty is a body without a soul.
Answer:
We think ‘liberty’ means only physical freedom. But even if a person is not physically free, his mind is working freely. Actually the freedom to think, speak and act to fulfil our wishes and goals is more important.

A free man really means a free-thinking man. We have heard of men speaking out against powerful people. They were jailed. But even in jail they wrote books. They expressed their views. We know of many such famous personalities like Gandhiji, Jawaharlal Nehru and Nelson Mandela.

Many of our Indian freedom fighters were executed for their ideas. But they did not keep quiet. They spoke out and inspired Indians to rise up against the colonial rulers. Their minds were free though they were physically in prison.

Liberty is freedom to anything for oneself without hurting other people’s liberty. We should not use freedom to do just anything we desire. That is not correct. Hence we must be aware of what is happening and speak against wrongs. When there is life, there is mind. When we have an intelligent mind, we should think.

‘Life, liberty, and thought – three persons in one substance, eternal, never-ending, and unceasing.’ Khalil Gibran.

(A6)

Question (i)
Take help from the sources available on the internet and make a list of proverbs and quotations about ‘road.’ [an example …]
Answer:
The road to success is not a path you find but a trail you blaze.
https : //www.bemytravelmuse.com/best- road-trip-quotes/
https : //www.goodreads.com/quotes/tag/ road-trip

Question (ii)
Read the poem ‘The Road Not Taken’ by Robert Frost.

Yuvakbharati English 12th Digest Chapter 2.1 Song of the Open Road Additional Important Questions and Answers

Read the poem and complete the activities given below:

Global Understanding:

Question 1.
Describe the mood of the speaker in the poem. Choose from the options given. There may be more than one possible option:
1. hopeful
2. thoughtful
3. serious
4. cheerful
5. regretful
6. upbeat
7. contemplative
8. buoyant
Answer:
1. hopeful
4. cheerful
6. upbeat
8. buoyant

Inference/Interpretation/Analysis:

Question 1.
Pick out the lines from the poem which indicate the past behaviour of the poet, which he now chooses to discontinue and discard. What do the thoughts indicate regarding the poet’s intentions for the future?
Answer:
The lines which the poet writes indicating his change in mind-set are:
1. ‘Henceforth I ask not good-fortune, I myself am good-fortune,
2. Henceforth I whimper no more, postpone no more, need nothing,
3. Done with indoor complaints, libraries, querulous criticisms,’
The poet realizes he has been discontented, complaining, blaming and criticizing others, as an excuse for his inaction. He had not taken charge of his own actions or his life.

Now he has a clear view of what he will do in the future, a different attitude to life. He has taken charge of both now. He is ready to leave behind all negativity and move ahead with hope and self-confidence.

Personal Response:

Question 1.
The poet says ‘strong and content’, ‘The earth, that is sufficient’. Describe your thoughts about yourself if you were starting out on life’s journey. Would ‘the earth be sufficient’ for you to being ‘strong and content’?
Answer:
I agree with the poet. The fact that I am reading and understanding the poem indicates I have a high-school education. People with much fewer advantages have accomplished great things. I can use the resources I have to become a good human, a useful citizen and find my way to go forward in life. Success and satisfaction does not mean making lots of money or becoming famous. If I can help fellow humans and give back to the country that has given me so much, I will be content.

Poetic Devices:

Paradox is a poetic device, which is defined as ‘a (logical) statement’ contradicting itself. It can i also be said to be a sentence that is opposed to the 1 common sense but yet can be true.

Question 1.
Pick out a line from the poem that is an example of paradox.
Answer:
‘Still here I carry my old delicious burdens’ is the line that is having a paradox ‘delicious’ and ‘burden’. Something delicious is pleasant, whereas ‘burden ’ reminds us of something difficult and unpleasant. But the poet wants to convey that his sweet memories are difficult to leave behind. They pull us back from going away. But still he will go, but he will carry his precious memories and still carry on his life’s journey.

Question 2.
Pick out the line where transferred epithet is used by the poet.
Answer:
‘Done with indoor complaints, libraries, querulous complaints.’
The phrase ‘indoor complaints’ describes the speaker who earlier had been enclosed indoors and complaining. Now he is ‘done’ -will no longer do that. Another phrase ‘querulous criticisms’ speaks of an irritated person constantly criticizing. The poet has decided he will no longer indulge in that also.

English Yuvakbharati 12th Full Digest Section 2 (Poetry)

• Song of the Open Road Class 11 English Solutions
• Indian Weavers Class 11 English Solutions
• The Inchcape Rock Class 11 English Solutions
• Have you Earned Your Tomorrow Class 11 English Solutions
• Father Returning Home Class 11 English Solutions
• Money Class 11 English Solutions
• She Walks in Beauty Class 11 English Solutions
• Small Towns and Rivers Class 11 English Solutions

Class 12 English Chapter 1.8 Voyaging Towards Excellence Question Answer Maharashtra Board

Balbharti Yuvakbharati English 12th Digest Chapter 1.8 Voyaging Towards Excellence Notes, Textbook Exercise Important Questions and Answers.

12th Std English Chapter 1.8 Brainstorming Question Answer

12th English Digest Chapter 1.8 Voyaging Towards Excellence Textbook Questions and Answers

Question 1.
There are different ways to travel from one place to another for different purposes. Discuss with your partner and match the words given in table A with their meanings in table B:

Answer:
(a) Cruise – a journey on a boat or ship to a number of places
(b) Expedition – a journey, especially by a group of people, for a specific purpose
(c) Camp – a place usually away from urban areas where tents are erected for shelter
(d) Trip – a brief pleasure outdoor visit
(e) Excursion – a short journey to a place with a particular purpose
(f) Picnic – a short visit to an outdoor place where people celebrate, enjoy and eat meals
(g) Voyage – a long journey on a ship

Question 2.
Discuss the following with your partner and complete the web.

Answer:

(A1)

Question (i)
Upbringing plays a very important role in shaping one’s life.
Answer:
The teacher will form two groups in the class. One group will speak in favour of the above topic while the other will speak against it. Debate brings out different perspectives, it does not mean one is right and other is wrong. You can take help of the following points and have a debate on it:

(A2)

Question (i)
Make a list of great Indian and foreign personalities who had a great impact on Achyut Godbole during his childhood.
Answer:

Question (ii)
Find the different techniques used by the writer to learn Science and Mathematics.
Answer:
The different techniques used by the writer to learn Science and Mathematics are:
(a) The writer used to appreciate the inherent beauty of these subjects.
(b) He found Newton’s law of motion beautiful and the Pythagorean Theorem elegant.
(c) The writer loved solving problems of Mathematics of the 9th standard when he was in the 7th.
(d) He used to love solving problems and used to enjoy finding out the most elegant method of solving them, even though I they were not a part of the curriculum.

Question (iii)
The writer faced numerous problems while communicating in English because-
Answer:
(a) He had his entire education in Marathi.
(b) His vocabulary was very weak, and pronunciation was terrible.
(c) His construction of sentences was very awkward.

Question (iv)
The writer was completely stumped because his:
Answer:
(a) vocabulary was very weak
(b) spoken English was quite pathetic
(c) pronunciation was terrible
(d) construction of sentences was very awkward

Question (v)
Due to the writer’s pathetic English speaking style, he:
Answer:
(a) felt quite lonely and terrified, in Mumbai in general, and IIT in particular.
(b) developed an inferiority complex
(c) felt depressed and diffident.
(d) wanted to run away from IIT and even Mumbai.

Question (vi)
Complete the following. The writer wanted to achieve mastery in English because-
Answer:
(a) he wanted to speak excellent, elegant and fluent English
(b) he would be able to achieve excellence and excel in anything he tried to do
(c) he need not have to feel afraid of anybody and start feeling at home in his hostel.

Question (vii)
Make a list of different steps that the writer undertook to improve his English speaking skills.
Answer:
To improve his English the writer:
(a) decided to also think in English before speaking in English.
(b) started reading English newspapers and English novels.
(c) studied etymology and phonetics and studied the roots of the words and how to pronounce them.
(d) used to stand in front of the mirror and practice speaking, realising his mistakes and correcting them himself all the time and improvising and improving day by day.

Question (viii)
Describe the writer’s achievements after achieving mastery over the English language.
Answer:
After achieving mastery over the English language:

1. His fear for English disappeared.
2. He started feeling quite confident about speaking in English at length with anybody.
3. He started feeling at home in his hostel.
4. He could give presentations with ease.
5. He negotiated and signed many contracts worldwide and ran large global software companies.
6. He headed software companies having thousands of software engineers worldwide.

Question (a)
Complete the table comparing the two different phases of the life of the writer- as an MD or Chief Executive Officer and an activist of Sarvodaya movement.
Answer:

Question (ix)
Complete the web highlighting the various opportunities you gained due to your good English speaking skills.

Answer:

Question (a)
Describe a situation or incident when you felt embarrassed for your lack of knowledge of a particular subject or incompetence in speaking English fluently.
Answer:
This happened after my Std X exams. I live in Latur, and I was visiting my cousins in Mumbai for the first time. In order to entertain me, they took me to a musical nite. Unfortunately, it was music show based on English songs, and I had no knowledge of it or interest in it. I love to listen to Hindi and Marathi songs only. They soon realized my lack of interest, and were sorry for their mistake. I was embarrassed about my complete lack of knowledge about English music.

(A3)

Question (i)
Fill in the blanks selecting the correct phrase from the alternatives given.
(feel out of place, speak at length, feel at home, sea of knowledge)
(a) By the end of the week she was beginning ………………… in her new job.
(b) When he lost his mother he was completely ……………… .
(c) Travelling can help to ………………….. .
(d) After my retirement I started ……………… as a social worker.
(e) Having faith in God ……………………. in difficult situations.
(f) To succeed in any competitive examination, one requires a sea of knowledge.
(g) The simple village girl ……………………. in a formal party.
(h) The work done by Sindhutai Sapkal …………………. of millions
(i) The teacher …………………….. explaining the concept.
(j) The speaker was ……………………… by the intelligent questions asked by the audience.
Answer:
(a) By the end of the week she was beginning to feel at home in her new job.
(b) When he lost his mother he was completely broken.
(c) Travelling can help to broaden one’s horizon.
(d) After my retirement I started my second innings as a social worker.
(e) Having faith in God keeps one going in difficult situations.
(f) To succeed in any competitive examination, one requires a sea of knowledge.
(g) The simple village girl felt out of place in a formal party.
(h) The work done by Sindhutai Sapkal touched the hearts of millions
(i) The teacher spoke at length explaining the concept.
(j) The speaker was completely stumped by the intelligent questions asked by the audience.

Question (ii)
Find out a word related to the game of cricket. List two meanings for it.

Answer:
Second innings:
1. general meaning: the second phase of life of an individual where he/she starts/ pursues a new or different career or the post retirement life.
2. related to cricket: when a team comes to bat for the second time in a test match

Question (iii)
Go through the text to find the antonyms of the words given in the grid and fill in the boxes. One is done for you.

Answer:

(A4)

Question (i)
Write whether the underlined verbs in the following sentences are Main verbs or Primary auxiliary verbs:
(a) I had a very simple upbringing. ………………
(b) I was immensely impressed. ………………..
(c) I had learnt from my childhood that money did not mean everything in life. …………………
(d) He was a convent educated guy. ……………….
(e) They did all the work in time. …………………..
(f) I had to achieve a lot in life. …………………….
Answer:
(a) Main verb
(b) Main verb
(c) Auxiliary verb
(d) Main verb
(e) Main verb
(f) Main verb

Question (a)
Fill in the blanks with appropriate modals according to the situations given in the following sentences:
Answer:

1. Take an umbrella. It might rain later.
2. People must not walk on the grass.
3. Could I ask you a question?
4. The signal has turned red. You ought to wait.
5. I was a sportsperson in my school days. I can play badminton.
6. I am going to the library. I will find my friend there.

Question (b)
Find from the extract, the sentences that show past habit.
Answer:
1. Poets like Vinda Karandikar, Mangesh Padgaonkar and Vasant Bapat used to visit our home.
2. They used to talk about Keshavsut…

(iii) Do as directed and rewrite the sentence:

Question (a)
I did not fully understand their discussions but I was immensely impressed. (Remove ‘but’.)
Answer:
Though I did not fully understand their discussions, I was immensely impressed.

Question (b)
I had decided that I would do nothing of this sort. (Remove ‘that’.)
Answer:
I had decided to do nothing of this sort.

Question (c)
My fear had vanished and I started feeling at home in my hostel. (Use ‘when’.)
Answer:
When my fear had vanished, I started feeling at home in my hostel.

Question (d)
It was only my self-esteem which stopped me. (Remove ‘which’.)
Answer:
Only my self-esteem stopped me.

Question (e)
I plunged into all these branches of knowledge. It was a period of renaissance.
(Join with ‘which’.)
Answer:
I plunged into all these branches of knowledge, which was a period of renaissance.

Question (f)
When I look back, there are a number of lessons that I cherish. (Remove ‘When’.)
Answer:
On looking back, I find that there are a number of lessons that I cherish.

Question (g)
There are hundreds who tell me that they understood the theory of relativity. (Remove ‘who’.)
Answer:
Hundreds tell me that they understood the theory of relativity.

(A5)

Question 1.
Go through the sample of the flyer given on page 91 of the textbook and prepare flyers on the topics given below.
Topics :
1. Yoga Class / Summer Hobby Class
2. Tree Plantation Drive
3. Cleanliness Drive
4. Help us to end Child Labour
5. Let’s get rid of the monsters – tobacco and alcohol

Use the following points:

• Details
• Special Features
• Why to choose us/Need of drive/Purpose of the mission
• Anything special
• Add your own points

Answer:
1. Yoga classes:
Divine Yoga Classes
First Floor, Vijai Towers, Opposite Railway Station, AAahim (West)
We have classes for all : from age 5 to 75 Men and women, girls and boys.

(A6)

Question 1.
Achyut Godbole has written many bestsellers that are famous far and wide. Read at least two books of your choice, make a summary of those books and submit.
(Students may attempt this on their own.)

Yuvakbharati English 12th Digest Chapter 1.8 Voyaging Towards Excellence Additional Important Questions and Answers

Read the extract and complete the activities given below:

Global Understanding:

Question 1.
Write if the following sentences are True or False. Rewrite the false sentences correctly:
1. The writer did not like Mathematics and Science.
2. The writer studied Mathematics and Science only for scoring maximum marks in exams.
3. The writer’s skill at solving problems helped him in his IIT entrance exam.
4. The writer scored 100% marks in Mathematics in every examination he appeared for.
Answer:
True sentence:
3. The writer’s skill at solving problems helped him in his IIT entrance exam.

False sentences:
1. The writer did not like Mathematics and Science.
2. The writer studied Mathematics and Science only for scoring maximum marks in exams.
4. The writer scored 100% marks in Mathematics in every examination he appeared for.

Corrected sentences:
1. The writer loved Mathematics and Science.
2. The writer studied Mathematics and Science not only for scoring maximum marks in exams, but also because he appreciated their inherent beauty.
4. The writer scored 100% marks in Mathematics in almost all the examinations he appeared for.

Question 2.
The writer’s joy was shortlived. Give reasons.
Answer:
In Solapur, where the writer spent his childhood, he had not seen any building which was more than three – storeyed. Mumbai however was full of skyscrapers, which made the writer uncomfortable. At IIT, most of the students and professors used to converse in English whereas the writer’s English was very poor, with a weak vocabulary, terrible pronunciation and very awkward construction of sentences.

Due to all this, he felt quite lonely and terrified in Mumbai in general and IIT in particular. He developed an inferiority complex and wanted to run away from IIT and even Mumbai. Thus, his joy at getting into IIT was shortlived.

Question 3.
Name the following from the extract:
Answer:

1. Management gurus : Alvin Toffler, Peter Drucker, C. K. Prahlad, Tom Peters
2. The founder of Infosys: Narayan Murthy
3. Two universities: Harvard, MIT (Massachusetts Institute of Technology)
4. A great technologist-Vincent Serf

Question 4.
Pick out the false sentences and rewrite them correctly:
1. The writer was more intelligent and well- j read than his friends.
2. The writer’s group was interested in many things.
3. The writer wanted to top the GRE and migrate to the U.S.
4. The writer possessed many books on various topics.
Answer:
False sentences:
1. The writer was more intelligent and well- read than his friends.
3. The writer wanted to top the GRE and migrate to the U.S.

Corrected sentences:
1. The writer’s friends were more intelligent and well-read than the writer.
3. The thought of topping the GRE and migrating to the U.S. never even touched the writer’s mind.

Question 5.
Complete the web: (the first letter of each quality has been given)
Answer:

Question 6.
Complete the web stating the principles of good management:
Answer:

Question 7.
What was the writer’s first love?
Answer:
to read and write on various subjects concerning human life and existence.

Question 8.
How many books has the writer written in Marathi?
Answer:
about 34 books

Question 9.
What was the name of the writer’s autobiography?
Answer:
Musafir.

Question 10.
Name any two values that the writer cherishes.
Answer:
humility, humanity

Complex Factual:

Question 1.
Give the writer’s opinion about:
arts, music and literature.
Answer:
The writer says that the arts are equally, if not more, important in our lives than science and technology. He also feels that arts, music and literature enrich our lives and put meaning into our existence. He loved music.

Question 2.
money.
Answer:
The writer feels that money is necessary, but does not mean everything in life.

Question 3.
List the achievements of the writer in Mathematics.
Answer:
1. The writer loved solving problems of Mathematics of the 9th standard when he was in the 7th.
2. The writer scored 100% marks in Mathematics in almost all the examinations that he appeared for, from the 1st standard until IIT, barring only a few times. He also stood 1st in the University in all subjects put together.

Question 4.
Describe the ‘very important’ thing that happened to the writer.
Answer:
When the writer was in his third year at IIT, he came in contact with about 15-20 extremely brilliant students/researchers/ professors from IIT, TIFR and BARC. They included top-ranking students from IIT, visiting professors in American Universities, very renowned mathematicians of the world and so on. This friendship had a lasting impression on his life. He came to know what real brilliance meant, and where he stood with regard to it.

Question 5.
Describe curiosity and humanity.
Answer:
Curiosity is important. It is only because of the human curiosity that we have been able to make such a great progress in science and technology, and social sciences. Humanity means concern for our fellow human beings; it means caring for and helping others whenever and wherever possible. This is important if we wish to live in a world that is happy and contented.

Question 6.
List the things that the writer said he learnt while running large companies.
Answer:
While running large companies the writer learnt:

1. The importance of teamwork
2. The necessity of leading from the front and setting a good example for the staff.
3. The need to treat subordinates and colleagues as friends.

Question 1.
Match the subjects in Column A with the title of the books in Column B:

Answer:

1. Management – Boardroom
2. Painting – Canvas
3. Western music – Symphony
4. Psychology – Manat
5. Mathematics – Ganiti
6. Science – Kimayagar
7. Indian music – Nadvedh
8. Western films – Limelight
9. English Literature – Zapoorza
10. Economics – Arthat

Inference/Interpretation/Analysis:

Question 1.
‘Nevertheless, culturally I had a rich childhood’. Explain the statement with reference to the extract.
Answer:
The writer says that he had a very simple upbringing in a lower middle-class family which did not have even basic amenities like a fan, refrigerator, etc. Even so, it was rich culturally because various poets, writers and musicians used to visit their home and there would be hours of discussions about music, literature, paintings, sculptures, etc. Famous writers, painters and musicians were discussed and this made the writer love the arts. He states that arts, music and literature enrich our lives and put meaning into our existence.

Question 2.
Complete the following:
The writer developed a problem-solving attitude because …………….
Answer:
The writer developed a problem-solving attitude because ……………..
1. He did not study subjects only for scoring maximum marks in the examinations.
He used to study these subjects or any subject for that matter for its inherent beauty.
2. He used to love solving problems andused to enjoy finding out the most elegant method of solving them.
3. He used to get involved in solving them.

Question 3.
Complete the following:
The writer was benefitted by the discussions with great people as it…
Answer:

1. made a lasting impact on his life
2. made him realize what real brilliance meant
3. broadened his horizons, and his aims and worldview became global
4. taught him a lesson in humility, hard work and a passion for excellence.

Question 4.
Explain why the author say that passing the ‘examination of life’ is more important than passing the college examination.
Answer:
The writer wished to understand the world and how it works. He also wished to serve India and her people. To do this, he would have to read and understand different branches of knowledge, to develop values like humility, humanity and rationalism. This was the ‘examination of life’ for him. This was far more important to him than just passing the IIT examination.

Question 5.
Mention a few ways in which the author touch the hearts of the people.
Answer:
The author’s books have brought about very good changes in the lives of thousands of readers. Hundreds have come out of depression and more than a dozen have given up thoughts of committing suicide and decided to start all afresh. There are hundreds who say that they understood the theory of relativity or Big Bang after reading his book on Science ‘Kimayagar’.

His book ‘Boardroom’ on Management has created at least 20 successful entrepreneurs. Then there are hundreds who can understand Economic Times or NDTV Profit after reading his book on economics ‘Arthat’.

Many have turned to Mathematics after reading his book ‘GanitV. The same is true about his books on Indian Music (Nadvedh), English Literature (Zapoorza), Painting (Canvas), Western Films (Limelight) and Western Music (Symphony) or books such as ‘Genius’ series, ‘Rakta’ or ‘Vitamins’ or ‘Anartha’. It is these reactions of thousands of readers that made him feel that has touched the hearts of thousands of people.

Question 6.
Describe the second innings of the writer in your own words.
Answer:
After working for software companies for many years, the writer wanted to return to his first love, i.e. reading and writing on various subjects concerning human life and existence. Therefore, he gave up two lucrative offers to become a writer. This is how his second innings as a writer in Marathi began. After this, he wrote about 34 books in Marathi. Most of them became bestsellers with tens of thousands of copies sold for each. These books brought about very good changes in the lives of thousands of readers.

Hundreds came out of depression and more than a dozen gave up thoughts of committing suicide and decided to start all afresh. Thousands more have been helped in the fields of science, economics, music, mathematics, etc. by the writer’s books. It is these reactions of thousands of readers and the feeling that he is touching their hearts that has kept him going.

Personal Response:

Question 1.
Describe what a ‘rich childhood’ mean to you.
Answer:
I think that a rich childhood is one where you get a lot of love and security at home. It could also be culturally rich, where you get to read or know music/books/theatre, etc. Basically, a rich childhood is one which has plenty of love, fun and friends. Money is secondary.

Question 2.
We should study any subject. Do you agree? Give your reasons.
Answer:
Every subject has its own inherent beauty and uses. We should study a subject because of its beauty. While Science and Technology are important to make our daily lives easy, arts, music and literature enrich our lives and put meaning into our existence. Every subject helps in some way in the progress of mankind.

Question 3.
Do you think that speaking English fluently and confidently is important? Discuss.
Answer:
Yes, it is. English is an international language, which the people of most countries understand. If we wish to go abroad, or have international exposure, we should know English in this competitive world. Even in India, knowledge of good English gives us a sense of confidence. It helps us to get jobs. It also helps us to get access to information from all parts of the world.

Question 4.
Name some of the top universities in the world.
Answer:
Some of the top universities in the world are: Harvard University, Stanford University, Massachusetts Institute of Technology, Oxford University, Cambridge University, Cornell University. Princeton University, etc.

Question 5.
Do you feel that arts, music and literature enrich our lives. Discuss.
Answer:
Art is all around us; it surrounds us. It provides us with a deeper understanding of our own emotions and those of others. It makes us more sensitive, softer and gentler. It enriches the quality of life and improves our physical and mental health. It connects us to others. Literature gives us an insight into the world of others, both in the present and the past.

Question 6.
Do you think that team work is important today? Explain with an example.
Answer:
Yes, today team work is very important in every sphere, whether it is in games or at work. Every individual has different talents and these separate talents come together when one is in a team. For example, in cricket, one person may be a good bowler, another a good batsman, a third a good fielder, etc. When all these people come together and play the game as a team, it leads to success. In an office too, only when we work in a team and contribute our respective talents can we complete projects.

Question 7.
Do you think passion is more important than wealth?
Answer:
Passion is certainly more important than wealth. Wealth can give the luxuries of life, but it cannot give mental peace and satisfaction. This can only be gained by having an interest in what we do, or in simple words, by loving our jobs. Hence, when one chooses a career, it is more important to choose one which we love rather than one which pays more.

Language Study:

Question 1.
Find from the extract, the sentences that show past habit.
Answer:
1. I used to study these subjects or any subject for that matter for its inherent beauty.
2. I used to get involved in solving them.
3. I used to love problem-solving and used to enjoy finding out the most elegant method of solving them.

Question 2.
These problems were not a part of the curriculum, but I enjoyed the whole process. (Rewrite using ‘though’.)
Answer:
Though these problems were not a part of the curriculum, I enjoyed the whole process.

Question 3.
This exam is completely based on your problem-solving ability and the ability to think not only logically but quickly and rapidly. (Pick out the adverbs of manner.)
Answer:
completely, logically, quickly, rapidly

Question 4.
Find from the text, the sentence that show past habit:
Answer:
Most of the students and professors used to converse in English.

Question 5.
Find from the extract, a sentence that shows past habit.
Answer:
I used to stand in front of the mirror and practise speaking.

Question 6.
I wanted to speak excellent, elegant and fluent English. (Rewrite using ‘that’.)
Answer:
I wanted to speak English that was excellent, elegant and fluent.

Question 7.
My fear had vanished and I started feeling at home in my hostel.
(Pick out the verbs and state the tense.)
Answer:
had vanished – past perfect tense; started – simple past tense

Question 8.
Find from the extract,the sentences that show past habit.
Answer:
1. Until that time I used to consider myself somewhat intelligent.
2. I used to visit MIT during lunch time to meet my friends.
3. I used to visit both of these Universities.
4. If you walked for an hour from there, you could reach Harvard Square near Harvard University. (Pick out the clauses and state their type.)
Answer:
you could reach Harvard Square near Harvard University-Main clause
If you walked for an hour from there- Subordinate adverb clause of condition

Question 9.
All the discussions with these greats broadened my horizon.
(Rewrite beginning ‘My horizon…………’)
Answer:
My horizon was broadened by all the discussions with these greats.

Question 10.
Find from the text, a sentence that show past habit.
Answer:
We used to discuss about relativity, Big Bang, aesthetics, literature, philosophy, economics and many other subjects every day until late into the nights.

Question 11.
I learnt these values during my IIT days.
(Rewrite beginning ‘These values’.)
Answer:
These values were learnt by me during my IIT days.

Question 12.
It is very difficult to become a master or an expert in all these subjects. (Rewrite using ‘not’.)
Answer:
It is not at all easy to become a master or an expert in all these subjects.

Question 13.
I made a few mistakes, but learnt a lot about motivation. (Rewrite as a complex sentence.)
Answer:
Though I made a few mistakes, I learnt a lot about motivation.

Question 14.
I learnt a lot of things when I was running these large companies.
(Pick out the subordinate clause and state its type.)
Answer:
when I was running these large companies – Subordinate adverb clause of time.

Question 15.
You need to lead from the front.
(Add a question tag.)
Answer:
You need to lead from the front, don’t you?

Question 16.
I had also written 4 books with 500-700 pages each on Information Technology published by Tata McGraw-Hill. (Pick out the predicate.)
Answer:
predicate-had also written 4 books with 500-700 pages each on Information Technology published by Tata McGraw-Hill.

Vocabulary:

Question 1.
From the extract, prepare a word register of at least 6 words for:
‘Household appliances and objects’:
Answer:
fan, refrigerator, geyser, dining table, gas stove, air conditioner.

Question 2.
Match the columns:

Answer:

Question 3.
Choose the correct noun forms from those given in brackets:

1. elegant (elegance/elegantly)
2. solve (solving/solution)
3. develop (developmental/development)
4. logically (logical/logic)
5. appear (appearance/apparently)
6. including (inclusive/inclusion)

Answer:

1. elegant – elegance
2. solve – solution
3. develop – development
4. logically – logic
5. appear – appearance
6. including – inclusion

Question 4.
Write the verb forms of the following:

1. maximum
2. examination
3. challenging
4. beauty
5. quickly
6. admission

Answer:

1. maximum – maximise
2. examination – examine
3. challenging – challenge
4. beauty – beautify
5. quickly – quicken
6. admission – admit

Question 5.
Find out a word related to the game of cricket. List two meanings for it.
Answer:
Scoring:
1. general meaning: getting something
2. related to cricket: gaining runs

Question 6.
Guess the meaning of:

1. inferiority complex
2. sophisticated
3. arrogant

Answer:

1. inferiority complex – a feeling that you are not as good, as intelligent, as attractive, etc. as other people
2. sophisticated – smart and polished
3. arrogant – unpleasantly proud

Question 7.
Find out a word related to the game of cricket. List two meanings for it.
Answer:
Stumped: (Note: The word is not in the lesson but in the question on page 86)
1. general meaning : to be unable to answer a question or solve a problem because it is too difficult
2. related to cricket: being stumped is a method of dismissing a batsman.

Question 8.
Guess the meaning:
1. negotiate
2. at ease
Answer:
1. negotiate – to have formal discussions with someone in order to reach an agreement with them
2. at ease – comfortable.

Question 9.
Find the full forms of:

1. IIT
2. TFIR
3. BARC
4. TCP
5. IP

Answer:

1. IIT: Indian Institute of Technology
2. TIFR: Tata Institute of Fundamental Research
3. BARC: Bhabha Atomic Research Centre
4. TCP: Transmission Control Protocol
5. IP: Internet Protocol

Question 10.
Find the meaning of: anything under the sun
Answer:
anything under the sun-anything at all.

Question 11.
Find the full form of: GRE
Answer:
GRE – Graduate Record Examination

Question 12.
Match the following:

Answer:

1. Sociology – the study of the development, structure, and functioning of human society.
2. Economics – the branch of knowledge concerned with the production, consumption, and transfer of wealth.
3. Psychology – the scientific study of the human mind and its functions.
4. Archaelogy – the scientific study of material remains of past human life and activities.

Question 13.
From the extract find four words that form their antonyms by adding a prefix:
Answer:

1. important × unimportant
2. successful × unsuccessful
3. possible × impossible
4. written × unwritten

Question 14.
Write the past participles of:

1. learn
2. write
3. change
4. make

Answer:

1. learn – learnt
2. write – written
3. change – changed
4. make – made

Question 15.
Find out a word related to the game of cricket. List two meanings for it.
Answer:
target setting:
1. general meaning: deciding something that one hopes or intends to accomplish
2. related to cricket: deciding the number of runs to be achieved.

Question 16.
Give the adjective forms of the following:

1. humanity
2. rationality
3. humility
4. equality
5. curiosity
6. knowledge

Answer:

1. humanity – humane
2. rationality – rational
3. humility – humble
4. equality – equal
5. curiosity – curious
6. knowledge – knowledgeable

Non-Textual Grammar:

Do as directed:

Question 1.
To their astonishment they found a hissing snake stopping their way. (Rewrite using the verb form of the underlined word.)
Answer:
They were astonished to find a hissing snake stopping their way.

Question 2.
The minister spotted his cheerful face in the crowd and called out to him. (Rewrite using the present participle form of the verb ‘to spot’.)
Answer:
The minister, spotting his cheerful face in the crowd, called out to him./Spotting his cheerful face in the crowd, the minister called out to him.

Question 3.
He is a great king.
(Rewrite as an exclamatory sentence.)
Answer:
What a great king he is

Spot the error in the following sentences and rewrite them correctly:

Question 1.
Even though the laptop is expensive, but I wish to buy it for my mother.
Answer:
Even though the laptop is expensive, I wish to buy it for my mother.

Question 2.
The story should not exceed more than 800 words.
Answer:
The story should not exceed 800 words.

English Yuvakbharati 12th Full Digest Section 1 (Prose)

Class 12 English Chapter 1.7 Why We Travel Question Answer Maharashtra Board

Balbharti Yuvakbharati English 12th Digest Chapter 1.7 Why We Travel Notes, Textbook Exercise Important Questions and Answers.

12th Std English Chapter 1.7 Brainstorming Question Answer

12th English Digest Chapter 1.7 Why We Travel Textbook Questions and Answers

Question 1.
Share your views on how travelling can be a hobby:
Answer:
Students can discuss their views on travelling, both in India and in foreign countries, and how it can be a leisure time activity.

Question 2.
Discuss in the class the benefits of travelling and complete the web:

Answer:

Make a list of your expectations when you travel to some new place:
Answer:
(a) Food should be delicious and available whenever hungry.
(b) Travelling should be easy and comfortable.
(c) Hotel accommodation should be inexpensive and clean.
(d) Weather should be sunny and pleasant.

Question 3.
Discuss in the class the various types of travels. Add your own to ones given below:

Answer:

(A1)

Question 1.
Read the first two paragraphs and write down the reasons one needs to travel.
Answer:
One needs to travel:

1. initially, to lose ourselves next, to find ourselves
2. to open our hearts and eyes and learn more about the world than our newspapers tell us.
3. to bring our ignorance and knowledge to cultures which are rich in ways different from ours.
4. to become young fools again
5. to slow time down and to get taken in to fall in love once more
6. to escape into open solitudes, into aimlessness, into accepting dangers and risks
7. to sharpen the edge of life, and to taste hardship
8. to leave all one’s beliefs and certainties at home, and see everything in a different light

(A2)

Question (i)
Read the sentence ‘If a diploma can famously ……………. in cultural relativism.’ of this extract on page 67 of the textbook. Pick the sentence which gives the meaning of the above statement from the alternatives given below.
(a) A diploma certificate can be used as a passport and a passport can be used as a diploma certificate.
(b) If one has a diploma, he does not need a passport and if he has a passport, he does not need a diploma.
(c) One can acquire permission to travel to foreign countries for educational purposes based on one’s academic achievements, and travelling to foreign countries enriches one the most regarding the knowledge and wisdom of the world.
Answer:
(c) One can acquire permission to travel to foreign countries for educational purposes based on one’s academic achievements, and travelling to foreign countries enriches one the most regarding the knowledge and wisdom of the world.

Question (ii)
Prepare a list of the litterateurs and their quotations mentioned by the writer in the extract.
Answer:
Names of the litterateurs: Camus, Christopher Isherwood
Quotations: Camus said, “What gives value to travel is fear”- Christopher Isherwood once said, “The ideal travel book should be perhaps a little like a crime story in which you’re in search of something.”

Question (iii)
‘The real voyage of discovery consists not in seeing new places but in seeing with new eyes.’ – Marcel Proust. Justify with the help of the text.
Answer:
This means that we don’t really have to discover new landscapes or new sights to be in the real process of discovery. Often, we simply need to change our perspective, the way we look at things, to understand them and to raise them to a new, exhilarating level.

Question (iv)
Read the third paragraph and find the difference between a tourist and a traveller as revealed through the complaints made by them.
Answer:
1. A tourist is someone who does not leave his assumptions at home and complains, ‘Nothing here is the way it is at home’.
2. A traveller is someone who leaves his assumptions at home but grumbles, ‘Everything here is the same as it is in Cairo – or Cuzco or Kathmandu.’

Question (v)
Write sentences from the extract conveying the fact that travelling brings together the various cultures of the different parts of the world.
Answer:
1. You can teach them what they have to celebrate as much as you celebrate what they have to teach.
2. This, I think, is how tourism, which so obviously destroys cultures, can also resuscitate or revive them, how it has created new “traditional” dances in Bali, and caused craftsmen in India to pay s new attention to their works.

Question (vi)
By quoting Camus, the writer has stated that travelling emancipates us from circumstances and all the habits behind which we hide. Write in detail your views about that.
Answer:
When we are at home, we have set ideas and habits, which we are reluctant to change. We dress in a particular way and we behave in a particular way, because the people around us know us and expect that behaviour. We hide behind all this. However, when we travel, no one knows us and there are no expectations about a particular type of behaviour, dress or habits. Hence, we have a feeling of freedom and emancipation from our circumstances and habits.

(A3)

Question (i)
Read the following groups of words:

1. crooked angle
2. censored limits
3. impoverished places
4. walking video screens
5. living newspapers
6. searching questions

Discuss in pairs and make a list of some more adjectives like this and make sentences using them.
Answer:
1. burnt cottage
2. disturbed night
3. hidden house
4. missing necklace
5. probing questions
6. standing instructions
Sentences:
1. burnt cottage – The mystery of the burnt cottage was finally solved.
2. disturbed night – Rohan had a disturbed night because of the noise from the road construction.
3. hidden house – I could see the hidden house only after climbing a hill.
4. missing necklace – The detective was sure that the missing necklace would be soon found.
5. probing questions – The lawyer asked the witness some probing questions.
6. standing instructions – The queen had given standing instructions that she was never to be disturbed while sleeping.

Question 1.
Read the following sentence and pick out the phrasal verb.
We travel, then, in part just to shake up our complacencies.
Answer:
shake-up

(A4)

Question 1.
Read the following sentences carefully and find out the infinitives :
(a) We travel, initially, to lose ourselves; and we travel, next, to find ourselves.
(b) We travel to bring what little we can, …………
(c) Yet one of the subtler beauties of travel is that it enables you to bring new eyes to the people you encounter.
Answer:
(a) to lose, to find
(b) to bring
(c) to bring

Question (ii)
Combine the two sentences into one using the word given in the brackets:
(a) I go to Iceland. I visit the lunar spaces within me. (to)
(b) We have the opportunity. We come into contact with more essential parts of ourselves, (of)
(c) Romantic poets inaugurated an era of travel. They were great apostles of open eyes.
(d) The travel spins us around. It shows us the sights and values ordinarily ignored, (showing)
Answer:
(a) I go to Iceland to visit the lunar spaces within me.
(b) We have the opportunity of coming into contact with more essential parts of ourselves.
(c) Romantic poets, being great apostles of open eyes, inaugurated an era of travel.
(d) The travel spins us around, showing us the sights and values ordinarily ignored.

Question (iii)
Read the sentences given below and state whether the underlined words are gerunds or present participles.
(a) As it’s a hot day, many people are swimming
(b) This is a swimming pool.
(c) It’s very bad that children are begging.
(d) Begging is a curse on humanity.
Answer:
(a) present participle
(b) present participle
(c) present participle
(d) gerund

(A5)

Question 1.
Write an email to your friends about your proposed trek. You can take help of the points given below. You can keep your parents informed about it by adding them in BCC.

• A trek in the forest of Kodaikanal
• Time and duration
• Type of trek (cycle/ motorbike/ walk)
• Facilities provided
• Last date for registration
• Fees

(A6)

Question 1.
There is a boom in ‘Travel and Tourism’ career. Find information about different options in this field.

(A7)

Question (i)
Find information about:
(a) Fa Hien
(b) Huen Tsang
(c) Ibn Batuta
(d) Marco Polo
(e) Sir Richard Burton

Question (ii)
Further reading:

• ‘Childe Harold’s Pilgrimage’ – Lord Byron
• ‘Gulliver’s Travels’ – Jonathan Swift
• ‘Twenty Thousand Leagues Under The Sea’ – Jules Verne
• ‘Travelling Souls’ – Brian Bouldrey

Yuvakbharati English 12th Digest Chapter 1.7 Why We Travel Additional Important Questions and Answers

Read the extract and complete the activities given below:

Global Understanding:

Question 1.
Write the name of the litterateur and his quotation mentioned by the writer in the extract.
Answer:
Name of the litterateur – George Santayana.
Quotation:
George Santayana writes, “We need sometimes to escape into open solitudes, into aimlessness, into the moral holiday of running some pure hazard, in order to sharpen the edge of life, to taste hardship, and to be compelled to work desperately for a moment at no matter what.”

Question 2.
Based on the extract, complete the web:
(The answers are given directly and underlined.)
Answer:

Question 3.
From the extract, write the names of:
Answer:
1. 2 litterateurs : Proust, Hazlitt
2. 2 places : Bali, Tibet

Question 4.
Pick out the false statements and write them correctly :
1. Holidays help you to appreciate your own home more.
2. Tourism can also revive cultures.
3. The writer spent many days in Bali in temples.
4. The writer finds Iceland full of chatter and routine.
Answer:
False statements:
3. The writer spent many days in Bali in temples.
4. The writer finds Iceland full of chatter and routine.

Corrected statements:
3. The writer spent many days in Tibet in temples.
4. The writer finds Iceland quiet and empty.

Question 5.
Write the name of the litterateur and his quotation mentioned by the writer in the extract.
Answer:
Name of the litterateur – Oliver Cromwell Quotation : “A man never goes so far as when he doesn’t know where he is going.”

Question 6.
Write if the following statements are True or False. Correct the false statements :
1. The posters at McDonald’s outlet in Kyoto have pictures of places in San Francisco.
2. The young people in Kyoto McDonald’s outlet look very American.
3. The writer was born in America.
4. Cities like Sydney and Toronto are a mix of many cultures.
True statements:
1. The posters at McDonald’s outlet in Kyoto have pictures of places in San Francisco.
4. Cities like Sydney and Toronto are a mix of many cultures.

False statements:
2. The young people in Kyoto McDonald’s outlet look very American.
3. The writer was born in America.

Corrected statements:
2. The young people in Kyoto McDonald’s outlet look very Japanese.
3. The writer was born in England.

Question 7.
Write from the extract:
Answer:
1. Names of 4 cities: Kyoto, Toronto, Sydney, Addis Ababa
2. Names of two food items: Teriyaki McBurgers, Bacon Potato Pies.

Question 8.
Write the name of the litterateurs and their quotations mentioned by the writer in the extract.
Answer:
Names of the litterateurs: Sir John Mandeville, Emerson, Thoreau and Sir Thomas Browne.
Quotations: Emerson said, “Travelling is a fool’s paradise.”
Thoreau said, “I have travelled a good deal in Concord.”
Sir Thomas Browne sagely put it, “We carry within us the wonders we seek without us. There is Africa and her prodigies in us.”

Complex Factual:

Question 1.
Write sentences from the extract conveying the fact that travelling brings together the various cultures of the different parts of the world :
Answer:
1. We can become a kind of carrier pigeon in transporting back and forth what every culture needs.
2. I find that I always take Michael Jordan posters to Kyoto, and bring woven ikebana baskets back to California.
3. We become walking video screens and living newspapers, the only channels that can take people out of the censored limits of their homelands.
4. In closed or impoverished places, like Pagan or Lhasa or Havana, we are the eyes and ears of the people we meet, their only contact with the world outside and, very often, the closest, quite literally, they will ever come to Michael Jackson or Bill Clinton.
5. Not the least of the challenges of travel, therefore, is learning how to import – and export – dreams with tenderness.
6. We carry values and beliefs and news to the places we go.

Question 2.
Complete the following:
Travel spins us round in two ways at once:
Answer:
Travel spins us round in two ways at once: It shows us the sights and values and issues that we might ordinarily ignore. It also shows us all the parts of ourselves that might otherwise grow rusty. For in travelling to a truly foreign place, we inevitably travel to moods and states of mind that we’d otherwise ignore.

Question 3.
Write sentences from the extract conveying the fact that travelling brings together the various cultures of the different parts of the world.
Answer:
1. For when we go to France, we often migrate to French, and the more childlike self, simple and polite, that speaking a foreign language educes.
2. Even when I’m not speaking pidgin English in Hanoi, I’m simplified in a positive way, and concerned not with expressing myself, but simply making sense.

Question 4.
Write sentences from the extract conveying the fact that travelling brings together the various cultures of the different parts of the world.
Answer:
1. When we go abroad we are objects of scrutiny as much as the people we scrutinize, and we are being consumed by the cultures we consume, as much on the road as when we are at home.
2. At the very least, we are objects of speculation (and even desire), who can seem as exotic to the people around us as they do to us.

Question 5.
Write the sentences from the extract conveying the fact that travelling brings together the various cultures of the different parts of the world.
Answer:
1. When you go to a McDonald’s outlet in Kyoto, you will find Teriyaki McBurgers and Bacon Potato Pies.
2. The placemats offer maps of the great temples of the city, and the posters all around broadcast the wonders of San Francisco.
3. And-most crucial of all-the young people eating their Big Macs, with baseball caps worn backwards, and tight 501 jeans, are still utterly and inalienably Japanese in the way they move, they nod, they sip their Oolong teas – and never to be mistaken for the patrons of a McDonald’s outlet in Rio, Morocco or Managua.
4. These days a whole new realm of exotica arises out of the way one culture colours and appropriates the products of another,
5. The other factor complicating and exciting all of this is people, who are, more and more, themselves as many-tongued and mongrel as cities like Sydney or Toronto or Hong Kong.
6. Besides, even those who don’t move around the world find the world moving more and more around them. Walk just six blocks, in Queens or Berkeley, and you’re travelling through several cultures in as many minutes; get into a cab outside the White House, and you’re often in a piece of Addis Ababa.

Question 6.
Complete the following:
Answer:
1. Travel is a voyage into the imagination and is the conspiracy of perception and imagination.
2. Sir John Mandeville never visited the Far East but yet gave colourful accounts of it.
3. Emerson and Thoreau insist that reality is our creation and we invent the places we see as much as we do the books we read.

Question 7.
Complete the following, giving examples: (The answer is given directly.) The finest recent travel books are those that:
Answer:
1. undertake a parallel journey, matching the physical steps of a pilgrimage with the metaphysical steps of a questioning e.g. in Peter Matthiessen’s great “The Snow Leopard”.
2. chronicle a trip to the farthest reaches of human strangeness e.g. Oliver Sacks’ “Island of the Color-Blind,” which features a journey not just to a remote atoll in the Pacific, but to a realm where people actually see light differently).

Inference/Interpretation/Analysis:

Question 1.
Guess the difference : travel and travail:
Answer:
Travel guides us towards a better balance of wisdom and compassion, of seeing the world clearly and truly. Travail means agony, or hard toil, which will be the result of laborious travelling and hardships.

Question 2.
Describe the changes that come into us because of travels, especially to foreign countries.
Answer:
When we go abroad, we stay up late, do impulsive things and leave ourselves open to various experiences. We live for the moment, without any past or future; only the present. We may even become mysterious-to others, at first, and sometimes even to ourselves, behaving in new ways. We feel younger, as if we have been reborn.

Question 3.
Explain in your own words how travel can be a kind of ‘monasticism’.
Answer:
‘Monasticism’ means living like monks, living a self-disciplined life that is isolated from other people. When we travel, even if we are living in a luxury hotel, we live more simply than we normally do at home. We have no more possessions than what we can carry, we surrender ourselves to chance, and to whatever may come in our way. Hence, travel can be a kind of ‘monasticism’.

Question 4.
Travelling abroad make us the object of scrutiny. Justify this statement,
Answer:
When we go abroad, the local people there are curious about us and our culture. We seem exotic and different to them and they scrutinize our ways and behaviour to learn and understand more about us.

Question 5.
The writer calls himself ‘many-tongued’ and ‘mongrel’. Give reasons.
Answer:
‘Many-tongued’ means that he knows many languages; ‘mongrel’ here means someone who has a mixed upbringing, someone of mixed cultures. The writer knows many languages. He was born of Indian parents, in England, and he moved to America when he was 7 years old. Hence, he says that he cannot really call himself an Indian, an American or an Englishman.

Question 6.
‘Get into a cab outside the White House, and you’re often in a piece of Addis Ababa.’ Explain the meaning of this sentence.
Answer:
Addis Ababa is the capital of Ethiopia, Africa. The sentence means that the driver of the cab outside the White House was probably an African American, may be originally from Africa.

Question 7.
“We carry within us the wonders we seek without us.” Explain.
Answer:
This means that all the wonders and emotions are within us, and if we wish to, we can tap these forces. Everything is within our own hearts and imagination. Everything is internal. Whatever we find outside has first to be inside us for us to experience it. There is no necessity for any separate outside happenings for us to feel anything.

Personal Response:

Question 1.
Name the places you would like to visit the most. Give reasons to support your answer.
Answer:
I like to travel but I have not had much opportunity yet. I love seeing new places and meeting new people. I would love to travel to the North-Eastern parts of India and to foreign countries. I am also a nature lover and would love seeing high mountains, clear lakes and green pastures.

Question 2.
‘Travel helps you to appreciate your own home more’. Justify this statement.
Answer:
Holidays, especially holidays abroad, can certainly help us to appreciate our own homes more. For example, if we go to the African desert and see the problems they have with potable water supply, we will appreciate our own water resources more. If we see the problems faced by people living in very cold climates, we will appreciate the heat in our country, and even be grateful for it.

Question 3.
Do you think that people travel more, or in a different way, as compared to people fifty years back? Explain your view.
Answer:
Yes, people certainly travel more today. They also travel for different reasons. Fifty years back, in India, people generally travelled only for religious reasons or to meet relatives and family. Travelling for sightseeing was rarer. Today, in addition to these reasons, people also travel for fun, relaxation and sight-seeing. People also go on holidays abroad, which was not done often earlier.

Question 4.
Do you think that we must always seek new experiences and new places? Or do you feel that the best place is home, and we must never move?
Answer:
If we just stick to our own homes, we will be like the frog in the pond, which thought its small pond was the whole world. This is not advisable in the world of today. To be happy and successful, we must be broad-minded and unbiased. We must see what the world and other cultures have to offer. We must try to imbibe the best from other cultures and places.

Language Study:

Question 1.
We carry values and beliefs and news to the places we go.
(Rewrite using ‘not only but also.)
Answer:
We carry not only values and beliefs but also news to the places we go.

Question 2.
Travel is the best way we have of rescuing the humanity of places.
(Use an infinitive in place of the gerund.)
Answer:
Travel is the best way we have to rescue the humanity of places.

Question 3.
The beauty of this process was best described by George Santayana.
(Rewrite beginning George Santayana)
Answer:
George Santayana best described the beauty of this process.

Question 4.
Yet for me the first great joy of travelling is simply the luxury of leaving all my beliefs and certainties at home. (Pick out the finite verb and say whether the sentence is simple, compound or complex.)
Answer:
finite verb-is; simple sentence

Question 5.
Pick out the phrasal verb from this sentence:
Abroad is the place where we stay up late.
Answer:
stay up

Question 6.
Travelling is a way to reverse time. (Identify the part of speech of the underlined word.)
Answer:
travelling – gerund

Question 7.
I tend to believe more abroad than I do at home. (Rewrite using as….as..)
Answer:
I tend not to believe as much at home as I do abroad.

Question 8.
Pick out the phrasal verb from these sentences:
Answer:
1. I remember, in fact, after my first trip to Southeast Asia, more than a decade ago, how I would come back to my apartment in New York.
2. All, in that sense, believed in, “being moved”
Answer:
1. come back
2. believed in

Question 9.
Anyone witnessing this strange scene would have drawn the right conclusion.
(Rewrite using ‘who’)
Answer:
Anyone who witnessed this strange scene would have drawn the right conclusion.

Question 10.
I remember how I would come back to my apartment in New York. (Rewrite using ‘used, to’.)
Answer:
I remember how I used to come back to my apartment in New York.

Question 11.
We have to carry our sense of destination. (Rewrite beginning‘Our sense….’)
Answer:
Our sense of destination has to be carried by us.

Question 12.
The most valuable Pacifies we explore will always be the vast expanses within us.
(Rewrite using more…than..)
Answer:
We will never explore more valuable Pacifies than the vast expanses within us.

Question 13.
It keeps the mind nimble. (Rewrite using the present perfect tense of the verb.)
Answer:
It has kept the mind nimble.

Vocabulary:

Question 1.
Guess the meaning: riches are differently dispersed
Answer:
cultures that are rich in ways different from ours.

Question 2.
Find out a past/present participle from the extract that has been used as an adjective :
Answer:
crooked angle (crooked-past participle)

Question 3.
Find out two pairs of antonyms from the extract:
Answer:
1. lose × find
2. ignorance × knowledge

Question 4.
Guess the difference between provisional and provincial.
Answer:
Provisional means temporary, whereas provincial means limited in outlook narrow.

Question 5.
Find out from the extract a few past / present participles that have been used as adjectives:
1. walking video screens
2. censored limits
3. living newspapers
4. impoverished places
Answer:
censored, impoverished – past participles used as adjectives
walking, living – present participles used as adjectives

Question 6.
Pick out four proper nouns for places from the extract.
Answer:
Kyoto, Pagan, Lhasa, Havana.

Question 7.
Find from the extract one word for the following :
1. A Japanese art of flower arrangement
2. Satisfaction of one with oneself or one’s own achievements.
Answer:
1. ikebana
2. complacencies

Question 8.
Complete the table with the words given in the brackets:
(values celebrate now deeply discovery apprehend wonderfully distant quietude foreign appreciative spins)
Answer:

Question 9.
Find out a past/present participle from the extract that has been used as an adjective:
Answer:
searching questions (searching – present participle)

Question 10.
Discuss the pun implied by the writer, ecstasy (ex-stasis):
Answer:
ecstasy – great joy. ex-stasis – previous period of inactivity or boredom. The words sound alike but have different meanings.

Question 11.
Guess the meaning:

1. many-tongued
2. mongrel
3. inheritance
4. notions

Answer:

1. many-tongued – a person who speaks many languages.
2. mongrel – (here) someone who has a mixed upbringing, someone of mixed cultures.
3. inheritance – the acquisition of a possession, condition, or trait from past generations.
4. notions – ideas.

Question 12.
Match the adjectives in Column A with the nouns in Column B, with reference to the extract:

Answer:

1. great temples
2. new realm
3. typical specimen
4. essential notions
5. synthetic versions
6. foreign world

Question 13.
Give the adjective forms of:

1. perception
2. imagination
3. friendship
4. reality

Answer:

1. perception – perceptive
2. imagination – imaginative
3. friendship – friendly
4. reality – realistic

Question 14.
Give the verb forms of:

1. perception
2. imagination
3. friendship
4. conspiracy

Answer:

1. perception – perceive
2. imagination – imagine
3. friendship – befriend
4. conspiracy – conspire

Question 15.
Guess the meaning:

1. atoll
2. prejudice
3. fosters

Answer:

1. atoll – a coral island consisting of a reef surrounding a lagoon
2. prejudice – bias
3. fosters – encourages

Question 17.
Find from the extract the antonyms of:

1. worthless
2. public
3. nearest
4. familiar
5. outside
6. slow

Answer:

1. worthless × valuable
2. public × private
3. nearest × farthest
4. familiar × unfamiliar
5. outside × inside
6. slow × quick

Do as directed:

Question 1.
The queen loved her people and looked after the affairs of her kingdom well.
(Rewrite using ‘who’.)
Answer:
The queen, who loved her people, looked after the affairs of her kingdom well.

Question 2.
But I want to test this. (Change the voice.)
Answer:
But I want this to be tested.

Question 3.
The husband had a small smile on his lips while the wife looked sad.
(Rewrite beginning with ‘Though’)
Answer:
Though the husband had a small smile on his lips, the wife looked sad.

Spot the error in the following sentences and rewrite them correctly:

Question 1.
You must neither tell me the whole story or at least the first part of it.
Answer:
You must either tell me the whole story or at least the first part of it.

Question 2.
No sooner did the Minister begin speaking, some rogues started shouting loudly.
Answer:
No sooner did the Minister begin speaking, than some rogues started shouting loudly.

English Yuvakbharati 12th Full Digest Section 1 (Prose)

Class 12 English Chapter 1.6 Into the Wild Question Answer Maharashtra Board

Balbharti Yuvakbharati English 12th Digest Chapter 1.6 Into the Wild Notes, Textbook Exercise Important Questions and Answers.

12th Std English Chapter 1.6 Brainstorming Question Answer

12th English Digest Chapter 1.6 Into the Wild Textbook Questions and Answers

Question 1.
Narrate in your class any of the incidents of your life when you were extremely terrified or awestruck.
Answer:
(Points: alone on a lonely road – lost somewhere – seeing a beautiful sunset – seeing beautiful mountains, etc.)

Question 2.
Complete the given table regarding the factors/situations/reasons – why you sometimes get scared and the factors that add to it. Give possible solutions:
Answer:

Question 3.
Given below are various activities which you can pursue as your hobby, passion, or profession. Complete the table accordingly:

Answer:

Question 4.
Match the following ‘Wildlife Sanctuaries’ with their locations:

Answer:

(A1)

Question (i)
In pairs, discuss the professions and challenges one can take happily if one is really passionate about the job.
(Points – professions: photography, environmental conservation, writing, reporting, music, choreography, etc. challenges – low salary, difficulties with organizations, uncooperative colleagues, severe competition, etc.

Question (ii)
In groups, organize a role play activity associated with ‘Wildlife Expert’/‘Wildlife Photographer’/ ‘Wildlife Conservator’, explaining the differences and similarities involved in their profession.
(Students can find out the details of each profession from the internet and organize a role play.)

(A2)

Question (ii)
Correct the false statements:
1. Earlier Shaaz was in the field of finance.
2. The writer saw the fight between the two leopards.
3. The photograph of the old leopard made Shaaz famous.
4. Saya is a black panther.
Answer:
False statements:
2. The writer saw the fight between the two leopards.
3. The photograph of the old leopard made Shaaz famous.
Corrected statements:
2. The writer did not see the fight between the two leopards.
3. The photograph of the young leopard made Shaaz famous.

Question (iii)
Complete the given web:

Answer:

Question (iv)
Complete the following:

Answer:

Question (v)
Complete the flow chart stating the reactions of the petrified Langurs due to the presence of the Leopard.

Answer:

Question (vi)
Complete the web, describing each step taken by the writer as a solitary traveller while moving in the jungle with great precaution:

Answer:

Question (vii)
Complete the table explaining the qualities that you would like to imbibe from Nature within yourself and provide the reasons for the same:
Answer:

(A3)

Question (i)
Choose the appropriate phrase/ expression from the extract given in the brackets: (time and again, to one’s heart’s content, in a jiffy)
(a) I was on a diet for some days but today I am going to eat ……………… .
(b) Every mother scolds her children …………… for the overuse of the mobile phone.
(c) All their educational problems were sorted out ………….. because of the funds given by an NGO.
(d) Raj ran at a ……………… to catch the train.
Answer:
I was on a diet for some days but today I am going to eat to my heart’s content.
Every mother scolds her children time and again for the overuse of the mobile phone.
All their educational problems were sorted out in a jiffy because of the funds given by an NGO.
Raj ran at a frantic speed to catch the train.

(A4)

(i) Begin the following sentences with the words given in the brackets:

Question (a)
I can guide visitors. (Visitors….)
Answer:
Visitors can be guided by me.

Question (b)
Animals are paying me back. (I……..)
Answer:
I am being paid back by animals.

Question (c)
Madegowda is employed by The Bison.
(The Bison )
Answer:
The Bison employs Madegowda.

Question (d)
Older leopards like Pardus carry away livestock from villages. (Livestock….)
Answer:
Livestock are carried away from villages by older leopards like Pardus.

Question (e)
I have lost almost 80 per cent of a season’s yield of sugarcane. (Almost 80 per cent.)
Answer:
Almost 80 per cent of a season’s yield of sugarcane has been lost by me.

Question (f)
Tracking an animal also teaches you life lessons. (Life lessons)
Answer:
Life lessons are also taught by tracking an animal.

Question (g)
Many things have been taught to me by the forests. (The forests)
Answer:
The forests have taught me many things.

Question (h)
Resentment among locals towards the animals is created by this. (This)
Answer:
This creates resentment among locals towards the animals.

(ii) Rewrite the sentences by using ‘not only…… but also’:

Question (i)
Rewrite the sentences by using ‘not only….but also’:
1. The petrified Langurs speeded to the trees near and far and secured their places on the treetops.
2. Umbarzara is the haven for Tigers, Leopards and Sloth Bears.
3. I crossed the cement pillar and stones stacked by the Forest Development Corporation.
Answer:
1. The petrified Langurs not only speeded to the trees near and far but also secured their places on the treetops.
2. Umbarzara is the haven not only for Tigers but also for Leopards and Sloth Bears.
3. I crossed not only the cement pillar but also the stones stacked by the Forest Development Corporation.

(A5)

Question (i)
Your college has decided to celebrate the World Environment Day. Mr. Kiran Purandare has been invited as the ‘Chief Guest’ for the event. Imagine you are the Secretary of the ‘Nature Club’ of your college and you have to conduct an interview of Mr. Kiran Purandare. Frame 8/10 questions for the same.
Answer:
Questions to interview Mr Kiran Purandare

Good morning, Sir. On behalf of the Nature Club of our college, I congratulate you on your achievements. We also loved your book ‘Sakha Nagzira’. I would like to ask you a few questions. May I? Thank you.

1. Please tell us something about the ‘Environmental Studies’ Course that you studied’.
2. Are there any such courses in India, especially in Maharashtra?
3. How did you get interested in the conservation of the environment?
4. Do you think that we, in Maharashtra, are doing enough to look after our environment?
5. How can we get permission to spend time inside sanctuaries?
6. You were mostly a solitary traveller inside the forest. What was the reason for this?
7. Are there any excursions/expeditions in which you are going to participate, in the near future?
8. How can we help you in your work?
9. Any tips/message for our Nature Club?

Thank you, sir, for answering our questions so frankly. We wish you all the best in your future endeavours.

Question (ii)
Imagine you have visited the jungles of Nagarhole. Write a report, to be published in your college magazine/in a local newspaper.
Answer:
A Week in a Jungle

Mysuru, 13 May: Four of us from N.S. College, Mysuru, spent a week at Nagarhole National Park (Rajiv Gandhi National Park), located in Kodagu District.

It was an exhilarating and educative week. The park is filled with waterfalls, hills, valleys, streams and forests. It is famous for its rich population of animals and birds. The Bengal Tiger, Indian Leopard, Sloth Bear, Striped Hyena, etc. are the predators that can be spotted in the park. Herbivores like Elephants, Chital, Sambar Deer and Barking Deer are also spotted around the national park.

As it was the month of May, and the water holes were drying up, plenty of animals visited the lake, and we had a grand time observing their habits from the machaan which was built for tourists. We were particularly careful not to disturb the environment by talking loudly or playing music. Hence, the animals were at their natural best. We were thrilled to see a pair of Bengal Tigers and a Leopard.

It was wonderful to see these majestic animals from such a close distance. It is truly an unforgettable experience. We could not see the Sloth Bear, but there were plenty of elephants and deer. After an experience like this one, all four of us have decided to visit various sanctuaries and take an avid interest in the wildlife of India.
– Shantanu Pratap.

Question (iii)
Shaaz has contributed towards conserving the wild animals and their habitat. Your college has decided to spread the message in society and arrange a rally. Prepare an ‘Appeal’ to ensure maximum participation informing about the day, date and other relevant details.
Answer:
Come One Come All!
Come With Friends And Family!

We need your help to save our planet!
Every species is essential for the survival of the planet.
Hence, we need to protect and conserve wild animals and their habitat.
You are the One With A Voice
Protect The Ones Without A Voice

Participate in our rally.
N.S. College Grounds To Forest Office
Date: 12 November Time: 9 a.m.
Save Animals-They Will Save You!

Question (iv)
Nature is a great teacher and a guide. Complete the mind map as instructed as per the titled concept:

Answer:

(A6)

Question (i)
Surf the net and obtain more information about the conservation work done by Shaaz. Prepare posters to inspire others and display them on your college notice board.

Question (ii)
Find out the information about the I qualification and eligibility required in the professions related to wildlife such as …………

• Forest officer/Ranger
• Wildlife photographer
• Environmentalist
• Geologist
• Tour Manager

Yuvakbharati English 12th Digest Chapter 1.6 Into the Wild Additional Important Questions and Answers

Read the extract and complete the activities given below:

Global Understanding:

Question 1.
Pick out the sentences that are false and write them correctly:
1. The narrator had made notes of the langurs in the region.
2. One has to be really alert while walking in the jungle.
3. The leopard was petrified.
4. There was a lot of noise in the jungle.
Answer:
False sentences:
1. The narrator had made notes of the langurs in the region.
3. The leopard was petrified.
Correct sentences:
1. The narrator had made notes of the birds in the region.
2. The langurs were petrified.

Question 2.
Complete the following:
Answer:
1. Shaaz named the leopards:
(a) Saya
(b) Scarface
(c) Pardus
2. The visitors are welcomed because they can volunteer to teach a skills training class of their choice. This enables locals to find employment either at the numerous wildlife resorts in the region or in a city.

Question 3.
Correct the false statements:
1. BCRTI was founded out of the genuine urge to conserve the habitat of the wild life.
2. Shaaz failed to utilize the finance incurred out of tourism.
3. According to the local agriculturist seeing is more essential than listening.
4. There was no specific buffer zone around Nagarhole.
Answer:
False statements:
2. Shaaz failed to utilize the finance incurred out of tourism.
3. According to the local agriculturist seeing is more essential than listening.
Corrected statements :
2. Shaaz put the finance incurred out of tourism to good use.
3. According to the local agriculturist listening is more essential than seeing.

Complex Factual:

Question 1.
Pick out from the extract four sentences that show that the writer was frightened.
Answer:

1. The evening breeze flew through my wet curled hair.
2. My stomach was aching.
3. My legs were trembling.
4. The shaking of limbs had lessened a bit.

Question 2.
Describe the meaning of the acronym BCRTI and explain its benefits to the local people.
Answer:
The BCRTI is ‘Buffer Conflict Resolution Trust of India’. It’s an agency that educates villagers who live on the fringe of the forest on the importance of conservation. Under the BCRTI umbrella, Shaaz provides locals with vocational training, with the aim of educating them on the merits of conservation and to help them benefit from tourist currency. The visitors at the resort are welcome to volunteer to teach a skills training class of their choice. The acquired skills enable locals to find employment.

Inference/Interpretation/Analysis:

Question 1.
Explain: I was alone here like a fox:
Answer:
Foxes are solitary creatures. They move around and hunt alone. In the same way, the narrator was alone; he had come to the forest alone to do his research, and now he was going back to the village all alone. Hence, he compares himself to a fox.

Question 2.
Give the meaning of the word ‘hide’ in the context and give reasons for its usage here.
Answer:
A hide is a camouflaged shelter used to get a close view of wildlife. It is a place built to look like its surrounding. The writer was observing birds and noting their behaviour. If he was visible, the birds would not come near him or act in a natural manner. Hence, he had to build a hide, conceal himself in it and then observe birds unnoticed.

Question 3.
Give reasons:
Answer:
1. After meeting Raju, the writer and Raju both felt relaxed because now there were two of them-four eyes and four hands with a stick-to find their way out of the jungle and to battle predators.
2. The time was dreadful because it was evening and the sun was setting. Being alone in the jungle at night time with predators all around was dreadful.

Question 4.
What is called ‘silver lining’ of the trail by the writer? Why?
Answer:
The writer had lost his way in the jungle and was desperate to find a village and civilization. Then he found a bright red soil trail with the marks of a bicycle wheel on it. These marks showed that there was a village nearby. To the frightened and desperate writer, this was like a ‘silver lining’.

Question 5.
The writer said, “There still exists a jungle where we can get lost, isn’t this our good luck?” What does he mean by this?
Answer:
Human beings have tried to take over all the natural areas of the world. We have encroached on jungles and forests, and there are human inhabitations within the jungles too. To find a jungle where there is no sign of human life, and one can still get lost, shows that there are some areas untouched by humans and left to nature. That is what the writer called ‘our good luck’.

Question 6.
Describe Shaaz’s meetings with Scarface.
Answer:
One day, at sunset, Shaaz and his companions went round a blind turn and saw an old leopard, well past his prime. Close to him was another very young, good-looking male leopard who was soon to come into his prime. It was like looking at the past and the present. It was clear that there was going to be a fight. However, they had to leave as it was sunset.

The next day, when Shaaz went back to the spot, sitting on the high rock was Scarface, blood dripping from a gash across his face. He sat there like he was the king of the jungle, and Shaaz knew that he had taken over from the old leopard, and it was a new journey for both of them.

Question 7.
Find: The Bison is
Answer:
The Bison is an eco-friendly wildlife camp in South India. It offers some great opportunities for youngsters to learn about the area, people, the man-animal conflict, eco-tourism and hotel management.

Personal Response:

Question 1.
Describe a safari you have been on or a trip through a forest. Narrate your experience in brief.
Answer:
I have gone to the Periyar National Park in Kerala. It is in the Western Ghats. This wildlife sanctuary is home to tigers and elephants. There are also deer, leopards and Indian bison. I have also been on a boat ride in the Periyar Lake. It was a wonderful experience to see tigers drinking at the watering holes. I really enjoyed the experience and will repeat it as soon as I can.

Question 2.
Have you ever been lost/lost your way? Narrate the experience.
Answer:
Yes, once when I was in Panchgani with my family I got lost. I decided to go for a walk alone. I set out without finding out the name of the road on which our hotel was situated. As I was walking, it suddenly began to rain heavily, and got quite dark. When I looked around I found that I was in a sort of a jungle. I was terrified; then I met a villager, but he could not help me. I did not even have my cellphone with me. I was in tears when all at once I saw my hotel. I had walked round in circles! I was very relieved. It was indeed a frightening experience.

Question 3.
How do you relax at the end of a tiring day? Give a brief description.
Answer:
At the end of a tiring day, I pick up a nice book or watch a good film on TV or Netflix. This relaxes me completely. If I go to sleep j directly, I am too tired and do not get good sleep. But if I spend half an hour or so unwinding, I really feel relaxed and sleepy.

Question 4.
Would you like to meet wild animals face to face? Give reasons to support your answer.
Answer:
No, I would not. I like to see wild animals only on TV. I feel that we should not intrude into their territory, and leave them to live in peace. Besides, they are wild and not tame, and one never knows how they may behave. I have read about a lot of people being killed by wild animals.

Language Study:

Question 1.
The surroundings were reminding me.
(Rewrite, beginning the sentence with ‘I…)
Answer:
I was being reminded by the surroundings.

Question 2.
I had apparently entered in the sanctum sanctorum of a miracle called leopard.
(Pick out the finite verb/s and state the tense.)
Answer:
had entered – past perfect tense.

Question 3.
Raju was amazed at my solitary visits to Umbarzara.
(Rewrite beginning ‘My solitary’)
Answer:
My solitary visits to Umbarzara amazed Raju.

Question 3.
Then we both resumed our walking tour, (Identify the part of speech of the underlined word.)
Answer:
walking-present participle acting as an adjective.

Question 4.
I found a bright red soil trail. (Rewrite beginning with‘A ’.)
Answer:
A bright red soil trail was found by me.

Question 5.
I had no other way to climb the hillock before me. (Rewrite as an affirmative sentence.)
Answer:
This was the only way I had to climb the hillock before me.

Question 6.
I climbed one more hillock and tried to locate signs of human civilization. (Rewrite beginning ‘Climbing’.)
Answer:
Climbing one more hillock, I tried to locate signs of human civilization.

Question 7.
The behaviour of the first black panther is being documented. (They….)
Answer:
They are documenting the behaviour of the first black panther.

Question 8.
All the research on the animal has been done through camera traps. (They….)
Answer:
They have done all the research on the animal through camera traps.

Question 9.
Shaaz recalls the incident with great clarity.
(Rewrite the sentence replacing the underlined expression with a single word.)
Answer:
Shaaz recalls the incident clearly.

Question 10.
Unfortunately, the sun was setting and we had to leave. (Rewrite using ‘because’.)
Answer:
Unfortunately, we had to leave because the sun was setting.

Question 11.
Use the word ‘guide’ as a noun and a verb in two separate sentences:
Answer:
1. We can guide children to behave well. {verb)
2. I hired a local guide to show me the sights of the palace, {noun)

Question 12.
The black panther has taught me patience. (Rewrite using the adjective form of the underlined word.)
Answer:
The black panther has taught me to be patient.

Question 13.
Listening is a sense far more important than sight. (Rewrite using ‘as…as…’)
Answer:
Sight is a sense not as important as listening.

Vocabulary:

Question 1.
Guess the meaning of the following words :

1. upheaval
2. predator
3. hovering
4. antelope

Answer:

1. upheaval – uproar; disturbance.
2. predator – an animal that preys on other animals.
3. hovering – fluttering in the air.
4. antelope – deer-like animal with hollow horns.

Question 2.
Give the meaning of the phrase ‘to stay put’ and use it in your own sentence.
Answer:
to stay put:
Meaning: remain somewhere without moving.
Sentence: My mother told me to stay put near the entrance when she went to buy the train ticket.

Question 3.
Write two adjectives from the extract used for the leopard.
Answer:
mighty, elusive.

Question 4.
Choose the correct option for: spooked –
(a) frightened
(b) happy
(c) angry
Answer:
frightened

Question 5.
Find the contextual meaning of‘stacked’:
Answer:
stacked – piled one on top of the other

Question 6.
Guess the meaning of ‘in a jiffy’:
Answer:
in a jiffy – in a moment; very soon

Question 7.
Make sentences of your own using the words:
1. slumped
2. stumbled
Answer:
1. slumped: I was so tired after the trek that I slumped onto my bed and fell I asleep immediately.
2. stumbled: I did not see the stone in the middle of the road and stumbled over it.

Question 8.
Guess the meaning of:
1. ‘felines’
2. chronicler
Answer:
1. felines: belonging to the cat family,
2. chronicler: a person who records something.

Question 9.
Pick out two pairs of antonyms from the : extract:
Answer:
1. old × young
2. past × present

Question 10.
Write the noun forms of:

1. famous
2. enviable
3. collect
4. including

Answer:

1. famous – fame
2. enviable – envy
3. collect – collection
4. including – inclusion

Question 11.
Write the adjective forms of the following:

1. incursion
2. territory
3. resentment
4. occasion
5. employment
6. region

Answer:

1. incursion – incursive
2. territory – territorial
3. resentment – resentful
4. occasion – occasional
5. employment – employable
6. region – regional ?

Question 12.
Choose the correct simple past tense forms of the following from the brackets:

1. teach – (teached, teaching, taught)
2. lose – (loser, lost, loose)
3. put – (put, putted, putting)
4. learn – (lean, learnt, learns)

Answer:

1. teach – taught
2. lose – lost
3. put – put
4. learn – learnt.

Non Textual Grammar:

Do as directed:

Question 1.
He had won a prize in the drawing competition. (Rewrite using the future perfect tense of the verb.)
Answer:
He will have won a prize in the drawing competition.

Question 2.
How could I call him a liar? (Rewrite as an assertive sentence.)
Answer:
I could not call him a liar.

Question 3.
All other things are unimportant. (Add a question tag.)
Answer:
All other things are unimportant, aren’t they?

Spot the error in the following sentences and rewrite them correctly:

Question 1.
Unless you do not listen to his advice, I am not going to help you.
Answer:
Unless you listen to his advice, I am not going to help you./If you do not listen to his advice, I am not going to help you.

Question 2.
Hardly had I reached the airport where I heard about the change in plans.
Answer:
Hardly had I reached the airport when I heard about the change in plans.

English Yuvakbharati 12th Full Digest Section 1 (Prose)