Category: Class 9

Balbharti Maharashtra State Board Class 9 Sanskrit Solutions Aamod Chapter 10 पितृभक्तः नचिकेताः Notes, Textbook Exercise Important Questions and Answers.

Maharashtra State Board Class 9 Sanskrit Aamod Solutions Chapter 10 पितृभक्तः नचिकेताः

Sanskrit Aamod Std 9 Digest Chapter 10 पितृभक्तः नचिकेताः Textbook Questions and Answers

भाषाभ्यास:

1. एकवाक्येन उत्तरत।

प्रश्न अ.
वाजश्रवाः कः ?
उत्तरम् :
वाजश्रवाः दानपर: ब्राह्मणः।

प्रश्न आ.
दक्षिणायां किं यच्छेत् इति नियमः ?
उत्तरम् :
दक्षिणायां सर्वदा प्रियं वस्तु यच्छेत् इति नियमः।

प्रश्न इ.
वाजश्रवसः पुत्रः कः ?
उत्तरम् :
बाजश्रवस: पुत्र: नचिकेताः।

प्रश्न ई.
तृतीयवररूपेण नचिकेताः किम् अयाचत ?
उत्तरम् :
तृतीयवररूपेण नचिकेता: आत्मज्ञानम् अयाचत।

प्रश्न उ.
बालः नचिकेताः कति दिनानि यावत् यमस्य प्रतीक्षाम् अकरोत् ?
उत्तरम् :
बाल: नचिकेता: त्रीणिदिनानि यावत् यमस्य प्रतीक्षाम् अकरोत्।

2. माध्यमभाषया उत्तरत।

प्रश्न अ.
नचिकेता: यमपुरं किमर्थम् अगच्छत् ?
उत्तरम् :
‘पितृभक्त: नचिकेता: ही लहान पण अतिशय प्रगल्भ अशा ज्ञानपिपासू नचिकेताची कथा आहे. नचिकेताने आपले वडील वाजश्रवा यांना विश्वजित् यज्ञ संपन्न झाल्यावर भाकड गायी दक्षिणा म्हणून देताना पाहिले. दक्षिणा म्हणून सर्वात प्रिय वस्तू द्यावी असा नियम होता, त्यामुळे अयोग्य दक्षिणा देण्याचे पाप लागून आपले वडील नरकात जातील की काय अशी नचिकेताला भिती वाटली.

त्याने वडिलांना विचारले “तुम्हाला सर्वात प्रिय असे काय आहे?” वडिलांनी त्याला लगेच सांगितले की नचिकेताच त्यांना सर्वात प्रिय आहे. नचिकेताने हे ऐकून त्यांना विचारले. “मग तुम्ही मला कोणाला दान करणार?” वडिलांनी दुर्लक्ष करुन सुद्धा नचिकेता तोच प्रश्न विचारत राहिला.

शेवटी चिडून वाजश्रवा म्हणाला “मी तुला मृत्यूला देईन!” वडील चिडून बोलत हे कळूनसुद्धा वडिलांच्या आज्ञेचे पालन करायचे आहेत म्हणून नचिकेता यमाच्या घरी गेला. नचिकेता इतका आज्ञाधारी मुलगा होता की वडिलांची आज्ञा मोडायची नाही म्हणून मृत्यूच्या घरी जाताना सुद्धा त्याने किंचितसाही विचार केला नाही. वडिलांच्या आज्ञेचे पालन करण्यासाठी तो अतिशय तत्पर होता.

In the lesson ‘पितृभक्त: नचिकेता:’ there is story of a small boy Nachiketa who was very thirsty for knowledge. Once the little Nachiketa saw his father giving the old, unmilkable cows in charity to the Brahmins after performing Vishwajit sacrifice.

But the rule was that the most beloved thing has to be given in donation. So Nachiketa was scared that his father might attain hell if he performs improper donation. So he asks his father what was the most dear to him. His father answered that Nachiketa was most dear to him.

So Nachika asked whom he would be given to. Nachiketa kept asking this again and again even when his father ignored him. Nachiketa didn’t give up. His father got angry and told him that he would give him to the death. He knew that his father said so in anger.

Still, he went to the abode of Yama to follow his Father’s order. Nachiketa was such a well-behaved son that he didn’t even think once before following his father’s order.

प्रश्न आ.
के त्रयः वरा: नचिकेतसा याचिताः ?
उत्तरम् :
‘पितृभक्त नचिकेता’ या पाठामध्ये यम-नचिकेता संवाद आला आहे. या संवादातून नचिकेताची जिज्ञासू वृत्ती दिसून येते. वडिलांची आज्ञा पाळण्यासाठी नचिकेता यमाच्या घरी गेला तेव्हा यम तिथे नव्हता. नचिकेताने काहीही न खाता पिता तीन दिवस यमाची वाट पाहिली. चौथ्या दिवशी यम परतला तेव्हा त्याला लहानग्या नचिकेताची खूप दया आली.

नचिकेता तीन दिवस तिथे थांबला म्हणून यमाने नचिकेताला तीन वर मागण्यास सांगितले. नचिकेताने वडिलांचा राग जाऊ दे असा पहिला वर मागितला आणि स्वर्ग प्राप्त करून देणारी अशी अग्निविद्या दुसरा वर म्हणून मागितली. तिसरा वर म्हणून नचिकेताने सामान्य माणसाला तसेच भल्या भल्या विद्वानांनासुद्धा मिळवण्यासाठी अशक्यप्राय असणारे असे आत्मज्ञान मागितले. नचिकेता वयाने लहान असला तरी सुद्धा त्याला असामान्य अशी बुद्धी आणि ज्ञानपिपासा लाभली होती.

In the story ‘पितृभक्त : नचिकेता:’ an incident of small Nachiketa who is eager to attain the ‘knowledge of self is told. When Nachiketa went to Antioch to obey his father’s order. But Yama was not there. Nachiketa waited there for three days, without eating or drinking anything.

When Yama returned on the fourth day his heart went out of compassion for Nachiketa. Yama offered Nachiketa three boons. Nachiketa asked to let his father’s anger get pacified as the first boon and the Agnividya as the second one.

As the third boon, he asked for knowledge of the self which was very difficult to attain even for the learned let alone a normal human being Even if he was young Nachiketa was blessed with immense maturity and great and thirst for knowledge.

Sanskrit Aamod Class 9 Textbook Solutions Chapter 10 पितृभक्तः नचिकेताः Additional Important Questions and Answers

एकवाक्येन उत्तरत।

प्रश्न 1.
वाजश्रवाः दक्षिणारूपेण का: अयच्छत् ?
उत्तरम् :
वाजश्रवा दक्षिणारूपेण दुग्धदाने असमर्था: दुर्बला: वृद्धा: च धेनू: अयच्छत्।

प्रश्न 2.
वाजश्रवस: प्रियः कः अस्ति?
उत्तरम् :
वाजश्रवस: प्रिय: स्वपुत्र: नचिकेता: अस्ति।

प्रश्न 3.
नचिकेता: किमर्थं यमपुरम् अगच्छत्?
उत्तरम् :
नचिकेताः पितुः आदेशपालनार्थ यमपुरम् अगच्छत्।

प्रश्न 4.
यमः किमर्थ चकित: अभवतः?
उत्तरम् :
अल्पवयसः बालस्य प्रगल्भा ज्ञानतृष्णां दृष्ट्वा यमः चकितः अभवतः।

प्रश्न 5.
यम: नचिकेतसे कति वरान् अयच्छत्?
उत्तरम् :
यम: नचिकेतसे त्रीन् वरान् अयच्छत्।

सत्यं वा असत्यं लिखत।

प्रश्न 1.

1. वाजश्रवाः नाम दानपर: द्विज: आसीत्।
2. वाजश्रवाः सबलाः धेनू: अयच्छत्।
3. असमीचीनदानेन पिता स्वर्ग गमिष्यति इति नचिकेतस: भीतिः ।
4. पिता क्रोधावेशे उक्तवान् इति नचिकेता: न अजानात् ।
5. नचिकेता: त्रीणि दिनानि यावत् यमस्य प्रतीक्षाम् अकरोत्।
6. पिता कुद्धः अभवत्।।
7. प्रथमवररूपेण नचिकेता: आत्मज्ञानम् अयाचत।
8. यमः तृतीयं वरं न अथच्छत्।

उत्तरम् :

1. सत्यम्
2. असत्यम्
3. असत्यम्
4. असत्यम्
5. सत्यम्
6. सत्यम्
7. असत्यम्
8. असत्यम्

कः कं वदति।

प्रश्न 1.

1. वत्स, त्वमेव मम प्रियतमः।
2. किं तव अतीव प्रियम्?
3. “तर्हि मां कस्मै दास्यति, भवान् ?”
4. “अहं त्वां मृत्यवे ददामि”।

उत्तरम् :

1. वाजश्रवाः नचिकेतसं वदति।
2. नचिकेता: वाजश्रवसं वदति।
3. नचिकेता: वाजश्रवसं वदति।
4. वाजश्रवाः नचिकेतसं वदति।

प्रश्न 2.
“स्वर्गसाधिकाम् अग्निविद्यां दत्त्वा माम् अनुगृह्णातु।”
उत्तरम् :
नचिकेता: यमं वदति।

शब्दस्य वर्णविग्रहं कुरुत।

• दक्षिणायाम् – द् + अ + क् + ष् + इ + ण् + आ + य् + आ + म्।
• असमर्थाः – अ + स् + अ + म् + अ + र् + थ् + आः।
• वाजश्रवाः – व् + आ + ज् + अ + श + र् + अ + व् + आ:।
• यज्ञम् – य् + अ + ज् + ञ् + अ + म्।
• क्रुद्धः – क् + र् + उ + द् + ध् + अः।
• नचिकेतसम् – न् + अ + व् + इ + क् + ए + त् + अ + स् + अ + म्।
• तर्हि – त् + अ + र् + ह् + इ।
• त्रिवारम् – त् + र् + इ + व् + आ + र् + अ + म्।
• क्षुधातेम – क् + ष् + उ + ध् + आ + र + त् + अ + म्।
• दृष्ट्वा – द् + ऋ + ष् + ट् + व् + आ।
• क्रोध: – क् + र + ओ + ध् + अः।
• प्रगल्भा – प् + र + अ + ग् + अ + ल् + भ् + आ।

प्रश्ननिर्माणं कुरुत।

1. वाजश्रवाः नाम दानपर: ब्राह्मणः आसीत्।
2. वाजश्रवाः विश्वजित्-यज्ञम् अकरोत्।
3. दक्षिणायां प्रियं वस्तु यच्छेत्।
4. अहं त्वां मृत्यवे दास्यामि।
5. स: यमपुरम् अगच्छत्।
6. स: त्रीणि दिनानि यावत् प्रतीक्षाम् अकरोत्।
7. पितुः आदेशपालनार्थ नचिकेताः यमपुरम् अगच्छत्।
8. चतुर्थ दिवसे यम: यमपुरं प्राप्तः।
9. नचिकेता: आत्मज्ञानम् अयाचत।
10. नचिकेतस: निर्णयः निश्चलः।

उत्तरम् :

1. क: दानपर: ब्राह्मण: आसीत् ?
2. वाजश्रवाः किम् अकरोत्?
3. दक्षिणायां कीदृशं वस्तु यच्छेत्?
4. अहं त्वां कस्मै दास्यामि?
5. सः कुत्र अगच्छत्?
6. स: कति दिनानि यावत् प्रतीक्षाम् अकरोत्?
7. नचिकेता: किमर्थं यमपुरम् अगच्छत्?
8. यमः कदा यमपुरं प्राप्त:?
9. नचिकेताः किम् अयाचत?
10. नचिकेतस: निर्णयः कीदृशः?

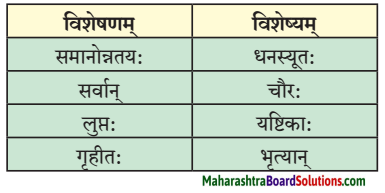
विशेषण-विशेष्य-सम्बन्धः।

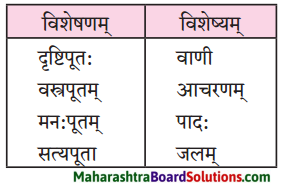
प्रश्न 1.
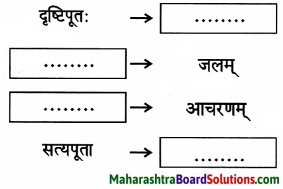
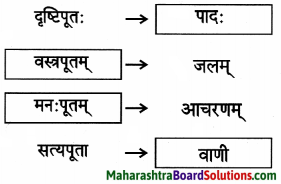
गद्यांशात् “धेनवः” इति पदस्य कृते विशेषणानि लिखत।
उत्तरम् :
असमर्थाः, दुर्बलाः, वृद्धाः।

प्रश्न 2.

उत्तरम् :

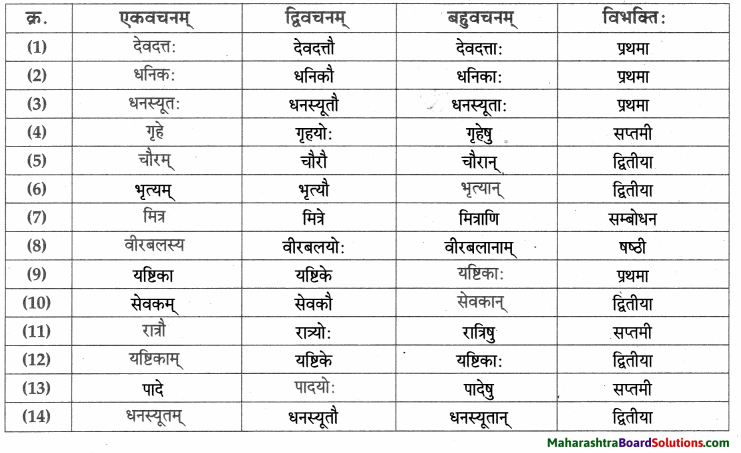
विभक्त्यन्तरूपाणि।

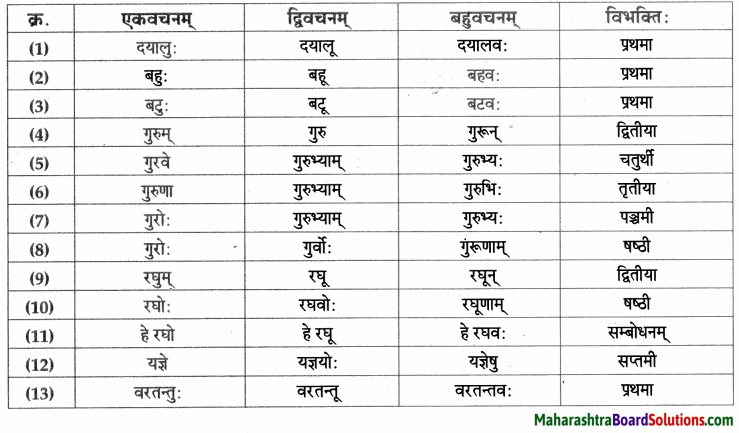
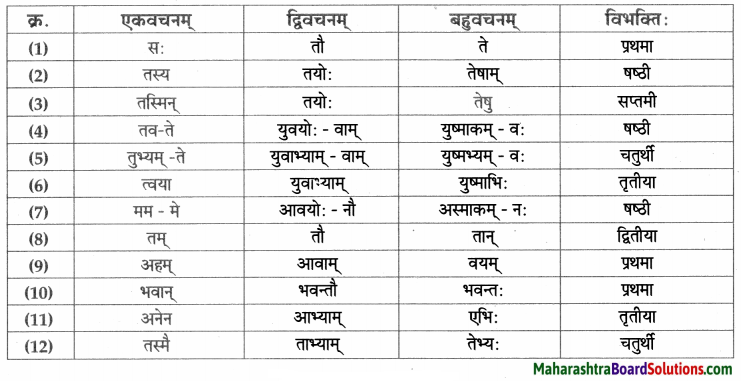
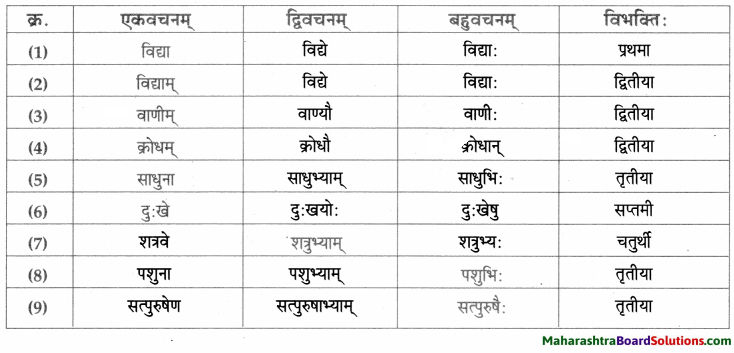
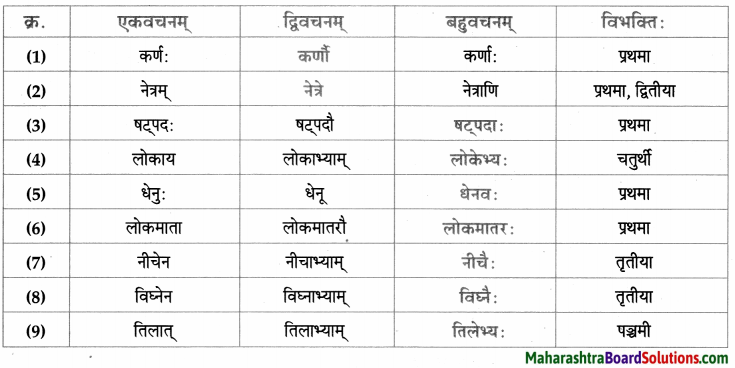
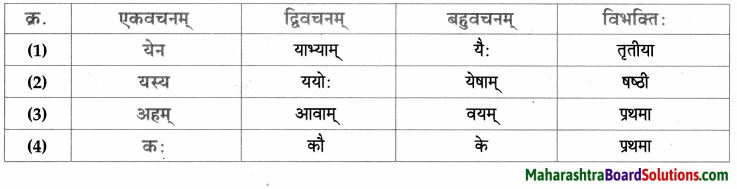
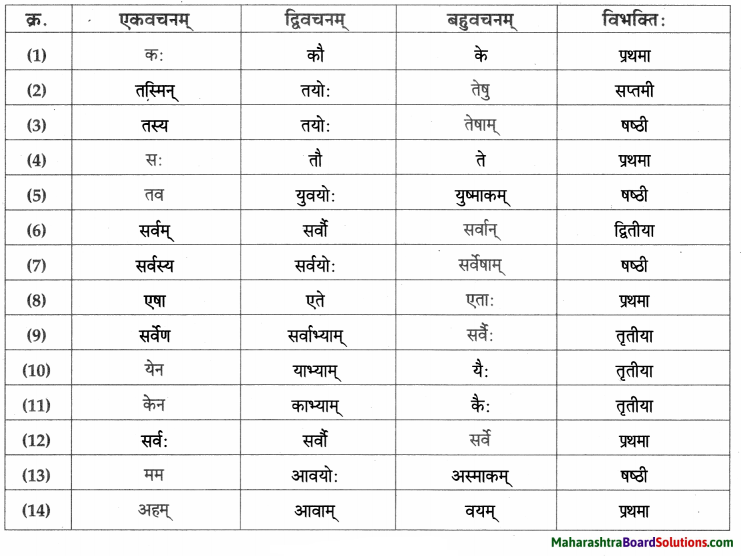
• प्रथमा – वाजश्रवाः, सः, बाह्मणः, वस्तु, पिता, पुत्रः, त्वम्, नचिकेताः, किम्, नचिकेताः, पिता, दिनानि, वाजश्रवाः, यमः हृदयम्, बालकः, मर्त्यः, ज्ञातुकामः, नचिकेताः।
• द्वितीया – पितरम्, यज्ञम, दक्षिणाम्, नचिकेतसम्, यमपुरम, प्रतीक्षाम्, वरम्, अग्निविद्याम्, माम्, प्रार्थनाम्, नचिकेतसम्।
• तृतीया – दक्षिणारूपेण, भीत्या, वाजश्रवसा, नचिकेतसा, आनन्देन, प्रलोभनैः।
• चतुर्थी – ब्राह्मणेभ्यः, कस्मै, मृत्यवे, तस्मै।
• पञ्चमी – तृतीयवरात्।
• षष्ठी – मम, तस्य, तव, यमस्य, पितुः, मम, जनकस्य, वाजश्रवसः, तस्य, नचिकेतसः।
• सप्तमी – दक्षिणायाम्, यज्ञे, यमपुरे, क्रोधावेशे, चतुर्थे, दिवसे, अन्ते।

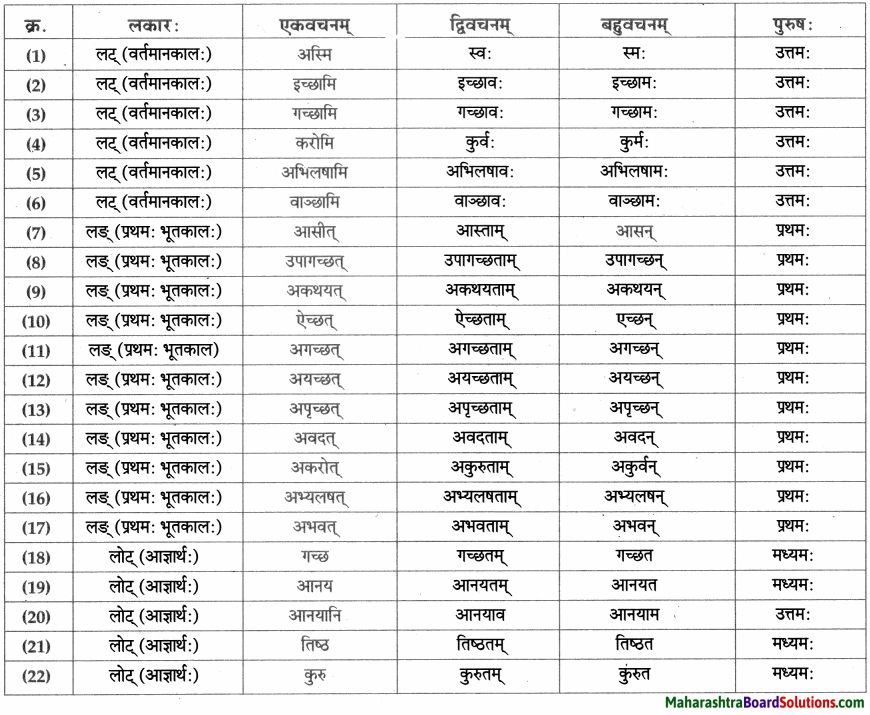
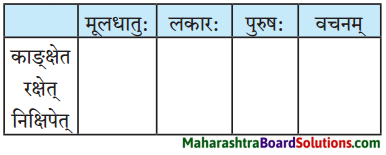
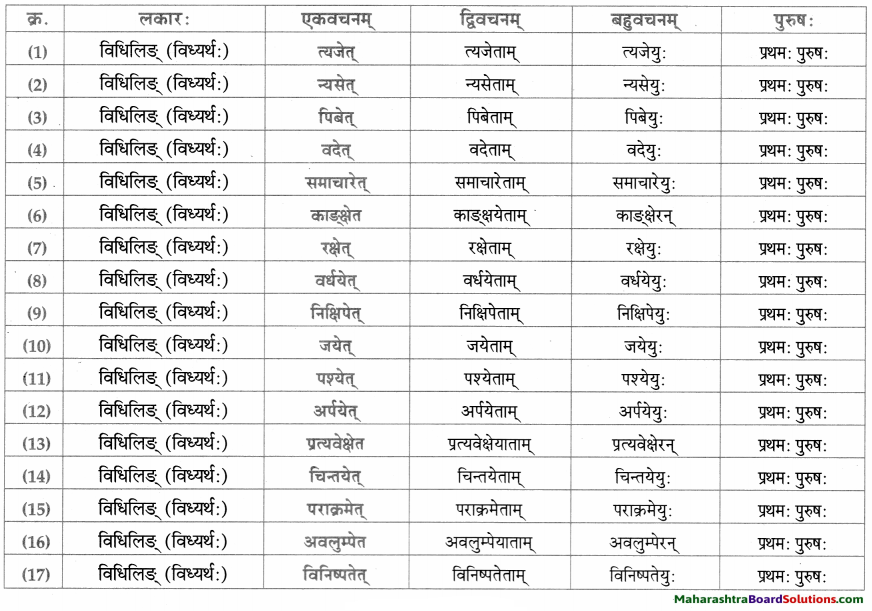
लकारं लिखत।

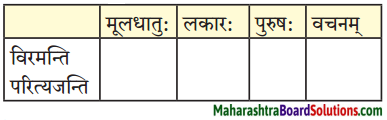
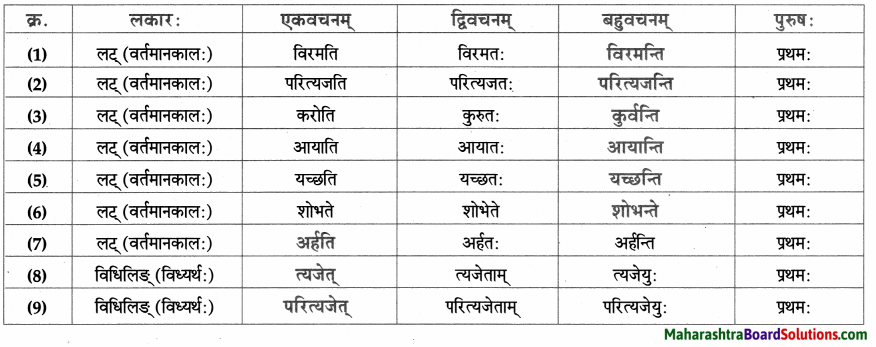
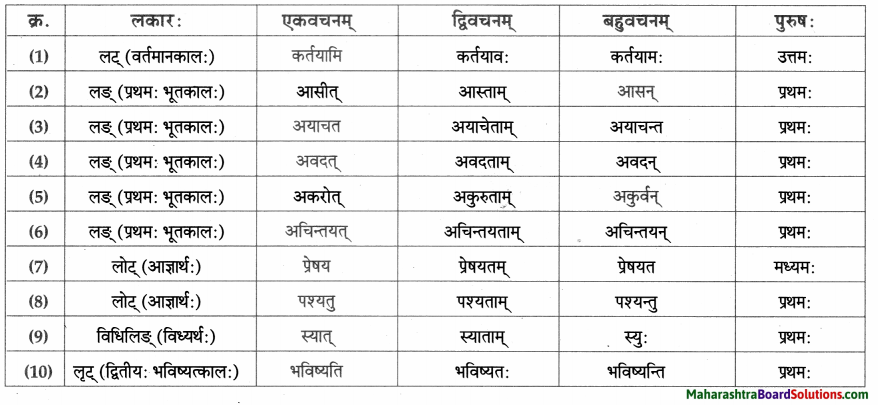
• आसीत् – अस् धातुः द्वितीयगणः परस्मैपदं लङ्लकार: प्रथमपुरुष: एकवचनम्।
• अकरोत् – कृ धातुः अष्टमगण: उभयपदम् अत्र परस्मैपदं प्रथमपुरुष: एकवचनम्।
• अयच्छत् – ‘दा-यच्छ्’ प्रथमगणः परस्मैपदं लङ्लकार: प्रथमपुरुष: एकवचनम्।
• गमिष्यति – गम्-गच्छ् धातुः प्रथमगणः परस्मैपदं लुट्लकार: प्रथमपुरुष: एकवचनम्।
• यच्छेत – दा-यच्छ् धातुः, प्रथमगणः, परस्मैपदं, विधिलिङ्लकार: प्रथमपुरुषः एकवचनम्।
• दास्यति – दा धातुः प्रथमगण: तृतीयगण: परस्मैपदं लुट्लकार: प्रथमपुरुष: एकवचनम्।
• ददामि – दा धातुः तृतीयगणः उभयपदम् अत्र परस्मैपदं लट्लकार: उत्तमपुरुषः एकवचनम्।
• अवदत् – वद् धातुः प्रथमगणः परस्मैपदं लङ्लकार: प्रथमपुरुष: एकवचनम्।
• अजानात् – ज्ञा धातुः नवमगणः उभयपदम् अत्र परस्मैपदं लङ्लकारः प्रथमपुरुष: एकवचनम्।
• अद्रवत् – द्रु-द्रव् धातुः प्रथमगणः परस्मैपदं लङ्लकार: प्रथमपुरुष: एकवचनम्।
• याचस्व – याच् धातुः प्रथमगण: आत्मनेपदं लोट्लकार: मध्यमपुरुषः एकवचनम्।
• अयाचत – याच् धातुः प्रथमगण: आत्मनेपदं लङ्लकार: प्रथमपुरुष: एकवचनम्।
• अनुगृह्यतु – अनु + ग्रह् धातुः नवमगण: उभयपदम् अत्र परस्मैपदं लोट्लकार : प्रथमपुरुष: एकवचनम्।
• उपादिशत्- उप् + दिश् धातुः षष्ठगण: उभयपदम् अत्र परस्मैपदं लङ्लकारः प्रथमपुरुष: एकवचनम्।

उचितं पर्यायं चिनुत ।

प्रश्न 1.
अहं त्वां ……………… ददामि।
(अ) मृत्यवे
(आ) इन्द्राय
उत्तरम् :
(अ) मृत्यवे

प्रश्न 2.
यमपुरे यमः ……………… ।
(अ) अनुपस्थितः
(आ) उपस्थितः
उत्तरम् :
(अ) अनुपस्थितः

प्रश्न 3.
नचिकेता: …………….. दिनानि यावत् प्रतीक्षाम् अकरोत्।
(अ) चत्वारि
(आ) त्रीणि
उत्तरम् :
(आ) त्रीणि

प्रश्न 4.
………….. यमपुरम् अगच्छत्।
(अ) भिक्षाटनार्थम्
(आ) आदेशपालनार्थम्
उत्तरम् :
(आ) आदेशपालनार्थम्

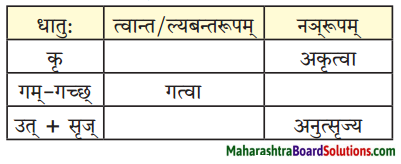
त्वान्त/ल्यबन्त/तुमन्त अव्ययानि।

समानार्थकशब्दं योजयित्वा वाक्यं पुनर्लिखत।

1. यज्ञ: – सः विश्वजित् – यज्ञम् अकरोत्। – स: विश्वजित्-यागम् अकरोत्।
2. पुत्रः – तस्य पुत्र: नचिकेता: अपश्यत्। – तस्य आत्मज: नचिकेता: अपश्यत् ।

व्याकरणम् :

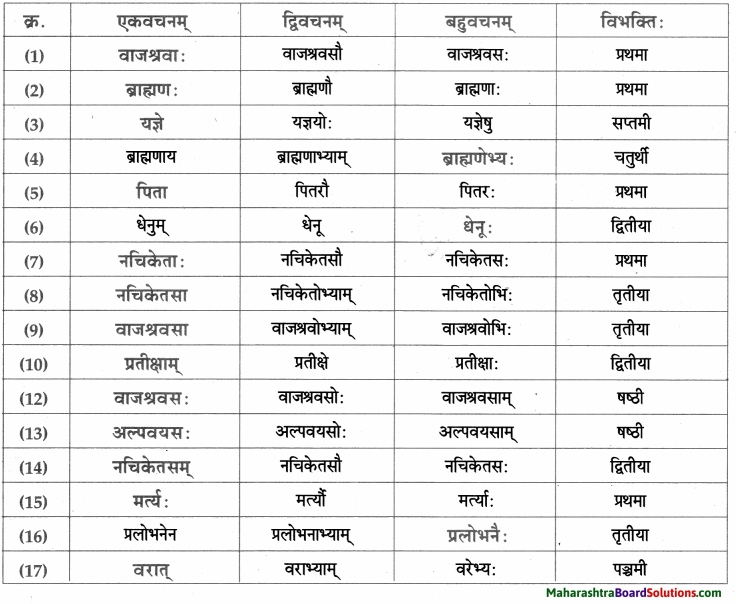
नाम – तालिका।

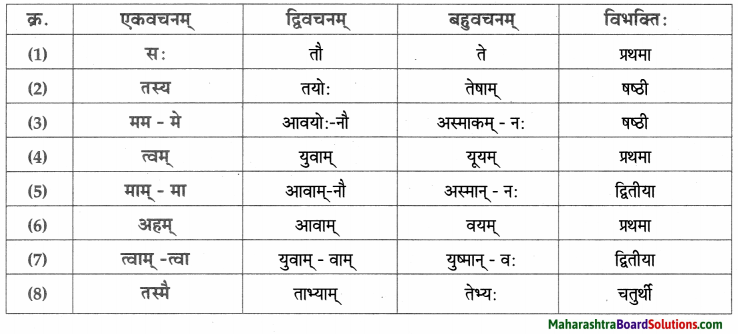
सर्वनाम – तालिका।

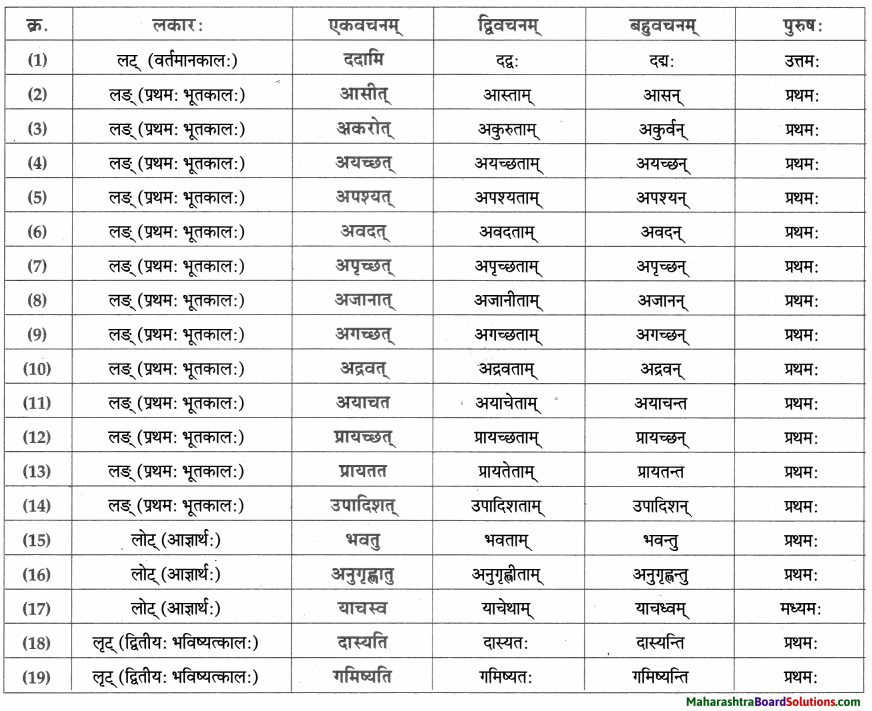
धातु – तालिका।

समासाः

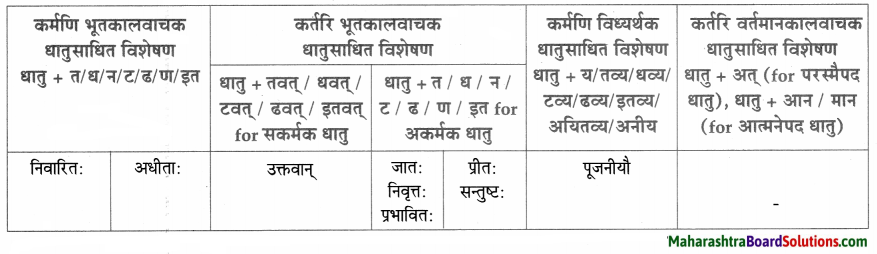
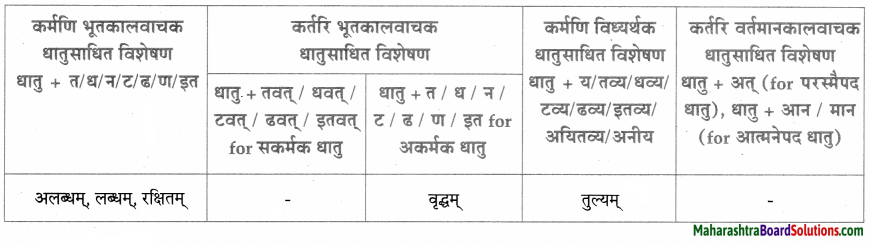
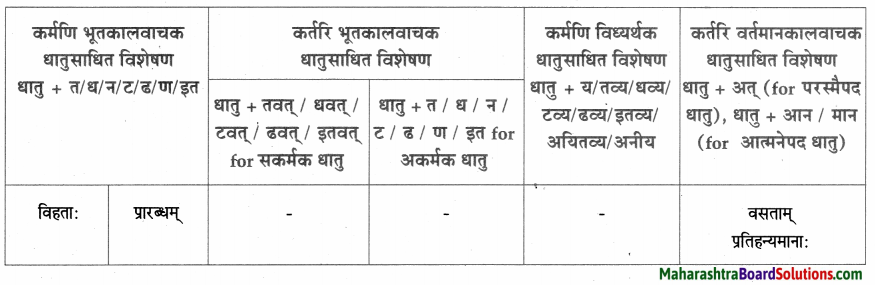
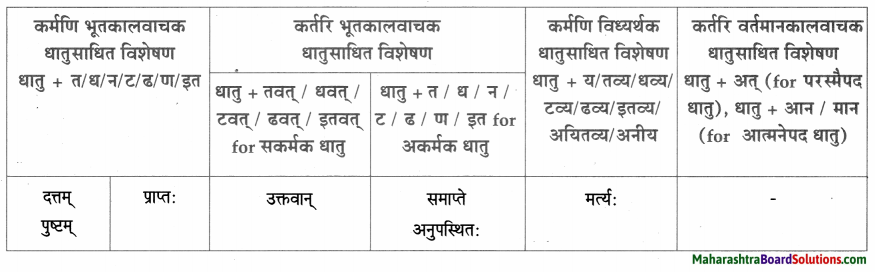
धातुसाधितविशेषणानि।

पितृभक्तः नचिकेताः Summary in Marathi and English

प्रस्तावना :

वेद, ब्राह्मणग्रंथ, आरण्यके, उपनिषदे प्राचीन भारतीय साहित्याचा भाग आहेत. त्यातील उपनिषदे भारतीय तत्त्वज्ञानाचे मूळ आहेतच शिवाय अनेक महत्त्वाची मूल्ये सांगणाऱ्या सुंदर कथा हे त्याचे वैशिष्य आहे नचिकेता हा एक लहान हुशार मुलगा आहे जो आपल्या वडिलांना पापापासून परावृत्त करण्याचा प्रयत्न करतो. ही पितृप्रेमाची कथा आपल्याला वडीलधाऱ्यांचा आदर करायला शिकवते. “पितृदेवो भव’ हे तत्त्व सांगतानाच ही कथा प्राचीन यज्ञसंस्थेविषयी, त्यातील दानाविषयी सुद्धा सांगते.

Our ancient Vedic literature comprises of the Vedas, Brahmanas, Aranyakas and Upanishad. The Upanishads are not just a collection of philosophical concepts, but rich treasures of knowledge. Through Upanishads, absolute values can be instilled as they contain many simple yet thought-provoking stories.

There are several Upanishads through tent of them are considered the main ones. One of the ten main Upanishads is Kathopanishad. The story presented here is a part of the famous dialogue between Yama and Nachiketa from the Kathopanishad.

Nachiketa uns a young intelligent lad who tried to prevent his father afar from committing a sin. This story is one of the best examples that conveys the value of love and respect towards the father. Not only does this story depict fugeat a but also presents in what form donation can be done.

परिच्छेद : 1

वाजश्रवाः …………………. प्रियतमः ।
वाजश्रवाः नाम दानपर: ब्राह्मण: आसीत्। एकदा स: विश्वजित्-यज्ञम् अकरोत्। समाप्ते यज्ञे सः ब्राह्मणेभ्य: दक्षिणाम् अयच्छत्। दक्षिणायां सर्वदा प्रियं वस्तु यच्छेत् इति नियमः। किन्तु पिता वाजश्रवाः तु दक्षिणारूपेण दुग्धदाने असमर्थाः दुर्बलाः वृद्धाः च धेनूः अयच्छत्। तस्य पुत्र: नचिकेता: तद् अपश्यत्। असमीचीनदानेन पिता मे नरकं गमिष्यति इति भीत्या सः पितरम् अपृच्छत्, “पितः, किं तव अतीव प्रियम्?” झटिति पिता अवदत, “वत्स, त्वमेव मम प्रियतमः।”

अनुवादः

वाजश्रवा नावाचा अतिश दानशूर ब्राह्मण होता. एकदा त्याने विश्वजितयज्ञ केला. यज्ञाच्या सांगतेच्या वेळी त्याने ब्राह्मणांना दक्षिणा दिली. दक्षिणेमध्ये नेहमी सर्वात प्रिय वस्तू द्यावी असा नियम आहे.

परंतु वाजश्रव्याने दक्षिणा म्हणून दूध न देऊ शकणाऱ्या, (भाकड) अशक्त आणि म्हाताऱ्या गायी दिल्या. त्याचा मुलगा नचिकेता याने ते पाहिले. अयोग्य दानामुळे माझे वडील नरकात जातील या भितीने त्याने वडिलांना विचारले, “बाबा! तुम्हाला सगळ्यात प्रिय काय आहे?” वडिलांनी पटकन उत्तर दिले, “तूच मला सर्वात प्रिय आहेस.”

There was a charitable Brahmin named Vajashrava. Once he performed the Vishwajit sacrifice When the sacrifice was over he gave donations to the brahmins. The rule is whatever is the dearest should be donated. But father Vajashrava gave old and weak cows which were unable to give milk in the form of donation.

His son Nachiketa saw that and due to the fear that his father might attain hell on account of improper donation he asked his father, “O father, what is most dear to you?” The father immediately answered, “Child! you are dear to me.

परिच्छेद : 2

नचिकेताः पुनः अपृच्छत् …………………. प्रतीक्षाम् अकरोत्।

नचिकेताः पुन: अपृच्छत, “तर्हि मां कस्मै दास्यति भवान् ?” वाजश्रवसा किमपि उत्तरं न दत्तम्। द्विवार त्रिवार नचिकेतसा तदेव पृष्टम् । तदा कुद्धः भूत्वा पिता नचिकेतसम् ‘अहं त्वां मृत्यवे ददामि| इति अवदत्। पिता क्रोधावेशे एवम् उक्तवान् इति नचिकेताः अजानत्। तथापि पितुः आदेशपालनार्थ सः यमपुरम् अगच्छत् । यमपुरे यमः अनुपस्थितः । बाल: नचिकेता: तत्रैव त्रीणि दिनानि यावत्, किमपि अभुक्त्वा अपीत्वा यमस्य प्रतीक्षाम् अकरोत् ।

अनुवादः

नचिकेताने पुन्हा विचारले, “मग मला तुम्ही कुणाला देणार?” वाजश्रवाने काहीच उत्तर दिले नाही. नचिकेताने दोन-तीनदा परत तेच विचारले. तेव्हा चिडून वडील नचिकेताला म्हणाले, “मी तुला मृत्यूला देईन!” वडील रागाच्या भरात असे म्हणाले हे नचिकेताला कळले. तरीसुद्धा वडिलांच्या आज्ञेचे पालन करण्यासाठी तो यमपुरी गेला. यमपुरात यम नव्हता. लहानगा नचिकेता तिथेच तीन दिवस काहीही न खाता पिता यमाची वाट पाहत थांबला.

Nachiketa asked again, “Then whom will you give me to?” Vajashrava didn’t answer. Nakita asked the same question two-three times again and again. Then the father who was angry said to Nachiketa, “I’ll give you to death.”

Nachiketa knew that the father said this due to anger, yet, he went to the abode of Yama to follow his father’s order. Yama was not there in Yamapura. Young Nachiketa stayed there for three days without eating or drinking anything waiting for Yama.

परिच्छेद : 3

चतुर्थे दिवसे …………………. उपदिशत्।

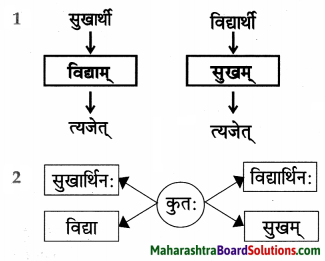
चतुर्थे दिवसे यमः यमपुरं प्राप्त: । क्षुधात पिपासात बालातिथिं दृष्ट्वा तस्य हृदयं करुणया अद्रवत्। यम: नचिकेतसे ‘प्रीन् वरान् याचस्व’ इति अवदत्। ततः बालकः प्रथमं वरम् अयाचत, “मम जनकस्य वाजश्रवसः मां प्रति क्रोधः शान्त: भवतु।”

“स्वर्गसाधिकाम् अग्निविद्यां दत्त्वा माम् अनुगृह्यतु’ इति द्वितीयं वरं स: अयाचत। यम: आनन्देन वरौ प्रायच्छत्। ततः तृतीयवररूपेण नचिकेताः आत्मज्ञानम् अयाचत । तस्य प्रार्थनां श्रुत्वा यमः चकितः। न कोऽपि मर्त्यः अद्यपर्यन्तं तद् ज्ञातुकामः । अल्पवयसः बालस्य कथमिव प्रगल्भा ज्ञानतृष्णा? यमः विविधप्रलोभनै: नचिकेतसं तृतीयवरात् निवारयितुं प्रायतत। किन्तु निश्चल: नचिकेतसः निर्णयः । अन्ते वरं दातुं वचनबद्धः यम: तस्मै ज्ञानिनामपि दुर्लभम् आत्मज्ञानम् उपादिशत्।

अनुवादः

चौथ्या दिवशी यम यमपुरी आला. ताहनेने, भुकेने व्याकूळ झालेल्या त्या लानग्या अतिथीला पाहून त्याचे हृदय दयेने पिळवटले. यम नचिकेताला म्हणला, “तीन वर माग!” तेव्हा नचिकेताने पहिला वर मागितला.

“माझ्या वडिलांचा वाजश्रवांचा माझ्यावरचा राग शांत होऊ दे.” “स्वर्ग साधून देणारी अग्निविद्या देऊन माझ्यावर अनुग्रह करा.” असा दुसरा वर त्याने मागितला. यमाने आनंदाने ते दोन वर दिले. त्यानंतर तिसरा वर म्हणून नचिकेताने आत्मज्ञान मागितले.

त्याची ही विनंती ऐकून यम चकित झाला. आजपर्यंत कोणताही मर्त्य मानव आजपर्यंत इतका ज्ञान इच्छिणारा नव्हता. इतक्या लहान मुलाची इतकी प्रगल्भ ज्ञानतृष्णा?

परावृत्त करण्याचा प्रयत्न केला. परंतु नचिकेताचा निश्चय पक्का होता. शेवटी वर देण्यासाठी वचनबद्ध असलेल्या यमाने त्याला भल्या भल्या ज्ञानींसाठी दुर्लभ असणाऱ्या आत्मज्ञानाचा उपदेश केला.

यमाने इतर अनेक प्रलोभने दाखवून नचिकेताला या तिसऱ्या वरापासून On fourth day Yama arrived at his abode. यमपुर : Seeing the thirsty, hungry young guest his heart went out with compassion. Yama said to Nachiketa, “Ask for three boons!” Then the boy asked the first boon.

“May my father Vajashrava’s anger be pacified.” “Please bless me with the heavenly Agnividya”, he asked for the second boon. Yama happily bestowed him with the two boons. Then Nachiketa asked for knowledge of the self as the third boon. Yama was astonished hearing his request. Till then no mortal wished to know that.

How does this small child have such mature thirst for knowledge? Yama tried to dissuade Nachiketa from the third boon by offering different temptations. But Nachiketa’s decision was firm. In the end, being bound to give him the boon as promised, Yama bestowed him with the knowledge which is rare to even the learned.

सन्धिविग्रहः

• तद् अपश्यत् – तत् + अपश्यत्
• त्वमेव – त्वम् + एव ।
• किमपि – किम् + अपि।
• तत्रैव – तत्र + एव।
• तदेव – तत् + एव।
• कथमिव – कथम् + इव।
• शानिनामपि – ज्ञानिनाम् + अपि।

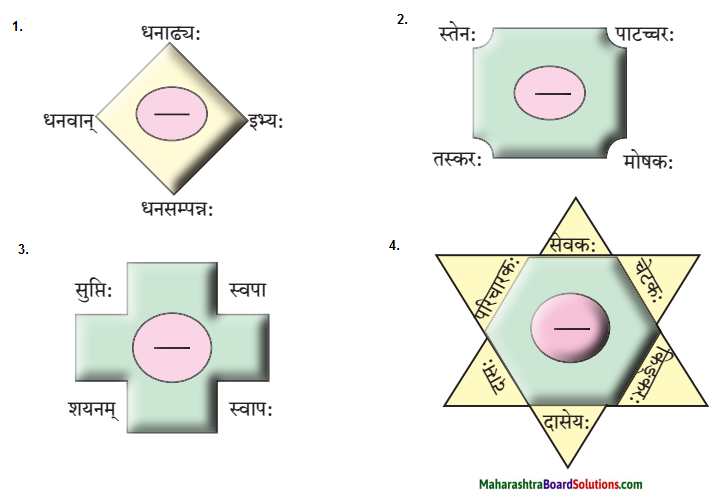
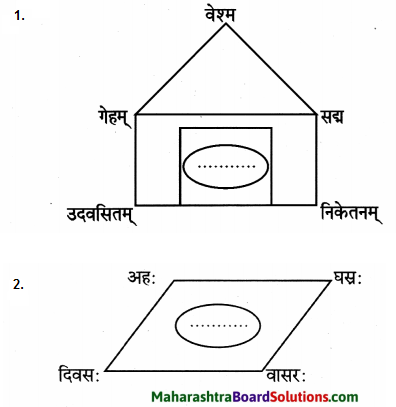
समानार्थकशब्दाः

1. नाम – अभिधानम्, आख्या, नामधेयम्।
2. सर्वदा – सदा, नित्यम्, सदैव ।
3. दुग्धम् – क्षीरम्, पयः।
4. वृद्धा – स्थविरा।
5. झटिति – सत्वरम्, तूर्णम्, आशु, शीघ्रम्।
6. ब्राह्मणः – द्विजाः, विप्रः, भूसुरः।
7. पिता – जन्मदाता, जनकः।
8. दुर्बलाः – निर्बलाः।
9. धेनुः – गौः।
10. दिनानि – दिवसाः।
11. जनक: – पिता।
12. श्रुत्वा – आकर्ण्य।
13. आनन्दः – हर्षः।
14. पुरम् – नगरी।

विरुद्धार्थकशब्दाः

1. समाप्ते × आरम्भे।
2. सर्वदा × क्वचित्।
3. प्रियम् × अप्रियम्।
4. दुर्बलाः × सबलाः।
5. वृद्धा × युवती।
6. नरक: × स्वर्ग:।
7. दिवसे × रात्रौ।
8. अनुपस्थितः × उपस्थितः।
9. आनन्दः × दु:खः।
10. निशल: × चञ्चलः।

शब्दार्थाः

1. वृद्धाः – old – म्हाताऱ्या
2. असमर्थाः – unable – असमर्थ
3. भीत्या – due to fear – भितीने
4. झटिति – fast – लवकर
5. यज्ञम् – sacrifice – यज्ञ
6. दक्षिणा – donation – दक्षिणा
7. नियमः – rule – नियम
8. दुर्बला – weak – अशक्त
9. धेनूः – cows – गायी
10. प्रियतमः – most dear – सर्वात प्रिय
11. कुद्धः – angry – रागावलेला
12. प्रतीक्षाम् अकरोत् – waited – वाट पाहिली
13. अभुक्त्वा – without eating – नखाता
14. अपीत्वा – without drinking – न पिता
15. यमपुरम् – abode of यम – यमनगर
16. अनुपस्थितः – absent – गैरहजर
17. क्षुधार्त: – overcome by hunger – भुकेने व्याकूळ
18. पिपासार्त: – overcome by thirst – तहानेने व्याकूळ
19. हृदयम् – heart – हृदय
20. वरान् – boon – वर
21. आत्मज्ञानम् – self-realisation – आत्मज्ञान
22. अतिथि: – guest – पाहुणा
23. अल्पवयसः – of young age – लहान
24. प्रगल्भा – mature – प्रगल्भ
25. ज्ञानतृष्या – thirst for knowledge – ज्ञानाची तहान
26. प्रलोभनम् – temptation – लालूच
27. निश्चल: – firm – पक्का
28. निवारयितुम् – to dissuade – परतवण्यासाठी
29. मर्त्यः – mortal – मानव

Balbharti Maharashtra State Board Class 9 Sanskrit Solutions Aamod Chapter 3 धन्यौ तौ दातृयाचकौ Notes, Textbook Exercise Important Questions and Answers.

Maharashtra State Board Class 9 Sanskrit Aamod Solutions Chapter 3 धन्यौ तौ दातृयाचकौ

Sanskrit Aamod Std 9 Digest Chapter 3 धन्यौ तौ दातृयाचकौ Textbook Questions and Answers

भाषाभ्यास:

1. एकवाक्येन उत्तरत।

प्रश्न अ.
वरतन्तुः ऋषिः कीदृशः आसीत् ?
उत्तरम् :
वरतन्तुःऋषि: अध्यापने निपुण : प्रकृत्या दवालुः च आसीत्।

प्रश्न आ.
कौत्सेन कति विद्याः अधीताः ?
उत्तरम् :
कौत्सेन चतुर्दशविद्या; अधीताः।

प्रश्न इ.
कौत्सः कस्य शिष्यः आसीत् ?
उत्तरम् :
कौत्सः वरतन्तो: शिष्यः आसीत्।

प्रश्न ई.
रघोः यज्ञस्य नाम किम् ?
उत्तरम् :
रघो: यज्ञस्य नाम विश्वजित्।

प्रश्न उ.
कः स्वर्णवृष्टिम् अकरोत् ?
उत्तरम् :
कुबेरः स्वर्णवृष्टिम् अकरोत् ।

2. प्रश्ननिर्माणं कुरुत।

प्रश्न अ.
वरतन्तुः अध्यापने निपुणः ।
उत्तरम् :
वरतन्तुः कस्मिन् निपुण:?

प्रश्न आ.
रघु: कौत्सस्य भक्त्या प्रभावितः।
उत्तरम् :
रघुः कस्य भक्त्या प्रभावितः?

3. अ. समूहेतरं पदं चिनुत लिखत च।

प्रश्न क.
यज्ञः, क्रतुः, सप्ततन्तुः वरतन्तुः।
उत्तरम् :
यज्ञः, क्रतुः, सप्ततन्तुः, वरतन्तुः – यज्ञः।

प्रश्न ख.
पर्जन्यः, वर्षा, दृष्टिः, वृष्टिः ।
उत्तरम् :
पर्जन्यः, वर्षा, दृष्टिः, वृष्टिः – दृष्टिः ।

प्रश्न ग.
विज्ञः, अज्ञः, अभिज्ञः, पटुः।
उत्तरम् :
विज्ञः, अज्ञः, अभिज्ञः, पटुः – अज्ञः।

प्रश्न घ.
माभृत्, याचकः, वनीयकः, मार्गणः ।
उत्तरम् :
माभृत, याचकः, वनीयकः, मार्गणः – क्षमाभृत्।

प्रश्न ङ.
कुबेरः, यागः, धनाधिपः, धनदः ।
उत्तरम् :
कुबेरः, यागः, धनाधिपः, धनदः – यागः।

आ. विरुद्धार्थकशब्दं लिखत।
प्रभूतम्, समीपम् ।

प्रश्न 1.
विरुद्धार्थकशब्दं लिखत।
प्रभूतम्, समीपम् ।
उत्तरम् :

• प्रभूतम् × अल्पम्
• समीपम् × दूरे

4. वाक्यं शुद्धं कुरुत।

प्रश्न अ.
अहं मुद्राः गुरुं दातुं ऐच्छम्।
उत्तरम् :
अहं मुद्रा: गुरवे दातुम् ऐच्छम् ।

प्रश्न आ.
वरतन्तुः कौत्सम् अकथयत् ।
उत्तरम् :
बरतन्तुः कौत्साय अकथयत्।

5. पाठात् उकारान्तनामानि विशेषणानि च चित्वा लिखत ।

प्रश्न 1.
पाठात् उकारान्तनामानि विशेषणानि च चित्वा लिखत ।
उत्तरम् :
‘धन्यौ तौ दातृयाचकौ’ या कथेला महाकवी कालिदासच्या ‘रघुवंशम्’ या महाकाव्याचा संदर्भ आहे. आपले गुरु बरतन्तु यांना दक्षिणा देण्यासाठी कौत्स रघूकडे जातो. मात्र सर्वस्वाचे दान केल्याने रघू कौत्साला मदत करू शकत नाही. तरीसुद्धा आपल्या पराक्रमाने ता देवांचा खजिनदार कुबेरावर स्वारी करण्याचा निश्चय करतो आणि कौत्साला मदत करण्याचे आश्वासन देतो.

रघूच्या पराक्रमाची पूर्ण जाणीव असलेला कुबेर त्याला घाबरून अगोदरच सुवर्णवृष्टी करतो. रघू कौत्साला सगळे सोने देऊ पाहतो. मात्र गुरुदक्षिणेसाठी आपल्याला फक्त चौदा कोटी सुवर्णमुद्रांची आवश्यकता असल्याचे सांगत अधिक दान घेण्याचे नमपणे आवश्यकता असल्याचे सांगत नाकारतो.

यज्ञामध्ये संपत्ती सढळहस्ते दान करणाऱ्या आणि सुवर्णवृष्टी होऊनही त्यातील कशाचीही इच्छा न बाळगणाऱ्या नि:स्वार्थी आणि दानशूर रघूचे आणि आवश्यकतेपेक्षा काहीही अधिक नको असलेल्या निरिच्छ कौत्साचे दर्शन होते. ही सत्पात्री आणि कुठल्याही स्वार्थाशिवाय दान कसे करावे, याचे आदर्श उदाहरण प्रस्तुत करते.

The story ‘erit at styret’ is based on ‘रघुवंशम्’ of कालिदास. Sage वरतन्तु’s disciple, air had approached King Raghu to seek help for giving Guru Dakshina. But was unable to help him immediately as he had given away all his wealth in the form of charity in the विश्वजित् sacrifice.

Yet, Raghuhad assured कोत्स of help and set to invade कुबेर, कुबेर, who was aware of रघु’s valour, showed gold coins abundantly even before the could attach him. E is ready to donate all of it but कौत्स modestly refused to take more than required. He took only fourteen crores gold coins as guru dakshina.

This story portrays the ideal, generous donor and selfless seeker where the donor is ready to offer everything he has but the seeker doesn’t want to take anything more than what is required. This story also emphasizes that charity should be done among the deserving ones. Values like charity and selflessness that have stood through ages strike us even today.

6. मञ्जूषात: उचितैः अव्ययैः कोष्टकं पूरयत ।

प्रश्न 1.
(उपगम्य, श्रुत्वा, दृष्ट्रा, आहूय, दातुम्, आदातुम्, परीक्षितुम्, विहाय, समाप्य)
उत्तरम् :

Sanskrit Aamod Class 9 Textbook Solutions Chapter 3 धन्यौ तौ दातृयाचकौ Additional Important Questions and Answers

एकवाक्येन उत्तरत।

प्रश्न 1.
तपोवने का ऋषिः आसीत् ?
उत्तरम् :
तपोवने वरतन्तुः नाम ऋषिः आसीत्।

प्रश्न 2.
वरतन्तो: आश्रमे कीदृशा: बटव: आसन्?
उत्तरम् :
वरतन्तो: आश्रमे बहवः मेधाविन: बटव: आसन्।

प्रश्न 3.
कौत्सः कः आसीत्?
उत्तरम् :
कौत्सः बदुः आसीत्।

प्रश्न 4.
कौत्सः कदा किमर्थं च गुरुम् उपागच्छत्?
उत्तरम् :
कौत्सः विद्याध्ययनं समाप्य गुरुदक्षिणां दातुम् उत्सुक: गुरुम् उपागच्छत्।

प्रश्न 5.
कौत्सः गुरवे स्वेच्छां कथम् अकथयत्?
उत्तरम् :
कौत्सः गुरवे स्वेच्छां सविनयम् अकथयत्।

प्रश्न 6.
वरतन्तुः केन भृशं प्रीतोऽस्ति?
उत्तरम् :
वरतन्तुः कौत्सस्य अध्ययनेन सेवया भृशं प्रीतोऽस्ति।

प्रश्न 7.
वरतन्तुः किं न इच्छति?
उत्तरम् :
वरतन्तुः कामपि दक्षिणां न इच्छति।

प्रश्न 8.
कौत्स: वारंवारं किम् ऐच्छत्?
उत्तरम् :
कौत्सः वारंवारं दक्षिणां दातुम् ऐच्छत्।

प्रश्न 9.
कौत्स: केन निवारितः?
उत्तरम् :
कौत्सः गुरुणा वरतन्तुना निवारितः।

प्रश्न 10.
कौत्स: कम् उपागच्छत्?
उत्तरम् :
कौत्स: गुरुम् उपागच्छत्।

प्रश्न 11.
कति सुवर्णमुद्रा: आनेतुं वरतन्तुः अकथयत्?
उत्तरम् :
चतुर्दशकोटिसुवर्णमुद्रा: आनेतुं वरतन्तुः अकथयत्।

प्रश्न 12.
चतुर्दशकोटिसुवर्णमुद्रा: दातुं क : समर्थ:?
उत्तरम् :
चतुर्दशकोटिसुवर्णमुद्रा: दातुं महाराजः रघुः समर्थः ।

प्रश्न 13.
कौत्सः कस्य समीपम् अगच्छत् ?
उत्तरम् :
कौत्सः रघो: समीपम् अगच्छत्।

प्रश्न 14.
दिग्विजयानन्तरं रघुः किम् अकरोत्?
उत्तरम् :
दिग्विजयानन्तरं रघुः “विश्वजित्’ नाम्नि यज्ञे अशेष धनं दानरूपेण अयच्छत्।

प्रश्न 15.
कं दृष्ट्वा कौत्स: निवृत्तः?
उत्तरम् :
रिक्तहस्तं रचुं दृष्ट्वा कौत्स: निवृत्तः।

प्रश्न 16.
रघुः कौत्सम् आहूय किम् अपृच्छत्?
उत्तरम् :
रघुः कौत्सम् आहूय आगमनस्य प्रयोजनम् अपृच्छत्।

प्रश्न 17.
कुत्र विश्राम कर्तुं रघुः कौत्साय अकथयत्?
उत्तरम् :
रघो: यज्ञशालायां विश्रामं कर्तुं रघुः कौत्साय अकथयत्।

प्रश्न 18.
रघुः केन / कथं प्रभावित: जात:?
उत्तरम् :
रघु: कौत्सस्य गुरुभक्त्या प्रभावितः जातः।

प्रश्न 19.
रघुः किं कर्तुं सङ्कल्पम् अकरोत् ?
उत्तरम् :
रघुः कुबेरम् आक्रान्तुम् सङ्कल्पम् अकरोत्।

प्रश्न 20.
कुबेर: किम् अकरोत्?
उत्तरम् :
कुबेर: रघो: भयात् आक्रमणात् पूर्वमेव प्रभूतां सुवर्णवृष्टिम् अकरोत्।

प्रश्न 21.
साकेतजनानां कृते को पूजनीयौ अभवताम्?
उत्तरम् :
साकेतजनानां कृते दानशूरः रघुः तथा निरिच्छ: कौत्सः पूजनीयौ अभवताम्।

प्रश्न 22.
कौत्सः कीदृशः आसीत्?
उत्तरम् :
कौत्स: नि:स्पृहः / निरिच्छ: आसीत्।

प्रश्न 23.
कथायाः किं नाम?
उत्तरम् :
कथायाः नाम धन्यौ तौ दात्याचकौ।

प्रश्न 24.
अत्र क: दाता?
उत्तरम् :
अत्र रघुः दाता।

प्रश्न 25.
अत्र क: याचकः?
उत्तरम् :
अत्र कौत्स : याचकः।

प्रश्ननिर्माणं कुरुत।

प्रश्न 1.
रघुः कौत्साय सर्वं सुवर्णं दातुम् ऐच्छत्।
उत्तरम् :
रघुः कौत्साय किं दातुम् ऐच्छत्?

प्रश्न 2.
अहं गुरुदक्षिणार्थ केवलं चतुर्दशकोटिसुवर्णमुद्राः अभिलषामि।
उत्तरम् :
अहं किमर्थं केवलं चतुर्दशकोटिसुवर्णमुद्राः अभिलषामि?

प्रश्न 3.
द्वावपि साकेतजनानां कृते पूजनीयौ अभवताम्।
उत्तरम् :
द्वावपि केषां कृते पूजनीयौ अभवताम्?

प्रश्न 4.
कस्मिंश्चित् तपोवने वरतन्तुः आसीत्।
उत्तरम् :
कुत्र वरतन्तुः आसीत्?

प्रश्न 5.
कौत्स: स्वस्य इच्छां गुरवे अकथयत्।
उत्तरम् :
कौत्स: स्वस्य इच्छां कस्मै अकथयत् ?

प्रश्न 6.
कौत्स परीक्षितुं बरतन्तुः अकथयत्।
उत्तरम् :
कं परीक्षितुं वरतन्तुः अकथयत्?

प्रश्न 7.
गुरोः वचनं श्रुत्वा कौत्स: चिन्ताकुलः जातः।
उत्तरम् :
कस्य वचनं श्रुत्वा कौत्स: चिन्ताकुलः जातः ।

सत्यं वा असत्यं लिखत।

प्रश्न 1.

1. वरतन्तु: नाम ऋषिः नदीतटे वसति स्म।
2. वरतन्तो: स्वभावे दयालुता आसीत्।
3. वरतन्तो: आश्रमे मूढाः बटव: आसन् ।
4. कौत्सः नाम बटुः तस्य सेवया गुरुं प्रसन्नम् अकरोत् ।
5. कौत्सः गुरवे किमपि दातुं न ऐच्छत्।
6. विद्याध्ययनस्य पश्चात् कौत्स: दक्षिणां दातुमैच्छत्।

उत्तरम् :

1. असत्यम्
2. सत्यम्
3. असत्यम्
4. सत्यम्
5. असत्यम्
6. सत्यम्

प्रश्न 2.

1. कौत्सेन चतसः विद्या: अधीताः।
2. गुरु: रजतमुद्राः इच्छति।
3. गुरुवचनं श्रुत्वा कौत्सः चिन्तितः जातः ।
4. रघुणा ‘अश्वमेधः’ यज्ञः कृतः ।
5. कौत्सस्य इच्छा पूरयितुं रघुः तत्परः।

उत्तरम् :

1. असत्यम्
2. असत्यम्
3. सत्यम्
4. असत्यम्
5. सत्यम्

प्रश्न 3.

1. रघो: गुरुभक्त्या कौत्सः प्रभावितः।
2. कुबेर: आक्रमणस्य पश्चात् सुवर्णवृष्टिम् अकरोत्।
3. कौत्स: केवलं चतुर्दशकोटिमुद्राः इच्छति।
4. याचक: अधिकं ग्रहीतुं न ऐच्छत्।
5. राजा सर्वस्वस्य दाता।
6. साकेतनगरी नाम अयोध्यानगरी।

उत्तरम् :

1. असत्यम्
2. असत्यम्
3. सत्यम्
4. सत्यम्
5. सत्यम्
6. सत्यम्

कः कं वदति।

प्रश्न 1.
गच्छ, स्वस्ति तुभ्यम्।
उत्तरम् :
बरतन्तु: गुरु: कौत्सं वदति।

प्रश्न 2.

1. “अत: चतुर्दशकोटिसुवर्णमुद्रा: आनय।”
2. “रघु प्रति गच्छामि।”
3. “रघो, अहं गुरुदक्षिणार्थ चतुर्दशकोटिसुवर्णमुद्राः गुरवे दातुमिच्छामि। किन्तु भवान् पूर्वमेव सर्वस्ववानम् अकरोत्। अत: अहम् अन्यत्र गच्छामि।”
4. “हे कौत्स, तिष्ठ। मम यज्ञशालायां विश्रामं कुरु । अहं निश्चयेन तव साहाय्यं करोमि।”

उत्तरम् :

1. बरतन्तु:/गुरु: कौत्सं वदति।
2. कौत्स: आत्मानं वदति।
3. कौत्सं रघु वदति।
4. रघुः कौत्सं वदति।

प्रश्न 3.
“भोः राजन्, अहं केवलं गुरुदक्षिणार्थं चतुर्दशकोटिसुवर्णमुद्राः अभिलषामि। न वाञ्छामि अधिकम्।”
उत्तरम् :
कौत्स: रघु वदति।

उचितं कारणं चित्वा वाक्यं पुनर्लिखत।

प्रश्न 1.
कौत्स: गुरुम् उपागच्छत् यतः ………..।
a. सः विद्याम् अध्येतुम् ऐच्छत्।
b. सः गुरवे दक्षिणां दातुम् ऐच्छत्।
उत्तरम् :
कौत्सः गुरुम् उपागच्छत् यतः सः गुरवे दक्षिणां दातुम् ऐच्छत्।

प्रश्न 2.
गुरु: वरतन्तु: अतीव प्रसन्नः अभवत् यतः ………..।
a. तस्य सर्वे शिष्या: मेधाविनः।
b. तस्मै कौत्सस्य सेवा अरोचत।
उत्तरम् :
गुरुः वरतन्तुः अतीव प्रसन्नः अभवत् यतः तस्मै कौत्सस्य सेवा अरोचत।

प्रश्न 3.
वरतन्तुः चतुर्दशकोटिसुवर्णमुद्राः इच्छति यतः……..।
a. स: निर्धन: आचार्य: आसीत्।
b. स: कौत्सं चतुर्दशविद्या: पाठितवान्।
उत्तरम् :
वरतन्तुः चतुर्दशकोटिसुवर्णमुद्राः इच्छति यतः सः कौत्सं चतुर्दशविद्या: पाठितवान्।

प्रश्न 4.
कौत्स: रघु प्रति गच्छति यतः……..,
a. स: “विश्वजित्’ यज्ञस्य मुख्यः पुरोहितः।
b. स: रघु सुवर्णमुद्राः याचितुम् ऐच्छत्।
उत्तरम् :
कौत्सः रघु प्रति गच्छति यतः, सः रघु सुवर्णमुद्रा: याचितुम् ऐच्छत्।

प्रश्न 5.
रघुःसुवर्णमुद्रा: तत्क्षणमेव दातुम् असमर्थः यतः……..।
a. स: सर्वस्वदानम् अकरोत्।
b. स: दानं दातुं नैच्छत्।
उत्तरम् :
रघुः सुवर्णमुद्राः तत्क्षणमेव दातुम् असमर्थः यतः सः सर्वस्वदानम् अकरोत्।

प्रश्न 6.
रघु: कुबेरमाकान्तुम् ऐच्छत् यतः ………..।
a. स: कौत्साय दानं दातुम् ऐच्छत्।
b. सः स्वस्य कृते धनम् ऐच्छत्।
उत्तरम् :
रघुः कुबेरमाकान्तुम् ऐच्छत् यतः सः कौत्साय दानं दातुम् ऐच्छत्।

प्रश्न 7.
कुबेर: सुवर्णवृष्टिम् अकरोत् यतः ……
a. स: कौत्सस्य गुरुभक्त्या प्रभावितः ।
b. स: रघो: तस्य आक्रमणात् च भीतः।
उत्तरम् :
कुबेर: सुवर्णवृष्टिम् अकरोत् यतः सः रघो: तस्य आक्रमणात् च भीतः।

प्रश्न 8.
राजा सर्वस्वं दातुम् ऐच्छत् यतः ………..।
a. स: पूर्वमेव धनान्यः आसीत्।
b. स: दानशील: आसीत्।
उत्तरम् :
राजा सर्वस्वं दातुम् ऐच्छत् यतः सः दानशील : आसीत्।

प्रश्न 9.
कौत्स: अधिकं नैच्छत् यतः ………..।
a. स: नि:स्पृहः आसीत्।
b. तस्य समीपे मुद्राः आसन्।
उत्तरम् :
कौत्स: अधिकं नैच्छत् यतः सः नि:स्पृहः आसीत्।

प्रश्न 10.
कौत्स: रघुः च पूजनीयौ अभवताम् यतः ………..।
a. तौ साकेतजनान् शत्रुभ्य: अरक्षताम्।
b. तयोः नि:स्पृहता, दानशूरता अवर्णनीया।
उत्तरम् :
कौत्सः रघुः च पूजनीयौ अभवताम् यतः तयोः नि:स्पृहता, दानशूरता अवर्णनीया।

शब्दस्य वर्णविग्रहं कुरुत।

• प्रकृत्या – प्+ र + क् + ऋ + त् + य् + आ।
• कश्चित् – क् + अ + श् + च् + इ + त्।
• कौत्सः – क् + औ + त् + स् + अः।
• चतुर्दशविद्या:- च् + अ + त् + र + द् + अ + श् + व् + इ + द् + य् + आः।
• श्रुत्वा – श् + र + उ + त् + व् + आ।
• गुरुभक्त्या – ग् + उ + र् + उ + भ् + अ + क् + त् + य् + आ।
• आक्रान्तुम् – आ + क् + + आ + न् + त् + उ + म्।
• नि:स्पृहः – न् + इ + स् + स् + प् + + + + अः।
• सङ्कल्पम् – स् + अ् + ङ् + क् + अ + ल् + प् + अ।
• द्वावपि – द् + व् + आ + व् + अ + प् + इ।

विशेषण – विशेष्य – सम्बन्धः ।

प्रश्न 1.

उत्तरम् :

त्वान्त/ल्यबन्त/तुमन्त अव्ययानि।

विभक्त्यन्तरूपाणि।

• प्रथमा – वरतन्तुः, ऋषिः, निपुणः, दयालुः, सः, कौत्सः, बटुः, गुरुः, प्रीतः, निवारितः, बटवः, मेधाविनः, वरतन्तुः, चतुर्दशविद्याः, अधीताः, मुद्राः, रघुः, अहम्, भवान्, रघुः, कौत्सः, राजा, दानशूरः, निरिच्छः, द्वौ, पूजनीयौ।
• द्वितीया – विद्याध्ययनम्, गुरुदक्षिणाम्, गुरुम्, काम, इच्छाम्, अन्याम्, तम्, महाराजम्, रघुम्, कुबेरम्, सङ्कल्पम्, प्रभूताम, सुवर्णवृष्टिम्, कौत्सम्।
• तृतीया – अध्ययनेन, सेवया, त्वया, अनेन, प्रसङ्गेन।
• चतुर्थी – गुरवे, गुरवे, तस्मै।
• षष्ठी – तस्य, स्वस्य, गुरोः, मम, तव, साकेतजनानाम्।
• सप्तमी – अध्यापने, आश्रमे, यज्ञे, यज्ञशालायाम्, रघोः, भयात्, आक्रमणात्।

समूहेतरपदं चिनुत।

1. दृष्ट्वा, अवलोक्य, द्रष्टुम्, विलोक्य – द्रष्टुम्।
2. गुरवे, वरतन्तवे, कौत्साय, रघवे – कौत्साय।

समानार्थकशब्द योजयित्वा वाक्यं पुनर्लिखत।

1. राजा – भोज: नाम राजा सुप्रसिद्धः ।
भोज: नाम पार्थिवः / भूपति:/क्ष्माभृत् सुप्रसिद्धः।

2. गुरुः – अहं गुरुं नमामि ।
अहं आचार्य /अध्यापकं नमामि ।

3. निपुणः – विनायक: चित्रकलायां निपुणः।
विनायक: चित्रकलायां पारङ्गत:/ कुशल:।

4. यज्ञः – युधिष्ठिरः यज्ञे दानम् अयच्छत्।
युधिष्ठिरः मखे/क्रतौ/यागे दानम् अयच्छन्।

5. कुबेरः – देवानां कोषाधिकारी कुबेरः।
देवानां कोषाधिकारी धनाधिप:/धनदः।

6. याचक:- याचक: दानं याचते।
वनीयक:/मार्गण: दानं याचते।

7. बचः – सज्जनानां वच: श्रवणीयम्।
सज्जनानां उक्ति: श्रवणीया।
सज्जनानां भाषितं/वचनं श्रवणीयम्।

8. प्रभूतम् – नरः प्रभूतं धनम् इच्छति।
नर: प्रचुरं/बहु धनम् इच्छति।

व्याकरणम् :

नाम – तालिका।

सर्वनाम – तालिका।

धातु – तालिका।

समासाः।

धातुसाधितविशेषणानि।

धन्यौ तौ दातृयाचकौ Summary in Marathi and English

प्रस्तावना :

महाकवी कालिदासांचे ‘रघुवंशम्’ हे महाकाव्य सुप्रसिद्ध आहे. त्यातील पाचव्या सर्गात महाराज रघू यांच्या आयुष्यात घडलेल्या प्रसंगांचे वर्णन कवीने केले आहे. रघू महाराजांनी विश्वजित यज्ञ करून त्या यज्ञात सर्वस्वाचे दान केले. त्यामुळे त्यांचा खजिना रिकामा झाला. त्यावेळी कौत्स नावाचा एक विद्यार्थी तेथे आला.

कौत्साने आपल्या गुरुंना दक्षिणा देण्यासाठी त्याने रघूपाशी धनाची इच्छा प्रकट केली. हाच प्रसंग येथे वर्णिला आहे. रघुव कौत्स यांच्या रूपाने दानशूरता व निःस्वार्थी वृत्तीचे दर्शन घडते.

Raghuvansham the epic poetry composed by Kalidasa is world famous There, in the fifth canto, the poet describes an incident that took place in the life of King Raghu. King Raghu had performed the Vishuvajit sacrifice and performed Sartastxadakshina that is he had given away all the wealth in the form of charity and had become completely empty.

His coffers too were completely empty. It was then that a young student named Kautsa came there. He wished for wealth in order to give it as Guru Dakshina. This very event is described here. Through this episode values like charity and selflessness are made live in the form of Raghu and Kausta respectively.

परिच्छेद : 1.

कस्मिंश्चित् ……………… ऐच्छत्।
कस्मिंश्चित् तपोवने वरतन्तुः नाम ऋषिः आसीत्। सः अध्यापने निपुणः प्रकृत्या दयालुः च आसीत्। तस्य आश्रमे बहवः मेधाविनः वटव: आसन्। तेषु कश्चित् कौत्स: नाम बटुः आसीत्। विद्याध्ययनं समाप्य गुरुदक्षिणां दातुमुत्सुक: कौत्सः गुरुम् उपागच्छत् । सविनयं च स्वस्य इच्छां गुरवे अकथयत् । तस्य वचः श्रुत्वा गुरुः उक्तवान्, “वत्स कौत्स, तव अध्ययनेन सेवया च भृशं प्रीतोऽस्मि । अन्य कामपि दक्षिणां नेच्छामि। गच्छ, स्वस्ति तुभ्यम् ।” गुरुणा वरतन्तुना निवारितः अपि कौत्स: वारंवार दक्षिणां दातुम् ऐच्छत्।

अनुवादः

कोण्या एका तपोवनात वरतंतू ऋषी होते. ते शिकवण्यात कुशल आणि स्वभावाने दयाळू होते. त्याच्या आश्रमात अनेक हुशार ब्राह्मण मुले होती. त्यापैकी कौत्स नावाचा कोणी एक ब्राह्मण मुलगा (बटू) होता. शिक्षण संपवून गुरुदक्षिणा देण्यास उत्सुक असलेला कौत्स गुरुंजवळ गेला.

आणि त्याने नम्रपणे स्वतःची इच्छा गुरुंना सांगितली. त्याचे बोलणे ऐकून गुरु म्हणाले, “बाळ कौत्स, तुझ्या अभ्यासाने आणि सेवेने अतिशय प्रसन्न झालो आहे. मला दुसरी कुठलीही दक्षिणा नको. तू जा, तुझे कल्याण असो.” वरतंतू गुरुंनी नको म्हणूनही (अडवूनही) कौत्साची दक्षिणा द्यायची वारंवार इच्छा होती.

In a certain penance grove there was a sage named Varatantu. He was skilled in teaching and compassionate by nature. There were many intelligent brahmin boys in his hermitage. Among them was a certain boy named Kautsa.

Kautsa who was eager to offer Guru Dakshina after completing his studies approached the Guru. And modestly told his Guru of his desire. Hearing his words the preceptor said, “Child Kautsa, I am extremely pleased by your studies and service.

I do not wish for any other Dakshina. Go, may all be well with you.” Despite being refused by the preceptor Varatantu, Kautsa again and again wished to offer Dakshina.

परिच्छेद : 2.

तदा ………………. करोमि।
तदा तं परीक्षितुं वरतन्तुः कथयत् – ” त्वया मम सकाशात् चतुर्दशविद्याः अधीताः । अत: चतुर्दशकोटिसुवर्णमुद्राः आनय।” गुरोः वचनं श्रुत्वा कौत्स: चिन्ताकुलः जातः । एतावती: सुवर्णमुद्राः कुत: आनयानि ? महाराज रघु विहाय न कोऽपि एतावती: मुद्राः दातुं समर्थः । अतः ‘रघु प्रति गच्छामि’ इति विचार्य कौत्स: रघो: समीपम् अगच्छत् । दिग्विजयानन्तरं रघुः ‘विश्वजित्’ नाम्नि यज्ञे अशेषं धनं दानरूपेण अयच्छत्।

रिक्तहस्तं रघु दृष्ट्वा कौत्स: निवृत्तः। रघुः तम् आहूय आगमनस्य प्रयोजनम् अपृच्छत्। तदा कौत्सः अवदत् “रघो, अहं गुरुदक्षिणार्थ चतुर्दशकोटिसुवर्णमुद्रा गुरवे दातुमिच्छामि। किन्तु भवान् पूर्वमेव सर्वस्वदानम् अकरोत्। अत: अहम् अन्यत्र गच्छामि।” रघुः अवदत्, “हे कौत्स, तिष्ठ। मम यज्ञशालायां विश्रामं कुरु । अहं निश्चयेन तव साहाय्यं करोमि।”

अनुवादः

तेव्हा त्याची परीक्षा घेण्यासाठी वरतंतू म्हणाले, तू माझ्याकडे चौदा विद्या शिकलास. म्हणून चौदा कोटी सुवर्णमुद्रा (सोन्याची नाणी) आण. गुरुंचे बोलणे ऐकून कौत्स चिंतित झाला. ‘एवढ्या सुवर्णमुद्रा मी कुठून आणू?’ महाराज रचूंशिवाय इतक्या सुवर्णमुद्रा देण्यास कोणीही समर्थ नाही.

म्हणून ‘मी रघूकडे जाता’ असा विचार करून कौत्स रघूजवळ गेला. दिग्विजयानंतर रघूने ‘विश्वजित्’ नावाच्या यज्ञात सगळे धन दानरूपाने दिले. मोकळ्या हातांच्या (दान देण्यास असमर्थ) रघूला पाहून कौत्स (तेथून) मागे फिरला. रघूने त्याला बोलावून (त्याच्या) येण्याचे कारण विचारले.

तेव्हा कौत्स म्हणाला, “अहो रघूमहाराज, गुरुदक्षिणेसाठी चौदा कोटी सुवर्णमुद्रा मी गुरुंना देऊ इच्छितो; पण आपण तर अगोदरच सर्वस्वाचे दान केलेत. म्हणून मी दुसरीकडे जातो.” रघू म्हणाले, “हे कौत्स, थांब. माझ्या यज्ञमंडपात तू विश्रांती घे. मी तुला नक्कीच मदत करतो.”

Then in order to test him, Varatantu said, “You have learnt the fourteen vidyas from me. So bring fourteen crore gold coins.” Hearing the words of the preceptor, Kautsa became worried.

From where shall I bring so many gold coins? None other than king Raghu will be able to give so many coins.’ Hence, thinking that ‘Ishall go to Raghu’ Kautsa went to Raghu.

After conquering the directions, Raghu gave away all the wealth in the form of charity in the Vishwajit sacrifice. Seeing Raghu empty-handed Kautsa turned back. Calling him Raghu ask him the purpose of his arrival.

Then Kautsa said, “O Raghu, I wish to give the preceptor fourteen crore gold coins as Guru Dakshina. But your respected one has given away everything in charity before itself. Hence I am going elsewhere”. Raghu replied, OKautsa, wait. Rest in the sacrificial hall. I shall surely help you”.

परिच्छेद : 3.

कौत्सस्य ……………… अभवताम्।
कौत्सस्य गुरुभक्त्या प्रभावित: रघुः कुबेरमाकान्तुं सङ्कल्पम् अकरोत्। कुबेरः रघो: भयात् आक्रमणात् पूर्वमेव प्रभूतां सुवर्णवृष्टिमकरोत्। तत् दृष्ट्वा सन्तुष्टः रघुः कौत्सम् आहूय सर्व सुवर्ण तस्मै दातुमैच्छत् । किन्तु नि:स्पृहः कौत्सः अवदत् – “भो: राजन, अहं केवलं गुरुदक्षिणार्थ चतुर्दशकोटिसुवर्णमुद्राः अभिलषामि।

न वाञ्छामि अधिकम्।” राजा सर्वस्वं दातुम् ऐच्छत् किन्तु याचक: अधिकमादातुं न अध्यलषत्। अनेन प्रसङ्गेन दानशूर; रघु तथा निरिच्छ: कौत्सः च द्वावपि साकेतजनानां (अयोध्यावासिना) कृते पूजनीयौ अभवताम्।

अनुवादः

कौत्साच्या गुरुभक्तीने प्रभावित झालेल्या रघूने कुबेरावर स्वारी करण्याचा निश्चय केला. रघूच्या भीतीने कुबेराने आक्रमणापूर्वीच मोठ्या प्रमाणावर सुवर्णवृष्टी (सोन्याच्या नाण्यांचा पाऊस) केली. ते पाहून प्रसन्न झालेल्या रघूने कौत्साला बोलावून त्याला सगळे सोने
देण्याची इच्छा व्यक्त केली.

पण निर्लोभी कौत्स म्हणाला, “हे राजन्, मला गुरुदक्षिणेसाठी फक्त चौदा कोटी सुवर्णमुद्रा पाहिजेत. त्यापेक्षा जास्त नको.” राजाची सर्वस्व दान करण्याची इच्छा होती, मात्र याचकाला अधिक स्वीकारण्याची इच्छा नव्हती. या प्रसंगामुळे दानशूर रघू तसेच निरिच्छ कौत्स हे दोघेही अयोध्यावासीयांसाठी वंदनीय झाले.

Raghu who was impressed by the devotion towards his preceptor decided to attack Kuber. Kubera out of fear of Raghu showered abundant gold coins before the attack itself. Seeing that, Raghu who was happy called Kautsa and wished to give him all the gold.

But the desireless Kautsa said, “O King, I only wish for fourteen crore gold coins as Guru Dakshina. I do not want more. King wished to give everything, but the seeker did not desire to take more. Due to this incident, the charitable Raghu and the selfless (desireless) Kautsa became respectable for the people of Saket (Ayodhya).

सन्धिविग्रहः

1. दातुमुत्सुक: – दातुम् + उत्सुक:
2. प्रीतोऽस्मि – प्रीतः + अस्मि।
3. कामपि – काम् + अपि।
4. नेच्छामि – न + इच्छामि।
5. कोऽपि – कः + अपि।
6. दातुमिच्छामि – दातुम् + इच्छामि।
7. पूर्वमेव – पूर्वम् + एव।
8. कुबेरमाकान्तुम् – कुबेरम् + आक्रान्तुम्।
9. सुवर्णवृष्टिमकरोत् – सुवर्णवृष्टिम् + अकरोत्।
10. अधिकमादातुम् – अधिकम् + आदातुम्।
11. द्वावपि – द्वौ + अपि।

समानार्थकशब्दाः

1. ऋषिः – मुनिः, साधुः, तपोधनः।
2. निपुणः – कुशलः, पारङ्गतः, प्रवीणः ।
3. प्रकृत्या – स्वभावेन/स्वभावतः।
4. श्रुत्वा – आकर्ण्य।
5. भृशम् – बहु, प्रभूतम्।
6. प्रीतः – प्रसन्नः।
7. वारंवारम् – पुनः पुनः।
8. वचः – उक्तिः , वचनम्।
9. गुरुः – आचार्यः, अध्यापकः।
10. सकाशात् – समीपे, निकटे, निकषा।
11. चिन्ताकुलः – चिन्तितः, चिन्ताग्रस्तः।
12. विचार्य – चिन्तयित्वा, मत्वा।
13. यज्ञः – क्रतुः, मखः, यागः।
14. अशेषम् – नि:शेषम्।
15. धनम् – वित्तम्, अर्थम्, द्रविणम्।
16. विश्रामः . विश्रान्तिः, अनायासः।
17. सङ्कल्पः – प्रतिज्ञा, निश्चयः ।
18. कनकम, हेम, काञ्चनम् – सुवर्णम्।
19. नि:स्पृहः – निरिच्छः ।
20. अभिलषामि – वाञ्छामि।
21. ग्रहीतुम् – आदातुम्।
22. दानी, दानवीरः – दानशूरः।
23. वन्दनीयौ – पूजनीयौ।
24. धनाधिपः, धनदः – कुबेरः।
25. राजा – पार्थिवः, माभृत, भूपः, महीक्षितः

विरुद्धार्थकशब्दाः

1. निपुण: × अकुशल:
2. दयालुः × कूरः
3. मेधाविनः × मूढाः, मूर्खा:
4. बहवः × अल्पाः, स्तोकाः
5. समाप्य × आरभ्य, प्रारभ्य
6. उत्सुक: × अनुत्सुकः
7. भृशम् × अल्पम्, स्तोकम् .
8. प्रीतः × कुद्धः
9. वारंवारम् × कदाचित्
10. असन्तुष्टः × सन्तुष्टः ।
11. न्यूनम्, अल्पम् × अधिकम्।
12. कृपणः × दानशूरः।
13. लोभी × निरिच्छ:, निस्पृहः।
14. नय × आनय।
15. निश्चिन्तः × चिन्ताकुलः।
16. शेषम् × अशेषम्।
17. पश्चात् × पूर्वम्।

शब्दार्थाः

1. तपोवनम् – penance grove – तपस्येकरिता वन
2. निपुणः – expert – कुशल
3. प्रकृत्या – by nature – स्वभावाने
4. मेधाविनः – intelligent – हुशार
5. बटुः – brahmin boy – ब्राह्मण मुलगा
6. समाप्य – having finished – संपवून
7. सविनयम् – politely – नम्रपणे
8. उपागच्छत् – approached, went near – जवळ गेला
9. श्रुत्वा – by hearing – ऐकून
10. उक्तवान् – said – म्हटले
11. भृशम् – a lot – अतिशय
12. स्वस्ति – may all be well – कुशल असो
13. निवारितः – refused – प्रतिबंधित, अडवलेला
14. परीक्षितुम् – to test – परीक्षा घेण्यासाठी
15. सकाशात् – near – कडे
16. अधीताः – learnt – शिकलेल्या
17. चिन्ताकुल: – worried – चिंतित
18. विहाय – except – शिवाय
19. एतावती – this much – इतक्या
20. विचार्य – after thinking – विचार करून
21. अशेषम् – all – सगळे
22. आहूय – after calling – बोलावून
23. प्रयोजनम् – purpose – हेतु
24. विश्रामः – rest – वित्रांती
25. सुवर्णमुद्राः – gold coins – सोन्याची नाणी
26. गुरुभक्त्या – by devotion towards the preceptor – गुरुभक्तीने
27. ‘आक्रान्तुम् – to invade, attack – आक्रमण करण्यासाठी
28. नि:स्पृहः – desireless – निरिच्छ, निर्लोभी
29. चिन्ताकुल: worried – चिंतित
30. पूजनीयौ respectable – बंदनीय
31. प्रभावितः – impressed – प्रभावित
32. सङ्कल्पम् अकरोत् – vowed – निशय केला
33. वाञ्छामि / अभिलषामि – I desire – मी इच्छितो
34. प्रभूता – a lot – पुष्कळ

Balbharti Maharashtra State Board Class 9 Sanskrit Solutions Aamod Chapter 4 विध्यर्थमाला Notes, Textbook Exercise Important Questions and Answers.

Maharashtra State Board Class 9 Sanskrit Aamod Solutions Chapter 4 विध्यर्थमाला

Sanskrit Aamod Std 9 Digest Chapter 4 विध्यर्थमाला Textbook Questions and Answers

भाषाभ्यासः

श्लोकः 1

1. एकवाक्येन उत्तरत।

प्रश्न अ.
विद्यार्थी किं त्यजेत् ?
उत्तरम् :
विद्यार्थी सुखं त्यजेत् ।

प्रश्न आ.
सुखार्थी किं त्यजेत् ?
उत्तरम् :
सुखार्थी विद्या त्यजेत् ।

2. सन्धिविग्रहं कुरुत।

प्रश्न 1.

1. त्यजेद्विद्याम्
2. त्यजेत्सुखम्
3. कुतो विद्या
4. कुतो विद्यर्थिनः

उत्तरम् :

1. त्यजेद्विद्याम् – त्यजेत् + विद्याम् ।
2. त्यजेत्सुखम् – त्यजेत् + सुखम् ।
3. कुतो विद्या – कुतः + विद्या ।
4. कुतो विद्यार्थिन: – कुतः + विद्यार्थिनः ।

3. समानार्थकशब्दं लिखत।

1. विद्या
2. विद्यार्थी

उत्तरम् :

1. विद्या – ज्ञानम्, शिक्षा ।
2. विद्यार्थी – छात्र:, शिष्यः, अन्तेवासी।

4. प्रश्ननिर्माणं कुरुत।

प्रश्न अ.
सुखार्थी विद्यां न लभते।
उत्तरम् :
सुखार्थी किं न लभते ?

प्रश्न आ.
विद्यार्थी सुखं न लभते।
उत्तरम् :
कः सुखं न लभते ।

श्लोक: 2.

1. एकवाक्येन उत्तरत।

प्रश्न अ.
कीदृशं जलं पिबेत् ?
उत्तरम् :
वस्त्रपूतं सुखं त्यजेत्।

प्रश्न आ.
कीदृशीं वाणी वदेत् ?
उत्तरम् :
सत्यपूतां वाणी वदेत्।

2. समानार्थकशब्दं चित्वा लिखत ।
वाक्, पवित्रम्, ऋतम्, उदकम् ।

प्रश्न 1.
समानार्थकशब्दं चित्वा लिखत ।
वाक्, पवित्रम्, ऋतम्, उदकम् ।
उत्तरम् :

• वाक् – वाणी।
• पवित्रम् – पूतम्।
• ऋतम् – सत्यम्।
• उदकम् – जलम्।

3. स्तम्भमेलनं कुरुत।

प्रश्न 1.

उत्तरम् :

श्लोकः 3

1. एकवाक्येन उत्तरत।

प्रश्न अ.
मनुजः कीदृशं धनं काङ्केत ?
उत्तरम् :
मनुज: अलब्ध धनं काक्षेत।

प्रश्न आ.
वृद्धं धनं कुत्र निक्षिपेत् ?
उत्तरम् :
वृद्धं धनं तीर्थेषु निक्षिपेत्।

2. क्रमानुसारं रचयत।

प्रश्न 1.

1. धनस्य रक्षणम्।
2. तीर्थेषु दानम्।
3. धनस्य इच्छा ।
4. धनस्य वर्धनम्।

उत्तरम् :

1. धनस्य इच्छा।
2. धनस्य रक्षणम् ।
3. धनस्य वर्धनम् ।
4. तीर्थेषु दानम् ।

3. पदपरिचयं लिखत।

उत्तरम् :
1. काङ्क्षत – काङ्क्ष धातुः प्रथमगण: आत्मनेपदं
विधिलिङ्लकार : प्रथमपुरुष: एकवचनम्।

2. रक्षेत् – रक्ष धातुः प्रथमगण: परस्मैपदं विधिलिङ्लकार:
प्रथमपुरुष: एकवचनम्।

3. निक्षिपेत् – नि + क्षिप् धातुः प्रथमगण: परस्मैपदं
विधिलिङ्लकारः प्रथमपुरुष: एकवचनम्।

श्लोकः 4

1. एकवाक्येन उत्तरत।

प्रश्न अ.
क्रोधं केन जयेत्?
उत्तरम् :
क्रोधं अक्रोधेन जयेत्।

प्रश्न आ.
दानेन किं जयेत् ?
उत्तरम् :
दानेन कदर्य जयेत्।

प्रश्न इ.
सत्येन किं जयेत्?
उत्तरम् :
सत्येन अनृतं जयेत्।

2. विरुद्धार्थकशब्द लिखत ।
क्रोधः, असाधुः, सत्यम्, दानम् ।
उत्तरम् :

• क्रोध: × अक्रोधः, क्षमा।
• असाधुः × साधुः।
• सत्यम् × अनृतम्।
• दानम् × कदर्यम् ।

3. श्लोकात् तृतीयान्तपदानि चित्वा लिखत ।
उत्तरम् :
तृतीया – अक्रोधेन, साधुना, दानेन, सत्येन

4. सन्धिविग्रहं कुरुत ।
चानृतम्।

प्रश्न 1.
चानृतम्।
उत्तरम् :
चानृतम् – च + अनृतम्।

श्लोक: 5

1. एकवाक्येन उत्तरत।

प्रश्न अ.
दुःखे कान् पश्येत्?
उत्तरम् :
दुःखे दुःखाधिकान् पश्येत्।

प्रश्न आ.
सुखाधिकान् कदा पश्येत् ?
उत्तरम् :
सुखाधिकान् सुखे पश्येत्।

2. सन्धिविग्रहं कुरुत।
शत्रुभ्यामिव, नार्पयेत्।
उत्तरम् :

• शत्रुभ्यामिव – शत्रुभ्याम् + इव।
• नार्पयेत् – न + अर्पयेत्।

3 विरुद्धार्थकशब्द लिखत ।
सुखम्, अधिकम्, शोकः, शत्रुः ।
उत्तरम् :

• सुखम्: × दु:खम्।
• अधिकम् × न्यूनम, अल्पम्, स्तोकम्।
• शोक: × हर्षः, आनन्दः।
• शत्रुः × मित्रम्, सखा, सुहृद्।

4. जालरेखाचित्रं पूरयत।

प्रश्न 1.

उत्तरम् :

श्लोकः 6

1. एकवाक्येन उत्तरत।

प्रश्न अ.
प्रत्यहं किं प्रत्यवेक्षेत ?
उत्तरम् :
प्रत्यहं आत्मन: चरितं प्रत्यवेक्षेत।

प्रश्न आ.
चरितं केन तुल्यं माऽस्तु ?
उत्तरम् :
चरितं पशुभि: तुल्यं माऽस्तु।

प्रश्न इ.
चरितं केन तुल्यम् अस्तु ?
उत्तरम् :
चरितं सत्पुरुषै : तुल्यम् अस्तु।

2. सन्धिं कुरुत।

प्रश्न अ.
पशुभिः + तुल्यम्
उत्तरम् :
पशुभिस्तुल्यम् – पशुभिः + तुल्यम् ।

प्रश्न आ.
किम् + नु
उत्तरम् :
किन्नु – किम् + नु।

प्रश्न इ.
सत्पुरुषैः + इति
उत्तरम् :
सत्पुरुषैरिति – सत्पुरुषैः + इति।

प्रश्न ई.
नरः + चरितम्
उत्तरम् :
नरश्चरितमात्मनः – नरः + चरितम् + आत्मनः ।

3 समानार्थकशब्दानां युग्मं चिनुत ।

प्रश्न 1.

उत्तरम् :

श्लोकः 7

1. एकवाक्येन उत्तरत।

प्रश्न अ.
नृपः अर्थान् कथं चिन्तयेत् ?
उत्तरम् :
नृपः अर्थान् बकवत् चिन्तयेत्।

प्रश्न आ.
नृपः कथं पराक्रमेत् ?
उत्तरम् :
नृपः सिंहवत् पराक्रमेत्।

प्रश्न इ.
नृपः कथम् अवलुम्पेत ?
उत्तरम् :
नृपः वृकवत् अवलुम्पेत।

प्रश्न ई.
नृपः कथं विनिष्पतेत् ?
उत्तरम् :
नृपः शशवत् विनिष्यतेत्।

2. लिङ्लकारस्य क्रियापदानि चिनुत ।

प्रश्न 1.
लिङ्लकारस्य क्रियापदानि चिनुत ।

3. श्लोकात् पशुद्वयं चिनुत लिखत च ।

प्रश्न 1.
श्लोकात् पशुद्वयं चिनुत लिखत च ।

4. सन्धिं कुरुत।

प्रश्न अ.
शशवत् + च
उत्तरम् :
शशवच्च – शशवत् + च।

प्रश्न आ.
च + अवलुम्पेत
उत्तरम् :
चावलुम्पेत – च + अवलुम्पेत।

प्रश्न इ.
चिन्तयेत् + अर्थान् ।
उत्तरम् :
बकवच्चिन्तयेदर्थान् – बकवत् + चिन्तयेत् + अर्थान् ।

Sanskrit Aamod Class 9 Textbook Solutions Chapter 4 विध्यर्थमाला Additional Important Questions and Answers

विभक्त्यन्तरूपाणि।

• प्रथमा – विद्या, सुखम्, विद्यार्थी, सुखार्थी।
• द्वितीया – विद्याम, सुखम्।

लकारं लिखत।

1. त्यजेत् – त्यज् धातुः प्रथमगणः परस्मैपदं विधिलिङ्लकार: प्रथमपुरुष: एकवचनम्।
2. न्यसेत् – न्यस् धातुः चतुर्थगण: परस्मैपदं विधिलिङ्लकार: प्रथमपुरुष: एकवचनम्।
3. पिबेत् – पा – पिब् धातुः प्रथमगणः परस्मैपदं विधिलिङ्लकारः प्रथमपुरुषः एकवचनम्।
4. वदेत् – वद् धातुः प्रथमगण: परस्मैपदं विधिलिङ्लकार: प्रथमपुरुषः एकवचनम।
5. समाचरेत् – सम् + आ + चर् धातुः प्रथमगणः परस्मैपदं विधिलिङ्लकारः प्रथमपुरुषः एकवचनम।
6. वर्धयेत् – वृध् – वर्धधातुः प्रथमगण: आत्मनेपदं प्रयोजकरूपम् विधिलिङ्लकारः प्रथमपुरुषः एकवचनम्।
7. जयेत् – जि – जय् धातुः प्रथमगण: परस्मैपदं विधिलिङ्लकार: प्रथमपुरुष: एकवचनम्।
8. पश्येत् – दृश् – पश्य् धातुः प्रथमगण: परस्मैपदं विधिलिङ्लकार: प्रथमपुरुष: एकवचनम्।
9. अयित् – ऋधातुः प्रथमगणः परस्मैपदं प्रयोजकरूपम्, विधिलिङ्लकारः प्रथमपुरुषः एकवचनम्।
10. प्रत्यवेक्षेत – प्रति + अव + ईश् धातुः प्रथमगण:आत्मनेपदं विधिलिङ्लकार : प्रथमपुरुष: एकवचनम्।
11. चिन्तयेत् – चिन्त् धातुः दशमगण: उभयपदम् अत्र परस्मैपदं विधिलिङ्लकार: प्रथमपुरुषः एकवचनम्।
12. पराक्रमेत् – परा + क्रम् धातुः प्रथमगणः परस्मैपदं विधिलिङ्लकार : प्रथमपुरुष: एकवचनम्।
13. अवलुम्पेत – अव + लुम्प् धातुः षष्ठगण: उभयपदम् अत्र आत्मनेपदं विधिलिङ्लकारः प्रथमपुरुषः एकवचनम्।
14. विनिष्पतेत् – वि + निस् + पत् धातुः प्रथमगण: परस्मैपदं विधिलिङ्लकार: प्रथमपुरुष: एकवचनम्।

पद्यांशं पठित्वा जालरेखाचित्रं पूरयत ।

प्रश्न 1.

उत्तरम् :

प्रश्न 2.

उत्तरम् :

प्रश्न 3.

उत्तरम् :

प्रश्न 4.

उत्तरम् :

प्रश्न 5.

उत्तरम् :

प्रश्न 6.

उत्तरम् :

प्रश्न 7.

उत्तरम् :

प्रश्ननिर्माणं कुरुत।

प्रश्न 1.
1. दृष्टिपूतं पादं न्यसेत्।
2. मन:पूतं समाचारेत्।
उत्तरम् :
1. कथं पादं न्यसेत?
2. मन:पूतं किं कुर्यात् ? (पद्यांशं पठित्वा जालरेखाचित्रं पूरयत। )

प्रश्न 2.
1. लब्धं धनं प्रयत्नतः रक्षेत्।
2. रक्षितं धनं सम्यक् वर्धयेत।
उत्तरम् :
1. लब्धं धनं कथं रक्षेत?
2. कीदृशं धनं सम्यक् वर्धयेत?

प्रश्न 3.
1. असाधुं साधुना जयेत्।
2. दानेन कदर्य जयेत्।
उत्तरम् :
1. असा, केन जयेत्?
2. दानेन किं जयेत्?

विधिलिङ् क्रियापदैः जालचित्रं पूरयत।

प्रश्न 1.

उत्तरम् :

विभक्त्यन्तरूपाणि

• प्रथम – नरः।
• द्वितीया – दुःखाधिकान्, सुखाधिकान्, आत्मानम्।
• तृतीया – पशुभिः, सत्पुरुषैः।
• चतुर्थी – शोकहर्षाभ्याम्, शत्रुभ्याम्।
• सप्तमी – दुःखे, सुखे।

प्रवनिर्माणं कुरुत।

प्रश्न 1.
शत्रुभ्याम् इव शोकहर्षाभ्याम् आत्मानं न अर्पयेत्।
उत्तरम् :
काभ्याम् इव शोकहर्षाभ्याम् आत्मानं न अर्पयेत्?

प्रश्न 2.

1. नर: आत्मनःचरितं प्रत्यवेक्षेत।
2. प्रत्यहम् आत्मनः चरितं प्रत्यवेक्षेत।
3. मे चरितं पशुभिः तुल्यम्।
4. मे चरितं सत्पुरुषै : तुल्यम्।
5. नृपः बकवत् अर्थान् चिन्तयेत्।
6. नृपः सिंह: इव पराक्रमेत् ।

उत्तरम् :

1. कआत्मनःचरितं प्रत्यवेक्षेत?
2. कदा आत्मन: चरितं प्रत्यवेक्षेत?
3. मे चरितं कै: तुल्यम्?
4. मे चरितं कै: तुल्यम्?
5. नृपः बकवत् कान् चिन्तयेत्?
6. नृपः कः इव पराक्रमेत्?

सूचनानुसारं कृती: कुरुत।

प्रश्न 1.
विशेषण – विशेष्य – सम्बन्धः।
‘धनम्’ इति शब्दस्य चत्वारि विशेषणनि चिनुत ।
उत्तरम् :
अलब्धम्, लब्धम्, रक्षितम्, वृद्धम्।

लेखनकौशलम् 

• हर्षः – वर्षाकाले हर्ष : भवेत्। वर्षाकाले प्रमोदः/ आनन्द: भवेत्।
• वचः – गुरोः वच: अनुकरणीयः। गुरोः व्याहार : अनुकरणीयः।
• शत्रुः – सः शत्रु: अतीव बलवान् आसीत्। सः रिपुः / वैरी अतीव बलवान् आसीत्।

व्याकरणम् :

नाम – तालिका।

धातु – तालिका।

समासाः।

धातुसाधितविशेषणानि।

विध्यर्थमाला Summary in Marathi and English

प्रस्तावना :

सुभाषिते हा संस्कृत साहित्याचा अविभाज्य भाग आहे. सुभाषिते कमी शब्दात खोल अर्थ सांगतात. सुभाषिते मनोरंजक तसेच माहितीपर असतात. काही सुभाषिते आपण कसे वागावे, काय करावे, काय करू नये हे सांगतात.

प्रस्तुत पद्य पाठामध्ये अशाच सुभाषितांचा समावेश आहे, जी आपल्याला काय करावे आणि काय करू नये ते सांगतात. “विध्यर्थ’ (विधि-अर्थ) हा शब्द आपल्याला क्रियेची गरज सांगतो.

We know that subhashitas that are an integral part of Sanskrit literature convey a very deep meaning. They are entertaining, as well as informative. Some subhashitas guide us as to how we should behave, what we should do and what are the things we should not do.

As the name suggests विध्यार्थमाला is a collection of beautiful slokas that tell us what we should do and what we should not do. The word foraf (विधि-अर्थ) tells the worth, necessity of an action.

श्लोकः 1

सुखार्थी ………………….. सुखम् ।।1।।

श्लोकः : सुखार्थी चेत् त्यजेद्विद्यां विद्यार्थी चेत् त्यजेत्सुखम्।
सुखार्थिनः कुतो विद्या कुतो विद्यार्थिनः सुखम् ।।1।। (अनुष्टुभ्)

अन्वयः सुखार्थी चेत् विद्यां त्यजेत्। विद्यार्थी चेत् सुखं त्यजेत्। सुखार्थिन: विद्या कुतः? विद्यार्थिनः सुखं कुतः?

अनुवादः

सुखाची इच्छा असणाऱ्याने विद्येचा त्याग करावा. विद्येची इच्छा असणाऱ्याने सुखाचा त्याग करावा. सुखाची इच्छा असणाऱ्यांस विद्या कुठून मिळणार? विद्येची इच्छा असणाऱ्यांस सुख कुठून मिळणार?

If a person desires comforts he should give up knowledge. If a person desires knowledge he should give up comforts. From where do the ones yearning for comforts get knowledge? From where do the ones desiring knowledge get comfort?

श्लोकः 2

दृष्टिपूतं …………………….. समाचारेत् ।।2।।

श्लोकः : दृष्टिपूतं न्यसेत् पादं वस्त्रपूतं पिबेत् जलम्।
सत्यपूतां वदेत् वाणीं मनःपूतं समाचारेत् ।।2।। (मनुस्मृतिः) (अनुष्टुभ)

अन्वयः दृष्टिपूतं पादं न्यसेत् । वस्त्रपूतं जल पिबेत् । सत्यपूतां वाणी वदेत् । मन:पूतं समाचरेत्।

अनुवादः

योग्यरीत्या पाहून पाय ठेवावा. वस्त्राने गाळून घेतलेले पाणी प्यावे. सत्याने पवित्र झालेली भाषा बोलावी आणि योग्य रीतीने विचार करुन (मनन करून) वर्तन करावे.

One should take a step after seeing. One should drink water purified by a cloth. One should speak words purified with truth and one should act after thinking.

श्लोकः 3

धनमलब्ध …………………….. निक्षिपेत् ।।3।।

श्लोकः : धनमलब्धं काङ्क्षत, लब्धं रक्षेत् प्रयत्नतः।
रक्षितं वर्धयेत् सम्यक्, वृद्ध तीर्थेषु निक्षिपेत् ।।3।। (अनुष्टुभ)

अन्वयः : अलब्धं धनं काहक्षेत। लब्ब (धन) प्रयत्नतः रक्षेत्। रक्षितं (धन) सम्यक् वर्धयेत्। वृद्धं (धन) तीर्थेषु निक्षिपेत्।।

अनुवादः

न मिळालेल्या धनाची इच्छा करावी. प्राप्त झालेल्या धनाचे प्रयत्नपुर्वक रक्षण करावे. रक्षण केलेले धन चांगल्या रीतीने वाढवावे. अधिक (वाढलेले) धन तीर्थक्षेत्री / चांगल्या ठिकाणी (कार्यात) दान करावे.

One should wish for wealth which is not obtained. One should protect that which is obtained with efforts. That which is protected should be enhanced properly and the wealth which is enhanced should be put into good use. (given in charity)

श्लोकः 4

अक्रोयेन ………………. चानृतम् ।।4।।
श्लोकः : अक्रोधेन जयेत् क्रोधम् असाधु साधुना जयेत्।
जयेत् कदयं दानेन जयेत् सत्येन चानृतम् ।।4।।(अनुष्टुभ्)

अन्वयः : अक्रोधेन क्रोधं जयेत् । साधुना असाधुं जयेत् । दानेन कदर्य जयेत् । सत्येन च अनृतम् जयेत्।

अनुवादः

क्रोधाला शांततेने (क्षमेने) जिंकावे, सज्जनाने दुष्टाला जिंकावे (चांगल्याने | वाईटाला जिंकावे), कंजूषपणाला दानाने जिंकावे आणि सत्याने असत्याला जिंकावे.

One should win over anger with calmness. One should win over the wicked with goodness. One should win over miserliness with charity and one should win over falsehood with truth.

श्लोकः 5

दुःखे ………………………… नार्पयेत् ।।5।।

श्लोकः : दुःखे दु:खाधिकान् पश्येत् सुखे पश्येत् सुखाधिकान्।
आत्मानं शोकहर्षाभ्यां शत्रुभ्यामिव नार्पयेत् ।।5।। (अनुष्टुभ)

अन्वयः दुःखे दुःखाधिकान् पश्येत्। सुखे सुखाधिकान् पश्येत् । (मानव:) शत्रुभ्याम् इव शोकहर्षाभ्याम् आत्मानं न अर्पयेत् ।

अनुवादः

दु:खात अधिक दुःख असलेल्याकडे पाहावे. सुखात अधिक सुख असलेल्याकडे पाहावे. माणसाने स्वत:ला शत्रूप्रमाणे असलेल्या दुःख व सुखाला समर्पित करू नये.

One would see an abundance of sorrow when sad. One would see an abundance of happiness when happy. Man should not surrender himself to sorrow and happiness which are like enemies.

श्लोकः 6

प्रत्यहं ……………………… सत्पुरुषैरिति ।।6।।

श्लोकः : प्रत्यहं प्रत्यवेक्षेत नरश्चरितमात्मनः ।
किन्नु मे पशुभिस्तुल्यं किन्नु सत्पुरुषैरिति ।।6।। (अनुष्टुभ)

अन्वयः नर: आत्मन: चरितं प्रत्यहं प्रत्यवेक्षेत किं नु मे (चरित) पशुभि: तुल्यम्? किं नु (मे चरित) सत्पुरुषैः (तुल्यम्) इति।

अनुवादः

मनुष्याचे स्वत:च्या चारित्र्याकडे (वर्तनाकडे) बारकाईने दररोज पाहावे (आणि विचारावे) “खरेच माझे बर्तन पशूसमान आहे की सज्जनांसमान?”
Man should observe his behaviour daily (and ask) “Did I behave like animals? Or did I behave like good people?”

श्लोकः 7

बकवच्चिन्तयेदर्थान् ……………… विनिष्यतेत् ।।7।।

श्लोकः बकवच्चिन्तयेदर्थान् सिंहवच्च पराक्रमेत् ।
वृकवच्चावलुम्पेत शशवच्च विनिष्पतेत् ।।7।। (अनुष्टुभ्)

अन्वयः (नृपः) बकवत् अर्थान् चिन्तयेत् सिंहवत् च पराक्रमेत् । वृकवत् अवलुम्पेत शशवत् च विनिष्यतेत्।

अनुवादः

बगळ्याप्रमाणे सिंहाप्रमाणे लांडग्याप्रमाणे सश्याप्रमाणे फाडावे, नामोहरम करावे बाहेर पडावे विचार करावा पराक्रम करावा (राजाने) बगळ्याप्रमाणे होणाऱ्या लाभाचा विचार करावा. सिंहाप्रमाणे पराक्रम गाजवावा. लांडग्याप्रमाणे शत्रूला फाडावे (नामोहरम कराव)(आणि) सश्याप्रमाणे शत्रूच्या व्यूहातून बाहेर पडावे.

(A king) One should think about the purpose like a crane. He should be brave like a lion. He should tear down the enemy like a wolf and should get out of the enemy’s array (व्यूह) like a rabbit.

सन्धिविग्रहः

• धनमलब्धम् – धनम् + अलब्धम् ।
• सिंहवच्च – सिंहवत् + च।
• वृकवच्च – वृकवत् + च।

विरुद्धार्थकशब्दाः

1. त्यजेत् × स्वीकुर्यात, गृह्णीयात् ।
2. सुखम् × दुःखम् ।
3. अलब्धम् × लब्धम्।
4. सत्यम् × असत्यम्।
5. पूतम् × मलिनम्, अस्वच्छम, अमङ्गलम् ।
6. सत्पुरुषाः × दुर्जनाः, खलाः, दुष्टाः।

समानार्थकशब्दाः

1. वाणी – वाक्, भाषा, ब्राह्मी, भारती, गिर् ।
2. पूतम् – पवित्रम्, पावनम् ।
3. सत्यम् – ऋतम् ।
4. जलम् – नीरम्, उदकम्, तोयम्, अम्बु, पयः ।
5. काक्षेत – इच्छेत्।
6. लब्धम् – प्राप्तम्।
7. धनम् – वित्तम्, अर्थम्, द्रविणम्।
8. सम्यक् – सुष्ठु ।
9. कोधः – रोषः।
10. असाधुः – दुष्ट, दुर्जनः।
11. कदर्यम् – कृपणता।
12. सत्यम् – ऋतम्।
13. असत्यम् – अनृतम्।
14. दु:खम् – शोकः।
15. हर्षः – आनन्दः।
16. शत्रुः – रिपुः, अरिः, वैरी।
17. अधिकम् – प्रभूतम्, बहु।
18. सिंहः – वनराजः, केसरी, मृगेन्द्रः।
19. शश: – शशकः।
20. प्रत्यहम् – प्रतिदिनम्।
21. नरः – मनुजः, पुरुषः।
22. चरितम् – वर्तनम्।
23. पशुः – प्राणी, मृगः।
24. तुल्यः – समः।
25. सत्पुरुषाः – सज्जनाः।

शब्दार्थाः

1. सुखार्थी – one who wishes happiness – सुखाची इच्छा असणारा
2. चेत् – if – जर
3. विद्या – knowledge – विद्या, ज्ञान
4. त्यजेत् – should leave – त्याग करावा
5. कुतः – from where/how – कुठून
6. सुखम् – happiness – सुख
7. दृष्टिपूतम् – after seeing (purified by sight) – नीट पाहून
8. न्यसेत् – should place – ठेवावे
9. समाचरेत् – should act – वागावे
10. काङ्क्षेत – should wish – इच्छा करावी
11. रक्षेत् – shoul protect – रक्षण करावे
12. प्रयत्नतः – with efforts – प्रयत्नपूर्वक
13. वर्धयेत् – should enhance – वाढवावे
14. सम्यक् – properly – योग्यरीत्या
15. क्रोध – anger – राग
16. अक्रोधेन – with calmness – शांततेने
17. असाधु – wicked – दुष्ट
18. कदर्यम् – miserliness – कंजूषपणा
19. अनृतम् – falsehood – असत्य
20. दुःखे – in sorrow – दुःखात
21. आत्मानम् – oneself – स्वत:ला
22. सुखे – in happiness – सुखात
23. शोकहर्षाभ्याम् – to sorrow and happiness – दु:ख व सुखाला
24. न अर्पयेत् – should not surrender – समर्पित करू नये
25. आत्मनः – of oneself – स्वत:चे
26. चरितम् – behaviour – वर्तन
27. प्रत्यहम् – everyday – दररोज
28. प्रत्यवेक्षेत – observe – परीक्षण करावे
29. तुल्यम् – like – सारखे, तुलना करण्यायोग्य
30. बकवत् – like a crane – बगळ्याप्रमाणे
31. सिंहवत् – like a lion – सिंहाप्रमाणे
32. वृकवत् – like a wolf – लांडग्याप्रमाणे
33. शशवत् – like a rabit – सश्याप्रमाणे
34. अवलुम्पेत – should tear down – फाडावे, नामोहरम करावे
35. विनिष्पतेत् – should get out of – बाहेर पडावे
36. चिन्तयेत् – should think – विचार करावा
37. पराक्रमेत् – should be brave – पराक्रम करावा

Balbharti Maharashtra State Board Class 9 Marathi Solutions Kumarbharti Chapter 5 एक होती समई Notes, Textbook Exercise Important Questions and Answers.

Maharashtra State Board Class 9 Marathi Kumarbharti Solutions Chapter 5 एक होती समई

9th Std Marathi Kumarbharati Digest Chapter 5 एक होती समई Textbook Questions and Answers

1. चौकटी पूर्ण करा:

प्रश्न 1.
चौकटी पूर्ण करा:
(अ) कोसबाडच्या टेकडीवरील समई म्हणून ओळख – [ ]
(आ) रोपट्याचा वटवृक्ष झालेली संस्था – [ ]
(इ) आयुष्याचा पाया भक्कम करणारे – [ ]
(ई) भाकरीच्या शोधात आयुष्य गमावणारे – [ ]
उत्तर:
(अ)अनुताई वाघ
(आ) बाल ग्रामशिक्षण केंद्र
(इ) प्राथमिक शिक्षण
(ई) आदिवासी बालक

2. खालील घटनांचे परिणाम लिहा:

प्रश्न 1.
खालील घटनांचे परिणाम लिहा:

उत्तर:

3. कार्यक्षेत्र लिहा:

प्रश्न 1.
कार्यक्षेत्र लिहा:

उत्तर:

4. का ते लिहा:

प्रश्न (अ)
शिक्षणक्षेत्रातील कार्यकर्त्यांना कोसबाडच्या टेकडीचं सातत्यानं आकर्षण राहिलं.
उत्तर:
शिक्षण सर्वांगीण असले पाहिजे. ते एकांगी असता कामा नये. तसेच, केवळ चाकोरीबद्ध रितीने न शिकवता अनेक प्रयोग केले पाहिजेत, असा दृष्टिकोन बाळगून अनुताईंनी कार्य केले. त्यांच्या या कार्याविषयी अनेकांना कुतूहल होते. म्हणून शिक्षणक्षेत्रातील कार्यकर्त्यांना कोसबाडच्या टेकडीचे सातत्याने आकर्षण राहिले.

प्रश्न (आ)
अनुताईंच्या कार्याचा तुम्हांला जाणवलेला विशेष सांगा.
उत्तर:
आपल्याकडे शिक्षण म्हणजे पुस्तकी शिक्षण असा समज घट्ट बसला आहे. खरे तर शिक्षण जीवन जगण्यासाठी व लाभलेले जीवन अधिक समृद्ध करण्यासाठी आवश्यक असते. त्यासाठी दिले जाणारे शिक्षण हे जीवनाभिमुख असले पाहिजे. ते जीवनाशी जोडले गेले पाहिजे. समाजात पूरक वातावरण तयार असले पाहिजे.

अंधश्रद्धा नष्ट झाली पाहिजे. वैज्ञानिक दृष्टिकोन वाढला पाहिजे. कुटुंबकल्याणाकडे लक्ष दिले पाहिजे. स्वच्छता व आरोग्य यांबाबत समाजात जागृती हवी. तसेच, लहान मुले, मूकबधिर व महिला या घटकांना सक्षम केले पाहिजे. इतके व्यापक भान अनुताईंना होते. म्हणून त्यांनी शालेय , शिक्षणाबरोबर अन्य सामाजिक क्षेत्रांकडे लक्ष दिले आणि तेथेही भरीव । काम केले. अनुताईंच्या कार्याचा हा फार मोठा विशेष आहे.

5. खालील शब्दांमधील कल्पना स्पष्ट करा:

प्रश्न 1.
खालील शब्दांमधील कल्पना स्पष्ट करा:
1. भातुकलीचा खेळ
2. ज्ञानयज्ञ
3. ज्ञानगंगा.
4. पाऊलखुणा.
उत्तर:
1. भातुकलीचा खेळ: लहान मुलांचा, विशेषतः मुलींचा खेळ. यात खोटा खोटा संसार उभारला जातो. संसारोपयोगी चिमुकली भांडी आणली जातात. प्रत्यक्ष संसारात मोठी माणसे जशी वावरतात, त्याचे अनुकरण करीत खेळ मांडला जातो. बाहुला-बाहुलीचे लग्नही लावले जाते. थोडक्यात, भातुकलीचा खेळ म्हणजे खोटा खोटा, आभासमय असा संसार.

2. ज्ञानयज्ञ: विधिपूर्वक अग्नी पेटवला जातो आणि त्यात आपल्या जवळच्या पदार्थांची आहुती दिली जाते. अग्नी ती आहुती परमेश्वरापर्यंत पोहोचवतो, अशी श्रद्धा आहे. अनुताईंनी शिक्षणप्रसाराचे कार्य सुरू केले. त्या कार्यात त्यांनी आपले सर्वस्व ओतले. यज्ञात आहुती देतात, तशी अनुताईंनी स्वत:च्या जीवनाची आहुती दिली. म्हणून त्यांचे कार्य म्हणजे ज्ञानयज्ञ होय.

3. ज्ञानगंगा: गंगा नदी पवित्र मानली जाते. गंगेचे पाणी प्याल्यास पुण्य मिळते, पाप नाहीसे होते अशी श्रद्धा आहे. गंगा नदी घरोघर पोहोचवणे म्हणजे सर्वांचे दु:ख, दैन्य दूर करणे असा अर्थ रूढ झाला आहे. अनुताईंनी आदिवासी बालकांपर्यंत शिक्षण नेले. एक प्रकारे त्यांचे जीवन अनुताईंनी पवित्र केले, म्हणून त्यांच्या कार्याला लाक्षणिक अर्थाने ज्ञानगंगा म्हटले आहे.

4. पाऊलखुणा: या शब्दाचा शब्दश: अर्थ, चालताना वाटेवर निर्माण झालेल्या पावलांच्या खुणा. त्या खुणांवरून, कोण चालत गेले, हे सांगता येते. अनुताईंनी शिक्षणप्रसाराचा जो मार्ग अवलंबिला तो मार्ग आणि त्यांनी काय, काय केले ते त्यांचे कार्य या गोष्टी म्हणजे, त्यांच्या ‘पाऊलखुणा’ आहेत. या पाऊलखुणा जपल्या पाहिजेत.

6. खालील ‌शब्दसमूहांसाठी‌ ‌एक‌ ‌शब्द‌ ‌लिहा‌:‌

प्रश्न 1.‌ ‌
खालील ‌शब्दसमूहांसाठी‌ ‌एक‌ ‌शब्द‌ ‌लिहा‌:‌
‌(अ) व्रताने‌ ‌स्वत:ला‌ ‌बांधणाऱ्या‌ ‌- [ ]
‌(आ) नेमाने‌ ‌स्वत:ला‌ ‌बांधणारा‌ ‌- [ ]
‌(इ) गावातील‌ ‌रहिवासी‌ ‌- [ ]
(ई) तिहाइताच्या‌ ‌भूमिकेतून‌ ‌बघणारा‌ ‌-‌ ‌[ ]
उत्तर:
(अ) व्रतस्थ‌ ‌
(आ) नेमस्त‌ ‌
(इ) ग्रामस्थ‌ ‌
(ई) भतटस्थ‌ ‌

7. खाली ‌दिलेल्या‌ ‌शब्दांचा‌ ‌उपसर्ग‌ ‌बदलून‌ ‌विरुद्धार्थी‌ ‌शब्द‌ ‌लिहा‌ ‌:‌ ‌

प्रश्न 1.‌ ‌
खाली ‌दिलेल्या‌ ‌शब्दांचा‌ ‌उपसर्ग‌ ‌बदलून‌ ‌विरुद्धार्थी‌ ‌शब्द‌ ‌लिहा‌ ‌:‌ ‌
उदा.,‌ 1.‌ ‌सापेक्ष‌ ‌×‌ ‌निरपेक्ष‌, ‌2.‌ ‌अनावृष्टी‌ ‌× ‌अतिवृष्टी.‌

1. अनाथ‌ ‌
2. दुश्चिन्ह‌ ‌
3. सुपीक‌ ‌
4. एकमत‌ ‌
5. पुरोगामी‌ ‌
6. स्वदेशी‌ ‌
7. विजातीय‌ ‌

उत्तर:

1. अनाथ × सनाथ
2. दुश्चिन्ह × सुचिन्ह
3. सुपीक × नापीक
4. एकमत × दुमत
5. पुरोगामी × प्रतिगामी
6. स्वदेशी × परदेशी
7. विजातीय × सजातीय

8. स्वमत:

प्रश्न (अ)
अनुताई वाघ यांना दिलेल्या समईच्या उपमेची सार्थकता तुमच्या शब्दांत लिहा.
उत्तर:
समईचा प्रकाश मंद, शांत, स्निग्ध असतो. तिच्या प्रकाशात शांत, निवांत वाटते. ती गाभारा उजळून टाकते. त्या शांत प्रकाशात बसावे आणि देवाचे नाव घ्यावे अशी इच्छा होते. तिचा प्रकाश भगभगीत नसतो. भगभगीत प्रकाशात मनाला शांती मिळतच नाही. अनुताई वाघांचे व्यक्तिमत्त्व समईसारखे होते. त्यांच्याजवळ डामडौल नव्हता. भपका नव्हता. त्या कडक शिस्तीच्या नव्हत्या. मुलांवर रागावून, त्यांना दम देऊन गप्प बसवणाऱ्या नव्हत्या. त्यांना आदिवासी मुलांबद्दल अमाप माया होती. त्यामुळे आदिवासी मुलांना अनुताईंच्या सहवासात असताना मायेची ऊब मिळे. अनुताईंचा सहवास त्या मुलांना जणू समईचा प्रकाशच वाटे. अनुताईंना दिलेली समईची उपमा यथार्थ आहे.

प्रश्न (आ)
‘समई हे सातत्याचे, संयमी वृत्तीचे आणि सामर्थ्याचे प्रतीक आहे.’ या विधानाबाबत तुमचे मत स्पष्ट करा.
उत्तर:
समई देवाजवळच लावली जाते. घरात प्रकाश मिळावा, म्हणून अन्य दिवे वापरतात; समई नव्हे. देवाजवळची, गाभाऱ्यातली समई सतत तेवती राहावी याची काळजी घेतली जाते. म्हणून सतत तेवणारी ती समई. समईमध्येच सातत्य सामावलेले आहे. समई संपूर्ण घर, संपूर्ण महाल किंवा संपूर्ण परिसर उजळून टाकण्याची ईर्षा बाळगत नाही. ती फक्त देवघर किंवा मंदिरातला गाभारा उजळते. पण उजळते म्हणजे झगझगीत प्रकाश पसरवीत नाही. तिचा मंद प्रकाश डोळ्यांना, मनाला शांत, निवांत करणारा असतो. मर्यादित प्रमाणात राहावे, ही तिची वृत्तीच जणू असते. म्हणून ती संयमी वाटते. समईच्या प्रकाशात असलेला परिसर उच्च, उदात्त भावनेने भारलेला असतो. ही भावना माणसाला फार मोठे समाधान देते. असे समाधान देता येणे हे समईचे सामर्थ्य आहे

उपक्रम:

प्रश्न 1.‌ ‌
आदिवासी मुलांच्या शिक्षणासाठी कार्यरत असणाऱ्या कोणत्याही एका संस्थेची माहिती मिळवा.

भाषाभ्यास:

उपमेय व उपमान यांच्यातील साधर्म्यावर आधारित काही अलंकारांचा आपण अभ्यास केला. आता इतर काही अलंकार पाहूया.

1. दृष्टान्त अलंकार:
खालील उदाहरण वाचा व समजून घ्या.
उदा., चंदनाचे हात । पायही चंदन
तुका म्हणे तैसा । सज्जनापासून
पाहता अवगुण । मिळेचिना (संत तुकाराम)

1. संत तुकाराम कोणत्या दोन गोष्टींची तुलना करतात?
[ ] आणि [ ]

2. (अ) चंदनाचा विशेष गुण – [ ]
(आ) संतांचा विशेष गुण – [ ]
चंदन सर्वांगाने सुगंधित-त्रिकालाबाधित सत्य
सज्जन व्यक्ती अंतर्बाह्य सज्जन असते हे पटवून देण्यासाठी वरील उदाहरण दिले आहे.

3. दृष्टान्त अलंकाराची वैशिष्ट्ये –
1. एखादी गोष्ट पटवून देणे.
2. ती पटवून देण्यासाठी समर्पक उदाहरणाचा वापर करणे.

4. एखादी गोष्ट पटवून देण्यासाठी त्याच अर्थाचे एखादे समर्पक उदाहरण दिले जाते, तेव्हा ‘दृष्टान्त’ अलंकार होतो.

प्रश्न 1.
खालील ओळी वाचा व चौकटी पूर्ण करा.
लहानपण देगा देवा । मुंगी साखरेचा रवा ।
ऐरावत रत्न थोर । त्यासी अंकुशाचा मार ।।

1. संत तुकाराम परमेश्वराजवळ हे मागणे मागतात – [ ]
2. रत्नासारख्या थोर ऐरावताला सहन करावा लागतो – [ ]
3. मुंगीला ही गोष्ट प्राप्त होते – [ ]
4. संत तुकाराम ही गोष्ट पटवून देतात – [ ]
5. मोठेपणातील यातना या उदाहरणाने पटवून देतात – [ ]

उत्तर:

1. [लहानपण दे]
2. [अंकुशाचा मार]
3. [साखरेचा रवा]
4. [नम्रपणा असावा]
5. [थोर ऐरावताला अंकुशाचा मार]

Marathi Kumarbharati Textbook Std 9 Answers Chapter 5 एक होती समई Additional Important Questions and Answers

उतारा क्र. 1

1. पुढील उतारा वाचून दिलेल्या सूचनांनुसार कृती करा :

कृती 1 : (आकलन)

प्रश्न 1.
चौकटी पूर्ण करा:

1. बालपणीच वैधव्य आलेल्या – [ ]
2. अनुताईंचे अश्रू पुसणाऱ्या – [ ]
3. प्राथमिक शाळेत कार्यकर्ती म्हणून काम करणाऱ्या – [ ]
4. ताराबाईंनी स्थापन केलेली संस्था – [ ]

उत्तर:

1. अनुताई वाघ
2. ताराबाई मोडक
3. अनुताई वाघ
4. बाल ग्रामशिक्षण केंद्र

प्रश्न 2.
अर्थ स्पष्ट करा:

1. वादळ झेलतात – ………………………………..
2. वादळ पचवतात – ………………………………….
3. ज्ञानयज्ञ तेवत ठेवला – …………………………………..
4. कोसबाडची टेकडी हळहळली – …………………………..

उत्तर:

1. मोठ्या संकटांना सामोरे जातात.
2. संकटांचे निवारण करतात.
3. ज्ञानप्रसाराचे कार्य दीर्घकाळ चालू ठेवले.
4. कोसबाडच्या टेकडीवरील आदिवासी हळहळले, ते व्यथित झाले.

कृती 2 : (आकलन)

प्रश्न 1.
आकृती पूर्ण करा:

उत्तर:

कृती 3 : (स्वमत/अभिव्यक्ती)

प्रश्न 1.
हा उतारा वाचल्यावर अनुताई वाघांची तुमच्या मनात निर्माण झालेली प्रतिमा तुमच्या शब्दांत लिहा.
उत्तर:
अनुताई वाघांचा काळ म्हणजे सुमारे 100 वर्षांपूर्वीचा काळ. त्या काळाला धरून अनुताईंचे लग्न वयाच्या तेराव्या वर्षी म्हणजे इयत्ता आठवीत असण्याच्या वयात झाले. शाळेत मित्रमैत्रिणींबरोबर शिकण्याचे व खेळण्याबागडण्याचे हे वय. पण त्यांना हा नैसर्गिक उत्सव सोडून लग्न करावे लागले. पण लग्न, संसार म्हणजे काय, हे कळण्याच्या आतच, म्हणजे सहा महिन्यांतच, त्यांच्या पतीचे निधन झाले. त्या विधवा झाल्या. त्या काळात विधवांचे जीवन खूप कष्टाचे, हलाखीचे व अपमानाचे होते. पण त्या वयातही त्या मनाने खंबीर राहिल्या. स्वत:ला खचू दिले नाही.

संकटांना तोंड देण्यासाठी स्वतः शक्तिमान असणे आवश्यक असते, हे त्यांनी ओळखले. स्वत:चे व्यक्तिमत्त्व अधिक बलशाली करण्यासाठी त्यांनी स्वतः शिक्षण घेतले. बाहेरून अभ्यास करून त्यांनी पदवी संपादन केली. त्या स्वत:चे दुःख कुरवाळत बसल्या नाहीत किंवा संकटांना शरणही गेल्या नाहीत. दुःखाला सामोरे जाण्याचा त्यांनी वेगळाच मार्ग निवडला. त्या ताराबाई मोडकांच्या कार्यात सामील झाल्या. त्यांनी आदिवासी बालकांना शिक्षणाच्या प्रवाहात आणायचे ठरवले. त्या कार्याला त्यांनी पूर्णपणे वाहून घेतले. यावरून त्यांच्या मनातील उच्च, उदात्त मूल्यांचे दर्शन घडते.

उतारा क्र. 2

पुढील उतारा वाचून दिलेल्या सूचनांनुसार कृती करा:

कृती 1 : (आकलन)

प्रश्न 1.
आकृतिबंध पूर्ण करा:

उत्तर:

प्रश्न 2.
चौकटी पूर्ण करा:
1. कपाळावर दारिद्र्याचा शाप असलेली – [ ]
2. प्रसिद्धीचा हव्यास नसलेल्या – [ ]
उत्तर:
1. आदिवासी बालके
2. अनुताई वाघ

प्रश्न 3.

उत्तर:

कृती 2: (आकलन)

प्रश्न 1.
चौकट पूर्ण करा:

उत्तर:

प्रश्न 2.
आकृती पूर्ण करा:

उत्तर:

कृती 3 : (स्वमत/अभिव्यक्ती)

प्रश्न 1.
दारिद्र्यात खितपत पडलेल्या बालकांना शिक्षणाच्या प्रवाहात आणण्यासाठी तुम्हांला या उताऱ्यावरून जाणवलेले उपाय लिहा.
उत्तर:
दारिद्र्यात खितपत पडलेल्या बालकांना प्रथम गरज असते ती मायेची. मायेच्या आधाराने त्यांच्यात ज्ञानाची ओढ निर्माण केली __ पाहिजे. अशा स्थितीत नेहमीचे चाकोरीबद्ध शिक्षक उपयोगाचे नाहीत. त्यांना शिकवण्याबरोबर मार्गदर्शन केले पाहिजे. त्यांच्या समस्या सोडवण्यासाठी कार्यकर्त्याची भूमिका घेतली पाहिजे. तसेच, सतत नवनवीन प्रयोग करीत राहिले पाहिजे. त्यासाठी शिक्षकांकडे दूरदृष्टी असली पाहिजे. प्रथम प्राथमिक शिक्षण भक्कम केले पाहिजे. या शिक्षकांनी प्रसिद्धीपासून दूर राहिले पाहिजे. या सर्व बाबी पाळल्या तर दारिद्र्यात खितपत पडलेल्या बालकांना चांगले शिक्षण देता येईल.

उतारा क्र. 3:

1. पुढील उतारा वाचून दिलेल्या सूचनांनुसार कृती करा:

कृती 1 : (आकलन)

प्रश्न 1.
का ते लिहा:
अन्य क्षेत्रांतही अनुताईंनी फार मोठे काम केले आहे.
उत्तर:
आपल्या शाळांमधून दिले जाणारे औपचारिक शिक्षण एकांगी आहे. या शिक्षणाने एक चांगला नागरिक घडवता येणे अशक्य आहे. म्हणून शिक्षणाशी संबंधित क्षेत्रांतही अनुताईंनी फार मोठे कार्य केले.

कृती 2 : (आकलन)

प्रश्न 1.
कल्पना स्पष्ट करा:
1. अंधश्रद्धा निर्मूलन
2. महिला विकास.
उत्तर:
1. अंधश्रद्धा निर्मूलन : अंधश्रद्धेमुळे माणसे चुकीच्या मार्गांनी जातात. स्वत:ची विचारशक्ती, विवेकबुद्धी गमावून बसतात. योग्य वेळी योग्य निर्णय घेत नाहीत. यांमुळे माणसांचे मोठ्या प्रमाणात नुकसान होते. सतत नुकसान, अपयश मिळत राहिल्याने ती हतबल होतात आणि पुन्हा अंधश्रद्धांच्या मागे लागतात. या परिस्थितीचा लबाड लोक गैरफायदा घेतात. ते दुबळ्या माणसांना लुबाडतात, म्हणून अंधश्रद्धा नष्ट करण्याचा प्रयत्न करणारी चळवळ, म्हणजे ‘अंधश्रद्धा निर्मूलन’ होय.

2. महिला विकास : शिक्षणाचा प्रसार होण्यासाठी महिलांच्या सहकार्याची नितांत गरज असते. त्यासाठी प्रथम महिला सुधारल्या पाहिजेत. महिला कमावत्या असतील, तर त्यांना आत्मविश्वास येतो. त्या शिक्षित असतील, तर त्यांना शिक्षणाचे महत्त्व कळते. दृष्टी व्यापक बनते. मग घरात शिक्षणासाठी अनुकूल वातावरण तयार होते. महिलांना उपजीविकेची साधने मिळवून देणे, शिकू इच्छिणाऱ्यांना शिक्षण देणे, विविध कौशल्ये आत्मसात करण्यास मदत करणे, विज्ञाननिष्ठ दृष्टिकोन रुजवणे, स्त्रीपुरुष समानतेचा दृष्टिकोन रुजवणे या गोष्टी प्राधान्याने महिला विकासात येतात.

प्रश्न 2.
आशय स्पष्ट करा:
अनेक मानसन्मान अनुताईंच्या शोधात भटकत राहिले.
उत्तर:
वेगवेगळ्या कर्तबगारी गाजवलेल्यांना शासन व समाज सन्मान देऊन त्यांचा गौरव करतात. कित्येकजण हे सन्मान मिळावेत म्हणून गैरमार्गाने प्रयत्न करतात. अनुताईंना मात्र कार्य करण्यातच रस होता, त्यांचे कार्यच एवढे उत्तुंग होते की, त्यांचा सन्मान करावा, असे सर्वांनाच वाटत होते. म्हणून अनुताईंनी न मागता अनेक सन्मान त्यांना मिळत गेले.

उतारा क्र. 4:

पुढील उतारा वाचून दिलेल्या सूचनांनुसार कृती करा:

कृती 1 : (आकलन)

प्रश्न 1.
का ते लिहा:
अनुताईंच्या कामाला प्राथमिक अवस्थेत विरोध झाला.
उत्तर:
अनुताईंच्या कामाला प्राथमिक अवस्थेत विरोध झाला. त्यामागे रूढी, परंपरा, अज्ञान व अंधश्रद्धा ही प्रमुख कारणे होती. प्रचंड अज्ञानामुळे लोकांना स्वतंत्र बुद्धीने विचार करता येत नाही. त्यामुळे ते अंधश्रद्धेने ग्रासलेले असतात. त्यांना नवीन सुधारणा नको असतात. सुधारणांमुळे आपले नुकसान होईल, अशी त्यांना भीती वाटते. म्हणून ते शिक्षणाला विरोध करतात.

कृती 2 : (आकलन)

प्रश्न 1.
पुढील बाबींची घातकता सांगा:
1. रूढी
2. परंपरा
3. अंधश्रद्धा
4. स्थितिशीलता.
उत्तर:
1. रूढी: रूढींमुळे माणसे विचार करीत नाहीत, चिकित्सा करीत नाहीत. घातक प्रथा तशाच राहतात.
2. परंपरा: पूर्वापार चालत आलेली जगण्याची रीत म्हणजे परंपरा. परंपराप्रिय माणसे नवीन गोष्टींना, सुधारणांना विरोध करतात.
3. अंधश्रद्धा: भूताखेतांच्या, देवधर्माच्या खूप जुन्या कल्पनांवर श्रद्धा ठेवणे म्हणजे ‘अंधश्रद्धा’. अंधश्रद्धाळू माणसे विज्ञाननिष्ठेकडे पाठ फिरवतात. अंधश्रद्धेतून चुकीचे निर्णय घेतात. त्यामुळे खूप नुकसान होते. कधी कधी माणसांचे प्राणही जातात. अंधश्रद्धेमुळे प्रगतीच्या मार्गात अडचणी निर्माण होतात.
4. स्थितिशीलता: आहे त्याच स्थितीला चिकटून राहणे आणि त्याच स्थितीत राहण्यात आनंद मानणे, म्हणजे ‘स्थितिशीलता’. या वृत्तीमुळे प्रगती, विकास होत नाही. किंबहुना प्रगतीला विरोध केला जातो.

प्रश्न 2.
अर्थ स्पष्ट करा:
1. ज्ञानाचा दिवा जपणे.
2. मनातील विविध प्रकारचा अंधार दूर करणे.
उत्तर:
1. ज्ञानाचा दिवा जपणे: दिव्यामुळे प्रकाश पडतो. अंधार दूर होतो. आपल्याला स्पष्टपणे सर्व दिसते. ज्ञानामुळेही सर्व गोष्टींचा उलगडा होतो. सर्व घटना, प्रसंग, माणसे, माणसांचे वागणे आपल्याला कळते. म्हणून ज्ञानाला दिवा म्हणतात. ज्ञानाचा दिवा जपणे म्हणजे ज्ञान वाढवत राहणे.
2. मनातील विविध प्रकारचा अंधार दूर करणे: मनात अज्ञानामुळे अंधार निर्माण होतो. कधी कधी अंधश्रद्धेने सत्य काय व असत्य काय हे कळत नाही. रूढींमुळेही हा गोंधळ उडतोच. भूताखेतांवर विश्वास ठेवल्यामुळेही मनात भीती निर्माण होते. हे सर्व अंधाराचेच प्रकार होत. या अंधारामुळे माणूस योग्य दिशेने प्रगती करू शकत नाही. ज्ञानामुळे हे सर्व अंधार नष्ट होतात. माणूस प्रगती करू शकतो.

कृती 3 : (स्वमत/अभिव्यक्ती)

प्रश्न 1.
अनुताईंच्या मार्गातील खडतरपणा तुमच्या शब्दांत लिहा.
उत्तर:
आदिवासींमध्ये कमालीचे दारिद्र्य असल्यामुळे कोणत्याही सोयीसुविधा उपलब्ध नव्हत्या. वर्ग घेण्यासाठी साधी जागा मिळत नसे. बसण्याच्या सोयी, खडू-फळा या गोष्टीही मिळत नसत. अनुताईंनी या स्थितीलाही खंबीरपणे तोंड दिले. जेथे मिळेल तेथे वर्ग घेतले. प्रसंगी झाडाखाली, कधी गोठ्यात, कधी झोपडीत, तर कधी उघड्याबोडक्या माळावर वर्ग घेतले.

सर्व भौतिक सोयींची वानवा होतीच. पण आदिवासींची मानसिकताही शिक्षणाला पूरक नव्हती. पोट भरण्यासाठी भटकावे लागत असल्याने मुलांना शिक्षणासाठी मोकळे ठेवणे त्यांना परवडत नसे. शिवाय, अज्ञान, अंधश्रद्धा व रूढी-परंपरा यांच्या प्रभावामुळेही आदिवासी लोक शिक्षणाकडे दुर्लक्ष करीत. त्यांना पुन:पुन्हा समजावून सांगून शिक्षणाकडे आणावे लागे. यात अनुताईंची बरीचशी शक्ती खर्च होई.

भाषाभ्यास:

(अ) व्याकरण घटकांवर आधारित कृती:

1. अलंकार:

प्रश्न 1.
पुढील ओळी वाचा व चौकटी पूर्ण करा:
1. चंदनाचे हात। पायही चंदन।
तुका म्हणे तैसा। सज्जनापासून।
पाहता अवगुण। मिळेचिना।। (संत तुकाराम)
2. संत तुकाराम कोणत्या दोन गोष्टींची तुलना करतात?
[ ] आणि [ ]

2. (अ) चंदनाचा विशेष गुण – [ ]
(आ) संतांचा विशेष गुण – [ ]
उत्तर:
1. [सज्जन] आणि [चंदन]
2. (अ) [सुगंधित]
(आ) [त्यांच्यात अवगुण नसतो]

2. समास:

प्रश्न 1.
तक्ता भरा: (उत्तरे अधोरेखित केली आहेत.)
उत्तर:

‌3. ‌शब्दसिद्धी‌:‌ ‌

प्रश्न 1.
‌उपसर्गघटित‌ ‌व‌ ‌प्रत्ययघटित‌ ‌यांत‌ ‌वर्गीकरण‌ ‌करा‌‌:‌
‌(नि:स्वार्थी,‌ ‌दिशाहीन,‌ ‌व्यावहारिक,‌ ‌प्रयत्न)‌ ‌
उत्तर‌:‌ ‌
उपसर्गघटित‌ ‌प्रत्ययघटित‌ ‌नि:स्वार्थी‌ ‌
दिशाहीन‌ ‌व्यावहारिक‌ ‌ प्रयत्न‌ ‌

4.‌ ‌वाक्प्रचार‌‌:

प्रश्न 1.
‌पुढील‌ ‌वाक्प्रचारांचा‌ ‌अर्थ‌ ‌सांगून‌ ‌वाक्यांत‌ ‌उपयोग‌ ‌करा‌‌:
‌1. ‌आयुष्य‌ ‌गमावणे‌ ‌
2. कोलमडून‌ ‌पडणे.‌
‌उत्तर‌:‌
‌1.‌ ‌आयुष्य‌ ‌गमावणे -‌ ‌अर्थ‌ ‌:‌ ‌जीवन‌ ‌संपवणे.‌ ‌
वाक्य‌:‌ ‌स्वातंत्र्यलढ्यामध्ये‌ ‌अनेक‌ ‌क्रांतिवीरांनी‌ ‌देशासाठी‌ ‌आपले‌ ‌आयुष्य‌ ‌गमावले.‌ ‌

2.‌ ‌कोलमडून‌ ‌पडणे‌ ‌-‌ ‌अर्थ‌ ‌:‌ ‌मनाने‌ ‌ढासळणे.‌ ‌
वाक्य‌:‌ ‌अतिवृष्टीने‌ ‌पिकांचा‌ ‌नाश‌ ‌झाल्यामुळे‌ ‌अनेक‌ ‌शेतकरी‌ ‌कोलमडून‌ ‌पडले.‌ ‌

(आ‌) भाषिक‌ ‌घटकांवर‌ ‌आधारित‌ ‌कृती‌ :

1.‌ ‌शब्दसंपत्ती‌:‌

प्रश्न 1.‌ ‌
पुढे‌ ‌दिलेल्या‌ ‌शब्दांचा‌ ‌उपसर्ग‌ ‌बदलून‌ ‌विरुद्धार्थी‌ ‌शब्द‌ ‌लिहा‌ ‌:‌ ‌
उदा.,‌ 1.‌ ‌सापेक्ष‌ ‌×‌ ‌निरपेक्ष‌, ‌2.‌ ‌अनावृष्टी‌ ‌× ‌अतिवृष्टी.‌
1. आरोह‌ ‌
2.‌ ‌दीर्घायुषी.‌ ‌
उत्तर:
1. आरोह × अवरोह
2. दीर्घायुषी × अल्पायुषी.

प्रश्न 2.‌ ‌
तक्ता पूर्ण करा:

उत्तर:

प्रश्न 3.‌ ‌
पुढील शब्दांतील अक्षरांपासून प्रत्येकी चार अर्थपूर्ण शब्द लिहा:
1. जाणीवपूर्वक
2. शिफारस.
उत्तर:
1. (1) जाणीव (2) पूर्व (3) जावक (4) कणी.
2. (1) फार (2) फास (3) रस (4) सर.

2. लेखननियम:

प्रश्न 1.‌ ‌
पुढील अशुद्ध शब्द लेखननियमांनुसार शुद्ध लिहा:

1. दुरदृष्टि
2. ओपचारिक
3. स्थीतीशिल
4. नीमुर्लन
5. भातूकलि
6. आदराजलि.

उत्तर:

1. दूरदृष्टी
2. औपचारिक
3. स्थितिशील
4. निर्मूलन
5. भातुकली
6. आदरांजली.

३. विरामचिन्हे:

प्रश्न 1.‌ ‌
नावे लिहा: (उत्तरे ठळक अक्षरांत दिली आहेत.)
1. [,] स्वल्पविराम
2. [;] अर्धविराम

एक होती समई Summary in Marathi

प्रस्तावना:

उत्तम कांबळे हे प्रसिद्ध लेखक व पत्रकार. त्यांना साहित्यनिर्मितीसाठी व पत्रकारितेसाठी अनेक पुरस्कार मिळाले आहेत. त्यांच्या साहित्यात गरीब, कष्टकरी सामान्य जनतेच्या जीवनाला प्राधान्याने स्थान मिळाले आहे. दीनवाणे, अगतिक जीवन लाभलेल्या तळागाळातील लोकांविषयी लेखकांना खूप आस्था आहे.

अनुताई वाघ (17 मार्च 1910-17 सप्टेंबर 1992) यांनी आदिवासी बालकांपर्यंत शिक्षणाची गंगा नेली. त्यासाठी त्यांनी आपले संपूर्ण आयुष्य वेचले. अनेक हालअपेष्टा सोसल्या. त्यांच्या कार्याचा परिचय प्रस्तुत पाठात करून देण्यात आला आहे.

शब्दार्थ:

1. व्रतस्थ – कठोरपणे एखादया व्रताचे आचरण करणारे.
2. निरपेक्ष – कार्य केल्याच्या बदल्यात काहीतरी मिळण्याची अपेक्षा न ठेवता.
3. स्थितिशील – कोणताही बदल होऊ न देता, आहे त्याच स्थितीत राहण्याची वृत्ती असलेले.
4. औपचारिक शिक्षण – पूर्व प्राथमिक, प्राथमिक, माध्यमिक, उच्च माध्यमिक असे शाळांमध्ये क्रमाने दिले जाणारे रूढ शिक्षण.

वाक्प्रचार व त्यांचे अर्थ:

1. कपाळावरील कुंकू पुसले जाणे – पतीला मृत्यू येणे, विधवा होणे.
2. डोळ्यांतले अश्रू पुसणे – दुःख दूर करणे, दुःख दूर करण्यास मदत करणे.
3. भविष्याचा वेध घेणे – भावी काळात काय काय होऊ शकेल याचा अंदाज बांधणे.

Balbharti Maharashtra State Board Class 9 Marathi Solutions Kumarbharti Chapter 18 हसरे दुःख Notes, Textbook Exercise Important Questions and Answers.

Maharashtra State Board Class 9 Marathi Kumarbharti Solutions Chapter 18 हसरे दुःख

9th Std Marathi Kumarbharati Digest Chapter 18 हसरे दुःख Textbook Questions and Answers

1. आकृतीत दिलेल्या प्रसंगाबाबत माहिती लिहून आकृतिबंध पूर्ण करा:

प्रश्न 1.

उत्तर:

प्रश्न 2.

उत्तर:

2. खाली दिलेल्या घटनांचा परिणाम लिहा:

प्रश्न 1.
खाली दिलेल्या घटनांचा परिणाम लिहा:

उत्तर:

3. कंसातील वाक्प्रचारांचा खाली दिलेल्या वाक्यांत योग्य उपयोग करा:

प्रश्न (अ)
कंसातील वाक्प्रचारांचा खाली दिलेल्या वाक्यांत योग्य उपयोग करा: (अवेहलना करणे, चेहरा पांढरा फटफटीत पडणे, पदार्पण करणे, स्तिमित होणे)

1. आंब्याच्या झाडाचे मालक समोरून येताना दिसताच कैऱ्या पाडणाऱ्या मुलांच्या चेहऱ्यावर भीती पसरली.
2. शालेय स्नेहसंमेलनात प्राचीने स्टेजवर पहिले पाऊल टाकले.
3. दिव्यांग मुलांची प्रदर्शनातील चित्रे पाहून प्रमुख पाहुणे थक्क झाले.
4. गुणवान माणसांचा अनादर करू नये.

उत्तर:

1. आंब्याच्या झाडाचे मालक समोरून येताना दिसताच कैऱ्या पाडणाऱ्या मुलांचे चेहरे पांढरे फटफटीत पडले.
2. शालेय स्नेहसंमेलनात प्राचीने स्टेजवर पदार्पण केले.
3. दिव्यांग मुलांची प्रदर्शनातील चित्रे पाहून प्रमुख पाहुणे स्तिमित झाले.
4. गुणवान माणसांची अवहेलना करू नये.

प्रश्न (ब)
पुढील वाक्यांतील अधोरेखित शब्दांचे लिंग बदलून वाक्ये पुन्हा लिहा :

1. तिच्यावर आलेला वाईट प्रसंग या चिमुकल्याने सावरला.
2. तिच्या गोड गळ्याने कधीही दगा दिला नाही.
3. नर्तकीचे नृत्य प्रेक्षणीय होते.
4. सवाई गंधर्व महोत्सव प्रसिद्ध गायकाच्या गायनाने रंगला.

उत्तर:

1. तिच्यावर आलेला वाईट प्रसंग या चिमुकलीने सावरला.
2. त्याच्या गोड गळ्याने कधीही दगा दिला नाही.
3. नर्तकाचे नृत्य प्रेक्षणीय होते.
4. सवाई गंधर्व महोत्सव प्रसिद्ध गायिकेच्या गायनाने रंगला.

4. स्वमत:

प्रश्न 1.
चार्लीच्या तुम्हांला जाणवलेल्या गुणांचे वर्णन तुमच्या शब्दांत करा.
उत्तर:
चार्ली हा मुळातच गुणी कलावंत होता. आपली ही ओळख त्याने पदार्पणातच करून दिली. त्या दिवशी आई गात असताना तो एकाग्रतेने गाणे ऐकत होता. मला तर वाटते की, तो आईबरोबर मनातल्या मनात गाणे गातच असावा. यासाठी एकाग्रता राखण्याची व आपल्या आवडत्या विषयाशी एकरूप होण्याची क्षमता लागते. ती चार्लीकडे होती. रंगमंचावरून प्रत्यक्ष गाण्याची वेळ आली, तेव्हा चार्लीने ते यशस्वी रितीने गायले. याचे कारण त्याला कार्यक्रम सादर करायचा नव्हता. त्याला गायचे होते. त्याच्यात गायनाची ऊर्मी होती. तो त्या गाण्याशी एकरूप झाला होता. म्हणून तो गाऊ शकला.

पैशांचा पाऊस पडला, तेव्हा त्याने पैसे गोळा करायला सुरुवात केली. प्रेक्षकांनाही तसे सांगितले. हा त्याच्या मनाचा निरागसपणा, निष्पापपणा होता. तो कलावंतच होता. कलेची ऊर्मी त्याच्यात होती. म्हणून त्याने नाचून दाखवले. नकला करून दाखवल्या. हे सर्व त्याने निरीक्षणातून मिळवले होते. त्याची निरीक्षणक्षमता अफाट होती. एकंदरीत पदार्पणातच त्याने आपले कलावंतपण सिद्ध केले.

प्रश्न 2.
स्टेज मॅनेजरच्या जागी तुम्ही आहात अशी कल्पना करून त्या प्रसंगात तुम्ही कसे वागाल, ते सविस्तर लिहा.
उत्तर:
स्टेज मॅनेजरने चार्लीला गाणे सादर करायला सांगितले, हे योग्यच होते. तो निर्णय योग्यच होता, हे चालीने आपल्या कामगिरीने सिद्ध केलेच. मात्र, मॅनेजरची एक गोष्ट मला पटली नाही आणि आवडलीही नाही. लिलीवर अनवस्था प्रसंग ओढवला, तेव्हा मॅनेजर गोंधळून गेला. त्याने प्रेक्षकांना शांत करण्यासाठी काहीही केले नाही. मी त्याच्या जागी असतो, तर पुढे झालो असतो. प्रेक्षकांची क्षमा मागितली असती. घडलेल्या प्रसंगात लिलीची कोणतीही चूक नव्हती, तिच्यावर कोसळलेली ती नैसर्गिक आपत्ती होती, हे सर्व त्यांना समजावून सांगितले असते. पंधरा मिनिटांची विश्रांती जाहीर केली असती. या अवधीत विचारविनिमय केला असता. लिलीला धीर दिला असता. मला वाटते, असेच व्हायला हवे होते.

प्रश्न 3.
‘हसरे दुःख’ या शीर्षकाचा तुम्हांला समजलेला अर्थ तुमच्या शब्दांत लिहा.
उत्तर:
लिली हार्ले ही एक मोठी कलावंत होती. गायन, पियानो वादन, नर्तन यांत ती निष्णात होती. कलावंत म्हणून जे मोठेपण असते, ते तिने मिळवले होते. या सामर्थ्याच्या बळावर तिने पैसा, कीर्ती मिळवली होती. हे सर्व एके दिवशी अचानक लुप्त झाले. तिचा आवाज हरवला आणि तिचे सर्वस्वच गेले. ती रात्र तिच्या दृष्टीने काळरात्र होती. दुःखाचा कडेलोट होता.

त्याच रात्री लिलीचा पाच वर्षांचा हरहुन्नरी मुलगा या संकटात तिच्या मदतीला धावून आला. कोसळलेला कार्यक्रम त्याने पुन्हा उभारला. त्याने गायन, अभिनय व नर्तन या कौशल्यांचे डोळे दिपवणारे दर्शन घडवले. कोणत्याही आईला आभाळ ठेंगणे वाटावे, असे दृश्य होते ते. नवा कलावंत उदयाला आला. आपल्या मुलाचा हा उदयकाळ म्हणजे सुखाचा सर्वोच्च बिंदू होता. एका बाजूला सुख होते. त्याच क्षणी दुसऱ्या बाजूला दु:ख होते. म्हणून या पाठाचे शीर्षक आहे – ‘हसरे दुःख’.

5. हसरे दुःख’ या पाठातील पाठवंशाचे नाट्यीकरण करून वर्गात सादरीकरण करा.

प्रश्न 1.
हसरे दुःख’ या पाठातील पाठवंशाचे नाट्यीकरण करून वर्गात सादरीकरण करा.

अपठित गद्य आकलन:

1. खालील उतारा काळजीपूर्वक वाचून त्याखालील कृती का.

प्रश्न (अ)
चोकटी पूर्ण करा. अश्मयुगातील माणसाने दगडाचा उपयोग करून बनवलेल्या वस्तू – [ ] [ ] [ ] [ ]

आमयुगात माणसाने आपले जीवन सुखाचे काम येण्यासाठी चुलीसाठी तीन दगड मांडण्यापासून मृताचे थडगे बांधण्यापर्यंत दगडाला नानातहांनी वापरले. त्यांची भांडीकुंडी केली. औते-हत्यारे बनवली आणि त्याचे दागदागिने देखील घडवले. साठक कोरून किंवा दगडाच्या भिंती रचून आपल्या निवान्याची सोय केली. माणसाच्या प्राथमिक गरजा भागल्यानंतर त्याला आपल्या सृजनशीलतेला आणि पूजावृत्तीला वाट कान दिल्याशिवाय राहवले नाही.

फुरसद मिळाली तशी तो लेगी खोदू लागला; शिल्पे कोरू लागला, घरांना कलात्मक आकार देऊ लागला. शिल्प आणि स्थापत्य या दोन्ही कला प्रयाप्रमाणे अशा दाडातून फुटल्या आणि विज्ञानाचा उगम झाला. एक सबंध युग दशहाने माणसाचे जीवन परोपरीने सुखाचे केल्यामुळे आणि माणसाच्या सृजनशीलतेला कला आणि विज्ञान यांचे उमाळे आल्यामुळे त्याला दगडच देव वाटून त्याने तो पूजला.

प्रश्न (आ)
माणसाला दगडच देव वाटण्याचे कारण उताऱ्याच्या आधारे व तुमच्या मते स्पष्ट करा.

भाषाभ्यास:

अनुस्वार लेखनावावतचे नियम:

1. खालील शब्द वाचा.

‘रंग’, ‘का’, ‘पंचमी’, ‘पंडित’, ‘अंधुज हे शब्द तत्सम आहेत. हे आपण पर-सवर्णानसुया लिहू शकतो, म्हणजे अनुस्वारानंतर देणाऱ्या अक्षराच्या वर्गातील अनुनासिक वापरून लिहू शकतो. उदा., रा. पडकर, पञ्चमी, पण्डित, अन्धुन असे. विशेषतः जुने साहित्य वाचले तर असे लेखन दिसते. परंतु, आजकाल अशी पर-सवनि लिहिण्याची पद्धत जुनी झाली आहे. त्याऐवजी अनुस्वारच वापरले जातात. खालील शब्दया कसे दिसतात! ‘निबन्य’, ‘आम्बा’, ‘वन’, ‘सम्म’, ‘दल्या हे शब्द वयायला विचित्र वाटतात ना! कारण हे तत्सम नाहीत. पर-सवर्ग लिहिण्याची पद्यत का तत्सम शब्दांपुरती मर्यादित आहे. संस्कृत नसलेले मराठी शब्द शोविंद देऊनच लिहावेत.

मराठीत स्पष्टोच्यारित अनुनासिकाबद्दल शीविंदू दयावा.

2. खालील शब्द वाचा.

‘सिंह’, ‘संगम’, मांस’, ‘संहार’ या शब्दांचा उच्चार करे तर खूप शाळा आहे ना? या शब्दांचे ‘सिंह’, कम’, भांबा’, ‘संहार’ उच्चार असे होतात आणि तसेच ते कायचे असतात पण लिहिताना हे शब्द तसे लिहू नयेत.

इ.इ.स., स. प. म. रयांच्यापूर्वी येणाऱ्या अनुस्वारांबद्दल केवळ शीविंदू दयावा.

पर – सवर्णाने लिहा:
घंटा, मंदिर, चंपा, चंचल, मंगल

अनुस्वार वापसन लिहा:
जगाल, घेण्डू, सञ्च, गोन्धळ, बम्ब

Marathi Kumarbharati Textbook Std 9 Answers Chapter 18 हसरे दुःख Additional Important Questions and Answers

उतारा क्र. 1

1. पुढील उतारा वाचून दिलेल्या सूचनांनुसार कृती करा:

कृती 1 : (आकलन)

प्रश्न 1.
आकृती पूर्ण करा:

उत्तर:

कृती 2 : (आकलन)

प्रश्न 1.
आकृती पूर्ण करा:

उत्तर:

कृती 3 : (स्वमत/अभिव्यक्ती)

प्रश्न 1.
प्रेक्षागारात घडलेला तो विपरीत प्रसंग लिली कथन करीत आहे, अशी कल्पना करून लिहा.
उत्तर:
त्या दिवशी माझे गाणे रंगात आले होते. माझे खूप चाहते आले होते. त्यांना संगीताचा आनंद भरभरून दयावा, असे मलाच वाटत होते. आनंदाने फुललेले श्रोत्यांचे चेहेरे पाहण्यातले सुख मी अनेकदा अनुभवले आहे. त्या दिवशीसुद्धा मी भरभरून गात होते. श्रोते डोलत होते. त्यांच्या चेहेऱ्यांवरचा आनंद मला दिसत होता. मीसुद्धा खुशीत होते. आजसुद्धा मी यशाचा आणखी एक टप्पा गाठणार होते, अशी माझी खात्री झाली होती आणि घडले भलतेच.

मधुर स्वरविलास चालू असतानाच अचानक मध्येच माझा आवाज चिरकला. कंठातून आवाजच येईना. स्वर आतल्या आत विरून जाऊ लागले. स्वरांनी वादयवृंदाची साथसंगत सोडून दिली. काही केल्या काही होईना. मी घुसमटले. आतल्या आत कोसळले. इतकी लांच्छनास्पद स्थिती मी कधीच अनुभवली नव्हती. श्रोत्यांना तोंड दाखवण्याचीही मला लाज वाटू लागली. मी कशीबशी खाली मान घालून विंगेत परतले.

उतारा क्र. 2

1. पुढील उतारा वाचून दिलेल्या सूचनांनुसार कृती करा:

कृती 1 : (आकलन)

प्रश्न 1.
चंडोल पक्ष्याच्या उदाहरणाला अनुसरून आकृती पूर्ण करा:

उत्तर:

प्रश्न 2.
विपरीत घटनेचे श्रोत्यांवरील परिणाम लिहा.

1. ……………………………
2. …………………………..
3. …………………………..
4. …………………………..

उत्तर:

1. काही काळानंतर श्रोत्यांना दम धरवेना. त्यांच्यात कुजबूज सुरू झाली.
2. श्रोते आरडाओरडा करू लागले. आरडाओरड वाढू लागली.
3. काही श्रोते लिलीचे गाणे भसाड्या आवाजात म्हणू लागले.
4. श्रोत्यांच्या गायनाला शिट्ट्यांची व आरोळ्यांची साथ मिळाली.

कृती 2 : (आकलन)

प्रश्न 1.
आकृती पूर्ण करा:

उत्तर:

प्रश्न 2.
यापूर्वीचा लिली हार्लेबाबतचा मॅनेजरचा अनुभव लिहा.
1. …………………….
2. ……………………
उत्तर:
1. लिली हार्ले एकदा रंगमंचावर गेली की, तिच्याकडे मॅनेजरला कधी बघावेच लागत नसे.
2. लिली रंगमंचावर उभी राहिली की, मॅनेजर निर्धास्तपणे दुसरीकडे बघायला मोकळा असे.

कृती 3 : (स्वमत/अभिव्यक्ती)

प्रश्न 1.
लिली हार्लेच्या बाबतीत घडलेल्या प्रसंगासारखा तुम्ही अनुभवलेला किंवा तुम्हांला ठाऊक असलेला प्रसंग सांगा.
उत्तर:
माझ्या आयुष्यातला तो प्रसंग मी कधीही विसरणार नाही. प्रस्तुत पाठ वाचला त्या वेळी मला तो तीव्रपणे आठवला. लिलीची काय अवस्था झाली असेल, हे मला पूर्णपणे कळले. गेल्याच्या गेल्या वर्षीची गोष्ट आहे ही. मी सातवीत होतो. जिल्हास्तरीय वक्तृत्वस्पर्धा होती. आमच्या शाळेतून मी सहभागी झालो होतो. सभागृह पूर्ण भरलेले होते. एकेकाचे नाव घेतले जायचे, तो यायचा आणि तडाखेबंद भाषण करून जायचा. ते पाहून माझ्या छातीत धडधडायचे. माझा क्रमांक जवळ येऊ लागला तशी माझी भीती वाढू लागली. माझे नाव पुकारले गेले आणि मी आतून धडपडलोच. व्यासपीठावर गेलो. माझे हातपाय थरथरायला लागले.

परीक्षक मला, “घाबरू नकोस. बोल तू.’ असा धीर देऊ लागले. त्याबरोबर माझी भीती आणखी वाढू लागली. मी कशीबशी तीनचार वाक्ये बोललो आणि पुढचे काही आठवेच ना! खरे तर मी भाषण चोख पाठ केले होते. सरांनी माझ्याकडून घोटवून घेतले होते. कोणाचाही ऑफ पिरिअड असला की माझे भाषण ठेवायचे. भरपूर सराव झाला होता. आईबाबा आणि काकाकाकीसुद्धा खूश होते माझ्यावर. हे सगळे आठवले. पण भाषण आठवेना. मी तेच तेच शब्द पुन्हा पुन्हा म्हणू लागलो. शब्दसुद्धा थरथरत येऊ लागले. अखेरीस मला रडू आले. मी तसाच खाली उतरलो आणि टेबलावर डोके टेकून खूप वेळ तसाच बसून राहिलो.

उतारा क्र. 3

1. पुढील उतारा वाचून दिलेल्या सूचनांनुसार कृती करा:

कृती 1 : (आकलन)

प्रश्न 1.
आकृती पूर्ण करा:

उत्तर:

प्रश्न 2.
पुढे दिलेल्या घटनांचे परिणाम लिहा:

उत्तर:

कृती 2 : (आकलन)

प्रश्न 1.
माहिती लिहा:
मॅनेजरला घडलेले लिलीचे दर्शन.
उत्तर:
लिलीची मुद्रा पांढरी पडली होती. आजवर तिच्या गोड गळ्याने तिला दगा दिला नव्हता. तिची एवढी अवहेलना झाली नव्हती! अपमानित अवस्थेत ती मुकाट्याने विंगेत परतली.

प्रश्न 2.
अर्थ स्पष्ट करा:
विदयुल्लता चमकावी आणि क्षणार्धात घनदाट अंधकारात विलीन होऊन जावी, असा प्रकार घडला होता.
उत्तर:
वीज चमकते तेव्हा आसमंत झळाळून जातो. लख्ख प्रकाश पडतो. पण वीज चमकून गेली की, मिट्ट काळोख होतो. प्रकाशाचा टिपूसही दिसत नाही. लिलीच्या बाबतीत असेच घडले. तिची कारकीर्द झळाळत होती. तिला नाव मिळत होते. पैसा मिळत होता. तिचे हे तेज क्षणार्धात नष्ट झाले. तिच्या तेजाचा पुसटसा बिंदूही प्रकट झाला नाही. मिट्ट काळोख पसरावा तसे झाले.

कृती 3 : (स्वमत/अभिव्यक्ती)

प्रश्न 1.
लिलीच्या या प्रसंगासंबंधात तिथे हजर असलेल्या एका रसिक श्रोत्याचे मनोगत लिहा.
उत्तर:
अरे देवा! काय घडले हे? विश्वासच बसत नाही. किती वेळा या लिलीचे कार्यक्रम मी पाहिले आहेत! किती वेळा गायन ऐकले आहे! प्रत्येक वेळी ती चार पावले पुढेच जात होती. तिची प्रगतीच होत होती. तिचे बहारदार नृत्य, रसाळ गायन, वातावरण प्रसन्न करणारा तिचा अभिनय! काय बोलावे त्याबद्दल? आता हा आनंद संपला. तिची अलौकिक कला लोप पावली.

असे कसे झाले? काय खाल्ले असेल तिने? तिच्या अन्नात कोणीतरी काहीतरी मिसळले नाही ना? एखादयाचे चांगले कोणाला पाहवत नाही. ते विनाकारण शत्रू बनतात आणि असा घात करतात. असा कोणी दुष्ट असेल, तर त्याला शोधलेच पाहिजे. छे, छे! अशी वेळ वैऱ्यावरसुद्धा येऊ नये. खरे म्हणजे हे फक्त लिलीचे नुकसान नाही. हे आम्हां रसिकांचेही नुकसान आहे. काय करणार? आलिया भोगासी…!

उतारा क्र. 4

1. पुढील उतारा वाचून दिलेल्या सूचनांनुसार कृती करा:

कृती 1 : (आकलन)

प्रश्न 1.
आकृती पूर्ण करा:

उत्तर:

प्रश्न 2.
पुढील वाक्यामागील भाव स्पष्ट करा:
मॅनेजरला ते माहीत का नव्हते?
उत्तर:
मॅनेजर लिलीला खूप आधीपासून ओळखत होता. तिचे अनेक कार्यक्रम त्याने जवळून पाहिले होते. कलावंत म्हणून असलेले तिचे मोठेपण त्याला माहीत होते. तिची असहायता, अगतिकता त्याला समजत होती. त्यामुळे तिने मॅनेजरजवळ दिलगिरी व्यक्त करण्याची गरज नव्हती. हा सर्व भाव त्या छोट्याशा एका वाक्यात आहे.

कृती 2 : (आकलन)

प्रश्न 1.
आकृती पूर्ण करा:

उत्तर:

कृती 3 : (स्वमत/अभिव्यक्ती)

प्रश्न 1.
मॅनेजरने घेतलेल्या निर्णयावर तुमचे मत नोंदवा.
उत्तर:
मॅनेजरने खरे तर फार मोठा धोका पत्करला होता. कारण चार्ली त्या वेळी 5 वर्षांचा होता. 5 वर्षांच्या मुलाची समज ती काय असणार? कला म्हणजे काय हे समजून घेणे त्याच्या बुद्धीच्या पलीकडची गोष्ट होती. कलेच्या सादरीकरणातील खाचाखोचा त्याला कळणे शक्यच नव्हते. तो सतत आईसोबत असल्याने आईचे गाणे त्याच्या कानांवर सततच पडत होते. बालबुद्धीनुसार तो ते गाणे सतत गुणगुणत, गात राहिला असणार. आईच्या गायनाचे अनुकरण करीत करीत त्याने तिचे गायन आत्मसात केले. ते केवळ आईचे गायन नव्हते, तर ते उत्तम गायन होते. मॅनेजरने हे पाहिले होते, ऐकले होते. त्याला चार्लीचा अंतर्यामी विश्वास वाटत होता. म्हणून त्याने पाच वर्षांच्या चार्लीला स्टेजवर आणले, असे माझे मत आहे.

उतारा क्र. 5

1. पुढील उतारा वाचून दिलेल्या सूचनांनुसार कृती करा:

कृती 1 : (आकलन)

प्रश्न 1.
आकृती पूर्ण करा:

उत्तर:

प्रश्न 2.
पुढील उद्गार कोणी, कोणाला उद्देशून काढले ते लिहा:
1. याच्या आईची प्रकृती अचानक बिघडली… तेव्हा तिचं अपुरं राहिलेलं गाणं आता हा पुरं करील!
2. मी आधी पैसे गोळा करतो आणि मग राहिलेलं गाणं म्हणून दाखवतो.
उत्तर:
1. स्टेज मॅनेजर – रसिक श्रोत्यांना.
2. चार्ली – रसिक श्रोत्यांना.

कृती 2 : (आकलन)

प्रश्न 1.
का ते लिहा:
1. श्रोत्यांनी स्टेजवर पैशांची उधळण केली.
2. चार्लीने ताबडतोब स्टेज मॅनेजरचा पाठलाग केला.
उत्तर:
1. चार्लीच्या गाण्याने सारे श्रोते भारावून गेले.
2. श्रोत्यांनी चार्लीच्या गायनासाठी स्टेजवर उधळलेले पैसे गोळा करून स्टेज मॅनेजर निघून गेला.

कृती 3 : (स्वमत/अभिव्यक्ती)

प्रश्न 1.
या उताऱ्यातून तुम्हांला जाणवणारे स्टेज मॅनेजरचे गुण लिहा.
उत्तर:
‘स्टेज मॅनेजर’ याला मराठीत ‘रंगमंच व्यवस्थापक’ म्हणतात. हा खरे तर व्यावसायिक. त्याचे काम खूप महत्त्वाचे असते. स्टेजवरचे पडदे, सर्व दिवे, ध्वनिव्यवस्था, वादयवृंदाची व्यवस्था, नेपथ्याची व्यवस्था वगैरे सर्व बाबी रंगमंच व्यवस्थापक सांभाळतो. हे काम करता करता त्याचे लिली व चार्ली यांच्याशी जिव्हाळ्याचे नाते निर्माण झाले आहे. लिलीच्या रंगमंच व्यवस्थापकाला मनुष्यस्वभावाची चांगली जाण आहे.

त्याला लिलीची कलेवरील निष्ठा आणि तिचे कलावंत म्हणून असलेले सामर्थ्य कळते. चार्लीची क्षमताही त्याने अचूक ओळखली. पाच वर्षांच्या चार्लीने पदार्पणातच आपली क्षमता सिद्ध केली. श्रोत्यांनी उधळलेले पैसे गोळा करून तो लिलीला नेऊन देतो. यात त्याचा प्रामाणिकपणा दिसतो. आलेल्या श्रोत्यांना-प्रेक्षकांना पूर्ण कार्यक्रम दाखवला पाहिजे, ही कर्तव्याची भावनाही त्याच्या मनात है असते. मुख्य म्हणजे व्यवहाराच्या पलीकडे जाऊन माणसांशी जिव्हाळ्याने वागण्याचा मोठा गुण त्याच्याकडे आहे.

उतारा क्र. 6

1. पुढील उतारा वाचून दिलेल्या सूचनांनुसार कृती करा :

कृती 1 : (आकलन)

प्रश्न 1.
आकृती पूर्ण करा:

उत्तर:

प्रश्न 2.
का ते लिहा:
1. चार्लीच्या जिवात जीव आला.
2. प्रेक्षकांनी थिएटर डोक्यावर घेतले.
उत्तर:
1. आपल्याला मिळालेले पैसे स्टेज मॅनेजर हडप करतो की काय, ही चार्लीला शंका आली. म्हणून त्याने त्याचा पाठलागही केला. पण मॅनेजरने ते पैसे चार्लीच्या आईकडे दिले. म्हणून चार्लीच्या जिवात जीव आला.
2. चार्लीच्या आईचा आवाज अचानक बसल्यामुळे तिचे गाणे अर्धवट राहिले. त्यामुळे श्रोत्यांचा विरस झाला होता. या पार्श्वभूमीवर चार्लीने उरलेले गाणे आईप्रमाणे हुबेहूब म्हटले. आणि चार्ली त्या वेळी अवघा पाच वर्षांचा होता. या सर्व बाबींमुळे श्रोते बेहद्द खूश झाले. त्यांनी आनंदाच्या भरात थिएटर डोक्यावर घेतले.

कृती 2 : (आकलन)

प्रश्न 1.
आकृती पूर्ण करा:

उत्तर:

प्रश्न 2.
आकृती पूर्ण करा:

उत्तर:

कृती 3 : (स्वमत/अभिव्यक्ती)

प्रश्न 1.
या उताऱ्यातून तुम्हांला जाणवणारे चार्लीचे स्वभावगुण लिहा.
उत्तर:
चार्लीचे वय पाच वर्षे होते. म्हणजे अज्ञानी बालकच तो. तो त्याच्या स्वभावाला अनुसरून नैसर्गिकपणे वागला. वास्तविक अशा समारंभाचे संकेत असतात. ते सर्वांनी पाळायचे असतात. पण चार्ली गाणे थांबवून पैसे गोळा करतो. पैसे घेऊन जाणाऱ्या मॅनेजरचा पाठलाग करतो. समारंभाचे संकेत मोडून तो बालसुलभ वृत्तीने वागतो. त्यामुळे गमतीदार विसंगती निर्माण होते. त्याची निरीक्षण शक्ती जबरदस्त आहे. म्हणून आईच्या गायनाची तो हुबेहूब नक्कल करतो. अन्य नकलाही करतो. रंगमंचावर वावरताना तो घाबरत नाही, गोंधळत नाही. कलावंताकडे असलेले हे महत्त्वाचे गुण त्याच्याकडे दिसतात.

उतारा क्र. 7

1. पुढील उतारा वाचून दिलेल्या सूचनांनुसार कृती करा:

कृती 1 : (आकलन)

प्रश्न 1.
आकृती पूर्ण करा:

उत्तर:

प्रश्न 2.
आकृती पूर्ण करा:

उत्तर:

कृती 2 : (आकलन)

प्रश्न 1.
आकृती पूर्ण करा:

उत्तर:

प्रश्न 2.
आकृती पूर्ण करा:

उत्तर:

भाषाभ्यास:

(अ) व्याकरण घटकांवर आधारित कृती:

1. समास:

प्रश्न 1.
तक्ता भरा:
उत्तर:

2. शब्दसिद्धी:

प्रश्न 1.
‘कार’ प्रत्यय असलेले चार शब्द लिहा.
उत्तर:

1. कथाकार
2. नाटककार
3. संगीतकार
4. शिल्पकार

3. वाक्प्रचार:

प्रश्न 1.
पुढील वाक्प्रचारांचा अर्थ सांगून वाक्यांत उपयोग करा:

1. नाचक्की होणे
2. भान हरपणे
3. लुप्त होणे
4. पाठ थोपटणे.

उत्तर:

1. नाचक्की होणे – अर्थ : अब्रू जाणे.
   वाक्य : सरांना उलट उत्तर देऊन सुरेशने स्वतःची नाचक्की केली.
2. भान हरपणे – अर्थ : जाणीव न उरणे.
   वाक्य: चित्र रंगवताना शालिनीचे भान हरपले.
3. लुप्त होणे – अर्थ : नाहीसे होणे.
   वाक्य: कडक उन्हाळ्यामुळे विहिरीतले पाणी लुप्त झाले.
4. पाठ थोपटणे – अर्थ : शाबासकी देणे.
   वाक्य : निबंधस्पर्धेत प्रथम क्रमांक पटकावणाऱ्या मालतीची सरांनी पाठ थोपटली.

(आ) भाषिक घटकांवर आधारित कृती:

1. शब्दसंपत्ती:

प्रश्न 1.
पुढील शब्दात लपलेले प्रत्येकी चार अर्थपूर्ण शब्द लिहा:

1. दुसरीकडे
2. लांबसडक
3. उदासवाण्या
4. पदन्यासात.

उत्तर:

प्रश्न 2.
विरुद्धार्थी शब्द लिहा:

1. बाहेर
2. गोड
3. धूसर
4. सुरेल
5. धाकटा
6. दूर.

उत्तर:

1. बाहेर × आत
2. गोड × कडू
3. धूसर × स्पष्ट
4. सुरेल × कर्कश
5. धाकटा × थोरला
6. दूर × जवळ.

2. लेखननियम:

प्रश्न 1.
अनुस्वार लेखनाबाबतचे नियम:
पुढील शब्द वाचा.
उत्तर:
‘रंग’, ‘पंकज’, ‘पंचमी’, ‘पंडित’, ‘अंबुज’ हे शब्द तत्सम आहेत. हे आपण पर-सवर्णानेसुद्धा लिहू शकतो. म्हणजे अनुस्वारानंतर येणाऱ्या अक्षराच्या वर्गातील अनुनासिक वापरून लिहू शकतो. उदा., रङ्ग, पङ्कज, पञ्चमी, पण्डित, अम्बुज असे. विशेषतः जुने साहित्य वाचले तर असे लेखन दिसते. परंतु, आजकाल अशी परसवर्णाने लिहिण्याची पद्धत जुनी झाली आहे. त्याऐवजी अनुस्वारच वापरले जातात. पुढील शब्द बघा कसे दिसतात!

‘निबन्ध’, ‘आम्बा’, ‘खन्त’, ‘सम्प’, ‘दगा’ हे शब्द बघायला विचित्र वाटतात ना! कारण हे तत्सम नाहीत. पर-सवर्ण लिहिण्याची पद्धत फक्त तत्सम शब्दांपुरती मर्यादित आहे. संस्कृत नसलेले मराठी शब्द शीर्षबिंदू देऊनच लिहावेत.

मराठीत स्पष्टोच्चारित अनुनासिकाबद्दल शीर्षबिंदू दयावा.

पुढील शब्द वाचा.

‘सिंह’, ‘संयम’, ‘मांस’, ‘संहार’ या शब्दांचा उच्चार खरे तर खूप वेगळा आहे ना? या शब्दांचे ‘सिंव्ह’, ‘संय्यम’, ‘मांव्स’, ‘संव्हार’ अनुस्वारांबद्दल केवळ शीर्षबिंदू दयावा.
असे उच्चार होत असले तरी लिहिताना हे शब्द तसे लिहू नयेत.

नियम : य्, र, ल, व्, श्, प्, स्, ह यांच्यापूर्वी येणाऱ्या अनुस्वारांबददल केवळ शीर्षबिंदू दयावा.

प्रश्न 1.
पुढील शब्द पर-सवर्णाने लिहा:

1. घंटा
2. मंदिर
3. चंपा
4. चंचल
5. मंगल.

उत्तर:

1. घण्टा
2. मन्दिर
3. चम्पा
4. चञ्चल
5. मङ्गल.

प्रश्न 2.
पुढील शब्द अनुस्वार वापरून लिहा:

1. जङ्गल
2. चेण्डू
3. सञ्च
4. गोन्धळ
5. बम्ब.

उत्तर:

1. जंगल
2. चेंडू
3. संच
4. गोंधळ
5. बंब.

प्रश्न 3.
पुढील शब्द लेखननियमांनुसार अचूक लिहा :

1. त्रिकालाबाधित
2. हास्यकल्लोळ
3. यत्किंचित
4. प्रकृती
5. कंठमाधुर्य.

उत्तर:

1. त्रीकाळाबाधीत
2. हस्यकलोल
3. यक्तिचीत
4. परक्रुती
5. कंठमाधूर्य.

3. विरामचिन्हे:

प्रश्न 1.
पुढील वाक्यात योग्य विरामचिन्हे वापरून वाक्य पुन्हा लिहा:
मॅनेजर म्हणाला छे छे तुम्ही आता स्टेजवर जाण्याची गरज नाही.
उत्तर:
मॅनेजर म्हणाला, “छे, छे! तुम्ही आता स्टेजवर जाण्याची गरज नाही.”

4. पारिभाषिक शब्द:

प्रश्न 1.
पुढील इंग्रजी पारिभाषिक शब्दांना मराठी प्रतिशब्द लिहा :
1. Children Theatre
2. Anniversary.
उत्तर:
1. बालरंगभूमी
2. वर्धापन दिन.

उपक्रम:

प्रश्न 1.
हसरे दु:ख’ या पाठातील पाठ्यांशाचे नाट्यीकरण करून वर्गात सादरीकरण करा.

हसरे दुःख Summary in Marathi

प्रस्तावना:

भा. द. खेर हे जुन्या पिढीतील एक सुप्रसिद्ध लेखक. त्यांनी विपुल लेखन केले आहे. त्यांचे काही लेखन पुढीलप्रमाणे:
कादंबऱ्या: ‘सुखाचा लपंडाव’, ‘प्रायश्चित्त’, ‘शुभमंगल’, ‘नंदादीप’, ‘वादळवारा’, ‘यज्ञ’, ‘अमृतपुत्र’.
अन्य लेखन: ‘आईन्स्टाईनचे नवे विश्व’, ‘गीताज्ञानदेवी’, ‘अपरोक्षानुभूती’, ‘अधांतरी’, ‘द प्रिन्सेस’ इत्यादी.

प्रस्तुत पाठात चार्ली चॅप्लिनचा कलेच्या प्रांतातील प्रवेशाचा प्रसंग चित्रित केला आहे. यातील दुर्दैवाचा भाग असा की, त्याच्या आईच्या कारकिर्दीचा दु:खद अंत झाला, त्या क्षणीच त्याची कलावंत म्हणून कारकीर्द सुरू झाली. एकच क्षण सुख आणि दु:ख यांनी भरलेला! म्हणून त्या प्रसंगातील भावनांना ‘हसरे दुःख’ असे नाव दिले आहे.

शब्दार्थ:

1. तेजोमय – तेजाने युक्त, तेजस्वी.
2. कंठमाधुर्य – कंठाचे माधुर्य, गळ्याचा गोडवा, म्हणजे आवाजाचा गोडवा.
3. विध – घायाळ.
4. विपरीत – उलट, विरुद्ध (वाईट या अर्थाने रूढ).
5. कावराबावरा – भीतीने बावरलेला, बुजलेला.
6. पदन्यास – पावलांची लयदार हालचाल.
7. अवहेलना – हेटाळणी.
8. नाचक्की – बदनामी.

वाक्प्रचार व त्यांचे अर्थ:

1. नजर खिळून राहणे – एकाग्रतेने पाहणे.
2. जिवाचा कान करणे – मन लावून ऐकणे.
3. भान हरपणे – गुंग होणे.
4. तंद्री लागणे – गुंग होणे.
5. रंगात येणे – तल्लीन होणे.
6. दम धरणे – धीर धरणे.
7. दम निघून जाणे – धीर सुटणे.

Balbharti Maharashtra State Board Class 9 Sanskrit Solutions Aamod Chapter 2 अव्ययमाला Notes, Textbook Exercise Important Questions and Answers.

Maharashtra State Board Class 9 Sanskrit Aamod Solutions Chapter 2 अव्ययमाला

Sanskrit Aamod Std 9 Digest Chapter 2 अव्ययमाला Textbook Questions and Answers

भाषाभ्यास:

श्लोक: 1

1. एकवाक्येन उत्तरत।

प्रश्न अ.
ईश्वरेण श्रोतुं किं दत्तम् ?
उत्तरम् :
ईश्वरेण श्रोतुं कर्णी दत्तौ।

प्रश्न आ.
आस्यं कीदृशम् ?
उत्तरम् :
आस्यं सुहास्यम्।

प्रश्न इ.
ईश्वरेण विहर्तुं किं दत्तम् ?
उत्तरम् :
ईश्वरेण विहाँ पादयुग्मं दत्तम्।

2. तालिकां पूरयत।

प्रश्न 1.

उत्तरम् :

3. मेलनं कुरुत।

प्रश्न 1.

श्लोकः 2

1. एकवाक्येन उत्तरत ।

प्रश्न अ.
के दूतत्वं कुर्वन्ति ?
उत्तरम् :
गुणा: दूतत्वं कुर्वन्ति।

प्रश्न आ.
के केतकीम् आजिघ्रन्ति ?
उत्तरम् :
षट्पदा: केतकीम् आजिवन्ति।

2. सत्यं वा असत्यं लिखत ।

प्रश्न अ.
सज्जना: दूतत्वं कुर्वन्ति।

प्रश्न आ.
षट्पदाः स्वयम् आयान्ति ।

प्रश्न इ.
सज्जनाः केतकीगन्धम् आजिघ्रन्ति ।

3. समानार्थकशब्दं चिनुत लिखत च ।
सज्जनाः, भ्रमरा:, आगच्छन्ति ।

प्रश्न 1.
समानार्थकशब्दं चिनुत लिखत च ।
सज्जनाः, भ्रमरा:, आगच्छन्ति ।
उत्तरम् :

• सज्जनाः – सन्तः, सुजनाः ।
• भ्रमराः – अलयः, भृगाः, मधुपाः, षट्पदाः।
• आगच्छन्ति – आयान्ति।

4. विरुद्धार्थकशब्दं लिखत।
गुणाः, दूरे, आयान्ति।

प्रश्न 1.
विरुद्धार्थकशब्दं लिखत।
गुणाः, दूरे, आयान्ति।
उत्तरम् :

• गुणाः × दोषाः, दुर्गुणाः।
• दूरे × समीपे, निकटे, निकषा।
• आयान्ति × गच्छन्ति, यान्ति।

श्लोकः 3

1. एकवाक्येन उत्तरत।

प्रश्न अ.
धेनवः किं भुक्त्वा दुग्धं यच्छन्ति ?
उत्तरम् :
धेनवः शुष्काणि तृणानि भुक्त्वा दुग्धं यच्छन्ति ।

प्रश्न आ.
धेनवः जलाशयात् किं पिबन्ति ?
उत्तरम् :
धेनव: जलाशयात् तोयं पिबन्ति ।

प्रश्न इ.
लोकमातर: का:?
उत्तरम् :
लोकमातरः धेनवः ।

2. श्लोकात् त्वान्त-अव्यये चित्वा लिखत ।

प्रश्न 1.
श्लोकात् त्वान्त-अव्यये चित्वा लिखत

3. वाक्यत: कर्ता, कर्म क्रियापदं च अन्विष्यत लिखत च ।
दुग्धं यच्छन्ति धेनवः।

प्रश्न 1.
वाक्यत: कर्ता, कर्म क्रियापदं च अन्विष्यत लिखत च ।
दुग्धं यच्छन्ति धेनवः।

4. एकवचने परिवर्तयत।
लोकमातरः धेनवः शुष्काणि तृणानि खादन्ति ।

प्रश्न 1.
लोकमातरः धेनवः शुष्काणि तृणानि खादन्ति ।

श्लोकः 4

1. एकवाक्येन उत्तरत।

प्रश्न अ.
मनुजेन किं न कर्तव्यम् ?
उत्तरम् :
मनुजेन परसन्ताप: न कर्तव्यः।

प्रश्न आ.
मनुजेन कुत्र न गन्तव्यम् ?
उत्तरम् :
मनुजेन खलमन्दिरं न गन्तव्यम्।

प्रश्न इ.
मनुजेन किम् अनुसर्तव्यम् ?
उत्तरम् :
मनुजेन सतां वर्त्म अनुसतव्यम् ।

2. तालिकां परयत।

प्रश्न 1.

उत्तरम् :

3. श्लोकात् अधोदत्तशब्दानां कृते समानार्थकशब्द चित्वा लिखत ।
गृहम्, दुष्टः, मार्गः, स्तोकम्, भूरि ।

प्रश्न 1.
श्लोकात् अधोदत्तशब्दानां कृते समानार्थकशब्द चित्वा लिखत ।
गृहम्, दुष्टः, मार्गः, स्तोकम्, भूरि ।

श्लोक: 5

1. श्लोकात् ल्यबन्त-अव्ययानि चिनुत ।

प्रश्न 1.
श्लोकात् ल्यबन्त-अव्ययानि चिनुत ।
उत्तरम् :

2. योग्यं रूपं चिनुत ।

प्रश्न अ.
षष्ठी- विहस्य/देवस्य।
उत्तरम् :
देवस्य।

प्रश्न आ.
चतुर्थी- विहाय/गेहाय।
उत्तरम् :
गेहाय।

प्रश्न इ.
प्रथमा- अहम्/कथम्।
उत्तरम् :
अहम्।

श्लोक: 6

1. एकवाक्येन उत्तरत।

प्रश्न अ.
के कार्य न प्रारभन्ते?
उत्तरम् :
नीचा: कार्य न प्रारभन्ते।

प्रश्न आ.
के मध्ये विरमन्ति?
उत्तरम् :
मध्या: मध्ये विरमन्ति।

प्रश्न इ.
के प्रारब्धं कार्यं न परित्यजन्ति ?
उत्तरम् :
उत्तमजनाः प्रारब्धं कार्य न परित्यजन्ति।

2. मञ्जूषात: उचितं पर्यायं चित्वा स्तम्भपूरणं कुरुत।

प्रश्न 1.
मञ्जूषात: उचितं पर्यायं चित्वा स्तम्भपूरणं कुरुत।

(न परित्यज्यन्ति, कार्यात्, न प्रारभन्ते, विरमन्ति)
उत्तरम् :

3. श्लोकात् प्रथमाविभक्तेः तथा तृतीयाविभक्तेः रूपाणि चिनुत लिखत च।

प्रश्न 1.
श्लोकात् प्रथमाविभक्तेः तथा तृतीयाविभक्तेः रूपाणि चिनुत लिखत च।
उत्तरम् :
तृतीया – अनुद्यमेन।

4. पदपरिचयं करूत।

5. वर्णविग्रहं कुरुत।
प्रारभ्य, विघ्नैः।

प्रश्न 1.
वर्णविग्रहं कुरुत।
प्रारभ्य, विघ्नैः।
उत्तरम् :

• प्रारभ्य – प् + र + आ + र् + अ + भ् + य् + अ।
• विघ्नः – व् + इ + थ् + न् + ऐः।

श्लोकः 7

1. एकवाक्येन उत्तरत।

प्रश्न अ.
स्थानभ्रष्टाः के के न शोभन्ते ?
उत्तरम् :
स्थानभ्रष्टा: दन्ताः, केशाः, नखाः, नराः न शोभन्ते।

प्रश्न आ.
किं विज्ञाय मतिमान् स्वस्थानं न परित्यजेत् ?
उत्तरम् :
स्थानभ्रष्टाः दन्ताः, केशाः, नखाः, नराः न शोभन्ते इति विज्ञाय मतिमान् स्वस्थानं न परित्यजेत्।

2. समानार्थकशब्दैः वाक्यं पुनर्लिखत ।
स्थानभ्रष्टाः दन्ताः केशा: नखाः नरा: न शोभन्ते ।

प्रश्न 1.
समानार्थकशब्दैः वाक्यं पुनर्लिखत ।
स्थानभ्रष्टाः दन्ताः केशा: नखाः नरा: न शोभन्ते ।
उत्तरम् :

• दन्ताः – रदनाः ।
• केशा: – कचा:, कुन्तलाः।
• नखाः – नखर:, शङ्कवः, कररुहाः।
• नराः – मानवाः, पुरुषाः।

3. श्लोकात प्रथमाविभक्ते: रूपाणि चित्वा लिखत ।

प्रश्न 1.
श्लोकात प्रथमाविभक्ते: रूपाणि चित्वा लिखत ।
उत्तरम् :
प्रथमा – स्थानभ्रष्टाः, दन्ताः, केशाः, नखाः, नराः, मतिमान्, विघ्नविहताः, मध्याः, प्रतिहन्यमानाः, उत्तमजनाः।

श्लोकः 8

1. एकवाक्येन उत्तरत।

प्रश्न अ.
नरः किं न त्यजेत् ?
उत्तरम् :
नर: स्वोद्योग न त्यजेत्।

प्रश्न आ.
अनुद्यमेन किं प्राप्तुं न शक्यते ?
उत्तरम् :
अनुद्यमेन तिलेभ्य: तैलं प्राप्तुं न शक्यते।

2. सत्यम् असत्यं वा इति लिखत ।

प्रश्न अ.
नरः दैवं सचिन्तयेत्।

प्रश्न आ.
नरः उद्यमं सश्चिन्तयेत्।

प्रश्न इ.
तिलेभ्य: तैलं प्राप्यते।

3. अमरकोषपङ्क्तिं लिखत । दैवम्, नरः ।

प्रश्न 1.
अमरकोषपङ्क्तिं लिखत । दैवम्, नरः ।
उत्तरम् :

• दैवम् – दिष्टम् भागधेयम्, भाग्यम्, नियतिः, विधिः।
• नरः – मनुष्यः, मानुषः, मर्त्यः ।

4. समानार्थकशब्दं चिनुत लिखत च ।
लब्धम्, आलस्यम्।

प्रश्न 1.
समानार्थकशब्दं चिनुत लिखत च ।
लब्धम्, आलस्यम्।

5. वर्णविग्रहं कुरुत।
सचिन्त्य, तिलेभ्यः।

प्रश्न 1.
वर्णविग्रहं कुरुत।
सचिन्त्य, तिलेभ्यः।
उत्तरम् :

• सञ्चिन्त्य – स् + अ + ञ् + च् + इ + न् + त् + य् + अ।
• तिलेभ्यः – त् + इ + ल् + ए + भ् + य् + अः।

Sanskrit Aamod Class 9 Textbook Solutions Chapter 2 अव्ययमाला Additional Important Questions and Answers

विशेषण-विशेष्य- सम्बन्धः ।

पृथक्करणम्। तालिकां पूरयत ।

प्रश्न निर्माणं कुरुत।

प्रश्न 1.
गुणाः दूतत्वं कुर्वन्ति।
उत्तरम् :
गुणाः किं कुर्वन्ति?

प्रश्न 2.
केतकीगन्धम् आघ्राय षट्पदाः आयान्ति ।
उत्तरम् :
किं कृत्वा षट्पदा: आयान्ति?

प्रश्न 3.
धेनवः लोकेभ्यः दुग्धं यच्छन्ति।
उत्तरम् :
धेनवः केभ्यः दुग्धं यच्छन्ति?

प्रश्न 4.
मनुजेन सतां वर्त्म अनुसतव्यम्।
उत्तरम् :
मनुजेन केषां वर्त्म अनुसतव्यम्?

प्रश्न 5.
नीचैः विघ्नभयेन न खलु प्रारभ्यते।
उत्तरम् :
कैः विघ्नभयेन न खलु प्रारभ्यते?

प्रश्न 6.

1. ईश्वरेण घ्राणं घातुं दत्तम्।
2. ईश्वरेण द्रष्टुं नेत्रे दत्ते।
3. ईश्वरेण दातुं हस्तयुग्मं दत्तम्।
4. ईश्वरेण चित्तं ध्यातुं दत्तम्।

उत्तरम् :

1. ईश्वरेण घ्राणं किमर्थं दत्तम्?
2. ईश्वरेण द्रष्टुं के दत्ते?
3. ईश्वरेण दातुं किं दत्तम्?
4. ईश्वरेण चित्तं किमर्थ दत्तम्?

विभक्त्यन्तरूपाणि।

• प्रथमा – गुणाः, षट्पदाः, धेनवः, लोकमातरः, स्वल्पम, बहु, षष्ठी, चतुर्थी, अहम, द्वितीया, नरः, कः, दैवम्।
• द्वितीया – दूतत्वम्, केतकीगन्धम्, तृणानि, तोयम, दुग्धम्, परसन्तापम, खलमन्दिरम्, वर्त्म, विघ्नभयेन, विनैः, स्वोद्योगम्।
• चतुर्थी – लोकेभ्यः।
• पञ्चमी – जलाशयात्, तिलेभ्यः।
• षष्ठी – सताम्, वसताम्, सताम्, यस्य।

पद्यांशं पठित्वा जालरेखाचित्रं पूरयत।

1.

2.

3.

लेखनकौशलम् :

समानार्थकशब्द योजयित्वा वाक्यं पुनर्लिखत।

• नासिका- बालकस्य नासिका दीर्घा। बालकस्य नासा / घोणा दीर्घा ।
• नेत्रम् – नेत्रे मुखस्य सौंदर्य वर्धयतः। लोचने / नयने मुखस्य सौंदर्य वर्धयतः।
• षट्पदा:- षट्पदाः रसपानं कर्तुम् आयान्ति। भ्रमराः । भृङ्गाः रसपान कर्तुम् आयान्ति।
• नराः – नराः स्वस्थानं न त्यजेयुः। मानवाः / मनुष्याः स्वस्थानं न त्यजेयुः।
• दैवम् – दैवं पुरुषकार्यम् एव अनुसरति। भाग्यं पुरुषकार्यम् एव अनुसरति।
• वर्त्म – सतां वर्त्म अनुत्सृज्य कार्य कुर्यात्। सतां मार्गम् अनुत्सृज्य कार्यं कुर्यात्।

व्याकरणम् :

नाम – तालिका।

सर्वनाम – तालिका।

धातु – तालिका।

समासाः

धातुसाधितविशेषणानि।

अव्ययमाला Summary in Marathi and English

प्रस्तावना :

सुभाषिते हे संस्कृत भाषेचे ठळक वैशिष्ट्य आहे. सुभाषिते केवळ गेय नसून कमी शब्दांत महत्त्वपूर्ण अर्थ पोहचवतात. प्रस्तुत अव्ययमालेमध्ये केवळ भाषासौंदर्यच दिसत नाही तर धातुंपासून बनणाऱ्या अव्ययांचे प्रयोजन सुद्धा दिसते. ह्यामध्ये प्रत्येक श्लोकात अव्ययांचा वापर केला आहे. ज्यात काही बदल होत नाही ती अव्यये. त्यांपैकी काही अव्यये धातुंपासून बनतात.

Subhashitas or good sayings form the most beautiful part of Sanskrit language. They are not only rhythmic and melodious but convey a very profound meaning in a few words. In this beautiful collection of slokas we shall not only see the beauty of language but also observe the use of avyayas that are derived from dhatus.

This अव्ययमाला has a theme where in each shloka contains some words which are अव्ययs formed from धातुs. अव्ययs are words that don’t change and these are अव्ययs that are formed from धातुs.

श्लोकः 1

श्रोतुं ……………………….. पातु ।।1।। [Greatness of the creation of the creator]

श्लोकः : श्रोतुं करें, वक्तुमास्यं सुहास्यं
घातुं घ्राणं पादयुग्मं विहर्तुम्।
द्रष्टुं नेत्रे हस्तयुग्मं च दातुं
ध्यातुं चित्तं येन सृष्टं स पातु।।1।। (शालिनी)

अन्वयः : येन श्रोतुं कर्णी, वक्तुं सुहास्यम् आस्य, घातुं घाणं, विहर्तुं पादयुग्मं, द्रष्टुं नेत्रे, दातुं हस्तयुग्मं ध्यातुं च वित्त सृष्ट सः (ईश्वरः) पातु।

अनुवादः

ऐकण्यासाठी कान, बोलण्यासाठी सुंदर हास्य असलेले तोंड, वास घेण्यासाठी नाक, फिरण्यासाठी दोन पाय, देण्यासाठी दोन हात आणि ध्यान करण्यासाठी मन ज्याने निर्माण केले तो (ईश्वर) (आमचे) रक्षण
करो.

May he (the Lord) protect us who has created two ears to hear, smiling face to speak, a nose to smell, a pair of feet to move around, two eyes to see, a pair of hands to give and a mind to think/contemplate.

श्लोकः 2.

गुणा: ……………… षट्पदाः ।।2।। [Virtues spread on their own]

श्लोकः : गुणा: कुर्वन्ति दूतत्वं दूरेऽपि वसतां सताम्।
केतकीगन्धमाघ्राय स्वयमायान्ति षट्पदाः ।।2।। (शाङ्गधरपद्धतिः) (अनुष्टुभ)

अन्वयः : दूरे वसताम् अपि सतां, गुणा: दूतत्वं कुर्वन्ति। (यथा) षट्पदाः केतकीगन्धम् आघ्राय (मधुपानाय) स्वयम् आयन्ति।

अनुवादः

दूरवर राहणाऱ्या सज्जनांचे गुण (त्यांचे) दूतत्व करतात. (जसे) भुंगे | केवड्याचा सुगंध घेऊन (मध पिण्यासाठी) स्वत:हून येतात.
Virtues become the messengers of the virtuous though residing far away. Just as having smelt the fragrance of Ketaki, the bees themselves come to it.

श्लोकः  3.

भुक्त्वा ……………. लोकमातरः ।।3।। [Great ones act for the welfare of others]

श्लोकः : भुक्त्वा तृणानि शुष्काणि पीत्वा तोयं जलाशयात्।
दुग्धं यच्छन्ति लोकेभ्यो धेनवो लोकमातरः।।3।। (अनुष्टुभ)

अन्वयः : धेनवः शुष्काणि तृणानि भुक्त्वा जलाशयात् तोयं पीत्वा लोकेभ्य: दुग्धं यच्छन्ति । (ता.) लोकमातर: (खलु)।

अनुवादः

गायी सुके गवत (चारा) खाऊन, जलाशयातील पाणी पिऊन लोकांना दूध देतात. (त्या) खरोखरच लोकमाता होत.

Cows who are indeed the mothers of the world give milk to people after eating dry grass and drinking water from the pond.

श्लोकः 4.

अक्रत्वा …………….. तद् बहु ।।4।। [All that is done in a good manner is valuable]

श्लोकः : अकृत्वा परसन्तापम् अगत्वा खलमन्दिरम्।
अनुत्सृज्य सतां वर्त्म यत्स्वल्पमपि तद् बहु।।4।। (शागधरपद्धतिः) (अनुष्टुभ्)

अन्वयः : परसन्तापं न कृत्वा, खलमन्दिरं न गत्वा, सतां वर्त्म न उत्सृज्य, यत् स्वल्पम् अपि (लभ्यते) तद् बहु (वर्तते)।

अनुवादः

इतरांना त्रास न देता,दुष्टाच्या घरी न जाता (मदत न घेता), सज्जनांचा मार्ग न सोडता जे काही थोडे मिळेल तेच पुष्कळ मानावे.

Even the little which is obtained without troubling others, without going to the house of the wicked (to ask for something), without leaving up the good path, is worth much.

श्लोकः 5.

यस्य षष्ठी ………….. कथम् ।।5।। [I can’t marry a person who is ignorant.]

श्लोकः : यस्य षष्ठी चतुर्थी च विहस्य च विहाय च।
अहं कथं द्वितीया स्यात्, द्वितीया स्यामहं कथम्।।5।। (अनुष्टुभ्)

अन्वयः : यस्य (कृते) विहस्य (इति) षष्ठी, विहाय (इति) चतुर्थी, अहं कथं च (इति) द्वितीया स्यात् (तस्य) अहं द्वितीया (पत्नी) कथं स्याम्?

अनुवादः

ज्याच्यासाठी विहस्य ही षष्ठी (विभक्ती) आणि विहाय ही चतुर्थी (विभक्ती) आहे (तसेच) अहम्, कथम् ही द्वितीया (विभक्ती) आहे त्याची मी द्वितीया (पत्नी) कशी होऊ?

स्पष्टीकरण वैय्याकरणी वेदवती तिच्या भावी पतीची परीक्षा घेणार होती. गौरांग या तिच्या होणाऱ्या नवऱ्याला तिने विचारले, विहस्य, विहाय आणि अहम् व कथम् ही कोणती रूपे आहेत? त्याला केवळ ‘देव शब्दाची रूपे पाठ असल्यामुळे षष्ठी, चतुर्थी व द्वितीया असे उत्तर दिले. तेव्हा वेदवतीने वरील उत्तर दिले. ती म्हणाली ज्यासाठी अहम् आणि कथम् द्वितीया आहेत, त्याची मी द्वितीया म्हणजेच पत्नी कशी होऊ?

How can I become the wife of a person for whom the word विहस्य is षष्ठी विभक्ति, विहाय is चतुर्थी विभक्ति and अहम् and कथम् are द्वितीया विभक्ति?

Explanation Vedavati, a lady well-versed with grammar wanted to test the groom she would be marrying.

In order to test the knowledge of the groom Gaurang, she asked him what the words विहस्य, विहाय and अहम्, कथम् were grammatically. Gaurang had only learnt the forms of the word and that too with great difficulty.

So, for him the words विहस्य and विहाय which are actually अव्ययs seemed to be षष्ठी and चतुर्थी विभक्ति like देवस्य and देवाय respectively and अहम् and कथम् seemed to be द्वितीया विभक्ति like देवम् SoVedavati remarked that she could not become the file meaning wife of such an ignorant person.

श्लोकः 6.

प्रारभ्यते न ……………. परित्यजन्ति ।।6।। [Effect of obstacles on different types of people]
श्लोकः : प्रारभ्यते न खलु विघ्नभयेन नीचैः
प्रारभ्य विघ्नविहता विरमन्ति मध्याः।
विघ्नैः पुनः पुनरपि प्रतिहन्यमानाः
प्रारब्धमुत्तमजना न परित्यजन्ति।।6।। (मुद्राराक्षसम्) (वसन्ततिलका)

अन्वयः : विघ्नभयेन खलु नीचैः (कार्य) न प्रारभ्यते। (कार्य) प्रारभ्य विघ्नविहताः (भूत्वा) मध्या: विरमन्ति। विजैः पुनः पुनः प्रतिहन्यमानाः अपि उत्तमजना: प्रारब्धं (कार्य) न परित्यजन्ति।

अनुवादः

संकटाच्या भीतीने कनिष्ठ प्रतींच्या लोकांकडून (कार्यांची) सुरुवात होत नाही. (कार्याची) सुरुवात करून संकटांनी घायाळ होऊन मध्यम प्रतीचे लोक (कार्य) सोडून देतात / कार्य थांबवतात. (परंतु) संकटांचा वेळोवेळी सामना करणारे उत्तम प्रतीचे लोक सुरु केलेले (कार्य) (कधीच) सोडून देत नाहीत.

The inferior do not start a task due to the fear of obstacles. The mediocre stop having started when faced with obstacles. The superior do not give up the task started, though hammered with obstacles again and again.

श्लोकः 7.

स्थानभ्रष्टा ………………. परित्यजेत् ।।7।। [Everything has its value only when it is in its right place]

श्लोकः : स्थानभ्रष्टा न शोभन्ते दन्ता: केशा नखा नराः।
इति विज्ञाय मतिमान् स्वस्थानं न परित्यजेत्।।7।। (हितोपदेश:) (अनुष्टुभ्)

अन्वयः स्थानभ्रष्टा: दन्ताः, केशाः, नखा: नराः च न शोभन्ते इति विज्ञाय मतिमान् (नर:) स्वस्थानं न परित्यजेत्।

अनुवादः

आपल्या स्थानापासून ढळलेले दात, केस, नखे आणि पुरुष शोभून दिसत नाहीत, हे जाणून बुद्धिमान माणसाने स्वत:चे स्थान सोडू नये.
Knowing that teeth, hair, nails and people that are not in the right place don’t look good, a wise person would not give up his place.

श्लोकः 8.

दैवमेवेति ……………… प्राप्तुमर्हति ।।8।।
श्लोकः : दैवमेवेति सज्ञिन्त्य न स्वोद्योगं नरस्त्य जेत् । [There is no replacement for effort]
अनुद्यमेन कस्तैलं तिलेभ्यः प्राप्तुमहीत ।।8।। (अनुष्टुभ्)

अन्वयः : दैवम् एव इति सञ्चिन्त्य नर: स्वोद्योगं न त्यजेत्। अनुद्यमेन तिलेभ्य: तैलं कः प्राप्तुम् अर्हति?

अनुवादः

मनुष्य प्रयत्नाशिवाय दैव (हेच यश देईल) असा विचार करून माणसाने स्वतःचे प्रयत्न सोडू नये. प्रयत्न न करता तिळांतून तेल मिळवण्यासाठी कोण बरे सक्षम / पात्र आहे? (तिळांत तेल हे असतेच, मात्र ते मिळवण्यासाठी त्यावर दाब द्यावाच लागतो.)

Man should not give up his own effort thinking that destiny is the only thing. Who can obtain oil from sesame seeds without crushing them (without effort)? [Though sesame seeds have abundant oil, one still needs to apply pressure on them to extract out that oil.]

सन्धिविग्रहः

1. स्थानभ्रष्टान – स्थानभ्रष्टाः + न।
2. वक्तुमास्यम् – वक्तुम् + आस्यम् ।
3. केतकीगन्धमानाय – केतकीगन्धम् + आघाय।
4. दूरेऽपि – दूरे + अपि।
5. स्वयमायान्ति – स्वयम् + आयान्ति।
6. लोकेभ्यो धेनवो लोकमातरः – लोकेभ्यः + धेनवः + लोकमातरः।
7. यत्स्वल्पमपि – यत् + स्वल्पम् + अपि ।
8. विघ्नविहता विरमन्ति – विघ्नविहताः + विरमन्ति।
9. पुनरपि – पुन: + अपि।
10. प्रारब्धमुत्तमजना न – प्रारब्धम् + उत्तमजनाः + न।
11. स्यामहम् – स्याम् + अहम् ।
12. केशा नखा नरा: – केशा: + नखा: + नराः।
13. दैवमेवेति – दैवम् + एव + इति।
14. नरस्त्यजेत् – नरः + त्यजेत्।
15. कस्तैलम् – कः + तैलम्।
16. प्राप्तुमर्हति – प्राप्तुम् + अर्हति।

समानार्थकशब्दाः

1. कर्णः – श्रोत्रम्, श्रुतिः, श्रवः, श्रवणम्।
2. आस्यम् – वदनम्, तुण्डम्, आननम्, मुखम्।
3. प्राणम् – नासिका, गन्धवहा, घोणा, नासा।
4. विहर्तुम् – भ्रमितुम्।
5. नेत्रम् – नयनम, लोचनम्, चक्षुः, अक्षः।
6. हस्त: – करः, पाणिः ।
7. पादः – चरणः।
8. चित्तम् – मनः, चेतः, अन्त:करणम्।
9. पातु – रक्षतु।
10. तृणानि – शष्पाणि।
11. धेनवः – गावः।
12. भुक्त्वा – खादित्वा।
13. मातर: – जनन्यः।
14. खलः – दुष्टः, दुर्जनः।
15. सताम् – सज्जनानाम्।
16. वर्त्म – मार्गः, अध्वा,
17. पन्थाः, पथः।
18. अनुत्सृज्य – अत्यक्त्वा।
19. स्वल्पम् – अल्पम्, स्तोकम्।
20. बहु – भूरि, अधिकम्।
21. मन्दिरम् – (अत्र) गृहम्।
22. विघ्नम् – सङ्कटम्, प्रत्यूहः ।
23. पुन: पुन: – वारंवारम् ।
24. द्वितीया – पत्नी, जाया ।
25. विहस्य – हसित्वा ।
26. विहाय – त्यक्त्वा ।
27. प्राप्तुम् – लब्धम्।
28. अनुद्यमः – आलस्यम्।
29. सताम् – सज्जनानाम्।
30. प्रारभ्य – आरभ्य।

विरुद्धार्थकशब्दाः

• शुष्काणि × आणि।
• खलः × सुजनः।
• स्वल्पम् × बहु।
• नीचा: × उत्तमाः।
• प्रारभ्य × समाप्य।
• प्रारब्धम् × समाप्तम्।
• परित्यजन्ति × स्वीकृर्वन्ति।
• अनुद्यमः × उद्यमः।

शब्दार्थाः

1. आस्यम् – mouth – तोंड
2. ध्राणम् – nose – नाक
3. घातुम् – to smell – वास घेण्यासाठी
4. पादः – foot/leg – पाय
5. युग्मम् – pair – जोडी
6. नेत्रे – eyes – डोळे
7. दातुम् – to give – देण्यासाठी
8. चित्तम् – mind – चित्त
9. विहर्तुम् – to wander – फिरण्यासाठी
10. सृष्टम् – created – निर्माण केले
11. षट्पदाः – bees – भुंगे
12. केतकी – fragrance of Ketaki – केवड्याचा
13. गन्धम् – (Screw pine) – सुवास
14. गुणाः – virtues – गुण
15. दूतत्वम् – as a messenger – दूताचे काम
16. सताम् – of good people – सज्जनांचे
17. तृणानि – grass – गवत
18. शुष्काणि – dry – सुकलेले
19. तोयम् – water – पाणी
20. धेनवः – cows – गायी
21. अकृत्वा – without doing – न करून
22. परसन्ताप: – troubling others – दुसऱ्याला त्रास, पीडा
23. अगत्वा – without going – न जाता
24. खलमन्दिर – abode of the wicked – दुष्टाचे घर
25. अनुत्सृज्य – without leaving – न सोडता
26. सताम् – of good people – सज्जनांचा
27. वर्ती – road, path – मार्ग
28. विहस्य – having smiled – हसून
29. बिहाय – having left – सोडून
30. द्वितीया – second, (here) wife – दुसरी, (इथे)पत्नी
31. विघ्न – obstacle – अडथळा
32. विघ्नविहता: – due to obstacles – अडथळ्यांनी हरलेले
33. प्रतिहन्यमानाः – hammered – मारा झालेले
34. मध्यमाः – mediocre – मध्यम प्रतीचे लोक
35. स्थानभ्रष्टा: – not in the proper place – स्थानापासून ढळलेले
36. विज्ञाय – after knowing – जाणून
37. मतिमान् – intelligent – बुद्धिमान
38. दैवम् – fortune – नशीब
39. सञ्चिन्त्य – thinking – विचार करून
40. नरः – man – मनुष्य
41. अनुद्यमेन – without effort – प्रयत्नशिवाय

Balbharti Maharashtra State Board Class 9 Marathi Solutions Kumarbharti Chapter 14 आदर्शवादी मुळगावकर Notes, Textbook Exercise Important Questions and Answers.

Maharashtra State Board Class 9 Marathi Kumarbharti Solutions Chapter 14 आदर्शवादी मुळगावकर

9th Std Marathi Kumarbharati Digest Chapter 14 आदर्शवादी मुळगावकर Textbook Questions and Answers

1. योग्य उदाहरण लिहा:

प्रश्न 1.

उत्तर:

प्रश्न 2.
योग्य उदाहरण लिहा:

उत्तर:

2. आकृती पूर्ण करा:

प्रश्न 1.

उत्तर:

प्रश्न 2.

उत्तर:

3. खाली काही उदाहरणे दिली आहेत. या उदाहरणावरून मुळगावकरांच्या व्यक्तिमत्त्वाचे तुम्हांला जाणवलेले पैलू लिहा:

प्रश्न (अ)

उत्तर:

प्रश्न (आ)

उत्तर:

4. वैशिष्ट्ये लिहा:

प्रश्न 1.
वैशिष्ट्ये लिहा:
(अ) लंडनच्या स्थापत्य विषयाची पदवी –
(आ) टेल्कोचा पुण्यातील कारखाना –
(इ) टेल्कोची परंपरा –
(ई) टेल्कोची मालमोटार –
उत्तर:
(अ) लंडनच्या पदवी परीक्षेच्या अभ्यासक्रमात पुस्तकी शिक्षण होतेच; शिवाय, प्रत्यक्ष कारखान्यात काम करावे लागे. मगच पदवी मिळत असे.
(आ) टेल्कोचा पुण्यातील कारखाना : उत्पादन व व्यवस्थापन या दोन्ही दृष्टींनी कारखाना पहिल्या दर्जाचा आहे, हा लौकिक मिळाला.
(इ) टेल्कोची परंपरा : सर्व दर्जाचे व्यवस्थापक कारखान्यात रोज फेरी मारत असत, ही टेल्कोची परंपरा होती.
(ई) टेल्कोची मालमोटार : टेल्कोची मालमोटार पहिल्या दर्जाची बनली व त्यात सतत सुधारणा होत गेली.

5. खालील वाक्यांतील अधोरेखित शब्दांचे विरुद्धार्थी शब्द लिहून, अर्थ न बदलता वाक्य पुन्हा लिहा.

(अ) मुळगावकर अबोल प्रवृत्तीचे होते.
(आ) मुळगावकर पदवी घेऊन आले, तेव्हा भारतात मंदीची लाट होती.
(इ) मुळगावकरांचे जीवन असमाधानी नव्हते.

6. अधोरेखित केलेल्या अर्थाचा वाक्प्रचार पाठातून शोधून लिहा.

(अ) प्रकृतीकडे दुर्लक्ष केल्यामुळे यश वारंवार आजारी पडत होता.
(आ) शेतीत खूप कष्ट केल्यामुळे यावर्षी रामरावांच्या कष्टाला चांगले फळ मिळाले.
(इ) आवाक्याबाहेरचे काम समीरने सन्मार्गाने पूर्ण केले.
(ई) स्वत:च्या तत्त्वांशी समझोता करणे योग्य नव्हे.
(अ) पाठात उल्लेख असलेल्या चिनी म्हणीतील विचार तुमच्या शब्दांत स्पष्ट करा. (आ) टेल्कोच्या मालमोटारीच्या ड्रायव्हरशी संवाद साधण्यामागे मुळगावकरांचे कोणते हेतू असावेत, असे तुम्हांस वाटते?

7. स्वमत.

प्रश्न (अ)
पाठात उल्लेख असलेल्या चिनी म्हणीतील विचार तुमच्या शब्दांत स्पष्ट करा.
उत्तर:
माणसे आपल्या भविष्याची तरतूद करून ठेवतात. ही तरतूद वेगवेगळ्या स्वरूपांत असते. पैशाच्या स्वरूपातील मदत फार मुळगावकरांनी सामाजिक कार्ये केलेली क्षेत्रे – उपयोगाला येत नाही. झाडे लावली, तर दरवर्षी फळाफुलांचे उत्पन्न मिळते. लाकूडही निर्माण होते. झाडांचा हा असा दरवर्षी नियमितपणे शेती शिक्षण आरोग्य फायदा होतो. मात्र, कोणत्या झाडांचा कधी, कसा व किती फायदा घ्यायचा, हे माणूसच ठरवतो. म्हणून माणूस चांगला घडलेला असेल, मुळगावकरांचे छंद – तर त्याला स्वत:ला या गोष्टीचा फायदा होतोच; शिवाय त्याच्या कुटुंबालाही होतो.

अशी व्यक्ती खूप कर्तबगार निघाली, तर त्या छायाचित्रण कला झाडे लावणे व्यक्तीचा अखंड समाजालाही फायदा होतो. म्हणून पैसे साठवून मुळगावकरांच्या छंदांची फलश्रुती ठेवण्यापेक्षा झाडेझुडपे लावली, तर त्यांचा माणसांना उपयोग होणारच. पण त्याहीपेक्षा माणसे घडवली, तर त्याचा खूप उपयोग होतो. म्हणजे त्यांनी काढलेली त्यांनी लावलेल्या माणसे तयार करणे, हा मानवी समाज घडवण्याचा मार्ग आहे. चिनी छायाचित्रे इतकी सुंदर आहेत झाडांनी पुण्याचा परिसर ई म्हणीमध्ये नेमके हेच सांगितले आहे. की त्यांची प्रदर्शने भरू अत्यंत नयनमनोहर शकतात.

प्रश्न (आ)
टेल्कोच्या मालमोटारीच्या ड्रायव्हरशी संवाद साधण्यामागे मुळगावकरांचे कोणते हेतू असावेत, असे तुम्हांस वाटते ?
उत्तर:
मालमोटारीचा ड्रायव्हर देशभर विविध प्रदेशांत हिंडत असतो. तो कधी जंगलातून प्रवास करतो, तर कधी वाळवंटी प्रदेशातून. उंचसखल प्रदेश, सपाट प्रदेश, दलदलीचा प्रदेश, अतिथंडीचा प्रदेश, प्रचंड पाऊस कोसळणारा प्रदेश अशा विविध प्रकारच्या परिसरांतून आपली मालमोटार प्रवास करीत असते.

अशा वेगवेगळ्या प्रकारच्या परिसरांतील वातावरणात आपली मालमोटार कशी चालत असेल? काही अडचणी निर्माण होत असतील का? मोटारीच्या स्वरूपात उणिवा राहिल्या असतील का? अशा प्रश्नांची उत्तरे ड्रायव्हरांशी केलेल्या संवादातून मिळतात. गाडीत काही उणिवा असतील तर त्या दूर करता येतात. आपली मोटार अधिकाधिक निर्दोष करण्याची संधी मिळते.

उपक्रम:

प्रश्न 1.
तुमच्या परिसरातील लघुउद्योजकांची मुलाखत घ्या.

भाषाभ्यास:

हस्व दीर्घ लेखनाबाबतचे नियम:

प्रश्न 1.
खालील शब्द वाचा.
कुस्ती, मुक्काम, पुष्कळ, शिस्त, दुष्काळ, पुस्तक, चिठ्ठी, डुक्कर, बिल्ला, चिक्की.
वरील प्रत्येक उदाहरणात एक जोडाक्षर आहे. या जोडाक्षरयुक्त अक्षरापूर्वीच्या अक्षराचे नीट निरीक्षण करा. काय आढळले? या अक्षरांतील उकार, इकार हे -हस्व आहेत.

मराठी शब्दांत जोडाक्षर असल्यास जोडाक्षरापूर्वीचे इकार, उकार, सामान्यतः हस्य असतात.

लक्षात ठेवा: तत्सम शब्दांतील जोडाक्षरापूर्वीचे इकार व उकार न्हस्व व दीर्घ अशा दोन्ही प्रकारचे आढळतात.
उदा., पुण्य, तीक्ष्ण, पूज्य

वर दिलेल्या वर्णनानुसार किमान दहा शब्द लिहा.

प्रश्न 2.
खालील शब्द वाचा.

चिंच, लिंबू, बिंदू, तुरुंग, उंच, लिंग, अरविंद, अरुंधती, दिंडी, पिंड, किंकाळी, चिंता, पिंड, पुरचुंडी, पुंगी, धुंद, चिंधी
वरील शब्द अनुस्वारयुक्त आहेत. यांतील अनुस्वारयुक्त अक्षराकडे नीट पाहिल्यास काय जाणवते ?
शब्द मराठी असो वा तत्सम. अनुस्वारयुक्त अक्षरे -हस्व आहेत.

मराठी व तत्सम शब्दांतील इकारयुक्त व उकारयुक्त अक्षरांवर अनुस्वार असल्यास सामान्यत: ती हस्य असतात, म्हणजेच ह्या अनुस्वारयुक्त अक्षरातील इकार, उकार -हस्व असतात. वर दिलेल्या वर्णनानुसार किमान दहा शब्द लिहा.

Marathi Kumarbharati Textbook Std 9 Answers Chapter 14 आदर्शवादी मुळगावकर Additional Important Questions and Answers

उतारा क्र. 1

1. पुढील उतारा वाचून दिलेल्या सूचनांनुसार कृती करा :

कृती 1 : (आकलन)

प्रश्न 1.
आकृतिबंध पूर्ण करा:

उत्तर:

प्रश्न 2.
कोण ते लिहा:
1. होऊन गेलेल्या बातमीवर अथवा घडामोडीवर परखड भाष्य करणारा.
2. समाजमनावर आपल्या कार्यकर्तृत्वाचा ठसा उमटवणारा.
उत्तर:
1. संपादक
2. समाजमनस्क व्यक्तिमत्त्व.

कृती 2 : (आकलन)

प्रश्न 1.
उत्तर लिहा:
संपादकाचे आवश्यक गुण:

1. बहुश्रुतता
2. ………………..
3. ………………..

उत्तर:

1. संपादकाचे आवश्यक गुण:
2. बहुश्रुतता
3. चिकित्सक विचार

प्रश्न 2.
आकृती पूर्ण करा:

उत्तर:

कृती 3 : (स्वमत/अभिव्यक्ती)

प्रश्न 1.
‘फॅक्ट्स आर् सेक्रेड बट कॉमेंट्स आर् फ्री’ या उक्तीचा तुम्हांला कळलेला अर्थ लिहा.
उत्तर:
वृत्तपत्रांनी बातमी देणे हे त्यांचे मूळ कर्तव्य आहे. वाचकांना आपल्या अवतीभवती, देशविदेशात घडणाऱ्या घडामोडी जाणून घेण्यात रस असतो. वृत्तपत्रांनी बातमीच्या रूपात या घडामोडींची माहिती दयायची असते. ही बातम देताना घटना जशी घडली तशी बातमीत ती आली पाहिजे. बातमीदाराने स्वत:चे विचार, कल्पना बातमीत मिसळू नयेत, अशी अपेक्षा असते. बातमीदाराने आपल्या आवडत्या राजकीय पक्षाची बातमी भरभरून दिली, तर तो त्या पक्षाचा प्रचार होईल. वाचकांना मात्र संबंधित घटना खऱ्या स्वरूपात कळणार नाहीत. हे गैर आहे.

थोडक्यात बातमीदाराने, पत्रकारांनी बातमीत भेसळ करता कामा नये. यालाच ‘फॅक्ट्स आर् सेक्रेड’ असे म्हटले आहे. पत्रकारांना स्वत:चे विचार, मते मांडायची असतील, तर ती त्यांनी अग्रलेखात मांडावीत. स्वतंत्र लेख लिहून मांडावीत. मात्र ही मतेसुद्धा तटस्थपणे व परखडपणे मांडली पाहिजेत. पत्रकारांना ते स्वातंत्र्य पूर्णपणे बहाल केलेले असते. यालाच ‘कॉमेंट्स आर फ्री’ असे म्हटले आहे.

उतारा क्र. 2

1. पुढील उतारा वाचून दिलेल्या सूचनांनुसार कृती करा:

कृती 1 : (आकलन)

प्रश्न 1.
कोष्टक पूर्ण करा:

उत्तर:

कृती 2 : (आकलन)

प्रश्न 1.
वैशिष्ट्ये लिहा:
1. मंदीच्या काळातील नोकऱ्या.
उत्तर:
1. मंदीच्या काळातील नोकरीत सुरुवातीला काही महिने विनावेतन काम करावे लागे व नंतर काही काळ अत्यल्प वेतन मिळत असे.

प्रश्न 2.
कोण ते लिहा:
1. टाटा कंपनीत येण्याचे मुळगावकरांना आमंत्रण देणारे.
2. ध्येयाच्या बाबतीत अजिबात तडजोड न करणारे.
उत्तर:
1. जे. आर. डी. टाटा
2. सुमंत मुळगावकर.

कृती 3 : (स्वमत/अभिव्यक्ती)

प्रश्न 1.
तुम्हांला जाणवलेले मुळगावकरांचे मोठेपण समजावून सांगा.
उत्तर:
मुळगावकरांनी शास्त्र शाखेची पदवी घेतली होती. पुढे ते लंडनला गेले आणि त्यांनी स्थापत्यशास्त्राची पदवी घेतली. त्या काळाचा विचार करता, हे खूप उच्च दर्जाचे शिक्षण त्यांनी मिळवले होते. लेखकांनी सांगितलेला आदर्शवाद जोपासण्याचा मुळगावकरांचा गुण यातून दिसून येतो. जे करायचे ते उत्तमच, हा त्यांचा ध्यास या कृतीतून दिसतो. उच्च शिक्षण घेतलेले असूनही त्यांना सुरुवातीला 6 महिने विनावेतन काम करावे लागले. या परिस्थितीने ते खचले नाहीत. निराश झाले नाहीत. अत्यल्प वेतनावरही त्यांनी काम केले. यातून त्यांची चिकाटी दिसते. आपल्या ध्येयाकडे जाताना येईल त्या संकटाला तोंड दयायची त्यांची तयारी होती.

या सर्व काळात मुळगावकरांनी आपली योग्यता सिद्ध केली होती. म्हणूनच सिमेंटचे अधिक कारखाने उभारण्याची जबाबदारी त्यांच्यावर सोपवली गेली. दुसऱ्या महायुद्धाच्या काळात युरोप-अमेरिकेत तंत्रज्ञांचे एक मंडळ तत्कालीन सरकारने पाठवले. त्यात मुळगावकरांचा समावेश होता. लक्षात घेण्यासारखी गोष्ट म्हणजे त्या मंडळात जे. आर. डी. टाटांसारखा दूरदृष्टीचा उदयोजकही होता. टाटांनी त्या प्रवासातच मुळगावकरांना टाटा कंपनीत येण्याचे आमंत्रण दिले. या घटनांवरून मुळगावकरांच्या मोठेपणाची सहज कल्पना येऊ शकेल.

उतारा क्र. 3

1. पुढील उतारा वाचून दिलेल्या सूचनांनुसार कृती करा:

कृती 2 : (आकलन)

प्रश्न 1.
उत्तर लिहा:
सलग बारा वर्षे मालमोटारींचे उत्पादन न करण्यामागील रहस्य:
उत्तर:
सलग बारा वर्षे मालमोटारींचे उत्पादन न करण्यामागील रहस्य: मुळगावकरांना केवळ कारखाना उभारायचा नव्हता; तर त्यांना एक उदयोग उभारायचा होता.

कृती 3 : (स्वमत अभिव्यक्ती)

प्रश्न 1.
मुळगावकरांची दिसून येणारी व्यवस्थापनातील दूरदृष्टी व कौशल्य समजावून सांगा.
उत्तर:
साधारणपणे बहुसंख्य उदयोजक भराभर उत्पादन तयार करतात आणि बाजारात आणतात. या घाईमुळे उत्पादनात दोष राहतात. कर्मचाऱ्यांना व अधिकाऱ्यांनाही एक वाईट सवय लागते. उत्पादनात उणिवा दिसल्या तरी तिकडे दुर्लक्ष करण्याची सवय लागते. अचूक काम करण्याची, काटेकोरपणे काम करण्याची इच्छा राहत नाही. उत्तम दर्जा हवा, हा आग्रहही हळूहळू राहत नाही. अशी कंपनी कधीही पहिल्या दर्जाची होऊ शकत नाही. म्हणून मुळगावकरांनी प्रथम उत्पादनावर भर दिला नाही. मूलभूत बाबी निर्माण करण्यावर भर दिला. याचा टेल्को कंपनीला फार मोठा फायदा झाला. यातच मुळगावकरांची दूरदृष्टी होती व कौशल्य होते.

उतारा क्र. 4

1. पुढील उतारा वाचून दिलेल्या सूचनांनुसार कृती करा:

कृती 1 : (आकलन)

प्रश्न 1.
मुळगावकरांचे स्वभावविशेष लिहा.

1. ………………………..
2. ………………………..
3. ………………………..
4. ………………………..

उत्तर:
मुळगावकरांचे स्वभावविशेष:

1. सौम्य प्रवृत्ती
2. मोजके बोलणे
3. आस्थेवाईकपणा
4. टापटीपपणा.

प्रश्न 3.
विधाने पूर्ण करा:
1. आपल्या कारखान्याला आदर्श करायचे असेल, तर …………………………….
2. आपल्या कारखान्याचे हित कशात आहे, हे लक्षात घेतले, तर ………………………….
उत्तर:
1. आपल्या कारखान्याला आदर्श करायचे असेल, तर कठोरपणे निर्णय घेणे आवश्यक असते.
2. आपल्या कारखान्याचे हित कशात आहे, हे लक्षात घेतले, तर कठोर निर्णय घेणे सोपे जाते.

कृती 2 : (आकलन)

प्रश्न 1.
पुढील घटनांचा परिणाम लिहा:

उत्तर:

प्रश्न 2.
विधाने पूर्ण करा:
1. ………………….. ही मोटार उदयोगाला मुळगावकरांनी दिलेली देणगी होय.
2. आपले उत्पादन अधिकाधिक सरस व्हावे, म्हणून ……………………….
उत्तर:
1. अनेक तंत्रज्ञ शिकून तयार झाले, ही मोटार उद्योगाला मुळगावकरांनी दिलेली देणगी होय.
2. आपले उत्पादन अधिकाधिक सरस व्हावे, म्हणून मुळगावकरांनी संशोधन विभागावर लक्ष केंद्रित केले.

उतारा क्र. 5

1. पुढील उतारा वाचून दिलेल्या सूचनांनुसार कृती करा:

कृती 2 : (आकलन)

प्रश्न 1.
आकृती पूर्ण करा:

उत्तर:

भाषाभ्यास:

(अ) व्याकरण घटकांवर आधारित कृती :

1. समास:

प्रश्न 1.
पुढील विग्रहावरून समास ओळखा:
उत्तर:

1. हळद, कुंकू वगैरे → समाहार वंद्व समास
2. पाच मुखांचा समूह → द्विगू समास
3. राव किंवा रंक → वैकल्पिक द्वंद्व समास
4. ऋषीसारखा राजा → कर्मधारय समास
5. देव आणि दानव → इतरेतर द्वंद्व समास

2. शब्दसिद्धी:

प्रश्न 1.
‘उपसर्गघटित, प्रत्ययघटित व अभ्यस्त’- प्रत्येकी दोन है शब्द लिहा.
उत्तर:

प्रश्न 2.
‘ज्ञ’ प्रत्यय लागलेले चार शब्द लिहा : जसे-तंत्रज्ञ.
उत्तर:

1. शास्त्रज्ञ
2. तत्त्वज्ञ
3. शिल्पज्ञ
4. मनोज्ञ

प्रश्न 3.
‘सद् (सत्)’ उपसर्ग लागलेले चार शब्द लिहा: जसे-सद्वर्तन.
उत्तर:

1. सद्विचार
2. सद्विवेक
3. सदाचार
4. सद्गुणी

3. वाक्प्रचार:

प्रश्न 1.
अधोरेखित केलेल्या अर्थाचा वाक्प्रचार पाठातून शोधून लिहा:

1. यशने आहाराकडे दुर्लक्ष केल्यामुळे तो वारंवार आजारी पडत होता.
2. शेतीत खूप कष्ट केल्यामुळे या वर्षी रामरावांच्या कष्टाला चांगले फळ मिळाले.
3. आवाक्याबाहेरचे काम समीरने सन्मार्गाने पूर्ण केले.
4. स्वत:च्या तत्त्वांशी समझोता करणे योग्य नव्हे.

उत्तर:

1. यशने आहाराची हेळसांड केल्यामुळे तो वारंवार आजारी पडत होता.
2. शेतीत खूप राबल्यामुळे या वर्षी रामरावांच्या कष्टाला चांगले फळ मिळाले.
3. आटोक्यात नसलेले काम समीरने सन्मार्गाने पूर्ण केले.
4. स्वत:च्या तत्त्वांशी तडजोड करणे योग्य नव्हे.

प्रश्न 2.
पुढील वाक्प्रचारांचा अर्थ सांगून वाक्यात उपयोग करा:

1. वाखाणणे
2. गाजावाजा करणे
3. प्रेरणा देणे.

उत्तर:

1. वाखाणणे – अर्थ : प्रशंसा करणे.
   वाक्य: सुधीरच्या चित्राची सरांनी खूप वाखाणणी केली.
2. गाजावाजा करणे – अर्थ : स्वत:ची टिमकी वाजवणे.
   वाक्य: आपल्या कर्तृत्वाचा गाजावाजा करणे अयोग्य आहे.
3. प्रेरणा देणे — अर्थ : स्फूर्ती देणे.
   वाक् : राजूच्या समाजसेवेच्या कार्याला आईने खूप प्रेरणा दिली.

(आ) भाषिक घटकांवर आधारित कृती:

1. शब्दसंपत्ती:

प्रश्न 1.
पुढील वाक्यांतील अधोरेखित शब्दांचे विरुद्धार्थी शब्द लिहून, अर्थ न बदलता वाक्य पुन्हा लिहा:

1. सौम्य प्रकृतीच्या मुळगावकरांना प्रसंगी कठोर निर्णय घेणे शक्य होत असे.
2. मुळगावकर अबोल प्रवृत्तीचे होते.
3. मुळगावकर पदवी घेऊन आले, तेव्हा भारतात मंदीची लाट होती.
4. मुळगावकरांचे जीवन असमाधानी नव्हते.

उत्तर:

1. सौम्य प्रकृतीच्या मुळगावकरांना प्रसंगी सौम्य निर्णय घेणे शक्य होत नसे. सौम्य प्रकृतीच्या मुळगावकरांना प्रसंगी सौम्य निर्णय घेणे अशक्य होत असे.
2. मुळगावकर बोलक्या प्रवृत्तीचे नव्हते.
3. मुळगावकर पदवी घेऊन आले, तेव्हा भारतात भरभराटीची लाट नव्हती.
4. मुळगावकरांचे जीवन समाधानी होते.

प्रश्न 2.
तक्ता भरा:

उत्तर:

प्रश्न 3.
कंसांतील योग्य विरुद्धार्थी शब्द निवडून लिहा:

1. सरस × …………………. (विरस, निरस, सुरस)
2. सचोटी × ………………. (लबाडी, गुणवान, दुर्गुणी)
3. अवाढव्य × …………….. (प्रचंड, विशाल, चिमुकले)
4. सुदैव × ………………… (सदैव, एकमेव, दुर्दैव)

उत्तर:

1. सरस × निरस
2. सचोटी × लबाडी
3. अवाढव्य × चिमुकले
4. सुदैव × दुर्दैव.

2. लेखननियम:

प्रश्न 1.
नियम 1 मध्ये दिलेल्या वर्णनानुसार किमान दहा शब्द लिहा.
उत्तर:

1. उल्लेख
2. मुद्दाम
3. किल्ला
4. जिल्हा
5. झिम्मा
6. कुत्रा
7. पुत्र
8. चित्र
9. दुर्जन
10. दिल्ली.

प्रश्न 2.
नियम 2 मध्ये दिलेल्या वर्णनानुसार किमान दहा शब्द लिहा.
उत्तर:

1. इंच
2. भिंत
3. कुंडी
4. शिंग
5. बिंब
6. बुंदी
7. रुंदी
8. उंदीर
9. टिंब
10. पिंप.

प्रश्न 3.
अचूक शब्द ओळखा:

1. प्रर्दशन, प्रदर्शन, परदर्शन, प्रदशर्न.
2. केंद्रित, केद्रीत, केद्रित, केंद्रीत.
3. सलागार, सल्लागर, सल्लागार, सलागर.
4. चिकीत्सक, चीकीत्सक, चिकिस्तक, चिकित्सक.
5. बहुश्रुतता, बहुश्रुतता, बहूश्रूतता, बहुश्रूतता.
6. व्यक्तीमत्त्व, व्यक्तिमत्व, व्यक्तिमत्त्व, व्यक्तीमत्व.

उत्तर:

1. प्रदर्शन
2. केंद्रित
3. सल्लागार
4. चिकित्सक
5. बहुश्रुतता
6. व्यक्तिमत्त्व.

3. विरामचिन्हे:

प्रश्न 1.
पुढील वाक्यातील चुकीची विरामचिन्हे दुरुस्त करून योग्य ती विरामचिन्हे घालून वाक्ये लिहा:
1. तो म्हणाला. मी! तिथे मुळीच येणार नाही,
2. छे, छे, मला नकोच हा वेगळा छंद.
उत्तर:
1. तो म्हणाला, “मी तिथे मुळीच येणार नाही.”
2. “छे! छे! मला नकोच हा वेगळा छंद!”

4. पारिभाषिक शब्द:

प्रश्न 1.
पुढील इंग्रजी पारिभाषिक शब्दांना मराठी प्रतिशब्द दया:

1. Plumber
2. Comedy
3. Magazine
4. Orientation.

उत्तर:

1. नळ-कारागीर
2. सुखात्मिका
3. मासिक-पत्रिका
4. उद्बोधन, निदेशन.

उपक्रम:

प्रश्न 1.
तुमच्या परिसरातील लघुउदयोजकाची मुलाखत घ्या.

आदर्शवादी मुळगावकर Summary in Marathi

प्रस्तावना:

गोविंद तळवलकर हे मराठीतील व इंग्रजीतील एक श्रेष्ठ संपादक. आंतरराष्ट्रीय घडामोडींचे चिकित्सक अभ्यासक, सामाजिक व राजकीय घडामोडींवर अधिकारवाणीने भाष्य करणारे व्यासंगी पत्रकार. इंग्रजी वाङ्मय, जागतिक राजकारण, विशेषतः रशियन राज्यक्रांती व रशियाची जडणघडण यांचा सखोल अभ्यास हे गोविंद तळवलकरांचे खास वैशिष्ट्य. पुरोगामी दृष्टिकोन, खोलवर चिकित्सा, नि:पक्षपाती भूमिका व धारदार लेखणी यांमुळे वृत्तपत्रसृष्टीत त्यांचा जबरदस्त दरारा निर्माण झाला होता. राजकारणी लोकांना त्यांचा खूप धाक वाटत असे. त्यांनी राजकारण्यांवर नैतिक अंकुश ठेवण्याचे काम केले.

गोविंद तळवलकरांनी विविध प्रकारचे लेखन केले आहे. अनेक कर्तृत्ववान व्यक्तींच्या कार्याचा परिचय करून देणारे लेखही त्यांनी लिहिले आहेत. प्रस्तुत ‘आदर्शवादी मुळगावकर’ हा पाठ अशाच प्रकारातला आहे. श्री. सुमंत मुळगावकर हे टाटा समूहातील टेल्को या कंपनीचे व्यवस्थापकीय संचालक होते. एखादी कंपनी स्थापन करायची आणि तिला नफा मिळवून दयायचा, एवढाच मर्यादित हेतू त्यांनी मनात बाळगला नाही. जे काही करायचे ते सर्वोत्तम, आदर्शच असले पाहिजे, असा त्यांचा ध्यास होता.

कंपनीच्या इमारतीची रचना कशी करायची, कर्मचाऱ्यांना कसे घडवायचे, उत्पादन प्रक्रिया कशी आखायची, अंतिम उत्पादन ग्राहकस्नेही कसे करायचे या सर्व बाबतीत ते आदर्शवादीच होते. यामुळे टेल्को कंपनीने संपूर्ण भारतात एक उत्कृष्ट कंपनी म्हणून लौकिक मिळवलाच; शिवाय, जागतिक पातळीवरही ‘उत्कृष्ट कंपनी’ असा शिक्का प्राप्त केला. अशा या सुमंत मुळगावकर या व्यक्तिमत्त्वाच्या कार्याचा व स्वभावगुणांचा परिचय या पाठात गोविंद तळवलकरांनी करून दिला आहे.

शब्दार्थ:

1. परखड – स्पष्ट, कोणाच्या दडपणाखाली न येता व कोणालाही खूश करण्याचा हेतू न बाळगता व्यक्त केलेले (मत, विचार इत्यादी).
2. बहुश्रुतता – खूप ऐकलेले, पाहिलेले, वाचलेले असणे.
3. समाजमनस्क – समाजाविषयी जागरूक मन असलेला.
4. आदर्श – आरसा; एखादी गोष्ट, तत्त्व, विचार यांची सर्वोत्कृष्ट अवस्था.
5. सचोटी – प्रामाणिकपणा, प्रांजळपणा.
6. निकडीचे – (निकडतातडी, ताबडतोबीची गरज) तातडीचे.
7. अवाढव्य – प्रचंड.
8. सौम्य – मृदू, कोमल.
9. हेळसांड – हयगय, दुर्लक्ष.

टिपा:

1. फॅक्ट्स आर् सेक्रेड, बट कॉमेंट्स आर् फ्री: ‘गार्डियन’ या जगप्रसिद्ध वर्तमानपत्राचे हे घोषवाक्य. फॅक्ट्स म्हणजे घटना, घडलेली गोष्ट. वर्तमानपत्राने घटना घडली, तशीच तिची बातमी दिली पाहिजे. बातमीत स्वत:ची मते, पूर्वग्रह, हेतू मिसळता कामा नयेत. जसे घडले तसे शोधून काढून प्रसिद्ध केले पाहिजे. वर्तमानपत्राची ही नीती असली पाहिजे. भगवद्गीता, बायबल, कुराण यांसारख्या धर्मग्रंथांतील वचने, त्यांतील शब्द हे पवित्र मानले जातात. त्यांत बदल करता कामा नये. त्यांची मोडतोड करून वेगळी रचना करता कामा नये. त्या ग्रंथांत मुळात जसे आहे, तसेच उद्धृत केले पाहिजे, असा दंडक असतो. या अर्थाने बातमीसुद्धा पवित्र असते. तिच्या पावित्र्याला धक्का लावता कामा नये. मात्र त्या बातमीवर, बातमीतील घटनांवर भाष्य करण्याचा संपादकांना अधिकार असतो. असा एकूण त्या घोषवाक्याचा अर्थ आहे.

2. मंदीची लाट: कोणत्या तरी कारणाने एखादे उत्पादन खपत नाही किंवा त्याचे पुरेसे उत्पादन होत नाही. त्यामुळे नफा कमी होतो. साहजिकच पगारकपात केली जाते किंवा नोकरभरती होत नाही किंवा नोकरकपात केली जाते. याचा परिणाम म्हणून लोकांच्या हातात कमी पैसा येतो. पैसा कमी असल्याने बाजारात मालाचा उठाव होत नाही. त्यामुळे संबंधित उदयोगाचा नफा कमी होतो. नोकरकपात होते. पुन्हा मागणी कमी होते… अशा रितीने हेच चक्र वेगाने चालू होते. बेकारी येते. उत्पादन थंडावते. समाजाची आर्थिक स्थिती डबघाईला येते. या स्थितीला ‘मंदी’ म्हणतात.

वाक्प्रचार व त्यांचे अर्थ:

1. कस लागणे – सामर्थ्य सिद्ध होणे, गुणवत्ता सिद्ध होणे.
2. मानवंदना देणे – आदरपूर्वक सन्मान करणे.
3. कटाक्ष असणे – आग्रह असणे.
4. जीव तोडून काम करणे – शरीराला कितीही त्रास झाला तरी त्याची पर्वा न करता कष्ट करणे, पराकोटीचे कष्ट करणे.
5. गाजावाजा होणे – अवाजवी प्रसिद्धी होणे.

Balbharti Maharashtra State Board Class 9 Sanskrit Solutions Aamod Chapter 1 सुष्ठु गृहीतः चौरः Notes, Textbook Exercise Important Questions and Answers.

Maharashtra State Board Class 9 Sanskrit Aamod Solutions Chapter 1 सुष्ठु गृहीतः चौरः

Sanskrit Aamod Std 9 Digest Chapter 1 सुष्ठु गृहीतः चौरः Textbook Questions and Answers

भाषाभ्यास:

1. उचितं पर्यायं चिनुत ।

प्रश्न 1.
कस्य धनस्यूत: लुप्त: ?
(अ) देवदत्तस्य
(आ) वीरबलस्य
(इ) भृत्यस्य
(ई) नृपस्य
उत्तरम् :
(अ) देवदत्तस्य

प्रश्न 2.
गृहे कति भृत्याः आसन् ?
(अ) पञ्च
(आ) सप्त
(इ) षड्
(ई) एक:
उत्तरम् :
(इ) षड्

प्रश्न 3.
वीरबलः कस्य मित्रम् ?
(अ) भृत्यस्य
(आ) धनिकस्य
(इ) यष्टिकायाः
(ई) चौरस्य
उत्तरम् :
(आ) धनिकस्य

प्रश्न 4.
‘श्व: मम चौर्यं प्रकटितं भवेत्।’ इति चिन्ता कस्य चित्ते जायते?
(अ) दासस्य
(आ) वीरबलस्य
(इ) धनिकस्य
(ई) नृपस्य
उत्तरम् :
(अ) दासस्य

2. कः कं वदति ?

प्रश्न 1.
“पश्यन्तु एता: मायायष्टिकाः।”
उत्तरम् :
वीरबल: सेवकान् वदति।

प्रश्न 2.
“मित्र, अद्य सायङ्काले तव सर्वान् भृत्यान् मम गृहं प्रेषय।”
उत्तरम् :
वीरबल: देवदत्तं वदति।

3. माध्यमभाषया उत्तरं लिखत । वीरबलेन चौरः कथं गृहीतः ?

प्रश्न 1.
माध्यमभाषया उत्तरं लिखत । वीरबलेन चौरः कथं गृहीतः ?
उत्तरम् :
बिरबल हा सम्राट अकबराचा अतिशय चतुर आणि हजरजबाबी मंत्री होता. त्याच्या चातुर्याच्या अनेक कथा प्रसिद्ध आहेत. त्यांपैकीच एक म्हणजे ‘सुगृहीत: चौर:’. बिरबलाने स्वत:च्या चातुर्यान कसा चोर पकडला, याबाबत ही गोष्ट आहे.

देवदत्त नावाच्या एका श्रीमंत माणसाची पैशाची पिशवी चोरीला गेल्यावर तो आपल्या सेवकांवर संशय घेतो. आपल्या सहा सेवकांपैकीच कोणी एक चोर असणार, याची त्याला खात्री असते. चोराला पकडण्यासाठी तो आपल्या मित्राकडे म्हणजे बिरबलाकडे मदत मागतो. त्यानुसार एके संध्याकाळी बिरबल त्या सहा नोकरांना आपल्या घरी बोलावून समान उंचीची एकेक काठी देतो.

त्या काठ्या जादूच्या असून तुमच्यापैकी जो कोणी चोर असेल, त्याची काठी अंगठ्याएवढी लांब होईल, अशी भीतीही दाखवतो. आपापल्या काठ्या घेऊन दुसऱ्या दिवशी सकाळी यावे असे तो सेवकांना सांगतो. सहापैकी पाच चोर रात्री निश्चिंतपणे झोपतात. मात्र खऱ्या चोराच्या मनात भीती निर्माण होते.

आपली काठी अंगठ्याएवढी लांब होऊन आपली चोरी उघडकीस येण्यापेक्षा अगोदरच काठी कापलेली बरी, असा विचार करून तो काठी कापतो. दुसऱ्या दिवशी बिरबल एकच आखूड काठी बघून चोराला ओळखतो आणि त्याला पकडतो. खजील झालेला चोर क्षमा मागतो आणि पैशाची पिशवी परत देतो.

माणसाची मानसिकता कशी असते हे बिरबल जाणत होता. चोराच्या मनात चांदणे याचा अर्थ जाणून बिरबलाने सर्व साधले. खरा चोर स्वत:ची चोरी उघडकीस येणार नाही यासाठी नक्कीच प्रयत्न करेल. मनुष्याची हीच मानसिकता लक्षात घेऊन बिरबलाने युक्ती केली. अशा प्रकारे केवळ आपल्या युक्तीच्या जोरावर बिरबल चोराला पकडण्यात यशस्वी होतो.

Birbal was a very clever and witty minister in Emperor Akbar’s court. There are several famous accounts of his cleverness. One among them is the story “The thief is well – caught’ – ‘सु गृहीत: चौर:’ This story revolves around Birbal’s cleverness correctly identifying the thief.

When Devdutta realised his money bag was missing he suspected that one of the six servants would be the culprit. To catch the thief, he took Birbal’s help.

Birbal used his understanding of human psychology that the real thief would always do something to conceal his theft. Knowing this Birbal gave the servants a stick each of the same length saying that those sticks were magical and only the thief’s stick would grow longer the next day. The real thief fell for this ploy and cut his stick so no one would know that he was the thief.

However, the next day the thief’s stick was shorter than the others’. Birbal easily identified the thief due to his short stick. Thus, Birbal used his cleverness and understanding of human behavior to catch the thief.

4. स्तम्भमेलनं कुरुत।

प्रश्न 1.

उत्तरम् :

5. विरुद्धार्थकशब्दानां युग्मं चिनुत लिखत च।

प्रश्न 1.

उत्तरम् :

• पूर्वम् × पश्चात्
• गताः × आगताः
• दीर्घा × हस्वा
• जागृतः × सुप्तः
• भृत्यः × स्वामी
• धनिकः × दरिद्रः

6. पाठात् समानार्थक शब्दं चित्वा रेखाचित्रं पूरयत ।

प्रश्न 1.

उत्तरम् :

1. धनिकः
2. चौरः
3. सुप्तः
4. भृत्य:

Sanskrit Aamod Class 9 Textbook Solutions Chapter 1 सुष्ठु गृहीतः चौरः Additional Important Questions and Answers

एकवाक्यन उत्तरत।

प्रश्न 1.
क: धनिकः आसीत्?
उत्तरम् :
देवदत्त : धनिकः आसीत्।

प्रश्न 2.
सेवका: कदा वीरबलस्य गृहम् अगच्छन् ?
उत्तरम् :
सेवका: सायकाले वीरबलस्य गृहम् अगच्छन्।

प्रश्न 3.
वीरबलेन सर्वेषां कृते का: आनीता:?
उत्तरम् :
वीरबलेन सर्वेषां कृते समानोन्नतय: मायायष्टिका: आनीताः ।

प्रश्न 4.
चौरस्य यष्टिका कीदृशी भविष्यति ?
उत्तरम् :
चौरस्य यष्टिका अगुलिमात्र दीर्घा भविष्यति।

प्रश्न 5.
रात्रौ सर्वे भृत्याः किम् अकुर्वन् ।
उत्तरम् :
रात्री सर्वे भृत्याः सुखेन निद्राम् अकुर्वन् ।

प्रश्न 6.
किं दृष्ट्वा वीरबालेन चौर: ज्ञात:?
उत्तरम्
लघुष्टिकां दृष्ट्वा वीरबालेन चौर: ज्ञातः।

प्रश्न 7.
अपराधी भृत्यः किम् अकरोत्?
उत्तरम्
अपराधी भृत्यः अपराधम् अङ्गीकृतवान् धनस्यूतं च प्रत्यर्पितवान्।

प्रश्न 8.
अयं गद्यांश: कस्मात् पाठात् उद्धृतः?
उत्तरम्
अयं गटांशः ‘सुष्ठु गृहीत : चौर: पाठात् उद्धृतः।

सत्यं वा असत्यं लिखत।

प्रश्न 1.

1. देवदत्तः निर्धनः आसीत्।
2. देवदत्तस्य धनस्यूत: चोरितः।
3. देवदत्तस्य गृहे षड्भृत्येषु एक: चौरः ।
4. वीरबल: देवदत्तं साहाय्यम् अयाचत।
5. यष्टिकाः भिन्नोन्नतयः आसन्।
6. सेवकै: यष्टिका: न स्वीकृताः।
7. चौरस्य यष्टिका पूर्वमेव दीर्घा।

उत्तरम् :

1. असत्यम्
2. सत्यम्
3. सत्यम्
4. असत्यम्
5. असत्यम्
6. असत्यम्
7. असत्यम्

प्रश्न 2.

1. षद् सेवका: सुखेन निद्याम् अकुर्वन्।
2. चौरेण यष्किा कीयत्वा हस्वा कृता।
3. सर्वेषां राष्टिका: दीर्घा: भूताः।
4. लघुष्टिकाया: साहाय्येन चौर: गृहीतः।
5. चौर क्षमा प्राथ्यं धनस्यूतं प्रत्यर्पितवान्।

उत्तरम :

1. असत्यम्
2. सत्यम्
3. असत्यम्
4. सत्यम्
5. सत्यम्

उचितं कारणं चित्वा वाक्यं पुनर्लिखत।

प्रश्न 1.
देवदत्तः वीरबलं साहाय्यम् अयाचत यत: ……..
a. देवदत्त: आरक्षक: आसीत्।
b. चतुर: वीरबल: देवदत्तस्य मित्रम् आसीत्।
उत्तरम् :
देवदत्त: वीरबलं साहाय्यम् अयाचत यत: चतुर: बीरबल: देवदत्तस्य मित्रम् आसीत्।

प्रश्न 2.
सर्वे सेवका: वीरबलस्य गृहम् अगच्छन् यतः …….
a. वीरबलेन भोजनसमारोहः आयोजितः ।
b. वीरबल: तान् परीक्षितुम् ऐच्छत्।
उत्तरम् :
सर्वे सेवका: वीरबलस्य गृहम् अगच्छन् यतः वीरबल: तान् परीक्षितुम् ऐच्छत्।

प्रश्न 3.
वीरबल: सर्वेभ्यः सेवकेभ्य: यष्टिकाम् अयच्छत् यतः ………..
a. सः चौरं ग्रहीतुम् ऐच्छत्।
b. सेवका: यष्टिकाम् अयाचन्त।
उत्तरम् :
वीरबल:सर्वेभ्य:सेवकेभ्य: यष्टिकाम् अयच्छत् यत: स: चौर ग्रहीतुम् ऐच्छत्।

प्रश्न 4.
एक सेवक: निद्रा न अकरोत् यतः
a. सः अस्वस्थः आसीत्।
b. ‘मम चौर्य प्रकटितं भवेत्’ इति विचारेण स: भीतः।
उत्तरम् :
एक: सेवक: निटांन अकरोत् यतः मम चौर्व प्रकटितं भवेत्’ इति विचारेण स: भीतः।

प्रश्न 5.
चौरेण यतिका लघूकता यतः …………।
a. स: चौयं प्रकटयितुं न ऐच्छत्।
b. तस्य यष्टिका पूर्वमेव दीर्घा आसीत्।
उत्तरम् :
चौरेण यष्टिका लाकृता यत:, स; चौर्य प्रकटयितुं न ऐच्छन्।

प्रश्न 6.
वीरबलेन चौर: सम्यक् ज्ञात: बत्तः …….
a. चौरस्य यष्टिका दोषों अभवत्।
b. चौरस्य यटिका हस्वा अभवत्।
उत्तरम् :
बीरबलेन चौर: सम्यक् ज्ञात: यत: चौरस्य यष्टिका हस्वा अभवत्।

कः कं वदति।

प्रश्न 1.
प्रात: मम चौर्य प्रकटितं भवेत्।
उत्तरम्
चौर:/सेवक: आत्मानं वदति।

सूचनानुसारं कृती: कुरुत।

शब्दस्य वर्णविग्रहं कुरुत।

1. देवदत्तः – द् + ए + व + अ + अ + त् + त् + अः।
2. धनस्यूतः – ध् + अ + न् + अ + स् + य् + ऊ + त् + अः।
3. सायङ्काले – स् + आ + य् + अ + ङ् + क् + आ + ल् +ए।
4. भृत्यान् – भ + ऋ + त् + य् + आ + न्।
5. यष्टिकाः – य् + अ + ष्  + ट् + इ + क् + आः।
6. एकस्मात् – ए + क् + अ + स् + म् + आ + त्।
7. ऋते – ऋ + त् + ए।
8. अङ्गुलिमात्रम् – अ+ ङ् + ग् + उ + ल् + इ + म् + आ + त् + र् + अ + म्।
9. कर्तयामि – क् + अ + र + त् + अ + य् + आ + म् + इ।
10. चिन्तयित्वा – च + इ + न् + त् + अ + य + इ + त् + व् + आ।
11. अन्येयुः – अ + न् + य् + ए + द् + य + उः।
12. ज्ञात: – ज् + ञ् + आ + त् + अः।

प्रश्ननिर्माणं कुरुत।

प्रश्न 1.

1. देवदत्तः धनिकः आसीत्।
2. देवदत्तस्य गृहे षट् भृत्याः आसन्।
3. चौर ग्रहीतुं देवदत्त: वीरबल साहाय्यम् अयाचत।
4. सर्वे सेवका: सायङ्काले वीरबलस्य गृहम् आगताः।
5. वीरबलेन सर्वेषां कृते समानोन्नतय: यष्टिका: आनीताः।

उत्तरम् :

1. कः धनिकः आसीत्?
2. देवदत्तस्य गृहे कति भृत्या: आसन्?
3. चौरं ग्रहीतुं देवदत्तः कं साहाय्यम् अयाचत?
4. सर्वे सेवका: सायडकाले कुत्र आगताः?
5. वीरबलेन सर्वेषां कृते कीदृश्य : यष्टिका: आनीताः?

प्रश्न 2.
रात्री सर्वे भृत्या: सुखेन निद्राम् अकुर्वन्।
उत्तरम् :
कदा सर्वे भृत्या: सुखेन निद्राम् अकुर्वन् ।

प्रश्न 3.
लघुष्टिकां दृष्ट्वा वीरबलेन चौर: सम्यक् ज्ञातः ।
उत्तरम् :
लघुष्टिकां दृष्ट्वा केन चौर: सम्यक् ज्ञात:।

प्रश्न 4.
भृत्य अपराधम् अङ्गीकृतवान् ।
उत्तरम् :
मृत्यः किम् अङ्गीकृतवान्?

विशेषण-विशेष्य-सम्बन्धः।

त्वान्त/ल्यबन्त/तुमन्त अव्ययानि।

विभक्त्यन्तरूपाणि।

• प्रथमा – देवदत्तः, धनिकः, धनस्यूतः, भृत्याः, षड, चौरः, वीरबलः, सेवकाः, यष्टिकाः, सः, एताः, मायायष्टिकाः, दीर्घा, सर्वे, भृत्याः, अहम, चौरः, भृत्यः, गृहीतः।
• द्वितीया – चौरम्, वीरबलम्, साहाय्यम्, सर्वान, भृत्यान, गृहम, सेवकान्, एकाम, यष्टिकाम्, निद्राम, चौर्यम्, यष्टिकाम्, लघुष्टिकाम, अपराधम्, धनस्यूतम्
• तृतीया – सुखेन, वीरबलेन, सर्वैः, वीरबलेन, येन, केन।
• पञ्चमी – एकस्मात्
• षष्ठी – मम, वीरबलस्य, स्वस्य, तस्य, वीरबलस्य, सर्वेषाम्, मम, देवदत्तस्य।
• सप्तमी – रात्री, पादयोः, तासु, प्रभाते, गृहे।

पाठात् समानार्थक शब्दं चित्वा रेखाचित्रं पूरयत।

प्रश्न 1.

उत्तरम् :
1. गृहम्
2. दिनः

समानार्थकशब्दं योजयित्वा वाक्यं पुनर्लिखत।

निद्रा – निद्रा बालकं पीडयति। स्वापः / सुप्तिः / स्वपा / शयनं बालकं पीडयति।
दिनः – अद्य रम्य: दिनः । अद्य रम्य: दिवस: / अहः।.

व्याकरणम्

नाम – तालिका।

सर्वनाम – तालिका।

धातु – तालिका।

समासाः।

धातुसाधितविशेषणानि।

सुष्ठु गृहीतः चौरः Summary in Marathi and English

प्रस्तावना :

मूल्य रुजविण्यासाठी, कौशल्यविकास तसेच मनोरंजनासाठी कथांचा परिणामकारकपणे वापर फार पूर्वीपासून होत आहे. प्रस्तुत कथेत एका चोराला पकडण्यासाठी बिरबलाने योजलेल्या युक्तीतून फक्त त्याचे चातुर्यच नव्हे तर त्याला असलेले मानवी स्वभावाचे ज्ञानही दिसून येते.

परिस्थिती अनुकूल असेपर्यंत आपल्या चुका लपवण्याचा मानवी स्वभाव असतो. या कथेतील चोराला पकडण्यासाठी बिरबल देवदत्ताच्या सहा सेवकांना काळ्या देतो आणि फक्त चोराचीच काठी बोटभर लांब होईल, अशी भीती घालतो. आपली चोरी लपविण्यासाठी खरा चोर अगोदरच काठी कापून टाकतो आणि दुसऱ्या दिवशी आखूड काठी बघून बिरबल चोराला ओळखतो.

Stories have been the medium of teaching values, skills and providing entertainment since ages. This story revolves around how Birbal used not just his cleverness, but also his knowledge of human behaviour to identify the thief.

A man always tries to hide his mistake or wrongdoing and therefore will not be at exse till he finds a way to take care of it. Birbal gave Deudutta’s six servants & stick each and said that only the thief’s stick would become longer the next day.

The real thief cut his stick so that he would not be caught. But Birbal immediately identified the thief, the one whose stick was shorter than the rest.

परिच्छेद : 1

देवदत्त: …………….. भविष्यति।

देवदत्त: नाम कोऽपि धनिकः आसीत्। एकदा तस्य धनस्यूतः लुप्तः । तस्य गृहे षड् भृत्याः आसन्। तेषु एव एक: चौरः स्यात्, इति तस्य मतम्। चौर ग्रहीतुं सः वीरबलं साहाय्यम् अयाचत । वीरबल: अवदत, “मित्र ! अद्य सायङ्काले तव सर्वान् भृत्यान् मम गृहं प्रेषय” इति। यथानिश्चितं सर्वे सेवका; वीरबलस्य गृहम् आगताः। वीरबलेन पूर्वमेव सर्वेषां कृते समानोन्नतय: यष्टिका: आनीताः । सः सेवकान् अवदत, “भोः पश्यन्तु, एताः मायायष्टिका: । तासु एका यष्टिकां स्वीकृत्य सर्वे: देवदत्तस्य गृहं गन्तव्यं , श्वः प्रभाते पुनरागन्तव्यम्। येन केनापि धनस्यूत: चोरित: स्यात् तस्य यष्टिका अङ्गुलिमात्रं दीर्घा भविष्यति।”

अनुवाद:

देवदत्त नावाचा कोणी एक श्रीमंत माणूस होता. एकदा त्याची पैशांची पिशवी (थैली) हरवली. त्यांच्या घरी सहा सेवक होते. त्यांच्यापैकीच कोणी एक चोर असेल, असे त्याचे मत होते.

चोराला पकडण्यासाठी त्याने विरबलाकडे मदत मागितली. बिरबल म्हणाला, “मित्रा, आज संध्याकाळी तुझ्या सर्व सेवकांना माझ्या घरी पाठव.” ठरल्याप्रमाणे सगळे सेवक बिरबलाच्या घरी आले. बिरबलाने अगोदरच सगळ्यांसाठी समान उंचीच्या काठ्या आणल्या होत्या.

तो सेवकांना म्हणाला, “हे बघा, या जादुई काठ्या आहेत. त्यातील एक काठी घेऊन सर्वांनी देवदत्ताच्या घरी जावे, उद्या सकाळी परत यावे. ज्या कोणाकडून पिशवी चोरली गेली असेल त्याची काठी बोटभर लांब होईल.”

There was a certain rich man name Devadutta. Once his money bag was missing. There were six servants in his house. It was his opinion that one among them would surely be the thief. He sought Birbal’s help in order to catch the thief. Birbal said, “O friend, send all your servants to my house today, in the evening.

As decided, all the servants came to Birbal’s house. Birbal had brought sticks of the same length for all of them in advance. He said to the servants, “O see, these are magical sticks.

Taking a stick among those, you all go back to Devadutta’s house and come again tomorrow morning. The stick of the one who has stolen the money bag will become longer by a finger.

सन्धिविग्रहः

• कोऽपि – कः + अपि।
• पूर्वमेव – पूर्वम् + एव।
• पुनरागन्तव्यम् – पुन: + आगन्तव्यम्।
• केनापि – केन + अपि।
• दृष्ट्वैव – दृष्ट्वा + एव।

समानार्थकशब्दाः

1. धनिकः – धनी, धनाक्यः, धनवान, धनसमपत्रः, सधन:,
2. इभ्यः, श्रीमान्।
3. भृत्यः – सेवकः, परिचारकः, दासः, दासेयः, किङ्करः,
4. चौरः – स्तेनः, तस्करः, मोषकः, पाटच्चरः।
5. मित्रम् – सखा, वयस्यः , सुहृद्।
6. गृहम् – गेहम्, सदनम्, निकेतनम्, वेश्म, आलयः।
7. अवदत् – अभणत्, अकथयत्।
8. प्रभाते – प्रात:काले।
9. सुष्टु – सम्यक्तया।
10. स्वीकृत्य – गृहीत्वा।
11. भः – अन्येयुः, अपरेयुः।
12. रात्रौ – निशायाम्।
13. निद्रा – स्वापः, स्वपा, शयनम् सुप्तिः।
14. अधुना – साम्पतम्, इदानीम्।
15. दृष्ट्वा – वीक्ष्य, विलोक्य, अवलोक्य।
16. ऋते – विना।
17. सुप्तः – निद्रितः, निद्राधीनः।
18. चौर्यम् – लण्ठनम्।

विरुद्धार्थकशब्दाः

• धनिकः × दरिद्रः, दीनः।
• दीर्घा × न्हस्वा
• आगताः × गताः, निर्गताः।
• भृत्यः × स्वामी।
• पूर्वम् × पश्चात्।
• स्वीकृत्य × त्यक्त्वा।
• श्वः × अद्य, ह्यः।
• मित्रम् × शत्रुः।
• सायङ्काले × प्रात:काले।
• रात्री × प्रभाते।
• सुखेन × चिन्तया, सचिन्तम्।
• निद्रा × जागृतिः।
• सुप्त: × जागृतः।

परिच्छेद : 2

रात्री ………… प्रत्यर्पितवान्।

रात्री सर्वे भृत्या: सुखेन निद्राम् अकुर्वन् ऋते एकस्मात् स: अचिन्तयत्, “व: प्रात: मम चौर्य प्रकटितं भवेत्। अत: अहम् अधुना एव मम यष्टिकाम् अङ्गलिमात्रं कर्तयामि।” इति चिन्तयित्वा तथा कृत्वा सः सुखेन सुप्तः। अन्येाः लघुष्टिकां दृष्ट्वैव वीरवलेन चौर: सम्यक् ज्ञात: गृहीत: च। अपराधी भृत्य: वीरबलस्य पादयोः पतित्वा स्वस्य अपराधम् अङ्गीकृतवान् धनस्यूतं च प्रत्यर्पितवान्।

अनुवादः

रात्री एकजण वगळता सगळे सेवक शांतपणे झोपले. त्याने विचार केला, “उद्या सकाळी माझी चोरी उघड होईल (प्रकाशात येईल). म्हणून मी आताच माझी काठी बोटभर कापतो.”

असा विचार करून ठरवल्याप्रमाणे करून तो शांतपणे झोपला. दुसऱ्या दिवशी आखूड काठी पाहून बिरबलाने चोराला उत्तमरीत्या (व्यवस्थित) ओळखले आणि पकडले. अपराधी सेवकाने बिरबलाच्या पाया पडून स्वतःचा अपराध मान्य केला आणि पैशांची (थैली) परत दिली.

At night except one, all the servants slept peacefully. He thought, “Tomorrow morning my theft will be revealed. So I shall cut my stick by a finger length now itself.” Thinking that, he did so and slept peacefully.

The next day just by looking at the short stick Birbal correctly recognised and caught the thief. The guilty servant fell at Birbal’s feet and accepted his mistake and returned the money bag.

शब्दार्थाः

1. धनिक – rich man – श्रीमंत
2. धनस्यूतः – money bag – पैशांची पिशवी(थैली)
3. भृत्याः – servants – सेवक
4. स्यात् – would be – असेल
5. ग्रहीतुम् – to catch – पकडण्यासाठी
6. अयाचत – sought/asked – याचना केली
7. अद्य – today – आज
8. प्रेषय – send – तू पाठव
9. गन्तव्यम – should – जावे
10. यथानिश्चितम् – as decided – ठरवल्याप्रमाणे
11. आगताः – came – आले
12. पूर्वमेव – in advance – अगोदरच
13. समानोन्नतयः – same length – समान उंचीच्या (मापाच्या)
14. यष्टिकाः – sticks – काठ्या
15. आनीताः – brought – आणल्या
16. मायायष्टिकाः – magical sticks – जादुई काठ्या
17. पुनरागन्तव्यम् – come again – पुन: यावे
18. स्वीकृत्य – taking – स्वीकार करून, घेऊन
19. अङ्गुलिमात्रम् – by a finger – बोटभर
20. श्चः – tomorrow – उद्या
21. चोरितः – stolen – चोरलेला
22. दीर्घा – long – लांब
23. भविष्यति – will become – होईल
24. ऋते – except – शिवाय
25. चौर्यम् – theft – चोरी
26. प्रकटितं भवेत् – will be revealed – उघड होईल
27. कर्तयामि – I shall cut – मी कापतो
28. चिन्तयित्वा – thinking – विचार करून
29. सुप्त: – slept – झोपला
30. अन्येयुः – the next day – दुसऱ्या दिवशी
31. दृष्ट्वा – looking – पाहून
32. सम्यक् – correctly – उत्तमरीत्या
33. ज्ञातः – recognised – ओळखला गेलेला
34. गृहीतः – caught – पकडला गेलेला
35. पतित्वा – falling – पडून
36. अङ्गीकृतवान् – accepted – मान्य केला / कबूल केला
37. प्रत्यर्पितवान् – returned – परत दिला

Balbharti Maharashtra State Board Class 9 Marathi Solutions Kumarbharti Chapter 19 प्रीतम Notes, Textbook Exercise Important Questions and Answers.

Maharashtra State Board Class 9 Marathi Kumarbharti Solutions Chapter 19 प्रीतम

9th Std Marathi Kumarbharati Digest Chapter 19 प्रीतम Textbook Questions and Answers

1. तुलना करा:

प्रश्न 1.
तुलना करा:

उत्तर:

2. कारणे लिहा:

प्रश्न 1.
कारणे लिहा:
(अ) प्रीतमला मराठी नीट येत नसे.
(आ) पोरकेपणाचे समान धागे लेखिकांना प्रीतमकडे खेचत होते.
उत्तर:
(अ) जन्मल्यापासून प्रीतम महाराष्ट्राबाहेर होता. त्या वर्षी तो प्रथमच महाराष्ट्रात आला होता.
(आ) प्रीतमची आई त्याच्या लहानपणीच वारली होती आणि लेखिकांचे वडीलही वारले होते. त्यामुळे प्रीतमचा पोरकेपणा त्यांना समजत होता.

3. प्रतिक्रिया लिहा:

प्रश्न 1.
प्रतिक्रिया लिहा:
(अ) प्रीतमच्या निबंधातील चुका बघून त्याच्या वर्गशिक्षिकेची प्रतिक्रिया.
(आ) अबोल प्रीतम भडाभडा बोलल्यानंतर वर्गशिक्षिकेची प्रतिक्रिया –
उत्तर:
(अ) प्रीतमच्या निबंधातील चुका बघितल्यावर बाईंनी त्याला थांबवून घेतले आणि आईवडिलांना घेऊन यायला सांगितले.
(आ) बाईंनी प्रीतमला जवळ घेतले. त्याच्या चेहेऱ्यावरून हात फिरवला.

4. लेखिकेच्या कृती व तिच्या कृतीतून अभिव्यक्त होणारे गुण यांची जुळणी करा:

प्रश्न 1.
लेखिकेच्या कृती व तिच्या कृतीतून अभिव्यक्त होणारे गुण यांची जुळणी करा:

5. प्रीतमला स्वतःबद्दल जाणीव असलेली पाठातील वाक्ये शोधा व लिहा.

प्रश्न 1.
प्रीतमला स्वतःबद्दल जाणीव असलेली पाठातील वाक्ये शोधा व लिहा.
उत्तर:
पाठातील वाक्ये अशी:
1. प्रीतम मान खाली घालून हळूच माझ्याकडे बघत होता.
2. मला मराठी नीट येत नसल्याने बाकी विषयही कळत नाहीत.
3. माझ्याबद्दल तक्रार गेली तर मामी खूप टाकून बोलते. मग मामा मला मारतात. मी नापास झालो, तर बाबांना सांगून ते मला बोर्डिंगात ठेवणार. तिकडे मुलांना खूप त्रास देतात. बाबांनी वारंवार विनंती केल्यामुळे मामांनी मला ठेवून घेतले आहे.
4. तो हळूच जवळ येऊन म्हणाला, “बाई, माझ्याकडे पैसे नव्हते, म्हणून माझ्या आईच्या वापरलेल्या बांगड्या अन् अत्तर मी तुम्हांला दिले. तिची तेवढीच आठवण माझ्यापाशी आहे. खास माझ्या स्वत:च्या वस्तू आहेत त्या.”
5. “या बाई म्हणजे माझ्या एकुलत्या एक कुटुंबीय आहेत. त्या भेटल्या नसत्या तर कॅप्टन लुथरा नावाचा आज कुणी अस्तित्वात नसता.”

6. खालील वाक्प्रचारांचा योग्य अर्थ लिहा:

प्रश्न (अ)
रया जाणे.
1. शोभा जाणे.
2. शोभा करणे.
3. शोभा देणे.
उत्तर:
2. शोभा जाणे

प्रश्न (आ)
संजीवनी मिळणे.
1. जीव घेणे.
2. जीवदान देणे.
3. जीव देणे.
उत्तर:
2. जीवदान देणे.

7. कंसांत दिलेल्या सूचनांप्रमाणे वाक्यांचे रूपांतर करा:

प्रश्न 1.
कंसांत दिलेल्या सूचनांप्रमाणे वाक्यांचे रूपांतर करा:

1. मुलांनी आईवडिलांची आज्ञा पाळावी. (आज्ञार्थी करा.)
2. आईने माझ्याकडे निराशेने पाहिले. (नकारार्थी करा.)
3. बापरे ! रस्त्यावर केवढी ही गर्दी ! (विधानार्थी करा.)
4. नेहमी खरे बोलावे. (प्रश्नार्थी करा.)

उत्तर:

1. मुलांनो, आईवडिलांची आज्ञा पाळा.
2. आईने माझ्याकडे आशेने पाहिले नाही.
3. रस्त्यावर खूपच गर्दी आहे.
4. नेहमी खरे बोलावे का?

8. स्वमत.

प्रश्न (अ)
प्रीतम आणि त्याच्या बाई यांच्यातील भावनिक नातेसंबंधांविषयी तुमचे मत सविस्तर लिहा.
उत्तर:
प्रीतमच्या बाईंना प्रीतमची नकारात्मक बाजूच प्रथम जाणवते. त्यामुळे त्यांच्या मनात त्याची नकारात्मक प्रतिमा निर्माण होते. परंतु त्याची खरी पार्श्वभूमी कळल्यावर त्यांच्या मनात कणव निर्माण होते. त्या त्याच्याशी सहृदयतेने वागू लागतात. त्याला भावनिक आधार देतात. सगळ्या मुलांनी वर्गणी काढून बाईंना भेटवस्तू दिली. प्रीतम त्याच्याजवळच्या आईच्या जुन्या बांगड्या बाईंना भेट देतो. आईविषयीच्या सर्व भावना त्या बांगड्यांमध्ये त्याने साठवलेल्या होत्या.

त्याच्या दृष्टीने ती अमूल्य वस्तू होती. ती तो बाईंना भेट म्हणून देतो. त्याच्या मनातला हा उच्च, उदात्त भाव बाईंच्या अंत:करणाचा ठाव घेतो. त्या त्याच्या भावनेचा गौरव करतात. अशा प्रकारे बाई त्याला प्रसंगाप्रसंगांतून आत्मविश्वास देतात. बाईंकडून भावनिक पाठबळ मिळते. त्याच्या जोरावर तो सेकंड लेफ्टनंट बनतो. आदराचे व प्रतिष्ठेचे स्थान प्राप्त करतो. या कारणाने त्याला बाई म्हणजे आपली आईच, असे मनोमन वाटते. बाईंना त्याच्यातील सद्गुणी, होतकरू मुलगा दिसतो. त्या त्याला तसे घडवत नेतात. बाई आणि प्रीतम दोघेही एकमेकांना तृप्तीचा, परिपूर्तीचा आनंद देतात.

प्रश्न (आ)
तुमच्या जीवनातील शिक्षकाचे स्थान स्पष्ट करा.
उत्तर:
आतापर्यंतच्या शिक्षकांपैकी दोन शिक्षक माझ्या लक्षात राहिले आहेत. त्या दोनपैकी एक होते माझे मराठीचे शिक्षक शार्दुल सर. ते नेहमी सांगत — वाक्यातले सर्व शब्द एकमेकांचे नातेवाईक असतात. काही दूरचे, काही जवळचे. त्यांच्या नात्यांप्रमाणे त्यांचा अर्थ ठरतो. ही नाती लक्षात घेत घेत वाचन करायचे असते, हेही त्यांनी सोदाहरण समजावून सांगितले. आता वाचन करताना मला कधीही अडखळायला होत नाही.

पाचवीत भेटले इंग्रजीचे श्रीरंग सर. त्यांनी शब्दांचे स्पेलिंग लक्षात ठेवण्याचे गुपितच सांगितले. त्यानुसार उच्चार कसे होतात, हेही समजावून सांगितले. इंग्रजी शब्द, इंग्रजी वाक्य उच्चारण्याची गोडी इतकी वाढू लागली की मला हळूहळू इंग्रजी बोलता येऊ लागले आहे. या शिक्षकांमुळे माझा अभ्यास चांगला होऊ लागला. माझा आत्मविश्वास वाढला. माझे आईबाबाही खूश आहेत. हे सर्व माझ्या या शिक्षकांमुळे घडले आहे.

उपक्रम:

प्रश्न 1.
‘प्रीतम’ या कथेचे नाट्यरूपांतर करा. वर्गात सादरीकरण करा.

प्रश्न 2.
कथेची मध्यवर्ती कल्पना तुमच्या शब्दांत लिहा.

Marathi Kumarbharati Textbook Std 9 Answers Chapter 19 प्रीतम Additional Important Questions and Answers

उतारा क्र. 1

1. पुढील उतारा वाचून दिलेल्या सूचनांनुसार कृती करा:

कृती 1 : (आकलन)

प्रश्न 1.
कारणे लिहा:
1. बाईंना प्रीतम लुथरा हे नाव वेगळे वाटले.
उत्तर:
1. सर्व मराठी मुलांमध्ये प्रीतम लुथरा हे अमराठी नाव असल्याने बाईंना ते वेगळे वाटले.

कृती 2 : (आकलन)

प्रश्न 1.
माहिती लिहा:
1. बाईंचे प्रीतमविषयी झालेले मत.
2. लहानपणापासूनच प्रीतमला आईवडिलांचे छत्र न लाभण्याचे कारण.
उत्तर:
1. प्रीतम दिवसेंदिवस आळशी व बेजबाबदार होत चालला होता.
2. लहानपणी म्हणजे प्रीतम साधारणपणे तीन वर्षांचा असताना त्याची आई वारली होती. वडील सैन्यात जवान असल्याने ते नेहमी सरहद्दीवर असत. तो सतत आईवडिलांपासून दूर राहत होता.

प्रश्न 2.
लेखिकेच्या कृती व तिच्या कृतीतून अभिव्यक्त होणारे गुण यांची जुळणी करा:

उत्तर:
1. कर्तव्यनिष्ठा.

प्रश्न 3.
कोष्टक पूर्ण करा:

उत्तर:

कृती 3 : (स्वमत/अभिव्यक्ती)

प्रश्न 1.
‘माणसाचे व्यक्तिमत्त्व त्याच्या भोवतालावर अवलंबून असते,’ हे विधान प्रीतम लुथरा यांच्या आधारे स्पष्ट करा.
उत्तर:
प्रीतम लुथरा हा सात वर्षांचा मुलगा. चार वर्षांपूर्वी त्याची आई वारली होती. म्हणजे त्या वेळी तो केवळ तीन वर्षांचा होता. आईचे प्रेम आणि तिचा आधार त्याला लाभलाच नव्हता. त्यात भर म्हणजे त्याचे वडील सैन्यात होते. ते नेहमी सरहद्दीवर असत. त्यांचाही त्याला सहवास लाभलेला नाही. आईवडिलांच्या सुरक्षित छत्रछायेत त्याला वावरायलाच मिळालेले नाही. कधी बंगाल, कधी पंजाब अशा भिन्न वातावरणात राहावे लागले. दुसरीत असताना तो महाराष्ट्रात आला होता.

अशा परिस्थितीमुळे तो सतत बुजरा राहिला. तो कोणात मिसळत नसे. कोणत्याही उपक्रमात भाग घेत नसे. वर्गात शिकताना खूपदा खिडकीबाहेर रिकाम्या आकाशाच्या तुकड्याकडे एकटक पाहत राही. तो एकलकोंडा, घुमा, अबोल बनला होता. मुक्तपणे खेळणारा-बागडणारा बालक न राहता, तो चारही बाजूंनी दबलेला, मनातून खचलेला बालक बनला होता. हे केवळ त्याच्या बाह्य परिस्थितीमुळे घडले होते. याचा अर्थ, माणसाच्या भोवतालची परिस्थिती माणसाला घडवते.

उतारा क्र. 2

1. पुढील उतारा वाचून दिलेल्या सूचनांनुसार कृती करा :

कृती 1 : (आकलन)

प्रश्न 1.
प्रतिक्रिया लिहा:
प्रीतमला कुणी नातेवाईक नाहीत, हे कळल्यावर बाईंची प्रतिक्रिया –
उत्तर:
बाईंचा आवाज एकदम खाली आला.

प्रश्न 2.
लेखिकांची कृती आणि त्यांच्या कृतीतून अभिव्यक्त होणारे गुण यांची जुळणी करा:

उत्तर:

कृती 2 : (आकलन)

प्रश्न 1.
का ते लिहा:
1. प्रीतमला मराठीखेरीज अन्य विषयसुद्धा येत नसत.
2. मामांनी प्रीतमला स्वत:कडे ठेवून घेतले.
उत्तर:
1. सर्व विषय मराठीतून शिकवले जात. प्रीतमला मराठी नीट येत नसे. त्यामुळे अन्य विषयसुद्धा येत नसत.
2. प्रीतमच्या बाबांनी वारंवार विनंती केल्यामुळे मामांनी प्रीतमला स्वत:कडे ठेवून घेतले.

प्रश्न 2.
कोण ते लिहा:

1. प्रीतमला टाकून बोलणाऱ्या
2. प्रीतमला मार देणारे
3. प्रीतमला घरी ठेवून घ्यावे, अशी मामांना विनंती करणारे
4. प्रीतमला मधल्या सुट्टीत मराठी शिकायला बोलावणाऱ्या

उत्तर:

1. प्रीतमला टाकून बोलणाऱ्या – मामी
2. प्रीतमला मार देणारे – मामा
3. प्रीतमला घरी ठेवून घ्यावे, अशी मामांना विनंती करणारे – बाबा
4. प्रीतमला मधल्या सुट्टीत मराठी शिकायला बोलावणाऱ्या – बाई

कृती 3 : (स्वमत/अभिव्यक्ती)

प्रश्न 1.
बाईंनी प्रीतमला मराठी शिकायला बोलावले, याबद्दल तुमचे मत लिहा.
उत्तर:
प्रीतमचे बाबा हे त्याचे एकुलते एक नातेवाईक. पण ते सैन्यात असल्यामुळे नेहमी देशाच्या सीमेवर असतात. मामा-मामी त्याला प्रेमाने वागवत नाहीत. परक्या भाषिकांमध्ये, परक्या वातावरणात तो राहतो. त्याला कोणाचाच आधार नाही. सगळीकडून तो दूर लोटला गेला होता. त्याला मायेची गरज होती. मायेला पारखा झाल्यामुळे त्याला कशातच गोडी वाटत नव्हती. त्यामुळे शिकण्यातही रस नव्हता. बाईंनी त्याला माया दिली. मराठी शिकवले. त्याला इतर विषयही कळू लागले. एकंदरीत कोणालाही प्रेमाने वागवल्यास तो आनंदाने जीवन जगतो. जगण्याची त्याची ताकद वाढते. म्हणून बाईंनी प्रीतमला मराठी शिकायला बोलावून त्याच्यात उमेद निर्माण केली, असे मला वाटते.

उतारा क्र. 3

1. पुढील उतारा वाचून दिलेल्या सूचनांनुसार कृती करा:

कृती 1 : (आकलन)

प्रश्न 1.
कारणे लिहा:
1. प्रीतमला इतर विषय समजू लागले.
2. आपुलकी वाटत नसतानाही मामा-मामी प्रीतमला खाऊ घालत.
उत्तर:
1. सर्व विषय मराठीतून शिकवले जात. त्याला मराठी येऊ लागले, तेव्हापासून त्याला इतर विषय समजू लागले.
2. प्रीतमचे बाबा पैसे पाठवत, म्हणून मामा-मामी त्याला खायला घालत.

प्रश्न 2.
विविध व्यक्तींच्या कृती व त्यांतून अभिव्यक्त होणारे गुण यांची जुळणी करा:

उत्तर:

कृती 2 : (आकलन)

प्रश्न 1.
पुढील घटनांचे परिणाम लिहा:

उत्तर:

प्रश्न 2.
फरक लिहा:

उत्तर:

कृती 3 : (स्वमत/अभिव्यक्ती)

प्रश्न 1.
प्रीतमच्या वर्तनातील बदल सांगून त्याबद्दलचे तुमचे मत लिहा.
उत्तर:
मधल्या सुट्टीत बाई शिकवू लागल्यापासून प्रीतम मन लावून शिकू लागला. त्याचे मराठीचे कौशल्य वाढले. त्यामुळे त्याला इतर विषयही समजू लागले. बाईंच्या प्रेमळ वागण्याने त्याला जणू संजीवनी मिळाली. त्याची प्रकृती सुधारली. तो आनंदाने वावरू लागला.

बाईंच्या लग्नानिमित्त शाळेतल्या मुलांनी एक छोटासा समारंभ केला. बाईंना एक छोटीशी भेटही दिली. त्यासाठी मुलांनी वर्गणीही काढली होती. त्यात प्रीतम सहभागी होऊ शकला नाही. मात्र, प्रत्यक्ष समारंभात प्रीतम आत्मविश्वासाने बाईंजवळ गेला. त्याने स्वत:च्या आईच्या जुन्या बांगड्या बाईंना भेट म्हणून दिल्या. या कृतीमागे त्याच्या मनात उदात्त भावना आहेत. तो आता दबलेला, खचलेला मुलगा राहिलेला नाही. तो आता समंजस, शहाणा, जाणता मुलगा बनला आहे. प्रीतममध्ये झालेला हा बदल बाईंच्या मायेमुळे झाला आहे. मुलांना धाकाने, दहशतीने न वागवता प्रेमाने वागवले, तर मुलांमध्ये चांगला बदल होतो, हे सर्वांनी लक्षात घ्यायला हवे.

उतारा क्र. 4

1. पुढील उतारा वाचून दिलेल्या सूचनांनुसार कृती करा:

कृती 1 : (आकलन)

प्रश्न 1.
पुढे दिलेली विधाने आणि त्यांतून अभिव्यक्त होणारे गुण यांच्या जोड्या लावा:

उत्तर:

प्रश्न 2.
पुढे दिलेल्या घटनेचा परिणाम लिहा:

उत्तर:

कृती 2 : (आकलन)

प्रश्न 1.
का ते सांगा:
1. प्रीतम ओशाळवाणा झाला.
2. प्रीतमने आईच्या वापरलेल्या बांगड्या बाईंना भेट दिल्या.
उत्तर:
1. प्रीतम ओशाळवाणा झाला, कारण जुन्या बांगड्या बघून सगळेजण हसू लागले.
2. प्रीतमने आईच्या वापरलेल्या जुन्या बांगड्या बाईंना भेट दिल्या, कारण त्याच्याकडे वर्गणी देण्यासाठी पैसे नव्हते.

प्रश्न 2.
कोण ते लिहा:
1. बाईंना दरवर्षी नव्या वर्षाच्या शुभेच्छा देणारा – ……………………..
2. प्रीतमला आईसारख्या वाटणाऱ्या – ……………………….
उत्तर:
1. प्रीतम
2. बाई.

कृती 3 : (स्वमत/अभिव्यक्ती)

प्रश्न 1.
‘ते धागे फुलत आमच्यामध्ये नाते विणत राहिले,’ हे विधान स्पष्ट करा.
उत्तर:
प्रीतमकडे पैसे नव्हते. पण बाईंविषयीची आपुलकी, कृतज्ञता व्यक्त करण्याची त्याची इच्छा तीव्र होती. म्हणून त्याने त्याच्याजवळची एकुलती एक खास वस्तू बाईंना भेट म्हणून दिली. बाईंनी तिचा प्रेमाने स्वीकार केला. दोघांच्याही मनातील भावना एकमेकांपर्यंत पोहोचल्या. असे प्रत्येक वेळेला होत गेले. प्रीतम चांगल्या रितीने मॅट्रिक झाला. त्याने एन. डी. ए. मध्ये प्रवेश घेतला. त्याची ही प्रगती बाईंना कळत होती आणि त्यांना आनंद होत होता. तो दरवर्षी शुभेच्छापत्र न चुकता पाठवायचा. त्याच्या भावना त्यांना कळत होत्या. अशा प्रकारे दोघांमधील आपुलकीची भावना घट्ट होत होती, वाढत होती. हा संपूर्ण भाव वर दिलेल्या विधानातून व्यक्त होतो.

उतारा क्र. 5

1. पुढील उतारा वाचून दिलेल्या सूचनांनुसार कृती करा :

कृती 1 : (आकलन)

प्रश्न 1.
कोण ते लिहा:
1. ट्रेनिंग संपवून सेकंड लेफ्टनंट झाला.
2. प्रीतमच्या छातीवर बिल्ला लावला जातो, तेव्हा जोराने टाळ्या वाजवतात.
उत्तर:
1. प्रीतम लुथरा.
2. बाई.

प्रश्न 2.
कोणाला ते लिहा:
1. पासिंग आऊट परेडच्या वेळी विशेष जागी बसवतात.
2. प्रीतमने पुण्याला येण्याचे विशेष निमंत्रण दिले होते.
उत्तर:
1. यशस्वी कॅडेटच्या आईवडिलांना.
2. बाईंना.

प्रश्न 3.
आकृती पूर्ण करा:

उत्तर:

कृती 2 : (आकलन)

प्रश्न 1.
आकृती पूर्ण करा:

उत्तर:

प्रश्न 2.
पुढील प्रसंगांतील भाव लिहा:

उत्तर:

प्रश्न 3.
का ते सांगा:

1. प्रीतमच्या सासुरवाडीच्या लोकांनी आईसाठी दिलेली साडी त्याने बाईंना दिली.
2. प्रीतम म्हणाला, “या बाई माझ्या एकुलत्या एक कुटुंबीय.”
3. प्रीतम म्हणाला, “केव्हाही मुलगा म्हणून हाक मारा, धावत येईन.”

उत्तर:

1. प्रीतम बाईंना आईच मानत होता.
2. प्रीतमचे एकही नातेवाईक नव्हते, पण बाई परक्या असूनही त्यांनी आईची माया दिली होती.
3. प्रीतमला मुलगा मानून त्यांनी त्याला भावनिक आधार दिला होता.

कृती 3 : (स्वमत/अभिव्यक्ती)

प्रश्न 1.
या उताऱ्यातून जाणवणारा, तुमच्या मते, महत्त्वाचा असलेला भाव स्पष्ट करा.
उत्तर:
स्टेशनवर बाईंना प्रीतमचे देखणे भरदार रूप जाणवते. आपण त्याच्या खांदयाखाली आहोत, हेही त्यांना जाणवते. कोणत्याही आईला आपला मुलगा देखणा, रुबाबदार व्हावा, आपल्यापेक्षा उंच व्हावा, असे वाटते. म्हणूनच प्रीतमला पाहताच बाई आनंदी होतात. आपल्या सर्व अडचणी दूर सारून त्या प्रीतमच्या लग्नाला हजर राहतात. बाई आता त्याच्या शाळेतल्या शिक्षिका राहत नाहीत. त्या मनोमन त्याची आई बनतात.

दुसऱ्या बाजूने पाहिले, तर प्रीतम बाईंचा मुलगा असल्याचे सुख अनुभवत असतो. तो त्यांना आई-बाबांच्या आसनावर बसवतो. “गेल्या जन्मी मी नक्कीच तुमचा मुलगा होतो,” असे म्हणतो. त्या आपल्या एकुलत्या एक कुटुंबीय आहेत, असे पत्नीला सांगतो. एखादया आईने आपल्या मुलाला घडवावे, तसे बाईंनी आपल्याला घडवले असे तो मानतो. आपल्याला मुलगा मिळाला, असे बाईंना वाटते; तर, आपल्याला आई मिळाली, असे प्रीतमला वाटते. दोघांनाही साफल्याचा आनंद मिळतो. आपण कृतार्थ झालो, असे दोघांनाही वाटते. हा भाव दोघांमधील नात्यातून संपूर्ण उताऱ्यात भरून राहिला आहे.

भाषाभ्यास:

(अ) व्याकरण घटकांवर आधारित कृती :

1. समास:

प्रश्न 1.
तक्ता पू+
उत्तर:

2. शब्दसिद्धी:

प्रश्न 1.
चार अभ्यस्त शब्द लिहा.
उत्तर:

1. कामधंदा
2. पाऊसपाणी
3. वारंवार
4. मधेमधे.

(आ) भाषिक घटकांवर आधारित कृती:

1. शब्दसंपत्ती:

प्रश्न 1.
एकवचन लिहा:

1. बांगड्या
2. साड्या
3. धागे
4. टाळ्या.

उत्तर:

1. बांगड्या – बांगडी
2. साड्या – साडी
3. धागे – धागा
4. टाळ्या – टाळी.

प्रश्न 2.
विरुद्धार्थी शब्द लिहा:

1. खाली
2. सुगंध
3. सावकाश
4. नापास.

उत्तर:

1. खाली × वर
2. सुगंध × दुर्गंध
3. सावकाश × जलद
4. नापास × पास.

2. लेखननियम:

प्रश्न 1.
अचूक शब्द निवडा:
उत्तर:
1. दृष्टीक्षेप, दृष्टिक्षेप, द्रुष्टीक्षेप, दृश्टिक्षेप. – दृष्टिक्षेप
2. सरहद्द, सराहद्द, सरहद, सारहद्द. – सरहद्द

3. विरामचिन्हे:

प्रश्न 1.
पुढील वाक्यात योग्य विरामचिन्हे घालून वाक्य पुन्हा लिहा:
तो म्हणाला बाई तुम्ही येणार म्हणून मला खात्री होती
उत्तर:
तो म्हणाला, “बाई, तुम्ही येणार म्हणून मला खात्री होती.”

4. पारिभाषिक शब्द:

प्रश्न 1.
योग्य पर्याय निवडा:
Honorable.
(अ) आदरणीय
(आ) माननीय
(इ) वंदनीय
(ई) प्रार्थनीय.
उत्तर:
माननीय.

प्रीतम Summary in Marathi

प्रस्तावना:

माधुरी शानभाग यांनी विविध प्रकारचे लेखन केले आहे. त्यात विज्ञानकथांचा आवर्जून उल्लेख करावा लागेल. मुलांमध्ये, तरुणांमध्ये विज्ञानाचा प्रसार व्हावा, म्हणून त्यांनी विज्ञानकथा लिहिल्या. प्रस्तुत पाठात प्रीतम नावाच्या मुलाची कथा आली आहे. त्या मुलाला आईवडिलांचे प्रेमळ छत्र लाभले नाही.

त्यातच, त्याला सतत बदलत्या वातावरणात राहावे लागले. याचा त्याच्या मनावर विपरीत परिणाम झाला. मनाचा कोंडमारा झालेल्या स्थितीत तो जगत राहिला. दरम्यान त्याला शाळेतल्या बाई भेटल्या. त्यांनी त्याला वात्सल्याची ऊब दिली. त्यामुळे त्याचे आयुष्य पूर्णपणे बदलले. तो एक कर्तबगार माणूस बनला. समाधानी आयुष्य जगू लागला. या संपूर्ण जीवनप्रवासाचे हृदयस्पर्शी चित्रण या कथेत आले आहे.

शब्दार्थ:

1. रया – तेज.
2. केळवण – लग्न होण्यापूर्वी नियोजित वधूवरांना त्यांचे नातेवाईक देतात ती मेजवानी.
3. दटावणे – दरडावणे, भीती घालणे.
4. टेलिपथी – जिव्हाळ्याच्या दोन व्यक्तींना एकाच वेळी मध्ये कोणतीही संपर्क व्यवस्था नसूनही एकच विचार सुचणे.
5. एकलकोंडा – कोणाशीही न मिसळणारा.
6. घुमा – बाहेरून शांत वाटणारा पण आतून धुसफुसणारा.

वाक्प्रचार व त्यांचे अर्थ:

1. रया जाणे – तेज जाणे, मूळ रुबाब जाणे.
2. खांदे पाडणे – निराश, दीनवाणा होणे.
3. टाकून बोलणे – मनाला दुःख होईल असे अपमानकारक बोलणे.
4. भडाभडा बोलणे – मनात साचलेले संधी मिळताच भराभर बोलून टाकणे.
5. अंग चोरून घेणे – अंग आक्रसून घेणे.

Balbharti Maharashtra State Board Class 9 Marathi Solutions Kumarbharti Chapter 12 महाराष्ट्रावरूनी टाक ओवाळून काया Notes, Textbook Exercise Important Questions and Answers.

Maharashtra State Board Class 9 Marathi Kumarbharti Solutions Chapter 12 महाराष्ट्रावरूनी टाक ओवाळून काया (पोवाडा)

9th Std Marathi Kumarbharati Digest Chapter 12 महाराष्ट्रावरूनी टाक ओवाळून काया Textbook Questions and Answers

1. वैशिष्टचे लिहा.

प्रश्न (अ)

उत्तर:

प्रश्न (आ)

उत्तर:

2. असत्य विधान ओळखा:

प्रश्न 1.
असत्य विधान ओळखा:
1. धुरंधर शिवरायांना स्मरावे.
2. असत्यास्तव शिंग फुकावे.
3. स्वातंत्र्याची आण घ्यावी.
4. जन्मभूमीचे उपकार फेडावे.
उत्तर:
2. असत्यास्तव शिंग फुकावे.

3. कवितेतून व्यक्त झालेली ‘महाराष्ट्राबद्दलची कृतज्ञता’ हा विचार स्पष्ट करा.

प्रश्न 1.
कवितेतून व्यक्त झालेली ‘महाराष्ट्राबद्दलची कृतज्ञता’ हा विचार स्पष्ट करा.
उत्तर:
महाराष्ट्र हे मंदिर आहे. त्याच्या पुढ्यात यशाची ज्योत पाजळते. महाराष्ट्राची धरती सोने पिकवणारी आहे नि वर निळ्या आकाशाची छाया आहे. गडकिल्ले महाराष्ट्रभूमीचे पोवाडे गातात.

रथीमहारथींनी तिला भूषवले आहे. अरबी समुद्र जिच्या चरणांशी लीन आहे. महाराष्ट्र हा धैर्यवंत शासनकर्त्यांचा, साधुसंतांचा, शाहिरांचा, कष्टकरी शेतकऱ्यांचा, त्यागाच्या सामर्थ्याचा व धुरंधर शिवरायांचा आहे. या प्रिय महाराष्ट्रासाठी छातीवर घाव झेलायला व त्यावर जान कुर्बान करायला मी तयार आहे. अशा प्रकारे कवितेतून महाराष्ट्राबद्दलची कृतज्ञता व्यक्त झाली आहे.

4. महाराष्ट्राची बलस्थाने तुमच्या शब्दांत लिहा.

प्रश्न 1.
महाराष्ट्राची बलस्थाने तुमच्या शब्दांत लिहा.
उत्तर:
या महाराष्ट्ररूपी मंदिरात यशाची ज्योती अखंड पाजळते आहे. नील अंबराच्या छायेखाली महाराष्ट्र ही सोने पिकवणारी धरती आहे. हिच्या कर्तृत्वाचे पोवाडे गडकिल्ले गातात. महारथी, शूर पराक्रमी योद्ध्यांनी या भूमीला वैभव प्राप्त करून दिले आहे. ही भूमी धैर्यवान शासनकर्त्यांची, कष्टकऱ्यांची, संतमहंत व शाहिरांची आहे. येथे पराक्रमाला त्यागाचे अस्तर आहे. अरबी समुद्र महाराष्ट्रभूमीच्या चरणांशी लीन आहे. स्वातंत्र्याचे रणशिंग फुकून महाराष्ट्राची मान ताठ ठेवणाऱ्या श्रीछत्रपती शिवरायांच्या प्रेरणेने उज्ज्वल झालेला हा महाराष्ट्र आहे. ही महाराष्ट्राची बलस्थाने आहेत.

5. काव्यसौंदर्य.

प्रश्न (अ)
‘धर ध्वजा करी ऐक्याची मनीषा जी महाराष्ट्राची’ या काव्यपंक्तीतील विचारसौंदर्य लिहा.
उत्तर:
मुंबईसह संयुक्त महाराष्ट्राची चळवळ सुरू झाली, तेव्हा त्याला काहीजणांनी विरोध दर्शवला. खूप साधकबाधक चर्चा झाली. परंतु मराठी मनाने संयुक्त महाराष्ट्र साकार करण्याचा ध्यास घेतला होता. निष्ठेने हे कार्य मराठी माणसे करीत होती. त्यांच्या एकजुटीत फूट पडू नये; म्हणून शाहीर म्हणतात, की ऐक्याचा हा झेंडा हातात घ्या. अशीच अवघ्या महाराष्ट्राची मनोकामना आहे. ती पूर्ण करण्यास कटिबद्ध होऊ या.

प्रश्न (आ)
कवितेतून व्यक्त होणाऱ्या रसाचे तुमच्या शब्दांत सोदाहरण वर्णन करा.
उत्तर:
या कवितेत जागोजागी वीररसाची प्रचीती येते. मराठी मन आंदोलनासाठी जागृत करण्याकरिता कवींनी वीररसाचा मुक्त वापर केला आहे. ‘कंबर बांधून ऊठ घाव झेलाया। महाराष्ट्रावरूनी टाक ओवाळून काया’ या पहिल्या दोन ओळींत शाहिरांनी मर्दमराठी मनाला प्राणार्पणाचे व मर्दुमकीचे आवाहन केले आहे. शिवरायांच्या कर्तृत्वाची ग्वाही दिली आहे. ‘करी कंकण बांधून साचे,’ ‘सत्यास्तव शिंग फुकाया,’ ‘पर्वत उलथून यत्नाचे,’ ‘धर ध्वजा करी ऐक्याची,’ ‘पाऊले टाक हिंमतीची,’ ‘घे आण स्वातंत्र्याची’ अशा प्रकारच्या ओळींमधून ओजगुण ओतप्रोत भरला आहे. मराठी मन पेटून उठेल अशा प्रकारे ही कविता वीररसाने ओतप्रोत भरली आहे.

6. अभिव्यक्ती.

प्रश्न (अ)
तुम्हांला जाणवलेल्या महाराष्ट्रातील अभिमानास्पद बाबींचे वर्णन करा.
उत्तर:
महाराष्ट्र हा दऱ्याखोऱ्यांचा प्रदेश आहे. संतांच्या शिकवणीने पावन झालेली महाराष्ट्रभूमी आहे. इथे पराक्रमाची व त्यागाची गाथा लिहिली गेली. नर्मदा, गोदावरी, कृष्णा, भीमा, वैनगंगा इत्यादी नदयांनी सुपीक केलेली महाराष्ट्राची भूमी आहे. येथे शौर्य व वैराग्य है हातात हात घालून नांदतात. विदयेचा उगम व प्रसार महाराष्ट्रातून आरंभी झाला.

भारताची सांस्कृतिक व ऐतिहासिक जडणघडण महाराष्ट्राने केली. महात्मा गांधी, लोकमान्य टिळक, महात्मा फुले, बाबासाहेब आंबेडकर या थोर विभूतींनी महाराष्ट्राचे वैचारिक वैभव व सामाजिक समता जोपासली. औदयोगिक क्रांती व सामाजिक क्रांतीचे महाराष्ट्र हे माहेरघर आहे. सत्य, शिव, सुंदर या मूल्यत्रयींची जपणूक करणे हे महाराष्ट्राचे ब्रीद आहे.

भाषाभ्यास:

वृत्तांतील लघुगुरूक्रम ठरवण्याचे काही नियम आहेत.

1. ‘पुस्तक’ या शब्दांतील लघुक्रम (-∪∪) असा आहे, कारण ‘पु’ हे अक्षर लघू असले, तरी पुढच्या ‘स्त’ या जोडाक्षराचा आघात मागील लघु स्वरावर येतो. त्यामुळे त्याच्या 2 मात्रा धराव्या लागतात. जर असा आघात येत नसेल, तर जे अक्षर म्हस्व आहे ते न्हस्वच राहते.
2. जोडाक्षरातील शेवटचा वर्णन्हस्व असेल, तर ते जोडाक्षर व्हस्व मानावे.
उदा., भास्कर (-∪∪) दीर्घ असेल, तर दीर्घ उदा., इच्छा (-∪∪).
3. लघु अक्षरावर अनुस्वार येत असेल किंवा त्यानंतर विसर्ग येत असेल तर ते गुरू मानावे.
उदा., नंतर (-∪∪) दुःखी (-∪∪).
4. कवितेच्या चरणातील शेवटचे अक्षर लघू असले तरी दीर्घ उच्चारले जाते. त्यामुळे ते गुरू किंवा दोन मात्रांचे मानतात.

मराठी पदयरचनेत अक्षरवृत्ते, छंदवृत्ते, मात्रावृत्ते किंवा जातिवृत्ते असे तीन प्रकार आढळतात.

Marathi Kumarbharati Textbook Std 9 Answers Chapter 12 महाराष्ट्रावरूनी टाक ओवाळून काया Additional Important Questions and Answers

1. पुढील कवितेच्या आधारे दिलेल्या सूचनांनुसार कृती करा:

कृती 1 : (आकलन)

प्रश्न 1.

उत्तर:

कृती 2 : (आकलन)

प्रश्न 1.
योग्य पर्याय निवडून विधाने पूर्ण करा:
1. हातात ……………….. ध्वजा धर.
(सामंजस्याची/वीरांची/एकजुटीची/ धुरंधराची)
2. मैदानात शिंग ……………. साठी फुकायचे आहे.
(हत्या /सत्या /विदया / असत्या)
3. महाराष्ट्रासाठी लढण्याची स्वातंत्र्याची ……………… घे.
(शपथ / तलवार/कंकण / स्वप्ने)
उत्तर:
1. हातात एकजुटीची ध्वजा धर.
2. मैदानात शिंग सत्यासाठी फुकायचे आहे.
3. महाराष्ट्रासाठी लढण्याची स्वातंत्र्याची शपथ घे.

प्रश्न 2.
चौकटी पूर्ण करा:

1. शिवरायांना म्हटले आहे – [ ]
2. पर्व आले आहे – [ ]
3. शेतकऱ्यांची दोन अवजारे – [ ] व [ ]
4. पर्वत उलथायचे आहेत – [ ]
5. तलवार आहे ती – [ ]

उत्तर:

1. धुरंधर
2. संयुक्त महाराष्ट्राचे
3. खुरपे व दोरी
4. प्रयत्नांचे
5. त्यागाची

कृती 3 : (दोन ओळींचा सरळ अर्थ)

प्रश्न 1.
तो अरबी सागर लागे जयाचे पाया
महाराष्ट्रावरूनी टाक ओवाळून काया
उत्तर:
महाराष्ट्राची महती गाताना शाहीर अण्णा भाऊ साठे म्हणतात – या महाराष्ट्राच्या चरणांना अरबी समुद्र वंदन करतो. त्या प्रिय महाराष्ट्रावर स्वत:चा जीव ओवाळून टाक. समर्पित हो.

1. पुढील कवितेवर दिलेल्या मुद्द्यांच्या आधारे कृती सोडवा:

प्रश्न 1.
कविता-महाराष्ट्रावरूनी टाक ओवाळून काया.
उत्तर:
महाराष्ट्रावरूनी टाक ओवाळून काया
1. प्रस्तुत कवितेचे कवी/कवयित्री → लोकशाहीर अण्णा भाऊ साठे.

2. कवितेचा विषय → या महाराष्ट्र गौरवगीतात शाहिरांनी महाराष्ट्राचा इतिहास, भूगोल, इथले नरवीर, मराठी मनाचा स्वभाव यांची ओजस्वी शब्दांत ओळख करून दिली आहे.

3. कवितेतील दोन शब्दांचे अर्थ →

1. काया = शरीर
2. धरा = धरणी
3. अंबर = आकाश
4. साचे = खरे
5. मनीषा = इच्छा
6. आण = शपथ.

4. कवितेतून मिळणारा संदेश → शिवरायांच्या कर्तृत्वाने गाजलेल्या महाराष्ट्रभूमीला वंदन करणे व तिचे पांग फेडणे, हे कर्तव्य आहे, असा संदेश या कवितेत दिला आहे. महाराष्ट्राच्या गौरवशाली परंपरेचे स्मरण करून मराठी मनाची एकजूट कायम ठेवावी, ही शिकवण दिली आहे.

5. कवितेची भाषिक वैशिष्ट्ये → हे महाराष्ट्राचे गौरवगीत ओजस्वी शब्दकळेत साकार केले आहे. बाहू स्फुरण पावतील, अशी आवाहनात्मक भाषेची वीण आहे. योग्य यमकांचा वापर करून गेयता आणली आहे. ‘या सत्यास्तव मैदानि शिंग फुकाया’ अशा सुभाषितप्रचुर भाषेचा बाज कायम ठेवला आहे. वीरश्रीयुक्त शब्दरचनेतून संपूर्ण कवितेत वीररसाचे दर्शन होते. ‘महाराष्ट्रास्तव लढण्याचे’ आवाहन काळजाला भिडते.

6. कवितेतून व्यक्त होणारा विचार → कर्तृत्ववान इतिहासाची आठवण ठेवून एकजुटीने महाराष्ट्रभूमीचे पांग फेडण्यासाठी जीव कुर्बान करावा हा विचार मांडला आहे.

7. कवितेतील दोन ओळींचा सरळ अर्थ:
महाराष्ट्र मंदिरापुढती। पाजळे याशीची ज्योती ।।
सुवर्णधरा खालती। निल अंबर भरले वरती ।।
→ महाराष्ट्रभूमीचा गौरव करताना शाहीर अण्णा भाऊ साठे म्हणतात की, महाराष्ट्र हे पवित्र मंदिर आहे. या मंदिरापुढे वीरपुरुषांनी बलिदान केलेल्या प्राणांची ज्योत जळत आहे. महाराष्ट्र ही सोन्याची अशी धरती आहे की त्या धरतीवर निळ्या आकाशाचे छत आहे.

8. कविता आवडण्याची वा न आवडण्याची कारणे → महाराष्ट्राचा बलशाली इतिहास, पवित्र भूमी, श्रीशिवरायांची धुरंधर राजनीती, कर्तव्याची जाण, भविष्याची ग्वाही अशी टप्प्याटप्याने उलगडणारी ही कविता आस्वादताना अंगात वीरश्री संचारते. तसेच उपकाराला स्मरून जीव ओवाळून टाकावा, अशी महाराष्ट्रभूमीचे नितांत सुंदर वर्णन असलेली व तेजस्वी शब्दांत आवाहक भावना रुजवणारी ही कविता मला आवडली.

कृतिपत्रिकेतील प्रश्न 2 (इ) साठी…

1. पुढील ओळींचे रसग्रहण तुमच्या शब्दांत करा:

प्रश्न 1.
‘महाराष्ट्र मंदिरापुढती । पाजळे याशीची ज्योती
सुवर्णधरा खालती । निल अंबर भरले वरती
गड पुढे पोवाडे गाती । भूषवी तिला महारथी’
उत्तर:
आशयसौंदर्य: महाराष्ट्र ही कर्तृत्वाची भूमी आहे. तिचे उपकार फेडण्यासाठी जीव कुर्बान करून टाका असे आवाहन शाहीर अण्णा भाऊ साठे यांनी या कवितेत ओजस्वी शब्दांत केले आहे. महाराष्ट्राच्या गौरवशाली परंपरेचे स्मरण व मराठी मनाची दृढ एकजूट . हा आशय प्रत्ययकारी शब्दांत मांडला आहे.

काव्यसौंदर्य: संयुक्त महाराष्ट्राच्या आंदोलनासाठी मराठी मनाला जागृत करताना शाहीर आवाहन करताना म्हणतात – महाराष्ट्रभूमी एक पवित्र मंदिर आहे. या मंदिरापुढे वीरपुरुषांनी आहुती दिलेल्या यज्ञाची ज्योत जळत आहे. महाराष्ट्र ही सोन्याची भूमी व त्यावर निळ्या आकाशाचे छत धरले आहे. म्हणजे ही नररत्नांची खाण आहे व त्यावर तारकांची छाया आहे. सर्व किल्ले महाराष्ट्राच्या यशाचे पोवाडे (स्तुतिगीते) गात आहेत. या भूमीला रथीमहारथी देशभक्तांनी सजवले आहे.

भाषिक वैशिष्ट्ये: संयुक्त महाराष्ट्राच्या चळवळीच्या पार्श्वभूमीवर हे महाराष्ट्राचे गौरवगीत ओजस्वी शब्दकळेत साकार केले आहे. बाहू स्फुरण पावतील, अशी आवाहनात्मक भाषेची वीण आहे. योग्य यमकांचा वापर करून गेयता आणली आहे. ‘या सत्यास्तव मैदानि शिंग फुकाया’ अशा सुभाषितप्रचुर भाषेचा बाज कायम ठेवला आहे. वीरश्रीयुक्त शब्दरचनेतून संपूर्ण कवितेत वीररसाचे दर्शन होते. ‘महाराष्ट्रास्तव लढण्याचे’ आवाहन काळजाला भिडते.

(अ) व्याकरण घटकांवर आधारित कृती:

• वाक्प्रचार / म्हणी:

प्रश्न 1.
पुढील म्हणी पूर्ण करा:
1. थेंबे थेंबे ………………..
2. …………… झोपा केला.
उत्तर:
1. थेंबे थेंबे तळे साचे.
2. बैल गेला नि झोपा केला.

(आ) भाषिक घटकांवर आधारित कृती:

1. शब्दसंपत्ती:

प्रश्न 1.
समानार्थी शब्द लिहा:

1. अंबर
2. ध्वज
3. मंदिर
4. तलवार.

उत्तर:

1. अंबर = आकाश
2. ध्वज = झेंडा
3. मंदिर = देऊळ
4. तलवार = समशेर.

प्रश्न 2.
शब्दांत लपलेले चार अर्थपूर्ण शब्द लिहा:
1. महाराष्ट्र
2. शासनकर्ता.
उत्तर:
1. महाराष्ट्र – महा, हारा, राष्ट्र, राम.
2. शासनकर्ता – शान, सन, कर्ता, नस.

2. लेखननियम:

प्रश्न 1.
अचूक शब्द निवडा:
1. संयूक्त, सयुंक्त, संयुक्त, संयुत्क.
2. जन्मभूमि, जम्नभूमी, जन्मभूमी, जन्मभुमी.
उत्तर:
1. संयुक्त
2. जन्मभूमी.

3. पारिभाषिक शब्द:

प्रश्न 1.
पुढील इंग्रजी पारिभाषिक शब्दांना मराठी प्रतिशब्द दया:

1. Bio-data
2. Event
3. Registered Letter
4. Dismiss.

उत्तर:

1. स्व-परिचय
2. घटना
3. नोंदणीकृत पत्र
4. बडतर्फ.

महाराष्ट्रावरूनी टाक ओवाळून काया Summary in Marathi

कवितेचा आशय:

संयुक्त महाराष्ट्राच्या चळवळीच्या वेळी मराठी मनाला जागृत करण्यासाठी अण्णा भाऊ साठे या लोकशाहिरांनी महाराष्ट्राची थोरवी सांगणारे हे गीत (कवन) लिहिले. त्यांनी ओघवत्या लोकभाषेतून महाराष्ट्राचा गौरव केला आहे.

शब्दार्थ:

1. काया – शरीर.
2. घाव – प्रहार.
3. मंदिर – देऊळ.
4. पुढती – पुढे.
5. पाजळे – जळते, तेवते.
6. याशीची – यशाची किंवा यज्ञाची.
7. सुवर्ण – सोने.
8. धरा – धरणी, धरती, जमीन.
9. निल – निळे.
10. अंबर – आकाश.
11. गड – किल्ले.
12. भूषवी – भूषवतात, मढवतात, सजवतात.
13. महारथी – थोर देशभक्त.
14. सागर – समुद्र.
15. जयाचे – ज्याच्या.
16. पाया – पायाला, चरणांना.
17. मायभूमि – मातृभूमी.
18. धीरांची – शूर धैर्यवंतांची.
19. शासनकर्ते – राज्यकर्ते.
20. श्रमाची – कष्टाची.
21. त्याग – नि:स्वार्थीपणे सर्व सोडून देणे.
22. स्मरून – आठवण करून.
23. धुरंधर – कुशल, तरबेज, प्रमुख.
24. पातले – आले.
25. कंकण – कडे, बांगडी.
26. साचे – खरे.
27. पर्वत – मोठे डोंगर.
28. उलथून – उचलून टाकणे.
29. यत्न – प्रयत्न.
30. सांधू – जोडू.
31. खंड – तुकडे.
32. सत्यास्तव – खरेपणासाठी.
33. ध्वजा – झेंड्याला.
34. करी – हातात.
35. ऐक्याची – एकजुटीची.
36. मनीषा – इच्छा.
37. हिंमत – धैर्य, जिद्द.
38. कणखर – मजबूत.
39. पोलाद – लोखंड.
40. आण – शपथ.
41. जाया – जाण्यासाठी.

टिपा:

1. पोवाडा – वीररसयुक्त शाहिरी कवन (काव्य).
2. अरबी सागर – भारताच्या पश्चिम किनारपट्टीलगत असलेल्या समुद्राचे नाव.
3. खुरपे – तण उपटण्यासाठीचे शेतकऱ्यांचे अवजार.
4. दोरी – (1) पेरणी-लावणीच्या वेळी शेतकरी कमरेला दोरी बांधतात. (2) मोटेचे पाणी काढण्यासाठी मोटेला बांधलेला दोरखंड.
5. शाहीर – वीररसयुक्त पोवाडे व शृंगाररसात्मक लावणी लिहिणारे व सादर करणारे कवी – गायक.
6. पर्व – विशिष्ट कालखंड.
7. संयुक्त महाराष्ट्र – मुंबईसह संयुक्त महाराष्ट्र होण्यासाठी मराठी माणसांनी घडवलेली चळवळ.
8. शिंग – रानरेड्याच्या (गवा) शिंगापासून बनवलेले वायुवादय – रणशिंग (तुतारी).

वाक्प्रचार व त्यांचे अर्थ:

1. काया ओवाळून टाकणे – जीव कुर्बान करणे.
2. स्वप्न साकार करणे – स्वप्न प्रत्यक्षात आणणे, मनात असलेले कार्य तडीस नेणे.
3. कंबर बांधणे (कसणे) – दृढ निश्चय करणे.
4. करी कंकण बांधणे – प्रतिज्ञा करणे, शपथ घेणे.
5. शिंग फुकणे – लढा देण्यास सुरुवात करणे.
6. आण घेणे – शपथ घेणे.
7. उपकार फेडणे – कृतज्ञतेने उपकारांची परतफेड करणे.

कवितेचा भावार्थ:

संयुक्त महाराष्ट्राच्या आंदोलनासाठी मराठी मनाला जागृत करताना शाहीर म्हणतात –
कंबर कसून तयार हो, दृढ निश्चय करून घाव झेलायला ऊठ. या प्रिय महाराष्ट्रासाठी जीव कुर्बान कर. ।।

या महाराष्ट्ररूपी मंदिरापुढे यज्ञाची (यशाची) ज्योत जळत आहे. सोन्याची (नररत्नांची खाण व कसदार) धरणी खाली नि वर निळे आकाश भरले आहे. सर्व किल्ले यशाचे पोवाडे गात आहेत. या भूमीला रथीमहारथी देशभक्तांनी सजवले आहे. या महाराष्ट्रभूमीच्या चरणांशी अरबी समुद्र वंदन करतो आहे, त्या प्रिय महाराष्ट्रासाठी प्राण
ओवाळून टाक.।।

ही माझी मातृभूमी धैर्यवंतांची आहे. वीर राज्यकर्त्यांची आहे. घाम गाळून कष्टाने हिचे आपण रक्षण केले आहे. ही शेतकऱ्यांच्या खुरप्यांची व दोरीची भूमी आहे. ही संतांची, शाहिरांची भूमी आहे. इथे त्यागरूपी तलवार फिरून राखलेली भूमी आहे. ज्या भूमीवर श्रीछत्रपती शिवाजी महाराजांनी अधिराज्य निर्माण केले त्या धुरंधर वीर शिवरायांचे कर्तृत्व आठवून या प्रिय महाराष्ट्रासाठी प्राणांची आहुती दे.।।

संयुक्त महाराष्ट्राचे पर्व आज सुरू झाले आहे. संयुक्त महाराष्ट्राचे स्वप्न साकार करण्यासाठी आम्ही हातात कंकण बांधून (घोर प्रतिज्ञा करून) खरोखर सज्ज झालो आहोत. प्रयत्नांचे पर्वत उलथून, प्रयत्नांची पराकाष्ठा करून आपण महाराष्ट्राचे खंड जोडून तो एकसंध, अखंड राखूया. या सत्यासाठी मैदानात संग्रामाला सुरुवात करण्यासाठी रणशिंग फुकले आहे. या महाराष्ट्रावर कुरवंडी ओवाळून टाकू.।।

महाराष्ट्राच्या इच्छेसाठी हातात एकजुटीचा झेंडा घे. हिमतीने, जिद्दीने पोलादासारखी मजबूत पावले टाक. महाराष्ट्रासाठी लढा करण्याची स्वातंत्र्याची शपथ घे. या जन्मभूमीचे उपकार फेडण्यासाठी सिद्ध हो. या प्रिय महाराष्ट्रासाठी तिच्यावर आपली काया ओवाळून टाक. बलिदान दे.