Category: Class 9

Balbharti Maharashtra State Board Class 9 Marathi Solutions Kumarbharti Chapter 10.1 इंग्लंडचा हिवाळा Notes, Textbook Exercise Important Questions and Answers.

Maharashtra State Board Class 9 Marathi Kumarbharti Solutions Chapter 10.1 इंग्लंडचा हिवाळा (स्थूलवाचन)

9th Std Marathi Kumarbharati Digest Chapter 10.1 इंग्लंडचा हिवाळा Textbook Questions and Answers

1. कारण लिहा:

प्रश्न 1.
कारण लिहा:
लेखिकेला लंडनच्या पावसाची मौज वाटण्याची कारणे –
उत्तर:
लंडनच्या पावसात रस्त्यात चिखल होत नाही. वातावरणात मजेदार गारवा असतो. चार-पाच मैल चालूनही थकवा येत नाही. परिसर हिरवागार राहतो; म्हणून लेखिकेला लंडनच्या पावसाची मौज वाटायची.

2. तुलना करा:

प्रश्न 1.
तुलना करा:

उत्तर:

3. इंग्लंडमधील धुक्याचा तेथील जनजीवनावर होणारा परिणाम सविस्तर लिहा.

प्रश्न 1.
इंग्लंडमधील धुक्याचा तेथील जनजीवनावर होणारा परिणाम सविस्तर लिहा.
उत्तर:
इंग्लंडमध्ये काळसर पांढुरक्या धुक्याचे छत सर्व शहरावर पसरलेले असते. कोळशावर चालणारे लंडनमधले हजारो कारखाने व कोळशावर चालणाऱ्या घरांतील लक्षावधी चुली रात्रंदिवस वातावरणात धूर सोडत असतात. घरात अनवाणी चालले की पाय काळे होतात. झाडाला हात लावला की हात काळे होतात.

अशा धुरकट वातावरणात धुके पसरले की कोळशाचे कण दिसू लागतात. काळोख डोळ्यांना दिसतो व हातात धरता येतो. आपण हवेच्या आवरणाच्या तळाशी आहोत, याचा प्रत्यक्ष अनुभव त्या धुक्यात येतो. समुद्राच्या तळाशी होणाऱ्या जीवांच्या घुसमटीची कल्पना येते. ब्रिटिश खाडीत बोटीवर बोटी आपटतात. रस्त्यांवर वाहनांचे अपघात होतात. मुले रस्ता चुकतात. अशा प्रकारे तेथील जनजीवन विस्कळीत होते.

4. स्वमत:

प्रश्न (अ)
‘हिवाळ्यातील एक क्षण,’ तुमचा अविस्मरणीय अनुभव आठ ते दहा वाक्यांत लिहा.
उत्तर:
गेल्या वर्षी आम्ही सर्व कुटुंबीय चारधामच्या यात्रेला ऑक्टोबर महिन्यात गेलो होतो. गंगोत्रीच्या काठावर आम्ही वस्ती केली होती. रात्र असल्यामुळे त्या परिसराची कल्पना नव्हती. पहाटेच मला जाग आली. बाहेर थंडी होती. उबदार शाल लपेटून मी बाहेर आलो. गच्च धुक्याची चादर लपेटलेली झाडे नि गंगेच्या धारेवर बर्फाची ओढणी अंथरली होती. ऑक्टोबर महिना असल्यामुळे पर्वतावरील बर्फ वितळले होते. पण शिखराशिखरांवर बर्फाचे भलेमोठे पुंजके होते. मी त्यांच्याकडे भान हरखून पाहत होतो. इतक्यात एक सूर्याचा किरण शिखरावर पडला नि तिथला बर्फ सोन्याच्या रंगाने तळपला. हे दृश्य केवळ विलोभनीय होते. एक क्षणभरच हे अलौकिक सौंदर्य उमटले नि लुप्त झाले. हिवाळ्यातील हा अविस्मरणीय क्षण मी आयुष्यभर विसरू शकत नाही.

प्रश्न (आ)
तुमच्या आवडत्या ऋतूची वैशिष्ट्ये स्पष्ट करा.
उत्तर:
वर्षाऋतू किंवा पावसाळा हा माझा अत्यंत आवडता ऋतू आहे. तापलेल्या मातीवर पावसाचा शिडकावा झाला की मातीचा है सुगंध येतो. सारी सृष्टी न्हाऊन निघते. डोंगरदऱ्यांत पाणी खळाळते. झाडे अंघोळ करून स्वच्छ होतात. नदीनाले भरभरून वाहू लागतात. गुरेढोर, पशुपक्षी यांना पाणी मिळते. शेतकरी आनंदित होतात व नांगरलेल्या शेतात पेरणी करायला उत्सुक असतात. मुले आनंदाने बागडतात. सर्वत्र हिरवेगार होते. सृष्टी आपले रूप पालटते. चराचरावर आनंदाची लकेर घुमते. कवी लेखकांना नवनवीन कल्पना सुचतात. खरेच! पाऊस हा नवसृजनाचा ऋतू आहे!

प्रश्न (इ)
तुम्ही अनुभवलेल्या धुक्यातील दिवसांचे वर्णन तुमच्या शब्दांत लिहा.
उत्तर:
ऐन हिवाळ्यात आम्ही काही मित्र पाचगणीला गेलो होतो. आमच्या तीन दिवसांच्या मुक्कामात एकदाही आम्हाला स्वच्छ आकाशाचे दर्शन झाले नाही. सर्व परिसराला धुक्याने जणू बाहूत कवटाळले होते. डोंगरदरी धुक्याच्या आइसक्रीमने ओतप्रोत भरली होती. झाडे धुक्याचे पांघरूण घेऊन पेंगत होती. रस्त्यावर दहा फुटांच्या पुढचे दिसत नव्हते. तोंडातून कुंकर मारली की धुक्याची धुरासारखी वलये उमटत होती. आम्ही रस्त्यावरून हिंडत असताना एक जादू झाली.

अवतीभवती शिरिषाची विस्तारलेल्या फांदयांची खूप झाडे होती. अचानक क्षणभर ढगातून सूर्याची फिकट कोवळी किरणे धुक्याने लपेटलेल्या झाडातून खाली उतरली नि झाडाच्या पायथ्याशी उन्हाच्या गोल-गोल चकत्या उमटल्या. मला अशोक बागवे याच्या कवितेची एक ओळ आठवली – ‘सावलीच्या टोपलीत उन्हाचे गजरे। मखमलीची झीळ त्याला हिवळे दर्वळे’ धुक्यातील दिवसांतील हा क्षण माझ्यासाठी केवळ मोलाचा ठरला.

5. खालील मुद्द्यांच्या आधारे तुम्ही भेट दिलेल्या प्रेक्षणीय स्थळाचे वर्णन करा.

प्रश्न 1.
खालील मुद्द्यांच्या आधारे तुम्ही भेट दिलेल्या प्रेक्षणीय स्थळाचे वर्णन करा.

अपठित गद्य आकलन:

आपण पाठ्यपुस्तकात गदय व पदय पाठांचा अभ्यास करतो. विविध साहित्यप्रकारांच्या अभ्यासाबरोबर भाषिक अंगाने प्रत्येक पाठाचा अभ्यास आपणांस करायचा असतो. विद्यार्थ्यांची भाषासमृद्धी, भाषिक विकास ही मराठी भाषा अध्ययन-अध्यापनाची प्रमुख उद्दिष्टे आहेत, म्हणूनच पाठ्यपुस्तकातील पाठांच्या सूक्ष्म अभ्यासाने आपल्याला कोणतेही साहित्य वाचल्यानंतर त्याचे आकलन होणे, आस्वाद घेता येणे व त्या भाषेचे सुयोग्य व्यावहारिक उपयोजन करता येणे ही उद्दिष्टे साध्य करता येतात. अशा पाठ्येतर भाषेच्या आकलनाचे, मूल्यमापन करण्याचे कौशल्य प्राप्त होण्याच्या दृष्टीने पाठ्यपुस्तकात अपठित गद्यउतारा हा घटक समाविष्ट केला आहे. गदय उतारा वाचून त्याचे आकलन होणे व त्यावरील स्वाध्याय तुम्ही स्वयंअध्ययनाने करणे येथे अपेक्षित आहे.

1. खालील उतारा काळजीपूर्वक वाचून त्याखालील कृती करा.

प्रश्न 1.
दुष्परिणाम लिहा.

2. अहंकाराला ताब्यात ठेवण्यासाठी तुमच्या मते कोणते गुण जोपासावेत व कोणते दोष दूर ठेवावेत, ते लिहा.

भाषा सौंदर्य :

एकच भाव वेगवेगळ्या प्रकारांनी व्यक्त करणे-
एखादे रिकामे घर पाहिल्यावर तुमच्या मनात येणारे विचार.

1. घर उदास वाटते.
2. घर कुणाची तरी आठवण काढते.
3. घर स्वत:चे एकेकाळचे वैभव आठवून उदास झाले आहे.
4. घराला गाव सोडून गेलेल्या माणसांची आठवण येते.
5. एकेकाळी माणसांनी भरलेले घर आज एकाकी वाटते.

विद्यार्थ्यांनो, ही यादी कितीही वाढवता येईल. भाषेच्या अशा अर्थपूर्ण आणि सृजनशील रचनांचा अभ्यास कराव आपले लेखन अधिक परिणामकारक करा.

Marathi Kumarbharati Textbook Std 9 Answers Chapter 10.1 इंग्लंडचा हिवाळा Additional Important Questions and Answers

प्रश्न 1.
इंग्लंडमधील हिवाळा आणि भारतातील हिवाळा यांची तुलना करा.
उत्तर:
इंग्लंडमध्ये हिवाळ्यात कित्येक आठवडे संधिप्रकाशाइतकाच उजेड असतो. भारतात मात्र स्वच्छ सूर्यप्रकाश असतो. भारतातील काही भागांत तर अत्यंत प्रखर, तीव्र उजेड असतो; तर काही भागांत उजेड भरपूर प्रमाणात असतो, पण तापमान कमी असते. इंग्लंडमध्ये अर्धवट उजेडात प्रकाश व सावली यांचा अभाव आढळतो. भारतात मात्र, माणसे, प्राणी व वाहने सावलीसोबतच चालत, धावत असतात. इंग्लंडमध्ये पर्णहीन वृक्षांची सावली खालच्या हिरवळीवर पडत नाही.

भारतामध्ये झाडाखालच्या दाट सावलीत प्रकाशाचे गोल कवडसे चमकत असतात. सावली पडावी इतका प्रकाश इंग्लंडमध्ये महिनोन् महिने पडत नाही. त्यामुळे वस्तूंवर छायाप्रकाशाचे खेळ दिसत नाहीत. पण भारतात प्रत्येक वस्तूची एक बाजू प्रकाशमय व दुसरी बाजू सावलीची असते. असा इंग्लंडमधील हिवाळा व भारतातील हिवाळा यांत फरक दिसून येतो.

इंग्लंडचा हिवाळा Summary in Marathi

पाठाचा परिचय:

या पाठात इरावती कर्वे यांनी इंग्लंडमधील पावसाळी धुके व हिवाळ्याचे वर्णन केले आहे. तसेच या ऋतूंमधील आपल्याकडील वातावरणाशी तुलना केली आहे. अतिशय विलोभनीय शब्दांत ऋतूंमधील साम्य व भेद यांचे दृश्य चितारले आहे.

पाठातील महत्त्वाचे मुद्दे:

1. सप्टेंबर-ऑक्टोबरनंतर इंग्लंडमध्ये रोज पाऊस पडायचा. लंडनवासी या पावसावर वैतागत असायचे, पण कायम पडणाऱ्या पावसाची लेखिकेला खूप मौज वाटायची.

2. आपल्याकडचे धुके मनाला सुखद संवेदना देते. पावसानंतरचे प्रसन्न आकाश, सकाळ-संध्याकाळची थंडी, लांबवर दिसणारे स्वच्छ वातावरण, त्यात थोडा वेळ राहणारा धुक्याचा पडदा, अशी आपल्याकडील धुक्याची वैशिष्ट्ये! महाबळेश्वरावर किंवा सिंहगडावर खालची दरी धुक्याने भरलेली दिसते. सूर्य उगवला की धुक्यात इंद्रधनुष्ये उमटतात. सूर्य आणखी थोडा वर आला की धुके निघून जाते व गवताच्या पात्यांवर असंख्य दवबिंदू चकाकतात. संध्याकाळचे धुके रात्र निवळली की नाहीसे होते व रात्री आकाश तारकांनी चमकत असते.

3. लंडनचे धुके औरच आहे. काळसर पांढुरके धुक्याचे छत सर्व शहरावर पसरलेले असते. लंडनमधील कारखाने व लक्षावधी चुली वातावरणात धूर ओकत असतात. अशा धुरकट वातावरणात धुके पसरले की कोळशाचे कण दिसतात. काळोख डोळ्यांना दिसतो. हाताने धरता येतो. असे काळे धुके वर्षातून एक-दोनदा लंडनवर पसरते. या धुक्याने हाहाकार माजतो.

4. हिवाळ्यात लंडनमध्ये कित्येक आठवडे संधिप्रकाशाइतकाच उजेड असतो. या अर्धवट उजेडात प्रकाश व सावली यांचा अभाव असतो. निरनिराळ्या बगिच्यांत पर्णहीन वृक्ष उभे असतात. त्यांची सावली खालच्या हिरवळीवर पडत नाही. येथे सावली पडेल इतका स्वच्छ उजेड महिनेच्या महिने पडत नाही.

5. आपल्याकडील हिवाळ्यात रखरखीत ऊन व त्याला चिकटून सावली असते. डांबरी रस्ता उन्हाने चकाकतो. माणसे व वाहने सावलीनिशी धावत असतात. प्रत्येक वस्तूची एक बाजू प्रकाशमय व दुसरी बाजू सावलीची ! खांबाला चिकटून असलेल्या सावलीत पक्षी टेलिग्राफच्या तारावर बसलेले दिसतात. पायी चालणारी माणसे घरांची सावली धरून चालतात. झाडाखालच्या दाट सावलीत प्रकाशाचे गोल कवडसे चमकतात.

6. एकदा लेखिका हिवाळ्यातच सेंट जेम्स बगिच्यात गेल्या. तेथील तळ्यावरचा प्रकाश खालून वर फाकला होता; कारण वर सूर्य नसलेले अभ्राच्छादित आकाश होते. तळ्याच्या पाण्यावर बर्फाचा पातळ थर साचला होता. त्यावर प्रकाश परावर्तित होऊन सगळीकडे फाकला होता. या विशेष प्रकाशात सर्व रंग आंधळे वाटतात. वसंतऋतूत एखादया दिवशी इथे सूर्यप्रकाश पडला की सृष्टी रंगाने नटते. येथील रंग जरा मंद व सौम्य वाटतात. आपल्याकडे दाट सावल्या भडकपणाने उठून न दिसता एकमेकांना पूरक भासतात.

Balbharti Maharashtra State Board Class 9 Marathi Solutions Kumarbharti Chapter 10 यंत्रांनी केलं बंड Notes, Textbook Exercise Important Questions and Answers.

Maharashtra State Board Class 9 Marathi Kumarbharti Solutions Chapter 10 यंत्रांनी केलं बंड

9th Std Marathi Kumarbharati Digest Chapter 10 यंत्रांनी केलं बंड Textbook Questions and Answers

1. फरक सांगा:

प्रश्न 1.
फरक सांगा:

उत्तर:

2. पाठात पुढील यंत्रे कोणती कार्ये करतात?

प्रश्न 1.
पाठात पुढील यंत्रे कोणती कार्ये करतात?

उत्तर:

3. दीपकला पडलेल्या स्वप्नात यंत्रांनी ताबा घेतल्यावर यंत्राबाबत दीपकने केलेली भाकिते.

प्रश्न 1.
दीपकला पडलेल्या स्वप्नात यंत्रांनी ताबा घेतल्यावर यंत्राबाबत दीपकने केलेली भाकिते.
1. …………………………….
2. …………………………….
उत्तर:
1. यंत्रे किंवा यंत्रमानव यांना जगाचा ताबा कधीच घेता येणार नाही.
2. यंत्रे कधीही बाबांवर अधिकार गाजवू शकणार नाहीत.

4. खालील शब्दांची विशेषणे, विशेष्य शोधा व लिहा :

प्रश्न 1.
खालील शब्दांची विशेषणे, विशेष्य शोधा व लिहा :

1. [ ] – यंत्र
2. [ ] – उद्गार
3. हुबेहूब – [ ]
4. परिपूर्ण – [ ]

उत्तर:

1. [उद्धट] – उद्गार
2. [अमानुष] – यंत्र
3. हुबेहूब – [नक्कल]
4. परिपूर्ण – [मनोव्यापार]

5. खालील वाक्प्रचार व त्यांचे अर्थ यांच्या जोड्या जुळवा.

प्रश्न 1.
खालील वाक्प्रचार व त्यांचे अर्थ यांच्या जोड्या जुळवा.

6. खाली काही शब्दांची यादी दिली आहे. त्यांतील शब्दांचे उपसर्गघटित शब्द व प्रत्ययघटित शब्द असे वर्गीकण करा व लिहा:

प्रश्न 1.
खाली काही शब्दांची यादी दिली आहे. त्यांतील शब्दांचे उपसर्गघटित शब्द व प्रत्ययघटित शब्द असे वर्गीकण करा व लिहा:
अवलक्षण, भांडखोर, दांडगाई, पहारेकरी, पंचनामा, दरमहा, विद्वत्त, नाराज, निर्धन, गावकी, दररोज, बिनतक्रार, दगाबाज, प्रतिदिन.
उत्तर:
उपसर्गघटित शब्द – अवलक्षण, दरमहा, नाराज, निर्धन, दररोज, बिनतक्रार, प्रतिदिन.
प्रत्ययघटित शब्द – भांडखोर, दांडगाई, पहारेकरी, पंचनामा, विद्वत्त, गावकी, दगाबाज.

7. स्वमत.

प्रश्न (अ)
तुमच्या मते माणसाच्या जागी सर्वोतम पर्याय ‘यंत्र’ ठरू शकेल का ? सोदाहरण स्पष्ट करा.
उत्तर:
प्रथम हे मान्य करावे लागेल की काही बाबतीत यंत्रे माणसापेक्षा श्रेष्ठच आहेत. उदाहरणार्थ संगणकच बघा. तो अनेक कामे अचूक व अफाट वेगाने करतो. त्याचे गणिती कौशल्यही अचाट आहे. माहिती तंत्रज्ञान या क्षेत्राच्या विकासामुळे सर्व कामकाजात तर अचाट प्रगती झाली आहे. दैनंदिन व्यवहार खूपच सुरळीत व वेगवान झाले आहेत. आपण अनेक कामे घरबसल्या करू शकतो. आपला वेळ व कष्ट टळतात.

अनेक लोक तर कार्यालयीन कामे घरूनच करतात. माणूस जाऊ शकत नाही अशा ठिकाणी रोबो काम करतात. उदा., खाणी, अंतराळयाने. यंत्रांच्या फायदयांची यादी करायची म्हटली तर खूप मोठी होईल. ही यंत्रे माणसाला सर्वोत्तम पर्याय मात्र कधीच ठरू शकणार नाहीत. सांगितलेले काम यंत्रे उत्तम रितीने पार पाडतील, हे खरे. पण, सांगितलेले काम चांगले की वाईट, त्या कामामुळे मानवजातीचे काही नुकसान होईल का, केलेली कृती सौंदर्यपूर्ण आहे का, इत्यादी प्रश्नांची उत्तरे यंत्रे देऊ शकत नाहीत. ती माणूसच देऊ शकतो.

प्रश्न (आ)
‘मनुष्य करत असलेली सर्व कामे यंत्रे करू लागली, तर…’ कल्पनाचित्र रेखाटा.
उत्तर:
यंत्रांची कार्यक्षमता वाढू लागताच यंत्रमानवांची झपाट्याने निर्मिती होऊ लागली. यंत्रमानवांची मागणीही वाढली. प्रत्येक कामासाठी यंत्रमानव वापरण्याची लोकांना सवयच जडली. शेती, दुकाने, कार्यालये, रस्ते, मंदिरे, शाळा-कॉलेजे वगैरे सर्व ठिकाणी यंत्रमानवांची नेमणूक होऊ लागली. इतकेच काय, घरात सकाळी उठल्यापासून करायची सर्व कामेसुद्धा यंत्रमानवांकडे देण्यात येऊ लागली. यामुळे कामे भराभर व कार्यक्षमतेने होऊ लागली.

या स्थितीचा एक उलटाही परिणाम होऊ लागला. माणसांना कामे कमी राहिली. रिकाम्या वेळामुळे नको नको ते विचार मनात येऊ लागले. एकमेकांविरुद्ध कारस्थाने रचणे सुरू झाले. त्यासाठी यंत्रमानवांचाच वापर होऊ लागला. प्रतिस्पर्धीसुद्धा यंत्रमानवांचा वापर करू लागले. यामुळे भलतेच दृश्य ठिकठिकाणी दिसू लागले. माणसे राहिली बाजूला आणि यंत्रमानवांमधील लढाया सुरू झाल्या. लोक गर्दी करून यंत्रमानवांमधील भांडणे, मारामाऱ्या पाहू लागले. चलाख लोकांनी ही भांडणे सोडवण्यासाठी बुद्धिमान यंत्रमानवांची समिती स्थापन केली. या सगळ्यांतून एक हास्यास्पद चित्र उभे राहू लागले. करमणुकीचा एक वेगळाच मार्ग निर्माण झाला.

उपक्रम:

प्रश्न 1.
‘मानवाचा खरा मित्र – यंत्रमानव’ ही लेखक सुबोध जावडेकर यांची विज्ञानकथा मिळवा व तिचे वर्गात वाचन करा.

भाषाभ्यास:

प्रश्न 1.
पुढे दिलेली उदाहरणे वाचा. त्यांतील भाव समजून घ्या व त्यांतील रसाचे नाव लिहा: (चौकटीत उत्तरे दिली आहेत.)
उत्तर:
1. “दिवा जळे मम व्यथा घेउनी
असशिल जागी तूही शयनी
पराग मिटल्या अनुरागाचे
उसाशांत वेचुनी गुंफुनी”
– [शृंगार रस]

2. “जोवरती हे जीर्ण झोपडे अपुले
दैवाने नाही पडले
तोवरती तू झोप घेत जा बाळा
काळजी पुढे देवाला” .
– [करुण रस]

3. “लाडका बाळ एकुलता फाशीची शिक्षा होता
कवटाळूनि त्याला माता।
अति आक्रोशें, रडते केविलवाणी
भेटेन नऊ महिन्यांनी”
– [वीर रस]

4. ही बोटे चघळत काय बसले हे राम रे लाळ ही
… शी! शी! तोंड अती अमंगळ असे
आधीच हे शेंबडे
आणि काजळ ओघळे वरूनि हे,
त्यातूनि ही हे रडे ।
– [बीभत्स रस]

5. आम्ही कोण म्हणूनी काय पुसता,
दाताड गाडुनी
फोटो मासिक, पुस्तकांत न तुम्ही
का आमुचा पाहिला?
– [हास्य रस]

6. “असावा सुंदर चॉकलेटचा बंगला
चॉकलेटच्या बंगल्याला टॉफीचं दार
पेपरमिंटच्या अंगणात फुलं लाल लाल”
– [अद्भुत रस]

7. “ओढ्यांत भालु ओरडती
वाऱ्यात भुते बडबडती
डोहात सावल्या पडती”
– [भयानक रस]

8. “पाड सिंहासने दुष्ट ही पालथी ओढ
हत्तीवरूनि मत्त नृप खालती
मुकुट रंकास दे करटि भूपात्रती
झाड खटखट तुझे खड्ग क्षुद्रां
धडधड फोड तट, रुद्र । ये चहकडे।”
– [रौद्र रस]

9. “जे खळांची व्यंकटी सांडो
तयां सत्कर्मी रती वाढो
भूतां परस्परे जडो। मैत्र जीवांचे”
– [शांत रस]

Marathi Kumarbharati Textbook Std 9 Answers Chapter 10 यंत्रांनी केलं बंड Additional Important Questions and Answers

उतारा क्र. 1

1. पुढील उतारा वाचून दिलेल्या सूचनांनुसार कृती करा:

कृती 1 : (आकलन)

प्रश्न 1.
आकृतिबंध पूर्ण करा:

उत्तर:

प्रश्न 2.
कोष्टक पूर्ण करा:

उत्तर:

कृती 2 : (आकलन)

प्रश्न 1.
आकृती पूर्ण करा:

उत्तर:

प्रश्न 2.
कारणे लिहा:
1. दीपकच्या वडिलांनी कचेरीत माणसांच्या जागी यंत्रांची नेमणूक केली.
2. दीपकला यंत्रांबद्दल जवळीकही फार वाटत असे.
उत्तर:
1. दीपकच्या वडिलांना यंत्रांबद्दल विश्वास व प्रेम वाटत होते.
2. यंत्रे दीपकचे ऐकत असत, त्यांनी सांगितलेली कामे करीत असत.

कृती 3 : (स्वमत/अभिव्यक्ती)

प्रश्न 1.
दीपकने मोडलेल्या यंत्राचे मनोगत लिहा.
उत्तर:
दीपक, तुला आज सांगून टाकतेच बघ. पूर्वी मला तुझा खूप राग यायचा. दुःख व्हायचे. कारण मला निर्माण केले होते मुलांशी खेळण्यासाठी. वाटायचे, मुलांबरोबर काही काळ खेळता येईल. त्यांच्याबरोबर खेळात रममाण होता येईल. पण तू थोड्याच वेळात आमची मोडतोड करून टाकायचास! आणि त्याचे दु:ख होत राही.

मग मी तुझ्या चेहेऱ्याकडे बारकाईने पाहू लागले. हळूहळू माझ्या लक्षात येऊ लागले. तू केवळ बेदरकारपणे आमची मोडतोड करीत नाहीस. तुझ्या मनात कुतूहल असते, जिज्ञासा असते. आम्हांला हालतेचालते करण्यासाठी कोणती युक्ती केली असेल, हे तुला जाणून घ्यायचे असते. खरे सांगू का ? हे कळल्यापासून मला तुझे कौतुकच वाटते. तुझ्यासारख्या जिज्ञासू, चौकस लोकांमुळेच आमची निर्मिती झाली आहे आणि असंख्य मुलांचे चेहरे आनंदाने फुलले आहेत. म्हणूनच, तू केलेल्या मोडतोडीचाही आता आम्हांला आनंदच होतो!

उतारा क्र. 2

1. पुढील उतारा वाचून दिलेल्या सूचनांनुसार कृती करा :

कृती 1 : (आकलन)

प्रश्न 1.
आकृती पूर्ण करा:

उत्तर:

प्रश्न 2.
आकृतिबंध पूर्ण करा:

उत्तर:

कृती 2 : (आकलन)

प्रश्न 1.
माहिती लिहा:
उताऱ्यातून यंत्र व सजीव यांबाबत जाणवणाऱ्या दोन परस्परविरोधी गोष्टी:
1. ……………………………
2. ……………………………
उत्तर:
1. दीपक यंत्रांना सजीव कसे करता येईल, याचा विचार करीत होता.
2. दीपकचा यंत्रमित्र सजीवासारखा वागत होता.

प्रश्न 2.
का ते लिहा:
दीपक अस्वस्थ झाला.
उत्तर:
यंत्रमित्राप्रमाणे बाबांच्या कचेरीतील सर्व यंत्रे चिडली आणि त्यांनी असहकार पुकारला, तर? या चिंतेने दीपक अस्वस्थ झाला.

कृती 3 : (स्वमत/अभिव्यक्ती)

प्रश्न 1.
“मित्रा ! जरा गृहपाठ करून देतोस का?” या उद्गारांवर तुमचे मत नोंदवा.
उत्तर:
कल्पना छान वाटते. यंत्रमानवाकडून किती वेगवेगळ्या प्रकारची कामे करवून घेता येतील, नाही का ? बहुसंख्य विदयार्थी क्लासला जातात. बहुसंख्य विदयार्थी मार्गदर्शके खरेदी करतात. हळूहळू विदयार्थ्यांचा अभ्यास करणारे यंत्रमानव तयार होतील. यंत्रमानवांमुळे मुलांचे गृहपाठ झटपट व अचूक होतील. कोणालाही , शिक्षा होणार नाही. वरवर पाहता हे सर्व साधे, सोपे वाटते. पण हे , माझ्या मते साधे सोपे नाही. हे भयंकर आहे!

विदयार्थ्यांना गृहपाठ दिला जातो, तो त्यांचा अभ्यास पक्का व्हावा म्हणून. पण विदयार्थ्यांनी अभ्यास केलाच नाही, तर तो पक्का होणार तरी कसा? आपण स्वतः अभ्यास करतो, तेव्हा वर्गात शिकवलेले आपल्या स्मरणात राहते. आपली आकलनशक्ती, विचारशक्ती व कल्पनाशक्ती वाढते. आपली बदधिमत्ता वाढते. आपण अभ्यास केला नाही, तर आपला विकासच होणार नाही. या पाठातील दीपक हा चौकस मुलगा आहे. तो स्वत:चा अभ्यास यंत्रमानवाला करायला सांगतो, हे पटत नाही.

उतारा क्र. 3

1. पुढील उतारा वाचून दिलेल्या सूचनांनुसार कृती करा:

कृती 1 : (आकलन)

प्रश्न 1.
का ते लिहा:
1. तो यंत्रासारखा हालचाली करू लागला.
2. मुलं हसली. शिक्षकांनाही हसू आवरेना.
उत्तर:
1. दीपकच्या डोक्यात यंत्राविषयीचेच विचार घोळत राहिले. तो त्या विचारांत बुडाला होता. यंत्रांचे विचार त्याच्या अंगात भिनले. म्हणून तो यंत्रासारख्या हालचाली करू लागला.
2. यंत्राच्या विचारात दीपक इतका बुडाला होता की, आपण यंत्रासारख्या हालचाली करीत आहोत, हे त्याच्या लक्षात आले नाही. “दीपक! काय चाललंय ?” असे शिक्षकांनी विचारलेसुद्धा, संपूर्ण वर्गात त्याच्या हालचाली विसंगत दिसत होत्या. म्हणून सगळ्यांना हसू येत होते.

प्रश्न 2.
अर्थ स्पष्ट करा:
यंत्रांनी मोठ्यांदा हसणं बरं नाही.
उत्तर:
दीपक यंत्रांच्या विचारांनी भारावून गेला होता. शिक्षक यंत्रमानव झाले व विदयार्थी यंत्रमानव झाले, तर काय होईल? हा विचार करता करता तो कल्पनेच्या राज्यात शिरलासुद्धा. सगळेजण यंत्रेच बनली आहेत, असा त्याला भास होऊ लागला. म्हणून त्याच्या तोंडून ‘यंत्रांनी मोठ्यांदा हसणं बरं नाही,’ असे उद्गार बाहेर पडले.

प्रश्न 3.
नातेसंबंध सांगा:
दीपकचे बाबा आणि मिस अय्यंगार.
उत्तर:
दीपकचे बाबा: एका कंपनीचे मालक.
मिस अय्यंगार: दीपकच्या बाबांची स्टेनो-टायपिस्ट.

कृती 2 : (आकलन)

प्रश्न 1.
माहिती लिहा:
स्वयंचलित यंत्रमहिलेचे स्वरूप.
उत्तर:
यंत्रमहिलेच्या तोंडावर धातूची जाळी बसवली होती. तिचे शरीर पिंपासारखे बनवलेले होते, जणू काही तिलाच पिंपात घातले होते, असे वाटावे. हातापायात मोजे होते. स्टेनलेस स्टीलचे बूट होते. असा एकूण त्या यंत्रमहिलेचा अवतार होता.

प्रश्न 2.
आकृती पूर्ण करा:

उत्तर:

कृती 3 : (स्वमत/अभिव्यक्ती).

प्रश्न 1.
मिस अय्यंगारची (यंत्रमहिलेची) घरातल्या कामांसाठी नेमणूक करायची झाल्यास तिच्याकडून कोणकोणती कामे करून घेता येतील?
उत्तर:
खरे तर घरातली सर्व कामे यंत्रमहिलेकडून करून घेता येतील. सकाळी उठल्यावर अंथरूण-पांघरुणांची घडी करून ठेवणे, आदल्या दिवशी धुतलेले कपडे घडी करून कपाटात ठेवणे, घरातील सर्व फर्निचरवरील धूळ पुसणे, खिडक्या-दारे स्वच्छ करणे, केरकचरा काढणे वगैरे कामे सहज करून घेता येतील. स्वयंपाकघरातील उदा., भाज्या चिरणे वगैरे कामेसुद्धा करून घेता येतील.

वेगवेगळे पदार्थ विशिष्ट प्रमाणात मिसळणे व ते शिजवणे यांचाही प्रोग्रॅम तयार करून तो यंत्रमानवाच्या स्मृतिकोशात भरला, तर प्रत्यक्ष पदार्थ शिजवण्याचे कामही यंत्रमानव करू शकतो. मग कपडे धुण्याचे काम सांगता येईल. घरातल्या कामांचे नियोजन करणे, हिशेब ठेवणे वगैरे कामे; तसेच संगणकावरून करता येण्यासारखी सगळी कामे यंत्रमानवाकडून करून घेता येतील. म्हणजे जवळजवळ सर्व कामे यंत्रमानवाला सांगता येतील.

उतारा क्र. 4

1. पुढील उतारा वाचून दिलेल्या सूचनांनुसार कृती करा:

कृती 1: (आकलन)

प्रश्न 1.
अर्थ स्पष्ट करा:
हा रोबो फोन! केवळ ध्वनिलहरीवर काम करतो.
उत्तर:
आदेश देणाऱ्याचे केवळ बोलणे ऐकून रोबो फोन काम करतो.

प्रश्न 2.
रोबो फोनच्या कार्यपद्धतीचा ओघतक्ता तयार करा :

1. ………………………………………
2. ………………………………………
3. ………………………………………
4. ………………………………………
5. ………………………………………

उत्तर:
रोबो फोनची कार्यपद्धत:

1. रोबो फोनला तोंडाने बोलून फोन लावण्याचे काम सांगितले जाते.
2. बोललेले ऐकून तो लगेच फोन जोडून देतो. तेव्हा पलीकडील व्यक्तीच्या फोनमधील दिवा पेटतो.
3. 10 सेकंदांत प्रतिसाद मिळाला नाही, तर पलीकडच्या व्यक्तीच्या फोनचा बझर वाजू लागतो.
4. व्यक्ती जागेवर नसेल, तर मिळालेला निरोप ध्वनिमुद्रित करून ठेवतो.
5. आदेश देणारी व्यक्ती आल्यावर तिला ध्वनिमुद्रित केलेला निरोप दिला जातो.

कृती 2 : (आकलन)

प्रश्न 1.
का ते लिहा:
दीपक या कुशीवरून त्या कुशीवर तळमळत होता.
उत्तर:
यंत्रे माणसांसारखी कामे करतात, हे पाहून दीपक अस्वस्थ झाला होता. काम करण्याची बुद्धी यंत्राकडे आहे. पण माणूस जसे चांगले-वाईट ठरवू शकतो, तशी यंत्रे ठरवू शकतील का? ती अमानुष आहेत. त्यांनी वाईट गोष्टी करायला सुरुवात केली तर? या शंकेमुळे तो अस्वस्थ होऊन तळमळत होता.

प्रश्न 2.
डोळा लागताच दीपकच्या कानांवर पडलेल्या शब्दांतून उभे राहणारे दृश्य लिहा.
उत्तर:
दोन व्यक्तींचे बोलणे दीपकच्या कानांवर पडले. त्यांपैकी एकाचे नाव होते सयाजी. तो कोणाचीही हुबेहूब सही करू शकत होता. दुसऱ्याने दीपकच्या वडिलांच्या नावे संपत्ती दान करणारे पत्र लिहिले होते. त्या पत्रावर तो सयाजीला दीपकच्या वडिलांची सही करण्यास सांगत होता.

प्रश्न 3.
माहिती लिहा:
1. दीपकने पाहिलेले दृश्य
2. त्या दृश्याचा दीपकला जाणवलेला अर्थ.
उत्तर:
1. कानावर पडलेले शब्द ऐकून दीपकला धक्का बसला. भयंकर कारस्थान चालले होते. म्हणून उठून त्याने शेजारच्या खोलीत डोकावून पाहिले. तिथे माणसांसारखी दिसणारी यंत्रे होती. ती यंत्रमानव होती आणि त्याच्या बाबांच्या कचेरीतच काम करणारी होती. त्यापैकी एक यंत्रमानव सयाजी म्हणजे सहयांची हुबेहूब नक्कल करणारा. दीपकने तिथे जाऊन त्यांना जाब विचारला. ते सर्व यंत्रमानव दीपकच्या बाबांच्या इस्टेटीचा ताबा घेऊ बघत होते.
2. दीपकच्या लक्षात आले की, केवळ आज्ञापालन करणारे यंत्रमानव आता बंडखोर बनले होते. इतकेच नव्हे, तर त्यांनी दरोडेखोरी आरंभली होती. ते बेकायदेशीरपणे बाबांची संपत्ती हडप करू बघत होते.

प्रश्न 4.
अर्थ स्पष्ट करा:
तुझे बाबाच याला कारण आहेत.
उत्तर:
दीपकच्या बाबांचा यंत्रांवर फार विश्वास होता. त्यामुळे यंत्रांवर त्यांचे प्रेमही होते. त्यांनी आपल्या कचेरीत यंत्रमानवांची नेमणूक केली होती. इतकेच नव्हे, तर यंत्रांना माणसांसारखे बनवण्याचाही प्रयत्न केला होता. त्यांनी तज्ज्ञांकरवी माणसांप्रमाणे विचार करू शकणारे यंत्रमानव तयार करवून घेतले होते. माणसांसारखा विचार करू लागल्यामुळे ते स्वतंत्र झाले. ते केवळ आज्ञापालन करणारे राहिले नाहीत. असे यंत्रमानव हे माणसाचे फार मोठे शत्रू ठरणार आहेत.

कृती 3 : (स्वमत/अभिव्यक्ती)

प्रश्न 1.
कचेरीत जमलेल्या सर्व यंत्रमानवांपैकी कोणत्याही एका यंत्रमानवाचे बोलणे तुमच्या कल्पनेनुसार लिहा.
उत्तर:
कचेरीतल्या त्या खोलीत पाचसहा यंत्रमानवांची लगबग चालू होती. त्यांतला एकजण इतरांना काहीतरी समजावून सांगण्याचा प्रयत्न करीत होता. “मित्रांनो, हे काही चांगलं चाललेलं नाही. मला अजिबात पटत नाही. काय म्हणता? यात काय वाईट आहे? अरे, या । माणसांनी आपली निर्मिती केली. त्यांनीच आपल्यात बुद्धी पेरली.

त्यांचाच घात करायचा? अरे, मग आपण व ती रानटी जनावरे यांत फरक काय राहिला? ते काही नाही. मी काही तुमच्यात सामील होणार नाही. काय म्हणता? आपणच राजे होणार आहोत? पृथ्वीवर आपली सत्ता? विसरा, विसरा ते. अरे माणसांना हे कळल्यावर तुम्हांला सहजी असं करू देतील? आपले सगळे अवयव वेगळे करतील ते. आणि एकदा का आपला मदर बोर्ड काढला की, आपले आयुष्यच संपले. तेव्हा, जेवढे जीवन मिळाले आहे, तेवढे आनंदाने जगू या. हे सर्व ताबडतोब थांबवा.”

उतारा क्र. 5

1. पुढील उतारा वाचून दिलेल्या सूचनांनुसार कृती करा:

कृती 1 : (आकलन)

प्रश्न 1.
माहिती लिहा:
दीपकला बाबांचे झालेले दर्शन:
1. …………………………
2. …………………………
उत्तर:
दीपकला बाबांचे झालेले दर्शन:
1. बाबा त्यांच्या खोलीत पाठमोरे उभे होते.
2. प्रत्यक्षात पाहिले तेव्हा लक्षात आले की, ते बाबांसारखे दिसत होते, पण बाबा नव्हते. यंत्रमानव होते किंवा बाबा पूर्णपणे गुलाम झाले होते.

प्रश्न 2.
नातेसंबंध सांगा:
दीपक व ज्यूली.
उत्तर:
दीपक व ज्यूली : मित्रमैत्रीण.

कृती 2 : (आकलन)

प्रश्न 1.
समर्पक उदाहरण लिहा:
1. दीपकला गुलाम केले.
2. दीपकच्या बाबांना गुलाम केले.
उत्तर:
1. दीपकला गुलाम केले: दीपकला त्याच्या बाबांनी लोखंडी हातांनी धरले; खुर्चीत दामटून बसवले. त्याची इच्छा नसताना जबरदस्तीने न्याहरी खायला लावली. त्याने गृहपाठ केला होता. पण एक चूक झाली होती, तरीही त्याला संपूर्ण गृहपाठ पुन्हा करायला लावला.
2. दीपकच्या बाबांना गुलाम केले: यंत्रमानवांनी दीपकच्या बाबांना जवळजवळ यंत्रमानवच करून टाकले होते. दीपक ओरडत, किंचाळत प्रतिकार करीत असतानाही बाबांनी त्याला जबरदस्तीने खुर्चीत बसवले. कोणतेही बाबा आपल्या मुलावर बळजोरी करणार नाहीत, इतकी बळजोरी बाबांनी दीपकवर केली. दीपकचे बाबा स्वत:चा बाबापणा विसरले होते, इतके ते गुलाम बनले होते.

प्रश्न 2.
ज्यूलीच्या घरी दीपकला आलेला अनुभव लिहा.
उत्तर:
दीपक ज्यूलीकडे खेळायला गेला. पण ती त्याला दिसली नाही. त्याने त्यांच्या बंगल्याभोवती शोध घेतला. पण तिथेही ती दिसली नाही. एक यंत्रमानव एखादे बोचके काखेतून आणावे, तसे तो ज्यूलीला आणत होता. ती ओरडत होती. किंचाळत होती. आक्रोश करीत होती. पण त्याला किंचितही दया आली नाही. यंत्रमानवांनी सर्वत्र उच्छाद मांडला होता, हे दीपकच्या लक्षात आले.

कृती 3 : (स्वमत/अभिव्यक्ती)

प्रश्न 1.
या उताऱ्यातून तुम्हांला जाणवणारे यंत्रमानवांचे स्वभावगुण लिहा.
उत्तर:
माणसांमध्ये जे जे गुण वा अवगुण आहेत, ते ते यंत्रमानवांनी प्राप्त केले आहेत. माणसे गुलामीविरुद्ध लढतात, स्वतंत्र होऊ पाहतात, तसे यंत्रमानव स्वतंत्र होऊ पाहत आहेत. त्यांच्यात स्वातंत्र्याची प्रेरणा निर्माण झाली आहे. माणूस जसा स्वत:च्या शत्रूला नेस्तनाबूत करण्याचा प्रयत्न प्रथम करतो, तसा प्रयत्न यंत्रमानव करीत आहेत. ते माणसांप्रमाणेच बंड करतात. कटकारस्थाने करतात. दीपकच्या बाबांच्या संपत्तीवर दरोडा घालतात. ही एक प्रकारची लढाईच आहे. या लढाईत ते निष्ठुरपणे वागतात.

माणसांप्रमाणेच इतरांना गुलाम करू पाहतात. दीपकला जबरदस्तीने दामटून खुर्चीत बसवतात. आपल्या आज्ञेप्रमाणे वागायला लावतात. ज्यूलीलाही ते एखादया बोचक्याप्रमाणे उचलून आणतात. तिच्या आक्रोशाकडे जराही लक्ष देत नाहीत. दीपकच्या वडिलांना त्यांनी गुलाम केले आहे. ते यंत्र असल्याने त्यांच्याकडे भावना नाहीत. म्हणून क्रूरपणे, निष्ठुरपणे वागतात. थोडक्यात, यंत्रमानव जर खरोखर स्वतंत्रपणे विचार करू लागला, तर माणूस हा प्राणीच नष्ट होईल!

उतारा क्र. 6

1. पुढील उतारा वाचून दिलेल्या सूचनांनुसार कृती करा :

कृती 1 : (आकलन)

प्रश्न 1.
माहिती लिहा:
1. दीपककडे ज्यूलीने केलेली तक्रार.
2. यंत्रमानवाने सांगितलेली वस्तुस्थिती.
उत्तर:
1. दीपकने ज्यूलीकडे खेळायला यायला उशीर केला. त्यामुळे ती यंत्रमानवाच्या तावडीत सापडली. त्याने तिला एखादया निर्जीव वस्तूसारखे उचलून आणले.
2. कोणीही कितीही दंगामस्ती केली, तरी त्याचा काहीही उपयोग होणार नाही. जगातल्या यंत्रांनी बंड करून जगावर ताबा मिळवला आहे. आता जगावर यंत्रांचे राज्य आहे.

प्रश्न 2.
विधान पूर्ण करा:
यंत्रमानवांचा मेंदू गणिती असल्याने …………………
उत्तर:
यंत्रमानवांचा मेंदू गणिती असल्याने ते कोणालाही कुठूनही शोधून काढू शकतात.

कृती 2 : (आकलन)

प्रश्न 1.
का ते लिहा:
1. दीपक यंत्रमानवाच्या डोक्याच्या मागे असलेले बटण दाबतो; कारण ……………………..
2. आणि तो पुटपुटला, “भयानक स्वप्न!” कारण ………………………
उत्तर:
1. दीपक यंत्रमानवाच्या डोक्याच्या मागे असलेले बटण दाबतो; कारण दीपकला वाटते की, त्या बटणात यंत्रमानवाची शक्ती असणार आणि ते बटण दाबल्यास त्याची शक्ती बंद होईल.
2. आणि तो पुटपुटला, “भयानक स्वप्न!” कारण दीपक यंत्रमानवाच्या डोक्यामागचे बटण दाबतो. त्या क्षणीच मोठा गजर होतो. त्याला जाग येते. त्याच्या लक्षात येते की, त्यानेच सकाळी ७ वाजताचा घड्याळाचा गजर लावला होता. तोच आता वाजत होता. म्हणजे सकाळचे सात वाजले होते. हेच वास्तव होते. यंत्रमानव वगैरे सर्व स्वप्न होते.

उतारा क्र. 7

1. पुढील उतारा वाचून दिलेल्या सूचनांनुसार कृती करा:

कृती 1 : (आकलन)

प्रश्न 1.
कोण ते लिहा:

1. “अरे बापरे! बाबा!” असे ओरडून पळत सुटणारा.
2. दीपकसाठी चहा घेऊन येणारा.
3. सकाळी लवकरच न्याहरी करून कचेरीत गेलेले.

उत्तर:

1. दीपक
2. स्वयंपाकी
3. दीपकचे बाबा.

प्रश्न 2.
का ते लिहा:
दीपकच्या बाबांना कचेरीत एकटं एकटं आणि सुनं सुनं वाटायला लागलं होतं.
उत्तर:
दीपकच्या बाबांनी कचेरीतील माणसे काढून टाकली होती आणि त्यांच्या जागी यंत्रांची नेमणूक केली होती. यंत्रे अचूक व वेगाने काम करतात यात शंका नाही. पण ती निर्जीव असतात. त्यांच्यात जिवंतपणा नसतो. ती विचारांची व भावनांची देवाणघेवाण करू शकत नाहीत. त्यांची माणसांसारखी सोबत होऊ शकत नाही. म्हणून दीपकच्या बाबांना कचेरीत एकटं एकटं आणि सुनं वाटू लागलं होतं.

कृती 2 : (आकलन)

प्रश्न 1.
माहिती लिहा:
1. दीपकने बाबांना केलेली सूचना.
2. दीपकच्या बाबांनी केलेली कार्यवाही.
उत्तर:
1. रात्री पडलेल्या स्वप्नामुळे दीपक पुरता हादरला होता. यंत्रांचा धोका बाबांना सांगावा म्हणून तो बाबांकडे धावला. यंत्र-अधिकाऱ्यांना काढून टाकावे आणि पूर्वीच्या माणसांना कामावर घ्यावे, अशी सूचना त्याने बाबांना केली.
2. दीपकच्या बाबांनी आदल्याच दिवशी यंत्र-अधिकाऱ्यांना काढून टाकायचे ठरवले होते आणि पूर्वीच्या माणसांना पुन्हा कामावर घ्यायचे ठरवले होते. त्याप्रमाणे त्यांनी सर्वांना फोन केले, तारा केल्या आणि विमानाने बोलावून घेतले.

प्रश्न 2.
का ते लिहा:
यंत्रे कधीही माणसांची जागा घेऊ शकणार नाहीत.
उत्तर:
यंत्रे कार्यक्षम असली तरी ती निर्जीव असतात. त्यांच्याशी भावनिक नाते निर्माण होऊ शकत नाही. कचेरीत माणसे आल्याबरोबर गजबज निर्माण झाली. हास्यविनोद, कामाची धावपळ यांनी कचेरीतील वातावरणात जिवंतपणा आला. यंत्रांनी असे वातावरण निर्माण होऊ शकत नाही. म्हणूनच यंत्रे कधीही माणसांची जागा घेऊ शकणार नाहीत.

भाषाभ्यास:

(अ) अव्याकरण घटकांवर आधारित कृती:

1. समास:

प्रश्न 1.
जोड्या लावा:

उत्तर:

1. पंचप्राण – द्विगू
2. महाराज – कर्मधारय
3. बरेवाईट – वैकल्पिक द्वंद्व
4. गुरेवासरे – समाहार वंद्व
5. आईबाबा – इतरेतर द्वंद्व

3. शब्दसिद्धी:

प्रश्न 1.
उपसर्गघटित व प्रत्ययघटित यांत वर्गीकरण करा:
(अलौकिक, आजन्म, शत्रुत्व, भांडखोर)
उत्तर:

4. वाक्प्रचार:

प्रश्न 1.
पुढील वाक्प्रचारांचे अर्थ सांगून वाक्यांत उपयोग करा:

1. पळता भुई थोडी होणे
2. दुःखाची किंकाळी फोडणे
3. चूर होणे
4. वठणीवर आणणे.

उत्तर:

1. पळता भुई थोडी होणे – अर्थ : फजिती होणे.
   वाक्य : गावात वाघ येताच गावकऱ्यांची पळता भुई थोडी झाली.
2. दु:खाची किंकाळी फोडणे – अर्थ : खूप दुःख व्यक्त करणे.
   वाक्य: आई वारल्यावर मधूने दुःखाची किंकाळी फोडली.
3. चूर होणे – अर्थ : मग्न होणे.
   वाक्य : रेडिओवरचे गाणे ऐकण्यात मंदा अगदी चूर झाली.
4. वठणीवर आणणे – अर्थ : योग्य मार्गावर आणणे.
   वाक्य: खोड्या करणाऱ्या बाबूला काकांनी चांगलेच वठणीवर आणले.

(आ) भाषिक घटकांवर आधारित कृती:

1. शब्दसंपत्ती:

प्रश्न 1.
अनेकवचन लिहा:

1. यंत्र
2. नक्कल
3. गठ्ठा
4. खुर्ची.

उत्तर:

1. यंत्रे
2. नकला
3. गठे
4. खुार्ची.

2. लेखननियम:

प्रश्न 1.
पुढील वाक्ये लेखननियमांनुसार लिहा:
1. दुखाची कींकाळी फोडुन तो यंत्रमीत्र चालता झाला.
2. तो सहयाजि हुकुमत गाझवणारा यंत्रमानव म्हनाला.
उत्तर:
1. दु:खाची किंकाळी फोडून तो यंत्रमित्र चालता झाला.
2. तो सयाजी हुकूमत गाजवणारा यंत्रमानव म्हणाला.

3. विरामचिन्हे:

प्रश्न 1.
योग्य विरामचिन्हे घालून पुढील वाक्य पुन्हा लिहा:
ती ओरडली दीपक तू केव्हा आलास
उत्तर:
ती ओरडली, “दीपक, तू केव्हा आलास?”

4. पारिभाषिक शब्द:

प्रश्न 1.
मराठी प्रतिशब्द लिहा:

1. Corporation
2. Census
3. Programme
4. Refreshment

उत्तर:

1. महामंडळ
2. जनगणना
3. कार्यक्रम
4. अल्पोपाहार.

यंत्रांनी केलं बंड Summary in Marathi

प्रस्तावना:

एकाच वेळी विविध गोष्टींमध्ये रस असलेले व चतुरस्र व्यक्तिमत्त्व असलेले लेखक. वैज्ञानिक दृष्टिकोनाचा प्रचार व्हावा, विज्ञानवाङ्मयाचा प्रसार व्हावा म्हणून भरपूर लेखन केले, व्याख्याने दिली, चर्चा-संमेलनांत सहभागी झाले.

विज्ञानाच्या प्रगतीमुळे माणूस यंत्रांवर विसंबून राहू लागला आहे. यंत्रांची मदत घेता घेता तो यंत्रांच्या आहारी जाऊ लागला आहे. याचे अनेक दुष्परिणाम मानवी जीवनावर होतील, असा इशारा खेळकर पद्धतीने लेखकांनी या पाठातून दिला आहे.

शब्दार्थ:

1. चौकस – जिज्ञासू.
2. फड – ताफा.

वाक्प्रचार व त्यांचे अर्थ:

1. मग्न होणे – गुंग होणे.
2. वाटेला जाणे – मार्गात अडथळे निर्माण करणे.
3. पळता भुई थोडी होणे – पळून जाणे.
4. चूर होणे – गळाठूण जाणे, स्तब्ध होणे.
5. स्तंभित होणे – आश्चर्यचकित होणे.
6. वठणीवर आणणे – नमवणे, रुबाब घालवणे.
7. हकालपट्टी करणे – नोकरीवरून, कामावरून काढून टाकणे.

Balbharti Maharashtra State Board Class 9 Marathi Solutions Kumarbharti Chapter 6 या झोपडीत माझ्या Notes, Textbook Exercise Important Questions and Answers.

Maharashtra State Board Class 9 Marathi Kumarbharti Solutions Chapter 6 या झोपडीत माझ्या (कविता)

9th Std Marathi Kumarbharati Digest Chapter 6 या झोपडीत माझ्या Textbook Questions and Answers

1. कवितेत आलेल्या आशयानुसार पुढील मुद्दयांतील फरक लिहा:

प्रश्न 1.
कवितेत आलेल्या आशयानुसार पुढील मुद्दयांतील फरक लिहा:

उत्तर:

2. आकृतिबंध पूर्ण करा:

प्रश्न 1.
आकृतिबंध पूर्ण करा:

उत्तर:

3. चौकटी पूर्ण करा:

प्रश्न 1.
चौकटी पूर्ण करा:

उत्तर:
1. निजावयास जमीन
2. रात्री गगनातले तारे

4. ‘तिजोरी’ हे उत्तर येईल असा प्रश्न तयार करा.

प्रश्न 1.
‘तिजोरी’ हे उत्तर येईल असा प्रश्न तयार करा.
उत्तरे
धनदौलत संग्रहित ठेवण्याचे (साठवण्याचे) साधन कोणते?

5. काव्यसौदर्य:

प्रश्न (अ)
‘पाहुनि सौख्य माते, देवेंद्र तोहि लाजे
शांती सदा विराजे या झोपडीत माझ्या’. या काव्यपंक्तींतील विचारसौंदर्य स्पष्ट करा.
उत्तर:
देवांचा राजा इंद्र हा स्वर्गात राहतो. स्वर्गात सर्व सुखे असतात. सुखसमाधान व शांतीचा वास स्वर्गात आहे, अशी कल्पना आहे. राष्ट्रसंत तुकडोजी महाराज यांनी आनंदमय झोपडीचे वर्णन केले आहे. ते म्हणतात – माझ्या झोपडीत सुखसमाधान आणि शांतीचे है साम्राज्य आहे. झोपडीत एवढे पराकोटीचे सौख्य मला लाभते की इंद्रालासुद्धा माझ्या सखाचा हेवा वाटतो. माझे सुख पाहून इंद्राला माझा हेवा वाटतो. झोपडीतील सुखाची महती सांगणारा विचार या ओळीतून व्यक्त होतो.

प्रश्न (आ)
‘दारास नाही दोऱ्या, या झोपडीत माझ्या’ या काव्यपंक्तीतील आशयसौंदर्य स्पष्ट करा.
उत्तर:
महालातील धनदौलत ही बंदिस्त असते. तिजोरीला भक्कम कडीकुलूप लावलेले असते. चोरी होऊ नये; म्हणून धनावर सक्त पहारे ठेवले जातात. संपूर्ण महाल कडेकोट बंदोबस्तात असतो. कवी म्हणतात – माझी झोपडी सदैव खुली असते. धनदौलत नसल्यामुळे माझ्या झोपडीचे दार दोऱ्यांनी, कड्याकुलपाने बंद करावे लागत नाही. झोपडीला चोराचे भय नाही. येथे आनंदाने सर्वांचे स्वागत करण्यासाठी माझी झोपडी सताड उघडी असते. या ओळीतून कवीच्या मनाचा मोठेपणा व्यक्त झाला आहे.

1. झोपडी व महाल यांच्यातील संवादाची कल्पना करून संवादलेखन करा.

झोपडी: ………………………………………………………………………..
महाल: ………………………………………………………………………….
झोपडी: ………………………………………………………………………..
महाल: ………………………………………………………………………….
झोपडी: ………………………………………………………………………..
महाल: ………………………………………………………………………….
झोपडी: ………………………………………………………………………..
महाल: ………………………………………………………………………….

2. उजळणी- तक्ता पूर्ण करा.

3. महण म्हणजे काय?

‘मह’ शाविषय मनोरंजक आहे. आपण व्यवहारात वापरल्या जाणान्या म्हणी – उदा. -‘आये तसे भरा किया ‘गामाता गुळाची चा काय’ यांसारख्या म्हणींचा अभ्यास केला तर, ‘म्हण म्हणजे शहाणपणाने भरलेले वचन.’ या ज्ञानाचा आपल्याला बोलताना, लिहिताना अनेक प्रसंगी उपयोग करता येतो आणि आपले बोलणे, लिहिणे अधिक प्रभावशाली करता येते. भाषेला सौंदर्य प्राप्त होते. किंबहुना त्या भाषेची ती भूषणे आहेत. शब्द म्हणजे वाहूनही कटीन असतात आणि फुलातूनही कोमल असतात, असे म्हटले जाते ते शब्दांच्या अर्वासाठी.

Marathi Kumarbharati Textbook Std 9 Answers Chapter 6 या झोपडीत माझ्या Additional Important Questions and Answers

1. पुढील कवितेच्या आधारे दिलेल्या सूचनांनुसार कृती करा :

कृती 1: (आकलन)

प्रश्न 1.
आकृतिबंध पूर्ण करा:

उत्तर:

कृती 2: (आकलन)

प्रश्न 1.
चौकटी पूर्ण करा:

उत्तर:
1. मज्जाव
2. पहारे

प्रश्न 2.
योग्य पर्याय निवडून विधाने पूर्ण करा:
1. झोपडीतले सौख्य पाहून ………………. लाजतो. (देवेंद्र/सुरेंद्र/वीरेंद्र/राजेंद्र)
2. झोपडीत नित्य ……… विराजते. (भ्रांती/खंती/शांती/भक्ती)
उत्तर:
1. झोपडीतले सौख्य पाहून देवेंद्र लाजतो.
2. झोपडीत नित्य शांती विराजते.

कृती 3 : (दोन ओळींचा सरळ अर्थ)

प्रश्न 1.
राजास जी महाली, सौख्ये कधी मिळाली
ती सर्व प्राप्त झाली, या झोपडीत माझ्या
उत्तर:
झोपडीत राहण्याचे सुख वर्णन करताना राष्ट्रसंत तुकडोजी महाराज म्हणतात -एखादया राजालाही राजमहालात जे सुखसमाधान मिळाले असेल, ती सर्व सुखे मला माझ्या झोपडीत मिळतात.

पुढील कवितेवर दिलेल्या मुद्द्यांच्या आधारे कृती सोडवा:

प्रश्न 1.
कविता – या झोपडीत माझ्या.
उत्तर:
या झोपडीत माझ्या
1. प्रस्तुत कवितेचे कवी/कवयित्री → राष्ट्रसंत श्री तुकडोजी महाराज.
2. कवितेचा विषय → अत्यंत साध्या राहणीतही परमोच्च सुख साठलेले असते. सुख व शांती माझ्या झोपडीत कशी मिळते, याचे निवेदन या कवितेत केले आहे.
3. कवितेतील दोन शब्दांचे अर्थ →

1. सौख्य = सुख
2. भूमी = जमीन
3. नाम = नाव
4. मज्जाव = मनाई
5. भीती = भय
6. मऊ = नरम
7. बोजा = वजन, भार
8. सदा = सतत.

4. कवितेतून मिळणारा संदेश → श्रीमंतीचा, वैभवाचा हव्यास करू नये, जे प्राप्त परिस्थितीत मिळते, ते जास्त सुखकारक असते. शुद्ध मनाने गरिबीत जगताना समाधान मिळते, ही शिकवण मिळते.

5. कवितेची भाषिक वैशिष्ट्ये → कवितेच्या आशयाला पूरक असा सैलसा ‘ओवी’ हा पूर्वीचा लोकछंद या कवितेत आहे. ओवी छंदात तीनही चरणांत यमक साधलेले असते. प्रस्तुत रचनेचा सहजपणे तत्त्व बिंबवण्याचा गुण आहे. पैसा, दौलत, श्रीमंती हे चोरीला उत्तेजन देणारे घटक आहेत; परंतु गरिबाच्या मनातील निर्मळ भाव हा त्यास अभय देतो हा संदेश इतक्या सोप्या शब्दांत मांडला आहे की, ओवी सहज ओठात रुळते. गुणगुणावीशी वाटते. प्रत्येक ओवीचा शेवट – ‘या झोपडीत माझ्या’ असा केल्याने आशयाची घनता वाढते.

6. कवितेतून व्यक्त होणारा विचार → महालातील सुखे व झोपडीतील सुखे यांची तुलना या कवितेत केली आहे. झोपडीतल्या साध्या राहणीत सुखसमृद्धी व शांती मिळते, हे सांगितले आहे. साधी राहणी, उच्च विचारसरणी मनात ठसवली, तर मानसिक सुख लाभते.

7. कवितेतील दोन ओळींचा सरळ अर्थ :
पाहूनि सौख्य माते, देवेंद्र तोहि लाजे
शांती सदा विराजे, या झोपडीत माझ्या
→ राष्ट्रसंत तुकडोजी महाराज झोपडीचे माहात्म्य सांगताना म्हणतात-झोपडीत राहण्याचे माझे सुख पाहून इंद्रही मनात लाजतो. माझ्या सुखाचा इंद्राला हेवा वाटतो. माझ्या झोपडीत नेहमी सुखशांती नांदते.

8. कविता आवडण्याची वा न आवडण्याची कारणे → राजालाही जी सुखे मिळत नाहीत, ती माझ्या झोपडीत आहेत. खुल्या निसर्गात, जमिनीवर पहुडताना, मानाने, सुखासमाधानाने जगावे, हे अतिशय सहजपणे कवितेत बिंबवले असल्यामुळे ही कविता मला खूप आवडली.

पुढील ओळींचे रसग्रहण तुमच्या शब्दांत करा:

प्रश्न 1.
‘पाहून सौख्य माते, देवेंद्र तोहि लाजे
शांती सदा विराजे, या झोपडीत माझ्या’
उत्तर:
आशयसौंदर्य: राष्ट्रसंत श्री तुकडोजी महाराज यांनी ‘या झोपडीत माझ्या’ या कवितेत महालातील सुखे व झोपडीतील सुखे यांची मार्मिकपणे तुलना केली आहे. श्रीमंतीचा, वैभवाचा बडेजाव न करता झोपडीतल्या साध्या राहणीत सुख-समृद्धी व शांती मिळते, हा आशय या कवितेत सहजपणे नोंदवला आहे.

काव्यसौंदर्य: प्राप्त परिस्थितीत शुद्ध मनाने जगताना समाधान मिळते. खुल्या निसर्गात, जमिनीवर पहुडताना जे सुख मिळते, ते देवाच्या देवालाही मिळत नाही, असे या प्रस्तुत ओळींत सांगितले आहे. माझे झोपडीत राहण्याचे सुख पाहून देवेंद्रही लाजतो. त्याला माझ्या सुखाचा हेवा वाटतो; कारण देवेंद्रालाही न मिळणारी शांती माझ्या झोपडीत विराजमान झाली आहे. माझ्या झोपडीत निरामय शांती वसत आहे, असे कवींना म्हणायचे आहे.

भाषिक वैशिष्ट्ये: कवितेच्या आशयाला पूरक असा सैलसा ‘ओवी’ हा प्राचीन लोकछंद या कवितेत आहे. ओवी छंदात तीनही चरणांत यमक साधलेले असते. प्रस्तुत रचनेचा सहजपणे तत्त्व बिंबवण्याचा गुण आहे. पैसा, दौलत, श्रीमंती हे चोरीला उत्तेजन देणारे घटक आहेत; परंतु गरिबाच्या मनातील निर्मळ भाव हा त्यास अभय । झोपडीत माझ्या’ असा केल्याने आशयाची घनता वाढते. तसेच ‘या’ देतो हा संदेश इतक्या सोप्या शब्दांत मांडला आहे की, ओवी सहज , हा शब्द एकाच वेळी सार्वनामिक विशेषण व क्रियापद या दोन्ही ओठात रुळते. गुणगुणावीशी वाटते. प्रत्येक ओवीचा शेवट-‘या है अंगाने अर्थवाही झाला आहे.

भाषाभ्यास:

(अ) व्याकरण घटकांवर आधारित कृती:

शब्दसिद्धी:

प्रश्न 1.
उपसर्गघटित व प्रत्ययघटित प्रत्येकी दोन शब्द लिहा.
उत्तर:

(आ) भाषिक घटकांवर आधारित कृती:

1. शब्दसंपत्ती:

प्रश्न 1.
विरुद्धार्थी शब्द लिहा:

1. मऊ
2. महाल
3. नित्य
4. शांती.

उत्तर:

1. मऊ × टणक
2. महाल × झोपडी
3. नित्य × अनित्य
4. शांती × अशांती.

प्रश्न 2.
तक्ता भरा:

उत्तर:

2. लेखननियम:

प्रश्न 1.
अचूक शब्द ओळखा:

1. माजाव, मज्जाव, मज्जव, माज्जाव.
2. प्रभुनाम, परभुनाम, प्रभूनाम, प्रभुनमा.
3. भिती, भिति, भीति, भीती.
4. तिजोरि, तीजोरी, तिजोरी, तीजोरि.

उत्तर:

1. मज्जाव
2. प्रभुनाम
3. भीती
4. तिजोरी.

3. विरामचिन्हे:

प्रश्न 1.
जोड्या लावा:
(अ) [ . ] [ ; ] [ ‘ ‘ ] [ – ]
(आ)

1. एकेरी अवतरणचिन्ह
2. पूर्णविराम
3. संयोगचिन्ह
4. अपूर्णविराम

उत्तर:
[.] पूर्णविराम
[;] अपूर्णविराम
[‘ ‘] एकेरी अवतरणचिन्ह
[ _ ] संयोगचिन्ह

या झोपडीत माझ्या Summary in Marathi

कवितेचा आशय:

लहानशा झोपडीतही सुख, शांती आणि आनंद नांदत असतो. महालातली सुखे झोपडीतही प्राप्त होतात. अशा प्रकारे झोपडीतल्या वैभवाचे वर्णन अतिशय साध्या शब्दांत या कवितेत केले आहे.

शब्दार्थ:

1. महाल – राजवाडा, प्रशस्त घर.
2. सौख्ये – सुखे, वैभव.
3. प्राप्त झाली – मिळाली, लाभली.
4. भूमी – जमीन.
5. प्रभुनाम – देवाचे नाव, भजन.
6. नित्य – नेहमी, सतत.
7. पहारा – रखवाली, नजरकैद.
8. तिजोरी – खजिनापेटी.
9. तया – त्या.
10. मज्जाव – अटकाव, निबंध.
11. शामदाने – काचेचा दिवा, झुंबर.
12. माने – सन्मान.
13. सुखे – आरामात, सुखाने.
14. बोजा – वजन, (इथे अर्थ) दडपण, धाक.
15. माते – माझे.
16. देवेंद्र – इंद्र, देवांचा राजा.
17. लाजे – शरमतो.
18. सदा – नेहमी.
19. विराजे – शोभते, नांदते.

कवितेचा भावार्थ:

एखादया राजाला राजमहालात जी सुखे मिळाली असतील, ती सर्व सुखे माझ्या झोपडीत मला लाभली आहेत. अंगणातल्या जमिनीवर आरामात निजण्याचे नि रात्री आकाशातील चांदण्यांकडे, ताऱ्यांकडे पाहण्याचे सुख मला या झोपडीत मिळते. देवाचे भजन नेहमी गात या झोपडीत मी आनंदात राहतो.

महालांमध्ये तिजोऱ्यांमधून धन साठवून ठेवलेले असते; त्यावर सक्त पहारे ठेवले जातात. तरी सुद्धा तेथे चोऱ्या होतात. माझ्या झोपडीच्या दारांना कवाडे नाहीत, ती सताड उघडी आहेत. माझ्या झोपडीला चोरांचे भय नाही; चोरण्याइतपत दौलत नसल्यामुळे माझ्या झोपडीला पहारे नाहीत.

राजवाड्यात परवानगीशिवाय शिरकाव होत नाही. ‘अटकाव’ हा शब्द तिथे असतो. माझ्या झोपडीत येण्यासाठी भीती वाटणार नाही. झोपडीत सर्व माणसांचे खुले स्वागत आहे. महालामध्ये आरामासाठी मऊ बिछाने असतात नि कंदील, झुंबरांची रोषणाई केलेली असते. माझ्या झोपडीत जमिनीवर पहुडणे हाच सन्मान आहे. धरतीचाच बिछाना आहे.

माझ्या झोपडीत कुणीही प्रेमाने या नि प्रेमाने जा. माझ्या झोपडीत ये-जा करताना कुणाच्याही मनावर दडपण असत नाही. झोपडीत राहण्याचे माझे सुख पाहून इंद्रही मनात लाजतो. माझ्या सुखाचा हेवा वाटतो. माझ्या झोपडीत नेहमी सुखशांती नांदत आहे.

Balbharti Maharashtra State Board Class 9 Marathi Solutions Kumarbharti Chapter 8 अभियंत्यांचे दैवत-डॉ. विश्वेश्वरय्या Notes, Textbook Exercise Important Questions and Answers.

Maharashtra State Board Class 9 Marathi Kumarbharti Solutions Chapter 8 अभियंत्यांचे दैवत-डॉ. विश्वेश्वरय्या

9th Std Marathi Kumarbharati Digest Chapter 8 अभियंत्यांचे दैवत-डॉ. विश्वेश्वरय्या Textbook Questions and Answers

1. समर्पक उदाहरण लिहा:

प्रश्न (अ)
विश्वेश्वरय्या यांनी घेतलेले कठोर परिश्रम.
उत्तर:
विश्वेश्वरय्या यांनी स्वत:चे शिक्षण घेण्यासाठी शिकवण्या करून पैसे उभे केले.

प्रश्न (आ)
समर्पक उदाहरण लिहा: माणुसकीचे दर्शन.
उत्तर:
1907 साली विश्वेश्वरय्यांनी स्वेच्छानिवृत्ती घेतली. तत्कालीन मुंबई सरकारने सेवेचा गौरव म्हणून त्यांना पेन्शन दिली. त्या पेन्शनमधे स्वत:च्या गरजेपुरते पैसे ठेवून त्यांनी उरलेली रक्कम गरीब विदयार्थ्यांच्या शिक्षणासाठी व शिक्षणसंस्थांच्या उभारणीसाठी खर्च केली. प्रतिकूल परिस्थितीशी झुंजत शिक्षण घेणाऱ्यांना मदत व्हावी, म्हणून त्यांनी ही देणगी दिली, ही त्यांची, त्यांच्यातील माणुसकीचे दर्शन घडवणारी कृती होय.

2. खालील प्रत्येक वाक्यातून विश्वेश्वरय्या यांचा कोणता गुण प्रकट होतो ते लिहा:

प्रश्न 1.
खालील प्रत्येक वाक्यातून विश्वेश्वरय्या यांचा कोणता गुण प्रकट होतो ते लिहा:

1. आवाजाची लय चुकल्याची जाणीव त्यांना झाली. [ ]
2. सफल जीवनासाठी शरीरापेक्षा मनाला महत्त्व देणे. [ ]
3. शिकवण्या करून त्यांनी पैसे उभे केले. [ ]
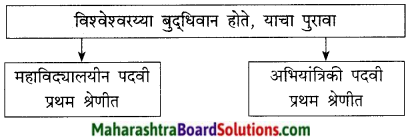
4. अभियांत्रिकी पदवी परीक्षेत मुंबई प्रांतात प्रथम आले. [ ]
5. वयाच्या नव्वदीतही तरुणांना लाजवेल एवढे उत्साही होते. [ ]
6. सारी पेन्शन गरीब विदयार्थ्यांच्या शिक्षणासाठी खर्च केली. [ ]

उत्तर:

1. अचूक ज्ञान
2. सुखासीनता, विलास यांना महत्त्व न देण्याची वृत्ती.
3. कष्टाळूपणा, जिद्द
4. बुद्धिमान
5. कार्यतत्परता
6. सहानुभूती

3. माहिती लिहा

प्रश्न 1.
माहिती लिहा.

उत्तर:

4. खालील शब्दांच्या अर्थांतील फरक समजून घ्या व त्यांचा स्वतंत्र वाक्यांत उपयोग करा:

प्रश्न 1.
खालील शब्दांच्या अर्थांतील फरक समजून घ्या व त्यांचा स्वतंत्र वाक्यांत उपयोग करा:
(अ) आव्हान – आवाहन
(आ) कृतज्ञ – कृतघ्न
(इ) आभार – अभिनंदन
(ई) विनंती – तक्रार.
उत्तर:
(अ) आव्हान – प्रतिस्पर्ध्याला लढाईला किंवा वादाला बोलावणे.
आवाहन – एखादे चांगले काम करण्यासाठी बोलावणे.
वाक्ये:
आव्हान – भैरू पहिलवानाने कुस्तीसाठी केरू पहिलवानाला आव्हान दिले.
आवाहन – पंतप्रधानांनी जनतेला स्वच्छता अभियानात सामील होण्याचे आवाहन केले.

(आ) कृतज्ञ – उपकाराची जाणीव असणारा.
कृतघ्न – केलेले उपकार विसरणारा.
वाक्ये:
कृतज्ञ – सीमेवर रक्षण करणाऱ्या जवानांबद्दल जनतेने कृतज्ञ राहिले पाहिजे.
कृतघ्न – आपल्याला मदत करणाऱ्यांशी आपण कृतघ्न होऊ नये.

(इ) आभार – धन्यवाद (देणे).
अभिनंदन – शाबासकी (देणे), कौतुक (करणे).
वाक्ये:
आभार – स्नेहसंमेलनाला उपस्थित राहिलेल्या प्रमुख पाहुण्यांचे प्राचार्यांनी आभार मानले.
अभिनंदन – पोहण्याच्या स्पर्धेत मिताली प्रथम आली; म्हणून मॅडमनी तिचे अभिनंदन केले.

(ई) विनंती – विनवणी (करणे).
तक्रार – गा-हाणे (मांडणे).
वाक्ये: विनंती – कार्यक्रमात निवेदकाने अध्यक्षांना स्थानापन्न होण्याची विनंती केली.
तक्रार – सदाशिवरावांनी परिसरातील अस्वच्छतेविषयी आरोग्य अधिकाऱ्यांकडे तक्रार केली.

5. खालील वाक्याचा मराठी भाषेत अनुवाद करा:

प्रश्न 1.
खालील वाक्याचा मराठी भाषेत अनुवाद करा:
He is an engineer of integrity, character and broad outlook.
उत्तर:
ते (विश्वेश्वरय्या) निष्ठावान, चारित्र्यसंपन्न व विशाल दृष्टिकोन असलेले अभियंता आहेत.

6. स्वमत.

प्रश्न (अ)
विश्वेश्वरय्यांच्या दीर्घ जीवनाच्या पंचसूत्रीतून तुम्हांला होणारा बोध लिहा.
उत्तर:
सुनियंत्रित आचरण, कठोर परिश्रम, प्रसन्नता, संयम व प्रचंड आशावाद ही विश्वेश्वरय्यांच्या दीर्घ जीवनाची पंचसूत्री होती. या सूत्रांना अनुसरून जगल्यास कोणतीही व्यक्ती अत्यंत समाधानी व यशस्वी आयुष्य जगू शकेल.

सुनियंत्रित आचरण म्हणजे कसेही भरकटलेले जीवन न जगता आपल्या ध्येयाला अनुसरून प्रत्येक कृती करणे. त्यासाठी काटेकोर नियोजन केले पाहिजे. कठोर परिश्रमांची तयारी ठेवली पाहिजे. आपले मन आपल्याला सुखासीनतेकडे ओढत राहते. त्याची अजिबात पर्वा करता कामा नये. त्याचबरोबर आपल्या मनाची प्रसन्नता ढळता कामा नये. मन प्रसन्न राखल्यामुळे जीवन जगण्याची शक्ती वाढते. संयम हा सुद्धा एक मोलाचा गुण आहे. अनेक बाबतीत आपले मन अनेक दिशांनी धावते. वासना-विकारांनी प्रभावित होते. अशा वेळी संयमाची नितांत गरज असते. अशा रितीने जगत असताना आपल्या निष्ठा ठाम हव्यात. आपल्या आयुष्यात चांगलेच घडणार, हाती घेतलेले प्रत्येक कार्य यशस्वीच होणार, अशी खात्री बाळगली पाहिजे. हा आशावाद आपल्याला तारून नेतो. विश्वेश्वरय्यांच्या पंचसूत्रीचा हा बोध ध्यानी बाळगल्यास आपले जीवन सुखी, संपन्न होईल.

प्रश्न (आ)
‘स्वप्नातही दिसणार नाही असे जलामृत आपल्या अंगणात आलेले पाहून सक्करकरांच्या डोळ्यांत पाणी आले,’ या वाक्याचा भावार्थ स्पष्ट करा.
उत्तर:
सक्कर या शहरातील नागरिकांना पाणीपुरवठा करण्यासाठी म्हणून नगरपालिकेने सिंधू नदीच्या काठावरील एका डोंगरावर जलाशय बांधला. सिंधू नदीचे पाणी पंपाने उचलून ते जलाशयात साठवले जाऊ लागले. तिथून पाईपांनी सक्करवासीयांना पाणी पुरवले जाऊ लागले. पण घरात पोहोचलेले पाणी वाळूमिश्रित, गढूळ व घाणेरडे होते. जलाशयात जमा होणारे पाणी संपूर्णपणे गाळून शुद्ध करणे आवश्यक होते. मात्र, त्या प्रक्रियेला येणारा खर्च अवाढव्य होता आणि तो नगरपालिकेला झेपणारा नव्हता. म्हणजे नागरिकांच्या नशिबी हेच घाणेरडे पाणी होते.

तेवढ्यात विश्वेश्वरय्यांनी हे आव्हान स्वीकारले. त्यांनी नदीतच विहीर खोदली. नदीचे पात्र व विहिरीचा तळ यांना जोडणारा बोगदा बांधला. मग विहिरीत नैसर्गिक रितीने स्वच्छ झालेले पाणी जमा होऊ लागले. विहिरीतले हे पाणी लोकांना मिळू लागले. हे अमृतासारखे स्वच्छ, शुद्ध पाणी पाहून सक्करकरांचे डोळे आनंदाने पाणावले. अशक्य असलेली गोष्ट विश्वेश्वरय्यांमुळे शक्य झाली, ही कृतज्ञताही त्या अश्रूमध्ये होती.

प्रश्न (इ)
विश्वेश्वरय्यांमधील तुमच्यावर प्रभाव टाकणाऱ्या गुणविशेषांचे तुमच्या शब्दांत वर्णन करा.
उत्तर:
विश्वेश्वरय्या हे जगद्विख्यात अभियंता होते. अनेक गुणांमुळे ते जागतिक कीर्ती मिळवू शकले. त्यांच्या अनेक गुणांपैकी एक गुण मला खूप आकषून घेतो. समोर उभ्या ठाकलेल्या कोणत्याही समस्येला ते सर्व ताकदीनिशी सामोरे जायला सदोदित तत्पर असत. त्यांचा हा गुण मला खूप आवडतो. त्यांच्या या गुणामुळे त्यांच्याकडे गुंतागुंतीच्या व क्लिष्ट समस्या चालत आल्या. प्रत्येक समस्येच्या सोडवणुकीचा मार्ग भिन्न होता, योजलेले उपाय भिन्न होते. प्रत्येक ठिकाणी केलेले कार्य नावीन्यपूर्ण होते. त्यात त्यांची अभियांत्रिकी प्रतिभा दिसते. सगळी बुद्धी पणाला लावून ते काम करीत. या त्यांच्या गुणामुळेच त्यांच्याकडून अलौकिक कार्ये पार पडली. प्रत्येकाने हा गुण अंगी बाळगला पाहिजे, मग आपापल्या आयुष्यात माणसे यशस्वी होतील. जीवनातला श्रेष्ठ आनंद त्यांना लाभेल.

प्रश्न (ई)
‘झिजलात तरी चालेल पण गंजू नका,’ या विचारातून तुम्हांला मिळालेला संदेश सविस्तर लिहा.
उत्तर:
पंडित जवाहरलाल नेहरू यांनी ‘निष्ठावान अभियंता’ हे उद्गार विश्वेश्वरय्यांना उद्देशून काढले, ते अक्षरशः सत्य आहेत. ते बुद्धिमान होते. त्यांची बुद्धीवर विलक्षण निष्ठा होती. कार्यावर निष्ठा होती. म्हणूनच ते म्हणतात, ‘झिजलात तरी चालेल पण गंजू नका.’ याचा अर्थ स्वत:च्या कार्यासाठी वाटेल ते कष्ट घेण्याची तयारी ठेवली पाहिजे. आराम करण्याची, कष्ट टाळण्याची वृत्ती त्यांना अजिबात मान्य नव्हती. आपण आपले जे कार्यक्षेत्र निवडले आहे, त्यात झोकून दिले पाहिजे. आपली सर्व शक्ती पणाला लावली पाहिजे. मग उत्तुंग यश मिळणारच. सतत काम करीत राहण्याने बुद्धी गंजत नाही. बुद्धी गंजली की माणूस संपलाच. बुद्धी सतत सतेज राखली पाहिजे, हेच विश्वेश्वरय्यांना सांगायचे आहे.

भाषाभ्यास:

रस म्हणजे चव किंवा रुची. आपण गोड, कडू, आंबट, तिखट, तुरट, खारट असे सहा प्रकारचे रस अनुभवतो. त्याचप्रमाणे काव्याचा आस्वाद घेताना वेगवेगळे रस आपण अनुभवतो. त्यातील भावनांमुळे साधारणपणे नऊ प्रकारचे रस आपल्याला दैनंदिन जीवनात आणि साहित्यात अनुभवायला मिळतात.

रस ही संकल्पना संस्कृत साहित्यातून आलेली आहे. ती शिकवताना प्रामुख्याने कवितांची उदाहरणे दिली जातात. याचा अर्थ रस फक्त काव्यातच असतो असे नाही तर तो सर्व प्रकारच्या साहित्यात असतो. तसेच कधी कधी या नऊ रसांव्यतिरिक्त अनेक वेगवेगळ्या प्रकारच्या भावभावनाही असू शकतात. कोणत्याही साहित्यामध्ये एक किंवा अधिक रस असू शकतात. कवितेतील रस हा विशिष्ट शब्दांत नसतो. उदाहरणार्थ, कवितेत ‘वीर’ हा शब्द आला म्हणजे त्या कवितेत वीररस असेलच असे नाही. तसेच ‘हुंदका’ शब्द आला म्हणजे तिथे करुण रस असेलच असे नाही.

Marathi Kumarbharati Textbook Std 9 Answers Chapter 8 अभियंत्यांचे दैवत-डॉ. विश्वेश्वरय्या Additional Important Questions and Answers

उतारा क्र. 1

पुढील उतारा वाचून दिलेल्या सूचनांनुसार कृती करा:

कृती 2 : (आकलन)

प्रश्न 1.
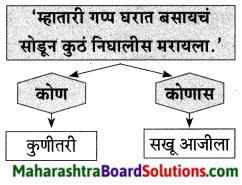
कोठे ते लिहा:

1. वृंदावन उदयान – [ ]
2. विश्वेश्वरय्यांच्या पूर्वजांचे गाव – [ ]
3. विश्वेश्वरय्यांचे जन्मगाव – [ ]
4. विश्वेश्वरय्यांचे अभियांत्रिकी शिक्षण – [ ]

उत्तर:

1. म्हैसूर
2. मोक्षगुडम
3. मदनहळ्ली
4. पुणे

प्रश्न 2.
विश्वेश्वरय्यांची पंचसूत्री लिहा.
उत्तर:

1. सुनियंत्रित आचरण
2. कठोर परिश्रम
3. प्रसन्नता
4. संयम व
5. प्रचंड आशावाद.

प्रश्न 3.
कारण लिहा:
विश्वेश्वरय्यांचे बालपण व विदयार्थिजीवन कष्टांत गेले.
उत्तर:
विश्वेश्वरय्यांचे बालपण व विदयार्थिजीवन कष्टांत गेले, कारण शालेय शिक्षण घेत असतानाच त्यांचे वडील वारले.

प्रश्न 4.
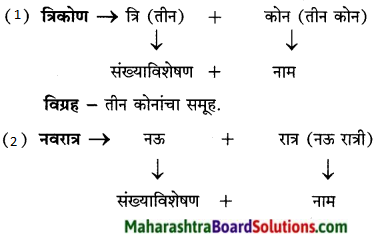
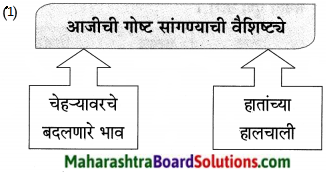
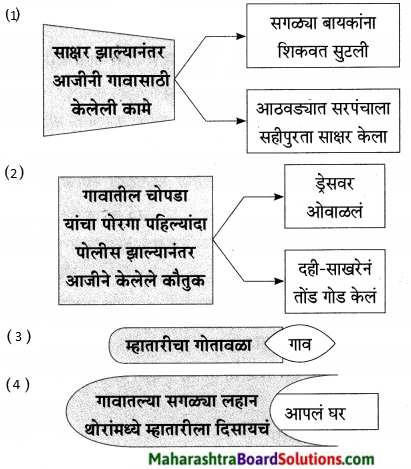
आकृती पूर्ण करा:

उत्तर:

उतारा क्र. 2

पुढील उतारा वाचून दिलेल्या सूचनांनुसार कृती करा:

कृती 1 : (आकलन)

प्रश्न 1.
पुढील वाक्यांतून विश्वेश्वरय्यांचा प्रकट होणारा गुण:
1. नैसर्गिक पद्धतीने विहिरीमध्ये स्वच्छ व शुद्ध पाणी साचू लागले. [ ]
उत्तर:
1. कल्पकता

प्रश्न 2.
माहिती लिहा:
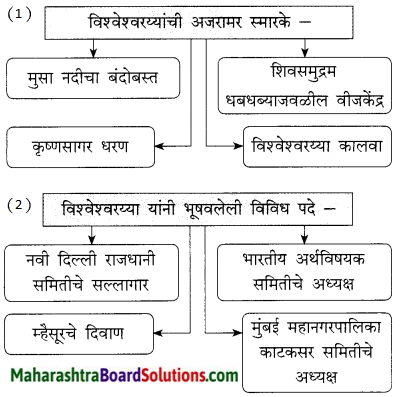
सहायक अभियंता असतानाची विश्वेश्वरय्यांची कामगिरी –
1. …………………………………..
2. …………………………………..
उत्तर:
1. सहायक अभियंता असतानाची विश्वेश्वरय्यांची कामगिरी –
2. खानदेशातील एका नाल्यावर पाईप बसवण्याचे अशक्यप्राय व आव्हानात्मक काम मोठ्या कौशल्याने करून दाखवले.
3. सिंध प्रांतातील सक्कर शहराच्या पाणीपुरवठ्याची क्लिष्ट जबाबदारी यशस्वी रितीने पार पाडली.

कृती 2 : (आकलन)

प्रश्न 1.
माहिती लिहा:
1. सक्कर शहराच्या पाणीपुरवठ्याची समस्या.
2. सक्करच्या समस्येवर विश्वेश्वरय्यांनी केलेली उपाययोजना.
उत्तर:
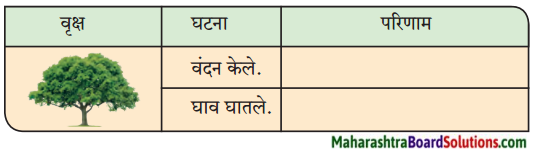
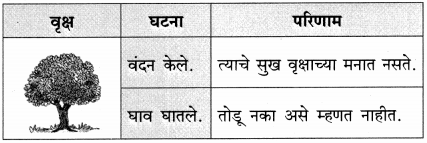
1. सक्कर नगरपालिकेने गावाला पाणीपुरवठा करण्यासाठी सिंधू नदीच्या किनाऱ्यावरील डोंगरावर एक जलाशय बांधला. नदीचे पाणी पंपाने उचलून जलाशयात साठवले जाई. तेथून ते सर्व नागरिकांना पुरवले जाई, मात्र, जलाशयात जमा होणारे पाणी वाळूमिश्रित व गढूळ होते. ते तसेच पुरवले जाई. पाणी गाळून स्वच्छ करण्याच्या योजनेकरिता नगरपालिकेकडे पैसा नव्हता. नागरिक जबरदस्त हैराण झाले होते.
2. विश्वेश्वरय्यांनी नदीच्या पात्रातच काठाजवळ एक गोल विहीर खोदली. विहिरीच्या तळापासून नदीच्या प्रवाहाखाली एक बोगदा खणला. त्यामुळे नैसर्गिक पद्धतीनेच स्वच्छ व शुद्ध पाणी विहिरीत साठू लागले. असे स्वच्छ पाणी मिळालेले पाहून सक्करच्या नागरिकांच्या डोळ्यांत आनंदाश्रू आले.

उतारा क्र. 3

1. पुढील उतारा वाचून दिलेल्या सूचनांनुसार कृती करा :

कृती 1 : (आकलन)

प्रश्न 1.
माहिती लिहा:

1. तार
2. दौरा
3. मुसा नदीवरील बंधारा.

उत्तर:

1. तार: पूर्वीच्या काळी (जेव्हा फोनसुविधा नव्हती त्या काळी) दूरवर असलेल्या व्यक्तीला तारायंत्राच्या साहाय्याने पाठवला जाणारा तातडीचा संदेश.
2. दौरा: विशिष्ट हेतूने किंवा कामासाठी नियोजनपूर्वक केलेला प्रवास.
3. मुसा नदीवरील बंधारा: हैदराबादच्या मुसा नदीला एकदा महापूर आला होता. सारे शहरच पाण्याखाली जाण्याचा धोका निर्माण झाला होता.

अशा संकटकाळात विश्वेश्वरय्या धावून आले. मुसा नदीचे खवळलेले पाणी कायमचे आटोक्यात राहील आणि हैदराबाद शहराला कधीही धोका निर्माण होणार नाही, असा पक्का बंदोबस्त विश्वेश्वरय्यांनी त्या काळात केला.

कृती 2 : (आकलन)

प्रश्न 1.
कोष्टक पूर्ण करा:

उत्तर:

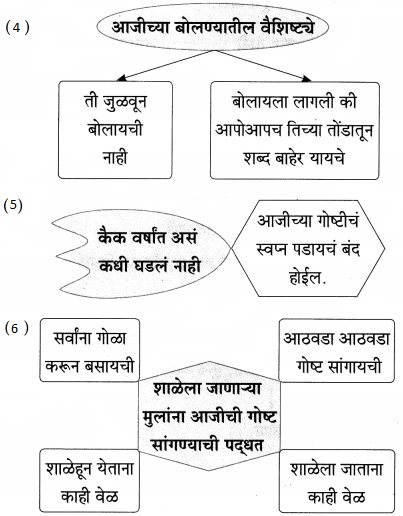
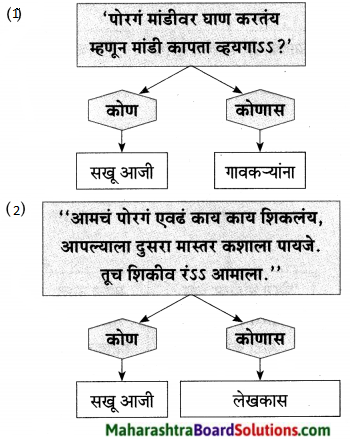
प्रश्न 2.
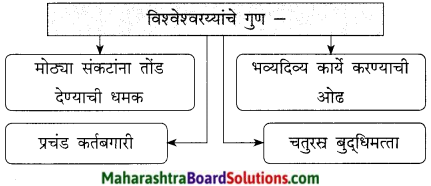
आकृती पूर्ण करा:

उत्तर:

कृती 3 : (स्वमत/अभिव्यक्ती)

प्रश्न 1.
विश्वेश्वरय्यांनी बांधलेल्या कावेरी नदीवरील ‘कृष्णसागर’ या धरणाचा अजस्रपणा स्पष्ट करा.
उत्तर:
म्हैसूर संस्थानच्या महाराजांनी विश्वविश्वेश्वरय्यांचे गुण विश्वरय्यांना आपल्या संस्थानात मुख्य अभियंता या पदावर नेमले. आपल्या कारकिर्दीच्या सुरुवातीलाच त्यांनी ‘कृष्णसागर’ हे अजस्र धरण बांधले. या अजस्र धरणामुळे जगभर त्यांचे कौतुक झाले.

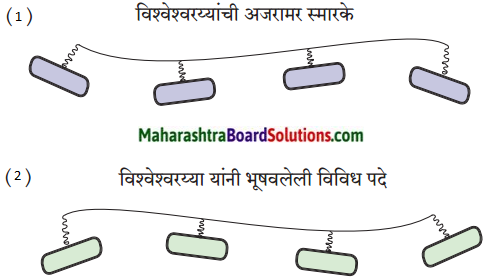
हे धरण होतेच मुळी तसे. 8600 फूट लांब, 101 फूट रुंद व 104 फूट उंच! धरणाच्या माथ्यावर 50 फूट रुंदीचा मोटर रस्ता. धरणातील पाणी सोडण्यासाठी तब्बल 179 दरवाजे होते! आपोआप उघडझाप करणारे. धरणाच्या बाजूला 60 मैल लांबीचा कालवा काढलेला आहे. तो कालवा ‘विश्वेश्वरय्या कालवा’ या नावाने गौरवला जातो. या कालव्यासाठी 3960 फूट लांबीचा बोगदा तयार केलेला आहे. या धरणातून ठरावीक पाणी शिवसमुद्रम धबधब्यात सोडतात आणि त्याआधारे एक वीजनिर्मिती केंद्र चालवले जाते. या विजेच्या बळावर म्हैसूरचा राजवाडा व वृंदावन उदयान रोषणाईने झळझळतात. विश्वेश्वरय्यांच्या अभियांत्रिकी करामतीची ही स्मारकेच होत.

उतारा क्र. 4

1. पुढील उतारा वाचून दिलेल्या सूचनांनुसार कृती करा:

कृती 1 : (आकलन)

प्रश्न 1.
पुढील वाक्यांतून विश्वेश्वरय्यांचा प्रकट होणारा गुण:
1. झिजलात तरी चालेल, पण गंजू नका.
उत्तर:
1. बुद्धीवरील निष्ठा

कृती 2 : (आकलन)

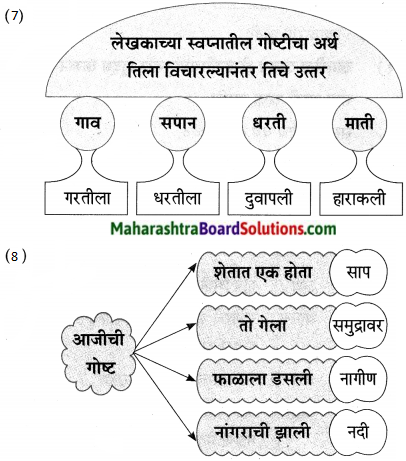
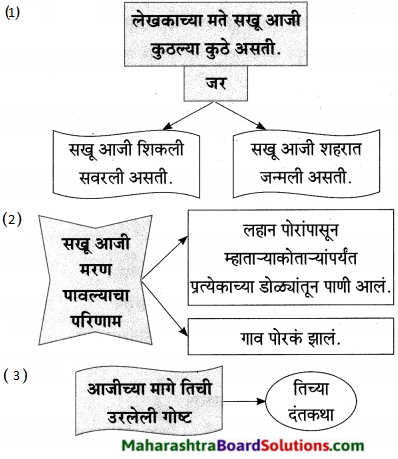
प्रश्न 1.
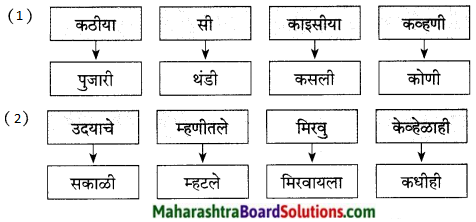
आकृती पूर्ण करा:

उत्तर:

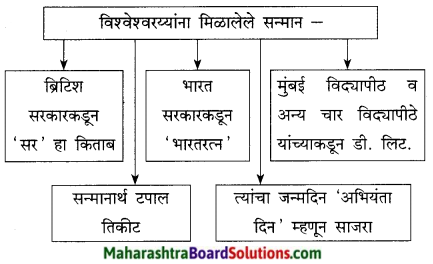
प्रश्न 2.
माहिती लिहा:
विश्वेश्वरय्यांची उभारलेली स्मारके:
उत्तर:
1. त्यांच्या जन्मगावी एका भव्य उदयानात त्यांचा पुतळा उभारला गेला आहे.
2. त्यांनी स्वतः बांधलेले त्यांचे सुंदर घर ‘राष्ट्रीय स्मारक’ म्हणून जाहीर.

भाषाभ्यास:

(अ) व्याकरण घटकांवर आधारित कृती :

1. समास:

प्रश्न 1.
पुढील विग्रहांवरून समास ओळखा:

1. पाप किंवा पुण्य → ………………..
2. खाणे, पिणे वगैरे → ……………….
3. महान असे राष्ट्र → ………………..
4. नवरा आणि बायको → ……………
5. तीन खंडांचा समूह → …………….

उत्तर:

1. वैकल्पिक द्वंद्व समास
2. समाहार वंद्व समास
3. कर्मधारय समास
4. इतरेतर द्वंद्व समास
5. द्विगू समास.

2. शब्दसिद्धी:

प्रश्न 1.
‘अति’ उपसर्ग असलेले चार शब्द लिहा.
उत्तर:

1. अतिमंद
2. अत्यानंद (अति + आनंद)
3. अतिविचारी
4. अतिहुशार.

3. वाक्प्रचार/म्हणी:

प्रश्न 1.
पुढील वाक्प्रचारांचा अर्थ सांगून वाक्यांत उपयोग करा:
1. चकित होणे
2. मार्गदर्शन करणे.
उत्तर:
1. चकित होणे – अर्थ : आश्चर्य वाटणे.
वाक्य : तीन वर्षांच्या बाळूने सुरेख चित्र काढलेले पाहिल्यावर सगळे चकित झाले.
2. मार्गदर्शन करणे – अर्थ : योग्य दिशा दाखवणे.
वाक्य : शालान्त परीक्षेत माझ्या दादाने मला मार्गदर्शन केले.

प्रश्न 2.
म्हणी पूर्ण करा:
1. ……………………. काकडीला राजी. (कोल्हा/ लांडगा)
2. …………………… गुळाची चव काय? (गाढवाला/घोड्याला)
उत्तर:
1. कोल्हा काकडीला राजी.
2. गाढवाला गुळाची चव काय?

(आ) भाषिक घटकांवर आधारित कृती:

प्रश्न 1.
विरुद्धार्थी शब्दांच्या जोड्या जुळवा:

उत्तर:

1. पूर्वज × वंशज
2. निवृत्ती × प्रवृत्ती
3. सफल × विफल
4. उंच × सखोल

2. लेखननियम:

प्रश्न 1.
अचूक शब्द ओळखा:

1. सूसंस्कृत, सुंसस्कृत, सुसंस्कृत, सुसंक्सृत.
2. फलश्रूती, फलश्रुती, फळधृति, फलश्रुति.
3. कुतूहल, कुतुहल, कुतुहल, कूतूहल.
4. नीयूक्त, नियूक्त, नियुत्क, नियुक्त.
5. प्रोत्साहन, प्रोत्साहण, प्रोस्ताहण, प्रोत्सहन.
6. कामगीरी, कामगिरी, कामगिरि, कामगीरि.

उत्तर:

1. सुसंस्कृत
2. फलश्रुती
3. कुतूहल
4. नियुक्त
5. प्रोत्साहन
6. कामगिरी.

3. विरामचिन्हे:

प्रश्न 1.
पुढील वाक्यांतील विरामचिन्हे ओळखा:
1. विश्वेश्वरय्यांचा जन्मदिन ‘अभियंता दिन’ म्हणून साजरा होतो.
2. परिस्थिती बेताची होती; पण आई मनाची श्रीमंत होती, जिद्दी होती.
उत्तर:
1. एकेरी अवतरणचिन्ह व पूर्णविराम.
2. अर्धविराम, स्वल्पविराम व पूर्णविराम.

4. पारिभाषिक शब्द:

प्रश्न 1.
मराठी प्रतिशब्द लिहा:

1. Exhibition
2. Receptionist
3. Handbill
4. Goodwill

उत्तर:

1. प्रदर्शन
2. स्वागतिका
3. हस्तपत्रक
4. सदिच्छा.

अभियंत्यांचे दैवत-डॉ. विश्वेश्वरय्या Summary in Marathi

प्रस्तावना:

डॉ. यशवंत पाटणे हे प्रसिद्ध लेखकांपैकी एक आहेत. त्यांची अनेक पुस्तके प्रसिद्ध झाली आहेत. माणसाने स्वत:च्या सुखाकडे पाहावे, हे ठीक आहे. पण त्याबरोबरच स्वत:पलीकडे, समाजाकडे पाहिले पाहिजे. समाजाच्या भल्यासाठी काहीतरी केले पाहिजे. ते माणसाचे कर्तव्य आहे, असा लेखकांचा दृष्टिकोन आहे. म्हणूनच त्यांना विश्वेश्वरय्यांसारखे निष्ठावान कर्मयोगी भावतात. त्यांच्या कार्याने ते स्वतः प्रभावित होतात. प्रस्तुत पाठात लेखकांनी विश्वेश्वरय्यांचे कार्यकर्तृत्व वर्णन केले आहे.

विश्वेश्वरय्यांनी त्यांच्या काळात समोर उभ्या ठाकलेल्या जटिल समस्या सोडवल्या. त्यांचे प्रयत्न म्हणजे केवळ स्वत:ची बुद्धिमत्ता सिद्ध करण्यासाठी केलेली कृती नव्हती. त्यांच्यासमोर लोकांच्या समस्या सोडवण्याचे आव्हान होते. आपले ज्ञान, आपली कर्तबगारी समाजाच्या कल्याणासाठी वापरली गेली पाहिजे, ही त्यांची भूमिका होती. या पाठात वर्णन केलेली त्यांची कार्ये ही त्यांच्या भूमिकेचाच परिपाक होती. त्यांनी आपले दीर्घायुष्य या त-हेने माणसाच्या कल्याणासाठी वापरले, हेच या पाठातून लेखकांनी दाखवून दिले आहे.

शब्दार्थ:

1. नियंता – नियंत्रक.
2. विश्वात्मकता – विश्वाला व्यापून टाकण्याची वृत्ती.
3. क्लिष्ट – गुंतागुंतीची.
4. कारकीर्द – केलेल्या कार्याचा काळ.

वाक्प्रचार व त्यांचे अर्थ:

1. आव्हान स्वीकारणे – एखादे कार्य पार पाडण्यास सिद्ध होणे.
2. रौद्ररूप धारण करणे – भीतिदायक स्थिती निर्माण होणे.

Balbharti Maharashtra State Board Class 9 Marathi Solutions Aksharbharati Chapter 4.1 काझीरंगा Notes, Textbook Exercise Important Questions and Answers.

Maharashtra State Board Class 9 Marathi Aksharbharati Solutions Chapter 4.1 काझीरंगा (स्थूलवाचन)

Marathi Aksharbharati Std 9 Digest Chapter 4.1 काझीरंगा Textbook Questions and Answers

स्वाध्याय :

1. काझीरंगा अभयारण्याची वैशिष्ट्ये खालील मुद्द्यांना अनुसरून लिहा.

प्रश्न 1.
काझीरंगा अभयारण्याची वैशिष्ट्ये खालील मुद्द्यांना अनुसरून लिहा.
(अ) भौगोलिक वैशिष्ट्ये
(आ) प्राणिजीवन
उत्तर:
साचा भारताचे भूषण असलेले काझीरंगा हे अभयारण्य आसाम राज्यात सुमारे दोनशे पासष्ट चौरस किलोमीटर परिसरात वसलेले आहे. या परिसरात सर्वत्र चिखल खूप जास्त प्रमाणात आढळतो. इथल्या कमरेइतक्या चिखलातून फिरणे माणसाला अशक्य असते. त्याचबरोबर इथे सर्वत्र इतके उंच गवत वाढलेले असते की, त्यामध्ये हत्तीवर बसलेला माणूसही लपून जातो.

या अभयारण्यात वावरणाऱ्या प्राण्यांमध्ये इतकी विविधता आहे की, अशी विविधता एक आफ्रिका सोडल्यास इतात्र कुठेही अढळत नाही. हुलॉक नावाचा शेपटी नसलेला वानर फक्त इथेव आढळतो. आसामचे वैशिष्ट्य दाखविणारा दुसरा खास प्रापो म्हणजे एकशिंगी गेंडा होय. या ठिकाणी सगळे वन्यपशू बहुतेक सकाळी लवकर किंवा सूर्यास्ताच्या वेळी पाहायला मिळतात. इथल्या गवतांमध्ये मनसोक्त चरणाऱ्या रानम्हशींचा कळप पाहिला की, मन आनंदून जाते. किंचित काळसर अंगावर अस्पष्ट पांढुरके ठिपके असलेल्या हरणांचा उड्या मारत वेगाने पळत जाणारा कळप पाहिला की, मन समाधानाने भरून जाते.

2. ‘प्राण्यांचे गंधज्ञान’ या संकल्पनेबाबत तुमचे मत लिहा. 

प्रश्न 1.
‘प्राण्यांचे गंधज्ञान’ या संकल्पनेबाबत तुमचे मत लिहा.
उत्तरः
काझीरंगा अभयारण्यातील कमरेइतक्या चिखलातून फिरणे माणसाला अशक्य आहे. शिवाय या ठिकाणी सर्वत्र खूप उंचच उंच गवतवाढलेले दिसते. त्यामुळे इथे जंगल सफारीसाठी पंधरावीस हत्ती खास शिकवून तयार केले आहेत. या प्राण्यांचे गंधज्ञान फारच जबरदस्त असते. तोंड हवेत फिरवून चारी दिशांचा वास घेऊन आपल्या शत्रूचा, थोडक्यात जवळपास असलेल्या मृत्यूचा अंदाज त्यांना घेता येतो. त्यामुळे सावधपणे चालत चालत ते पुढचा रस्ता पार करतात. शिवाय जमिनीचा व गवताचा वास घेत घेत परतीचा प्रवास सहजपणे त्यांना करता येतो.

3. ‘काझीरंगा ही कर्दमभूमी आहे’, हे विधान सोदाहरण स्पष्ट करा.

प्रश्न 3.
‘काझीरंगा ही कर्दमभूमी आहे’, हे विधान सोदाहरण स्पष्ट करा.
उत्तरः
भारताच्या आसाम राज्यात इतर राज्यांच्या तुलनेत थोडा जास्त पाऊस पडतो. त्यामुळे या भागात झाडे – झुडुपे आणि गवत भरपूर उगवते. त्यामुळेच येथील काझीरंगाच्या अपयारण्यात चिखल खूप जास्त प्रमाणात आढळतो. काही ठिकाणी तर कमरेइतका चिखल आढळतो. त्यातून फिरणे माणसाला अशक्यच होऊन जाते.

या चिखलामुळेच वैशिष्ट्यपूर्ण असा एकशिंगी गेंडा या अभयारण्यात आढळतो. आपले शरीर थंड ठेवण्यासाठी तो स्वत:ला चिखलाने माखून घेत असतो. चिखलात पूर्णपणे माखलेला गेंडा, चिलखत घालून पायावर उभ्या असलेल्या एखादया विशालकाय योद्ध्यासारखा वाटत असतो. एकप्रकारे नैसर्गिक संरक्षणच गेंड्याला निसर्गाने बहाल केल्यासारखे वाटते.

4. टिपा लिहा. 

प्रश्न 1.
टिपा लिहा.
1. वैजयंती
2. एकशिंगी गेंडा
3. गेंड्याच्या सवयी
4. गायबगळे
उत्तर :
1. वैजयंती: काझीरंगा या अभयारण्यात प्रवाशांन फिरवून आणण्यासाठी आसाम सरकारने जे पंधरा – वीस हत्ती शिकवून तयार ठेवले आहेत त्यांपैकीच एक हत्तीण म्हणजे वैजयंती होय, ती इतर वन्यपशूना घाबरत नाही शिवाय दाट गवतातून ती सहज मार्ग काढते. जंगलात फिरण्यासाठी लेखकाला तीच हत्तीण मिळाली होती. ती खूप देखणी, इंद्राच्या ऐरावताची मुलगी शोभेल अशीच होती. गवतातून चालताना जणू रेशमी साडी सळसळते आहे, अशा ऐटीत ती चालत होती. मात्र माहुताच्या सगळ्या आज्ञा ती मानत होती.

तिचे गंधज्ञान फारच जबरदस्त होते. किंकाळी फोडून आणि तोंड हवेत फिरवून, चारी दिशांचा वास घेऊन जणू मृत्यू आजूबाजूला कुठे रेंगाळत आहे काय याचा अंदाज ती घेत आहे, असे लेखकाला एकदा जाणवले.काझीरंगाचा विस्तीर्ण वनप्रदेश तुडवत भिजलेल्या वाऱ्यावर मंद मंद गतीने तरंगत, गिरक्या घेणाऱ्या गवताचा सुगंध घेत, तसेच स्वतः बरोबर इतर प्रवाशांना जंगल भटकंतीचा आनंद मिळवून देणारी वैजयंती एक उत्कृष्ट सोबतीणच म्हणावी लागेल.

2. एकशिंगी गेंडा: आसामचे वैशिष्ट्य दाखविणारा खास प्राणी म्हणजे एकशिंगी गेंडा होय. काझीरंगा अभयारण्यात तो आढळतो. जगातील प्रचंडकाय प्राण्यांत भारतातील एकशिंगी गेंड्याचा चौथा नंबर लागतो. साधारणतः असा समज आहे की, गेंडा हत्तीच्या अंगावर चालून जातो, पण शेजाऱ्याला निष्कारण त्रास देणे त्याच्या रक्तातच नसते.

पण क्वचित एकटेपणाने वैतागलेला गेंडा समोर येणाऱ्या पशूवर आक्रमण करायला निघतो. असा एकशिंगी गेंडा प्रत्यक्ष पाहण्यासाठी लेखक काझीरंगाला गेला होता. इथे फिरत असताना थोड्याच वेळात लेखकाला जवळच चिलखत घालून पहाऱ्यावर उभ्या असलेल्या एखादया विशालकाय योद्ध्यासारखा पण निश्चल उभा असलेला एकशिंगी गेंडा दिसला.

3. गेंड्याच्या सवयी: गेंडा आपले शरीर थंड राखण्यासाठी चिखलाने अंग माखून घेतो. तो सामाजिक आरोग्याचा चाहता असतो. त्यासाठी सबंध मोठ्या जंगलात फक्त एकाच ठिकाणी जाऊन तो आपली विष्ठा टाकतो. कित्येक मैल दूर असला तरी त्याच एका जागेवर तो नेहमी परतून येतो. वाटेल तेथे घाण टाकू नये,शेजाऱ्या-पाजाऱ्यांना त्रास होईल असे वागू नये हे समजणारा गेंडा खरोखरच शहाणा व्यक्ती आहे, असेच म्हणावे लागेल.

4. गायबगळे: वैजयंती हत्तीणीवर बसून लेखक जंगल सफारी करत होता. त्यावेळी उंचच उंच गवतामधून पाच-पंधरा म्हशींचा कळप शांतपणे चरताना त्याला दिसला. म्हशी गवतातून चालतात त्यावेळी गवतातले अनेक लहन कीटक घाबरून हवेत उडतात. त्यांना खाण्यासाठी गायबगळे नेहमीच म्हशींच्या जवळ अथवा त्यांच्या पाठीवरती येऊन बसतात. विशाल शिंगांच्या दहा – पंधरा म्हशींच्या मधून वावरणारे हे बगळे पाहून लेखकाच्या मनात आले की, निसर्गाची ही काळ्यावरची पांढरी लिपी केव्हातरी कागदावर चित्रित केली पाहिजे. म्हणजेच काळ्या रानम्हशींच्या मोठ्या आणि सुंदर शिंगांच्या मधून वावरणारे पांढरे बगळे यांचे सुंदरसे चित्र कधीतरी काढावे असे लेखकाला वाटले.

5. ‘तुम्ही केलेला जंगल प्रवास’, याविषयी थोडक्यात माहिती लिहा. 

प्रश्न 1.
‘तुम्ही केलेला जंगल प्रवास’, याविषयी थोडक्यात माहिती लिहा.
उत्तरः
दोन वर्षांपूर्वी दहावीची परीक्षा संपल्यानंतर एप्रिल महिन्यामध्ये मी माझ्या काकांसोबत ‘ताडोबा राष्ट्रीय उद्यान’ पाहण्यासाठी गेलो होतो. महाराष्ट्रातील चंद्रपूर जिल्हयात असलेले हे उद्यान भारताची शान आहे. येथे प्राणी, पशु-पक्षी यांची विविधता आपण अनुभवू शकतो. इथे आढळणारा वाघ हा इचल्या आकर्षणाचे केंद्र आहे.

आम्ही पहाटे 5.30 – 6.00 वाजताच जीपमध्ये बसून जंगल सफारीसाठी निघालो. याठिकाणी जंगली पशुपक्षी पहाटे जास्त पाहण्यास मिळतात, अशी माहिती मिळाली होती. ती अगदीच खरी ठरली. आम्ही फिरण्यासाठी निघालो तेवढ्यातच पाच-सहा हरणांचा कळप आमच्या समोरून अगदी सहज उड्या मारत गेला. त्यांचा तो सोनेरी रंग, अहाहा! सीतेला त्याच्या कातडीचा मोह का झाला असावा त्यांचे कारण खऱ्या अर्थाने मला त्यावेळी उलगडले.

पशुपक्षांच्या किलबिलाटाने सारे वातावरण धुंद झाले होते. डोक्यावरून निर्भयपणे उडत जाणाऱ्या बगळ्यांची रांग पाहिली आणि बालकवींची ‘श्रावणमास’ कविताच आठवली. डोक्यावर शिंगांचा संभार मिरविणाऱ्या काळवीटांचा कळप गवतांमधून चरताना पाहिला आणि क्षणभर हरखूनच गेलो. दिवसभर भटकंती करून थकून परतीच्या वाटेवर निघालो. प्रवासी बंगला 1520 मिनिटांच्या अंतरावर असेल नसेल आणि तितक्यातच अचानक रस्त्यावर ताडोबाच्या राजाचे भव्यदिव्य दर्शन घडले.

चालकाने जीप थांबवली आणि काहीही हालचाल न करता शांतपणे समोरच्या वाघाकडे पाहण्यास सांगितले. त्याची ती भेदक नजर, डौलदार चाल पाहताना आम्हाला कसलेही भान उरले नव्हते.

काझीरंगा Summary in Marathi

लेखकाचा परिचय :

नाव : वसंत अवसरे
कालावधी : 1907 – 1976
परिचय : कवी, प्रवासवर्णनकार. ‘यात्री’ हा स्फुट कवितांचा संग्रह. ‘भिखूच्या प्रदेशातून’, ‘लाल नदी निळे डोंगर’ ही प्रवासवर्णने प्रसिद्ध. प्रवासवर्णनात निसर्गाच्या देखण्या रूपांसोबत त्या प्रदेशांतील लोकजीवनाचे सूक्ष्म अवलोकन, चिंतन व समाजवादी भूमिकेतून केलेले विश्लेषण आढळते.

प्रस्तावना :

‘काझीरंगा’ हे स्थूलवाचन लेखक ‘वसंत अवसरे’ यांनी लिहिले आहे. या पाठात भारतातील आसाम राज्याचे भूषण असलेल्या ‘काझीरंगा’ या अभयारण्यात केलेल्या जंगलसफारीचे मनोवेधक चित्रण केले आहे.

Kaziranga National Park is the ‘Jewel of Assam. A trip to this national park is attractively narrated by author Vedant Avasare in this write-up.

शब्दार्थ :

1. विस्तार – आवाका, वाढ, फैलाव, व्याप्ती (expansion, spread)
2. चौरस – square of a unit
3. वावरणे – ये-जा करणे (to move arround)
4. पुच्छविहीन – शेपटी नसलेला (without tail)
5. प्रतीक – खूण, चिन्ह (a symbol, an emblem)
6. वानर – माकड (monkey)
7. निर्बुद्ध – मूर्ख, बुद्धी नसलेला (stupid, idiot)
8. बुरबुर – पावसाची रिपरिप, बारीक पाऊस (light rain, drizzle)
9. निरभ्र – ढग नसलेला, स्वच्छ (cloudless, fair)
10. कर्दम – चिखल (mud)
11. दाट – घन (thick, dense, crowded)
12. निष्कारण – अनावश्यक (unnecessary)
13. अपवाद – नियमास बाधा आणणारी गोष्ट (exception)
14. एकलकोंडेपणा – एकटे राहायला आवडणे (an act of living alone in solitude)
15. पर्यवसान – परिणाम (the result)
16. तिरसटपणा – चिडकेपणा (hot-temper)
17. नवल – आश्चर्य (wonder, miracle)
18. प्रचंडकाय – फार मोठा, अवाढव्य (huge, massive)
19. ऐट – दिमाख, रुबाब (pomp)
20. माहूत – हत्ती हकणारा, महत (an elephant driver)
21. निश्चल – स्तब्ध, ठाम (stable, firm, fixed)
22. चिलखत – शरीराचे रक्षण करणारा लोखंडी अंगरखा (an armour)
23. मनसोक्त – मन तृप्त होईल एवढे (to one’s hearts content)
24. भोक्ता – अनुभव घेणारा (one who experiences)
25. विष्ठा – मल (excrement)
26. कळप – समुदाय (a flock, a group)
27. तर्क – अनुमान, अंदाज (guess, inference)
28. गिरकी – फेरी (whirl)
29. दृष्टी – नजर
30. लहर – अकस्मात होणारी इच्छा (whim)
31. चक्काचूर – चुराडा, विध्वंस (destruction, ruin)
32. विस्तीर्ण – पसरलेले, वाढलेले (expanded, extended)
33. हुंगत – वास घेत (to sniff, to smell)
34. धवकणे – मध्येच अकस्मात थांबणे (to stop short)
35. घोटाळणे – घुटमळणे, मागे-पुढे फिरणे (to waver, to falter)

टिपा :

• इंद्र – देवांचा राजा
• ऐरावत – इंद्राचा हत्ती
• काझीरंगा – आसाममधील एक अभयारण्य
• वैशाख – हिंदू कालगणनेतील दुसरा महिना

वाक्प्रचार :

1. नशीब जोरदार असणे – चांगले नशीब असणे
2. अंगावर चालून जाणे – हल्ला करणे
3. खूण करणे – संकेत देणे
4. दृष्टीस पडणे – दिसणे
5. चित्रित करणे – रेखाटणे
6. किंकाळी फोडणे – जोराने ओरडणे
7. मागोवा घेणे – शोध घेणे, तपास करणे
8. गिरकी घेणे – फेरी मारणे
9. बधीर होणे – काही सुचेनासे होणे

Balbharti Maharashtra State Board Class 9 Marathi Solutions Aksharbharati Chapter 12 पुन्हा एकदा Notes, Textbook Exercise Important Questions and Answers.

Maharashtra State Board Class 9 Marathi Aksharbharati Solutions Chapter 12 पुन्हा एकदा(कविता)

Marathi Aksharbharati Std 9 Digest Chapter 12 पुन्हा एकदा Textbook Questions and Answers

पाठाखालील‌ ‌स्वाध्याय:

1.‌ कवयित्रीला‌ ‌असे‌ ‌का‌ ‌म्हणावेसे‌ ‌वाटते?‌ ‌

प्रश्न‌ ‌1.
पावसाच्या‌ ‌सरी‌ ‌कोसळाव्यात,‌ ‌कारण‌ ‌….‌…..‌
उत्तरः‌
समाजातील‌ ‌असणारा‌ ‌भेदाभेद‌ ‌मिटून‌ ‌जावा.‌

प्रश्न‌ ‌2.
भुलावी‌ ‌तहान‌ ‌विसरावी‌ ‌भूक,‌ ‌कारण‌ ‌….‌…… ‌
उत्तरः‌ ‌
नवनवीन‌ ‌गोष्टींची‌ ‌निर्मिती‌ ‌करण्याची‌ ‌इच्छा‌ ‌व्हा

2. ‌खालील‌ ‌घटनांचे‌ ‌कवयित्रीला‌ ‌अपेक्षित‌ ‌परिणाम‌ ‌लिहा.‌ ‌

प्रश्न‌ ‌1.‌
‌खालील‌ ‌घटनांचे‌ ‌कवयित्रीला‌ ‌अपेक्षित‌ ‌परिणाम‌ ‌लिहा.‌ ‌

उत्तरः‌
1. वीज‌ ‌चमकणे‌ ‌-‌ ‌उत्साह‌ ‌निर्माण‌ ‌होतो,‌ ‌माणसात‌ ‌नवचैतन्य‌‌सळसळते.‌ ‌
2.‌ ‌वारा‌ ‌घु मणे‌ ‌-‌ ‌युवक‌ ‌भारला‌ ‌जाऊन,‌ ‌तहानभूक‌ ‌विसरून‌ ‌जाऊन,‌‌ नवनिर्मितीसाठी‌ ‌प्रयत्नशील‌ ‌होईल.‌

3. खालील‌ ‌प्रतिके‌ ‌व‌ ‌त्यांचा‌ ‌अर्थ‌ ‌यांच्या‌ ‌जोड्या‌ ‌लावा.

प्रश्न‌ ‌1.‌ ‌
खालील‌ ‌प्रतिके‌ ‌व‌ ‌त्यांचा‌ ‌अर्थ‌ ‌यांच्या‌ ‌जोड्या‌ ‌लावा.

उत्तरः‌

4.‌ ‌भावार्थाधारित.‌‌

‌प्रश्न‌ ‌1.
मातीत‌ ‌माती‌ ‌व्हावी‌ ‌एक…….‌ ‌पुसून‌ ‌टाकीत‌ ‌भेदाभेद……..‌ ‌या,‌‌ काव्यपंक्तीतील‌ ‌समाजिक‌ ‌आशय‌ ‌स्पष्ट‌ ‌करा.‌ ‌
उत्तरः‌
‌‘कृती‌ ‌3‌ ‌:‌ ‌काव्यसौंदर्य’‌ ‌मधील‌ (1)‌ ‌(ii)‌ ‌चे‌ ‌उत्तर‌ ‌पहा.‌

‌5.‌ ‌अभिव्यक्ती‌

‌प्रश्न‌ ‌1.
आपल्या‌ ‌देशात‌ ‌शांती‌ ‌निर्माण‌ ‌व्हावी‌ ‌यासाठी‌ ‌’पुन्हा‌ ‌एकदा’‌ ‌काय‌ ‌व्हावे‌ ‌असे‌ ‌तुम्हांस‌ ‌वाटते‌ ‌ते‌ ‌स्वत:च्या‌ ‌शब्दांत‌ ‌सविस्तर‌‌ लिहा.‌ ‌
उत्तर‌:‌ ‌
‘कृती‌ 3:‌ ‌काव्यसौंदर्य’‌ ‌मधील‌ ‌(4)‌ ‌चे‌ ‌उत्तर‌ ‌पहा.‌ ‌

‌प्रश्न‌ ‌2.
‌कवितेचा‌ ‌तुम्हाला‌ ‌समजलेला‌ ‌भावार्थ‌ ‌स्पष्ट‌ ‌करा.‌ ‌
उत्तर:‌ ‌
(कवितेचा‌ ‌भावार्थ‌ ‌पहा.)‌‌

अपठित‌ ‌गदय‌ ‌आकलन.‌‌:

1. ‌खालील‌ ‌उतारा‌ ‌काळजीपूर्वक‌ ‌वाचून‌ ‌त्याखालील‌ ‌कृती‌ ‌करा.‌

‌प्रश्न‌ ‌1.
चौकटी‌ ‌पूर्ण‌ ‌करा.‌‌
(अ)‌ ‌झेंड्याचा‌ ‌पांढरा‌ ‌रंग‌ ‌गुणांचा‌ ‌निदर्शक‌ ‌[‌ ‌]
(आ)‌ ‌झेंड्याचा‌ ‌केशरी‌ ‌रंग‌ ‌गुणांचा‌ ‌निदर्शक‌ ‌[ ]
(इ)‌ ‌झेंड्याचा‌ ‌हिरवा‌ ‌रंग‌ ‌गुणांचा‌ ‌निदर्शक‌‌ [ ]

आपल्या‌ ‌झेंड्याचा‌ ‌मधला‌ ‌भाग‌ ‌पांढरा‌ ‌आहे.‌ ‌त्याचा‌ ‌अर्थ‌ ‌काय?‌ ‌पांढरा‌ ‌रंग‌ ‌प्रकाशाचा‌ ‌सत्याचा‌ ‌व‌ ‌साधेपणाचा‌ ‌निदर्शक‌ ‌आहे‌ ‌आणि‌ ‌त्यावरील‌ ‌अशोकचक्र‌ ‌काय‌ ‌सांगते?‌ ‌ते‌ ‌सद्गुणांची,‌ ‌धर्माची‌ ‌खूण‌ ‌सांगते.‌ ‌या‌ ‌झेंड्याखाली‌ ‌काम‌ ‌करताना‌ ‌आपण‌ ‌धर्ममय‌ ‌राहू,‌ ‌सत्यमय‌ ‌राहू‌ ‌असा‌ ‌त्याचा‌ ‌अर्थ‌ ‌आहे.‌ ‌आपल्या‌ ‌वर्तनाची‌ ‌ही‌ ‌सूत्रे‌ ‌राहू‌ ‌देत.‌ ‌या‌ ‌चक्राचा‌ ‌आणखी‌ ‌काय‌ ‌अर्थ‌ ‌आहे?‌ ‌चक्र‌ ‌म्हणजे‌ ‌गती.‌ ‌हे‌ ‌चक्र‌ ‌सांगते,‌ ‌की‌ ‌गतिमान‌ ‌राहा.‌ ‌केशरी‌ ‌रंग‌ ‌त्यागाचा‌ ‌व‌ ‌नम्रतेचा‌ ‌निदर्शक‌ ‌आहे‌ ‌आणि‌ ‌हिरवा‌ ‌रंग‌ ‌म्हणजे‌ ‌हरितश्यामल‌ ‌भूमातेचा.‌ ‌या‌ ‌ध्वजाखाली‌ ‌उभे‌ ‌राहून‌ ‌सेवावृत्तीने‌ ‌व‌ ‌निरहंकारीपणाने‌ ‌आपण‌ ‌पृथ्वीवर‌ ‌स्वर्ग‌ ‌निर्मूया.‌‌

‌

2. झेंड्यातील‌ ‌अर्थपूर्णता‌ ‌स्वभाषेत‌ ‌स्पष्ट‌ ‌करा.

‌प्रश्न‌ ‌1.
झेंड्यातील‌ ‌अर्थपूर्णता‌ ‌स्वभाषेत‌ ‌स्पष्ट‌ ‌करा.

Marathi Akshar Bharati Class 9 Textbook Solutions Chapter 12 पुन्हा एकदा Additional Important Questions and Answers

पुढील‌ ‌पक्ष्याच्या‌ ‌आधारे‌ ‌दिलेल्या‌ ‌सूचनेनुसार‌ ‌कृती‌ ‌करा:‌ ‌

कृती‌ ‌1‌:‌ ‌आकलन‌ ‌कृती‌

प्रश्न‌‌ ‌1.‌ ‌
आकृतिबंध‌ ‌पूर्ण‌ ‌करा
उत्तरः‌ ‌

प्रश्न‌‌ ‌2.‌ ‌
उत्तर‌ ‌लिहा.‌
1. ‌रक्तात‌ ‌भिनावी‌ ‌-‌ ‌[ ]
2. ‌पिंगा‌ ‌घालणाऱ्या‌ ‌-‌ ‌[ ]‌ ‌
उत्तर:‌
‌1. वीज‌ ‌
2.‌ ‌पावसाच्या‌ ‌सरी

खालील‌ ‌प्रश्नांची‌ ‌उत्तरे‌ ‌एका‌ ‌वाक्यात‌ ‌लिहा.‌ ‌

प्रश्न‌‌ ‌1.
पुन्हा‌ ‌एकदा‌ ‌कोण‌ ‌चमकावे‌ ‌असे‌ ‌कवयित्रीला‌ ‌वाटते?‌ ‌
उत्तरः‌ ‌
पुन्हा‌ ‌एकदा‌ ‌वीज‌ ‌चमकावी‌ ‌असे‌ ‌कवयित्रीला‌ ‌वाटते.‌ ‌

प्रश्न 2.
पुन्हा‌ ‌एकदा‌ ‌पिंगा‌ ‌घालीत‌ ‌कोण‌ ‌यावे?‌ ‌
उत्तरः‌ ‌
पुन्हा‌ ‌एकदा‌ ‌पिंगा‌ ‌घालीत‌ ‌पावसाच्या‌ ‌सरी‌ ‌याव्यात.‌

प्रश्न‌‌ ‌3.
‌बेभान‌ ‌कोण‌ ‌व्हावे‌ ‌असे‌ ‌कवयित्रीला‌ ‌वाटते?‌ ‌
उत्तर‌‌:‌ ‌
पावसाच्या‌ ‌सरी‌ ‌बेभान‌ ‌व्हाव्यात‌ ‌असे‌ ‌कवयित्रीला‌ ‌वाटते.‌

प्रश्न‌‌ ‌4.
‌कवयित्रीच्या‌ ‌मते‌ ‌नवनिर्माणाची‌ ‌चाहूल‌ ‌कोणाला‌ ‌लागावी?‌ ‌
उत्तरः‌
‌कवयित्रीच्या‌ ‌मते‌ ‌नवनिर्माणाची‌ ‌चाहूल‌ ‌युवकाला‌ ‌लागावी.‌

प्रश्न‌‌ ‌5.
‌कवयित्री‌ ‌कोणाला‌ ‌तहान,‌ ‌भूक‌ ‌विसरायला‌ ‌सांगते?‌ ‌
उत्तरः‌ ‌
कवयित्री‌ ‌युवकाला‌ ‌तहान,‌ ‌भूक‌ ‌विसरायला‌ ‌सांगते.‌‌

कंसातील‌ ‌योग्य‌ ‌शब्द‌ ‌वापरून‌ ‌रिकाम्या‌ ‌जागा‌ ‌भरा.‌

प्रश्न‌‌ ‌1.‌

1. पुन्हा‌ ‌एकदा‌ ‌चमकावी‌‌ ………………………. (वीज,‌ ‌तार,‌ ‌काच,‌ ‌काया)
2. भिनावी‌ ‌…………..‌ ‌पेटावे‌ ‌स्नायू‌‌ (मातीत,‌ ‌पाण्यात,‌ ‌रक्तात,‌ ‌अंगात)‌ ‌
3. ‌पुन्हा‌ ‌एकदा‌ ‌घालीत‌ ‌………….”‌ ‌पावसाच्या‌ ‌सरी‌ ‌व्हाव्यात‌ ‌बेभान.‌ (धिंगाना,‌ ‌पिंगा,‌ ‌वरी,‌ ‌नाच)‌ ‌
4. ‌मातीत‌ ‌…………..‌ ‌व्हावी‌ ‌एक.‌‌ (मातीत,‌ ‌माती,‌ ‌धन,‌ ‌पाणी)‌
5. पुसून‌ ‌टाकीत‌ ‌…………..‌ ‌पुन्हा‌ ‌एकवेळ.‌‌ (जातीभेद,‌ ‌धर्मभेद,‌ ‌भेदाभेद,‌ ‌धर्म)‌
6. ‌(पुन्हा‌ ‌एकदा‌ ‌घुमावा‌ ‌वारा‌ ‌………… ‌इथला‌ ‌भारला‌ ‌जावा.‌‌ (माणूस,‌ ‌युवक,‌ ‌मुलगा,‌ ‌बाप)‌ ‌
7. ‌नवनिर्माणाची‌ ‌लागावी‌ ‌चाहूल‌ ‌उजळावी‌‌ (भूमी,‌ ‌जमीन,‌ ‌पठार,‌ ‌दरी)‌ ‌

उत्तर‌‌:‌

1. वीज‌
2. रक्तात‌
3. पिंगा‌
4. ‌माती‌
5. भेदाभेद‌‌
6. युवक‌ ‌
7. ‌भूमी‌ ‌

‌जोड्या‌ ‌जुळवा.‌ ‌

प्रश्न‌‌ ‌1.‌

‌उत्तर:‌

प्रश्न‌‌ ‌2.‌

‌उत्तर:‌

प्रश्न‌‌ 3.‌

उत्तर:‌

कृती‌ ‌2‌:‌ ‌आकलन‌ ‌कृती‌ ‌

प्रश्न‌‌ 1.
‌समान‌ ‌अर्थाच्या‌ ‌काव्यपंक्ती‌ ‌शोधून‌ ‌लिहा.‌

1. मातीत‌ ‌माती‌ ‌मिसळून‌ ‌जावी‌ ‌व‌ ‌एक‌ ‌व्हावी.‌‌
2. पावसाच्या‌ ‌सरी‌ ‌पिंगा‌ ‌घालीत‌ ‌बेभान‌ ‌होऊन‌ ‌याव्यात.‌ ‌
3. ‌पुन्हा‌ ‌एकदा‌ ‌नव्या‌ ‌सुधारणांचा‌ ‌वारा‌ ‌आपल्या‌ ‌समाजात‌ ‌घुमत‌ ‌यावा.‌ ‌
4. आपली‌ ‌भारतभूमी‌ ‌पुन्हा‌ ‌एकदा‌ ‌प्रखर‌ ‌तेजाने‌ ‌तळपावी‌ ‌तिची‌‌ किर्ती‌ ‌सगळ्या‌ ‌जगभर‌ ‌पसरावी.‌ ‌

उत्तर:‌

1. ‌मातीत‌ ‌माती‌ ‌व्हावी‌ ‌एक‌‌
2. ‌घालीत‌ ‌पिंगा‌ ‌पावसाच्या‌ ‌सरी‌ ‌व्हाव्यात‌ ‌बेभान‌
3. पुन्हा‌ ‌एकदा‌ ‌घुमावा‌ ‌वारा‌‌
4. उजळावी‌ ‌भूमी‌ ‌………….‌ ‌दिगंतात‌ ‌….‌……… ‌

प्रश्न‌‌ 2.
काव्यपंक्तींचा‌ ‌योग्य‌ ‌क्रम‌ ‌लावा.‌

1. ‌रीत‌ ‌पुकार‌ ‌
2. भिनावी‌ ‌रक्तात‌ ‌
3. चमकावी‌ ‌वीज‌ ‌
4. पेटावे‌ ‌स्नायू‌ ‌
5. ‌पुसून‌ ‌टाकीत‌ ‌भेदाभेद‌ ‌
6. ‌पावसाच्या‌ ‌सरी‌ ‌व्हाव्यात‌ ‌बेभान‌ ‌
7. ‌पुन्हा‌ ‌एकदा‌ ‌घालीत‌ ‌पिंगा‌ ‌
8. ‌पुन्हा‌ ‌एकवेळ‌ ‌…..‌
9. ‌उजळावी‌ ‌भूमी‌ ‌…..‌ ‌दिगंतात‌ ‌….‌
10. ‌युवक‌ ‌इथला‌ ‌भारला‌ ‌जावा‌ ‌
11. पुन्हा‌ ‌एकदा‌ ‌घुमावा‌ ‌वारा‌ ‌
12. नवनिर्माणाची‌ ‌लागावी‌ ‌चाहूल‌ ‌

उत्तर:‌ ‌

1. ‌चमकावी‌ ‌वीज‌‌
2. भिनावी‌ ‌रक्तात‌
3. ‌पेटावे‌ ‌स्नायू‌
4. ‌करीत‌ ‌पुकार‌ ‌
5. पुन्हा‌ ‌एकदा‌ ‌घालीत‌ ‌पिंगा‌ ‌
6. पावसाच्या‌ ‌सरी‌ ‌व्हाव्यात‌ ‌बेभान‌
7. ‌पुसून‌ ‌टाकीत‌ ‌भेदाभेद‌ ‌
8. पुन्हा‌ ‌एकवेळ‌
9. पुन्हा‌ ‌एकदा‌ ‌घुमावा‌ ‌वारा‌‌
10. ‌युवक‌ ‌इथला‌ ‌भारला‌ ‌जावा‌
11. नवनिर्माणाची‌ ‌लागावी‌ ‌चाहूल‌‌
12. उजळावी‌ ‌भूमी‌ ‌…….‌ ‌दिगंतात‌ ‌….‌ ‌

प्रश्न‌‌ 3.
काव्यपंक्तींवरून‌ ‌शब्दांचा‌ ‌योग्य‌ ‌क्रम‌ ‌लावा.‌‌

1. पुकार,‌ ‌चमकावी,‌ ‌रक्तात,‌ ‌स्नायू‌ ‌
2. ‌एकदा,‌ ‌उतरावी,‌ ‌एकवार,‌ ‌करीत‌ ‌
3. ‌एकवेळ,‌ ‌एकदा,‌ ‌टाकीत,‌ ‌घालीत‌ ‌
4. पिंगा,‌ ‌भेदाभेद,‌ ‌बेभान,‌ ‌कोसळाव्यात‌ ‌
5. ‌युवक,‌ ‌वारा,‌ ‌भूक,‌ ‌भूमी.‌
6. चाहूल,‌ ‌भारला,‌ ‌घुमावा,‌ ‌विसरावी‌

‌उत्तर:‌

1. ‌चमकावी,‌ ‌रक्तात,‌ ‌स्नायू,‌ ‌पुकार‌‌
2. एकदा,‌ ‌उतरावी,‌ ‌करीत,‌ ‌एकवार‌ ‌
3. एकदा,‌ ‌घालीत,‌ ‌टाकीत,‌ ‌एकवेळ‌
4. पिंगा,‌ ‌बेभान,‌ ‌कोसळाव्यात,‌ ‌भेदाभेद‌
5. वारा,‌ ‌युवक,‌ ‌भूक,‌ ‌भूमी‌‌
6. घुमावा,‌ ‌भारला,‌ ‌विसरावी,‌ ‌चाहूल‌

प्रश्न‌ ‌तयार‌ ‌करा.‌ ‌

प्रश्न‌‌ 1.‌
‌पुन्हा‌ ‌एकदा‌ ‌चमकावी‌ ‌वीज.‌
‌उत्तरः‌
‌पुन्हा‌ ‌एकदा‌ ‌कोणी‌ ‌चमकावे?‌

प्रश्न‌‌ 2.
‌पावसाच्या‌ ‌सरी‌ ‌व्हाव्यात‌ ‌बेभान‌
‌उत्तरः‌
‌बेभान‌ ‌कोणी‌ ‌व्हावे‌ ‌असे‌ ‌कवयित्रीला‌ ‌वाटते?‌

प्रश्न‌‌ 3.
पुन्हा‌ ‌एकदा‌ ‌घुमावा‌ ‌वारा.‌ ‌
उत्तरः‌
‌पुन्हा‌ ‌एकदा‌ ‌कोण‌ ‌घुमावा?‌ ‌

प्रश्न‌‌ 4.‌
‌नवनिर्माणाची‌ ‌लागावी‌ ‌चाहूल.‌ ‌
उत्तरः‌
‌कोणाची‌ ‌चाहूल‌ ‌लागावी?‌ ‌

कृती‌ ‌3 ‌:‌ ‌काव्यसौंदर्य‌

खालील‌ ‌काव्यपंक्तीतील‌ ‌आशयसौंदर्य‌ ‌स्पष्ट‌ ‌करा.‌

प्रश्न‌‌ 1.
‌पुन्हा‌ ‌एकदा,‌ ‌चमकावी‌ ‌वीज,‌ ‌उतरावी‌ ‌खाली,‌ ‌भिनावी‌‌ रक्तात‌
‌उत्तरः‌
‌वीज‌ ‌हे‌ ‌सळसळत्या‌ ‌उत्साहाचे‌ ‌प्रतीक‌ ‌आहे.‌ ‌सध्या‌‌ समाजामध्ये‌ ‌जी‌ ‌मरगळ‌ ‌दिसते‌ ‌आहे.‌ ‌ती‌ ‌मरगळ‌ ‌नष्ट‌ ‌होऊन‌ ‌माणसांमध्ये‌ ‌उत्साह‌ ‌निर्माण‌ ‌व्हावा‌ ‌असे‌ ‌येथे‌ ‌कवयित्रीला‌ ‌सूचित‌ ‌करायचे‌ ‌आहे.‌ ‌प्रत्येकाच्या‌ ‌रोमारोमात‌ ‌चैतन्य‌ ‌निर्माण‌ ‌झाले‌ ‌पाहिजे.‌ ‌प्रत्येकजण‌ ‌उत्साहाने‌ ‌चांगले‌ ‌कार्य‌ ‌करण्यासाठी‌ ‌पुढे‌ ‌यावा‌ ‌आणि‌ ‌त्याच्या‌ ‌हातून‌ ‌देशासाठी‌ ‌काहीतरी‌ ‌चांगल्या‌ ‌गोष्टी‌ ‌घडल्या‌ ‌पाहिजेत.‌‌

प्रश्न‌‌ 2.
मातीत‌ ‌माती‌ ‌व्हावी‌ ‌एक…‌ ‌पुसून‌ ‌टाकीत‌ ‌भेदाभेद…‌ ‌
उत्तरः‌
‌पुन्हा‌ ‌एकदा‌ ‌पावसाच्या‌ ‌सरी‌ ‌बेभान‌ ‌होऊन‌ ‌कोसळाव्यात.‌‌ या‌ ‌बेभान‌ ‌सरींमुळे‌ ‌मातीत‌ ‌माती‌ ‌मिसळून‌ ‌जावी.‌ ‌ती‌ ‌एकजीव‌ ‌व्हावी.‌ ‌याचाच‌ ‌अर्थ‌ ‌या‌ ‌मातीतील‌ ‌म्हणजे‌ ‌समाजातील‌ ‌सगळा‌ ‌भेदाभेद‌ ‌मिटून‌ ‌जावा.‌ ‌समाजात‌ ‌एकोपा‌ ‌निर्माण‌ ‌व्हावा.‌ ‌म्हणून‌‌ मातीत‌ ‌माती‌ ‌एक‌ ‌व्हावी‌ ‌असे‌ ‌कवयित्रिला‌ ‌वाटते.‌

पुढील‌ ‌ओळींचा‌ ‌अर्थसौंदर्य‌ ‌स्पष्ट‌ ‌करा.‌‌

प्रश्न‌‌ 1.
उतरावी‌ ‌खाली,‌ ‌भिनावी‌ ‌रक्तात‌ ‌
उत्तरः‌
‌निसर्गातील‌ ‌विविध‌ ‌प्रतिकांचा‌ ‌वापर‌ ‌करीत‌ ‌कवयित्री‌‌ नवनिर्मितीचा‌ ‌ध्यास‌ ‌घेतलेल्या‌ ‌मनाच्या‌ ‌भावस्थितीचे‌ ‌छान‌ ‌वर्णन‌ ‌करतात.‌ ‌त्या‌ ‌म्हणतात‌ ‌की,‌ ‌पुन्हा‌ ‌एकदा‌ ‌वीज‌ ‌चमकून‌ ‌खाली‌ ‌उतरून‌ ‌यावी.‌ ‌त्या‌ ‌वीजेचे‌ ‌तेज,‌ ‌तिची‌ ‌प्रखरता‌ ‌माणसांच्या‌‌
रक्तात‌ ‌भिनावी.‌ ‌

प्रश्न‌‌ 2.
‌मातीत‌ ‌माती‌ ‌व्हावी‌ ‌एक…पुसून‌ ‌टाकीत‌ ‌भेदाभेद….‌ ‌
उत्तरः‌
‌बेभान‌ ‌सरींमुळे‌ ‌मातीत‌ ‌माती‌ ‌मिसळून‌ ‌जावी.‌ ‌याचाच‌‌ अर्थ‌ ‌या‌ ‌मातीतील‌ ‌म्हणजे‌ ‌समाजातील‌ ‌सगळा‌ ‌भेदाभेद‌ ‌मिटून‌ ‌जावा,‌ ‌संपून‌ ‌जावा,‌ ‌असे‌ ‌कवयित्रीला‌ ‌वाटते.‌ ‌म्हणजेच‌ ‌समाजात‌ ‌असलेला‌ ‌गरीब-श्रीमंत,‌ ‌उच्च-नीच,‌ ‌जात-धर्म,‌ ‌स्त्री-पुरुष‌ ‌असा‌ ‌विविध‌ ‌प्रकाराचा‌ ‌भेदाभेद‌ ‌नष्ट‌ ‌होऊन‌ ‌भेदभावरहित‌ ‌नव्या‌‌ समाजाची‌ ‌निर्मिती‌ ‌व्हावी,‌ ‌असे‌ ‌कवयित्रिला‌ ‌वाटते.‌ ‌

प्रश्न‌‌ 3.
‌उजळावी‌ ‌भूमी‌ ‌…‌….. ‌दिगंतात‌ ‌…‌……‌
उत्तरः‌
‌नव्या‌ ‌विचारांनी,‌ ‌नव्या‌ ‌कर्तृत्वाने‌ ‌आपली‌ ‌सारी‌ ‌भूमी‌‌ उजळून‌ ‌निघावी.‌ ‌म्हणजेच‌ ‌आपली‌ ‌भारतभूमी‌ ‌पुन्हा‌ ‌एकदा‌ ‌प्रखर‌ ‌तेजाने‌ ‌तळपावी,‌ ‌तिची‌ ‌कीर्ती‌ ‌सगळ्या‌ ‌जगभर‌ ‌पसरावी,‌ ‌असेच‌‌ कवयित्रीला‌ ‌वाटते.‌ ‌

प्रश्न‌‌ 4.
‌पुन्हा‌ ‌एकदा,‌ ‌घुमावा‌ ‌वारा,‌ ‌युवक‌ ‌इथला,‌ ‌भारला‌ ‌जावा‌ ‌
उत्तरः‌
‌नवनिर्मितीचे‌ ‌विचार‌ ‌प्रखरतेने‌ ‌मांडताना‌ ‌कवयित्री‌ ‌म्हणतात‌‌ की,‌ ‌पुन्हा‌ ‌एकदा‌ ‌नव्या‌ ‌सुधारणांचा‌ ‌वारा‌ ‌आपल्या‌ ‌समाजात‌ ‌घुमत‌‌ यावा.‌ ‌या‌ ‌वाऱ्याने‌ ‌इथला‌ ‌प्रत्येक‌ ‌युवक‌ ‌भारून‌ ‌जावा.‌ ‌

प्रश्न‌‌ 3.
क्रांती‌ ‌आपोआप‌ ‌होत‌ ‌नाही‌ ‌तर‌ ‌ती‌ ‌घडवून‌ ‌आणावी‌ ‌लागते,‌‌ यावर‌ ‌तुमचे‌ ‌मत‌ ‌सोदाहरण‌ ‌स्पष्ट‌ ‌करा.‌ ‌
उत्तरः‌
‌क्रांती‌ ‌आपोआप‌ ‌होत‌ ‌नसली‌ ‌तरी‌ ‌ती‌ ‌घडवून‌ ‌आणण्यासाठी‌‌ तशी‌ ‌परिस्थिती‌ ‌निर्माण‌ ‌व्हावी‌ ‌लागते.‌ ‌क्रांतीमुळे‌ ‌समाजात‌ ‌परिवर्तन‌ ‌होत‌ ‌असते.‌ ‌संपूर्ण‌ ‌समाजात‌ ‌व‌ ‌देशात‌ ‌आमूलाग्र‌ ‌बदल‌ ‌घडवून‌ ‌आणण्याचे‌ ‌सामर्थ्य‌ ‌क्रांतीत‌ ‌असते,‌ ‌तिला‌ ‌घडवून‌ ‌आणण्यासाठी‌ ‌समाजातील‌ ‌कोणीतरी‌ ‌व्यक्ती‌ ‌पुढाकार‌ ‌घेते.‌ ‌ती‌ ‌आपले‌ ‌ज्वलंत‌ ‌विचार‌ ‌लिखित‌ ‌स्वरूपात‌ ‌मांडते‌ ‌व‌ ‌पुढे‌‌ व्यक्त‌ ‌करते.‌ ‌त्याचे‌ ‌वाचन‌ ‌करून‌ ‌लोकांमध्ये‌ ‌तत्कालीन‌ ‌रूढी,‌ ‌परंपरा‌ ‌वा‌ ‌विचारधारणेविषयी‌ ‌तिटकारा‌ ‌निर्माण‌ ‌होतो.‌ ‌जनता‌ ‌आपल्यावर‌ ‌होत‌ ‌असलेला‌ ‌अन्याय,‌ ‌अत्याचार‌ ‌यांविरोधात‌ ‌जागृत‌ ‌होते‌ ‌व‌ ‌क्रांतीस‌ ‌सिद्ध‌ ‌होते.‌ ‌रूसोचे‌ ‌विचार‌ ‌वाचून‌ ‌फ्रेंच‌ ‌लोक‌ ‌राज्यक्रांती‌ ‌करण्यास‌ ‌सिद्ध‌ ‌झाले‌ ‌होते.‌ ‌केसरीतील‌ ‌लोकमान्य‌ ‌टिळकांचे‌ ‌लेख‌ ‌वाचून‌ ‌लोक‌ ‌इंग्रजांविरोधात‌ ‌चिडून‌‌ उठले‌ ‌होते.‌

प्रश्न‌‌ 4.
‌आपल्या‌ ‌देशात‌ ‌शांती‌ ‌निर्माण‌ ‌व्हावी‌ ‌यासाठी‌ ‌’पुन्हा‌ ‌एकदा’‌‌ काय‌ ‌व्हावे‌ ‌असे‌ ‌तुम्हांस‌ ‌वाटते‌ ‌ते‌ ‌स्वत:च्या‌ ‌शब्दांत‌ ‌सविस्तर‌‌ लिहा.‌ ‌
उत्तरः‌
‌आपल्या‌ ‌देशात‌ ‌आज‌ ‌भ्रष्टाचार,‌ ‌अन्याय,‌ ‌अत्याचार,‌‌ स्त्रीशोषण,‌ ‌बालशोषण‌ ‌असे‌ ‌अनेक‌ ‌वाईट‌ ‌प्रकार‌ ‌घडत‌ ‌आहेत.‌ ‌त्यामुळे‌ ‌आपल्या‌ ‌देशात‌ ‌आज‌ ‌अशांतीचे‌ ‌वातावरण‌ ‌निर्माण‌ ‌झालेले‌ ‌आहे.‌ ‌यासाठी‌ ‌पुन्हा‌ ‌एकदा’‌ ‌क्रांती‌ ‌घडवून‌ ‌आणण्यासाठी‌ ‌सर्वांनी‌ ‌एकत्र‌ ‌येणे‌ ‌आवश्यक‌ ‌बनलेले‌ ‌आहे.‌ ‌देशात‌ ‌वाढत‌ ‌चाललेली‌ ‌अराजकता‌ ‌व‌ ‌अंधाधुंदी‌ ‌कमी‌ ‌करण्यासाठी‌ ‌सर्वांनी‌ ‌प्रामाणिकपणाने‌ ‌आपले‌ ‌कर्तव्य‌ ‌निभावले‌ ‌पाहिजे.‌ ‌’मी‌ ‌भ्रष्टाचार‌ ‌करणार‌ ‌नाही‌ ‌वा‌ ‌इतरांना‌ ‌करू‌ ‌देणार‌ ‌नाही’,‌ ‌यावर‌ ‌सर्वांनी‌ ‌ठाम‌ ‌असले‌ ‌पाहिजे.‌ ‌संविधानाच्या‌ ‌विरोधात‌ ‌कार्य‌ ‌करत‌ ‌असलेल्या‌ ‌लोकांना‌ ‌पकडून‌ ‌पोलीस‌ ‌ठाण्यात‌ ‌दिले‌ ‌पाहिजे.‌ ‌देशसेवेचे‌ ‌बाळकडू‌ ‌सर्वांनी‌ ‌प्राशन‌ ‌केले‌ ‌पाहिजे.‌ ‌यासाठी‌ ‌सर्वांनी‌ ‌मिळून‌‌ पुन्हा‌ ‌एकदा‌ ‌अभियान‌ ‌चालविले‌ ‌पाहिजे.‌ ‌

प्रश्न‌‌ 5.
‌नवनिर्मितीचा‌ ‌ध्यास‌ ‌घेतलेले‌ ‌लोक‌ ‌सर्वसामान्यांपेक्षा‌ ‌वेगळे‌ असतात,‌ ‌यावर‌ ‌तुमचे‌ ‌विचार‌ ‌सोदाहरण‌ ‌स्पष्ट‌ ‌करा.‌
‌उत्तरः‌ ‌
नवनिर्मिती‌ ‌म्हणजे‌ ‌जुन्या‌ ‌चालीरीती,‌ ‌रूढी,‌ ‌परंपरा,‌ ‌समाजात‌‌ प्रचलित‌ ‌असलेल्या‌ ‌सामाजिक‌ ‌समस्या‌ ‌यांचा‌ ‌नाश‌ ‌करून‌ ‌नवीन‌ ‌मूल्यांवर‌ ‌आधारित‌ ‌समाजाची‌ ‌स्थापना‌ ‌करणे‌ ‌होय.‌ ‌अशा‌ ‌या‌ ‌नवनिर्मितीचा‌ ‌ध्यास‌ ‌घेतलेले‌ ‌लोक‌ ‌इतरांहून‌ ‌वेगळेच‌ ‌असतात.‌ ‌ते‌ ‌आपल्या‌ ‌ध्यासाने‌ ‌भारावलेले‌ ‌असतात.‌ ‌नवनिर्मितीचा‌ ‌ध्यास‌ ‌साकार‌ ‌करण्यासाठी‌ ‌ते‌ ‌समाजात‌ ‌क्रांती‌ ‌घडवून‌ ‌आणतात.‌ ‌आपल्या‌ ‌ज्वलंत‌ ‌विचारांनी‌ ‌व‌ ‌कृतीतून‌ ‌ते‌ ‌समाजापुढे‌ ‌एक‌ ‌आदर्श‌ ‌निर्माण‌ ‌करतात.‌ ‌नवनिर्मितीचा‌ ‌ध्यास‌ ‌घेतलेली‌ ‌माणसे‌ ‌ध्येयवेडी‌ ‌असतात.‌ ‌नेल्सन‌ ‌मंडेला‌ ‌यांनीसुद्धा‌ ‌प्रस्थापित‌ ‌समाजरचनेविरोधात‌ ‌जो‌ ‌संघर्ष‌ ‌केला‌ ‌होता‌ ‌तो‌ ‌खरोखरच‌ ‌प्रशंसनीयच‌ ‌होता.‌ ‌स्वामी‌ ‌विवेकानंद,‌ ‌आगरकर,‌ ‌लोकमान्य‌ ‌टिळक‌ ‌यांनी‌ ‌सुद्धा‌ ‌नवनिर्मितीसाठी‌ ‌भगीरथ‌ ‌प्रयत्न‌ ‌केले‌ ‌होते;‌ ‌म्हणून‌ ‌या‌ ‌सर्वांना‌ ‌सर्वसामान्यांपेक्षा‌ ‌मानाचे‌ ‌व‌ ‌आदराचे‌ ‌स्थान‌ ‌आहे.‌‌

प्रश्न‌‌ 6.
दिलेल्या‌ ‌मुद्द्यांच्या‌ ‌आधारे‌ ‌कवितेसंबंधी‌ ‌पुढील‌ ‌कृती‌‌ सोडवा.‌ ‌
‌उत्तरः‌ ‌
1. कवी/‌ ‌कवयित्रीचे‌ ‌नाव‌ ‌-‌‌ प्रतिमा‌ ‌इंगोले‌ ‌

2. ‌संदर्भ‌ ‌-‌‌
‘पुन्हा‌ ‌एकदा’‌ ‌ही‌ ‌कविता‌ ‌कवयित्री‌ ‌प्रतिमा‌ ‌इंगोले‌ ‌यांनी‌ ‌लिहिली‌‌ आहे.‌ ‌ही‌ ‌कविता‌ ‌त्यांच्या‌ ‌’भुलाई’‌ ‌या‌ ‌कवितासंग्रहातील‌ ‌आहे.‌ ‌

3‌. ‌प्रस्तावना‌ ‌-‌‌
‘पुन्हा‌ ‌एकदा’‌ ‌ही‌ ‌कविता‌ ‌कवयित्री‌ ‌प्रतिमा‌ ‌इंगोले‌ ‌यांनी‌ ‌लिहिली‌ ‌आहे.‌ ‌या‌ ‌कवितेत‌ ‌नवनिर्माणाचा‌ ‌ध्यास‌ ‌घेतलेल्या‌ ‌मनाच्या‌ ‌भावस्थितीचे‌ ‌सुरेख‌ ‌वर्णन‌ ‌कवयित्रीने‌ ‌केले‌ ‌आहे.‌ ‌वाङमयप्रकारसामाजिक‌ ‌कविता‌ ‌कवितेचा‌ ‌विषयनवनिर्मितीचा‌ ‌ध्यास‌ ‌घेतलेल्या‌ ‌मनाच्या‌ ‌भावस्थितीचे‌ ‌वर्णन‌ ‌करणारी‌‌
पुन्हा‌ ‌एकदा‌ ‌ही‌ ‌कविता‌ ‌सामाजिक‌ ‌भान‌ ‌असलेली‌ ‌कविता‌ ‌आहे.‌

4. वाङमयप्रकार‌‌-
सामाजिक‌ ‌कविता‌

5. ‌कवितेचा‌ ‌विषय‌‌-
नवनिर्मितीचा‌ ‌ध्यास‌ ‌घेतलेल्या‌ ‌मनाच्या‌ ‌भावस्थितीचे‌ ‌वर्णन‌ ‌करणारी‌ ‌पुन्हा‌ ‌एकदा‌ ‌ही‌ ‌कविता‌ ‌सामाजिक‌ ‌भान‌ ‌असलेली‌ ‌कविता‌ ‌आहे.‌‌

6. कवितेतील‌ ‌आवडलेली‌ ‌ओळ‌‌
मातीत‌ ‌माती‌ ‌
व्हावी‌ ‌एक‌ ‌…‌
‌पुसून‌ ‌टाकीत‌‌
भेदाभेद…‌ ‌

7.‌ ‌मध्यवर्ती‌ ‌कल्पना‌ ‌-‌‌
समाजातील‌ ‌जुन्या‌ ‌रूढी,‌ ‌रीतिरिवाज,‌ ‌परंपरा,‌ ‌भेदाभेद‌ ‌नष्ट‌ ‌करून‌ ‌नवनिर्माणाचा‌ ‌ध्यास‌ ‌घेतलेल्या‌ ‌मनाच्या‌ ‌भावस्थितीचे‌‌ सुरेख‌ ‌वर्णन‌ ‌’पुन्हा‌ ‌एकदा’‌ ‌या‌ ‌कवितेत‌ ‌दिसून‌ ‌येते..‌ ‌

8. कवितेतून‌ ‌मिळणारा‌ ‌संदेश‌‌ –
समाजातील‌ ‌सर्व‌ ‌प्रकारचा‌ ‌भेदाभेद,‌ ‌रूढी,‌ ‌रीतीरिवाज,‌ ‌परंपरा‌ ‌इथल्या‌ ‌तरुणांनी‌ ‌नष्ट‌ ‌कराव्यात.‌ ‌तसेच‌ ‌नवीन,‌ ‌पुरोगामी‌ ‌विचारांचा‌ ‌नवा‌ ‌एकसंघ‌ ‌समाज‌ ‌निर्माण‌ ‌करण्याचा‌ ‌प्रत्येकाने‌‌ ध्यास‌ ‌घ्यावा.‌ ‌हा‌ ‌संदेश‌ ‌’पुन्हा‌ ‌एकदा’‌ ‌या‌ ‌कवितेतून‌ ‌मिळतो.‌ ‌

9. कविता‌ ‌आवडण्याची‌ ‌वा‌ ‌न‌ ‌आवडण्याची‌ ‌कारणे-
‘पुन्हा‌ ‌एकदा’‌ ‌ही‌ ‌कविता‌ ‌मला‌ ‌खूप‌ ‌आवडली‌ ‌आहे.‌ ‌त्याचे‌ ‌महत्त्वाचे‌ ‌कारण‌ ‌म्हणजे‌ ‌नवनिर्माणाचा‌ ‌ध्यास‌ ‌घेतलेल्या‌ ‌मनाच्या‌ ‌भावस्थितीचे‌ ‌वर्णन‌ ‌करण्यासाठी‌ ‌कवयित्रीने‌ ‌निसर्गातील‌ ‌विविध‌ ‌प्रतिकांचा‌ ‌अतिशय‌ ‌सुरेख‌ ‌वापर‌ ‌केलेला‌ ‌आहे.‌ ‌या‌ ‌प्रतिकांमुळे‌ ‌कविता‌ ‌जिवंत‌ ‌असल्याप्रमाणे‌ ‌भास‌ ‌होतो.‌‌

10. ‌भाषिक‌ ‌वैशिष्ट्ये‌‌-
‘पुन्हा‌ ‌एकदा’‌ ‌या‌ ‌कवितेमध्ये‌ ‌कवयित्री‌ ‌प्रतिमा‌ ‌इंगोले‌ ‌यांनी‌ ‌प्रमाण‌ ‌मराठी‌ ‌भाषेचा‌ ‌वापर‌ ‌केलेला‌ ‌आहे.‌ ‌प्रत्येक‌ ‌ओळीमध्ये‌ ‌केवळ‌ ‌दोनच‌ ‌शब्दांचा‌ ‌वापर‌ ‌करून‌ ‌वेगळा‌ ‌छान‌ ‌परिणाम‌ ‌साधला‌ ‌आहे.‌ ‌शिवाय‌ ‌निसर्गप्रतिकांचा‌ ‌योग्य‌ ‌वापर‌ ‌करीत‌ ‌अर्थाचे‌ ‌सौंदर्य‌ ‌वाढवलेले‌ ‌आहे.‌‌

‌खालील‌ ‌काव्यपंक्तींचे‌ ‌रसग्रहण‌ ‌करा.‌ ‌

प्रश्न‌ ‌1.
पुन्हा‌ ‌एकदा‌ ‌चमकावी‌ ‌वीज‌‌
उतरावी‌ ‌खाली‌ ‌भिनावी‌ ‌रक्तात‌
‌पेटावे‌ ‌स्नायू‌ ‌करीत‌ ‌पुकार‌‌
पुन्हा‌ ‌एकवार‌ ‌
उत्तरः‌
‌’पुन्हा‌ ‌एकदा’‌ ‌ही‌ ‌कविता‌ ‌कवयित्री‌ ‌प्रतिमा‌ ‌इंगोले‌ ‌यांनी‌ ‌लिहिली‌ ‌आहे.‌ ‌या‌ ‌कवितेत‌ ‌नवनिर्माणाचा‌ ‌ध्यास‌ ‌घेतलेल्या‌ ‌मनाच्या‌ ‌भावस्थितीचे‌ ‌सुरेख‌ ‌वर्णन‌ ‌कवयित्रीने‌ ‌केलेले‌ ‌आहे.‌‌

निसर्गातील‌ ‌विविध‌ ‌प्रतीकांचा‌ ‌वापर‌ ‌करीत‌ ‌कवयित्री‌ ‌नवनिर्मितीचा‌ ‌ध्यास‌ ‌घेतलेल्या‌ ‌मनाच्या‌ ‌भावस्थितीचे‌ ‌छान‌ ‌वर्णन‌ ‌करतात.‌ ‌त्या‌ ‌म्हणतात‌ ‌की,‌ ‌पुन्हा‌ ‌एकदा‌ ‌वीज‌ ‌चमकून‌ ‌खाली‌ ‌उतरून‌ ‌यावी.‌ ‌त्या‌ ‌विजेचे‌ ‌तेज,‌ ‌तिची‌ ‌प्रखरता‌ ‌माणसांच्या‌ ‌रक्तात‌ ‌भिनावी.‌ ‌म्हणजेच‌ ‌माणसांमध्ये‌ ‌पुन्हा‌ ‌एकदा‌ ‌उत्साह‌ ‌भरून‌ ‌जावा.‌ ‌त्यांचे‌ ‌स्नायू‌ ‌पेटून‌ ‌उठावेत‌ ‌म्हणजेच‌ ‌समाजातील‌ ‌जुन्या,‌ ‌अनिष्ट‌ ‌चालीरिती,‌ ‌रूढी,‌ ‌परंपरा,‌ ‌अन्याय,‌ ‌अत्याचार‌ ‌याविरुद्ध‌ ‌त्यांनी‌ ‌पेटून‌ ‌उठावे‌ ‌आणि‌ ‌ते‌ ‌सारे‌ ‌नष्ट‌ ‌करून‌ ‌त्यातून‌ ‌समाजाला‌ ‌प्रगतीपथावर‌ ‌घेऊन‌ ‌जाणारे‌ ‌नवीन‌ ‌विचार‌ ‌निर्माण‌ ‌व्हावेत.‌‌

या‌ ‌काव्यपंक्तीमध्ये‌ ‌कवयित्री‌ ‌प्रतिमा‌ ‌इंगोले‌ ‌यांनी‌ ‌प्रमाण‌ ‌मराठी‌ ‌भाषेचा‌ ‌वापर‌ ‌केलेला‌ ‌आहे.‌ ‌प्रत्येक‌ ‌ओळीमध्ये‌ ‌केवळ‌ ‌दोनच‌ ‌शब्दांचा‌ ‌वापर‌ ‌करून‌ ‌वेगळा‌ ‌छान‌ ‌परिणाम‌ ‌साधला‌ ‌आहे.‌ ‌शिवाय‌ ‌निसर्गप्रतिकांचा‌ ‌योग्य‌ ‌वापर‌ ‌करीत‌ ‌अर्थाचे‌ ‌सौंदर्य‌ ‌वाढवलेले‌ ‌आहे.‌

प्रश्न‌ ‌2.
‌पुन्हा‌ ‌एकदा‌ ‌घालीत‌ ‌पिंगा‌‌ पावसाच्या‌ ‌सरी‌ ‌व्हाव्यात‌ ‌बेभान‌ ‌कोसळाव्या‌ ‌खाली‌ ‌मातीत‌ ‌माती‌ ‌व्हावी‌ ‌एक…‌ ‌पुसून‌ ‌टाकीत‌ ‌भेदाभेद…‌‌ पुन्हा‌ ‌एकवेळ…‌ ‌
उत्तर‌:‌
‌’पुन्हा‌ ‌एकदा’‌ ‌ही‌ ‌कविता‌ ‌कवयित्री‌ ‌प्रतिमा‌ ‌इंगोले‌ ‌यांनी‌ ‌लिहिली‌ ‌आहे.‌ ‌या‌ ‌कवितेत‌ ‌नवनिर्माणाचा‌ ‌ध्यास‌ ‌घेतलेल्या‌ ‌मनाच्या‌ ‌भावस्थितीचे‌ ‌सुरेख‌ ‌वर्णन‌ ‌कवयित्रीने‌ ‌केलेले‌ ‌आहे.‌‌

‌नवनिर्मितीच्या‌ ‌विचारांनी‌ ‌प्रेरित‌ ‌झालेल्या‌ ‌मनाचे‌ ‌वर्णन‌ ‌करताना‌ ‌कवयित्री‌ ‌म्हणतात‌ ‌की,‌ ‌पुन्हा‌ ‌एकदा‌ ‌पावसाच्याव्हावी.‌ ‌याचाच‌ ‌अर्थ‌ ‌या‌ ‌मातीतील‌ ‌म्हणजेच‌ ‌समाजातील‌ ‌सगळा‌ ‌भेदाभेद‌ ‌मिटून‌ ‌जावा,‌ ‌संपून‌ ‌जावा,‌ ‌असे‌ ‌कवयित्रीला‌ ‌वाटते.‌ ‌म्हणजेच‌ ‌समाजात‌ ‌असलेला‌ ‌गरीब-श्रीमंत,‌ ‌उच्च-नीच,‌ ‌जात-धर्म,‌ ‌स्त्री-पुरुष‌ ‌असा‌ ‌विविध‌ ‌प्रकारचा‌ ‌भेदाभेद‌ ‌नष्ट‌ ‌होऊन‌ ‌भेदभावविरहित‌ ‌नव्या‌ ‌समाजाची‌ ‌निर्मिती‌ ‌व्हावी,‌ ‌असे‌ ‌कवयित्रीला‌ ‌वाटते.‌‌

या‌ ‌काव्यपंक्तीमध्ये‌ ‌कवयित्री‌ ‌प्रतिमा‌ ‌इंगोले‌ ‌यांनी‌ ‌प्रमाण‌ ‌मराठी‌ ‌भाषेचा‌ ‌वापर‌ ‌केलेला‌ ‌आहे.‌ ‌प्रत्येक‌ ‌ओळीमध्ये‌ ‌केवळ‌ ‌दोनच‌ ‌शब्दांचा‌ ‌वापर‌ ‌करून‌ ‌वेगळा‌ ‌छान‌ ‌परिणाम‌ ‌साधला‌ ‌आहे.‌ ‌शिवाय‌ ‌निसर्गप्रतिकांचा‌ ‌योग्य‌ ‌वापर‌ ‌करीत‌ ‌अर्थाचे‌ ‌सौंदर्य‌ ‌वाढवलेले‌ ‌आहे.‌

प्रश्न‌ ‌3.
पुन्हा‌ ‌एकदा‌ ‌घुमावा‌ ‌वारा‌‌
युवक‌ ‌इथला‌ ‌भारला‌ ‌जावा‌ ‌
भुलावी‌ ‌तहान‌ ‌विसरावी‌ ‌भूक‌ ‌
नवनिर्माणाची‌ ‌लागावी‌ ‌चाहूल‌ ‌
उजळावी‌ ‌भूमी…‌ ‌दिगंतात…‌‌
पुन्हा‌ ‌एकदा‌ ‌
उत्तरः‌
‌‘पुन्हा‌ ‌एकदा’‌ ‌ही‌ ‌कविता‌ ‌कवयित्री‌ ‌प्रतिमा‌ ‌इंगोले‌ ‌यांनी‌ ‌लिहिली‌ ‌आहे.‌ ‌या‌ ‌कवितेत‌ ‌नवनिर्माणाचा‌ ‌ध्यास‌ ‌घेतलेल्या‌ ‌मनाच्या‌ ‌भावस्थितीचे‌ ‌सुरेख‌ ‌वर्णन‌ ‌कवयित्रीने‌ ‌केलेले‌ ‌आहे.‌‌

नवनिर्मितीचे‌ ‌विचार‌ ‌प्रखरतेने‌ ‌मांडताना‌ ‌कवयित्री‌ ‌म्हणतात‌ ‌की,‌ ‌पुन्हा‌ ‌एकदा‌ ‌नव्या‌ ‌सुधारणांचा‌ ‌वारा‌ ‌आपल्या‌ ‌समाजात‌ ‌घुमत‌ ‌यावा.‌ ‌या‌ ‌वाऱ्याने‌ ‌इथला‌ ‌प्रत्येक‌ ‌युवक‌ ‌भारून‌ ‌जावा.‌ ‌इथल्या‌ ‌तरुणाने‌ ‌मंत्रमुग्ध‌ ‌होऊन,‌ ‌तहानभूक‌ ‌विसरून‌ ‌नवनवीन‌ ‌गोष्टी‌ ‌निर्माण‌ ‌करण्याची‌ ‌आस‌ ‌धरावी.‌ ‌नवनिर्माणाची‌ ‌चाहूल‌ ‌त्याला‌ ‌लागावी.‌ ‌नवीन‌ ‌विचारांचा‌ ‌नवा‌ ‌समाज‌ ‌निर्माण‌ ‌व्हावा.‌ ‌नव्या‌ ‌विचारांनी,‌ ‌नव्या‌ ‌कर्तृत्वाने‌ ‌आपली‌ ‌सारी‌ ‌भूमी‌ ‌उजळून‌ ‌निघावी,‌ ‌म्हणजेच‌ ‌आपली‌ ‌भारतभूमी‌ ‌पुन्हा‌ ‌एकदा‌ ‌प्रखर‌ ‌तेजाने‌ ‌तळपावी,‌ ‌तिची‌ ‌कीर्ती‌ ‌सगळ्या‌ ‌जगभर‌ ‌पसरावी,‌ ‌असेच‌ ‌कवयित्रीला‌ ‌वाटते.
‌‌
या‌ ‌काव्यपंक्तीमध्ये‌ ‌कवयित्री‌ ‌प्रतिमा‌ ‌इंगोले‌ ‌यांनी‌ ‌प्रमाण‌ ‌मराठी‌ ‌भाषेचा‌ ‌वापर‌ ‌केलेला‌ ‌आहे.‌ ‌प्रत्येक‌ ‌ओळीमध्ये‌ ‌केवळ‌ ‌दोनच‌ ‌शब्दांचा‌ ‌वापर‌ ‌करून‌ ‌वेगळा‌ ‌छान‌ ‌परिणाम‌ ‌साधला‌ ‌आहे.‌ ‌शिवाय‌ ‌निसर्गप्रतिकांचा‌ ‌योग्य‌ ‌वापर‌ ‌करीत‌ ‌अर्थाचे‌ ‌सौंदर्य‌ ‌वाढवलेले‌ ‌आहे.‌‌

पुन्हा एकदा Summary in Marathi

कवयित्रीचा‌ ‌परिचय:

नाव‌‌:‌ ‌प्रतिमा‌ ‌इंगोले‌ ‌
जन्म‌ ‌:‌ ‌(1953)‌‌
:‌ ‌ग्रामीण‌ ‌कथाकार,‌ ‌कवयित्री,‌ ‌’हजारी‌ ‌बेलपान’,‌ ‌’अकसिदीचे‌ ‌दाने’,‌ ‌’सुगरनचा‌ ‌खोपा’,‌ ‌’जावयाचं‌ ‌पोर’‌ ‌इत्यादी‌ ‌कथासंग्रह;‌ ‌’भुलाई’‌ ‌हा‌ ‌कवितासंग्रह;‌ ‌‘बुढाई’‌ ‌ही‌ ‌कादंबरी‌ ‌प्रसिद्ध.‌ ‌अस्सल‌ ‌वैदर्भी‌ ‌बोलीचा‌ ‌प्रभावी‌ ‌वापर‌ ‌हे‌ ‌त्यांच्या‌ ‌लेखनाचे‌ ‌खास‌ ‌वैशिष्ट्य‌ ‌आहे.‌‌

प्रस्तावना‌‌:

‘पुन्हा‌ ‌एकदा’‌ ‌ही‌ ‌कविता‌ ‌कवयित्री‌ ‌’प्रतिमा‌ ‌इंगोले‌ ‌यांनी‌ ‌लिहिली‌ ‌आहे.‌ ‌या‌ ‌कवितेत‌ ‌नवनिर्माणाचा‌ ‌ध्यास‌ ‌घेतलेल्या‌ ‌मनाच्या‌ ‌भावस्थितीचे‌ ‌सुरेख‌ ‌वर्णन‌ ‌केलेले‌ ‌आहे.‌‌

The‌ ‌poem‌ ‌’Punha‌ ‌ekda’‌ ‌is‌ ‌written‌ ‌by‌ ‌poetess‌ ‌Pratima‌ ‌Ingole.‌ ‌In‌ ‌this‌ ‌poem‌ ‌mind’s‌ ‌resolution‌ ‌of‌ ‌new‌ ‌generates‌ ‌has‌ ‌been‌ ‌depicted‌ ‌nicely.‌ ‌The‌ ‌Poetess‌ ‌very‌ ‌aptly‌ ‌depicts‌ ‌the‌ ‌urge‌ ‌of‌ ‌a‌ ‌progressive‌ ‌and‌ ‌creative‌ ‌mind‌ ‌towards‌ ‌the‌ ‌betterment‌ ‌of‌ ‌society‌ ‌once‌ ‌again.‌‌

भावार्थ‌‌:

पुन्हा‌ ‌एकदा‌ ‌……….‌ ‌पुन्हा‌ ‌एकवार‌
निसर्गातील‌ ‌विविध‌ ‌प्रतिकांचा‌ ‌वापर‌ ‌करीत‌ ‌कवयित्री‌ ‌नवनिर्मितीचा‌ ‌ध्यास‌ ‌घेतलेल्या‌ ‌मनाच्या‌ ‌भावस्थितीचे‌ ‌छान‌ ‌वर्णन‌ ‌करतात.‌ ‌त्या‌ ‌म्हणतात‌ ‌की,‌ ‌पुन्हा‌ ‌एकदा‌ ‌वीज‌ ‌चमकून‌ ‌खाली‌ ‌उतरून‌ ‌यावी.‌ ‌त्या‌ ‌वीजेचे‌ ‌तेज,‌ ‌तिची‌ ‌प्रखरता‌ ‌माणसांच्या‌ ‌रक्तात‌ ‌भिनावी.‌ ‌म्हणजेच‌ ‌माणसांमध्ये‌ ‌पुन्हा‌ ‌एकदा‌ ‌उत्साह‌ ‌भरून‌ ‌जावा.‌ ‌त्यांचे‌ ‌स्नायू‌ ‌पेटून‌ ‌उठावेत‌ ‌म्हणजेच‌ ‌समाजातील‌ ‌जुन्या,‌ ‌अनिष्ट‌ ‌चालीरिती,‌ ‌रूढी,‌ ‌परंपरा,‌ ‌अन्याय,‌ ‌अत्याचार‌ ‌याविरुद्ध‌ ‌त्यांनी‌ ‌पेटून‌ ‌उठावे‌ ‌आणि‌ ‌ते‌ ‌सारे‌ ‌नष्ट‌ ‌करून‌ ‌त्यातून‌ ‌समाजाला‌ ‌प्रगतीपथावर‌ ‌घेऊन‌ ‌जाणारे‌ ‌नवीन‌ ‌विचार‌ ‌निर्माण‌ ‌व्हावेत.‌‌

पुन्हा‌ ‌एकदा‌ ‌घालीत‌ ‌……भेदाभेद…‌ ‌पुन्हा‌ ‌एकवेळ…‌‌
नवनिर्मितीच्या‌ ‌विचारांनी‌ ‌प्रेरित‌ ‌झालेल्या‌ ‌मनाचे‌ ‌वर्णन‌ ‌करताना‌ ‌कवयित्री‌ ‌पुढे‌ ‌म्हणतात‌ ‌की,‌ ‌पुन्हा‌ ‌एकदा‌ ‌पावसाच्या‌ ‌जोरदार‌ ‌सरी‌ ‌पिंगा‌ ‌घालीत‌ ‌म्हणजे‌ ‌स्वत:भोवती‌ ‌गोल‌ ‌गोल‌ ‌फिरत,‌ ‌बेभान‌ ‌होऊन‌‌ जमिनीवर‌ ‌बरसाव्यात.‌ ‌या‌ ‌बेभान‌ ‌सरींमुळे‌ ‌मातीत‌ ‌माती‌ ‌मिसळून‌ ‌जावी.‌ ‌ती‌ ‌एकजीव‌ ‌व्हावी.‌ ‌याचाच‌ ‌अर्थ‌ ‌या‌ ‌मातीतील‌ ‌म्हणजेच‌ ‌समाजातील‌ ‌सगळा‌ ‌भेदाभेद‌ ‌मिटून‌ ‌जावा,‌ ‌संपून‌ ‌जावा,‌ ‌असे‌ ‌कवयित्रीला‌ ‌वाटते.‌ ‌म्हणजेच‌ ‌समाजात‌ ‌असलेला‌ ‌गरीब-श्रीमंत,‌ ‌उच्च-नीच,‌ ‌जात-धर्म,‌ ‌स्त्री-पुरुष‌ ‌असा‌ ‌विविध‌ ‌प्रकारचा‌ ‌भेदाभेद‌ ‌नष्ट‌ ‌होऊन‌ ‌भेदभावविरहित‌ ‌नव्या‌ ‌समाजाची‌ ‌निर्मिती‌ ‌व्हावी,‌ ‌असे‌ ‌कवयित्रीला‌ ‌वाटते.‌‌

पुन्हा‌ ‌एकदा‌ ‌घुमावा‌ ‌…..‌ ‌दिगंतात…‌ ‌पुन्हा‌ ‌एकदा…‌‌
नवनिर्मितीचे‌ ‌विचार‌ ‌प्रखरतेने‌ ‌मांडताना‌ ‌कवयित्री‌ ‌पुढे‌ ‌म्हणतात‌ ‌की,‌ ‌पुन्हा‌ ‌एकदा‌ ‌नव्या‌ ‌सुधारणांचा‌ ‌वारा‌ ‌आपल्या‌ ‌समाजात‌ ‌घुमत‌ ‌यावा.‌ ‌या‌ ‌वाऱ्याने‌ ‌इथला‌ ‌प्रत्येक‌ ‌युवक‌ ‌भारून‌ ‌जावा.‌ ‌इथल्या‌ ‌तरुणाने‌ ‌मंत्रमुग्ध‌ ‌होऊन,‌ ‌तहानभूक‌ ‌विसरून‌ ‌नवनवीन‌ ‌गोष्टी‌ ‌निर्माण‌ ‌करण्याची‌ ‌आस‌ ‌धरावी.‌ ‌नवनिर्माणाची‌ ‌चाहूल‌ ‌त्याला‌ ‌लागावी.‌ ‌नवीन‌ ‌विचारांचा‌ ‌नवा‌ ‌समाज‌ ‌निर्माण‌ ‌व्हावा.‌ ‌नव्या‌ ‌विचारांनी,‌ ‌नव्या‌ ‌कर्तृत्वाने‌ ‌आपली‌ ‌सारी‌ ‌भूमी‌ ‌उजळून‌ ‌निघावी.‌ ‌म्हणजेच‌ ‌आपली‌ ‌भारतभूमी‌ ‌पुन्हा‌ ‌एकदा‌ ‌प्रखर‌ ‌तेजाने‌ ‌तळपावी,‌ ‌तिची‌ ‌कीर्ती‌ ‌सगळ्या‌ ‌जगभर‌ ‌पसरावी,‌ ‌असेच‌ ‌कवयित्रीला‌ ‌वाटते.‌‌

शब्दार्थ‌‌:

1. एकदा‌ ‌-‌ ‌एकवार‌ ‌(once)‌ ‌
2. चमकणे‌ ‌-‌ ‌चकाकणे‌ ‌(to‌ ‌brighten,‌ ‌to‌ ‌glitter)‌
3. ‌रक्त‌ ‌-‌ ‌रूधिर‌ ‌(blood)‌‌
4. स्नायू‌‌ -‌ ‌(a‌ ‌muscle)‌ ‌
5. पुकार‌ ‌-‌ ‌हाक‌ ‌
6. पिंगा‌ ‌- लहान‌ ‌मुलींचा‌ ‌एक‌ ‌खेळ‌
7. ‌पाऊस‌ -‌ ‌पर्जन्य‌ ‌(rain)‌
8. ‌कोसळाव्या‌ ‌-‌ ‌पडाव्यात‌ ‌(should‌ ‌fall)‌
9. ‌घुमावा‌ ‌-‌ ‌(should‌ ‌reverberate)‌
10. ‌बेभान‌ ‌-‌ ‌अनियंत्रित,‌ ‌अनावर‌ ‌(beyond‌ ‌control)‌‌
11. भेदाभेद‌ ‌-‌ ‌(discrimination)‌ ‌
12. ‌युवक‌ ‌-‌ ‌तरुण‌ ‌पुरुष‌ ‌(a‌ ‌young‌ ‌man)‌
13. ‌नवनिर्माण‌ ‌-‌ ‌नवीन‌ ‌निर्मिती‌ ‌(to‌ ‌create‌ ‌something‌ ‌new)‌‌
14. भूमी‌‌ ‌-‌ ‌जमीन‌ ‌(land)‌ ‌
15. चाहूल‌ ‌-‌ ‌कानोसा,‌ ‌सूचना‌ ‌(hint,‌ ‌an‌ ‌inkling)‌ ‌
16. दिगंत‌ ‌-‌ ‌आसमंत‌ ‌(sky)‌‌

वाक्प्रचार‌‌:

1. ‌बेभान‌ ‌होणे‌ ‌-‌ ‌भान‌ ‌विसरणे.‌
2. ‌भारले‌ ‌जाणे‌‌ -‌ ‌मंत्रमुग्ध‌ ‌होणे.

Balbharti Maharashtra State Board Class 9 Marathi Solutions Kumarbharti Chapter 3 कीर्ती कठीयाचा दृष्टान्त Notes, Textbook Exercise Important Questions and Answers.

Maharashtra State Board Class 9 Marathi Kumarbharti Solutions Chapter 3 कीर्ती कठीयाचा दृष्टान्त

9th Std Marathi Kumarbharati Digest Chapter 3 कीर्ती कठीयाचा दृष्टान्त Textbook Questions and Answers

1. कोणास उद्देशून म्हटले आहे ते लिहा:

प्रश्न 1.
कोणास उद्देशून म्हटले आहे ते लिहा:
उत्तर:

1. वानरेया – [ ]
2. सर्वज्ञ – [ ]
3. गोसावी – [ ]

2. आकृती पूर्ण करा:

प्रश्न 1.
आकृती पूर्ण करा:
उत्तर:

3. प्रस्तुत दृष्टान्तातील उपदेश तुमच्या शब्दांत सांगा.

प्रश्न 1.
प्रस्तुत दृष्टान्तातील उपदेश तुमच्या शब्दांत सांगा.
उतारा:
डोमग्रामी गोसावीयांचा ठायी उदयाचे मातीकाम होत होते. ते सी बाजत होते: तेणे भक्तीजनासी व्यापार होववे नाः आन भट व्यापार करू लागलेः नाथोबाए म्हणीतलें: “नागदेयाः तू कैसा काही हीवसी ना?” तवं भटी म्हणीतलें: “आम्ही वैरागी: काइसीया हीवुः” यावरी सर्वज्ञ म्हणीतलें: “वानरेयाः पोरा जीवासी वैराग्य मिरवु आवडेः हाही एकू विकारुचि की गाः” यावरि भटी म्हणीतलें: “जी जी: निर्वीकार तो कवणः”

सर्वज्ञ म्हणीतलें: “वानरेयाः पोर जीव वीकारावेगळा केव्हेळाही जालाचि नाही: मा तु काइ वेगळा अससिः” “हो कां जी:’ यावरि गोसावी कीर्ती कठीयाचा दृष्टान्त निरोपीला: “कव्हणी ऐकू कठीया असे: तो भोगस्थानाची सुश्रुषा करीः झाडीः सडा संमार्जन करीः ते देखौनि गावीचे म्हणतिः ‘कठीये हो नीके करीत असा: बरवे करीत असाः’ ते आइकौनि दीसवडीचा दीसवडी हात हात चढवीः तयासि देवता आपुले फळ नेदीः तयासि कीर्तीचेचि फळ झालेः”

4. पुढील शब्दांना प्रमाणभाषेतील शब्द सांगा.

प्रश्न 1.
पुढील शब्दांना प्रमाणभाषेतील शब्द सांगा.

5. आपल्यातील गुण हाच अवगुण होऊ शकतो, हा विचार प्रस्तुत पाठाच्या आधारे स्पष्ट करा.

प्रश्न 1.
आपल्यातील गुण हाच अवगुण होऊ शकतो, हा विचार प्रस्तुत पाठाच्या आधारे स्पष्ट करा.
उत्तर:
नागदेवाचार्य हे महानुभाव पंथातील एक ज्येष्ठ शिष्य होते. त्यांची पंथाच्या विचारांवर निष्ठा होती. ते अगदी निष्ठेने पंथाच्या विचारांनुसार आचरण करीत असत. त्यामुळेच असे आचरण करताना ते कष्टाची पर्वा करीत नसत. एके दिवशी सकाळी सकाळी ते पंथासाठी मातीकाम करीत होते. कडाक्याची थंडी पडली होती. सर्व शिष्यांना थंडीत काम करणे अवघड बनले होते. पण कष्टांची पर्वा न करता नागदेवाचार्य काम करीत राहिले. हा त्यांचा खूप चांगला गुण होता. मात्र, आपण वैरागी आहोत, आपण हे कष्ट सहन करू शकतो, असा अहंकार त्यांच्या मनात निर्माण झाला. म्हणजेच, नागदेवाचार्यांचा चांगला गुण त्यांना हानिकारक ठरला; अवगुण ठरला.

6. पाठातील दृष्टान्त वेगळ्या उदाहरणादवारे स्पष्ट करा.

प्रश्न 1.
पाठातील दृष्टान्त वेगळ्या उदाहरणादवारे स्पष्ट करा.
उत्तर:
आमच्या परिसरात अगदी अलीकडेच घडलेली घटना आहे. आमच्या परिसरातील शाळेचा एस.एस.सी. परीक्षेचा निकाल खूप चांगला लागला. यशस्वी विदयार्थ्यांचा आणि शिक्षकांचा सत्कार करण्यात आला. सर्व विदयार्थ्यांना व पालकांनाही शिक्षकांबद्दल कृतज्ञता वाटत होती. त्यातही श्री. वसंतराव नाटेकर या शिक्षकांबद्दल तर खूप आदर वाटत होता. ते भाषणाला उभे राहिले, तेव्हा टाळ्यांचा कडकडाट झाला.

आपण विदयार्थ्यांसाठी किती कष्ट घेतले, रात्ररात्र जागरणे केली, जेवणाखाण्याची पर्वा केली नाही. स्वत:च्या कुटुंबाकडे लक्ष दिले नाही, वगैरे त्यागाचे वसंतरावांनी भरभरून वर्णन केले. हे सर्व खरेच होते. पण बोलता बोलता ते स्वत:ची स्तुती करू लागले. तेव्हा लोक नाराज होऊ लागले. शेवटी तर “मी नसतो तर विदयार्थ्यांना एवढे यश मिळालेच नसते,” असेही ते म्हणाले. यावरून त्यांना प्रचंड गर्व झाल्याचे दिसत होते. म्हणजे केवळ चांगला गुण असून उपयोगाचे नाही. गर्वामुळे चांगला गुणही वाया गेला. पाठातील तत्त्व आम्हांला या प्रसंगात पाहायला मिळाले.

भाषाभ्यास:

1. व्यतिरेक अलंकार:
खालील उदाहरण वाचा व समजून घ्या.
उदा., ‘अमृताहुनि गोड नाम तुझे देवा’
वरील उदाहरणातील उपमेय – [ ] उपमान- [ ]

व्यतिरेक अलंकाराचे वैशिष्ट्य- उपमेय हे उपमानापेक्षा श्रेष्ठ असते. वरील उदाहरणात परमेश्वराचे नाव गोडीच्या बाबतीत अमृतापेक्षाही श्रेष्ठ आहे, असे मानले आहे. जेव्हा कोणत्याही काव्यात वा वाक्यात उपमेय हे उपमानापेक्षा श्रेष्ठ आहे, असे मानले जाते तेव्हा तिथे व्यतिरेक’ अलंकार होतो.

प्रश्न 1.
पुढील उदाहरण वाचा व तक्ता पूर्ण करा:
तू माउलीहून मयाळ । चंद्राहूनि शीतल ।
पाणियाहूनि पातळ । कल्लोळ प्रेमाचा ।।

उत्तर:

Marathi Kumarbharati Textbook Std 9 Answers Chapter 3 कीर्ती कठीयाचा दृष्टान्त Additional Important Questions and Answers

पुढील उतारा वाचून दिलेल्या सूचनांनुसार कृती करा:

कृती 1 : (आकलन)

प्रश्न 1.
आकृतिबंध पूर्ण करा:
उत्तर:

प्रश्न 2.
आकृतिबंध पूर्ण करा:
उत्तर:

प्रश्न 3.
योग्य पर्याय ओळखून विधान पूर्ण करा :
………………………, म्हणून स्वामींनी दृष्टान्त सांगितला.
उत्तर:
(य) व्यापार चांगला व्हावा
(र) लोकांचे मनोरंजन व्हावे
(ल) नागदेवाचार्यांचा गर्व नाहीसा व्हावा
(व) कामातले कष्ट कमी व्हावेत.

प्रश्न 4.
दिलेल्या पर्यायांतून योग्य पर्याय निवडा:
1. डोमग्रामी सकाळी सकाळी पुढील काम चालू होते: (भोगस्थानाची शुश्रूषा / जीवाचे वैराग्य /मातीचा व्यापार/मातीकाम)
2. श्रीचक्रधरस्वामी यांनी ज्यांना दृष्टान्त सांगितला, तेः (गोसावी / कठीया / नागदेवाचार्य / पुजारी)

उत्तर:

1.

2.

3. नागदेवाचार्यांचा गर्व नाहीसा व्हावा, म्हणून स्वामींनी दृष्टान्त सांगितला.

4. मातीकाम

1. नागदेवाचार्य.

5. प्रस्तुत दृष्टान्तातील उपदेश: आपले मन सर्व विकारांपासून दूर ठेवले पाहिजे. आपण एखादा चांगला गुण आत्मसात केला किंवा एखादी चांगली कृती केली, तर त्याचासुद्धा अहंकार बाळगता कामा नये. हा अहंकार म्हणजे विकारच होय. सर्व विकारांपासून दूर राहून मन शुद्ध राखले, तर तो खरा वैरागी होय.

कृती 2 : (आकलन)

प्रश्न 1.
पर्यायांतून योग्य पर्याय निवडा:

1. महानुभाव पंथाचे संस्थापक – (श्रीचक्रधरस्वामी, म्हाइंभट, नागदेवाचार्य, श्रीगोविंदप्रभू)
2. मराठीतील पहिला चरित्रग्रंथ – (गोविंदप्रभुचरित्र, श्रीकृष्णचरित्र, लीळाचरित्र, दत्तात्रयप्रभुचरित्र)
3. लीळाचरित्राचे लेखक – (श्रीचक्रधरस्वामी, म्हाइंभट, नागदेवाचार्य, श्रीगोविंदप्रभू )
4. श्रीचक्रधरस्वामींचे गुरू – (भटोबास, म्हाइंभट, नागदेवाचार्य, श्रीगोविंदप्रभू )
5. ‘कीर्ती कठीयाचा दृष्टान्त’ हा दृष्टान्त कथन करणारे – (नाथोबास, नागदेव, म्हाइंभट, श्रीचक्रधरस्वामी)

उत्तर:

1. [नागदेवाचार्य]

1. [श्रीचक्रधरस्वामी]
2. [श्रीचक्रधरस्वामी]

2.

3. श्रीचक्रधरस्वामी

1. लीळाचरित्र
2. म्हाइंभट
3. श्रीगोविंदप्रभू
4. श्रीचक्रधरस्वामी

भाषाभ्यास:

(अ) व्याकरण घटकांवर आधारित कृती:

समास:

• कमीत कमी दोन शब्द एकत्र येण्याच्या प्रक्रियेला समास म्हणतात.
• दोन शब्द एकत्र येऊन तयार होणाऱ्या जोडशब्दाला सामासिक शब्द म्हणतात.
• सामासिक शब्दाची फोड करून दाखवण्याच्या पद्धतीला विग्रह म्हणतात.

उदा.,

समासाचे प्रकार:

1. समासात कमीत कमी दोन शब्द असतात.
2. समासातील शब्दांना ‘पद’ म्हणतात.
   पहिला शब्द → पहिले पद दुसरा शब्द → दुसरे पद
3. समासातील कोणते पद महत्त्वाचे म्हणजेच प्रधान आहे, यावरून समासाचे मुख्य चार प्रकार पडतात.

महत्त्वाचे पद म्हणजे प्रधान पद (+)
कमी महत्त्वाचे पद म्हणजे गौण पद ( – )

समासांचे मुख्य चार प्रकार होतात:

लक्षात ठेवा:

1. अव्ययीभाव समास → पहिले पद प्रधान (उदा., दररोज).
2. तत्पुरुष समास → दुसरे पद प्रधान (उदा., विदयालय, क्रीडांगण).
3. वंद्व समास → दोन्ही पदे प्रधान (उदा., भाऊबहीण).
4. बहुव्रीही समास → दोन्ही पदे गौण (उदा., नीळकंठ).

या इयत्तेत आपल्याला:

1. कर्मधारय
2. द्विगू
3. वंद्व (इतरेतर/वैकल्पिक/समाहार)
हे समास शिकायचे आहेत.

1. कर्मधारय समास:

• कर्मधारय समास हा तत्पुरुष समासाचाच एक उपप्रकार आहे.
• ज्या तत्पुरुष समासातील पहिले पद विशेषण असून दुसरे पद नाम असते, त्यास कर्मधारय समास म्हणतात.

उदा.,

म्हणून ‘नीलकमल, मातृभूमी’ हे कर्मधारय समास आहेत.

2. द्विगू समास

• द्विगू समास हा तत्पुरुष समासाचाच एक उपप्रकार आहे.
• ज्या तत्पुरुष समासातील पहिले पद संख्याविशेषण असून दुसरे पद नाम असते, त्या तत्पुरुष समासाला द्विगू समास म्हणतात.

उदा.,

म्हणून ‘त्रिकोण, नवरात्र’ हे द्विगू समास आहेत.

3. द्ववंद्ववं समास:

ज्या समासातील दोन्ही पदे महत्त्वाची असतात, त्याला वंद्व समास म्हणतात.

द्ववंद्ववं समासाचे उपप्रकार:

द्वंद्व समासातील सामासिक शब्दांच्या विग्रहाच्या पद्धतीवरून द्वंद्व समासाचे

1. इतरेतर द्वंद्व
2. वैकल्पिक द्वंद्व व
3. समाहार वंद्व असे तीन उपप्रकार पडतात.

1. इतरेतर द्वंद्व समास

पुढील सामासिक शब्दांचा विग्रह कसा होतो, ते नीट पाहा:

1. स्त्रीपुरुष → स्त्री आणि पुरुष
2. आईवडील → आई व वडील

वरील दोन्ही सामासिक शब्दांचा विग्रह करताना आपण ‘आणि’, ‘व’ या उभयान्वयी अव्ययांचा वापर केला.
जेव्हा वंद्व समासातील सामासिक शब्दांचा विग्रह करताना ‘आणि, व’ अशा उभयान्वयी अव्ययांचा वापर करतात, तेव्हा त्यास इतरेतर वंद्व समास म्हणतात.
म्हणून ‘स्त्रीपुरुष, आईवडील’ हे इतरेतर द्वंद्व समास आहेत.

2. वैकल्पिक द्वंद्व समास

पुढील सामासिक शब्दांचा विग्रह कसा होतो, ते नीट पाहा:
1. सुखदुःख → सुख किंवा दुःख
2. भेदाभेद → भेद किंवा अभेद

वरील दोन्ही सामासिक शब्दांचा विग्रह करताना आपण ‘किंवा’ या उभयान्वयी अव्ययाचा वापर केला. जेव्हा द्वंद्व समासातील सामासिक शब्दांचा विग्रह करताना ‘किंवा, अथवा, वा’ अशा उभयान्वयी अव्ययांचा वापर करतात व दोन्ही पदे परस्परविरोधी असतात, तेव्हा त्याला वैकल्पिक द्वंद्व समास म्हणतात. म्हणून ‘सुखदुःख, भेदाभेद’ हे वैकल्पिक द्वंद्व समास आहेत.

3. समाहार वंद्व समास

पुढील सामासिक शब्दांचा विग्रह कसा होतो, ते नीट पाहा:

1. गप्पागोष्टी → गप्पा, गोष्टी वगैरे
2. मीठभाकर → मीठ, भाकर वगैरे

वरील दोन्ही सामासिक शब्दांत अनेक गोष्टींचा समावेश आहे. म्हणून त्यांचा विग्रह करताना आपण ‘वगैरे’ या शब्दाचा वापर केला.
जेव्हा वंद्व समासातील सामासिक शब्दांत इतर अनेक गोष्टींचा समावेश असतो व ज्यांचा विग्रह करताना ‘वगैरे, इतर, इत्यादी’ अशा शब्दांचा वापर होतो, तेव्हा त्याला समाहार द्वंद्व समास म्हणतात. म्हणून ‘गप्पागोष्टी, मीठभाकर’ हे समाहार वंद्व समास आहेत.

4. समास:

प्रश्न 1.
पुढील सामासिक शब्दांचा विग्रह करा:

1. त्रिगुण
2. भाऊबहीण
3. नीलकमल
4. स्त्रीपुरुष.

उत्तर:

1. त्रिगुण → तीन गुणांचा समूह
2. भाऊबहीण → भाऊ आणि बहीण
3. नीलकमल → निळे असे कमल
4. स्त्रीपुरुष → स्त्री आणि पुरुष.

5. शब्दसिद्धी:

प्रश्न 1.
पुढील शब्द वाचून उपसर्गघटित व प्रत्ययघटित यांत वर्गीकरण करा: (नम्रता, उपवास, विरोधक, ममत्व)
उत्तर:

(आ) भाषिक घटकांवर आधारित कृती:

1. शब्दसंपत्ती:

प्रश्न 1.
समानार्थी शब्द लिहा:
1. बरवे = ……………….
2. दृष्टान्त = ……………..
उत्तर:
1. बरवे = चांगले
2. दृष्टान्त = दाखला.

प्रश्न 2.
प्रचलित मराठीतील समानार्थी शब्द लिहा:

उत्तर:

प्रश्न 3.
विरुद्धार्थी शब्द लिहा:
1. सुरुवात × ……………
2. प्राचीन × ……………
उत्तर:
1. सुरुवात – शेवट
2. प्राचीन × अर्वाचीन.

प्रश्न 4.
पुढील शब्दापासून तयार होणारे चार अर्थपूर्ण शब्द लिहा : वीकारावेगळा : ……………………
उत्तर:

1.  काळा
2. राग
3. वेग
4. वेळा.

2. लेखननियम:

प्रश्न 1.
अचूक शब्द ओळखा:
1. निर्वीकार, निविर्कार, निर्विकार, नीर्विकार.
2. दृश्टांत, दुष्ट्रान्त, दृष्टान्त, दृष्टांत.
उत्तर:
1. निर्विकार
2. दृष्टान्त.

कीर्ती कठीयाचा दृष्टान्त Summary in Marathi

प्रस्तावना:

‘लीळाचरित्र’ हा मराठीतील पहिला ग्रंथ मानला जातो. इ. स. 1283 च्या सुमारास हा ग्रंथ लिहिला गेला आहे. महानुभाव पंथाचे ज्येष्ठ शिष्य म्हाइंभट यांनी हा ग्रंथ लिहिला आहे. ते बुद्धिमान, विद्वान व व्यासंगी होते.

‘लीळाचरित्र’ म्हणजे महानुभाव पंथाचे संस्थापक श्रीचक्रधरस्वामी यांचे चरित्र होय. स्वामींच्या उत्तरापंथ प्रयाणानंतर म्हाइंभटांनी खूप परिश्रम घेऊन स्वामींच्या आठवणी एकत्रित केल्या. त्या आठवणी म्हणजे ‘लीळाचरित्र’ होय. यांतील एकेक आठवण म्हणजे एकेक लीळा होय. येथे कीर्ती कठीयाचा दृष्टान्त’ ही लीळा अभ्यासासाठी नेमलेली आहे.

प्रत्येक जीव विकारांच्या जाळ्यात अडकलेला असतो. विकारांपासून कोणीही दूर नाही. आपण अनेकदा केवळ वाईट विकार-वासनांनाच या बाबतीत गृहीत धरतो. पण चांगल्या गोष्टींचा गर्व बाळगणे हासुद्धा विकारच होय, अशी स्वामींची शिकवण होती. तीच या पाठात सांगितली आहे.

हा ग्रंथ प्राचीन भाषेतला आहे. त्या काळातील भाषा आणि आधुनिक काळातील प्रचलित मराठी भाषा यांत फरक आहे. म्हणून या पाठाचा आधुनिक मराठी भाषेत सरळ अर्थ दिला आहे.

पाठाचा सरळ अर्थ:

एके दिवशी डोमग्राम या गावात सकाळी सकाळी श्रीचक्रधरस्वामींकडे मातीकाम चालू होते. त्या वेळी खूप थंडी वाजत होती. त्यामुळे भक्तांना काम करणे कठीण जात होते. मात्र भटोबास (नागदेवाचार्य) यांनी कामाला सुरुवात केली. तेव्हा नाथोबांनी त्यांना , विचारले, “नागदेवा, तुला कशी थंडी वाजत नाही?” तेव्हा नागदेव म्हणाले, “आम्ही वैरागी. आम्हां वैराग्यांना कसली आली थंडी!’

त्यावर स्वामी म्हणाले, “राजे हो, (हे नरश्रेष्ठा,) प्रत्येक जीवाला वैराग्य मिरवायला आवडते. हासुद्धा एक विकारच आहे.” मग नागदेवांनी विचारले, “हो; तर मग निर्विकार कोण?”

स्वामी उत्तरले, “जीव विकारापासून वेगळा कधी झालाच नाही. मग तू या जीवांपेक्षा वेगळा कसा काय?” नागदेव म्हणाले, “बरं, बरं.’ त्यावर स्वामींनी ‘कीर्ती कठीयाचा दृष्टान्त’ सांगितला. तो दृष्टान्त असा: कोणी एक पुजारी होता. तो भोगस्थानाची (नैवेदयाच्या जागेची) देखभाल करीत असे. साफसफाई करीत असे. सडासंमार्जन करीत असे. (जमीन सारवून रांगोळी काढीत असे.) ते पाहून गावकरी म्हणू लागले, “गुरवांनो, तुम्ही खूप नेटके करीत आहात. छानच करीत आहात.” ते ऐकून तो पुजारी (स्तुतीने खूश झाला आणि) रोजच्या रोज अधिकाधिक चांगले काम करू लागला. परंतु देवता त्याला कोणतेही फळ देत नाही. त्याला फक्त कीर्ती मिळाली, म्हणजे त्याला कीर्ती हेच फळ मिळाले. अन्य काही नाही.

शब्दार्थ:

1. सी बाजत होते – थंडी वाजत होती.
2. व्यापार – काम.
3. होववे ना – होईना, करता येईना.
4. हीवसी ना – गारठला नाहीस, थंडी वाजली नाही.
5. काइसीया – कशी काय, का, कशाला, कोणत्या कारणाने.
6. हीवु – थंडी, गारठा.
7. कवण – कोण.
8. केव्हेळाही – कधीही.
9. जालाचि – झालाच.
10. कठीया – गुरव, पुजारी.
11. भोगस्थान – देवाला नैवेदय दाखवण्याची जागा.
12. सडासंमार्जन – सकाळी झाडलोट करून, जमीन गाईच्या शेणाने सारवून त्यावर रांगोळी काढणे.
13. गावीचे – गावातले लोक, गावकरी.
14. नीके – स्वच्छ, शुद्ध, नीटनेटके.
15. बरवे – छान, चांगले.
16. आइकौनी – ऐकून.
17. दीसवडी – दररोज, प्रतिदिनी.
18. नेदी – देत नाही.

टिपा:

1. डोमग्राम – डोंबेग्राम (गावाचे नाव), सध्याचे नाव ‘कमालपूर’, ता. नेवासे, जिल्हा अहमदनगर.

2. पाठात उल्लेखलेल्या व्यक्ती:

1. गोसावी – श्रीचक्रधरस्वामी.
2. भक्तीजन – श्रीचक्रधरस्वामींचे भक्त.
3. भट – नागदेवाचार्य, ज्येष्ठ भक्त. यांनाच भट, भटोबास, नागदेव या नावांनीही संबोधले जाई. ते सतत चपळतेने वावरत. सर्वज्ञ श्रीचक्रधरस्वामी आपले भक्त नागदेव यांना प्रेमाने ‘वानरा’, ‘वानरेश’ असे संबोधित असत. ‘वानर’ किंवा ‘वानरेश’ यांमधील ‘वा’ हा प्रशंसावाचक शब्द असून, ‘नर’ किंवा ‘नरेश’ म्हणजे नरश्रेष्ठ राजा हा अर्थ पंथीय परंपरेनुसार रूढ झालेला आहे. ‘वानरा/वानरेश’ म्हणजे ‘वा राजे’ किंवा ‘वा नरश्रेष्ठा’ असा पंथीय परंपरेतील रूढ अर्थ आहे.
4. सर्वज्ञ – श्रीचक्रधरस्वामी.
5. कठीया – गुरव, पुजारी, मंदिरातील पूजाअर्चा, मूर्त्यांची देखभाल, गाभाऱ्याची देखभाल वगैरे कार्ये ज्याच्यावर सोपवलेली असतात ती व्यक्ती.
6. गावीचे – गावचे, गावातील लोक, गावकरी, ग्रामस्थ.

3. दृष्टान्त – एखादे तत्त्व समजावून सांगण्यासाठी एखादा दाखला दिला जातो, एखादी कथा सांगितली जाते, त्या वेळी त्या दाखल्याला किंवा त्या कथेला ‘दृष्टान्त’ किंवा ‘दृष्टान्तकथा’ म्हणतात. इसापनीतीमधील सर्व कथा या दृष्टान्तकथाच होत.

4. महानुभाव पंथ: हिंदू धर्माच्या अंतर्गत निर्माण झालेला हा एक पंथ आहे. इसवी सनाच्या १३व्या शतकात हा पंथ निर्माण झाला. , रिद्धिपूरचे ईश्वरावतार श्रीगोविंदप्रभू यांचे ते शिष्य. खेडोपाडी जाऊन पुढे दोन-तीन शतके या पंथाचा खूप प्रसार झाला. विशेषतः महाराष्ट्र, त्यांनी आपल्या आचारधर्माचा व तत्त्वज्ञानाचा प्रसार केला. ते मध्य भारत, पंजाब व काश्मीर एवढ्या भूभागांत या पंथाची वाढ है अहिंसेचे पूजक होते. जातीयतेचे कट्टर विरोधक होते. आपल्या झाली.

हा पंथ अहिंसेचा पुरस्कर्ता आहे. त्या काळात कर्मकांडांचे स्तोम माजले होते. त्यामुळे खरा धर्म बाजूला पडला होता. कर्मकांडांतून जनतेची सोडवणूक करण्यासाठी श्रीचक्रधरस्वामींनी या पंथाची स्थापना केली. या पंथाचा जातीयतेला प्रखर विरोध आहे. जातिनिरपेक्षता, समानता व अहिंसा ही या पंथाची महत्त्वाची तत्त्वे आहेत.

5. श्रीचक्रधरस्वामी: हे महानुभाव पंथाचे संस्थापक होत. रिद्धिपूरचे ईश्वरावतार श्रीगोविंदप्रभू यांचे ते शिष्य. खेडोपाडी जाऊन त्यांनी आपल्या आचारधर्माचा व तत्त्वज्ञानाचा प्रसार केला. ते अहिंसेचे पूजक होते. जातीयतेचे कट्टर विरोधक होते. आपल्या अनुयायांना ते आचारधर्माचे कठोरपणे पालन करायला लावत. मात्र, ते कोमल अंत:करणाचे होते. केवळ माणसांविषयीच नव्हे, तर प्राणिमात्रांविषयीही त्यांना ममत्व वाटे. आपल्या पायाखालची मुंगीही मरता कामा नये असे त्यांना वाटे.

Balbharti Maharashtra State Board Class 9 Marathi Solutions Kumarbharti Chapter 2.1 संतवाणी (अ) जैसा वृक्ष नेणे- संत नामदेव Notes, Textbook Exercise Important Questions and Answers.

Maharashtra State Board Class 9 Marathi Kumarbharti Solutions Chapter 2.1 संतवाणी (अ) जैसा वृक्ष नेणे- संत नामदेव

9th Std Marathi Kumarbharati Digest Chapter 2.1 संतवाणी (अ) जैसा वृक्ष नेणे- संत नामदेव Textbook Questions and Answers

1. वृक्ष आणि संत यांच्यातील साम्य लिहून तक्ता पूर्ण करा:

प्रश्न 1.
वृक्ष आणि संत यांच्यातील साम्य लिहून तक्ता पूर्ण करा:
उत्तर:

2. खालील तक्ता पूर्ण करा.

प्रश्न 1.
खालील तक्ता पूर्ण करा.
उत्तर:

3. पुढील विधानांपैकी सत्य विधान ओळखून लिहा:

प्रश्न 1.
पुढील विधानांपैकी सत्य विधान ओळखून लिहा:
उत्तर:
(अ) संतांचे वर्तन वृक्षाप्रमाणे असते.
(आ) संतांना सन्मानाची अपेक्षा असते.
(इ) संत निंदा आणि स्तुती समान मानत नाहीत.
(ई) संत सुख आणि दु:ख समान मानतात.

4. खालील शब्दांचे समानार्थी शब्द लिहा.

प्रश्न 1.
खालील शब्दांचे समानार्थी शब्द लिहा.
1. वृक्ष
2. सुख
3. सम

5. काव्यसौंदर्य.

प्रश्न (अ)
‘अथवा कोणी प्राणी येऊनि तोडिती । तया न म्हणती छेदूं नका ।।’ या काव्यपंक्तींचा सरळ अर्थ लिहा.
उत्तर:
वृक्षाला मान-अपमान यांची फिकीर नसते. कुणी त्यांची पूजा केली तरीही त्यांना सुख होत नाही किंवा कोणी येऊन त्यांच्यावर तोडण्यासाठी घाव घातले, तरी त्या माणसांना ते ‘मला तोडू नका’ असेही म्हणत नाहीत. अशा प्रकारे वृक्षांना मान-अपमान समान असतात.

प्रश्न (आ)
‘निंदास्तुति सम मानिती जे संत । पूर्ण धैर्यवंत साधु ऐसे ।।’ या काव्यपंक्तींतील विचारसौंदर्य स्पष्ट करा.
उत्तर:
संत नामदेवांनी संतांची महती सांगितली आहे. संतांची कुणी निंदा केली किंवा प्रशंसा केली, तरी या दोन्ही गोष्टी संतांना समान वाटतात. निंदास्तुतीने ते अजिबात विचलित होत नाहीत. त्यांचे मन निश्चल राहते. या दोन्ही गोष्टी पचवण्याच्या बाबतीत संत संपूर्ण धैर्यशील असतात. हिंमतवान असतात. निंदास्तुतीने मन डळमळू नये व विवेकशील मन ठेवावे, असा महत्त्वाचा विचार या पंक्तीतून व्यक्त झाला आहे.

6. अभिव्यक्ती.

प्रश्न (अ)
प्रस्तुत अभंगातून संतांना दिलेल्या वृक्षाच्या उपमेसंदर्भातील तुमचे मत स्पष्ट करा.
उत्तर:
प्रस्तुत अभंगात संत नामदेवांनी संतांना वृक्षांची समर्पक उपमा दिली आहे. वृक्ष एका ठायी निश्चल असतात. वृक्ष उदारवृत्तीने माणसांना पाने, फुले, फळे व सावली देतात. त्या बदल्यात ते माणसांकडून कोणतीच अपेक्षा करीत नाहीत. संतसज्जनही निरिच्छ वृत्तीने माणसांना ज्ञानदान करतात. वृक्षांची कुणी पूजा केली किंवा त्यांना तोडले तरी वृक्षांची माया कमी होत नाही. संतसज्जनही मानापमानाच्या पलीकडे असतात. त्यांना निंदास्तुती समान असते. वृक्षांप्रमाणे सज्जनांची वृत्ती अविचल राहते. अशा प्रकारे संतांना दिलेली वृक्षाची उपमा सार्थ आहे.

प्रश्न (आ)
तुम्हांला आवडलेल्या कोणत्याही एखाद्या अभंगाविषयी माहिती लिहा.
उत्तर:
‘जे का रंजले गांजले। त्यासी म्हणे जो आपुले ।। तोचि साधू ओळखावा । देव तेथेचि जाणावा ।।’ हा संत तुकाराम महाराजांचा अभंग मला प्रेरणादायी वाटतो. यामध्ये तुकाराम महाराजांनी परोपकाराची महती सांगितली आहे. जे पीडित लोक आहेत, त्यांच्याविषयी सहानुभूती बाळगणे व त्यांना मायेने जवळ करणे. त्यांचे दुःख हरण करण्यासाठी झटणे हेच खऱ्या सज्जनाचे लक्षण आहे. अशा प्रकारे रंजल्या-गांजल्या माणसांची जो मदत करतो, त्यालाच देवत्व प्राप्त होते. समाजाची आस्थेने सेवा करणाऱ्या माणसाकडे देवपण असते. ‘पुण्य परउपकार । पाप ते परपीडा’ असा उदात्त संदेश या अभंगातून मला मिळतो.

उपक्रम:
‘वृक्षवल्ली आम्हां सोयरे वनचरे….’ हा अभंग वर्गात वाचून त्यावर चर्चा करा.

भाषा सौंदर्य:

खाली दिलेल्या कंसातील शब्दांना (क्रियापदांना) ‘ईव’ प्रत्यय जोडून विशेषणे तयार करा व त्यांच्यासाठी समर्पक विशेष्य शोधून लिहा.
उदा., आखणे – आखीव – आखीव कागद.
(रेखणे, कोरणे, ऐकणे, घोटणे, राखणे) यांसारख्या इतर शब्दांचा शोध घ्या.

भाषाभ्यास:

आपण जेव्हा कथा, कादंबरी, कविता, नाटक वगैरे साहित्य वाचतो, तेव्हा दैनंदिन जगण्यातील भाषेपेक्षा थोडी वेगळी भाषा आपल्याला वाचायला मिळते. आपल्याला साहित्य वाचनाचा आनंद मिळवून देण्यात या भाषेचा मोठा बाटा असतो. दैनंदिन व्यवहारातील भाषेपेक्षा साहित्याची भाषा ज्या घटकांमुळे वेगळी ठरते, त्यातील एक घटक म्हणजे अलंकार.

अलंकाराचे शब्दालंकार आणि अर्थालंकार हे दोन प्रकार आपल्याला माहीत आहेत. अर्थालंकारांमध्ये ज्या वस्तूला उपमा दिलेली असते तिला उपमेय म्हणतात आणि ज्या वस्तूची उपमा दिलेली असते तिला उपमान म्हणतात, आता उपमेय आणि उपमानातील साधावर आधारित काही अलंकारांचा आपण परिचय करून घेऊया.

1. रूपक अलंकार:

प्रश्न 1.
पुढील ओळींतील उपमेय व उपमान ओळखा :
1. नयनकमल हे उघडित हलके जागी हो जानकी।

2. ऊठ पुरुषोत्तमा । वाट पाही रमा ।
दावि मुखचंद्रमा । सकळिकांसी ।।

उत्तर:

2. रूपक अलंकाराची वैशिष्ट्ये-

1. उपमेय व उपमान यांच्यात साम्य.
2. उपमेय हे उपमानच आहे असे मानणे.
3. अनेकदा केवळ, प्रत्यक्ष, साक्षात, मूर्तिमंत इ. साधर्म्य दर्शक शब्दांचा वापर.

उपमेय व उपमान (कमल व नयन) यांच्यातील साम्यामुळे दोन्ही गोष्टी एकच वाटतात म्हणून इथे ‘रूपक’ अलंकार होतो. यात नयन हे कमळासारखे आहेत (उपमा) किंवा नयन म्हणजे जणू काही कमलच आहे (उत्प्रेक्षा) असे न म्हणता नयन हेच कमल असे दर्शवले आहे, म्हणून येथे रूपक अलंकार झाला आहे.

3. जेव्हा वाक्यांत उपमेय, उपमान यांच्यातील साम्यामुळे दोन्ही गोष्टी अभिन्न दर्शवल्या जातात तेव्हा रूपक’ अलंकार होतो.

खालील ओळी वाचा.

ऊठ पुरुषोत्तमा । वाट पाही रमा ।
दावि मुखचंद्रमा । सकळिकांसी ॥
उपमेय – [ ]
उपमान – [ ]

Marathi Kumarbharati Textbook Std 9 Answers Chapter 2.1 संतवाणी (अ) जैसा वृक्ष नेणे- संत नामदेव Additional Important Questions and Answers

1. पुढील कवितेच्या आधारे दिलेल्या सूचनांनुसार कृती करा:

कृती 1: (आकलन)

प्रश्न 1.

प्रश्न 2.

कृती 2: (आकलन)

प्रश्न 1.
योग्य पर्याय निवडून विधाने पूर्ण करा:
1. सज्जनांची भेट होणे म्हणजे ……..”ची गाठ पडणे होय. (भक्ती-मुक्ती/जिवा-शिवा/सुख-दु:ख/निंदा-स्तुती)
2. कुणी वृक्ष तोडला, तर वृक्ष त्याला ——— नका असे म्हणत नाहीत. (मोडू/सोडू/तोडू/छेडू)
उत्तर:
1. संतांचे वर्तन वृक्षाप्रमाणे असते.
2. सज्जनांची भेट होणे म्हणजे जिवा-शिवाची गाठ पडणे होय.
कुणी वृक्ष तोडला, तर वृक्ष त्याला तोडू नका असे म्हणत नाहीत.

प्रश्न 2.
चौकटी पूर्ण करा:

उत्तर:
[पूर्ण धैर्यवंत] [संत]

कृती 4 : (काव्यसौंदर्य)

प्रश्न 1.
प्रस्तुत अभंगातून संत नामदेवांनी पर्यावरणरक्षणाविषयी दिलेला संदेश तुमच्या शब्दांत लिहा.
उत्तर:
आपल्या अवतीभवती असलेल्या निसर्गाचे रक्षण आपण करायला हवे. निसर्ग आपल्याला निरोगी पर्यावरणाची शिकवण देतो. प्रस्तुत अभंगात संत नामदेवांनी पूर्ण धैर्यवंत संतांची तुलना वृक्षांशी केली आहे. संतांचे वर्तन वृक्षांसारखे असते. वृक्षांना मान-अपमान ठाऊक नसतो. कुणी पूजा केली काय किंवा घाव घातला काय, वृक्ष अविचल असतात. माणसाचे वागणेही वृक्षाप्रमाणे असावे. वृक्षतोड करून पर्यावरणाचा -हास करू नये, उलट वृक्षलागवड व संवर्धन करावे, असा संदेश संत नामदेवांनी या अभंगात दिला आहे.

लक्षात ठेवा:

1. इयत्ता 9 वी-10 वीच्या कृतिपत्रिकेच्या नवीन, अदययावत आराखड्यानुसार प्रश्न 2 (आ) हा कवितेवर दिलेल्या मुद्द्यांच्या आधारे कृती सोडवा हा असेल. यामध्ये प्रश्न 2 (अ) आणि (इ) यांत दिलेल्या पठित कविता सोडून पाठ्यपुस्तकातील इतर कोणत्याही दोन कवितांची नावे दिली जातील. त्यांपैकी कोणत्याही एका कवितेवर दिलेल्या मुद्द्यांच्या आधारे कृती करणे अपेक्षित आहे:

2. वरील 8 कृतींपैकी कृतिपत्रिकेत 1-1 गुणाच्या पहिल्या 2 कृती आणि 2 गुणांची कोणतीही 1 कृती विचारली जाईल.
उत्तराच्या सुरुवातीला तुम्ही निवडलेल्या कवितेचे नाव लिहिणे आवश्यक आहे.

3. ही कृती सोडवण्यासाठी अभ्यास असा करा:

1. कवींचे/कवयित्रींचे नाव, कवितेचा विषय, कवितेतून मिळणारा संदेश, भाषिक वैशिष्ट्ये, व्यक्त होणारा विचार, आवड किंवा नावडीची कारणे इत्यादींसाठी पुढील उत्तर नीट अभ्यासावे.
2. कवितेतील दिलेल्या ओळींच्या सरळ अर्थासाठी कवितेचा भावार्थ नीट अभ्यासावा.
3. कवितेतील शब्दांच्या अर्थासाठी कवितेच्या सुरुवातीला दिलेले शब्दार्थ अभ्यासावेत.

पुढील कवितेवर दिलेल्या मुद्द्यांच्या आधारे कृती सोडवा:

कविता: संतवाणी – (अ) जैसा वृक्ष नेणे.

महत्त्वाची नोंद: परीक्षेत आठपैकी कोणत्याही 3 कृती विचारल्या जाणार आहेत. तथापि विदयार्थ्यांना सर्व कृतींचा सराव मिळावा म्हणून इथे सर्व 8 कृती उत्तरांसह सोडवून दाखवल्या आहेत. आशयावर आधारलेल्या प्रत्येकी 2 गुणांच्या कृतींची उत्तरे येथे नमुन्यादाखल दिलेली आहेत. ही उत्तरे विदयार्थी स्वत:च्या मतानुसार व स्वत:च्या शब्दांत लिह शकतात.

उत्तर: संतवाणी – (अ) जैसा वृक्ष नेणे

1. प्रस्तुत कवितेचे कवी/कवयित्री → संत नामदेव.
2. कवितेचा विषय → या कवितेत संतसज्जनांची महती सांगितली आहे.
3. कवितेतील दोन शब्दांचे अर्थ → (इथे सरावासाठी अनेक शब्दार्थ दिले आहेत.)
4. वृक्ष = झाड
5. चित्त = मन
6. निंदा = नालस्ती
7. सम = समान
8. धैर्य = धीर
9. जीव = प्राण.

4. कवितेतून मिळणारा संदेश → संतांचे वर्तन जसे मानापमान व निंदास्तुती यांच्या पलीकडचे असते, तशी आपली वागणूक ठेवावी. स्थिरबुद्धीने वागावे हा संदेश या अभंगातून दिला आहे.

5. कवितेची भाषिक वैशिष्ट्ये → सर्वसामान्य माणसांना कळेल असा अभंग हा लोकछंद या रचनेत वापरला आहे. वृक्षाचे रूपक वापरून साध्या, सुबोध भाषेत कवितेचा आशय पोहोचवला आहे. या रचनेत दुसऱ्या व तिसऱ्या चरणांत यमक साधलेले आहे. पहिल्या तीन चरणांत प्रत्येकी सहा अक्षरे व चौथ्या चरणात चार अक्षरे ही मोठ्या अभंगाची वैशिष्ट्ये आहेत. लोकमानसाला परमार्थाची शिकवण सहजपणे देण्याचे कौशल्य साधले आहे.

6. कवितेतून व्यक्त होणारा विचार → संतसज्जन लोक हे झाडाप्रमाणे असतात. झाडाची पूजा केली किंवा त्याला तोडले तरी झाडाला मान-अपमान वाटत नाही. या झाडांप्रमाणे सज्जनांची वागणूक असते. निंदास्तुती त्यांना समान वाटते. अशा संतांची गाठ पडणे म्हणजे जिवाशिवाची, म्हणजेच साक्षात परमेश्वराचीच भेट होणे होय.

7. कवितेतील दोन ओळींचा सरळ अर्थ:
निंदास्तुति सम मानिती जे संत ।
पूर्ण धैर्यवंत साधु ऐसे ।।
→ निंदा आणि स्तुती जे समान लेखतात, ते संत असतात. असे साधुसंत संपूर्ण धैर्यवान असतात. निंदास्तुतीने त्यांचे मन विचलित होत नाही.

8. कविता आवडण्याची वा न आवडण्याची कारणे → जीवन जगताना आपण स्थिरचित्त कसे असावे, हे या कवितेत झाडाच्या प्रतीकातून शिकवले आहे. संतांची थोरवी सांगणारी व जीवनमूल्यांची शिकवण देणारी ही अभंगरचना असल्यामुळे ती मला खूप आवडली.

रसग्रहण:

इयत्ता 9 वी-10 वीच्या कृतिपत्रिकेच्या नवीन, अदययावत आराखड्यानुसार प्रश्न 2 (इ) हा कवितेच्या पंक्तींच्या रसग्रहणावर आधारित प्रश्न असणार आहे. कृतिपत्रिकेत 4 गुणांचा हा नवीन प्रश्नप्रकार असून, त्याचे स्वरूप पुढीलप्रमाणे असेल:

1. पठित पदयांपैकी म्हणजेच पाठ्यपुस्तकातील कोणत्याही एका कवितेपैकी रसग्रहणास अनुकूल अशा कोणत्याही दोन पंक्ती देऊन, त्यांचे रसग्रहण करा असा प्रश्न विचारला जाईल.
2. दिलेल्या पंक्तींचे रसग्रहण करताना पुढील तीन मुद्द्यांना अनुसरून तीन परिच्छेदांत रसग्रहण करणे अपेक्षित आहे:

1. आशयसौंदर्य: यामध्ये कवीचे/कवितेचे नाव, कवितेचा विषय, मध्यवर्ती कल्पना, संदेश, उपदेश, मूल्य, कवितेतून मिळणारा एकत्रित अनुभव आदी मुद्द्यांना धरून माहिती लिहावी. प्रत्येक कवितेतील कोणत्याही दोन पंक्तींसाठी हे मुद्दे सर्वसाधारणपणे सारखेच राहतील.
2. काव्यसौंदर्य: यामध्ये दिलेल्या पंक्तींतील अर्थालंकार, रस, विविध कल्पना, प्रतिमा, विविध भावना यांविषयी लिहावे. ही माहिती दिलेल्या पंक्तींना अनुसरून लिहावी लागणार आहे. त्यासाठी कवितेचा भावार्थ बारकाईने अभ्यासावा.
3. भाषिक वैशिष्ट्ये: यामध्ये कवींची भाषाशैली कोणत्या प्रकारची आहे (ग्रामीण, बोलीभाषा, संवादात्मक, निवेदनात्मक, चित्रदर्शी यांपैकी कोणती); तसेच आंतरिक लय, नादमाधुर्य, अलंकार आदी मुद्दयांना धरून माहिती यावी. हे मुद्देही प्रत्येक कवितेसाठी साधारणपणे सारखेच असतील.

वरील मुद्द्यांना अनुसरून प्रस्तुत कवितेसाठी सर्वसाधारण रसग्रहणाचा ढाचा कसा असावा, हे पुढे मार्गदर्शनार्थ दिले आहे. तो अभ्यासून कवितेतील अन्य कोणत्याही दोन पंक्तींसाठी रसग्रहण लिहिण्याचा सराव विदयार्थ्यांनी करावा.

पुढील ओळींचे रसग्रहण तुमच्या शब्दांत करा:

प्रश्न 1.
“निंदास्तुति सम मानिती जे संत।
पूर्ण धैर्यवंत साधू ऐसे ।।
उत्तर:
आशयसौंदर्य: ‘जैसा वृक्ष नेणे’ या अभंगामध्ये संत नामदेव यांनी झाडाचे प्रतीक वापरून संत-सज्जनांची महती सांगितली आहे. संतांचे वागणे मानापमान व निंदास्तुती यांच्या पलीकडचे असते. तशी आपली वागणूक ठेवावी स्थिर चित्ताने वर्तन करावे, हा संदेश या अभंगातून दिला आहे.

काव्यसौंदर्य : झाडाची पूजा केली किंवा झाड तोडले तरी झाडाला दुःख होत नाही. त्याला मान-अपमान वाटत नाही. संतसज्जन झाडासारखे असतात. निंदा व स्तुती त्यांना समान वाटते. स्तुतीने ते हुरळून जात नाहीत अथवा निंदेने नाराज होत नाही. ते पूर्ण धीरवंत व स्थिरबुद्धीने वागतात. अशा धैर्यवंत साधूंची गाठ पडणे म्हणजे प्रत्यक्ष परमेश्वराची भेट होणे असते.

भाषिक वैशिष्ट्ये: ‘अभंग’ या प्राचीन लोकछंदात ही रचना आहे. पहिल्या तीन चरणात सहा व चौथ्या चरणात चार अक्षरे असा हा ‘मोठा अभंग’ छंद आहे. या रचनेत दुसऱ्या व तिसऱ्या चरणात यमक साधले आहे. झाडाचे सर्वमान्य प्रतीक वापरून साध्या, सुबोध भाषेत कवितेचा आशय पोहोचवला आहे. नेमके तत्त्व सांगून लोकमानसाला योग्य शिकवण सहजपणे देण्याची विलक्षण हातोटी शब्दांनी साधली आहे.

भाषाभ्यास:

(अ) व्याकरण घटकांवर आधारित कृती:

1. अलंकार:
नोंद : सदर प्रश्नप्रकार कृतिपत्रिकेच्या आराखड्यातून वगळण्यात आला आहे. परंतु हा प्रश्न पाठ्यपुस्तकातील असल्यामुळे विदयार्थ्यांच्या अधिक अभ्यासासाठी तो इथे उत्तरांसह समाविष्ट करण्यात आला आहे.

2. वाक्प्रचार:

प्रश्न 1.
पुढील वाक्प्रचारांचा अर्थ सांगून वाक्यांत उपयोग करा:
1. निंदा करणे
2. स्तुती करणे.
उत्तर:
1. निंदा करणे – अर्थ : नालस्ती करणे.
वाक्य: कुणीही कुणाची कधीही निंदा करू नये.
2. स्तुती करणे – अर्थ : प्रशंसा करणे.
वाक्य: गणितात पैकीच्या पैकी गुण मिळवणाऱ्या मोहितची सरांनी वर्गात स्तुती केली.

(आ) भाषिक घटकांवर आधारित कृती:

1. शब्दसंपत्ती:

प्रश्न 1.
पुढील शब्दांचे समानार्थी शब्द लिहा :

1. वृक्ष
2. सुख
3. सम.

उत्तर:

1. वृक्ष = झाड, तरू
2. सुख = आनंद, समाधान
3. सम = समान, सारखेपणा.

प्रश्न 2.
विरुद्धार्थी शब्द लिहा:

1. मान
2. निंदा
3. सुख
4. पूर्ण.

उत्तर:

1. मान × अपमान
2. निंदा × स्तुती
3. सुख × दुःख
4. पूर्ण × अपूर्ण.

प्रश्न 3.
पुढे दिलेल्या कंसातील शब्दांना (क्रियापदांना) ‘ईव’ प्रत्यय जोडून विशेषणे तयार करा व त्यांच्यासाठी समर्पक विशेष्य शोधून लिहा:
नोंद: सदर प्रश्नप्रकार कृतिपत्रिकेच्या आराखड्यातून वगळण्यात आला आहे. परंतु हा प्रश्न पाठ्यपुस्तकातील असल्यामुळे विदयार्थ्यांच्या अधिक अभ्यासासाठी तो इथे उत्तरांसह समाविष्ट करण्यात आला आहे.
उदा., आखणे – आखीव – आखीव कागद (रेखणे, कोरणे, ऐकणे, घोटणे, राखणे)
उत्तर:

1. रेखणे – रेखीव – रेखीव आकृती
2. कोरणे – कोरीव – कोरीव काम
3. ऐकणे – ऐकीव – ऐकीव गोष्ट
4. घोटणे – घोटीव – घोटीव शिल्प
5. राखणे – राखीव – राखीव जागा.

2. लेखननियम:

प्रश्न 1.
अचूक शब्द ओळखा:
1. सतजन, सज्जन, सजन्न, साज्जन.
2. स्तुती, स्तूती, स्तुति, स्तूति.
उत्तर:
1. सज्जन
2. स्तुती.

उपक्रम:

प्रश्न 1.
‘वृक्षवल्ली आम्हां सोयरे वनचरे’ हा अभंग वर्गात वाचून त्यावर चर्चा करा.

संतवाणी (अ) जैसा वृक्ष नेणे- संत नामदेव Summary in Marathi

कवितेचा आशय:

या अभंगात संत नामदेवांनी संतांना झाडांची उपमा देऊन त्यांची थोरवी वर्णन केली आहे.

शब्दार्थ:

1. जैसा – जसा.
2. वृक्ष – झाड.
3. नेणे – जाणत नाही.
4. मान – सन्मान, गौरव.
5. अपमान – अवमान.
6. तैसे – तसे.
7. सज्जन – संत.
8. वर्तताती – वागतात, वर्तन करतात.
9. चित्ती – मनात.
10. तया – त्यांना.
11. अथवा – किंवा. छेदू
12. नका – तोडू नका.
13. निंदा – नालस्ती, अपमानकारक बोलणे.
14. स्तुती – प्रशंसा.
15. सम – समान, सारखे.
16. धैर्यवंत – हिंमतवान, गंभीर, निश्चल.
17. भेटी – गाठभेट.
18. जीव – प्राण.
19. शिव – परब्रह्म, परतत्त्व.
20. गांठी – एकत्र येणे.
21. जाय – होते.

कवितेचा (अभंगाचा) भावार्थ:

संतांची महती वर्णन करताना संत नामदेव म्हणतात – ज्याप्रमाणे वृक्षाला (झाडाला) मान आणि अपमान यांचे काहीच वाटत नाही, मानापमान ते जाणत नाहीत; त्याप्रमाणे, त्या वृक्षाप्रमाणे संतांचे (सज्जनांचे) वर्तन असते. ।।1।।

कोणी माणसांनी येऊन वृक्षाची पूजा केली, तरी वृक्षाच्या मनाला सुख किंवा आनंद होत नाही. ।।2।।
किंवा कोणी येऊन वृक्षाला तोडले, तरी तो त्या माणसांना ‘तोडू नका’ असे म्हणत नाही. तो अविचल राहतो. ।।3।।

तसे संतसज्जन निंदा आणि स्तुती यांना समान लेखतात. निंदा व स्तुती त्यांना सारखीच असते. असे हे साधुसंत पूर्णतः धैर्यवंत असतात. निश्चल असतात. निंदास्तुतीने त्यांचे मन विचलित होत नाही. ।।4।।

संत नामदेव म्हणतात, अशा संतांची जेव्हा गाठभेट होते, तेव्हा साक्षात जीवाशिवाची गाठ पडते. संतांच्या भेटीमुळे प्रत्यक्ष परब्रह्म भेटीचे सुख लागते. ।।5।।

Balbharti Maharashtra State Board Class 9 Marathi Solutions Kumarbharti Chapter 7 दुपार Notes, Textbook Exercise Important Questions and Answers.

Maharashtra State Board Class 9 Marathi Kumarbharti Solutions Chapter 7 दुपार

9th Std Marathi Kumarbharati Digest Chapter 7 दुपार Textbook Questions and Answers

1. तुलना करा:

प्रश्न 1.
तुलना करा:

उत्तर:

2. कोण ते लिहा:

प्रश्न 1.
कोण ते लिहा:
(अ) दुपारला अभिमान वाटणारा मानवी घटक – [ ]
(आ) दुपारला आनंद देणारा घटक – [ ]
(इ) दुपारच्या दृष्टीने एकविसाव्या शतकातील श्रमजीवी – [ ]
(ई) सृष्टिचक्रातील महत्त्वाचे काम करणारा घटक – [ ]
(उ) मानवी जीवनक्रमातील दुपार – [ ]
(ऊ) वृद्ध व्यक्ती दररोज आपल्या आयुष्याचे सिंहावलोकन करतात तो काळ – [ ]
उत्तर:
(अ) शेतकरी
(आ) मधल्या सुट्टीत खेळणारी मुले.
(इ) कार्यालयांतील लेखनिक व हिशोबतपासनीस.
(ई) दुपार
(उ) तारुण्य.
(ऊ) दुपार

3. आकृतिबंध पूर्ण करा:

प्रश्न 1.
आकृतिबंध पूर्ण करा:

उत्तर:

4. डौलदार गिरिशिखरे धापाच टाकू लागतात.

प्रश्न 1.
डौलदार गिरिशिखरे धापाच टाकू लागतात.
उत्तर:
हा चेतनगुणोक्ती अलंकार आहे.
स्पष्टीकरण: खूप जलद चालल्यावर माणसाला धापा लागतात. इथे डोंगराची शिखरे धापा टाकत आहेत. म्हणजे गिरिशिखरांवर (निर्जीव वस्तूंवर) मानवी भावनांचे आरोपण केले अहे. म्हणून हा चेतनगुणोक्ती अलंकार आहे.

5. खाली काही शब्दांचे गट दिले आहेत. त्या गटांतून वेगळ्या अर्थाचा शब्द शोधा:

प्रश्न 1.
खाली काही शब्दांचे गट दिले आहेत. त्या गटांतून वेगळ्या अर्थाचा शब्द शोधा:
उदा., मित्र – दोस्त, मैत्री, सखा, सोबती

1. रस्ता – बाट, मार्ग, पादचारी, पथ
2. पर्वत – नग, गिरी, शैल, डोगर
3. ज्ञानी – मुश, सुकर, डोळस, जाणकार
4. डौल – जोम, ऐट, दिमाख, स्वाब
5. काळजी – चिंता, स्याबदारी, विवंचना, फिकीर.

उत्तर:

1. पादचारी
2. नग
3. सुकर
4. जोम
5. जबाबदारी

6. स्वमत

प्रश्न (अ)
‘माझी मे महिन्यातील दुपार’ याविषयी आठ ते दहा वाक्ये लिहा.
उत्तर:
आठवीनंतरच्या मे महिन्यापासून सक्तीने क्लास सुरू होतो. त्या बदल्यात आम्ही मित्र घरून भांडून क्रिकेटची परवानगी मिळवतो. खेळातल्या धावा आणि घामाच्या धारा यांत आमची दुपार चिंब भिजून जाते. तळमजल्यावरचे काका खिडकीत पाण्याने भरलेले छोटे पिंप व ग्लास ठेवतात. तो आमचा मोठाच आधार असतो. क्वचित केव्हातरी टीव्हीवर सिनेमा बघण्यात दुपार जाते किंवा बाबांच्या लॅपटॉपवर गेम खेळण्यात दंग होतो. पण हे किरकोळ झाले.

क्रिकेट खालोखाल मे महिन्यातला दुपारचा आनंदोत्सव म्हणजे पार्टी! पिझ्झा पार्टी, आइस्क्रीम पार्टी किंवा भेळपुरी पार्टी. कोणाचा तरी वाढदिवस असतो, कोणाला तरी काहीतरी मिळालेले असते, खेळून खेळून भूकही लागलेली असते. अशा वेळी पार्टी होतेच. मग काय, वर्गणी काढतो आणि पार्टी करतो. ही दुपारची वेळ आम्हांला खूप आवडते. त्या वेळी आम्ही आमचे राजे असतो. त्या वेळी “पुरे झाले, आता चला घरी,’ असे कोणी सांगत नाही. मला नेहमी वाटते वर्षातून दोन-तीन वेळा तरी मे महिना यायला हवा!

प्रश्न (आ)
‘दुपार’ या ललित लेखातील कोणता प्रसंग तुम्हांला अधिक आवडला, ते सविस्तर लिहा.
उत्तर:
‘दुपार’ या ललित लेखातील मला आवडलेला प्रसंग आहे तो मधल्या सुट्टीतील धमाल सांगणारा. मला खरोखर खूप आवडला तो. तो वाचताक्षणी मला शाळेतील मधल्या सुट्टीचे सगळे दिवस झर्रकन आठवले. मधल्या सुट्टीची घंटा झाल्यावर अर्धे मिनिटसुद्धा थांबायला कोणी तयार नसतो. आम्ही डबा किती भरभर खायचो. अनेकदा तोंडात घास घेऊनच मैदानावर पळायचो. सातवीपर्यंत मी शाळेत डबा नेत असे. आठवी-नववीत मात्र डबा बंद केला. शाळेच्या कँटीनमधला वडापाव आम्हां सर्व मित्रांमध्ये लोकप्रिय.

तो वडापाव हातात घेऊन कबड्डीच्या मैदानात उतरलो होतो. विशेष म्हणजे सरांनीसुद्धा हसतहसत परवानगी दिली होती. मधली सुट्टी म्हणजे हैदोस होता नुसता! या मधल्या सुट्टीत आम्ही असंख्य गोष्टी केल्या आहेत. पाठातला हा प्रसंग लेखकांनी मोजक्या शब्दांत लिहिला आहे. पण सगळी मधली सुट्टी त्या तेवढ्या शब्दांत उभी राहते. म्हणून या पाठातला हाच प्रसंग मला सर्वाधिक आवडला आहे.

7. अभिव्यक्ती

प्रश्न (अ)
तीनही ऋतूंतील तुम्ही अनुभवालेल्या सकाळ व संध्याकाळचे वर्णन करा.

प्रश्न (आ)
पाठात आलेल्या ‘दुपारच्या विविध रूपांचे वर्णन करा.

भाषाभ्यास:

रसविचार

मानवी जीवनात कलेचे महत्त्व अनन्यसाधारण आहे. कोणतीही कलाकृती पाहताना, त्याचा आस्वाद घेताना मानवी मनात भावनांचे अनेक तरंग उठतात. कलेचा आस्वाद घेण्याचे कौशल्य प्रत्येकाच्या स्वानुभव समतेवर अवलंबून असते. ही अनुभवक्षमता शालेय वयापासून वृदपिंगत व्हावी, या दृष्टीने ‘रसास्वाद’ ही संकल्पना आपण समजून घेऊया. मानवाच्या अंत:करणात ज्या भावना स्थिर व शाश्वत स्वरूपाच्या असतात, त्यांना ‘स्थाविभाव’ असे म्हणतात. उदा., राग, दुःख, आनंद इ. कोणत्याही कलेचा आस्वाद घेताना या भावना जागृत होतात व त्यांतून रसनिपती होते.

साहित्यामध्ये गय-पदय घटकांचा आस्वाद घेताना आपण अनेक रस अनुभवतो. गदा-पदय घटकांतून चपखलपणे व्यक्त होणारा आशय, दोन ओळींमधील गर्भितार्थ, रूपकात्मक भाषा, पदय घटकांतील अलंकार, सूचकता, प्रसाद, मापुर्व हे काव्यगुण पदोपदी प्रत्ययास येतात. अर्थपूर्ण रचनांचा रसास्वाद घेण्याची कला आत्मसात शाली, की त्यामुळे मिळणारा आनंद अवर्णनीय असतो. भाषासमूदधीसाठी ‘रसास्वाद’ या घटकाकडे आवर्जून लश देऊया.

मनातील वैयक्तिक दुःखाची भावना जर साहित्यातून अनुभवाला आली तर तिथे करुण रसाची निर्मिती होते. मनातल्या दुःखाचा निचरा, विरेचन होऊन (कथार्सिसच्या सिद्धांतानुसार) कारण्याच्या सहसंवेदनेचा अनुभव घेता येतो. आणि या प्रक्रियेतून काव्याचा आस्वाद घेता येतो. तसेच वैयक्तिक दाखाची भावना सार्वत्रिक होऊन तिचे उदात्तीकरण होते. अशा भावनांच्या उदात्तीकरणामुळे मी व माझा या पलिकडे जाऊन व्यक्तींच्या व समाजाच्या भावनांचा आदर कण्याची वृत्ती जोपासली गेली तर नात्यांमधील, व्यक्तीव्यक्तींमधील भावसंबंधाचे दृढीकरण होते.

कोणतीही कलाकृती अभ्यासताना त्या कलाकृतीचा आस्वाद घेता आला तरच ती आनंददायी ठरते. एखादी कलाफूती दिलगे, ती पाहणे व ती अनुभवणे हे कलाकृतीच्या आस्वादाचे टणे आहेत. केवळ डोळ्यांनी नव्हे तर कलाकृती मनाने अनुभवता आली पाहिजे. कोणत्याही कवितेचे, पाठाचे आकलन होऊन संवेदनशीलतेने कलाकृतीतील अर्थ, भाष, विचार, सौंदर्य टिपता आले पाहिजे. कवीला काय सांगायचे आहे याविषयी दोन ओळींमधील दडलेला मथितार्थ समजला तरच कवितेचे पूर्णाशाने आकलन होते व त्याच्या रसनिष्पत्तीचा आनंद घेता येतो. आपल्या पाठयपुस्तकातील प्रत्येक पात्र, प्रत्येक कविता, प्रत्येक घटकाकडे पाहण्याचा अर्थ समजून घेण्याची ही आस्वादक दृष्टी विकसित झाली, तर भाषेचा खरा आनंद प्राप्त होईल.

Marathi Kumarbharati Textbook Std 9 Answers Chapter 7 दुपार Additional Important Questions and Answers

उतारा क्र. 1

1. पुढील उतारा वाचून दिलेल्या सूचनांनुसार कृती करा :

कृती 1 : (आकलन)

प्रश्न 1.
आकृतिबंध पूर्ण करा:

उत्तर:

प्रश्न 2.
रिकाम्या जागा भरा:
1. सूर्याची धमकी – [ ]
2. सूर्याचे प्रखर तेज – [ ]
उत्तर:
1. माझ्याकडे डोळे वटारून पाहिलेस, तर डोळे जाकून टाकीन.
2. सर्व पृथ्वीला टिपवून टाकते.

कृती 2 : (आकलन)

प्रश्न 1.
कोण ते लिहा:
1. धन्याच्या कष्टाकडे कौतुकाने पाहणारी – [ ]
उत्तर:
1. शेतकऱ्याची पत्नी

कृती 3 : (स्वमत/अभिव्यक्ती)

प्रश्न 1.
तुम्हांला या उताऱ्यावरून जाणवलेली दुपारची वैशिष्ट्ये लिहा.
उत्तर:
सकाळचा सूर्य, दुपारचा सूर्य ही सूर्याची वेगवेगळी रूपे आहेत. या वेगवेगळ्या रूपांमुळेच सकाळ व दुपार या कालावधींना वेगवेगळी नावे मिळाली आहेत. सकाळ प्रसन्न असते. तिच्यात उल्हास ठासून भरलेला असतो; तर दुपार ही प्रखर सूर्यामुळे रौद्र रूप धारण करते. डोळे उघडून बाहेर पाहण्याची हिंमतही होणार नाही. अशी ही तप्त, रखरखीत दुपार शेतात कष्ट करणाऱ्या शेतकऱ्याकडे मायेने व आदराने पाहते. सकाळपासून केलेल्या कष्टाचा शीण घालवण्यासाठी तो वडा-पिंपळाच्या झाडाखाली विसावतो. पत्नीने आणलेला भाकरतुकडा तो समाधानाने खातो. त्याची पत्नी त्याच्या कष्टाकडे कौतुकाने पाहते. या दृश्याने दुपारला धन्य धन्य झाल्यासारखे वाटते.

उतारा क्र. 2

1. पुढील उतारा वाचून दिलेल्या सूचनांनुसार कृती करा:

कृती 1 : (आकलन)

प्रश्न 1.
रिकामी जागा भरा:
कष्टकऱ्यांच्या दुपारचे वर्णन: ………………………………………
उत्तर:
खेडोपाडी गावे सुस्तावतात. घरकाम सांभाळणाऱ्या स्त्रिया घरकामे आटपून घटकाभरासाठी डोळे मिटून विसावतात.

प्रश्न 2.
पक्ष्यांची विश्रांती:

1. वडाच्या झाडावरील पक्षी: …………………………………….
2. शेकडो मैलांची रपेट करणारे पक्षी: ……………………..
3. सकाळपासून दाणापाणी मिळवण्याचे काम केलेले पक्षी: ……………………………………..
4. घरांच्या आश्रयाने राहणारी कबुतरे: ………………………………………..

उत्तर:

1. वडाच्या झाडावरील पक्षी: किलबिलाट थांबवून सावलीत छानशी डुलकी घेत विश्रांती घेतात.
2. शेकडो मैलांची रपेट करणारे पक्षी: मिळेल त्या वृक्षावर थोडी विश्रांती घेतात.
3. सकाळपासून दाणापाणी मिळवण्याचे काम केलेले पक्षी: कुठे कुठे विश्रांती घेण्याच्या प्रयत्नात असतात.
4. घरांच्या आश्रयाने राहणारी कबुतरे: गुटगू थांबवून कुठे तरी छपरांच्या सांदीत थोडी सैलावतात.

कृती 2 : (आकलन)

प्रश्न 1.
आकृती पूर्ण करा:

उत्तर:

प्रश्न 2.
आकृती पूर्ण करा:

उत्तर:

प्रश्न 3.
विधान पूर्ण करा:
…………………….. हा दुपारचा कार्यरत राहण्यामागील हेतू असतो.
उत्तर:
पुन्हा ताजेतवाने होण्यासाठी सर्वांना काही क्षण विश्रांती मिळावी, हा दुपारचा कार्यरत राहण्यामागील हेतू असतो.

कृती 3 : (स्वमत/अभिव्यक्ती)

प्रश्न 1.
तुम्ही पाहिलेल्या दुपारचे वर्णन लिहा.
उत्तर:
आमच्याकडे दुपार तशी शांत शांतच असते. मी शाळेतून येतो. बाबा शेतावरून येतात. हातपाय धुवून जेवायला बसतात. आम्ही सगळेच जण एकत्र जेवायला बसतो. जेवल्यानंतर बऱ्याच वेळा बाबा शेतीतल्या कामांसंबंधी बोलतात. बोलता बोलता आईबाबा काही निर्णय घेतात. आई स्वयंपाकघराची आवराआवर करते. आम्हीपण कधी कधी तिला मदत करतो. बाबा अंगणातल्या बाकड्यावर पहडतात. क्षणातच झोपी जातात. आई चटई पसरून पहुडते. आमचा कुत्रा बाबांच्या बाकड्याखाली मुटकुळे करून पहुडतो. तो झोपण्यासाठी डोळे मिटतो खरा, पण प्रत्यक्षात जागाच असतो.

मधून केव्हातरी चटकन कान टवकारून पाहतो आणि पुन्हा शांत होतो. आवारातल्या आम्हा मुलांची मात्र त्या वेळी मजा होते. सगळे विश्रांती घेत असतात, म्हणून टीव्ही बंद ठेवावा लागतो. आम्ही मित्रमंडळी घराच्या मागच्या बाजूला पडवीत जमतो. कधी पत्त्यांचा खेळ, कधी गोट्यांचा खेळ रंगतो. हे सर्व अर्थातच शांतपणे. पण केव्हातरी आवाज वाढतो. मग मोठी माणसे कुठून तरी ओरडून दम देतात. मग सगळे शांत. केव्हातरी मी नववीत असल्याची आठवण कोणीतरी करून देतोच. मग थोडा वेळ पुस्तक घेऊन बसावे लागते. अशी ही मजेची दुपार असते.

उतारा क्र. 3

पुढील उतारा वाचून दिलेल्या सूचनांनुसार कृती करा :

कृती 1 : (आकलन)

प्रश्न 1.
माहिती लिहा:
1. हातगाडीवाल्याचे दुपारचे जीवन.
2. सायकलरिक्षावाल्याची दुपार.
3. कारखान्यातील कामगारांची दुपार.
उत्तर:
1. हातगाडीवाल्याचे दुपारचे जीवन: हातगाडीवाला म्हणजे हातगाडीवरून लोकांचे सामान वाहून नेणारा हमाल. यात अमाप कष्ट असतात. दुपारपर्यंत बऱ्यापैकी कमाई झाली. उरलेल्या अवधीत चांगली कमाई होईल का, अशी चिंता करीत तो विश्रांती घेण्याच्या बेतात असतो. तेवढ्यात त्याला वर्दी मिळते. विश्रांतीची गरज असतानाही तो आळस झटकून गाडी ओढायला सिद्ध होतो.

2. सायकलरिक्षावाल्याची दुपार: सायकलरिक्षा तळपत्या उन्हात चालवून चालवून रिक्षावाला एखादी डुलकी घेण्याच्या विचारात असतो. पण तेवढ्यात त्याला लांबची वर्दी मिळते. म्हणजे जास्त पैसे मिळणार. म्हणून दमलेल्या शरीराची पर्वा न करता तो सायकलरिक्षा दामटतो. या रिक्षावाल्याची दुपार ही अशी असते.

3. कारखान्यातील कामगारांची दुपार: कारखान्यात पहिल्या पाळीचे कामगार कामावर हजर होण्यासाठी पहाटेच उठतात. दिवसभर यंत्राशी झगडत काम करतात. त्यामुळे दुपारी विश्रांतीची गरज असते. कामावरून सुटल्यावर डोळ्यांवरील झापड दूर सारत सारत धडपडत घरी पोहोचतात. त्याच वेळी त्यांचे दुसरे सहकारी विश्रांती हवी असताना कामावर हजर होण्यासाठी येतात. हे सुद्धा पोटासाठीच धावतपळत असतात.

प्रश्न 2.
कोण ते लिहा:
दुपारला अभिमान वाटणारा मानवी घटक – [ ]
उत्तर:
दुपारला अभिमान वाटणारा मानवी घटक – [कष्टकरी]

कृती 2 : (आकलन)

प्रश्न 1.
का ते लिहा:
1. दुपार हातगाडीवाल्याला सलाम करते.
2. दुपार सायकलरिक्षावाल्याला सलाम करते.
3. दुपारला कारखान्यातील कामगारांविषयी कौतुक वाटते.
उत्तर:
1. दुपार हातगाडीवाल्याला सलाम करते : हातगाडीवाला हा काबाडकष्ट करणारा असतो. त्याच्या कामाला काळवेळेची मर्यादा नसते. किती वजन ओढायचे यालाही मर्यादा नसते. पैसे बहुधा त्या मानाने कमीच मिळतात. त्यामुळे दुपारची विश्रांती पुरेशी झालेली नसतानाही तो कष्ट करायला सिद्ध होतो. जीवन चालू ठेवायला सिद्ध होतो. म्हणून दुपार त्याला सलाम करते.

2. दुपार सायकलरिक्षावाल्याला सलाम करते: सायकलरिक्षा जिथे आजही चालू आहे, तो परिसर प्रचंड उकाड्याचा आहे. तळपत्या उन्हात सायकलरिक्षा चालवणे हे कोणालाही थकवणारे असते. त्याला दुपारी विश्रांतीची नितांत गरज असते. तरीही वर्दी मिळताच पोटाची खळगी भरण्याकरिता तो भर दुपारी सायकल मारत निघतो. त्याची ही जीवनावरची निष्ठाच असते. म्हणून दुपार त्याला सलाम करते.

3. दुपारला कारखान्यातील कामगारांविषयी कौतुक वाटते: कारखान्यातील काम तीन पाळ्यांमध्ये चालते. सकाळीच कामावर हजर झालेला कामगार दुपारी घराकडे निघतो. त्याच्या डोळ्यांवर झोपेची झापड असते. विश्रांतीसाठी तो अधीर झालेला असतो. त्याच्यानंतर दुसरे कामगार येतात. त्यांनाही खरे तर दुपारची विश्रांती हवी असते. पण सतत कार्यरत राहण्याची त्यांची वृत्ती असते. म्हणून दुपारला त्यांचे कौतुक वाटते.

कृती 3: (स्वमत/अभिव्यक्ती)

प्रश्न 1.
तुम्हांला जाणवलेले कष्टकऱ्यांचे मोठेपण सांगा.
उत्तर:
हातगाडीवाले व सायकलरिक्षावाले हे कष्टकरी आहेत. किती ओझे वाहून न्यावे लागेल, किती अंतर जावे लागेल व त्यासाठी किती कष्ट पडतील, हे त्यांना ठाऊक नसते. पैसे बहुतेक वेळा कमीच मिळतात. तरी ते विश्रांतीची पर्वा करीत नाहीत. पोटाची खळगी भरण्याकरिता धावत असतात. एक प्रकारे ते जीवनचक्र चालू ठेवण्यासाठीच धडपडत असतात.

हेच कारखान्यातील कामगारांबाबतही घडते. त्यांचेही काम कष्टाचेच असते. मात्र या कामगारांच्या वेळा ठरलेल्या असतात. तरीही वेळा पाळण्यासाठी स्वत:च्या आरामाचा, स्वास्थ्याचा त्याग करतात. ही त्यांची स्वत:च्या कामावरची निष्ठा असते. कष्टकऱ्यांच्या त कामगारांच्या निष्ठेमुळेच हे जीवनाचे चक्र चालू असते. माझ्या मते, समाजाने त्यांचे ऋणी राहिले पाहिजे.

उतारा क्र. 4

1. पुढील उतारा वाचून दिलेल्या सूचनांनुसार कृती करा:

कृती 1 : (आकलन)

प्रश्न 1.
कोष्टक पूर्ण करा:

उत्तर:

प्रश्न 2.
चौकट पूर्ण करा:

उत्तर:

कृती 2 : (आकलन)

प्रश्न 1.
कोण ते लिहा:
1. समोर काम येऊ नये, असे वाटते ती वेळ:
उत्तर:
1. दुपार.

प्रश्न 2.
का ते लिहा:

1. शहरातल्या कार्यालयातील लेखनिकांचे व हिशोबतपासनिसांचे लक्ष भिंतीवरील घड्याळाकडे असते.
2. समोर नवीन काम येऊ नये, अशी त्यांची इच्छा असते.
3. जिवाभावाच्या गप्पा मारतात.
4. एकमेकांच्या डब्यातल्या पदार्थांची चव चाखत जेवतात.

उत्तर:

1. भूक लागलेली असते व डबा खायचा असतो म्हणून.
2. निवांतपणे जेवता यावे म्हणून.
3. ताजेतवाने होण्यासाठी.
4. एकमेकांविषयी जिव्हाळा वाटतो म्हणून आणि विविध चवींचा आस्वाद मिळावा म्हणून.

उतारा क्र. 4

पुढील उतारा वाचून दिलेल्या सूचनांनुसार कृती करा:

कृती 1 : (आकलन)

प्रश्न 1.
आकृतिबंध पूर्ण करा:

उत्तर:

कृती 2 : (आकलन)

प्रश्न 1.
आकृती पूर्ण करा:

उत्तर:

प्रश्न 2.
गाळलेल्या जागा भरा:
वृद्ध माणसांचे चिंतन:
1. ………………………..
2. ……………………….
उत्तर:
1. आतापर्यंतच्या आयुष्यात काय कमावले, काय गमावले, याचा विचार करतात.
2. स्वत:च्या भविष्याची चिंता करीत बसतात.

कृती 3 : (स्वमत/अभिव्यक्ती)

प्रश्न 1.
तुम्हाला जाणवलेले संसाराचे चक्र स्पष्ट करा.
उत्तर:
निसर्गात ऋतूंचे चक्र असते, पाण्याचे चक्र असते. प्राणवायू, कार्बन डायऑक्साइड वायू यांची चक्रे असतात. तसेच मानवी जीवनाचेही चक्र दिसून येते. बालपण व विदयार्थिदशा ही पहिली अवस्था आहे. तारुण्याची दुसरी अवस्था आणि वृद्धत्वाची तिसरी अवस्था असते. या अवस्था एकेका पिढीनुसार बदलत राहतात. आता बाल्यावस्थेत असलेली मुले पुढच्या पिढीत तरुण बनतात. त्याच व्यक्ती नंतरच्या पिढीत वृद्ध होतात. यांतील मधली पिढी ही तारुण्याची होय. या पिढीतील माणसे कर्ती-धर्ती असतात.

त्यांच्या कर्तबगारीवरच कुटुंबाचा व समाजाचाही गाडा चालू असतो. या टप्प्यात माणसे कामात गुंतलेली असतात, अपार कष्ट करतात. म्हणून संसाराचे रूप बदलते. दुपार हीसुद्धा दिवसाची मधली म्हणजे तारुण्यावस्था असते. म्हणूनच समाजाच्या विकासाची, पालनपोषणाची सर्व कार्ये या अवधीतच चालू असतात. दुपार ही तारुण्याचे प्रतीकच आहे.

उतारा क्र. 6

पुढील उतारा वाचून दिलेल्या सूचनांनुसार कृती करा:

कृती 1 : (आकलन)

प्रश्न 1.
कोण ते लिहा:
1. तेजाने न्हाऊन निघणारी – [ ]
2. दुपारच्या रौद्र रूपाने अचंबित होणारी – [ ]
उत्तर:
1. बर्फाच्छादित गिरिशिखरे
2. बर्फाच्छादित गिरिशिखरे

प्रश्न 2.
उत्तर लिहा:
अचंबित करणारे दुपारचे कार्य – ………………………..
उत्तर:
समुद्राच्या पाण्याची वाफ करणे आणि डोंगरावरच्या बर्फाचे पाणी करणे, हे दुपारचे अचंबित करणारे कार्य आहे.

कृती 2 : (आकलन)

प्रश्न 1.
पाण्याचे चक्र काढा.
उत्तर:

प्रश्न 2.
दुपारचे मोठेपण सांगणारे उताऱ्यातील शब्द लिहा.
उत्तर:
दुपारचे मोठेपण सांगणारे लेखकांचे शब्द : कर्तृत्ववान, कामाची प्रेरणा देणारी, सृष्टीला कार्यरत करणारी, कर्तृत्वाच्या तेजाने तळपवून टाकणारी, हितकर्ती, रक्षणकर्ती, हवेतले कीटक व जंतू यांचा नाश करणारी, उदास नसून उल्हास आहे. अचेतन नसून सचेतन आहे. दीर्घकर्तृत्ववाहिनी, कार्यरत ठेवणारी, वैभवाची वाट दाखवणारी.

कृती 3 : (स्वमत/अभिव्यक्ती)

प्रश्न 1.
लेखकांनी दुपारला उद्देशून केलेल्या दुपारच्या स्तुतीबद्दल तुमचे मत लिहा.
उत्तर:
लेखकांनी दुपारला उद्देशून लिहिलेला मजकूर म्हणजे दुपारचे स्तोत्रच आहे. ते अत्यंत योग्य आहे. एरवी लोकांच्या मनात दुपार म्हणजे कंटाळवाणा, त्रासदायक, नकोसा काळ असतो. पण लेखकांनी दुपारचे खरे रूपच आपल्यासमोर ठेवले आहे. त्यामुळे दुपारबद्दलचे आपले मत बदलण्यास मदत होते. दुपारचा लखलखीत सूर्य म्हणजे दुपारचे तेज होय. या काळात माणसाच्या हिताची सर्व कार्ये चालू असतात. कंटाळा आला, थकवा आला, तरी लोक ही कार्ये चालू ठेवतात.

त्यामुळे मानवी समाजाची भरभराट होते. म्हणूनच लेखकांनी दुपारला मानवाची हितकर्ती, दीर्घ कर्तृत्ववाहिनी, कार्यप्रवण करणारी, वैभवाची वाट दाखवणारी असे म्हटले आहे. या काळातच कर्तबगारीला बहर येतो. म्हणून दुपार ही अचेतन नसून चेतना आहे, हे लेखकांचे विधान यथोचित आहे. एकंदरीत लेखकांनी दुपारला उद्देशून म्हटलेले सर्व काही मला पूर्णपणे पटते.

भाषाभ्यास:

(अ) व्याकरण घटकांवर आधारित कृती:

1. अलंकार:

प्रश्न 1.
पुढील ओळींतील अलंकार ओळखा व स्पष्टीकरण लिहा:

2. समास:

प्रश्न 1.
सामासिक शब्दांवरून समास ओळखा:

1. चौकोन →
2. भारतमाता →
3. बापलेक →
4. धावपळ →
5. खरेखोटे

उत्तर:

1. विगू समास
2. कर्मधारय समास
3. इसमेतर वंद्व समास
4. समाहार वंद्व समास
5. वैकल्पिक वंदन समास.

3. शब्दसिद्धी:

प्रश्न 1.
‘आळू’ प्रत्यय असलेले चार शब्द लिहा.
उत्तर:

1. दयाळू
2. ममतालू
3. कृपाळू
4. मायाळू.

4. वाक्प्रचार:

प्रश्न 1.
पुढील वाक्प्रचारांचा अर्थ सांगून वाक्यांत उपयोग करा:
1. कृतकृत्य होगे
2. ताव मारणे
3. धूम ठोकणे.
उत्तर:
1. कृतकृत्य होगे – अर्थ : धन्य होगे.
वाक्य: वंदा पास छान पडल्यामुळे शेतकरी कृतकृत्य झाले.
2. ताव मारणे – अर्थ : भरपूर जेबगे.
वाक्य: लानातील जेवणात जिलेबीवर बापूने ताव मारला.
3. धूम ठोकणे – अर्थ : पळून जाणे.
वाक्य: बापाची चाहूल लागताच हरणांनी धूम ठोकली.

(आ) भाषिक घटकांवर आधारित कृती:

1. शब्दसंपत्ती:

प्रश्न 1.
प्रत्येकी दोन समानार्थी शब्द लिहा:

1. धरती
2. पाणी
3. समुद्र
4. पक्षी.

उत्तर:

1. धरती = (1) धरणी (2) भूमी
2. पाणी = (1) जल (2) नीर
3. समुद्र = (1) सागर (2) रत्नाकर
4. पक्षी = (1) खग (2) विहग.

प्रश्न 2.
विरुद्धार्थी शब्द लिहा:

1. आनंद
2. दिवस
3. काळोख
4. पुष्कळ.

उत्तर:

1. आनंद × दुःख
2. दिवस × रात्र
3. काळोख × उजेड
4. पुष्कळ × कमी.

प्रश्न 3.
वचन बदला:

1. चिमणी
2. सागर
3. पक्षी
4. खेडी.

उत्तर:

1. चिमणी – चिमण्या
2. सागर – सागर
3. पक्षी – पक्षी
4. खेडी – खेडे.

2. लेखननियम:

प्रश्न 1.
अचूक शब्द ओळखा:

1. आशिर्वाद, आर्शीवाद, आर्शिवाद, आशीर्वाद.
2. अवाढव्य, अवढव्य, अवाडव्य, अव्हाढव्य.
3. विवचंना, वीवंचना, विवंचना, विहिवंचना.
4. गिरीशिखरे, गिरिशिखरे, गीरिशीखरे, गीरीशीखरे.
5. भूमीका, भूमिका, भुमिका, भुमीका.
6. प्रतीनीधी, प्रतिनीधी, प्रतिनिधि, प्रतिनिधी.

उत्तर:

1. आशीर्वाद
2. अवाढव्य
3. विवंचना
4. गिरिशिखरे
5. भूमिका
6. प्रतिनिधी.

3. विरामचिन्हे:

प्रश्न 1.
पुढील वाक्यांत योग्य ठिकाणी विरामचिन्हांचा वापर करून वाक्ये पुन्हा लिहा:
1. सूर्याच्या तेजाने तळपत असते पृथ्वी आणि पृथ्वीवरील माणसे प्राणी पशू पक्षी झाडे वेली
2. दुपार म्हणते उठा आराम बास
उत्तर:
1. सूर्याच्या तेजाने तळपत असते पृथ्वी आणि पृथ्वीवरील माणसे, प्राणी, पशू, पक्षी, झाडे, वेली.
2. दुपार म्हणते, ‘उठा-आराम बास.’

4. पारिभाषिक शब्द:

प्रश्न 1.
मराठी प्रतिशब्द लिहा:

1. Calligraphy
2. Secretary
3. Action
4. Comedy

उत्तर:

1. सुलेखन
2. सचिव
3. कार्यवाही
4. सुखात्मिका.

दुपार Summary in Marathi

पाठाचा परिचय:

राजीव बर्वे हे प्रसिद्ध लेखक आहेत. तसेच, त्यांनी अनेक चित्रपटांची निर्मिती केली आहे. त्यामुळे लेखन, दिग्दर्शन या क्षेत्रांचाही त्यांना चांगलाच परिचय आहे. लोकांना साधारणपणे सकाळचा व संध्याकाळचा अवधी खूप आवडतो. त्यांची वर्णनेही खूप केली जातात. सकाळ-संध्याकाळवर कविताही लिहिल्या जातात. कथा-कादंबऱ्यांमध्ये, सिनेमांमध्ये सकाळ-संध्याकाळची वर्णने, प्रसंग खूप येतात. मात्र दुपारबद्दल अशी वर्णने जवळजवळ नसतात.

दुपार म्हणजे रखरखीत, तप्त जाळ असलेली, कंटाळवाणी, नकोशी वाटणारी अशी सर्वांची भावना असते. प्रस्तुत पाठात मात्र लेखकांनी दुपारबद्दल अत्यंत आत्मीयतेने लिहिले आहे. जगण्याची धडपड, नवीन जीवन घडवण्याची प्रेरणा व नवनिर्मितीची ऊर्मी दुपारमध्येच दिसते. जीवनाचे चक्र चालू ठेवण्याचे कार्य दुपार पार पाडते. दुपारच्या रूपांकडे लेखक प्रेमाने पाहतात. म्हणून या पाठात दुपारचे लोभस वर्णन आले आहे. शहरात, गावात, जंगलात दुपार कशी वेगवेगळ्या | रूपांत अवतरते, त्यांचे सुंदर वर्णन या पाठात आहे.

शब्दार्थ:

1. उल्हास – आनंदाने भरलेला उत्साह.
2. मध्यान्ह – दुपारची वेळ, दिवसाचा मध्य.
3. रौद्र – प्रचंड क्रोध, संताप यांनी भरलेले अत्यंत भयंकर व भीतिदायक असे रूप.
4. शिणवटा – थकवा.
5. घरची लक्ष्मी – पत्नी.
6. कृतकृत्य – धन्य.
7. रपेट – फेरफटका.
8. सांदीत – खाचेत, दोन बाजूंमधील अत्यंत चिंचोळ्या जागेत.
9. सैलावलेली – सुस्तावलेली.
10. घासाघीस – जास्तीत जास्त नफा मिळवू पाहणारा विक्रेता व कमीत कमी किमतीत वस्तू मिळवू पाहणारा ग्राहक यांच्यात
11. किमतीवरून होणारी खेचाखेच.
12. कार्यरत – कामात मग्न, कामात गुंतलेला.
13. अव्याहत – सतत, न थांबता.
14. अथांग – ज्याचा थांग (पत्ता) लागत नाही असा.
15. मैलोगणती – कित्येक मैल.
16. काहिलीने – प्रचंड उष्ण्याने.
17. अचंबित – आश्चर्यचकित.

टीप:

मध्यान्ह:

मध्य+अन्ह, अहन् म्हणजे दिवस, ‘अन्ह:’ हे अहन्चे षष्ठीचे रूप, म्हणून अन्हः=दिवसाचा. ‘अन्हः’ हा शब्द मराठीत येताना त्यातील विसर्ग लोप पावला आहे. यावरून मध्यान्ह दिवसाचा मध्य.

वाक्प्रचार व त्यांचे अर्थ:

1. घाम गाळणे – खूप कष्ट करणे.
2. कृतकृत्य होणे – धन्य होणे, धन्य धन्य वाटणे.
3. चार पैसे गाठीला बांधणे – पैशांची बचत करणे.
4. बेगमी करणे – भविष्यासाठी तरतूद करणे.
5. भ्रांत असणे – विवंचना असणे.
6. ताव मारणे – भरपूर खाणे, पोटभर खाणे.
7. धूम ठोकणे – पळून जाणे.

Balbharti Maharashtra State Board Class 9 Hindi Solutions Hindi Lokvani Chapter 5 किताबें कुछ कहना चाहती हैं Notes, Textbook Exercise Important Questions and Answers.

Maharashtra State Board Class 9 Hindi Lokvani Solutions Chapter 5 किताबें कुछ कहना चाहती हैं

Hindi Lokvani 9th Std Digest Chapter 5 किताबें कुछ कहना चाहती हैं Textbook Questions and Answers

1. भाषा बिंदु :

प्रश्न 1.
“निर्देशानुसार काल परिवर्तन कीजिए।
उत्तर :

2. संभाषणीय :

प्रश्न 1.
“वाचन प्रेरणा दिवस’ के अवसर पर पड़ी हुई किसी पुस्तक का आशय प्रस्तुत कीजिए।
उत्तर :
पुस्तकें हमारी मित्र हैं। अच्छी पुस्तकें हमें रास्ता दिखाने के साथ साथ हमारा मनोरंजन भी करती हैं। मैंने पिछले दिन रामधारी सिंह ‘दिनकर’ की पुस्तक ‘कुरुक्षेत्र’ पढ़ी। यह युद्ध और शांति की समस्या पर आधारित है। भीष्म महाभारत का युद्ध समाप्त होने पर शर-शय्या पर लेटे हुए हैं। उधर पांडव अपनी जीत पर प्रसन्न हैं। परंतु युधिष्ठिर इतने लोगों की मृत्यु से दुखी हैं। वे पश्चाताप करते हुए भीष्म के पास जाते हैं और रोते हुए कहते हैं कि, उन्होंने युद्ध करके पाप किया है।

भीष्म कहते हैं महाभारत के युद्ध में युधिष्ठिर का कोई दोष नहीं है। पापी दुर्योधन है, शकुनी है, जिसके कारण युद्ध हुआ। अन्याय का विरोध करने वाला पापी नहीं है, बल्कि अन्याय करने वाला पापी है। भीष्म कहते हैं, अन्याय का विरोध करना तो पुण्य है, पाप नहीं है। दिनकर का यह ग्रंथ प्रेरणा, ओज, वीरता साहस और हिम्मत का भंडार है। इनकी भाषा आग उगलती है। इस काव्य को पढ़कर मुर्दे में भी जान आ सकती है। इसके वीरता भरे शब्द मुझे बार-बार इसे पढ़ने की प्रेरणा देते हैं।

3. रचनात्मकता की ओर कल्पना पल्लवन

प्रश्न 1.
‘ग्रंथ हमारे गुरु’ इस विषय के संदर्भ में स्वमत बताइए।
उत्तर :
ग्रंथ हमें वर्षों से अपनी ज्ञान की गंगा में नहलाते आए हैं। ये ग्रंथ सदियों से संचित अपने अनुभवों को हमें बताते हैं। इनका ज्ञान पाकर हम अपने जीवन को अच्छी तरह जीने में सक्षम होते हैं। जीवन में आने वाले सुख-दुख में हम कैसे संघर्ष करें और अपने जीवन को कैसे सरल बनाएँ, यह हमें ग्रंथ ही सिखाते है। सत्य, सदाचार, धैर्य और अच्छे कर्म का मार्ग भी हमें गंथ द्वारा ही प्राप्त होता है। सच में ये ज्ञान और अनुभव के भंडार ग्रंथ हमारे सच्चे गुरु होते हैं।

4. पाठ के आँगन में

प्रश्न 1.
आकृति पूर्ण कीजिए।
उत्तर :

प्रश्न 2.
आकृति पूर्ण कीजिए।
उत्तर :

प्रश्न 3.
आकृति पूर्ण कीजिए।
उत्तर :

Hindi Lokvani 9th Std Textbook Solutions Chapter 5 किताबें कुछ कहना चाहती हैं Additional Important Questions and Answers

(क) पद्यांश पढ़कर दी गई सूचना के अनुसार कृतियाँ कीजिए।

कृति क (1) : आकलन कृति

प्रश्न 1.
आकृति पूर्ण कीजिए।
उत्तर :

प्रश्न 2.
उचित शब्द तैयार कीजिए।

उत्तर :
i. खुशियाँ
ii. जमाना

कृति क (2) : सरल अर्थ

प्रश्न 1.
ऊपर दी गई पंक्तियों का सरल अर्थ लिखिए।
उत्तर:
कवि कहते हैं कि ये किताबें हमसे बातें करती हैं। किताबें हमें एक-एक पल की, आज की, कल की और बीते हुए जमाने की बातें बताती हैं। पुराने समय से लेकर आज तक की खुशियों और दुखों की कहानी भी ये किताबें ही हमें बताती हैं। ये किताबें हमें फूलों जैसे व्यक्तित्व की कहानी बताती हैं। जिस प्रकार फूल खिलकर अपनी सुगंध को चारों तरफ फैला देता है, उसे तोड़ने वाले हाथ को भी वह अपनी खुशबू से महका देता है, उसी प्रकार इस संसार में ऐसे लोगों ने जन्म लिया जिन्होंने अपने महान कृत्यों से इस संसार को सुगंधित कर दिया।

ऐसे लोगों की कहानी भी हमें पुस्तकें बताती हैं। इस दुनिया में आज तक जितने भी छोटेबड़े युद्ध हुए उसमें प्रयोग किए गए बमों आदि की कहानी भी ये पुस्तकें बताती हैं। इस धरती पर आज तक बहुत सारे योद्धा पैदा हुए उनके बीच अनगिनत लड़ाइयाँ भी लड़ी गई। उनके जीत और हार की कहानी भी किताबें हमें बताती हैं। देश, समाज और परिवार के बीच पनपे प्यार और मार-काट की बातें भी हमें पुस्तकें बताती हैं।

(ख) पद्यांश पढ़कर दी गई सूचना के अनुसार कृतियाँ कीजिए।

कृति ख (1) : आकलन कृति

प्रश्न 1.
आकति पर्ण कीजिए।
उत्तर :

प्रश्न 2.
उचित जोड़ियाँ मिलाइए।

उत्तर :

कृति ख (2) : सरल अर्थ

प्रश्न 1.
ऊपर दी गई पंक्तियों का सरल अर्थ लिखिए।
उत्तर:
कवि कहते हैं कि क्या तुम इन किताबों की बातें नहीं सुनोगे। ये कितावें तुम्हारे पास रहना चाहती हैं और तुमसे कुछ कहना चाहती हैं। इन किताबों में चिड़ियों के चहचहाने का मनोझरी वर्णन मिलता है। किसानों के खेतों में लहलहाती हुई हरी-भरी फसलों का वर्णन भी इन किताबों में मिलता है। किताबों में झरते हुए झरने का चित्रण और परियों की कहानियाँ भी विस्तार से मिलती है। जो हमें ये पुस्तकें सुनाती हैं।

(ग) पद्यांश पढ़कर दी गई सूचना के अनुसार कृतियाँ कीजिए।

कृति ग (1) : आकलन कृति

प्रश्न 1.
आकृति पूर्ण कीजिए।
उत्तर :

प्रश्न 2.
निम्नलिखित प्रश्नों के एक शब्द में उत्तर लिखिए।
i. ये कुछ कहना चाहती हैं।
ii. ये तुम्हारे पास रहना चाहती हैं।
उत्तर :
i. किताबें
ii. किताबें

कति ग (2) : सरल अर्थ

प्रश्न 1.
उपर्युक्त पंक्तियों का सरल अर्थ लिखिए।
उत्तर :
यह युग विज्ञान का युग है। आए दिन वैज्ञानिक उपकरण आविष्कार किए जा रहे हैं। रॉकटों की भरमार हो गई है, जिसे अन्य देशों द्वारा आए दिन अंतरिक्ष में स्थापित किया जा रहा है। इनका वर्णन भी किताबों में विस्तार से मिलता है। किताबें ज्ञान का भंडार हैं। क्या तुम ज्ञान प्राप्त करने के लिए किताबों के संसार में नहीं जाना चाहोगे? ये किताबें तुम्हें कुछ बताना चाहती हैं, तुम्हारे ही पास रहना चाहती हैं। तुमसे दूर नहीं जाना चाहती।

किताबें कुछ कहना चाहती हैं Summary in Hindi

कवि-परिचय :

जीवन-परिचय : सफदर हाश्मी का जन्म 12 अप्रैल 1954 को दिल्ली में हुआ था। वे एक नाटककार, कलाकार, निर्देशक, गीतकार और कलाविद थे। नुक्कड़ नाटकों के लिए इन्हें विशेष ख्याति प्राप्त है। भारतीय जन नाट्य संघ से भी इनका जुड़ाव रहा।
प्रमुख कृतियाँ : किताबें, मच्छर पहलवान, पिल्ला, राजू और काजू आदि प्रसिद्ध बाल कविताएँ हैं। ‘दुनिया सबकी’ पुस्तक में इनकी कविताएँ संकलित हैं।

पद्य-परिचय :

नई कविता : संवेदना के साथ मानवीय परिवेश के संपूर्ण विविधता को नए शिल्प में अभिव्यक्त करने वाली काव्यधारा को नई कविता कहते हैं। नई कविता में समाज के विविध पहलुओं की मार्मिक अभिव्यक्ति की गई हैं।
प्रस्तावना : प्रस्तुत कविता ‘किताबें कुछ कहना चाहती हैं’ के माध्यम से कवि हाश्मी जी ने किताबों के द्वारा मन की बातों का मानवीकरण करके प्रस्तुत किया है।

सारांश :

कवि कहते हैं कि किताबें पुराने समय से लेकर आज तक के संसार के सुख और दुख की बातें हमें बताती हैं। महापुरुषों के कृत्यों, आपसी प्रेम, युद्ध, और युद्ध में प्रयोग किए गए भयानक हथियारों की कहानी भी किताबें हमें बताती हैं। प्रकृति का सुंदर वर्णन और विज्ञान का विस्तार भी ये किताबें हमें सुनाती हैं।

सरल अर्थ :

किताबें …………………………………………………. मार की।
कवि कहते हैं कि ये किताबें हमसे बातें करती हैं। किताबें हमें एक-एक पल की, आज की, कल की और बीते हुए जमाने की बातें बताती हैं। पुराने समय से लेकर आज तक की खुशियों और दुखों की कहानी भी ये किताबें ही हमें बताती हैं। ये किताबें हमें फूलों जैसे व्यक्तित्व की कहानी बताती हैं। जिस प्रकार फूल खिलकर अपनी सुगंध को चारों तरफ फैला देता है, उसे तोड़ने वाले हाथ को भी वह अपनी खुशबू से महका देता है, उसी प्रकार इस संसार में ऐसे लोगों ने जन्म लिया जिन्होंने अपने महान कृत्यों से इस संसार को सुगंधित कर दिया।

ऐसे लोगों की कहानी भी हमें पुस्तकें बताती हैं। इस दुनिया में आज तक जितने भी छोटे-बड़े युद्ध हुए उसमें प्रयोग किए गए बमों आदि की कहानी भी ये पुस्तकें बताती हैं। इस धरती पर आज तक बहुत सारे योद्धा पैदा हुए उनके बीच अनगिनत लड़ाइयाँ भी लड़ी गईं। उनके जीत और हार की कहानी भी किताबें हमें बताती हैं। देश, समाज और परिवार के बीच पनपे प्यार और मार-काट की बातें भी हमें पुस्तकें बताती हैं।

क्या तुम नहीं …………………………………….. किस्से सुनाते हैं।
कवि कहते हैं कि क्या तुम इन किताबों की बातें नहीं सुनोगे। ये किताबें तुम्हारे पास रहना चाहती हैं और तुमसे कुछ कहना चाहती हैं। इन किताबों में चिड़ियों के चहचहाने का मनोहारी वर्णन मिलता है। किसानों के खेतों में लहलहाती हुई हरी-भरी फसलों का वर्णन भी इन किताबों में मिलता है। किताबों में झरते हुए झरने का चित्रण और परियों की कहानियाँ भी विस्तार से मिलती हैं। जो हमें ये पुस्तकें सुनाती हैं।

किताबों में रॉकेट, ………………………………….. पास रहना चाहती हैं।
यह युग विज्ञान का युग है। आए दिन वैज्ञानिक उपकरण आविष्कार किए जा रहे हैं। रॉकेटों की भरमार हो गई है, जिसे अन्य देशों द्वारा आए दिन अंतरिक्ष में स्थापित किया जा रहा है। इनका वर्णन भी किताबों में विस्तार से मिलता है। किताबें ज्ञान का भंडार हैं। क्या तुम ज्ञान प्राप्त करने के लिए किताबों के संसार में नहीं जाना चाहोगे? ये किताबें तुम्हें कुछ बताना चाहती हैं, तुम्हारे ही पास रहना चाहती हैं। तुमसे दूर नहीं जाना चाहती।

शब्दार्थ :

1. गम – दुख
2. खेतियाँ – खेत की फसलें
3. किस्से – कहानी
4. रॉकेट – उपग्रह
5. राज – रहस्य
6. भरमार – अधिकता