Category: Class 9

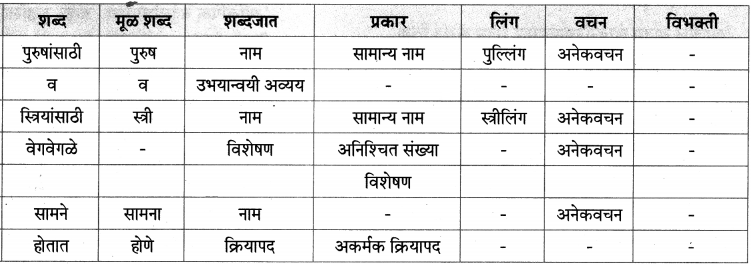
Balbharti Maharashtra State Board Class 9 Marathi Solutions Aksharbharati Chapter 5 व्यायामाचे महत्त Notes, Textbook Exercise Important Questions and Answers.

Maharashtra State Board Class 9 Marathi Aksharbharati Solutions Chapter 5 व्यायामाचे महत्त(कविता)

Marathi Aksharbharati Std 9 Digest Chapter 5 व्यायामाचे महत्त Textbook Questions and Answers

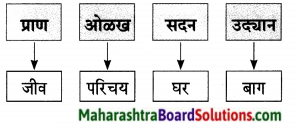
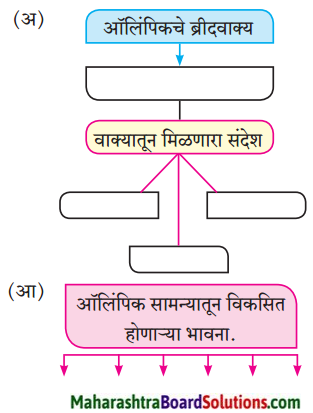
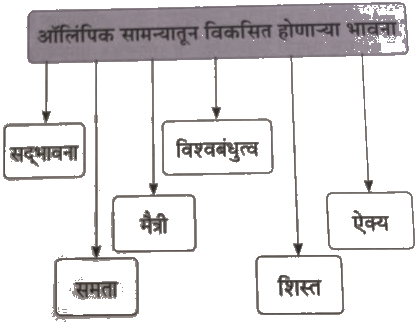
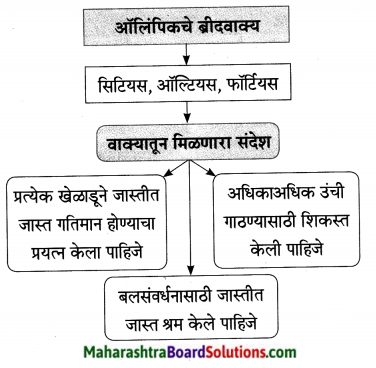
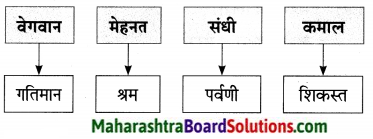
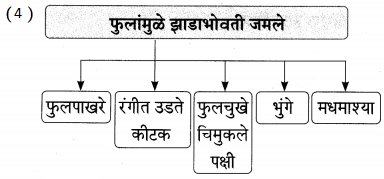
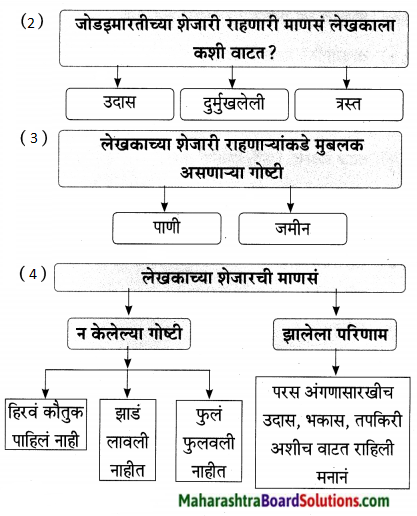
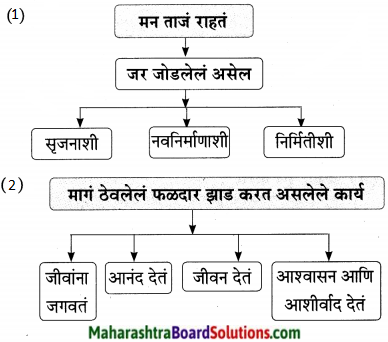
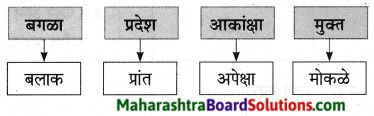
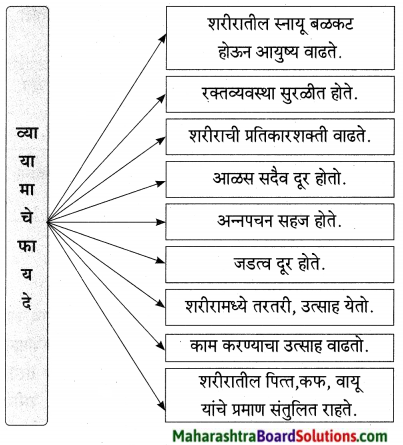
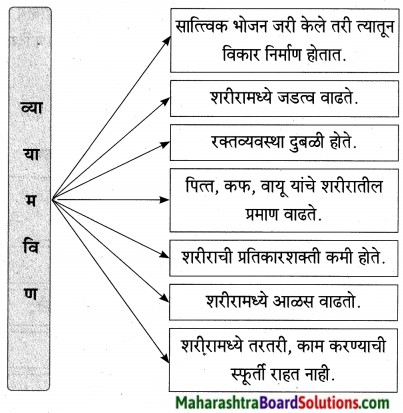
1. व्यायामाचे फायदे दर्शवणारा आकृतिबंध पूर्ण करा.

प्रश्न 1.
व्यायामाचे फायदे दर्शवणारा आकृतिबंध पूर्ण करा.

उत्तर:

2. चूक की बरोबर ते लिहा.

प्रश्न 1.
चूक की बरोबर ते लिहा.
(अ) व्यायाम सर्वांकरता उपयुक्त असतो.
(आ) व्यायामाने जडत्व वाढते.
(इ) व्यायामाने स्नायू अशक्त होतात.
(ई) व्यायामाने प्रतिकारशक्ती वाढते.
उत्तर:
(अ) बरोबर
(आ) चूक
(इ) चूक
(ई) बरोबर

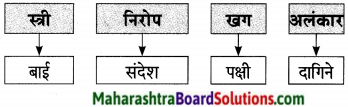
3. शब्दसमूहांबद्दल एक शब्द चौकटीत लिहा.

प्रश्न 1.
शब्दसमूहांबद्दल एक शब्द चौकटीत लिहा.
(अ) आरोग्य देणारी –
(आ) विरोध करण्याची क्षमता असलेली शक्ती –
(इ) स्वत:ची कामे स्वत:करणारा –
(ई) एका अंगाने केलेला विचार –
उत्तर:
(अ) आरोग्यदायी
(आ) प्रतिकारशक्ती
(इ) स्वावलंबी
(ई) एकांगी

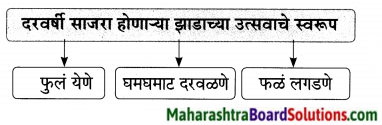
4. व्यायाम न करण्याचे तोटे लिहून आकृती पूर्ण करा.

प्रश्न 1.
व्यायाम न करण्याचे तोटे लिहून आकृती पूर्ण करा.

उत्तर:

5. भावार्थाधारित

प्रश्न (अ)
व्यायामाचे महत्त्व तुमच्या शब्दांत लिहा.
उत्तरः
मानवी जीवनात व्यायामाचे अनन्यसाधारण महत्त्व आहे. व्यायामाचे महत्त्व संपूर्ण जगाने मान्य केले आहे. व्यायामामुळे शरीरातील आळस, कंटाळा दूर होतो. शरीरामध्ये तरतरी, उत्साह येतो. व्यायामामुळे अन्नपचन सहजपणे होते. शरीरात स्थूलपणा वाढत नाही. रक्तव्यवस्था सुरळीत होते. शरीरातील स्नायू बळकट मजबूत होऊन आपले आयुष्य वाढते. शिवाय शरीरातील पित्त, कफ, वायू यांचे प्रमाण संतुलित राहण्यास मदत होते. त्यामुळे शरीराची प्रतिकारशक्ती वाढते आणि काम करण्याचा उत्साह वाढतो. त्यामुळे दररोज व्यायाम करणे आवश्यक आहे.

प्रश्न (आ)
‘व्यायामे अंगी वाढे स्फूर्ति। कार्य करण्याची।।’ या पंक्तीतील तुम्हांला समजलेला अर्थ लिहा.
उत्तरः
तुकडोजी महाराज म्हणतात की, व्यायामामुळे आपल्या शरीराला बळकटी प्राप्त होऊन रोग प्रतिकारकशक्ती वाढते. येणाऱ्या आजारांचा, संकटांचा आपण सहज सामना करू शकतो. त्याचबरोबर शरीर सुदृढ झाल्यामुळे आपण स्वावलंबीसुद्धा बनतो. आपल्या व्यक्तिगत कामासाठी आपल्याला दुसऱ्या कोणावर अवलंबून राहण्याची आवश्यकता राहत नाही. या नियमित व्यायामामुळे शरीरातील आळस कंटाळा दूर होऊन शरीर ताजेतवाने बनते. शिवाय कोणत्याही कामामध्ये उत्साह जाणवतो. म्हणजेच कोणतेही काम करण्याची शरीरातील जोश, स्फूर्ती वाढते.

प्रश्न (इ)
‘आरोग्यम् धनसंपदा’ या उक्तीतील विचाराचा विस्तार करा.
उत्तरः
संध्याकाळी दिवेलागणीच्या वेळी देवाजवळ बसून घराघरात ‘शुभं करोति कल्याणम्’ ही दिव्याची प्रार्थना म्हटली जाते. ‘आरोग्यम् धनसंपदा’ ही त्यातीलच एक पंक्ती आहे. प्रार्थना करताना जणू आपण परमेश्वराकडून आरोग्यरूपी धनसंपदेची अपेक्षा करत असतो. पण अवघ्या जगाने मान्य केले आहे की उत्तम आरोग्य प्राप्त करणे हे आपल्याच हातात आहे. त्यासाठी नियमितपणे योग्य व्यायाम करणे गरजेचे आहे. व्यायामामुळे अन्नपचन व्यवस्थित होते. रक्तव्यवस्था सुरळीत होते. शरीरातील स्नायू बळकट होऊन शरीराची प्रतिकारशक्ती वाढते. शिवाय शरीरातील पित्त, कफ, वायू यांचे प्रमाण संतुलित राहते. शरीरामध्ये तरतरी, उत्साह वाढतो. या व्यायामामुळेच उत्तम आरोग्याची प्राप्ती आपणाला होते. आपल्याला लाभलेले उत्तम आरोग्य ही खऱ्या अर्थाने आपली धनसंपदाच असते.

भाषाभ्यास:

समासात कमीत कमी दोन शब्द असावे लागतात. त्याला ‘पद’ असे म्हणतात. त्या दोन पदांपैकी कोणत्या पदाला प्राधान्य आहे यावरून समासाचे प्रकार ठरतात.

यावर्षी आपल्याला ‘अव्ययीभाव’ आणि ‘वंद्व’ हे दोन समास समजून घ्यायचे आहेत.

Marathi Akshar Bharati Class 9 Textbook Solutions Chapter 5 व्यायामाचे महत्त Additional Important Questions and Answers

पुढील पक्ष्याच्या आधारे दिलेल्या सूचनेनुसार कृती करा:

कृती 1 : आकलन कृती

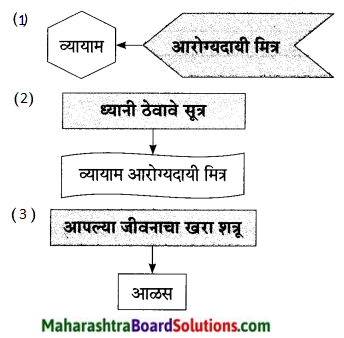
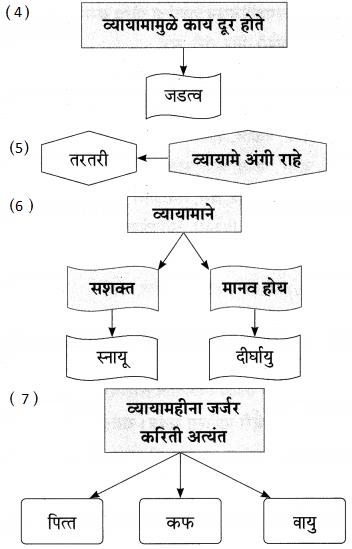
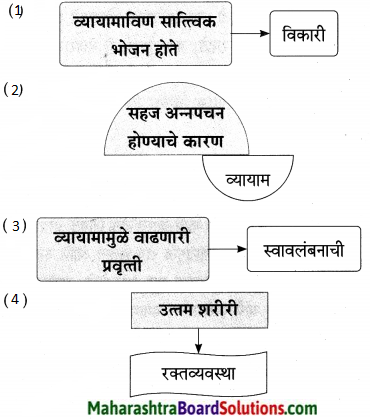
प्रश्न 1.
आकृतिबंध पूर्ण करा.
उत्तरः

प्रश्न 2.
उत्तरे लिहा.
उत्तरः

खालील प्रश्नांची उत्तरे एका वाक्यात लिहा.

प्रश्न 1.
सर्वप्रकारे, सर्व ठिकाणी कोणाला वैरी मानावे असे कवी म्हणतो?
उत्तरः
सर्वप्रकारे, सर्व ठिकाणी आळसाला वैरी मानावे असे कवी म्हणतो.

प्रश्न 2.
व्यायामाविण काय विकारी होते असे कवी म्हणतो?
उत्तरः
व्यायामाविण सात्त्विक भोजन विकारी होते असे कवी म्हणतो.

प्रश्न 3.
व्यायामामुळे शरीरातील रक्तव्यवस्था कशी होते?
उत्तर:
व्यायामामुळे शरीरातील रक्तव्यवस्था उत्तम म्हणजे व्यवस्थित होते.

प्रश्न 4.
व्यायामामुळे माणसाचे आयुष्य कसे होते?
उत्तरः
व्यायामामुळे माणसाचे आयुष्य दीर्घ होते.

कंसातील योग्य शब्द वापरून रिकाम्या जागा भरा.

प्रश्न 1.

1. व्यायाम आरोग्यदायी ……………… । हे ध्यानी ठेवावे सूत्र। (सखा, सोबती, मित्र, सवंगडी)
2. आळस …………… मानिला सर्वत्र। सर्वतोपरी।। (सखा, दुश्मन, वैरी, सोबती)
3. व्यायामाविण सात्त्विक भोजन। तेहि मारी …………… होऊन । (अविकारी, शुद्ध, बदल, विकारी)
4. व्यायामे होय अग्निदीपन। ……………. सहजचि।। (अन्नपचन, हवन, शरीरसंपदा, भूक)
5. व्यायामे जडत्व जाई दूरी। व्यायामे अंगी राहे …………..। (ताजेपणा, तरतरी, दुबळेपण, आळस)
6. व्यायामहीना पित्त, …………,वायु। जर्जर करिती अत्यंत।। (सर्दी, पडसे, ज्वर, कफ)
7. व्यायामे वाढे प्रतिकार शक्ति। ……………. प्रवृत्ति। (परावलंबनाची, स्वावलंबनाची, रोगराईची, आजाराची)

उत्तर:

1. मित्र
2. वैरी
3. विकारी
4. अन्नपचन
5. तरतरी
6. कफ
7. स्वावलंबनाची

कृती 2 : आकलन कृती

समान अर्थाच्या काव्यपंक्ती शोधून लिहा.

प्रश्न 1.

1. व्यायामाअभावी सत्त्वगुणी जेवणही शरीरास उपयोगी नाही.
2. आळस हा माणसाचा शत्रू आहे, हे सगळया जगाने मान्य केलेले आहे.
3. व्यायामाने शरीरामध्ये तरतरी येते.
4. व्यायामाने मानवाचे आयुष्य वाढते.
5. व्यायामाने चांगल्या प्रवृत्ती जोपासल्या जातात.

उत्तर:

1. व्यायामाविण सात्त्विक भोजन। तेहि मारी विकारी होऊन।।
2. आळस वैरी मानिला सर्वत्र। सर्वतोपरी।।
3. व्यायामे अंगी राहे तरतरी।
4. व्यायामे मानव होय दीर्घायु।
5. व्यायाम वाढे प्रतिकार शक्ति। स्वावलंबनाची प्रवृत्ति।

प्रश्न 2.
जोड्या जुळवा.

उत्तरः

प्रश्न 3.
जोड्या जुळवा.

उत्तरः

प्रश्न 4.
काव्यपंक्तींचा योग्य क्रम लावा.

1. व्यायाम आरोग्यदायी मित्र । हे ध्यानी ठेवावे सूत्र।
2. व्यायामे होय अग्निदीपन । अन्नपचन सहजचि।।
3. आळस वैरी मानिला सर्वत्र। सर्वतोपरी।।
4. व्यायामाविण सात्त्विक भोजन। तेहि मारी विकारी होऊन।
5. रक्तव्यवस्था उत्तम शरीरी । वाढे विचारी सजीवपण।।
6. व्यायामहीना पित्त, कफ, वायु । जर्जर करिती अत्यंत।।
7. व्यायामाने सशक्त स्नायु । व्यायामे मानव होय दीर्घायु।
8. व्यायामे जडत्त्व जाई दूरी । व्यायामे अंगी राहे तरतरी।

उत्तरः

1. व्यायाम आरोग्यदायी मित्र । हे ध्यानी ठेवावे सूत्र।
2. आळस वैरी मानिला सर्वत्र। सर्वतोपरी।।
3. व्यायामाविण सात्त्विक भोजन। तेहि मारी विकारी होऊन।
4. व्यायामे होय अग्निदीपन। अन्नपचन सहजचि।।
5. व्यायामे जडत्त्व जाई दूरी । व्यायामे अंगी राहे तरतरी ।
6. रक्तव्यवस्था उत्तम शरीरी । वाढे विचारी सजीवपण ।।
7. व्यायामाने सशक्त स्नायु । व्यायामे मानव होय दीर्घायु ।
8. व्यायामहीना पित्त, कफ, वायु । जर्जर करिती अत्यंत ।।

प्रश्न 5.
काव्यपंक्तीवरून शब्दांचा योग्य क्रम लावा.

1. सर्वतोपरी, मित्र, वैरी, सूत्र
2. अग्निदीपन, विकारी, भोजन, अन्नपचन
3. सजीवपण, अंगी, उत्तम, तरतरी
4. कार्य, प्रवृत्ति, शक्ति, प्रतिकार
5. जर्जर, मानव, कफ, सशक्त

उत्तर:

1. मित्र, सूत्र, वैरी, सर्वतोपरी
2. जन, विकारी, अग्निदीपन, अन्नपचन
3. अंगी, तरतरी, उत्तम, सजीवपण
4. प्रतिकार, शक्ति, प्रवृत्ति, कार्य .
5. सशक्त, मानव, कफ, जर्जर

कृती 3: काव्यसौंदर्य

खालील काव्यपंक्तीतील आशयसौंदर्य स्पष्ट करा.

प्रश्न 1.
आळस वैरी मानिला सर्वत्र। सर्वतोपरी।।
उत्तरः
आळस हा आपल्या जीवनाचा खरा शत्रू आहे, हे सगळ्या जगाने मान्य केलेले आहे. व्यायामामुळेच आळस दूर होऊन शरीर आरोग्यपूर्ण होते.

प्रश्न 2.
व्यायामाविण सात्त्विक भोजन। तेहि मारी विकारी होऊन।
उत्तरः
आरोग्य व्यवस्थित राहावे म्हणून आपण सात्त्विक आहार घेत असतो. या सात्त्विक भोजनाने आपले शरीर व मन छान स्वस्थ राहते; पण तुकडोजी महाराज म्हणतात, की अशा भोजनासोबतच व्यायामही केला पाहिजे. नाहीतर अशा भोजनामुळेही आपणस विविध विकार, विविध आजार होऊ शकतात.

प्रश्न 3.
व्यायामहीना पित्त, कफ, वायु। जर्जर करिती अत्यंत।।
उत्तरः
जर आपण व्यायाम करीत नसू तर आपल्या शरीरात पित्त, कफ, वायू यांचे प्रमाण कमी-जास्त होऊ लागते. पित्त, कफ, वायू यांच्या असंतुलित प्रमाणामुळे रोग होतात आणि आपण आजारी पडतो. त्यामुळे आपल्याला खूप त्रास होतो. व्यायामामुळे पित्त, कफ, वायू यांचे शरीरातील प्रमाण योग्य व संतुलित राहण्यास मदत होते.

प्रश्न 4.
व्यायामे अंगी वाढे स्फूर्ति। कार्य करण्याची।।
उत्तरः
तुकडोजी महाराज म्हणतात, की व्यायामामुळे आपल्या शरीराला बळकटी प्राप्त होऊन रोगप्रतिकारकशक्ती वाढते. येणाऱ्या आजारांचा, संकटांचा आपण सहज सामना करू शकतो. त्याचबरोबर शरीर सुदृढ झाल्यामुळे आपण स्वावलंबीसुद्धा बनतो. आपल्या व्यक्तिगत कामासाठी आपल्याला दुसऱ्या कोणावर अवलंबून राहण्याची आवश्यकता राहत नाही. या नियमित व्यायामामुळे शरीरातील आळस, कंटाळा दूर होऊन ताजेतवाने बनते. शिवाय कोणत्याही कामांमध्येही उत्साह जाणवतो.

पुढील ओळींचा अर्थ स्पष्ट करा.

प्रश्न 1.
व्यायाम आरोग्यदायी मित्र । हे ध्यानी ठेवावे सूत्र ।
उत्तरः
राष्ट्रसंत श्री तुकडोजी महाराज यांनी आपल्यासारख्या सामान्य माणसांना आपल्या जीवनातील व्यायामाचे महत्त्व साध्या, सरळ भाषेत समजावून सांगितले आहे. ते म्हणतात की, व्यायाम हा आपल्याला सुखाचे आयुष्य देणारा आरोग्यदायी मित्र आहे. हे सूत्र आपण कायम लक्षात ठेवणे गरजेचे आहे.

प्रश्न 2.
व्यायामे जडत्व जाई दूरी । व्यायामे अंगी राहे तरतरी।
उत्तरः
आपण व्यायाम नियमितपणे करायला हवा. योग्य व पुरेसा व्यायाम आपण नियमित केला नाही तर शरीरामध्ये जडत्व म्हणजेच स्थूलपणा वाढत जातो. नियमीत व्यायामामुळे स्थूलपणा कमी होऊन शरीर सुडौल होते. तसेच आळस दूर होऊन अंगामध्ये तरतरी म्हणजेच उत्साह भरतो.

प्रश्न 3.
व्यायामे वाढे प्रतिकार शक्ति । स्वावलंबनाची प्रवृत्ति ।।
उत्तरः
तुकडोजी महाराज म्हणतात की, व्यायामामुळे आपल्या शरीराला बळकटी प्राप्त होऊन रोगप्रतिकारक शक्ती वाढते. येणाऱ्या आजारांचा, संकटांचा आपण सहज सामना करू शकतो. त्याचबरोबर शरीर सुदृढ झाल्यामुळे आपण स्वावलंबीसुद्धा बनतो.

प्रश्न 4.
व्यायामाचे मानवी जीवनातील महत्त्व थोडक्यात सांगा.
उत्तरः
व्यायाम म्हणजे शारीरिक कसरत. व्यायाम फक्त मनुष्याचे शरीरच सुदृढ करीत नाही तर तो व्यक्तीला मनाने देखील बळकट करीत असतो. व्यायाम मन एका ठिकाणी केंद्रित करण्याचे महत्त्वाचे साधन आहे. जर का व्यक्तीचे मन बळकट व स्वस्थ असेल तर ती व्यक्ती शरीराने देखील बळकट होते. व्यायाम काम, क्रोध, वासना, ईर्ष्या, द्वेष, मत्सर व मोह यांपासून मनुष्याचे संरक्षण करतो. माणसाची आत्मिकशक्ती जोपासण्याचे काम व्यायामामुळे शक्य होते. व्यायाम माणसाचे मन, मनगट व मेंदू यांवर समतोल नियंत्रण ठेवतो त्यामुळे व्यक्तीचा व्यक्तिमत्त्व विकास होतो.

प्रश्न 5.
व्यायामाचे शरीराला होणारे फायदे तुमच्या शब्दात लिहा.
उत्तरः
‘आरोग्यम् धनसंपदा’ म्हणजे स्वस्थ शरीर हेच माणसाचे वैभव आहे. सुदृढ आरोग्य माणसाची धनसंपदा आहे. माणसाचे आरोग्य तेव्हाच चांगले व स्वस्थ राहू शकते जेव्हा तो मानसिक व शारीरिकदृष्ट्या बळकट व मजबूत असेल. त्यासाठी नियमितपणे व्यायाम करणे गरजेचे असते. नियमित व्यायाम करणारी व्यक्ती आजारी पडत नाही. ती शरीराने व मनाने नेहमी स्वस्थ राहते. नियमित व्यायाम केल्याने आरोग्य सुदृढ तर राहतेच शिवाय माणूस दीर्घायू होतो. म्हातारपणी सुद्धा माणूस स्वबळावर सर्व शारीरिक क्रिया पार पाडू शकतो. म्हणूनच ‘आरोग्यम् धनसंपदा’ असे जे म्हटले गेलेले आहे ते खरेच आहे.

प्रश्न 6.
दिलेल्या मुद्द्यांच्या आधारे कवितेसंबंधी पुढील कृती सोडवा.
उत्तरः
1. कवी / कवयित्रीचे नाव – राष्ट्रसंत तुकडोजी महाराज (माणिक बंडोजी ठाकूर)

2. संदर्भ – ‘व्यायामाचे महत्त्व’ ही कविता राष्ट्रसंत तुकडोजी महाराज यांनी लिहिली आहे. ही कविता त्यांच्या ‘ग्रामगीता’ या पुस्तकातून घेतली आहे.

3. प्रस्तावना – ‘व्यायामाचे महत्त्व’ ही कविता राष्ट्रसंत तुकडोजी महाराज यांनी लिहिली आहे. मानवी जीवनातील व्यायामाचे महत्त्व या कवितेतून तुकडोजी महाराजांनी प्रभावीपणे मांडले आहे.

4. वाङमयप्रकार – ‘व्यायामाचे महत्त्व’ ही कविता म्हणजे ‘ओव्या’ आहेत.

5. कवितेचा विषय – व्यायामाचे शरीरावर होणारा सकात्मक परिणाम दर्शविणारी राष्ट्रसंत तुकडोजी महाराज यांची ‘व्यायामाचे महत्त्व’ ही कविता म्हणजे आदर्श ‘ओव्या’ आहेत.

6. कवितेतील आवडलेली ओळ – व्यायामे वाढे प्रतिकार शक्ती । स्वावलंबनाची प्रवृत्ति ।।
व्यायामे अंगी वाढे स्फूर्ति । कार्य करण्याची ।।

7. मध्यवर्ती कल्पना – आरोग्यासाठी व्यायाम अतिशय आवश्यक गोष्ट आहे. व्यायामामुळे शरीरातील रोगप्रतिकारशक्ती वाढते. शिवाय पित्त, कफ, वायू या गोष्टींचे शरीरातील प्रमाण संतुलित राहून शरीर बलवान होते. अशा प्रकारचे मानवी जीवनातील व्यायामाचे महत्त्व दर्शविणारी राष्ट्रसंत तुकडोजी महाराज यांची ‘व्यायामाचे महत्त्व’ ही सुंदर कविता आहे.

8. कवितेतून मिळणारा संदेश – सुदृढ आरोग्य हवे असेल तर व्यायाम करणे आवश्यक आहे. व्यायामामुळे अन्नपचन सहज होते. शिवाय स्थूलपणा कमी होऊन रक्तव्यवस्था उत्तम कार्य करते त्याचबरोबर शरीराचे स्नायू बळकट होऊन रोगप्रतिकार शक्ती वाढते. अंगामधला आळस दूर होऊन स्फूर्ती वाढते. अशाप्रकारे व्यायामामुळे शरीरावर सकारात्मक परिणाम होत असतो म्हणून दररोज व्यायाम करणे आवश्यक आहे. असा संदेश व्यायामाचे महत्त्व’ या कवितेतून आपणास मिळतो.

9. कविता आवडण्याची वा न आवडण्याची कारणे – ‘व्यायामाचे महत्त्व’ ही कविता मला खूप आवडली आहे. याचे महत्त्वाचे कारण म्हणजे आपले आयुष्य उजळून टाकणाऱ्या व्यायामाचे महत्त्व राष्ट्रसंत तुकडोजी महाराजांनी अतिशय सोप्या भाषेत पटवून दिले आहे. त्यांचे शरीरप्रकृतीचे बारीक निरीक्षण मनाला भावणारे आहे.

10. भाषिक वैशिष्ट्ये – ‘व्यायामाचे महत्त्व’ या कवितेमध्ये राष्ट्रसंत तुकडोजी महाराजांनी साध्या आणि सोप्या भाषेचा वापर केला आहे. शिवाय ही कविता ‘ओवी’ रूपात असल्यामुळे प्रत्येक ओवीमध्ये चार चरण दिसून येतात. त्याचबरोबर ‘यमक’ अलंकाराचा वापर शोभून दिसतो.

खालील काव्यपंक्तींचे रसग्रहण करा.

प्रश्न 1.
व्यायाम आरोग्यदायी मित्र। हे ध्यानी ठेवावे सूत्र।
आळस वैरी मानिला सर्वत्र । सर्वतोपरी।।
उत्तरः
‘व्यायामाचे महत्त्व’ ही कविता राष्ट्रसंत श्री तुकडोजी महाराज यांनी लिहिली आहे. मानवी जीवनातील व्यायामाचे महत्त्व या कवितेतून कवीने स्पष्ट केले आहे.

‘राष्ट्रसंत श्री तुकडोजी महाराज’ यांनी आपल्यासारख्या सामान्य माणसांना आपल्या जीवनातील व्यायामाचे महत्त्व साध्या, सरळ भाषेत समजावून सांगितले आहे. ते म्हणतात की, व्यायाम हा आपल्याला सुखाचे आयुष्य देणारा आरोग्यदायी मित्र आहे. हे सूत्र आपण कायम लक्षात ठेवणे गरजेचे आहे. कारण आळस हा आपल्या जीवनाचा खरा शत्रू आहे, हे सगळया जगाने मान्य केलेले आहे. व्यायामामुळेच आळस दूर होऊन शरीर आरोग्यपूर्ण होते.

‘व्यायामाचे महत्त्व’ या कवितेमध्ये राष्ट्रसंत तुकडोजी महाराजांनी साध्या आणि सोप्या भाषेचा वापर केला आहे. शिवाय ही कविता ‘ओवी’ रूपात असल्यामुळे प्रत्येक ओवीमध्ये चार चरण दिसून येतात. त्याचबरोबर ‘यमक’ अलंकाराचा वापर शोभून दिसतो.

प्रश्न 2.
व्यायामाविण सात्त्विक भोजन। तेहि मारी विकारी होऊन।
व्यायामे होय अग्निदीपन। अन्नपचन सहजचि।।
उत्तरः
‘व्यायामाचे महत्त्व’ ही कविता राष्ट्रसंत श्री तुकडोजी महाराज यांनी लिहिली आहे. मानवी जीवनातील व्यायामाचे महत्त्व या कवितेतून कवीने स्पष्ट केले आहे.

आरोग्य व्यवस्थित राहावे म्हणून आपण सात्त्विक आहार घेत असतो. या सात्त्विक भोजनाने आपले शरीर व मन छान स्वस्थ राहते. पण तुकडोजी महाराज म्हणतात की, अशा भोजनासोबतच व्यायामही केला पाहिजे. नाहीतर अशा भोजनामुळेही आपणास विविध विकार, विविध आजार होऊ शकतात. सात्त्विक भोजनासोबतच चांगला, योग्य व्यायाम केला तर पोटातील जठाराग्नी चांगला प्रदिप्त होतो. म्हणजे पोटातील अग्नी चांगला पेटून आपल्या अन्नाचे सहज पचनही होते. अन्नाचे अपचन होऊन होणारे विकार व्यायामामुळे टाळता येतात.

‘व्यायामाचे महत्त्व’ या कवितेमध्ये राष्ट्रसंत तुकडोजी महाराजांनी साध्या आणि सोप्या भाषेचा वापर केला आहे. शिवाय ही कविता ‘ओवी’ रूपात असल्यामुळे प्रत्येक ओवीमध्ये चार चरण दिसून येतात. त्याचबरोबर ‘यमक’ अलंकाराचा वापर शोभून दिसतो.

प्रश्न 3.
व्यायामे जडत्व जाई दूरी। व्यायामे अंगी राहे तरतरी।
रक्तव्यवस्था उत्तम शरीरी। वाढे विचारी सजीवपण।।
उत्तरः
‘व्यायामाचे महत्त्व’ ही कविता राष्ट्रसंत श्री तुकडोजी महाराज यांनी लिहिली आहे. मानवी जीवनातील व्यायामाचे महत्त्व या कवितेतून कवीने स्पष्ट केले आहे.

आपण व्यायाम नियमितपणे करायला हवा. योग्य व पुरेसा व्यायाम आपण केला नाही तर शरीरामध्ये जडत्व म्हणजेच स्थूलपणा वाढत जातो. नियमित व्यायामामुळे स्थूलपणा कमी होऊन शरीर सुडौल होते. तसेच आळस दूर होऊन अंगामध्ये तरतरी म्हणजेच उत्साह भरतो. तुकडोजी महाराज पुढे म्हणतात की, व्यायामामुळे शरीरातील रक्तव्यवस्था व्यवस्थित होते. रक्तप्रवाह सुरळीत होऊन रक्ताशी संबंधित विकार दूर होतात आणि आपले आयुष्य वाढते.

‘व्यायामाचे महत्त्व’ या कवितेमध्ये राष्ट्रसंत तुकडोजी महाराजांनी साध्या आणि सोप्या भाषेचा वापर केला आहे. शिवाय ही कविता ‘ओवी’ रूपात असल्यामुळे प्रत्येक ओवीमध्ये चार चरण दिसून येतात. त्याचबरोबर ‘यमक’ अलंकाराचा वापर शोभून दिसतो.

प्रश्न 4.
व्यायामे जडत्व जाई दूरी। व्यायामे अंगी राहे तरतरी।
रक्तव्यवस्था उत्तम शरीरी। वाढे विचारी सजीवपण।।
उत्तरः
‘व्यायामाचे महत्त्व’ ही कविता राष्ट्रसंत श्री तुकडोजी महाराज यांनी लिहिली आहे. मानवी जीवनातील व्यायामाचे महत्त्व या कवितेतून कवीने स्पष्ट केले आहे.

आपण व्यायाम नियमितपणे करायला हवा. योग्य व पुरेसा व्यायाम आपण केला नाही तर शरीरामध्ये जडत्व म्हणजेच स्थूलपणा वाढत जातो. नियमित व्यायामामुळे स्थूलपणा कमी होऊन शरीर सुडौल होते. तसेच आळस दूर होऊन अंगामध्ये तरतरी म्हणजेच उत्साह भरतो. तुकडोजी महाराज पुढे म्हणतात की, व्यायामामुळे शरीरातील रक्तव्यवस्था प्रवाही होते. रक्तप्रवाह सुरळीत होऊन रक्ताशी संबंधित विकार दूर होतात आणि आपले आयुष्य वाढते.

‘व्यायामाचे महत्त्व’ या कवितेमध्ये राष्ट्रसंत तुकडोजी महाराजांनी साध्या आणि सोप्या भाषेचा वापर केला आहे. शिवाय ही कविता ‘ओवी’ रूपात असल्यामुळे प्रत्येक ओवीमध्ये चार चरण दिसून येतात. त्याचबरोबर ‘यमक’ अलंकाराचा वापर शोभून दिसतो.

प्रश्न 5.
व्यायामाने सशक्त स्नायु। व्यायामे मानव होय दीर्घायु।
व्यायामहीना पित्त, कफ, वायु। जर्जर करिती अत्यंत।।
उत्तरः
‘व्यायामाचे महत्त्व’ ही कविता राष्ट्रसंत श्री तुकडोजी महाराज यांनी लिहिली आहे. मानवी जीवनातील व्यायामाचे महत्त्व या कवितेतून कवीने स्पष्ट केले आहे.

नियमित व योग्य व्यायामामुळे आपल्या शरीरातील स्नायूंना बळकटी प्राप्त होते. सगळे स्नायू सशक्त होत जातात. माणसाला आजारपण येत नाही. याच व्यायामामुळे मानवाला दीर्घायुष्य प्राप्त होते, असे तुकडोजी महाराज म्हणतात. आपण जर व्यायाम करीत नसू तर आपल्या शरीरात पित्त, कफ, वायू यांचे प्रमाण कमी-जास्त होऊ लागते. पित्त, कफ, वायू यांच्या असंतुलित प्रमाणामुळे रोग होतात आणि आपण आजारी पडतो. त्यामुळे आपल्याला खूप त्रास होतो. व्यायामामुळे पित्त, कफ, वायू यांचे शरीरातील प्रमाण योग्य व संतुलित राहण्यास मदत होते.

‘व्यायामाचे महत्त्व’ या कवितेमध्ये राष्ट्रसंत तुकडोजी महाराजांनी साध्या आणि सोप्या भाषेचा वापर केला आहे. शिवाय ही कविता ‘ओवी’ रूपात असल्यामुळे प्रत्येक ओवीमध्ये चार चरण दिसून येतात. त्याचबरोबर ‘यमक’ अलंकाराचा वापर शोभून दिसतो.

प्रश्न 6.
व्यायाम वाढे प्रतिकार शक्ति। स्वावलंबनाची प्रवत्ति।
व्यायामे अंगी वाढे स्फूर्ति। कार्य करण्याची।।
उत्तरः
‘व्यायामाचे महत्त्व’ ही कविता राष्ट्रसंत श्री तुकडोजी महाराज यांनी लिहिली आहे. मानवी जीवनातील व्यायामाचे महत्त्व या कवितेतून कवीने स्पष्ट केले आहे.

तुकडोजी महाराज म्हणतात की, व्यायामामुळे आपल्या शरीराला बळकटी प्राप्त होऊन रोग प्रतिकारक शक्ती वाढते. येणाऱ्या आजारांचा, संकटांचा आपण सहज सामना करू शकतो. त्याचबरोबर शरीर सुदृढ झाल्यामुळे आपण स्वावलंबीसुद्धा बनतो. आपल्या व्यक्तिगत कामासाठी आपल्याला दुसऱ्या कोणावर अवलंबून राहण्याची आवश्यकता राहत नाही. या नियमित व्यायामामुळे शरीरातील आळस, कंटाळा दूर होऊन शरीर ताजेतवाने बनते. शिवाय कोणत्याही कामामध्ये उत्साह जाणवतो. म्हणजेच कोणतेही काम करण्याची शरीरातील जोश, स्फूर्ती वाढते.

‘व्यायामाचे महत्त्व’ या कवितेमध्ये राष्ट्रसंत तुकडोजी महाराजांनी साध्या आणि सोप्या भाषेचा वापर केला आहे. शिवाय ही कविता ‘ओवी’ रूपात असल्यामुळे प्रत्येक ओवीमध्ये चार चरण दिसून येतात. त्याचबरोबर ‘यमक’ अलंकाराचा वापर शोभून दिसतो.

व्यायामाचे महत्त Summary in Marathi

कवीचा‌ ‌परिचय‌:

‌नाव‌:‌ ‌राष्ट्रसंत‌ ‌श्री‌ ‌तुकडोजी‌ ‌महाराज‌ ‌(‌ ‌माणिक‌ ‌बंडोजी‌ ‌ठाकूर)‌ ‌
कालावधी‌:‌ ‌‌1909-1968
संतकवी,‌ ‌समाजसुधारक.‌ ‌अंधश्रद्धा,‌ ‌जातिभेद,‌ ‌धर्मभेद‌ ‌यांसारख्या‌ ‌समाजविघातक‌ ‌गोष्टींवर‌ ‌हल्ले‌ ‌चढवून‌ ‌त्यांनी‌ ‌देशभक्ती,‌ ‌अहिंसा‌ ‌व‌ ‌आत्मसंयम‌ ‌यांचे‌ ‌पाठ‌ ‌दिले.‌ ‌गावागावातून‌ ‌’गुरुदेव‌ ‌सेवा‌ ‌मंडळे’‌ ‌स्थापना‌ ‌केली.‌ ‌या‌ ‌कार्याबद्दल‌ ‌जनतेने‌ ‌त्यांना‌ ‌’राष्ट्रसंत’‌ ‌ही‌ ‌उपाधी‌ ‌देऊन‌ ‌त्यांचा‌ ‌गौरव‌ ‌केला.‌ ‌त्यांची‌ ‌‘अनुभवसागर’,‌ ‌’भजनावली’,‌ ‌’सेवास्वधर्म’,‌ ‌’राष्ट्रीय‌ ‌भजनावली’‌ ‌इत्यादी‌ ‌पुस्तके‌ ‌प्रकाशित‌ ‌आहेत.‌ ‌शिक्षण,‌ ‌भेदाभेद‌ ‌व‌ ‌अस्पृश्यता‌ ‌निर्मूलन,‌ ‌अंधश्रद्धा‌ ‌निर्मूलन,‌ ‌स्वच्छता,‌ ‌सर्वधर्मसमभाव‌ ‌यांविषयी‌ ‌कळकळीचे‌ ‌आवाहन‌ ‌करणारा‌ ‌व‌ ‌अज्ञानी‌ ‌जनतेला‌ ‌वात्सल्ययुक्त‌ ‌भूमिकेतून‌ ‌लोकशिक्षण‌ ‌देणारा‌ ‌त्यांचा‌ ‌’ग्रामगीता’‌ ‌हा‌ ‌ग्रंथ‌ ‌खेडोपाडी‌ ‌आदराने‌ ‌वाचला‌ ‌जातो.‌ ‌

प्रस्तावना‌:

‘व्यायामाचे‌ ‌महत्त्व’‌ ‌ही‌ ‌कविता‌ ‌राष्ट्रसंत‌ ‌श्री‌ ‌तुकडोजी‌ ‌महाराज‌ ‌यांनी‌ ‌लिहिली‌ ‌आहे.‌ ‌मानवी‌ ‌जीवनातील‌ ‌व्यायामाचे‌ ‌महत्त्व‌ ‌या‌ ‌कवितेतून‌ ‌कवीने‌ ‌स्पष्ट‌ ‌केले‌ ‌आहे.‌ ‌

Rashtrasant‌ ‌Shri‌ ‌Tukdoji‌ ‌Maharaj‌ ‌has‌ ‌written‌ ‌this‌ ‌poem‌ ‌called‌ ‌’Vyayamache‌ ‌Mahatva’.‌ ‌The‌ ‌poet‌ ‌has‌ ‌explained‌ ‌the‌ ‌importance‌ ‌of‌ ‌exercise‌ ‌in‌ ‌human‌ ‌life‌ ‌through‌ ‌this‌ ‌poem.‌ ‌

भावार्थ:

व्यायाम आरोग्यदायी …….. सर्वतोपरी ।।
‘राष्ट्रसंत श्री तुकडोजी महाराज’ यांनी आपल्यासारख्या सामान्य माणसांना आपल्या जीवनातील व्यायामाचे महत्त्व साध्या, सरळ भाषेत समजावून सांगितले आहे. ते म्हणतात की, व्यायाम हा आपल्याला सुखाचे आयुष्य देणारा आरोग्यदायी मित्र आहे. हे सूत्र आपण कायम लक्षात ठेवणे गरजेचे आहे. कारण आळस हा आपल्या जीवनाचा खरा शत्रू आहे, हे सगळ्या जगाने मान्य केलेले आहे. व्यायामामुळेच आळस दूर होऊन शरीर आरोग्यपूर्ण होते.

व्यायामाविण सात्त्विक ……. अन्नपचन सहजचि ।।
आरोग्य व्यवस्थित राहावे म्हणून आपण सात्त्विक आहार घेत असतो. या सात्त्विक भोजनाने आपले शरीर व मन छान स्वस्थ राहते. पण तुकडोजी महाराज म्हणतात की, अशा भोजनासोबतच व्यायामही केला पाहिजे, नाहीतर अशा भोजनामुळेही आपणास विविध विकार, विविध आजार होऊ शकतात. सात्त्विक भोजनासोबतच चांगला, योग्य व्यायाम केला तर पोटातील जठाराग्नी चांगला प्रदिप्त होतो. म्हणजे पोटातील अग्नी चांगला पेटून आपल्या अन्नाचे सहज पचनही होते. अन्नाचे अपचन होऊन होणारे विकार व्यायामामुळे टाळता येतात.

व्यायामे जडत्व ……… विचारी सजीवपण ।।
आपण व्यायाम नियमितपणे करायला हवा. योग्य व पुरेसा व्यायाम आपण केला नाही तर शरीरामध्ये जडत्व म्हणजेच स्थूलपणा वाढत जातो. नियमित व्यायामामुळे स्थूलपणा कमी होऊन शरीर सुडौल होते. तसेच आळस दूर होऊन अंगामध्ये तरतरी म्हणजेच उत्साह भरतो. तुकडोजी महाराज पुढे म्हणतात की, व्यायामामुळे शरीरातील रक्तव्यवस्था व्यवस्थित होते. रक्तप्रवाह सुरळीत होऊन रक्ताशी संबंधित विकार दूर होतात आणि आपले आयुष्य वाढते.

व्यायामाने सशक्त स्नायु ……. करिती अत्यंत ।।
नियमित व योग्य व्यायामामुळे आपल्या शरीरातील स्नायूंना बळकटी प्राप्त होते. सगळे स्नायू सशक्त होत जातात. माणसाला आजारपण येत नाही. याच व्यायामामुळे मानवाला दीर्घायुष्य प्राप्त होते, असे तुकडोजी महाराज म्हणतात. आपण जर व्यायाम करीत नसू तर आपल्या शरीरात पित्त, कफ, वायू यांचे प्रमाण कमी-जास्त होऊ लागते. पित्त, कफ, वायू यांच्या असंतुलित प्रमाणामुळे रोग होतात आणि आपण आजारी पडतो. त्यामुळे आपल्याला खूप त्रास होतो. व्यायामामुळे पित्त, कफ, वायू यांचे शरीरातील प्रमाण योग्य व संतुलित राहण्यास मदत होते..

व्यायामे वाढे ……. कार्य करण्याची ।।
तुकडोजी महाराज म्हणतात की, व्यायामामुळे आपल्या शरीराला बळकटी प्राप्त होऊन रोग प्रतिकारक शक्ती वाढते. येणाऱ्या आजारांचा, संकटांचा आपण सहज सामना करू शकतो. त्याचबरोबर शरीर सुदृढ झाल्यामुळे आपण स्वावलंबीसुद्धा बनतो. आपल्या व्यक्तिगत कामासाठी आपल्याला दुसऱ्या कोणावर अवलंबून राहण्याची आवश्यकता राहत नाही. या नियमित व्यायामामुळे शरीरातील आळस, कंटाळा दूर होऊन शरीर ताजेतवाने बनते. शिवाय कोणत्याही कामामध्ये उत्साह जाणवतो. म्हणजेच कोणतेही काम करण्याची शरीरातील जोश, स्फूर्ती वाढते.

शब्दार्थ:

1. अपघात – दुर्घटना (an accident)
2. व्यायाम – कसरत, कवायत, शारीरिक मेहनत देणारी क्रिया (Physical exercise)
3. महत्त्व – मोल (importance)
4. उपाधी – पदवी (a title)
5. गौरव – मानसन्मान, सन्मान (honour, respect)
6. आरोग्य – स्वास्थ्य (health)
7. ध्यानी – (येथे अर्थ) लक्षात, मनात (in mind)
8. सूत्र – पद्धत, रीत (formula, key)
9. आळस – सुस्ती (laziness)
10. वैरी – शत्रू (an enemy)
11. मानिला – मानला (considered, regarded)
12. विण – (येथे अर्थ) शिवाय (without)
13. सात्त्विक – पवित्र, शुद्ध (holy, pure)
14. भोजन – जेवण (food, meals)
15. विकारी – (येथे अर्थ) आजारी (sick, ill, ailing)
16. दीपन – पेटणे, ज्वलन
17. अन्न – खादयपदार्थ (food)
18. पचन – जिरण्याची क्रिया (digestion)
19. जडत्व – जडता, जडपणा, स्थूलपणा (heaviness)
20. अंग – शरीर (body)
21. तरतरी – (येथे अर्थ) चपळाई, चलाखी, उत्साह (sharpness, smartness, freshness)
22. रक्त – रुधिर (blood)
23. उत्तम – अत्यंत चांगले, उत्कृष्ट (best, excellent)
24. शरीर – काया, देह (body)
25. सजीव – जिवंत (living, organic)
26. सशक्त – मजबूत, ताकदवान (strong, powerful)
27. स्नायू – (muscle)
28. मानव – मनुष्य (human)
29. दीर्घायु – प्रदीर्घ जीवन (a long life)
30. पित्त – अन्नपचनास मदत करणारा एक पिवळा द्रव, एक शरीर दोष (bile)
31. जर्जर – (येथे अर्थ) त्रस्त, पीडित
32. प्रतिकार शक्ती – विरोध करणारी ताकद (resistance power)
33. स्वावलंबन – आत्मावलंबन (self-dependence)
34. प्रवृत्ति – कल (tendency)
35. स्फूर्ति – प्रेरक शक्ती (inspiration)
36. कार्य – कृती, काम, क्रिया (an act, work)

Balbharti Maharashtra State Board Class 9 Marathi Solutions Aksharbharati Chapter 15 माझे शिक्षक व संस्कार Notes, Textbook Exercise Important Questions and Answers.

Maharashtra State Board Class 9 Marathi Aksharbharati Solutions Chapter 15 माझे शिक्षक व संस्कार

Marathi Aksharbharati Std 9 Digest Chapter 15 माझे शिक्षक व संस्कार Textbook Questions and Answers

1. खालील वाक्यांचा संदर्भासहित अर्थ स्पष्ट करा.

प्रश्न (अ)
शाळेच्या बागा’ लेखकांसारख्या मुलांच्या जिवावर उभ्या होत्या.
उत्तरः
संदर्भ – शंकरराव खरात यांच्या ‘माझे शिक्षक व संस्कार’ या पाठातून हे वाक्य घेतले आहे. शाळेच्या ‘बागा’ उभारताना लेखक व इतर मुलांचे लाभलेले योगदान या वाक्यातून दिसून येते.

अर्थ – लेखक व लेखकांसारखी हाडा-पिंडाने मोठी असलेली मुले कष्टाच्या कामात कणखर होती. विहिरीचं पाणी दोन-दोन तास राहाटेने ओढून, बागेतल्या फुलझाडांना, फळझाडांना ती मुले पाणी देत असत. त्यामुळे ती फुलझाडे-फळझाडे तरारून उभी राहत होती. बागेला संरक्षण मिळावे; म्हणून मुले बागेतील जमीन कुदळी, टिकावाने खोदायची. त्याचे वाफे करायची व बागेसभोवार बांध घालायची. अशी सर्व कष्टाची कामे केल्यामुळे शाळेच्या ‘बागा’ लेखकांसारख्या मुलांच्या जिवावर उभ्या होत्या, असे म्हटले आहे.

प्रश्न (आ)
लेखक सातारा जिल्हयातील औंधला जायच्या विचारात होते.
उत्तरः
संदर्भ – शंकरराव खरात यांच्या अर्थ – लेखक गावच्या शाळेत शिकत होते. तेथे उत्तम शिक्षणाची सोय होती. शिक्षकही चांगले होते. योग्य मार्गदर्शन व उत्तम संस्कार ते वेळोवेळी मुलांवर करत असत. पण लेखकांना पुढील शिक्षण घ्यायचे होते. पुढील शिक्षणाची सोय गावच्या शाळेत नव्हती म्हणून लेखक सातारा जिल्ह्यात औंधला जायच्या विचारात होते.

2. जोड्या जुळवा.

प्रश्न 1.
जोड्या जुळवा.

उत्तरः

3. चौकटी पूर्ण करा.

प्रश्न 1.
चौकटी पूर्ण करा.
पाठावरून तुम्हाला जाणवलेली लेखकाची स्वभाववैशिष्ट्ये लिहा.

उत्तर:

1. कष्टाळू
2. आज्ञाधारक
3. हरहुन्नरी
4. समंजस

4. खालील परिणाम ज्या घटनेचे आहेत, त्या घटना लिहा.

प्रश्न (अ)
परिणाम – हिरमुसले होऊन लेखक कुस्तीच्या मैदानातून माघारी फिरले.
उत्तरः
घटना – मैदानात कुणीतरी लेखकांना जातीवरून हटकले.

प्रश्न (आ)
परिणाम – लेखकाची मान खाली गेली होती.
उत्तरः
घटना – प्रौढ साक्षरतेचा वर्ग बंद ठेवून त्याठिकाणी धूलिवंदनाच्या दिवशी तमाशा चालला होता. ते पाहून रायगावकर मास्तर मागे वळले.

5. समर्पक उदाहरण लिहा.

प्रश्न (अ)

उत्तरः
उदाहरण – लेखक कुस्तीची लढत लढण्यासाठी मैदानात उतरले असता त्यांना कुणीतरी ओळखले व हटकले.

प्रश्न (आ)

उत्तरः
उदाहरण- बागेतील फुलझाडांना वफळझाडांना पाणी देण्यासाठी लेखक व त्यांचे मित्र विहिरीचे पाणी दोन-दोन तास राहाटाने ओढून काढत.

प्रश्न 6.
आकृतिबंध पूर्ण करा.

उत्तर:

1. समाज निद्रिस्त आहे.
2. खेळात जात न पाहता कौशल्य पाहावे.
3. हा भेदाभेद नष्ट होईल.
4. बहिष्कृतांनाही खेळात-स्पर्धेत मानाने बोलावले जाईल.

पश्न 7.
चौकटीतील वाक्प्रचारांचा अर्थ लिहा.

1. दरारा असणे
2. हिरमुसले होणे
3. उद्धृत करणे
4. समुपदेशन करणे

उत्तर:

1. वचक असणे.
2. नाराज होणे.
3. उल्लेख करणे.
4. मार्गदर्शन करणे.

8. स्वमत.

पश्न 1.
विदयार्थ्यांच्या व्यक्तिमत्त्व विकासात शिक्षकांची भूमिका महत्त्वाची आहे, या विधानाबाबत तुमचे मत सोदाहरण स्पष्ट करा.
उत्तरः
उतारा 1 मधील कृती 4 : स्वमतचे उत्तर पहा.

पश्न 2.
शिक्षक व विदयार्थी यांच्यातील नातेसंबंधाविषयी तुमच्या संकल्पना स्पष्ट करा.
उत्तरः
उतारा 3 मधील कृती 4 : स्वमतचे उत्तर पहा.

उपक्रम:

तुमचे प्राथमिक शाळेतील शिक्षक आठवा व त्यांतील अविस्मरणीय शिक्षकांशी संबंधित असलेल्या तुमच्या आठवणी लिहा.

भाषाभ्यास:

पश्न 1.
अधोरेखित शब्दांविषयी खालील माहिती भरून तक्ता पूर्ण करा.

Marathi Akshar Bharati Class 9 Textbook Solutions Chapter 15 माझे शिक्षक व संस्कार Additional Important Questions and Answers

1. पुढील उताऱ्याच्या आधारे दिलेल्या सूचनेनुसार कृती करा:

कृती 1 : आकलन कृती

प्रश्न 1.
आकृतिबंध पूर्ण करा.
उत्तर:

प्रश्न 2.
उताऱ्यानुसार वाक्यांचा क्रम लावा.

1. श्री. गोळीवडेकर मास्तर आमच्यावर प्रेम करायचे.
2. शाळेच्या ‘बागा’ आमच्यासारख्या मुलांच्या जिवावरच तर उभ्या होत्या.
3. मी माझी गावची शाळा सोडणार होतो.
4. कात्रे मास्तरांच्या घरी माझे वडील लाकडं फोडायला जायचे.

उत्तर:

1. मी माझी गावची शाळा सोडणार होतो.
2. कात्रे मास्तरांच्या घरी माझे वडील लाकडं फोडायला जायचे.
3. शाळेच्या ‘बागा’ आमच्यासारख्या मुलांच्या जिवावरच तर उभ्या होत्या.
4. श्री. गोळीवडेकर मास्तर आमच्यावर प्रेम करायचे.

खालील प्रश्नांची उत्तरे एका वाक्यात लिहा.

प्रश्न 1.
लेखकांचा पुढील शिक्षणासाठी कोठे जाण्याचा विचार होता?
उत्तरः
लेखकांचा पुढील शिक्षणासाठी औंध (जि. सातारा) येथील हायस्कूलमध्ये जाण्याचा विचार होता.

प्रश्न 2.
लेखकांचे वडील कोणाकडे लाकडे फोडायला जायचे?
उत्तर:
लेखकांचे वडील कात्रे मास्तरांच्या घरी लाकडे फोडायला जायचे.

प्रश्न 3.
शाळेच्या बागा’ कोणाच्या जिवावर उभ्या होत्या?
उत्तर:
शाळेच्या बागा’ लेखकासारख्या मुलांच्या जिवावर उभ्या होत्या.

प्रश्न 4.
कंसातील योग्य शब्द वापरून रिकाम्या जागा भरा.
1. श्री. ……….. मास्तर मला मराठी पाचवीत होते. (गोळीवडेकर, पाटकर, देशमुख, कात्रे)
2. श्री. हणमंतराव देशमुखांनी मला इंग्रजी ………… भाषांतर शिकवले. (तराडकरांचे, तर्खडकरांचे, कठिण शब्दांचे, परिच्छेदाचे)
उत्तर:
1. गोळीवडेकर
2. तर्खडकरांचे

कृती 2 : आकलन कृती

1. योग्य पर्याय निवडून विधाने पूर्ण करा.

प्रश्न 1.
आम्ही मुलं वयानं तसंच ……………….
(अ) आडदांड मोठाड.
(ब) मजबूत कणखर.
(क) हाडा-पिंडाने मोठाड.
(ड) बांधा मोठाड.
उत्तर:
आम्ही मुलं वयानं तसंच हाडा-पिंडाने मोठाड.

प्रश्न 2.
लेखकांना यश मिळणार याची ………………
(अ) खात्री होती.
(ब) माहिती होती.
(क) समज होती.
(ड) कल्पना होती.
उत्तर:
लेखकांना यश मिळणार याची खात्री होती.

प्रश्न 3.
कोण ते लिहा.
उत्तर:

प्रश्न 4.
आकृतिबंध पूर्ण करा.
उत्तर:

4. चूक की बरोबर लिहा.

प्रश्न 1.
1. कात्रे मास्तरांच्या घरी लेखकांचे वडील साफ सफाई करायला जायचे.
2. गोळीवडेकर मास्तर इतिहास भूगोल शिकवायचे.
उत्तर:
1. चूक
2. बरोबर

कृती 3 : व्याकरण कृती

प्रश्न 1.
खालील वाक्ये लेखननियमांनुसार शुद्ध करून लिहा.
आम्ही मूल वयानं तसंच हाडा-पींडाने मोठाड.
उत्तर:
आम्ही मुलं वयानं तसंच हाडा-पिंडाने मोठाड,

प्रश्न 2.
अचूक शब्द लिहा.
1. शेतीतज्ज्ञ, शेतितज्ञ, शेतीतदज्ञ, शेतीतज्ञ
2. तखडकर, तरखडकर, तर्खडकर, तरखरकर
उत्तर:
1. शेतीतज्ज्ञ
2. तर्खडकर

प्रश्न 3.
अधोरेखित शब्दाचा समानार्थी शब्द लिहून वाक्य पुन्हा लिहा.
त्यांची व माझी जवळची ओळख होती.
उत्तरः
त्यांचा व माझा जवळचा परिचय होता.

प्रश्न 4.
अधोरेखित शब्दाचा विरुद्धार्थी शब्द लिहून वाक्य पुन्हा लिहा.
यश मिळणार याची लेखकांना खात्री होती.
उत्तर:
अपयश मिळणार याची लेखकांना खात्री होती.

प्रश्न 5.
अधोरेखित शब्दाची जात ओळखा.
अबब! केवढा मोठा साप.
उत्तरः
केवलप्रयोगी अव्यय.

प्रश्न 6.
तक्ता पूर्ण करा.
उत्तरः

प्रश्न 7.
तक्ता पूर्ण करा.
उत्तरः

प्रश्न 8.
कंसातील सूचनेनुसार बदल करा.
गोळीवडेकर मास्तर इतिहास, भूगोल शिकवायचे. (काळ ओळखा.)
उत्तरः
भूतकाळ

प्रश्न 9.
पर्यायी शब्द लिहा.
उत्तरः

कृती 4 : स्वमत

प्रश्न 1.
विदयार्थ्यांच्या व्यक्तिमत्त्व विकासात शिक्षकांची भूमिका महत्त्वाची आहे. या विधानाबाबत तुमचे मत सोदाहरण स्पष्ट करा.
उत्तरः
शिक्षक विदयार्थ्यांचे व्यक्तिमत्त्व घडवित असतात. त्यांना ज्ञान देऊन त्यांच्यावर योग्य ते संस्कार करत असतात. मुलांना योग्य प्रकारे मार्गदर्शन करून पुढील आयुष्यासाठी त्यांना तयार करत असतात. मानवी मूल्यांचे योग्य ते आदर्श मुलांसमोर उभे करण्याचे सामर्थ्य शिक्षकांत असते; त्यामुळेच विदयार्थ्यांच्या व्यक्तिमत्त्वाची जडणघडण होते. एखादया गोष्टीबद्दल विचार करण्याची सकारात्मक मानसिकता तयार होते. शिक्षक स्वत:च्या आचरणातून मुलांसमोर एक आदर्श निर्माण करण्याचे कार्य करतात. त्यामुळे मुलांना प्रेरणा मिळते व ते आपल्या शिक्षकांचे अनुकरण करतात. अशा प्रकारे मुलांच्या व्यक्तिमत्त्वाला सुडौल आयाम देण्याचे कार्य शिक्षकच करतात.

पुढील उताऱ्याच्या आधारे दिलेल्या सूचनेनुसार कृती करा:

कृती 1 : आकलन कृती

प्रश्न 1.
आकृतिबंध पूर्ण करा.
उत्तरः

प्रश्न 2.
कोण ते लिहा.
उत्तरः

प्रश्न 3.
उताऱ्यानुसार वाक्यांचा क्रम लावा.

1. परीक्षेच्या निकालाच्या दृष्टीने त्यांनी शाळेची चांगली प्रगती केली.
2. औंधला शिकायला जाणार म्हणून मी श्री. नाईक मास्तरांना भेटलो.
3. शिस्तप्रिय हेडमास्तरांनी माझ्या शाळेला चांगलीच शिस्त लावली.
4. ते सदानकदा विदयार्थ्यांना समुपदेश करत.

उत्तर:

1. शिस्तप्रिय हेडमास्तरांनी माझ्या शाळेला चांगलीच शिस्त लावली.
2. ते सदानकदा विदयार्थ्यांना समुपदेश करत.
3. परीक्षेच्या निकालाच्या दृष्टीने त्यांनी शाळेची चांगली प्रगती केली.
4. औंधला शिकायला जाणार म्हणून मी श्री. नाईक मास्तरांना भेटलो.

खालील प्रश्नांची उत्तरे एका वाक्यात लिहा.

प्रश्न 1.
लेखकांच्या शाळेत कोणाचा दरारा होता?
उत्तरः
लेखकांच्या शाळेत हेडमास्तर श्री. नाईक यांचा दरारा होता.

प्रश्न 2.
शाळेची दुसरी घंटा होताच हेडमास्तर श्री. नाईक काय करत असत?
उत्तरः
शाळेची दुसरी घंटा होताच हेडमास्तर श्री. नाईक हातात छडी घेऊन शाळेच्या दारात थांबत असत.

कंसातील योग्य शब्द वापरून रिकाम्या जागा भरा.

प्रश्न 1.
1. नाईक मास्तरांनी केलेला ………….. लेखक कधीच विसरू शकत नाही. (संस्कार, हितोपदेश, प्रयोग, अभिनय)
2. …………. मास्तरांसारखे ते कधीही इतर सार्वजनिक कार्यात पडत नसत. (श्री. हणमंतराव देशमुख, कात्रे, श्री. नाईक, श्री. रायगावकर)
उत्तर‌:‌
1. ‌हितोपदेश‌
2.‌ ‌श्री.‌ ‌रायगावकर‌ ‌

कृती‌ 2 ‌:‌ ‌आकलन‌ ‌कृती‌ ‌

प्रश्न 1.
योग्य‌ ‌पर्याय‌ ‌निवडून‌ ‌विधाने‌ ‌पूर्ण‌ ‌करा.‌ ‌
श्री.‌ ‌नाईक‌ ‌मास्तरांनी‌ ‌केलेला‌ ‌हितोपदेश‌ ‌लेखक‌ ‌कधीच‌ ‌विसरू‌ ‌शकत‌ ‌नाहीत;‌ ‌कारण‌ ‌……………….‌
‌(अ)‌ ‌शिस्तीच्या‌ ‌दृष्टीने‌ ‌कसं‌ ‌वागावे,‌ ‌जीवनात‌ ‌आपली‌ ‌प्रगती‌ ‌कशी‌ ‌करून‌ ‌घ्यावी.‌ ‌
(ब)‌ ‌सगळी‌ ‌कष्टाची‌ ‌कामे‌ ‌श्री.‌ ‌नाईक‌ ‌मास्तर‌ ‌करत‌ ‌असत.‌
‌(क)‌ ‌शाळेत‌ ‌दरारा‌ ‌असे,‌ ‌ते‌ ‌शिस्तीचे‌ ‌भोक्ते‌ ‌होते.‌
‌(ड)‌ ‌शाळेची‌ ‌दुसरी‌ ‌घंटा‌ ‌होताच‌ ‌ते‌ ‌हातात‌ ‌छडी‌ ‌घेऊन‌ ‌शाळेच्या‌ ‌दारात‌ ‌थांबत‌ ‌असत.‌
‌उत्तर:‌
‌श्री.‌ ‌नाईक‌ ‌मास्तरांनी‌ ‌केलेला‌ ‌हितोपदेश‌ ‌लेखक‌ ‌कधीच‌ ‌विसरू‌ ‌शकत‌ ‌नाहीत;‌ ‌कारण‌ ‌शिस्तीच्या‌ ‌दृष्टीने‌ ‌कसं‌ ‌वागावे,‌ ‌जीवनात‌ ‌आपली‌ ‌प्रगती‌ ‌कशी‌ ‌करून‌ ‌घ्यावी.‌

प्रश्न 2.
आकृतिबंध‌ ‌पूर्ण‌ ‌करा.‌ ‌
‌उत्तर:‌

प्रश्न 3.
आकृतिबंध‌ ‌पूर्ण‌ ‌करा.‌ ‌
‌उत्तर:‌

‌चूक‌ ‌की‌ ‌बरोबर‌ ‌लिहा.‌

प्रश्न 1.
1.‌ ‌हेडमास्तर‌ ‌श्री.‌ ‌नाईक‌ ‌मास्तर‌ ‌यांचा‌ ‌शाळेत‌ ‌दरारा‌ ‌नसे.‌
2. ‌औंधला‌ ‌शिकायला‌ ‌जाणार‌ ‌म्हणून‌ ‌लेखक‌ ‌श्री.‌ ‌नाईक‌ ‌मास्तरांना‌ ‌भेटले.‌ ‌
उत्तर:‌
1. चूक‌ ‌
2. ‌बरोबर‌

‌कृती‌ ‌3 ‌:‌ ‌व्याकरण‌ ‌कृती‌

प्रश्न 1.
खालील‌ ‌वाक्य‌ ‌लेखननियमांनुसार‌ ‌शुद्ध‌ ‌करून‌ ‌लिहा.‌ ‌
या‌ ‌शिस्तप्रीय‌ ‌हेडमास्तरांनी‌ ‌माझ्या‌ ‌शाळेला‌ ‌चांगलीच‌ ‌शीस्त‌ ‌लावली.‌ ‌
उत्तर:‌
‌या‌ ‌शिस्तप्रिय‌ ‌हेडमास्तरांनी‌ ‌माझ्या‌ ‌शाळेला‌ ‌चांगलीच‌ ‌शिस्त‌ ‌लावली.‌ ‌

प्रश्न 2.
अचूक शब्द लिहा.
1. शिस्तप्रीय, शिस्तप्रिय, शीस्तप्रिय, शिस्तप्रिरय
2. मार्गदर्शन, मार्गदरशन, मारगदशन, मागदर्शन
उत्तर:
1. शिस्तप्रिय
2. मार्गदर्शन

अधोरेखित शब्दांचा समानार्थी शब्द लिहून वाक्ये पुन्हा लिहा.

प्रश्न 1.
हेडमास्तर श्री. नाईक मास्तर यांचा शाळेत वचक असे.
उत्तर:
हेडमास्तर श्री. नाईक मास्तर यांचा शाळेत दरारा असे.

प्रश्न 2.
परीक्षेच्या निकालाच्या दृष्टीने त्यांनी शाळेची चांगली सुधारणा केली.
उत्तरः
परीक्षेच्या निकालाच्या दृष्टीने त्यांनी शाळेची चांगली प्रगती केली.

अधोरेखित शब्दाचा विरुद्धार्थी शब्द लिहून वाक्य पुन्हा लिहा.

प्रश्न 1.
अधोरेखित शब्दाचा विरुद्धार्थी शब्द लिहून वाक्य पुन्हा लिहा.
परीक्षेच्या निकालाच्या दृष्टीने त्यांनी शाळेची अधोगती केली.
उत्तरः
परीक्षेच्या निकालाच्या दृष्टीने त्यांनी शाळेची प्रगती केली.

अधोरेखित शब्दाची जात ओळखा.

प्रश्न 1.
मी कधीच विसरू शकत नाही.
उत्तर:
सर्वनाम.

प्रश्न 2.
आम्हां मुलांसाठी वेगळी तालीम होती.
उत्तर:
विशेषण.

प्रश्न 3.
तक्ता पूर्ण करा.
उत्तर:

प्रश्न 4.
तक्ता पूर्ण करा.
उत्तर:

खालील वाक्यात अधोरेखित शब्दांऐवजी पाठात आलेले योग्य वाक्प्रचार शोधून वाक्य पुन्हा लिहा.

प्रश्न 1.
रामला समिरने मार्गदर्शन केले.
उत्तरः
रामला समिरने समुपदेशन केले.

प्रश्न 2.
हेडमास्तर श्री. नाईक यांचा शाळेत वचक होता.
उत्तरः
हेडमास्तर श्री. नाईक यांचा शाळेत दरारा होता.

कंसातील सूचनेनुसार बदल करा.

प्रश्न 1.
कंसातील सूचनेनुसार बदल करा.
ते शिस्तीचे कडे भोक्ते होते. (काळ ओळखा.)
उत्तरः
भूतकाळ.

प्रश्न 2.
पर्यायी शब्द लिहा.
उत्तरः

कृती 4 : स्वमत

प्रश्न 1.
शाळा ही विदयार्थ्यांवर संस्कार करणारे एक प्रमुख केंद्र असते या विधानावर तुमचे विचार स्पष्ट करा.
उत्तर:
शाळा विदयेचे माहेरघर असते. शाळेत शिकविणारे शिक्षक हे मुलांना विद्या देण्याचे कार्य करत असतात. जवळपास विदयार्थी रोज पाच ते सहा तास शाळेत असतात. एवढा वेळ मुलांवर संस्कार करण्यासाठी पुरेसा असतो. शिक्षक शिकवित असलेल्या विविध विषयांच्या माध्यमातून मुलांवर संस्कार करीत असतात. शाळेमध्ये होत असलेल्या निरनिराळ्या कार्यक्रमातून मुलांवर संस्कार होत असतात. तसेच शाळेमार्फत आयोजित केलेल्या शैक्षणिक सहलींतून मुलांवर संस्कार होत असतात. म्हणून शाळा हे विदयार्थ्यांवर संस्कार करणारे प्रमुख केंद्र आहे.

पुढील उताऱ्याच्या आधारे दिलेल्या सूचनेनुसार कृती करा:

कृती 1 : आकलन कृती

प्रश्न 1.
आकृतिबंध पूर्ण करा.
उत्तर:

प्रश्न 2.
उताऱ्यानुसार वाक्यांचा क्रम लावा.

1. “अरे! आज धूलिवंदन! हे चालायचेच!’
2. प्रौढ वर्गाच्या कंदिलाच्या प्रकाशात तमाशा चालला होता.
3. शिमग्याच्या धुळवडीला प्रौढ वर्गात तमाशाचा फड उभा राहिला.
4. मी हिरमुसला होऊन माघारी गेलो.

उत्तर:

1. मी हिरमुसला होऊन माघारी गेलो.
2. शिमग्याच्या धुळवडीला प्रौढ वर्गात तमाशाचा फड उभा राहिला.
3. प्रौढ वर्गाच्या कंदिलाच्या प्रकाशात तमाशा चालला होता.
4. “अरे! आज धूलिवंदन! हे चालायचेच!’

खालील प्रश्नांची उत्तरे एका वाक्यात लिहा.

प्रश्न 1.
लेखकांची समजूत कोणी काढली?
उत्तरः
लेखकांची समजूत श्री. रायगावकरांनी काढली.

प्रश्न 2.
रायगावकर मास्तर लेखकांना पाहून काय म्हणाले?
उत्तरः
“अरे! आज धूलिवंदन! हे चालायचेच!” असे रायगावकर मास्तर लेखकांना म्हणाले.

कंसातील योग्य शब्द वापरून रिकाम्या जागा भरा.

प्रश्न 1.
1. ‘अरे, समाज अजून ………… आहे. (निद्रिस्त, झोपलेला, जागा, आंधळा)
2. “………….. तू हे ध्यानात ठेव.” (शाम!, शंकर!, नाईक!, देशपांडे!)
उत्तर:
1. निद्रिस्त
2. शंकर!

प्रश्न 2.
आकृतिबंध पूर्ण करा.
उत्तर:

कृती 2: आकलन कृती

योग्य पर्याय निवडून विधाने पूर्ण करा.

प्रश्न 1.
एका थोराड मुलाला, ‘याला जोड, याला जोड’ म्हणून …..
(अ) फडात फिरवत होते.
(ब) मैदानात फिरवत होते.
(क) अंगणात फिरवत होते.
(ड) रस्त्यावर फिरवत होते.
उत्तर:
एका थोराड मुलाला, ‘याला जोड, याला जोड’ म्हणून फडात फिरवत होते.

प्रश्न 2.
श्री रायगावकर मास्तर चटकन परत फिरले; कारण …………………
(अ) प्रौढ वर्गाच्या कंदिलाच्या प्रकाशात तमाशा चालला होता.
(ब) शाळेत कंदिलाच्या प्रकाशात तमाशा चालला होता.
(क) प्रौढ वर्गात कंदिलाच्या प्रकाशात लावणी चालली होती.
(ड) सार्वजनिक ठिकाणी कंदिलाच्या प्रकाशात ढोल-ताशाचं वाक्य वाजत होते.
उत्तर:
श्री रायगावकर मास्तर चटकन परत फिरले; कारण प्रौढ वर्गाच्या कंदिलाच्या प्रकाशात तमाशा चालला होता.

प्रश्न 3.
चूक की बरोबर ते लिहा.
1. त्या दिवशी प्रौढ साक्षरतेचा वर्ग चालू होता.
2. सरांनी लेखकांना केलेला उपदेश लेखक कधीच विसरू शकत नव्हते.
उत्तर:
1. चूक
2. बरोबर

प्रश्न 4.
कोण कोणास म्हणाले ते लिहा.
उत्तर:

कृती 3 : व्याकरण कृती

खालील वाक्ये लेखननियमांनुसार शुद्ध करून लिहा.

प्रश्न 1.
1. लेखक हिरमूसला होऊन माघारि गेला.
2. त्या दीवशी प्रौढ साक्षरतेचा वरग बंद होता.
उत्तर:
1. लेखक हिरमुसला होऊन माघारी गेला.
2. त्या दिवशी प्रौढ साक्षरतेचा वर्ग बंद होता.

प्रश्न 2.
अचूक शब्द लिहा.
1. वस्तीतील, वस्तितिल, वस्तीतिल, वस्तितील
2. धूलीवंदन, धुलिवंदन, धूलिवंदन, धुलीवंदन
उत्तर:
1. वस्तीतील
2. धूलिवंदन

प्रश्न 3.
समानार्थी शब्द लिहा.
उत्तर:

1. शिक्षण – संस्कार
2. कसब – कौशल्य
3. झोप – निद्रा
4. घटना – प्रसंग
5. विभाग – वर्ग
6. पोक्त – प्रौढ

प्रश्न 4.
विरुद्धार्थी शब्द लिहा.
उत्तर:

1. बालक × प्रौढ
2. रात्री × दिवसा
3. वर × खाली

प्रश्न 5.
खालील वाक्यातील अधोरेखित शब्दाचे वचन बदलून वाक्य पुन्हा लिहा.
त्या विदयेच्या मंदिरात तमाशा उभा कसा …….?
उत्तर:
त्या विद्येच्या मंदिरात तमाशे उभे कसे …………?

प्रश्न 6.
तक्ता पूर्ण करा.
उत्तर:

प्रश्न 7.
तक्ता पूर्ण करा.
उत्तर:

प्रश्न 8.
खालील वाक्यात अधोरेखित शब्दांऐवजी पाठात आलेला योग्य वाक्प्रचार शोधून वाक्य पुन्हा लिहा.
रमेशला कब्बडी खेळायला न मिळाल्याने तो नाराज झाला.
उत्तर:
रमेशला कब्बडी खेळायला न मिळाल्याने तो हिरमुसला.

प्रश्न 9.
वाक्यातील काळ ओळखा.
समाज अजून निद्रिस्त आहे.
उत्तरः
वर्तमानकाळ.

प्रश्न 10.
काळ बदला.
सरांनी मला उपदेश केला होता. (वर्तमानकाळ करा.)
उत्तर:
सर मला उपदेश करत आहेत.

प्रश्न 11.
पर्यायी शब्द लिहा.
उत्तर:

कृति 4 : स्वमत

प्रश्न 1.
शिक्षक व विद्यार्थी यांच्यातील नातेसंबंधाविषयी तुमच्या संकल्पना स्पष्ट करा.
उत्तर:
शिक्षक विदयार्थ्यांना ज्ञान देत असतात. कळत-नकळत त्यांच्यावर संस्कार करत असतात. विदयार्थी सुद्धा शिक्षकांनी दिलेले ज्ञान आत्मसात करत असतात व संस्काराचे पालन करत असतात. त्यामुळेच त्यांच्यात एक प्रकारचे जिव्हाळ्याचे व स्नेहाचे संबंध निर्माण होत असतात. त्यांच्यात गुरू-शिष्याचे नाते निर्माण होते. विदयार्थी आपल्या शिक्षकांनी दिलेल्या सगळ्या सूचनांचे व निर्देशांचे पालन करत असतात. त्यांचे विचार स्वत:च्या जीवनात उतरवत असतात. त्यांचा आपल्या शिक्षकांवर विश्वास असतो. त्यामुळेच एका श्रद्धेच्या दृष्टिकोनातून ते आपल्या शिक्षकांकडे पाहत असतात. अशा प्रकारे विदयार्थ्यांसाठी त्याचे शिक्षक हे मात्या-पित्याची भूमिका बजावित असतात.

माझे शिक्षक व संस्कार Summary in Marathi

लेखकाचा परिचय:

नाव: शंकरराव खरात
कालावधी: 1921-2001
कथाकार, कादंबरीकार, लेखक, दलित चळवळीत सक्रिय सहभाग. ‘तडीपार’, ‘सांगावा’, ‘आडगावचे पाणी’ इत्यादी कथासंग्रह, ‘झोपडपट्टी’, ‘फूटपाथ नं. १’, ‘माझं नाव’, इत्यादी कादंबऱ्या, ‘तराळ-अंतराळ’ हे आत्मचरित्र.

प्रस्तावना:

‘माझे शिक्षक व संस्कार’ हा पाठ लेखक शंकरराव खरात यांनी लिहिला आहे. शालेय वयात शिक्षकांकडून केल्या जाणाऱ्या संस्कारांचे महत्त्व प्रस्तुत पाठातून लेखकाने व्यक्त केले आहे.

‘Maze Shikshak va Sanskar’ article is written by Shankarrao Kharat. The importance of teacher and his nurturing is narrated in this article.

शब्दार्थ:

1. संस्कार – सद्गुण (virtue)
2. रहिवासी – निवासी (resident)
3. प्रयत्न – परिश्रम (effort)
4. यश – (success)
5. सल्ला – उपदेश (advice)
6. सडपातळ – किरकोळ अंगाचा (slim)
7. विकार – आजार, रोग (illness, disease)
8. भाषांतर – एका भाषेतील मजकुराचे वा ग्रंथाचे दुसऱ्या भाषेत केलेले रूपांतर (translation)
9. शेतीतज्ज्ञ – शेतीविषयक सखोल ज्ञान असणारा (Agro expert)
10. बाग – बगीचा, उदयान (a garden)
11. परिचय – ओळख (an introduction)
12. मोठाड – (huge, massive)
13. कष्ट – मेहनत (hard work)
14. कणखर – मजबूत (strong, tough)
15. निकाल – (result)
16. हितोपदेश – कल्याणकारक सल्ला (counselling)
17. उपकृत – ज्याला मदत केली आहे असा (obliged)
18. उद्धृत – उदाहरण म्हणून केलेला (quoted as anextract)
19. तालीम – शारीरिक व्यायाम (exercise)
20. हंगाम – मोसम, ऋतू (season)
21. इनाम – बक्षीस (prize)
22. लढत – (लढाई), झुंज (fight)
23. हिरमुसणे – निराश होणे (get nervous, to feel dejected)
24. निद्रा – (sleep)
25. शिमगा – होळीचा सण (the Holi festival)
26. वस्ती – वसाहत (colony, settlement)
27. साक्षर – अक्षरओळख असलेला (literate)
28. कल्पना – योजना (येथे अर्थ) माहिती, पूर्व सूचना (idea, planning)
29. रहाट – विहिरीतून पाणी काढण्याची यंत्रणा (चाक)

टिपा:

1. तमाशा – बव्हंशी विनोद व शृंगार यांचा अविष्कार करणारा लोककलेचा नाटकासारखा प्रकार
2. धूलिवंदन – (धुलवड) हिंदूंचा एक सण, परस्परांवर धूळ, रंग इ. उडवण्याचा खेळ
3. तर्खडकर – दादोबा पांडूरंग तर्खडकर हे मराठी व्याकरण लेखक आणि समाजसुधारक होते
4. स्काउट – भारत स्काउट गाइड (संस्थापक – बेडेन पावेल, एक शैक्षणिक चळवळ)
5. कुस्ती – महाराष्ट्राच्या मातीत मुरलेला एक खेळ
6. तमाशाचा फड – तमाशा किंवा इतर लोककला सादर केली जाते ती जागा
7. कुस्तीचा फड – कुस्तीच्या स्पर्धा जिथे खेळल्या जातात ती जागा

वाक्प्रचार:

1. दरारा असणे – वचक असणे
2. हिरमुसले होणे – नाराज होणे
3. उद्धृत करणे – उल्लेख करणे
4. समुपदेशन करणे – मार्गदर्शन करणे
5. प्रगती करणे – सुधारणा करणे
6. मान खाली जाणे – शरमेने मान झुकणे

Balbharti Maharashtra State Board Class 9 Marathi Solutions Aksharbharati Chapter 6 ऑलिंपिक वर्तुळांचा गोफ Notes, Textbook Exercise Important Questions and Answers.

Maharashtra State Board Class 9 Marathi Aksharbharati Solutions Chapter 6 ऑलिंपिक वर्तुळांचा गोफ

Marathi Aksharbharati Std 9 Digest Chapter 6 ऑलिंपिक वर्तुळांचा गोफ Textbook Questions and Answers

1. आकृतिबंध पूर्ण करा.

प्रश्न 1.
आकृतिबंध पूर्ण करा.

उत्तरः
(अ)

(आ)

2. योग्य पर्याय निवडून वाक्ये पुन्हा लिहा.

प्रश्न 1.
योग्य पर्याय निवडून वाक्ये पुन्हा लिहा.
1. पहिले ऑलिंपिक व्हिलेज ………….. येथे वसले. (ग्रीस, मेलबोर्न, फ्रान्स, अमेरिका)
2. पहिले ऑलिंपिक सामने ………….. साली झाले. (1894, 1956, इ.स.पूर्व७७६, इ.स. पूर्व 394)
उत्तर:
1. मेलबोर्न
2. इ.स.पूर्व 776

3. खालील वाक्य वाचा. अधोरेखित केलेल्या शब्दांबाबत माहिती भरून तक्ता पूर्ण करा. एखादया शब्दाला खालील मुद्दे लागू नसतील तर तिथे – हे चिन्ह लिहा. उदा., ‘व’ यासाठी लिंग, वचन, विभक्ती सगळीकडे – हे चिन्ह येईल.

प्रश्न 1.
पुरुषांसाठी व स्त्रियांसाठी वेगवेगळे सामने होतात.

उत्तरः

4. स्वमत

प्रश्न (अ)
‘ऑलिंपिक म्हणजे विश्वबंधुत्व’ ही संकल्पना स्पष्ट करा.
उत्तरः
मानवाच्या सर्वांगीण व्यक्तिमत्त्व विकासात खेळाचे महत्त्वाचे स्थान आहे. त्यामुळेच सर्व स्तरांवर खेळले जाणारे क्रीडासामने हे जगभरातील क्रीडाप्रेमींचे लक्ष वेधून घेतात. संपूर्ण जगभरातील क्रीडासामन्यांत, ऑलिंपिक क्रीडासामन्यांना एक मानाचे स्थान आहे. या ऑलिंपिक सामन्यांचे स्वतंत्र निशाण म्हणजे, एक भलामोठा ध्वज असतो. ध्वजाच्या पांढऱ्याशुभ्र रंगावर लाल, पिवळ्या, निळ्या, हिरव्या व काळ्या रंगांची वर्तुळे एकमेकांत गुंफलेली असतात. ही पाच वर्तुळे म्हणजे जगातील पाच खंड आणि ध्वजाचा पांढराशुभ्र रंग म्हणजे विशाल अंतराळ होय. जगभरातील सर्व राष्ट्रांतील सुमारे पाच ते सहा हजार खेळाडू या सामन्यांमध्ये भाग घेतात. देशादेशांतील मैत्री वाढून त्यांच्यात मित्रत्वाची स्पर्धा व्हावी यासाठी ऑलिंपिक सामने दर चार वर्षांनी वेगवेगळ्या देशात भरवले जातात.

या सामन्यांच्या व्यवस्थेसाठी एक आंतरराष्ट्रीय ऑलिंपिक समिती नेमलेली असते. या स्पर्धांत भाग घेणाऱ्या प्रत्येक देशाचे एक ते तीन प्रतिनिधी या समितीमध्ये असतात. या सामन्यांसाठी लागणारा सारा पैसा स्पर्धक देश उभा करतात. क्रीडेच्या क्षेत्रात जातिभेद नाही, धर्मभेद नाही की वर्णभेद नाही. येथे सर्वांना समान संधी मिळते. ऑलिंपिकच्या मैदानावर खेळाडू खेळत असतात तेव्हा खेळाडूंना पराक्रमाचा व प्रयत्नवादाचा संदेश देणारा ध्वज डौलाने फडकत असतो. त्या ध्वजावरील पाच खंडांची पाच वर्तुळे समतेचा व विश्वबंधुत्वाचा संदेश जगाला देत असतात.

उपक्रम:

सन 2016 साली झालेल्या ऑलिंपिक सामन्यातील सुवर्ण, रजत व कांस्यपदक मिळवणाऱ्या खेळाडूंची माहिती आंतरजालाचा वापर करून खालील तक्त्यात लिहा.

Marathi Akshar Bharati Class 9 Textbook Solutions Chapter 6 ऑलिंपिक वर्तुळांचा गोफ Additional Important Questions and Answers

पुढील उताऱ्याच्या आधारे दिलेल्या सूचनेनुसार कृती करा:

कृती 1: आकलन कृती

प्रश्न 1.
आकृतिबंध पूर्ण करा.
उत्तरः

प्रश्न 2.
जोड्या जुळवा.

उत्तर:

1. येण्याजाण्यासाठी
2. पाच वर्तुळे
3. ऑलिंपिक सामन्यांचे
4. विशाल अंतराळ

खालील प्रश्नांची उत्तरे एका वाक्यात लिहा.

प्रश्न 1.
संपूर्ण जगभरातील क्रीडासामन्यात कशाला मानाचे स्थान आहे?
उत्तरः
संपूर्ण जगभरातील क्रीडासामन्यात ऑलिंपिक क्रीडासामन्यांना मानाचे स्थान आहे.

प्रश्न 2.
ऑलिंपिकच्या ध्वजावर किती रंगांची वर्तुळे काढण्यात आली आहेत?
उत्तर:
ऑलिंपिकच्या ध्वजावर पाच रंगांची वर्तुळे काढण्यात आली आहेत.

प्रश्न 3.
लेखकांची मोटार भरधाव वेगाने कुठे जात होती?
उत्तर:
लेखकांची मोटार ऑलिंपिक गावाकडे भरधाव वेगाने जात होती.

प्रश्न 4.
कंसातील योग्य शब्द वापरून रिकाम्या जागा भरा.
1. मनुष्याच्या सर्वांगीण व्यक्तिमत्त्व विकासात महत्त्व अनन्यसाधारण आहे. (क्रीडेचे, मेहनतीचे, कामाचे, शाळेचे)
2. …………. गावाकडे आमची मोटार भरधाव वेगाने जात होती. (वडिलांच्या, आवडत्या, ऑलिंपिक, दूरच्या)
उत्तर:
1. क्रीडेचे
2. ऑलिंपिक

प्रश्न 5.
सहसंबंध लिहा.
1. शुभ्रधवल : पार्श्वभूमी :: विशाल : …………….
2. प्रचंड : गर्दी :: भलामोठा : ………………
उत्तर:
1. अंतराळ
2. ध्वज

कृती 2 : आकलन कृती

प्रश्न 1.
योग्य पर्याय निवडून विधान पूर्ण करा.
गर्दी प्रचंड असली तरी रहदारीला अडचण मुळीच नव्हती; कारण ……………………….
(अ) येण्याजाण्यासाठी एकच रस्ता होता.
(ब) रस्त्यावर सिग्नल होते.
(क) लोकांमध्ये शिस्त होती.
(ड) येण्याजाण्यासाठी वेगवेगळे रस्ते होते.
उत्तरः
गर्दी प्रचंड असली तरी रहदारीला अडचण मुळीच नव्हती, कारण येण्याजाण्यासाठी वेगवेगळे रस्ते होते.

प्रश्न 2.
काय ते लिहा.

1. उंच स्तंभावर फडकणारा – [ ]
2. ध्वजावरील पांढऱ्याशुभ्र पार्श्वभूमीवर एकमेकांत गुंफलेली – [ ]
3. जगभरातील क्रीडाप्रेमींचे लक्ष वेधून घेणारे – [ ]

उत्तर:

1. ऑलिंपिकच्या सामन्यांचा भलामोठा ध्वज
2. पाच रंगांची वर्तुळे
3. सर्व स्तरांवर खेळले जाणारे क्रीडासामने

प्रश्न 3.
चूक की बरोबर ते लिहा.
1. संपूर्ण जगभरातील क्रीडासामन्यांत आशियाई क्रीडासामन्यांना एक मानाचे स्थान आहे.
2. ही पाच वर्तुळे म्हणजे जगातील पाच खंड.
उत्तर:
1. चूक
2. बरोबर

कृती 3 : व्याकरण कृती

प्रश्न 1.
खालील वाक्य लेखननियमांनुसार शुद्ध करून लिहा. ऑलिपिंक सामन्यांचे ते स्वतंत्र निशान होते.
उत्तर:
ऑलिंपिक सामन्यांचे ते स्वतंत्र निशाण होते.

प्रश्न 2.
उताऱ्यातील दोन विशेषणे शोधून लिहा.
उत्तर:

1. मानाचे
2. लाल
3. पिवळा
4. निळा
5. हिरवा
6. काळा
7. वेगवेगळे
8. भलामोठा
9. पांढऱ्याशुभ्र
10. पाच
11. विशाल
12. एक

प्रश्न 3.
अचूक शब्द लिहा.
1. क्रिडासामने, क्रीडासामने, क्रीडासामणे, कीडासामने – [ ]
2. क्षितिज, क्षीतिज, क्षितीज, शितिज – [ ]
उत्तर:
1. क्रीडासामने
2. क्षितिज

प्रश्न 4.
लिंग बदला
मैत्रीण – [ ]
उत्तर:
मित्र

प्रश्न 5.
समानर्थी शब्द लिहा.

1. ठिकाण – [ ]
2. क्रीडांगण – [ ]
3. खूण – [ ]
4. नयन – [ ]

उत्तर:

1. स्थान
2. मैदान
3. निशाण
4. डोळे

प्रश्न 6.
विरुद्धार्थी शब्द लिहा.

1. अपमान × [ ]
2. पराजय × [ ]
3. बुटके × [ ]
4. विकेंद्रित × [ ]

उत्तर:

1. मान
2. जय
3. उंच
4. केंद्रित

प्रश्न 7.
उताऱ्यातील दोन अनेकवचनी शब्द शोधून लिहा.
उत्तर:

1. क्रीडासामने
2. रस्ते
3. वर्तुळे
4. डोळे

प्रश्न 8.
खालील अधोरेखित शब्दांची जात ओळखा.
तसे आमचे डोळे समोरील क्षितिजाकडे लागले.
उत्तरः
आमचे – सर्वनाम, डोळे – नाम

प्रश्न 9.
वाक्यातील काळ ओळखा.
ऑलिंपिक गावाकडे आमची मोटार भरधाव वेगाने जात होती.
उत्तर:
भूतकाळ

प्रश्न 10.
वाक्यातील काळ बदला. (वर्तमानकाळ करा)
येण्याजाण्यासाठी वेगवेगळे रस्ते होते.
उत्तरः
येण्याजाण्यासाठी वेगवेगळे रस्ते आहेत.

कृती 4 : स्वमत

प्रश्न 1.
मनुष्याच्या सर्वांगीण व्यक्तिमत्त्व विकासात क्रीडेचे महत्त्व अनन्यसाधारण असते, यावर तुमचे विचार स्पष्ट करा.
उत्तरः
क्रीडा व्यक्तिविकासांचे महत्त्वाचे साधन आहे. खेळ खेळल्याने व्यक्ती चपळ, सुदृढ व प्रवीण बनते. मैदानी खेळ जसे की, क्रिकेट, बॉस्केट बॉल, हॉकी वा कबड्डी अशा प्रकारचे विविध खेळ खेळल्याने मनुष्याचे शरीर लवचीक बनते. खेळ खेळल्याने एक प्रकारची शक्ती अंगात निर्माण होते. व्यक्तीमध्ये वक्तशीरपणा येतो. एकतेचे महत्त्व कळते. एखादया खेळात चांगल्या प्रकारचे प्रावीण्य व कौशल्य मिळविल्यास प्रसिद्धी मिळते. खेळ खेळणे म्हणजे एक प्रकारची कसरतच असते, त्यामुळे शरीराचा नियमितपणे व्यायाम होत असतो. खेळामुळे व्यक्तीच्या शारीरिक व मानसिक क्रियांचे संतुलन राखले जाते. म्हणून मनुष्याच्या सर्वांगीण व्यक्तिमत्त्व विकासात क्रीडेचे महत्त्व अनन्यसाधारण असते.

पुढील उताऱ्याच्या आधारे दिलेल्या सूचनेनुसार कृती करा:

कृती 1 : आकलन कृती

प्रश्न 1.
आकृतिबंध पूर्ण करा.
उत्तरः

खालील प्रश्नांची उत्तरे एका वाक्यात लिहा.

प्रश्न 1.
ऑलिंपिकचे ब्रीदवाक्य कशावर लिहिलेले आहे?
उत्तर:
ऑलिंपिकच्या ध्वजावर ऑलिंपिकचे ब्रीदवाक्य लिहिलेले आहे.

प्रश्न 2.
ऑलिंपिकच्या ब्रीदवाक्यातील ‘ऑल्टियस’ या शब्दाचा अर्थ काय होतो?
उत्तर:
ऑलिंपिकच्या ब्रीदवाक्यातील ‘ऑल्टियस’ या शब्दाचा अर्थ ‘उच्चता’ असा होतो.

प्रश्न 3.
ऑलिंपिक सामने म्हणजे कोणासाठी एक पर्वणीच असते?
उत्तर:
ऑलिंपिक सामने म्हणजे क्रीडापटू आणि क्रीडाशौकिनांसाठी एक पर्वणीच असते.

प्रश्न 4.
कंसातील योग्य शब्द वापरून रिकाम्या जागा भरा.
1. या ध्वजस्तंभाजवळ एक स्फूर्तिदायक …………. सतत तेवत असते. (मशाल, दगड, चिन्ह, पताका)
2. …………. सुमारे सत्तर ते ऐंशी हजार प्रेक्षक बसण्याची सोय असते. (मैदानात, तलावाजवळ, खोल्यांमध्ये, प्रेक्षागारात)
उत्तर:
1. मशाल
2. प्रेक्षागारात

प्रश्न 5.
काय ते लिहा.
1. ‘सिटियस, ऑल्टियस, फॉर्टियस’ असा संदेश देणारा
2. ध्वजस्तंभाजवळ सतत तेवत असणारी –
उत्तर:
1. ऑलिंपिकचा ध्वज
2. मशाल

कृती 2 : आकलन कृती

प्रश्न 1.
चूक की बरोबर ते लिहा.
1. जिंकण्यासाठी जास्तीत जास्त श्रम केले पाहिजेत.
2. पोहण्याच्या शर्यतीसाठी चार-पाच तलावही बांधलेले असतात.
उत्र:
1. चूक
2. बरोबर

प्रश्न 2.
ऑलिंपिक ब्रीदवाक्यातील शब्द आणि त्याचे अर्थ यांचे वर्गीकरण करा.

उत्तर:

प्रश्न 3.
आकृतिबंध पूर्ण करा.
उत्तर:

प्रश्न 4.
सहसंबंध लिहा.
कमी : जास्त :: गैरसोय : …………….
उत्तरः
सोय

कृती 3 : व्याकरण कृती

प्रश्न 1.
खालील वाक्य लेखननियमांनुसार शुद्ध करून लिहा.
या ध्वजावर ऑलीपिकचे ब्रिदवाक्य लिहिलेले आहे.
उत्तर:
या ध्वजावर ऑलिंपिकचे ब्रीदवाक्य लिहिलेले आहे.

प्रश्न 2.
उताऱ्यातील दोन नामे लिहा.
उत्तर:

1. ध्वज
2. खेळाडू
3. मशाल
4. क्रीडापटू
5. पृथ्वी
6. राष्ट्र
7. स्त्री
8. तलाव
9. प्रेक्षक
10. ब्रीदवाक्य
11. लोक
12. पर्वणी
13. संदेश

प्रश्न 3.
अचूक शब्द लिहा.
1. गतिनामता, गतिमानता, गतीमानता, गतीतानमा – [ ]
2. परवणी, पर्वणि, पर्वणी, र्पवणी – [ ]
उत्तर:
1. गतिमानता
2. पर्वणी

प्रश्न 4.
लिंग बदला
पुरुष – [ ]
उत्तर:
स्त्री

प्रश्न 5.
समानार्थी शब्द लिहा.
1. कष्ट – [ ]
2. देश – [ ]
उत्तर:
1. श्रम
2. राष्ट्र

प्रश्न 6.
विरुद्धार्थी शब्द लिहा.
कमी × [ ]
उत्तरः
जास्त

प्रश्न 7.
उताऱ्यातील दोन अनेकवचनी शब्द शोधून लिहा.
उत्तर:
1. खेळाडू
2. सामने

प्रश्न 8.
खालील अधोरेखित शब्दांच्या जाती ओळखा.
असा संदेश हा ध्वज खेळाडूंना देत असतो.
उत्तर:
ध्वज – नाम, देत असतो – क्रियापद

प्रश्न 9.
खालील वाक्यातील काळ ओळखा.
या ध्वजावर ऑलिंपिकचे ब्रीदवाक्य लिहिलेले आहे.
उत्तर:
वर्तमानकाळ

प्रश्न 10.
वाक्यातील काळ बदला. (भूतकाळ करा)
या ध्वजस्तंभाजवळ एक स्फूर्तिदायक मशाल सतत तेवत आहे.
उत्तरः
या ध्वजस्तंभाजवळ एक स्फूर्तिदायक मशाल सतत तेवत होती.

प्रश्न 11.
पर्यायी शब्द लिहा.
उत्तरः

कृती 4 : स्वमत

प्रश्न 1.
गतिमानता, उच्चता व तेजस्विता ही तीन सूत्रे खेळाडूंसाठी फार आवश्यक असतात, या कथनावर तुमचे विचार स्पष्ट करा.
उत्तरः
खेळाडू म्हटला म्हणजे तो कुशल, चपळ, प्रवीण व तरबेज असला पाहिजे. यासाठी खेळाडूला गतिमान होणे आवश्यक असते. प्रत्येक खेळाडूने आपआपल्या खेळात प्रावीण्य मिळविण्यासाठी खेळाचा जास्तीत जास्त सराव केला पाहिजे की जेणेकरून त्याच्या खेळ खेळण्याच्या गतीत वाढ होईल. खेळाडूने आपल्या खेळात कौशल्य संपादन करण्यासाठी प्रयत्नांची शिकस्त केली पाहिजे, तसेच त्याने स्वत:चे शरीर सुदृढ बनविण्यासाठी जास्तीत जास्त श्रम केले पाहिजेत. खेळाडूला नियमित व्यायाम करणे फारच गरजेचे असते जेणेकरून एक विशिष्ट प्रकारचे तेज त्याच्या शरीरात निर्माण होईल. अशा प्रकारे गतिमानता, उच्चता व तेजस्विता ही तीन सूत्रे खेळाडूंसाठी फार आवश्यक असतात.

पुढील उताऱ्याच्या आधारे दिलेल्या सूचनेनुसार कृती करा:

कृती 1 : आकलन कृती

प्रश्न 1.
आकृतिबंध पूर्ण करा.
उत्तरः

प्रश्न 2.
उत्तर लिहा.
उत्तरः

प्रश्न 3.
जोड्या जुळवा.
उत्तरः

प्रश्न 4.
आकृतिबंध पूर्ण करा.
उत्तरः

खालील प्रश्नांची उत्तरे एका वाक्यात लिहा.

प्रश्न 1.
प्रेक्षकांच्या श्रमपरिहारासाठी ‘ऑलिंपिक व्हिलेज’ येथे कोणती सोय करण्यात आली आहे ?
उत्तरः
प्रेक्षकांच्या श्रमपरिहारासाठी ‘ऑलिंपिक व्हिलेज’ येथे सुसज्ज अशी उपाहारगृहे तयार करण्यात आली आहेत.

प्रश्न 2.
‘ऑलिंपिक व्हिलेज’ वसवण्याची कल्पना कोठे मांडण्यात आली?
उत्तर:
‘ऑलिंपिक व्हिलेज’ वसवण्याची कल्पना मेलबोर्न येथे मांडण्यात आली.

प्रश्न 3.
ऑलिंपिक सामने किती वर्षांनी होतात?
उत्तर:
ऑलिंपिक सामने दर चार वर्षांनी होतात.

कंसातील योग्य शब्द वापरून रिकाम्या जागा भरा.

प्रश्न 1.
1. ‘ऑलिंपिक व्हिलेज’वसवण्याची कल्पना इ. स. … मध्ये मेलबोर्न येथे मांडण्यात आली. (1957, 1956, 1976, 1946)
2. इ.स.पूर्व ७७६ मध्ये हे सामने झाल्याची पहिली नोंद ………… देशाच्या इतिहासात सापडते. (ग्रीस, जर्मनी, ऑस्ट्रेलिया, भारत)
उत्तर:
1. 1956
2. ग्रीस

सहसंबंध लिहा.

प्रश्न 1.
विशाल : मैदान :: असंख्य : …………………
इ.स.पूर्व ७७६: सामने सुरू झाले :: इ.स.पूर्व 394: ………………….
उत्तर:
1. खोल्या
2. सामने बंद पडले

प्रश्न 2.
पुढे दिलेल्या सालातील घडलेल्या घटना लिहा.
उत्तर:

कृती 2 : आकलन कृती

प्रश्न 1.
योग्य पर्याय निवडून विधान पूर्ण करा.
इ.स.पूर्वी 394 मध्ये ऑलिंपिक सामने बंद पडले; कारण …………..
(अ) पुढे ग्रीक सत्तेचा हास झाला.
(ब) खेळाडू जखमी होतात.
(क) जागेअभावी
(ड) अंतर्गत राजकारणांमुळे
उत्तरः
इ.स.पूर्वी 394 मध्ये ऑलिंपिक सामने बंद पडले; कारण पुढे ग्रीक सत्तेचा -हास झाला.

प्रश्न 2.
कोण ते लिहा.
1. इ.स. 1956 मध्ये मेलबोर्न येथे वसवण्यात आलेले – [ ]
2. ऑलिव्ह वृक्षाच्या फांदीची माळ घालून, गौरव करण्यात येणारे – [ ]
उत्तर:
1. ऑलिंपिक व्हिलेज
2. यशस्वी खेळाडू ऑलिव्ह

प्रश्न 3.
कोष्टक पूर्ण करा.
उत्तर:

प्रश्न 4.
आकृतिबंध पूर्ण करा.
उत्तर:

प्रश्न 5.
चूक की बरोबर लिहा.
1. ‘ऑलिंपिक व्हिलेज’ वसवण्याची कल्पना इ.स. 1957 मध्ये मेलबोर्न येथे मांडण्यात आली.
2. पूर्वी ऑलिंपिक सामने पाच दिवस चालत.
उत्तर:
1. चूक
2. बरोबर

कृती 3 : व्याकरण कृती

खालील वाक्ये लेखननियमांनुसार शुद्ध करून लिहा.

प्रश्न 1.
1. पहीले ‘ऑलिंपिक विलेज’ तिथलेच.
2. पुढे ग्रीक सतेचा हास झाला.
उत्तर:
1. पहिले ‘ऑलिंपिक व्हिलेज’ तिथलेच.
2. पुढे ग्रीक सत्तेचा -हास झाला.

प्रश्न 2.
उताऱ्यातील दोन विशेषणे शोधून लिहा.
उत्तरः

1. असंख्य
2. सुसज्ज
3. विशाल
4. मोठे
5. अनेक
6. यशस्वी
7. प्रचंड

प्रश्न 3.
अचूक शब्द लिहा.
1. राहदारी, रहादारी, रहदारी, रदारी – [ ]
2. उपहारगृह, उपाहारगृह, उपाहरगृह, उपहरगृह – [ ]
उत्तर:
1. रहदारी
2. उपाहारगृह

प्रश्न 4.
समानार्थी शब्द लिहा.
1. भव्य – [ ]
2. रस्ते – [ ]
उत्तर:
1. विशाल
2. सडका

प्रश्न 5.
विरुद्धार्थी शब्द लिहा.
1. लहान ×
2. अयशस्वी ×
उत्तर:
1. मोठे
2. यशस्वी

प्रश्न 6.
उताऱ्यातील दोन अनेकवचनी शब्द शोधून लिहा.
उत्तर:

1. शहरे
2. सडका
3. लोहमार्ग
4. खेळाडू
5. खोल्या
6. इमारती
7. वसतिगृहे
8. प्रेक्षक
9. उपाहारगृहे
10. सामने

प्रश्न 7.
वाक्यातील काळ बदला. (भविष्यकाळ करा)
ऑलिंपिक सामने दर चार वर्षांनी होतात.
उत्तर:
ऑलिंपिक सामने दर चार वर्षांनी होतील.

प्रश्न 8.
पर्यायी शब्द लिहा.
उत्तर:

कृती 4 : स्वमत

प्रश्न 1.
ऑलिंपिकमध्ये यशस्वी झालेल्या भारतीय खेळाडूंचा आपल्या देशात कशा प्रकारे सन्मान केला जातो, यावर थोडक्यात तुमचे विचार लिहा.
उत्तरः
आपल्या भारत देशात ऑलिंपिकमध्ये यशस्वी झालेले अनेक खेळाडू आहेत. त्यांना ऑलिंपिक मध्ये कांस्य पदक मिळो, वा रजत पदक मिळो वा सुवर्ण पदक. संपूर्ण भारत देश त्यांचे स्वागत करण्यास सुसज्ज होतो. खेळाडू ज्या राज्यातील असतो, ते राज्य तर त्यांना सरकारी खात्यात मोठमोठ्या पदांवर नियुक्त करते. तसेच लाखो रुपयांची धनराशी देखील दिली जाते. भारत सरकार त्यांना अर्जुन पुरस्कार किंवा पद्मभूषण देऊन त्यांचा आदरसत्कार करते. भारतातील विविध संस्था आपआपल्या कुवतीनुसार त्यांचा यथोचित सत्कार करतात. देशातील सर्व राज्यांत त्यांना सन्मान दिला जातो.

पुढील उताऱ्याच्या आधारे दिलेल्या सूचनेनुसार कृती करा:

कृती 1 : आकलन कृती

प्रश्न 1.
उत्तरे लिहा.
1. इ.स. 1894 साली या देशात ‘ऑलिंपिक काँग्रेस’ भरवण्यात आली होती.
2. ऑलिंपिक सामन्यांचे पुनरुज्जीवन करणारे क्रीडातज्ज्ञ –
उत्तर:
1. फ्रान्स
2. कुबर टीन

प्रश्न 2.
उताऱ्यानुसार वाक्यांचा क्रम लावा.

1. 1896 पासून ऑलिंपिक सामने दर चार वर्षांनी वेगवेगळ्या देशांत भरवले जातात.
2. इ.स. 1894 साली फ्रान्स देशात एक ऑलिंपिक काँग्रेस भरवण्यात आली होती.
3. प्राचीन ऑलिंपिक सामन्यांप्रमाणेच यापुढे आंतरराष्ट्रीय क्रीडास्पर्धा भरवाव्यात असे ठरले.
4. कुबर टीन नावाच्या फ्रेंच क्रीडातज्ज्ञाने या काँग्रेसमध्ये ऑलिंपिक सामन्यांचे पुनरुज्जीवन केले.

उत्तर:

1. इ.स. 1894 साली फ्रान्स देशात एक ऑलिंपिक काँग्रेस भरवण्यात आली होती.
2. कुबर टीन नावाच्या फ्रेंच क्रीडातज्ज्ञाने या काँग्रेसमध्ये ऑलिंपिक सामन्यांचे पुनरुज्जीवन केले.
3. प्राचीन ऑलिंपिक सामन्यांप्रमाणेच यापुढे आंतरराष्ट्रीय क्रीडास्पर्धा भरवाव्यात असे ठरले.
4. 1896 पासून ऑलिंपिक सामने दर चार वर्षांनी वेगवेगळ्या देशांत भरवले जातात.

खालील प्रश्नांची उत्तरे एका वाक्यात लिहा.

प्रश्न 1.
कोणत्या साली आधुनिक जगाला ऑलिंपिक सामन्यांची आठवण झाली?
उत्तर:
इ.स. 1894 साली आधुनिक जगाला ऑलिंपिक सामन्यांची आठवण झाली.

प्रश्न 2.
ऑलिंपिक सामन्यांचे पुनरुज्जीवन कोणी केले?
उत्तर:
‘कुबर टीन’ नावाच्या फ्रेंच क्रीडातज्ज्ञाने ऑलिंपिक सामन्यांचे पुनरुज्जीवन केले.

कंसातील योग्य शब्द वापरून रिकाम्या जागा भरा.

प्रश्न 1.
1. ………. पासून ऑलिंपिक सामने दर चार वर्षांनी वेगवेगळ्या देशांत भरवले जातात. (1895, 1796, 1986, 1896)
2. ………… सामन्यांसाठी लागणारा खर्च फारच मोठा असतो. (अंतर्गत, विदेशी, देशी, ऑलिंपिक)
उत्तर:
1. 1896
2. ऑलिंपिक

सहसंबंध लिहा.

प्रश्न 1.
1. फ्रान्स : नाम :: अनेक :
2. वेगवेगळे : सामने :: पैसा :
उत्तर:
1. विशेषण
2. स्पर्धक देश

कृती 2 : आकलन कृती

प्रश्न 1.
योग्य पर्याय निवडून विधान पूर्ण करा.
1896 पासून ऑलिंपिक सामने ……………
(अ) दर पाच वर्षांनी वेगवेगळ्या देशांत भरवले जातात.
(ब) दर सहा वर्षांनी वेगवेगळ्या देशांत भरवले जातात.
(क) दर चार वर्षांनी वेगवेगळ्या देशांत भरवले जातात.
(ड) दर सात वर्षांनी वेगवेगळ्या देशांत भरवले जातात.
उत्तरः
1896 पासून ऑलिंपिक सामने दर चार वर्षांनी वेगवेगळ्या देशांत भरवले जातात.

प्रश्न 2.
कोण ते लिहा.

1. मैत्रीचा मंत्र सांगणारे – [ ]
2. ऑलिंपिक सामन्यांच्या व्यवस्थेसाठी नेमलेली समिती – [ ]
3. इ.स. 1894 साली ‘ऑलिंपिक काँग्रेस’ भरवण्यात आलेला देश – [ ]

उत्तर:

1. ऑलिंपिक सामने
2. ‘आंतरराष्ट्रीय ऑलिंपिक समिती’
3. फ्रान्स

प्रश्न 3.
चूक की बरोबर ते लिहा.
1. ऑलिंपिक सामन्यासांठी लागणारा सर्व पैसा स्पर्धक देश उभा करतात.
2. ऑलिंपिक सामन्यांत पुरुषांसाठी व स्त्रियांसाठी एकत्र सामने होतात.
उत्तर:
1. बरोबर
2. चूक

कृती 3 : व्याकरण कृती

प्रश्न 1.
खालील वाक्ये लेखननियमांनुसार शुद्ध करून लिहा.
1. हा सर्व पैशा स्पधर्क देश उभा करतात.
2. त्या काँगेसला अनेक राष्ट्रांचे प्रतिनीधी हजर होते.
उत्तर:
1. हा सर्व पैसा स्पर्धक देश उभा करतात.
2. त्या काँग्रेसला अनेक राष्ट्रांचे प्रतिनिधी हजर होते.

प्रश्न 2.
उताऱ्यातील दोन नामे शोधून लिहा.
उत्तर:

1. फ्रान्स
2. ऑलिंपिक
3. काँग्रेस
4. कुबर टीन
5. क्रीडातज्ज्ञ
6. देश
7. खेळ
8. पुरुष
9. स्त्रिया

प्रश्न 3.
अचूक शब्द लिहा.
1. मित्रत्वाची, मीत्रत्वाची, मित्रत्वाचि, मितरत्वाचि
2. आंतराष्ट्रीय, आंतरराष्ट्रीय, आंतरराष्ट्रिय, आंतराष्ट्रिय
उत्तर:
1. मित्रत्वाची
2. आंतरराष्ट्रीय

प्रश्न 4.
समानार्थी शब्द लिहा.

1. स्मरण – [ ]
2. उपस्थित – [ ]
3. ताकद – [ ]
4. दोस्ती – [ ]

उत्तर:

1. आठवण
2. हजर
3. बल
4. मैत्री

प्रश्न 5.
विरुद्धार्थी शब्द लिहा.

1. प्राचीन ×
2. गैरहजर ×
3. जमा ×
4. दुश्मनी ×

उत्तर:

1. आधुनिक
2. हजर
3. खर्च
4. मैत्री

प्रश्न 6.
उताऱ्यातील दोन अनेकवचनी शब्द शोधून लिहा.
उत्तर:

1. सामने
2. प्रतिनिधी
3. देश

प्रश्न 7.
तक्ता पूर्ण करा.
उत्तर:

प्रश्न 8.
तक्ता पूर्ण करा.
उत्तर:

प्रश्न 9.
वाक्यातील काळ ओळखा.
1. त्या वर्षी फ्रान्स देशात एक ‘ऑलिंपिक काँग्रेस’ भरवण्यात आली होती.
2. या सामन्यांत निरनिराळ्या एकवीस खेळांची तरतूद आहे.
उत्तर:
1. भूतकाळ
2. वर्तमानकाळ

कृती 4 : स्वमत

प्रश्न 1.
‘ऑलिंपिक खेळांची वैशिष्ट्ये स्पष्ट करा.
उत्तरः
‘ऑलिंपिक’ हा खेळ दर 4 वर्षांनी खेळला जातो. या खेळात संपूर्ण जग सहभागी होते. प्रत्येक देशातील खेळाडू स्पर्धक म्हणून ऑलिंपिकमध्ये सहभागी होतात. प्रत्येक देशाचे अन्य देशांशी मैत्रीचे व जिव्हाळ्याचे संबंध निर्माण व्हावेत, म्हणून या क्रीडास्पर्धा भरविल्या जातात. स्त्री व पुरुष यांना या खेळात समान संधी दिली जाते. येथे कोणत्याही प्रकारचा भेदभाव नसतो. संपूर्ण जगात प्रेम, आपुलकी, जिव्हाळा, समता, सद्भावना, शिस्त, ऐक्य व मैत्री वाढीस लागावी हाच या स्पर्धेचा प्रमुख उद्देश असतो. संपूर्ण विश्व हे एक कुटुंबच आहे म्हणून एकमेकांशी बंधुभावाने वागले पाहिजे, अशी ही स्पर्धा आपणांस प्रेरणा देते.

पुढील उताऱ्याच्या आधारे दिलेल्या सूचनेनुसार कृती कराः

कृती 1 : आकलन कृती

प्रश्न 1.
आकृतिबंध पूर्ण करा.
उत्तरः

प्रश्न 2.
उत्तरे लिहा.
1. सर्वांना समान संधी मिळणारे क्षेत्र –
2. मानवी रेल्वे इंजिन’ अशी ख्याती मिळवलेला – ___
उत्तर:
1. क्रीडा
2. एमिल झेटोपेक

प्रश्न 3.
आकृतिबंध पूर्ण करा.
उत्तर:

खालील प्रश्नांची उत्तरे एका वाक्यात लिहा.

प्रश्न 1.
हेलसिंकी येथे ऑलिंपिक सामने कोणत्या साली झाले होते?
उत्तरः
1952 साली हेलसिंकी येथे ऑलिंपिक सामने झाले होते.

प्रश्न 2.
झेटोपेकने कोणत्या नावाने ख्याती मिळविली होती?
उत्तरः
झेटोपेकने ‘मानवी रेल्वे इंजिन’ या नावाने ख्याती मिळविली.

कंसातील योग्य शब्द वापरून रिकाम्या जागा भरा.

प्रश्न 1.
1. ……….”वर्ण, त्याचा देश हे सर्व विसरून साऱ्या जगाने त्याची प्रशंसा केली. (ध्यानचंदचा, कुबरचा, ओवेन्सचा, झेटोपेकचा)
2. एमिल झेटोपेक हा ……….. खेळाडू. (बर्लिनचा, अमेरिकेचा, भारताचा, झेकोस्लोव्हाकियाचा)
उत्तर:
1. ओवेन्सचा
2. झेकोस्लोव्हाकियाचा

प्रश्न 2.
सहसंबंध लिहा.
1. 1936: बर्लिन :: 1952 : ……………….
2. समान : संधीः: नवे :
उत्तर:
1. हेलसिंकी
2. उच्चांक

प्रश्न 3.
शब्दसमूहासाठी एक शब्द चौकटीत लिहा.
उत्तर:
शिल्प तयार करणारा – [शिल्पकार]

प्रश्न 4.
पुढील खेळाडूंचे त्यांच्या देशांनुसार वर्गीकरण करा.
(जेसी ओवेन्स, अमेरिका, एमिल झेटोपेक, झेकोस्लोव्हाकिया)
उत्तर:

आकलन कृती

प्रश्न 1.
योग्य पर्याय निवडून विधान पूर्ण करा.
क्रीडेच्या क्षेत्रात सर्वांना समान संधी मिळते; कारण …………………
(अ) क्रीडेच्या क्षेत्रात जातिभेद, धर्मभेद, वर्णभेद होतो.
(ब) क्रीडेच्या क्षेत्रात पंच असतात.
(क) क्रीडेच्या क्षेत्रात जातिभेद नाही, धर्मभेद नाही की वर्णभेद नाही.
(ड) क्रीडेच्या क्षेत्रात न्याय असतो.
उत्तरः
क्रीडेच्या क्षेत्रात सर्वांना समान संधी मिळते; कारण क्रीडेच्या क्षेत्रात जातिभेद नाही, धर्मभेद नाही की वर्णभेद नाही.

प्रश्न 2.
कोण ते लिहा.
1. अमेरिकेतील वंशाने आफ्रिकी असणारा खेळाडू – [ ]
2. 1936 मध्ये ऑलिंपिक सामने भरलेले ठिकाण – [ ]
उत्तर:
1. जेसी ओवेन्स
2. बर्लिन

प्रश्न 3.
आकृतिबंध पूर्ण करा.
उत्तर:

प्रश्न 4.
चूक की बरोबर लिहा.
1. क्रीडेच्या क्षेत्रात जातिभेद, धर्मभेद, वर्णभेद केला जातो.
2. जेसी ओवेन्स हा झेकोस्लोव्हाकियाचा खेळाडू.
उत्तर:
1. चूक
2. चूक

कृती 3 : व्याकरण कृती

प्रश्न 1.
खालील वाक्य लेखननियमांनुसार शुद्ध करून लिहा.
अमेरीकेच्या यशाचा तो मोठा शिप्लकार ठरला.
उत्तर:
अमेरिकेच्या यशाचा तो मोठा शिल्पकार ठरला.

प्रश्न 2.
उताऱ्यातील दोन विशेषणे शोधून लिहा.
उत्तर:

1. मोठा
2. साऱ्या
3. नवा
4. एक

प्रश्न 3.
अचूक शब्द लिहा.
1. क्रिडेच्या, क्रीडेच्या, कीरडेच्या, किड्रेच्या
2. अजिक्यपदे, अंजिक्यपदे, अजिंक्यपदे, अजीक्यपदे
उत्तर:
1. क्रीडेच्या
2. अजिंक्यपदे

प्रश्न 4.
खालील वाक्यांतील अधोरेखित शब्दांचे समान अर्थ लिहून वाक्य पुन्हा लिहा.
1. साऱ्या जगाने ओवेन्सची स्तुती केली.
2. क्रीडेच्या विभागात जातिभेद नाही.
उत्तर:
1. साऱ्या जगाने ओवेन्सची प्रशंसा केली.
2. क्रीडेच्या क्षेत्रात जातिभेद नाही.

प्रश्न 5.
विरुद्धार्थी शब्द लिहा.

1. असमान ×
2. जुने ×
3. लहान ×
4. निंदा ×
5. अनादर ×

उत्तर:

1. समान
2. नवे
3. मोठा
4. कौतुक
5. आदर

प्रश्न 6.
उताऱ्यातील दोन अनेकवचनी शब्द शोधून लिहा.
उत्तर:
1. नवे
2. देश

प्रश्न 7.
तक्ता पूर्ण करा.
उत्तर:

प्रश्न 8.
तक्ता पूर्ण करा.
उत्तर:

प्रश्न 9.
वाक्प्रचाराचा अर्थ लिहून वाक्यात उपयोग करा.
ख्याती मिळविणे
उत्तर:
अर्थ: प्रसिद्धी मिळविणे.
वाक्य: सायना नेहवालने बॅडमिंटन या खेळामध्ये ख्याती मिळविली.

प्रश्न 10.
वाक्यातील काळ ओळखा.
1. येथे सर्वांना समान संधी मिळते.
2. क्रीडेच्या क्षेत्रात जातिभेद नाही, धर्मभेद नाही की वर्णभेद नाही.
उत्तर:
1. वर्तमानकाळ
2. वर्तमानकाळ

प्रश्न 11.
पर्यायी शब्द लिहा.
उत्तर:

कृती 4 : स्वमत

प्रश्न 1.
क्रीडेच्या क्षेत्रात जातिभेद, धर्मभेद व वर्णाला थारा नसतो. सर्वांना समान संधी हेच क्रीडेचे ब्रीदवाक्य असते, त्यावर तुमचे विचार स्पष्ट करा.
उत्तरः
क्रीडा सर्वांसाठी मुक्त असते. क्रीडेचे सर्वांना स्वातंत्र्य असते. तेथे जातिभेद, धर्मभेद व वर्णभेदाला मुळीच स्थान नसते. सर्वांना समान संधी उपलब्ध करून देणे हेच क्रीडेचे ब्रीदवाक्य असते. प्रत्येक खेळाडू हा आपआपल्या क्षमतेनुसार व कुवतीनुसार खेळात पारंगत होत असतो व त्यावरूनच त्याची श्रेणी ठरविली जाते. आपल्या भारत देशात विविध प्रांतातील विविध धर्माचे खेळाडू आहेत. आज आपल्या देशात क्रिकेट संघ, हॉकी संघ, कबड्डी संघ अशा विविध खेळांचे संघ आहेत. या संघातून खेळणारे खेळाडू हे भारताच्या विविध प्रांतातील आहेत. तेथे जात, पात, भाषा, धर्म किंवा राज्य यांना मुळीच स्थान नाही.

पुढील उताऱ्याच्या आधारे दिलेल्या सूचनेनुसार कृती करा:

कृती 1 : आकलन कृती

प्रश्न 1.
आकृतिबंध पूर्ण करा.
उत्तरः

प्रश्न 2.
जोड्या जुळवा.

उत्तरः

खालील प्रश्नांची उत्तरे एका वाक्यात लिहा.

प्रश्न 1.
अबेबे बिकिला हा कुठला खेळाडू होता?
उत्तरः
अबेबे बिकिला हा आफ्रिकेतील इथियोपियाचा खेळाडू होता.

प्रश्न 2.
ध्वजावरील पाच वर्तुळे जगाला कोणता संदेश देत असतात?
उत्तर:
ध्वजावरील पाच वर्तुळे समतेचा व विश्वबंधुत्वाचा संदेश जगाला देत असतात.

कंसातील योग्य शब्द वापरून रिकाम्या जागा भरा.

प्रश्न 1.
1. …………. या स्त्री खेळाडूने तर 1948 साली ऑलिंपिकचे मैदान दणाणून सोडले. (अॅनी बँकर्स, फनी बँकर्स, फॅनी बेकर्स, मॅनी बॅकर्स)
2. भारताने …………….. स्पर्धेत अनेक वर्षे अजिंक्यपद टिकवले.
(कबड्डीच्या, नेमबाजीच्या, हॉकीच्या, धावण्याच्या)
उत्तर:
1. फॅनी बँकर्स
2. हॉकीच्या

सहसंबंध लिहा.

प्रश्न 1.
1. अबेबे बिकिला : लांब पल्ल्याची शर्यत :: फॅनी बँकर्स : …………………
2. प्रयत्नवादाचा संदेश देणारा : ध्वजः: क्षुद्र विचारांचा अहंकार घालवणारी : ………………….
उत्तर:
1. 100 व 200 मीटर शर्यत
2. ज्योत

प्रश्न 2.
पुढील खेळाडूंशी संबंधित असणारे खेळ लिहा.
उत्तर:

कृती 2 : आकलन कृती

प्रश्न 1.
योग्य पर्याय निवडून विधान पूर्ण करा.
त्या ध्वजावरील पाच खंडांची पाच वर्तुळे ………………..
(अ) समतेचा व विश्वबंधुत्वाचा संदेश खेळाडूंना देत असतात.
(ब) असमतेचा व विश्वबंधुत्वाचा संदेश खेळाडूंना देत असतात.
(क) समतेचा व शत्रुत्वाचा संदेश खेळाडूंना देत असतात.
(ड) समतेचा व विश्वबंधुत्वाचा संदेश जगाला देत असतात.
उत्तर:
त्या ध्वजावरील पाच खंडांची पाच वर्तुळे समतेचा व विश्वबंधुत्वाचा संदेश जगाला देत असतात.

प्रश्न 2.
कोण ते लिहा.
1. अनवाणी पायाने लांब पल्ल्याची शर्यत जिंकणारा – [ ]
2. सुप्रसिद्ध भारतीय हॉकी खेळाडू. – [ ]
उत्तर:
1. अबेबे बिकिला
2. ध्यानचंद

प्रश्न 3.
आकृतिबंध पूर्ण करा.
उत्तर:

चूक की बरोबर लिहा.

प्रश्न 1.
1. त्या ध्वजावरील पाच खंडांची सहा वर्तुळे समतेचा :
विश्वबंधुत्वाचा संदेश जगाला देत असतात.
2. अबेबे बिकिला हा आशियातील खेळाडू होता.
उत्तर:
1. चूक
2. चूक

कृती 3: व्याकरण कती

प्रश्न 1.
खालील वाक्य लेखननियमांनुसार शुद्ध करून लिहा.
भारताने हॉकिच्या स्पर्धेत अनेक वर्षे अजिक्यपद टिकवले.
उत्तर:
भारताने हॉकीच्या स्पर्धेत अनेक वर्षे अजिंक्यपद टिकवले.

प्रश्न 2.
उताऱ्यातील दोन सर्वनामे शोधून लिहा.
उत्तर:
1. त्याने
2. यांचे

प्रश्न 3.
अचूक शब्द लिहा.
1. वतुळे, तुळे, वर्तुळे, वरतुळे
2. प्रयन्तवादाचा, प्रयत्नवादाचा, प्रत्यनवादाचा, प्रयत्नवदाचा
उत्तर:
1. वर्तुळे
2. प्रयत्नवादाचा

प्रश्न 4.
समानार्थी शब्द लिहा.

1. क्रीडांगण- [ ]
2. निरोप – [ ]
3. झेंडा – [ ]
4. क्रीडापटू – [ ]

उत्तर:

1. मैदान
2. संदेश
3. ध्वज
4. खेळाडू

प्रश्न 5.
विरुद्धार्थी शब्द लिहा.

1. हाताने ×
2. उजेड ×
3. कुप्रसिद्ध ×

उत्तर:

1. पायाने
2. अंधकार
3. सुप्रसिद्ध

प्रश्न 6.
उताऱ्यातील दोन अनेकवचनी शब्द शोधून लिहा.
उत्तरः

1. वर्षे
2. खेळाडू
3. वर्तुळे

प्रश्न 7.
तकता पूर्ण करा.
उत्तरः

प्रश्न 8.
तकता पूर्ण करा.
उत्तरः

प्रश्न 9.
खालील दिलेल्या वाक्याचा काळ ओळखा.
सुप्रसिद्ध भारतीय हॉकी खेळाडू ध्यानचंद यांचे नाव कित्येक वर्षे जगात सर्वांच्या जिभेवर नाचत होते.
उत्तरः
भूतकाळ

कृती 4 : स्वमत

प्रश्न 1.
‘ऑलिंपिक वर्तुळांचा गोफ’ यातून तुम्हांला कोणती प्रेरणा मिळतो, हे थोडक्यात सांगा.
उत्तरः
पाच वर्तुळे एकमेकांत गुंफून त्याचा गोफ बनवून ती ऑलिंपिकच्याध्वजावर रेखाटली आहेत. ही पाचवर्तुळे जगातील पाच खंडांचे प्रतीक आहेत. जणू हे पाच खंड एकमेकांशी मैत्रीने व प्रेमाने जुळले गेलेले आहेत असे या गोफातून दिसून येते. ही वर्तुळे जणू आपणास समतेचा, ऐक्याचा व विश्वबंधुत्वाचा संदेश देतात. जगातील सर्व लोकांशी प्रेमाने, समतेने, सद्भावनेने व आपुलकीने वागण्यास शिकवितात. संपूर्ण विश्व हे आपले कुटुंबच आहे, असे जणू आपणास सांगतात. या पाच वर्तुळांच्या जवळच तेवत असणारी ज्योत आपल्या हृदयातून क्षुद्र विचारांचा अंधकार मिटविण्यास स्वयंसिद्ध होते.

ऑलिंपिक वर्तुळांचा गोफ Summary in Marathi

लेखकाचा परिचय:

कालावधी: 1929-2015
प्रसिद्ध लेखक, विकेट सामन्यांचे समालोचक, ‘पहिले शतक’, ‘कुमारांचे खेळ’, ‘क्रिकेटमधील नवलका’ इत्यादी

प्रस्तावना:

आलपिक वर्तुळाचा गोफ हा पाठ लेखक बाळ ज. पडित’ यांनी लिहिला आहे. या पाठात ऑलिपिक सामन्यांची सुरुवात कारको झाली ?, हे सामने भरवण्यामागील उद्दिष्टे कोणती?, ऑलिपिक वर्तुळांचा अर्थ काय? या सर्वांचा आढावा प्रस्तुत पाठातून लेखकांनी घेतला आहे. प्रस्तुत पाठातून जागतिक ऑलिंपिक क्रीडास्पर्धाविषयीची माहिती दिली आहे.

Olympic Vartulancha Goph is written by writer Bal J. Pandit. This write-up answers many questions like how and why Olympic matches started? What were the motives to organise these matches? What do the famous Olympic Circles signify? etc. This write-up also renders useful information about International Olympic Sports competitions.

शब्दार्थ:

1. गोफ – एकात एक अडकवलेल्या कड्या (chain)
2. वर्तुळ – गोल (round, circle)
3. सामने – स्पर्धा, स्पर्धात्मक खेळ (tournaments matches)
4. समालोचक – सामन्यांचे धावते वर्णन करणारा व्यक्ती (commentator)
5. शतक – शंभर ही संख्या (a century)
6. मनुष्य – मानव, माणूस (human being)
7. सर्वांगीण – सर्व अंगांनी परिपूर्ण (all round)
8. व्यक्तिमत्त्व – व्यक्तित्व (personality)
9. अनन्यसाधारण – अलौकिक, असामान्य (remarkable, unique)
10. स्तर – पातळी, घर (layer, grade, level)
11. रसिक – गुणग्राहक (alover of good things)
12. उद्दिष्ट – उद्देश, हेतू, प्रयोजन (purpose, object, intention)
13. लक्ष – अवधान (attention)
14. केंद्रित – एकवटलेले (centered)
15. पारंगत – निष्णात, प्रवीण (well-versed, skilled, proficient)
16. मानकरी – आदरणीय व्यक्ती (person deserving honour and respect)
17. धीरगंभीर – शांत परंतु ठाम निश्चय असलेला (serious)
18. खांब (a pillar, a column)
19. ध्वज – झेंडा, निशाण (a flag)
20. मुक्त, मोकळा (independent, free)
21. शुभ्रधवल – सफेद (white)
22. पार्श्वभूमी – मागील बाजू (backround)
23. गुंफणे – माळेत एकत्र ओवणे (to string together)
24. खंड – मोठा विस्तृत भूप्रदेश (a continent)
25. विशाल – मोठा, विस्तृत (great, vast, large)
26. अंतराळ – आकाश, अवकाश (the sky, the space)
27. ब्रीदवाक्य – घोषवाक्य (aslogan)
28. गतिमान – गतियुक्त (moving, dynamic)
29. उच्चता – वरचा दर्जा, श्रेष्ठत्व (excellence)
30. तेजस्विता – चकचकीतपणा (brightness, brilliance, glorious)
31. स्फूर्तिदायक – प्रेरणादायक (inspirational)
32. मशाल – दिवटी (a torch)
33. तेवत – जळत (lit)
34. पर्वणीय – (येथे अर्थ) सणाचा दिवस (a festival)
35. खेळाडू – खेळातील एक गडी (a player)
36. पोहणे – तरणे (to swim)
37. तलाव – तळे, जलाशय (a tank)
38. प्रचंड – फार मोठा, अवाढव्य (huge, massive)
39. प्रेक्षक – पाहणारा (a spectator)
40. वसतिगृह – भोजन निवास गृह (hostel)
41. उपाहार गृह – restaurant
42. नोंद – टाचण (an entry)
43. गौरव – सन्मान (respect, honour)
44. भेदभाव – परकेपणाची भावना (discrimination)
45. हास – नाश, अवनती (ruin, decline)
46. प्रतिनिधी – मुखत्यार (representative)
47. क्रीडातज्ज्ञ – खेळ तज्ज्ञ (sports expert)
48. पुनरुज्जीवन – दुसरा जन्म (rebirth, reincarnation)
49. शरीरसंपदा – शरीरातील जोम (physical strength)
50. स्पर्धा – चढाओढ (competition)
51. आंतरराष्ट्रीय – राष्ट्रा-राष्ट्रांतील (international)
52. सद्भावना – चांगला विचार (goodness, goodwill)
53. विश्वबंधुत्व – universalism
54. ऐक्य – एकजूट, एकोपा (unity)
55. तरतूद – तजवीज, व्यवस्था (arrangement, preparation)
56. स्पर्धक – आव्हान देणारा (competitor)
57. वर्णभेद – वर्णावरून श्रेष्ठ-कनिष्ठ ठरवणे (racial discrimination)
58. संधी – मौका (chance)
59. वंश – कुल, कुटुंब (race, family)
60. ख्याती – प्रसिद्धी, कीर्ती, थोरवी (reputation)
61. अजिंक्य – जिंकता येण्यास कठीण (invincible)
62. पराक्रम – शौर्य, प्रताप (bravery)

टिपा:

1. मेलबोर्न – ऑस्ट्रेलियाच्या व्हिक्टोरिया राज्यातील सर्वात जास्त लोकसंख्या असलेले शहर

2. ग्रीस – दक्षिणपूर्व युरोपमधील एजियन आणि आयोनियन समुद्रातील हजारो द्वीपसमुहांचा देश. आकारमानाच्या दृष्टीने जगातील 97 व्या क्रमांकाचा देश. याची राजधानी ‘अथेन्स’ ही आहे.

3. ऑलिव्ह – भूमध्य खोऱ्यात आढळणारी वृक्षाची लहान जमात. त्याच्या ऑलिव्ह फळांपासून मिळणाऱ्या ऑलिव्ह तेलासाठी हे वृक्ष प्रसिद्ध आहे.

4. फ्रान्स – पश्चिम युरोपमधील एक देश. पॅरिस हे याच्या |
राजधानीचे शहर आहे.

5. मॅरेथॉन – लांब पल्ल्याच्या धावण्याच्या शर्यती.

6. कुबर टीन – हे एक फ्रेंच शिक्षक व इतिहासकार होते. आणि आंतरराष्ट्रीय ऑलिम्पिक समितीचे संस्थापक होते. त्यांना आधुनिक ऑलिंपिक खेळांचे जनक मानले जाते.

7. जेसी ओवेन्स – (1913-1980) यांचा जन्म 12 सप्टेंबर 1913 रोजी अलबामा येथे झाला.

8. बर्लिन – जर्मनीच्या राजधानीचे शहर

9. एमिल झेटोपेक – (1912-2000), 1952 च्या हेलसिंकीतील उन्हाळी ऑलिंपिकमध्ये तीन प्रकारचे सुवर्ण पदक जिंकणारा झेकोस्लोव्हाकियाचा खेळाडू.

10. इथियोपिया – ग्रेट रिफ्ट व्हॅलीद्वारे विभाजित झालेला आफ्रिका खंडातील देश, प्राचीन संस्कृतीचे ठिकाण.

11. फॅनी बँकर्स – (1918-2004), ही एक डच खेळाडू होती. वयाच्या 30 व्या वर्षी दोन मुलांची माता असताना तिने 1948 उन्हाळी ऑलिंपिकमध्ये चार सुवर्ण पदके जिंकली.

12. ध्यानचंद – (1905-1979) प्रसिद्ध भारतीय हॉकीपटू. यांचा जन्मदिवस ‘राष्ट्रीय क्रीडादिन’ म्हणून साजरा केला जातो.

13. अबेबे बिकिला – (1932-1973), 1960 उन्हाळी ऑ लिंपिकमध्ये त्याने अनवाणी पायाने शर्यत जिंकून जागतिक विक्रम नोंदविला

वाक्प्रचार:

1. लक्ष वेधून घेणे – आकषून घेणे
2. पारंगत होणे – निपुण होणे
3. साक्ष देणे – ग्वाही देणे
4. शिकस्त करणे – कठोर मेहनत करणे
5. गौरव करणे – सत्कार करणे, सन्मान करणे
6. हास होणे – नाश पावणे
7. पुनरुज्जीवन करणे – नव्याने निर्माण करणे
8. ख्याती मिळविणे – प्रसिद्धी मिळविणे
9. दणाणून सोडणे – गाजवणे

Balbharti Maharashtra State Board Class 9 Marathi Solutions Aksharbharati Chapter 12.1 व्हेनिस Notes, Textbook Exercise Important Questions and Answers.

Maharashtra State Board Class 9 Marathi Aksharbharati Solutions Chapter 12.1 व्हेनिस (स्थूलवाचन)

Marathi Aksharbharati Std 9 Digest Chapter 12.1 व्हेनिस Textbook Questions and Answers‌‌

1.‌ ‌टिपा‌ ‌लिहा.

प्रश्न‌ ‌1.‌ ‌
टिपा‌ ‌लिहा.‌ ‌
1.‌ ‌ग्रँड‌ ‌कॅनॉल‌ ‌
2. व्हेनिसच्या‌ ‌स्टेशन‌ ‌बाहेरचा‌ ‌परिसर‌ ‌
उत्तर:‌
‌1.‌ ‌ग्रँड‌ ‌कॅनॉल‌:‌
व्हेनिस‌ ‌स्टेशनच्या‌ ‌बाहेर‌ ‌रस्त्याऐवजी‌ ‌एखादया‌ ‌विस्तीर्ण‌ ‌नदीसारखा‌ ‌प्रचंड‌ ‌कालवा‌ ‌दिसतो.‌ ‌त्यालाच‌ ‌’ग्रँड‌ ‌कॅनॉल’‌ ‌म्हणतात.‌ ‌त्यात‌ ‌अनेक‌ ‌पॉटर‌ ‌टॅक्सी‌ ‌म्हणजे‌ ‌लहान‌ ‌मोटार‌ ‌लाँचीस‌ ‌आणि‌ ‌मोठ्या‌ ‌यांत्रिक‌ ‌नावा‌ ‌उभ्या‌ ‌असतात.‌ ‌प्रवासी‌ ‌पोटात‌ ‌घेऊन‌ ‌या‌ ‌नावा‌ ‌उत्साहाने‌ ‌याच‌ ‌कॅनॉलवर‌ ‌ये-जा‌ ‌करत‌ ‌असतात.‌ ‌प्रेमात‌ ‌पडलेल्या‌ ‌युगुलांना‌ ‌विजेच्या‌ ‌वेगाने‌ ‌सुसाट‌ ‌घेऊन‌ ‌जाणाऱ्या‌ ‌मोटर‌ ‌लाँचेसपर्यंत‌ ‌वेगाच्या‌ ‌अनेक‌ ‌प्रकारच्या‌ ‌नावा‌ ‌या‌ ‌ग्रँड‌ ‌कॅनॉलवर‌ ‌प्रवास‌ ‌करत‌ ‌असतात.‌ ‌

या‌ ‌कॅनॉलच्या‌ ‌पाण्यात‌ ‌नेहमीच‌ ‌तारुण्य‌ ‌सळसळताना‌ ‌दिसते.‌ ‌या‌ ‌ग्रँड‌ ‌कॅनॉलच्या‌ ‌किनाऱ्यावर‌ ‌खुा‌ ‌टाकलेल्या‌ ‌दिसतात.‌ ‌या‌ ‌चार‌ ‌खुर्त्यांच्यामध्ये‌ ‌टेबल‌ ‌आणि‌ ‌त्यावर‌ ‌रंगीबेरंगी‌ ‌प्रचंड‌ ‌छत्री‌ ‌ठेवलेली‌ ‌आढळते.‌ ‌या‌ ‌खुर्त्यांवर‌ ‌बसून‌ ‌बिअर‌ ‌किंवा‌ ‌कॉफी‌ ‌घेत‌ ‌पाण्यातून‌ ‌प्रवास‌ ‌करणाऱ्या‌ ‌नावांकडे‌ ‌पाहणे‌ ‌सगळ्यांना‌ ‌मनापासून‌ ‌आवडते.‌ ‌

2. व्हेनिसच्या‌ ‌स्टेशन‌ ‌बाहेरचा‌ ‌परिसरः‌‌
‘व्हेनिस’‌ ‌स्टेशनच्या‌ ‌बाहेर‌ ‌रस्ता‌ ‌नाहीच.‌ ‌एखादया‌ ‌विस्तीर्ण‌ ‌नदीसारखा‌ ‌पसरलेला‌ ‌एक‌ ‌प्रचंड‌ ‌कालवा‌ ‌आहे.‌ ‌त्यालाच‌ ‌’ग्रँड‌ ‌कॅनॉल’‌ ‌म्हणतात.‌ ‌लेखक‌ ‌तेथे‌ ‌पोहोचला‌ ‌तेव्हा‌ ‌या‌ ‌कॅनॉलमध्ये‌ ‌अनेक‌ ‌पॉटर‌ ‌टॅक्सी‌ ‌म्हणजे‌ ‌लहान‌ ‌मोटर‌ ‌लाँचीस‌ ‌आणि‌ ‌मोठ्या‌ ‌यांत्रिक‌ ‌नावा‌ ‌उभ्या‌ ‌होत्या.‌ ‌’व्हेनिझिया-व्हेनिझिया,‌ ‌पियाझापियाझा’‌ ‌असा‌ ‌यांचा‌ ‌पुकार‌ ‌चालला‌ ‌होता.‌ ‌टॅक्सीपेक्षा‌ ‌बस‌ ‌स्वस्त‌ ‌पडणार‌ ‌त्यामुळे‌ ‌इतर‌ ‌अनेक‌ ‌प्रवाशांप्रमाणे‌ ‌मोठ्या‌ ‌बोटीचे‌ ‌तिकीट‌ ‌घेऊन‌ ‌लेखक‌ ‌बोटीत‌ ‌बसला.‌ ‌दोनएकशे‌ ‌प्रवासी‌ ‌पोटात‌‌ घेऊन‌ ‌नाव‌ ‌जोरात‌ ‌पुढे‌ ‌निघाली‌ ‌होती.‌ ‌

2. ‌खालील‌ ‌मुद्द्यांच्या‌ ‌आधारे‌ ‌व्हेनिसचे‌ ‌वर्णन‌ ‌लिहा.‌ ‌

प्रश्न‌ ‌1.‌
‌खालील‌ ‌मुद्द्यांच्या‌ ‌आधारे‌ ‌व्हेनिसचे‌ ‌वर्णन‌ ‌लिहा.‌ ‌
(अ)‌ ‌व्हेनिस‌ ‌म्हणजे‌ ‌अफाट‌ ‌जलदर्शन‌‌ [ ]
(ब)‌ ‌व्हेनिस‌ ‌म्हणजे‌ ‌अवर्णनीय‌ ‌शहर‌ ‌[ ]
उत्तरः‌ ‌
व्हेनिस‌ ‌म्हणजे‌ ‌केवळ‌ ‌कालव्यांचेच‌ ‌नव्हे‌ ‌तर‌ ‌कालव्यातही‌‌ तरंगणारे‌ ‌शहर‌ ‌आहे.‌ ‌या‌ ‌शहरात‌ ‌एकही‌ ‌मोटार‌ ‌नाही‌ ‌कारणया‌ ‌शहरात‌ ‌खऱ्या‌ ‌अर्थाने‌ ‌रस्तेच‌ ‌नाहीत.‌ ‌इथे‌ ‌जिकडे‌ ‌तिकडे‌ ‌पाणरस्तेच‌ ‌आहेत.‌ ‌या‌ ‌पाणरस्त्यांवरच‌ ‌अनेक‌ ‌छोट्या-मोठ्या‌ ‌नावा‌ ‌उत्साही‌ ‌प्रवाशांना‌ ‌घेऊन‌ ‌ये-जा‌ ‌करत‌ ‌असतात.‌ ‌व्हेनिसचे‌ ‌रस्ते‌ ‌म्हणजे‌ ‌पाणरस्ते‌ ‌असतात‌ ‌याची‌ ‌कल्पना‌ ‌नसलेला‌ ‌एक‌ ‌मुनीम‌ ‌एकदा‌ ‌लंडनहून‌ ‌व्हेनिसला‌ ‌विमानाने‌ ‌आला.‌ ‌रस्त्यावर‌ ‌सगळीकडे‌ ‌पाणीच‌ ‌पाणी‌ ‌झालेले‌ ‌पाहून‌ ‌त्याने‌ ‌आपल्या‌ ‌मालकाला‌ ‌तार‌ ‌केली,‌ ‌“व्हेनिसमध्ये‌ ‌पूर‌ ‌आला‌ ‌आहे.‌ ‌सगळे‌ ‌रस्ते‌ ‌पाण्यानं‌ ‌तुडुंब‌ ‌भरले‌ ‌आहेत.‌ ‌

परत‌ ‌येऊ‌ ‌की‌ ‌पूर‌ ‌ओसरेपर्यंत‌ ‌वाट‌ ‌पाहू‌ ‌ते‌ ‌कळवा!”‌ ‌जिकडे‌ ‌पाहावे‌ ‌तिकडे‌ ‌पाणी‌ ‌आणि‌ ‌पाणीच‌ ‌दिसते.‌ ‌व्हेनिस‌ ‌म्हणजे‌ ‌खऱ्या‌ ‌अर्थाने‌ ‌अफाट‌ ‌जलदर्शन‌ ‌आहे.‌ ‌अशा‌ ‌या‌ ‌व्हेनिसच्या‌ ‌हवेत‌ ‌गारवा‌ ‌असतो.‌ ‌इथल्या‌ ‌वाऱ्यात‌ ‌उत्साही‌ ‌आणि‌ ‌मनात‌ ‌संगीत‌ ‌नाचत‌ ‌असते.‌ ‌तसेच‌ ‌सभोवार‌ ‌पसरलेल्या‌ ‌पाण्यात‌ ‌तारुण्याची‌ ‌सळसळ‌ ‌दिसते.‌ ‌त्यामुळेच‌ ‌व्हेनिस‌ ‌शहराचे‌ ‌वर्णन‌‌ शब्दांत‌ ‌करताच‌ ‌येत‌ ‌नाही.‌ ‌

3.‌ ‌खालील‌ ‌संकल्पना‌ ‌स्पष्ट‌ ‌करा.‌

प्रश्न‌ ‌1.‌
‌व्हेनिस‌ ‌म्हणजे‌ ‌हिया-माणकांच्या‌ ‌ढिगासारखा‌ ‌बेटांचा‌‌ पुंजका‌ ‌………….‌
‌उत्तरः‌
‌व्हेनिस‌ ‌या‌ ‌शहरात‌ ‌सर्वत्र‌ ‌पाणीच‌ ‌पाणी‌ ‌दिसते.‌ ‌पाण्यावर‌‌ तरंगणारे‌ ‌हे‌ ‌अद्भूत‌ ‌शहर‌ ‌आहे.‌ ‌हा‌ ‌गाव‌ ‌म्हणजे‌ ‌खऱ्या‌ ‌अर्थाने‌ ‌शहर‌ ‌नाहीच.‌ ‌तर‌ ‌अनेक‌ ‌छोट्या-छोट्या‌ ‌बेटांचा‌ ‌समूहच‌ ‌आहे.‌ ‌अनेक‌ ‌कालवे‌ ‌आणि‌ ‌त्यांना‌ ‌जोडणारे‌ ‌पूल‌ ‌यामुळे‌ ‌हे‌ ‌शहर‌ ‌खुलून‌ ‌दिसते.‌ ‌मधूनच‌ ‌चर्च‌ ‌किंवा‌ ‌जुना‌ ‌राजवाडा‌ ‌यांची‌ ‌टोके‌ ‌आभाळात‌ ‌घुसल्याप्रमाणे‌ ‌वाटणारे‌ ‌हे‌ ‌शहर‌ ‌मखमली‌ ‌सागरावर‌ ‌टाकलेल्या‌ ‌हिऱ्या-माणकांच्या‌ ‌ढिगासारखे‌ ‌लांबून‌ ‌दिसते.‌ ‌म्हणूनच‌ ‌जो‌ ‌कोणी‌ ‌इथे‌ ‌येतो‌ ‌तो‌ ‌निळ्या‌ ‌पाण्यात‌ ‌तरंगणाऱ्या‌ ‌या‌ ‌शहराच्या‌ ‌प्रेमात‌‌ पडतो.‌ ‌

प्रश्न‌ ‌2.‌ ‌
व्हेनिस‌ ‌म्हणजे‌ ‌निरुयोगी‌ ‌शहर‌ ………………… ‌.‌ ‌
उत्तरः‌
‌युरोप‌ ‌खंडातले‌ ‌पाण्यावर‌ ‌तरंगणारे‌ ‌जगातले‌ ‌एकमेव‌ ‌शहर‌‌ म्हणजे‌ ‌’व्हेनिस’‌ ‌होय.‌ ‌इथे‌ ‌सर्वत्र‌ ‌पाणरस्तेच‌ ‌आहेत.‌ ‌इथल्या‌ ‌कालव्यांमधून‌ ‌अनेक‌ ‌लहान-मोठ्या‌ ‌नावा‌ ‌उत्साही‌ ‌प्रवाप‌‌ बसून‌ ‌बिअर‌ ‌किंवा‌ ‌कॉफी‌ ‌घेत‌ ‌समोरून‌ ‌सरकणाऱ्या‌ ‌विविध‌ ‌आकारांच्या‌ ‌आणि‌ ‌अनंत‌ ‌प्रकारांचे‌ ‌उतारू‌ ‌म्हणजेच‌ ‌प्रवासी‌ ‌वाहून‌ ‌नेणाऱ्या‌ ‌नावांची‌ ‌ये-जा‌ ‌पाहत‌ ‌बसायचे.‌ ‌तीच‌ ‌गंमत‌ ‌या‌ ‌नावांमधून‌ ‌प्रवास‌ ‌करणाऱ्यानांही‌ ‌पाहायला‌ ‌मिळते.‌ ‌डेकवर‌ ‌येऊन‌ ‌किनाऱ्यावरच्या‌ ‌निरुदयोगी‌ ‌संथ,‌ ‌शांत,‌ ‌चित्रविचित्र‌ ‌प्रवाशांच्याकडे‌ ‌पाहत‌ ‌पुढे-पुढे‌ ‌सरकायचे.‌ ‌हे‌ ‌शहर‌ ‌निरुदयोग्यांसाठीच‌ ‌आहे,‌ ‌असे‌ ‌वाटते‌ ‌कारण‌ ‌इथे‌ ‌येणाऱ्या‌ ‌प्रवाशांना‌ ‌कसलीही‌ ‌घाई-गर्दी‌ ‌नसते.‌ ‌न्यूयॉर्क,‌ ‌मुंबई,‌ ‌हाँगकाँग‌ ‌अशा‌ ‌शहरांतल्या‌ ‌धावपळीपासून‌ ‌हे‌‌ पूर्णपणे‌ ‌वेगळे‌ ‌शांत‌ ‌असे‌ ‌शहर‌ ‌आहे.‌

4. ‘व्हेनिस’हे‌ ‌पाण्यातले‌ ‌जगातले‌ ‌एकमेव‌ ‌शहर‌ ‌आहे.‌‌ पाठाच्या‌ ‌आधारे‌ ‌या‌ ‌विधानाची‌ ‌सत्यता‌ ‌पटवून‌ ‌दया.‌ ‌

‌प्रश्न‌ ‌1.‌ ‌
‘व्हेनिस’हे‌ ‌पाण्यातले‌ ‌जगातले‌ ‌एकमेव‌ ‌शहर‌ ‌आहे.‌‌ पाठाच्या‌ ‌आधारे‌ ‌या‌ ‌विधानाची‌ ‌सत्यता‌ ‌पटवून‌ ‌दया.‌ ‌
उत्तरः‌
‌व्हेनिस‌ ‌हे‌ ‌पाण्यातले‌ ‌असे‌ ‌जगातले‌ ‌एकमेव‌ ‌अद्भूत‌‌ शहर‌ ‌आहे.‌ ‌या‌ ‌शहरात‌ ‌एकही‌ ‌मोटार‌ ‌नाही.‌ ‌वाहतूक‌ ‌नियंत्रण‌ ‌करणारा‌ ‌पोलीस‌ ‌नाही.‌ ‌ट्रॅफिक‌ ‌लाईट्स‌ ‌नाहीत‌ ‌आणि‌ ‌रस्त्यावर‌ ‌धक्काबुक्की‌ ‌नाही‌ ‌असे‌ ‌हे‌ ‌जगातले‌ ‌एकमेव‌ ‌शहर‌ ‌आहे‌ ‌कारण‌ ‌याला‌ ‌खऱ्या‌ ‌अर्थाने‌ ‌रस्तेच‌ ‌नाहीत.‌ ‌इथे‌ ‌फक्त‌ ‌कालवे‌ ‌आहेत‌ ‌आणि‌ ‌त्यांना‌ ‌जोडणारे‌ ‌पूल‌ ‌आहेत.‌ ‌आईच्या‌ ‌गळ्यात‌ ‌मुलाने‌ ‌लडिवाळपणे‌ ‌प्रेमळपणे‌ ‌हात‌ ‌टाकावे‌ ‌तसे‌ ‌हे‌ ‌पूल‌ ‌आहेत.‌

‌येथील‌ ‌पाणरस्त्यांतूनच‌ ‌अनेक‌ ‌लहान-मोठ्या‌ ‌यांत्रिक‌ ‌नावा‌ ‌हौशी‌ ‌प्रवाशांना‌ ‌तसेच‌ ‌प्रेमात‌ ‌पडलेल्या‌ ‌युगुलांना‌ ‌सुसाट‌ ‌वेगाने‌ ‌घेऊन‌ ‌जात-येत‌ ‌असतात.‌ ‌येथील‌ ‌हवेत‌ ‌गारवा‌ ‌असतो.‌ ‌वाऱ्यात‌ ‌उत्साह‌ ‌असतो.‌ ‌मनात‌ ‌संगीत‌ ‌असते‌ ‌आणि‌ ‌विशेष‌ ‌म्हणजे‌ ‌सभोवार‌ ‌परसलेल्या‌ ‌पाण्यात‌ ‌तारुण्याचा‌ ‌उत्साह‌ ‌दिसून‌ ‌येतो.‌ ‌त्यामुळेच‌ ‌निळ्या‌ ‌पाण्यावर‌ ‌तरंगणारे‌ ‌हे‌ ‌शहर‌ ‌सोडताना‌ ‌उगाच‌ ‌मनाला‌ ‌हुरहुर‌ ‌वाटते.‌‌

5. तुम्ही‌ ‌पाहिलेल्या‌ ‌तुम्हाला‌ ‌आवडलेल्या‌ ‌कोणत्याही‌‌ स्थळाचे‌ ‌वर्णन‌ ‌तुमच्या‌ ‌शब्दांत‌ ‌करा.‌ ‌

प्रश्न‌ ‌1.‌ ‌
तुम्ही‌ ‌पाहिलेल्या‌ ‌तुम्हाला‌ ‌आवडलेल्या‌ ‌कोणत्याही‌‌ स्थळाचे‌ ‌वर्णन‌ ‌तुमच्या‌ ‌शब्दांत‌ ‌करा.‌ ‌
उत्तरः ‌
‌मागच्या‌ ‌रविवारी‌ ‌माझ्या‌ ‌ताईच्या‌ ‌सासुरवाडीला‌ ‌जाण्याचा‌‌ योग‌ ‌आला.‌ ‌कोकणातील‌ ‌दापोली‌ ‌तालुक्यातील‌ ‌’आंबिवली’‌ ‌हे‌ ‌तिचे‌ ‌सासर.‌ ‌डोंगराच्या‌ ‌कुशीत‌ ‌वसलेले,‌ ‌निसर्गसौंदत्या‌ ‌निसर्गसौंदर्याने‌ ‌मी‌ ‌मोहूनच‌ ‌गेलो.‌ ‌सर्वत्र‌ ‌धुके‌ ‌पसरलेले‌ ‌होते.‌ ‌डोंगराच्या‌ ‌पलिकडून‌ ‌सूर्य‌ ‌हळूहळू‌ ‌वर‌ ‌येत‌ ‌होता.‌ ‌आकाश‌ ‌सोनेरी‌ ‌रंगाने‌ ‌रंगून‌ ‌गेले‌ ‌होते.‌ ‌मी‌ ‌खूप‌ ‌आनंदी‌ ‌झालो‌ ‌होतो.‌ ‌शहरातील‌ ‌सिमेंट‌ ‌काँक्रिटच्या‌ ‌जंगलात‌ ‌वाढलेल्या‌ ‌माझ्यासारख्या‌ ‌मुलाला‌‌ त्या‌ ‌सौंदर्याचा‌ ‌हेवा‌ ‌वाटू‌ ‌लागला.‌ ‌

भाषाभ्यास‌‌:

विरामचिन्हे‌:

प्रश्न‌ ‌1.
‌खालील‌ ‌वाक्ये‌ ‌वाचा‌ ‌व‌ ‌अभ्यासा.‌‌
1. आवडले‌ ‌का‌ ‌तुला‌ ‌हे‌ ‌पुस्तक‌ ‌
2. ‌हो‌ ‌जेवणानंतर‌ ‌मी‌ ‌सर्व‌ ‌गोष्टी‌ ‌वाचणार‌ ‌आहे‌ ‌जया‌ ‌म्हणाली‌ ‌
3.‌ ‌वडील‌ ‌म्हणाले‌ ‌ज्ञानेश्वरी‌ ‌कुणी‌ ‌लिहिली‌ ‌तुला‌ ‌ठाऊक‌ ‌आहे‌ ‌का‌‌
वरील‌ ‌संवाद‌ ‌वाचताना‌ ‌वाक्य‌ ‌कुठे‌ ‌संपते,‌ ‌प्रश्न‌ ‌आहे‌ ‌की‌ ‌उद्गार‌ ‌आहे,‌ ‌हे‌ ‌काहीच‌ ‌कळत‌ ‌नाही‌ ‌कारण‌ ‌या‌ ‌वाक्यात‌ ‌विरामचिन्हे‌ ‌नाहीत.‌ ‌बोलताना‌ ‌काही‌ ‌विधाने‌ ‌करताना,‌ ‌प्रश्न‌ ‌विचारताना,‌ ‌आश्चर्य,‌ ‌हर्ष,‌ ‌क्रोध‌ ‌आदी‌ ‌भावना‌ ‌व्यक्त‌ ‌करताना‌ ‌माणूस‌ ‌त्या‌ ‌त्या‌ ‌ठिकाणी‌ ‌कमी‌ ‌अधिक‌ ‌वेळ‌ ‌थांबतो,‌ ‌म्हणून‌ ‌तोच‌ ‌आशय‌ ‌लिहून‌ ‌दाखवताना‌ ‌वाचकालाही‌ ‌कळावा,‌ ‌यासाठी‌ ‌विरामचिन्हांचा‌ ‌वापर‌ ‌केला‌ ‌जातो.‌

प्रश्न‌ ‌2.
‌वरील‌ ‌वाक्यातील‌ ‌चिन्हे‌ ‌आणि‌ ‌त्यांची‌ ‌नावे‌ ‌यांचा‌ ‌तक्ता‌ ‌तयार‌ ‌करा.‌‌

Marathi Akshar Bharati Class 9 Textbook Solutions Chapter 12.1 व्हेनिस Additional Important Questions and Answers

प्रश्न‌ ‌1.
धावपळीच्या‌ ‌शहरी‌ ‌जीवनातून‌ ‌वेळ‌ ‌काढून‌ ‌मनुष्य‌ ‌निसर्गरम्य‌‌ शांत‌ ‌ठिकाणांना‌ ‌भेट‌ ‌देत‌ ‌असतो.‌ ‌यावर‌ ‌तुमचे‌ ‌विचार‌ ‌लिहा.‌
‌उत्तरः‌
‌शहरी‌ ‌जीवन‌ ‌हे‌ ‌धकाधकीचे‌ ‌व‌ ‌धावपळीचे‌ ‌जीवन‌ ‌आहे.‌‌ या‌ ‌जीवनात‌ ‌माणसाला‌ ‌आराम‌ ‌नाही.‌ ‌दिवस‌ ‌रात्र‌ ‌कामेच‌ ‌कामे‌ ‌त्यास‌ ‌करावी‌ ‌लागतात.‌ ‌कोणत्याच‌ ‌प्रकारचा‌ ‌विरंगुळा‌ ‌त्यास‌ ‌अनुभवायास‌ ‌मिळत‌ ‌नाही.‌ ‌कोणत्याही‌ ‌प्रकारची‌ ‌करमणूक‌ ‌नाही.‌ ‌मनुष्य‌ ‌अशा‌ ‌प्रकारच्या‌ ‌जीवनाला‌ ‌कंटाळतो‌ ‌व‌ ‌तो‌ ‌तीन‌ ‌ते‌ ‌चार‌ ‌दिवस‌ ‌का‌ ‌होईना‌ ‌निसर्गरम्य‌ ‌शांत‌ ‌स्थळाला‌ ‌भेट‌ ‌देतो.‌ ‌निसर्ग‌ ‌मानवाला‌ ‌ताजे‌ ‌टवटवीत‌ ‌व‌ ‌प्रसन्न‌ ‌करतो.‌ ‌तो‌ ‌माणसाचा‌ ‌सर्व‌ ‌थकवा‌ ‌वा‌ ‌वेदना‌ ‌दूर‌ ‌करून‌ ‌त्यात‌ ‌ऊर्जा‌ ‌निर्माण‌ ‌करतो.‌ ‌जीवनात‌ ‌उमेदीने‌ ‌उभी‌ ‌राहण्याची‌ ‌प्रेरणा‌ ‌देतो.‌ ‌म्हणून‌ ‌मनुष्य‌ ‌धावपळीच्या‌ ‌शहरी‌ ‌जीवनातून‌ ‌वेळ‌ ‌काढून‌ ‌निसर्गरम्य‌ ‌शांत‌ ‌ठिकाणांना‌ ‌भेट‌ ‌देत‌‌ असतो.‌

‌प्रश्न‌ ‌2.‌
‌तुम्हांला‌ ‌कधी‌ ‌एखादया‌ ‌शहराला‌ ‌भेट‌ ‌दिल्यानंतर‌ ‌ते‌‌ सोडताना‌ ‌मनात‌ ‌हुरहुर‌ ‌निर्माण‌ ‌झालेली‌ ‌आहे‌ ‌का?‌ ‌तुमचा‌‌ अनुभव‌ ‌कथन‌ ‌करा.‌
‌उत्तरः‌
मी‌ ‌गेल्या‌ ‌वर्षी‌ ‌माझ्या‌ ‌कुटुंबासोबत‌ ‌दुबईला‌ ‌गेलो‌ ‌होतो.‌ ‌दुबई‌‌ हे‌ ‌जगातील‌ ‌एक‌ ‌भव्य‌ ‌व‌ ‌दिव्य‌ ‌असे‌ ‌शहर‌ ‌आहे.‌ ‌रात्रीच्या‌ ‌वेळी‌ ‌सत्र‌ ‌दिव्यांची‌ ‌रोषणाई‌ ‌पाहून‌ ‌आपले‌ ‌डोळे‌ ‌दिपून‌ ‌जातात.‌ ‌ओसाड‌ ‌वाळवंटावर‌ ‌वसलेले‌ ‌हे‌ ‌शहर‌ ‌पाहून‌ ‌सर्वजण‌ ‌आश्चर्यचकित‌ ‌होतात.‌ ‌उंचच‌ ‌उंच‌ ‌गगनचुंबी‌ ‌इमारती‌ ‌पाहून‌ ‌मन‌ ‌थक्क‌ ‌होते.‌ ‌तसेच‌ ‌समुद्रातील‌ ‌पाण्यावर‌ ‌वसलेले‌ ‌बुर्ज‌ ‌खलिफा‌ ‌हे‌ ‌पंचतारांकित‌ ‌हॉटेल‌ ‌पाहून‌ ‌मल‌ ‌धन्य‌ ‌होते.‌ ‌दुबई‌ ‌येथील‌ ‌म्युजियम‌ ‌स्नो‌ ‌वर्ल्ड‌ ‌क्रीडा‌ ‌झोन‌ ‌पाहून‌ ‌मनाला‌ ‌सुखद‌ ‌आश्चर्याचा‌ ‌धक्का‌ ‌बसतो.‌ ‌

जागोजागी‌ ‌विविध‌ ‌प्रकारची‌ ‌सुंदर‌ ‌सुंदर‌ ‌झाडे‌ ‌लावून‌ ‌तयार‌ ‌केलेली‌ ‌उदयाने‌ ‌पाहताना‌ ‌मन‌ ‌अगदी‌ ‌भरून‌ ‌येते.‌ ‌रंगीबेरंगी‌ ‌फुलझाडे‌ ‌पाहून‌ ‌मन‌ ‌टवटवीत‌ ‌होते.‌ ‌दुबई‌ ‌येथील‌ ‌चौफेर‌ ‌रस्त्यावरून‌ ‌गाड्या‌ ‌अगदी‌ ‌भरधाव‌ ‌वेगाने‌ ‌पुढेच‌ ‌पुढे‌ ‌सरसावताना‌ ‌पाहून‌ ‌मनाला‌ ‌एक‌ ‌प्रकारची‌ ‌भुरळच‌ ‌पडते.‌ ‌असे‌ ‌हे‌ ‌शहर‌ ‌सोडताना‌ ‌माझ्या‌ ‌मनात‌ ‌एक‌ ‌प्रकारची‌ ‌हुरहुर‌ ‌निर्माण‌ ‌झालेली‌ ‌होती.‌ ‌निघताना‌ ‌असेच‌ ‌वाटत‌ ‌होते‌ ‌की‌ ‌याच‌ ‌स्थळी‌ ‌राहावे.‌‌

व्हेनिस Summary in Marathi

लेखकाचा‌ ‌परिचय‌:

1. नाव‌‌:‌ ‌रमेश‌ ‌राजाराम‌ ‌मंत्री‌ ‌
2. कालावधी‌:‌ ‌1924-1998
3. परिचय‌:‌ ‌कथाकार,‌ ‌प्रवासवर्णनकार,‌ ‌विनोदी‌ ‌लेखक.‌ ‌’थंडीचे‌ ‌दिवस’,‌ ‌’सुखाचे‌ ‌दिवस’,‌ ‌’नवरंग’‌ ‌इत्यादी‌ ‌प्रवासवर्णने‌ ‌प्रसिद्ध.‌‌ 1979 ‌साली‌ ‌एकाच‌ ‌वर्षात‌ ‌34 ‌पुस्तके‌ ‌प्रकाशित‌ ‌करण्याचा‌ ‌विक्रम‌ ‌त्यांच्या‌ ‌नावावर‌ ‌आहे.‌‌

प्रस्तावना‌‌:

‘व्हेनिस’‌ ‌हे‌ ‌स्थूलवाचन‌ ‌लेखक‌ ‌रमेश‌ ‌मंत्री’‌ ‌यांनी‌ ‌लिहिले‌ ‌आहे.‌ ‌या‌ ‌पाठात‌ ‌युरोप‌ ‌खंडातील‌ ‌’व्हेनिस’‌ ‌या‌ ‌पाण्यावर‌ ‌तरंगणाऱ्या‌ ‌शहरातील‌ ‌वातावरण,‌ ‌हवामान,‌ ‌निसर्गसौंदर्य‌ ‌व‌ ‌जीवनमान‌ ‌याचे‌ ‌धुंद‌ ‌वर्णन‌ ‌आले‌ ‌आहे.‌‌

The‌ ‌writer‌ ‌of‌ ‌’Vhenis’‌ ‌is‌ ‌’Ramesh‌ ‌Mantri’.‌ ‌He‌ ‌has‌ ‌explained‌ ‌about‌ ‌the‌ ‌atmosphere,‌ ‌weather,‌ ‌natural‌ ‌beauty‌ ‌and life style of vhenis in this chapter.

‌शब्दार्थ‌‌:

1. चिकार‌ ‌-‌ ‌विपुल,‌ ‌भरपूर,‌ ‌पुष्कळ‌ ‌(abundant,‌ ‌plentifly)‌ ‌
2. बिहाड‌ ‌-‌ ‌वास्तव्य‌ ‌(a‌ ‌residence‌ ‌in‌ ‌a‌ ‌lodging)‌
3. ‌इरादा‌ ‌-‌ ‌बेत,‌ ‌हेतू,‌ ‌उद्देश‌ ‌(intention,‌ ‌aim,‌ ‌object)‌ ‌
4. ‌औपचारिक -‌ ‌उपचार‌ ‌म्हणून‌ ‌पाळलेला,‌ ‌वरवरचा‌ ‌कृत्रिम‌ ‌(formal,‌‌ artificial)‌ ‌
5. कालवा‌ ‌-‌ ‌नदीचे‌ ‌पाणी‌ ‌शेत‌ ‌इत्यादींना‌ ‌पुरवणारा‌ ‌पाट‌ ‌किंवा‌ ‌ओहोळ‌‌ (a‌ ‌water‌ ‌course,‌ ‌canal)‌ ‌
6. नाव‌ ‌-‌ ‌नौका,‌ ‌होडी‌ ‌(a‌ ‌boat)‌
7. ‌युगुल‌ ‌-‌ ‌जोडपे,‌ ‌जोडी‌ ‌(a‌ ‌couple)‌ ‌
8. विस्तीर्ण‌ ‌-‌ ‌अफाट‌ ‌(enlarged)‌
9. ‌पुकार‌ ‌-‌ ‌हाकाटी‌ ‌(a‌ ‌call)‌ ‌
10. उत्साह‌ ‌-‌ ‌जोश,‌ ‌जोम‌ ‌(enthusiasm,‌ ‌energy)‌ ‌
11. तारुण्य‌ ‌-‌ ‌तरुणपण,‌ ‌जवानी‌ ‌(youthful‌ ‌state)‌ ‌
12. अद्भूत‌ ‌-‌ ‌अपूर्व,‌ ‌अलौकिक‌ ‌(strange)‌ ‌
13. एकमेव‌ ‌-‌ ‌एकच‌ ‌एक‌ ‌(the‌ ‌only‌ ‌one)‌
14. ‌निरुदयोगी‌ ‌-‌ ‌कामकाज‌ ‌नसलेला‌ ‌(unemployed)‌‌
15. तुडुब‌ ‌-‌ ‌काठोकाठ,‌ ‌परिपूर्ण‌ ‌(quite‌ ‌full)‌
16. ‌सुसाट‌ ‌-‌ ‌जोरात‌ ‌किंवा‌ ‌वेगात‌ ‌(with‌ ‌great‌ ‌speed)‌
17. ‌लाडिक‌ ‌-‌ ‌लडिवाळपणे‌ ‌(doting‌ ‌affection,‌ ‌fondness)‌ ‌
18. पुंजका‌ ‌-‌ ‌गुच्छा‌ ‌(cluster)‌ ‌
19. निवांत‌ ‌-‌ ‌शांत‌ ‌(still,‌ ‌quiet)‌
20. ‌अलिप्त‌ ‌-‌ ‌अलग,‌ ‌वेगळा‌ ‌(separate)‌‌
21. मुनीम‌ ‌- ‌व्यवस्थापक‌ ‌(a‌ ‌manager)‌ ‌
22. अफाट‌ ‌-‌ ‌प्रचंड,‌ ‌विशाल‌ ‌(huge,‌ ‌vast)‌ ‌
23. मुक्काम‌ ‌-‌ ‌राहण्याचे,‌ ‌वास्तव्याचे‌ ‌ठिकाण‌ ‌(a‌ ‌place‌ ‌of‌ ‌residence)‌‌

टिपा‌:

1. ‌व्हेनिस‌‌ -‌ ‌पूर्वोत्तर‌ ‌इटलीतील‌ ‌एक‌ ‌शहर‌ ‌आणि‌ ‌व्हेनेटो‌ ‌प्रांताची‌ ‌राजधानी,‌ ‌हा‌ ‌नदया‌ ‌आणि‌ ‌कालव्यांमुळे‌ ‌वेगळ्या‌ ‌झालेल्या‌ ‌118 ‌लहान‌ ‌बेटांचा‌ ‌समूह‌‌ आहे.‌‌
2. ‌पोर्टर्स‌ ‌-‌ ‌म्हणजेच‌ ‌वाहक‌ ‌किंवा‌ ‌हमाल,‌ ‌जे‌ ‌इतरांच्या‌ ‌वस्तू‌‌ वाहून‌ ‌नेतात.‌ ‌
3. ‌ग्रँड‌ ‌कॅनॉल‌ ‌-‌ ‌एक‌ ‌जागतिक‌ ‌वारसा‌ ‌स्थळ.‌ ‌जगातील‌ ‌सर्वात‌‌ लांब‌ ‌कालवा‌ ‌किंवा‌ ‌कृत्रिम‌ ‌नदी‌ ‌आणि‌ ‌प्रसिद्ध‌‌ पर्यटन‌ ‌स्थळ.‌ ‌
4. ‌व्हेनिझिया‌ ‌-‌ ‌इटलीतील‌ ‌एक‌ ‌बंदर‌ ‌
5. ‌पियाझा‌ ‌-‌ ‌(Piazza)‌ ‌पियाझा‌ ‌सॅन‌ ‌मार्को‌ ‌(Piazza‌ ‌san‌‌ marco).‌ ‌ज्याला‌ ‌इंग्रजीत‌ ‌सेंट‌ ‌मार्क‌ ‌स्क्वेअर‌ ‌(st.‌ ‌Mark’s‌ ‌Square)‌ ‌असेही‌ ‌ओळखले‌ ‌जाते.‌‌ पर्यटनासाठी‌ ‌हे‌ ‌एक‌ ‌आकर्षक‌ ‌चौक‌ ‌आहे.‌ ‌
6. ‌अर्थतज्ज्ञ‌ ‌-‌ ‌अर्थ‌ ‌विषयक‌ ‌माहिती‌ ‌असणारे‌ ‌व‌ ‌त्याबाबत‌‌ सल्ला‌ ‌देऊ‌ ‌शकणारे‌ ‌अर्थशास्त्राचे‌ ‌विद्वान.‌
7. ‌लिरा‌ ‌-‌ ‌1861 ते‌ ‌2002 ‌च्या‌ ‌दरम्यान‌ ‌असलेले‌‌ इटलीतील‌ ‌चलन.‌ ‌
8. ‌रोम‌ ‌-‌ ‌इटलीच्या‌ ‌राजधानीचे‌ ‌शहर
9. माणिक‌ ‌-‌ ‌हे‌ ‌सर्वोत्तम‌ ‌रत्न‌ ‌मानले‌ ‌जाते.‌ ‌याला‌ ‌इंग्रजीत‌ ‌रुबी‌‌ (ruby)‌ ‌असे‌ ‌म्हणतात.‌ ‌लाल‌ ‌रंगाचा‌ ‌माणिक‌‌ सर्वाधिक‌ ‌मौल्यवान‌ ‌असतो.‌ ‌
10. न्यूयॉर्क‌ ‌-‌ ‌अमेरिकेतील‌ ‌सर्वात‌ ‌दाट‌ ‌लोकवस्ती‌ ‌असलेले‌ ‌शहर‌
11. मुंबई‌ ‌-‌ ‌भारताची‌ ‌आर्थिक‌ ‌राजधानी‌ ‌आणि‌ ‌दाट‌‌ लोकवस्तीचे‌ ‌शहर‌‌
12. ‌हाँगकाँग‌ ‌-‌ ‌चीन‌ ‌देशातील‌ ‌एक‌ ‌स्वायत्त‌ ‌प्रदेश‌ ‌
13. ‌लंडन‌ ‌-‌ ‌इंग्लंडच्या‌ ‌राजधानीचे‌ ‌शहर‌‌

वाक्प्रचार‌‌:

1.‌ ‌हूरहूर‌ ‌वाटणे‌ ‌-‌ ‌चिंता‌ ‌वाटणे

Balbharti Maharashtra State Board Class 9 Marathi Solutions Aksharbharati Chapter 4 जी. आय. पी. रेल्वे Notes, Textbook Exercise Important Questions and Answers.

Maharashtra State Board Class 9 Marathi Aksharbharati Solutions Chapter 4 जी. आय. पी. रेल्वे

Marathi Aksharbharati Std 9 Digest Chapter 4 जी. आय. पी. रेल्वे Textbook Questions and Answers

स्वाध्याय :

1. रिकाम्या जागी योग्य पर्याय लिहून वाक्य पूर्ण करा.

प्रश्न 1.
रिकाम्या जागी योग्य पर्याय लिहून वाक्य पूर्ण करा.
1. भारतात सर्वांत पहिली रेल्वे …………… येथून सुटली. (ठाणे, मुंबई, कर्जत, पुणे)
2. रेल्वेकडे लोकांना आकर्षित करण्यासाठी …………….. ठेवले. (तिकीट, बक्षीस, इनाम, प्रलोभन)
उत्तर :
1. मुंबई
2. इनाम

2. आकृतिबंध पूर्ण करा. 

प्रश्न 1.
आकृतिबंध पूर्ण करा.

उत्तर :

3. आकृती पूर्ण करा.

प्रश्न 1.
आकृती पूर्ण करा.

उत्तर :

4. खालील शब्दांसाठी पाठात आलेले पर्यायी शब्द शोधून लिहा.

प्रश्न 4.
खालील शब्दांसाठी पाठात आलेले पर्यायी शब्द शोधून लिहा.

उत्तर :

5. कारणे लिहा.

प्रश्न अ.
रेल्वेचा प्रवास धोक्याचा नाही हे पटवण्यासाठी रेल्वेच्या कारभाऱ्यांनी खूप आटापिटा केला.
उत्तर :
स्वातंत्र्यपूर्वकाळात भारतीय लोकांवर अंधश्रद्धांचा प्रभाव खूप जास्त होता. पहिली रेल्वे मुंबई ते ठाणे अशी धावली, तेव्हा ही गाडी म्हणजे इंग्रजांची विलायती भुताटकी आहे. मुंबईला नव्या इमारती आणि पूल बांधताहेत. त्यांच्या पायांत गाडायला जिवंत माणसे फूस लावून नेण्याचा हा डाव आहे अशा अफवा त्यावेळी पसरल्या होत्या. म्हणूनच रेल्वे प्रवासासाठी लोक तयार होत नव्हते. अशावेळी रेल्वेचा प्रवास धोक्याचा नाही हे पटवण्यासाठी रेल्वेच्या कारभाऱ्यांना खूप आटापिटा करावा लागला.

प्रश्न आ.
इंग्रजांनी देऊ केलेली मुंबई-ठाणे रेल्वे प्रवासाची इनामे काही दिवसांनी बंद करण्यात आली.
उत्तर :
रेल्वे प्रवासाबाबत लोकांमध्ये अनेक चित्रविचित्र अफवा पसरल्या होत्या. त्यामुळे रेल्वे प्रवासासाठी लोक तयार होत नव्हते. कितीही समजावले तरी लोकांचे समाधान काही होत नव्हते. शेवटी दर माणशी एक रुपया इनाम आणि मोफत प्रवासाची योजना सुरू केली. पैशाच्या लालुचीने ठाण्याचे आणि मुंबईचे लोक आगगाडीने जाऊ लागले की, त्यांच्या घरचे लोक आजूबाजूला उभे राहून खूप रडायचे.

त्यांची समजूत काढणे खूप त्रासाचे असायचे. एकदा ते प्रवासी ठाणे-मुंबईची सफर करून सुखरूप परत आले की चौकशी करणाऱ्यांचे घोळके त्यांच्याभोवती जमायचे. रुपयांचे इनाम पुढे आठ आण्यांवर आले. नंतर चार आणे झाले आणि नंतर रेल्वे प्रवासाची लोकांची भीती निघून गेल्याचे पाहून इनामे बंद करण्यात आली.

6. स्वमत

प्रश्न अ.
रेल्वेचा शोध देशाच्या आर्थिक विकासाला गती देणारा ठरला,’ तुमचे मत लिहा.
उत्तर :
आपल्या भारत देशाची आर्थिक राजधानी मुंबई ही होय. याच मुंबईहून पहिली रेल्वे 18 एप्रिल, 1853 या दिवशी मुंबई ते ठाणे अशी धावली होती. या रेल्वेमुळेच ठाणे ते मुंबई हा दिवसभराचा प्रवास अवघा सव्वा तासावर आला. याच रेल्वेने मुंबई -पुणे ही दोन शहरे जोडून टाकली. कारखानदारी, व्यापार, नोकरीधंदा यांमध्ये प्रचंड वाढ झाली.

व्यापारी मंडळी, नोकरदार मंडळी यांचे कामधंदयाचा निमित्ताने येणे-जाणे वाढले, वेळेची बचत झाली, कामाचा पसारा वाढला.कच्च्या व पक्क्या मालाची वाहतूक या रेल्वेमुळे सहजपणे होऊ लागली. त्यामुळेच या शहरांची प्रगती वेगाने होऊ लागली. एकूणच देशाच्या प्रगतीमध्ये भरच पडत गेली. नंतरच्या काळामध्ये रेल्वेचे जाळेच संपूर्ण देशभर विणले गेले. त्याचाच परिणाम म्हणून देशाचा आर्थिक विकास झपाट्याने होऊ लागला. देशाच्या आर्थिक विकासाला गती देण्यामध्ये रेल्वेचे योगदान फार मोलाचे आहे.

प्रश्न आ.
स्वातंत्र्यपूर्वकाळात भारतीयांवर असलेल्या अंधश्रद्धांच्या प्रभावासंबंधी तुमचे विचार स्पष्ट करा.
उत्तर :
स्वातंत्र्यपूर्वकाळात भारतीय जनमानसांवर अंधश्रद्धांचा फार मोठा पगडा होता. कोणताही आधुनिक बदल सहजासहजी स्वीकारला जात नव्हता. पांरपरिक गोष्टींवर लोकांचा जास्त विश्वास होता.जमशेटजी जिजीभाई आणि जगन्नाथ नाना शंकरशेट यांच्या प्रयत्नाने सुरू झालेल्या रेल्वेला, भारतीयांनी सुरुवातीला इंग्रजांनी सुरू केलेली वाफेची गाडी म्हणजे विलायती भुताटकी आहे. असे म्हटले. लोकांना ठाणे-मुंबई रेल्वे प्रवासाची सवय व्हावी, गोडी लागावी म्हणून मोफत प्रवास रेल्वेच्या अधिकाऱ्यांनी सुरू केला होता.

त्यावेळी मुंबईला नव्या इमारती नि पूल बांधताहेत, त्यांच्या पायांत जिवंत गाडायला फूस लावून माणसे नेण्याचा हा साळसूद डाव आहे, असा विचार केला जात होता. याचाच अर्थ नवी इमारत किंवा नवा पूल बांधायचा असला तर त्याच्या मजबुतीसाठी त्याच्या पायामध्ये माणसांना जिवंत गाडावे लागते किंवा त्यांचा बळी दयावा लागतो, अशी विचित्र अंधश्रद्धा स्वातंत्र्यपूर्वकाळात भारतीयांमध्ये होती.

प्रश्न इ.
तुमच्या मते रेल्वेप्रवासाचे असलेले फायदे व तोटे सविस्तर लिहा.
उत्तर :
(उतारा 4 मधील कृती 4 : स्वमतचे उत्तर पहा.)

Marathi Akshar Bharati Class 9 Textbook Solutions Chapter 4 जी. आय. पी. रेल्वे Additional Important Questions and Answers

पुढील उताऱ्याच्या आधारे दिलेल्या सूचनेनुसार कृती कराः

कृती 1 : आकलन कृती

प्रश्न 1.
आकृतिबंध पूर्ण करा.
उत्तर :

प्रश्न 2.
उत्तरे लिहा.

1. आगीनगाडी निघणार त्या मुहूर्ताचा दिवस – [ ]
2. कलियुगातला हा विंग्रेजी चमत्कार पाहायला आ वासून उभे असलेले – [ ]
3. एकेरी रस्ता – [ ]

उत्तर :

1. दिनांक 18 एप्रिल सन 1853 (सोमवार)
2. लोक
3. मुंबई ते ठाणे

प्रश्न 3.
उताऱ्यानुसार घटनांचा क्रम लावा.

1. बरोबर पाच वाजता आगगाडीने कूक शिटीचा कर्णा कुंकून आपल्या भकभक, फकफक प्रवासाला सुरुवात केली.
2. मुंबई प्रांतात रेल्वे असावी असा उठाव झाला.
3. सन 1853 मध्ये ग्रेट इंडियन पेनिनशुला रेल्वेचा एकेरी रस्त्याचा छोटा फाटा सुरू झाला.
4. मुहूर्ताचा दिवस जाहीर झाला.

उत्तर :

1. मुंबई प्रांतात रेल्वे असावी असा उठाव झाला.
2. सन 1853 मध्ये ग्रेट इंडियन पेनिनशुला रेल्वेचा एकेरी रस्त्याचा छोटा फाटा सुरू झाला.
3. मुहूर्ताचा दिवस जाहीर झाला.
4. बरोबर पाच वाजता आगगाडीने कूऽक शिटीचा कर्णा फुकून आपल्या भकभक, फकफक प्रवासाला सुरुवात केली.

प्रश्न 4.
खालील प्रश्नांची उत्तरे एका वाक्यात लिहा.
i. मुंबई प्रांतात रेल्वे असावी असा उठाव मुंबईला प्रथम कोणी केला?
उत्तर :
मुंबई प्रांतात रेल्वे असावी असा उठाव मुंबईला प्रथम सर जमशेटजी जिजीभाई आणि जगन्नाथ नाना शंकरशेट यांनी केला.

ii. लोकांना कोणती कल्पना अचंब्याची वाटली?
उत्तर :
लोखंडी रुळावरून इंग्रज आगीनगाडी चालवणार, ही कल्पना लोकांना अचंब्याची वाटली. –

iii. किती वाजता पहिली आगगाडी मुंबईहून निघाली?
उत्तर :
सायंकाळी 5 वाजता पहिली आगगाडी मुंबईहून निघाली.

प्रश्न 5.
कंसातील योग्य शब्द वापरून रिकाम्या जागा भरा,

1. ……….. मध्ये ग्रेट इंडियन पेनिनशुला रेल्वेचा पहिला छोटा फाटा मुंबई ते ठाणे-पर्यंत एकेरी रस्त्याचा तयार झाला. (सन-1835, सन – 1853, सन-1930, सन – 1630)
2. दहा डब्यांची ………….. खुशाल चालली आहे. (माळका, माळ, मालिका, शृंखला)
3. बरोबर पाच वाजता आगगाडीने कूऽक ………….. कुंकून आपल्या भकभक, फकफक प्रवासाला सुरुवात केली. (गाडीचा कर्णा, शिटीचा कर्णा, इंजिनाचा कर्णा, डन्याचा कर्णा)

उत्तर :

1. सन – 1853
2. माळका
3. शिटीचा कर्णा

प्रश्न 6.
शब्दजाल पूर्ण करा.
उत्तर :

कृती 2 : आकलन कृती

प्रश्न 1.
योग्य पर्याय निवडून विधाने पूर्ण करा.
i. लोखंडी रुळावरून इंग्रज आगीनगाडी चालवणार, ही कल्पनाच…………..
(अ) लोकांना धक्कादायक होती.
(ब) लोकांना मोठी अचंब्याची होती.
(क) रेल्वे कर्मचाऱ्यांना मोठी अचंब्याची होती.
(ड) लेखकाला मोठी अचंब्याची होती.
उत्तर :
(क) रेल्वे कर्मचाऱ्यांना मोठी अचंब्याची होती.

ii. विस्तव आणि पाणी यांची सांगड घालून
(अ) विग्रेजांनी वाफेलाच गाडी ओढायला लावले!
(ब) विंग्रेजांनी पाण्यालाच गाडी ओढायला लावले!
(क) विंग्रजांनी हवेलाच गाडी ओढायला लावले!
(ड) विंग्रजांनी बाप्पाला गाडी ओढायला लावले!
उत्तर :
(अ) विग्रेजांनी वाफेलाच गाडी ओढायला लावले!

प्रश्न 2.
चूक की बरोबर ते लिहा.

1. 19 एप्रिल सन 1953, सोमवार रोजी सायंकाळी 4 वाजता पहिली आगगाडी मुंबईहून निघाली.
2. इंजिनावर अंग्रेजांचे मोठे निशाण फडकत आहे
3. मुंबई ते पुणे दुतर्फा लाखांवर लोक कलियुगातला हा विंग्रेजी चमत्कार पाहायला आ वासून उभे होते.
4. विस्तव आणि पाणी यांची सांगड घालून विंग्रेजांनी वाफेलाच गाडी ओढायला लावले!

उत्तर :

1. चूक
2. बरोबर
3. चूक
4. बरोबर

कृती 3 : व्याकरण कृती

प्रश्न 1.
खालील वाक्ये लेखननियमांनुसार शुद्ध करून लिहा.
i. हि कल्पनाच लोकांना मोठी आचंब्याचि वाटली.
ii. कमल आहे बूवा या विंग्रेजांची!
उत्तर :
i. ही कल्पनाच लोकांना मोठी अचंब्याची वाटली.
ii. कमाल आहे बुवा या विग्रेजांची!

प्रश्न 2.
अचूक शब्द लिहा.

1. पेनिनशुला, पेनीनशुला, पेनिनशूला, पेनिशूला
2. झुकझूक, झुकझूख, झुकझुक, झूकझूक
3. मुहुर्ताचा, मुहुरताचा, मुहुतार्चा, मुहूर्ताचा
4. विंग्रेजी, ईग्रजी, वीग्रजी, विग्रेजि

उत्तर :

1. पेनिनशुला
2. झुकझुक
3. मुहूर्ताचा
4. विंग्रेजी

प्रश्न 3.
वचन बदला.

1. डबा – [ ]
2. निशाण – [ ]
3. रेडे – [ ]
4. तोरण – [ ]

उत्तर :

1. डबे
2. निशाणे
3. रेडा
4. तोरणे

प्रश्न 4.
समानार्थी शब्द लिहा.

1. युक्ती – [ ]
2. सुमन – [ ]
3. पताका – [ ]
4. जल – [ ]
5. आग – [ ]

उत्तर :

1. कल्पना
2. फूल
3. निशाण
4. पाणी
5. विस्तव

प्रश्न 5.
विरुद्धार्थी शब्दांच्या जोड्या जुळवा.

उत्तर :

प्रश्न 6.
उताऱ्यातील दोन अनेकवचनी शब्द शोधून लिहा.
उत्तर :

1. निशाणे
2. डबे
3. खुर्ध्या
4. लोक
5. तोरणे

प्रश्न 7.
तक्ता पूर्ण करा.
उत्तर :

प्रश्न 8.
वाक्प्रचारांचा अर्थ लिहून वाक्यांत उपयोग करा.
i. आ वासून उभे असणे
ii. पाठबळ असणे
उत्तर :
i. अर्थ : आश्चर्य वाटणे
वाक्य : जादूचे प्रयोग पाहायला लोक आ वासून उभे होते.

ii. अर्थ : पाठिंबा असणे.
वाक्य : सह्याद्रीचे पाठबळ होते म्हणून शिवाजी महाराजांनी स्वराज उभारले.

प्रश्न 9.
खालील दिलेल्या वाक्यांचा काळ ओळखा.
i. ही कल्पनाच लोकांना मोठी अचंब्याची वाटली.
ii. हा विंग्रेजी चमत्कार पाहायला आ वासून उभे होते.
उत्तर :
i. भूतकाळ
ii. भूतकाळ

प्रश्न 10.
पर्यायी शब्द लिहा.
उत्तर :

कृती 4 : स्वमत

प्रश्न 1.
रेल्वेचा शोध देशाच्या आर्थिक विकासाला गती देणारा ठरला. तुमचे मत लिहा.
उत्तर :
रेल्वेचा शोध हे 19 व्या शतकातले फार मोठे आश्चर्य होय. रेल्वेचा शोध लागल्यामुळे विस्तव व पाणी यांच्या समन्वयातून तयार होणाऱ्या वाफेवर रेल्वे गाडी चालू लागली. कमीत कमी वेळात ती लांब लांबचा प्रवास करू लागली. त्यामुळे लोकांचा वेळ वाचु लागला. व्यापारी वर्ग व्यापारासाठी रेल्वेचा वापर करू लागले. अवजड यंत्रे, निरनिराळ्या वस्तू यांची रेल्वेने वाहतूक होऊ लागली.

त्यामुळे त्यांची व्यापारात भरभराट होऊ लागली. दळणवळण सुलभ व प्रगत झाल्यामुळे देशाच्या आर्थिक विकासात हातभार लावला जाऊ लागला. देशाची आर्थिक प्रगती होऊ लागली. म्हणून रेल्वेचा शोध देशाच्या आर्थिक विकासाला गती देणारा ठरला.

पुढील उताऱ्याच्या आधारे दिलेल्या सूचनेनुसार कृती करा:

कृती 1 : आकलन कृती

प्रश्न 1.
आकृतिबंध पूर्ण करा.
उत्तर :

प्रश्न 2.
उत्तर लिहा.
लोकात कशाचे पीक पिकले होते?
उत्तर :
लोकात भलत्याच कंड्या नि अफवांचे पीक पिकले होते

प्रश्न 3.
उताऱ्यानुसार घटनांचा क्रम लावा.

1. दुसऱ्या दिवसापासून लोकांना मोफत ठाणे ते मुंबई आणि परत नेण्या-आणण्याची दबंडी पिटण्यात आली.
2. मुहूर्तावर निघालेली पहिली आगगाडी ठाण्याला जाऊन मुंबईला सुखरूप परत आली.
3. एक दोन दिवस सरकारी कचेरीतले कारकून, व्यापाऱ्यांच्या पेडीवरचे गुमास्ते यांना मुंबई ते ठाण्याला नेऊन परत आलेले लोकांना दाखवले.
4. लोकांत भलत्याच कंड्या नि अफवांचे पीक पिकले होते.

उत्तर :

1. मुहूर्तावर निघालेली पहिली आगगाडी ठाण्याला जाऊन मुंबईला सुखरूप परत आली.
2. दुसऱ्या दिवसापासून लोकांना मोफत ठाणे ते मुंबई आणि परत नेण्या-आणण्याची दवंडी पिटण्यात आली.
3. लोकांत भलत्याच कंड्या नि अफवांचे पीक पिकले होते.
4. एक दोन दिवस सरकारी कचेरीतले कारकून, व्यापाऱ्यांच्या पेढीवरचे गुमास्ते यांना मुंबई ते ठाण्याला नेऊन परत आलेले लोकांना दाखवले.

प्रश्न 4.
खालील प्रश्नांची उत्तरे एका वाक्यात लिहा.
i. दुसऱ्या दिवसापासून कोणती दवंडी पिटण्यात आली?
उत्तर :
दुसऱ्या दिवसापासून लोकांना मोफत ठाणे ते मुंबई आणि परत नेण्या-आणण्याची दवंडी पिटण्यात आली.

ii. विंग्रेजांची विलायती भुताटकी कोणती आहे?
उत्तर :
वाफेची गाडी ही विंग्रेजांची विलायती भुताटकी आहे.

प्रश्न 5.
कंसातील योग्य शब्द वापरून रिकाम्या जागा भरा.

1. वाफेची गाडी ही विंग्रेजांची विलायती ……………. आहे. (भुताटकी, राक्षस, यंत्र, मशीन)
2. तेवढ्यानेही कोणाचे …………… होईना. (समाधान, कौतुक, दुःख, नवल)
3. मुहूर्तावर निघालेली पहिली आगगाडी ठाण्याला जाऊन …………… सुखरूप परत आली. (पुण्याला, मुंबईला, रत्नागिरीला, कोल्हापुरला)
4. मुंबईला नव्या इमारती नि ………… बांधताहेत. (बांध, धरण, पूल, रस्ते)

उत्तर :

1. भुताटकी
2. समाधान
3. मुंबईला
4. पूल

प्रश्न 6.
सहसंबंध लिहा.
कचेरीतले कारकून :: व्यापाऱ्यांच्या पेढीवरचे : ……………….
उत्तर :
गुमास्ते

कृती 2 : आकलन कृती

प्रश्न 1.
कोण ते लिहा.

1. सरकारी कचेरीतले – [ ]
2. व्यापाऱ्यांच्या पेढीवरचे – [ ]
3. विंग्रेजांची विलायती भुताटकी – [ ]
4. खूप आटापीटा करणारे – [ ]

उत्तर :

1. कारकून
2. गुमास्ते
3. बाफेची गाडी
4. रेल्वेचे कारभारी

प्रश्न 2.
आकृतिबंध पूर्ण करा.
उत्तर :

प्रश्न 3.
सत्य वा असत्य ते लिहा.

1. आगगाडीत बसणे धोक्याचे आहे.
2. लोकांत भलत्याच कंड्या नि अफवांचे पीक पिकले होते.
3. वाफेच्या गाडीत बसायचा लोकांना धीर झाला.

उत्तर :

1. असत्य
2. सत्य
3. असत्य

कृती 3 : व्याकरण कृती

प्रश्न 1.
लेखननियमांनुसार वाक्ये शुद्ध करून लिहा.
i. लोकांत भलत्याच कंड्या नी अफवांचे पिक पिकले होते,
ii. तेवढ्यानेही कोणाचे समधान होइना.
उत्तर :
i. लोकांत भलत्याच कंड्या नि अफवांचे पीक पिकले होते.
ii. तेवढ्यानेही कोणाचे समाधान होईना.

प्रश्न 2.
अचूक शब्द लिहा.

1. साळसूद, साळसुद, साळखुद, साळखूद
2. मुहूरतावर, मुहूर्तावर, मुहुर्तावर, मुहर्तावर
3. सुखरूप, सूखरूप, सुरुप, सुकरुप

उत्तर :

1. साळसूद
2. मुहूर्तावर
3. सुखरूप

प्रश्न 3.
समानार्थी शब्दांच्या जोड्या जुळवा.

उत्तर :

प्रश्न 4.
विरुद्धार्थी शब्दांच्या जोड्या जुळवा.

1. दुःखाचा × [ ]
2. उशीरा × [ ]
3. जुन्या × [ ]
4. मृत × [ ]
5. मूर्ख × [ ]
6. असमाधान × [ ]

उत्तर :

1. सुखाचा
2. लवकर
3. नव्या
4. जिंवत
5. शहाणे
6. समाधान

प्रश्न 5.
उताऱ्यातील दोन अनेकवचनी शब्द शोधून लिहा.
उत्तर :

1. कारकून
2. गुमास्ते
3. इमारती
4. पूल

प्रश्न 6.
तक्ता पूर्ण करा.
उत्तर :

प्रश्न 7.
वाक्प्रचारांचा अर्थ लिहा.

1. दवंडी पिटणे
2. फूस लावणे
3. समाधान होणे

उत्तर :

1. जाहीर घोषणा करणे
2. गुप्तपणे/फसवून उत्तेजन देणे
3. तृप्त होणे

प्रश्न 8.
काळ बदला. (वर्तमानकाळ करा)
लोकांच्या मनात भलत्याच कंड्या नि अफवांचे पीक पिकले होते.
उत्तर :
लोकांच्या मनात भलत्याच कंड्या नि अफवांचे पीक पिकले आहे.

प्रश्न 9.
पर्यायी शब्द लिहा.
उत्तर :

कृती 4 : स्वमत

प्रश्न 1.
स्वातंत्र्यपूर्व काळात भारतीयांवर असलेल्या अंधश्रद्धांच्या प्रभावांसंबंधी तुमचे विचार स्पष्ट करा.
उत्तर :
स्वातंत्र्यपूर्वकाळात भारत देशात अंधश्रद्धेचे साम्राज्य होते. अंधश्रद्धेने समाजाला पोखरून काढलेले होते. सती जाणे, मांजर आडवे जाणे, केशवपन करणे, विधवेचे दर्शन होणे अशा कितीतरी प्रकारच्या अंधश्रद्धा देशात आ वासून उभ्या होत्या. भारतीय लोक निरक्षर असल्यामुळे ते या सर्व प्रकारच्या अंधश्रद्धांना बळी पडत होते. अर्धश्रद्धेचा लोकांवर इतका पगडा होता की त्यांची मानसिकताच जणू मृतप्राय झालेली होती.

देशाला स्वातंत्र्य मिळण्याअगोदर या अंधश्रदधेने अनेक भारतीयांचे बळी घेतलेले होते. तरी देखील तत्कालीन लोक डॉक्टरकडे न जाता ढोंगी, साधू व मांत्रिकांवरच विश्वास ठेवत असत. खरोखरच देश स्वतंत्र होण्याअगोदर अंधश्रद्धा हा भारतीय समाजाला लागलेला एक फार मोठा कलंक होता आणि त्याचा प्रभाव कमी करण्याकरीता अनेक समाजसुधारकांना आपल्या जिवाचे रान करावे लागले होते.

पुढील उताऱ्याच्या आधारे दिलेल्या सूचनेनुसार कृती करा:

कृती 1 : आकलन कृती

प्रश्न 1.
आकृतिबंध पूर्ण करा.
उत्तर :

प्रश्न 2.
उत्तरे लिहा.
i. आजूबाजूला उभी राहून ठणाण धाय मोकलणारी
ii. समजूत काढता काढता टेकीला यायचे –
उत्तर :
i. घरची माणसे
ii. रेल्वेचे अधिकारी

प्रश्न 3.
उताऱ्यानुसार घटनांचा क्रम लावा.

1. पैशाच्या लालुचीने ठाण्याच्या घंटाळीवरचे आणि मुंबईचे लोक आगगाडीने जाऊ लागले.
2. इनामे बंद झाली नि सर्रास तिकिटे चालू केली.
3. दर माणशी एक रुपया इनाम आणि मोफत प्रवासाचा डंका वाजला,
4. समजूत काढता काढता रेल्वेचे अधिकारी अगदी टेकीला यायचे.

उत्तर :

1. दर माणशी एक रुपया इनाम आणि मोफत प्रवासाचा डंका वाजला.
2. पैशाच्या लालुचीने ठाण्याच्या घंटाळीवरचे आणि मुंबईचे लोक आगगाडीने जाऊ लागले.
3. समजूत काढता काढता रेल्वेचे अधिकारी अगदी टेकीला यायचे.
4. इनामे बंद झाली नि सर्रास तिकिटे चालू केली.

प्रश्न 4.
खालील प्रश्नांची उत्तरे एका वाक्यात लिहा.
i. इनामे बंद का झाली?
उत्तर :
रेल्वे प्रवास करताना लोकांचा धीर चेपला म्हणून इनामे बंद झाली.

ii. ठाणे-मुंबईच्या बैलांच्या खटारगाडीचा प्रवास किती दिवस खायचा?
उत्तर :
ठाणे-मुंबईच्या बैलांच्या खटारगाडीचा प्रवास तब्बल एक दिवस खायचा.

प्रश्न 5.
कंसातील योग्य शब्द वापरून रिकामी जागा भरा.
मग मात्र लोकांची …………… लागली. (झुंबड, तुंबड, चंगळ, मौज)
उत्तर :
झुंबड

प्रश्न 6.
शब्दसमूहासाठी एक शब्द चौकटीत लिहा.
i. प्रवास करणारी व्यक्ती –
उत्तर :
प्रवासी

b

कृती 2 : आकलन कृती

प्रश्न 1.
योग्य पर्याय निवडून विधाने पूर्ण करा.
i. समजूत काढता काढता रेल्वेचे ……………
(अ) अधिकारी अगदी टेकौला यायचे.
(व) पदाधिकारी अगदी टेकीला यायचे.
(क) अधिकारी अगदी आनंदी असायचे.
(ड) अधिकारी दु:खी व्हायचे.
उत्तर :
(अ) अधिकारी अगदी टेकौला यायचे.

ii. अवध्या सव्वा तासात ठाण्याचा असामी …………..
(अ) पुण्याला येऊ जाऊ लागला.
(व) कोल्हापूरला येऊ जाऊ लागला.
(क) मुंबईला येऊ जाऊ लागला.
(ड) ठाण्याला येऊ जाऊ लागला.
उत्तर :
(क) मुंबईला येऊ जाऊ लागला.

प्रश्न 2.
आकृतिबंध पूर्ण करा.
उत्तर :

प्रश्न 3.
एका वाक्यात उत्तर लिहा.
ठाण्याचा आसामी मुंबईला किती तासात येऊ जाऊ लागला?
उत्तर :
ठाण्याचा असामी मुंबईला अवघ्या सव्वा तासात येऊ जाऊ लागला.

प्रश्न 4.
सत्य वा असत्य ते लिहा.
i. अखेर दर माणशी दोन रुपया इनाम आणि मोफत प्रवासाचा डंका वाजवला.
ii. घरची माणसे आजूबाजूला उभी राहून ठणाण धाय मोकलायची.
उत्तर :
i. असत्य
ii. सत्य

कृती 3 : व्याकरण कृती

प्रश्न 1.
खालील वाक्य लेखननियमांनुसार शुद्ध करून लिहा.
पैशाच्या लालूचीने ठाण्याच्या घंटाळिवरचे आणि मुंबईचे लोक आगगाडीने जाऊ लागले.
उत्तर :
पैशाच्या लालुचीने ठाण्याच्या घंटाळीवरचे आणि मुंबईचे लोक आगगाडीने जाऊ लागले.

प्रश्न 2.
उताऱ्यातील दोन विशेषणे शोधून लिहा.
उत्तर :

1. मोफत
2. दर
3. एक

प्रश्न 3.
अचूक शब्द लिहा.
i. खटारगाडीचा, कटारगाडीचा, खटारगाडिचा, खटारडीचा
ii. आजूबाजुला, आजुबाजुला, आजूबाजूला, आजुबाजूला.
उत्तर :
i. खटारगाडीचा
ii. आजूबाजूला

प्रश्न 4.
समानार्थी शब्द लिहा.

1. बक्षीस – [ ]
2. तपास – [ ]
3. धिटाई – [ ]
4. दिन – [ ]

उत्तर :

1. इनाम
2. चौकशी
3. धीर
4. दिवस

प्रश्न 5.
विरुद्धार्थी शब्द लिहा.

1. सुरुवात × [ ]
2. विकत × [ ]
3. रात्र × [ ]
4. मागे × [ ]

उत्तर :

1. अखेर
2. मोफत
3. दिवस
4. पुढे

प्रश्न 6.
उताऱ्यातील दोन अनेकवचनी शब्द शोधून लिहा.
उत्तर :

1. लोक
2. माणसे
3. इनामे
4. अधिकारी
5. घोळके
6. तिकिटे

प्रश्न 7.
तक्ता पूर्ण करा.
उत्तर :

प्रश्न 8.
तक्ता पूर्ण करा.
उत्तर :

प्रश्न 9.
वाक्प्रचारांचा अर्थ लिहून वाक्यात उपयोग करा,
i. धाय मोकलून रडणे
ii. झुंबड उडणे
उत्तर :
i. अर्थ : मोठमोठ्याने रडणे.
वाक्य : आपल्या आवडत्या कुत्र्याचा अपघात झालेला पाहून रजनी धाय मोकलून रडू लागली.

ii. अर्थ : गर्दी करणे.
वाक्य : माकडाचे खेळ पाहण्यासाठी लहान मुलांची झुंबड उडाली होती.

प्रश्न 10.
काळ बदला. (भविष्यकाळ करा)

1. ते प्रवासी ठाणे-मुंबईची सफर करून सुखरूप परत येतात.
2. लोकांची झुंबड लागली होती.
3. नंतर चार आणे झाले.

उत्तर :

1. ते प्रवासी ठाणे-मुंबईची सफर करून सुखरूप परत येतील.
2. लोकांची झुंबड लागेल.
3. नंतर चार आणे होतील.

प्रश्न 11.
पर्यायी शब्द लिहा.
उत्तर :

कृती 4 : स्वमत

प्रश्न 1.
नवीन तंत्रज्ञानाशी मानवाची लगेचच मैत्री होत नाही, असे तुम्हांस वाटते का? स्पष्ट करा.
उत्तर :
तंत्रज्ञान हे नेहमीच बदलत असते. त्यात प्रगती होत असते. नवीन तंत्रज्ञान मानवासाठी एक चमत्कार असतो. त्याच्याशी जवळीक साधण्यासाठी मनुष्याला थोडाफार वेळ लागतो. त्याची रीत, पद्धत वा तंत्र समजून घेण्यासाठी मानवाला थोडा उशीर लागतो. ज्याप्रमाणे देशात सर्वप्रथम रेल्वे सुरू झाली तेव्हा लोकांच्या मानसिकतेत बदल व्हायला व तिचा वापर करण्यास लोकांना फार वेळ लागला होता. त्याप्रमाणे आता एवढा वेळ वा आश्चर्य वाटत नाही पण तरीही नवीन तंत्रज्ञान म्हटले की ते शिकण्यास वा जाणून घेण्यास थोडाफार वेळ लागतोच,

पुढील उताऱ्याच्या आधारे दिलेल्या सूचनेनुसार कृती कराः

कृती 1 : आकलन कृती

प्रश्न 1.
आकृतिबंध पूर्ण करा.
उत्तर :

प्रश्न 2.
उत्तरे लिहा.
i. पुणे ते मुंबईचा रेल्वे प्रवास तासांत व्हायचा – [ ]
ii. घाट – उतरणीला किती तास लागायचे – [ ]
उत्तर :
i. अठरा
ii. चार

प्रश्न 3.
जोड्या जुळवा.

उत्तर :

प्रश्न 4.
उताऱ्यानुसार घटनांचा क्रम लावा.

1. मोठ्या थाटामाटाने ओपणिंग शिरोमणि’ करण्यात आला.
2. ज्याला त्याला मोठे नवल वाटायचे.
3. आगगाडीत बसून झुकझुक करीत खुशाल मुंबईला रवाना व्हायचे
4. मुंबई-पुण्याचा रेल्वेप्रवास ज्यारीने चालू झाला.

उत्तर :

1. मोठ्या थाटामाटाने ‘ओपणिंग शिरोमणि’ करण्यात आला.
2. मुंबई-पुण्याचा रेल्वेप्रवास ज्यारीने चालू झाला.
3. आगगाडीत बसून झुकझुक करीत खुशाल मुंबईला रवाना व्हायचे.
4. ज्याला त्याला मोठे नवल वाटायचे.

प्रश्न 5.
खालील प्रश्नाचे उत्तरे एका वाक्यात लिहा.
i. कोणत्या रस्त्याचा ‘ओपणिंग शिरोमणि’ मोठ्या थाटामाटाने करण्यात आला?
उत्तर :
खंडाळ्याहून पुण्यापर्यंतच्या सपाटीच्या रस्त्याचा ‘ओपणिंग शिरोमणि’ मोठ्या थाटामाटाने करण्यात आला.

ii. घाट-उतरणीची सुखसोय नि सरबराई पाहण्याचे कंत्राट कोणी घेतले होते?
उत्तर :
घाट-उतरणीची सुखसोय नि सरबराई पाहण्याचे कंत्राट मुंबईच्या करशेटजी जमशेटजी यांनी घेतले होते.

प्रश्न 6.
कंसातील योग्य शब्द वापरून रिकाम्या जागा भरा.

1. ……… काम चालले असतानाच मुंबई-पुण्याचा रेल्वेप्रवास ज्यारीने चालू झाला. (मेळघाटाचे, कशेडी घाटाचे, फोंडाघाटाचे, बोरघाटाचे)
2. खंडाळ्याहून पुण्यापर्यंचा सपाटीचा रेल्वे-रस्ता सन …………. च्या फेब्रुवारीत पुरा झाला. (1858, 1850, 1860, 1958)
3. सगळा काफिल्ला ………… आला. (देवगिरीला, खोपवलीला, सोनखडीला, राजगीरीला)

उत्तर :

1. बोरघाटाचे
2. 1858
3. खोपवलीला

कृती 2: आकलन कृती

प्रश्न 1.
योग्य पर्याय निवडून विधाने पूर्ण करा.
i. खंडाळा-पुण्याच्या दरम्यान खडकी आणि तळेगाव अशी ………………
(अ) दोन स्टेशने ठेवण्यात आली.
(ब) दोन उपाहारगृहे ठेवण्यात आली.
(क) दोन माणसे ठेवण्यात आली.
(ङ) दोन ठिकाणे ठेवण्यात आली.
उत्तर :
(अ) दोन स्टेशने ठेवण्यात आली.

ii. पुणे ते मुंबईचा रेल्वे प्रवास
(अ) अवघ्या वीस तासांत व्हायचा.
(ब) अवघ्या दहा तासांत व्हायचा.
(क) अवघ्या अठरा तासांत व्हायचा.
(ड) अवघ्या तीस तासांत व्हायचा.
उत्तर :
(क) अवघ्या अठरा तासांत व्हायचा.

प्रश्न 2.
कोण ते लिहा.
i. बोरघाट पोखरण्याची योजना करणारे – [ ]
ii. प्रवाशांची घाट-उतरणीची सुखसोय नि सरबराई पाहण्याचे कंत्राट घेणारे – [ ]
उत्तर :
i. इंजिनीयर (इजनेर) लोक
ii. करशेटजी जमशेटजी

प्रश्न 3.
आकृतिबंध पूर्ण करा.
उत्तर :

प्रश्न 4.
सत्य वा असत्य ते लिहा.

1. पुणे ते मुंबईचा रेल्वे प्रवास अवघ्या अठरा तासांत व्हायचा.
2. रस्ता दुहेरीच होता.
3. आगगाडीत बसून झुकझुक करीत खुशाल मुंबईला रवाना व्हायचे.

उत्तर :

1. सत्य
2. असत्य
3. सत्य

कृती 3 : व्याकरण कृती

प्रश्न 1.
खालील वाक्ये लेखननियमांनुसार शुद्ध करून लिहा.
i. त्याचाहि मोठ्या थाटामाटाने ‘ओपणींग शिरोमणि’ करण्यात आला.
ii. बोरघाटाचे काम चालले असतानाच मुंबई-पूण्याचा रेल्वेप्रवास जारीने चालू झाला,
उत्तर :
i. त्याचाही मोठ्या थाटामाटाने ओपणिंग शिरोमणि’ करण्यात आला.
ii. बोरघाटाचे काम चालले असतानाच मुंबई-पुण्याचा रेल्वेप्रवास ज्यारीने चालू झाला.

प्रश्न 2.
अचूक शब्द लिहा.
i. खंड्याळाहून, खंडाळ्याहून, खंडाळायाहून, खंड्याळहुन
ii. उतरणीची, उतरणिची, उतरणिचि, उतरणिच
उत्तर :
i. खंडाळ्याहून
i. उतरणीची

प्रश्न 3.
समानार्थी शब्द लिहा.

1. कर्म – [ ]
2. आश्चर्य – [ ]
3. गंमत – [ ]
4. बेत – [ ]

उत्तर :

1. काम
2. नवल
3. मौज
4. योजना

प्रश्न 4.
विरुद्धार्थी शब्द लिहा.
i. बंद × [ ]
ii. दुहेरी × [ ]
उत्तर :
i. चालू
ii. एकेरी

प्रश्न 5.
उताऱ्यातील दोन अनेकवचनी शब्द शोधून लिहा.
उत्तर :

1. लोक
2. पालख्या
3. डोल्या
4. खुर्ध्या
5. स्टेशने

प्रश्न 6.
तक्ता पूर्ण करा.
उत्तर :

प्रश्न 7.
वाक्प्रचारांचा अर्थ लिहा.

1. रवाना होणे
2. नवल वाटणे
3. योजना आखणे

उत्तर :

1. निघून जाणे
2. आश्चर्य वाटणे
3. बेत आखणे

प्रश्न 8.
वाक्यांतील काळ ओळखा.
i. रस्ता एकेरीच होता.
ii. ज्याला त्याला मोठे नवलच वाटायचे,
उत्तर :
i. भूतकाळ
ii. भूतकाळ

प्रश्न 9.
पर्यायी शब्द लिहा.
उत्तर :

कृती 4 : स्वमत

प्रश्न 1.
तुमच्या मते रेल्वेप्रवासाचे असलेले फायदे व तोटे सविस्तर सांगा.
उत्तर :
रेल्वेमुळे प्रवास लवकर आणि सुखाचा होतो. बाकी गाड्यांच्या तुलनेत रेल्वेचा प्रवास जास्त सुरक्षित असतो. हा प्रवास स्वस्त आणि कमी खर्चिक असतो. एकाच वेळी अनेक शेकडो प्रवासी एकत्रितपणे प्रवास करू शकतात. शिवाय हलक्या तसेच वजनाने जड अशा वस्तू प्रवासात सुरक्षितपणे नेता येतात. रेल्वे फक्त शहराशहरांशी जोडलेली असल्याने गाव-खेड्यांपर्यंत प्रवास करता येत नाही. लांबच्या प्रवासासाठी तिकिट आधीच आरक्षित करावे लागते. अचानक प्रवास करायचा झाल्यास आपल्याला त्रास सहन करावा लागतो. लांबच्या प्रवासासाठी मर्यादित गाड्या असतात. दुर्घटना झाल्यास एकाच वेळी शेकडो प्रवाशांच्या जीवाला धोका असतो. पावसात रेल्वे यंत्रणा विस्कळीत होते व प्रवाशांना याचा त्रास सहन करावा लागतो.

जी. आय. पी. रेल्वे Summary in Marathi

लेखकाचा परिचय :

नाव : केशव सीताराम ठाकरे
कालावधी : 1885 – 1973 इतिहासकार, नाटककार, वृत्तपत्रकार, व्यंगचित्रकार, समाजसुधारक, फर्डे वक्ते. ‘कुमारिकांचे शाप’, ‘भिक्षुकशाहीचे बंड’ हे वैचारिक ग्रंथ; ‘खरा ब्राम्हण’, ‘टाकलेले पोर’, ही नाटके; ‘ग्रामण्यांचा सावंत इतिहास’, ‘हिंदवी स्वराज्याचा खून’, ‘कोंदडाचा टणत्कार’ इत्यादी इतिहासविषयक पुस्तके; ‘संत रामदास’, पंडिता रमाबाई, ‘संत गाडगेमहाराज’ इत्यादी चरित्रात्मक लेखन; ‘माझी जीवनगाथा’ हे आत्मचरित्र प्रसिद्ध.

प्रस्तावना :

सन 1853 मध्ये इंग्रजांनी मुंबई ते ठाणे असा एकेरी रेल्वेमार्ग तयार केला. लोखंडी रुळावरून वाफेच्या जोरावर धावणारी रेल्वे पाहून लोकांना होणारे नवल, रेल्वेविषयी पसरलेल्या अफवा व त्यातून मार्ग काढत सुरू झालेला रेल्वे प्रवास, याचे अतिशय सुंदर, मार्मिक व ओघवत्या शैलीत वर्णन लेखकांनी प्रस्तुत पाठात केले आहे.

In the year 1853, british started single railway track between Mumbai to Thane. Marvel of people watching running railway with help of steam, rumours about railway and finally after many hazards starting journey of railway, have beautifully narrated by writer in very easy and subtle language

शब्दार्थ:

1. रूळ – लोहमार्ग (a railway line)
2. मार्मिक – सूक्ष्म, भेदक (pointed)
3. ओघवते – प्रवाही (flowing)
4. शैली – पद्धत, रीत (style, mode)
5. प्रांत – प्रदेश, विभाग (territory)
6. उठाव – बंड (an outbreak)
7. नामांकित – प्रख्यात (famous, reputed)
8. पाठबळ – भक्कम पाठिंबा (strength of backing. good support)
9. फाटा – भाग (part)
10. आगीनगाडी – रेल्वे, वाफेवर चालणारी रेल्वे (railway train)
11. अचंबा – आश्चर्य, विस्मय (surprise, wonder)
12. मुहूर्त – मंगलदायक, शुभ असा क्षण (an auspicious moment)
13. शृंगार – शोभा, थाट (decoration, adornment)
14. जामानिमा – पोशाख (dress)
15. दुतर्फा – दोन्ही बाजूस (to both sides)
16. – चार युगांपैकी चौथे युग (the forth age)
17. विंग्रजी – इंग्रजी (British)
18. विस्तव – (येथे अर्थ) आग (fire)
19. सांगड – एकत्र जुळणी, जोडणी (Joining together)
20. धीर – धैर्य, संयम (patience, daring)
21. दवंडी – जाहीर घोषणा (a public announcement)
22. सुखाचा – आनंदाचा (happy)
23. कारभारी – (येथे अर्थ) व्यवस्थापक (a manager)
24. आटापीटा – कष्ट, मेहनत, परिश्रम (efforts, hardwork)
25. कंड्या . अफवा, गप्पा (rumours.gossip)
26. भुताटकी – भुतांची किंवा पिशाच्चांची करामत
27. फूस – गुप्तपणे दिलेले उत्तेजन (secret instigation)
28. साळसूद . साधा, प्रामाणिक (honest, simple, innocent)
29. कचेरी – कार्यालय (an office)
30. पेढी – जेथे पैशाच्या देवघेवीचे व्यवहार होतात ते ठिकाण (a place wherer money transactions take place)
31. कारकून – लेखनकाम हिशेब इ. करणारा सेवक (aderk)
32. गुमास्ते – मुनीम (agent)
33. डंका – गाजावाजा, प्रसिद्धी (publicity)
34. लालूच – लोभीपणा (greediness)
35. घोळके – समुदाय, जमाव (groups)
36. आठ आणे – पन्नास पैसे
37. सर्रास – कित्येकवेळा, वारंवार (very frequently)
38. असामी – व्यक्ती (person)
39. झुंबड – आतोनात गर्दी (great crowd, rush)
40. इंजनेर – इंजिनीयर पोखरणे – खणणे, उकरणे (to dig)
41. योजना – बेत (a plan, a programme)
42. सपाट – समतल, उंचसखल नसलेला (flat, smooth)
43. ओपणिंग शिरोमणि – उद्घाटन सोहळा (Opening ceremony)
44. काफिल्ला – प्रवाशांचा तांडा (a group of travellers)
45. सरबराई – पाहुणचार, आदरातिथ्य (hospitality)
46. कंत्राट – मक्ता , ठेका (contract)

टिपा :

1. सर जमशेटजी जिजीभाई – हे प्रसिद्ध पारशी भारतीय व्यापारी होते. ते परोपकारी होते. चीनसोबत व्यापार करून मोठ्या प्रमाणात संपत्ती निर्माण करण्यात ते ऐतिहासिकदृष्ट्या प्रसिद्ध आहेत.
2. जगन्नाथ नाना शंकरशेट – (10 ऑक्टोबर, 1800 – 31 जुलै, 1865). हे मराठी शिक्षणतज्ज्ञ, उद्योगपती होते. मुंबई शहराच्या घडणीत त्यांचा मोठा वाटा मानला जातो.
3. मोरारजी गोकुळदास – हे मुंबईतील कापड उद्योगाचे एक संस्थापक होते. मुंबईत त्यांच्या नावाची एक गिरणी होती.
4. आदमजी पीरभाई – सर आदमजी पीरभाई हे भारतीय उद्योगपती, परोपकारी आणि मुंबईतील दाऊदी बोहरा समाजाचे प्रतिनिधी होते.
5. डेविड ससून – डेविड ससून 1817 ते 1892 दरम्यान बगदादचे खजिनदार होते. मुंबईला स्थलांतरित झाल्यावर ते यहुदी समाजाचा नेता बनले. त्यांच्या नावाचे मुंबईला एक बंदर आहे. (Sassoon dock)
6. बोरघाट – सहयाद्री पर्वतामधला एक घाटरस्ता. हा रस्ता रायगड जिल्ह्यातील खोपोली गावाला व पुणे जिल्हयातील लोणावळा गावाला जोडतो. या घाटाला सामान्यतः खंडाळ्याचा घाट असे म्हटले जाते.

वाक्प्रचार :

1. पाठबळ असणे – पाठिंबा असणे
2. अचंबा वाटणे – आश्चर्य वाटणे
3. जाहीर करणे – घोषित करणे, प्रसिद्ध करणे
4. जामानिमा करणे – नटणे, सर्व पोशाख घालून तयार होणे.
5. आ वासणे – आश्चर्यचकित होणे
6. सांगड घालणे – एकत्र जुळणी करणे
7. दवंडी पिटणे – प्रचार/ प्रसार करणे
8. फूस लावणे – गुप्तपणे/ फसवून उत्तेजन देणे
9. डंका वाजवणे – प्रसिद्धी/ प्रसार करणे
10. धाय मोकलून रडणे – जोरजोरात रडणे
11. टेकीला येणे – शौण होणे, अतिशय थकवा येणे
12. धीर चेपणे – भीती नाहीशी होणे
13. झुंबड होणे – अतोनात गर्दी होणे
14. रवाना होणे – मार्गस्थ होणे
15. नवल वाटणे – आश्चर्य वाटणे

98Balbharti Maharashtra State Board Class 9 Marathi Solutions Aksharbharati Chapter 16 शब्दांचा खेळ Notes, Textbook Exercise Important Questions and Answers.

Maharashtra State Board Class 9 Marathi Aksharbharati Solutions Chapter 16 शब्दांचा खेळ (स्थूलवाचन)

Marathi Aksharbharati Std 9 Digest Chapter 16 शब्दांचा खेळ Textbook Questions and Answers

1. खालील‌ ‌वाक्यांचा‌ ‌अर्थ‌ ‌स्पष्ट‌ ‌करा.‌

प्रश्न‌ ‌(अ)
बाहुलीचे‌ ‌शेकोटीजवळ‌ ‌लोटलेले‌ ‌तुकडे‌ ‌हेलनने‌ ‌गोळा‌ ‌केले.‌ ‌
उत्तरः‌
‌हेलनने‌ ‌रागाच्या‌ ‌भरात‌ ‌बाहुली‌ ‌बाईंकडून‌ ‌हिसकावून‌ ‌ती‌ ‌जमिनीवर‌ ‌आपटली.‌ ‌त्यामुळे‌ ‌बाहुलीचे‌ ‌तुकडे‌ ‌तुकडे‌ ‌झाले‌ ‌होते.‌ ‌पण‌ ‌बाईंच्या‌ ‌सान्निध्यात‌ ‌लेखिकेला‌ ‌एक‌ ‌नवीन‌ ‌दृष्टी‌ ‌मिळाली‌ ‌होती.‌ ‌त्यामुळे‌ ‌आपल्या‌ ‌हातून‌ ‌घडलेल्या‌ ‌चुकीची‌ ‌लेखिकेला‌ ‌जाणीव‌ ‌झाली‌ ‌व‌ ‌वाईटही‌ ‌वाटले.‌ ‌दारापाशी‌ ‌येताच‌ ‌तिला‌ ‌त्या‌ ‌बाहुलीची‌ ‌आठवण‌ ‌आली.‌ ‌त्यामुळेच‌ ‌बाहुलीचे‌ ‌शेकोटीजवळ‌ ‌लोटलेले‌ ‌तुकडे‌ ‌हेलनने‌ ‌गोळा‌ ‌केले.‌ ‌

प्रश्न‌ (‌आ‌)
‌हव्याशा‌ ‌क्षणी‌ ‌हेलन‌ ‌प्रेमाच्या‌ ‌प्रकाशात‌ ‌न्हाऊन‌ ‌निघाली.‌ ‌
उत्तरः‌
‌बाई-अनी‌ ‌मॅन्सफिल्ड‌ ‌सुलिव्हॅन‌ ‌जीवनात‌ ‌येण्यापूर्वी‌ ‌हेलनचे‌ ‌मन‌ ‌राग‌ ‌व‌ ‌कडवटपणानं‌ ‌भरलेले‌ ‌होते.‌ ‌स्वत:च्या‌ ‌भविष्यासाठी‌ ‌स्वत:शीच‌ ‌चाललेल्या‌ ‌सततच्या‌ ‌झगड्यानं‌ ‌हेलन‌ ‌थकून‌ ‌गेली‌ ‌होती.‌ ‌तिचं‌ ‌आयुष्य‌ ‌म्हणजे‌ ‌धुक्यात‌ ‌सापडलेल्या‌ ‌जहाजासारखे‌ ‌झाले‌ ‌होते.‌ ‌होकायंत्र‌ ‌व‌ ‌बंदर‌ ‌याबद्दल‌ ‌हेलनला‌ ‌काहीच‌ ‌कल्पना‌ ‌नव्हती.‌ ‌अशा‌ ‌या‌ ‌निराश,‌ ‌भवितव्य‌ ‌नसलेल्या‌ ‌आयुष्यात‌ ‌अगदी‌ ‌योग्य‌ ‌वेळी‌ ‌बाई‌ ‌ॲनी‌ ‌मॅन्सफिल्ड‌ ‌सुलिव्हॅन‌ ‌यांचा‌ ‌प्रवेश‌ ‌झाला,‌ ‌ज्यांनी‌ ‌हेलनच्या‌ ‌जीवनात‌ ‌मायेची‌ ‌पाखर‌ ‌घातली.‌ ‌अक्षर,‌ ‌शब्द‌ ‌यांचे‌ ‌ज्ञान‌ ‌झाले.‌ ‌त्यामुळे‌ ‌हेलनच्या‌ ‌जीवनात‌ ‌शिक्षणाचा‌ ‌प्रवेश‌ ‌झाला.‌ ‌म्हणून‌ ‌लेखिका‌ ‌हेलन‌ ‌सांगते‌ ‌हव्याशा‌ ‌क्षणी‌ ‌हेलन‌ ‌प्रेमाच्या‌ ‌प्रकाशात‌ ‌न्हाऊन‌ ‌निघाली.‌ ‌

2. ‌w-a-t-e-r‌ ‌शब्द‌ ‌हेलन‌ ‌कशी‌ ‌शिकली‌ ‌हे‌ ‌लिहून‌ ‌आकृती‌ ‌पूर्ण‌ ‌करा.‌ ‌

प्रश्न‌ ‌1.‌
‌w-a-t-e-r‌ ‌शब्द‌ ‌हेलन‌ ‌कशी‌ ‌शिकली‌ ‌हे‌ ‌लिहून‌ ‌आकृती‌ ‌पूर्ण‌ ‌करा.‌ ‌

उत्तरः‌

‌3. जोड्या‌ ‌जुळवा.‌

प्रश्न‌ ‌1.‌
‌जोड्या‌ ‌जुळवा.‌

उत्तरः‌

4. ‌फरक‌ ‌स्पष्ट‌ ‌करा.‌ ‌

प्रश्न‌ ‌1.‌
‌फरक‌ ‌स्पष्ट‌ ‌करा.‌ ‌

उत्तर:‌

5. खालील‌ ‌गटातील‌ ‌लेखननियमांनुसार‌ ‌योग्य‌ ‌शब्द‌ ‌लिहा.‌ ‌

प्रश्न‌ ‌1.‌ ‌
खालील‌ ‌गटातील‌ ‌लेखननियमांनुसार‌ ‌योग्य‌ ‌शब्द‌ ‌लिहा.‌ ‌
‌(अ) शिरीष,‌ ‌शिरिश,‌ ‌शिरीश,‌ ‌शीरीष‌ ‌= [ ]
(‌आ‌) ‌पुनर्वसन,‌ ‌पूनर्वसन,‌ ‌पुनर्वसन,‌ ‌पुनरवसन‌ ‌= [ ]
(इ)‌ ‌पारांपारिक,‌ ‌पारंपरिक,‌ ‌पारंपारीक,‌ ‌पारंपरीक‌ = [ ]
(ई)‌ ‌क्रिडांगण,‌ ‌क्रीडांगण,‌ ‌क्रिडागण,‌ ‌क्रिडांगन‌ ‌= [ ]
उत्तर‌‌:
‌(अ) शिरीष‌ ‌
(‌आ‌)‌ ‌पुनर्वसन‌
(इ)‌ ‌पारंपरिक‌
(ई)‌ ‌क्रीडांगण‌ ‌

6. खालील‌ ‌वाक्यांतील‌ ‌काळ‌ ‌ओळखा.‌ ‌

प्रश्न‌ ‌1.‌ ‌
खालील‌ ‌वाक्यांतील‌ ‌काळ‌ ‌ओळखा.‌ ‌
‌(अ) काल‌ ‌शब्द‌ ‌शिकून‌ ‌घेतले.‌ ‌
(‌आ‌)‌‌ ‌सकाळी‌ ‌आई‌ ‌माझ्या‌ ‌खोलीत‌ ‌येऊन‌ ‌गेली.‌ ‌
(इ)‌ ‌आयुष्यात‌ ‌पहिल्यांदाच‌ ‌मला‌ ‌उदया‌ ‌कधी‌ ‌उगवेल‌ ‌याची‌ ‌उत्कंठा‌ ‌लागली.‌ ‌
उत्तर‌‌:‌
‌(अ) भूतकाळ‌
(‌आ‌)‌‌ ‌भूतकाळ‌ ‌
(इ) ‌भूतकाळ‌

7.‌ ‌स्वमत.‌ ‌

प्रश्न‌ ‌1.‌ ‌
तुमच्या‌ ‌मते‌ ‌हेलन‌ ‌केलर‌ ‌आयुष्यात‌ ‌पहिल्यांदा‌ ‌’उदयाची’‌ ‌वाट‌ ‌का‌ ‌पहात‌ ‌असेल?‌
‌उत्तर‌:‌
‌उतारा‌ ‌6‌ ‌मधील‌ ‌कृती‌ ‌4‌ ‌:‌ ‌स्वमतचे‌ ‌उत्तर‌ ‌पहावे‌ ‌

प्रश्न‌ ‌2.‌ ‌
‘अनी‌ ‌सुलिव्हॅन‌ ‌नसत्या‌ ‌तर‌ ‌हेलन‌ ‌घडली‌ ‌नसती’‌ ‌विधानाची‌ ‌सत्यता‌ ‌पटवून‌ ‌दया.‌
‌उत्तरः‌ ‌
उतारा‌ 4‌ ‌मधील‌ ‌कृती‌ ‌4 ‌:‌ ‌स्वमतचे‌ ‌उत्तर‌ ‌पहावे‌ ‌

‌8.‌ ‌अभिव्यक्ती‌

प्रश्न‌ 1. ‌
तुमच्या‌ ‌मते‌ ‌दिव्यांग‌ ‌मुलांना‌ ‌भाषाशिक्षणात‌ ‌येणारे‌ ‌संभाव्य‌ ‌अडथळे‌ ‌लिहा.‌ ‌
उत्तरः‌ ‌
कोणतीही‌ ‌भाषा‌ ‌शिकताना‌ ‌त्या‌ ‌भाषेची‌ ‌मुळाक्षरे‌ ‌त्यांचे‌ ‌उच्चार‌ ‌माहीत‌ ‌असणे‌ ‌किंवा‌ ‌शिकणे‌ ‌अतिशय‌ ‌आवश्यक‌ ‌असते.‌ ‌जर‌ ‌मुलगा‌ ‌किंवा‌ ‌मुलगी‌ ‌यांना‌ ‌बहिरेपणा‌ ‌असेल‌ ‌तर‌ ‌उच्चारातील‌ ‌आवाज,‌ ‌स्वर‌ ‌ऐकू‌ ‌न‌ ‌आल्याने‌ ‌मुळाक्षरांचे‌ ‌उच्चार‌ ‌ज्ञान‌ ‌होत‌ ‌नाही.‌ ‌मुलगा‌ ‌किंवा‌ ‌मुलगी‌ ‌यांना‌ ‌अंधत्व‌ ‌असेल‌ ‌तर‌ ‌अक्षर‌ ‌ओळखही‌ ‌होत‌ ‌नाही.‌ ‌मुकेपणा‌ ‌जर‌ ‌मुलांमध्ये‌ ‌असेल‌ ‌तर‌ ‌मुळाक्षरांचे,‌ ‌शब्दांचे‌ ‌उच्चार‌ ‌ज्ञान‌ ‌होत‌ ‌नाही.‌ ‌बोलणे,‌ ‌वाचणे,‌ ‌लिहिणे,‌ ‌ऐकणे‌ ‌यातून‌ ‌भाषेचे‌ ‌ज्ञान‌ ‌व‌ ‌भाषेची‌ ‌समृद्धी‌ ‌मुलांना‌ ‌प्राप्त‌ ‌होत‌ ‌असते.‌ ‌परंतु‌ ‌दिव्यांग‌ ‌मुलांना‌ ‌मात्र‌ ‌त्यांच्यातील‌ ‌शारीरिक‌ ‌अपंगत्वामुळे‌ ‌भाषाशिक्षणास‌ ‌मुकावे‌ ‌लागते.‌ ‌

प्रश्न‌ 2. ‌
‌’सर्वसामान्य‌ ‌मुलांबरोबर‌ ‌दिव्यांग‌ ‌मुलांना‌ ‌शिक्षणाची‌ ‌समान‌ ‌संधी‌ ‌दयायला‌ ‌हवी’.‌ ‌या‌ ‌विचाराचे‌ ‌सामाजिक‌ ‌महत्त्व‌ ‌जाणा‌ ‌व‌ ‌ते‌ ‌शब्दबद्ध‌ ‌करा.‌
‌उत्तरः‌
‌उतारा‌ ‌5‌ ‌मधील‌ ‌कृती‌ ‌4‌ ‌:‌ ‌स्वमतचे‌ ‌उत्तर‌ ‌पहावे.‌ ‌

Marathi Akshar Bharati Class 9 Textbook Solutions Chapter 16 शब्दांचा खेळ Additional Important Questions and Answers

1. पुढील उताऱ्याच्या आधारे दिलेल्या सूचनेनुसार कृती करा:

कृती 1 : आकलन कृती

प्रश्न 1.
आकृतिबंध पूर्ण करा.
उत्तर:

प्रश्न 2.
उत्तर लिहा.
उत्तर:

उताऱ्यानुसार घटनांचा क्रम लावा.

प्रश्न 1.

1. लेखिका दारापाशी जाऊन पायऱ्यांवर वाट पाहत राहिली.
2. त्या दिवशी लेखिका दुपारी पोर्चमध्ये उभी होती.
3. काहीतरी वेगळं घडणार याचा लेखिकेला साधारण अंदाज आला होता.

उत्तर:

1. त्या दिवशी लेखिका पोर्चमध्ये उभी होती.
2. काहीतरी वेगळं घडणार याचा लेखिकेला साधारण अंदाज आला होता.
3. लेखिका दारापाशी जाऊन पायऱ्यांवर वाट पाहत राहिली.

खालील प्रश्नांची उत्तरे एका वाक्यात लिहा.

प्रश्न 1.
लेखिकेच्या जीवनातील महत्त्वाचा दिवस कोणता?
उत्तर:
शिक्षिका ॲनी मॅन्सफिल्ड सुलिव्हॅन ज्या दिवशी लेखिकेला शिकवायला आल्या तो दिवस लेखिकेच्या जीवनातील अतिशय महत्त्वाचा दिवस होता.

प्रश्न 2.
लेखिकेला कशाची कल्पना नव्हती?
उत्तर:
लेखिकेला भविष्यात तिच्यासाठी काय चमत्कार लिहून ठेवलाय याची कल्पना नव्हती.

प्रश्न 3.
3 मार्च, 1887 रोजी दुपारी लेखिका कोठे उभी होती?
उत्तरः
3 मार्च, 1887 रोजी दुपारी लेखिका पोर्चमध्ये उभी होती.

प्रश्न 4.
लेखिकेला आठवं वर्ष लागायला किती महिने बाकी होते?
उत्तर:
लेखिकेला आठवं वर्ष लागायला तीन महिने बाकी होते.

प्रश्न 5.
लेखिकेची बोटं कळ्यांवरून कशी फिरली?
उत्तरः
वसंत ऋतूचं स्वागत करायलाच उमलाव्यात तशी लेखिकेची बोटं कळ्यांवरून फिरली.

प्रश्न 6.
कंसातील योग्य शब्द वापरून रिकाम्या जागा भरा.

1. भविष्यात माझ्यासाठी काय ……लिहून ठेवलाय, याची काही मला कल्पना नव्हती. (अभिवादन, नमस्कार, आशीर्वाद, चमत्कार)
2. म्हणून मी दारापाशी जाऊन …………. वाट पाहत राहिले. (आतुरतेने, पायऱ्यांवर, खिडकीपाशी, पोर्चवर)
3. मला आठवं वर्ष लागायला …………. महिने बाकी हो. (एक, चार, तीन, पाच)

उत्तर:

1. चमत्कार
2. पायऱ्यांवर
3. तीन

कृती 2. आकलन कृती

योग्य पर्याय निवडून विधाने पूर्ण करा.

प्रश्न 1.
आयुष्यातला महत्त्वाचा दिवस म्हणजे माझ्या …………………….
(अ) बाई सुलिव्हॅन अॅनी मॅन्सफिल्ड मला शिकवायला आल्या तो दिवस.
(ब)‌ ‌बाई‌ ‌मॅन्सफिल्ड‌ ‌सुलिव्हॅन‌ ‌अॅनी‌ ‌मला‌ ‌शिकवायला‌ ‌आल्या‌ ‌तो‌ ‌दिवस.‌ ‌
(क)‌ ‌बाई‌ ‌ॲनी‌ ‌मॅन्सफिल्ड‌ ‌सुलिव्हॅन‌ ‌मला‌ ‌शिकवायला‌ ‌आल्या‌ ‌तो‌ ‌दिवस.‌ ‌
(ड)‌ ‌बाई‌ ‌मॅन्सफिल्ड‌ ‌अॅनी‌ ‌सुलिव्हॅन‌ ‌मला‌ ‌शिकवायला‌ ‌आल्या‌ ‌तो‌ ‌दिवस.‌ ‌
उत्तर:‌ ‌
आयुष्यातला‌ ‌महत्त्वाचा‌ ‌दिवस‌ ‌म्हणजे‌ ‌माझ्या‌ ‌बाई‌ ‌ॲनी‌ ‌मॅन्सफिल्ड‌ ‌सुलिव्हॅन‌ ‌मला‌ ‌शिकवायला‌ ‌आल्या‌ ‌तो‌ ‌दिवस.‌ ‌

प्रश्न 2.
भविष्यात‌ ‌माझ्यासाठी‌ ‌काय‌ ‌चमत्कार‌ ‌लिहून‌ ‌ठेवलाय,‌ ‌…………….‌
‌(अ)‌ ‌याची‌ ‌काही‌ ‌मला‌ ‌कल्पना‌ ‌नव्हती.‌ ‌
(ब)‌ ‌याची‌ ‌काही‌ ‌मला‌ ‌कल्पना‌ ‌होती.‌ ‌
(क)‌ ‌याची‌ ‌काही‌ ‌मला‌ ‌हळूहळू‌ ‌कल्पना‌ ‌आली‌ ‌होती.‌ ‌
(ड)‌ ‌याची‌ ‌मला‌ ‌पुरेपूर‌ ‌कल्पना‌ ‌होती.‌
‌उत्तरः‌
‌भविष्यात‌ ‌माझ्यासाठी‌ ‌काय‌ ‌चमत्कार‌ ‌लिहून‌ ‌ठेवलाय,‌ ‌याची‌ ‌काही‌ ‌मला‌ ‌कल्पना‌ ‌नव्हती.‌ ‌

प्रश्न 3.
कोण‌ ‌ते‌ ‌लिहा.‌
‌उत्तरः‌

प्रश्न 4.
सत्य‌ ‌वा‌ ‌असत्य‌ ‌ते‌ ‌लिहा.‌ ‌-‌
1. लेखिका‌ ‌दारापाशी‌ ‌जाऊन‌ ‌पायऱ्यांवर‌ ‌वाट‌ ‌पाहत‌ ‌राहिली.‌
2. लेखिकेला‌ ‌आठवं‌ ‌वर्ष‌ ‌लागायला‌ ‌पाच‌ ‌महिने‌ ‌बाकी‌ ‌होते.‌ ‌
उत्तर:‌
1. सत्य‌
2. असत्य‌

‌कृती‌ ‌3:‌ ‌व्याकरण‌ ‌कृती‌

‌खालील‌ ‌वाक्ये‌ ‌लेखननियमांनुसार‌ ‌शुद्ध‌ ‌करून‌ ‌लिहा.‌

प्रश्न 1.
मला‌ ‌आठवं‌ ‌वर्ष‌ ‌लागायला‌ ‌तिन‌ ‌महीने‌ ‌बाकी‌ ‌होते.‌
‌उत्तरः‌ ‌
मला‌ ‌आठवं‌ ‌वर्ष‌ ‌लागायला‌ ‌तीन‌ ‌महिने‌ ‌बाकी‌ ‌होते.‌

प्रश्न 2.
दोन‌ ‌अगदी‌ ‌परस्परविरोधि‌ ‌आयूष्यं‌ ‌कशी‌ ‌एकत्र‌ ‌येतात.‌ ‌
उत्तरः‌
‌दोन‌ ‌अगदी‌ ‌परस्परविरोधी‌ ‌आयुष्यं‌ ‌कशी‌ ‌एकत्र‌ ‌येतात.‌

प्रश्न 3.
उताऱ्यातील‌ ‌दोन‌ ‌विशेषणे/नामे/सर्वनामे‌ ‌शोधून‌ ‌लिहा.‌ ‌
उत्तर:‌

1. ‌सर्वनामे:‌ ‌मी,‌ ‌माझ्या,‌ ‌मला,‌ ‌माझी‌ ‌
2. ‌नामे:‌ ‌आई,‌ ‌पोर्च,‌ ‌दार,‌ ‌पायरी,‌ ‌ऊन‌ ‌
3. ‌विशेषणे:‌ ‌शांत,‌ ‌लगबग‌

प्रश्न 4.
अचूक‌ ‌शब्द‌ ‌लिहा.
1. भविषयात,‌ ‌भवीष्यात,‌ ‌भविष्यात,‌ ‌भवविष्यात‌ ‌
2. चमत्कार,‌ ‌चमतकार,‌ ‌चत्मकार,‌ ‌चममकार‌ ‌
उत्तर:‌
1. ‌भविष्यात‌ ‌
2.‌ ‌चमत्कार‌ ‌

‌खालील‌ ‌शब्दांसाठी‌ ‌पाठात‌ ‌आलेले‌ ‌समान‌ ‌अर्थाचे‌ ‌शब्द‌ ‌शोधा.‌ ‌

प्रश्न 1.
‌खालील‌ ‌शब्दांसाठी‌ ‌पाठात‌ ‌आलेले‌ ‌समान‌ ‌अर्थाचे‌ ‌शब्द‌ ‌शोधा.‌
उत्तर:‌

प्रश्न 5.
विरुद्धार्थी‌ ‌शब्द‌ ‌लिहा.‌ ‌

1. 1. असाधारण ×
2. सावली‌ ‌×
3. रात्र‌ ×
4. ‌शांत‌ ×

उत्तर:‌ ‌

1. ‌साधारण‌
2. ‌ऊन‌
3. ‌दिवस‌ ‌
4. ‌अशांत‌

प्रश्न 6.
उताऱ्यातील‌ ‌दोन‌ ‌अनेकवचनी‌ ‌शब्द‌ ‌शोधून‌ ‌लिहा.‌ ‌
उत्तर:‌

1. ‌महिने‌
2. पायऱ्या‌
3. ‌जाळ्या‌
4. सवयी‌ ‌
5. कळ्यां‌ ‌
6. खाणाखुणा‌
7. ‌आठवणी‌ ‌
8. ‌बोटं‌ ‌

प्रश्न 7.
‌तक्ता‌ ‌पूर्ण‌ ‌करा.‌
उत्तर:‌

प्रश्न 8.
तक्ता‌ ‌पूर्ण‌ ‌करा.‌ ‌
उत्तर:‌

खालील‌ ‌वाक्यांत‌ ‌कंसातील‌ ‌वाक्प्रचारांचा‌ ‌वापर‌ ‌करा.‌ ‌(नवल‌ ‌वाटणे,‌ ‌कल्पना‌ ‌नसणे)‌ ‌

प्रश्न 1.
1. भविष्यात‌ ‌काय‌ ‌करायचे‌ ‌आहे‌ ‌याची‌ ‌रमेशला‌ ‌काहीही‌ ‌माहिती‌ ‌नव्हती.‌
‌2.‌ ‌आकाशात‌ ‌पसरलेलं‌ ‌इंद्रधनुष्य‌ ‌पाहून‌ ‌सर्वांना‌ ‌आश्चर्य‌ ‌वाटले.‌ ‌
उत्तर:‌
‌1.‌ ‌भविष्यात‌ ‌काय‌ ‌करायचे‌ ‌आहे‌ ‌याची‌ ‌रमेशला‌ ‌काहीही‌ ‌कल्पना‌ ‌नव्हती.‌
2.‌ ‌आकाशात‌ ‌पसरलेलं‌ ‌इंद्रधनुष्य‌ ‌पाहून‌ ‌सर्वांना‌ ‌नवल‌ ‌वाटले.‌ ‌

काळ‌ ‌बदला.‌ ‌

प्रश्न 1.
याची‌ ‌काही‌ ‌मला‌ ‌कल्पना‌ ‌नव्हती.‌ ‌(भविष्यकाळ‌ ‌करा)‌ ‌
उत्तर:‌
‌याची‌ ‌काही‌ ‌कल्पना‌ ‌मला‌ ‌नसेल.‌ ‌

प्रश्न 2.
आज‌ ‌काहीतरी‌ ‌वेगळं‌ ‌घडणार‌ ‌याचा‌ ‌मला‌ ‌साधारणअंदाज‌ ‌आला.‌ ‌(भविष्यकाळ‌ ‌करा)‌ ‌
उत्तर:‌ ‌
आज‌ ‌काहीतरी‌ ‌वेगळं‌ ‌घडणारं‌ ‌याचा‌ ‌मला‌ ‌साधारण‌ ‌अंदाज‌ ‌येईल.‌ ‌

प्रश्न 3.
पर्यायी‌ ‌शब्द‌ ‌लिहा.‌ ‌
उत्तर:‌ ‌

‌कृती‌ ‌4‌ ‌:‌ ‌स्वमत‌ ‌

प्रश्न 1.
तुमच्या‌ ‌आठवणीतला‌ ‌महत्त्वाचा‌ ‌दिवस‌ ‌कोणता‌ ‌व‌ ‌का‌ ‌याबद्दल‌ ‌तुमचे‌ ‌विचार‌ ‌व्यक्त‌ ‌करा.‌ ‌
उत्तर:‌ ‌
माझ्या‌ ‌आठवणीतला‌ ‌महत्त्वाचा‌ ‌दिवस‌ 10‌ ‌डिसेंबर,‌ ‌2015 आहे.‌ ‌त्याला‌ ‌कारणही‌ ‌तसेच‌ ‌आहे.‌ ‌या‌ ‌दिवशी‌ ‌मला‌ ‌आंतर-‌ ‌विदयालयीन‌ ‌भाषण‌ ‌स्पर्धेत‌ ‌प्रथम‌ ‌पारितोषिक‌ ‌मिळाले‌ ‌व‌ ‌ते‌ ‌ही‌ ‌महाराष्ट्र‌ ‌राज्याच्या‌ ‌मुख्यमंत्र्यांच्या‌ ‌हस्ते!‌ ‌मला‌ ‌आतापर्यंतच्या‌ ‌विदयार्थी‌ ‌जीवनात‌ ‌मिळालेले‌ ‌हे‌ ‌पहिलेच‌ ‌बक्षीस‌ ‌होते.‌ ‌त्यामुळे‌ ‌मला‌ ‌या‌ ‌दिवसाचे‌ ‌विशेष‌ ‌आकर्षण‌ ‌आहे.‌ ‌प्रथमच‌ ‌आयुष्यात‌ ‌मिळालेल्या‌ ‌पहिल्या‌ ‌यशाचा‌ ‌हा‌ ‌दिवस‌ ‌आहे.‌ ‌तो‌ ‌मी‌ ‌कधी‌ ‌विसरणे‌ ‌शक्यच‌ ‌नाही.‌ ‌मला‌ ‌आजही‌ ‌आठवतोय‌ ‌तो‌ ‌दिवस.‌ ‌माझे‌ ‌भाषण‌ ‌ऐकून‌ ‌सर्वांनी‌ ‌माझे‌ ‌कौतुक‌ ‌केले.‌ ‌स्वतः‌ ‌मुख्यमंत्र्यांनी‌ ‌माझे‌ ‌भाषण‌ ‌ऐकून‌ ‌भविष्यात‌ ‌मला‌ ‌नेता‌ ‌होण्यास‌ ‌सांगितले.‌ ‌म्हणून‌ ‌हा‌ ‌माझ्या‌ ‌आयुष्यातील‌ ‌महत्त्वाचा‌ ‌दिवस‌ ‌आहे.‌ ‌

‌पुढील‌ ‌उताऱ्याच्या‌ ‌आधारे‌ ‌दिलेल्या‌ ‌सूचनेनुसार‌ ‌कृती‌ ‌करा:‌ ‌

कृती‌ ‌1‌ ‌:‌ ‌आकलन‌ ‌कृती‌ ‌

प्रश्न 1.
‌आकृतिबंध‌ ‌पूर्ण‌ ‌करा.‌ ‌
उत्तर:‌

प्रश्न 2.
जोड्या‌ ‌जुळवा.‌

उत्तर:‌

प्रश्न 3.
उताऱ्यानुसार‌ ‌घटनांचा‌ ‌क्रम‌ ‌लावा.‌

1. प्रेमाच्या‌ ‌प्रकाशात‌ ‌लेखिका‌ ‌न्हाऊन‌ ‌निघाली.‌ ‌
2. ‌लेखिकेच्या‌ ‌आत्म्याचं‌ ‌नि:शब्द‌ ‌आक्रंदन‌ ‌चालायचं.‌ ‌
3. लेखिकेकडे‌ ‌होकायंत्र‌ ‌वगैरे‌ ‌काहीचं‌ ‌नव्हतं.‌
4. मन‌ ‌रागानं‌ ‌आणि‌ ‌कडवटपणानं‌ ‌व्यग्र‌ ‌झालं‌ ‌होतं.‌ ‌

उत्तर:‌

1. ‌मन‌ ‌रागानं‌ ‌आणि‌ ‌कडवटपणानं‌ ‌व्यग्र‌ ‌झालं‌ ‌होतं.‌ ‌
2. लेखिकेकडे‌ ‌होकायंत्र‌ ‌वगैरे‌ ‌काहीचं‌ ‌नव्हतं.‌
3. ‌लेखिकेच्या‌ ‌आत्म्याचं‌ ‌नि:शब्द‌ ‌आक्रंदन‌ ‌चालायचं‌ ‌
4. ‌प्रेमाच्या‌ ‌प्रकाशात‌ ‌लेखिका‌ ‌न्हाऊन‌ ‌निघाली.‌

खालील‌ ‌प्रश्नांची‌ ‌उत्तरे‌ ‌एका‌ ‌वाक्यात‌ ‌लिहा.‌ ‌

प्रश्न 1.
‌लेखिका‌ ‌कशाने‌ ‌थकून‌ ‌गेली‌ ‌होती?‌
‌उत्तरः‌
‌लेखिका‌ ‌स्वत:शीच‌ ‌चाललेल्या‌ ‌सततच्या‌ ‌झगड्यानं‌ ‌अगदी‌ ‌थकून‌ ‌गेली‌ ‌होती.‌

‌प्रश्न 2.
शिक्षणाला‌ ‌सुरुवात‌ ‌होण्यापूर्वी‌ ‌लेखिकेची‌ ‌अवस्था‌ ‌कशी‌ ‌होती?‌ ‌
उत्तरः‌
‌शिक्षणाला‌ ‌सुरुवात‌ ‌होण्याआधी‌ ‌लेखिकेची‌ ‌अवस्था‌ ‌धुक्यात‌ ‌सापडलेल्या‌ ‌जहाजासारखी‌ ‌होती.‌ ‌

‌प्रश्न 3.
लेखिका‌ ‌कशाच्या‌ ‌प्रकाशात‌ ‌न्हाऊन‌ ‌निघाली?‌ ‌
उत्तर:‌
‌लेखिका‌ ‌प्रेमाच्या‌ ‌प्रकाशात‌ ‌न्हाऊन‌ ‌निघाली.‌ ‌

‌प्रश्न 4.
कंसातील‌ ‌योग्य‌ ‌शब्द‌ ‌वापरून‌ ‌रिकाम्या‌ ‌जागा‌ ‌भरा.‌

1. ‌नेमक्या‌ ‌त्याच‌ ‌हव्याश्या‌ ‌क्षणी‌ ‌…………..‌ ‌प्रकाशात‌ ‌मी‌ ‌न्हाऊन‌ ‌निघाले.‌ ‌(मोकळ्या,‌ ‌अंधकार,‌ ‌प्रेमाच्या,‌ ‌रागाच्या)‌
2. किनारा‌ ‌गाठेपर्यंत‌ ‌….‌…………..‌ ‌असतो.‌ ‌q(ताण,‌ ‌त्रास,‌ ‌व्यग्र,‌ ‌धुकं)‌ ‌
3. ‌छाती‌ ‌…‌…….‌….‌ ‌असते.‌ ‌(घाबरत,‌ ‌धडधडत,‌ ‌धडपडत,‌ ‌धबधबत)‌ ‌
4. असं‌ ‌माझ्या‌ ‌……………… नि:शब्द‌ ‌आक्रंदन‌ ‌चालायचं.‌ ‌(जीवनाचं,‌ ‌आत्म्याचं,‌ ‌मनाचं,‌ ‌जीवाचं)‌

उत्तर:‌

1. ‌प्रेमाच्या‌ ‌
2. ताण‌ ‌
3. धडधडत‌
4. आत्म्याचं‌ ‌

कृती‌ ‌2‌ ‌:‌ ‌आकलन‌ ‌कृती‌

योग्य‌ ‌पर्याय‌ ‌निवडून‌ ‌विधाने‌ ‌पूर्ण‌ ‌करा.‌

‌प्रश्न 1.
शिक्षणाला‌ ‌सुरुवात‌ ‌होण्याआधी‌ ‌माझी‌ ‌अवस्था‌ ‌……………..‌ ‌
(अ)‌ ‌त्या‌ ‌धुक्यात‌ ‌न‌ ‌सापडलेल्या‌ ‌जहाजासारखी‌ ‌होती.‌ ‌
(ब)‌ ‌त्या‌ ‌धुक्यात‌ ‌सापडलेल्या‌ ‌बोटीसारखी‌ ‌होती.‌
‌(क)‌ ‌त्या‌ ‌धुक्यात‌ ‌न‌ ‌सापडलेल्या‌ ‌बोटीसारखी‌ ‌होती.‌ ‌
(ड)‌ ‌त्या‌ ‌धुक्यात‌ ‌सापडलेल्या‌ ‌जहाजासारखी‌ ‌होती.‌ ‌
उत्तरः‌
‌शिक्षणाला‌ ‌सुरुवात‌ ‌होण्याआधी‌ ‌माझी‌ ‌अवस्था‌ ‌त्या‌ ‌धुक्यात‌ ‌सापडलेल्या‌ ‌जहाजासारखी‌ ‌होती.‌ ‌

‌प्रश्न 2.
सहज‌ ‌स्पर्श‌ ‌करता‌ ‌येईल‌ ‌अशा‌ ‌पांढऱ्या‌ ‌…………..‌ ‌
(अ)‌ अंधारानं‌ ‌आपल्याला‌ ‌वेढलंय‌ ‌आणि‌ ‌तशा‌ ‌धुक्यातून‌ ‌जहाज‌ ‌वाट‌ ‌काढत‌ ‌किनाऱ्याच्या‌ ‌विरूद्ध‌ ‌दिशेनं‌ ‌येत‌ ‌असतं.‌ ‌
(ब)‌ अंधारानं‌ ‌आपल्याला‌ ‌वेढलंय‌ ‌आणि‌ ‌तशा‌ ‌धुक्यातून‌ ‌जहाज‌ ‌वाट‌ काढत‌ ‌किनाऱ्याच्या‌ ‌दिशेनं‌ ‌येत‌ ‌असतं.‌
‌(क)‌ ‌अंधारानं‌ ‌आपल्याला‌ ‌वेढलंय‌ ‌आणि‌ ‌तशा‌ ‌धुक्यातून‌ ‌जहाज‌ ‌वाट‌ ‌न‌ ‌काढता‌ ‌किनाऱ्याच्या‌ ‌दिशेनं‌ ‌येत‌ ‌असतं.‌
‌(ड)‌ ‌अंधारानं‌ ‌आपल्याला‌ ‌वेढलंय‌ ‌आणि‌ ‌तशा‌ ‌धुक्यातून‌ ‌जहाज‌ ‌वाट‌ ‌न‌ ‌काढता‌ ‌किनाऱ्याच्या‌ ‌विरूद्ध‌ ‌दिशेनं‌ ‌येत‌ ‌असतं.‌
‌उत्तरः‌
‌सहज‌ ‌स्पर्श‌ ‌करता‌ ‌येईल‌ ‌अशा‌ ‌पांढऱ्या‌ ‌अंधारानं‌ ‌आपल्याला‌ ‌वेढलंय‌ ‌आणि‌ ‌तशा‌ ‌धुक्यातून‌ ‌जहाज‌ ‌वाट‌ ‌काढत‌ ‌किनाऱ्याच्या‌ ‌दिशेनं‌ ‌येत‌ ‌असतं.‌

‌प्रश्न 3.
परिच्छेदावरून‌ ‌खालील‌ ‌विधाने‌ ‌चूक‌ ‌की‌ ‌बरोबर‌ ‌ते‌ ‌लिहा.‌ ‌

1. ‌स्वत:शीच‌ ‌चाललेल्या‌ ‌सततच्या‌ ‌झगड्यानं‌ ‌लेखिकाअगदी‌ ‌थकून‌ ‌गेली‌ ‌होती.‌
2. ‌किनारा‌ ‌गाठेपर्यंत‌ ‌ताण‌ ‌नसतो.
3. ‌लेखिकेकडे‌ ‌होकायंत्र‌ ‌असल्यामुळे‌ ‌बंदर‌ ‌किती‌ ‌जवळ‌ ‌आहे‌ ‌हे‌ ‌काळायला‌ ‌मार्ग‌ ‌होता.‌ ‌

उत्तर:

1. ‌बरोबर‌
2. ‌चूक‌ ‌
3. ‌चूक‌

‌कृती‌ ‌3 ‌:‌ ‌व्याकरण‌ ‌कृती‌ ‌

खालील‌ ‌वाक्ये‌ ‌लेखननियमांनुसार‌ ‌शुद्ध‌ ‌करून‌ ‌लिहा.‌

‌प्रश्न 1.
कीनारा‌ ‌गाठेपरर्यत‌ ‌ताण‌ ‌असतो.‌ ‌
उत्तरः‌ ‌
किनारा‌ ‌गाठेपर्यंत‌ ‌ताण‌ ‌असतो.‌ ‌

‌प्रश्न 2.
स्वत:शीच‌ ‌चाललेल्या‌ ‌सततच्या‌ ‌झगड्यानं‌ ‌मि‌ ‌अगदि‌ ‌थकून‌ ‌गेले‌ ‌होते.‌ ‌
उत्तरः‌ ‌
स्वत:शीच‌ ‌चाललेल्या‌ ‌सततच्या‌ ‌झगड्यानं‌ ‌मी‌ ‌अगदी‌ ‌थकून‌ ‌गेले‌ ‌होते.‌ ‌

‌प्रश्न 3.
उताऱ्यातील‌ ‌दोन‌ ‌विशेषणे/नामे/सर्वनामे‌ ‌शोधून‌ ‌लिहा.‌
उत्तरः‌ ‌

1. ‌‌सर्वनामे:‌ ‌स्वतः,‌ ‌माझी,‌ ‌मी‌ ‌
2. ‌नामे:‌ ‌मन,‌ ‌प्रकाश,‌ ‌शिक्षण,‌ ‌जहाज,‌ ‌धुकं‌ ‌
3. विशेषणे:‌ ‌व्यग्र,‌ ‌दाट,‌ ‌नाम‌ ‌

‌अचूक‌ ‌शब्द‌ ‌लिहा.‌ ‌

‌प्रश्न 1.
आतम्याचं,‌ ‌आत्म्याचं,‌ ‌आत्माचं,‌ ‌आतमयाचं‌
‌उत्तर:‌
‌आत्म्याचं‌ ‌

‌प्रश्न 2.
लुकलुकत्या,‌ ‌लूकलूकत्या,‌ ‌लुकलुकत्या,‌ ‌लुकलुकत्या‌ ‌
उत्तर‌‌:‌
‌लुकलुकत्या‌ ‌

अधोरेखित‌ ‌शब्दाचा‌ ‌समानार्थी‌ ‌शब्द‌ ‌लिहून‌ ‌वाक्य‌ ‌पुन्हा‌ ‌लिहा.‌ ‌

‌प्रश्न 1.
दाट‌ ‌धुकं‌ ‌असताना‌ ‌तुम्ही‌ ‌कधी‌ ‌सागरावर‌ ‌गेलायत?‌ ‌
उत्तरः‌
‌दाट‌ ‌धुकं‌ ‌असताना‌ ‌तुम्ही‌ ‌कधी‌ ‌समुद्रावर‌ ‌गेलायत?‌ ‌

‌प्रश्न 2.
अधोरेखित‌ ‌शब्दाचा‌ ‌विरुद्धार्थी‌ ‌शब्द‌ ‌वापरून‌ ‌वाक्य‌ ‌पुन्हा‌ ‌लिहा.‌
‌शिक्षणाला‌ ‌सुरुवात‌ ‌होण्याआधी‌ ‌माझी‌ ‌अवस्था‌ ‌त्या‌ ‌धुक्यात‌ ‌सापडलेल्या‌ ‌जहाजासारखी‌ ‌होती.‌ ‌
उत्तर:‌ ‌
शिक्षणाचा‌ ‌शेवट‌ ‌होण्याआधी‌ ‌माझी‌ ‌अवस्था‌ ‌त्या‌ ‌धुक्यात‌ ‌सापडलेल्या‌ ‌जहाजासारखी‌ ‌होती.‌ ‌

‌प्रश्न 3.
अधोरेखित‌ ‌शब्दाची‌ ‌जात‌ ‌ओळखा.‌ ‌
राम‌ ‌व‌ ‌शाम‌ ‌दोघे‌ ‌मित्र‌ ‌आहेत.‌ ‌
उत्तर:‌
‌उभयान्वयी‌ ‌अव्यय‌ ‌

‌प्रश्न 4.
तक्ता‌ ‌पूर्ण‌ ‌करा.‌ ‌
उत्तर:‌

‌प्रश्न 5.
‌तक्ता‌ ‌पूर्ण‌ ‌करा.‌ ‌
उत्तर:‌

‌प्रश्न 6.
वाक्प्रचारांचा‌ ‌अर्थ‌ ‌लिहा.‌
1. ‌व्यग्र‌ ‌होणे‌ ‌- [ ]
2. ताण‌ ‌असणे‌ ‌-‌ ‌[ ]
उत्तर:‌
1. व्यस्त‌ ‌होणे‌
2. भार‌ ‌असणे,‌ ‌तणाव‌ ‌असणे‌ ‌

‌

प्रश्न 7.
वाक्यातील‌ ‌काळ‌ ‌ओळखा.‌ ‌
तेही‌ ‌कळायला‌ ‌काही‌ ‌मार्ग‌ ‌नव्हता.‌ ‌
उत्तर‌‌:‌
‌भूतकाळ‌ ‌

‌प्रश्न 8.
पर्यायी‌ ‌शब्द‌ ‌लिहा.‌ ‌
उत्तर‌‌:‌

कृती‌ ‌4 ‌:‌ ‌स्वमत‌ ‌

‌प्रश्न 1.
तुमची‌ ‌अवस्था‌ ‌कधी‌ ‌धुक्यात‌ ‌सापडलेल्या‌ ‌जहाजासारखी‌ ‌झाली‌ ‌आहे‌ ‌का?‌ ‌त्यातून‌ ‌तुम्ही‌ ‌मार्ग‌ ‌काढण्याचा‌ ‌कसा‌ ‌प्रयत्न‌ ‌केलात‌ ‌हे‌ ‌थोडक्यात‌ ‌लिहा.‌
उत्तर‌‌:‌
जीवन‌ ‌म्हटले‌ ‌म्हणजे‌ ‌संघर्ष‌ ‌हा‌ ‌आलाच.‌ ‌लहान‌ ‌असो‌ ‌किंवा‌ ‌मोठे.‌ ‌संकटे‌ ‌ही‌ ‌सर्वांवरच‌ ‌येत‌ ‌असतात.‌ ‌त्यावेळी‌ ‌आपली‌ ‌अवस्था‌ ‌धुक्यात‌ ‌सापडलेल्या‌ ‌जहाजासारखी‌ ‌होत‌ ‌असते.‌ ‌काय‌ ‌करावे‌ ‌व‌ ‌काय‌ ‌नाही‌ ‌याबद्दल‌ ‌नेमके‌ ‌काय‌ ‌ते‌ ‌सुचतच‌ ‌नाही.‌ ‌गोंधळून‌ ‌जाणारी‌ ‌स्थिती‌ ‌निर्माण‌ ‌होते.‌ ‌लहानपणी‌ ‌एकदा‌ ‌आईबरोबर‌ ‌बाजारात‌ ‌गेलेलो‌ ‌असताना‌ ‌गर्दीमुळे‌ ‌मी‌ ‌आईपासून‌ ‌दुरावलो‌ ‌व‌ ‌रडत‌ ‌रडत‌ ‌आईला‌ ‌शोधत‌ ‌राहिलो.‌ ‌मला‌ ‌आई‌ ‌कुठेच‌ ‌दिसली‌ ‌नाही.‌ ‌माझी‌ ‌अवस्था‌ ‌त्यावेळी‌ ‌खरोखरच‌ ‌धुक्यात‌ ‌सापडलेल्या‌ ‌जहाजासारखीच‌ ‌झाली‌ ‌होती.‌ ‌लोकांनी‌ ‌माझ्याभोवती‌ ‌गर्दी‌ ‌केली.‌ ‌मला‌ ‌माझे‌ ‌नाव‌ ‌विचारले‌ ‌मी‌ ‌रडत‌ ‌रडत‌ ‌त्यांना‌ ‌गणपती‌ ‌मंदिराजवळ‌ ‌राहतो‌ ‌असे‌ ‌सांगितले‌ ‌दोन‌ ‌व्यक्ती‌ ‌मला‌ ‌मंदिराजवळ‌ ‌घेऊन‌ ‌आल्या.‌ ‌तेथेही‌ ‌गर्दी‌ ‌जमली‌ ‌होती.‌ ‌माझी‌ ‌आई‌ ‌तेथे‌ ‌बसून‌ ‌रडत‌ ‌होती.‌ ‌आईला‌ ‌पाहून‌ ‌मी‌ ‌तिला‌ ‌घट्ट‌ ‌मिठी‌ ‌मारली.‌ ‌

पुढील‌ ‌उताऱ्याच्या‌ ‌आधारे‌ ‌दिलेल्या‌ ‌सूचनेनुसार‌ ‌कृती‌ ‌करा:‌ ‌

कृती‌ ‌1 ‌:‌ ‌आकलन‌ ‌कृती‌

‌प्रश्न 1.
आकृतिबंध‌ ‌पूर्ण‌ ‌करा.‌ ‌
उत्तर‌‌:‌

‌प्रश्न 2.
‌सहसंबंध‌ ‌लिहा.‌
1. ‌मायेची:‌ ‌पाखर‌ ‌::‌ ‌बालसुलभ‌ ‌: …………..
2.‌ ‌हॅट‌ ‌:‌ ‌शब्द‌ ‌::‌ ‌बसणं‌ ‌:‌ ‌………………….
‌उत्तर:‌
1. आनंद‌ ‌
2.‌ ‌क्रियापद

उताऱ्यानुसार‌ ‌घटनांचा‌ ‌क्रम‌ ‌लावा.‌

‌प्रश्न 1.

1. ‌अंध‌ ‌मुलांनी‌ ‌लेखिकेला‌ ‌एक‌ ‌बाहुली‌ ‌दिली‌ ‌होती.‌ ‌
2. ‌बोटांच्या‌ ‌खेळाद्वारे‌ ‌लेखिका‌ ‌शब्द‌ ‌व‌ ‌क्रियापदं‌ ‌शिकली.‌ ‌
3. ‌दुसऱ्या‌ ‌दिवशी‌ ‌सकाळीच‌ ‌बाई‌ ‌लिखिकेला‌ ‌आपल्या‌ ‌खोलीत‌ ‌घेऊन‌ ‌गेल्या.‌
4. ‌बाईंनी‌ ‌लेखिकेच्या‌ ‌हातावर‌ ‌स्वत:च्या‌ ‌बोटांनी‌ ‌अक्षरं‌ ‌जुळवली.‌ ‌

उत्तर:‌

1. ‌दुसऱ्या‌ ‌दिवशी‌ ‌सकाळीच‌ ‌बाई‌ ‌लिखिकेला‌ ‌आपल्या‌ ‌खोलीत‌ ‌घेऊन‌ ‌गेल्या.‌
2. ‌अंध‌ ‌मुलांनी‌ ‌लेखिकेला‌ ‌एक‌ ‌बाहुली‌ ‌दिला‌ ‌होती.‌
3. ‌बाईंनी‌ ‌लेखिकेच्या‌ ‌हातावर‌ ‌स्वत:च्या‌ ‌बोटांनी‌ ‌अक्षरं‌ ‌जुळवली.‌
4. ‌बोटांच्या‌ ‌खेळाद्वारे‌ ‌लेखिका‌ ‌शब्द‌ ‌व‌ ‌क्रियापदं‌ ‌शिकली.‌

खालील‌ ‌प्रश्नांची‌ ‌उत्तरे‌ ‌एका‌ ‌वाक्यात‌ ‌लिहा.‌

‌प्रश्न 1.
बाहुली‌ ‌कोणी‌ ‌सजवली‌ ‌होती?‌
‌उत्तर:‌ ‌
बाहुली‌ ‌लॉरा‌ ‌ब्रिजमननं‌ ‌सजवली‌ ‌होती.‌ ‌

‌प्रश्न 2.
लेखिकेच्या‌ ‌बाई‌ ‌शिकविण्याबरोबरच‌ ‌काय‌ ‌करायला‌ ‌आल्या‌ ‌होत्या?‌ ‌
उत्तर:‌ ‌
लेखिकेच्या‌ ‌बाई‌ ‌शिकविण्याबरोबर‌ ‌लेखिकेवर‌ ‌मायेची‌ ‌पाखर‌ ‌घालायला‌ ‌आल्या‌ ‌होत्या.‌

‌प्रश्न 3.
लेखिकेला‌ ‌कोणता‌ ‌खेळ‌ ‌आवडला?‌ ‌
उत्तरः‌ ‌
लेखिकेला‌ ‌बोटांचा‌ ‌खेळ‌ ‌खूप‌ ‌आवडला.‌

‌प्रश्न 4.
कंसातील‌ ‌योग्य‌ ‌शब्द‌ ‌वापरून‌ ‌रिकाम्या‌ ‌जागा‌ ‌भरा.‌

1. ……….‌ ‌हा‌ ‌बोटांचा‌ ‌खेळ‌ ‌मला‌ ‌फार‌ ‌आवडला.‌ ‌(P-I-N,‌ ‌m-u-q, d-O-1-1,‌ ‌W-A-T-E-R)‌
2. त्याहीपेक्षा‌ ‌जास्त‌ ‌माझ्यावर‌ ‌…………‌ ‌पाखर‌ ‌घालायला.‌ ‌(मायेची,‌ ‌प्रेमाची,‌ ‌अभिमानाची,‌ ‌आनंदाची)‌ ‌
3. धावतच‌ ‌…………. उतरून‌ ‌मी‌ ‌आईपाशी‌ ‌गेले!‌ ‌(घाट,‌ ‌शिडी,‌ ‌पायरी,‌ ‌जिना)‌
4. मी‌ ‌फक्त‌ ‌बोटांनी‌ ‌बाईंचं‌ ‌………….’‌ ‌करत‌ ‌होते.‌ ‌ (अंधानुकरण,‌ ‌चित्रीकरण,‌ ‌अनुकरण,‌ ‌छायाचित्र)‌ ‌

उत्तर‌:‌

1. d-O-1-1‌ ‌
2. मायेची
3. जिना
4. ‌अनुकरण‌

कृती‌ ‌2‌: ‌आकलन‌ ‌कृती‌ ‌

योग्य‌ ‌पर्याय‌ ‌निवडून‌ ‌विधाने‌ ‌पूर्ण‌ ‌करा.‌

‌प्रश्न 1.
‌त्या‌ ‌मला‌ ‌शिकवायला‌ ‌आल्या‌ ‌होत्या,‌ ‌……………..‌ ‌
(अ)‌ ‌त्याहीपेक्षा‌ ‌जास्त‌ ‌माझ्यावर‌ ‌ममतेची‌ ‌पाखर‌ ‌घालायला!‌ ‌
(ब)‌ त्याहीपेक्षा‌ ‌जास्त‌ ‌माझ्यावर‌ ‌प्रेमाची‌ ‌पाखर‌ ‌घालायला!‌ ‌
(क)‌ ‌त्याहीपेक्षा‌ ‌जास्त‌ ‌माझ्यावर‌ ‌मायेची‌ ‌पाखर‌ ‌घालायला!‌
‌(ड)‌ ‌त्याहीपेक्षा‌ ‌जास्त‌ ‌माझ्यावर‌ ‌आनंदाची‌ ‌पाखर‌ ‌घालायला!‌
‌उत्तरः‌
‌त्या‌ ‌मला‌ ‌शिकवायला‌ ‌आल्या‌ ‌होत्या,‌ ‌त्याहीपेक्षा‌ ‌जास्त‌ ‌माझ्यावर‌ ‌मायेची‌ ‌पाखर‌ ‌घालायला!‌ ‌

‌प्रश्न 2.
‌शेवटी‌ ‌जेव्हा‌ ‌एकदा‌ ‌मी‌ ‌ती‌ ‌अक्षरं‌ ‌बरोबर‌ ‌काढली‌ ‌तेव्हा‌ ‌………………
(अ)‌ ‌बालसुलभ‌ ‌अभिमान‌ ‌आणि‌ ‌आनंदानं‌ ‌फुलून‌ ‌आले.‌ ‌
(ब)‌ ‌बालसुलभ‌ ‌आनंद‌ ‌आणि‌ ‌अभिमानानं‌ ‌फुलून‌ ‌आले.‌
‌(क)‌ ‌बालसुलभ‌ ‌आनंद‌ ‌आणि‌ ‌अभिमानानं‌ ‌हळूहळू‌ ‌फुलून‌ ‌आले.‌ ‌
‌(ड)‌ ‌बालसुलभ‌ ‌आनंद‌ ‌आणि‌ ‌अभिमानानं‌ ‌अचानक‌ ‌फुलून‌ ‌आले.‌
‌उत्तरः‌ ‌
शेवटी‌ ‌जेव्हा‌ ‌एकदा‌ ‌मी‌ ‌ती‌ ‌अक्षरं‌ ‌बरोबर‌ ‌काढली‌ ‌तेव्हा‌ ‌बालसुलभ‌ ‌आनंद‌ ‌आणि‌ ‌अभिमानानं‌ ‌फुलून‌ ‌आले.‌ ‌

‌प्रश्न 3.
आकृतिबंध‌ ‌पूर्ण‌ ‌करा.‌ ‌
‌उत्तरः‌ ‌

‌प्रश्न 4.
कोण‌ ‌ते‌ ‌लिहा.‌ ‌
‌उत्तरः‌ ‌

‌प्रश्न 1.
परिच्छेदावरून‌ ‌सत्य‌ ‌वा‌ ‌असत्य‌ ‌ते‌ ‌लिहा.‌ ‌

1. ‌लेखिकेला‌ ‌बोटांचा‌ ‌खेळ‌ ‌खूपच‌ ‌आवडला.‌ ‌
2. ‌बाहुली‌ ‌अनी‌ ‌सुलिव्हॅनने‌ ‌सजवली.‌
3. लेखिका‌ ‌धावतच‌ ‌जिना‌ ‌उतरून‌ ‌बाईंपाशी‌ ‌आली.‌ ‌
4. प्रत्येक‌ ‌वस्तूला‌ ‌काहीतरी‌ ‌नाव‌ ‌असतं,‌ ‌हे‌ ‌लेखिकेच्या‌ ‌लक्षातं‌ ‌आलं.‌ ‌

उत्तर:‌

1. ‌सत्य‌
2. ‌असत्य‌ ‌
3. असत्य‌
4. सत्य‌

‌कृती‌ ‌3‌‌:‌ ‌व्याकरण‌ ‌कृती‌

‌प्रश्न 1.
खालील‌ ‌वाक्य‌ ‌लेखननियमांनुसार‌ ‌शुद्ध‌ ‌करून‌ ‌लिहा.‌ ‌
माझ्या‌ ‌जवल‌ ‌कुणितरि‌ ‌येतयसं‌ ‌मला‌ ‌जाणवलं.‌
‌उत्तरः‌
‌माझ्या‌ ‌जवळ‌ ‌कुणीतरी‌ ‌येतयसं‌ ‌मला‌ ‌जाणवलं.‌ ‌

‌प्रश्न 2.
उताऱ्यातील‌ ‌शब्दांच्या‌ ‌जाती‌ ‌शोधून‌ ‌लिहा.‌ ‌
‌उत्तरः‌

1. नामे:‌ ‌बाई,‌ ‌हात,‌ ‌आई,‌ ‌बोटं‌
2. ‌सर्वनामे:‌ ‌मी,‌ ‌माझ्या,‌ ‌मला‌ ‌
3. ‌विशेषणे:‌ ‌मायेची,‌ ‌दुसऱ्या,‌ ‌अंध‌ ‌
4. ‌शब्दयोगी‌ ‌अव्यय:‌ ‌आईपाशी,‌ ‌तिच्यासमोर,‌ ‌बाईबरोबर‌ ‌

‌प्रश्न 3.
अचूक‌ ‌शब्द‌ ‌लिहा.‌
1.‌ ‌सुलिव्हॅन,‌ ‌सूलिव्हॅन,‌ ‌सुलीव्हॅन,‌ ‌सूलीव्हॅन‌ ‌
2. ‌इन्स्टिट्युशन,‌ ‌इन्स्टिट्यूशन,‌ ‌इनसिस्टूशन,‌ ‌इनस्टूक्षण‌ ‌
उत्तर‌:‌
1. सुलिव्हॅन‌
2. ‌इन्स्टिट्यूशन‌

‌प्रश्न 4.
लिंग‌ ‌बदला.‌
उत्तर‌:‌

‌प्रश्न 5.
‌समानार्थी‌ ‌शब्दांच्या‌ ‌जोड्या‌ ‌लावा.‌ ‌

उत्तर‌:‌

प्रश्न 6.
‌विरुद्धार्थी‌ ‌शब्द‌ ‌लिहा.‌
1. डोळस‌ ‌×
2.‌ ‌चढणे‌ ‌×
उत्तर:‌
1.‌ ‌अंध‌
‌2.‌ ‌उतरणे‌

‌प्रश्न 7.
उताऱ्यातील‌ ‌दोन‌ ‌अनेकवचनी‌ ‌शब्द‌ ‌शोधून‌ ‌लिहा.‌ ‌
उत्तर‌‌:‌
1. बोटांनी‌
2. मुलांनी‌

‌प्रश्न 8.
‌तक्ता‌ ‌पूर्ण‌ ‌करा.‌ ‌
उत्तर‌‌:‌

‌प्रश्न 9.
तक्ता‌ ‌पूर्ण‌ ‌करा.‌ ‌
उत्तर‌‌:‌

‌प्रश्न 10.
खालील‌ ‌वाक्यात‌ ‌अधोरेखित‌ ‌शब्दांऐवजी‌ ‌पाठात‌ ‌आलेले‌ ‌योग्य‌ ‌वाक्प्रचार‌ ‌शोधून‌ ‌वाक्य‌ ‌पुन्हा‌ ‌लिहा.‌ ‌
शेजारच्या‌ ‌काकू‌ ‌नेहमीच‌ ‌आमच्यावर‌ ‌प्रेम‌ ‌करतात.‌ ‌
उत्तर:‌
‌शेजारच्या‌ ‌काकू‌ ‌नेहमीच‌ ‌आमच्यावर‌ ‌मायेची‌ ‌पाखर‌ ‌घालतात.‌

‌प्रश्न 11.
वाक्यातील‌ ‌काळ‌ ‌ओळखा.‌ ‌
मी‌ ‌एक‌ ‌शब्द‌ ‌जुळवत‌ ‌होते.‌ ‌
उत्तरः‌
‌भूतकाळ‌

‌प्रश्न 12.
काळ‌ ‌बदला.‌ ‌(भविष्यकाळ‌ ‌करा)‌ ‌
प्रत्येक‌ ‌वस्तूला‌ ‌काहीतरी‌ ‌नाव‌ ‌असतं,‌ ‌हे‌ ‌माझ्या‌ ‌लक्षात‌ ‌आलं.‌
‌उत्तरः‌
‌प्रत्येक‌ ‌वस्तूला‌ ‌काहीतरी‌ ‌नाव‌ ‌असतं,‌ ‌हे‌ ‌माझ्या‌ ‌लक्षात‌ ‌येईल.‌

‌प्रश्न 13.
पर्यायी‌ ‌शब्द‌ ‌लिहा.‌ ‌
‌उत्तरः‌

कृती‌ ‌4 ‌:‌ ‌स्वमत‌

‌प्रश्न 1.
‌’दिव्यांग‌ ‌मुलांना‌ ‌भाषाशिक्षणात‌ ‌येणारे‌ ‌संभाव्य‌ ‌अडथळे’‌ ‌यावर‌ ‌तुमचे‌ ‌मत‌ ‌लिहा.‌ ‌
उत्तरः‌
‌दिव्यांग‌ ‌मुले‌ ‌ही‌ ‌विशेषकरून‌ ‌मुकी,‌ ‌बहिरी‌ ‌व‌ ‌अंध‌ ‌असतात.‌ ‌त्यामुळे‌ ‌त्यांना‌ ‌शिकविणे‌ ‌ही‌ ‌एक‌ ‌प्रकारे‌ ‌तारेवरची‌ ‌कसरतच‌ ‌असते.‌ ‌त्यांना‌ ‌शिक्षण‌ ‌घेताना‌ ‌विविध‌ ‌अडचणी‌ ‌येत‌ ‌असतात.‌ ‌एकतर‌ ‌प्रत्यक्ष‌ ‌वस्तू‌ ‌पाहण्यासाठी‌ ‌त्यांच्याकडे‌ ‌दृष्टी‌ ‌नसते,‌ ‌त्यामुळे‌ ‌त्यांना‌ ‌दृष्टीच्या‌ ‌रूपातून‌ ‌प्रत्यक्ष‌ ‌अनुभव‌ ‌उपलब्ध‌ ‌करून‌ ‌देणे‌ ‌सहज‌ ‌शक्य‌ ‌नसते.‌ ‌अशा‌ ‌वेळी‌ ‌त्यांना‌ ‌शिकविताना‌ ‌स्पर्शाच्या‌ ‌माध्यमातून‌ ‌प्रत्यक्ष‌ ‌अनुभव‌ ‌देणे‌ ‌आवश्यक‌ ‌असते.‌ ‌स्वत:‌ ‌दिव्यांग‌ ‌मुलांनाही‌ ‌भाषेचे‌ ‌ज्ञान‌ ‌प्राप्त‌ ‌करून‌ ‌घेताना‌ ‌अशा‌ ‌प्रकारच्या‌ ‌प्रत्यक्ष‌ ‌अनुभवांशी‌ ‌समायोजन‌ ‌साधावे‌ ‌लागते.‌ ‌त्यांना‌ ‌भाषाशिक्षण‌ ‌प्राप्त‌ ‌करून‌ ‌घेण्यासाठी‌ ‌अथक‌ ‌प्रयत्न‌ ‌करावे‌ ‌लागतात.‌ ‌ते‌ ‌हळूहळू‌ ‌शब्द‌ ‌शिकत‌ ‌असतात.‌ ‌त्यांची‌ ‌सर्वसामान्य‌ ‌मुलांपेक्षा‌ ‌ज्ञान‌ ‌प्राप्त‌ ‌करून‌ ‌घेण्याची‌ ‌गती‌ ‌कमी‌ ‌असते.‌ ‌

पुढील‌ ‌उताऱ्याच्या‌ ‌आधारे‌ ‌दिलेल्या‌ ‌सूचनेनुसार‌ ‌कृती‌ ‌कराः‌:

‌कृती‌ ‌1 ‌:‌ ‌आकलन‌ ‌कृती‌ ‌

‌प्रश्न 1.
आकृतिबंध‌ ‌पूर्ण‌ ‌करा.‌ ‌
उत्तरः‌

‌खालील‌ ‌प्रश्नांची‌ ‌उत्तरे‌ ‌एका‌ ‌वाक्यात‌ ‌लिहा.‌ ‌

‌प्रश्न 1.
बाईंनी‌ ‌लेखिकेच्या‌ ‌मांडीवर‌ ‌ठेवलेली‌ ‌बाहुली‌ ‌कशी‌ ‌होती?‌ ‌
उत्तर:‌
‌बाईंनी‌ ‌लेखिकेच्या‌ ‌मांडीवर‌ ‌ठेवलेली‌ ‌बाहुली‌ ‌जुनी,‌ ‌चिंध्या‌ ‌झालेली‌ ‌होती.‌ ‌

‌प्रश्न 2.
लेखिकेला‌ ‌केव्हा‌ ‌उकळ्या‌ ‌फुटू‌ ‌लागल्या?‌
‌उत्तर:‌
‌बाहुलीचे‌ ‌तुकडे‌ ‌होऊन‌ ‌आपल्या‌ ‌पायांशी‌ ‌पडलेले‌ ‌जाणवल्यानंतर‌ ‌लेखिकेला‌ ‌उकळ्या‌ ‌फुटू‌ ‌लागल्या.‌

‌प्रश्न 3.‌
लिखिकेच्या‌ ‌निश्चल‌ ‌आणि‌ ‌अंधाऱ्या‌ ‌जगात‌ ‌कोणत्या‌ ‌भावना‌ ‌उगवणे‌ ‌कठिण‌ ‌होते?‌ ‌
उत्तर:‌
‌लेखिकेच्या‌ ‌निश्चल‌ ‌आणि‌ ‌अंधाऱ्या‌ ‌जगात‌ ‌हळव्या‌ ‌व‌ ‌हळूवार‌ ‌भावना‌ ‌उगवणे‌ ‌कठिण‌ ‌होते.‌ ‌

‌प्रश्न 4.‌
‌बाईंनी‌ ‌लेखिकेच्या‌ ‌बाहुलीचे‌ ‌तुकडे‌ ‌कुठे‌ ‌लोटले?‌
‌उत्तर‌‌:‌
‌बाईंनी‌ ‌लेखिकेच्या‌ ‌बाहुलीचे‌ ‌तुकडे‌ ‌झाडून‌ ‌शेकोटी‌ ‌जवळच‌ ‌एका‌ ‌बाजूला‌ ‌लोटले.‌ ‌

कंसातील‌ ‌योग्य‌ ‌शब्द‌ ‌वापरून‌ ‌रिकाम्या‌ ‌जागा‌ ‌भरा.‌ ‌

‌प्रश्न 1.‌
1. एवढा‌ ‌थयथयाट‌ ‌करूनही‌ ‌ना‌ ‌खंत‌ ‌ना‌ ‌खेद‌ ‌असाच‌ ‌माझा‌ ‌होता.‌ ‌(विचार,‌ ‌आदरभाव,‌ ‌आविर्भाव,‌ ‌अविचार)‌ ‌
2.‌ ‌माझा‌ ‌हा‌ ‌गोंधळ‌ ‌बघून‌ ‌त्यांचा‌ ‌………….‌ ‌झाला.‌ ‌(हिरमोड,‌ ‌थयथयाट,‌ ‌खेद,‌ ‌खंत)‌
‌उत्तर:‌ ‌
1.‌ ‌आविर्भाव‌
‌2.‌ ‌हिरमोड‌ ‌

कृती 2:‌ ‌आकलन‌ ‌कृती

‌योग्य‌ ‌पर्याय‌ ‌निवडून‌ ‌विधाने‌ ‌पूर्ण‌ ‌करा.‌ ‌

‌प्रश्न 1.‌
माझा‌ ‌हा‌ ‌गोंधळ‌ ‌बघून‌ ‌त्यांचा‌ ‌हिरमोड‌ ‌झाला‌ ‌…………….‌
‌(अ)‌ ‌आणि‌ ‌त्यांनी‌ ‌तो‌ ‌विषय‌ ‌तेवढ्यावर‌ ‌ठेवला‌ ‌नाही.‌ ‌
(ब)‌ ‌आणि‌ ‌त्यांनी‌ ‌तो‌ ‌विषय‌ ‌ तेवढ्यावरच‌ ‌न‌ ‌ठेवता‌ ‌पुढे‌ ‌चालूच‌ ‌ठेवला.‌
‌(क)‌ ‌आणि‌ ‌त्यांनी‌ ‌तो‌ ‌विषय‌ ‌तेवढ्यावरच‌ ‌ठेवला.‌
‌(ड)‌ ‌आणि‌ ‌त्यांनी‌ ‌तो‌ ‌विषय‌ ‌तेवढ्यावर‌ ‌आटपून‌ ‌घेतला.‌ ‌
उत्तर:‌
‌माझा‌ ‌हा‌ ‌गोंधळ‌ ‌बघून‌ ‌त्यांचा‌ ‌हिरमोड‌ ‌झाला‌ ‌आणि‌ ‌त्यांनी‌ ‌तो‌ ‌ विषय‌ ‌तेवढ्यावरच‌ ‌ठेवला.‌

‌प्रश्न 2.‌
त्या‌ ‌बाहुलीचे‌ ‌तुकडे‌ ‌होऊन‌ ‌माझ्या‌ ‌पायांशी‌ ‌पडलेले‌ ‌……‌…… ‌
(अ)‌ ‌मला‌ ‌जाणवल्यावर‌ ‌मला‌ ‌उकळ्या‌ ‌फुटू‌ ‌लागल्या.‌
‌(ब)‌ ‌मला‌ ‌जाणवल्यावर‌ ‌मला‌ ‌आनंदानी‌ ‌उकळ्या‌ ‌फुटू‌ ‌लागल्या.‌
‌(क)‌ ‌मला‌ ‌जाणवल्यावर‌ ‌मला‌ ‌रागाच्या‌ ‌उकळ्या‌ ‌फुटू‌ ‌लागल्या.‌
‌(ड)‌ ‌मला‌ ‌जाणवल्यावर‌ ‌मला‌ ‌नकळत‌ ‌उकळ्या‌ ‌फुटू‌ ‌लागल्या.‌ ‌
उत्तरः‌ ‌
त्या‌ ‌बाहुलीचे‌ ‌तुकडे‌ ‌होऊन‌ ‌माझ्या‌ ‌पायांशी‌ ‌पडलेले‌ ‌मला‌ ‌जाणवल्यावर‌ ‌मला‌ ‌उकळ्या‌ ‌फुटू‌ ‌लागल्या.‌

‌प्रश्न 3.‌
कोण‌ ‌ते‌ ‌लिहा.‌ ‌
उत्तरः‌ ‌

‌प्रश्न 4.‌
‌सत्य‌ ‌वा‌ ‌असत्य‌ ‌ते‌ ‌लिहा.‌ ‌

1. ‌बाईंनी‌ ‌लेखिकेची‌ ‌जुनी‌ ‌चिंध्या‌ ‌झालेली‌ ‌बाहुली‌ ‌लेखिकेच्या‌ ‌मांडीवर‌ ‌ठेवली.‌
2. ‌लेखिकेचा‌ ‌गोंधळ‌ ‌बघून‌ ‌बाईंचा‌ ‌हिरमोड‌ ‌झाला‌ ‌नाही.‌ ‌
3. ‌लेखिकेची‌ ‌डोकेदुखी‌ ‌गेल्यानं‌ ‌लेखिकेलाच‌ ‌हायसं‌ ‌वाटलं.‌ ‌

उत्तर:‌

1. ‌सत्य‌
2. ‌असत्य‌
3. ‌सत्य‌

‌कृती‌ ‌3 ‌:‌ ‌व्याकरण‌ ‌कृती‌

खालील‌ ‌वाक्ये‌ ‌लेखननियमांनुसार‌ ‌शुद्ध‌ ‌करून‌ ‌लिहा.‌

‌प्रश्न 1.‌
आता‌ ‌पून्हा‌ ‌बाहुलीवरून‌ ‌त्यांचं‌ ‌शीकवणं‌ ‌सुरू‌ ‌झालं‌ ‌होतं.‌ ‌
उत्तरः‌
‌आता‌ ‌पुन्हा‌ ‌बाहुलीवरून‌ ‌त्यांचं‌ ‌शिकवणं‌ ‌सुरू‌ ‌झालं‌ ‌होतं.‌

‌प्रश्न 2.‌
‌मि‌ ‌माझी‌ ‌नवी‌ ‌बाहुली‌ ‌हिसकावून‌ ‌जमीनिवर‌ ‌आपटली.‌ ‌
उत्तरः‌ ‌
मी‌ ‌माझी‌ ‌नवी‌ ‌बाहुली‌ ‌हिसकावून‌ ‌जमिनीवर‌ ‌आपटली.‌ ‌

‌प्रश्न 3.
उताऱ्यातील‌ ‌दोन‌ ‌सर्वनामे‌ ‌शोधून‌ ‌लिहा.‌
‌उत्तर:‌ ‌

1. ‌मी‌ ‌
2. ‌माझी‌ ‌
3. ‌त्यांनी‌ ‌
4. ‌तो‌ ‌
5. ‌हे‌
6. ‌ते‌ ‌
7. ‌माझ्या‌
8. ‌मला‌

‌प्रश्न 4.
अचूक‌ ‌शब्द‌ ‌लिहा.‌ ‌
आवीर्भाव,‌ ‌आविर्भाव,‌ ‌आविभाव,‌ ‌आविभाव‌
‌उत्तरः‌
‌आविर्भाव‌ ‌

‌प्रश्न 5.
समानार्थी‌ ‌शब्द‌ ‌लिहा.‌

1. ‌त्रास‌ ‌-‌ ‌[ ]‌ ‌
2. ‌दुःख‌ ‌-‌ ‌[ ]
3. ‌गलका‌ ‌- [ ]

उत्तर:‌

1. ‌पीडा‌ ‌
2. ‌खेद‌
3. ‌गोंधळ‌

‌प्रश्न 6.
अधोरेखित‌ ‌शब्दाचा‌ ‌समानार्थी‌ ‌शब्द‌ ‌लिहून‌ ‌वाक्य‌ ‌पुन्हा‌ ‌लिहा.‌ ‌
वाटलं,‌ ‌बर‌ ‌झालं,‌ ‌एकदाचा‌ ‌त्रास‌ ‌गेला.‌ ‌
उत्तरः‌
‌वाटलं,‌ ‌बरं‌ ‌झालं,‌ ‌एकदाची‌ ‌पीडा‌ ‌गेली.‌

‌प्रश्न 7.
विरुद्धार्थी‌ ‌शब्द‌ ‌लिहा.‌
‌

1. ‌आनंद‌ ‌× [ ]
2. ‌नवी‌ ‌× [ ]
3. ‌नंतर‌ ‌× [ ]

उत्तर:‌ ‌

1. ‌खेद‌ ‌
2. ‌जुनी‌ ‌
3. ‌आधी‌

‌‌प्रश्न 8.
उताऱ्यातील‌ ‌दोन‌ ‌अनेकवचनी‌ ‌शब्द‌ ‌शोधून‌ ‌लिहा.‌ ‌
उत्तर:‌ ‌
1. ‌बाहुल्यांना‌
‌2.‌ ‌तुकडे‌

‌‌प्रश्न 9.
‌तक्ता‌ ‌पूर्ण‌ ‌करा.‌ ‌
उत्तर:‌ ‌

‌‌प्रश्न 10.
तक्ता‌ ‌पूर्ण‌ ‌करा.‌ ‌
उत्तर:‌ ‌

‌‌प्रश्न 11.
वाक्प्रचार‌ ‌व‌ ‌अर्थ‌ ‌यांच्या‌ ‌योग्य‌ ‌जोड्या‌ ‌जुळवा.‌

‌‌प्रश्न 12.
‌वाक्यातील‌ ‌काळ‌ ‌ओळखा.‌ ‌
माझी‌ ‌डोकेदुखी‌ ‌गेल्यानं‌ ‌मलाही‌ ‌हायसं‌ ‌वाटलं.‌ ‌
उत्तर:‌
‌भूतकाळ‌ ‌

‌‌प्रश्न 13.
काळ‌ ‌बदला.‌ ‌(वर्तमानकाळ‌ ‌करा)‌ ‌
ती‌ ‌बाहुली‌ ‌माझी‌ ‌नावडती‌ ‌होती.‌
‌उत्तरः‌
‌ती‌ ‌बाहुली‌ ‌माझी‌ ‌नावडती‌ ‌आहे.‌

कृती‌ ‌4 :‌ ‌स्वमत‌ ‌

‌‌प्रश्न 1.
‘अनी‌ ‌सुलिव्हॅन‌ ‌नसत्या‌ ‌तर‌ ‌हेलन‌ ‌घडली‌ ‌नसती’‌ ‌या‌ ‌विधानाची‌ ‌सत्यता‌ ‌पटवून‌ ‌या.‌
‌उत्तरः‌
‌हेलन‌ ‌केलर‌ ‌ही‌ ‌मुळातच‌ ‌दिव्यांग‌ ‌मुलगी‌ ‌होती.‌ ‌त्यामुळे‌ ‌तिच्या‌ ‌शिक्षणात‌ ‌बऱ्याच‌ ‌अडचणी‌ ‌येत‌ ‌होत्या.‌ ‌तिला‌ ‌साधी‌ ‌अक्षर,‌ ‌शब्द‌ ‌ओळखही‌ ‌करणे‌ ‌अतिशय‌ ‌कठीण‌ ‌होते.‌ ‌त्यामुळे‌ ‌तिला‌ ‌एक‌ ‌असा‌ ‌शिक्षक‌ ‌हवा‌ ‌होता‌ ‌की,‌ ‌जो‌ ‌तिच्या‌ ‌शारीरिक‌ ‌दुर्बलतेला‌ ‌समजून‌ ‌तिची‌ ‌शिक्षणात‌ ‌मदत‌ ‌करेल.‌ ‌ॲनी‌ ‌मन्सफिल्ड‌ ‌सुलिव्हॅन‌ ‌या‌ ‌अशाच‌ ‌शिक्षिका‌ ‌तिला‌ ‌लाभल्या‌ ‌होत्या.‌ ‌अनी‌ ‌सुलिव्हॅन‌ ‌यांनी‌ ‌सर्वप्रथम‌ ‌तिच्यावर‌ ‌आपल्या‌ ‌मायेची‌ ‌पाखर‌ ‌घातली.‌ ‌शिकविताना‌ ‌तिच्या‌ ‌आवडीनुसार‌ ‌तिच्या‌ ‌कलानुसार‌ ‌घेत‌ ‌घेत‌ ‌तिला‌ ‌शिकविले.‌

‌हेलनचा‌ ‌शिक्षणात‌ ‌जेव्हा‌ ‌जेव्हा‌ ‌गोंधळ‌ ‌व्हायचा‌ ‌तेव्हा‌ ‌तेव्हा‌ ‌बाई‌ ‌संयम‌ ‌बाळगायच्या.‌ ‌हेलनची‌ ‌शिक्षणातील‌ ‌दुर्बलता‌ ‌लक्षात‌ ‌घेऊन‌ ‌बाईनी‌ ‌केवळ‌ ‌अक्षर,‌ ‌शब्द‌ ‌ओळख‌ ‌करून‌ ‌न‌ ‌देता‌ ‌त्यांच्या‌ ‌अर्थाची‌ ‌ही‌ ‌ओळख‌ ‌करून‌ ‌दिली.‌ ‌बाहुली,‌ ‌पाणी‌ ‌यांच्या‌ ‌प्रत्यक्ष‌ ‌अनुभवाद्वारे‌ ‌अर्थ‌ ‌समजून‌ ‌देण्याचा‌ ‌प्रयत्न‌ ‌केला.‌ ‌परिणामी‌ ‌हेलनच्या‌ ‌अंधाराने‌ ‌भरलेल्या‌ ‌आयुष्यात‌ ‌नवीन‌ ‌भवितव्याची‌ ‌पालवी‌ ‌फुटली‌ ‌केवळ‌ ‌बाईंमुळेच.‌ ‌म्हणून‌ ‌’अॅनी‌ ‌सुलिव्हॅन‌ ‌नसत्या‌ ‌तर‌ ‌हेलन‌ ‌घडली‌ ‌नसती’‌ ‌हे‌ ‌वाक्य‌ ‌सत्य‌ ‌वाटते.

‌पुढील‌ ‌उताऱ्याच्या‌ ‌आधारे‌ ‌दिलेल्या‌ ‌सूचनेनुसार‌ ‌कृती‌ ‌करा:‌ ‌

कृती‌ ‌1‌ ‌:‌ ‌आकलन‌ ‌कृती‌

प्रश्न‌ ‌1.‌
आकृतिबंध‌ ‌पूर्ण‌ ‌करा.‌ ‌
‌उत्तरः‌

प्रश्न‌ ‌2. ‌
उताऱ्यानुसार‌ ‌घटनांचा‌ ‌क्रम‌ ‌लावा.‌

1. ‌एका‌ ‌चैतन्यमय‌ ‌जिवंत‌ ‌शब्दानं‌ ‌लेखिकेच्या‌ ‌आत्म्याला‌ ‌जशी‌ ‌जाग‌ ‌आली.‌ ‌
2. ‌उन्हात‌ ‌जायला‌ ‌मिळणार‌ ‌या‌ ‌विचाराने‌ ‌लेखिका‌ ‌टुणटुण‌ ‌उड्या‌ ‌मारू‌ ‌लागली.‌
3. ‌गमावलेली‌ ‌स्मृती‌ ‌परत‌ ‌येण्याचा‌ ‌थरार‌ ‌लेखिकेने‌ ‌अनुभवला.‌
4. ‌फुलांचा‌ ‌सुगंध‌ ‌दरवळत‌ ‌होता.‌ ‌

उत्तर‌‌:‌

1. ‌उन्हात‌ ‌जायला‌ ‌मिळणार‌ ‌या‌ ‌विचाराने‌ ‌लेखिका‌ ‌टुणटुण‌ ‌उड्या‌ ‌मारू‌ ‌लागली.‌ ‌
2. ‌फुलांचा‌ ‌सुगंध‌ ‌दरवळत‌ ‌होता.‌
3. ‌गमावलेली‌ ‌स्मृती‌ ‌परत‌ ‌येण्याचाथरार‌ ‌लेखिकेने‌ ‌अनुभवला.‌ ‌
4. ‌एका‌ ‌चैतन्यमय‌ ‌जिवंत‌ ‌शब्दानं‌ ‌लेखिकेच्या‌ ‌आत्म्याला‌ ‌जशी‌ ‌जाग‌ ‌आली.‌

‌खालील‌ ‌प्रश्नांची‌ ‌उत्तरे‌ ‌एका‌ ‌वाक्यात‌ ‌लिहा.‌ ‌

प्रश्न‌ ‌1.
लेखिका‌ ‌आनंदानं‌ ‌टुणटुण‌ ‌उड्या‌ ‌का‌ ‌मारू‌ ‌लागली?‌ ‌
उत्तर:‌ ‌
बाहेर‌ ‌छान‌ ‌उबदार‌ ‌उन्हात‌ ‌जायला‌ ‌मिळणार‌ ‌या‌ ‌विचारानं‌ ‌लेखिका‌ ‌आनंदानं‌ ‌टुणटुण‌ ‌उड्या‌ ‌मारू‌ ‌लागली.‌

प्रश्न‌ ‌2.
लेखिका‌ ‌व‌ ‌बाई‌ ‌विहिरीपाशी‌ ‌कशा‌ ‌पोहोचल्या?‌
‌उत्तर:‌ ‌
पाऊलवाटेनं‌ ‌जात‌ ‌लेखिका‌ ‌व‌ ‌बाई‌ ‌विहिरीपाशी‌ ‌पोहोचल्या.‌

कंसातील‌ ‌योग्य‌ ‌शब्द‌ ‌रिकाम्या‌ ‌जागी‌ ‌भरा.‌

प्रश्न‌ ‌1.
1.‌ ‌त्यांच्या‌ ‌फुलांचा‌ ‌सुगंध‌ ‌……….होता.‌ ‌(भावलेला,‌ ‌पसरलेला,‌ ‌दरवळत,‌ ‌आवडलेला)‌ ‌
2.‌ ‌मी‌ ‌एकदम‌ ‌…………”उभी‌ ‌राहिले.‌ ‌(स्तब्ध,‌ ‌निश्चल,‌ ‌शांत,‌ ‌निशब्द)‌ ‌
उत्तर:‌
‌1. ‌दरवळत‌ ‌
2. निश्चल‌

सहसंबंध‌ ‌लिहा.‌ ‌

प्रश्न‌ ‌1.
1. ‌सुंगंधी‌ ‌:‌ ‌फुले‌ ‌::‌ ‌उबदार‌ ‌:‌ ……………………
2. स्पष्ट‌ ‌:‌ ‌अस्पष्ट‌ ‌::‌ ‌मृत‌ ‌:‌ ‌……………………
उत्तर:‌ ‌
1. उन्ह‌ ‌
2. जिवंत‌ ‌

कृती‌ ‌2‌ ‌:‌ ‌आकलन‌ ‌कृती‌ ‌

प्रश्न‌ ‌1.
योग्य‌ ‌पर्याय‌ ‌निवडून‌ ‌विधान‌ ‌पूर्ण‌ ‌करा.‌ ‌
बाईंनी‌ ‌माझी‌ ‌हॅट‌ ‌माझ्या‌ ‌हातात‌ ‌ठेवल्यावर‌ ‌मी‌ ‌ओळखलं‌ ‌….‌………………‌
(अ)‌ ‌आता‌ ‌बाहेर,‌ ‌पावसात‌ ‌जायचंय.‌
‌(ब)‌ ‌आता‌ ‌बाहेर,‌ ‌तप्त‌ ‌उन्हात‌ ‌जायचंय.‌ ‌
(क)‌ ‌आता‌ ‌बाहेर,‌ ‌छान‌ ‌उबदार‌ ‌उन्हात‌ ‌जायचंय.‌
‌(ख)‌ ‌आता‌ ‌बाहेर,‌ ‌थंडीत‌ ‌जायचंय.‌ ‌
उत्तर‌:‌
‌बाईंनी‌ ‌माझी‌ ‌हॅट‌ ‌माझ्या‌ ‌हातात‌ ‌ठेवल्यावर‌ ‌मी‌ ‌ओळखलं‌ ‌आता‌ ‌बाहेर,‌ ‌छान‌ ‌उबदार‌ ‌उन्हात‌ ‌जायचंय.‌

प्रश्न‌ ‌2.
‌कोण‌ ‌ते‌ ‌लिहा.‌ ‌
उत्तर‌:‌

प्रश्न‌ ‌3.
‌कारणे‌ ‌दया.‌ ‌
उत्तर‌:‌

चूक‌ ‌की‌ ‌बरोबर‌ ‌ते‌ ‌लिहा.‌ ‌

प्रश्न‌ ‌1.
1. त्यांच्या‌ ‌फुलांचा‌ ‌दुर्गंध‌ ‌दरवळत‌ ‌होता.‌
2. पाऊलवाटेनं‌ ‌जात‌ ‌लेखिका‌ ‌व‌ ‌बाई‌ ‌विहिरीपाशी‌ ‌आल्या.‌ ‌
उत्तर:‌
1. ‌चूक‌
2. बरोबर‌

‌कृती‌ ‌3‌ ‌:‌ ‌व्याकरण‌ ‌कृती‌

‌प्रश्न‌ ‌1.
खालील‌ ‌वाक्य‌ ‌लेखननियमांनुसार‌ ‌शुद्ध‌ ‌करून‌ ‌लिहा.‌ ‌
पण‌ ‌लोकरच‌ ‌ते‌ ‌दुर‌ ‌होणार‌ ‌होते.‌ ‌
उत्तर‌:
पण‌ ‌लौकरच‌ ‌ते‌ ‌दूर‌ ‌होणार‌ ‌होते.‌

‌प्रश्न‌ 2.
उताऱ्यातील‌ ‌दोन‌ ‌विशेषणे‌ ‌शोधून‌ ‌लिहा.‌ ‌
उत्तर:‌ ‌

1. छान‌ ‌
2. ‌उबदार‌ ‌
3. ‌वेलीच्या‌
4. ‌थंडगार‌
5. इतके‌ ‌
6. ‌गमावलेली‌ ‌
7. जिवंत‌ ‌
8. ‌चैतन्यमय‌ ‌

‌प्रश्न‌ 3. ‌
अचूक‌ ‌शब्द‌ ‌लिहा.‌
1.‌ ‌निश्चल,‌ ‌नीश्चल,‌ ‌निचल,‌ ‌निश्चल‌ ‌
2.‌ ‌चेतन्यमय,‌ ‌चैतनमय,‌ ‌चैतन्यमय,‌ ‌चेतनमय‌ ‌
उत्तर:‌
1. निश्चल‌ ‌
2. ‌चैतन्यमय‌ ‌

प्रश्न‌ 4. ‌
‌समानार्थी‌ ‌शब्द‌ ‌लिहा.‌ ‌

1. मार्ग‌ ‌-‌ ‌[ ]
2. जल‌ ‌-‌ ‌[ ]
3. आठवण‌ ‌-‌ ‌[ ]
4. उजेड‌ ‌-‌ ‌[ ]‌

‌उत्तर:‌

1. वाट‌
2. पाणी‌ ‌
3. स्मृती‌ ‌
4. ‌प्रकाश‌ ‌

प्रश्न‌ 5. ‌
विरुद्धार्थी‌ ‌शब्द‌ ‌लिहा.‌ ‌

1. आत‌ ‌×‌
2. ‌जलद‌ ‌×
3. ‌रात्र‌ ‌×
4. ‌जवळ‌ ‌×

उत्तर‌:‌

1. ‌बाहेर‌ ‌
2. सावकाश‌ ‌
3. ‌दिवस‌
4. ‌दूर‌

प्रश्न‌ 6.
अधोरेखित‌ ‌शब्दाचा‌ ‌विरुद्धार्थी‌ ‌शब्द‌ ‌लिहून‌ ‌वाक्य‌ ‌पुन्हा‌ ‌लिहा.‌
‌इतके‌ ‌दिवस‌ ‌आपण‌ ‌काहीतरी‌ ‌विसरून‌ ‌गेलो‌ ‌हातो,‌ ‌याची‌ ‌स्पष्ट‌ ‌जाणीव‌ ‌झाली.‌
‌उत्तरः‌
‌इतके‌ ‌दिवस‌ ‌आपण‌ ‌काहीतरी‌ ‌विसरून‌ ‌गेलो‌ ‌होतो,‌ ‌याची‌ ‌अस्पष्ट‌ ‌जाणीव‌ ‌झाली.‌ ‌

प्रश्न‌ 7.
उताऱ्यातील‌ ‌दोन‌ ‌अनेकवचनी‌ ‌शब्द‌ ‌शोधून‌ ‌लिहा.‌ ‌
उत्तर:‌

1. ‌जाळ्या‌
2. ‌फुलांचा‌
3. ‌बोटांनी‌

प्रश्न‌ 8.
तक्ता‌ ‌पूर्ण‌ ‌करा.‌ ‌
उत्तर:‌

प्रश्न‌ 9.
‌तक्ता‌ ‌पूर्ण‌ ‌करा.‌ ‌
उत्तर:‌

प्रश्न‌ 10.
कंसातील‌ ‌वाक्प्रचारांचा‌ ‌अर्थ‌ ‌लिहून‌ ‌वाक्यात‌ ‌उपयोग‌ ‌करा.‌ ‌ (निश्चल‌ ‌उभे‌ ‌राहणे,‌ ‌आनंदाची‌ ‌उधळण‌ ‌करणे)‌ ‌
उत्तर:‌
1. ‌निश्चल‌ ‌उभे‌ ‌राहणे‌ ‌-‌ ‌स्तब्ध‌ ‌उभे‌ ‌राहणे‌ ‌
वाक्य:‌ ‌बाबा‌ ‌रागावले‌ ‌आहेत‌ ‌हे‌ ‌ओळखून‌ ‌सीमा‌ ‌त्यांच्यासमोर‌ ‌निश्चल‌ ‌उभी‌ ‌राहिली.‌ ‌
उत्तर‌:‌
2. आनंदाची‌ ‌उधळण‌ ‌करणे‌ ‌-‌ ‌आनंद‌ ‌पसरवणे
वाक्यः‌ ‌त्या‌ ‌पहिल्या‌ ‌पावसाने‌ ‌सगळीकडे‌ ‌आनंदाची‌ ‌उधळण‌ ‌केली‌ ‌होती.‌

‌प्रश्न‌ 11.
‌वाक्यातील‌ ‌काळ‌ ‌ओळखा.‌ ‌
अजूनही‌ ‌तसे‌ ‌ह्या‌ ‌वाटेत‌ ‌बरेच‌ ‌अडथळे‌ ‌होते.‌ ‌
उत्तरः‌
‌भूतकाळ‌ ‌

‌प्रश्न‌ 12.
‌काळ‌ ‌बदला.‌ ‌(भविष्यकाळ‌ ‌करा)‌ ‌
त्यांच्या‌ ‌फुलांचा‌ ‌सुगंध‌ ‌दरवळत‌ ‌होता.‌ ‌
उत्तरः‌
‌त्यांच्या‌ ‌फुलांचा‌ ‌सुगंध‌ ‌दरवळेल.‌ ‌

‌प्रश्न‌ 13.
‌पर्यायी‌ ‌शब्द‌ ‌लिहा.
उत्तरः‌

कृती‌ ‌4‌ ‌:‌ ‌स्वमत‌ ‌

‌प्रश्न‌ 1.
‘सर्वसामान्य‌ ‌मुलांबरोबर‌ ‌दिव्यांग‌ ‌मुलांना‌ ‌शिक्षणाची‌ ‌समान‌ ‌संधी‌ ‌द्यायला‌ ‌हवी’‌ ‌या‌ ‌विचाराचे‌ ‌सामाजिक‌ ‌महत्त्व‌ ‌जाणा‌ ‌व‌ ‌ते‌ ‌शब्दबद्ध‌ ‌करा.‌ ‌
उत्तर:‌
‌निसर्गनियमानुसार‌ ‌तसेच‌ ‌कायद्यानुसार‌ ‌प्रत्येकाला‌ ‌शिक्षणाचा‌ ‌समान‌ ‌अधिकार‌ ‌आहे.‌ ‌त्यामुळे‌ ‌सर्वसामान्य‌ ‌मुले‌ ‌किंवा‌ ‌दिव्यांग‌ ‌मुले‌ ‌हा‌ ‌भेदभाव‌ ‌आपण‌ ‌करू‌ ‌शकत‌ ‌नाही.‌ ‌पण‌ ‌तसे‌ ‌झाल्यास‌ ‌दिव्यांग‌ ‌मुले‌ ‌ही‌ ‌त्यांच्या‌ ‌प्राथमिक‌ ‌हक्कापासून‌ ‌वंचित‌ ‌होतील,‌ ‌त्यांच्यामध्ये‌ ‌न्यूनगंडाची,‌ ‌स्वत:मध्ये‌ ‌काहीतरी‌ ‌कमतरता‌ ‌आहे‌ ‌ही‌ ‌भावना‌ ‌निर्माण‌ ‌होईल.‌ ‌परिणामी‌ ‌समाजातील‌ ‌एक‌ ‌महत्त्वाचा‌ ‌घटक‌ ‌समाजापासून‌ ‌दूर‌ ‌होईल,‌ ‌त्यामुळे‌ ‌दिव्यांग‌ ‌मुलांना‌ ‌शिक्षणाची‌ ‌समान‌ ‌संधी‌ ‌द्यायला‌ ‌हवी.‌ ‌शिक्षणामुळे‌ ‌त्यांच्यातील‌ ‌न्यूनगंड‌ ‌कमी‌ ‌होऊन‌ ‌ते‌ ‌आपल्या,‌ ‌दिव्यंगावर‌ ‌मात‌ ‌करतील‌ ‌व‌ ‌ते‌ ‌स्वावलंबी‌ ‌बनतील.‌ ‌त्यांच्यामध्ये‌ ‌शिक्षणामुळे‌ ‌स्वाभिमान‌ ‌जागृत‌ ‌होईल.‌ ‌शिक्षणामुळे‌ ‌त्यांना‌ ‌समाजात‌ ‌मानाचे‌ ‌स्थान‌ ‌मिळेल.‌ ‌परिणामी‌ ‌समाजाची,‌ ‌देशाची‌ ‌प्रगती‌ ‌होण्यास‌ ‌मोठी‌ ‌मदत‌ ‌मिळेल.‌ ‌त्यामुळेच‌ ‌सर्वसामान्य‌ ‌मुलांबरोबर‌ ‌दिव्यांग‌ ‌मुलांना‌ ‌शिक्षणाची‌ ‌समान‌ ‌संधी‌ ‌द्यायला‌ ‌हवी.‌

‌पुढील‌ ‌उताऱ्याच्या‌ ‌आधारे‌ ‌दिलेल्या‌ ‌सूचनेनुसार‌ ‌कृती‌ ‌कराः‌ ‌

कृती‌ ‌1‌ ‌:‌ ‌आकलन‌ ‌कृती‌ ‌

‌प्रश्न‌ 1.
आकृतिबंध‌ ‌पूर्ण‌ ‌करा.‌
उत्तर:‌

‌‌‌प्रश्न‌ 2.
कारणे‌ ‌दया.‌ ‌
उत्तर:‌

‌‌‌प्रश्न‌ 3.
उताऱ्यानुसार‌ ‌वाक्यांचा‌ ‌क्रम‌ ‌लावा.‌

1. आयुष्यात‌ ‌पहिल्यांदाच‌ ‌मला‌ ‌उदया‌ ‌कधी‌ ‌उगवतोय‌ ‌ह्याची‌ ‌उत्कंठा‌ ‌लागून‌ ‌राहिली‌ ‌होती.‌ ‌
2. दारापाशी‌ ‌आल्यावर‌ ‌मला‌ ‌मी‌ ‌मोडलेल्या‌ ‌बाहुलीची‌ ‌आठवण‌ ‌आली.‌ ‌
3. ‌मला‌ ‌जशी‌ ‌एक‌ ‌वेगळीच‌ ‌नवी‌ ‌दृष्टी‌ ‌मिळाली‌ ‌होती.‌
4. ‌‌तो‌ ‌दिवस‌ ‌माझ्या‌ ‌दृष्टीनं‌ ‌फार‌ ‌नाट्यमय‌ ‌होता.‌ ‌

उत्तर:‌

1. मला‌ ‌जशी‌ ‌एक‌ ‌वेगळीच‌ ‌नवी‌ ‌दृष्टी‌ ‌मिळाली‌ ‌होती.‌ ‌
2. दारापाशी‌ ‌आल्यावर‌ ‌मला‌ ‌मी‌ ‌मोडलेल्या‌ ‌बाहुलीची‌ ‌आठवण‌ ‌झाली.‌ ‌
3. तो‌ ‌दिवस‌ ‌माझ्या‌ ‌दृष्टीनं‌ ‌फार‌ ‌नाट्यमय‌ ‌होता.‌ ‌
4. आयुष्यात‌ ‌पहिल्यांदाच‌ ‌मला‌ ‌उदया‌ ‌कधी‌ ‌उगवतोय‌ ‌ह्याची‌ ‌उत्कंठा‌ ‌लागून‌ ‌राहिली‌ ‌होती.‌ ‌

खालील‌ ‌प्रश्नांची‌ ‌उत्तरे‌ ‌एका‌ ‌वाक्यात‌ ‌लिहा.‌

‌‌‌प्रश्न‌ 1.
लेखिकेचे‌ ‌मन‌ ‌कोणत्या‌ ‌गोष्टींसाठी‌ ‌आतुर‌ ‌झाले‌ ‌होते?‌ ‌
उत्तर:‌
‌लेखिकेचे‌ ‌मन‌ ‌नवीन‌ ‌गोष्टी‌ ‌शिकण्यासाठी‌ ‌आतुर‌ ‌झाले‌ ‌होते.‌

‌‌‌प्रश्न‌ 2.
दारापाशी‌ ‌आल्यावर‌ ‌लेखिकेला‌ ‌कशाची‌ ‌आठवण‌ ‌आली?‌ ‌
उत्तरः‌ ‌
दारापाशी‌ ‌आल्यावर‌ ‌लेखिकेला‌ ‌तिनेच‌ ‌मोडलेल्या‌ ‌बाहुलीची‌ ‌आठवण‌ ‌आली.‌ ‌

‌‌‌प्रश्न‌ 3.
लेखिकेला‌ ‌कोणती‌ ‌उत्कंठा‌ ‌लागून‌ ‌राहिली‌ ‌होती?‌ ‌
उत्तरः‌
‌लेखिकेला‌ ‌आयुष्यात‌ ‌पहिल्यांदाच‌ ‌उदया‌ ‌कधी‌ ‌उगवतोय‌ ‌याची‌ ‌उत्कंठा‌ ‌लागून‌ ‌राहिली‌ ‌होती.‌

कंसातील‌ ‌योग्य‌ ‌शब्द‌ ‌वापरून‌ ‌रिकाम्या‌ ‌जागा‌ ‌भरा.‌ ‌

‌‌‌प्रश्न‌ 1.
1.‌ ‌आयुष्यात‌ ‌नव्यानं‌ ‌आलेल्या‌ ‌या‌ ‌शब्दांनी‌ ‌माझ्या‌ ‌….‌……….. ‌पालवी‌ ‌फुटली.‌ ‌(भावविश्वात,‌ ‌विश्वात,‌ ‌जगात,‌ ‌आयुष्यात)‌
2.‌ ‌तो‌ ‌दिवस‌ ‌माझ्या‌ ‌दृष्टीनं‌ ‌फार‌ ‌………..‌ ‌होता.‌ ‌(आनंददायी,‌ ‌चैतन्यमय,‌ ‌नाट्यमय,‌ ‌पश्चात्तापाचा)‌ ‌
उत्तर:‌
1. ‌भावविश्वात‌
‌2.‌ ‌नाट्यमय‌ ‌

‌‌‌प्रश्न‌ 2.
सहसंबंध‌ ‌लिहा.‌ ‌
नवीन‌ ‌:‌ ‌गोष्टी‌ ‌::‌ ‌नवा‌ ‌:‌ …………………
उत्तरः‌ ‌
विचार‌ ‌

कृती‌ ‌2 ‌:‌ ‌आकलन‌ ‌कृती‌ ‌

‌योग्य‌ ‌पर्याय‌ ‌निवडून‌ ‌विधाने‌ ‌पूर्ण‌ ‌करा.‌

‌‌‌प्रश्न‌ 1.
आता‌ ‌प्रत्येक‌ ‌गोष्टीला‌ ‌नाव‌ ‌होतं‌ ‌……‌ ‌
(अ)‌ ‌आणि‌ ‌प्रत्येक‌ ‌नावातून‌ ‌उमलत‌ ‌होता‌ ‌एकेक‌ ‌नवा‌ ‌विचार!‌
‌(ब)‌ ‌आणि‌ ‌उमलत‌ ‌होता‌ ‌एकेक‌ ‌नवा‌ ‌विचार‌ ‌प्रत्येक‌ ‌नावातून‌ ‌!‌
‌(क)‌ ‌आणि‌ ‌नावा-नावातून‌ ‌उमलत‌ ‌होता‌ ‌एकेक‌ ‌नवा‌ ‌विचार!‌ ‌
(ड)‌ ‌आणि‌ ‌एकेक‌ ‌नवा‌ ‌विचार‌ ‌उमलत‌ ‌होता‌ ‌प्रत्येक‌ ‌नावातून‌ ‌!‌ ‌
उत्तरः‌
‌आता‌ ‌प्रत्येक‌ ‌गोष्टीला‌ ‌नाव‌ ‌होतं‌ ‌आणि‌ ‌नावा-नावातून‌ ‌उमलत‌ ‌होता‌ ‌एकेक‌ ‌नवा‌ ‌विचार!‌

‌‌‌प्रश्न‌ 2.
चाचपडत‌ ‌शेकोटीजवळ‌ ‌लोटलेले‌ ‌बाहुलीचे‌ ‌…….‌…………… ‌.‌
‌(अ)‌ ‌तुकडे‌ ‌गोळा‌ ‌करून‌ ‌मी‌ ‌उचलले.‌
‌(ब)‌ ‌मी‌ ‌तुकडे‌ ‌गोळा‌ ‌करून‌ ‌उचलले.‌
‌(क)‌ ‌तुकडे‌ ‌गोळा‌ ‌करून‌ ‌मी‌ ‌उचलले.‌ ‌
(ड)‌ ‌तुकडे‌ ‌मी‌ ‌गोळा‌ ‌करून‌ ‌उचलले.‌
‌उत्तरः‌ ‌
चाचपडत‌ ‌शेकोटीजवळ‌ ‌लोटलेले‌ ‌बाहुलीचे‌ ‌तुकडे‌ ‌मी‌ ‌गोळा‌ ‌करून‌ ‌उचलले.‌

‌‌‌प्रश्न‌ 3.
‌कोण‌ ‌ते‌ ‌लिहा.‌ ‌
‌उत्तरः‌ ‌

‌चूक‌ ‌वा‌ ‌बरोबर‌ ‌ते‌ ‌लिहा.‌ ‌

‌‌‌प्रश्न‌ 1.

1. ‌लेखिकेचे‌ ‌मन‌ ‌नवीन‌ ‌गोष्टी‌ ‌शिकण्यासाठी‌ ‌आतुर‌ ‌झालं‌ ‌होतं.‌
2. ‌लेखिकेला‌ ‌आज‌ ‌जशी‌ ‌एक‌ ‌वेगळीच‌ ‌नवी‌ ‌दृष्टी‌ ‌मिळाली‌ ‌नव्हती.‌ ‌
3. ‌दारापाशी‌ ‌आल्यावर‌ ‌लेखिका‌ ‌मोडलेल्या‌ ‌बाहुलीची‌ ‌आठवण‌ ‌विसरली.‌ ‌

उत्तर:‌

1. ‌बरोबर‌
2. ‌चूक‌
3. ‌चूक‌ ‌

कृती‌ ‌3 ‌:‌ ‌व्याकरण‌ ‌कृती‌

‌‌‌प्रश्न‌ 1.
‌खालील‌ ‌वाक्य‌ ‌लेखननियमांनुसार‌ ‌शुद्ध‌ ‌करून‌ ‌लिहा.‌ ‌
त्याच‌ ‌दिवशी‌ ‌मी‌ ‌खुप‌ ‌नवे‌ ‌शब्द‌ ‌शिकुन‌ ‌घेतले.‌ ‌
उत्तरः‌
‌त्याच‌ ‌दिवशी‌ ‌मी‌ ‌खूप‌ ‌नवे‌ ‌शब्द‌ ‌शिकून‌ ‌घेतले.‌ ‌

‌‌‌प्रश्न‌ 2.
उताऱ्यातील‌ ‌दोन‌ ‌नामे‌ ‌शोधून‌ ‌लिहा.‌ ‌
उत्तरः‌

1. ‌विहीर‌
2. ‌बाहुली‌
3. ‌डोळे‌
4. ‌शब्द‌ ‌
5. ‌आई‌ ‌
6. ‌बाबा‌ ‌
7. ‌बहीण‌ ‌
8. ‌बाबा‌ ‌
9. रात्र‌
10. पलंग‌

प्रश्न‌ 3.
‌अचूक‌ ‌शब्द‌ ‌लिहा.‌ ‌
1.‌ ‌कशोशीनं,‌ ‌कसोशिनं,‌ ‌कशोशिनं,‌ ‌कसोशीनं‌ ‌
2.‌ ‌पच्चात्ताप,‌ ‌पश्चाताप,‌ ‌पश्चात्ताप,‌ ‌पश्चत्ताप‌ ‌
उत्तर:‌
1. कसोशीनं‌ ‌
2.‌ ‌पश्चात्ताप‌

प्रश्न‌ 4.
समानार्थी‌ ‌शब्द‌ ‌लिहा.‌ ‌

1. नयन‌ ‌-‌ [ ]
2. ‌रजनी‌ ‌-‌ ‌[ ]
3. नजर‌ ‌-‌ ‌[ ]‌ ‌
4. मेहनत‌ ‌-‌ ‌[ ]

उत्तर:‌

1. डोळा‌ ‌
2. रात्र‌ ‌
3. ‌दृष्टी‌ ‌
4. ‌प्रयत्न‌ ‌

प्रश्न‌ 5. ‌
विरुद्धार्थी‌ ‌शब्द‌ ‌लिहा.

1. ‌जुने‌ ‌×
2. ‌विस्मरण‌ ‌×
3. ‌बरोबर‌ ‌×
4. ‌अनिश्चित‌ ‌×

‌उत्तर:‌

1. ‌नवीन‌
2. ‌आठवण‌
3. ‌चूक‌
4. ‌निश्चित‌ ‌

प्रश्न‌ 6. ‌
उताऱ्यातील‌ ‌दोन‌ ‌अनेकवचनी‌ ‌शब्द‌ ‌शोधून‌ ‌लिहा.‌ ‌
उत्तर:‌

1. ‌तुकडे‌ ‌
2. ‌डोळे‌ ‌
3. ‌नवे‌
4. ‌शब्द‌
5. ‌आठवणी‌ ‌

प्रश्न‌ 7. ‌
तक्ता‌ ‌पूर्ण‌ ‌करा.‌ ‌
उत्तर:‌

प्रश्न‌ 8. ‌
तक्ता‌ ‌पूर्ण‌ ‌करा.‌ ‌
उत्तर:‌

प्रश्न‌ 9. ‌
पर्यायी‌ ‌शब्द‌ ‌लिहा.‌ ‌
उत्तर:‌

कृती‌ ‌4‌ ‌:‌ ‌स्वमत‌

प्रश्न‌ 1. ‌
‌तुमच्या‌ ‌मते‌ ‌हेलन‌ ‌केलर‌ ‌आयुष्यात‌ ‌पहिल्यांदा‌ ‌’उदयाची’‌ ‌वाट‌ ‌का‌ ‌पाहत‌ ‌असेल?‌ ‌
उत्तरः‌ ‌
हेलन‌ ‌केलर‌ ‌ही‌ ‌एक‌ ‌दिव्यांग‌ ‌मुलगी‌ ‌होती.‌ ‌आंधळेपणा,‌ ‌बहिरेपणा‌ ‌व‌ ‌मुकेपणा‌ ‌यामुळे‌ ‌तिच्या‌ ‌संपूर्ण‌ ‌आयुष्यात‌ ‌अंधार‌ ‌पसरलेला‌ ‌होता.‌ ‌परंतु‌ ‌शिक्षिका‌ ‌अनी‌ ‌मॅन्सफिल्ड‌ ‌सुलिव्हन‌ ‌यांच्यामुळे‌ ‌तिला‌ ‌शब्दांची‌ ‌ओळख‌ ‌झाली.‌ ‌नवीन‌ ‌शब्द‌ ‌कळू‌ ‌लागले.‌ ‌परिचित‌ ‌अपरिचित‌ ‌वस्तूंची‌ ‌नावे‌ ‌तिला‌ ‌कळू‌ ‌लागली,‌ ‌त्यामुळे‌ ‌अंधाराने‌ ‌भरलेल्या‌ ‌तिच्या‌ ‌जगामध्ये‌ ‌नवचैतन्य‌ ‌निर्माण‌ ‌झाले.‌ ‌त्यामुळेच‌ ‌हेलनच्या‌ ‌आयुष्यात‌ ‌नव्यानं‌ ‌आलेल्या‌ ‌या‌ ‌शब्दांनी‌ ‌तिच्या‌ ‌भावविश्वात‌ ‌पालवी‌ ‌फुटली.‌ ‌अंधाराने‌ ‌भरलेल्या‌ ‌आयुष्यात‌ ‌जे‌ ‌घडले‌ ‌नव्हते‌ ‌ते‌ ‌घडले.‌ ‌या‌ ‌सर्व‌ ‌कारणांमुळे‌ ‌हेलन‌ ‌केलर‌ ‌आयुष्यात‌ ‌पहिल्यांदा‌ ‌’उदयाची’‌ ‌वाट‌ ‌पाहत‌ ‌असेल‌ ‌असे‌ ‌वाटते.‌ ‌

शब्दांचा खेळ Summary in Marathi

‌लेखकाचा‌ ‌परिचय‌:
‌ ‌
नाव‌:‌ ‌हेलन‌ ‌केलर‌ ‌
कालावधी‌:‌ ‌(1880-1968)
परिचय‌:‌ ‌विसाव्या‌ ‌शतकावर‌ ‌आपल्या‌ ‌अलौकिक‌ ‌कार्याने‌ ‌आणि‌ ‌व्यक्तिमत्त्वामुळे‌ ‌ज्या‌ ‌लोकोत्तर‌ ‌व्यक्तींचा‌ ‌प्रभाव‌ ‌पडला,‌ ‌त्यामध्ये‌ ‌हेलन‌ ‌केलर‌ ‌यांचे‌ ‌नाव‌ ‌अग्रगण्य‌ ‌आहे.‌ ‌अंधत्व,‌ ‌मुकेपणा‌ ‌आणि‌ ‌बधिरत्व‌ ‌अशा‌ ‌तिहेरी‌ ‌अपंगत्वाशी‌ ‌सामना‌ ‌देत‌ ‌त्यांनी‌ ‌आपले‌ ‌शिक्षण‌ ‌पूर्ण‌ ‌केले.‌ ‌अंधारातून‌ ‌प्रकाशाकडे‌ ‌नेणाऱ्या‌ ‌हेलन‌ ‌केलर‌ ‌यांच्या‌ ‌शिक्षणाच्या‌ ‌थक्क‌ ‌करणाऱ्या‌ ‌अनुभवांनी‌ ‌युक्त‌ ‌अशा‌ ‌’the‌ ‌story‌ ‌of‌ ‌my‌ ‌life’‌ ‌या‌ ‌आत्मकथनाचा‌ ‌मराठी‌ ‌अनुवाद‌ ‌श्री.‌ ‌माधव‌ ‌कर्वे‌ ‌यांनी‌ ‌’माझी‌ ‌जीवनकहाणी’‌ ‌या‌ ‌पुस्तकरूपाने‌ ‌केला‌ ‌आहे.‌

‌प्रस्तुत‌ ‌उतारा‌ ‌’माझी‌ ‌जीवनकहाणी‌ ‌-‌ ‌हेलन‌ ‌केलर,‌ ‌अनुवाद‌ ‌-‌ ‌माधव‌ ‌कर्वे,‌ ‌या‌ ‌पुस्तकातून‌ ‌घेतला‌ ‌आहे.‌ ‌

प्रस्तावना‌:

‘शब्दांचा‌ ‌खेळ’‌ ‌हा‌ ‌उतारा‌ ‌श्री‌ ‌माधव‌ ‌कर्वे‌ ‌यांनी‌ ‌लिहिलेल्या‌ ‌हेलन‌ ‌केलर‌ ‌यांच्या‌ ‌आत्मवृत्ताच्या‌ ‌अनुवादातून‌ ‌घेतला‌ ‌आहे.‌ ‌या‌ ‌पाठात‌ ‌हेलन‌ ‌केलर‌ ‌यांना‌ ‌अपंगत्वामुळे‌ ‌भाषा‌ ‌शिक्षणात‌ ‌येणारे‌ ‌अडथळे‌ ‌व‌ ‌हे‌ ‌अडथळे‌ ‌दूर‌ ‌करण्यासाठी‌ ‌त्यांनी‌ ‌व‌ ‌त्यांच्या‌ ‌शिक्षिकेने‌ ‌केलेले‌ ‌प्रयत्न‌ ‌याचे‌ ‌वर्णन‌ ‌येथे‌ ‌केले‌ ‌आहे.‌ ‌

The‌ ‌extract‌ ‌’Shabdancha‌ ‌Khel’‌ ‌is‌ ‌taken‌ ‌from‌ ‌the‌ ‌translation‌ ‌of‌ ‌the‌ ‌autobiography‌ ‌of‌ ‌Helen‌ ‌Keller.‌ ‌Helen‌ ‌Keller‌ ‌became‌ ‌deaf‌ ‌and‌ ‌blind‌ ‌at‌ ‌the‌ ‌age‌ ‌of‌ ‌19‌ ‌months.‌ ‌This‌ ‌extract‌ ‌tells‌ ‌us‌ ‌about‌ ‌the‌ ‌extraordinary‌ ‌and‌ ‌remarkable‌ ‌struggle‌ ‌of‌ ‌Helen‌ ‌and‌ ‌her‌ ‌teacher,‌ ‌to‌ ‌overcome‌ ‌her‌ ‌shortcomings‌ ‌in‌ ‌learning‌ ‌language.‌ ‌

शब्दार्थ‌:

1. नवल‌ ‌-‌ ‌आश्चर्य‌ ‌(wonder)‌ ‌
2. पोर्च‌ ‌-‌ ‌द्वारमंडप‌ ‌(porch)‌ ‌
3. अपेक्षा‌ ‌-‌ ‌इच्छा‌ ‌(ambition‌ ‌,‌ ‌wish)‌ ‌
4. खाणाखुणा‌ ‌-‌ ‌येचे‌ ‌अर्थ‌ ‌खुणा,‌ ‌इशारा‌ ‌(signs,‌ ‌marks)‌
5. ‌लगबग‌ ‌-‌ ‌घाई‌ ‌व‌ ‌गडबड‌ ‌(hurry,‌ ‌hustle)‌ ‌
6. अंदाज‌ ‌-‌ ‌सुमार,‌ ‌अदमास‌ ‌(rough‌ ‌estimate)‌ ‌
7. कडवटपणा‌ ‌-‌ ‌कडूपणा‌ ‌(bitterness)‌ ‌
8. व्यग्र‌ ‌-‌ ‌व्यस्त,‌ ‌गुंग‌ (engrossed)‌ ‌
9. झगडा‌ ‌-‌ ‌भांडण‌ ‌(dispute)‌
10. ‌दाट‌ ‌-‌ ‌घन‌ ‌(thick,‌ ‌dense)‌ ‌
11. स्पर्श‌ ‌-‌ ‌संपर्क‌ ‌(touch)‌
12. ‌किनारा‌ ‌-‌ ‌काठ‌ ‌(a‌ ‌bank)‌
13. ‌ताण‌ ‌- दबाव‌ ‌(strain,‌ ‌tension)‌
14. ‌नि:शब्द‌ ‌-‌ ‌काही‌ ‌न‌ ‌बोलता,‌ ‌शांत‌ ‌(silent)‌ ‌
15. आक्रंदन‌ ‌-‌ ‌तीव्र‌ ‌शोक,‌ ‌आक्रोश‌ ‌(wailing)‌ ‌
16. न्हाणे‌ ‌-‌ ‌नाहणे,‌ ‌स्नान‌ ‌करणे‌ ‌(to‌ ‌bathe)‌ ‌
17. पाखर‌ ‌-‌ ‌येथे‌ ‌अर्थ‌ ‌सावली‌ ‌(shade)‌
18. ‌जिना‌ ‌-‌ ‌पायऱ्या‌ ‌(staircase)‌
19. ‌चिंध्या‌ ‌-‌ ‌फाटलेले‌ ‌वस्त्र‌ ‌(strips‌ ‌of‌ ‌clothes)‌ ‌
20. तानमान‌ ‌-‌ ‌स्थलकाल,‌ ‌परिस्थितीची‌ ‌अनुकूल‌ ‌संधी‌
21. ‌हिसकावणे‌ ‌-‌ ‌खेचून‌ ‌घेणे‌ ‌(to‌ ‌take‌ ‌away‌ ‌forcibly)‌
22. ‌पीडा‌ ‌-‌ ‌त्रास,‌ ‌वेदना‌ ‌(trouble,‌ ‌pain)‌ ‌
23. खंत‌ ‌-‌ ‌दु:ख‌ ‌(regret)‌
24. ‌खेद‌ ‌-‌ ‌दु:ख‌ ‌(regret)‌ ‌
25. आविर्भाव‌ ‌-‌ ‌हावभाव‌ ‌(expression)‌ ‌
26. निश्चल‌ ‌-‌ ‌स्तब्ध,‌ ‌अढळ‌ ‌(stable,‌ ‌firm,‌ ‌still)‌
27. ‌हळवे‌ ‌-‌ ‌नाजूक‌ ‌(sentimental)‌
28. ‌उबदार‌ ‌-‌ ‌गरम‌ ‌करणारे‌ ‌(warm)‌
29. ‌टुणटुण‌ ‌-‌ ‌लहान-लहान‌ ‌उड्या‌ ‌मारत‌ ‌(hoppingly)‌ ‌
30. पाऊलवाट‌ ‌-‌ ‌पायवाट‌ ‌(path)‌ ‌
31. दरवळत‌ ‌-‌ ‌सर्वत्र‌ ‌पसरत‌ ‌
32. धारा‌ ‌-‌ ‌प्रवाह‌ ‌(flow)‌ ‌
33. ओघळ‌ ‌-‌ ‌बारीक‌ ‌प्रवाह‌ ‌(streamlet)‌
34. ‌अस्पष्ट‌ ‌-‌ ‌स्पष्ट‌ ‌नसलेले‌ ‌(unclear)‌ ‌
35. जाणीव‌ ‌-‌ ‌आकलन,‌ ‌बोध‌ ‌(realization)‌
36. ‌स्मृती‌ ‌-‌ ‌आठवण‌ ‌(memory)‌
37. ‌थरार‌ ‌-‌ ‌(thrill)‌ ‌
38. उसळणे‌ ‌-‌ ‌वर‌ ‌जाणे‌ ‌(to‌ ‌rise‌ ‌up)‌ ‌
39. चैतन्यमय‌ ‌-‌ ‌उत्साही‌ ‌(enthusiastic)‌ ‌
40. उधळणे‌ ‌-‌ ‌येचे‌ ‌अर्थ‌ ‌उडवणे‌ ‌(to‌ ‌throw)‌
41. ‌अडथळे‌ ‌-‌ ‌अडचणी‌ ‌(problems,‌ ‌obstacles)‌ ‌
42. चाचपडत‌ ‌-‌ ‌येथे‌ ‌अर्थ‌ ‌हातांनी‌ ‌स्पर्श‌ ‌करणे‌ ‌/‌ ‌शोधणे‌ ‌
43. पश्चात्ताप‌ ‌-‌ ‌खेद‌ ‌(remorse)‌ ‌
44. भावविश्व‌ ‌-‌ ‌भावनेतील‌ ‌जग‌ ‌
45. नाट्यमय‌ ‌-‌ ‌नाट्यपूर्ण‌ ‌(dramatic)‌ ‌
46. पलंग‌ ‌-‌ ‌खाट‌ ‌(bedstead,‌ ‌coach)‌
47. ‌शेकोटी‌ ‌-‌ ‌जाळ‌ ‌(a‌ ‌little‌ ‌warming‌ ‌fire)‌

‌टिपा‌:‌

1. अनी‌ ‌मॅन्सफिल्ड‌ ‌सुलिव्हॅन‌ ‌-‌ ‌लेखिका‌ ‌हेलन‌ ‌केलर‌ ‌यांची‌ ‌शिक्षिका‌ ‌
2. हनीसकल‌ ‌वेल‌ ‌-‌ ‌सुगंधी‌ ‌फुलांची‌ ‌वेल‌ ‌
3. होकायंत्र‌ ‌-‌ ‌दिशा‌ ‌ओळखण्यासाठी‌ ‌गलबतावर‌ ‌वापरले‌ ‌जाणारे‌ ‌यंत्र‌ ‌
4. पर्किन्स‌ ‌इन्स्टिट्यूशन‌ ‌-‌ ‌या‌ ‌संस्थेची‌ ‌स्थापना‌ ‌1929 मध्ये‌ ‌झाली.‌ ‌ही‌ ‌अमेरिकेतील‌ ‌सर्वांत‌ ‌जुनी‌ ‌अंध‌ ‌व्यक्तींसाठी‌ ‌असलेली‌ ‌शाळा‌ ‌आहे.‌

वाक्प्रचार‌:

1. नवल‌ ‌वाटणे‌ ‌-‌ ‌आश्चर्य‌ ‌वाटणे
2. अंदाज‌ ‌येणे‌‌ ‌-‌ ‌साधारण‌ ‌कल्पना‌ ‌येणे‌ ‌ ‌
3. कल्पना‌ ‌नसणे‌ ‌-‌ ‌माहित‌ ‌नसणे‌ ‌
4. व्यग्र‌ ‌होणे‌ ‌-‌ ‌व्यस्त‌ ‌असणे,‌ ‌मग्न/गुंग‌ ‌असणे‌ ‌
5. थकून‌ ‌जाणे‌ -‌ ‌दमणे‌ ‌
6. ताण‌ ‌असणे‌ ‌-‌ ‌तणाव‌ ‌असणे‌
7. ‌छाती‌ ‌धडधडणे‌ ‌-‌ ‌भीती‌ ‌वाटणे‌ ‌
8. मायेची‌ ‌पाखर‌ ‌घालणे‌ ‌-‌ ‌प्रेम‌ ‌करणे‌ ‌
9. अभिमानानं‌ ‌फुलून‌ ‌येणे‌ ‌-‌ ‌खूप‌ ‌आनंद‌ ‌होणे‌ ‌
10. अनुकरण‌ ‌करणे‌ ‌-‌ ‌नक्कल‌ ‌करणे‌ ‌
11. खाणाखुणा‌ करणे‌ ‌-‌ ‌इशारा‌ ‌करणे‌ ‌
12. उकळ्या‌ ‌फुटणे‌ ‌-‌ ‌खूप‌ ‌आनंद‌ ‌होणे‌ ‌
13. हिसकावून‌ ‌घेणे‌ ‌‌-‌ ‌खेचून‌ ‌घेणे‌
14. ‌खंत‌ ‌नसणे‌ ‌-‌ ‌दु:ख‌ ‌नसणे‌ ‌
15. आनंदाची‌ ‌उधळण‌ ‌करणे‌ ‌-‌ ‌आनंद‌ ‌पसरवणे‌
16. ‌आतुर‌ ‌होणे‌ ‌-‌ ‌उत्सुक‌ ‌होणे‌ ‌
17. नवी‌ ‌दृष्टी‌ ‌मिळणे‌ ‌-‌ ‌नवीन‌ ‌दिशा‌ ‌मिळणे‌ ‌
18. पश्चात्ताप‌ ‌होणे‌ ‌-‌ ‌खेद‌ ‌वाटणे/वाईट‌ ‌वाटणे/पस्तावा‌ ‌वाटणे‌
19. ‌पालवी‌ ‌फुटणे‌ ‌-‌ ‌नवीन‌ ‌उत्साह‌ ‌निर्माण‌ ‌होणे‌
20. ‌उत्कंठा‌ ‌लागणे‌ ‌-‌ ‌उत्सुकता‌ ‌लागणे.‌ ‌
21. हिरमोड‌ ‌होणे‌ ‌-‌ ‌नाराज‌ ‌होणे‌ ‌
22. कसोशीने‌ ‌प्रयत्न‌ ‌करणे‌ ‌-‌ ‌खूप‌ ‌कष्ट‌ ‌करणे‌ ‌
23. आतुर‌ ‌होणे‌ ‌-‌ ‌उत्सुक‌ ‌होणे‌ ‌

Balbharti Maharashtra State Board Class 9 Marathi Solutions Kumarbharti Chapter 2.2 संतवाणी (आ) धरिला पंढरीचा चोर-संत जनाबाई Notes, Textbook Exercise Important Questions and Answers.

Maharashtra State Board Class 9 Marathi Kumarbharti Solutions Chapter 2.2 संतवाणी (आ) धरिला पंढरीचा चोर-संत जनाबाई

9th Std Marathi Kumarbharati Digest Chapter 2.2 संतवाणी (आ) धरिला पंढरीचा चोर-संत जनाबाई Textbook Questions and Answers

1. खाली दिलेल्या शब्दांसाठी उपमा लिहा:

प्रश्न 1.
खाली दिलेल्या शब्दांसाठी उपमा लिहा:
उत्तर:

2. जोड्या लावा:

प्रश्न 1.
जोड्या लावा:
उत्तर:

3. काव्यसौंदर्य.

प्रश्न (अ)
सोहं शब्दाचा मारा केला। विठ्ठल काकुलती आला।।’ या ओळीतील सरळ अर्थ लिहा.
उत्तर:
संत जनाबाईंनी भक्तीचा दोर श्रीविठ्ठलाच्या गळ्यात अडकवून त्याला हृदयाच्या बंदिखान्यात कोंडला. श्रीविठ्ठल हृदयातून जाऊ नये, म्हणून त्याच्यावर ‘तू म्हणजे मीच’ या अहंभावाचा मारा केला. त्यामुळे विठ्ठल विनवणी करू लागला की, मी तुझ्या हृदयात राहीन, पण सोहं शब्दांचा मारा थांबव.

प्रश्न (आ)
‘जनी म्हणे बा विठ्ठला। जीवे न सोडी मी तुला ।।’ या ओळींतून व्यक्त झालेला कवयित्रीचा भाव स्पष्ट करा.
उत्तर:
संत जनाबाईंना श्रीविठ्ठल आपल्या हृदयात कायमचा राहावा, असे वाटत होते. म्हणून त्यांनी भक्तीचा दोर विठ्ठलाच्या गळ्यात बांधून त्याला हृदयाच्या कैदखान्यात कोंडला. शिक्षा म्हणून शब्दरचनेची बेडी त्याच्या पायात घातली व सोहं शब्दाचा मार दिला. शेवटी श्रीविठ्ठल हृदयातून जाऊ नये; म्हणून त्याला जिवंत न सोडण्याची प्रेमळ धमकी दिली. या शेवटच्या उपायाने तरी श्रीविठ्ठलाने मनात घर करून राहावे, असे संत जनाबाईंना वाटत होते. *

प्रश्न (इ)
प्रस्तुत अभंगातून कवयित्रीच्या मनातील श्रीविठ्ठलाविषयीच्या कोणत्या भावभावना दिसून येतात, ते लिहा.
उत्तर:
श्रीविठ्ठलाने आपल्या मनात कायम रहिवास करावा, असे संत जनाबाई यांना वाटते आहे. त्यासाठी एक वेगळाच उपाय त्यांनी योजला. त्यांनी विठ्ठलरूपी चोराला भक्तीचा दोर गळ्यात बांधून धरून आणला व हृदयाच्या बंदिखान्यात डांबला. तो पळून जाऊ नये म्हणून त्याच्या पायात शब्दांची जुळणी करून बेडी घातली. त्याच्यावर सोहं शब्दाचा मारा केला. इतकेच नव्हे; तर त्याला जीवे न सोडण्याची समज दिली. अशा प्रकारे प्रस्तुत अभंगातून संत जनाबाईंचा श्रीविठ्ठलाप्रती असणारा पराकोटीचा उत्कट भाव व्यक्त झाला आहे.

4. अभिव्यक्ती.

प्रश्न (अ)
मानवी जीवनातील निष्ठा, भक्ती आणि प्रयत्न यांचे असलेले महत्त्व तुमच्या शब्दांत लिहा.
उत्तर:
माणसाला आपल्या ध्येयावर अपार निष्ठा हवी. एखादे कार्य करताना त्याविषयी भक्तिभाव हवा. भक्तीमुळे माणसाच्या मनाला अहंकाराचा स्पर्श होत नाही व मन निष्ठेशी लीन होते. निष्ठा व भक्तीच्या जोडीला प्रयत्नांची पराकाष्ठा हवी. मानवी जीवनात निष्ठा, भक्ती व प्रयत्न या तीनही मूल्यांना नितांत महत्त्व आहे. जीवन कृतार्थ व सफल करायचे असेल, तर या तीन मूल्यांचे आचरण करायला हवे.

उपक्रम:
आंतरजालाच्या साहाय्याने महाराष्ट्रातील संत कवयित्रींची माहिती मिळवा.

Marathi Kumarbharati Textbook Std 9 Answers Chapter 2.2 संतवाणी (आ) धरिला पंढरीचा चोर-संत जनाबाई Additional Important Questions and Answers

पुढील कवितेच्या आधारे दिलेल्या सूचनांनुसार कृती करा:

कृती 1 : (आकलन)

प्रश्न 1.
चौकटी पूर्ण करा:

उत्तर:

1. पंढरीचा चोर
2. बंदिखाना
3. हृदयाचा
   1. शब्दांची
   2. सोहं शब्दाचा

कृती 2 : (आकलन)

प्रश्न 1.
पुढील विधाने योग्य पर्याय निवडून पूर्ण करा:
1. पंढरीचा चोर म्हणजे (श्रीकृष्ण/श्रीविष्णू /महादेव/श्रीविठ्ठल) .
2. श्रीविठ्ठल काकुलती आला; कारण
(अ) त्याच्या पायात बेडी घातली.
(आ) त्याला हृदयात कोंडला होता.
(इ) त्याच्यावर सोहं शब्दांचा मारा केला.
(ई) त्याच्या गळ्यात दोर बांधला.

उत्तर:

1. विठ्ठलाला धरले – भक्तीच्या दोराने
   1. विठ्ठल काकुलती आला – ‘तू म्हणजे मीच’ या शब्दाने
   2. विठ्ठलाच्या पायी घातली बेडी – शब्दरचनेच्या जुळणीने.
2. पंढरीचा चोर म्हणजे श्रीविठ्ठल.
   1. श्रीविठ्ठल काकुलती आला; कारण त्याच्यावर सोहं शब्दांचा मारा केला.

पुढील कवितेवर दिलेल्या मुद्द्यांच्या आधारे कृती सोडवा:

कविता: संतवाणी- (आ) धरिला पंढरीचा चोर.
उत्तर: संतवाणी-(आ) धरिला पंढरीचा चोर

1. प्रस्तुत कवितेचे कवी/कवयित्री → संत जनाबाई.
2. कवितेचा विषय → विठ्ठलाचे प्रेम व जवळीक लाभावी, म्हणून त्याला मनाच्या बंदिखान्यात कोंडून ठेवणे.

3. कवितेतील दोन शब्दांचे अर्थ →

1. बेडी = साखळी
2. जीव = प्राण
3. पाय = पद
4. हृदय = जिव्हार.

4. कवितेतून मिळणारा संदेश → भक्तिरसाचे उत्कट उदाहरण या अभंगातून प्रत्ययाला येते. परमेश्वर व भक्त यांचा संबंध अतूट असावा, केवळ नामस्मरण व जवळीक असावी, या भावनेचा परमोच्च बिंदू गाठला आहे.

5. कवितेची भाषिक वैशिष्ट्ये → पहिल्या चरणात सात ते आठ अक्षरे आणि दुसऱ्या चरणात नऊ-दहा अक्षरे असणारा, दोन्ही चरणांत यमक असलेला, हा ‘छोटा अभंगा’चा लोकछंद प्रकार संत जनाबाईंनी सहजपणे अभिव्यक्त केला आहे. या अभंगातील हृदयाच्या बंदिखान्याचे रूपक अत्यंत बहारदारपणे वठवले आहे. चोर, कैदखाना, मार देणे, बंदिस्त ठेवणे असे अनुक्रमे फुलत जाणारे भाव लोभस आले आहेत, शिवाय ‘सोहं शब्दाचा मारा केला’ यातील गहन तत्त्वज्ञान सहजपणे मांडले आहे. श्रीविठ्ठलाचा सहवास मिळावा, म्हणून केलेले लटके भांडण नाट्यमयरीत्या साकार केले आहे.

6. कवितेतून व्यक्त होणारा विचार → श्रीविठ्ठलाचा कायम सहवास मिळावा व त्याच्याशी प्रेमळ संवाद व्हावा, म्हणून श्रीविठ्ठलाला चोर समजून हृदयाच्या बंदिखान्यात बंदिस्त करणे व त्याच्याशी लटके भांडण करणे. चोर-शिपाई या रूपकांतून श्रीविठ्ठलाचा निरंतर सहवास. विठ्ठल हृदयात कायम राहावा हा भक्तिभाव.

7. कवितेतील दोन ओळींचा सरळ अर्थ:

‘सोहं शब्दाचा मारा केला।
विठ्ठल काकुलती आला ।।
→ संत जनाबाई यांनी श्रीविठ्ठलाला हृदयाच्या बंदिखान्यात कोंडून ठेवला. त्यावर अहंकारी शब्दांचा मारा केला. तेव्हा विठ्ठल जनाबाईंची व्याकुळ होऊन विनवणी करू लागला.

8. कविता आवडण्याची वा न आवडण्याची कारणे → श्रीविठ्ठलाच्या गळ्यात दोर बांधून त्याला हृदयाच्या बंदिखान्यात कैद करणे, ही संत जनाबाईंची श्रीविठ्ठलाच्या बाबतीत असलेली प्रेमळ आसक्ती अतिशय उत्कटपणे साधली आहे. ‘प्राण गेला तरी तुला मी सोडणार नाही,’ या निवेदनातून विठ्ठल कायम मनात वसावा, ही आंतरिक ओढ सहजपणे व सार्थपणे या अभंगात व्यक्त झाली आहे. त्यामुळेच संत जनाबाईंचा हा अभंग मला फार आवडला.

पुढील ओळींचे रसग्रहण तुमच्या शब्दांत करा:

प्रश्न 1.
‘हृदय बंदिखाना केला।
आंत विठ्ठल कोंडिला।।’
उत्तर:
आशयसौंदर्य: श्रीविठ्ठलाचे प्रेम व जवळीक सदैव लाभावी म्हणून त्याला हृदयाच्या बंदिखान्यात कायम कोंडून ठेवणे, हा आशय व्यक्त करणारा ‘धरिला पंढरीचा चोर’ हा संत जनाबाई यांचा वेगळा अभंग आहे. भक्त आणि परमेश्वराचे दृढ नाते कसे असावे, याची शिकवण या अभंगातून जनसामान्यांना मिळते.

काव्यसौंदर्य: श्रीविठ्ठलाचा कायम सहवास मिळावा म्हणून या पंढरीच्या चोराला मी पकडले आहे व त्याला माझ्या हृदयाच्या कैदखान्यात डांबून ठेवले आहे. असे संत जनाबाई निरागसपणे सहज म्हणतात. भक्तिरसाचे उत्कट उदाहरण या ओळींमधून प्रत्ययाला येते. श्रीविठ्ठल निरंतर मनात राहावा, म्हणून हे लटके भांडण अतिशय लोभसवाणे झाले आहे.

भाषिक वैशिष्ट्ये: पहिल्या चरणात सात ते आठ अक्षरे आणि दुसऱ्या चरणात नऊ-दहा अक्षरे असणारा, दोन्ही चरणांत यमक असलेला, हा ‘छोटा अभंगा’चा प्राचीन लोकछंद संत जनाबाईंनी सहजपणे अभिव्यक्त केला आहे. या अभंगातील चोर व हृदयाच्या बंदिखान्याचे रूपक अत्यंत बहारदारपणे वठवले आहे. चोर, कैदखाना, मार देणे, बंदिस्त ठेवणे असे अनुक्रमे फुलत जाणारे भाव लोभस आले आहेत, शिवाय ‘सोहं शब्दाचा मारा केला’ यातील गहन तत्त्वज्ञान सहजपणे मांडले आहे. श्रीविठ्ठलाचा सहवास मिळावा म्हणून केलेले लटके भांडण नाट्यमयरीत्या साकार केले आहे.

भाषाभ्यास:

(आ) भाषिक घटकांवर आधारित कृती:

1. शब्दसंपत्ती:

प्रश्न 1.
विरुद्धार्थी शब्द लिहा:

1. आत
2. चोर
3. सोडणे.

उत्तर:

1. आत × बाहेर
2. चोर × साव
3. सोडणे × धरणे.

प्रश्न 2.
वचन ओळखा:

1. जुड्या
2. दोर
3. हृदय
4. बंदिखाने.

उत्तर:

1. अनेकवचन
2. एकवचन
3. एकवचन
4. अनेकवचन.

2. लेखननियम:

प्रश्न 1.
अचूक शब्द ओळखा:
1. बंदीखाना, बंदिखाना, बंधिखाना, बंदिकाना.
2. पंन्ढरी, पंढरी, पंढरि, पंडरी.
उत्तर:
1. बंदिखाना
2. पंढरी.

उपक्रम:

प्रश्न 1.
आंतरजालाच्या साहाय्याने महाराष्ट्रातील स्त्री-संत कवयित्रींची माहिती मिळवा.

संतवाणी (आ) धरिला पंढरीचा चोर-संत जनाबाई Summary in Marathi

कवितेचा आशय:

पंढरीचा विठ्ठल सदैव हृदयात राहावा; म्हणून त्याला बंदिवान करण्याची आस संत जनाबाईंनी या अभंगात व्यक्त केली आहे. त्यासाठी चोर-शिपायाचे रूपक कवितेत वापरले आहे.

शब्दार्थ:

1. गळां – गळ्यामध्ये.
2. बंदिखाना – तुरुंग, कैदखाना.
3. कोंडिला – डांबून ठेवला.
4. शब्दें – शब्दांनी.
5. जवाजुडी – कड्यांची साखळी.
6. पायीं – पायात.
7. बेडी – जखडून ठेवण्याची साखळी, साखळदंड.
8. सोहं – अहंकार, मीपणा, व्यर्थ अभिमान.
9. काकुलती – विनवणी करणे.
10. बा – अरे.
11. जीवें न सोडी – जिवंत सोडणार नाही.

कवितेचा (अभंगाचा) भावार्थ:

श्रीविठ्ठलाबरोबर सुखसंवादरूपी लटके भांडण करताना संत जनाबाई म्हणतात:

गळ्यात भक्तीचा दोर बांधून मी पंढरीच्या चोराला (श्रीविठ्ठलाला) पकडले आहे. ।।1।।
माझ्या हृदयाचा कैदखाना करून मी त्यात विठ्ठलाला डांबून ठेवले आहे. ।।2।।
या पंढरीच्या चोराला शिक्षा म्हणून मी शब्द जुळवून साखळी केली व विठ्ठलाच्या पायात भक्कम बेडी घातली आहे. (भजन गाऊन विठ्ठलाला आपलेसे करण्याचा प्रयत्न केला आहे.) ।।3।।
विठ्ठलावर मी (अहंकारी) अहंपणाचा भडिमार केला. ‘तू म्हणजे मीच’ असे सांगितले. तेव्हा विठ्ठल व्याकुळ झाला. विनवणी करू लागला. ।।4।।
संत जनाबाई म्हणतात – अरे, विठ्ठला, मी तुला जिवंत सोडणार नाही. (माझ्या मनात कायम तुझा वास राहील, अशी तजवीज करणार आहे.) ।।5।।

Balbharti Maharashtra State Board Class 9 Marathi Solutions Aksharbharati Chapter 13 तिफन Notes, Textbook Exercise Important Questions and Answers.

Maharashtra State Board Class 9 Marathi Aksharbharati Solutions Chapter 13 तिफन(कविता)

Marathi Aksharbharati Std 9 Digest Chapter 13 तिफन Textbook Questions and Answers‌

‌1. खालील‌ ‌अर्थाच्या‌ ‌शब्दसमुहाला‌ ‌कवितेतील‌ ‌योग्य‌ ‌शब्द‌‌ दया.‌ ‌

प्रश्न‌ ‌1. ‌
खालील‌ ‌अर्थाच्या‌ ‌शब्दसमुहाला‌ ‌कवितेतील‌ ‌योग्य‌ ‌शब्द‌‌ दया.‌ ‌

1. ‌पेरणीसाठी‌ ‌लागणारे‌ ‌बियाणे‌ ‌…….‌………… ‌
2. ‌शेतकरी‌ ‌पेरणीसाठी‌ ‌वापरतो‌ ‌ते‌ ‌अवजार‌ ‌…………………
3. पाराबती‌ ‌करते‌ ‌त्या‌ ‌दोन‌ ‌कृती‌ ‌……………, …………………..

उत्तर:

1. ‌बजवाई‌
2. ‌तिफण‌‌
3. पोटाला‌ ‌वटी‌ ‌बांधणे,‌ ‌झोळी‌ ‌काठीला‌ ‌टांगणे‌ ‌

2.‌ ‌खालील‌ ‌ओळींतील‌ ‌अधोरेखित‌ ‌संकल्पना‌ ‌स्पष्ट‌ ‌करा.‌ ‌

प्रश्न‌ ‌1. ‌‌
‌काकरात‌ ‌बिजवाई‌ ‌जस‌ ‌हासरं‌ ‌चांदन.‌ ‌
उत्तरः‌ ‌
ज्याप्रमाणे‌ ‌आकाशात‌ ‌चांदणं‌ ‌चमकत‌ ‌असतं,‌ ‌त्याचप्रमाणे‌‌ शेतकऱ्याला‌ ‌शेतात‌ ‌पेरलेले‌ ‌बियाणे‌ ‌चमकत‌ ‌आहे,‌ ‌हसत‌ ‌आहे‌‌ असे‌ ‌वाटते.‌

प्रश्न‌ ‌2. ‌‌
काया‌ ‌ढेकलात‌ ‌डोया‌ ‌हिर्व‌ ‌सपन‌ ‌पाहेते.‌ ‌
उत्तरः‌
‌शेतकरी‌ ‌भर‌ ‌दिवसा‌ ‌(शेतात)‌ ‌स्वप्न‌ ‌पाहत‌ ‌आहे.‌ ‌शेतकऱ्याची‌‌ काळी‌ ‌कसदार‌ ‌सुपीक‌ ‌जमीन‌ ‌आहे.‌ ‌त्या‌ ‌जमिनीत‌ ‌हिरवंगार‌ ‌शेत‌‌ पिकवून‌ ‌खूप‌ ‌धान्य‌ ‌मिळवयाचं‌ ‌त्याचं‌ ‌स्वप्न‌ ‌आहे.‌ ‌

3. या‌ ‌कवितेत‌ ‌आलेले‌ ‌वहाडी‌ ‌बोलीतील‌ ‌शब्द‌ ‌शोधा‌ ‌व‌ ‌त्यांना‌ ‌प्रमाणभाषेतील‌ ‌शब्द‌ ‌लिहा.‌‌

प्रश्न‌ 1.‌ ‌
या‌ ‌कवितेत‌ ‌आलेले‌ ‌वहाडी‌ ‌बोलीतील‌ ‌शब्द‌ ‌शोधा‌ ‌व‌ ‌त्यांना‌ ‌प्रमाणभाषेतील‌ ‌शब्द‌ ‌लिहा.‌‌

उत्तरः‌

‌

4. कवितेच्या‌ ‌आधारे‌ ‌खालील‌ ‌तक्ता‌ ‌पूर्ण‌ ‌करा.‌

प्रश्न‌ 1.‌
‌कवितेच्या‌ ‌आधारे‌ ‌खालील‌ ‌तक्ता‌ ‌पूर्ण‌ ‌करा.‌

उत्तरः‌

5.‌ ‌अभिव्यक्ती‌ ‌

प्रश्न‌ ‌1.‌
‘काया‌ ‌ढेकलात‌ ‌डोया‌ ‌हिर्व‌ ‌सपान‌ ‌पाहेते’‌ ‌या‌ ‌ओळीतील‌‌ भावार्थ‌ ‌स्पष्ट‌ ‌करा.‌ ‌
उत्तर:‌
‌कृती‌ ‌3:‌ ‌काव्यसौंदर्य,‌ ‌प्रश्न‌ ‌(1)‌ ‌मधील‌ ‌(vi)‌ ‌चे‌ ‌उत्तर‌ ‌पाहा.‌ ‌

प्रश्न‌ ‌2.‌
‘काटा‌ ‌पायात‌ ‌रुतते‌ ‌लाल‌ ‌रगत‌ ‌सांडते‌ ‌हिर्व‌ ‌सपन‌ ‌फुलते’‌ ‌या‌‌ ओळीचा‌ ‌संदर्भ‌ ‌स्पष्ट‌ ‌करा.‌ ‌
उत्तरः‌ ‌
कृती‌ ‌3‌ ‌:‌ ‌काव्यसौंदर्य,‌ ‌प्रश्न‌ ‌(1)‌ ‌मधील‌ ‌(v)‌ ‌चे‌ ‌उत्तर‌ ‌पाहा

भाषाभ्यास‌:

प्रश्न‌ ‌1.‌
‌खालील‌ ‌वाक्ये‌ ‌वाचा.‌
‌1. ‌मी‌ ‌शाळा‌ ‌जातो.‌ ‌
2.‌ ‌मी‌ ‌शाळेत‌ ‌जातो.‌ ‌

ही‌ ‌दोन‌ ‌वाक्ये‌ ‌तुम्ही‌ ‌वाचलीत.‌ ‌यांपैकी‌ ‌पहिले‌ ‌वाक्य‌ ‌चुकीचे‌ ‌आहे‌ ‌आणि‌ ‌ दुसरे‌ ‌वाक्य‌ ‌बरोबर‌ ‌आहे.‌ ‌या‌ ‌दोन्ही‌ ‌वाक्यांमध्ये‌ ‌काय‌ ‌फरक‌ ‌आहे?‌ ‌पहिल्या‌ ‌वाक्यात‌ ‌’शाळा’‌ हा‌ ‌शब्द‌ ‌आहे.‌ ‌दुसऱ्या‌ ‌वाक्यात‌ ‌’शाळा’‌ ‌या‌ ‌शब्दाला‌ ‌’-त’‌ ‌हा‌ ‌प्रत्यय‌ ‌लागला‌ ‌आहे.‌

प्रश्न‌ 2.‌ ‌ ‌
खालील‌ ‌वाक्ये‌ ‌वाचा.‌ ‌
1. ‌राम‌ ‌मित्राशी‌ ‌बोलतो.‌
2.‌ ‌रेश्मा‌ ‌पालीला‌ ‌घाबरते.‌ ‌
3. ‌कल्पना‌ ‌दुकानात‌ ‌जाते.‌

या‌ ‌वाक्यांमध्ये,‌ ‌मित्र,‌ ‌पाल,‌ ‌दुकान‌ ‌या‌ ‌नामांना‌ ‌अनुक्रमे‌ ‌-शी,‌ ‌-ला,‌ ‌-त‌ ‌हे‌ ‌प्रत्यय‌ ‌जोडलेले‌ ‌आहेत.‌ ‌ प्रत्यय‌ ‌लागण्यापूर्वी‌ ‌या‌ ‌शब्दांमध्ये‌ ‌काही‌ ‌बदल‌ ‌झाले‌ ‌आहेत.‌ ‌उदा.,‌ ‌मित्र~मित्रा-,‌ ‌पाल~पाली-,‌ ‌दुकान~दुकाना-‌ ‌शब्दाला‌ ‌प्रत्यय‌ ‌लागण्यापूर्वी‌ ‌होणाऱ्या‌ ‌या‌ ‌बदलाला‌ ‌शब्दाचे‌ ‌सामान्यरूप‌ ‌ म्हणतात.‌ ‌शब्दाच्या‌ ‌मूळ‌ ‌रूपाला‌ ‌सरळरूप‌ ‌म्हणतात.‌ ‌उदा.,‌ ‌’दुकान’‌ ‌हे‌ ‌सरळरूप‌ ‌आणि‌ ‌ दकाना-‌ ‌हे‌ ‌सामान्यरूप.‌ ‌

नामांना‌ ‌किंवा‌ ‌सर्वनामांना‌ ‌लागणारे‌ ‌प्रत्यय‌ ‌अनेक‌ ‌प्रकारचे‌ ‌असतात.‌ ‌-ला,-त,-ने,-शी,-चा,-ची,-चे‌ ‌इत्यादी.‌ ‌नामांना‌ ‌व‌ ‌सर्वनामांना‌ ‌प्रत्ययांबरोबरच‌ ‌शब्दयोगी‌ ‌अव्यये‌ ‌जोडली‌ ‌जातात.‌ ‌तेव्हासुद्धा‌ ‌सामान्यरूप‌ ‌होते.‌ ‌

Marathi Akshar Bharati Class 9 Textbook Solutions Chapter 13 तिफन Additional Important Questions and Answers

पुढील‌ ‌पक्ष्याच्या‌ ‌आधारे‌ ‌दिलेल्या‌ ‌सूचनेनुसार‌ ‌कृती‌ ‌करा:‌

‌कृती‌ ‌1 ‌:‌ ‌आकलन‌ ‌कृती‌ ‌

प्रश्न‌ ‌1.‌
आकृतिबंध‌ ‌पूर्ण‌ ‌करा.
‌उत्तरः‌

प्रश्न‌ 2.‌
चौकटी‌ ‌पूर्ण‌ ‌करा.‌‌
‌उत्तरः‌

प्रश्न‌ 3.‌
उत्तर‌ ‌लिहा.‌‌
‌उत्तरः‌
नंदी‌ ‌बैलांच्या‌ ‌जोडीला‌ ‌हाकणारा‌ ‌-‌ ‌[सदाशीव‌]

‌खालील‌ ‌प्रश्नांची‌ ‌उत्तरे‌ ‌एका‌ ‌वाक्यात‌ ‌लिहा.‌‌

प्रश्न‌ 1.‌
कोण‌ ‌रडत‌ ‌आहे?‌ ‌
उत्तरः‌
‌तानुलं‌ ‌रडत‌ ‌आहे.‌

प्रश्न‌ 2.‌
‌पाराबतीने‌ ‌पोटाला‌ ‌काय‌ ‌बांधले‌ ‌आहे?‌ ‌
उत्तर:‌
‌पाराबतीने‌ ‌पोटाला‌ ‌वटी‌ ‌बांधली‌ ‌आहे.‌

प्रश्न‌ 3.‌
शेतात‌ ‌पेरलेले‌ ‌धान्य‌ ‌कवीला‌ ‌कसे‌ ‌वाटत‌ ‌आहे?‌ ‌
उत्तरः‌
‌शेतात‌ ‌पेरलेले‌ ‌धान्य‌ ‌कवीला‌ ‌जणू‌ ‌हसरे‌ ‌चांदणे‌ ‌वाटत‌ ‌आहे.‌

प्रश्न‌ 4.‌
जीवाला‌ ‌कोणाची‌ ‌भूल‌ ‌पडत‌ ‌आहे?‌
‌उत्तरः‌ ‌
जीवाला‌ ‌मातीच्या‌ ‌कस्तुरीच्या‌ ‌वासाची‌ ‌भूल‌ ‌पडत‌ ‌आहे.‌ ‌

प्रश्न‌ 5.‌
भिजलेली‌ ‌ढेकळं‌ ‌पायाला‌ ‌कशाप्रमाणे‌ ‌भासतात?‌ ‌
उत्तरः‌
‌भिजलेली‌ ‌ढेकळं‌ ‌पायाला‌ ‌लोण्याप्रमाणे‌ ‌भासतात.‌ ‌.‌‌

प्रश्न‌ 6.‌
शेतकरी‌ ‌काळ्या‌ ‌ढेकळात‌ ‌काय‌ ‌पाहत‌ ‌आहे?‌ ‌
उत्तर:‌
‌शेतकरी‌ ‌काळ्या‌ ‌ढेकळात‌ ‌हिरवं‌ ‌सपन‌ ‌पाहत‌ ‌आहे.‌

प्रश्न‌ 7.‌
‌योग्य‌ ‌पर्याय‌ ‌शोधून‌ ‌रिकाम्या‌ ‌जागा‌ ‌भरा.‌

1. नंदी‌ ‌बैलाच्या‌ ‌जोळीले‌ ‌…….”‌ ‌हकालते.‌‌ (महादेव,‌ ‌सदाशीव,‌ ‌शीव,‌ ‌शेतकरी)‌ ‌
2. …………….‌ ‌काटीले‌ ‌टांगते‌ ‌त्यात‌ ‌तानुलं‌ ‌लळते.‌‌ (मोळी,‌ ‌चोळी,‌ ‌झोयी,‌ ‌पताका)‌
3. काया‌ ‌मातीत‌ ‌मातीत‌ ‌…………….’‌ ‌चालते.‌‌ (गोफन,‌ ‌रापन,‌ ‌चाखन,‌ ‌तिफन)‌ ‌
4. सरीवरी‌ ‌सरी‌ ‌येती‌‌ ……………….. न्हातीधुती‌ ‌होते.‌‌ (माती,‌ ‌धरनी,‌ ‌काया,‌ ‌पृथ्वी)‌ ‌
5. ‌मैना‌ ‌वाटुली‌ ‌पाहेते‌ ‌..‌…………..‌ ‌‌तिफन‌ ‌हानते.‌‌ (राघू,‌ ‌शूक,‌ ‌सदाशीव,‌ ‌पाराबती)‌
6. ‌वला‌ ‌टाकती‌ ‌तिफन‌ ‌………………‌ ‌वखर‌ ‌पाहेते.‌‌ (शितू,‌ ‌राघू,‌ ‌चंदू,‌ ‌मैना)‌ ‌
7. ‌डोया‌ ‌सपन‌ ‌पाहेते‌ ‌…..‌…………‌ ‌पायात‌ ‌रुतते.‌‌ (खिळा,‌ ‌मोळा,‌ ‌चूक,‌ ‌काटा)‌ ‌

उत्तर:‌

1. सदाशीव‌
2. ‌झोयी‌
3. तिफन‌ ‌
4. माती‌
5. राघू‌‌
6. शितू‌ ‌
7. ‌काटा‌‌

कृती‌ ‌2:‌ ‌आकलन‌ ‌कृती‌ ‌

प्रश्न‌ 1.‌
‌समान‌ ‌अर्थाच्या‌ ‌काव्यपंक्ती‌ ‌शोधून‌ ‌लिहा.‌

1. आकाशात‌ ‌विजा‌ ‌चमकत‌ ‌असतात.‌ ‌जणू‌ ‌त्यांचा‌ ‌थयथय‌‌ नाच‌ ‌चालू‌ ‌असतो.‌
2. ‌काठीला‌ ‌टांगलेल्या‌ ‌झोळीत‌ ‌झोका‌ ‌घेणारे‌ ‌बाळ‌ ‌रडत‌ ‌आहे.‌
3. ‌पावसाच्या‌ ‌सरीवर‌ ‌सरी‌ ‌कोसळत‌ ‌आहेत‌ ‌जणू‌ ‌या‌ ‌सरी‌ ‌मातीला‌‌ अंघोळ‌ ‌घालत‌ ‌आहेत.‌ ‌
4. शेतकरी‌ ‌तिफन‌ ‌चालवत‌ ‌आहे.‌ ‌पाऊस‌ ‌बरसत‌ ‌आहे.‌‌
5. शेतकरी‌ ‌तिफणीत‌ ‌बीज‌ ‌टाकत‌ ‌आहे.‌ ‌त्याचं‌ ‌लक्ष‌ ‌जमिनीवर‌‌ ढेकळं‌ ‌फोडत‌ ‌पुढे‌ ‌जाणाऱ्या‌ ‌वखरावर‌ ‌आहे.‌ ‌
6. त्याचं‌ ‌हिरवं‌ ‌स्वप्न‌ ‌(धान्य‌ ‌पिकवण्याचं)‌ ‌खरं‌ ‌झालं‌ ‌आहे.‌ ‌

उत्तर:‌

1. ईज‌ ‌नाचते‌ ‌थयथय.‌‌
2. झोयी‌ ‌काटीले‌ ‌टांगते‌ ‌त्यात‌ ‌तानुलं‌ ‌लळते.‌ ‌
3. सरीवरी‌ ‌सरी‌ ‌येती‌ ‌माती‌ ‌न्हातीधुती‌ ‌होते.‌‌
4. राघू‌ ‌तिफन‌ ‌हानते‌ ‌ढग‌ ‌बरसते.‌
5. ‌वला‌ ‌टाकती‌ ‌तिफन‌ ‌शितू‌ ‌वखर‌ ‌पाहेते.‌‌
6. ‌हिर्व‌ ‌सपन‌ ‌फुलते‌ ‌ढग‌ ‌बरसते.‌ ‌

जोड्या‌ ‌जुळवा.‌

प्रश्न‌ 1.

उत्तर:‌

प्रश्न‌ 2.

उत्तर:‌

प्रश्न‌ 3.

उत्तर:‌

काव्यपंक्तींचा‌ ‌योग्य‌ ‌क्रम‌ ‌लावा.‌

प्रश्न‌ 1.
काव्यपंक्तींचा‌ ‌योग्य‌ ‌क्रम‌ ‌लावा.‌
उत्तर:‌

1. ‌त्यात‌ ‌तानुलं‌ ‌लळते‌ ‌ढग‌ ‌बरसते.‌‌
2. ईज‌ ‌नाचते‌ ‌थयथय‌ ‌ढग‌ ‌ढोल‌ ‌वाजवते.‌
3. वटी‌ ‌बांधून‌ ‌पोटाले‌ ‌पाराबती‌ ‌उनारते.‌ ‌
4. काया‌ ‌मातीत‌ ‌मातीत‌ ‌तिफन‌ ‌चालते‌ ‌तिफन‌ ‌चालते.‌
5. ‌राघू‌ ‌तिफन‌ ‌हानते‌ ‌ढग‌ ‌बरसते.‌ ‌
6. ‌काकरात‌ ‌बिजवाई‌ ‌जसं‌ ‌हासरं‌ ‌चांदनं‌ ‌
7. सरीवरी‌ ‌सरी‌ ‌येती‌ ‌माती‌ ‌न्हातीधुती‌ ‌होते.‌
8. ‌मैना‌ ‌वाटुली‌ ‌पाहेते‌ ‌राघू‌ ‌तिफन‌ ‌हानते.‌‌
9. ‌हिर्व‌ ‌सपन‌ ‌फुलते‌ ‌ढग‌ ‌बरसते.‌ ‌
10. वला‌ ‌टाकती‌ ‌तिफन‌ ‌शितू‌ ‌वखर‌ ‌पाहेते.‌‌
11. काया‌ ‌ढेकलात‌ ‌डोया‌ ‌हिर्व‌ ‌सपन‌ ‌पाहेते.‌‌
12. ‌पानी‌ ‌भिजलं‌ ‌ढेकूल‌ ‌लोनी‌ ‌पायाले‌ ‌पाटते.‌

‌उत्तर:‌

1. ‌‌काया‌ ‌मातीत‌ ‌मातीत‌ ‌तिफन‌ ‌चालते‌ ‌तिफन‌ ‌चालते.‌‌
2. ‌ईज‌ ‌नाचते‌ ‌थयथय‌ ‌ढग‌ ‌ढोल‌ ‌वाजवते.‌ ‌
3. ‌वटी‌ ‌बांधून‌ ‌पोटाले‌ ‌पाराबती‌ ‌उनारते.‌
4. ‌‌त्यात‌ ‌तानुलं‌ ‌लळते‌ ‌ढग‌ ‌बरसते.‌ ‌
5. काकरात‌ ‌बिजवाई‌ ‌जसं‌ ‌हासरं‌ ‌चांदनं‌ ‌
6. सरीवरी‌ ‌सरी‌ ‌येती‌ ‌माती‌ ‌न्हातीधुती‌ ‌होते.‌
7. मैना‌ ‌वाटुली‌ ‌पाहेते‌ ‌राघू‌ ‌तिफन‌ ‌हानते.‌
8. राघू‌ ‌तिफन‌ ‌हानते‌ ‌ढग‌ ‌बरसते.‌
9. ‌वला‌ ‌टाकती‌ ‌तिफन‌ ‌शितू‌ ‌वखर‌ ‌पाहेते.‌
10. ‌पानी‌ ‌भिजलं‌ ‌ढेकूल‌ ‌लोनी‌ ‌पायाले‌ ‌वाटते.‌ ‌
11. ‌काया‌ ‌ढेकलात‌ ‌डोया‌ ‌हिर्व‌ ‌सपन‌ ‌पाहेते.‌‌
12. हिर्व‌ ‌सपन‌ ‌फुलते‌ ‌ढग‌ ‌बरसते.‌

काव्यपंक्तीवरून‌ ‌शब्दांचा‌ ‌योग्य‌ ‌क्रम‌ ‌लावा.‌‌

प्रश्न‌ 1.
काव्यपंक्तीवरून‌ ‌शब्दांचा‌ ‌योग्य‌ ‌क्रम‌ ‌लावा.‌‌

1. बरसते,‌ ‌टांगते,‌ ‌हकालते,‌ ‌उनारते
2. ढोल,‌ ‌तानुलं,‌ ‌पाराबती,‌ ‌सदाशीव‌‌
3. बरसते,‌ ‌गोंदन,‌ ‌पाहेते,‌ ‌चांदनं‌ ‌
4. राघू,‌ ‌मैना,‌ ‌माती,‌ ‌कस्तुरीचा‌ ‌
5. तिफन,‌ ‌ढग,‌ ‌काटा,‌ ‌डोया‌ ‌
6. वखर,‌ ‌वला,‌ ‌लोनी,‌ ‌हिर्व‌

उत्तर:‌

1. हकालते,‌ ‌उनारते,‌ ‌टांगते,‌ ‌बरसते‌‌
2. ढोल,‌ ‌सदाशीव,‌ ‌पाराबती,‌ ‌तानुलं‌ ‌
3. चांदनं,‌ ‌गोंदन,‌ ‌पाहेते,‌ ‌बरसते‌ ‌
4. ‌माती,‌ ‌कस्तुरीचा,‌ ‌मैना,‌ ‌राघू‌
5. तिफन,‌ ‌डोया,‌ ‌काटा,‌ ‌ढग‌‌
6. वला,‌ ‌वखर,‌ ‌लोनी,‌ ‌हिर्व‌

प्रश्न‌ ‌तयार‌ ‌करा.‌ ‌

प्रश्न‌ 1.
‌झोयी‌ ‌काटीले‌ ‌टांगते.‌ ‌
उत्तरः‌
‌काटीला‌ ‌काय‌ ‌टांगते?‌

प्रश्न‌ 2.
काया‌ ‌मातीत‌ ‌तिफन‌ ‌चालते.‌
‌उत्तरः‌
‌काया‌ ‌मातीत‌ ‌काय‌ ‌चालते?‌

प्रश्न‌ 3.
‌तिचा‌ ‌कस्तुरीचा‌ ‌वास‌ ‌भूल‌ ‌जीवाले‌ ‌पाळते.‌ ‌
उत्तर:‌
‌कोणता‌ ‌वास‌ ‌जिवाला‌ ‌भूल‌ ‌पाडत‌ ‌आहे?‌ ‌

प्रश्न‌ 4.
धरतीच्या‌ ‌आंगोपांगी‌ ‌लाळानौसाचं‌ ‌गोंदनं‌ ‌
उत्तरः‌
‌कोणाच्या‌ ‌आंगोपांगी‌ ‌लाळानौसाचं‌ ‌गोंदनं‌ ‌आहे?‌‌

प्रश्न‌ 5.
वला‌ ‌टाकती‌ ‌तिफन‌ ‌शितू‌ ‌वखर‌ ‌पाहेते.‌
‌उत्तरः‌
‌शितू‌ ‌काय‌ ‌पाहत‌ ‌आहे?‌ ‌

कृती‌ ‌3‌:‌ ‌काव्यसौंदर्य‌

खालील‌ ‌काव्यपंक्तीतील‌ ‌आशयसौंदर्य‌ ‌स्पष्ट‌ ‌करा.‌ ‌

प्रश्न‌ 1.
‌काया‌ ‌मातीत‌ ‌मातीत‌ ‌तिफन‌ ‌चालते‌ ‌तिफन‌ ‌चालते‌‌ ईज‌ ‌नाचते‌ ‌थयथय‌ ‌ढग‌ ‌ढोल‌ ‌वाजवते‌ ‌
उत्तरः‌ ‌
शेतकऱ्याच्या‌ ‌कष्टकरी‌ ‌जीवनाचे‌ ‌व‌ ‌निसर्गाचे‌ ‌नितांत‌‌ सुंदर‌ ‌व‌ ‌जिवंत‌ ‌चित्र‌ ‌कवी‌ ‌आपल्या‌ ‌डोळ्यांसमोर‌ ‌उभे‌ ‌करतात.‌ ‌शेतकऱ्याचे‌ ‌संपूर्ण‌ ‌जीवन‌ ‌हे‌ ‌शेतीवर‌ ‌आणि‌ ‌पर्यायाने‌ ‌पावसावर‌ ‌अवलंबून‌ ‌असते.‌‌ शेतीची‌ ‌नांगरणी‌ ‌आटोपून‌ ‌पाऊस‌ ‌सुरू‌ ‌झाल्याने‌ ‌शेतकरी‌ ‌धान्याची‌ ‌पेरणी‌ ‌करत‌ ‌असतो.‌ ‌शेतात‌ ‌बैलांच्या‌ ‌मदतीने‌ ‌तिफन‌ ‌चालवून‌ ‌पेरणी‌ ‌चालू‌ ‌असते.‌ ‌आकाशात‌ ‌विजा‌ ‌चमकत‌ ‌असतात.‌ ‌जणू‌ ‌त्यांचा‌ ‌थयथय‌ ‌नाच‌ ‌चालू‌ ‌आहे‌ ‌असे‌ ‌वाटते.‌ ‌ढगांचा‌ ‌होणारा‌‌ गडगडाट‌ ‌ऐकून‌ ‌ढग‌ ‌ढोल‌ ‌वाजवत‌ ‌आहेत,‌ ‌असे‌ ‌कवीला‌ ‌वाटते.‌ ‌

प्रश्न‌ 2.‌ ‌
झोयी‌ ‌काटीले‌ ‌टांगते‌ ‌त्यात‌ ‌तानुलं‌ ‌लळते.‌‌ त्यात‌ ‌तानुलं‌ ‌लळते‌ ‌ढग‌ ‌बरसते‌ ‌
उत्तरः‌
‌पार्वतीने‌ ‌(शेतकऱ्याच्या‌ ‌पत्नीने)‌ ‌आपले‌ ‌रडणारे‌ ‌छोटे‌ ‌बाळ‌‌ झोळीत‌ ‌ठेवले‌ ‌आहे.‌ ‌ती‌ ‌झोळी‌ ‌तिने‌ ‌काठीला‌ ‌टांगून‌ ‌ठेवली‌ ‌आहे.‌ ‌झोळीत‌ ‌झोका‌ ‌घेणारे‌ ‌बाळ‌ ‌रडत‌ ‌आहे.‌ ‌आकाशात‌ ‌ढग‌ ‌बरसू‌ ‌लागले‌ ‌आहे.‌ ‌पाऊस‌ ‌सुरू‌ ‌झाला‌ ‌आहे.‌ ‌शेतकरी‌ ‌शेतीच्या‌‌ कामात‌ ‌मग्न‌ ‌झाला‌ ‌आहे.‌

प्रश्न‌ 3.‌ ‌
काकरात‌ ‌बिजवाई‌ ‌जसं‌ ‌हासरं‌ ‌चांदनं‌ ‌
उत्तरः‌
‌काळ्या‌ ‌मातीत‌ ‌तिफन‌ ‌चालवून‌ ‌शेतकरी‌ ‌धान्य‌ ‌पेरतो.‌ ‌हे‌‌ पेरलेले‌ ‌धान्य‌ ‌म्हणजे‌ ‌जणू‌ ‌काही‌ ‌हसरं‌ ‌चांदणं‌ ‌आहे.‌ ‌शिवारात‌ ‌पेरलेले‌ ‌बियाणं‌ ‌हे‌ ‌आकाशात‌ ‌चमकणाऱ्या‌ ‌चांदण्यासारखं‌ ‌भासत‌‌ आहे‌ ‌असे‌ ‌कवीला‌ ‌वाटते.‌

प्रश्न‌ 4.‌ ‌
‌सरीवरी‌ ‌सरी‌ ‌येती‌ ‌माती‌ ‌न्हातीधुती‌ ‌होते.‌ ‌
उत्तरः‌
‌पावसाची‌ ‌सुरुवात‌ ‌झाली‌ ‌आहे,‌ ‌त्यामुळे‌ ‌पावसाच्या‌ ‌पडणाऱ्या‌‌ सरी‌ ‌जमिनीवर‌ ‌बरसत‌ ‌आहेत.‌ ‌धरणी‌ ‌ओली‌ ‌चिंब‌ ‌झाली‌ ‌आहे.‌ ‌भिजून‌ ‌गेली‌ ‌आहे.‌ ‌जणू‌ ‌या‌ ‌पावसाच्या‌ ‌सरी‌ ‌मातीला‌ ‌न्हाऊ‌ ‌घालत‌‌ आहेत,‌ ‌असे‌ ‌कवीला‌ ‌वाटते.‌

प्रश्न‌ 5.‌ ‌
‌काटा‌ ‌पायात‌ ‌रूतते‌ ‌लाल‌ ‌रगत‌ ‌सांडते‌ ‌हिर्व‌ ‌सपन‌ ‌फुलते.‌
‌उत्तरः‌
‌आपल्या‌ ‌कष्टाने,‌ ‌मेहनतीने‌ ‌हे‌ ‌शेत‌ ‌हिरवेगार‌ ‌होऊन‌ ‌उठेल,‌‌ शेतात‌ ‌धान्य‌ ‌डोलू‌ ‌लागेल‌ ‌असे‌ ‌स्वप्न‌ ‌डोळ्यांनी‌ ‌पाहत‌ ‌असताना‌ ‌किंवा‌ ‌मनात‌ ‌तसा‌ ‌विचार‌ ‌चालू‌ ‌असताना‌ ‌अचानक‌ ‌शेतकऱ्याच्या‌ ‌पायात‌ ‌काटा‌ ‌टोचतो.‌ ‌काटा‌ ‌टोचल्यामुळे‌ ‌पायातून‌ ‌लाल‌ ‌रक्त‌ ‌येऊ‌ ‌लागते;‌ ‌पण‌ ‌शेतकऱ्याला‌ ‌ती‌ ‌वेदना‌ ‌जाणवत‌ ‌नाही.‌ ‌कारण‌‌ त्याच्या‌ ‌कष्टातून,‌ ‌श्रमातून‌ ‌हिरव्यागार‌ ‌शेताचे‌ ‌स्वप्न‌ ‌सत्यात‌‌ उतरेल‌ ‌असा‌ ‌त्याला‌ ‌विश्वास‌ ‌वाटतो.‌

प्रश्न‌ 6.‌ ‌
‌काया‌ ‌ढेकलात‌ ‌डोया‌ ‌हिर्व‌ ‌सपान‌ ‌पाहेते.‌ ‌
उत्तरः‌
‌पाऊस‌ ‌आल्यामुळे‌ ‌तिफन‌ ‌धरली‌ ‌जाते‌ ‌आणि‌ ‌बियाणाची‌‌ पेरणी‌ ‌होते.‌ ‌मातीच्या‌ ‌काळ्या‌ ‌ढेकळात‌ ‌चालताना‌ ‌ती‌ ‌ढेकळं‌ ‌पावसाने‌ ‌भिजली‌ ‌आहेत.‌ ‌त्यामुळे‌ ‌पायाला‌ ‌ती‌ ‌मऊ‌ ‌लोण्यासारखी‌ ‌जाणवतात.‌ ‌या‌ ‌ढेकळातून‌ ‌आता‌ ‌हिरवंगार‌ ‌पीक‌ ‌येईल‌ ‌असं‌ ‌स्वप्न‌ ‌शेतकरी‌ ‌पाहत‌ ‌आहे.‌ ‌या‌ ‌ओळीतून‌ ‌शेतकऱ्याचा‌ ‌आशावाद‌‌ दिसून‌ ‌येतो.‌

‌पुढील‌ ‌ओळींचा‌ ‌अर्थ‌ ‌स्पष्ट‌ ‌करा.‌

प्रश्न‌ 1.‌ ‌
‌ईज‌ ‌नाचते‌ ‌थयथय‌ ‌ढग‌ ‌ढोल‌ ‌वाजवते.‌ ‌
उत्तरः‌
‌शेताची‌ ‌नांगरणी‌ ‌आटोपून‌ ‌पाऊस‌ ‌सुरू‌ ‌झाल्याने‌ ‌शेतकरी‌‌ धान्याची‌ ‌पेरणी‌ ‌करत‌ ‌असतो.‌ ‌शेतात‌ ‌बैलांच्या‌ ‌मदतीने‌ ‌तिफन‌ ‌चालवून‌ ‌पेरणी‌ ‌चालू‌ ‌असते.‌ ‌काळ्या‌ ‌मातीत‌ ‌तिफन‌ ‌चालत‌ ‌असते.‌ ‌आकाशात‌ ‌विजा‌ ‌चमकत‌ ‌असतात‌ ‌जणू‌ ‌त्यांचा‌ ‌थयथय‌ ‌नाच‌ ‌चालू‌ ‌असतो.‌ ‌त्याचवेळी‌ ‌ढगांचा‌ ‌गडगडाट‌ ‌ऐकू‌ ‌येऊ‌ ‌लागतो‌‌ जणू‌ ‌ढग‌ ‌ढोल‌ ‌वाजवत‌ ‌आहेत‌ ‌असे‌ ‌वाटते.

प्रश्न‌ 2.‌ ‌
‌नंदी‌ ‌बैलाच्या‌ ‌जोळीले‌ ‌सदाशीव‌ ‌हकालते.
उत्तरः‌ ‌
पाऊस‌ ‌आल्यामुळे‌ ‌पेरणीसाठी‌ ‌सदाशीव‌ ‌म्हणजेच‌ ‌शेतकरी‌‌ यार‌ ‌झालेला‌ ‌आहे.‌ ‌तो‌ ‌आपल्या‌ ‌शेतामध्ये‌ ‌स्वत:‌ ‌नंदीबैलाच्या‌‌ जोडीला‌ ‌तिफन‌ ‌चालवत‌ ‌आहे.‌ ‌

प्रश्न‌ 3.‌ ‌‌
धरतीच्या‌ ‌आंगोपांगी‌ ‌लाळानौसाचं‌ ‌गोंदनं‌ ‌
उत्तरः‌
‌पेरलेले‌ ‌धान्य‌ ‌जणू‌ ‌हसणारं‌ ‌चांदणं‌ ‌वाटत‌ ‌आहे.‌ ‌शिवाय‌ ‌पेरलेले‌‌ ते‌ ‌धान्य‌ ‌पाहून‌ ‌असे‌ ‌वाटते,‌ ‌जणू‌ ‌धरतीच्या‌ ‌अंगावर‌ ‌लाडाने,‌‌ कौतुकाने‌ ‌नवसाचे‌ ‌छान‌ ‌गोंदण‌ ‌केलेले‌ ‌आहे.‌ ‌

प्रश्न‌ 4.‌ ‌‌
मैना‌ ‌वाटुली‌ ‌पाहेते‌ ‌राघू‌ ‌तिफन‌ ‌हानते‌ ‌
उत्तरः‌
‌शेतकऱ्याची‌ ‌बायको‌ ‌संध्याकाळच्या‌ ‌वेळी‌ ‌घरी‌ ‌आपल्या‌‌ राघूची‌ ‌म्हणजेच‌ ‌शेतकऱ्याची‌ ‌मनापासून‌ ‌वाट‌ ‌पाहते‌ ‌आहे.‌ ‌ती‌ ‌घरी‌ ‌वाट‌ ‌पाहते‌ ‌पण‌ ‌इकडे‌ ‌शेतात‌ ‌हा‌ ‌शेतकरी‌ ‌तिफन‌ ‌चालवत‌‌ आहे.‌ ‌पाऊस‌ ‌बरसत‌ ‌आहे.‌ ‌

प्रश्न‌ 5.‌ ‌‌
बैल,‌ ‌काळी‌ ‌माती,‌ ‌तिफन‌ ‌आणि‌ ‌शेत‌ ‌यांमध्येच‌ ‌शेतकरी‌‌ राजाचा‌ ‌संसार‌ ‌गुरफटलेला‌ ‌असतो.‌ ‌तुमचे‌ ‌विचार‌ ‌लिहा.‌ ‌
उत्तरः‌
शेतकरी‌ ‌म्हटला‌ ‌म्हणजे‌ ‌शेत‌ ‌हे‌ ‌आलेच.‌ ‌शेत‌ ‌आले‌ ‌की,‌‌ माती,‌ ‌बैल‌ ‌व‌ ‌तिफन‌ ‌असे‌ ‌सर्व‌ ‌काही‌ ‌आले.‌ ‌शेतकरी‌ ‌राजाचे‌ ‌विश्व‌ ‌यांतच‌ ‌गुरफटलेले‌ ‌असते.‌ ‌दिवसभर‌ ‌बैलांच्या‌ ‌मदतीने‌ ‌शेत‌ ‌नांगरताना‌ ‌त्याचे‌ ‌अनवाणी‌ ‌पाय‌ ‌काळ्या‌ ‌मातीला‌ ‌स्पर्श‌ ‌करीत‌ ‌असतात.‌ ‌तिफन‌ ‌हातात‌ ‌घेऊन‌ ‌शेत‌ ‌नांगरताना‌ ‌त्याला‌‌ सुखाची‌ ‌अनुभूती‌ ‌येत‌ ‌असते.‌ ‌पेरणी,‌ ‌नागरणी,‌ ‌कापणी,‌ ‌मळणी‌ ‌यांशिवाय‌ ‌दुसरे‌ ‌काहीही‌ ‌त्यास‌ ‌सुचत‌ ‌नसते.‌ ‌म्हणून‌ ‌शेतकरी‌ ‌राजाचा‌ ‌संसार‌ ‌हा‌ ‌बैल,‌ ‌काळी‌ ‌माती,‌ ‌तिफन‌ ‌आणि‌ ‌शेत‌ ‌यांमध्ये‌ ‌गुरफटलेला‌ ‌असतो.‌ ‌

प्रश्न‌ 6.‌ ‌‌
पावसाच्या‌ ‌दिवसातील‌ ‌मातीच्या‌ ‌सुगंधाचा‌ ‌तुम्ही‌ ‌जरूर‌ ‌आस्वाद‌ ‌घेतला‌ ‌असेल.‌ ‌त्यावेळी‌ ‌तुम्हांला‌ ‌झालेल्या‌‌ आनंदाचे‌ ‌वर्णन‌ ‌करा.‌ ‌
उत्तरः‌ ‌
पाऊस‌ ‌पडण्याअगोदर‌ ‌माती‌ ‌उन्हात‌ ‌तापून‌ ‌गरम‌ ‌झालेली‌‌ असते.‌ ‌तिच्यातून‌ ‌गरम‌ ‌वाफा‌ ‌निघत‌ ‌असतात.‌ ‌पण‌ ‌जेव्हा‌ ‌पावसाला‌ ‌सुरुवात‌ ‌होते‌ ‌आणि‌ ‌तप्त‌ ‌धरती‌ ‌पावसात‌ ‌न्हाऊन‌ ‌निघते,‌ ‌तेव्हा‌ ‌मातीतून‌ ‌निघणारा‌ ‌सुगंध‌ ‌आपणास‌ ‌मोहून‌ ‌टाकतो‌ ‌व‌ ‌तो‌ ‌कस्तुरीच्या‌ ‌सुगंधाप्रमाणे‌ ‌सारा‌ ‌आसमंत‌ ‌दरवळून‌ ‌टाकतो.‌ ‌जणू‌ ‌धरणी‌ ‌मातेने‌ ‌त्यात‌ ‌स्नानच‌ ‌केलेले‌ ‌असते.‌ ‌मी‌ ‌प्रत्येक‌ ‌वर्षी‌ ‌पावसात‌ ‌न्हाऊन‌ ‌निघालेल्या‌ ‌मातीच्या‌ ‌सुगंधाचा‌ ‌आस्वाद‌ ‌घेतलेला‌ ‌आहे.‌ ‌त्या‌ ‌प्रत्येक‌ ‌वेळी‌ ‌माझे‌ ‌मन‌ ‌प्रसन्न‌ ‌व‌ ‌टवटवीत‌ ‌झालेले‌ ‌आहे.‌‌ माझ्या‌ ‌मनात‌ ‌एक‌ ‌प्रकारचा‌ ‌जोश‌ ‌व‌ ‌उत्साह‌ ‌निर्माण‌ ‌झालेला‌ ‌आहे.‌‌ ‌

प्रश्न‌ 7.‌ ‌‌‌
‌शेतकरीच‌ ‌नसता‌ ‌तर‌ ‌हिरवे‌ ‌सपन‌ ‌फुललेच‌ ‌नसते.‌ ‌या‌‌ विधानाचा‌ ‌तुम्हांला‌ ‌समजलेला‌ ‌अर्थ‌ ‌सांगा.‌ ‌
उत्तरः‌ ‌
शेतकरीच‌ ‌नसता‌ ‌तर‌ ‌हिरवे‌ ‌सपन‌ ‌फुललेच‌ ‌नसते.‌ ‌हिरवे‌‌ सपन‌ ‌म्हणजे‌ ‌शेतात‌ ‌बहरून‌ ‌आलेले‌ ‌पीक.‌ ‌जर‌ ‌शेतकरी‌ ‌नसता‌ ‌तर‌ ‌शेती‌ ‌कोणीच‌ ‌करू‌ ‌शकले‌ ‌नसते.‌ ‌मग‌ ‌पेरणी,‌ ‌नागरणी,‌ ‌कापणी‌ ‌व‌ ‌मळणी‌ ‌या‌ ‌प्रक्रिया‌ ‌कोणालाही‌ ‌पूर्ण‌ ‌करता‌ ‌आल्याच‌ ‌नसत्या.‌ ‌देशातील‌ ‌लोकांना‌ ‌अन्नधान्य‌ ‌खाण्यास‌ ‌मिळालेच‌ ‌नसते.‌ ‌त्यामुळे‌ ‌लोकांची‌ ‌अन्नान्न‌ ‌दशा‌ ‌झाली‌ ‌असती.‌ ‌संपूर्ण‌ ‌मानव‌ ‌जीवनच‌ ‌संपुष्टात‌ ‌आले‌ ‌असते.‌ ‌खरेच‌ ‌शेतकऱ्याशिवाय‌ ‌मानवी‌ ‌जीवनाची‌ ‌कल्पनाच‌ ‌करता‌ ‌आली‌ ‌नसती.‌‌

प्रश्न‌ 8.‌ ‌‌‌
‌दिलेल्या‌ ‌मुद्द्यांच्या‌ ‌आधारे‌ ‌कवितेसंबंधी‌ ‌पुढील‌ ‌कृती‌‌ सोडवा.‌
उत्तरः‌
1. ‌कवी‌ ‌/‌ ‌कवयित्रीचे‌ ‌नाव‌ ‌-‌‌
विठ्ठल‌ ‌वाघ‌ ‌

2. ‌संदर्भ‌ ‌-‌‌
‘तिफन’‌ ‌ही‌ ‌कविता‌ ‌कवी‌ ‌’विठ्ठल‌ ‌वाघ‌ ‌यांनी‌ ‌लिहिली‌ ‌आहे.‌ ‌ही‌‌ कविता‌ ‌त्यांच्या‌ ‌काळ्या‌ ‌मातीत‌ ‌मातीत’‌ ‌या‌ ‌कवितासंग्रहातील‌ ‌आहे.‌ ‌

3.‌ ‌प्रस्तावना‌ ‌-‌‌
‘तिफन’‌ ‌ही‌ ‌कविता‌ ‌कवी‌ ‌’विठ्ठल‌ ‌वाघ’‌ ‌यांनी‌ ‌लिहिली‌ ‌आहे.आहे.‌ ‌पावसाच्या‌ ‌आगमनाने‌ ‌शेतकऱ्यांची‌ ‌होणारी शेतीच्या‌ ‌कामांची‌ ‌लगबग‌ ‌याचे‌ ‌चित्रदर्शी‌ ‌वर्णन‌ ‌या‌ ‌कवितेत‌‌ कवीने‌ ‌केले‌ ‌आहे.‌ ‌

4. वाङ्मयप्रकार‌‌ –
‘तिफन’‌ ‌ही‌ ‌कविता‌ ‌एक‌ ‌‘लोकगीत’‌ ‌आहे.‌

5. ‌कवितेचा‌ ‌विषय‌‌ –
शेतकरी,‌ ‌कष्टकरी‌ ‌लोकजीवनाचे‌ ‌चित्रण‌ ‌करणारी‌ ‌’तिफन’‌ ‌ही‌‌ एक‌ ‌ग्रामीण‌ ‌कविता‌ ‌आहे.‌

6. कवितेतील‌ ‌आवडलेली‌ ‌ओळ‌‌ –
सरीवर‌ ‌सरी‌ ‌येती‌ ‌माती‌ ‌न्हातीधुती‌ ‌होते‌‌
तिचा‌ ‌कस्तुरीचा‌ ‌वास‌ ‌भूल‌ ‌जीवाले‌ ‌पाळते‌

7.‌ ‌मध्यवर्ती‌ ‌कल्पना‌ ‌-‌‌
पडणाऱ्या‌ ‌पावसावर,‌ ‌शेतीवर‌ ‌शेतकऱ्याचे‌ ‌सारे‌ ‌जीवन‌ ‌अवलंबून‌ ‌असते.‌ ‌पाऊस‌ ‌आल्यावर‌ ‌त्याची‌ ‌शेतीच्या‌ ‌कामाची‌ ‌धांदल‌ ‌सुरू‌ ‌होते.‌ ‌पेरणी,‌ ‌बैलांविषयीचे‌ ‌प्रेम,‌ ‌पावसाच्या‌ ‌दिवसांतील‌ ‌मातीचा‌ ‌सुगंध,‌ ‌शेतकऱ्यांचे‌ ‌स्वप्न,‌ ‌शेतीच्या‌ ‌कामांची‌ ‌लगबग‌ ‌याचे‌ ‌सुंदर‌ ‌चित्र‌ ‌’तिफन’‌ ‌कवितेत‌ ‌दिसून‌ ‌येते.‌ ‌

8. कवितेतून‌ ‌मिळणारा‌ ‌संदेश‌‌ –
शेतकरी‌ ‌खूप‌ ‌कष्टाने‌ ‌शेतात‌ ‌धान्य‌ ‌पिकवत‌ ‌असतो.‌ ‌आपल्या‌ ‌अनेक‌ ‌सुखाचा,‌ ‌आनंदाचा‌ ‌तो‌ ‌त्याग‌ ‌करत‌ ‌असतो.‌ ‌प्रसंगी‌ ‌रडणाऱ्या‌ ‌मुलांकडे‌ ‌दुर्लक्ष‌ ‌करून,‌ ‌आपल्या‌ ‌जखमांना‌ ‌विसरून‌ ‌तो‌ ‌शेतीची‌ ‌कामे‌ ‌करत‌ ‌असतो.‌ ‌खूप‌ ‌यातना,‌ ‌त्रास‌ ‌सोसून‌ ‌आपल्या‌ ‌ताटात‌ ‌भाजी-भाकरीची‌ ‌सोय‌ ‌करणाऱ्या‌ ‌शेतकऱ्यांचा‌ ‌आपण‌ ‌आदर‌ ‌केला‌ ‌पाहिजे.‌ ‌तो‌ ‌मातीत‌ ‌कष्ट‌ ‌करतो‌ ‌म्हणून‌ ‌आपण‌ ‌पोटभर‌ ‌जेऊ‌ ‌शकतो,‌ ‌हे‌ ‌आपण‌ ‌कधीही‌ ‌विसरू‌ ‌नये.‌ ‌हा‌ ‌संदेश‌ ‌‘तिफन’‌ ‌या‌ ‌कवितेतून‌ ‌आपणास‌ ‌मिळतो.‌ ‌

9. कविता‌ ‌आवडण्याची‌ ‌वा‌ ‌न‌ ‌आवडण्याची‌ ‌कारणे‌‌ –
“तिफन’‌ ‌ही‌ ‌कविता‌ ‌मला‌ ‌खूप‌ ‌आवडली‌ ‌आहे.‌ ‌त्याचे‌ ‌कारण‌ ‌म्हणजे‌ ‌हे‌ ‌एक‌ ‌लोकगीत‌ ‌आहे.‌ ‌छान‌ ‌चालीवर‌ ‌आपण‌ ‌ते‌ ‌गाऊ‌ ‌शकतो.‌ ‌शिवाय‌ ‌ही‌ ‌कविता‌ ‌वाचत‌ ‌असताना‌ ‌शेतकऱ्याचे‌‌ आयुष्य‌ ‌आपल्या‌ ‌डोळ्यांसमोर‌ ‌उभे‌ ‌राहते.‌

10. ‌भाषिक‌ ‌वैशिष्ट्ये‌‌ –
‘तिफन’‌ ‌या‌ ‌कवितेमध्ये‌ ‌कवी‌ ‌’विठ्ठल‌ ‌वाघ’‌ ‌यांनी‌ ‌वहाडी‌ ‌बोलीचा‌ ‌छान‌ ‌वापर‌ ‌केला‌ ‌आहे.‌ ‌या‌ ‌कवितेमध्ये‌ ‌यमक‌ ‌अलंकाराचा‌ ‌वापर‌ ‌करून‌ ‌छान‌ ‌परिणाम‌ ‌साधला‌ ‌आहे.‌ ‌शिवाय‌ ‌इथे‌ ‌चित्रदर्शी‌ ‌शैली‌ ‌दिसून‌ ‌येते.‌‌

खालील‌ ‌काव्यपंक्तींचे‌ ‌रसग्रहण‌ ‌करा.सोडवा.‌ ‌

प्रश्न‌ ‌1.‌ ‌
काया‌ ‌मातीत‌ ‌मातीत‌ ‌तिफन‌ ‌चालते‌‌
ईज‌ ‌नाचते‌ ‌थयथय‌ ‌ढग‌ ‌ढोल‌ ‌वाजवते‌ ‌
उत्तरः‌ ‌
‘तिफन’‌ ‌ही‌ ‌कविता‌ ‌कवी‌ ‌’विठ्ठल‌ ‌वाघ’‌ ‌यांनी‌ ‌लिहिली‌ ‌आहे.‌ ‌पावसाच्या‌ ‌आगमनाने‌ ‌शेतकऱ्यांना‌ ‌होणारा‌ ‌आनंद‌ ‌शिवाय‌ ‌शेतीच्या‌ ‌कामांची‌ ‌लगबग‌ ‌याचे‌ ‌सुंदर‌ ‌चित्रदर्शी‌ ‌वर्णन‌ ‌या‌ ‌कवितेत‌ ‌दिसून‌ ‌येते.‌‌

शेतकऱ्याच्या‌ ‌कष्टकरी‌ ‌जीवनाचे‌ ‌व‌ ‌निसर्गाचे‌ ‌नितांत‌ ‌सुंदर‌ ‌व‌ ‌जिवंत‌ ‌चित्र‌ ‌कवी‌ ‌आपल्या‌ ‌डोळ्यांसमोर‌ ‌उभे‌ ‌करतात.‌ ‌शेतकऱ्याचे‌ ‌संपूर्ण‌ ‌जीवन‌ ‌हे‌ ‌शेतीवर‌ ‌आणि‌ ‌पर्यायाने‌ ‌पावसावर‌ ‌अवलंबून‌ ‌असते.‌ ‌त्यामुळे‌ ‌पाऊस‌ ‌सुरू‌ ‌झाला‌ ‌की‌ ‌त्याच्या‌ ‌शेतीच्या‌ ‌कामाची‌ ‌लगबग‌ ‌सुरू‌ ‌होते.‌ ‌पाऊस‌ ‌सुरू‌ ‌झाल्याने‌ ‌शेताची‌ ‌नांगरणी‌ ‌आटोपून‌ ‌शेतकरी‌ ‌धान्याची‌ ‌पेरणी‌ ‌करत‌ ‌असतो.‌ ‌शेतात‌ ‌बैलांच्या‌ ‌मदतीने‌ ‌तिफन‌ ‌चालवून‌ ‌पेरणी‌ ‌चालू‌ ‌असते.‌ ‌काळया‌ ‌मातीत‌ ‌तिफन‌ ‌चालत‌ ‌असते.‌ ‌आकाशात‌ ‌विजा‌ ‌चमकत‌ ‌असतात‌ ‌जणू‌ ‌त्यांचा‌ ‌थयथय‌ ‌नाच‌ ‌चालू‌ ‌असतो.‌ ‌त्याचवेळी‌ ‌ढगांचा‌ ‌गडगडाट‌ ‌ऐकू‌ ‌येऊ‌ ‌लागतो.‌ ‌जणू‌ ‌ढग‌ ‌ढोल‌ ‌वाजवत‌ ‌आहेत‌ ‌असे‌ ‌वाटते.‌‌

या‌ ‌काव्यपंक्तीमध्ये‌ ‌कवी‌ ‌’विठ्ठल‌ ‌वाघ’‌ ‌यांनी‌ ‌व-हाडी‌ ‌बोलीचा‌ ‌छान‌ ‌वापर‌ ‌केला‌ ‌आहे.‌ ‌या‌ ‌कवितेमध्ये‌ ‌यमक‌ ‌अलंकाराचा‌ ‌वापर‌ ‌करून‌ ‌छान‌ ‌परिणाम‌ ‌साधला‌ ‌आहे.‌ ‌शिवाय‌ ‌इथे‌ ‌चित्रदर्शी‌ ‌शैली‌ ‌दिसून‌ ‌येते.‌ ‌

प्रश्न‌ 2.‌ ‌
नंदी‌ ‌बैलाच्या‌ ‌जोळीले‌ ‌सदाशीव‌ ‌हकालते‌‌
वटी‌ ‌बांधून‌ ‌पोटाले‌ ‌पाराबती‌ ‌उनारते‌ ‌
वटी‌ ‌पोटाले‌ ‌बांधते‌ ‌झोयी‌ ‌काटीले‌ ‌टांगते‌
‌झोयी‌ ‌काटीले‌ ‌टांगते‌ ‌त्यात‌ ‌तानुलं‌ ‌लळते‌‌
त्यात‌ ‌तानुलं‌ ‌लळते‌ ‌ढग‌ ‌बरसते‌ ‌
उत्तरः‌ ‌
‘तिफन’‌ ‌ही‌ ‌कविता‌ ‌कवी‌ ‌’विठ्ठल‌ ‌वाघ’‌ ‌यांनी‌ ‌लिहिली‌ ‌आहे.‌ ‌पावसाच्या‌ ‌आगमनाने‌ ‌शेतकऱ्यांना‌ ‌होणारा‌ ‌आनंद‌ ‌शिवाय‌ ‌शेतीच्या‌ ‌कामांची‌ ‌लगबग‌ ‌याचे‌ ‌सुंदर‌ ‌चित्रदर्शी‌ ‌वर्णन‌ ‌या‌ ‌कवितेत‌ ‌दिसून‌ ‌येते.‌‌

पाऊस‌ ‌आल्यामुळे‌ ‌पेरणीसाठी‌ ‌सदाशीव‌ ‌हा‌ ‌शेतकरी‌ ‌तयार‌ ‌झालेला‌ ‌आहे.‌ ‌तो‌ ‌आपल्या‌ ‌शेतामध्ये‌ ‌नंदीबैलाच्या‌ ‌जोडीला‌ ‌तिफन‌या‌ ‌काव्यपंक्तीमध्ये‌ ‌कवी‌ ‌’विठ्ठल‌ ‌वाघ’‌ ‌यांनी‌ ‌वहाडी‌ ‌बोलीचा‌ ‌छान‌ ‌वापर‌ ‌केला‌ ‌आहे.‌ ‌या‌ ‌कवितेमध्ये‌ ‌यमक‌ ‌अलंकाराचा‌ ‌वापर‌ ‌करून‌ ‌छान‌ ‌परिणाम‌ ‌साधला‌ ‌आहे.‌ ‌शिवाय‌ ‌इथे‌ ‌चित्रदर्शी‌ ‌शैली‌ ‌दिसून‌ ‌येते.‌ ‌

प्रश्न‌ 3.‌ ‌
काकरात‌ ‌बिजवाई‌ ‌जसं‌ ‌हासरं‌ ‌चांदनं‌‌
घरतीच्या‌ ‌अंगोपांगी‌ ‌लाळानौसाचं‌ ‌गोंदन‌ ‌
उत्तरः‌ ‌
‘तिफन’‌ ‌ही‌ ‌कविता‌ ‌कवी‌ ‌’विठ्ठल‌ ‌वाघ’‌ ‌यांनी‌ ‌लिहिली‌ ‌आहे.‌ ‌पावसाच्या‌ ‌आगमनाने‌ ‌शेतकऱ्यांना‌ ‌होणारा‌ ‌आनंद‌ ‌शिवाय‌ ‌शेतीच्या‌ ‌कामांची‌ ‌लगबग‌ ‌याचे‌ ‌सुंदर‌ ‌चित्रदर्शी‌ ‌वर्णन‌ ‌या‌ ‌कवितेत‌ ‌दिसून‌ ‌येते.‌‌

पाऊस‌ ‌सुरू‌ ‌झाल्यामुळे‌ ‌सदाशीव‌ ‌शेतकऱ्याने‌ ‌शेतात‌ ‌नंदीबैलाच्या‌ ‌साथीने‌ ‌तिफन‌ ‌जोडून‌ ‌पेरणीला‌ ‌सुरुवात‌ ‌केली‌ ‌आहे.‌ ‌या‌ ‌पेरणीच्या‌ ‌कामात‌ ‌त्याची‌ ‌पत्नी‌ ‌पार्वती‌ ‌त्याला‌ ‌साथ‌ ‌देत‌ ‌आहे.‌ ‌त्यांनी‌ ‌शेतात‌ ‌पेरलेले‌ ‌धान्य‌ ‌जणू‌ ‌हसणारं‌ ‌चांदणं‌ ‌वाटत‌ ‌आहे.‌ ‌शिवाय‌ ‌पेरलेले‌ ‌ते‌ ‌धान्य‌ ‌पाहून‌ ‌असे‌ ‌वाटते‌ ‌जणू‌ ‌धरतीच्या‌ ‌अंगावर‌ ‌लाडाने,‌ ‌कौतुकाने‌ ‌नवसाचे‌ ‌छान‌ ‌गोंदण‌ ‌केलेले‌ ‌आहे.‌‌

‌या‌ ‌काव्यपंक्तीमध्ये‌ ‌कवी‌ ‌’विठ्ठल‌ ‌वाघ’‌ ‌यांनी‌ ‌वहाडी‌ ‌बोलीचा‌ ‌छान‌ ‌वापर‌ ‌केला‌ ‌आहे.‌ ‌या‌ ‌कवितेमध्ये‌ ‌यमक‌ ‌अलंकाराचा‌ ‌वापर‌ ‌करून‌ ‌छान‌ ‌परिणाम‌ ‌साधला‌ ‌आहे.‌ ‌शिवाय‌ ‌इथे‌ ‌चित्रदर्शी‌ ‌शैली‌ ‌दिसून‌ ‌येते.‌‌

प्रश्न‌ 4.‌ ‌
सरीवरी‌ ‌सरी‌ ‌येती‌ ‌माती‌ ‌न्हातीधुती‌ ‌होते‌‌
तिचा‌ ‌कस्तुरीचा‌ ‌वास‌ ‌भूल‌ ‌जीवाले‌ ‌पाळते‌ ‌
भूल‌ ‌जीवाले‌ ‌पाळते‌ ‌वाट‌ ‌सांजीले‌ ‌पाहेते‌ ‌
मैना‌ ‌वाटुली‌ ‌पाहेते‌ ‌राघू‌ ‌तिफन‌ ‌हानते‌‌
राघू‌ ‌तिफन‌ ‌हानते‌ ‌ढग‌ ‌बरसते‌ ‌
उत्तरः‌
‌’तिफन’‌ ‌ही‌ ‌कविता‌ ‌कवी‌ ‌’विठ्ठल‌ ‌वाघ’‌ ‌यांनी‌ ‌लिहिली‌ ‌आहे.‌ ‌पावसाच्या‌ ‌आगमनाने‌ ‌शेतकऱ्यांना‌ ‌होणारा‌ ‌आनंद‌ ‌शिवाय‌ ‌शेतीच्या‌ ‌कामांची‌ ‌लगबग‌ ‌याचे‌ ‌सुंदर‌ ‌चित्रदर्शी‌ ‌वर्णन‌ ‌या‌ ‌कवितेत‌ ‌दिसून‌ ‌येते.‌‌

पावसाला‌ ‌चांगली‌ ‌सुरुवात‌ ‌झाली‌ ‌आहे.‌ ‌सर्वत्र‌ ‌पावसाच्या‌ ‌सरीवर‌ ‌सरी‌ ‌कोसळत‌ ‌आहेत.‌ ‌जणू‌ ‌या‌ ‌सरी‌ ‌मातीला‌ ‌न्हाऊ‌ ‌घालत‌ ‌आहेत.‌ ‌या‌ ‌बरसणाऱ्या‌ ‌सरींमुळे‌ ‌माती‌ ‌चिंब‌ ‌भिजून‌ ‌गेली‌ ‌आहे.‌ ‌या‌ ‌मातीचा‌ ‌कस्तुरीसारखा‌ ‌सुगंध‌ ‌सर्वत्र‌ ‌पसरलेला‌ ‌आहे.‌ ‌हा‌ ‌सुगंध‌ ‌जीवाला‌ ‌भूल‌ ‌पाडत‌ ‌आहे,‌ ‌मन‌ ‌मोहीत‌ ‌करत‌ ‌आहे.‌ ‌इकडे‌ ‌भिजलेल्या‌ ‌मातीचा‌ ‌सुगंध‌ ‌मनाला‌ ‌धुंद‌ ‌करत‌ ‌आहे‌ ‌तर‌ ‌तिकडे‌ ‌संध्याकाळच्या‌ ‌वेळी‌ ‌मैना‌ ‌म्हणजेच‌ ‌शेतकऱ्याची‌ ‌बायको‌ ‌घरी‌ ‌आपल्या‌ ‌राघूची‌ ‌म्हणजेच‌ ‌शेतकऱ्याची‌ ‌मनापासून‌ ‌वाट‌ ‌पाहते‌ ‌आहे.‌ ‌ती‌ ‌घरी‌ ‌वाट‌ ‌पाहते‌ ‌पण‌ ‌इकडे‌ ‌शेतात‌ ‌हा‌ ‌शेतकरी‌ ‌तिफन‌ ‌चालवत‌ ‌आहे‌ ‌आणि‌ ‌आकाशातून‌ ‌छान‌ ‌पाऊस‌ ‌बरसत‌ ‌आहे.‌‌

या‌ ‌काव्यपंक्तीमध्ये‌ ‌कवी‌ ‌’विठ्ठल‌ ‌वाघ’‌ ‌यांनी‌ ‌व-हाडी‌ ‌बोलीचा‌ ‌छान‌ ‌वापर‌ ‌केला‌ ‌आहे.‌ ‌या‌ ‌कवितेमध्ये‌ ‌यमक‌ ‌अलंकाराचा‌ ‌वापर‌ ‌करून‌ ‌छान‌ ‌परिणाम‌ ‌साधला‌ ‌आहे.‌ ‌शिवाय‌ ‌इथे‌ ‌चित्रदर्शी‌ ‌शैली‌ ‌दिसून‌ ‌येते.

‌

प्रश्न‌ 5.‌ ‌
वला‌ ‌टाकती‌ ‌तिफन‌ ‌शितू‌ ‌वखर‌ ‌पाहेते‌‌
पानी‌ ‌भिजलं‌ ‌ढेकूल‌ ‌लोनी‌ ‌पायाले‌ ‌वाटते‌‌
काया‌ ‌ढेकलात‌ ‌डोया‌ ‌हिर्व‌ ‌सपन‌ ‌पाहेते‌ ‌
उत्तर:‌
‌’तिफन’‌ ‌ही‌ ‌कविता‌ ‌कवी‌ ‌‘विठ्ठल‌ ‌वाघ’‌ ‌यांनी‌ ‌लिहिली‌ ‌आहे.‌ ‌पावसाच्या‌ ‌आगमनाने‌ ‌शेतकऱ्यांना‌ ‌होणारा‌ ‌आनंद‌ ‌शिवाय‌ ‌शेतीच्या‌ ‌कामांची‌ ‌लगबग‌ ‌याचे‌ ‌सुंदर‌ ‌चित्रदर्शी‌ ‌वर्णन‌ ‌या‌ ‌कवितेत‌ ‌दिसून‌ ‌येते.‌‌

शेतीची‌ ‌नांगरणी‌ ‌करून‌ ‌शेतकरी‌ ‌शेतात‌ ‌धान्याची‌ ‌पेरणी‌ ‌करत‌ ‌आहे.‌ ‌बैलांच्या‌ ‌मदतीने‌ ‌तिफन‌ ‌चालवून‌ ‌पेरणी‌ ‌सुरू‌ ‌आहे.‌ ‌तिफनीतून‌ ‌धान्य‌ ‌जमिनीमध्ये‌ ‌पेरले‌ ‌जाते.‌ ‌त्यानंतर‌ ‌नांगरणी‌ ‌केल्यामुळे‌ ‌मातीची‌ ‌छोटी-मोठी‌ ‌ढेकळं‌ ‌जी‌ ‌जमिनीतून‌ ‌वर‌ ‌आलेली‌ ‌असतात‌ ‌ती‌ ‌फोडून‌ ‌त्याची‌ ‌माती‌ ‌या‌ ‌पेरलेल्या‌ ‌धान्यावर‌ ‌हळूच‌ ‌सारली‌ ‌जाते,‌ ‌त्याला‌ ‌वखरणी‌ ‌म्हणतात.‌ ‌पेरणी‌ ‌करणाऱ्या‌ ‌शेतकऱ्याचे‌ ‌तिकडेही‌ ‌लक्ष‌ ‌आहे.‌ ‌पडणाऱ्या‌ ‌पावसामुळे‌ ‌माती‌ ‌भिजलेली‌ ‌आहे.‌ ‌पाण्याने‌ ‌भरलेली‌ ‌ही‌ ‌मातीची‌ ‌ढेकळं‌ ‌पायाला‌ ‌लोण्याप्रमाणे‌ ‌वाटतात.‌ ‌या‌ ‌मातीच्या‌ ‌काळ्या‌ ‌ढेकळातच‌ ‌शेतकरी‌ ‌उदयाच्या‌ ‌नव्या‌ ‌हिरव्यागार‌ ‌पिकाचं‌ ‌हिरवं‌ ‌स्वप्न‌ ‌पाहू‌ ‌लागतो.‌‌

या‌ ‌काव्यपंक्तीमध्ये‌ ‌कवी‌ ‌’विठ्ठल‌ ‌वाघ’‌ ‌यांनी‌ ‌वहाडी‌ ‌बोलीचा‌ ‌छान‌ ‌वापर‌ ‌केला‌ ‌आहे.‌ ‌या‌ ‌कवितेमध्ये‌ ‌यमक‌ ‌अलंकाराचा‌ ‌वापर‌ ‌करून‌ ‌छान‌ ‌परिणाम‌ ‌साधला‌ ‌आहे.‌ ‌शिवाय‌ ‌इथे‌ ‌चित्रदर्शी‌ ‌शैली‌ ‌दिसून‌ ‌येते.‌

‌प्रश्न‌ 6.‌ ‌
काया‌ ‌ढेकलात‌ ‌डोया‌ ‌हिर्व‌ ‌सपन‌ ‌पाहेते‌‌
डोया‌ ‌सपन‌ ‌पाहेते‌ ‌काटा‌ ‌पायात‌ ‌रुतते‌ ‌
काटा‌ ‌पायात‌ ‌रुतते‌ ‌लाल‌ ‌रगत‌ ‌सांडते‌ ‌हिर्व‌ ‌सपन‌ ‌फुलते‌‌
हिर्व‌ ‌सपन‌ ‌फुलते‌ ‌ढग‌ ‌बरसते‌ ‌
उत्तर:‌
‌’तिफन’‌ ‌ही‌ ‌कविता‌ ‌कवी‌ ‌’विठ्ठल‌ ‌वाघ’‌ ‌यांनी‌ ‌लिहिली‌ ‌आहे.‌ ‌पावसाच्या‌ ‌आगमनाने‌ ‌शेतकऱ्यांना‌ ‌होणारा‌ ‌आनंद‌ ‌शिवाय‌ ‌शेतीच्या‌ ‌कामांची‌ ‌लगबग‌ ‌याचे‌ ‌सुंदर‌ ‌चित्रदर्शी‌ ‌वर्णन‌ ‌या‌ ‌कवितेत‌ ‌दिसून‌ ‌येते.

बैलांच्या‌ ‌मदतीने‌ ‌शेतीची‌ ‌नांगरणी‌ ‌आटोपून‌ ‌शेतकरी‌ ‌धान्याची‌ ‌पेरणी‌ ‌करत‌ ‌असतो.‌ ‌पेरणी‌ ‌करून‌ ‌झाल्यावर‌ ‌मातीच्या‌ ‌काळ्या‌ ‌ढेकळातच‌ ‌शेतकरी‌ ‌उदयाच्या‌ ‌नव्या‌ ‌हिरव्यागार‌ ‌पिकाचं‌ ‌हिरवं‌ ‌स्वप्न‌ ‌पाहू‌ ‌लागतो.‌ ‌आपल्या‌ ‌कष्टाने,‌ ‌मेहनतीने‌ ‌हे‌ ‌शेत‌ ‌हिरवेगार‌ ‌होऊन‌ ‌उठेल,‌ ‌शेतात‌ ‌धान्य‌ ‌डोलू‌ ‌लागेल‌ ‌असे‌ ‌स्वप्न‌ ‌डोळ्यांनी‌ ‌पाहत‌ ‌असताना‌ ‌किंवा‌ ‌मनात‌ ‌तसा‌ ‌विचार‌ ‌चालू‌ ‌असताना‌ ‌अचानक‌ ‌त्याच्या‌ ‌पायात‌ ‌काटा‌ ‌टोचतो.‌ ‌काटा‌ ‌टोचल्यामुळे‌ ‌पायातून‌ ‌लाल‌ ‌रक्त‌ ‌येऊ‌ ‌लागते.‌ ‌पण‌ ‌शेतकऱ्याला‌ ‌ती‌ ‌वेदना‌ ‌जाणवत‌‌ नाही.‌ ‌कारण‌ ‌त्याच्या‌ ‌कष्टातून,‌ ‌श्रमातून‌ ‌त्याच्या‌ ‌हिरव्यागार‌ ‌शेताचे‌ ‌स्वप्न‌ ‌सत्यात‌ ‌उतरेल‌ ‌असा‌ ‌त्याला‌ ‌विश्वास‌ ‌वाटतो.‌ ‌पाऊस‌ ‌पडतो,‌ ‌ढग‌ ‌बरसू‌ ‌लागतात‌ ‌आणि‌ ‌त्या‌ ‌शेतकऱ्याचे‌ ‌हिरवे‌ ‌स्वप्न‌ ‌खरे‌ ‌होऊ‌ ‌लागते.‌‌

या‌ ‌काव्यपंक्तीमध्ये‌ ‌कवी‌ ‌’विठ्ठल‌ ‌वाघ’‌ ‌यांनी‌ ‌वहाडी‌ ‌बोलीचा‌ ‌छान‌ ‌वापर‌ ‌केला‌ ‌आहे.‌ ‌या‌ ‌कवितेमध्ये‌ ‌यमक‌ ‌अलंकाराचा‌ ‌वापर‌ ‌करून‌ ‌छान‌ ‌परिणाम‌ ‌साधला‌ ‌आहे.‌ ‌शिवाय‌ ‌इथे‌ ‌चित्रदर्शी‌ ‌शैली‌ ‌दिसून‌ ‌येते.‌‌

पाठाखालील‌ ‌स्वाध्याय‌‌:

‌अभिव्यक्ती‌:

प्रश्न‌ ‌1.‌
‘काया‌ ‌ढेकलात‌ ‌डोया‌ ‌हिर्व‌ ‌सपान‌ ‌पाहेते’‌ ‌या‌ ‌ओळीतील‌‌ भावार्थ‌ ‌स्पष्ट‌ ‌करा.‌ ‌
उत्तर:‌
‌कृती‌ ‌3:‌ ‌काव्यसौंदर्य,‌ ‌प्रश्न‌ ‌(1)‌ ‌मधील‌ ‌(vi)‌ ‌चे‌ ‌उत्तर‌ ‌पाहा.‌ ‌

तिफन Summary in Marathi

कवीचा‌ ‌परिचय‌:

नाव‌‌: विठ्ठल‌ ‌वाघ‌
जन्म‌‌:‌ ‌1945
‌सुप्रसिदध‌ ‌कवी‌ ‌व‌ ‌लेखक.‌ ‌’काळ्या‌ ‌मातीत‌ ‌मातीत’,‌ ‌’पंढरीच्या‌ ‌वाटेवर’,‌ ‌’कपाशीची‌ ‌चंद्रफुले’,‌ ‌’पाऊसपाणी’‌ ‌हे‌ ‌कवितासंग्रह;‌ ‌’अंधारयात्रा’‌ ‌हे‌ ‌नाटक;‌ ‌’डेबू’‌ ‌ही‌ ‌कादंबरी;‌ ‌’वहाड‌ ‌बोली‌ ‌आणि‌ ‌इतिहास’,‌ ‌’वहाडी‌ ‌म्हणी’‌ ‌इत्यादी‌ ‌पुस्तके‌ ‌प्रसिद्ध.‌‌

प्रस्तावना‌‌:

‘तिफन’‌ ‌ही‌ ‌कविता‌ ‌कवी‌ ‌’विठ्ठल‌ ‌वाघ’‌ ‌यांनी‌ ‌लिहिली‌ ‌आहे.‌ ‌पावसाच्या‌ ‌आगमनाने‌ ‌शेतकऱ्यांना‌ ‌होणारा‌ ‌आनंद‌ ‌शिवाय‌ ‌शेतीच्या‌ ‌कामांची‌ ‌लगबग‌ ‌याचे‌ ‌सुंदर‌ ‌चित्रदर्शी‌ ‌वर्णन‌ ‌या‌ ‌कवितेत‌ ‌दिसून‌ ‌येते.‌‌

Poet‌ ‌Vitthal‌ ‌Wagh‌ ‌has‌ ‌written‌ ‌the‌ ‌poem‌ ‌’Tiphan’.‌ ‌This‌ ‌poem‌ ‌describes‌ ‌a‌ ‌picture‌ ‌of‌ ‌rural‌ ‌area‌ ‌at‌ ‌the‌ ‌onset‌ ‌of‌ ‌the‌ ‌monsoons.‌ ‌A‌ ‌farmer’s‌ ‌joy‌ ‌knows‌ ‌no‌ ‌bounds‌ ‌as‌ ‌the‌ ‌monsoon‌ ‌showers‌ ‌drench‌ ‌his‌ ‌farm‌ ‌thoroughly.‌ ‌The‌ ‌poem‌ ‌depicts‌ ‌the‌ ‌various‌ ‌activities‌ ‌of‌ ‌the‌ ‌farmer‌ ‌and‌ ‌that‌ ‌of‌ ‌his‌ ‌wife‌ ‌in‌ ‌sowing‌ ‌seeds‌ ‌in‌ ‌the‌ ‌farm.‌ ‌The‌ ‌rain‌ ‌showers‌ ‌kindle‌ ‌the‌ ‌hope‌ ‌of‌ ‌an‌ ‌abundant‌ ‌green‌ ‌crop‌ ‌in‌ ‌the‌ ‌farmer’s‌ ‌mind.‌‌

भावार्थ‌‌:

काया‌ ‌मातीत‌ ‌……‌ ‌ढोल‌ ‌वाजवते‌ ‌
शेतकऱ्याच्या‌ ‌कष्टकरी‌ ‌जीवनाचे‌ ‌व‌ ‌निसर्गाचे‌ ‌नितांत‌ ‌सुंदर‌ ‌व‌ ‌जिवंत‌ ‌चित्र‌ ‌कवी‌ ‌आपल्या‌ ‌डोळ्यांसमोर‌ ‌उभे‌ ‌करतात.‌ ‌शेतकऱ्याचे‌ ‌संपूर्ण‌ ‌जीवन‌ ‌हे‌ ‌शेतीवर‌ ‌आणि‌ ‌पर्यायाने‌ ‌पावसावर‌ ‌अवलंबून‌ ‌असते.‌ ‌त्यामुळे‌ ‌पाऊस‌ ‌सुरू‌ ‌झाला‌ ‌की‌ ‌त्याच्या‌ ‌शेतीच्या‌ ‌कामाची‌ ‌लगबग‌ ‌सुरू‌ ‌होते.‌

शेताची‌ ‌नांगरणी‌ ‌आटोपून‌ ‌पाऊस‌ ‌सुरू‌ ‌झाल्याने‌ ‌शेतकरीधान्याची‌ ‌पेरणी‌ ‌करत‌ ‌असतो.‌ ‌शेतात‌ ‌बैलांच्या‌ ‌मदतीने‌ ‌तिफन‌ ‌चालवून‌ ‌पेरणी‌ ‌चालू‌ ‌असते.‌ ‌काळ्या‌ ‌मातीत‌ ‌तिफन‌ ‌चालत‌ ‌असते.‌ ‌आकाशात‌ ‌विजा‌ ‌चमकत‌ ‌असतात‌ ‌जणू‌ ‌त्यांचा‌ ‌थयथय‌ ‌नाच‌ ‌चालू‌ ‌असतो.‌ ‌त्याचवेळी‌ ‌ढगांचा‌ ‌गडगडाट‌ ‌ऐकू‌ ‌येऊ‌ ‌लागतो‌ ‌जणू‌ ‌ढग‌ ‌ढोल‌ ‌वाजवत‌ ‌आहेत‌ ‌असे‌ ‌वाटते.‌‌

नंदी‌ ‌बैलाच्या‌ ‌…..‌ ‌ढग‌ ‌बरसते‌
]पाऊस‌ ‌आल्यामुळे‌ ‌पेरणीसाठी‌ ‌सदाशीव‌ ‌म्हणजेच‌ ‌शेतकरी‌ ‌तयार‌ ‌झालेला‌ ‌आहे.‌ ‌तो‌ ‌आपल्या‌ ‌शेतामध्ये‌ ‌नंदीबैलाच्या‌ ‌जोडीला‌ ‌तिफन‌ ‌बांधून‌ ‌हाकारत‌ ‌आहे.‌ ‌त्यावेळी‌ ‌सदाशीवची‌ ‌पत्नी‌ ‌पार्वती‌ ‌आपल्या‌ ‌पोटाला‌ ‌पदराची‌ ‌ओटी‌ ‌बांधून‌ ‌त्यात‌ ‌बियाणे‌ ‌घेऊन‌ ‌पेरणी‌ ‌करत‌ ‌आहे.‌‌
आपले‌ ‌रडणारे‌ ‌छोटे‌ ‌बाळ‌ ‌पार्वतीने‌ ‌झोळीत‌ ‌ठेवले‌ ‌आहे.‌ ‌ती‌ ‌झोळी‌ ‌तिने‌ ‌काठीला‌ ‌टांगून‌ ‌ठेवली‌ ‌आहे.‌ ‌झोळीत‌ ‌झोका‌ ‌घेणारे‌ ‌बाळ‌ ‌रडत‌ ‌आहे‌ ‌आणि‌ ‌आकाशातून‌ ‌ढग‌ ‌बरसू‌ ‌लागले‌ ‌आहेत.‌ ‌पाऊस‌ ‌सुरू‌ ‌झाला‌ ‌आहे.‌‌

काकरात‌ ‌बिजवाई‌ ‌……‌ ‌हानते‌ ‌ढग‌ ‌बरसते‌ ‌
पाऊस‌ ‌सुरू‌ ‌झाल्यामुळे‌ ‌सदाशीव‌ ‌शेतकऱ्याने‌ ‌शेतात‌ ‌नंदीबैलाच्या‌ ‌साथीने‌ ‌तिफन‌ ‌जोडून‌ ‌पेरणीला‌ ‌सुरुवात‌ ‌केली‌ ‌आहे.‌ ‌या‌ ‌पेरणीच्या‌ ‌कामात‌ ‌त्याची‌ ‌पत्नी‌ ‌पार्वती‌ ‌त्याला‌ ‌साथ‌ ‌देत‌ ‌आहे.‌ ‌त्यांनी‌ ‌शेतात‌ ‌पेरलेले‌ ‌धान्य‌ ‌जणू‌ ‌हसणारं‌ ‌चांदणं‌ ‌वाटत‌ ‌आहे.‌ ‌शिवाय‌ ‌पेरलेले‌ ‌ते‌ ‌धान्य‌ ‌पाहून‌ ‌असे‌ ‌वाटते‌ ‌जणू‌ ‌धरतीच्या‌ ‌अंगावर‌ ‌लाडाने,‌ ‌कौतुकाने‌ ‌नवसाचे‌ ‌छान‌ ‌गोंदण‌ ‌केलेले‌ ‌आहे.‌‌

पुढे‌ ‌कवी‌ ‌म्हणतात‌ ‌की,‌ ‌आता‌ ‌पावसाला‌ ‌चांगली‌ ‌सुरुवात‌ ‌झाली‌ ‌आहे.‌ ‌सर्वत्र‌ ‌पावसाच्या‌ ‌सरीवर‌ ‌सरी‌ ‌कोसळत‌ ‌आहेत.‌ ‌जणू‌ ‌या‌ ‌सरी‌ ‌मातीला‌ ‌न्हाऊ‌ ‌घालत‌ ‌आहेत.‌ ‌या‌ ‌बरसणाऱ्या‌ ‌सरींमुळे‌ ‌माती‌ ‌चिंब‌ ‌भिजून‌ ‌गेली‌ ‌आहे.‌ ‌या‌ ‌मातीचा‌ ‌कस्तुरीसारखा‌ ‌सुगंध‌ ‌सर्वत्र‌ ‌पसरलेला‌ ‌आहे.‌ ‌हा‌ ‌सुगंध‌ ‌जीवाला‌ ‌भूल‌ ‌पाडत‌ ‌आहे,‌ ‌मन‌ ‌मोहीत‌ ‌करत‌ ‌आहे.‌‌

इकडे‌ ‌भिजलेल्या‌ ‌मातीचा‌ ‌सुगंध‌ ‌मनाला‌ ‌धुंद‌ ‌करत‌ ‌आहे‌ ‌तर‌ ‌तिकडे‌ ‌संध्याकाळच्या‌ ‌वेळी‌ ‌मैना‌ ‌म्हणजेच‌ ‌शेतकऱ्याची‌ ‌बायको‌ ‌घरी‌ ‌आपल्या‌ ‌राघूची‌ ‌म्हणजेच‌ ‌शेतकऱ्याची‌ ‌मनापासून‌ ‌वाट‌ ‌पाहते‌ ‌आहे.‌ ‌ती‌‌ घरी‌ ‌वाट‌ ‌पाहते‌ ‌पण‌ ‌इकडे‌ ‌शेतात‌ ‌हा‌ ‌शेतकरी‌ ‌तिफन‌ ‌चालवत‌ ‌आहे.‌ ‌पाऊस‌ ‌बरसत‌ ‌आहे.‌‌

वला‌ ‌टाकती‌ ‌तिफन‌ ‌…..‌ ‌फुलते‌ ‌ढग‌ ‌बरसते‌
‌शेतीची‌ ‌नांगरणी‌ ‌करून‌ ‌शेतकरी‌ ‌शेतात‌ ‌धान्याची‌ ‌पेरणी‌ ‌करत‌ ‌आहे.‌ ‌बैलांच्या‌ ‌मदतीने‌ ‌तिफन‌ ‌चालवून‌ ‌पेरणी‌ ‌सुरू‌ ‌आहे.‌ ‌तिफनीतून‌ ‌धान्य‌ ‌जमिनीमध्ये‌ ‌पेरले‌ ‌जाते.‌ ‌त्यानंतर‌ ‌नांगरणी‌ ‌केल्यामुळे‌ ‌मातीची‌ ‌छोटी-मोठी‌ ‌ढेकळं‌ ‌जी‌ ‌जमिनीतून‌ ‌वर‌ ‌आलेली‌ ‌असतात‌ ‌ती‌ ‌फोडून‌ ‌त्याची‌ ‌माती‌ ‌या‌ ‌पेरलेल्या‌ ‌धान्यावर‌ ‌हळूच‌ ‌सारली‌ ‌जाते,‌ ‌त्याला‌ ‌वखरणी‌ ‌म्हणतात.‌ ‌पेरणी‌ ‌करणाऱ्या‌ ‌शेतकऱ्याचे‌ ‌तिकडेही‌ ‌लक्ष‌ ‌आहे.‌ ‌पडणाऱ्या‌ ‌पावसामुळे‌ ‌माती‌ ‌भिजलेली‌ ‌आहे.‌ ‌पाण्याने‌ ‌भरलेली‌ ‌ही‌‌ मातीची‌ ‌ढेकळं‌ ‌पायाला‌ ‌लोण्याप्रमाणे‌ ‌वाटतात.‌ ‌या‌ ‌मातीच्या‌ ‌काळ्या‌ ‌ढेकळातच‌ ‌शेतकरी‌ ‌उदयाच्या‌ ‌नव्या‌ ‌हिरव्यागार‌ ‌पिकाचं‌ ‌हिरवं‌ ‌स्वप्न‌ ‌पाहू‌ ‌लागतो.‌

आपल्या‌ ‌कष्टाने,‌ ‌मेहनतीने‌ ‌हे‌ ‌शेत‌ ‌हिरवेगार‌ ‌होऊन‌ ‌उठेल,‌ ‌शेतात‌ ‌धान्य‌ ‌डोलू‌ ‌लागेल‌ ‌असे‌ ‌स्वप्न‌ ‌डोळ्यांनी‌ ‌पाहत‌ ‌असताना‌ ‌किंवा‌ ‌मनात‌ ‌तसा‌ ‌विचार‌ ‌चालू‌ ‌असताना‌ ‌अचानक‌ ‌शेतकऱ्याच्या‌ ‌पायात‌ ‌काटा‌ ‌टोचतो.‌ ‌काटा‌ ‌टोचल्यामुळे‌ ‌पायातून‌ ‌लाल‌ ‌रक्त‌ ‌येऊ‌ ‌लागते.‌ ‌पण‌ ‌शेतकऱ्याला‌ ‌ती‌ ‌वेदना‌ ‌जाणवत‌ ‌नाही.‌ ‌कारण‌ ‌त्याच्या‌ ‌कष्टातून,‌ ‌श्रमातून‌ ‌त्याच्या‌ ‌हिरव्यागार‌ ‌शेताचे‌ ‌स्वप्न‌ ‌सत्यात‌ ‌उतरेल‌ ‌असा‌ ‌त्याला‌ ‌विश्वास‌ ‌वाटतो.‌ ‌पाऊस‌ ‌पडतो,‌ ‌ढग‌ ‌बरसू‌ ‌लागतात‌ ‌आणि‌ ‌त्या‌ ‌शेतकऱ्याचे‌ ‌हिरवे‌ ‌स्वप्न‌ ‌खरे‌ ‌होऊ‌ ‌लागते.‌‌

शब्दार्थ‌‌:

1. काया‌ ‌-‌ ‌काळ्या‌ ‌(black)‌
2. ‌पानी‌ ‌-‌ ‌पाणी‌ ‌
3. ईज‌ ‌-‌ ‌वीज‌ ‌(lightning)‌ ‌
4. जोळीले‌ ‌-‌ ‌जोडीने‌ ‌(together,‌ ‌with)‌‌
5. वटी‌ ‌-‌ ‌ओटी‌‌ ‌
6. पोटाले‌ ‌-‌ ‌पोटाला‌ ‌
7. पाराबती‌ ‌-‌ ‌पार्वती‌
8. ‌काटीले‌ ‌-‌ ‌काठीला‌ ‌
9. लळते‌ ‌-‌ ‌रडते‌ ‌(is‌ ‌crying)‌ ‌
10. वाटुली‌ ‌पाहेते‌ ‌-‌ ‌वाट‌ ‌पाहते‌ ‌(is‌ ‌waiting)‌ ‌
11. झोयी‌ ‌-‌ ‌झोळी‌ ‌(traditional‌ ‌cradle)‌ ‌
12. तानुलं‌ ‌-‌ ‌तान्हुलं,‌ ‌छोटे‌ ‌बाळ‌ ‌
13. लोनी‌ ‌- लोणी‌ ‌(butter)‌ ‌
14. बिजवाई‌ ‌-‌ ‌बियाणं‌‌
15. चांदनं‌ ‌-‌ ‌चांदणं‌ ‌(moon‌ ‌light)‌ ‌
16. लाळानौसाचं‌ ‌-‌ ‌लाडा‌ ‌नवसाचं‌ ‌
17. जीवाले‌ ‌-‌ ‌जीवाला‌ ‌(here-mind)‌ ‌
18. डोया‌ ‌-‌ ‌डोळा‌ ‌(eye)‌ ‌
19. तिफन‌ ‌-‌ ‌धान्य‌ ‌पेरणीसाठीचे‌ ‌तीन‌ ‌नळकांड्या‌ ‌असलेले‌‌ शेतीचे‌ ‌अवजार‌
20. ‌नौसाचं‌ ‌-‌ ‌नवसाचं‌ ‌
21. रगत‌ ‌-‌ ‌रक्त‌ ‌(blood)‌
22. ‌सपन‌ ‌-‌ ‌स्वप्न‌ ‌(dream)‌ ‌
23. सांजीले‌ ‌-‌ ‌सायंकाळी‌ ‌(evening)‌ ‌
24. हानते‌ ‌-‌ ‌हाकतो‌ ‌(moving‌ ‌forward)
25. हिर्व‌‌ -‌ ‌हिरवं‌ ‌(green)‌ ‌
26. काकरात‌ ‌-‌ ‌शेतात‌ ‌
27. कस्तुरी‌ ‌-‌ ‌कस्तुरीमृगाच्या‌ ‌नाभीत‌ ‌उत्पन्न‌ ‌होणारे‌ ‌एक‌ ‌सुगंधी‌‌ द्रव्य‌ ‌(an‌ ‌aromatic‌ ‌substance)

Balbharti Maharashtra State Board Class 9 Marathi Solutions Aksharbharati Chapter 14 ते जीवनदायी झाड Notes, Textbook Exercise Important Questions and Answers.

Maharashtra State Board Class 9 Marathi Aksharbharati Solutions Chapter 14 ते जीवनदायी झाड

Marathi Aksharbharati Std 9 Digest Chapter 14 ते जीवनदायी झाड Textbook Questions and Answers

1.‌ ‌कारणे‌ ‌लिहा.‌

‌प्रश्न‌ ‌1.
‌लेखकाला‌ ‌लिंबाचे‌ ‌झाड‌ ‌जीवनदायी‌ ‌वाटले,‌ ‌कारण‌ ‌…..‌………‌
उत्तरः‌
‌लेखकाला‌ ‌लिंबाचे‌ ‌झाड‌ ‌जीवनदायी‌ ‌वाटले,‌ ‌कारण‌ ‌आजूबाजूचा‌ ‌सगळा‌ ‌प्रदेश‌ ‌उन्हाचा‌ ‌असला‌ ‌तरी‌ ‌लिंबाचे‌ ‌ते‌ ‌झाड‌ ‌लसलशीत‌ ‌हिरवेगार‌ ‌आणि‌ ‌चैतन्यमय‌ ‌होते.‌ ‌

‌प्रश्न‌ ‌2.
पारव्याची‌ ‌जोडी‌ ‌लिंबाच्या‌ ‌झाडावर‌ ‌राहते,‌ ‌कारण‌ ‌…..‌……………. ‌
उत्तरः‌
‌भोवतालच्या‌ ‌रखरखीत‌ ‌वातावरणात‌ ‌ते‌ ‌लिंबाचं‌ ‌झाड‌ ‌एक‌ ‌थंड‌ ‌असा‌ ‌आश्रय‌ ‌होता.‌ ‌

‌प्रश्न‌ ‌3.
‌लेखकाला‌ ‌खिडकी‌ ‌लावून‌ ‌घ्यावी‌ ‌असे‌ ‌वाटले,‌ ‌कारण‌ ‌…..‌…………. ‌
उत्तर:‌ ‌
लिंबाच्या‌ ‌एका‌ ‌छोट्या‌ ‌फांदीवर‌ ‌मधमाश्यांचं‌ ‌पोळंही‌ ‌रचलं‌ ‌जाऊ‌ ‌लागलं.‌

2. चौकट‌ ‌पूर्ण‌ ‌करा.‌ ‌

‌प्रश्न‌ ‌1.
चौकट‌ ‌पूर्ण‌ ‌करा.‌ ‌

उत्तर:‌ ‌

3.‌ ‌लिंबाच्या‌ ‌झाडाला‌ ‌खालील‌ ‌वैशिष्ट्ये‌ ‌कोणी‌ ‌कोणी‌ ‌प्राप्त‌ ‌करून‌ ‌दिली.‌ ‌

‌प्रश्न‌ ‌1.
संगीतमय‌ ‌झाड‌ ‌
उत्तरः‌
‌चिमण्या‌ ‌आणि‌ ‌इतर‌ ‌पक्षी‌ ‌

प्रश्न‌ 2.
‌आश्रयदायी‌ ‌झाड‌ ‌
उत्तर:‌
‌गोगलगाई,‌ ‌पारवा,‌ ‌चिमण्या,‌ ‌बुलबुल,‌ ‌पोपट,‌ ‌मुंग्या,‌ ‌किटक,‌ ‌किडे,‌ ‌साप,‌ ‌कुत्री,‌ ‌खार,‌ ‌फुलपाखरे,‌ ‌भुंगे,‌ ‌मधमाशी,‌ ‌माणसे‌ ‌इ.‌ ‌

प्रश्न‌ 3.
आश्वासक‌ ‌झाड‌ ‌
उत्तरः‌
‌तुरेदार‌ ‌बुलबुल‌ ‌आणि‌ ‌पोपट‌ ‌

प्रश्न‌ 4. ‌
जीवनदायी‌ ‌झाड‌
‌उत्तरः‌
‌सर्व‌ ‌सजीव‌ ‌

4. परसदार‌ ‌या‌ ‌शब्दापासून‌ ‌चार‌ ‌अर्थपूर्ण‌ ‌शब्द‌ ‌तयार‌ ‌करा.‌ ‌

प्रश्न‌ ‌1.‌ ‌
परसदार‌ ‌या‌ ‌शब्दापासून‌ ‌चार‌ ‌अर्थपूर्ण‌ ‌शब्द‌ ‌तयार‌ ‌करा.‌ ‌
उत्तरः‌
‌दार,‌ ‌सरदार,‌ ‌रस,‌ ‌दास,‌ ‌पर,‌ ‌सर,‌ ‌सदा‌ ‌

5. पाठात‌ ‌वर्णन‌ ‌आलेल्या‌ ‌दोन‌ ‌कुटुंबाची‌ ‌दिलेल्या‌ ‌मुददयांच्या‌ ‌आधारे‌ ‌तुलना‌ ‌करा.‌ ‌

प्रश्न‌ ‌1.
पाठात‌ ‌वर्णन‌ ‌आलेल्या‌ ‌दोन‌ ‌कुटुंबाची‌ ‌दिलेल्या‌ ‌मुददयांच्या‌ ‌आधारे‌ ‌तुलना‌ ‌करा.‌ ‌

उत्तरः‌

7. चूक‌ ‌की‌ ‌बरोबर‌ ‌ते‌ ‌लिहा.‌

‌प्रश्न‌ ‌1.‌ ‌
चूक‌ ‌की‌ ‌बरोबर‌ ‌ते‌ ‌लिहा.‌

1. परसदारी‌ ‌पाण्याचा‌ ‌हापसा‌ ‌असलेल्या‌ ‌शेजाऱ्यांची‌ ‌बाग‌ ‌फुललेली‌ ‌होती.‌
2. ‌इतर‌ ‌पक्ष्यांच्या‌ ‌त्रासामुळे‌ ‌पारव्याची‌ ‌जोडी‌ ‌लिंबाच्या‌ ‌झाडावरून‌ ‌हलली.‌
3. लिंबाचं‌ ‌झाड‌ ‌लावणारी‌ ‌स्त्री‌ ‌अत्यंत‌ ‌हळवी‌ ‌होती.‌
4. ‌लिंबाच्या‌ ‌झाडावर‌ ‌मधमाश्या‌ ‌कधी‌ ‌कुणाला‌ ‌चावल्या‌ ‌नाहीत.‌ ‌

उत्तर‌‌:‌

1. चूक‌
2. चूक‌
3. ‌बरोबर‌ ‌
4. बरोबर‌ ‌

8. स्वमत‌ ‌

‌प्रश्न‌ ‌1.‌ ‌
1. ‌वृक्ष‌ ‌व‌ ‌मानवी‌ ‌जीवन‌ ‌यांच्यातील‌ ‌परस्परसंबंधांविषयी‌ ‌तुमचे‌ ‌मत‌ ‌सोदाहरण‌ ‌स्पष्ट‌ ‌करा.‌ ‌(उतारा‌ ‌2‌ ‌मधील‌ ‌कृती‌ ‌4:‌ ‌स्वमतचे‌ ‌उत्तर‌ ‌पहा.)‌ ‌‌
2. ‌झाड‌ ‌सजीवांसाठी‌ ‌जीवनदायी‌ ‌केंद्र‌ ‌कसे‌ ‌बनू‌ ‌शकते,‌ ‌हे‌ ‌विधान‌ ‌पटवून‌ ‌द्या.‌ ‌(उतारा‌ ‌4‌ ‌मधील‌ ‌कृती‌ ‌4:‌ ‌स्वमतचे‌ ‌उत्तर‌ ‌पहा.)‌

9. अभिव्यक्ती.

‌प्रश्न‌ ‌1.‌ ‌
लेखकाच्या मुलाने पारव्यांच्या जोडीचा आश्रय – त्यांचे घरटे वारंवार पाहिल्यामुळे पारव्याचे जोडपे हळूहळू दिसेनासे झाले. ही घटना तुम्हाला काय सांगते, ते स्पष्ट करा.

Marathi Akshar Bharati Class 9 Textbook Solutions Chapter 14 ते जीवनदायी झाड Additional Important Questions and Answers

पुढील‌ ‌उताऱ्याच्या‌ ‌आधारे‌ ‌दिलेल्या‌ ‌सूचनेनुसार‌ ‌कृती‌ ‌करा:‌ ‌

कृती‌ ‌1 ‌:‌ ‌आकलन‌ ‌कृती‌

‌प्रश्न 1.‌ ‌
आकृतिबंध‌ ‌पूर्ण‌ ‌करा.‌ ‌
उत्तर:‌

‌प्रश्न 2.‌ ‌
उत्तर‌ ‌लिहा.‌ ‌
आसमंत‌ ‌तापून‌ ‌जाण्याचे‌ ‌कारण‌ ……………..
‌उत्तरः‌ ‌
त्या‌ ‌भागात‌ ‌उन्हाळा‌ ‌जास्त‌ ‌होता.‌ ‌

‌प्रश्न 3.‌ ‌
जोड्या‌ ‌जुळवा.‌ ‌

उत्तर:‌

खालील‌ ‌प्रश्नांची‌ ‌उत्तरे‌ ‌एका‌ ‌वाक्यात‌ ‌लिहा.‌

‌प्रश्न 1.‌ ‌
‌लेखकाच्या‌ ‌घरामागे‌ ‌कशाचे‌ ‌झाड‌ ‌होते?‌ ‌
उत्तर‌‌:‌
‌लेखकाच्या‌ ‌घरामागे‌ ‌लिंबाचे‌ ‌झाड‌ ‌होते.‌

‌प्रश्न 2.‌ ‌
आसपासची‌ ‌झाडे‌ ‌पाणी‌ ‌नसल्याने‌ ‌कशी‌ ‌झाली‌ ‌होती?‌ ‌
उत्तरः‌ ‌
आसपासची‌ ‌झाडे‌ ‌पाणी‌ ‌नसल्याने‌ ‌मलूल‌ ‌झाली‌ ‌होती.‌ ‌

कंसातील‌ ‌योग्य‌ ‌शब्द‌ ‌वापरून‌ ‌रिकाम्या‌ ‌जागा‌ ‌भरा.‌ ‌

‌प्रश्न 1.‌ ‌
1. ‌प्रदेश‌ ‌सगळा‌ ‌…………. होता.‌ ‌ (उन्हाचा,‌ ‌पावसाचा,‌ ‌सावलीचा,‌ ‌वाऱ्याचा)‌ ‌
2.‌ ‌सगळीकडं‌ ‌…………‌ ‌कोरडी‌ ‌जमीन.‌ ‌ (आर्द्र,‌ ‌ओलसर,‌ ‌तांबडी,‌ ‌शुष्क)‌ ‌
उत्तर:‌
‌1.‌ ‌उन्हाचा‌ ‌
2.‌ ‌शुष्क

सहसंबंध‌ ‌लिहा.‌

‌प्रश्न 1.‌ ‌
1. मलूल‌ ‌आणि‌ ‌काळपट‌ ‌हिरवी‌ ‌:‌ ‌झाडे‌ ‌::‌ ‌
शुष्क‌ ‌कोरडी‌ ‌:‌ ‌……‌……………..
‌2. ‌आर्द्र‌ ‌:‌ ‌शुष्क‌ ‌::‌ ‌ओली‌ ‌:‌ …………….. ‌
उत्तर:‌
1. ‌जमीन‌ ‌
2.‌ ‌कोरडी

कृती‌ ‌2‌:‌ ‌आकलन‌ ‌कृती‌ ‌

‌प्रश्न 1.‌ ‌
योग्य‌ ‌पर्याय‌ ‌निवडून‌ ‌विधान‌ ‌पूर्ण‌ ‌करा.‌ ‌
आसपासची‌ ‌जमीन‌ ‌तापून‌ ‌करपून‌ ‌तपकिरी‌ ‌पडलेली‌ ‌दिसे;‌ ‌ कारण‌ ‌………………‌ ‌
(अ)‌ ‌प्रदेश‌ ‌सगळा‌ ‌सावलीचा‌ ‌होता.‌ ‌
(ब)‌ ‌प्रदेश‌ ‌सगळा‌ ‌उन्हाचा‌ ‌होता.‌ ‌
(क)‌ ‌प्रदेश‌ ‌सगळा‌ ‌चैतन्यमय‌ ‌होता.‌
‌(ड)‌ ‌प्रदेश‌ ‌सगळा‌ ‌शुष्क‌ ‌होता.‌ ‌
उत्तरः‌ ‌
आसपासची‌ ‌जमीन‌ ‌तापून‌ ‌करपून‌ ‌तपकिरी‌ ‌पडलेली‌ ‌दिसे;‌ ‌कारण‌ ‌प्रदेश‌ ‌सगळा‌ ‌उन्हाचा‌ ‌होता.‌ ‌

‌प्रश्न 2.‌ ‌
‌काय‌ ‌ते‌ ‌लिहा.‌ ‌
लेखकाच्या‌ ‌घरामागचे‌ ‌झाड‌ ‌
उत्तर:‌
‌लिंबाचे‌ ‌

‌प्रश्न 3.‌ ‌
आकृतिबंध‌ ‌पूर्ण‌ ‌करा.‌ ‌
उत्तर:‌

चूक‌ ‌की‌ ‌बरोबर‌ ‌ते‌ ‌लिहा.‌ ‌

‌प्रश्न 1.‌ ‌
खिडकीलगतच‌ ‌होतं‌ ‌ते‌ ‌काटेरी‌ ‌आणि‌ ‌बोराच्या‌ ‌फळांनी‌ ‌गच्च‌ ‌लगडलेलं‌ ‌असं.‌ ‌
उत्तरः‌ ‌
चूक‌ ‌

‌प्रश्न 2.‌ ‌
त्या‌ ‌भागात‌ ‌एकूणच‌ ‌उन्हाळा‌ ‌जास्त.‌ ‌आसमंत‌ ‌तापून‌ ‌जाई.‌ ‌
उत्तर:‌ ‌
बरोबर‌

‌कृती‌ ‌3:‌ ‌व्याकरण‌ ‌कृती‌ ‌

‌प्रश्न 1.‌ ‌
खालील‌ ‌वाक्ये‌ ‌लेखननियमांनुसार‌ ‌शुद्ध‌ ‌करून‌ ‌लिहा.‌ ‌
1. ‌घरसूद्धा‌ ‌तापुन‌ ‌निघे‌
2. लींब‌ ‌म्हणजे‌ ‌कडुलिंब‌ ‌नव्हे.‌ ‌
उत्तर:‌ ‌
1.‌ ‌घरसुद्धा‌ ‌तापून‌ ‌निघे.‌
2. ‌लिंब‌ ‌म्हणजे‌ ‌कडूलिंब‌ ‌नव्हे.‌ ‌

‌प्रश्न 2.‌ ‌
उताऱ्यातील‌ ‌दोन‌ ‌सर्वनामे‌ ‌शोधून‌ ‌लिहा.‌ ‌
उत्तरः‌ ‌

1. ‌मी‌
2. ‌त्या‌
3. ‌आपण‌
4. ‌ते‌ ‌
5. ‌ती‌
6. या‌ ‌

अचूक‌ शब्द‌ ‌लिहा.‌

‌प्रश्न 1.‌
वीलक्षण,‌ ‌विलक्शन,‌ ‌विलक्षण,‌ ‌विलक्षन‌ ‌
उत्तर‌‌:‌
‌विलक्षण‌ ‌

‌प्रश्न 2.‌
‌पार्श्वभूमी,‌ ‌पाशभूमी,‌ ‌पाश्वभूमी,‌ ‌पार्श्वभुमी‌ ‌
उत्तरः‌
‌पार्श्वभूमी‌

समानार्थी‌ ‌शब्द‌ ‌लिहा.‌ ‌

‌प्रश्न 1.‌

1. ‌वृक्ष‌ ‌-‌ ‌[ ]
2. प्रांत‌ ‌-‌ [ ]
3. सदन‌ ‌-‌ ‌[ ]‌
4. ‌आकाश‌ ‌-‌ ‌[ ]‌ ‌

उत्तर:‌

1. झाड‌ ‌
2. प्रदेश‌ ‌
3. ‌घर‌ ‌
4. आसमंत‌ ‌

अधोरेखित‌ ‌शब्दाचा‌ ‌विरुद्धार्थी‌ ‌शब्द‌ ‌लिहून‌ ‌वाक्य‌ ‌पुन्हा‌ ‌लिहा.‌ ‌

‌प्रश्न 1.‌
मी‌ ‌राहत‌ ‌होतो‌ ‌त्या‌ ‌घराच्या‌ ‌मागं‌ ‌एक‌ ‌लिंबाचं‌ ‌झाड‌ ‌होतं.‌ ‌
उत्तरः‌ ‌
मी‌ ‌राहत‌ ‌होतो‌ ‌त्या‌ ‌घराच्या‌ ‌पुढं‌ ‌एक‌ ‌लिंबाचं‌ ‌झाड‌ ‌होतं.‌

विरुद्धार्थी‌ ‌शब्द‌ ‌लिहा.‌ ‌

‌प्रश्न 1.‌

1. आर्द्र‌ ‌×‌ [ ]
2. पुढं‌ × [ ]
3. ‌उदास‌ ‌× ‌[ ]
4. ‌मृत्युमय‌ ‌× [ ]

उत्तर:‌

1. शुष्क‌
2. मागं‌ ‌
3. चैतन्यमय‌ ‌
4. जीवनमय‌

‌‌प्रश्न 7.‌ ‌
अधोरेखित‌ ‌शब्दाची‌ ‌जात‌ ‌ओळखा.‌ ‌
ते‌ ‌झाड‌ ‌म्हणजे‌ ‌विलक्षण‌ ‌जीवनमय‌ ‌आणि‌ ‌जीवनदायी‌ ‌वाटे.‌ ‌
उत्तर:‌ ‌
उभयान्वयी‌ ‌अव्यय‌ ‌

‌पुढील‌ ‌विशेषणे‌ ‌कशासाठी‌ ‌वापरण्यात‌ ‌आली‌ ‌ते‌ ‌लिहा.‌

‌‌प्रश्न 1.
‌लसलशीत‌ ‌हिरवंगार‌ ‌
उत्तरः‌ ‌
लिंबाचं‌ ‌झाड‌

‌‌प्रश्न 2.
‌शुष्क‌ ‌कोरडी‌ ‌
उत्तर:‌ ‌
जमीन‌ ‌

‌‌प्रश्न 3.
तक्ता‌ ‌पूर्ण‌ ‌करा.‌ ‌
उत्तर:‌ ‌

‌‌प्रश्न 4.
‌तक्ता‌ ‌पूर्ण‌ ‌करा.‌ ‌
उत्तर:‌

‌‌‌प्रश्न 5.
वाक्यातील‌ ‌काळ‌ ‌ओळखा.‌ ‌
मी‌ ‌राहत‌ ‌होतो‌ ‌त्या‌ ‌घराच्या‌ ‌मागं‌ ‌एक‌ ‌लिंबाचं‌ ‌झाड‌ ‌होतं.‌
‌उत्तर‌:‌
‌भूतकाळ‌ ‌

‌‌‌प्रश्न 6.
पर्यायी‌ ‌शब्द‌ ‌लिहा.‌ ‌
‌उत्तर‌:‌

कृती‌ ‌4: स्वमत‌ ‌

‌‌‌प्रश्न 1.
झाडे‌ ‌जीवनदायी‌ ‌असतात‌ ‌या‌ ‌विधानावर‌ ‌तुमचे‌ ‌मत‌ ‌व्यक्त‌ ‌करा.‌ ‌
उत्तरः‌ ‌
झाड‌ ‌म्हटले‌ ‌म्हणजे‌ ‌हिरवळ‌ ‌आलीच.‌ ‌हिरवा‌ ‌रंग‌ ‌हा‌ ‌समृद्धीचा‌ ‌व‌ ‌संपन्नतेने‌ ‌नटलेला‌ ‌असतो.‌ ‌झाडे‌ ‌स्वत:च‌ ‌जीवनमय‌ ‌असतात,‌ ‌ती‌ ‌जीवनदायी‌ असतात.‌ ‌स्वत:च्या‌ ‌जीवनातून‌ ‌ती‌ ‌इतरांचे‌ ‌जीवन‌ ‌फुलवित‌ ‌असतात.‌ ‌इतरांना‌ ‌जीवन‌ ‌जगण्याची‌ ‌प्रेरणा‌ ‌देत‌ ‌असतात.‌ ‌स्वत:च्या‌ ‌दातृत्वातून‌ ‌ती‌ ‌इतरांना‌ ‌जणू‌ ‌जीवनच‌ ‌दान‌ ‌करीत‌ ‌असतात.‌ ‌झाडे‌ ‌सजीवांना‌ ‌प्राणवायू‌ ‌देतात.‌ ‌फळे‌ ‌व‌ ‌फुले‌ ‌अर्पण‌ ‌करत‌ ‌असतात.‌ ‌एक‌ ‌उत्साह,‌ ‌उमंग‌ ‌व‌ ‌प्रसन्नता‌ ‌माणसाच्या‌ ‌मनात‌ ‌निर्माण‌ ‌करतात.‌ ‌त्यांच्याकडे‌ ‌पाहिले‌ ‌की,‌ ‌माणसांचे‌ ‌मन‌ ‌प्रसन्न‌ ‌व‌ ‌टवटवीत‌ ‌होते.‌ ‌अशाप्रकारे‌ ‌झाडे‌ ‌जीवनदायी‌ ‌असतात.‌ ‌

‌

पुढील‌ ‌उताऱ्याच्या‌ ‌आधारे‌ ‌दिलेल्या‌ ‌सूचनेनुसार‌ ‌कृती‌ ‌करा:‌

‌कृती‌ ‌1‌:‌ ‌आकलन‌ ‌कृती‌ ‌

प्रश्न 1‌.
आकृतिबंध‌ ‌पूर्ण‌ ‌करा.‌
उत्तरः‌ ‌

योग्य‌ ‌पर्याय‌ ‌निवडून‌ ‌विधाने‌ ‌पूर्ण‌ ‌करा.‌ ‌

प्रश्न 1.
जमिनीत‌ ‌नेमकी‌ ‌तिथंच‌ ‌ओल‌ ‌असे;‌ ‌कारण‌ ‌…………………..
(अ)‌ ‌पावसाचं‌ ‌पाणी‌ ‌सगळं‌ ‌त्या‌ ‌झाडाला‌ ‌जाई.‌
‌(ब)‌ ‌गच्चीवरचं‌ ‌पाणी‌ ‌सगळं‌ ‌त्या‌ ‌झाडाला‌ ‌जाई.‌ ‌
(क)‌ ‌मोरीचं‌ ‌पाणी‌ ‌सगळं‌ ‌त्या‌ ‌झाडाला‌ ‌जाई.‌
‌(ड)‌ ‌अंगणातलं‌ ‌पाणी‌ ‌सगळं‌ ‌त्या‌ ‌झाडाला‌ ‌जाई.‌ ‌
उत्तरः‌ ‌
जमिनीत‌ ‌नेमकी‌ ‌तिथंच‌ ‌ओल‌ ‌असे;‌ ‌कारण‌ ‌मोरीचं‌ ‌पाणी‌ ‌सगळं‌ ‌त्या‌ ‌झाडाला‌ ‌जाई.‌

प्रश्न 2.
आज‌ ‌इथं‌ ‌दिसलेला‌ ‌शंख‌ ‌उदया‌ ‌तिथं‌ ‌दिसे;‌ ‌कारण‌ ‌………‌……..
‌(अ)‌ ‌रात्रीतून‌ ‌तो‌ ‌बराच‌ ‌सरकलेला‌ ‌असे.‌
‌(ब)‌ ‌तो‌ ‌पाठीवर‌ ‌शंख‌ ‌घेत‌ ‌असे.‌
‌(क)‌ ‌तो‌ ‌रात्रीचाच‌ ‌चालत‌ ‌असे.‌ ‌
(ड)‌ ‌त्याला‌ ‌उचलून‌ ‌दुसरीकडे‌ ‌ठेवले‌ ‌जाई.‌ ‌
उत्तरः‌ ‌
आज‌ ‌इथं‌ ‌दिसलेला‌ ‌शंख‌ ‌उदया‌ ‌तिथं‌ ‌दिस;‌ ‌कारण‌ ‌रात्रीतून‌ ‌तो‌ ‌बराच‌ ‌सरकलेला‌ ‌असे.‌ ‌

उत्तरे‌ ‌लिहा.‌ ‌

प्रश्न 1.
1. ‌लेखकाचा‌ ‌आणि‌ ‌लहान‌ ‌मुलांचा‌ ‌हा‌ ‌कौतुकाचा‌ ‌कार्यक्रम‌ ‌होऊन‌ ‌बसला‌ ‌……………‌ ‌
2.‌ ‌झाडाखाली‌ ‌असणारी‌ ‌वस्ती‌ ‌…..‌……………. ‌
उत्तर:‌ ‌
1. ‌गोगलगाईंचा‌ ‌प्रवास‌ ‌निरखणं‌ ‌
2.‌ ‌गोगलगाईंची‌

जोड्या‌ ‌जुळवा.‌

प्रश्न 1.
‌जोड्या‌ ‌जुळवा.‌

उत्तर:‌ ‌

उताऱ्यानुसार‌ ‌घटनांचा‌ ‌क्रम‌ ‌लावा.‌

प्रश्न 1.

1. लहान-मोठे‌ ‌अनेक‌ ‌शंख‌ ‌मग‌ ‌दिसून‌ ‌येऊ‌ ‌लागले.‌ ‌
2. ‌मोरीचं‌ ‌पाणी‌ ‌सगळं‌ ‌त्या‌ ‌झाडाला‌ ‌जाई.‌ ‌
3. ‌त्या‌ ‌ओलसर‌ ‌जमिनीत‌ ‌मला‌ ‌काही‌ ‌शंख‌ ‌दिसू‌ ‌लागले.‌ ‌
4. ‌त्यामुळे‌ ‌जमिनीत‌ ‌नेमकी‌ ‌तिथंच‌ ‌ओल‌ ‌असे.‌ ‌

उत्तर:‌ ‌

1. मोरीचं‌ ‌पाणी‌ ‌सगळं‌ ‌त्या‌ ‌झाडाला‌ ‌जाई.‌ ‌
2. ‌त्यामुळे‌ ‌जमिनीत‌ ‌नेमकी‌ ‌तिथंच‌ ‌ओल‌ ‌असे.‌
3. ‌त्या‌ ‌ओलसर‌ ‌जमिनीत‌ ‌मला‌ ‌काही‌ ‌शंख‌ ‌दिसू‌ ‌लागले.‌ ‌
4. ‌लहान-मोठे‌ ‌अनेक‌ ‌शंख‌ ‌मग‌ ‌दिसून‌ ‌येऊ‌ ‌लागले.‌

‌खालील‌ ‌प्रश्नांची‌ ‌उत्तरे‌ ‌एका‌ ‌वाक्यात‌ ‌लिहा.‌‌

प्रश्न 1.
फांदीवरील‌ ‌गोगलगाई‌ ‌कोणत्या‌ ‌रंगानं‌ ‌बरबटलेल्या‌ ‌असत?‌ ‌
उत्तरः‌ ‌
फांदीवरील‌ ‌गोगलगाई‌ ‌चिकट‌ ‌रंगानं‌ ‌बरबटलेल्या‌ ‌असत.‌

प्रश्न 2.
‌लिंबाचं‌ ‌झाड‌ ‌कोणाच्या‌ ‌दिलाशाचं‌ ‌केंद्र‌ ‌झालं‌ ‌होतं?‌ ‌
उत्तर:‌ ‌
लिंबाचं‌ ‌झाड‌ ‌सजीवांच्या‌ ‌दिलाशाचं‌ ‌केंद्र‌ ‌झालं‌ ‌होतं.‌ ‌

प्रश्न 3.
लिंबाखालच्या‌ ‌ओलसर‌ ‌जमिनीत‌ ‌लेखकाला‌ ‌कोणता‌ ‌सजीव‌ ‌दिसला?
उत्तरः‌
‌लिंबाखालच्या‌ ‌ओलसर‌ ‌जमिनीत‌ ‌लेखकाला‌ ‌शंख‌ ‌हा‌ ‌सजीव‌ ‌दिसला.‌ ‌

कंसातील‌ ‌योग्य‌ ‌शब्द‌ ‌वापरून‌ ‌रिकाम्या‌ ‌जागा‌ ‌भरा.‌

प्रश्न 1.
1.‌ ‌गोगलगाई‌ ‌शंख‌ ‌……………… घेऊन‌ ‌चालतात.‌ ‌ (मानेवर,‌ ‌खांदयावर,‌ ‌पायांवर,‌ ‌पाठीवर)‌
2. ‌त्या‌ ‌झाडाखाली‌ ‌…………..‌ ‌सावली‌ ‌असे.‌ ‌ (काळीकुट्ट,‌ ‌काळीमिट्ट,‌ ‌काळीभोर,‌ ‌काळीकुळकुळीत)‌ ‌
उत्तर:‌ ‌
1. ‌पाठीवर‌ ‌
2.‌ ‌काळीभोर‌ ‌

सहसंबंध‌ ‌लिहा.‌ ‌

प्रश्न 1.
दिलाशाचं‌ ‌:‌ ‌केंद्र‌ ‌::‌ ‌काळीभोर‌ ‌:‌ ‌………..‌ ‌
उत्तर‌‌:‌
‌सावली.‌ ‌

कृती‌ ‌2‌:‌ ‌आकलन‌ ‌कृती‌ ‌

प्रश्न 1.
कोण‌ ‌ते‌ ‌लिहा.‌ ‌
गोगलगाईंचा‌ ‌प्रवास‌ ‌पाहणारे.‌
उत्तर‌:‌
‌लेखक‌ ‌आणि‌ ‌लहान‌ ‌मुले.‌

प्रश्न 2.
आकृतिबंध‌ ‌पूर्ण‌ ‌करा.‌
उत्तर‌:‌

प्रश्न 3.‌
चूक‌ ‌की‌ ‌बरोबर‌ ‌ते‌ ‌लिहा.‌ ‌
1. त्यामुळे‌ ‌जमिनीत‌ ‌नेमकी‌ ‌तिथंच‌ ‌ओल‌ ‌असे.‌ ‌
2. ‌आज‌ ‌इथं‌ ‌दिसलेला‌ ‌शंख‌ ‌उदया‌ ‌दिसेनासा‌ ‌होई.‌ ‌
उत्तर:‌
‌1.‌ ‌बरोबर‌
2.‌ ‌चूक‌

‌कृती‌ 3:‌ ‌व्याकरण‌ ‌कृती‌ ‌

खालील‌ ‌वाक्ये‌ ‌लेखननियमांनुसार‌ ‌शुद्ध‌ ‌करून‌ ‌लिहा.‌ ‌

प्रश्न 1.‌
‌रात्रितून‌ ‌तो‌ ‌बराच‌ ‌सकरलेला‌ ‌असे.‌ ‌
उत्तरः‌
‌रात्रीतून‌ ‌तो‌ ‌बराच‌ ‌सरकलेला‌ ‌असे.‌

प्रश्न 2.‌
त्यामुळं‌ ‌जमीनीत‌ ‌नेमकि‌ ‌तिथंच‌ ‌ओल‌ ‌असे.
उत्तरः‌ ‌
त्यामुळे‌ ‌जमिनीत‌ ‌नेमकी‌ ‌तिथंच‌ ‌ओल‌ ‌असे.‌

‌उताऱ्यातील‌ ‌दोन‌ ‌सर्वनामे‌ ‌शोधून‌ ‌लिहा.‌ ‌

प्रश्न 1.‌
उताऱ्यातील‌ ‌दोन‌ ‌सर्वनामे‌ ‌शोधून‌ ‌लिहा.‌
उत्तरः‌ ‌

1. ‌माझ्या‌ ‌
2. त्या‌
3. ‌मला‌ ‌
4. ‌तो‌
5. ‌मी‌ ‌
6. ‌त्यांचा‌ ‌

‌अचूक‌ ‌शब्द‌ ‌लिहा.‌

प्रश्न 1.‌
1. दिलशाचं,‌ ‌दीलशाचं,‌ ‌दिलाशाचं,‌ ‌दिलाशचं‌ ‌(ii)‌ ‌कोतुकाचा,‌ ‌
2. कौतुकाचा,‌ ‌कौतूकाचा,‌ ‌कौतुकचा‌ ‌
उत्तर‌:‌
1. दिलाशाचं‌
2. कौतुकाचा‌ ‌

‌समानार्थी‌ ‌शब्द‌ ‌लिहा.‌ ‌

प्रश्न 1.‌

1. जल‌ ‌-‌ ‌[ ]
2. निशा‌ ‌-‌ [ ]
3. वसाहत‌ ‌-‌ ‌[ ]
4. छाया‌ ‌-‌ ‌[ ]

‌उत्तर:‌

1. पाणी‌ ‌
2. ‌रात्र‌ ‌
3. वस्ती‌
4. सावली‌ ‌

‌विरुद्धार्थी‌ ‌शब्द‌ ‌लिहा.‌

प्रश्न 1.‌

1. ‌खोटं‌ ‌× [ ]
2. दिवस‌ ‌× [ ]
3. निंदा‌ ‌× [ ]
4. वर‌ × [ ]

उत्तर:‌ ‌

1. खरं‌
2. रात्र‌
3. ‌कौतुक‌ ‌
4. ‌खाली‌ ‌

उताऱ्यातील‌ ‌अनेकवचनी‌ ‌शब्द‌ ‌शोधून‌ ‌लिहा.‌ ‌

प्रश्न 1.‌
उताऱ्यातील‌ ‌अनेकवचनी‌ ‌शब्द‌ ‌शोधून‌ ‌लिहा.‌ ‌
उत्तरः‌
‌शंख‌

प्रश्न 2.‌ ‌
तक्ता‌ ‌पूर्ण‌ ‌करा.‌ ‌
उत्तरः‌

प्रश्न 3.‌ ‌
तक्ता‌ ‌पूर्ण‌ ‌करा.‌ ‌
उत्तरः‌

प्रश्न 4.‌ ‌
अधोरेखित‌ ‌शब्दांच्या‌ ‌जाती‌ ‌ओळखा.‌
1. आज‌ ‌इथं‌ ‌दिसलेला‌ ‌शंख‌ ‌उदया‌ ‌तिथं‌ ‌दिसे.‌ ‌
2.‌ ‌त्यांचा‌ ‌प्रवास‌ ‌निरखणं‌ ‌हा‌ ‌माझा‌ ‌आणि‌ ‌लहान‌ ‌मुलांचा‌ ‌कौतुकाचा‌ ‌कार्यक्रम‌ ‌होऊन‌ ‌बसला‌ ‌होता.‌ ‌
उत्तर‌:‌
1. ‌नाम‌ ‌
2. ‌सर्वनाम‌

प्रश्न 5.‌ ‌
वाक्यातील‌ ‌काळ‌ ‌ओळखा.‌ ‌
त्यांचा‌ ‌प्रवास‌ ‌निरखणं‌ ‌हा‌ ‌माझा‌ ‌आणि‌ ‌लहान‌ ‌मुलांचा‌ ‌कौतुकाचा‌ ‌कार्यक्रम‌ ‌होऊन‌ ‌बसला‌ ‌होता.‌
‌उत्तरः‌ ‌
भूतकाळ‌

प्रश्न 6.‌ ‌
सहसंबंध‌ ‌लिहा.‌ ‌
मला‌ ‌:‌ ‌सर्वनाम‌ ‌::‌ ‌शंख‌ ‌:‌ ‌………‌ ‌
उत्तरः‌
‌नाम‌ ‌

प्रश्न 7.‌ ‌
पर्यायी‌ ‌शब्द‌ ‌लिहा.‌ ‌
उत्तरः‌

कृती‌ ‌4‌:‌ ‌स्वमत‌ ‌

प्रश्न 1.‌ ‌
वृक्ष‌ ‌व‌ ‌मानवी‌ ‌जीवन‌ ‌यांच्यातील‌ ‌परस्परसंबंधाविषयी‌ ‌तुमचे‌ ‌मत‌ ‌सोदाहरण‌ ‌स्पष्ट‌ ‌करा.
उत्तरः‌
‌वृक्ष‌ ‌व‌ ‌मानवी‌ ‌जीवन‌ ‌यांचे‌ ‌परस्परसंबंध‌ ‌अतूट‌ ‌आहेत.‌ ‌वृक्षांशिवाय‌ ‌मानवाच्या‌ ‌जीवनाची‌ ‌कल्पनाच‌ ‌करता‌ ‌येणार‌ ‌नाही.‌ ‌त्यांच्याशिवाय‌ ‌माणसाचे‌ ‌आस्तित्त्वच‌ ‌राहणार‌ ‌नाही.‌ ‌वृक्ष‌ ‌मानवास‌ ‌प्राणवायू‌ ‌देतात‌ ‌त्यामुळेच‌ ‌माणसास‌ ‌श्वसनास‌ ‌वायू‌ ‌मिळतो.‌ ‌प्राचीन‌ ‌काळापासून‌ ‌पाहिले‌ ‌तर‌ ‌आपल्या‌ ‌लक्षात‌ ‌येईल‌ ‌की,‌ ‌ऋषीमुनींनी‌ ‌याच‌ ‌वृक्षाच्या‌ ‌खाली‌ ‌बसून‌ ‌तप‌ ‌केलेले‌ ‌आहे.‌ ‌त्यांना‌ ‌दिव्यत्वाचा‌ ‌साक्षात्कार‌ ‌या‌ ‌वृक्षामुळेच‌ ‌झालेला‌ ‌आहे.‌ ‌गौतम‌ ‌बुद्धांना‌ ‌ज्ञान‌ ‌बोधिसत्व‌ ‌वृक्षांच्या‌ ‌खालीच‌ ‌मिळाले‌ ‌आहे.‌ ‌तुकोबांनी‌ ‌आपली‌ ‌अभंगरचना‌ ‌वृक्षाच्या‌ ‌सान्निध्यात‌ ‌बसूनच‌ ‌लिहिलेली‌ ‌आहे.‌ ‌’वृक्षवल्ली‌ ‌आम्हा‌ ‌सोयरी’‌ ‌असे‌ ‌ते‌ ‌आनंदाने‌ ‌म्हणतात.‌ ‌

पुढील‌ ‌उताऱ्याच्या‌ ‌आधारे‌ ‌दिलेल्या‌ ‌सूचनेनुसार‌ ‌कृती‌ ‌करा:‌ ‌

कृती‌ ‌1‌:‌ ‌आकलन‌ ‌कृती‌

प्रश्न 1.‌ ‌
‌आकृतिबंध‌ ‌पूर्ण‌ ‌करा.‌
उत्तरः‌

‌उत्तरे‌ ‌लिहा.‌ ‌

प्रश्न 1.‌
‌त्यांच्यामुळे‌ ‌झाड‌ ‌नेहमी‌ ‌गजबजलेलं‌ ‌असे.‌ ‌
उत्तर:‌
‌चिमण्या‌ ‌आणि‌ ‌इतर‌ ‌पक्षी‌ ‌

प्रश्न 2.‌
लिंबाच्या‌ ‌काटेरी‌ ‌झाडात‌ ‌घरटे‌ ‌बांधणारी‌ ‌जोडी.‌ ‌
उत्तरः‌
‌पारव्याची‌ ‌

प्रश्न 3.‌
‌जोड्या‌ ‌जुळवा.‌

‌उत्तर:‌

प्रश्न 4.
उताऱ्यानुसार‌ ‌घटनांचा‌ ‌क्रम‌ ‌लावा.‌ ‌

1. मग‌ ‌ते‌ ‌जोडपं‌ ‌हळूहळू‌ ‌दिसेनासं‌ ‌झालं.‌ ‌
2. त्या‌ ‌जोडीनं‌ ‌काड्याकाड्यांचं‌ ‌एक‌ ‌घरटं‌ ‌त्या‌ ‌लिंबाच्या‌ ‌काटेरी‌ ‌झाडात‌ ‌बांधायला‌ ‌सुरुवात‌ ‌केली.‌ ‌
3. लेखकाचा‌ ‌मुलगा‌ ‌तिथं‌ ‌वारंवार‌ ‌जाऊन‌ ‌पाही.‌
4. ‌लवकरच‌ ‌एक‌ ‌पारव्याची‌ ‌जोडी‌ ‌त्या‌ ‌गर्द‌ ‌हिरव्या‌ ‌आश्चर्यात‌ ‌दिलासा‌ ‌शोधू‌ ‌लागली.‌ ‌

उत्तर‌:‌

1. लवकरच‌ ‌एक‌ ‌पारव्याची‌ ‌जोडी‌ ‌त्या‌ ‌गर्द‌ ‌हिरव्या‌ ‌आश्चर्यात‌ ‌दिलासा‌ ‌शोधू‌ ‌लागली.‌
2. ‌त्या‌ ‌जोडीनं‌ ‌काड्याकाड्यांचं‌ ‌एक‌ ‌घरटं‌ ‌त्या‌ ‌लिंबाच्या‌ ‌काटेरी‌ ‌झाडात‌ ‌बांधायला‌ ‌सुरुवात‌ ‌केली.‌ ‌
3. लेखकाचा‌ ‌मुलगा‌ ‌तिथं‌ ‌वारंवार‌ ‌जाऊन‌ ‌पाही.‌ ‌
4. ‌मग‌ ‌ते‌ ‌जोडपं‌ ‌हळूहळू‌ ‌दिसेनासं‌ ‌झालं.‌

खालील‌ ‌प्रश्नांची‌ ‌उत्तरे‌ ‌एका‌ ‌वाक्यात‌ ‌लिहा.‌ ‌

प्रश्न 1.
गर्द‌ ‌हिरव्या‌ ‌आश्चर्यात‌ ‌कोण‌ ‌दिलासा‌ ‌शोधू‌ ‌लागली?‌ ‌
उत्तर‌‌:‌
‌एक‌ ‌पारव्याची‌ ‌जोडी‌ ‌गर्द‌ ‌हिरव्या‌ ‌आश्चर्यात‌ ‌दिलासा‌ ‌शोधू‌ ‌लागली.‌ ‌

प्रश्न 2.
पारव्याचं‌ ‌जोडपं‌ ‌हळूहळू‌ ‌दिसेनासं‌ ‌का‌ ‌झालं?‌ ‌
उत्तर‌‌:‌
‌लेखकाचा‌ ‌मुलगा‌ ‌वारंवार‌ ‌त्यांना‌ ‌जाऊन‌ ‌पाही‌ ‌म्हणून‌ ‌मग‌ ‌ते‌ ‌जोडपं‌ ‌हळूहळू‌ ‌दिसेनासं‌ ‌झालं.‌

प्रश्न 3.
लिंबाच्या‌ ‌झाडाजवळ‌ ‌नेहमी‌ ‌कोणते‌ ‌पक्षी‌ ‌दिसत?‌ ‌
उत्तर‌‌:‌
‌लिंबाच्या‌ ‌झाडाजवळ‌ ‌नेहमी‌ ‌तुरेदार‌ ‌बुलबुल‌ ‌आणि‌ ‌पोपट‌ ‌हे‌ ‌पक्षी‌ ‌दिसत.‌ ‌

‌कंसातील‌ ‌योग्य‌ ‌शब्द‌ ‌वापरून‌ ‌रिकाम्या‌ ‌जागा‌ ‌भरा.‌

प्रश्न 1.
‌1.‌ ‌जणू‌ ‌गातं‌ ‌बहरतं‌ ‌…………. झाड.‌ ‌(लययुक्त,‌ ‌सुरेल,‌ ‌संगीतमय,‌ ‌तालयुक्त)‌ ‌
2.‌ ‌लुकलुकत्या‌ ‌नजरेची‌ ‌………….‌ ‌दृष्टीस‌ ‌पडे‌ ‌‌(चिमणी,‌ ‌पारवी,‌ ‌बुलबुल,‌ ‌लांडोर)‌ ‌
उत्तर:‌
‌1.‌ ‌संगीतमय‌ ‌
2.‌ ‌पारवी‌ ‌

सहसंबंध‌ ‌लिहा.‌

प्रश्न 1.
1. ‌लुकलुकती‌ ‌:‌ ‌नजर‌ ‌::‌ ‌बहरतं‌ ‌:‌ ‌……………….
2.‌ ‌शेवट‌ ‌:‌ ‌सुरुवात‌ ‌::‌ ‌थंड‌ ‌:‌ ‌……………………..
उत्तर:‌
1.‌ ‌झाड‌
‌2.‌ ‌तप्त‌

प्रश्न 2.
शब्दजाल‌ ‌पूर्ण‌ ‌करा.‌ ‌
उत्तर:‌

कृती‌ ‌2‌:‌ ‌आकलन‌ ‌कृती‌

प्रश्न 1.
योग्य‌ ‌पर्याय‌ ‌निवडून‌ ‌विधान‌ ‌पूर्ण‌ ‌करा.‌ ‌
ते‌ ‌जोडपं‌ ‌हळूहळू‌ ‌दिसेनासं‌ ‌झालं;‌ ‌कारण‌ ‌…………………
(अ) माझा‌ ‌मुलगा‌ ‌तिथं‌ ‌वारंवार‌ ‌जाऊन‌ ‌पाही.‌ ‌
(ब) झाड‌ ‌हळूहळू‌ ‌सुकत‌ ‌गेलं.‌
‌(क)‌ ‌लोक‌ ‌वारंवार‌ ‌तिथं‌ ‌जाऊन‌ ‌पाहत.‌ ‌
(ड) उन्हाळा‌ ‌वाढत‌ ‌गेला.‌ ‌
उत्तर‌:‌
‌ते‌ ‌जोडपं‌ ‌हळूहळू‌ ‌दिसेनासं‌ ‌झालं;‌ ‌कारण‌ ‌माझा‌ ‌मुलगा‌ ‌तिथं‌ ‌वारंवार‌ ‌जाऊन‌ ‌पाही.‌

प्रश्न 2.
‌आकृतिबंध‌ ‌पूर्ण‌ ‌करा.‌ ‌
उत्तर‌:‌

चूक‌ ‌की‌ ‌बरोबर‌ ‌ते‌ ‌लिहा.‌ ‌

प्रश्न 1.
1. ‌तुरेदार‌ ‌पोपट‌ ‌आणि‌ ‌बुलबुल‌ ‌नेहमी‌ ‌तिथं‌ ‌दिसत.‌ ‌
2.‌ ‌मग‌ ‌जोडपं‌ ‌हळूहळू‌ ‌दिसेनासं‌ ‌झालं.‌
उत्तर:‌
1. चूक‌
2. ‌बरोबर‌ ‌

कृती‌ ‌3 ‌:‌ ‌व्याकरण‌ ‌कृती‌ ‌

प्रश्न 1.
खालील‌ ‌वाक्य‌ ‌लेखननियमांनुसार‌ ‌शुद्ध‌ ‌करून‌ ‌लिहा.‌ ‌चिमन्या‌ ‌आणि‌ ‌इतर‌ ‌पक्षी‌ ‌यांनी‌ ‌ते‌ ‌झाड‌ ‌नेहमि‌ ‌गजबजलेलं‌ ‌असे.‌ ‌
उत्तर:‌
‌चिमण्या‌ ‌आणि‌ ‌इतर‌ ‌पक्षी‌ ‌यांनी‌ ‌ते‌ ‌झाड‌ ‌नेहमी‌ ‌गजबजलेलं‌ ‌असे.‌ ‌

प्रश्न 2.
उताऱ्यातील‌ ‌दोन‌ ‌विशेषणे‌ ‌शोधून‌ ‌लिहा.‌ ‌
उत्तर:‌

1. ‌एक‌ ‌
2. ‌गर्द‌ ‌
3. काटेरी‌ ‌
4.  ‌गुंजांच्या‌ ‌
5. लुकलुकत्या
6. संगीतमय
7. तुरेदार
8. आश्वसनाचं‌ ‌
9. विश्वासाचं‌ ‌
10. अनेक‌
11. एकमेव‌ ‌

‌अचूक‌ ‌शब्द‌ ‌लिहा.‌

‌प्रश्न 1.
आस्वासन,‌ ‌आश्वाशन,‌ ‌आश्वासन,‌ ‌अश्वासन‌ ‌
उत्तर‌‌:‌
‌आश्वासन‌ ‌

‌प्रश्न 2.
लुकलुकत्या,‌ ‌लूकलूकत्या,‌ ‌लुकलुकत्या,‌ ‌लुकलकूत्या‌ ‌
उत्तर‌:‌ ‌
लुकलुकत्या‌

‌समानार्थी‌ ‌शब्द‌ ‌लिहा.‌ ‌

‌प्रश्न 1.

1. ‌दरवाजा‌ ‌-‌ ‌[ ] ‌
2. बाट‌ ‌-‌ ‌[ ]
3. ‌नयन‌ ‌- [ ]
4. नेहमी‌ ‌- [ ]

उत्तर:‌

1. ‌‌दार‌ ‌
2. ‌गर्दै‌
3. ‌डोळे‌
4. ‌वारंवार‌ ‌

‌विरुद्धार्थी‌ ‌शब्द‌ ‌लिहा.‌

‌प्रश्न 1.

1. ‌शेवट‌ ‌×
2. ‌गरम‌ ‌×
3. ‌कधीकपी‌ ‌×
4. ‌भरभर‌ ‌×‌ ‌

उत्तर:‌

1. सुरुवात‌
2. ‌थंड‌
3. ‌नेहमी‌ ‌
4. ‌हळूहळू‌ ‌

‌प्रश्न 6.
‌उत्ताऱ्यातील‌ ‌दोन‌ ‌अनेकवचनी‌ ‌शब्द‌ ‌शोधून‌ ‌लिहा.‌ ‌
उत्तर:‌
1. ‌चिमण्या‌
2.‌ ‌पक्षी‌

अधोरेखित‌ ‌शब्दांच्या‌ ‌जाती‌ ‌ओळखा.‌ ‌

‌प्रश्न 7.
लुकलुकत्या‌ ‌नजरेची‌ ‌पारवी‌ ‌दृष्टीस‌ ‌पडे‌ ‌
उत्तर:‌
‌विशेषम‌ ‌

‌प्रश्न 8.
तुरेवर‌ ‌बुलबुल‌ ‌आणि‌ ‌पोपट‌ ‌नेहमी‌ ‌तिथं‌ ‌दिसत.‌ ‌
उत्तर:‌ ‌
उभयान्वयी‌ ‌अव्यय‌

‌

प्रश्न 9.
तक्ता‌ ‌पूर्ण‌ ‌करा.‌ ‌
उत्तर:‌ ‌

‌प्रश्न 10.
‌तक्ता‌ ‌पूर्ण‌ ‌करा.‌ ‌
उत्तर:‌ ‌

‌प्रश्न 11.
‘आश्वासन‌ ‌देणे’‌ ‌या‌ ‌वाक्प्रचाराचा‌ ‌अर्थ‌ ‌लिहून‌ ‌वाक्यात‌ ‌उपयोग‌ ‌करा.‌
‌उत्तर:‌ ‌
आश्वासन‌ ‌देणे‌ ‌-‌ ‌हमी‌ ‌देणे‌ ‌
बाक्य:‌ ‌निवडणूक‌ ‌जवळ‌ ‌आल्याने‌ ‌नेतेमंडळी‌ ‌कोरडी‌ ‌आश्वासने‌ ‌देत‌ ‌होती.‌

‌प्रश्न 12.
खालील‌ ‌वाक्यात‌ ‌अधोरेखित‌ ‌शब्दांऐवजी‌ ‌पाठात‌ ‌आलेला‌ ‌योग्य‌ ‌वाक्प्रचार‌ ‌शोधून‌ ‌वाक्य‌ ‌पुन्हा‌ ‌लिहा.‌ ‌
गुंजांच्या‌ ‌डोळयांची,‌ ‌लुकलुकत्या‌ ‌नजरेची‌ ‌परवी‌ ‌नजरेस‌ ‌पडे.‌ ‌
उत्तरः‌
‌गुंजांच्या‌ ‌डोळांची,‌ ‌लुकलुकत्या‌ ‌नजरेची‌ ‌पारवी‌ ‌दृष्टीस‌ ‌पडे.‌ ‌

‌प्रश्न 13.
वान्यातील‌ ‌काळ‌ ‌ओळखा.‌ ‌
भोवतालच्या‌ ‌रखरखीतून‌ ‌त्या‌ ‌जोडीनं‌ ‌एक‌ ‌थंड‌ ‌असा‌ ‌आश्रय‌ ‌शोधून‌ ‌काढला‌ ‌होता,‌ ‌
उत्तर:‌
‌भूतकाळ‌ ‌

‌प्रश्न 14.
भविष्यकाळ‌ ‌करा.‌ ‌
तुरेवार‌ ‌बुलबुल‌ ‌अपि‌ ‌पोपट‌ ‌नेहमी‌ ‌विच‌ ‌दिसत.‌ ‌
उत्तरः‌
‌तुरेवर‌ ‌बुलबुल‌ ‌अपि‌ ‌पोपट‌ ‌नेहमी‌ ‌तिच‌ ‌दिसतील.‌ ‌

कृती‌ ‌4‌ ‌:‌ ‌स्वमत‌

प्रश्न 1.
झाई‌ ‌जणू‌ ‌पक्ष्यांना‌ ‌जगण्यासाठी‌ ‌नवं‌ ‌आश्वासक‌ ‌निमंत्रण‌ ‌देतात‌ ‌या‌ ‌विधानावर‌ ‌तुमचे‌ ‌स्वमत‌ ‌लिहा.‌ ‌
उत्तरः‌
‌झाडे‌ ‌आणि‌ ‌पक्षी‌ ‌यांचे‌ ‌एकमेकांशी‌ ‌अतूट‌ ‌नाते‌ ‌असते.‌ ‌रेशमाचे‌ ‌बंधच‌ ‌जणू‌ ‌त्यांच्यात‌ ‌गुरफटलेले‌ ‌असतात,‌ ‌पक्षी‌ ‌वातावरणात‌ ‌विहार‌ ‌करतात.‌ ‌झाड‌ ‌हेव‌ ‌त्यांचे‌ ‌वित्रामाचे‌ ‌व‌ ‌वास्तव्याचे‌ ‌विकाण‌ ‌असते.‌ ‌सर्व‌ ‌पक्षी‌ ‌झाडांवर‌ ‌बसून‌ ‌किलबिलाट‌ ‌करतात‌ ‌तेक्का‌ ‌असे‌ ‌वाटते‌ ‌की,‌ ‌जणू‌ ‌पक्ष्यांची‌ ‌शाळाच‌ ‌भरलेली‌ ‌आहे.‌ ‌ऊन‌ ‌वारा‌ ‌व‌ ‌पाऊस‌ ‌यांचसून‌ ‌स्वत:चे‌ ‌रक्षण‌ ‌करण्यासाठी‌ ‌पक्षी‌ ‌झाडांवर‌ ‌आपली‌ ‌घरटी‌ ‌बांधतात.‌ ‌झाडाची‌ ‌फळे‌ ‌खातात.‌ ‌झाड‌ ‌हेच‌ ‌त्यांच्या‌ ‌संरक्षणाचे‌ ‌एकमेव‌ ‌साधन‌ ‌असते.‌ ‌जणू‌ ‌झाडेच‌ ‌हिरवीगार‌ ‌होऊन‌ ‌डोलत‌ ‌त्यांना‌ ‌आपल्याकडे‌ ‌बोलावत‌ ‌असतात.‌

पुढील‌ ‌उताऱ्याच्या‌ ‌आधारे‌ ‌दिलेल्या‌ ‌सूचनेनुसार‌ ‌कृती‌ ‌करा:‌

‌कृती‌ 1 ‌:‌ ‌आकलन‌ ‌कृती‌

प्रश्न 1.
आकृतिबंध‌ ‌पूर्ण‌ ‌करा.‌ ‌
उत्तरः‌

उत्तरे‌ ‌लिहा.‌ ‌

प्रश्न 1.
‌लेखकाला‌ ‌झाडाच्या‌ ‌बाबतीत‌ ‌हे‌ ‌पहायला‌ ‌मिळाले‌ ‌नाही.‌ ‌
उत्तर‌:‌
‌फुलांपासून‌ ‌ते‌ ‌फळांपर्यंतचा‌ ‌सगळा‌ ‌जीवनप्रवास‌

प्रश्न 2.
राहत्या‌ ‌घराच्या‌ ‌मागे‌ ‌लिंबाचे‌ ‌झाड‌ ‌लावणारी.‌
‌उत्तरः‌
‌दाक्षिणात्य‌ ‌स्त्री‌ ‌

प्रश्न 3.
‌जोड्या‌ ‌जुळवा.‌ ‌

उत्तरः‌

‌खालील‌ ‌प्रश्नांची‌ ‌उत्तरे‌ ‌एका‌ ‌वाक्यात‌ ‌लिहा.‌

प्रश्न 1.
झाडाखाली‌ ‌कोणाचे‌ ‌एक‌ ‌वेगळेच‌ ‌विश्व‌ ‌होते?‌ ‌
उत्तर:‌
‌झाडाखाली‌ ‌मुंग्यांचे‌ ‌एक‌ ‌वेगळेच‌ ‌विश्व‌ ‌होते.‌ ‌

प्रश्न 2.
‌कशामुळे‌ ‌झाडाभोवती‌ ‌पंखधारी‌ ‌चिमुकल्या‌ ‌पऱ्या‌ ‌उडू‌ लागल्या?‌ ‌
उत्तरः‌
‌फुलांमुळे‌ ‌झाडाभोवती‌ ‌पंखधारी‌ ‌चिमुकल्या‌ ‌पऱ्या‌ ‌उडू‌ ‌लागल्या.‌

प्रश्न 3.
लेखकाला‌ ‌केव्हा‌ ‌खिडकी‌ ‌लावून‌ ‌घ्यावी‌ ‌असे‌ ‌वाटू‌ ‌लागले?‌ ‌
उत्तरः‌
‌झाडाच्या‌ ‌फांदीवर‌ ‌मधमाश्यांनी‌ ‌छोटे‌ ‌पोळे‌ ‌रचल्यावर‌ ‌लेखकाला‌ ‌खिडकी‌ ‌लावून‌ ‌घ्यावी‌ ‌असे‌ ‌वाटू‌ ‌लागले.‌ ‌

प्रश्न 4.
‌लिंबाच्या‌ ‌झाडाची‌ ‌कोणती‌ ‌व्याख्या‌ ‌झाली‌ ‌होती?‌ ‌
उत्तर:‌ ‌
‘सजीवांसाठी‌ ‌जीवनदायी‌ ‌केंद्र’‌ ‌अशी‌ ‌लिंबाच्या‌ ‌झाडाची‌ ‌व्याख्या‌ ‌झाली‌ ‌होती.‌ ‌

प्रश्न 5.
लिंबाचे‌ ‌झाड‌ ‌लावलेल्या‌ ‌स्त्रीनं‌ ‌त्याला‌ ‌कशाच्या‌ ‌मर्यादा‌ ‌घातल्या‌ ‌नव्हत्या?‌ ‌
उत्तर:‌
‌लिंबाचे‌ ‌झाड‌ ‌लावलेल्या‌ ‌स्त्रीनं‌ ‌त्याला‌ ‌कडूपणाच्या‌ ‌आणि‌ ‌कंजुषीच्या‌ ‌मर्यादा‌ ‌घातलेल्या‌ ‌नव्हत्या.

कंसातील‌ ‌योग्य‌ ‌शब्द‌ ‌वापरून‌ ‌रिकाम्या‌ ‌जागा‌ ‌भरा.‌ ‌

प्रश्न 1.
1. …………….‌ ‌लगडलेलं‌ ‌ते‌ ‌झाड‌ ‌दृष्ट‌ ‌लागण्यासारखं‌ ‌होतं.‌ ‌(फुलांनी,‌ ‌फळांनी,‌ ‌फांदयांनी,‌ ‌फुलपाखरांनी)‌ ‌
2.‌ ‌फुलांमुळे‌ ‌लवकरच‌ ‌त्या‌ ‌झाडाभोवती‌ ‌पंखधारी‌ ‌चिमुकल्या‌ ‌………………..‌ ‌उडू‌ ‌लागल्या.‌ ‌(चेटकिणी,‌ ‌पऱ्या,‌ ‌चिमण्या,‌ ‌लांडोरी)‌ ‌
3. ‌एकदा‌ ‌पाहत‌ ‌असताना‌ ‌…………..‌ ‌कात‌ ‌आढळून‌ ‌आली‌ ‌(पालीची,‌ ‌पक्ष्यांची,‌ ‌मगरीची,‌ ‌सापाची)‌
‌उत्तर:‌
1. ‌फळांनी‌
2. ‌पऱ्या‌
3. ‌सापाची‌

प्रश्न ‌2.‌ ‌
सहसंबंध‌ ‌लिहा.‌ ‌
अनेकरंगी‌ ‌:‌ ‌किडे‌ ‌::‌ ‌चिमुकल्या‌ ‌:‌ ‌………‌ ‌
उत्तर:‌
‌पऱ्या‌

प्रश्न ‌3.‌ ‌
शब्दसमूहासाठी‌ ‌एक‌ ‌शब्द‌ ‌चौकटीत‌ ‌लिहा.‌ ‌
पंख‌ ‌धारण‌ ‌केलेली‌ ‌-‌ ‌[ ]
उत्तर‌‌:‌
‌पंखधारी‌ ‌

कृती‌ ‌2:‌ ‌आकलन‌ ‌कृती‌ ‌

प्रश्न 1.
योग्य‌ ‌पर्याय‌ ‌निवडून‌ ‌विधान‌ ‌पूर्ण‌ ‌करा.‌ ‌
आसपासचे‌ ‌लोक‌ ‌येत,‌ ‌लिंबाची‌ ‌फळं‌ ‌मुक्तपणे‌ ‌घेऊन‌ ‌जात,‌ ‌कारण ….‌……….. ‌
(अ)‌ ‌मुक्त-मोकळं‌ ‌झाड‌ ‌तिनं‌ ‌जणू‌ ‌कडूपणाच्या‌ ‌आणि‌ ‌कंजुषीच्या‌ ‌मर्यादा‌ ‌घातलेल्या‌ ‌नव्हत्या.‌
‌(ब) मुक्त-मोकळं‌ ‌झाड‌ ‌तिनं‌ ‌जणू‌ ‌सर्व‌ ‌बंधने‌ ‌घातली‌ ‌नव्हती.‌
(क)‌ ‌मुक्त-मोकळं‌ ‌झाड‌ ‌तिनं‌ ‌जणू‌ ‌कडूपणाच्या‌ ‌आणि‌ ‌कंजुषीच्या‌ ‌मर्यादा‌ ‌घातलेल्या‌ ‌होत्या.‌ ‌
(ड) ती‌ ‌फळेच‌ ‌रसाळ‌ ‌होती.‌ ‌
उत्तर‌:‌
‌आसपासचे‌ ‌लोक‌ ‌येत,‌ ‌लिंबाची‌ ‌फळं‌ ‌मुक्तपणे‌ ‌घेऊन‌ ‌जात,‌ ‌कारण‌ ‌मुक्त-मोकळं‌ ‌झाड‌ ‌तिनं‌ ‌जणू‌ ‌कडूपणाच्या‌ ‌आणि‌ ‌कंजुषीच्या‌ ‌मर्यादा‌ ‌घातलेल्या‌ ‌नव्हत्या.‌

प्रश्न 2.
आकृतिबंध‌ ‌पूर्ण‌ ‌करा.‌ ‌
उत्तर‌:‌

प्रश्न 3.
कोण‌ ‌ते‌ ‌लिहा.‌ ‌

1. ‌अद्भूत‌ ‌फळदार‌ ‌आश्वासन‌ ‌घेऊन‌ ‌आलेली.‌ ‌
2. ‌छोट्या‌ ‌फांदीवर‌ ‌पोळं‌ ‌रचणाऱ्या‌ ‌
3. ‌सजीवांसाठी‌ ‌जीवनदायी‌ ‌केंद्र.‌ ‌
4. ‌लिंबाचे‌ ‌झाड‌ ‌लावणारी.‌ ‌

उत्तर:‌

1. ‌फुले‌ ‌
2. ‌मधमाश्या‌ ‌
3. ‌लिंबाचे‌ ‌झाड‌ ‌
4. ‌दाक्षिणात्य‌ ‌स्त्री‌

प्रश्न 4.
आकृतिबंध‌ ‌पूर्ण‌ ‌करा.‌ ‌
उत्तर:‌

चूक‌ ‌की‌ ‌बरोबर‌ ‌ते‌ ‌लिहा.‌ ‌

प्रश्न 1.

1. ‌माणसंही‌ ‌त्या‌ ‌झाडाकडं‌ ‌आकर्षित‌ ‌होत‌ ‌होती.‌ ‌
2. ‌झाडाखाली‌ ‌मुंग्यांचंही‌ ‌एक‌ ‌वेगळंच‌ ‌विश्व‌ ‌होतं.‌ ‌
3. ‌तिनं‌ ‌त्या‌ ‌झाडाला‌ ‌कुंपण‌ ‌घातलं‌ ‌होतं.‌

‌उत्तर:‌

1. ‌बरोबर‌ ‌
2. ‌बरोबर‌
3. ‌चूक‌ ‌

कृती‌ ‌3‌:‌ ‌व्याकरण‌ ‌कृती‌ ‌

प्रश्न 1.
‌खालील‌ ‌वाक्य‌ ‌लेखननियमांनुसार‌ ‌शुद्ध‌ ‌करून‌ ‌लिहा.‌ ‌
पण‌ ‌थंड‌ ‌सावलित‌ ‌कुत्रिही‌ ‌तिथं‌ ‌विसाव्याला‌ ‌येत.‌ ‌
उत्तरः‌ ‌
पण‌ ‌थंड‌ ‌सावलीत‌ ‌कुत्रीही‌ ‌तिथं‌ ‌विसाव्याला‌ ‌येत.‌

प्रश्न 2.
‌उताऱ्यातील‌ ‌दोन‌ ‌विशेषणे‌ ‌शोधून‌ ‌लिहा.‌
‌उत्तरः‌ ‌

1. वेगळंच‌
2. ‌थंड‌ ‌
3. सगळं‌
4. ‌‌चिमुकली‌ ‌
5. वासाची‌
6. ‌अद्भूत‌ ‌
7. फळदार‌ ‌
8. छोट्या‌
9. ‌‌मागं‌
10. जीवनदायी‌ ‌
11. ‌मुक्त-मोकळं‌ ‌
12. आसपासचे‌ ‌
13. लगडलेलं‌ ‌

प्रश्न 3.
अचूक‌ ‌शब्द‌ ‌लिहा.‌
1. ‌जिवनदायी,‌ ‌जीवनदयी,‌ ‌जीवनदायी,‌ ‌जीवनदायि‌ ‌
2. ‌रंगित,‌ ‌रगीत,‌ ‌रगित,‌ ‌रंगीत‌ ‌
उत्तर:‌
1. ‌जीवनदायी‌ ‌
2. ‌रंगीत‌ ‌

प्रश्न 4. ‌
समानार्थी‌ ‌शब्द‌ ‌लिहा.‌

1. ‌छाया‌ ‌-‌ [ ]
2. ‌विश्रांती‌ ‌-‌ [ ]
3. ‌सुमन‌ ‌-‌ [ ]
4. ‌वसाहत‌ ‌-‌ ‌[ ]

उत्तर:‌

1. सावली‌
2. ‌विसावा‌ ‌
3. फूल‌
4. ‌वस्ती‌

अधोरेखित‌ ‌शब्दाचा‌ ‌समानार्थी‌ ‌शब्द‌ ‌लिहून‌ ‌वाक्य‌ ‌पुन्हा‌ ‌छाया‌ ‌लिहा.‌ ‌

प्रश्न 5.
झाडाखाली‌ ‌मुंग्यांचंही‌ ‌एक‌ ‌वेगळंच‌ ‌विश्व‌ ‌होतं.‌ ‌
उत्तरः‌
‌झाडाखाली‌ ‌मुंग्यांचंही‌ ‌एक‌ ‌वेगळंच‌ ‌जग‌ ‌होतं.‌

विरुद्धार्थी‌ ‌शब्द‌ ‌लिहा.‌ ‌

प्रश्न 6.

1. रंगहीन‌ ‌×‌
2. ‌तिखट ×
3. ‌वर‌ ‌×‌
4. ‌मोठ्या‌ ×

उत्तर:‌

1. ‌रंगीत‌ ‌
2. ‌गोड‌ ‌
3. ‌खाली‌ ‌
4. ‌छोट्या‌ ‌

प्रश्न 7.
उताऱ्यातील‌ ‌दोन‌ ‌अनेकवचनी‌ ‌शब्द‌ ‌शोधून‌ ‌लिहा.‌ ‌
उत्तर:‌ ‌

1. ‌किडे‌
2. ‌कुत्री‌ ‌
3. फुलं‌ ‌
4. पऱ्या‌
5. फुलपाखरं‌ ‌
6. ‌कीटक‌ ‌
7. ‌भुंगे‌
8. ‌फळं‌
9. ‌माणसं‌ ‌
10. ‌पशू‌ ‌
11. ‌पक्षी‌
12. ‌खारी‌
13. ‌गोगलगाई‌ ‌

प्रश्न 8.
तक्ता‌ ‌पूर्ण‌ ‌करा.‌ ‌
उत्तर:‌ ‌

प्रश्न 9.
तक्ता‌ ‌पूर्ण‌ ‌करा.‌ ‌
उत्तर:‌ ‌

प्रश्न 10. ‌
खालील‌ ‌वाक्यात‌ ‌अधोरेखित‌ ‌शब्दांऐवजी‌ ‌पाठात‌ ‌आलेला‌ ‌योग्य‌ ‌वाक्प्रचार‌ ‌शोधून‌ ‌वाक्य‌ ‌पुन्हा‌ ‌लिहा.‌
‌माणसंही‌ ‌त्या‌ ‌झाडाकडं‌ ‌ओढली‌ ‌जात‌ ‌होती.‌ ‌
‌उत्तरः‌ ‌
माणसंही‌ ‌त्या‌ ‌झाडाकडं‌ ‌आकर्षित‌ ‌होत‌ ‌होती.‌

प्रश्न 11. ‌
वाक्यातील‌ ‌काळ‌ ‌ओळखा.‌ ‌
माणसंही‌ ‌त्या‌ ‌झाडाकडं‌ ‌आकर्षित‌ ‌होत‌ ‌होती.‌ ‌
उत्तर:‌
‌भूतकाळ‌ ‌

प्रश्न 12.
काळ‌ ‌बदला.‌ ‌(भविष्यकाळ‌ ‌करा)‌ ‌
आसपासचे‌ ‌लोक‌ ‌येत,‌ ‌लिंबाची‌ ‌फळं‌ ‌मुक्तपणे‌ ‌घेऊन‌ ‌जात.‌
‌उत्तरः‌
‌आसपासचे‌ ‌लोक‌ ‌येतील,‌ ‌लिंबाची‌ ‌फळं‌ ‌मुक्तपणे‌ ‌घेऊन‌ ‌जातील.‌ ‌

प्रश्न 13.‌ ‌
सहसंबंध‌ ‌लिहा.‌ ‌
स्त्री‌ ‌:‌ ‌नाम‌ ‌::‌ ‌त्या‌ ‌:‌ ……………………
‌उत्तरः‌ ‌
सर्वनाम‌ ‌

प्रश्न 14.‌ ‌
पर्यायी‌ ‌शब्द‌ ‌लिहा.‌ ‌
‌उत्तरः‌ ‌

कृती‌ ‌4‌ ‌:‌ ‌स्वमत‌ ‌

प्रश्न 1.‌ ‌
झाड‌ ‌सजीवांसाठी‌ ‌जीवनदायी‌ ‌केंद्र‌ ‌कसे‌ ‌बनू‌ ‌शकते‌ ‌हे‌ ‌विधान‌ ‌पटवून‌ ‌दया.‌ ‌
उत्तरः‌ ‌
झाडे‌ ‌सजीवांना‌ ‌चैतन्य‌ ‌देतात.‌ ‌सजीवांची‌ ‌मते‌ ‌प्रफुल्लित‌ ‌करतात.‌ ‌झाडे‌ ‌सजीवांच्या‌ ‌जीवनात‌ ‌आल्हाददायक‌ ‌गोडवा‌ ‌निर्माण‌ ‌करण्याचे‌ ‌कार्य‌ ‌करतात.‌ ‌या‌ ‌झाडांवर‌ ‌पर्यावरणातील‌ ‌अनेक‌ ‌कीटक,‌ ‌पक्षी,‌ ‌माणसं‌ ‌व‌ ‌इतर‌ ‌प्राणी‌ ‌आश्रय‌ ‌घेतात.‌ ‌असंख्य‌ ‌पशु-पक्षी,‌ ‌साप,‌ ‌खारी‌ ‌अनेक‌ ‌प्रकारचे‌ ‌कीटक‌ ‌व‌ ‌गोगलगाईंसाठी‌ ‌झाडे‌ ‌वरदान‌ ‌ठरतात.‌ ‌या‌ ‌सर्वांच्या‌ ‌विसाव्याचे‌ ‌केंद्र‌ ‌झाडेच‌ ‌असतात.‌ ‌झाडांभोवती‌ ‌रंगीबेरंगी‌ ‌फुलपाखरे‌ ‌उडताना‌ ‌दिसतात.‌ ‌जणू‌ ‌झाडांना‌ ‌पाहूनच‌ ‌ती‌ ‌नर्तन‌ ‌करत‌ ‌आहेत.‌ ‌असे‌ ‌वाटते.‌ ‌या‌ ‌सर्व‌ ‌प्रकारच्या‌ ‌सजीवांसाठी‌ ‌झाडे‌ ‌आपले‌ ‌सर्वस्व‌ ‌बहाल‌ ‌करत‌ ‌असतात..

पुढील‌ ‌उताऱ्याच्या‌ ‌आधारे‌ ‌दिलेल्या‌ ‌सूचनेनुसार‌ ‌कृती‌ ‌करा:‌ ‌

कृती‌ ‌1 ‌:‌ ‌आकलन‌ ‌कृती‌

प्रश्न 1.‌ ‌
आकृतिबंध‌ ‌पूर्ण‌ ‌करा.‌ ‌
उत्तरः‌ ‌

प्रश्न 2.‌ ‌
उत्तरे‌ ‌लिहा.‌
1. लखकाच्या‌ ‌‌शेजारी‌ ‌राहत‌ ‌असलेल्या‌ ‌लोकांनी‌ ‌कधी‌ ‌कसला‌ ‌प्रयत्न‌ ‌केला‌ ‌नाही?
2. लेखक‌ ‌का‌ ‌चकित‌ ‌होऊन‌ ‌गेला?‌ ‌
3. ‌झाड‌ ‌लावलेली‌ ‌बाई‌ ‌आपल्यामागे‌ ‌काय‌ ‌ठेवून‌ ‌गेली?‌ ‌
उत्तर:‌
1. ‌हिरवा‌ ‌आनंद‌ ‌पसरवण्याचा‌ ‌
2. ‌झाडाला‌ ‌आलेलं‌ ‌महत्त्व‌ ‌पाहून‌ ‌
3. ‌अद्भूत‌ ‌नाट्य‌

प्रश्न 3.‌ ‌
जोड्या‌ ‌जुळवा.‌