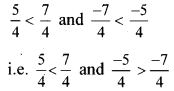Balbharti Maharashtra State Board Class 8 Maths Solutions covers the Practice Set 1.2 8th Std Maths Answers Solutions Chapter 1 Rational and Irrational Numbers.
Practice Set 1.2 8th Std Maths Answers Chapter 1 Rational and Irrational Numbers
Question 1.
Compare the following numbers.
i. 7, -2
ii. 0, \(\frac { -9 }{ 5 }\)
iii. \(\frac { 8 }{ 7 }\), 0
iv. \(-\frac{5}{4}, \frac{1}{4}\)
v. \(\frac{40}{29}, \frac{141}{29}\)
vi. \(-\frac{17}{20},-\frac{13}{20}\)
vii. \(\frac{15}{12}, \frac{7}{16}\)
viii. \(-\frac{25}{8},-\frac{9}{4}\)
ix. \(\frac{12}{15}, \frac{3}{5}\)
x. \(-\frac{7}{11},-\frac{3}{4}\)
Solution:
i. 7, -2
If a and b are positive numbers such that a < b, then -a > -b.
Since, 2 < 7 ∴ -2 > -7
ii. 0, \(\frac { -9 }{ 5 }\)
On a number line, \(\frac { -9 }{ 5 }\) is to the left of zero.
∴ 0 > \(\frac { -9 }{ 5 }\)
iii. \(\frac { 8 }{ 7 }\), 0
On a number line, zero is to the left of \(\frac { 8 }{ 7 }\) .
∴ \(\frac { 8 }{ 7 }\) > 0
iv. \(-\frac{5}{4}, \frac{1}{4}\)
We know that, a negative number is always less than a positive number.
∴ \(-\frac{5}{4}<\frac{1}{4}\)
v. \(\frac{40}{29}, \frac{141}{29}\)
Here, the denominators of the given numbers are the same.
Since, 40 < 141
∴ \(\frac{40}{29}<\frac{141}{29}\)
vi. \(-\frac{17}{20},-\frac{13}{20}\)
Here, the denominators of the given numbers are the same.
Since, 17 < 13
∴ -17 < -13
∴ \(-\frac{17}{20}<-\frac{13}{20}\)
vii. \(\frac{15}{12}, \frac{7}{16}\)
Here, the denominators of the given numbers are not the same.
LCM of 12 and 16 = 48

Alternate method:
15 × 16 = 240
12 × 7 = 84
Since, 240 > 84
∴ 15 × 16 > 12 × 7
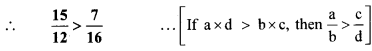
viii. \(-\frac{25}{8},-\frac{9}{4}\)
Here, the denominators of the given numbers are not the same.
LCM of 8 and 4 = 8
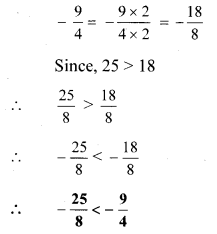
ix. \(\frac{12}{15}, \frac{3}{5}\)
Here, the denominators of the given numbers are not the same.
LCM of 15 and 5 = 15
x. \(-\frac{7}{11},-\frac{3}{4}\)
Here, the denominators of the given numbers are not the same.
LCM of 11 and 4 = 44
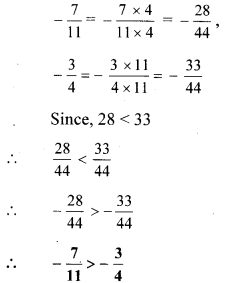
Maharashtra Board Class 8 Maths Solutions Chapter 1 Rational and Irrational Numbers Practice Set 1.2 Questions and Activities
Question 1.
Verify the following comparisons using a number line. (Textbook pg. no, .3)
i. 2 < 3 but – 2 > – 3
ii. \(\frac{5}{4}<\frac{7}{4}\) but \(\frac{-5}{4}<\frac{-7}{4}\)
Solution:

We know that, on a number line the number to the left is smaller than the other.
∴ 2 < 3 and -3 < -2
i.e. 2 < 3 and -2 > -3