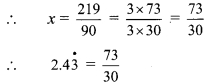Balbharti Maharashtra State Board Class 9 Maths Solutions covers the Practice Set 2.1 Algebra 9th Class Maths Part 1 Answers Solutions Chapter 2 Real Numbers.
Practice Set 2.1 Algebra 9th Std Maths Part 1 Answers Chapter 2 Real Numbers
Question 1.
Classify the decimal form of the given rational numbers into terminating and non-terminating recurring type.

Solution:
i. Denominator = 5 = 1 x 5
Since, 5 is the only prime factor denominator.
the decimal form of the rational number \(\frac { 13 }{ 5 }\) will be terminating type.
ii. Denominator = 11 = 1 x 11
Since, the denominator is other than prime factors 2 or 5.
∴ the decimal form of the rational number \(\frac { 2 }{ 11 }\) will be non-terminating recurring type.
iii. Denominator = 16
= 2 x 2 x 2 x 2
Since, 2 is the only prime factor in the denominator.
∴ the decimal form of the rational number \(\frac { 29 }{ 16 }\) will be terminating type.
iv. Denominator = 125
= 5 x 5 x 5
Since, 5 is the only prime factor in the denominator.
the decimal form of the rational number \(\frac { 17 }{ 125 }\) will be terminating type.
v. Denominator = 6
= 2 x 3
Since, the denominator is other than prime factors 2 or 5.
∴ the decimal form of the rational number \(\frac { 11 }{ 6 }\) will be non-terminating recurring type.
Question 2.
Write the following rational numbers in decimal form.
![]()
![]()
![]()
![]()
![]()
Solution:
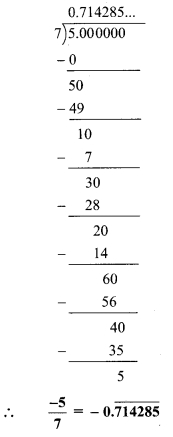
i. \(\frac { -5 }{ 7 }\)
ii. \(\frac { 9 }{ 11 }\)
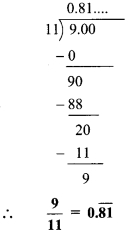
iii. √5

iv. \(\frac { 121 }{ 13 }\)
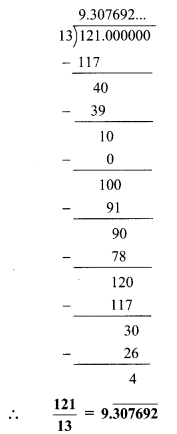
v. \(\frac { 29 }{ 8 }\)
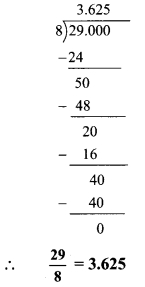
Question 3.
Write the following rational numbers in \(\frac { p }{ q }\) form.

Solution:
i. Let x = \(0.\dot { 6 }\) …(i)
∴ x = 0.666…
Since, one number i.e. 6 is repeating after the decimal point.
Thus, multiplying both sides by 10,
10x = 6.666…
∴ 10 x 6.6 …(ii)
Subtracting (i) from (ii),
10x – x = 6.6 – 0.6
∴ 9x = 6
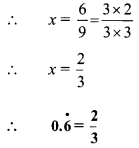
ii. Let x = \(0.\overline { 37 }\)
∴ x = 0.3737…
Since, two numbers i.e. 3 and 7 are repeating after the decimal point.
Thus, multiplying both sides by 100,
100x = 37.3737……
∴ 100x = \(37.\overline { 37 }\) ……(ii)
Subtracting (i) from (ii),
100x – x = \(37.\overline { 37 }\) – \(0.\overline { 37 }\)
∴ 99x = 37
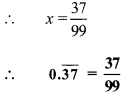
iii. Letx = \(3.\overline { 17 }\) …(i)
∴ x = 3.1717…
Since, two numbers i.e. 1 and 7 are repeating after the decimal point.
Thus, multiplying both sides by 100,
100x = 317.1717…
∴ 100x= 317.17 …(ii)
Subtracting (i) from (ii),
100x – x = \(317.\overline { 17 }\) – \(3.\overline { 17 }\)
∴ 99x = 314
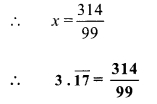
iv. Let x = \(15.\overline { 89 }\) …….. (i)
∴ x = 15.8989…
Since, two numbers i.e. 8 and 9 are repeating after the decimal point.
Thus, multiplying both sides by 100,
100x= 1589.8989…
∴ 100x = \(1589.\overline { 89 }\) …(ii)
Subtracting (i) from (ii),
100x – x = \(1589.\overline { 89 }\) – \(15.\overline { 89 }\)
∴ 99x = 1574
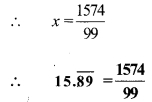
v. Let x = \(2.\overline { 514 }\)
∴ x = 2.514514…
Since, three numbers i.e. 5, 1 and 4 are repeating after the decimal point.
Thus, multiplying both sides by 1000,
1000x = 2514.514514…
1000x = \(2514.\overline { 514 }\) ….(ii)
Subtracting (i) from (ii),
1000x – x = \(2514.\overline { 514 }\) – \(2.\overline { 514 }\)
∴ 999x = 2512
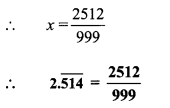
Question 1.
How to convert 2.43 in \(\frac { p }{ q }\) form ? (Textbook pg. no. 20)
Solution:
Let x = 2.43
In 2.43, the number 4 on the right side of the decimal point is not recurring.
So, in order to get only recurring digits on the right side of the decimal point, we will multiply 2.43 by 10.
∴ 10x = 24.3 …(i)
∴ 10x = 24.333…
Here, digit 3 is the only recurring digit. Thus, by multiplying both sides by 10, 100x = 243.333…
∴ 100x= 243.3 …(ii)
Subtracting (i) from (ii),
100x – 10x = 243.3 – 24.3
∴ 90x = 219