Balbharti Maharashtra State Board Class 9 Maths Solutions covers the Practice Set 3.6 Algebra 9th Class Maths Part 1 Answers Solutions Chapter 3 Polynomials.
Practice Set 3.6 Algebra 9th Std Maths Part 1 Answers Chapter 3 Polynomials
Question 1.
Find the factors of the polynomials given below:
i. 2x2 + x – 1
ii. 2m2 + 5m – 3
iii. 12x2 + 61x + 77
iv. 3y2 – 2y – 1
v. √3x2 + 4x + √3
vi. \(\frac { 1 }{ 2 }\)x2 – 3x + 4
Solution:
i. 2x2 + x – 1
= 2x2 + 2x – x – 1
= 2x(x + 1)- 1(x + 1)
= (x + 1)(2x – 1)
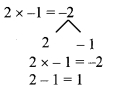
ii. 2m2 + 5m – 3
= 2m2 + 6m – m – 3
= 2m(m + 3) – 1(m + 3)
= (m + 3)(2m – 1)
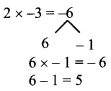
iii. 12x2 + 61x + 77
= 12x2 + 28x + 33x + 77
= 4x(3x + 7) 4 + 11(3x + 7)
= (3x + 7)(4x + 11)
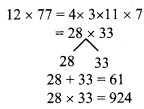
iv. 3y2 – 2y – 1
= 3y2 – 3y + y – 1
= 3y(y – 1) + 1 (y – 1)
= (y – 1)(3y + 1)
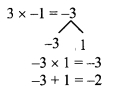
v. √3×2 + 4x + √3
= √3×2 + 3x + x + √3
= √3×2 + √3 x √3x + x + √3
= √3x(x + √3) + 1 ( x + √3 )
= (x + √3)(√3x + 1)
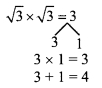
vi. \(\frac { 1 }{ 2 }\) x2 – 3x + 4
= \(\frac { 1 }{ 2 }\) x2 – 2x – x + 4
= \(\frac{1}{2} x^{2}-\frac{2 \times 2}{2} x-x+4\)
= \(\frac { 1 }{ 2 }\) x(x – 4) – 1 (x – 4)
= (x – 4) (\(\frac { 1 }{ 2 }\) x – 1)
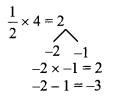
Alternate method
\(\frac { 1 }{ 2 }\) x2 – 3x + 4 = \(\frac { 1 }{ 2 }\) (x2 – 6x + 8)
= \(\frac { 1 }{ 2 }\) (x2 – 4x – 2x + 8)
= \(\frac { 1 }{ 2 }\) [x(x – 4) – 2(x – 4)]
= \(\frac { 1 }{ 2 }\) (x – 2)(x – 4)
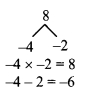
Question 2.
Factorize the following polynomials.
i. (x2 – x)2 – 8(x2 – x) + 12
iii. (x2 – 6x)2 – 8(x2 – 6x + 8) – 64
v. (y + 2) (y – 3) (y + 8) (y + 3) + 56
vii. (x – 3) (x – 4)2 (x – 5) – 6
Solution:
i. (x2 – x)2 – 8(x2 – x) + 12
= m2 – 8m + 12 …[Putting x2 – x = m]
= m2 – 6m – 2m + 12
= m(m – 6) – 2(m – 6)
= (m – 6)(m – 2)
= (x2 – x- 6) (x2 – x- 2) …[Replacing m = x2 -x]
= (x2 – 3x + 2x – 6) (x2 – 2x + x – 2)
= [x(x – 3) + 2(x – 3)] [x(x – 2) + 1 (x-2)]
= (x – 3) (x + 2) (x – 2) (x + 1)
ii. (x – 5)2 – (5x – 25) – 24
= (x – 5)2 – (5x – 25) – 24
= (x – 5)2 – 5(x – 5) – 24
= m2 – 5m – 24 … [Putting x – 5 = m]
= m2 – 8m + 3m – 24
= m(m – 8) + 3(m – 8)
= (m – 8) (m + 3)
= (x – 5 – 8) (x – 5 + 3) … [Replacing m = x – 5]
= (x – 13) (x – 2)
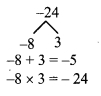
iii. (x2 – 6x)2 – 8(x2 – 6x + 8) – 64
= m2 – 8(m + 8)-64 …[Putting x2 – 6x = m]
= m2 – 8m – 64 – 64
= m2 – 8m – 128
= m2 – 16m + 8m- 128
= m(m – 16) + 8(m – 16)
= (m – 16)(m + 8)
= (x2 – 6x – 16) (x2 – 6x + 8) … [Replacing m = x2 – 6x]
= (x2 – 8x + 2x – 16) (x2 – 4x – 2x + 8)
= [x(x – 8) + 2(x – 8)] [x(x – 4) – 2(x – 4)]
= (x – 8) (x + 2) (x – 4) (x – 2)
iv. (x2– 2x + 3) (x2 – 2x + 5) – 35
= (m + 3) (m + 5) – 35 … [Putting x2 – 2x = m]
= m (m + 5) + 3(m + 5) – 35
= m2 + 5m + 3m + 15 – 35
= m2 + 8m – 20
= m2 + 10m – 2m – 20
= m(m + 10) – 2(m + 10)
= (m + 10) (m – 2)
= (x2 – 2x + 10) (x2 – 2x – 2) … [Replacing m = x2 – 2x]
v. (y + 2) (y – 3) (y + 8) (y + 3) + 56
= (y + 2)(y + 3)(y – 3)(y + 8) + 56
= (y2 + 3y + 2y + 6) (y2 + 8y – 3y – 24) + 56
= (y2 + 5y + 6) (y2 + 5y – 24) + 56
= (m + 6) (m – 24) + 56 … [Putting y2 + 5y = m]
= m (m – 24) + 6 (m – 24) + 56
= m2 – 24m + 6m – 144 + 56
= m2 – 18m – 88
= m2 – 22m + 4m – 88
= m(m – 22) + 4(m – 22)
= (m – 22) (m + 4)
= (y2 + 5y – 22)(y2 + 5y + 4) … [Replacing m = y2 + 5y]
= (y2 + 5y – 22) (y2 + 4y + y + 4)
= (y2 + 5y – 22) [y(y + 4) + 1(y + 4)]
= (y2 + 5y – 22) (y + 4) (y + 1)
vi. (y2 + 5y) (y2 + 5y – 2) – 24
= (m)(m – 2) – 24 … [Putting y2 + 5y = m]
= m2 – 2m – 24
= m2 – 6m + 4m – 24
= m(m – 6) + 4(m – 6)
= (m – 6) (m + 4)
= (y2 + 5y – 6) (y2 + 5y + 4) … [Replacing m = y2 + 5y]
= (y2 + 6y – y – 6) (y2 + 4y + y + 4)
= [y(y + 6) – 1(y + 6)] [y(y + 4) + 1(y + 4)]
= (y + 6) (y – 1) (y + 4) (y + 1)
vii. (x – 3) (x – 4)2 (x – 5) – 6
= (x – 3) (x – 5) (x – 4)2 – 6
= (x2 – 5x – 3x + 15) (x2 – 8x + 16) – 6
= (x2 – 8x + 15) (x2 – 8x + 16) – 6
= (m + 15) (m+ 16) – 6 … [Putting x2 – 8x = m]
= m (m + 16) + 15 (m + 16) – 6
= m2 + 16m + 15m + 240 – 6
= m2 + 31m + 234
= m2 + 18m + 13m + 234
= m(m + 18) + 13(m + 18)
= (m + 18) (m + 13)
= (x2 – 8x + 18) (x2 – 8x + 13) … [Replacing m = x2 – 8x]