Balbharti Maharashtra State Board Class 9 Maths Solutions covers the Practice Set 6.1 Algebra 9th Class Maths Part 1 Answers Solutions Chapter 6 Financial Planning.
Practice Set 6.1 Algebra 9th Std Maths Part 1 Answers Chapter 6 Financial Planning
Question 1.
Alka spends 90% of the money that she receives every month, and saves ₹ 120. How much money does she get monthly?
Solution:
Let Alka’s monthly income be ₹ x.
Alka spends 90% of the money that she receives every month.
∴ Amount spent by Alka = 90% of x
= \(\frac { 90 }{ 100 }\) × x = 0.9x 100
Now, Savings = Income – Expenditure
∴ 120 = x – 0.9x
∴120 = 0.1 x
∴ \(x=\frac{120}{0.1}=\frac{120 \times 10}{0.1 \times 10}\)
∴ x = 1200
Alka gets ₹ 1200 monthly.
Question 2.
Sumit borrowed a capital of ₹ 50,000 to start his food products business. In the first year he suffered a loss of 20%. He invested the remaining capital in a new sweets business and made a profit of 5%. How much was his profit or loss computed on his original capital ?
Solution:
Original capital borrowed by Sumit = ₹ 50000
Sumit suffered a loss of 20% in his food products business.
∴ Loss suffered in the first year = 20% of 50000
= \(\frac { 20 }{ 100 }\) × 50000
= ₹10000
Remaining capital = Original capital – loss suffered = 50000- 10000
= ₹ 40000
Sumit invested the remaining capital i.e. ₹ 40,000 in a new sweets business. He made a profit of 5%.
Profit in sweets business = 5% of 40000
= \(\frac { 5 }{ 100 }\) x 40000 100
= ₹ 2000
New capital with Sumit after the profit in new sweets business = 40000 + 2000 = ₹42000
Since, the new capital is less than the original capital, we can conclude that Sumit suffered a loss.
Total loss on original capital = Original capital – New capital
= 50000 – 42000 = ₹ 8000
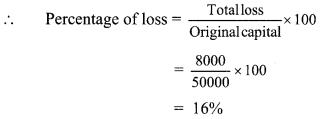
∴ Sumit suffered a loss of 16% on the original capital.
Question 3.
Nikhil spent 5% of his monthly income on his children’s education, invested 14% in shares, deposited 3% in a bank and used 40% for his daily expenses. He was left with a balance of ₹ 19,000. What was his income that month?
Solution:
Let the monthly income of Nikhil be ₹ x.
Nikhil invested 14% in shares and deposited 3% in a bank.
∴ Total investment = (14% + 3%) of x
= 17% of x
= \(\frac { 17 }{ 100 }\) × x
= 0.1 7 x
Nikhil spent 5% on his children’s education and used 40% for his daily expenses.
∴ Total expenditure = (5% + 40%) of x
= 45% of x
= \(\frac { 45 }{ 100 }\) × x
= 0.45x
Amount left with Nikhil = 19,000
Amount left with Nikhil = Income – (Total investment + Total expenditure)
∴ 19000 = x – (0.17x + 0.45x)
∴ 19000 = x – 0.62x ,
∴ 19000 = 0.38x
∴ \(x=\frac{19000}{0.38}=\frac{19000 \times 100}{0.38 \times 100}=\frac{1900000}{38}\)
= 50000
∴ The monthly income of Nikhil is ₹ 50000.
Question 4.
Mr. Sayyad kept ₹ 40,000 in a bank at 8% compound interest for 2 years. Mr. Fernandes invested ₹ 1,20,000 in a mutual fund for 2 years. After 2 years, Mr. Fernandes got ₹ 1,92,000. Whose investment turned out to be more profitable?
Solution:
Mr. Sayyad:
Mr. Sayyad kept ₹ 40,000 in a bank at 8% compound interest for 2 years P = ₹ 40000, R = 8%, n = 2 years
∴ Compound interest (I)
= Amount (A) – Principal (P)
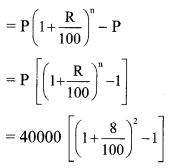
= 40000 [(1 +0.08)2 – 1]
= 40000 [(1.08)2 – 1]
= 40000(1.1664 – 1)
= 40000 (0.1664)
= ₹ 6656
∴ Mr. Sayyad’s percentage of profit Interest

Mr. Fernandes:
Amount invested by Mr. Fernandes in mutual fund = ₹ 120000
Amount received by Mr. Fernandes after 2 years = ₹ 192000
∴ Profit earned by Mr. Fernandes
= Amount received – Amount invested
= 192000- 120000
= ₹72000
∴ Mr. Fernandes percentage of profit Profit earned
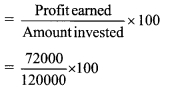
= 60%
From (i) and (ii),
Investment of Mr. Fernandes turned out to be more profitable.
Question 5.
Sameera spent 90% of her income and donated 3% for socially useful causes. If she was left with ₹ 1750 at the end of the month, what was her actual income ?
Solution:
Let the actual income of Sameera be ₹ x.
Sameera spent 90% of her income and donated 3%.
∴ Sameera’s total expenditure
= (3% + 90%) of x
= 93% of x
= \(\frac { 93 }{ 100 }\) × x
= 0.93x
Now, Savings = Income – Expenditure
∴ 1750 = x-0.93x
∴ 1750 = 0.07x
\(x=\frac{1750}{0.07}=\frac{1750 \times 100}{0.07 \times 100}=\frac{175000}{7}=25000\)
∴ The actual income of Sameera is ₹ 25000.
Maharashtra Board Class 9 Maths Chapter 6 Financial Planning Practice Set 6.1 Intext Questions and Activities
Question 1.
Amita invested some part of ₹ 35000 at 4% and the rest at 5% interest for one year. Altogether her gain was ₹ 1530. Find out the amounts she had invested at the two different rates. Write your answer in words. (Textbook pg. no. 97)
Solution:
Let the amount invested at the rate of 4% and 5% be ₹ x and ₹ y respectively.
According to the first condition, total amount invested = ₹ 35000
∴ x + y = 35000 …(i)
According to the second condition,
total interest received at 4% and 5% is ₹ 1530.
∴ 4 % of x + 5 % of y = 1530
∴ \(\frac { 4 }{ 100 }\) x x + \(\frac { 5 }{ 100 }\) x y = 1530
∴ 4x + 5y = 153000 …(ii)
Multiplying equation (i) by 4, we get
4x + 4y = 140000 …(iii)
Subtracting equation (iii) from (ii),
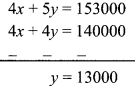
Substituting y = 13000 in equation (i),
x + 13000 = 35000
∴ x = 35000 – 13000 = 22000
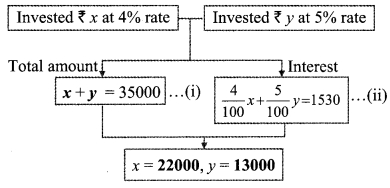
∴ Amita invested ₹ 22000 at the rate of 4% and ₹ 13000 at the rate of 5%.