Balbharti Maharashtra State Board Class 9 Maths Solutions covers the Practice Set 3.4 Geometry 9th Class Maths Part 2 Answers Solutions Chapter 3 Triangles.
Practice Set 3.4 Geometry 9th Std Maths Part 2 Answers Chapter 3 Triangles
Question 1.
In the adjoining figure, point A is on the bisector of ∠XYZ. If AX = 2 cm, then find AZ.
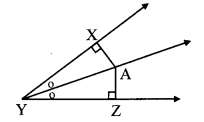
Solution:
AX = 2 cm [Given]
Point A lies on the bisector of ∠XYZ. [Given]
Point A is equidistant from the sides of ∠XYZ. [Every point on the bisector of an angle is equidistant from the sides of the angle]
∴ A Z = AX
∴ AZ = 2 cm
Question 2.
In the adjoining figure, ∠RST = 56°, seg PT ⊥ ray ST, seg PR ⊥ ray SR and seg PR ≅ seg PT. Find the measure of ∠RSP.
State the reason for your answer.
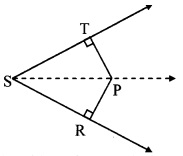
Solution:
seg PT ⊥ ray ST, seg PR ⊥ ray SR [Given]
seg PR ≅ seg PT
∴ Point P lies on the bisector of ∠TSR [Any point equidistant from the sides of an angle is on the bisector of the angle]
∴ Ray SP is the bisector of ∠RST.
∠RSP = 56° [Given]
∴ ∠RSP = \(\frac { 1 }{ 2 }\)∠RST
= \(\frac { 1 }{ 2 }\) x 56°
∴ ∠RSP = 28°
Question 3.
In ∆PQR, PQ = 10 cm, QR = 12 cm, PR triangle. 8 cm. Find out the greatest and the smallest angle of the triangle.
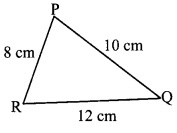
Solution:
In ∆PQR,
PQ = 10 cm, QR = 12 cm, PR = 8 cm [Given]
Since, 12 > 10 > 8
∴ QR > PQ > PR
∴ ∠QPR > ∠PRQ > PQR [Angle opposite to greater side is greater]
∴ In ∆PQR, ∠QPR is the greatest angle and ∠PQR is the smallest angle.
Question 4.
In ∆FAN, ∠F = 80°, ∠A = 40°. Find out the greatest and the smallest side of the triangle. State the reason.
Solution:
In ∆FAN,
∠F + ∠A + ∠N = 180° [Sum of the measures of the angles of a triangle is 180°]
∴ 80° + 40° + ∠N = 180°
∴ ∠N = 180° – 80° – 40°
∴∠N = 60°
Since, 80° > 60° > 40°
∴ ∠F > ∠N > ∠A
∴ AN > FA > FN [Side opposite to greater angle is greater]
∴ In ∆FAN, AN is the greatest side and FN is the smallest side.
Question 5.
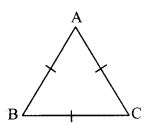
Prove that an equilateral triangle is equiangular.
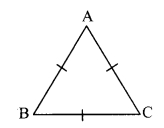
Given: ∆ABC is an equilateral triangle.
To prove: ∆ABC is equiangular
i.e. ∠A ≅ ∠B ≅ ∠C …(i) [Sides of an equilateral triangle]
In ∆ABC,
seg AB ≅ seg BC [From (i)]
∴ ∠C = ∠A (ii) [Isosceles triangle theorem]
In ∆ABC,
seg BC ≅ seg AC [From (i)]
∴ ∠A ≅ ∠B (iii) [Isosceles triangle theorem]
∴ ∠A ≅ ∠B ≅ ∠C [From (ii) and (iii)]
∴ ∆ABC is equiangular.
Question 6.
Prove that, if the bisector of ∠BAC of ∆ABC is perpendicular to side BC, then AABC is an isosceles triangle.
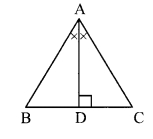
Given: Seg AD is the bisector of ∠BAC.
seg AD ⊥ seg BC
To prove: AABC is an isosceles triangle.
Proof.
In ∆ABD and ∆ACD,
∠BAD ≅ ∠CAD [seg AD is the bisector of ∠BAC]
seg AD ≅ seg AD [Common side]
∠ADB ≅ ∠ADC [Each angle is of measure 90°]
∴ ∆ABD ≅ ∆ACD [ASA test]
∴ seg AB ≅ seg AC [c. s. c. t.]
∴ ∆ABC is an isosceles triangle.
Question 7.
In the adjoining figure, if seg PR ≅ seg PQ, show that seg PS > seg PQ.
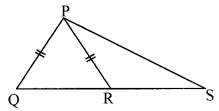
Solution:
Proof.
In ∆PQR,
seg PR ≅ seg PQ [Given]
∴ ∠PQR ≅ ∠PRQ ….(i) [Isosceles triangle theorem]
∠PRQ is the exterior angle of ∆PRS.
∴ ∠PRQ > ∠PSR ….(ii) [Property of exterior angle]
∴ ∠PQR > ∠PSR [From (i) and (ii)]
i.e. ∠Q > ∠S ….(iii)
In APQS,
∠Q > ∠S [From (iii)]
∴ PS > PQ [Side opposite to greater angle is greater]
∴ seg PS > seg PQ
Question 8.
In the adjoining figure, in AABC, seg AD and seg BE are altitudes and AE = BD. Prove that seg AD = seg BE.
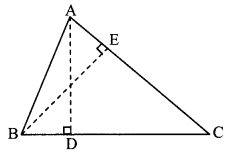
Solution:
Proof:
In ∆ADB and ∆BEA,
seg BD ≅ seg AE [Given]
∠ADB ≅ ∠BEA = 90° [Given]
seg AB ≅ seg BA [Common side]
∴ ∆ADB ≅ ∆BEA [Hypotenuse-side test]
∴ seg AD ≅ seg BE [c. s. c. t.]
Maharashtra Board Class 9 Maths Chapter 3 Triangles Practice Set 3.4 Intext Questions and Activities
Question 1.
As shown in the given figure, draw ∆XYZ such that side XZ > side XY. Find which of ∠Z and ∠Y is greater. (Textbook pg. no. 41)
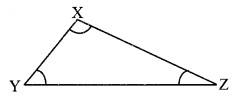
Answer:
From the given figure, ∠Z = 25° and ∠Y = 51°
∴ ∠Y is greater.