Balbharti Maharashtra State Board Class 9 Maths Solutions covers the Practice Set 5.3 Geometry 9th Class Maths Part 2 Answers Solutions Chapter 5 Quadrilaterals.
Practice Set 5.3 Geometry 9th Std Maths Part 2 Answers Chapter 5 Quadrilaterals
Question 1.
Diagonals of a rectangle ABCD intersect at point O. If AC = 8 cm, then find BO and if ∠CAD = 35°, then find ∠ACB.
Solution:
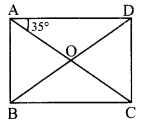
i. AC = 8 cm …(i) [Given]
□ABCD is a rectangle [Given]
∴ BD = AC [Diagonals of a rectangle are congruent]
∴ BD = 8 cm [From (i)]
BO = \(\frac { 1 }{ 2 }\) BD [Diagonals of a rectangle bisect each other]
∴ BO = \(\frac { 1 }{ 2 }\) x 8
∴ BO = 4 cm
ii. side AD || side BC and seg AC is their transversal. [Opposite sides of a rectangle are parallel]
∴ ∠ACB = ∠CAD [Alternate angles]
∠ACB = 35° [ ∵∠CAD = 35°]
∴ BO = 4 cm, ∠ACB = 35°
Question 2.
In a rhombus PQRS, if PQ = 7.5 cm, then find QR. If ∠QPS 75°, then find the measures of ∠PQR and ∠SRQ.
Solution:
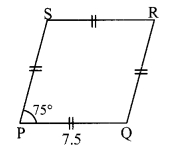
i. PQ = 7.5 cm [Given]
□PQRS is a rhombus. [Given]
∴ QR = PQ [Sides of a rhombus are congruent]
∴ QR = 7.5 cm
ii. ∠QPS = 75° [Given]
∠QPS + ∠PQR = 180° [Adjacent angles of a rhombus are supplementary]
∴ 75° + ∠PQR = 180°
∴ ∠PQR = 180° – 75°
∴ ∠PQR =105°
iii. ∠SRQ = ∠QPS [Opposite angles of a rhombus]
∴ ∠SRQ = 75°
∴ QR = 7.5 cm, ∠PQR = 105°,
∠SRQ = 75°
Question 3.
Diagonals of a square IJKL intersects at point M. Find the measures of ∠IMJ, ∠JIK and ∠LJK.
Solution:
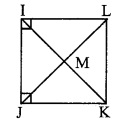
□IJKL is a square. [Given]
∴ seg IK ⊥ seg JL [Diagonals of a square are perpendicular to each other]
∠ IMJ=90°
∠ JIL 90° ……. (i) [Angle of a square]
ii. ∠JIK = \(\frac { 1 }{ 2 }\)∠JIL [Diagonals of a square bisect the opposite angles]
∠JIK = \(\frac { 1 }{ 2 }\) (90°) [From (i)
∴ ∠JIK = 45°
∠IJK = 90° (ii) [Angle of a square]
iii. ∠LJK = \(\frac { 1 }{ 2 }\)∠IJK [Diagonals of a square bisect the opposite angles]
∠LJK = \(\frac { 1 }{ 2 }\) (90°) [From (ii)]
∴ ∠LJK = 45°
∴ ∠LJK = 90°, ∠JIK = 45°, ∠LJK=45°
Question 4.
Diagonals of a rhombus are 20 cm and 21 cm respectively, then find the side of rhombus and its Perimeter.
Solution:
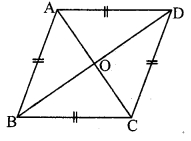
i. Let □ABCD be the rhombus.
AC = 20 cm, BD = 21 cm

ii. In ∆AOB, ∠AOB = 90° [Diagonals of a rhombus are prependicular to each other]
∴ AB2 = AO2 + BO2 [Pythagoras theorem]

iii. Perimeter of □ABCD
= 4 x AB = 4 x 14.5 = 58 cm
∴ The side and perimeter of the rhombus are 14.5 cm and 58 cm respectively.
Question 5.
State with reasons whether the following statements are ‘true’ or ‘false’.
i. Every parallelogram is a rhombus.
ii. Every rhombus is a rectangle,
iii. Every rectangle is a parallelogram.
iv. Every square is a rectangle,
v. Every square is a rhombus.
vi. Every parallelogram is a rectangle.
Answer:
i. False.
All the sides of a rhombus are congruent, while the opposite sides of a parallelogram are congruent.
ii. False.
All the angles of a rectangle are congruent, while the opposite angles of a rhombus are congruent.
iii. True.
The opposite sides of a parallelogram are parallel and congruent. Also, its opposite angles are congruent.
The opposite sides of a rectangle are parallel and congruent. Also, all its angles are congruent.
iv. True.
The opposite sides of a rectangle are parallel and congruent. Also, all its angles are congruent.
All the sides of a square are parallel and congruent. Also, all its angles are congruent.
v. True.
All the sides of a rhombus are congruent. Also, its diagonals are perpendicular bisectors of each other.
All the sides of a square are congruent. Also, its diagonals are perpendicular bisectors of each other.
vi. False.
All the angles of a rectangle are congruent, while the opposite angles of a parallelogram are congruent.