Complex Numbers Class 11 Commerce Maths 1 Chapter 3 Exercise 3.3 Answers Maharashtra Board
Balbharati Maharashtra State Board 11th Commerce Maths Solution Book Pdf Chapter 3 Complex Numbers Ex 3.3 Questions and Answers.
Std 11 Maths 1 Exercise 3.3 Solutions Commerce Maths
Question 1.
If ω is a complex cube root of unity, show that
(i) (2 – ω)(2 – ω2) = 7
(ii) (2 + ω + ω2)3 – (1 – 3ω + ω2)3 = 65
(iii) \(\frac{\left(\mathbf{a}+\mathbf{b} \omega+\mathbf{c} \omega^{2}\right)}{\mathbf{c}+\mathbf{a} \omega+\mathbf{b} \omega^{2}}\) = ω2
Solution:
ω is the complex cube root of unity.
∴ ω3 = 1 and 1 + ω + ω2 = 0
Also, 1 + ω2 = -ω, 1 + ω = -ω2 and ω + ω2 = -1
(i) L.H.S. = (2 – ω)(2 – ω2)
= 4 – 2ω2 – 2ω + ω3
= 4 – 2(ω2 + ω) + 1
= 4 – 2(-1) + 1
= 4 + 2 + 1
= 7
= R.H.S.
(ii) L.H.S. = (2 + ω + ω2)3 – (1 – 3ω + ω2)3
= [2 + (ω + ω2)]3 – [-3ω + (1 + ω2)]3
= (2 – 1)3 – (-3ω – ω)3
= 13 – (-4ω)3
= 1 + 64ω3
= 1 + 64(1)
= 65
= R.H.S.
(iii) L.H.S. =\(\frac{\left(\mathbf{a}+\mathbf{b} \omega+\mathbf{c} \omega^{2}\right)}{\mathbf{c}+\mathbf{a} \omega+\mathbf{b} \omega^{2}}\)
= \(\frac{a \omega^{3}+b \omega^{4}+c \omega^{2}}{c+a \omega+b \omega^{2}}\) ……[∵ ω3 = 1, ω4 = ω]
= \(\frac{\omega^{2}\left(c+a \omega+b \omega^{2}\right)}{c+a \omega+b \omega^{2}}\)
= ω2
= R.H.S.
![]()
Question 2.
If ω is a complex cube root of unity, find the value of
(i) ω + \(\frac{1}{\omega}\)
(ii) ω2 + ω3 + ω4
(iii) (1 + ω2)3
(iv) (1 – ω – ω2)3 + (1 – ω + ω2)3
(v) (1 + ω)(1 + ω2)(1 + ω4)(1 + ω8)
Solution:
ω is the complex cube root of unity.
∴ ω3 = 1 and 1 + ω + ω2 = 0
Also, 1 + ω2 = -ω, 1 + ω = -ω2 and ω + ω2 = -1
(i) ω + \(\frac{1}{\omega}\)
= \(\frac{\omega^{2}+1}{\omega}\)
= \(\frac{-\omega}{\omega}\)
= -1
(ii) ω2 + ω3 + ω4
= ω2 (1 + ω + ω2)
= ω2 (0)
= 0
(iii) (1 + ω2)3
= (-ω)3
= -ω3
= -1
(iv) (1 – ω – ω2)3 + (1 – ω + ω2)3
= [1 – (ω + ω2)]3 + [(1 + ω2) – ω]3
= [1 – (-1)]3 + (-ω – ω)3
= 23 + (-2ω)3
= 8 – 8ω3
= 8 – 8(1)
= 0
(v) (1 + ω)(1 + ω2)(1 + ω4)(1 + ω8)
= (1 + ω)(1 + ω2)(1 + ω)(1 + ω2) …..[∵ ω3 = 1, ω4 = ω]
= (-ω2)(-ω)(-ω2)(-ω)
= ω6
= (ω3)2
= (1)2
= 1
Question 3.
If α and β are the complex cube roots of unity, show that α2 + β2 + αβ = 0.
Solution:
α and β are the complex cube roots of unity.

∴ α – β = -1
L.H.S. = α2 + β2 + αβ
= α2 + 2αβ + β2 + αβ – 2αβ ……[Adding and subtracting 2αβ]
= (α2 + 2αβ + β2) – αβ
= (α + β)2 – αβ
= (-1)2 – 1
= 1 – 1
= 0
= R.H.S.
![]()
Question 4.
If x = a + b, y = αa + βb and z = aβ + bα, where α and β are the complex cube roots of unity, show that xyz = a3 + b3.
Solution:
x = a + b, y = αa + βb, z = aβ + bα
α and β are the complex cube roots of unity.
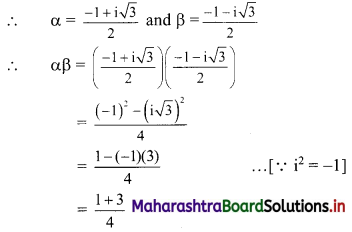

Question 5.
If ω is a complex cube root of unity, then prove the following:
(i) (ω2 + ω – 1)3 = -8
(ii) (a + b) + (aω + bω2) + (aω2 + bω) = 0
Solution:
ω is the complex cube root of unity.
∴ ω3 = 1 and 1 + ω + ω2 = 0
Also, 1 + ω2 = -ω, 1 + ω = -ω2 and ω + ω2 = -1
(i) L.H.S. = (ω2 + ω – 1)3
= (-1 – 1)3
= (-2)3
= -8
= R.H.S.
![]()
(ii) L.H.S. = (a + b) + (aω + bω2) + (aω2 + bω)
= (a + aω + aω2) + (b + bω + bω2)
= a(1 + ω + ω2) + b(1 + ω + ω2)
= a(0) + b(0)
= 0
= R.H.S.
Maharashtra State Board 11th Commerce Maths
- Sets and Relations Ex 1.1 11th Commerce Maths
- Sets and Relations Ex 1.2 11th Commerce Maths
- Sets and Relations Miscellaneous Exercise 1 11th Commerce Maths
- Functions Ex 2.1 11th Commerce Maths
- Functions Miscellaneous Exercise 2 11th Commerce Maths
- Complex Numbers Ex 3.1 11th Commerce Maths
- Complex Numbers Ex 3.2 11th Commerce Maths
- Complex Numbers Ex 3.3 11th Commerce Maths
- Complex Numbers Miscellaneous Exercise 3 11th Commerce Maths