Bhagya

Balbharti Maharashtra State Board Class 9 Hindi Solutions Lokbharti Chapter 8 उड़ान Notes, Textbook Exercise Important Questions and Answers.

Maharashtra State Board Class 9 Hindi Lokbharti Solutions Chapter 8 उड़ान

Hindi Lokbharti 9th Std Digest Chapter 8 उड़ान Textbook Questions and Answers

पठनीय:

प्रश्न 1.
‘दहेज’ जैसी सामाजिक समस्याओं को समझते हुए इसके संदर्भ में जनजागृति करने हेतु घोषवाक्यों का वाचन कीजिए।

श्रवणीय:

प्रश्न 1.
हिंदी-मराठी भाषा के प्रमुख गजलकारों की गजल रचना सुनिए और सुनाइए।

कल्पना पल्लवन:

प्रश्न 1.
‘मैं चिड़िया बोल रही हूँ इस विषय पर स्वयंप्रेरणा से लेखन कीजिए।

आसपास:

प्रश्न 1.
अंतरजाल की सहायता लेकर कोई कविता पढ़िए और निम्न मुद्दों के आधार पर आशय स्पष्ट कीजिए:

पाठ के आँगन में…

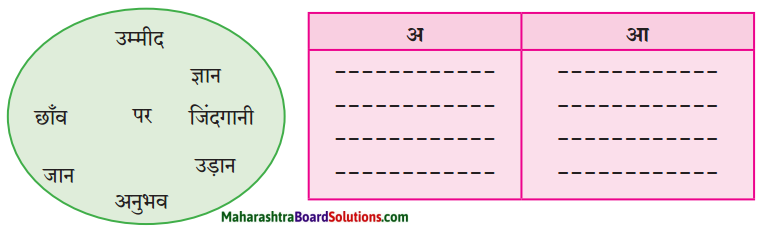
1. सूचना के अनुसार कृतियाँ कीजिए।

प्रश्न 1.
सही पर्याय चुनकर लिखिए।
परों में शक्ति हो तो ………..
उत्तर:
(क) उपलब्ध नभ को नापना है।
(ख) उपलब्ध जल को नापना है।
(ग) भू को नापना है।

प्रश्न 2.
सुलगते आप, बाहर से …………
(क) तपन नहीं माँगा करते।
(ख) अगन नहीं माँगा करते।
(ग) बुझन नहीं माँगा करते।
उत्तर:
1. परों में शक्ति हो तो उपलब्ध नभ को नापना है।
2. सुलगते आप, बाहर से अगन नहीं माँगा करते।

प्रश्न 3.
निम्नलिखित काव्य पंक्तियों का सरल भावार्थ लिखिए। अँधेरे के इलाके में ………….. नमन माँगा नहीं करते।
भावार्थ:
प्रस्तुत गजल में कवि कहते हैं, “इंसान के पास स्वाभिमान का होना बेहद जरूरी होता है। उसे अँधेरे के इलाके में किरण नहीं माँगनी चाहिए। यानी जब संकट की स्थिति आ जाएँ; तब इंसान को स्वयं ही उसके साथ संघर्ष करना चाहिए। किसी से मदद नहीं मांगनी चाहिए। जहाँ पर कंटकों का यानी काँटों का बन होता है; वहाँ पर काँटों के अलावा कुछ नहीं होता है। वहाँ पर सुमन नहीं हो सकते हैं। अर्थात संकट की परिस्थितियों में सर्वत्र काँटे-ही-काँटे होते हैं। वहाँ पर दुख-दर्द व पीड़ा ही होती है। वहाँ पर हम सुख की अपेक्षा नहीं कर सकते।”

“जो व्यक्ति सचमुच आदर का अधिकारी है उसके सामने दुसरे लोगों के मस्तक अपने आप झुक जाते हैं। ऐसे व्यक्ति को किसी से नमन या आदर मांगने की जरूरत नहीं होती बल्कि उसे तो अपने आप आदर मिल जाता है। व्यक्ति के पास विनम्रता होनी चाहिए।”

प्रश्न 4.
कविता द्वारा दिया गया संदेश अपने शब्दों में लिखिए।
उत्तरः
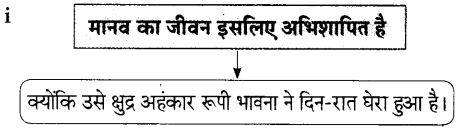
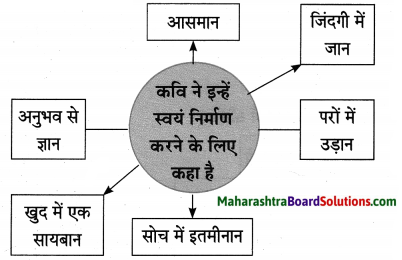
प्रस्तुत कविता के माध्यम से कवि ने व्यक्ति को मानवीय गुणों को स्वीकार करने के लिए कहा है। स्वाभिमान, विनम्रता, दूरदृष्टि, बुलंद हौसले आदि गुणों को स्वीकार करने से व्यक्ति प्रगति की ऊंची उड़ान भर सकता है। फिर उसके लिए कुछ भी असंभव नहीं होगा। जिस व्यक्ति के पास मानवीय गुण होते हैं उन्हें किसी के भी पास हाथ फैलाने की आवश्यकता नहीं होती है। ऐसे लोगों को समाज में मान-सम्मान कीर्ति व यश अपने आप मिल जाता है। अत: व्यक्ति के पास मानवीय गुणों का होना जरूरी होता है।

प्रश्न 5.
कविता में प्रयुक्त विरामचिह्नों के नाम लिखकर उनका वाक्य में प्रयोग कीजिए।
उत्तरः
(,) – अल्पविराम
बाक्य: राम ने दुकान से शक्कर, मिठाई व खजूर लाए।
(|) – पूर्णविराम
वाक्य: अजय शहर गया है।

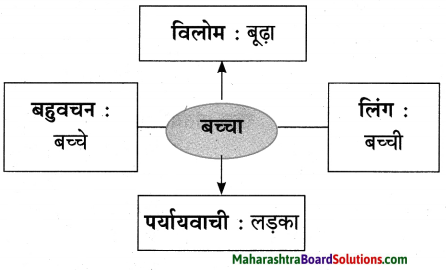
प्रश्न 6.
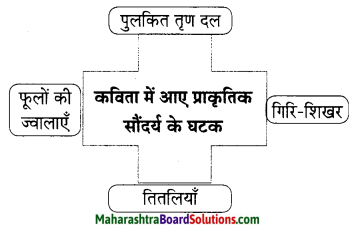
संजाल

उत्तरः

कल्पना पल्लवन:

प्रश्न 1.
“”मैं चिड़िया बोल रही हूँ।” इस विषय पर स्वयंप्रेरणा से लेखन कीजिए।
उत्तरः
“पंछी बनू उड़ती फिरूं मस्त गगन में
आज मैं आजाद हूँ दुनिया के चमन में।”

मुझे आज भी याद है पुरानी फिल्म का यह गीत । सचमुच पंछी बनकर खुले आसमान में विचरण करना सभी को अच्छा लगेगा। किसी की कुछ भी रोक-टोक नहीं और नहीं किसी-का कुछ झंझट । बस सिर्फ आसमान में स्वच्छंद होकर उड़ना। बताओ किसे अच्छा नहीं लगेगा? संध्या समय पीपल के नीचे बैठकर मेरे मन में ये विचार आ ही रहे थे तभी अचानक पीपल के पेड़ पर बैठी एक चिड़िया ने ची-चीं करते हुए मुझे आवाज दी और वह मेरे समक्ष आकर बैठ गई। फिर अपने बारे में कहने लगी।

“मैं हूँ नन्ही-सी, प्यारी-सी चिड़िया। इस पेड़ पर ही मेरा निवास है। देख रही हो वह घोंसला? कितने प्यार से मैंने बनाया है! उसका निर्माण करने के लिए मुझे तकरीबन एक महीना लगा है। न जाने मैंने कहाँ-कहाँ से उसे तैयार करने के लिए सामग्री इकट्ठा की है? बस ईश्वर ही इस बात का साक्षी है। मैंने अपनी चोंच में तिनका-तिनका लाकर स्वयं के लिए सुंदर भवन का निर्माण किया है। उस घोंसले में मेरे दो अंडे हैं। अब जल्द ही दो नन्हे-मुन्ने बच्चे मेरे घर आएँगे। अब मैं उन्हीं का इंतजार कर रही हूँ।

पीपल के इस पेड़ पर पहले मेरे कई भाई-बहन रहा करते थे। तोता, मैना आदि मेरे भाई बहन मनुष्य द्वारा निर्मित प्रदूषण के शिकार हो गए। अब न इस पेड़ पर कोई तोता आकर बैठता है और न कोई मैना। कौओं की भी काँव-काँव अब पहले जैसे सुनाई नहीं दे रही है। मनुष्य ने अपने स्वार्थ के लिए पेड़ों की अंधाधुंध कटाई की। इसका परिणाम यह हुआ कि पक्षियों की संख्या कम होती गई। अब तो शहरों से पक्षी नदारद हो गए हैं।

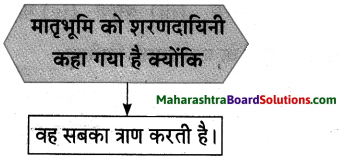
मैंने सुना है कि कुछ संस्थाएँ पक्षी-दर्शन जैसे कार्यक्रमों का आयोजन करती रहती हैं और कर्नाला पक्षी अभयारण्य जैसे स्थलों पर जाती रहती है। लेकिन मेरी प्यारी बहना, सच कहूँ तो वहाँ पर भी अब पहले जैसे पंछी नहीं रहें। पहले जैसे पंछियों का कलरव अब सुनाई नहीं देता है। इसके लिए इंसान ही जिम्मेदार है। यह सब उसी के कार्य का परिणाम है। यदि इंसान अपने किए कराए से बाज नहीं आएगा; तो भविष्य में अपने लिए गड्ढा स्वयं ही खोद लेगा।

हम ही इस सुंदर धरती का अंश हैं। हमें भी जीवन जीने का अधिकार है। आखिर हम भी एक जीव हैं। इंसान को कोई अधिकार नहीं है कि वह हमारे अधिकार को छीन लें। उसे प्राकृतिक संतुलन के बारे में सोचना चाहिए। जब इंसान “जिओ और जीने दो” इस सूत्र को अपनाएगा तब उसका जीवन भी खुशहाल हो जाएगा और यह प्यारी धरती फिर से ‘सुजलाम् सुफलाम्’ बन जाएगी।

Hindi Lokbharti 9th Answers Chapter 8 उड़ान Additional Important Questions and Answers

(क) पद्यांश पढ़कर दी गई सूचना के अनुसार कृतियाँ कीजिए।

कृति (1) आकलन कृति

प्रश्न 1.
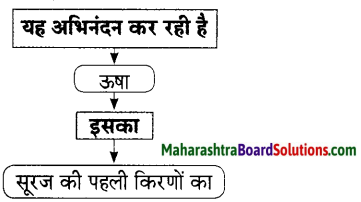
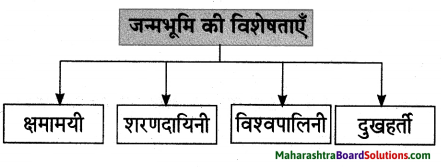
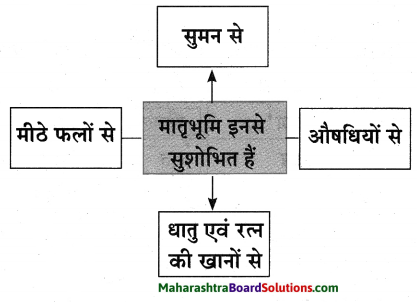
आकृति पूर्ण कीजिए।
उत्तर:

कृति (2) आकलन कृति

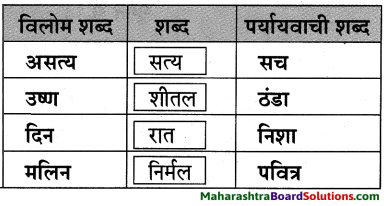
प्रश्न 1.
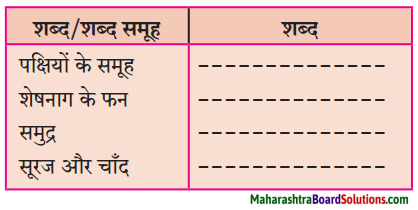
समझकर लिखिए।
उत्तर:

कृति (3) भावार्थ

प्रश्न 1.
निम्नलिखित पंक्तियों का भावार्थ अपने शब्दों में लिखिए। परों में शक्ति …………….. गगन माँगा नहीं करते।
भावार्थः
प्रस्तुत गजल में कवि कहते हैं, “जिनके पंखों में शक्ति होती है वे संपूर्ण आसमान को नाप लेते हैं। यानी जिनके पास साहस व वीरता होती है या जिनके हौसले बुलंद होते हैं; वे असंभव कार्य को संभव करते हैं। जैसे कि आसमान में विचरण करना या उड़ना तो पंछियों का काम होता है और वे तो गगन में नित्य संचार करते रहते हैं। उन्हें उड़ने के लिए किसी से गगन माँगने की आवश्यकता नहीं होती है अर्थात जहाँ चाह, वहाँ राह अपने आप निर्माण हो जाती है।’

(ख) पद्यांश पढ़कर सूचना के अनुसार कृतियाँ कीजिए।

कृति (1) आकलन कृति

1. सही विकल्प चुनकर लिखिए।

प्रश्न 1.
व्यक्ति को इसके सपने अपने आप आते हैं ……………
उत्तर:
(क) जिससे वह मन व प्राण से प्यार करता है।
(ख) जिससे वह नफरत करता है।
(ग) जिससे वह सहायता की अपेक्षा करता है।

प्रश्न 2.
ये अग्नि की माँग नहीं करते हैं …….
(क) जिन्होंने पश्चात्ताप की अग्नि में जलना स्वीकार किया है।
(ख) जिन्होंने पश्चात्ताप की अग्नि में जलना अस्वीकार किया है।
(ग) जन्होंने पश्चात्ताप की अग्नि में दूसरों को जलाना तय किया
उत्तर:
1. व्यक्ति को इसके सपने अपने आप आते हैं जिससे वह मन व प्राण से प्यार करता है।
2. ये अग्नि की माँग नहीं करते हैं जिन्होंने पश्चात्ताप की अग्नि में जलना स्वीकार किया है।

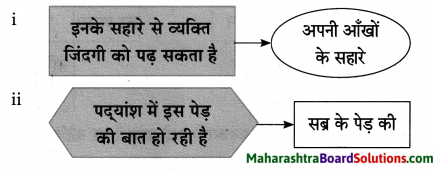
कृति (2) आकलन कृति

प्रश्न 1.
पद्यांश पढ़कर ऐसे दो प्रश्न तैयार कीजिए जिनके उत्तर
निम्न शब्द हों।
1. निमंत्रण
2. पश्चात्ताप
उत्तर:
1. किसके बिना सपने अपने आप आते हैं?
2. पद्यांश में किस अग्नि में जलने की बात हो रही है?

कृति (4) भावार्थ

प्रश्न 1.
निम्नलिखित पंक्तियों का भावार्थ अपने शब्दों में लिखिए। जिसे मन प्राण …………….. माँगा नहीं करते।
भावार्थ:
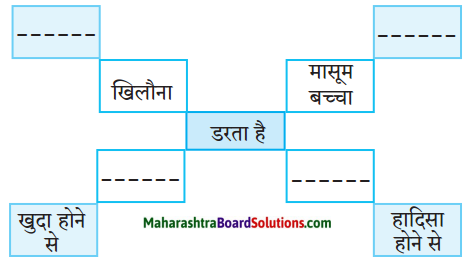
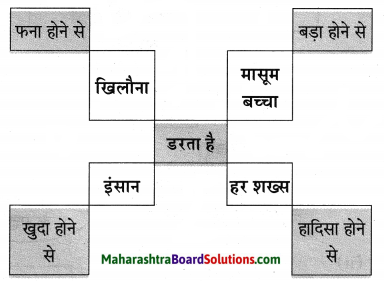
जिन लोगों ने अपने आप को पश्चात्ताप की आग में जलना स्वीकार कर लिया है, उन्हें कैसे कोई रोक सकता है? ऐसे लोग पश्चात्ताप की अग्नि में अंदर से सुलगते रहते हैं; लेकिन वे बाहर से अग्नि की माँग नहीं करते हैं। पश्चात्ताप की अग्नि से बढ़कर कोई दूसरी अग्नि नहीं हो सकती।

(ग) पद्यांश पढ़कर सूचना के अनुसार कृतियाँ कीजिए।

कृति (1): आकलन कृति

प्रश्न 1.
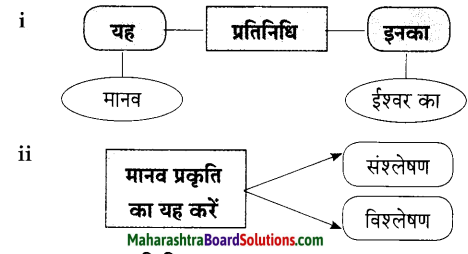
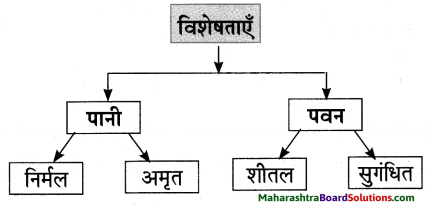
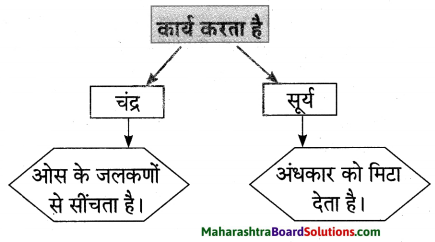
समझकर लिखिए।
उत्तर:

प्रश्न 2.
आकृति पूर्ण कीजिए।
उत्तर:

कृति (3): भावार्थ

प्रश्न 1.
निम्नलिखित पंक्तियों का भावार्थ अपने शब्दों में लिखिए। खुशबू देती है …………….. धूपदान होती है।
भावार्थ:
प्रस्तुत पंक्ति ‘उड़ान’ इस गजल से ली गई है और इसके कवि चंद्रसेन विराट जी हैं। धूप जब जलता है; तब वह सभी को खुशबू देता है। शायर की जिंदगी भी धूपदान की तरह होती है। वह अपनी शायरी से लोगों के जीवन में खुशबू भर देता है।”

पद्य-विश्लेषण:

• कविता का नाम – उड़ान
• कविता की विधा – गजल
• पसंदीदा पंक्ति – एक बहरे को एक गूंगा दे, जिंदगी वो बयान होती है।
• पसंदीदा होने का कारण – उपर्युक्त पंक्ति मुझे बेहद पसंद है क्योंकि उसमें एकदूसरे की सहायता करने से जिंदगी बड़े आराम से कटती है।
• कविता से प्राप्त संदेश या प्रेरणा – प्रस्तुत कविता से प्रेरणा मिलती है कि व्यक्ति को स्वाभिमानी व विनम्र होना चाहिए। उसके हौसले बुलंद होने चाहिए। उसे मानवीय गुणों को अपनाकर स्वयं का जीवन सुंदर बनाना चाहिए।

उड़ान Summary in Hindi

कवि-परिचय:

जीवन-परिचय: कवि चंद्रसेन विराट जी हिंदी साहित्य के आधुनिक रचनाकारों में से एक हैं। इनका जन्म ३ दिसंबर १९३६ को इंदौर मध्य
प्रदेश में हुआ। ये हिंदी साहित्य जगत में गजलकार के रूप में प्रसिद्ध हैं। इन्होंने अपनी गजलों में आम आदमी के जीवन
को अभिव्यक्त करने का सफल प्रयास किया है। इन्होंने गजल के साथ-साथ गीतों का भी लेखन किया है।

प्रमुख कृतियाँ: गीत संग्रह – ‘मेंहदी रची हथेली’, ‘स्वर के सोपान’, ‘मिट्टी मेरे देश की’, ‘धार के विपरीत’ आदि; गजल संग्रह – ‘आस्था
के अमलतास’, ‘कचनार की टहनी’, ‘न्याय कर मेरे समय’ आदि; मुक्तक संग्रह – कुछ पलाश कुछ पाटल, ‘कुछ सपने’, ‘कुछ सच’ आदि।

पदय-परिचय:

गजल: गजल काव्य विधा का एक प्रकार है। एक ही बहर और वजन के अनुसार लिखे गए शेरों के समूह को ‘गजल’ कहते हैं। गजल
के पहले शेर को ‘मतला’ और अंतिम शेर को ‘मकता’ कहते हैं।

प्रस्तावना: ‘उड़ान’ इस गजल में गजलकार चंद्रसेन विराट जी ने मानवीय मूल्यों के दर्शन करवाए हैं। व्यक्ति के पास स्वाभिमान, विनम्रता, दूरदृष्टि व बुलंद हौसले होने चाहिए। इन गुणों से ही जीवन में व्यक्ति ऊँचा उठता है।

सारांश:

प्रस्तुत कविता गजल विधा में लिखी गई है। व्यक्ति के पास मानवीय गुणों का होना बहुत जरूरी होता है। मानवीय गुणों के कारण व्यक्ति का व्यक्तित्व विकसित होता है। व्यक्ति के पास स्वाभिमान का होना बेहद जरूरी होता है। स्वाभिमान के कारण व्यक्ति ऊँचा उठता है। जिसके पास विनम्रता होती है; उसे समाज में आदर अपने आप मिलता है। जिनके हौसले बुलंद होते हैं; उनके लिए असंभव कुछ भी नहीं होता। जीवन में व्यक्ति को एक-दूसरे की सहायता करनी चाहिए। जीवन में सभी को खुशी देने का प्रयास करना चाहिए। आखिर चार दिन की जिंदगी होती है। उसी में स्वयं खुश रहकर दूसरों के भी जीवन में खुशियाँ भर देनी चाहिए।

शब्दार्थ:

1. अगन – अग्नि, आग
2. सायबान – छाया देने वाला
3. बयान – वक्तव्य
4. तीर – बाण
5. कमान – धनुष
6. इलाका – क्षेत्र
7. कंटक – काँटा
8. आदर – सम्मान
9. पर – पंख
10. थकान – थकावट
11. शायर – शायरी लिखने वाला

भावार्थ:

अँधेरे के इलाके में ………………. सुमन माँगा नहीं करते।

प्रस्तुत गजल में कवि कहते हैं, “इंसान के पास स्वाभिमान का होना बेहद जरूरी होता है। उसे अँधेरे के इलाके में किरण नहीं माँगनी चाहिए। यानी जब संकट की स्थिति आ जाए; तब इंसान को स्वयं ही उसके साथ संघर्ष करना चाहिए। किसी से मदद नहीं माँगनी चाहिए। जहाँ पर कंटकों का यानी काँटों का वन होता है वहाँ पर काँटों के अलावा कुछ नहीं होता है। वहाँ पर सुमन नहीं हो सकते हैं। अर्थात संकट की परिस्थितियों में सर्वत्र काँटे-ही-काँटे होते हैं। वहाँ पर दुख-दर्द व पीड़ा ही होती है। वहाँ पर हम सुख की अपेक्षा नहीं कर सकते।

Balbharti Maharashtra State Board Class 9 Hindi Solutions Lokbharti Chapter 3 इनाम Notes, Textbook Exercise Important Questions and Answers.

Maharashtra State Board Class 9 Hindi Lokbharti Solutions Chapter 3 इनाम

Hindi Lokbharti 9th Std Digest Chapter 3 इनाम Textbook Questions and Answers

मौलिक सृजन :

प्रश्न 1.
“प्राकृतिक संसाधन मानव के लिए वरदान।’ इस विषय पर स्वमत लिखिए।
उत्तरः
सच ही कहा गया है कि प्राकृतिक संसाधन मानव के लिए वरदान होता है। सूर्य की रोशनी, हवा, मिट्टी, पानी, लकड़ी, तेल, कोयला, जीवश्म, ईधन, खनिज, वनस्पति और अन्य पदार्थ प्राकृतिक संसाधन होते हैं क्योंकि ये सन्न प्रकृति द्वारा इसान को उपहार के रूप में मिले हैं। ये प्रकृति में प्राकृतिक रूप में पाए जाते हैं। इन्हें मनुष्य द्वारा निर्मित नहीं किया जा सकता। मानव सभ्यता, शहरीकरण, तकनीकीकरण, औद्योगिकीकरण के लिए इन संसाधनों का इस्तेमाल करता है।

इंसान की मूलभूत आवश्यकताओं को पूरा करने का कार्य प्राकृतिक संसाधन करते हैं। इनके कारण ही आज मनुष्य प्रगति कर सका है। इंसान के जीवन को खुशहाल एवं समृद्ध करने में प्राकृतिक संसाधन सहायता करते हैं। इनके कारण ही इस धरती पर जीवन संभव हुआ है। अत: प्राकृतिक संसाधन मानव के लिए वरदान हैं।

आसपास :

प्रश्न 1.
आपके गाँव-शहर को जहाँ से बिजली आपूर्ति होती है, उस केंद्र के बारे में जानकारी प्राप्त करके टिप्पणी तैयार कीजिए।

संभाषणीय :

प्रश्न 1.
‘ईधन की बचत, समय की माँग है।’ इस विषय पर अपना मत व्यक्त कीजिए।

उत्तरः
सचमुच आज के इस तकनीकी युग में ईधन की बचत समय की माँग हो गई है। यदि हमने आने वाले समय में ईंधन की बचत नहीं की तो हमें बहुत बड़ी समस्या का सामना करना पड़ेगा। हमारे देश में ईंधन की सौमित मात्रा ही उपलब्ध है। अत: मानव का दायित्व है कि वह उसकी बचत करे। ईंधन की बचत करने के लिए हमें पब्लिक बस या रेल से सफर करना चाहिए। अपनी गाड़ियों को व्यर्थ में चालू करके नहीं छोड़ना चाहिए। हमें छोटी दूरी के लिए साइकिल का इस्तेमाल करना चाहिए। अगर हम ईंधन की बचत करेंगे; तो वह आगे आने वाले पीढ़ी को उपलब्ध हो सकेगा। ईधन की बचत करने से हम पर्यावरण को भी दूषित होने से बचा सकते हैं।

लेखनीय :

प्रश्न 1.
समुद्री लहरों से विद्युत निर्मिति के बारे में टिप्पणी तैयार कीजिए। संदर्भ यू ट्यूब से लीजिए।
उत्तरः
समुद्री लहरों से विद्युत की निर्मिति की जाती है। इसे ‘जलविद्युत ऊर्जा’ कहते हैं। समुद्र की लहरें ऊर्जा का एक प्रमुख स्रोत है। भारत एक उष्ण कटिबंधीय देश है। इसी कारण सतह के पानी व गहरे समुद्र के बीच तापमान में लगातार भिन्नता रहती है। इसका फायदा ऊर्जा निर्माण करने के लिए किया जाता है। समुद्री धाराओं में बड़े पैमाने पर फ्लोटिंग विलवणीकरण संयंत्र का कार्यान्वयन किया जा रहा है जिस कारण जलविद्युत ऊर्जा की निर्मिती हो रही है।

पठनीय :

प्रश्न 1.
दैनंदिन जीवन में उपयोग में लाए जाने वाले विविध उपकरणों के आविष्कारकों और उनके कार्यो की जानकारी प्राप्त करके पढ़िए ।

पाठ के आँगन में :

1. सूचना के अनुसार कृतियाँ पूर्ण कीजिए :

प्रश्न क.
पाठ में आए और हिंदी में प्रयुक्त होने वाले पाँच-पाँच विदेशी एवं संकर शब्दों की सूची।

उत्तर:

विदेशी शब्द	संकर शब्द
1. रेफ्रीजरेटर	मोहल्लेदार
2. टेलीफोन	छायादार
3. एक्सपर्ट	लाठीचार्ज
4. क्यूब	वर्षगाँठ
5. आइसक्रीम	रेलगाडी

प्रश्न ख.
वाक्य में कि, की के स्थान को स्पष्ट कीजिए।
‘माँ ने कहा कि बच्चों ने आम की आईसक्रीम तैयार की।’
उत्तर:
कि – समुच्चयबोधक अव्यय
की – संबंधकारक
की – क्रिया

प्रश्न ग.
रेफ्रीजरेटर आने के पूर्व घरवालों के विचार।
उत्तर:

प्रश्न घ.
रेफ्रीजरेटर आने के बाद घर की स्थिति।
उत्तरः
कृति ग (1) का आकलन देखिए।

पाठ से आगे :

प्रश्न 1.
प्रशंसापत्र/पुरस्कार/इनाम के प्रसंग का कक्षा में वर्णन कीजिए।

भाषा बिंदु :

प्रश्न 1.
दिए गए आकृति के अनुसार रचना की दृष्टि से सरल, संयुक्त, मिश्र अन्य वाक्य पाठ से खोजकर तालिका पूर्ण कीजिए।

उत्तरः
छात्र स्वयं पाठ में से सरल, संयुक्त एवं मिश्र वाक्य ढूँढ़कर लिखेंगे।

Hindi Lokbharti 9th Answers Chapter 3 इनाम Additional Important Questions and Answers

(क) परिच्छेद पढ़कर सूचना के अनुसार कृतियाँ कीजिए।

कृति (1) आकलन कृति

प्रश्न 1.
आकृति पूर्ण कीजिए।
उत्तरः

प्रश्न 2.
समझकर लिखिए।
उत्तरः

कृति (2) आकलन कृति

प्रश्न 1.
आकृति पूर्ण कीजिए।
उत्तरः

प्रश्न 2.
किसने, किससे कहा?
i. “तुम तो खयाली पुलाव पका रहे हो।”
उत्तर:
लेखक ने अपनी पत्नी से कहा।

ii. “हमारे टेलीफोन तो तुम ही हो।”
उत्तरः
लेखक की पत्नी ने लेखक से कहा।

प्रश्न 3.
सत्य-असत्य लिखिए।
i. लेखक की पत्नी के अनुसार जिसका उत्तर सबसे अच्छा होगा, उसे इनाम मिलेगा।
ii. रेफ्रीजरेटर के लिए घरेलू पावर की जरूरत होती है।
उत्तर:
i. असत्य
ii. सत्य

कृति (3) शब्द संपदा

प्रश्न 1.
समानार्थी शब्द लिखिए।
i. प्रतियोगिता
ii. जुगाड़
iii. पत्नी
iv. रात
उत्तर :
i. स्पर्धा
ii. व्यवस्था
iii. भार्या
iv. निशा

प्रश्न 2.
विरुद्धार्थी शब्द लिखिए।
i. दिन × …
ii. देसी × …..
उत्तरः
i. रात
ii. विदेशी

प्रश्न 3.
वचन बदलिए।
i. लॉटरी
ii. दाम
उत्तर:
i. लॉटरियाँ
ii. दाम

प्रश्न 4.
निम्नलिखित शब्दों में प्रयुक्त प्रत्यय पहचानिए।
i. प्रतियोगिता
ii. विदेशी
उत्तर:
i. ‘ता’ प्रत्यय
ii. ‘ई’ प्रत्यय

प्रश्न 5.
निम्नलिखित शब्दों में उचित प्रत्यय लगाकर नए शब्द तैयार कीजिए।
i. अच्छा
ii. भारत
उत्तर:
i. अच्छा + आई – अच्छाई
ii. भारत + ईय – भारतीय

प्रश्न 6.
‘कल्पना में खोए रहना।’ इस अर्थ का गद्यांश में प्रयुक्तं मुहावरा है।
उत्तरः
खयाली पुलाव पकाना।

कृति (4) स्वमत अभिव्यक्ति

प्रश्न 1.
क्या खयाली पुलाव पकाना अच्छी बात होती है ? इस पर आधारित अपने विचार लिखिए।
उत्तरः
‘खयाली पुलाव पकाना’ यानी कल्पना में खोए रहना। कल्पना में खोए रहना उचित बात नहीं होती है। कल्पना के सहारे जीने से किसी भी प्रकार का लाभ नहीं होता है। इंसान को कल्पना जरूर करनी चाहिए पर उस कल्पना को यथार्थ में लाने का निश्चय भी करना चाहिए। सिर्फ कल्पना करके खयाली पुलाव पकाना यानी कि जीवन की सच्चाई से दूर भागना होता है। अत: स्पष्ट है कि खयाली पुलाव पकाना अच्छी बात नहीं होती है।

(ख) परिच्छेद पढ़कर दी गई सूचना के अनुसार कृतियाँ कीजिए।

कृति (1) आकलन कृति

प्रश्न 1.
समझकर लिखिए।
उत्तर:

प्रश्न 2.
सही पर्याय चुनकर लिखिए।
अमिता खिलखिलाई क्योंकि ……………………।
(क) वह रेफ्रीजरेटर में बर्फ जमाएगी।
(ख) वह रेफ्रीजरेटर में रोजाना आइसक्रीम जमाएगी।
(ग) वह रेफ्रीजरेटर से रोजाना ठंडा पानी पीएगी।
उत्तर:
अमिता खिलखिलाई क्योंकि वह रेफ्रीजरेटर में रोजाना आइसक्रीम जमाएगी।

कृति (2) आकलन कृति

प्रश्न 1.
कृति पूर्ण कीजिए।
उत्तर:

प्रश्न 2.
सहसंबंध लिखिए।
पहले आने वालों के लिए : शिंकजी :: शौकीनों के लिए :
उत्तरः
चाय

प्रश्न 3.
समझकर लिखिए।
उत्तर:

कृति (3) शब्द संपदा

प्रश्न 1.
वचन बदलिए।

1. ताली
2. बोतलें
3. पत्नी
4. बहू

उतर:

1. तालियाँ
2. बोतल
3. पत्नियाँ
4. बहुएँ

प्रश्न 2.
लिंग बदलिए।
i. पड़ोसी
ii. बहू
उत्तर:
i. पड़ोसन
ii. बेटा

प्रश्न 3.
निम्नलिखित शब्दों में उचित उपसर्ग लगाकर नए शब्द तैयार कीजिए।
i. शक
ii. नम
उत्तर:
i. बे + शक – बेशक
ii. वि + नम् = विनम्

प्रश्न 4.
प्रत्यय पहचानिए।
i. खिलखिलाई
ii. रोजाना
iii. भाग्यवान
उत्तर:
i. आई
ii. आना
iii. वान

प्रश्न 5.
समानार्थी शब्द लिखिए।
i. किस्मत
ii. शक
उत्तर:
i. भाग्य
ii. संशय

प्रश्न 6.
मानक वर्तनी के अनुसार शब्द लिखिए।
i. परबंध
ii. ठण्डा
उत्तर:
i. प्रबंध
ii. ठंडा

कृति (4) स्वमत अभिव्यक्ति

प्रश्न 1.
‘यदि रेफ्रीजरेटर न होते …..’ अपने विचार लिखिए।
उत्तरः
रेफ्रीजरेटर खाद्य पदार्थों को ठंडा बनाए रखता है एवं उन्हें खराब होने से बचाता है। यदि रेफ्रीजरेटर नहीं होते, तो खाद्य पदार्थों को ठंडा बनाए रखने में समस्या निर्माण हो जाती और फिर वे खराब हो जाते। रेफ्रीजरेटर के न होने से इंसान को ठंडा पानी भी पीने के लिए उपलब्ध नहीं होता। आज बाजार में आइसक्रीम के जो फैमिली पैक मिल रहे हैं। वे उपलब्ध नहीं होते। रेफ्रीजरेटर के न होने से आइसक्रीम भी तैयार नहीं हो सकती थी। गर्मियों के दिनों में इंसान की हालत बिगड़ जाती। शरबत व फलों के जूस बहुत दिनों तक नहीं रहते। इस प्रकार रेफ्रीजरेटर नहीं होते, तो इंसानों को बहुत तकलीफ होती थी।

(ग) परिच्छेद पढ़कर सूचना के अनुसार कृतियाँ कीजिए।

कृति (1) आकलन कृति

प्रश्न 1.
समझकर लिखिए।
उत्तरः

प्रश्न 2.
सत्य-असत्य लिखिए।
i. हेमंत के अनुसार देवी की मानता का आशीर्वाद था रेफ्रीजरेटर।
ii. अरुण का रिश्तेदार रेफ्रीजरेटर कंपनी में नौकरी करता है।
उत्तर:
i. असत्य
ii. सत्य

कृति (2) आकलन कृति

प्रश्न 1.
किसने, किससे कहा?
i. “मैंने फिर दुबारा दिमाग पर जोर नहीं डाला।”
उत्तरः
कुढ़मगज ने लेखक से कहा।

ii. “हमें भी बता दें।”
उत्तर:
पड़ोस की एक महिला ने लेखक से कहा।

प्रश्न 2.
समझकर लिखिए।
उत्तरः

कृति (3) शब्द संपदा

प्रश्न 1.
निम्नलिखित शब्दों के भिन्नार्थक शब्द लिखिए।
i. अरुण
ii. तिरछा
उत्तर:
i. लाल, सूर्य
ii. टेढा, वक्र, बाँका

प्रश्न 2.
समानार्थी शब्द लिखिए।

1. बिजली
2. बेटा
3. हाथी

उत्तर:

1. विदयुत
2. पुत्र
3. गज, हस्ती

प्रश्न 3.
प्रत्यय पहचानिए।
i. रिश्तेदार
ii. पूलकर
उत्तर:
i. ‘दार’ प्रत्यय
ii. ‘कर’ प्रत्यय

प्रश्न 4.
‘अनु’ उपसर्ग से निर्मित दो शब्द लिखिए।
उत्तर:
i. अनुबंध
ii. अनुचित

प्रश्न 5.
निम्नलिखित मुहावरे का अर्थ लिखकर उसका वाक्य में प्रयोग कीजिए।
i. जली-कटी सुनाना
उत्तर:
अर्थ : खरी-खोटी सुनाना।
वाक्यः रामू से गलती क्या हो गई, सभी उसे जली-कटी सुनाने लगे।

प्रश्न 6.
निम्नलिखित शब्द मानक वर्तनी के अनुसार लिखिए।

1. शककी
2. इन्क
3. मुफ्त
4. काण्टा

उत्तर:

1. शक्की
2. इंक
3. मुफ्त
4. काँटा

कृति (4) स्वमत अभिव्यक्ति

प्रश्न 1.
‘पड़ोसियों की आदत होती है, निंदा करने की!’ क्या आप इस कथन से सहमत हैं? अपने विचार लिखिए।
उत्तर:
संकट की घड़ी में पड़ोसी अपने रिश्तेदारों की अपेक्षा तुरंत सहायता के लिए उपस्थित हो जाते हैं। भले ही यह बात सच हो लेकिन अपने पास में रहने वालों की निंदा करने से भी वे कभी बाज नहीं आते। आप कितनी भी अच्छी तरह से उनके साथ रहें या उनके साथ अच्छा व्यवहार करें; फिर भी वे आपकी निंदा करना नहीं छोड़ेंगे। निंदा करना उनकी आदत होती है।

अपने पड़ोस में रहने वाले किसी व्यक्ति ने नई गाड़ी खरीदी हो या कुछ अन्य नई वस्तु घर पर लाई हो; तो वे जल-भूनकर राख हो जाते हैं और उस व्यक्ति के बारे में भला-बुरा कहने लगते हैं। इसलिए उपर्युक्त वाक्य से मैं सहमत हूँ। (विद्यार्थी अपने व्यक्तिगत विचार स्वतंत्र रूप से भी लिख सकते हैं।)

(घ) परिच्छेद पढ़कर दी गई सूचना के अनुसार कृतियाँ कीजिए।

कृति (1) आकलन कृति

प्रश्न 1.
कृति पूर्ण कीजिए।
उत्तर:

प्रश्न 2.
सहसंबंध लिखिए।
i. शांति बुआ : आटा :: लाला दीनदयाल : ……………
उत्तर:
मिठाई का बोइया

कृति घ (2): आकलन कृति

प्रश्न 1.
समझकर लिखिए।
उत्तर:

प्रश्न 2.
सही पर्याय चुनकर लिखिए।
i. लाला जी ने आइस्क्रीम नहीं खाई क्योंकि ………….।
(क) उन्हें सर्दी हो जाती है।
(ख) उन्हें बुखार चढ़ जाता है।
(ग) उनके दाँत चीसने लगते हैं।
उत्तर:
(ग) उनके दाँत चीसने लगते हैं।

ii. पत्नी का दिल बाग-बाग हो गया क्योंकि ………….।
(क) शांति बुआ आटे का कटोरा रेफ्रीजरेटर में रखना चाहती थी।
(ख) शांति बुआ बिना बुलाए लेखक के घर आई थी।
(ग) शांति बुआ रेफ्रीजरेटर का ठंडा पानी पीना चाहती थी।
उत्तर:
(क) शांति बुआ आटे का कटोरा रेफ्रीजरेटर में रखना चाहती थी।

कृति (3) शब्द संपदा

प्रश्न 1.
निम्नलिखित शब्दों के अर्थ गद्यांश से ढूँढकर लिखिए।

1. प्रसन्नता
2. संध्या
3. दया

उत्तर:

1. खुशी
2. शाम
3. कृपा

प्रश्न 2.
लिंग बदलिए।
i. भगवान
ii. लाला
उत्तर:
i. भगवती
ii. ललाइन

प्रश्न 3.
बचन बदलिए।
i. चिंता
ii. तश्तरी
उत्तर:
i. चिंताएँ
ii. तश्तरियाँ

प्रश्न 4.
प्रत्यय पहचानिए।
i. जल्दबाज
उत्तर:
‘बाज’ प्रत्यय

प्रश्न 5.
उपसर्ग लगाकर नए शब्द लिखिए।
i. कृपा
ii. दुआ
उत्तर:
i. अवकृपा
ii. बदुआ

प्रश्न 6.
मुहावरे का अर्थ लिखकर उसका वाक्य में प्रयोग कीजिए।
i. मिसरी घोलकर बोलना
उत्तरः
अर्थः मीठी-मीठी बातें करना।
वाक्यः रामलाल अपने स्वार्थ हेतु सभी से मिसरी घोलकर बोलते हैं।

(छ) परिच्छेद पड़कर दी गई सूचना के अनुसार कृतियाँ कीजिए।

कृति (1) आकलन कृति

प्रश्न 1.
आकृति पूर्ण कीजिए।
उत्तरः

प्रश्न 2.
सहसंबंध लिखिए।
i. लखनऊ : चमनलाल :: कोलकाता : ….
उत्तर:
बनर्जी

कृति (2) आकलन कृति

प्रश्न 1.
गद्यांश के आधार पर ऐसे प्रश्न तैयार कीजिए कि जिनके उत्तर निम्न शब्द हो।
i. सिंधी आलू
ii. स्कूल
उत्तर:
i. कैलाश को क्या अच्छे लगते हैं?
ii. हेमंत-अमिता कहाँ गए थे?

प्रश्न 2.
सत्य-असत्य लिखिए।
i. सिल्वर क्रीम बनर्जी बाबू ने खाई।
ii. सिंधी आलू लेखक की पत्नी ने बनवाए थे।
उत्तर:
i. असत्य
ii. असत्य

कृति (3) शब्द संपदा

प्रश्न 1.
लिंग बदलिए।
i. भाभी
ii. पत्ति
उत्तर:
i. भैया
ii. पत्नी

प्रश्न 2.
प्रत्यय पहचानिए।
i. मूर्खता
ii. बिगड़कर
उत्तर:
i. ‘ता’ प्रत्यय
ii. ‘कर’ प्रत्यय

प्रश्न 3.
विलोम शब्द लिखिए।
i. वास्तव × ……….
ii. फायदा × …………
उत्तरः
i. काल्पनिक
ii. नुकसान

प्रश्न 4.
समानार्थी शब्द लिखिए।

1. स्कूल
2. निराश
3.  आँख
4. लाचारी

उत्तर:

1. विद्यालय
2. उदास
3. नयन
4. बेबसी

प्रश्न 5.
गोश में ‘महत्त्वहीन’ इस अर्थ से संबंधित कहावत है।
उत्तरः
ऐरा-गैरा नत्थू खैरा

कृति (4) स्वमत अभिव्यक्ति

प्रश्न 1.
‘आधुनिक युग में समाचार उड़ती बीमारी से भी तेज फैलते हैं।’ अपने विचार लिखिए।
उत्तर:
आधुनिक युग विज्ञान व तकनीकी का युग है। आज मानव सभ्यता प्रगति की ओर अग्रसर है। इस युग में संचार माध्यमों का अत्यधिक प्रचार-प्रसार हुआ है। संचार माध्यमों ने विश्व की दूरियों को समेटकर बहुत छोटा कर दिया है। जितनी जल्दी से कोई भी संक्रामक बीमारी नहीं फैल सकती है; उतनी जल्दी से समाचार देश के कोने-कोने में फैलते हैं। दूरदर्शन के विविध चैनल, समाचार पत्र, मोबाइल फोन, एस. एम. एस., ट्विटर, ई-मेल आदि के जरिए समाचार तुरंत पलभर में संपूर्ण देश में फैल जाते हैं। आज हम अपने देश में बैठे हुए भी दूसरे देशों में होने वाली घटनाओं से तुरंत अवगत हो जाते हैं।

(च) परिच्छेद पढ़कर सूचना के अनुसार कृतियाँ कीजिए।

कृति (1) आकलन कृति

प्रश्न 1.
जोड़ियाँ मिलाइए।

(अ)	(ब)
1. रमा	(क) मिठाई
2. रामानुज	(ख) पराठे
3. शांति बुआ	(ग) साग
4. चक्रवर्ती	(घ) पनीर

उत्तरः

(अ)	(ब)
1. रमा	(ख) पराठे
2. रामानुज	(क) मिठाई
3. शांति बुआ	(घ) पनीर
4. चक्रवर्ती	(ग) साग

कृति (2) आकलन कृति

प्रश्न 1.
घटनाक्रमानुसार वाक्य लिखिए।

1. अब लेखक के घर के पास भी कोई नहीं फटकता है।
2. लेखक ने पनीर फेंक दिया था।
3. लेखक की पत्नी ने पराठे साधु को दिए थे।
4. लेखक ने मिठाई घर पर पधारे अपने मित्रों को दे दी।

उत्तर:

1. लेखक ने पनीर फेंक दिया था।
2. लेखक ने मिठाई घर पर पधारे अपने मित्रों को दे दी।
3. लेखक की पत्नी ने पराठे साधु को दिए थे।
4. अब लेखक के घर के पास भी कोई नहीं फटकता है।

प्रश्न 2.
आकृति पूर्ण कीजिए।
उत्तरः

कृति (3) शब्द संपदा

प्रश्न 1.
निम्नलिखित शब्दों के अर्थ गद्यांश से ढूँड़कर लिखिए।

1. आशीर्वाद
2. वर्षा
3. परेशान
4. वस्तु

उत्तर:

1. आशीष
2. बारिश
3. तंग
4. चीज

प्रश्न 2.
बिलोम लिखिए।
i. कल x ………….
ii. विश्वास x …………
उत्तर:
i. आज
ii. अविश्वास

प्रश्न 3.
वचन बदलिए।
i. बीमारी
i. शंका
उत्तर:
i. बीमारियाँ
ii. शंकाएँ

प्रश्न 4.
प्रत्यय पहचानिए।
i. बीमारी
ii. लाचारी
उत्तर:
i. ‘ई’ प्रत्यय
ii. ‘ई’ प्रत्यय

प्रश्न 5.
लिंग बदलिए।

1. साधु
2. चाचा
3. बुआ

उत्तर:

1. साध्वी
2. चाची
3. फूफा

कृति (4) स्वमत अभिव्यक्ति

प्रश्न 1.
‘जैसे के साथ तैसा व्यवहार करना चाहिए।’ इस पर आधारित अपने विचार लिखिए।
उत्तर:
‘जैसे के साथ तैसा’ यह एक कहावत है। इसका अर्थ है कि जो व्यक्ति आपके साथ जिस प्रकार का व्यवहार करता हो, ठीक उसी प्रकार आपको भी उसके साथ व्यवहार करना चाहिए। यदि कोई व्यक्ति आपसे आत्मीयता एवं सादगी से पेश आता है, तो आपको भी उसके साथ आत्मीयता एवं सादगी से पेश आना चाहिए। यदि कोई आपको सभी के सामने भला बुरा कहे और आपका अपमान करें, तो आपको भी उसके साथ उसी प्रकार का व्यवहार करना चाहिए और सभी के समक्ष उसे खरी-खोटी सुनानी चाहिए। जब आप ऐसा करेंगे; तब वह व्यक्ति दुबारा आपके साथ दुर्व्यवहार करने की नहीं सोचेगा। कभी-कभी हमें दूसरों की अक्ल ठिकाने लाने के लिए उनके साथ वैसा ही व्यवहार करना पड़ता है।

भाषाई कौशल पर आधारित पाठगत कृतियाँ

प्रश्न 1.
अव्ययों का अपने बाक्यों में प्रयोग कीजिए।
i. कि
ii. अब
उत्तर:
i. मैंने कहा कि तुम अपना काम करो।
ii. अब तो मुझे चलना चाहिए।

प्रश्न 2.
काल परिवर्तन कीजिए।

1. भारत में धूम मच गई है। (अपूर्ण भूतकाल)
2. तुम तो खयाली पुलाव पका रहे हो। (सामान्य भूतकाल)
3. तुम्हारे पराठे दे दिए। (सामान्य भविष्यकाल)
4. अब मेरे घर के पास भी कोई नहीं फटक रहा था। (अपूर्ण वर्तमानकाल)
5. चिंता ने चेतन की चिता सजा दी। (पूर्ण वर्तमानकाल)
6. मैं जगह कर लूँगा। (पूर्ण भूतकाल)
7. साधु आशीष देकर चला गया। (संयुक्त वाक्य)
8. सबेरे एक साधु आ गए। (मिश्र वाक्य)

उत्तर:

1. भारत में धूम मच रही थी।
2. तुमने तो खयाली पुलाव पकाया।
3. तुम्हारे पराठे दे दूंगा।
4. अब मेरे घर के पास भी कोई नहीं फटक रहा है।
5. चिंता ने चेतन की चिता सजा दी है।
6. मैंने जगह कर ली थी।
7. साधु ने आशीष दिया और चला गया।
8. जैसे ही सबेरा हुआ वैसे ही एक साधु आ गए।

प्रश्न 3.
निम्नलिखित वाक्यों के रचना की दृष्टि से भेद लिखिए।

1. जैसे ही एक जाता था; वैसे ही दो आते थे।
2. यह सब लॉटरी का प्रताप था।
3. “सुना है तुम्हारा रेफ्रीजरेटर आ गया है?”
4. मुझसे नहीं खाई जाएगी।

उत्तर :

1. मिश्र वाक्य
2. साधारण वाक्य
3. प्रश्नार्थक वाक्य
4. निषेधार्थक वाक्य

प्रश्न 4.
रेखांकित शब्दों के भेद पहचानिए।
i. मैं बर्फ के क्यूब चूसूंगा।
ii. कुछ शौकीनों के लिए चाय बनी।
उत्तर:
i. मैं – सर्वनाम; बर्फ – द्रव्यवाचक संज्ञा
ii. कुछ – अनिश्चित संख्यावाचक विशेषण;
बनी – सकर्मक क्रिया

प्रश्न 5.
अव्यय पहचानिए।
i. जरा इधर तो सुन।
ii. कटोरा ले लिया गया और रेफ्रीजरेटर में रख दिया गया।
उत्तर:
i. इधर – क्रियाविशेषण अव्यय
ii. और – समुच्चयबोधक अव्यय

इनाम Summary in Hindi

लेखक-परिचय :

जीवन-परिचय : अरुण जी का जन्म 3 जनवरी 1928 को मेरठ, उत्तर प्रदेश में हुआ था। आधुनिक हिंदी लेखकों में इनका महत्त्वपूर्ण स्थान है। हिंदी साहित्य में आधुनिक कहानीकार एवं उपन्यासकार के रूप में श्रीमान अरुण जी का नाम उल्लेखनीय है। कहानियाँ एवं उपन्यास लिखना आपका शौक है। आपके समग्र साहित्य की 14 पुस्तकों का संकलन प्रकाशित हो चुका है। आपकी कलम ने साहित्य के विविध विधाओं को अनुग्रहित किया है।
प्रमुख कृतियाँ : एकांकी संकलन – ‘मेरे नवरस’; कहानी संग्रह – ‘बृहद हास्य संकलन’।

गद्य-परिचय :

हास्य-व्यंग्यात्मक निबंध : ‘हास्य-व्यंग्य’ का अर्थ ही है उपहास करना। अत: इस प्रकार के निबंध में उपहास को प्रधानता दी जाती है। इसमें किसी विषय का तार्किक एवं बौद्धिक विवेचनापूर्ण लेखन किया जाता है।
प्रस्तावना : प्रस्तुत कहानी ‘इनाम’ के माध्यम से लेखक अरुण जी ने रेफ्रीजरेटर को माध्यम बनाकर लोगों के आचरण एवं व्यवहार पर करारा व्यंग्य किया है।

सारांश :

प्रस्तुत पाठ एक हास्य-व्यंग्यात्मक निबंध है। भारतीय समाज में तरह-तरह की विसंगतियाँ पाई जाती हैं। इस पाठ के द्वारा लेखक ने रेफ्रीजरेटर का आधार लेकर समाज में पाई जाने वाली विसंगतियों पर हास्य के माध्यम से करारा व्यंग्य किया है। एक भारतीय कंपनी रेफ्रीजरेटर की प्रसिद्धि के लिए विदेशी विज्ञापन पद्धति का सहारा लेती है। इसके लिए प्रतियोगिता का आयोजन करती है। लेखक भी इसमें सम्मिलित होते हैं और वे जीत जाते हैं। इसी कारण उन्हें एक रेफ्रीजरेटर मुफ़्त में मिल जाता है।

मुफ़्त में मिले रेफ्रीजरेटर को देखने के लिए उनके घर में पास-पड़ोस एवं सगे-संबंधियों का तांता लग जाता है। घर आए लोगों की आव-भगत एवं उन्हें रेफ्रीजरेटर का ठंडा पानी पिलाते-पिलाते लेखक का परिवार तंग आ जाता है। इतना ही नहीं, आस-पास रहने वाले लोग उनके फ्रीज में ढेर सारी चीजें रखते हैं। अंत में लेखक को एक तरकीब सूझती है और वे लोगों द्वारा रखी गई चीज़ों का इस्तेमाल करना शुरू कर देते हैं। इस कारण अब लोग उनकी फ्रीज में अपनी चीजें रखना बंद कर देते हैं।

शब्दार्थ :

1. जुगाड़ – व्यवस्था, प्रबंध
2. दरख्वास्त – अर्ज, अरजी
3. भंभड़ – शोरशराबा
4. अमानत – धरोहर
5. प्रतियोगिता – स्पर्धा
6. प्रतियोगी – प्रतिस्पर्धी
7. बिजली – विद्युत
8. लाचारी – बेबसी

मुहावरे :

• जली-कटी सुनाना – खरी-खोटी सुनाना।
• मिसरी घोलकर बोलना – मीठी-मीठी बातें करना।
• खयाली पुलाव पकाना – कल्पना में खोए रहना, स्वप्नरंजन करना।

कहावत :

ऐरे गैरे नत्थू खैरे – महत्त्वहीन

Balbharti Maharashtra State Board Class 10 Hindi Solutions Hindi Lokvani Chapter 2 कलाकार Notes, Textbook Exercise Important Questions and Answers.

Maharashtra State Board Class 10 Hindi Lokvani Solutions Chapter 2 कलाकार

Hindi Lokvani 10th Std Digest Chapter 2 कलाकार Textbook Questions and Answers

स्वाध्याय :

सूचना के अनुसार कृतियाँ कीजिए :

1. संजाल पूर्ण कीजिए।

प्रश्न 1.
संजाल पूर्ण कीजिए।

उत्तर:

2. परिणाम लिखिए :

प्रश्न 1.
बीमार सेठानी पर धूनी की चुटकी भर राख का…..
उत्तर:
सकारात्मक प्रभाव पड़ा और धीरे-धीरे उसकी तबीयत सुधरने लगी।

प्रश्न 2.
बहुरूपिये की वास्तविकता जानने के उपरांत सेठ जी की स्थिति –
उत्तरः
वह आश्चर्य के मारे आसमान से गिरा।

3. निम्नलिखित विधान सही करके लिखिए।

प्रश्न 1.
बहुरूपिये हू-ब-हू उसी तरह का व्यवहार करके प्राय: लोगों को भ्रम में नहीं डालते थे।
उत्तर:
बहुरूपिये हू-ब-हू उसी तरह का व्यवहार करके प्रायः लोगों को भ्रम में डालते थे।

प्रश्न 2.
एक बार सेठ जी बीमार हो गए।
उत्तर:
एक बार सेठानी बीमार हो गई।

प्रश्न 3.
सेठानी कभी-कभी आने लगी।
उत्तर:
सेठ रोज आने लगा।

प्रश्न 4.
साधु ने झगड़ा करके सेठ को लौटा दिया।
उत्तरः
साधु ने समझा-बुझाकर सेठ को लौटा दिया।

प्रवाह तालिका पूर्ण कीजिए।

प्रश्न 1.
प्रवाह तालिका पूर्ण कीजिए।

उत्तर:

5. निम्नलिखित वाक्यों को घटनाक्रम के अनुसार लिखिए।

प्रश्न 1.
निम्नलिखित वाक्यों को घटनाक्रम के अनुसार लिखिए।

1. सेठजी द्वारा सेठानी को साधु के पास ले जाना।
2. बहुरूपिये का साधु का रूप लेना।
3. सेठानी का बीमार होना।
4. धीरे-धीरे सेठानी की तबीयत सुधरना।

उत्तर:

1. बहुरूपिये का साधु का रूप लेना।
2. सेठानी का बीमार होना
3. सेठजी द्वारा सेठानी को साधु के पास ले जाना।
4. धीरे-धीरे सेठानी की तबीयत सुधरना।

6. इन कृदंत शब्दों की मूल क्रियाएँ लिखिए।

प्रश्न 1.
इन कृदंत शब्दों की मूल क्रियाएँ लिखिए।

1. झुकाव = [ ]
2. सोच = [ ]
3. बनावट = [ ]
4. लगाव = [ ]

उत्तर:

1. झुकाव = [झुकाना या झुकना]
2. सोच = [सोचना]
3. बनावट = [बनवाना]
4. लगाव = [लगना]

7. ‘कला के प्रति ईमानदारी ही सच्चे कलाकार की पहचान है।’ विषय पर अपने विचार लिखिए। 

प्रश्न 1.
‘कला के प्रति ईमानदारी ही सच्चे कलाकार की पहचान है।’ विषय पर अपने विचार लिखिए।
उत्तरः
कलाकार उसे कहते हैं जो कला का ज्ञाता हो, जिसे अपनी कला के सिवा अन्य कुछ नहीं भाता हो। अपनी कला का बेहतर प्रदर्शन करके लोगों का मनोरंजन करना ही उसका मुख्य उद्देश्य होता है। फिर वह कलाकार, अभिनेता हो या फिर कोई बहुरूपिया। उसकी कला ही उसकी पहचान होती है। इसलिए उसे अपनी पहचान एवं अस्तित्व को कभी नहीं खोना चाहिए। चरित्र निर्माण एवं संस्कार करने में कलाकार की भूमिका अनन्यसाधारण होती

है। इसलिए वह अपनी कला के माध्यम से लोगों पर अपनी अमिट छाप छोड़ता है। यदि वह अपनी कला के प्रति ईमानदार नहीं होता अथवा उसका सहारा लेकर गलत कार्य करता है, तो इससे उसकी कला का अपमान होता है। अत: वह हमेशा अपना व्यक्तिगत स्वार्थ त्यागकर, अपने पेशे के प्रति ईमानदारी पर अधिक बल देता है। इसी कारण समाज में उसकी प्रतिष्ठा बढ़ती है और सभी उसका और उसकी कला का सम्मान करते हैं।

अभिव्यक्ति :

प्रश्न 1.
‘सहयोग से कठिन कार्य की पूर्ति होती है।’ विषय पर अपने विचार शब्दांकित कीजिए।
उत्तर:
मनुष्य एक सामाजिक प्राणी है जिसकी उन्नति सहयोग की बुनियाद पर निर्भर है। सहयोग भावना मानवता का प्रतीक है। किसी भी व्यक्ति को सहयोग करना एवं उसे सहायता पहुँचाना सबसे बड़ा धर्म होता है। हमें सबकी समान भाव से मदद करनी चाहिए। सहयोग से बहुत बड़े-बड़े कार्य पूर्ण होते हैं। सहयोग से पुल का निर्माण होता है, बड़ी-बड़ी इमारतें सहयोग के बल पर ही बनती हैं।

सहयोग से व्यक्ति, समाज व राष्ट्र की उन्नति होती है। सहयोग के बल पर ही आधुनिक भारत का नवनिर्माण संभव है। गाँधी जी ने सभी भारतीयों का सहयोग पाकर ही इस देश को अंग्रेजों के शासन से मुक्त कराया तथा हमें आजादी दिला पाने में सफल रहे। सहयोग असंभव को संभव कर देता है। अत: सभी को इसका पालन करना चाहिए।

भाषाबिंदु :

प्रश्न 1.
पाठ में प्रयुक्त तीन-तीन क्रियाविशेषण अव्यय व संबंधसूचक अव्यय बकर उनका स्वतंत्र वाक्य में प्रयोग कीजिए।
उत्तर:
1. क्रियाविशेषण अव्यय :

• धीरे-धीरे : गाड़ी धीरे-धीरे जा रही थी।
• एक बार : एक बार मैं बहुत बीमार हो गया था।
• अब : अब मैं जा रहा हूँ।

2. संबंधसूचक अव्यय :

• के लिए : मैंने उसके लिए खिलौने लाए।
• की तरफ : मैंने तुरंत उसकी तरफ देखा।
• के नीचे : पेड़ के नीचे एक लड़का बैठा था।

उपयोजित लेखन :

प्रश्न 1.
आपके विद्यालय की सैर का वर्णन करने वाला पत्र अपनी सहेली या अपने मित्र को लिखिए। (पत्र निम्न प्रारूप में हों।)

उत्तर:

10 जुलाई, 2018
प्रिय मित्र राहुल,
सप्रेम नमस्ते।
तुम कैसे हो? बहुत दिन हो गए लेकिन तुम्हारा पत्र नहीं मिला। आशा करता हूँ कि तुम ठीक होगे। मैं भी कुशल हूँ। मेरी चिंता मत करना राहुल, हमारे विद्यालय ने महाबलेश्वर की सैर आयोजित की थी। सैर तीन दिन की थी। दिनांक 25 जून को हम सुबह 7 बजे महाबलेश्वर की ओर निकले। करीबन शाम के 4 बजे तक हम महाबलेश्वर पहुंच गए थे। महाबलेश्वर के बारे में तुम्हें क्या बताऊँ? बहुत ही रम्य प्राकृतिक स्थल है महाबलेश्वर । वहाँ की वादियाँ एवं घाटियाँ देखकर मेरा मनमयूर नाचने लगा था।

सघन वृक्ष देखने लायक थे। चारों ओर का वातावरण बड़ा ही शांत और खुशनुमा था। हवा में ठंडक व ताज़गी थी। पेड़ों पर उछल-कूद करने वाले बंदरों की सेना देखकर मैं आनंदविभोर हो गया। वहाँ का रम्य वातावरण एवं मित्रों के साथ घूमते-घूमते तीन दिन कैसे बीत गए, इस बात का मुझे पता ही नहीं चला।

जैसे ही छुट्टियाँ शुरू हो जाएगी; वैसे ही तुम मेरे घर पर आना। फिर हम मिलकर खूब खेलेंगे। तुम्हारे माता जी एवं पिता जी को मेरा सादर प्रणाम।
तुम्हारा प्रिय मित्र,
विजय मेहता
पता : 201, गीता महल,
कृष्ण नगर,
मुंबई : 400 012
vijay-44@gmail.com

Hindi Lokvani 10th Std Textbook Solutions Chapter 2 कलाकार Additional Important Questions and Answers

(अ) गद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए।

कृति अ (1) : आकलन कृति

प्रश्न 1.
कृति पूर्ण कीजिए।
उत्तर:

प्रश्न 2.
निम्नलिखित विधान सही करके लिखिए।

i. बहुरूपियों के बारे में सभी नहीं जानते हैं।
उत्तर:
बहुरूपियों के बारे में हम सब जानते हैं।

प्रश्न 3.
समझकर लिखिए।
i. गद्यांश में इस प्रांत की लोक कथाओं का जिक्र हुआ है।
उत्तर:
राजस्थान

कृति अ (2) : शब्द संपदा

प्रश्न 1.
निम्नलिखित शब्दों के अर्थ गद्यांश में से ढूँढ़कर लिखिए।

1. पेशा
2. नगर
3. इनाम
4. धोखा

उत्तर:

1. व्यवसाय
2. शहर
3. उपहार
4. विश्वासघात

प्रश्न 2.
अनेक शब्दों के लिए एक शब्द लिखिए।
i. कपड़े धोने का पेशा करनेवाली एक जाति –
ii. अनेक प्रकार के रूप धारण करने वाला –
उत्तर:
i. धोबी
ii. बहुरूपिया

प्रश्न 3.
निम्नलिखित शब्दों के विलोम शब्द लिखिए।

1. सफलता × ……….
2. व्यवहार × ……….
3. भीतर × ……….

उत्तर:

1. असफलता
2. अव्यवहार
3. बाहर

प्रश्न 4.
निम्नलिखित शब्द से उपसर्ग व प्रत्यययुक्त शब्द बनाइए।
i. व्यवहार
ii. रूप
उत्तर:
i. उपसर्गयुक्त शब्द : अव्यवहार, प्रत्यययुक्त शब्द : व्यावहारिक
ii. उपसर्गयुक्त शब्द : कुरूप, प्रत्यययुक्त शब्द : रूपवान

कृति अ (3) : स्वमत अभिव्यक्ति

प्रश्न 1.
‘बहुरूपियों का पेशा अब समाप्त होता जा रहा है।’ अपने विचार लिखिए।
उत्तर:
पुराने जमाने में मनोरंजन के साधन सीमित होते थे। सिनेमा हॉल, दूरदर्शन, संगणक या मोबाइल जैसे अत्याधुनिक एवं मन बहलाने वाले साधन कम थे। वास्तव में मनोरंजन की दुनिया बहुत छोटी थी। पहले पुराने संस्कार एवं विधियों का अनुकरण किया जाता था। लोक कथाओं एवं लोक कलाओं का अनुकरण करने में सभी को आनंद मिलता था। लेकिन अब जमाना बदल गया है। लोगों की मनोरंजन को लेकर मानसिकता बदल गई है।

विज्ञान व तकनीकी ने मानव सभ्यता में परिवर्तन ला दिया है। इस कारण पहले जिस प्रकार बहुरूपिया द्वार-द्वार पर जाकर अपनी कलाबाजी एवं हुनर को प्रदर्शित करता था, उस प्रकार अब द्वार पर बुहरूपिया नहीं आता है। उसकी कलाबाजी एवं हुनर को देखने के लिए लोगों के पास पर्याप्त समय भी नहीं है। आपाधापी के इस युग में जहाँ अपनों के लिए वक्त नहीं है, वहाँ बहुरूपिए के करतब देखने के लिए किसी के पास समय नहीं है। इसलिए बहुरूपियों का पेशा अब समाप्त होता जा रहा है।

(आ) गद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए।

कृति आ (1): आकलंन कृति

प्रश्न 1.
संजाल पूर्ण कीजिए।
उत्तर:

प्रश्न 2.
कृति पूर्ण कीजिए।
उत्तर:

कृति आ (2) : शब्द संपदा

प्रश्न 1.
निम्नलिखित शब्दों के पर्यायवाची शब्द लिखिए।

1. भस्म
2. साधु
3. उपदेश
4. समाचार

उत्तर:

1. राख
2. सज्जन
3. सलाह
4. खबर

प्रश्न 2.
अनेक शब्दों के लिए एक शब्द लिखिए।

1. तीन आड़ी रेखाओं का तिलक .
2. कमर में बाँधने का एक प्रकार का वस्त्र –
3. जिसने संसार को त्यागा है –

उत्तर:

1. त्रिपुंड
2. लँगोटी
3. संसारत्यागी

प्रश्न 3.
विलोम शब्द लिखिए।

1. कीर्ति × ……….
2. आशीर्वाद × ………….
3. साधु × …………..
4. नगर × ………….

उत्तर:

1. अपकीर्ति
2. शाप
3. गाँव

प्रश्न 4.
गद्यांश में प्रयुक्त पर्यायवाची शब्द को ढूँढ़कर लिखिए।
उत्तर:
i. सिर, माथा

प्रश्न 5.
वचन बदलिए।

1. डेरा
2. झोपड़ी
3. बगीचा
4. सफलता

उत्तर:

1. डेरे
2. झोपड़ियाँ
3. बगीचे
4. सफलताएँ

प्रश्न 6.
निम्नलिखित शब्दों में से उपसर्ग छाँटकर लिखिए।
i. महात्मा
ii. उपदेश
उत्तर:
i. महा
ii. उप

प्रश्न 7.
गद्यांश से प्रयुक्त शब्द-युग्म +डकर लिखिए।
उत्तरः
i. कभी-कभी
ii. धीरे-धीरे

प्रश्न 8.
निम्नलिखित शब्द के लिए अनेकार्थी शब्द लिखिए। –
i. रूप
उत्तरः
सूरत, प्रकृति, खूबसूरत, समान।।

प्रश्न 9.
गद्यांश में से तत्सम शब्द ढूँढ़कर लिखिए।
उत्तरः
संसार, कीर्ति, साधु

कृति आ (3) : स्वमत अभिव्यक्ति

प्रश्न 1.
‘साधु माला, जटा, त्रिपुंड, कमंडल, तिलक, भस्म क्यों धारण करते हैं? अपने विचार लिखिए।
उत्तर:
भारत में हिंदू साधुओं का एक विशेष पहनावा होता है। भारतीय संस्कृति की परंपरा के अनुसार ये माला, जटा, त्रिपुंड, कमंडल, तिलक, भस्म आदि का प्रयोग करके स्वयं को संसारत्यागी

कहलवाते हैं। हिंदू समाज में तुलसी की माला का विशेष महत्व होता है। अतः साधुओं के हाथ व गले में माला होती है। जटा, भस्म व कमंडल का सीधा संबंध भगवान शिव से होता है। भगवान शिव अपने शरीर पर भस्म लगाते थे। हिंदू संप्रदाय में तिलक का भी अपना विशेष महत्त्व होता है। धार्मिक कार्य एवं ईश्वर की उपासना करने के पश्चात माथे पर तिलक लगाया जाता है। माला, जटा, त्रिपुंड, कमंडल, तिलक, भस्म आदि का आध्यात्मिक महत्त्व भी है। इनके प्रयोग से व्यक्ति शुद्ध आचरण करने लगता है। अत: साधु उपर्युक्त साधनों को धारण करते हैं।

(इ) गद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए।

कृति इ (1) : आकलन कृति

प्रश्न 1.
गद्यांश पड़कर ऐसे प्रश्न तैयार कीजिए जिनके उत्तर निम्नलिखित शब्द हों –
i. सेठ
ii. सेठानी
उत्तर:
i. अविश्वास से कौन हँस पड़ा?
ii. कौन बीमार हो गई?

प्रश्न 2.
सही विकल्प चुनकर वाक्य पूर्ण कीजिए।
i. सेठ साधु को मिलने के लिए तैयार हो गया क्योंकि…..
(अ) दुनियाभर के इलाज कराने के बाद भी उसकी माँ ठीक नहीं हुई।
(आ) दुनियाभर के इलाज कराने के बाद भी उसकी बेटी ठीक नहीं हुई।
(इ) दुनियाभर के इलाज कराने के बाद भी उसकी पत्नी ठीक नहीं हुई।
उत्तर:
सेठ साधु को मिलने के लिए तैयार हो गया क्योंकि दुनियाभर के इलाज कराने के बाद भी उसकी पत्नी ठीक नहीं हुई।

प्रश्न 3.
निम्नलिखित विधान सही करके लिखिए।

i. बड़ी प्रसन्नता से सेठ साधु को मिलने गया।
उत्तर:
हारकर सेठ साधु से मिलने गया।

प्रश्न 4.
किसने, किससे कहा?
i. “सेठानी को जीवनदान दीजिए।”
उत्तर:
सेठ ने साधु से कहा।

ii. “ऐसे ढोंगी जाने यहाँ कितने आते रहते हैं।”
उत्तर:
सेठ ने व्यक्ति से कहा।

कृति इ (2) : शब्द संपदा

प्रश्न 1.
गद्यांश में से शब्द-युग्म ढूँढ़कर लिखिए।
उत्तर:
i. कभी-कभी
ii. वैद्य-डॉक्टर

प्रश्न 2.
वचन बदलिए।
i. सेठानी
ii. पेशा
उत्तर:
i. सेठानियाँ
i. पेशे

प्रश्न 3.
गद्यांश में से प्रत्यययुक्त शब्द ढूँढकर लिखिए।
उत्तर:

1. जीवनदान : प्रत्यय : दान
2. करोड़पति : प्रत्यय : पति
3. बेईमानी : प्रत्यय : ई

प्रश्न 4.
‘अविश्वास’ इस शब्द में निहित उपसर्ग प्रत्यय को पहचानकर संबंधित उपसर्ग लगाकर अन्य दो शब्द तैयार कीजिए।
उत्तरः
अविश्वास : प्रत्यय : अ, नए शब्द : अकारण, अप्रसन्न

प्रश्न 5.
निम्नलिखित गद्यांश में प्रयुक्त लिंग शब्द की जोड़ी ढूँढकर लिखिए।
उत्तरः
सेठ-सेठानी

प्रश्न 6.
निम्नलिखित गद्यांश में प्रयुक्त पर्यायवाची शब्दों की जोड़ी ढूँढकर लिखिए।
उत्तर:
i. वैद्य-डॉक्टर
ii. चरण-पाँव

प्रश्न 7.
नीचे दिए शब्द के लिए श्रुतिसम भिन्नार्थक शब्द लिखिए।
i. संपत्ति
ii. अब
उत्तर:
i. संप्रति
ii. आब

प्रश्न 8.
निम्नलिखित शब्दों के अनेकार्थी शब्द लिखिए।
i. डोली
ii. जीवन
उत्तर:
i. एक क्रिया जो ‘डोलना’ से संबंधित है, पालकी
ii. पानी, जिंदगी

कृति इ (3) : स्वमत अभिव्यक्ति

प्रश्न 1.
‘क्या कोई साधु बीमार व्यक्ति को स्वस्थ करने की शक्ति रखता है।’ विधान को वर्तमान समय के संदर्भ में अपने विचार लिखिए।
उत्तर:
आज का युग विज्ञान एवं तकनीकी का युग है। आज हमारे समाज में साधु और तांत्रिक के वेश में कुछ ढोंगी भी देखने को मिलते हैं। वे दूसरे की अज्ञानता और सीधेपन का लाभ उठाकर पैसा कमाते हैं। ऐसे में यदि घर का कोई व्यक्ति बीमार हो जाए, तो उसे साधु या तांत्रिक के पास ले जाना उचित नहीं है। फिर भी लोग अंधविश्वास के कारण बीमार व्यक्ति को साधु महाराज के पास लेकर जाते हैं। साधु के पास कोई भी ऐसी अद्भुत शक्ति नहीं होती है। वह तो सिर्फ उसके पास आने वाले व्यक्ति

को आशीर्वाद दे सकता है और ईश्वर से उनके कष्ट हरने की प्रार्थना कर सकता है। इससे ज्यादा उसके हाथ में कुछ नहीं होता है। फिर भी लोग उस पर विश्वास रखते हैं। हमें समाज में चारों ओर फैले कुछ ढोंगी साधुओं से बचना चाहिए और बीमार व्यक्ति को डॉक्टर के पास लेकर जाना चाहिए तथा डॉक्टर से उसका इलाज करवाना चाहिए।

(ई) गद्यांश को पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए।

कृति ई (1): आकलन कृति

प्रश्न 1.
परिणाम लिखिए।

i. सेठानी की तबीयत ठीक हो जाने पर …..
उत्तरः
सेठ का साधु पर गहरा विश्वास हो गया और वह रोज साधु के पास आने लगा।

प्रश्न 2.
गद्यांश पढ़कर ऐसे प्रश्न तैयार कीजिए जिनके उत्तर निम्न शब्द हों –
i. सात-आठ
ii. धन
उत्तर:
i. सेठानी की तबीयत कितने दिनों में ठीक हो गई?
ii. क्या बढ़ने से लोभ भी उतना ही बढ़ता है?

प्रश्न 3.
संजाल पूर्ण कीजिए।
उत्तर:

कृति ई (2) : शब्द संपदा

प्रश्न 1.
निम्नलिखित वाक्य में विराम चिह्नों का उचित प्रयोग कीजिए।
i. साधु ने सेठ से कहा सच्चा सुख धन का त्याग करने में है अपना ध्यान भगवान के चरणों में लगा दो
उत्तरः
साधु ने सेठ से कहा, “सच्चा सुख धन का त्याग करने में है; अपना ध्यान भगवान के चरणों में लगा दो।”

प्रश्न 2.
निम्नलिखित शब्दों के पर्यायवाची शब्द लिखिए।

1. भगवान
2. विश्वास
3. संसार
4. लोभ

उत्तर:

1. ईश्वर
2. भरोसा
3. जग
4. लालच

प्रश्न 3.
गद्यांश में से शब्द-युग्म ढूँढ़कर लिखिए।
उत्तर:
i. सात-आठ
ii. धीरे-धीरे

प्रश्न 4.
नीचे दिए शब्द के लिए श्रुतिसम भिन्नार्थक शब्द लिखिए।
i. सात
ii. समाधी
उत्तर:
i. साथ
ii. समधी

प्रश्न 5.
‘बीमारी’ इस शब्द में से प्रत्यय अलग कीजिए और संबंधित प्रत्यय लगाकर अन्य दो शब्द बनाइए।
उत्तरः
बीमारी : शब्द : बीमार प्रत्यय : ई अन्य शब्द : लोभी, संबंधी

प्रश्न 6.
अनेक शब्दों के लिए एक शब्द लिखिए।
i. योगसाधना द्वारा अंतर्ध्यान लगाकर बैठना –
उत्तरः
समाधी

कृति ई (3) : स्वमत अभिव्यक्ति

प्रश्न 1.
‘जीवन का सच्चा सुख धन का त्याग करने में है।’ विषय पर अपने विचार लिखिए।
उत्तरः
उपर्युक्त बिल्कुल शतप्रतिशत: सही है। जीवन का सच्चा सुख धन का त्याग करने में ही है। जिस व्यक्ति को धन का लोभ नहीं होता है; वह धन का कभी भी संचय नहीं करता है। जैसे-जैसे उसके पास धन आ जाता है; वैसे-वैसे वह धन दीन-दुखियों में बाँट देता है। दीन-दुखियों के चेहरे पर संतोष देखकर उसे अथाह खुशी मिलती है। ऐसा व्यक्ति सच्चे सुख का अनुभव करता है। जीवन में जो भी महान पुरुष हुए हैं, उन्होंने कभी भी धन का संचय नहीं किया था। आजीवन उन्होंने मानवता की भलाई हेतु ही कार्य किया। आखिर यह संसार एक माया है। धन का लोभ आदमी को आदमी नहीं रहने देता। जो व्यक्ति जितना धन का संचय करता है; उतना ही उसका लोभ बढ़ता जाता है।

(उ) गद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए।

कृति उ (1): आकलन कृति

प्रश्न 1.
कारण लिखिए।
i. सेठ का संसार से मन फिर गया।
उत्तर:
क्योंकि साधु महाराज के उपदेश का उस पर सकारात्मक असर पड़ा।

प्रश्न 3.
उचित जोड़ियाँ लगाइए।

‘अ’	‘ब’
1. बैलगाड़ियों	(क) कपट
2. सच्चा	(ख) झुंड
3. साधु	(ग) ज्ञान
4. झूठ	(घ) उपदेश

उत्तरः

‘अ’	‘ब’
1. बैलगाड़ियों	(ख) झुंड
2. सच्चा	(ग) ज्ञान
3. साधु	(घ) उपदेश
4. झूठ	(क) कपट

कृति उ (2) : शब्द संपदा

प्रश्न 1.
निम्नलिखित शब्दों के पर्यायवाची शब्द लिखिए।

1. प्रणाम
2. कुटी
3. असलियत
4. मंदिर

उत्तर:

1. नमस्कार
2. झोपड़ी
3. सच्चाई
4. देवालय

प्रश्न 2.
नीचे दिए हुए शब्द के विलोम शब्द लिखिए।
i. शिष्य × ……….
ii. सच्चा × ……….
उत्तर:
i. गुरु
ii. झूठा

प्रश्न 4.
‘असलियत’ शब्द में प्रत्यय अलग कीजिए और संबंधित प्रत्यय लगाकर अन्य दो शब्द तैयार कीजिए।
उत्तर:
असलियत : प्रत्यय : इयत, अन्य शब्द: इनसानियत, हैवानियत

प्रश्न 5.
नीचे दिए गए तत्सम शब्दों के तद्भव रूप लिखिए।
i. सुवर्ण
ii. उष्ट्र
उत्तर:
i. सोना
ii. ऊँट

प्रश्न 6.
नीचे दिए गए शब्द का श्रुतिसम भिन्नार्थक शब्द लिखिए।
i. चरण
उत्तर:
चारण

कृति उ (3) : स्वमत अभिव्यक्ति

प्रश्न 1.
‘हृदय परिवर्तन व्यक्ति को सत्मार्ग की ओर अग्रसित करता है।’ विषय पर अपने विचार लिखिए।
उत्तर:
हृदय परिवर्तन एक ऐसी प्रक्रिया है, जिससे व्यक्ति का स्वभाव, उसकी बुराइयाँ आदि सब कुछ अच्छाई में परिवर्तित हो जाती हैं। हृदय परिवर्तन व्यक्ति के व्यक्तित्व को संपूर्णत: नया आयाम देता है। भगवान बौद्ध के उपदेश का अंगुलिमाल के हृदय पर सकारात्मक प्रभाव पड़ा और उसका हृदय परिवर्तन हो गया। मोहनदास गांधी का भी हृदय परिवर्तन हुआ और वे महात्मा गांधी बने। दीन-दुखियों का दुख देखकर मदर टेरेसा का भी हदय परिवर्तन हुआ था।

जिस व्यक्ति का हृदय परिवर्तन हो जाता है वह व्यक्ति सत्मार्ग की ओर अग्रसित हो जाता है और फिर वह अपने जीवन में कभी भी बुराइयों को अपनाता नहीं। वह अपने जीवन में सत्संग कर दूसरों के जीवन में खुशहाली निर्माण करता है। जिसका हृदय परिवर्तन हो जाता है वह दूसरों की सेवा निःस्वार्थ भाव से करता है। हृदय परिवर्तन व्यक्ति के जीवन का सबसे बड़ा परिवर्तन होता है।

(ऊ) गद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए।

कृति ऊ (1): आकलन कृति

प्रश्न 1.
गद्यांश पढ़कर ऐसे प्रश्न तैयार कीजिए जिनके उत्तर निम्नलिखित शब्द हों –
i. धन
ii. सेठ जी
उत्तर:
i. साधु के अनुसार मिट्टी क्या है?
ii. बहुरूपिये के अनुसार चतुर आदमी कौन है?

प्रश्न 2.
परिणाम लिखिए।
i. बहुरूपिये ने सेठ जी से धन नहीं लिया –
उत्तर:
सेठ की आँखों में आँसू आ गए।

प्रश्न 3.
निम्नलिखित विधान सही करके लिखिए।

ii. प्रसन्न भाव से बहुरूपिया सिर ऊँचा करके खड़ा था।
उत्तर:
अपराधी भाव से बहुरूपिया सिर झुकाए खड़ा था।

प्रश्न 4.
कारण लिखिए।
i. बहुरूपिये ने सेठ से अपना इनाम माँगा।
उत्तर:
क्योंकि उसने सेठ जैसे चतुर आदमी को धोखा दे दिया था और अपनी कला का सम्मान चाहता था।

कृति ऊ (2) : शब्द संपदा

प्रश्न 1.
गद्यांश में से शब्द-युग्म ढूँढकर लिखिए।
उत्तर:
i. समझा-बुझाकर
ii. इधर-उधर

प्रश्न 2.
विलोम शब्द लिखिए।

1. बड़ा × ………….
2. स्वीकार × ……….
3. इनाम × …………..
4. चतुर × ……………

उत्तर:

1. छोटा
2. अस्वीकार
3. हर्जाना
4. मूर्ख

प्रश्न 3.
पर्यायवाची शब्द लिखिए।
i. कसूर
ii. इनाम
उत्तर :
i. गलती
ii. उपहार

प्रश्न 4.
गोश में से ऐसे दो शब्द ढूँढकर लिखिए जिनके वचन परिवर्तित नहीं होते।
उत्तर:
सिर, इनाम

प्रश्न 5.
अनेक शब्दों के लिए एक शब्द लिखिए।
i. वस्तु पर से अपना स्वत्व हटा लेना –
उत्तर:
त्याग

प्रश्न 6.
निम्नलिखित शब्द के अनेकार्थी शब्द लिखिए।
i. माया
उत्तर:
माया, धन, देवी, लक्ष्मी

(ए) गद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए।

कृति ए (1) : आकलन कृति

प्रश्न 1.
गद्यांश के आधार पर वाक्य पूर्ण कीजिए।
i. अगर बहुरूपिया सेठ जी की संपत्ति लेकर भाग जाता …..
उत्तर:
अगर बहुरूपिया सेठ जी की संपत्ति लेकर भाग जाता तो उसके रूप में खोट आ सकती थी।

ii. बहुरूपिए ने रूप को सच्चा रखने के लिए
उत्तर:
बहुरूपिए ने रूप को सच्चा रखने के लिए संपत्ति का त्याग कर दिया था।

प्रश्न 2.
कारण लिखिए।
i. बहुरूपिया अब खुशी से इनाम ले सकता है।
उत्तर:
क्योंकि उसने अपने बहुरूपिये का काम पूरा कर लिया था।

प्रश्न 3.
निम्नलिखित गलत विधान सही करके लिखिए।
i. सेठानी बहुरूपिये के आशीर्वाद से ठीक हो गई थी।
उत्तर:
सेठानी और सेठ का विश्वास और संयोग इनके मिलन से सेठानी ठीक हो गई थी।

ii. दुर्जन व्यक्ति की तरह बहुरूपिये ने साधु का रूप त्याग दिया था।
उत्तर:
सच्चे महत्मा की तरह बहुरूपिये ने साधु का रूप त्याग दिया था।

कृति ए (2) : शब्द संपदा

प्रश्न 1.
निम्नलिखित वाक्य में विराम चिह्नों का उचित प्रयोग कीजिए।
i. बहुरूपिये ने सेठ से कहा अब आप जो इनाम मुझे देंगे खुशी से ले लूँगा
उत्तर:
बहुरूपिये ने सेठ से कहा, “अब आप जो इनाम मुझे देंगे, खुशी से ले लूंगा।”

प्रश्न 2.
दिए गए गद्यांश में से विदेशी शब्द ढूँढकर लिखिए।
उत्तर:
अशर्फी

प्रश्न 3.
निम्नलिखित शब्द में उचित उपसर्ग व प्रत्यय लगाकर नए शब्द तैयार कीजिए।
i. नम
ii. संतुष्ट
उत्तर:
i. उपसर्गयुक्त शब्द: विनम्र, प्रत्यययुक्त शब्द: नम्रता
ii. उपसर्गयुक्त शब्द: असंतुष्ट, प्रत्यययुक्त शब्दः संतुष्टि

प्रश्न 4.
विलोम शब्द लिखिए।
i. विश्वास ×
ii. नम्रता ×
उत्तर:
i. अविश्वास
ii. अशिष्टता

प्रश्न 5.
निम्नलिखित अनेक शब्दों के लिए एक शब्द लिखिए।
i. सोने का सिक्का –
उत्तर:
अशर्फी

कृति ए (3) : स्वमत अभिव्यक्ति

प्रश्न 1.
‘हमें अपने व्यवसाय के प्रति ईमानदार होना चाहिए।’ अपने विचार लिखिए।
उत्तर:
‘व्यवसाय’ का अर्थ है काम-धंधा एवं पेशा। व्यवसाय से व्यक्ति को रोजगार प्राप्त होता है। व्यवसाय एक नैतिक उत्तरदायित्व होता है। लाभ कमाने के ध्येय से व्यवसाय किया जाता है। व्यवसाय के कई प्रकार हैं। जैसे कि अध्यापन, डॉक्टरी, चित्रकारी आदि तरह-तरह के व्यवसाय हैं। व्यक्ति किसी भी व्यवसाय का चयन करें, पर उसे अपने व्यवसाय के प्रति ईमानदार होना चाहिए। उसे अपना काम निष्ठा एवं विश्वास से करना चाहिए। उसके मन में अपने व्यवसाय के प्रति अपनत्व की भावना होनी चाहिए तथा प्रतिकूल परिस्थिति में भी वह अपने व्यवसाय की नैतिकता में सतर्क रहे। जो व्यक्ति अपने व्यवसाय के प्रति ईमानदार होता है; वह राष्ट्रीय विकास हेतु अपना योगदान देने में सक्षम होता है। व्यवसाय के प्रति ईमानदार रहने से व्यक्ति का व्यवसाय समाज में प्रतिष्ठित स्थान प्राप्त कर लेता है। अत: हमें व्यवसाय के प्रति ईमानदार होना चाहिए।

कलाकार Summary in Hindi

लेखक – परिचय :

जीवन-परिचय : राजेंद्र यादव जी का जन्म सन 1929 में उत्तर प्रदेश के आगरा शहर में हुआ। आप साठोत्तरी पीढ़ी के जाने-माने उपन्यासकार एवं साहित्यकार हैं। राजेंद्रजी हिंदी के सर्वाधिक लोकप्रिय संपादक भी थे। इन्होंने ‘नई कहानी’ के नाम से हिंदी साहित्य में एक नई विधा का सूत्रपात भी किया था। इन्होंने ‘हम’ पत्रिका का पुनः प्रकाशन किया और यह कार्य अपने जीवन के अंतिम समय तक यानी पूरे 27 वर्ष तक जारी रखा। हिंदी अकादमी दिल्ली द्वारा आपको समग्र लेखन के लिए ‘सर्वोच्च शलाका सम्मान’ प्रदान किया गया।
प्रमुख कृतियाँ : ‘जहाँ लक्ष्मी कैद है. ‘छोटे-छोटे ताजमहल’, ‘किनारे से किनारे तक (कहानी संग्रह), ‘सारा आकाश’, ‘शह और मात’। तथा ‘उखड़े हुए लोग’ (उपन्यास) आदि।

गद्य-परिचय :

कहानी : कहानी साहित्य की एक महत्वपूर्ण विधा है। जीवन की किसी एक घटना के रोचक वर्णन को ‘कहानी’ कहते हैं। कहानी का उद्देश्य उपदेश देना और मनोरंजन करना माना जाता है। कहानी का लक्ष्य मानव जीवन की विभिन्न समस्याओं और ! संवेदनाओं को व्यक्त करना होता है।
प्रस्तावना : ‘कलाकार’ इस कहानी में लेखक राजेंद्र यादव जी ने बहुरूपिए के माध्यम से बताया है कि श्रेष्ठ कलाकार को अपनी कला के प्रति ईमानदार रहना चाहिए अर्थात व्यक्ति का कोई भी पेशा या व्यवसाय हो; उसे उसके प्रति ईमानदार होना चाहिए।

सारांश :

‘कलाकार’ एक कहानी है। यह कहानी हमें अपनी कला और व्यवसाय के प्रति ईमानदार रहने की प्रेरणा देती है। इस कहानी का नायक एक बहुरूपिया है। तरह-तरह के रूप धारण कर लोगों का मनोरंजन करना उसका पेशा है। वह अपनी कला में माहिर है। एक बार वह साधु के जैसा हू-ब-रूप धारण करके नगर के बाहर डेरा लगाकर बैठ जाता है। धीरे-धीरे लोग उसके बारे में जानने लगते हैं और उससे मिलने आने लगते हैं। चारों तरफ उसका नाम फैल जाता है। नगर में रहने वाले एक सेठ की पत्नी बीमार पड़ जाती है।

डॉक्टर एवं वैद्यों द्वारा इलाज करने पर भी वह ठीक नहीं होती है। आखिर सेठ अपनी पत्नी को लेकर साधु महाराज के पास आते हैं। संयोग वश सेठानी की तबीयत सुधरने लगता हा सात-आठ दिना म उसका तबीयत ठीक हो जाती है। अब सेठ पूरी निष्ठा से साधु महाराज का भक्त बन जाता है। साधु महाराज उसे मोह-माया को त्यागने के लिए कहते हैं। साधु के उपदेश का सेठ पर गहरा असर होता है और वह एक दिन अपनी सारी संपत्ति लेकर साधु के पास आता है। वह अपनी संपत्ति साध महाराज को दान करना चाहता है। लेकिन साधु उसे विनम्रता से ठुकरा देता है।

अब साधु को लगता है कि उसने अपनी कला का बेहतर प्रदर्शन करके सेठ जैसे चतुर आदमी को धोखा दे दिया है। अत: वह साधु का वेश त्यागकर सेठ के पास अपना इनाम माँगता है और सेठ को सब कुछ सच बता देता है। उसकी बातों को सुनकर सेठ आश्चर्यचकित हो जाते हैं। वे बहुरूपिए से कहते है कि अगर वह चाहता; तो उनका सारा धन लेकर भाग सकता था। तब बहुरूपिया कहता है कि यदि वह ऐसा करता, तो उसके रूप में खोट आ सकती थी। रूप को सच्चा रखने के लिए उसने धन का त्याग कर दिया था। फिर भी सेठ जी की समझ में कुछ नहीं आ रहा था कि यह कैसा बहुरूपिया है। जो करोड़ों की संपत्ति छोड़कर अशर्फियों के इनाम के लिए इतना प्रसन्न और संतुष्ट है।

शब्दार्थ :

1. बहुरूपिया – तरह-तरह के रूप धारण करने वाला
2. जिक्र – चर्चा
3. पेशा – व्यवसाय, उद्यम
4. नगर – शहर
5. इनाम – उपहार
6. धोखा – फरेब
7. भस्म – राख
8. साधु – सज्जन
9. उपदेश – सलाह
10. समाचार – खबर
11. अशर्फी – मूल्यवान धातु के सिक्के
12. प्रणाम – नमस्कार
13. कुटी – झोपड़ी
14. असलियत – सच्चाई
15. मंदिर – देवालय
16. कमाल – सर्वोत्तम
17. इनाम – उपहार
18. धिक्कारना – झिड़कना
19. शुभचिंतक – किसी कार्य/व्यक्ति के बारे में अच्छा सोचने वाला
20. धूनी – साधुओं द्वारा बनाया गया अग्निकुंड

मुहावरे :

1. डेरा लगाना – निवास के लिए जम जाना।
2. आसमान से गिरना – आश्चर्यचकित होना।

Balbharti Maharashtra State Board Class 10 Hindi Solutions Hindi Lokvani Chapter 6 अति सोहत स्याम जू Notes, Textbook Exercise Important Questions and Answers.

Maharashtra State Board Class 10 Hindi Lokvani Solutions Chapter 6 अति सोहत स्याम जू

Hindi Lokvani 10th Std Digest Chapter 6 अति सोहत स्याम जू Textbook Questions and Answers

सुचना के अनुसर क्रुतिया कीजिए।

1. संजाल पूर्ण कीजिए।

प्रश्न 1.
संजाल पूर्ण कीजिए।

उत्तरः

2. कृति पूर्ण कीजिए।

प्रश्न 1.
कृति पूर्ण कीजिए।

उत्तरः

3. कवि यहाँ और यह बनकर रहना चाहते हैं –

प्रश्न 1.
कवि यहाँ और यह बनकर रहना चाहते हैं –
उत्तर:
(अ) गोकुल में ग्वाला बनकर रहना चाहते हैं।
(आ) गोकुल के बने में पशु बनकर चरना चाहते हैं।
(इ) गोकुल में स्थित गिरिधर पर्वत का पत्थर बनकर रहना चाहते हैं।
(ई) यमुना के किनारे पर स्थित किसी कंदब के पेड़ पर पक्षी बनकर रहना चाहते हैं।

प्रश्न 4.

उत्तरः

प्रश्न 5.
पद्य में इस अर्थ में आए शब्द लिखिए।

1. शोभा देता है
2. ग्वाल-बालाएँ
3. गोरस देने वाली
4. शुक मुनि

उत्तरः

1. सोहत
2. अहीर की छोहरियाँ
3. धेनु
4. सुक

6. निम्न शब्दों के भिन्न-भिन्न अर्थ लिखिए:

प्रश्न 1.
निम्न शब्दों के भिन्न-भिन्न अर्थ लिखिए:
image 7

प्रश्न 2.
शब्द समूह के लिए एक शब्द लिखिए:

1. जिसके कोई खंड नहीं होते – …..
2. छाछ रखने का छोटा पात्र – ………
3. जिसका कोई अंत नहीं होता – ……
4. जो सदैव चलता रहता है – ……….

7. कृदंत व तद्धित शब्दों के मूल शब्द पहचानकर लिखिए।

प्रश्न 1.
कृदंत व तद्धित शब्दों के मूल शब्द पहचानकर लिखिए।

उत्तरः
झगड़ालू, मुस्कान, सांस्कृतिक, रसीला,
खिलाड़ी, कहानी, जगमगाहट, सुखी।

कृदंत शब्द	तद्धित शब्द
1. जगमगाना	1. रस
2. मुस्कुराना	2. झगड़ा
3. कहना	3. संस्कृति
4. खेलना	4. सुख

8. किसी एक पद का सरल अर्थ लिखिए।

प्रश्न 1.
किसी एक पद का सरल अर्थ लिखिए।
सेस, गनेस ……………
…………… नाच नचावें।
उत्तरः
कवि रसखान कहते हैं कि कृष्ण तो प्रेमरूपी भक्ति के प्यासे हैं। शेषनाग, गणेश, शिव, सूर्य एवं इंद्र जिसके गुणों की हमेशा प्रशंसा करते हैं; जिन्हें अनादि, अनंत, अखंड, अछेद, अभेद और सुवेद बनाते हैं, ब्रह्म ऋषि नारद, शुकदेव व महाकवि व्यास जैसे तपस्वी जिनके नाम की निरंतर रट लगाते रहते हैं और प्रयत्न करने के बावजूद भी उनका पार नहीं पा सकें, ऐसे कृष्ण को अहीर कन्याएँ (ग्वालिने) कटोरे भर छाछ के लिए नाच नचाती हैं।

Hindi Lokvani 10th Std Textbook Solutions Chapter 6 अति सोहत स्याम जू Additional Important Questions and Answers

(अ) निम्नलिखित पद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए।

कृति (1): आकलन कृति

1. कृति पूर्ण कीजिए।

प्रश्न 1.
कवि यहाँ और यह बनकर रहना चाहते हैं –
उत्तर:
(अ) गोकुल में ग्वाला बनकर रहना चाहते हैं।
(आ) गोकुल के बने में पशु बनकर चरना चाहते हैं।
(इ) गोकुल में स्थित गिरिधर पर्वत का पत्थर बनकर रहना चाहते हैं।
(ई) यमुना के किनारे पर स्थित किसी कंदब के पेड़ पर पक्षी बनकर रहना चाहते हैं।

प्रश्न 2.
समझकर लिखिए।
उत्तर:

कृति अ (2): शब्दसंपदा

प्रश्न 1.
निम्नलिखित शब्दों के अर्थ लिखिए।

1. मानुष
2. कालिंदी
3. गिरि
4. धेनु
5. पाहन

उत्तर:

1. मानव
2. यमुना
3. पर्वत
4. गाय
5. पत्थर

प्रश्न 2.
वचन बदलिए।
1. बसेरा
2. डाल
उत्तर:
1. बसेरे
2. डालें

प्रश्न 3.
पद्यांश में प्रयुक्त तत्सम शब्द ढूँढ़कर लिखिए।
उत्तर:

1. धेनु
2. गिरि
3. खग
4. नित

प्रश्न 4.
निम्नलिखित शब्दों में उचित प्रत्यय लगाइए।
1. गाँव
2. गोकुल
उत्तर:
1. गाँववासी
2. गोकुलवासी

कृति (3): स्वमत अभिव्यक्ति

प्रश्न 1.
‘अपने आराध्य की जन्मभूमि से सभी को लगाव होता है।’ अपने विचार लिखिए।
उत्तर:
आराध्य वह होता है जिसकी हम आराधना करते हैं। आराध्य के बिना जीवन का अर्थ प्राप्त नहीं हो सकता। अतः प्रत्येक व्यक्ति के अपने-अपने आराध्य होते हैं। अपने आराध्य की जन्मभूमि से लगाव होना, स्वाभाविक है। प्रति वर्ष हजारों-लाखों लोग अयोध्या, मथुरा-ब्रज आदि देवस्थान और अपने आराध्य देव के देवस्थलों की यात्रा करते हैं।

अपने आराध्य की जन्मभूमि को भेंट देकर लोग इसमें अपनी धन्यता समझते हैं। वहाँ पर जाकर उन्हें दिव्य आनंद की अनुभूति होती है। साधकों को ऐसा लगता है मानो वे स्वर्ग में ही आ पहुँचे हैं। आराध्य की जन्मभूमि भक्तों के लिए तीर्थस्थल होती है। ऐसे तीर्थस्थलों पर जाकर भक्त मानसिक शांति का अनुभव करते हैं। अत: अपने आराध्य की जन्मभूमि सभी को प्रिय होती है।

(आ) निम्नलिखित पद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए।

कृति आ (1): आकलन कृति

प्रश्न 1.
संजाल पूर्ण कीजिए।
उत्तर:

प्रश्न 2.
समझकर लिखिए।
उत्तर:

कृति (2): शब्दसंपदा

प्रश्न 1.
निम्नलिखित शब्दों के भिन्न अर्थ लिखिए।
1. चोटी
2. निधि
उत्तर:
1. स्त्री के सिर के गूंथे हुए बाल, पर्वत शिखा
2. संपत्ति, आश्रयस्थान

प्रश्न 2.
निम्नलिखित तद्भव शब्द का तत्सम रूप लिखिए।
काग
उत्तर:
काक

प्रश्न 3.
उचित प्रत्यय लगाकर नया शब्द लिखिए।
1. कला
2. सुंदर
उत्तर:
1. कलापूर्ण
2. सुंदरता

प्रश्न 4.
वचन बदलिए।
1. चोटी
2. कला
उत्तर:
1. चोटियाँ
2. कलाएँ

प्रश्न 5.
निम्नलिखित शब्दों के अर्थ लिखिए।
1.धूरि
2. निधि
उत्तर:
1. धूल
2. संपत्ति

कृति आ (3): स्वमत अभिव्यक्ति

प्रश्न 1.
‘बाल कृष्ण का मनोहारी वर्णन करते हुए कवि ने कृष्ण के प्रति अपनी भक्ति समर्पित कर दी है।’ कथन का स्पष्टीकरण कीजिए।
उत्तरः
कवि रसखान कृष्ण के असाधारण भक्त थे। उन्होंने अपनी रचनाओं के माध्यम से अपनी भक्ति को कृष्ण के प्रति समर्पित कर दिया था। भगवान कृष्ण की लीलाओं से सभी परिचित है। उन्होंने गोकुल में जन्म लिया था और वे जन्म से ही अपने भक्तों का उद्धार करते रहे। अत: उनकी बालसुलभ क्रियाएँ एवं उनकी बचपन की लीलाओं का मनोहारी वर्णन कर सभी पाठकों को कृष्ण भक्ति में एकाकार करना कृष्ण प्रेमी कवियों का प्रमुख लक्ष्य रहा और साथ ही अपने इष्ट का वर्णन करते हुए उसके साथ एकाकार होना यह भी प्रमुख उद्देश्य रहा। कवि रसखान इससे अपवाद नहीं हैं। उन्होंने बड़ी ही तन्मयता से कृष्ण के बालरूप का मनोहारी वर्णन करके अपनी भक्ति को कृष्ण के चरणों में समर्पित कर दिया है।

(इ) पद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए।

कृति इ (1): आकलन कृति

प्रश्न 1.
संजाल पूर्ण कीजिए।
उत्तरः

प्रश्न 2.
निम्नलिखित शब्द पढ़कर ऐसे दो प्रश्न तैयार कीजिए जिनके उत्तर निम्न शब्द हों –
1. ग्वाले
2. कृष्ण
उत्तरः
1. कौन पुकार कर हँस रहे थे?
2. कवि की आँखों में किसकी छबि बस गई है?

3. कारण लिखिए।

प्रश्न 1.
कवि रसखान की आँखें बौरा हो गई हैं।
उत्तरः
कृष्ण के आकर्षक एवं मनोहारी रूप को देखकर कवि रसखान की आँखें बौरा हो गई हैं।

कृति (2): शब्दसंपदा

प्रश्न 1.
वचन बदलिए।
1. वनमाला
2. मूर्ति
उत्तरः
1. वनमालाएँ
2. मूर्तियाँ

प्रश्न 2.
निम्नलिखित शब्दों के पर्यायवाची शब्द लिखिए।

1. पाग
2. भाल
3. हिय
4. नैन

उत्तरः

1. पगड़ी
2. मस्तक
3. हृदय
4. आँखें

कृति (3): स्वमत अभिव्यक्ति

प्रश्न 1.
बाल कृष्ण की छबि देखकर अपने मन में आए विचारों को अभिव्यक्त कीजिए।
उत्तरः
बाल कृष्ण भगवान कृष्ण का बचपन का रूप था, जो मोहक एवं सभी को अपनी ओर आकर्षित करता था। मैंने कई बार बाल कृष्ण की छबि देखी है। इतना ही नहीं, मैंने दूरदर्शन पर कई धारावाहिक भी देखे हैं; जिसमें कृष्ण के बालरूप को बड़े ही मनोहारी एवं आकर्षक रूप में दर्शाया गया है। बाल कृष्ण के सुंदर व मुग्ध रूप को देखकर मैं आनंदविभोर हो गया हूँ। कोमल, श्यामल रंग, हाथ में बाँसुरी लिए हुए वे बहुत आकर्षक लगते है। उनकी छबि दिव्य और बड़ी ही मोहक है।

(ई) पद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए।

कृति (1): आकलन कृति

प्रश्न 1.
कृति पूर्ण कीजिए।
उत्तरः

कृति (2): शब्दसंपदा

प्रश्न 1.
निम्नलिखित शब्दों के अर्थ लिखिए।
1. अहीर
2. दिनेश
उत्तरः
1. ग्वाला
2. सूर्य

प्रश्न 2.
शब्द समूह के लिए एक शब्द लिखिए।
1. जिसके कोई खंड नहीं होते –
2. जिसका कोई अंत नहीं होता –
3.  छाछ रखने का छोटा पात्र –
4.  जो सदैव चलता रहता है –
उत्तरः
1. अखंड
2. अनंत
3. छछिया
4. निरंतर

प्रश्न 3.
निम्नलिखित शब्द में उचित उपसर्ग व प्रत्यय लगाइए।
खंड:
उत्तरः
उपसर्गयुक्त शब्द : अखंड
प्रत्यययुक्त शब्द : अखंडता

प्रश्न 4.
पद्यांश में से उपसर्गयुक्त शब्द ढूँढ़कर लिखिए।
उत्तरः

1. अनंत
2. अभेद
3. अखंड
4. अनादि

प्रश्न 5.
निम्नलिखित शब्द के भिन्न अर्थ लिखिए।
व्यास
उत्तरः
महर्षि व्यास, कथावाचक, ज्यामिति

कृति (3): स्वमत अभिव्यक्ति

प्रश्न 1.
‘ईश्वर सच्चे और निष्कपट भक्ति का प्यासा होता है।’ कथन विषय पर अपने विचार लिखिए।
उत्तरः
ईश्वर सच्चे प्रेम का भूखा होता है। वह सच्चे मन से की गई भक्ति पर प्रसन्न होता है और अपने भक्तों को स्वयं के दर्शन कराता है। उसे पाने के लिए हमें दिन-रात उसके नाम का जप करने की जरूरत नहीं होती। उसका दिन-रात भजन करना भी आवश्यक नहीं होता। उसे तो सच्चा भक्त कभी भी सच्चे हृदय से पुकार सकता है।

जब अंतर्मन से निकलने वाली पुकार में सच्चे मन की भक्ति की एकाग्रता हो, तो वह स्वयं अपने भक्तों की पुकार पर सहायता के लिए आ जाता है। गोकुल में रहने वाली ग्वालिने कृष्ण से सच्चे हृदय से प्रेम करती थीं। अत: वे उनके साथ नाचते-गाते थे और उनसे माखन पाने के लिए हठ करते थे। संत कबीर ने भी अपनी रचनाओं के द्वारा यही समझाया है कि ईश्वर को पाने के लिए हमें धार्मिक आडंबरों की जरूरत नहीं होती। उसे तो सच्चे हृदय से प्राप्त किया जा सकता है।

अति सोहत स्याम जू Summary in Hindi

कवि-परिचय:

जीवन-परिचय: रसखान जी का जन्म सन १५९० में उत्तर प्रदेश के पिहानी, मथुरा में हुआ। इनका मूलनाम सैयद इब्राहिम था। ये भगवान श्रीकृष्ण के अनन्यसाधारण भक्त थे। हिंदी के कृष्ण भक्त तथा रीतिकालीन रीतिमुक्त कवियों में इनका प्रमुख स्थान है। इनकी अधिकांश रचनाएँ भगवान कृष्ण के लिए समर्पित हैं। इनकी रचनाओं में भक्ति एवं श्रृंगार रस की प्रधानता है। इन्होंने श्रीकृष्ण के सगुण रूप को बड़े ही मनोहारी ढंग से अभिव्यक्त किया है।

प्रमुख कृतियाँ: ‘प्रेमवाटिका’ (दोहे), ‘सुजान रसखान’ (कवित्त, सवैया) आदि।

पद्य-परिचय:

सवैया: सवैया मात्रिक छंद का एक प्रकार है। इसमें चार चरण होते हैं । प्रत्येक चरण में २२ से २६ वर्ण होते हैं। रीतिकाल में ।
विभिन्न प्रकार के सवैया प्रचलित रहे हैं।

प्रस्तावना: ‘अति सोहत स्याम जू’ इस रचना में कवि रसखान ने श्रीकृष्ण की जन्मभूमि के प्रति लगाव, बालकृष्ण का मनोहारी वर्णन ।
एवं उसे पाने के लिए हृदय में सच्ची भक्ति की आवश्यकता जैसे बिंदुओं का विस्तार से सुंदर वर्णन किया है।

सारांश:

कवि रसखान भगवान श्रीकृष्ण के अनन्यसाधारण भक्त थे। उन्हें श्रीकृष्ण की जन्मभूमि के प्रति बेहद लगाव है। वे कृष्ण-भक्ति में एकाकार हो गए हैं। वे श्रीकृष्ण से अलग होना नहीं चाहते हैं। वे सदैव उनका सानिध्य चाहते हैं। इसलिए वे अगले जन्म में किसी भी योनी में जन्म लें फिर भी वे गोकुल से अलग होना नहीं चाहते। वे गोकुल में उपस्थित किसी भी प्राकृतिक अंश में बस जाना चाहते हैं। कवि रसखान ने बालकृष्ण का अत्यंत मनोहारी वर्णन किया है।

कृष्ण के आकर्षक एवं मनोहारी रूप को देखकर कवि रसखान की आँखे उन्मुक्त हो गई हैं। श्रीकृष्ण सच्ची भक्ति के द्वारा तुरंत मिल सकते हैं। उन्हें पाने के लिए भक्त को सच्चे हृदय से उन्हें पुकारने की आवश्यकता होती है। श्रीकृष्ण सच्ची भक्ति के प्यासे हैं। उनके दर्शन के लिए निरंतर जाप की आवश्यकता नहीं होती। श्रीकृष्ण भी सच्चे भक्त की पुकार सुनकर उसकी सहायता के लिए तत्पर हो जाते हैं। इस प्रकार प्रस्तुत रचना के माध्यम से कवि रसखान ने अपनी भक्ति श्रीकृष्ण के चरणों में समर्पित कर दी है।

भावार्थ:

1. मानुष …………………….. कूल कंदब की डारन।।

कवि रसखान कृष्णभक्त थे। उन्हें श्रीकृष्ण के जन्मभूमि के प्रति बेहद लगाव है। वे प्रत्येक स्थिति में श्रीकृष्ण का सानिध्य चाहते हैं। वे । भगवान कृष्ण की आराधना करते हुए कहते हैं कि यदि अगले जन्म में मनुष्य बनूँ, तो गोकुल के ग्वालों और गायों के बीच रहना पसंद करूँगा। ,
यदि मैं पशु की योनि में जन्म लेता हूँ, तो हमेशा नंद की गायों के साथ चरना चाहूँगा। यदि मैं पत्थर बनूँ, तो उसी पर्वत का पत्थर बनूँ जिसे । इंद्र के कारण भगवान कृष्ण ने अपनी उँगली पर धारण कर लिया था। यदि पक्षी बनूँ, तो यमुना के किनारे पर स्थित किसी कंदब के पेड़ की । डाल पर अपना बसेरा निर्माण करूँ।

2. धूरि भरे अति ……………….. माखन रोटी।

कवि रसखान ने प्रस्तुत पंक्तियों के माध्यम से बालकृष्ण का अत्यंत मनोहारी वर्णन किया है। बालकृष्ण धूल से सने हुए अत्यंत मोहक लग रहे हैं। उनके सिर पर चोटी शोभायमान हो रही है। उन्होंने कमर में पीली धोती पहनी हुई है तथा पैरों में पैजनियाँ बज रही है। वे पूरे आँगन में खाते-खेलते घूम रहे हैं। रसखान कहते हैं कि उनकी छवि देखकर कामदेव अपनी करोड़ों कलाओं की निधि निछावर करते हैं। सचमुच । वह कौआ बहुत ही भाग्यशाली है जो बालकृष्ण के हाथ से माखन रोटी को छीन कर ले उड़ा है।

3. सोहत हे चॅदवा ………………………. माँझ बसी है।

कवि रसखान कृष्ण के बालरूप का वर्णन करते हुए कहते हैं कि उनके सिर पर मोर मुकुट शोभायमान है। उन्होंने अपने सिर पर बड़ी । सुंदर पगड़ी बाँध रखी है। उनके मस्तक पर गायों के पैरों से उड़नेवाली धूल वैसे ही शोभा दे रही है जैसे हृदय पर वनमाला शोभित हो रही है। कृष्ण के आकर्षक एवं मनोहारी रूप को देखकर कवि रसखान की आँखे मारे खुशी के पागल हो गई हैं। उनकी बंद आँखों को देखकर ग्वाले उन्हें पुकारकर हँस रहे हैं, मानो वे उन्हें अपनी आँखा से पलकों के घूघट खोलने के लिए कह रहे हैं। किंतु कवि रसखान के सामने समस्या यह है कि वे अपनी पलकें नहीं खोल सकते क्योंकि कृष्ण की छवि उनकी आँखों में बस गई है।

4. सेस, गनेस ………………… नाच नचावें।

कवि रसखान कहते हैं कि कृष्ण तो प्रेमरूपी भक्ति के प्यासे हैं। शेषनाग, गणेश, शिव, सूर्य एवं इंद्र जिनके गुणों की हमेशा प्रशंसा करते हैं; जिन्हें अनादि, अनंत, अखंड अछेद, अभेद और सुवेद बताते हैं। ब्रह्म ऋषि नारद, शुकदेव व महाकवि व्यास जैसे तपस्वी जिनके नाम को निरंतर रटते रहते हैं और प्रयत्न करने के बावजूद भी उनका पार नहीं पा सके, ऐसे कृष्ण को अहीर कन्याएँ (ग्वालिने) कटोरे भर । छाछ के लिए नाच नचाती हैं।

शब्दार्थ:

1. मानुष – मानव
2. धूरि – धूल
3. हिय – हृदय
4. गिरि – पर्वत
5. पाग – पगड़ी
6. अहीर – ग्वाला, आभीर
7. धेनु – गाय
8. भाल – मस्तक
9. पाहन – पत्थर
10. दिनेश – सूर्य
11. छाछिया – छाछ रखने का छोटा पात्र
12. वारत – निछावर करना
13. लसी – सुशोभित होना
14. बिलोकत – देखना
15. पचिहारे – हार जाना
16. जू – जी
17. पीरी – पीले रंग की
18. कछोटी – कमर में लपेटी जानेवाली धोती
19. दृग – आँख
20. कूल – तट, किनारा
21. काग – कौआ

Balbharti Maharashtra State Board Class 8 Geography Solutions Chapter 9 Map Scale Notes, Textbook Exercise Important Questions and Answers.

Maharashtra State Board Class 8 Geography Solutions Chapter 9 Map Scale

Class 8 Geography Chapter 9 Map Scale Textbook Questions and Answers

1. 

Map Scale Std 8 Question a.
Classify maps showing the following areas into small scale or large scale:
(1) Building (2) School (3) Country of India (4) Church (5) Mall (6) World map (7) Garden (8) Dispensary (9) Maharashtra state (10) The north sky at night.
Answer:
The classification of maps showing the given areas is as follows:
(A) Small scale maps:

1. Country of India
2. World map
3. Maharashtra state
4. The north sky at night.

(B) Large scale maps :

1. Building
2. School
3. Church
4. Mall
5. Garden!
6. Dispensary.

Map Scale Class 8 Geography Question b.
There are two maps with respective scales of 1cm = 100 m and 1cm = 100 km. Give well reasoned answer as to which of them would be a large scale map and which a small scale map. Recognize the types of maps.
Answer:
A. Out of the two maps with respective scales of 1 cm = 100 m and 1 cm = 100 km, a map with respective scale of 1 cm = 100 m would be a large scale map.
B. Reasons :

1. 1 metre is equal to 100 centimetres and 100 metre is equal to 10000 centimetres.
2. Thus, the value of the given verbal scale (1cm = 100 m) is 1 : 10000 in numerical terms (scale).
3. A map having a numerical scale of 1 : 10,000 or less than it is called large scale map. Therefore, 1cm = 100 m would be a large scale map.

C. Types of maps :

1. Maps of villages, church, agricultural fields, etc. are the large scale maps.
2. Maps of state, country, continent, world, etc. are the small scale maps.

2. Using a map of India from the atlas measure straight Line distance between the following cities and complete the table below.

Question a.

Answer:

Cities	Distance on a map	Actual distance
1. Mumbai to Bangaluru	0.98 cm	980 km
2. Vijaypura to Jaipur	2 cm	2000 km
3. Hyderabad to Surat	0.9 cm	900 km
4. Ujjain to Shimla	1.14 cm	1140 km
5. Patna to Raipur	0.75 cm	750 km
6. Delhi to Kolkata	1 cm	1000 km

3. 

Map Scale Std 8 Questions And Answers Question a.
The distance between two points A and B on the ground is 500 m. Show this distance on paper by a line of 2 cm. Express the map scale by any one method and mention it.
Answer:

Question b.
Convert verbal scale of 1cm = 53 km to a numerical scale.
Answer:

1. 1 kilometre is equal to 100000 centimetres. Therefore, 53 kilometres is equal to 5300000 centimetres.
2. Therefore, the verbal scale of 1 cm = 53 km can be converted to a numerical scale as – 1 : 5300000.

Class 8 Geography Chapter 9 Map Scale Question c.
Convert numerical scale of 1 : 10000000 to a verbal scale in the metric system.
Answer:

1. 100000 centimetres is equal to 1 kilometre. Thus, 10000000 centimetres is equal to 100 kilometres.
2. Therefore, numerical scale of 1 : 10000000 to a verbal scale in the metric system can be converted as 1 cm = 100 km.

4. Help them, using road and railway maps of the state of Maharashtra. Use the scale given in the maps.

Std 8 Geography Chapter 9 Map Scale Question a.
Ajay wants to arrange a family trip. Beed-Aurangabad-Dhule-Nasik Mumbal-Pune-Solapur-Beed. He wants to visit tourist places along this route. The cost of the vehicle is Rs 12/- per km. What would be the approximate cost of travel?

Map Scale Questions And Answers Question b.
Saloni has been asked to organize a trip by her teacher. She has selected Nagpur Chandrapur-Nanded-Washim-Akola Malkapur. What would be the total coverage in kilometers?

Geography Class 8 Chapter 9 Question c.
Vishawasrao is transporting goods in a vehicle from Alibag (district Raigad) to Naldurg (district – Osmanabad). How many km. will he be covering aproximately for a to and fro travel?

Projects:

Map Scale Questions Question a.
Measure the length and breadth of your school. Prepare a sketch according to scale. Show different parts of your school on the sketch.

Maharashtra State Board Class 8 Geography Solutions Question b.
With the help of google maps find the distance between your village and your neighbouring village. Represent all the three methods of map scale on paper.

Class 8 Geography Chapter 9 Map Scale Additional Important Questions and Answers

Mark ✓ the box next to the right alternative:
(Note: The answers are given directly.)

Question a.
Which of the following factor’s map will be a large scale map?
(a) Temple [ ]
(b) State [ ]
(c) Nation [ ]
(d) Continent [ ]
Answer:
(a) Temple [✓]

Question b.
Which of the following scale indicates small scale map?
(a) 1 : 100 [ ]
(b) 1 : 1000 [ ]
(c) 1 : 10000 [ ]
(d) 1 : 100000 [ ]
Answer:
(d) 1 : 100000 [✓]

Answer the following questions in one sentence each:

Question a.
What is verbal scale?
Answer:
A scale in which distances are expressed with the use of words indicating measurement is called verbal scale.

Question b.
What is numerical scale?
Answer:
A scale in which distances are expressed as ratio is called numerical scale.

Question c.
What is linear scale?
Answer:
A scale in which distances are expressed by drawing graphical scale is called linear scale.

Question d.
What is large scale map?
Answer:
A map in which a particular part of ground covers comparatively more area is called large scale map.

Question e.
What is small scale map?
Answer:
A map in which a particular part of ground covers comparatively less area is called small scale map.

Write short notes on:

Question a.
Verbal scale.
Answer:
1. A scale in which distances are expressed with the use of words indicating measurement is called verbal scale.
2. For example, 1cm = 100 km.

3. In verbal scale, the word indicating measurement on the left hand side indicates the distance between any two points on a s map. On the other hand, the word indicating 1 measurement on the right hand side! indicates the ground distance between those two points.

4. When the map is reduced or enlarged by taking its photo copy, the verbal scale on the original map does not change.

Question b.
Numerical scale.
Answer:

1. Numerical scale: A scale in which distances are expressed as ratio is called numerical scale.
2. For example, 1:10000. It is also known as representative fraction.
3. In numerical scale, the same measuring unit is used for the figures on the left hand side and right hand side. However, no words are used to indicate this measuring unit.
4. In numerical scale, number 1 on the left hand side indicates the distance between any two points on a map. On the other hand, the number 10000 on the right hand side indicates the ground distance between those two points.
5. When the map is reduced or enlarged by taking its photo copy, the numerical scale on the original map does not change.

Question c.
Linear scale.
Answer:

1. A scale in which distances are expressed by drawing graphical scale is called linear scale.
2. For example,
   
3. Compass or blade of grass is used if the ruler is not available for the measurement.
4. A thread is used for measuring the curved distances between two points shown in a map.
5. When the map is reduced or enlarged by taking its photo copy, the linear scale drawn on the original map changes as per the changing size of the map.

Highlight differences /Distinguish between the following:

Question a.
Large scale map and Small scale map.
Answer:

Question b.
Numerical scale and Linear scale.
Answer:

Study the following map /figure/graph and answer the following questions:

Study the Figure and answer the following questions:

Question a.
How much is the ground distance between Mumbai and Gondia?
Answer:
The ground distance between Mumbai and Gondia is approximately 810 kilometres.

Question b.
How much is the distance between Satara and Sangli on a map?
Answer:
The distance between Satara and Sangli on a map is approximately 1.5 centimetres.

Thought-Provoking Question:

Think about it. 

Question a.
What is the need to use map scale? Think about it and write a paragraph.
Answer:

1. If the map scale is not mentioned in a map, it will become difficult to know the ground (actual) distance between any two points shown in a map.
2. Map scale is important element of a map. It facilitates map reading.
3. If the map scale is mentioned in a map, it will become very easy to understand the ground (actual) distance between any two points shown in a map.

Open-Ended Question:

Question a.
Which of the following scale will you prefer to use: (a) Verbal scale (b) Numerical scale (c) Linear scale?
Answer:

1. Different measuring units are used in different countries of the world. Due to linguistic differences, particular verbal scale or linear scale may not be used with ease in all the countries.
2. Numerical scale is a global scale. It can be used universally. Therefore, we will prefer numerical scale.

Balbharti Maharashtra State Board Class 7 History Solutions Chapter 10 The Expansion of the Maratha Power Notes, Textbook Exercise Important Questions and Answers.

Maharashtra State Board Class 7 History Solutions Chapter 10 The Expansion of the Maratha Power

Class 7 History Chapter 10 The Expansion of the Maratha Power Textbook Questions and Answers

1. Write the meaning:

The Expansion Of The Maratha Power Question Answer  Question 1.
Chauthai.
Answer:
One fourth part of the revenue

The Expansion Of The Maratha Power Question 2.
Sardeshmukhi.
Answer:
One tenth part of the revenue

2. Write the answer in one word:

Class 7 History Chapter 10 The Expansion Of The Maratha Power Question 1.
Balaji was from this town in Konkan.
Answer:
Shrivardhan

The Expansion Of The Maratha Power Class 7 Question 2.
He ruled Bundelkhand.
Answer:
King Chhatrasal

10 The Expansion Of The Maratha Power Question 3.
Bajirao died at this place.
Answer:
Raverkhedi

The Expansion Of The Maratha Power Answer Question 4.
He defeated the Portuguese.
Answer:
Chimajiappa

3. Write about them in your own words:

10. The Expansion Of The Maratha Power Question 1.
KanhojiAngre
Answer:

• Kanhoji Angre was the chief of the Maratha Navy.
• He choose Maharani Tarabai’s side.
• He attacked areas which belong to Shahu Maharaj.
• Shahu Maharaj appointed Balaji as Peshwa.
• Balaji was sent against Kanhoji.
• Balaji diplomatically turned Kanhoji towards Shahu Maharaj’s side.

Question 2.
The Battle of Palkhed
Answer:

• Mughal Emperor Farukhsear appointed Nijam-ul-Mulk as the Subhedar of Deccan.
• The Emperor gave Marathas the right to collect chauthai, Sardeshmukhi from the Mughals.
• The Nizam was against it.
• Bajirao decided to attack the Nizam and he defeated Nizam at Palkhed near Aurangabad.

Question 3.
Balaji Vishwanath:
Answer:

• Balaji Vishwanath was a prominent Maratha Sardar.
• He hailed from Shrivardhan, a town in Konkan.
• He was industrious and experienced.
• He convinced many Sardars to join hands with Shahu Maharaj.
• Kanhoji Angre, the chief of the Maratha Navy was against Shahu Maharaj and sided with Maharani Tarabai.
• He was sent against Kanhoji.
• Balaji avoided the war and diplomatically turned Kanhoji towards Shahu Maharaj’s side.

Question 4.
Bajirao I
Answer:
(i) After the death of Balaji Vishwanath, Shahu Maharaj made Bajirao I Peshwa in CE1720.

(ii) He expanded the Maratha Empire during his tenure of 20 years.

(iii) Nizam, the Subhedar of Deccan did not allow the Marathas the right to collect chauthai and sardeshmukhi.

(iv) Bajirao attacked Nizam and defeated him at Palkhed near Aurangabad.

(v) Under the leadership of his brother Chimajiappa. Bajirao sent Malharrao Holkar,: Ranoji Shinde and Udaji Pawar to strengthen the position of the Marathas in Malwa.

(vi) Mughal Subhedar Mohammad Khan Bangush attacked on Bundelkhand. The king of Bundelkhand, Chhatrasal requested Bajirao to help him.

(vii) Bajirao defeated Bangush. The King Chhatrasal honoured Bajirao on large scale.

4. Give reasons:

Question 1.
Two separate Maratha States were formed.
Answer:
(i) There was a battle between Shahu Maharaj and Maharani Tarabai for the throne/gadi.

(ii) Shahu Maharaj won the battle and captured Satara.

(iii) He got himself crowned and Satara became the capital of the Maratha kingdom.

(iv) In 1710, Maharani Tarabai declared her minor son Shivaji II as Chhatrapati at Panhalgad. Since then, a separate state of Kolhapur apart from Satara state came into existence in the Maratha Empire.

Question 2.
Azamshah released Chattrapati Shahu Maharaj from his custody.
Answer:
(i) Azamshah thought that if he released Shahu Maharaj from his custody, then there will be a fight between Maharani Tarabai and Shahu Maharaj for the throne of Chhatrapati.

(ii) The Maratha power will become weak and therefore Azamshah released Chhatrapati Shahu Maharaj from his custody.

Question 3.
Delhi Darbar needed the help of the Marathas.
Answer:
(i) The Mughal Empire was threatened by the north-west Irani and Afgani attacks.

(ii) Local kings like Pathans, Rajputs, Jats and Rohilas also posed a threat for them.

(iii) The internal competition and tussle in die court also weakened the Mughal powers. Hence, Delhi Darbar needed the help Marathas.

Activity:

Get a biography of Maharani Tarabai and present an inspiring event in her life.

Class 7 History Chapter 10 The Expansion of the Maratha Power Additional Important Questions and Answers

Complete the sentence by choosing the appropriate word from the options given below:

Question 1.
Chhatrapati Shahu Maharaj had got himself crowned at _______.(Pune, Satara, Malwa)
Answer:
Satara

Question 2.
At the time of Aurangzeb’s death, Shahajada _______ was in the south. (Azamshah, Aurangzeb, Farukhsear)
Answer:
Azamshah

Question 3.
Maharani Tarabai declared her minor son as Chhatrapati _______ at Panhala. (Shivaji II, Savai, Madhavrao)
Answer:
Shivaji II

Question 4.
_______ became the Subhedar of the Deccan. (Nijam-ul-Mulk, Farukhsear, Madhavrao)
Answer:
Nijam-ul-Mulk

Question 5.
Bajirao sent his brother ________ to subdue the Portuguese. (Chimajiappa, Malharrao Holkar, Ranoji Shinde)
Answer:
Chimajiappa

Question 6.
Bajirao defeated _________ of Bundelkhand. (Bangush, Nadir Shah, Farukhsear)
Answer:
Bangush

Question 7.
When Kanhoji Angre attacked Shahu Maharaj, he sent ______ against Kanhoji Angre. (Balaji Vishwanath, Bajirao, Shahu Maharaj)
Answer:
Balaji Vishwanath

Question 8.
After the death of Balaji Vishwanath, Shahu Maharaj made ________ as the Peshwa. (Chimajiappa, Bajirao I, Udaji Pawar)
Answer:
Bajirao I

Question 9.
Iran’s Emperor ___________ attack on India. (Nadirshah, Abdulla (Hassan), Hussein Ali)
Answer:
Nadirshah

Question 10.
After the death of Aurangzeb ________ and ______ dominated the Mughal Court.(Abdulla (Hasan), Hussein Ali, Nijam-Ul-Mulk)
Answer:
Abdulla (Hasan) and Hussein Ali

Question 11.
After the death of Emperor Aurangzeb the fight for __________ started between his sons. (Delhi’s throne, Chauthai-Sardeshmukhi, Subhedar of Deccan)
Answer:
Delhi’s throne

Question 12.
Prince Shahu was in the custody of _________ (Maharani Tarabai, Azamshah, Bahadur Shah)
Answer:
Azamshah

Question 13.
_______ became the capital of Maratha kingdom. (Satara, Kolhapur, Pune)
Answer:
Satara

Question 14.
__________was the chief of the Maratha Navy. (Balaji, Vishwanath, Kanhoji Angre, Bajirao I)
Answer:
Kanhoji Angre

Question 15.
Bajirao took his last breath at _______ (Raverkhedi, Bhopal, Palkhed)
Answer:
Raverkhedi

Question 16.
________ established the Maratha domination in North India by his bravery.
(Chimajiappa, Bajirao, King Chhatrasal)
Answer:
Bajirao

Match the following:

Question 1.

Column ‘A’	Column ‘B’
(1) Shahu Maharaj (2)Shivaji II (3) Nijam-ul-Mulk (4) Nadir Shah	(a)  Iran’s Emperor (b)  Satara (c) Panhalgad (d)  Subhedar of Deccan

Answer:
1 – b
2 – c
3 – a
4 – d

Question 2.

Column ‘A’	Column ‘B’
(1) King Chhatrasal (2)The Battle of Bhopal (3) Chauthai (4) Sardeshmukhi	(a)     One fourth part of the income (b)     Bundelkhand (c)     Bajirao (d)     One tenth part of the income.

Answer:
1 – b
2 – d
3 – a
4 – c

Explain the meanings of:

Question 1.
Subhedar.
Answer:
Historical rank in the army

Question 2.
Sanad.
Answer:
Authority

Write the answer in one word:

Question 1.
These places were under Portuguese rule.
Answer:
Vasai and Thane

Question 2.
The Emperor of Iran who invaded India.
Answer:
Nadir Shah

Question 3.
He was the chief of the Maratha Navy.
Answer:
KanhojiAngre

Question 4.
He was a great warrior.
Answer:
Bajirao

Question 5.
He was the first Peshwa.
Answer:
Balaji Vishwanath

Question 6.
The second Peshwa.
Answer:
Bajirao

Question 7.
Aurangzeb’s son.
Answer:
Shahajada Azamshah

Question 8.
Tarabai proclaimed her younger son as.
Answer:
Chhatrapati Shivaji II

Answer the following in one sentences:

Question 1.
Who was in the custody of Azamshah?
Answer:
Prince Shahu was in the custody of Azamshah.

Question 2.
What was the new political policy of Marathas?
Answer:
The new political policy of the Marathas was to protect and expand their own Empire instead of fighting with Mughal powers.

Question 3.
What had weakened the Mughal powers?
Answer:
The threat from local kings, internal competition and tussle in the court weakened the Mughal powers.

Question 4.
Who was Kanhoji Angre?
Answer:
Kanhoji Angre was the Chief of the Maratha Navy.

Question 5.
With whose help did Balaji receive the authority to recover Chauthai and Sardeshmukhi?
Answer:
With the help of Sayyid brothers, Abdulla (Hassan) and Hussein Ali, Balaji received the authority to recover Chauthai and Sardeshmukhi.

Question 6.
Whom did Bajirao send to Malwa to strengthen the position of the Marathas?
Answer:
Bajirao sent Malharrao Holkar, Ranoji Shinde and Udaji Pawar under the leadership of his x brother Chimajiappa to Malwa to strengthen the position of Marathas.

Question 7.
Whose help did King Chhatrasal seek to protect his kingdom Bundelkhand.
Answer:
The King Chhatrasal requested Bajirao to protect his kingdom Bundelkhand.

Question 8.
Which parts from Konkan coastal area were under Portuguese rule?
Answer:
Vasai and Thane from Konkan coastal area were under Portuguese rule.

Question 9.
Whom did Bajirao send to defeat Portuguese? ‘
Answer:
Bajirao sent his brother Chimajiappa to defeat the Portuguese.

Question 10.
What rights did Balaji get from the Mughal Emperor?
Answer:
Balaji got from the Mughal Emperor the sanads to collect Chauthai and Sardeshmukhi

Question 11.
Why did Chhatrasal ask Balaji for help?
Answer:
Mohammad Khan Bangush, the Mughal Subhedar of Allahabad attacked Bundelkhand and defeated Chhatrasal. So, Chhatrasal asked Balaji for help.

Question 12.
Where did Bajirao defeat the Nizam?
Answer:
Bajirao defeated the Nizam at Palkhed near Aurangabad.

Question 13.
What were the great qualities of Bajirao?
Answer:
Bajirao was a great warrior, a powerful ruler who established the Maratha dominance in North.

Write notes on the following:

Question 1.
The Battle of Bhopal
Answer:

• The emperor became restless due to Bajirao’s attack.
• He called the Nizam to protect Delhi.
• The Nizam attacked Bajirao with his large army.
• Bajirao defeated him at Bhopal.
• The Nizam agreed to secure the sanad of Malwa subhedari to Marathas from the Badshah.

Give explanations for the following:

Question 1.
Portuguese.
Answer:

• Vasai and Thane from Konkan coastal area were under Portuguese rule.
• Portuguese rulers used to exploit people.

Question 2.
King Chhatrasal requested Bajirao for help.
Answer:

• King Chhatrasal established his own kingdom in Bundelkhand.
• Mughal Subhedar Mohammad Khari Bangush attacked Bundelkhand and defeated king Chhatrasal.
• Hence, King Chhatrasal requested Bajirao for help.

Question 3.
Shahu Maharaj knew the integrities of the Mughals.
Answer:

• The early part of Shahu Maharaj’s life was spent in Mughal camps.
• He has seen Mughal politics from close quarters.
• He was aware of the strong and weak points of the Mughal empire very well.
• He also knew some influential people in Mughal Darbar.
• All these factors helped him in the changing circumstances to decide the new direction for Maratha politics.

Answer the following in short:

Question 1.
How did Balaji Vishwanath turned Kanhoji towards the side of Shahu Maharaj?
Answer:

• Kanhoji Angre was the chief of the Maratha Navy.
• He chose Maharani Tarabai’s side.
• He attacked areas which belonged to Shahu Maharaj.
• Shahu Maharaj sent Balaji Vishwanath against Kanhoji.
• Balaji avoided the war and won Kanhoji towards the side of Shahu Maharaj.

Question 2.
Why did Bajirao decide to attack Delhi?
Answer:

• The Marathas established their supremacy in Malwa and Bundelkhand.
• Bajirao demanded Malwa Subhedari from the Badshah (Emperor).
• The Emperor rejected his demand Hence Bajirao decided to attack Delhi.

Balbharti Maharashtra State Board Class 9 Hindi Solutions Lokbharti Chapter 6 निसर्ग वैभव Notes, Textbook Exercise Important Questions and Answers.

Maharashtra State Board Class 9 Hindi Lokbharti Solutions Chapter 6 निसर्ग वैभव (पूरक पठन)

Hindi Lokbharti 9th Std Digest Chapter 6 निसर्ग वैभव Textbook Questions and Answers

पठनीय :

प्रश्न 1.
निम्न शब्द पढ़िए। शब्द पढ़ने के बाद जो भाव आपके मन में आते हैं वे कक्षा में सुनाइए।

कल्पना पल्लवन :

प्रश्न 1.
किसी कार्यालय में नौकरी पाने हेतु साक्षात्कार देने वाले और लेने वाले व्यक्तियों के बीच होने वाला संवाद लिखिए।
उत्तर:

• उम्मीदवार – नमस्ते श्रीमान।
• अधिकारी – नमस्ते। आइए बैठिए।
• उम्मीदवार – जो शुक्रिया।
• अधिकारी – आपका नाम?
• उम्मीदवार – श्री राजेश तिवारी
• अधिकारी – आप अपने कार्य अनुभव के बारे में बताइए।
• उम्मीदवार – इस समय मैं वेद कंपनी में क्लर्क के पद पर काम कर रह्य हूँ। इस पद पर काम करते हुए मुझे तीन वर्ष पूर्ण हो गए हैं। इस प्रकार मेरे पास तीन वर्ष का अनुभव है।
• अधिकारी – क्या आप बता सकते हैं कि एक आदर्श कर्मचारी की कौन-कौन-सी विशेषताएँ होती हैं?
• उम्मीदवार – एक आदर्श कर्मचारी के पास अपने काम के प्रति निष्ठा लगन एवं मेहनत से काम करने का जज्बा होता है।
• अधिकारी – यदि हम आपको कंपनी में क्लर्क के पद पर नियुक्त करेंगे तो आप किस प्रकार स्वयं को अन्य कर्मचारियों से श्रेष्ठ साबित कर सकेंगे?
• उम्मीदवार – मैं अपनी पूरी लगन एवं ईमानदारी से अपने कार्य को पूर्ण करूंगा। कंपनी के प्रत्येक कार्य को मैं बड़े चाव के साथ पूरा करने का प्रयास करूंगा। इस प्रकार मैं अपनी मेहनत से अपने आप को अन्य कर्मचारियों से श्रेष्ठ साबित करने का प्रयास करूंगा।
• अधिकारी – ठीक है। धन्यवाद!
• उम्मीदवार – धन्यबाद ! श्रीमान महोदय।

पाठ के आँगन में :

1. सूचना के अनुसार कृतियाँ पूर्ण कीजिए :

प्रश्न क.
संजाल

उत्तर:

प्रश्न ख.
कविता की पंक्तियों को उचित क्रमानुसार लिखकर प्रवाह तत्जा पूर्ण कीजिए।
1. परिचित मरकत आँगन में
2. अभिशापित हो उसका जीवन?
3. अनिल स्पर्श से पुलकित तृणदल
4. निश्चल तरंग-सी स्तंभित

उत्तर:

2. कविता द्वारा प्राप्त संदेश लिखिए। 

प्रश्न 1.
कविता द्वारा प्राप्त संदेश लिखिए।
उत्तरः
प्रस्तुत कविता के माध्यम से कवि ने मनुष्य के हृदय में प्रकृति प्रेम उत्पन्न करने का प्रयास किया है। प्रकृति में चारों ओर सौंदर्य भरा पड़ा है और उस सौंदर्य की अनुभूति कराने के लिए मनुष्य को प्रकृति की ओर जाना चाहिए। मनुष्य को प्रकृति से हमेशा खुश एवं प्रसन्न रहने की प्रेरणा लेनी चाहिए। मनुष्य को एक-दूसरे से नफरत नहीं करनी चाहिए। उसे अपने मन से क्षुद्र भावों को त्यागकर प्रकृति की भाँति विशाल हृदय रखना चाहिए। मानव के मन से वैश्विक प्रेम व परोपकार की भावना साकार करना ही इस कविता का उद्देश्य है।

3. कविता के तृतीय चरण का भावार्थ सरल हिंदी में लिखिए। 

प्रश्न 1.
कविता के तृतीय चरण का भावार्थ सरल हिंदी में लिखिए।
उत्तर:
पर्वत जीवन पर बिखरी हुई प्राकृतिक सुषमा का आनंद लूटते समय कवि को सहज ही एक बात याद आ जाती है। वह यह कि जड़ जीवन में यानी प्रकृति में अपार सौंदर्य भरा पड़ा है पर मानव जीवन में दुख का भाव क्यों है? उसका मन विषण्णता से भरा क्यों पड़ा है? अत: कवि मनुष्य को कहता है कि, उसे प्रकृति से सीख लेनी चाहिए। उसे मानव प्रकृति का पुन: संश्लेषण-विश्लेषण करना चाहिए। देखा जाए तो मनुज ईश्वर का प्रतिनिधि है फिर भी उसका जीवन अभिशापित है। शायद इसलिए कि उसे क्षुद्र अहंकार रूपी भावना ने दिन-रात घेरा हुआ है। इसी कारण वह विश्व चेतना से दूर चला गया है और वह अकेला पड़ गया है।

श्रवणीय :

प्रश्न 1.
नीरज जी द्वारा लिखित कोई कविता यू ट्यूब पर सुनिए और उसके केंद्रीय भाव पर चर्चा कीजिए।

भाषा बिंदु :

प्रश्न 1.
निम्नलिखित मुहावरे या कहावतों में से अनुपयुक्त शब्द काटकर उपयुक्त शब्द लिखिए।

उत्तर:

1. टोपी पहनाना।
2. नजर बंद करना।
3. आटा गीला होना।
4. आँख की किरकिरी होना।
5. आसमान सर पर उठाना।
6. आग-पानी का बैर।

Hindi Lokbharti 9th Answers Chapter 6 निसर्ग वैभव Additional Important Questions and Answers

(क) पद्यांश पढ़कर सूचना के अनुसार कृतियाँ कीजिए।

कृति (1) आकलन कृति

प्रश्न 1.
समझकर लिखिए।
उत्तर:

प्रश्न 2.
समझकर लिखिए।
उत्तर:

प्रश्न 3.
संजाल पूर्ण कीजिए।
उत्तरः

कृति (2) स्वमत अभिव्यक्ति

प्रश्न 1.
‘आपका देखा हुआ प्राकृतिक स्थल’ इस विषय पर अपने विचार व्यक्त कीजिए।
उत्तरः
प्राकृतिक स्थल पर घूमने जाने का मला ही कुछ और है। मैंने कौसानी की यात्रा की थी। कौसानी उत्तराखंड में स्थित एक प्राकृतिक स्थल है। चारों ओर हरियाली व सघन वृक्षों को देखकर मानव मन प्रफुल्लित हो जाता है। रंग-बिरंगे फूल और आस-पास मैंडराने वाले भौरे देखकर बहुत प्रसन्नता होती है। कोहरा हट जाने पर कौसानी से हिमालय के दर्शन होते हैं। श्वेत बर्फ की राशि देखकर मानव मन बाग-बाग हो जाता है। सचमुच धरती पर अगर कहीं स्वर्ग है तो बस वह कौसानी में ही है।

(ख) पद्यांश पढ़कर सूचना के अनुसार कृतियाँ कीजिए।

कृति (1) आकलन कृति

प्रश्न 1.
समझकर लिखिए।
उत्तरः

प्रश्न 2.
कृति पूर्ण कीजिए।
उत्तरः

प्रश्न 3.
प्रस्तुत पद्यांश पढ़कर ऐसे दो प्रश्न तैयार कीजिए कि
जिनके उत्तर निम्न शब्द हों
i. साँझ
ii. नीले
उत्तर:
i. पर्वतों की घाटियों में कौन छिप जाती है?
ii. छाया कौन-से रंग की है?

कृति (2) स्वमत अभिव्यक्ति

प्रश्न 1.
‘प्रकृति अपने अनंत हाथों से मनुष्य पर उपार करती आ रही है।’ इस कथन की सार्थकता स्पष्ट कीजिए।
उत्तरः
प्रकृति साक्षात ईश्वर का दूसरा रूप है। प्रकृति मानव पर उपकार करती आ रही है। नदी, तालाब, सागर, पेड, फूल-फल, जंगल, पहाड़, पवन, सूर्य की किरण ये सब प्रकृति के अंश हैं। इनके माध्यम से प्रकृति ने मनुष्य को बहुत कुछ दिया है और दे रही है। मनुष्य को जीवन जीने के लिए अन्न, पानी एवं अन्य मूलभूत वस्तुएँ प्रकृति से ही मिलती है। मनुष्य को साँस लेने के लिए जिस प्राणवायु की जरूरत होती है वह भी प्रकृति से ही प्राप्त होती है। आयुर्वेदिक दवाएँ प्रकृति से मिलती हैं। अतः प्रकृति अपने अनंत ह्यथों से मनुष्य पर उपकार करती आ रही है। यह विधान पूर्णत: सत्य है।

(ग) पद्यांश पढ़कर सूचना के अनुसार कृतियाँ कीजिए।

कृति (1) आकलन कृति

प्रश्न 1.
आकृति पूर्ण कीजिए।
उत्तरः

प्रश्न 2.
कृति पूर्ण कीजिए।
उत्तरः

प्रश्न 3.
सत्य-असत्य लिखिए।
i. पक्षी फल चखना शुरू कर देते हैं।
ii. गिलहरियाँ फूलों को कुतरना शुरू कर देती है।
उत्तर:
i. सत्य
ii. असत्य

कृति (2) स्वमत अभिव्यक्ति

प्रश्न 1.
‘पर्वतीय जीवन में अनोखा व अद्भुत आनंद भरा होता है।’ इस कथन पर अपने विचार व्यक्त कीजिए।
उत्तरः
पर्वतीय प्रदेश सभी को अच्छे लगते हैं। सभी पर्वतीय प्रदेशों की यात्रा करना पसंद करते हैं। पर्वतीय प्रदेशों का आरोह व अवरोहण करना सभी को भाता है। पर्वतीय प्रदेश में चारों ओर हरियाली होती है। बड़े-बड़े वृक्ष एवं उन पर कलरव करने वाले पक्षियों को देखकर हमारे आँखों की तृप्ति हो जाती है। पर्वतीय प्रदेशों में बहने वाली हवा शीतल होती है। वह मानव के मन में अद्भुत प्रेरणा निर्माण करती है। पर्वतीय प्रदेश मानव हृदय को उमंग, ताजगी व उल्लास से भर देते हैं। अत: पर्वतीय जीवन में अनोखा व अदभुत आनंद भरा होता है।

(घ) पद्यांश पढ़कर सूचना के अनुसार कृतियाँ कीजिए।

कृति (1) आकलन कृति

प्रश्न 1.
कृति पूर्ण कीजिए।
उत्तरः

प्रश्न 2.
कृति पूर्ण कीजिए।
उत्तरः

प्रश्न 3.
समझकर लिखिए।
उत्तरः

कृति (2) स्वमत अभिव्यक्ति

प्रश्न 1.
‘मानव प्रकृति से दूर चला जा रहा है।’ क्या आप इस कथन से सहमत हैं ? अपने विचार लिखिए।
उत्तर:
जी हाँ, आज मानव प्रकृति से दूर चला जा रहा है। विज्ञान एवं तकनीकी के इस युग में मानव ने भले ही आसमान को छू लिया है। फिर भी प्रकृति के साथ खिलवाड़ कर उसने धरती को सौदर्यहीन कर दिया है। मानव ईया, दवेष, जलन, नफरत एवं अहंकार के कारण इतना स्वार्थी हो गया है कि वह प्रकृति के एहसान को भी भूल गया है। अपना स्वार्थ पूर्ण करने के लिए मानव एक-दूसरे का लहू बहाने से भी पीछे नहीं हटता है। अपनी इच्छाएं पूर्ण न होने के कारण वह हृदय से विषण्ण एवं दुखी हो जाता है। प्रकृति में सर्वत्र सौदर्य बिखरा हुआ है। इस तथ्य को भी वह भूल जाता है। अत: स्पष्ट है कि मानव प्रकृति से दूर चला जा रहा है।

निसर्ग वैभव Summary in Hindi

कवि-परिचय :

जीवन-परिचय : सुमित्रानंदन पंत का जन्म २0 मई 1900 को कौसानी उत्तराखंड में हुआ था। आप प्रकृति के सुकुमार कवि थे। आप छायावादी युग के चार स्तंभों में से एक हैं। आपको प्रकृति ने ही कविता लिखने की प्रेरणा दी थी। आपको साहित्य के सर्वश्रेष्ठ ज्ञानपीठ पुरस्कार से सम्मानित किया गया है।
प्रमुख कृतियाँ : काव्य संग्रह – ‘वीणा’, ‘गुंजन’, ‘पल्लव’, ‘ग्राम्या’, ‘चिदंबरा’, ‘कला और बूढ़ा चाँद’ आदि, उपन्यास – ‘हार’.
आत्मकथात्मक संस्मरण – ‘साठ वर्ष : एक रेखांकन’

पद्य-परिचय :

कविता : भावों का आविष्कार कराने वाली, हृदय में आनंद की अनुभूति निर्माण कराने वाली एवं रस का साक्षात्कार कराने वाली साहित्य की विधा ‘कविता’ कहलाती है। कविता मनुष्य के भावों की सहज अभिव्यक्ति है।

प्रस्तावना : प्रस्तुत कविता में महाकवि पंत जी ने प्राकृतिक सुषमा का बड़ा ही मनोहारी एवं अद्भुत वर्णन किया है। प्रकृति के प्रत्येक अंश में सौंदर्य भरा पड़ा है। उस अनुभूति का एहसास मनुष्य को तभी होगा जब वह प्रकृति की ओर आकर्षित होगा।

सारांश :

प्रस्तुत कविता प्राकृतिक सौंदर्य के प्रति मनुष्य के मन में आकर्षण निर्माण करती है। प्रकृति में ही ईश्वर का अंश विराजमान है, इस तथ्य को साकार करने वाली यह रचना है। महाकवि पंत जी प्रकृति के पुजारी थे। उन्होंने इस कविता के द्वारा प्रकृतिरम्य अनुभूति का साक्षात्कार तो करवाया ही है साथ में प्राकृतिक सौंदर्य का वर्णन करते समय आध्यात्मिकता की ओर पाठकों का ध्यान खींचकर उन्हें दुख, दर्द, व्यथा, नैराश्य एवं विषण्णता आदि पर विचार करने के लिए भी विवश कर दिया है।

प्रकृति के कण-कण में अपार सौंदर्य भरा पड़ा है। देखा जाए तो प्रकृति जड जग का अंश है और मानव जीवन तो चेतन जग का रूप है। फिर भी मानव जीवन में सर्वत्र विषण्णता छायी हुई है। ऐसा क्यों? मनुज को ही स्वयं इसका उत्तर ढूँढ़ने के लिए कवि ने विवश कर दिया है। इसीलिए यह कविता छायावाद का एक अनुपम उदाहरण है।

भावार्थ :

कितनी सुंदरता बिखरी ………………. वन प्रिय कोयल!
पंत जी प्रकृति के सुकुमार कवि थे। वे जानते हैं कि प्रकृति जगत में सौंदर्य बिखेरने वाला ईश्वर ही है। अतः कवि ईश्वर को संबोधित करते हुए कहते हैं, “हे ईश्वर ! प्राकृतिक जगत में सुंदरता बिखरी हुई है। पहाड़ों की चोटियों पर फैली सूरज की धूप घाटी की ओर लोट रही है और उसके डाँव में स्वयं को चुपचाप लिपटाए हुई है। धूप और छाँव का मानो मिलन हो रहा है। “हवा सर्वत्र बह रही है। उसके स्पर्श से हरी घास पुलकित यानी रोमांचित हो गई है। नदी मधुर संगीत का गान करती हुई स्वच्छंद बह रही है। प्रतिदिन प्रकृति की अनुपम शोभा का आनंद वन-भू उठा रही है।”

“चारों ओर लाल रंग के फूल खिले हुए हैं। फूलों का लाल रंग ज्वालाओं का निर्माण कर रहा है। उन्हें देखकर मनुष्य के आँखों की तृप्ति होती है यानी मनुष्य के आँखों को ठंडक मिलती है। भौरे भी अपने दल के साथ आकर गुंजन कर रहे हैं। वे फूलों की कलियों पर बैठकर अपने होंठों से मधु पान कर रहे हैं। लाल रंग के फूलों ने तितलियों को भी अपनी ओर आकर्षित कर लिया है। वे भी फूलों पर मंडरा रही हैं। ऐसे में दूर किसी पेड़ की पत्तियों की छाँव में बैठकर वन प्रिय कोयल रुक-रुककर अपना गीत गा रही है।”

लेटी नीली ………………. कर संध्यावंदन!
कवि पंत प्रकृति की सुषमा का वर्णन करते हुए कहते हैं, “आसमान में सर्वत्र नीले रंग के बादल दिखाई दे रहे हैं। इसी कारण नीले रंग की छाया दिखलाई पड़ती है। इस नीले रंग की छाया ने सूर्य के किरणों को अपने आप में समा लिया है। सूर्य के किरणों का सुनहरा रंग नीली छाया के साथ एकाकार हो गया है। इस विहंगम दृश्य को देखने के बाद ऐसा प्रतीत होता है कि नीले व सुनहरे रंग का आवरण निश्चल तरंग की तरह आसमान में निर्माण हुआ है।

ऐसे में सवेरा होने से पहले सर्वप्रथम सुनहरी किरण सर्वत्र छा जाती है। मानो उसका अभिनंदन करने के लिए ऊषा तैयार हो जाती है। इस अद्भुत दृश्य को देखने के लिए साँझ भी उत्सुक रहती है। इसीलिए वह वहीं आकर छिप जाती है। ऐसा प्रतीत होता है कि ऊषा निर्जन वन में संध्या को भी वंदन करती है।”

अपलक तारापथ ………………. मरकत आँगन में!
कवि पंत कहते हैं, “संध्या के बाद रात्रि का समय शुरू हो जाता है। आसमान में बिना पलक झपकाए असंख्य तारे दिखाई देने लगते हैं। उनके साथ चंद्रमा भी आसमान में आ जाता है। उस पूर्ण रूप में आसमान में बहुत की सुंदर तारे दिखलाई देने लगते हैं। ऐसा लगता है मानो वह एक दर्पण ही हो जिसमें असंख्य तारे अपने आप को निहार रहे हों। रात्रि के समय पर्वतों पर बहने वाली हवा भी पर्वतों के कंधों पर सो जाती है। पर्वतों पर दिखाई देने वाली यह प्राकृतिक सुषमा सभी को सम्मोहित कर देती है।

सचमुच पर्वत जीवन में अद्भुत एवं अनोखा विस्मय भरा पड़ा हुआ है। रात्रि के पश्चात फिर से सवेरा हो जाता है। पक्षी फल चखना शुरू कर देते हैं। गिलहरियाँ नए पत्तों को कुतरना शुरू कर देती हैं। धरती रूपी रत्न पर सभी वन-पशु प्रसन्न दिखाई देने लगते हैं।”

स्वाभाविक ………………. मानव मन निश्चित!
पर्वत जीवन पर बिखरी हुई प्राकृतिक सुषमा का आनंद लुटते समय कवि को सहज ही एक बात याद आ जाती है। वह यह कि जड़ जीवन में यानी प्रकृति में अपार सौंदर्य भरा पड़ा है पर मानव जीवन में दुख का भाव क्यों है? उसका मन विषण्णता से भरा क्यों पड़ा है? अतः कवि मनुष्य से कहते हैं कि उसे प्रकृति से सीख लेनी चाहिए। मनुष्य को प्रकृति का संश्लेषण-विश्लेषण करना चाहिए। देखा जाए तो मनुष्य ईश्वर का प्रतिनिधि है फिर भी उसका जीवन अभिशापित है। शायद इसलिए कि उसे क्षुद्र अहंकार रूपी भावना ने दिन-रात घेरा हुआ है। इसी कारण वह विश्व चेतना से दूर चला गया है और वह अकेला पड़ गया है।

शब्दार्थ :

1. श्लक्ष्ण – मधुर
2. अनिल – पवन
3. अहरह – प्रतिदिन
4. मुकुल – कली
5. मँझधार – बीचोबीच, लहरों के बीच
6. शैल – पर्वत
7. समीरण – पवन
8. मरकत – पन्ना (एक रत्न)
9. निर्जन – वीरान
10. अपलक – बिना पलक झपकाए
11. वैचित्र्य – अनोखापन
12. गिरि शिखर – पहाड़ों की चोटियाँ
13. वन-भू – जंगल या कानन
14. शीतल – ठंड
15. ऊषा – सुबह होने से पूर्व आसमान में सूर्य की लाल आभा फैल जाती है वह समय
16. खग – पक्षी
17. जड़ जग – सृष्टि
18. चेतन जग – संसार
19. विषण्ण – व्यथित या निराश

Balbharti Maharashtra State Board Class 10 Hindi Solutions Hindi Lokvani Chapter 1 मातृभूमि Notes, Textbook Exercise Important Questions and Answers.

Maharashtra State Board Class 10 Hindi Lokvani Solutions Chapter 1 मातृभूमि

Hindi Lokvani 10th Std Digest Chapter 1 मातृभूमि Textbook Questions and Answers

स्वाध्याय :

सूचना के अनुसार कृतियाँ कीजिए :

1. कृति पूर्ण कीजिए।

प्रश्न 1.
फूलों की विशेषताएँ

उत्तर:

प्रश्न 2.
जन्मभूमि की विशेषताएँ

उत्तर:

2. इन शब्द – शब्द समूहों के लिए कविता में प्रयुक्त शब्द लिखिए।

प्रश्न 1.
इन शब्द – शब्द समूहों के लिए कविता में प्रयुक्त शब्द लिखिए।

उत्तर:

शब्द समूह	शब्द
पक्षियों के समूह	खग वंद
शेषनाग के फन	सिंहासन
समुद्र	रत्नाकर
सूरज और चाँद	युग मुकुट

3. कृति पूर्ण कीजिए।

प्रश्न 1.
कृति पूर्ण कीजिए।

उत्तर:

4. संजाल पूर्ण कीजिए।

प्रश्न 1.
संजाल पूर्ण कीजिए।

उत्तर:

5. एक शब्द के लिए शब्द समूह लिखिए।

प्रश्न 1.
एक शब्द के लिए शब्द समूह लिखिए।
i. विश्वपालिनी = ……………………
ii. भयनिवारिणी = ………………….
उत्तर:
i. विश्व का पालन करने वाली
ii. भय का निवारण करने वाली

6. चौखट में प्रयुक्त शब्दों को सूचना के अनुसार परिवर्तन करके लिखिए। 

प्रश्न 1.
चौखट में प्रयुक्त शब्दों को सूचना के अनुसार परिवर्तन करके लिखिए।

उत्तर:

6. ‘हे शरणदायिनी देवी तू, करती सबका त्राण है।’ पंक्ति से प्रकट होने वाला भाव लिखिए। 

प्रश्न 2.
‘हे शरणदायिनी देवी तू, करती सबका त्राण है।’ पंक्ति से प्रकट होने वाला भाव लिखिए।
उत्तरः
इस पंक्ति से कृतज्ञता का भाव व्यक्त होता है। मातृभूमि ने हमें सब कुछ दिया है। इसके बदले में उसने हमसे कुछ भी नहीं लिया है। अत: उसके अनंत उपकारों के प्रति कृतज्ञ होकर कवि ने उसकी प्रार्थना करते हुए कहा है कि वह शरणदायिनी देवी है और जो उसकी शरण में आता है; वह उसकी रक्षा करती है।

उपयोजित लेखन :

प्रश्न 1.
‘मैं पंछी बोल रहा हूँ…’ इस विषय पर निबंध लिखिए।
उत्तर:
“मैं हूँ एक पंछी… प्रकृति का एक अंश…। इस धरती पर चारों ओर स्वच्छंद विचरण करने का अधिकार ईश्वर ने मुझे भी प्रदान किया है। अब तो बूढ़ा हो गया हूँ। मुझे आज भी याद है, मेरा जन्म आम के पेड़ पर बने घोंसले में हुआ था। जब मेरा जन्म हुआ था; तब मेरे माता-पिता बहुत खुश थे। मेरे साथ मेरे और दो भाई भी थे, लेकिन अब वे जीवित नहीं है। वे काल के गाल में समा गए हैं। आहिस्ता-आहिस्ता मैं बड़ा हुआ। बड़ा होने के बाद मेरे पंखों में शक्ति आ गई और मैं स्वच्छंद होकर खुले आसमान में उड़ने लगा।

समुद्र के ऊपरी हिस्से पर उड़ते समय मुझे बहुत खुशी होती थी। समुद्र से ऊपर उड़ने वाली लहरों के साथ मैं भी नर्तन करता था। कितना अच्छा लगता था मुझे उस समय! मैंने अन्य पक्षियों के साथ आम के पेड़ पर अपना घोंसला बनाया व बड़े ही प्यार से वहाँ पर रहने लगा। पेड़ की सुखद हरियाली में मुझे बेहद मजा आता था। अन्य पक्षियों के साथ मौज-मस्ती करते समय मैं फूला न समाता था। मेरी यह खुशी अधिक दिन तक नहीं रही। भाग्य को कुछ और ही मंजूर था।

एक दिन सरकारी अधिकारी आम के पेड़ के पास छान-बीन करने आए। न जाने उनकी आपस में क्या बातें हुई? उनके चले जाने के चार-पाँच दिन के बाद आम के पेड़ की कटाई करने के लिए कर्मचारी आए। उन्होंने बड़ी ही निर्दयता से पेड़ को जड़ से अलग कर दिया। इस कारण आम के पेड़ पर रहने वाले मेरे जैसे कई पक्षी बेघर हो गए। हम सब पंछी निराश एवं दुखी हो गए। कई पक्षियों ने घोंसले में शिशुओं को जन्म दिया था। पेड़ के गिरने के साथ उन्होंने भी इस संसार से विदा लिया।

अपने दोस्त एवं परिजनों की बुरी अवस्था देखकर मैं भी व्यथित हो गया हूँ। अब मैं अपने जीवन की अंतिम साँसें गिन रहा हूँ। मेरे जैसे कई खग-बूंद काल के गाल में समा गए हैं। हमारी कई प्रजातियाँ नामशेष रह गई हैं। इंसान को प्रकृति के साथ खिलवाड़ नहीं करना चाहिए। यदि ऐसा ही होता रहा, तो एक दिन पर्यावरण संतुलन बिगड़ जाएगा और समस्त जीवन खतरे में पड़ जाएगा। इसलिए पर्यावरण की रक्षा करना प्रत्येक मानव का कर्तव्य होना चाहिए। यही मेरा सबके लिए संदेश है।”

Hindi Lokvani 10th Std Textbook Solutions Chapter 1 मातृभूमि Additional Important Questions and Answers

(अ) निम्नलिखित पद्यांश पढ़कर दी गई सूचनाओं के का अनुसार कृतियाँ कीजिए।

कृति अ (1): आकलन कृति

प्रश्न 1.
कृति पूर्ण कीजिए।
उत्तर:

प्रश्न 2.
समझकर लिखिए।
उत्तर:

प्रश्न 3.
पद्यांश में प्रयुक्त प्राकृतिक घटकों के नाम लिखिए।
उत्तर:
अंबर, सूर्य, चंद्र, रत्नाकर, नदियाँ, फूल, तारे, खग, पयोद

कृति अ (2) : शब्द संपदा

प्रश्न 1.
निम्नलिखित शब्दों के अर्थ लिखिए।

1. अंबर
2. हरित
3. मेखला
4. सर्वेश
5. मुकुट

उत्तर:

1. आसमान
2. हरा
3. करधनी
4. ईश्वर
5. ताज

प्रश्न 2.
विलोम शब्द लिखिए।

1. प्रेम ×………….
2. सगुण × ………..
3. सत्य × ………..

उत्तर:

1. द्वेष
2. निर्गुण
3. असत्य

प्रश्न 3.
निम्नलिखित अनेक शब्दों के लिए एक शब्द लिखिए।

1. धागे आदि की करधनी
2. जिसमें मूल्यवान रत्नों का संचय है –
3. राजा के सिंहासनारोहण का अनुष्ठान –

उत्तर:

1. मेखला
2. रत्नाकर
3. अभिषेक

प्रश्न 4.
निम्नलिखित तत्सम शब्द का तद्भव शब्द लिखिए।
i. हरित
ii. काम
उत्तर:
i. हरा
ii. कार्य

प्रश्न 5.
निम्नलिखित शब्द के अनेकार्थी शब्द लिखिए।
i. फन
ii. शेष
उत्तर:
i. फन: साँप का फन, हुनर
ii. शेष : बचा हुआ, छोड़ा हुआ

कृति अ (3) : स्वमत अभिव्यक्ति

प्रश्न 1.
हम अपने देश को ‘मातृभूमि’ कहते हैं। अपने विचार लिखिए।
उत्तर:
हम भारतवासी संस्कृति से जुड़े लोग हैं। हम अपने देश को माता कहकर पुकारते हैं। हमारी मातृभूमि हमें जीवन देती है। वह हमें प्राकृतिक संसाधनों का भंडार उपलब्ध कराती है। सबकुछ देने वाली मातृभूमि हमारी जननी है। वहीं हमारी माता है। आमतौर पर एक बच्चे को अपने पिता की अपेक्षा माता से अधिक लगाव होता है। उसी प्रकार का लगाव हमें अपनी धरती से होता है। उसमें हम अपनापन एवं ममत्व ढूँढ़ते हैं। हमारा अपनी देश की धरती से अटूट नाता होता है। हमारे वेदों में भी ‘नमो मातृ भूम्यै’ ऐसा कहा गया है। अपनी मातृभूमि के प्रति अपनी भावना व्यक्त करते हुए भगवान कृष्ण ने भी कहा है: ‘ऊधौ मोहिं ब्रज विसरत नाहिं।’

(आ) निम्नलिखित पद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए।

कृति आ (1): आकलन कृति

प्रश्न 1.
समझकर लिखिए।
उत्तर:

प्रश्न 2.
गलत विधान सही करके लिखिए।
i. मातृभूमि पर प्रकृति के एक के बाद एक अदभुत दृश्य देखने को मिलते हैं।
उत्तरः
मातृभूमि पर छ: ऋतुओं के एक-के-बाद एक अद्भुत दृश्य देखने को मिलते हैं।

ii. मातृभूमि का धरातल बंजर है। जो किसी रोएँदार मखमल के कपड़े से कम नहीं है।
उत्तर:
मातृभूमि का धरातल हरियाली से भरा है; जो किसी रोएँदार मखमल के कपड़े से कम नहीं है।

कृति आ (2) : शब्द संपदा

प्रश्न 1.
कविता में इस अर्थ में आए शब्द लिखिए।

1. शुद्ध
2. पानी
3. श्रेष्ठ
4. हवा
5. अंधकार
6. सूर्य

उत्तर:

1. निर्मल
2. नीर
3. उत्तम
4. पवन
5. तम
6. तरणि

प्रश्न 2.
उपसर्ग व प्रत्यय लगाकर नए शब्द तैयार कीजिए।
i. गंध
उत्तर:
उपसर्गयुक्त शब्द : सुगंध
प्रत्यययुक्त शब्द : सुगंधित

प्रश्न 3.
पाश में से ऐसे दो शब्द ढूँढकर लिखिए कि जिनके वचन में परिवर्तन नहीं होता हो ।
उत्तर:
i. दिन
ii. पवन

प्रश्न 4.
विलोम शब्द लिखिए।
i. शीतल × ………
ii. सुगंध × ……….
उत्तर:
i. उष्ण
ii. दुर्गध

प्रश्न 5.
पद्यांश में प्रयुक्त विलोम शब्दों की जोड़ियाँ लिखिए।
उत्तर :
i. दिन × रात
i. तम × प्रकाश

प्रश्न 6.
नीचे दिए हुए शब्द का श्रुतिसम भिन्नार्थक शब्द लिखिए।
i. कम
ii. दिन
उत्तर:
i. क्रम
ii. दीन

कति आ (3) : स्वमत अभिव्यक्ति

प्रश्न 1.
‘छ: ऋतुओं ने भारत भूमि अर्थात हमारी मातृभूमि के सौंदर्य में चार चाँद लगा दिए हैं।’ अपने विचार लिखिए।
उत्तरः
भारत भूमि पर प्रकृति की विशेष कृपा है। विश्व में हमारी ही मातृभूमि ऐसी है जहाँ पर छः ऋतुओं का नियमित रूप से आगमन होता है। सभी ऋतुओं में अनोखी छटा देखने को मिलती है। वसंत, ग्रीष्म, वर्षा, शरद, हेमंत व शिशिर इन छ: ऋतुओं के एक-के-बाद एक अद्भुत दृश्य देखने को मिलते हैं। वसंत में फूलों का खिलना व पौधों का हरा-भरा होना आदि दृश्यों से मातृभूमि की शोभा देखने लायक होती है। ग्रीष्म ऋतु में फल व मेवे पकते हैं। बागों में आमों के फल लगते हैं।

वर्षा ऋतु में बारिश होती है। फसलों के लिए पानी मिलता है। पेड़ पौधे खुश और हरे-भरे हो जाते हैं। शरद ऋतु में कास के फूलों से धरती सज उठती है। मौसम सुहावना हो जाता है। हेमंत में बीज अंकुरित होते हैं। ओस की बूंदें गिरने लगती हैं। शिशिर में कड़ाके की ठंड पड़ती है। घना कोहरा छा जाता है। इस प्रकार मातृभूमि पर छ: ऋतुएँ सदैव अपना-अपना सौंदर्य बिखेरती रहती हैं।

(इ) पद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए।

कृति इ (1): आकलन कृति

प्रश्न 1.
निम्नलिखित शब्द पढ़कर ऐसे दो प्रश्न तैयार कीजिए जिनके उत्तर निम्न शब्द हों –
i. औषधियाँ
ii. वसुधा-धरा
उत्तर:
i. एक-से-एक निराली क्या प्राप्त हैं?
ii. पद्यांश में मातृभूमि के लिए प्रयुक्त नाम लिखिए।

प्रश्न 2.
सत्य-असत्य लिखिए।
i. मनुष्य को आवश्यक सभी पदार्थ मातृभूमि से मिलते हैं।
ii. भारत भूमि में धातुओं की खानें नहीं हैं।
उत्तर:
i. सत्य
i. असत्य

कृति इ. (2) : शब्द संपदा

प्रश्न 1.
पद्यांश में से उपसर्गयुक्त शब्द ढूँढकर लिखिए।
उत्तर:

1. सुखद
2. सुमन
3. सरस

प्रश्न 2.
निम्नलिखित तत्सम शब्द ढूंढकर लिखिए।
उत्तर:

1. सुमन
2. सरस
3. वसुधा
4. धातु

प्रश्न 3.
निम्नलिखित शब्दों के पर्यायवाची लिखिए।

1. खान
2. निराली
3. सुरभित

उत्तर:

1. खदान
2. अनोखी
3. सुगंधित

प्रश्न 4.
नीचे दिए हुए शब्दों के अनेकार्थी शब्द लिखिए।
i. खान
ii. फल
उत्तर:
i. खान : खदान, खजाना
ii. फल : परिणाम, आम या अन्य फल

प्रश्न 5.
विलोम शब्द लिखिए।
i. आवश्यक × ………
i. सरस × ……
उत्तर:
i. अनावश्यक
ii. नीरस

प्रश्न 6.
अनेक शब्दों के लिए एक शब्द लिखिए।
i. सुख देने वाला –
ii. सब कुछ धारण करने वाली –
उत्तर:
i. सुखद
ii. धरा

कृति इ (3) : स्वमत अभिव्यक्ति

प्रश्न 1.
‘धरती पर उपलब्ध संसाधनों का हमें उचित ध्यान रखना चाहिए।’ विषय पर अपने विचार लिखिए।
उत्तरः
प्रकृति से प्राप्त संसाधनों को प्राकृतिक संसाधन कहा जाता है। हवा, पानी, खनिज, लकड़ी, मिट्टी, तेल, वनस्पति, जीवाश्म ईंधन व ऊर्जा आदि प्राकृतिक संसाधनों के उदाहरण है। हमें प्राकृतिक का इस्तेमाल सोच-समझकर ही करना चाहिए। उन्हें व्यर्थ में बरबाद करने से आगे चलकर मनुष्य जीवन ही खतरे में पड़ सकता है। सभ्यता के इस युग में लोगों ने अपनी आँखे बंद करके प्राकृतिक संसाधनों का अमर्यादित दोहन करना शुरू कर दिया है। पेड़ों की अंधाधुंध कटाई हो रही है। पेड़ों की कटाई के विपरीत प्रभाव के कारण प्रदूषण एवं वर्षा की कमी हो रही है। इसलिए जीवन को संभव बनाना है, तो हमें धरती पर उपलब्ध संसाधनों का उचित उपयोग करना होगा।

(ई) पद्यांश पड़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए।

कृति ई (1): आकलन कृति

प्रश्न 1.
समझकर लिखिए।
उत्तर:

कृति ई (2) : शब्द संपदा

प्रश्न 1.
निम्नलिखित शब्दों के अर्थ लिखिए।

1. विभव
2. जननी
3. विश्व
4. प्रेम

उत्तर:

1. संपन्न
2. माता
3. संसार
4. प्यार

प्रश्न 2.
विलोम शब्द लिखिए।
i. भय × …………
ii. दया ×……
उत्तर:
i. साहस
ii. निर्दयता

प्रश्न 3.
एक शब्द के लिए शब्द समूह लिखिए।
i. क्षमामयी
ii. शांतिकारिणी
उत्तर:
i. क्षमा करने वाली
ii. शांति निर्माण करने वाली

प्रश्न 4.
निम्नलिखित शब्द के अनेकार्थी शब्द लिखिए।
i. क्षेम
उत्तर:
i. क्षेम : कुशल मंगल, सुख

कृति ई (3): स्वमत अभिव्यक्ति

प्रश्न 1.
‘हमारी मातृभूमि के प्रति जिम्मेदारी है।’ अपने विचार लिखिए।
उत्तर:
मातृभूमि हमारी सर्वस्व है। उस पर सब कुछ अर्पण करने की भावना हमारे पास होनी चाहिए। मातृभूमि के प्रति प्रेम व सम्मान की भावना होनी चाहिए। हमें मन, वचन व कर्म से राष्ट्रहित के लिए कार्य करते रहना चाहिए। मातृभूमि की रक्षा के लिए हमें सदैव तैयार रहना चाहिए। यदि कोई हमारी मातृभूमि की ओर आँख उठाकर देखने की कोशिश करें, तो हमें सजग होकर उसका प्रतिकार करना चाहिए।

जब हम मातृभूमि के प्रति दायित्व एवं जिम्मेदारियों को ध्यान में रखेंगे, तो शीघ्र ही हमारा देश प्रगति के पथ पर बढ़ेगा और विश्व में हमारी मातृभूमि की कीर्ती फैलेगी। हमें अपने कर्तव्य पालन के साथ-साथ दूसरे लोगों को भी मातृभूमि के प्रति कर्तव्यनिष्ठ एवं जिम्मेदार बनाने हेतु प्रयास करना चाहिए। इस प्रकार मातृभूमि की शान बढ़ाने हेतु हमें उसके प्रति जिम्मेदार होना चाहिए।

मातृभूमि Summary in Hindi

कवि-परिचय :

जीवन-परिचय : मैथिलीशरण गुप्त जी का जन्म झाँसी जिले के चिरगाँव में हुआ था। गुप्त जी खड़ी बोली हिंदी में काव्य रचना करने वाले, प्रथम कवि थे। अपने साहित्य में उपेक्षित नारी जीवन की व्यथा एवं वेदना को अभिव्यक्त करने का महान कार्य इन्होंने किया। यह राज्यसभा के मनोनीत सदस्य थे। इनकी रचनाओं में राष्ट्रीय चेतना, भारत का गौरवशाली इतिहास व संस्कृति प्रतिबिंबित होती हैं। महात्मा गांधी द्वारा इन्हें राष्ट्रकवि’ की पदवी से सम्मानित किया गया है।

प्रमुख कृतियाँ : ‘साकेत’ (महाकाव्य), ‘यशोधरा’, ‘जयद्रथ वध’, ‘पंचवटी’, ‘भारत-भारती’, (खंडकाव्य), ‘रंग में भंग’, ‘राजा प्रजा’ (नाटक) आदि।

पद्य-परिचय :

खड़ी बोली। ब्रज भाषा के स्थान पर खड़ी बोली को अपनी कविताओं की काव्य भाषा बनाकर कवियों ने उसकी क्षमता से सभी को परिचित कराने का कार्य किया। देशभक्ति, राष्ट्रीयता, बंधुत्व भावना, गांधीवाद, मानवता आदि मूल्यों को अभिव्यक्त करने का कार्य खड़ी बोली काव्य ने किया। प्रस्तावना । ‘मातृभूमि’ इस कविता में राष्ट्रकवि गुप्त जी ने भारतभूमि का गौरवगान किया है। हम भारतीय भारतभूमि को ‘मातृभूमि’ कहकर संबोधित करते हैं। हमें मातृभूमि के प्रति कृतज्ञ भाव रखकर उस पर अपना सर्वस्व न्योछावर करने का संदेश कविता के माध्यम से दिया गया है।

सारांश :

‘मातृभूमि’ कविता के द्वारा भारत की धरती का सुंदर और मनोहारी चित्रण करते हुए गुणगान किया गया है। भारत की भूमि हरियाली, नदियों, सागरों, फूलों और फलों, सुगंधित व शीतल पवन, चाँदनी के प्रकाश आदि से सुशोभित है। मातृभूमि सत्य का स्वरूप है और वह सर्वशक्तिमान ईश्वर की सगुण मूर्ति है। मातृभूमि पर उपलब्ध प्राकृतिक स्रोतों से जो जल मिल रहा है; वह अमृत के समान उत्तम है। यहाँ पर छ: अतुओं के एक के बाद एक अद्भुत दृश्य देखने को मिलते हैं।

भारत की भूमि विविध खाद्ययान्नों, धन-धान्य व प्राकृतिक संसाधनों से परिपूर्ण है। इसलिए मातृभूमि का ‘वसुधा’ एवं ‘धरा’ कहा जाता है। मातृभूमि क्षमामयी, दयामयी व सुखदायिनी है। वह अमृत, वात्सल्य व प्रेम की मूर्ति स्वरूप है। वह सबका दुख हरने वाली है। वह सबके जीवन को सुख-समृद्धि से भर देती है। इस प्रकार मातृभूमि के हम पर अनंत उपकार हैं। वह हमारी जननी है और हम उसकी संतान हैं।

भावार्थ :

नीलांबर परिधान …………………………………… मूर्ति सर्वेश की।
मातृभूमि भारतमाता के सुंदर रूप का वर्णन करते हुए राष्ट्रकवि गुप्त जी कहते हैं, “मात्रभूमि ने हरे रंग का परिधान धारण किया है और उनके सिर पर नीला अंबर शोभायमान है। आसमान में उदित होने वाले सूर्य व चंद्र उसके युग मुकुट है व सागर करधनी के रूप में उसकी शोभा बढ़ा रहे हैं। प्रेम रूपी प्रवाह के साथ नदियाँ बह रही हैं और चारों और सुंदर फूल खिले हैं; आसमान में रात्रि के समय प्रकाशित होने वाले तारों से मातृभूमि का सुंदर रूप और भी खिल रहा है।

मातृभूमि की महिमा का गुणगान कलरव के रूप में तरह-तरह के पक्षी कर रहे हैं। मातृभूमि का सिंहासन शेषनाग का फन है। बारिश के रूप में बादल इस मातृभूमि का अभिषेक कर रहे हैं। ऐसी भारतभूमि पर हमारा सब कुछ न्योछावर है। सचमुच, ऐसी गौरवमयी मातृभूमि सत्य का स्वरूप है और वह सर्वशक्तिमान ईश्वर की सगुण मूर्ति है।

ति निर्मल तेरा ……………………………… तम का नाश है।
मातृभूमि पर उपलब्ध प्राकृतिक स्रोतों से तो जल मिल रहा है। वह अमृत के समान उत्तम है। इस मातृभूमि पर बहने वाली शीतल-मंद व सुंगधित पवन मनुष्य के सारे कष्टों को दूर भगाती है। वसंत, ग्रीष्म, वर्षा, शरद, हेमंत व शिशिर इन छ: अतुओं के एक के बाद एक अदभुत दृश्य देखने को मिलते हैं। मातृभूमि का धरातल हरियाली से भरा हुआ है; जो किसी रोएँदार मखमल के कपड़े से कम नहीं है। रात में चंद्र का प्रकाश मातृभूमि को पवित्र ओस रूपी जलकणों से सींचता रहता है और दिन में सूर्य उदय होकर अंधकार को मिटा देता है।

सुरभित, सुंदर ………………………………………. नाम यथार्थ हैं।
मातृभूमि पर सुगंधित, सुंदर व सुखद सुमन खिलते हैं और अलग-अलग प्रकार के रसीले व अमृत के समान मीठे फल उगते हैं। यहाँ पर एक से एक निराली व अदभुत औषधियाँ उपलब्ध हैं। मातृभूमि पर धातु एवं श्रेष्ठ रत्नों की खानें हैं। सभी भारतवासियों को जिन-जिन पदार्थों एवं वस्तुओं की आवश्यकता होती है वे सारे पदार्थ एवं वस्तुएँ यहाँ पर विपुल मात्रा में उपलब्ध हैं। इसलिए मातृभूमि को वंसुधा-धरा’ कहा गया है। ये नाम उसके लिए पूरी तरह से उपयुक्त और सत्य भी है।

क्षमामयी …………………………………. तू प्राण है।
मातृभूमि क्षमामयी, दयामयी व सुखदायिनी है। वह अमृत, वात्सल्य व प्रेम से भरी हुई है। वह ऐश्वर्य देने वाली शक्ति हैं; वह विश्व का पालन करने वाली देवी है और सबका दुख हरने वाली दुखहर्ती है। वह भय का निवारण करती है शांति निर्माण करती है और सबके जीवन को सुख-समृद्धि से भर देती है। मातृभूमि शरणदायिनी देवी है अर्थात वह सभी को शरण देती है। वह सबको संकटों से मुक्ति दिलाती है सबकी रक्षा करने वाली हैं। हम सब इस मातृभूमि की संतान है। यह हम सबकी जननी है; यह हमारी नवचेतना है; यह हमारा प्राण है।

शब्दार्थ :

1. अंबर – आसमान
2. हरित – हरा
3. पट – वस्व
4. निशा मेखला – करधनी
5. सगुण – गुणयुक्त
6. सर्वेश – ईश्वरी
7. मुकुट – ताज
8. निर्मल – पवित्र, शुद्ध
9. खग – पक्षी
10. परिधान – वस्त्र, कपड़ा
11. रत्नाकर – सागर
12. पयोद – बादल, मेघ
13. सुचि – पवित्र, शुद्ध
14. सुधा शक – अमृत, जल
15. नीर – पानी
16. उत्तम – श्रेष्ठ
17. पवन – हवा
18. फर्श – धरातल
19. तम – अंधकार, अंधेरा
20. तरणि – सूर्य
21. खान – खदान
22. निराली – अनोखी
23. सुरभित – सुगंधित, सौरभित
24. वैभव – संपन्नता, बहुतायत
25. जननी – माता
26. विश्व – संसार

Balbharti Maharashtra State Board Class 8 English Solutions Chapter 3.4 Leisure Notes, Textbook Exercise Important Questions, and Answers.

Maharashtra State Board Class 8 English Solutions Chapter 3.4 Leisure

Class 8 English Chapter 3.4 Leisure Textbook Questions and Answers

Leisure Poem 8th Std Warming Up:

1. Discuss in groups and share with one another:

Leisure Poem Questions And Answers Class 8 Question 1.
The daily routine of your mother and father on working days
Answer:
(Points: what time they get up – what time they leave for work – what time they return home – have lunch – dinner – bedtime, etc.)

3.4 Leisure Questions And Answe Question 2.
How your family relaxes on weekends
Answer:
(Points: rest at home – visit relatives – shopping – malls – movies – gardens – catch up on housework, etc.)

Std 8 English Poem Leisure Question 3.
When you go for a picnic, what and how do you enjoy it?
Answer:
(Points: go to the beach/mall /garden/movies etc. – relax and enjoy by yourself – sing songs – go in big groups – go as a family – go to restaurants for food, etc.)

Leisure Question Answers Class 8 Question 4.
Do you spend time admiring and thinking over the beauties of nature? Elaborate on your response.
Answer:
(Points: no beautiful nature around/ gardens nearby – like enjoying natural beauties – prefer city life – like animals and birds – visit zoos and parks. etc.)

2. When a poet I writer attempts (o describe something in words, so that it appeals to our five senses (sight, smell, hearing, touch, taste) he/she has used a des ice called Imager.
For example a host of golden daffodils’.
to a chasm, deep and vast and wide’.
Go through other poems in your textbook or other books and find outlines that contain Imagery. Write them does n along with the name of the poem and line/stanza number.
Answer:
Students can attempt this activity on their own.

3. Prepare un Acrostic from the word ‘Leisure’. The words should be related to what one likes to do in free time:

1. L ………..
2. E ………….
3. I …………
4. S ………..
5. U ………..
6. Reading stories
7. E …………

Answer:

1. Laze around
2. Enjoy movies
3. Initiate games
4. Sleep
5. Undertake to clean house
6. Read stories
7. Exercise

1. Say Where:

Question a.
………… do the cows and sheep stand? …………..
Answer:
Beneath the branches of trees.

Question b.
………… do squirrels store their food? ………….
Answer:
In the grass.

Question c.
………….. do stars shine in the daytime …………..
Answer:
In the streams.

Question d.
………….. does Beauty’s smile begin? ……………….
Answer:
In her eyes.

2. Think and answer in your own words:

Question a.
What could have inspired the poet to compose this poem? Do you think it relates to our present-day life? Defend your choice.
Answer:
The poet must have seen the busy lives of people around him, who are always in a hurry and have no leisure to look at the beauty around. Yes, it certainly relates to our present life, which keeps getting busier and busier. Today, with the Internet, the mobile phone, the computer, and social networking sites, our lives are getting more I and more artificial and further from nature than ever before.

Question b.
Which line proves that in our busy lives we do not even have a fraction of a second to enjoy nature’s beauty?
Answer:
The lines are :
No time to see, when woods we pass
Where squirrels hide their nuts in the grass?
No time to see, in broad daylight,
Are streams full of stars, like skies at night?
No time to turn at Beauty’s glance,
And watch her feet, how they can dance?
No time to wait till her mouth can
Enrich that smile her eyes began.

Question c.
‘Beauty’ in stanza 5 to 6 can refer to a beautiful maiden as well as nature itself. Explain when and how nature ‘dances’ and also ‘smiles’.
Answer:
Nature dances during spring and: summer, when the leaves of trees and the flowers sway in the breeze. Nature smiles at the beginning of spring when the plants begin to once again bloom slowly.

Question d.
Why does the poet call our life ‘poor’?
Answer:
The poet calls our life ‘poor’ because we are always anxious and under stress. We are completely cut off from nature and cannot relax and enjoy its beauty. He feels that this type of life is a ‘poor’ life.

3. You have learned that when u human attribute is given to anything that is not a human being or it is spoken of as a person, the Figure of Speech used is culled as ‘Personification’:

Question a.
Pick out two examples of Personification from the poem
Answer:
(i) ‘No time to turn at Beauty’s glance, I And watch her feet, how they can; dance?’ Nature has been given the human qualities of ‘glancing’ and ‘dancing’.
(ii) ‘No time to wait till her mouth can Enrich the smile her eyes began.’ Nature has been given the human quality of ‘smiling’.

Question b.
Pick out from the poem, two examples of each of the following Figures of Speech:

3.4 Leisure Question 1.
Alliteration
Answer:
(i) We have no time to stand and stare.’ Repetition of the sound of the letter ‘s’.
(ii) ‘Streams full of stars, like skies at; night.’ Repetition of the sound of the letter ‘s’.

8th Standard English Poem Leisure Notes Question 2.
Simile
Answer:
(i) ‘And stare as long as sheep or cows.’ Here, a direct comparison has been made between sheep and cows.
(ii) ‘Streams full of stars, like skies at night.’ Here, a direct comparison has been made to the night skies.

Leisure Poem 8th Std Question 3.
Metaphor
Answer:
(i) ‘No time to turn at Beauty’s; glance.’ Here nature has been implicitly compared to a beautiful woman.
(ii) ‘Enrich the smile her eyes began.’ Here the blooming of flowers has been implicitly compared to a woman smiling.

Question c.
The poet opens his poem with a question. Is the question asked to receive some answer? No. It is a question used to emphasize and stress the fact that modern man has no time to enrich his life from nature. Such a device used by poets falls under the Figure of Speech called ‘Interrogation
or ‘Rhetorical Question’. Refer to the poem ‘The Pilgrim’ and find examples of Interrogation.
Answer:
‘What is this life, if full of care,
We have no time to stand and stare?’
Here the poet asks a question to emphasize and stress the fact that modern man has no time to appreciate nature.
(Note: The lines in stanzas 2,3,4,5 and 6 are also examples of Interrogation.)

4. Say where the images from mature given in the poem exist:

Air/Land/Water

Question a.
beneath the thoughts …………..
Answer:
Land

Question b.
squirrel hide nuts in grass …………
Answer:
Land

Question c.
streams in day time ………..
Answer:
Water

Question d.
stars/ skies at night …………
Answer:
Air

5. Make a paraphrase of the poem ‘Leisure’ in your own simple words. Write down in your notebook.
Answer:
In this poem, the poet, W.H. Davies, questions the type of life we are leading if we have no time to appreciate the beauties of nature. He says that we have no time to stand beneath the trees and stare as sheep and cows do. When we are walking through the woods we have no time to watch where the squirrels hide their food in the grass. We have no time to look at streams that sparkle and a twinkle in broad daylight and appear to be full of stars like the skies at night.

We have no time to watch when a beautiful young girl dances, or wait for her lips to complete the smile which started in her eyes. (We can also say that ‘Beauty’ is nature, and we have no time to see trees swaying In the breeze or flowers blooming slowly.)
In the concluding lines, the poet repeats that our life is a poor life if it is full of cares and worries with no time to appreciate and enjoy the beauty of nature.

Class 8 English Chapter 3.4 Leisure Additional Important Questions and Answers

Complex Factual Activities:

Class 8 English Leisure Question 1.
What does the poet want us to stare at and gain from it?
Answer:
The poet wants us to spare some time from our busy schedules to look at the beauty of nature and enjoy it.

Leisure Class 8 Question 2.
Enlist the beautiful things in nature that we overlook.
Answer:
We overlook:

1. squirrels hiding their food in the grass
2. twinkling and sparkling streams
3. a beautiful girl smile and dance/trees swaying in the breeze and flowers blooming slowly.

8th Standard English Poem Leisure Question 3.
Analysis/ Appreciation Of The Poem
Answer:

1. Poem and poet: ‘Leisure’ by William Henry Davies.
2. Theme: The poet regrets that ours is a poor life if it is full of cares and worries and we have no time to appreciate and enjoy the beauty of nature.
3. Tone: Serious and analytical; reflective poem.
4. Structure and stanzas: The stanzas are of two lines each; seven couplets with lines of equal length.
5. Rhyme and Rhythm: The rhyme scheme is aa, bb, cc, and so on, with the ending words of each couplet rhyming.
6. Language and Imagery: The language is simple; the poem has many figures of speech and is full of imagery when the poet describes the beauty of nature.
7. Figures of Speech: Alliteration, Personification, Simile, Metaphor, Repetition, Interrogation.

Balbharti Maharashtra State Board Class 10 Hindi Solutions Hindi Lokvani Chapter 4 दो गजलें Notes, Textbook Exercise Important Questions and Answers.

Maharashtra State Board Class 10 Hindi Lokvani Solutions Chapter 4 दो गजलें

Hindi Lokvani 10th Std Digest Chapter 4 दो गजलें Textbook Questions and Answers

स्वाध्याय :

सूचना के अनुसार कृतियाँ कीजिए :

1. कृति पूर्ण कीजिए।

प्रश्न 1.
कृति पूर्ण कीजिए।

उत्तर:

2. संजाल पूर्ण कीजिए।

प्रश्न 1.
संजाल पूर्ण कीजिए।

उत्तर:

3. कृति में दिए गज़ल में प्रयुक्त शब्दों की उचित जोड़ियाँ क्रमशः अ और आ तालिका में लिखिए।

प्रश्न 1.
कृति में दिए गज़ल में प्रयुक्त शब्दों की उचित जोड़ियाँ क्रमशः अ और आ तालिका में लिखिए।

उत्तर:

अ	आ
छाँव	उम्मीद
अनुभव	ज्ञान
पर	उड़ान
जान	जिंदगानी

4. उचित शब्द का चयन करते हुए वाक्य पूर्ण कीजिए।
(मिट्टी, कैद, बंदी, रिहा, छूटना)

प्रश्न 1.
उचित शब्द का चयन करते हुए वाक्य पूर्ण कीजिए।
(मिट्टी, कैद, बंदी, रिहा, छूटना)
i. अजब ये जिंदगी की ……….. है।
ii. रिहाई माँगता है और ……….. होने से डरता है।
उत्तर:
i. कैद
ii. रिहा

5. सूचना के अनुसार शब्द में परिवर्तन कीजिए।

प्रश्न 1.
सूचना के अनुसार शब्द में परिवर्तन कीजिए।

उत्तर:

6. ‘जीवन में डर की जगह सावधानी एवं साहस चाहिए।’ विषय पर अपने विचार व्यक्त कीजिए। 

प्रश्न 1.
‘जीवन में डर की जगह सावधानी एवं साहस चाहिए।’ विषय पर अपने विचार व्यक्त कीजिए।
उत्तर:
डर वह भावना है; जो इंसान को कमजोर बना देती है और साहस वह भावना होती है; जो इंसान के हौसलों में उड़ान पैदा करती है। व्यक्ति को अपने जीवन में डर का त्याग कर साहस और सावधानी को अपनाना चाहिए। उसे प्रत्येक काम साहस के साथ सावधानीपूर्वक करना चाहिए। सावधानी बरतने से व्यक्ति के सारे काम सुचारू रूप से पूर्ण होते हैं। साहस असंभव कार्य को भी संभव बनाने की शक्ति रखता है। जो व्यक्ति अपने जीवन में साहस को नहीं अपनाता है: वह व्यक्ति कभी भी सफल नहीं होता। जीवन में कई सफल व्यक्ति हैं, जिन्होंने डर की जगह सावधानी एवं साहस को अपनाकर संसार में अद्भुत कार्य करके सभी को अपने प्रभावी व्यक्तित्व से प्रेरित किया।

भाषा बिंदु :

प्रश्न 1.
निम्नलिखित वाक्यों के रचना के अनुसार भेद लिखिए।

1. वह आदमी भी उस गाँव में रहने के लिए तैयार हो गया। [ ]
2. स्टेशन मास्टर ने सिग्नल नहीं दिया और गाड़ी आउटर पर खड़ी रही। [ ]
3. मजे की बात यह है कि एक समाचारपत्र के कितने उपयोग हो सकते हैं। [ ]
4. वह पशु-पक्षियों के बीच बातें करता दिखाई देता। [ ]
5. आप उस गाँव में जाएंगे तो आपको उस खोए हुए आदमी की वहाँ स्थापित मूर्ति दिख जाएगी। [ ]
6. नींद आती रहती है, जाती रहती है और रह-रहकर टूटने के बावजूद उसमें लय बनी होती है। [ ]

उत्तर:

1. सरल वाक्य
2. संयुक्त वाक्य
3. मिश्र वाक्य
4. सरल वाक्य
5. मित्र वाक्य
6. संयुक्त वाक्य

प्रश्न 2.
पाठों में आए रचना के अनुसार वाक्यों के दो-दो उदाहरण लिखिए।
उत्तरः
1. सरल वाक्य :
i. इससे मेरा भी मन बड़ा दुखी होता है।
ii. मैंने सबकी बात सुनी है।

2. मिश्र वाक्य :
i. जैसी करनी वैसी भरनी।
ii. हमें चाहिए कि हम हवा और पानी को अपना दोस्त बनाकर उन्हें नुकसान न पहुँचाएँ।

3. संयुक्त वाक्य :
i. सोना तो मिट्टी है और मिट्टी का मोह पालकर आज तक किसी ने शांति नहीं पाई।
ii. लोग उसके दर्शन को आने लगे और धीरे-धीरे चारोंतरफ साधु का यश फैल गया।

प्रश्न 3.
निम्नलिखित वाक्यों के अर्थ के अनुसार भेद लिखिए।

1. सुबह उठता हूँ तो थोड़ी ताजगी महसूस होती है। [ ]
2. अरे, वहीं अटके रहोगे, मुझसे बात नहीं करोगे? [ ]
3. कई दिनों तक मैं तुम्हारे चौके में नहीं गई। [ ]
4. ठीक है, मुकदमें की कार्यवाही शुरू करें। [ ]
5. अरे! हवा रानी, नाराज मत हो। [ ]
6. इस बात के लिए ये गाँववाले ही जिम्मेदार हैं। [ ]
7. अधिक वर्षा के लिए कौन जिम्मेदार है? [ ]
8. अच्छा! निकलती हूँ बस पाँच मिनट चाहिए मुझे तैयार होने के लिए। [ ]
9. हौं राजीव, आओ बैठो।
10. यह एक भोले इंसान का विश्वास नहीं था।

उत्तर:

1. विधानार्थक वाक्य
2. प्रश्नार्थक वाक्य
3. निषेधार्थक वाक्य
4. आज्ञार्थक वाक्य
5. आज्ञार्थक वाक्य
6. विधानार्थक वाक्य
7. प्रश्नार्थक वाक्य
8. विस्मयादिबोधक वाक्य
9. आज्ञार्थक वाक्य
10. निषेधार्थक वाक्य

प्रश्न 4.
पाठों में आए अर्थ के अनुसार वाक्यों के दो-दो उदाहरण लिखिए।
उत्तरः
1. विधानार्थक वाक्य :
i. मैं तेजी से वहाँ जाती हूँ।
ii. महाराज यह आरोप झूठा है।

2. आज्ञार्थक वाक्य :
i. पहले पानी को बुलाया जाए।
ii. सेठ मेरा इनाम दें।

3. निषेधार्थक वाक्य :
i. कहीं भी कोई नहीं था।
ii. उसमें भी मेरा कुछ नहीं है।

4. प्रश्नार्थक वाक्य :
i. तू कौन है?
ii. उसकी माया में मुझे क्यों फँसाता है?

5. विस्मयादिबोधक वाक्य :
i. काश, अपने गाँव-शहर में हमें भी ऐसा ‘खोया हुआ आदमी’ मिल जाता!
ii. हाँ महाराज! आज सब शिकायतें हवा और पानी के बारे में हैं।

6. संदेहसूचक वाक्य :
i. शायद मैं खो गया हूँ।
ii. संभव है कि पानी दूषित होने से बच जाए।

उपयोजित लेखन :

प्रश्न 1.
अपने विद्यालय में आयोजित की जानेवाली क्रीड़ा प्रतियोगिताओं का आयोजक के नाते विज्ञापन तैयार कीजिए।

उत्तरः

Hindi Lokvani 10th Std Textbook Solutions Chapter 4 दो गजलें Additional Important Questions and Answers

(अ) पद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए।

कृति अ (1): आकलन कृति

प्रश्न 1.
समझकर लिखिए।
उत्तरः

प्रश्न 2.
पद्यांश में प्रयुक्त प्राकृतिक घटकों के नाम
उत्तरः

कृति अ (2) : शब्दसंपदा

प्रश्न 1.
निम्नलिखित शब्दों के अर्थ लिखिए।

1. आसमान
2. पर
3. इतमीनान
4. सोच

उत्तरः

1. अंबर
2. पंख
3. तसल्ली
4. विचार

प्रश्न 2.
पद्यांश में प्रयुक्त ऐसे दो शब्द लिखिए जिनके वचन परिवर्तित नहीं होते हैं।
उत्तर:
i. पेड़
ii. पर

प्रश्न 3.
निम्नलिखित अनेक शब्दों के लिए एक शब्द लिखिए।
i. हवा में उड़ने की क्रिया
उत्तरः
i. उड़ान

प्रश्न 4.
निम्नलिखित शब्द के अनेक अर्थ लिखिए।
i. फल
ii. पर
उत्तर:
i. फल : खाने का फल, परिणाम
ii. पर : परंतु, पंख

कृति अ (3) : स्वमत अभिव्यक्ति

प्रश्न 1.
‘अनुभव सबसे बड़ा शिक्षक होता है।’ अपने विचार लिखिए।
उत्तरः
जीवन-रूपी यात्रा में सीखने के लिए कोई किताब साथ नहीं होती। व्यक्ति अपने अनुभवों से ही सीखता है। व्यक्ति जीवन में कार्य करते समय कई गलतियाँ करता रहता है। उन गलतियों से उसका अनुभव समृद्ध हो जाता है। वह फिर से उन गलतियों को नहीं दोहराता। वह अपनी गलतियों से बहत सारी बातें सीखता है और स्वयं के अनुभव को समृद्ध बनाता है। अनुभव सोने के समान होता है।

जिस प्रकार सोना तप-तप कर तैयार हो जाता है उसी प्रकार अनुभव दिन-रात की मेहनत एवं लगन से प्राप्त किया जाता है। व्यक्ति के जीवन में आने वाले अच्छे-बुरे अनुभव उसके मार्गदर्शक बनते हैं। अनुभव से मिलने वाला ज्ञान व्यक्ति को सफलता के शिखर पर पहुँचा देता है। अनुभवहीन ज्ञान जीवन की सच्चाई के सामने टिक नहीं पाते। अत: अनुभव ही सबसे बड़ा शिक्षक होता है।

(आ) पद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए।

कृति आ (1): आकलन कृति

प्रश्न 1.
कृति पूर्ण कीजिए।
उत्तरः

प्रश्न 2.
समझकर लिखिए।
उत्तरः

प्रश्न 3.
निम्नलिखित गलत विधान सही करके लिखिए।
i. प्रकृति ने हमें जिंदगी बख्शी है।
उत्तरः
ईश्वर ने हमें जिंदगी बख्शी है।

ii. ईश्वर सायबान निर्माण करेगा।
उत्तर:
इंसान सायबान निर्माण करेगा।

कृति आ (2) : शब्द संपदा

प्रश्न 1.
कविता में इस अर्थ में आए शब्द लिखिए।

1. संसार
2. स्वयं
3. आशा
4. ईश्वर

उत्तर:

1. दुनिया
2. खुद
3. उम्मीद
4. खुदा

प्रश्न 2.
निम्नलिखित तत्सम शब्द का तद्भव रूप लिखिए।
i. छाया
उत्तर:
i. छाँव

प्रश्न 3.
निम्नलिखित अनेक शब्दों के लिए एक शब्द लिखिए।
i. घर के आगे छाया हेतु बनाया गया छप्पर
उत्तर:
i. सायबान

कृति आ (3) : स्वमत अभिव्यक्ति

प्रश्न 1.
‘व्यक्ति को जीवन में आत्मनिर्भर होना चाहिए। उसे दूसरों से मदद की अपेक्षा नहीं रखनी चाहिए।’ अपने विचार लिखिए।
उत्तर:
आत्मनिर्भर यानी स्वावलंबी। व्यक्ति को अपने जीवन में आत्मनिर्भर होना चाहिए। उसे दूसरों पर आश्रित नहीं होना चाहिए। यदि व्यक्ति अपने जीवन में दूसरों पर आश्रित रहता है, तो वह तरक्की नहीं कर सकता है। आत्मनिर्भर बनने के लिए व्यक्ति में दृढ़ इच्छा शक्ति का होना जरूरी होता है। आत्मनिर्भर व्यक्ति सदैव कोशिश करते रहता है। इसलिए वह सफलता की मंजिल हासिल करने में सफल हो जाता है। वह भाग्य के भरोसे नहीं बैठता है। आत्मनिर्भर बनकर वह अपनी क्षमताओं का विकास कर लेता है। अब्राहम लिंकन व नेपोलियन जैसे महापुरुषों का जन्म निर्धन परिवार में हुआ था। उन्होंने जीवन में आत्मनिर्भर बनकर सफलता की सीढ़ी हासिल की। इसलिए प्रत्येक व्यक्ति को अपने जीवन में आत्मनिर्भर होना चाहिए।

(इ) पद्यांश पढ़कर दी गई सूचनाओं के अनुसार कृतियाँ कीजिए।

कृति इ (1): आकलन कृति

प्रश्न 1.
निम्नलिखित शब्द पढ़कर ऐसे दो प्रश्न तैयार कीजिए जिनके उत्तर निम्न शब्द हों –
i. अजब
ii. रिहाई
उत्तर:
i. जिंदगी की कैद कैसी है?
ii. दुनिया का हर इंसान क्या माँगता है?

प्रश्न 2.
पद्यांश के आधार पर समझकर लिखिए।
i. इंसान के बस और काबू में ये नहीं है –
ii. हर शख्स इसका बना खिलौना है –
उत्तर:
i. इंसान के बस में जिंदगी नहीं है और काबू में मौत नहीं है।
ii. मिट्टी का

कृति इ (2) : शब्द संपदा

प्रश्न 1.
निम्न शब्दों में उचित उपसर्ग का प्रयोग कीजिए।

1. मौत
2. पल
3. काबू

उत्तर:

1. बेमौत
2. हरपल
3. बेकाबू

प्रश्न 2.
निम्नलिखित तत्सम शब्द का तद्भव रूप लिखिए।
i. मृदा
उत्तर:
i. मिट्टी

प्रश्न 3.
निम्नलिखित शब्दों के पर्यायवाची लिखिए।

1. फना
2. मौत
3. रिहाई
4. काबू

उत्तर:

1. नष्ट
2. मृत्यु
3. मुक्ति
4. नियंत्रण

प्रश्न 4.
विलोम शब्द लिखिए।
i. बड़ा × ……….
i. जिंदगी × ………….
उत्तर:
i. छोटा
ii. मौत

कृति आ (3) : स्वमत अभिव्यक्ति

प्रश्न 1.
बचपन की दुनिया और बड़ों की दुनिया में क्या अंतर है? अपने विचार लिखिए।
उत्तर:
बचपन की दुनिया में मासूमियत होती है और बड़ों की दुनिया मुश्किलों और परेशानियों से भरी होती है। बचपन जीवन की एक ऐसी अवस्था होती है; जहाँ पर जीवन का मस्ती से आनंद लिया जाता है और बड़ों की दुनिया जिम्मेदारियों से भरी होती है। कई लोगों को इस कारण जिंदगी कैद के समान लगती है।

लेकिन बच्चों के लिए जिंदगी खुशियाँ एवं प्यार लेकर आती है। मुस्कुराना, शरारत करना, रूठना और फिर सब भुलाकर एक हो जाना; ये बच्चों की पहचान होती है। वहीं बड़ों के जीवन में ईर्ष्या, द्वेष एवं कलह होता है। बच्चे दुनियादारी के झमेलों से दूर होते हैं, तो बड़ों की दुनिया कई प्रकार के झमेले में उलझती रहती है।

दो गजलें Summary in Hindi

कवि-परिचय :

जीवन-परिचय : राजेश रेड्डी जी का जन्म सन १९५२ में महाराष्ट्र के नागपुर में हुआ था। राजेश जी हिंदी, अंग्रेजी व उर्दू भाषा के ज्ञाता हैं। जगबीती को आपबीती में परिवर्तित कर गज़ल लिखने में रेड्डी जी कुशल माने जाते हैं। ये विविध भारती, मुंबई से भी जुड़े हैं। इन्होंने अपनी प्रतिभा से गज़ल एवं नाटक विधा को समृद्ध किया है।
प्रमुख कृतियाँ : ‘उड़ान’, ‘आसमान से आगे’, ‘वजूद’ (गज़ल संग्रह) आदि।

पद्य-परिचय :

गज़ल : ‘गज़ल’ यह अरबी साहित्य की प्रसिद्ध काव्य-विधा है। गज़ल एक ही बहर और वज़न के अनुसार लिखे गए शेरों का समूह है। इसके पहले शेर को मतला कहते हैं। गज़ल के अंतिम शेर को मक़्ता कहते हैं।
प्रस्तावना : ‘दो गज़लें’ इस गज़ल में दो गज़लें सम्मिलित की गई हैं। पहले गज़ल से हमें यह संदेश मिलता है कि व्यक्ति के पास कोई भी कार्य करने से पहले जोश, उत्साह, ज्ञान, आत्मविश्वास आदि का होना जरूरी होता है। दूसरी गज़ल में कवि ने बताया है कि बचपन मासूमियत से भरा होता है। बड़े होने पर परेशानियाँ आती हैं, जिस कारण इंसान अनेक प्रकार की परेशानियों से घिर जाता है।

सारांश :

‘दो गज़लें’ यह एक गज़ल है। इस गज़ल के द्वारा कवि कहता है कि व्यक्ति को कोई भी कार्य करने से पहले अपने आप में जोश, उत्साह, आत्मविश्वास आदि का निर्माण करना चाहिए। व्यक्ति को कोई भी कार्य करने से पहले अपनी आँखों से जिंदगी को पढ़ लेना चाहिए। खुद के अनुभवों से प्राप्त ज्ञान के बिना कार्य की पूर्ति नहीं होती। जीवन में संयम व धैर्य का बहुत बड़ा महत्त्व होता है। कवि मानवतावादी है। अत: वह मानव की भलाई की कामना रखता है।

व्यक्ति को दूसरों से अपेक्षा रखने के बजाय स्वयं आत्मनिर्भर होना चाहिए। प्रत्येक व्यक्ति को ऐसी वाणी में सबके साथ वार्तालाप करना चाहिए कि उसके विचार दूसरों के हृदय में सदा के लिए बस जाए। कवि इस गज़ल के माध्यम से कहता है कि आज का व्यक्ति दुख, तकलीफों और परेशानियों से चारों ओर से घिर चुका है। दुनिया-समाज में पड़कर व्यक्ति की बचपन जैसी मासूमियत खोने लगी है। वह नश्वर है। फिर भी उसकी महत्वाकांक्षा पूरी होती नहीं दिखती। वह अपनी ही जिंदगी में कैद हो गया है। वह मुक्ति भी पाना चाहता है. और इच्छाओं को भी नष्ट करना नहीं चाहता।

भावार्थ :

पहले इक आसमान …………………… उड़ान पैदा कर।
व्यक्ति को कोई भी कार्य करने से पहले अपने आप में जोश, उत्साह व आत्मविश्वास उत्पन्न करना चाहिए। इसलिए कवि कहते हैं कि व्यक्ति को अपने परों में यानी मन में हौसला भरने से पहले आसमान यानी सकारात्मक परिस्थिति उत्पन्न कर लेनी चाहिए। सकारात्मक परिस्थिति व आत्मविश्वास के बिना व्यक्ति सफलता की ऊंची मंजिल हासिल नहीं कर सकता।

अपनी आँखों से ………………. पैदा कर।
व्यक्ति को कोई भी कार्य करने से पहले अपनी आँखों से जिंदगी को पढ़ लेना चाहिए। स्वयं के अनुभवों से प्राप्त ज्ञान के बिना कार्य की पूर्ति नहीं होती। व्यक्ति का अनुभव समृद्ध होना बेहद जरूरी है। अनुभव समृद्ध व्यक्ति के पास ज्ञान का भंडार होता है। अनुभवों के द्वारा ही व्यक्ति को ज्ञान की प्राप्ति होती है।

सब के पेड़ ………………… पैदा कर।
जीवन में संयम व धैर्य का बहुत ही महत्त्व होता है। संयम व धैर्य के बिना मनुष्य को मनचाहे फल की प्राप्ति नहीं हो सकती। कहा भी । गया है कि सब्र का फल मीठा होता है। धैर्य और संयम से आज नहीं तो कल सब का फल जरूर मिलता है। इसलिए व्यक्ति की सोच में भी इतमीनान यानी तसल्ली होनी चाहिए। उसे कोई भी कार्य करने से पहले तसल्ली से सोचना चाहिए।

ऐ खुदा! ………………………… पैदा कर।
कवि इंसान का भला चाहता है। वह नहीं चाहता कि इंसान दुख-दर्द में अपना जीवन व्यतीत करे। इंसान के जीवन में खुशहाली आए । इसलिए कवि ईश्वर से ऐसे सुंदर संसार की कामना करता है; जहाँ पर व्यक्ति सुख-चैन के साथ अपना जीवन जी सके।

तूने बख्शी है …………………….. पैदा कर।
कवि मानवतावादी है। अत: वह मानव की भलाई की कामना रखता है। वह ईश्वर से कहता है, “हे ईश्वर, तूने सभी को जिंदगी का । अनमोल उपहार दिया है। अत: तू ही इस जिंदगी में जान भरने का कार्य कर । तू ही लोगों में जिंदादिली निर्माण कर; ताकि लोग इस जिंदगी के सफर का आनंद ले सकें।

छोड़ दुनिया से ………………….. पैदा कर।
व्यक्ति को जीवन में किसी से भी, कोई भी उम्मीद नहीं रखनी चाहिए। व्यक्ति को दूसरों से उम्मीद रखने के बजाय स्वयं आत्मनिर्भर होना चाहिए। व्यक्ति को दूसरों से सहायता की अपेक्षा नहीं रखनी चाहिए; बल्कि स्वयं ही प्रकाशित होकर स्वयं की जिंदगी को उज्ज्वल बनाना चाहिए। दूसरों से छाँव की अपेक्षा रखने के बजाय स्वयं ही सायबान बनकर खुद को और दूसरों के जीवन में भी छाँव उत्पन्न करनी चाहिए।

दिल से निकले ………………… पैदा कर।
व्यक्ति की वाणी सरल, सहज और मीठी होनी चाहिए। उसके बोलने वाले शब्द दिल से निकले होने चाहिए। यदि वह इस प्रकार वाणी : का प्रयोग करेगा, तो निश्चित ही वह दूसरों की निगाहों में और दिलों में आसानी से जगह प्राप्त कर लेगा।

यहाँ हर शख्स …………………. डरता है।
कवि कहते हैं कि हर इंसान अपनी मृत्यु से सदा भयभीत रहता है। वह अपने ऊपर होनेवाले हादसों और आपदाओं से डरता रहता है। । 5. आखिर इंसान मिट्टी से बना हुआ एक खिलौना ही तो है। उसे एक दिन टूटना ही है। फिर भी वह न जाने क्यों नष्ट होने से डरता रहता है।

मेरे दिल के किसी ……………………… डरता है।
बचपन की मासूमियत सभी को प्यारी और अच्छी लगती है। उसे कोई भी भूलना नहीं चाहता। हर व्यक्ति के दिल में कहीं न कहीं बचपना छिपा रहता है। लेकिन बड़ों की दुनिया जो दुख और तकलीफों से भरी है, उसे देखकर वह अपने बचपन को कहीं न कहीं बचाए रखना चाहता । है। वह बड़ों की दुनिया के साथ बड़ा होना नहीं चाहता क्योंकि बड़ों की दुनिया में मासूमियत नहीं होती।

शब्दार्थ :

1. आसमान – अंबर
2. पर – पंख
3. सोच – विचार
4. इतमीनान – तसल्ली , ढाढ़स
5. जहान – संसार, जगत
6. खुदा – ईश्वर
7. उम्मीद – आशा, भरोसा
8. खुद – स्वयं
9. हादिसा – आपदा
10. फना – नष्ट
11. मौत – मृत्यु
12. रिहाई – मुक्ति
13. काबू – नियंत्रण, वश
14. सायबान – घर के आगे छाया हेतु बनाया हुआ छप्पर
15. जान – प्राण, जीवन
16. सब्र – सबर, संयम, धैर्य