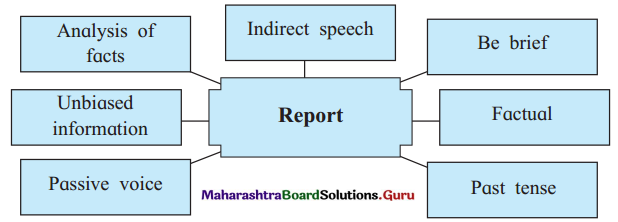
Class 11 English Chapter 3.1 Expansion of Ideas Question Answer Maharashtra Board
Balbharti Yuvakbharati English 11th Digest Chapter 3.1 Expansion of Ideas Notes, Textbook Exercise Important Questions and Answers.
11th Std English Chapter 3.1 Brainstorming Question Answer
11th English Digest Chapter 3.1 Expansion of Ideas Textbook Questions and Answers
Question 1.
Discuss the different ideas connoted by the word ‘season’.
Answer:
- A season is a division of the year based on weather, ecology etc.
- India experiences six seasons round the year, namely, summer (grisha), rainy season (varsha), early autumn (sharad), late autumn (hemanta), winter (sheet), spring (vasanta).
- The change of season allows many people to plan their activities (not shifting of house during rainy season), food, recreation, celebrations, etc.
![]()
Question 2.
Select a season of your choice and give the following details:
- Time of the year –
- Characteristics- crops, festivals etc.
- Features/changes – climate/weather/temperature etc.
- Advantages/Disadvantages-
Answer:
| Winter | |
| Duration | October to January |
| Climate | Cold |
| Crops | Wheat, Onion, Grapes, Sunflower |
| Work | Sowing seeds |
| Festivals | Diwali, Dashera, Christmas, Makarsankranti |
| Advantages | Cool weather useful for the growth of crop, rebirth of natural scenery |
Question 3.
Mention some proverbs associated with the word season, guess their meanings and write them along with a sentence of your own.
Answer:
(a) Make hay while the sun shines.
1. Meaning: Make the most benefit out of an opportunity
2. Sentence: Having got admission in a good college you should make hay while the sun shines.
(b) For everything there is a season
1. Meaning: For everything there is appropriate time.
2. Sentence: This is not the time to waste it talking to your friend, you must know, for everything ‘
there is a season
(c) No winter lasts for ever, no spring skips its turn.
1. Meaning: bad days do not stay for ever, as spring always replaces winter in the natural course of
nature.
2. Sentence: Cheer up, my friend, as no winter lasts for ever, no spring skips its turn.
![]()
Express your views and opinions in favor and against the topic.
Question (i)
Are sports essential in Jr. Colleges?
Answer:
Favour: (a) Sports help in increasing the physical and mental ability of students.
(b) Sports boost confidence and keep sportspersons fit for everyday living.
(c) Sports teach students team work.
Against: (a) Concentrating on sports is a waste of time. Students should focus on their career.
(b) Focus on entrance exams to persue better career opportunities.
Question (ii)
Are college council elections essential in Jr. Colleges?
Answer:
Favour: (a) The college council elections train the students to take up leadership roles and help them develop decisiveness.
Against: (a) Through elections in colleges children will follow the wrong path.
(b) They will be affected by national politics.
(c) Might get into bad company.
Question (iii)
Is cell-phone the need of the times?
Answer:
Favour: (a) Cell-phone has become the main and the fastest source of communication.
(b) Without a cell-phone one may feel crippled as it is repository of essential data and also is a source of knowledge.
Against: (a) Regular use of cell-phones affects our health conditions.
(b) Increases crimes.
![]()
Question (iv)
Should the ‘Earn and Learn’ concept be mandatory for students?
Answer:
Favour:
(a) It can make students economically independent.
(b) It can develop perseverance among students.
(c) Students will be aware of the value of money and hard work.
Against:
(a) This is an age for enjoyment.
(b) Students should concentrate on their health and family time.
(A1)
Question 1.
Expand the idea inherent in the following proverbs:
Answer:
1. A Bad Workman Blames his Tools
This proverb is an useful guide in practical life. It has been generally found that an incompetent person always grumbler. If a student does not do well in examination, he/she sometimes takes an easy resort to blame game that the question paper is tough. The person never admits that the preparation has not been up to the mark. On the other side, a sincere and good workman never tries to find excuses for his mediocre or bad performance. He probably thinks grumbling is a confession of his personal weakness.
Difficulties are parts and parcels of our lives and we have to learn to overcome by putting our best foot forward rather than finding fault with others or may be unfavourable situations. It is better to find out the reason for the performance which is not up to the mark. One has to find out the remedy for the shortcomings and need to have the faith on one’s ownself to raise the bar of his execution.
If the tools are bad, they can be mended, not by grumbling but by removing the defects. A good workman does exactly that and does not waste time complaining. “Patience and perseverance can fetch definite rewards. Everything is possible to achieve for a sincere worker whereas all things are impossible for a lazy person who is always on the look out for a scapegoat to bear the blame of his own failure.
2. One Should Eat to Live, Not Live to Eat – (Franklin)
We all have heard the proverb “health is wealth”. A sound mind can only exist in a sound body. If we are healthy, we can handle any situation in life. Eating plays a major role in maintaining a person’s health. The eating habits depend on own discretion and if we are conscious about the decision where to stop, “this far and no farther”, we can avoid many critical conditions of life with a healthy body. That is the biggest wealth any person can have.
But one needs a strong willpower not to live just to eat. The temptations are spread all around us. Some people have the habit of eating to their heart’s content and consoling themselves saying that it is just one day only. But they are greedy enough to forget their promise easily at the sight of mouth-watering dishes and continue their theory of “living to eat”.
Apparently, to some people, the eating habits do not need to be given so much importance, because they feel that the modern technologies used in the gyms will compensate for the loss of over-eating. Work hard in the gym and you can eat anything, is their motto of life. So, after coming out of the gym, they consume a big mug of cold coffee with cream from a reputed coffee shop and do not feel guilty about it. Not only home-cooked delicious foods, but all sorts of junk foods are included in their list of foods. Food is essential for one’s survival but excess of anything is bad. It is not about restrictions only, it is about how one can balance and enjoy the food.
3. If Winter Comes, Can Spring be Far Behind? – (Shelley)
Think positive and live happy, celebrate life ideally this should be the motto of a person’s life. But how many of us honestly follow this motto? Life, indeed, is beautiful but it does not move in a straight line. There has to be ups and downs and both these ups as well as downs have something to teach us, as P.B. Shelley said, “If winter comes, can spring be far behind?”. These are the natural courses of life. One has to follow the other as one season follows the other.
Life has problems and every problem is bound to have some solutions if we can try to see the brighter side. “No one makes a lock without a key. That is why God won’t give you problems without solutions.” In God’s own world also, if severe winter creates difficulties, He has kept the spring ready to bring smile on the faces of those who faced the difficult situations bravely. Winter, being the symbol of destruction here, spring will bring with it abundance everywhere.
Our duty is to maintain our patience and wait with hope for welcoming the good days because “At the end of every tunnel, there is light”. Night follows Day, that is also God’s design. If we crumble with the pressure of frustration and make ourselves fatigued, how will we enjoy the brightness of the day or the charming weather of the spring?
4. Beauty is Truth, Truth is Beauty – (Keats)
“Ode on a Grecian Urn”, the immortal poem of the poet John Keats, brings out a fact of life, that has its own beauty where joys and sorrows live together. He shows in the poem, the pictures on the urn has paintings of a combination of happiness and sadness to depict the truth of human life. A work of art has the power to express this truth of life so explicity.
“Beauty lies in the eyes of the beholder”. The person who is seeing the beauty can interpret it his or her own way, but the truth will remain the same. Truth is the permanent and ultimate beauty in the world and no one has the power to destroy it.
So, to ignore truth will be a futile attempt and only the inward beauty has the power to be the ever-lasting truth and the outward appearances are momentary. But our thoughts want to find out the truth and our feelings are inspired by the beauty. Thus, thought and feeling, truth and beauty need to go hand in hand.
5. Fools Rush in Where Angels Fear to Tread – (Alexander Pope)
“Experience is the best teacher”. The inexperienced people do not judge the pros and cons of the situation and take a step without much thinking. The experienced people become mature enough to take. a cautious step before taking a hasty decision. Their experience has taught them to “wait and watch” and then decide whether to avoid or get involved.
“A little learning is a dangerous thing”. The prudent and intelligent person think twice before opening their mouth and are also good observers. They are actually “afraid” but they are also careful that their actions should be safe and so they stay away from unnecessary risks. Even if they take risk believing “no risk, no gain”, they are capable of measuring the extent of the risk to reach their final decision. But a so called “fool” or rather an unwise person does not bother to think and can be easily influenced to do stupid things to invite problems in life.
“Ignorance” is not always “bliss”, since ignorance can lead to a irreversible damage. But, if a wise person is ignorant about certain things, he knows how to keep a distance from the unknown territory. The proverb actually tries to create an awareness against quick decisions or may be judgements, because every step of life is important. One wrong step, taken in a hurry, can lead to a major set back which probably will bring the disaster. History stands proof for that.
![]()
(A2)
Question 1.
Complete the tabular columns to specify Dos and Don’ts associated with ‘Expansion of Ideas’.
Answer:
| Expansion of ideas | |
| Dos | Don’ts |
| 1. Begin impressively | 1. Don’t go off-track |
| 2. Use clear symbolism | 2. Do not remove topic sentence |
| 3. Focus on words and expression | 3. Do not add irrelevant points |
| 4. Should be unity and clarity of thoughts | 4. Don’t use too many ideas |
Yuvakbharati English 11th Digest Chapter 3.1 Expansion of Ideas Additional Important Questions and Answers
Question 1.
Expand the idea inherent in the following proverbs:
Answer:
(i) Rome was not Built in a Day
Big cities cannot be built very quickly. This actually refers to jobs that we undertake, our careers, our life and our achievements.
Just as Rome was not built in a day, so also our career, our life and our ambitions cannot be achieved in a short period of time. We must bear in mind, before we take up a project, that hard work has to go into making any endeavor a success. Success is 99% perspiration and 1% inspiration. We are aware of this, but do we honestly put in hard work or do we keep putting off our hard work for another day?
Rome took years to be built and once it was built it turned out to be a city beyond compare. Its beauty and its allure was incomparable. This was and is the result of dedication and hard work. We will achieve our goal and rise to the top only, and only if we understand the meaning of dedication, perseverance and hard work.
The three D’s must always be in our mind when we undertake a task to be done. The three D’s are- Dedication, Determination and Devotion. We will be able to touch the stars if we work hard and devote ourselves to the task ahead of us. We should not think of finishing our job in haste because haste makes waste. Only our determination and hard work will help us to achieve our aim in life.
(ii) Cut Your Coat According to Your Cloth
This proverb is something that all of us must bear in mind and abide by. The message that is given is that we must not spend beyond our means but be very careful with our expenditure.
The explanation is that if we give a piece of cloth to a tailor to stitch a coat, he will first measure the cloth and tell us whether it is possible, for him to make the coat we have asked for or not. If the cloth is insufficient, he will not be able to stitch the coat.
The same is the case with our income and expenses. We must always stay within the limits and not spend more than we can afford to or we will end up repenting. I know of a young man who wanted everything he saw advertised and he kept on buying the articles on installment-basis. Finally, he realized that the total amount he had to pay by way of the installments exceeded his income. The young man borrowed the money to make up the deficit.
How long could he go on in this way? His loans increased. People refused to give him more loans, since he could not pay back what he had already borrowed. Finally no one could wait to get the money they had given him on loan. He lost everything he had bought on installments and he landed in jail. His entire life had become one big mess – No money, no friends.
Could we too, end up like this young man? Yes, we could end up like this if we do not keep a track of the money we have and if we do not spend according to our means. This proverb teaches us to economies and to be frugal. We must learn how to manage our resources and live within our means. This will surely keep us out of trouble.
(iii) Empty Vessels Make the Most Sound
We have experienced this fact a number of times at home or even in school. When we strike on an empty vessel, we get a sonorous deep sound and if we strike on a vessel that is full of some liquid, we get only a dull thud. The above adage is metaphorically and literary correct.
We see around us people with no knowledge or very little knowledge making themselves heard above the rest and when they are questioned we realise that all is empty talk, they are just ignorant people who are trying to impress the crowd. Those who really have the knowledge are the ones who are not making a loud noise. They check out on the situation and open their mouths. What they say is the correct thing. They have knowledge and they use it wisely and correctly.
When we are in company, we must not try to prove to all present there, that we are the best, there is no one as knowledgeable as we are. We must use our etiquette and let the others have their say. We must realise that there are many who have more knowledge than we do.
It is very important to learn that when in company, we must give others the chance to have their say and not monopolies all the time such people are respected by others.
(iv) As you Sow, So shall you Reap
If we want to earn good things in life, we must do good things. If a farmer wants to cultivate rice, he will sow rice and not wheat. There was once a person who was not well to do and was really downtrodden and poor. This man had a very large heart. Whatever little food he got, he shared with others. There were times when he went without food, but he saw to it, that the beggars around had food to eat.
The neighbours observed this and decided to help this poor, warm-hearted person. They gave him an education. The man studied very hard and did well. The neighbours were very pleased. They gave him a job and he did very well. This man however never forgot the beggars and always bought them food and clothing.
Soon the poor man rose higher and higher and became the manager of the factory. He helped all the poor and even started a special “Society for the poor”. The man helped others and in return, he was helped. All of us must do well if we expect others to do good to us.
English Yuvakbharati 11th Digest Pdf Section 3 (Writing Skills)





 Question (vi)
Question (vi)