Oscillations Class 12 Exercise Question Answers Solutions Maharashtra Board
Balbharti Maharashtra State Board 12th Physics Textbook Solutions Chapter 5 Oscillations Textbook Exercise Questions and Answers.
Class 12 Physics Chapter 5 Exercise Solutions Maharashtra Board
Physics Class 12 Chapter 5 Exercise Solutions
1. Choose the correct option.
i) A particle performs linear S.H.M. starting from the mean position. Its amplitude is A and its time period is T. At the instance when its speed is half the maximum speed, its displacement x is
(A) \(\frac{\sqrt{3}}{2}\)A
(B) \(\frac{2}{\sqrt{3}}\)
(C) A/2
(D) \(\frac{1}{\sqrt{2}}\)
Answer:
(A) \(\frac{\sqrt{3}}{2}\)A
ii) A body of mass 1 kg is performing linear S.H.M. Its displacement x (cm) at t (second) is given by x = 6 sin (100t + π/4). Maximum kinetic energy of the body is
(A) 36 J
(B) 9 J
(C) 27 J
(D) 18 J
Answer:
(D) 18 J
![]()
iii) The length of second’s pendulum on the surface of earth is nearly 1 m. Its length on the surface of moon should be [Given: acceleration due to gravity (g) on moon is 1/6 th of that on the earth’s surface]
(A) \(\frac{1}{6}\) m
(B) 6 m
(C) \(\frac{1}{36}\) m
(D) \(\frac{1}{\sqrt{6}}\) m.
Answer:
(A) \(\frac{1}{6}\) m
iv) Two identical springs of constant k are connected, first in series and then in parallel. A metal block of mass m is suspended from their combination. The ratio of their frequencies of vertical oscillations will be in a ratio
(A) 1:4
(B) 1:2
(C) 2:1
(D) 4:1
Answer:
(B) 1:2
v) The graph shows variation of displacement of a particle performing S.H.M. with time t. Which of the following statements is correct from the graph?
(A) The acceleration is maximum at time T.
(B) The force is maximum at time 3T/4.
(C) The velocity is zero at time T/2.
(D) The kinetic energy is equal to total energy at time T/4.
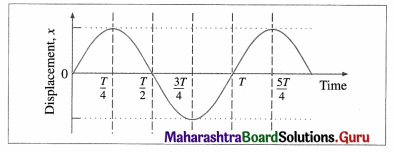
Answer:
(B) The force is maximum at time 3T/4.
2. Answer in brief.
i) Define linear simple harmonic motion.
Answer:
Definition: Linear simple harmonic motion (SHM) is defined as the linear periodic motion of a body, in which the force (or acceleration) is always directed towards the mean position and its magnitude is proportional to the displacement from the mean position.
OR
A particle is said to execute linear SHM if the particle undergoes oscillations about a point of stable equilibrium, subject to a linear restoring force always directed towards that point and whose magnitude is proportional to the magnitude of the displacement of the particle from that point.
Examples : The vibrations of the tines (prongs) of a tuning fork, the oscillations of the needle of a sewing machine.
![]()
ii) Using differential equation of linear S.H.M, obtain the expression for
(a) velocity in S.H.M.,
(b) acceleration in S.H.M.
Answer:
The general expression for the displacement of a particle in SHM at time t is x = A sin (ωt + α) … (1)
where A is the amplitude, ω is a constant in a particular case and α is the initial phase.
The velocity of the particle is

Equation (2) gives the velocity as a function of x.
The acceleration of the particle is
a = \(\frac{d v}{d t}\) = \(\frac{d}{d t}\) [Aω cos (ωt + α) J at at
∴ a = – ω2 A sin (ωt + α)
But from Eq. (1), A sin (ωt + α) = x
∴ a = -ω2x … (3)
Equation (3) gives the acceleration as a function of x. The minus sign shows that the direction of the acceleration is opposite to that of the displacement.
iii) Obtain the expression for the period of a simple pendulum performing S.H.M.
Answer:
An ideal simple pendulum is defined as a heavy point mass suspended from a rigid support by a weightless, inextensible and twistless string, and set oscillating under gravity through a small angle in a vertical plane.
In practice, a small but heavy sphere, called the bob, is used. The distance from the point of suspension to the centre of gravity of the bob is called the length of the pendulum.
Consider a simple pendulum of length L1 – suspended from a rigid support O. When displaced from its initial position of rest through a small angle θ in a vertical plane and released, it performs oscillations between two extremes, B and C, as shown in below figure. At B, the forces on the bob are its weight \(m \vec{g}\) and the tension \(\overrightarrow{F_{1}}\) in the string. Resolve \(m \vec{g}\) into two components : mg cos θ in the direction opposite to that of the tension and mg sin θ perpendicular to the string.
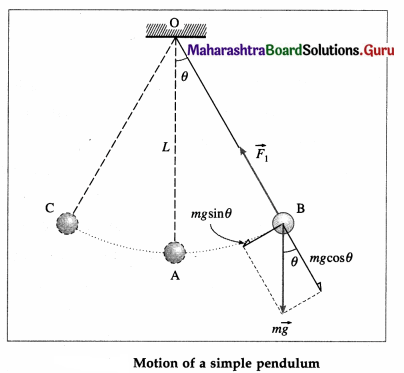
mg cos θ balanced by the tension in the string. mg sin θ restores the bob to the equilibrium position.
Restoring force, F = – mg sin θ
If θ is small and expressed in radian,
sin θ \(\approx\) θ = \(\frac{\text { arc }}{\text { radius }}\) = \(\frac{\mathrm{AB}}{\mathrm{OB}}\) = \(\frac{x}{L}\)
∴ F = – mgθ = -mg\(\frac{x}{L}\) …. (1)
Since m, g and L are constant,
F ∝ (-x) …. (2)
Thus, the net force on the bob is in the direction opposite to that of displacement x of the bob from its mean position as indicated by the minus sign, and the magnitude of the force is proportional to the magnitude of the displacement. Hence, it follows that the motion of a simple pendulum is linear SHM.
Acceleration, a = \(\frac{F}{m}\) = –\(\frac{g}{L}\)x … (3)
Therefore, acceleration per unit displacement
= |\(\frac{a}{x}\)| = \(\frac{g}{L}\) ….. (4)
Period of SHM,
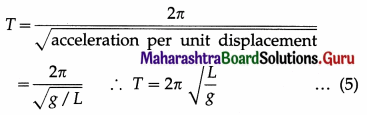
This gives the expression for the period of a simple pendulum.
![]()
iv) State the laws of simple pendulum.
Answer:
The period of a simple pendulum at a given place is
T = 2π\(\sqrt{\frac{L}{g}}\)
where L is the length of the simple pendulum and g is the acceleration due to gravity at that place. From the above expression, the laws of simple pendulum are as follows :
(1) Law of length : The period of a simple pendulum at a given place (g constant) is directly proportional to the square root of its length.
∴ T ∝\(\sqrt{L}\)
(2) Law of acceleration due to gravity : The period of a simple pendulum of a given length (L constant) is inversely proportional to the square root of the acceleration due to gravity.
∴ T ∝ \(\frac{1}{\sqrt{g}}\)
(3) Law of mass : The period of a simple pendulum does not depend on the mass or material of the bob of the pendulum.
(4) Law of isochronism : The period of a simple pendulum does not depend on the amplitude of oscillations, provided that the amplitude is small.
v) Prove that under certain conditions a magnet vibrating in uniform magnetic field performs angular S.H.M.
Answer:
Consider a bar magnet of magnetic moment μ, suspended horizontally by a light twistless fibre in a region where the horizontal component of the Earth’s magnetic field is Bh. The bar magnet is free to rotate in a horizontal plane. It comes to rest in approximately the North-South direction, along Bh. If it is rotated in the horizontal plane by a small
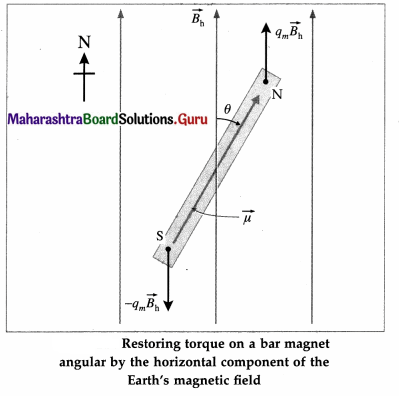
displacement θ from its rest position (θ = 0), the suspension fibre is twisted. When the magnet is released, it oscillates about the rest position in angular or torsional oscillation.
The bar magnet experiences a torque \(\tau\) due to the field Bh. Which tends to restore it to its original orientation parallel to Bh. For small θ, this restoring torque is
\(\tau\) = – μBh sin θ = – μBhμ …. (1)
where the minus sign indicates that the torque is opposite in direction to the angular displacement θ. Equation (1) shows that the torque (and hence the angular acceleration) is directly proportional in magnitude of the angular displacement but opposite in direction. Hence, for small angular displacement, the oscillations of the bar magnet in a uniform magnetic field is simple harmonic.
Question 3.
Obtain the expression for the period of a magnet vibrating in a uniform magnetic field and performing S.H.M.
Answer:
Definition : Angular SHM is defined as the oscillatory motion of a body in which the restoring torque responsible for angular acceleration is directly proportional to the angular displacement and its direction is opposite to that of angular displacement.
The differential equation of angular SHM is
I\(\frac{d^{2} \theta}{d t^{2}}\) + cθ = 0 ….. (1)
where I = moment of inertia of the oscillating body, \(\frac{d^{2} \theta}{d t^{2}}\) = angular acceleration of the body when its angular displacement is θ, and c = torsion constant of the suspension wire,
∴ \(\frac{d^{2} \theta}{d t^{2}}\) + \(\frac{c}{I}\)θ = 0
Let \(\frac{c}{I}\) = ω2, a constant. Therefore, the angular frequency, ω = \(\sqrt{c / I}\) and the angular acceleration,
a = \(\frac{d^{2} \theta}{d t^{2}}\) = -ω2θ … (2)
The minus sign shows that the α and θ have opposite directions. The period T of angular SHM is
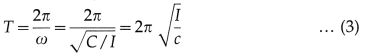
This is the expression for the period in terms of torque constant. Also, from Eq. (2),

Question 4.
Show that a linear S.H.M. is the projection of a U.C.M. along any of its diameter.
Answer:
Consider a particle which moves anticlockwise around a circular path of radius A with a constant angular speed ω. Let the path lie in the x-y plane with the centre at the origin O. The instantaneous position P of the particle is called the reference point and the circle in which the particle moves as the reference circle.
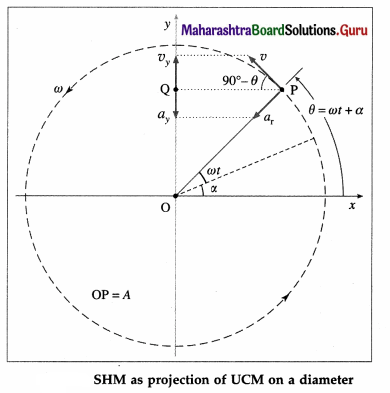
The perpendicular projection of P onto the y-axis is Q. Then, as the particle travels around the circle, Q moves to-and-fro along the y-axis. Line OP makes an angle α with the x-axis at t = 0. At time t, this angle becomes θ = ωt + α.
The projection Q of the reference point is described by the y-coordinate,
y = OQ = OP sin ∠OPQ, Since ∠OPQ = ωt + α, y = A sin(ωt + α)
which is the equation of a linear SHM of amplitude A. The angular frequency w of a linear SHM can thus be understood as the angular velocity of the reference particle.
The tangential velocity of the reference particle is v = ωA. Its y-component at time t is vy = ωA sin (90° – θ) = ωA cos θ
∴ vy = ωA cos (ωt + α)
The centripetal acceleration of the reference particle is ar = ω2A, so that its y-component at time t is ax = ar sin ∠OPQ
∴ ax = – ω2A sin (ωt + α)
![]()
Question 5.
Draw graphs of displacement, velocity and acceleration against phase angle, for a particle performing linear S.H.M. from (a) the mean position
(b) the positive extreme position. Deduce your conclusions from the graph.
Answer:
Consider a particle performing SHM, with amplitude A and period T = 2π/ω starting from the mean position towards the positive extreme position where ω is the angular frequency. Its displacement from the mean position (x), velocity (v) and acceleration (a) at any instant are
x = A sin ωt = A sin\(\left(\frac{2 \pi}{T} t\right)\) (∵ω = \(\frac{2 \pi}{T}\))
v = \(\frac{d x}{d t}\) = ωA cos ωt = ωA cos\(\left(\frac{2 \pi}{T} t\right)\)
a = \(\frac{d v}{d t}\) = -ω2 A sin ωt = – ω2A sin\(\left(\frac{2 \pi}{T} t\right)\) as the initial phase α = 0.
Using these expressions, the values of x, v and a at the end of every quarter of a period, starting from t = 0, are tabulated below.
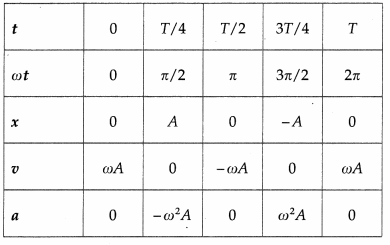
Using the values in the table we can plot graphs of displacement, velocity and acceleration with time.
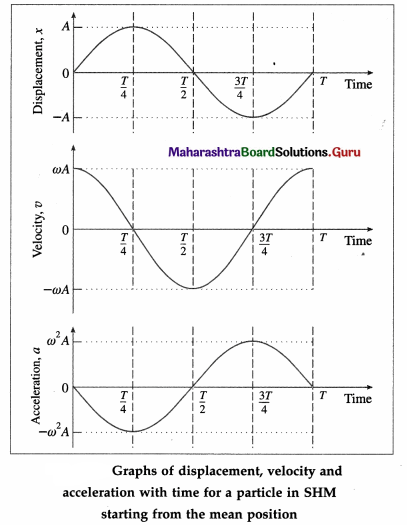
Conclusions :
- The displacement, velocity and acceleration of a particle performing linear SHM are periodic (harmonic) functions of time. For a particle starting at the mean position, the x-t and a-t graphs are sine curves. The v-t graph is a cosine curve.
- There is a phase difference of \(\frac{\pi}{2}\) radians between x and v, and between v and a.
- There is a phase difference of π radians between x and a.

Consider a particle performing linear SHM with amplitude A and period T = 2π/ω, starting from the positive extreme position, where ω is the angular frequency. Its displacement from the mean position (x), velocity (y) and acceleration (a) at any instant (t) are
x = A cos ωt = A cos \(\left(\frac{2 \pi}{T} t\right)\) (∵ω = \(\frac{2 \pi}{T}\))
v = -ωA sin ωt = – ωA sin \(\left(\frac{2 \pi}{T} t\right)\)
a = -ω2A cos ωt = -ω2A cos \(\left(\frac{2 \pi}{T} t\right)\)
Using these expressions, the values of x, y and a at the end of every quarter of a period, starting from t = 0, are tabulated below.
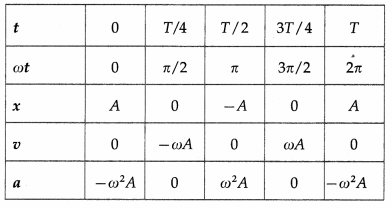
Using these values, we can plot graphs showing the variation of displacement, velocity and acceleration with time.
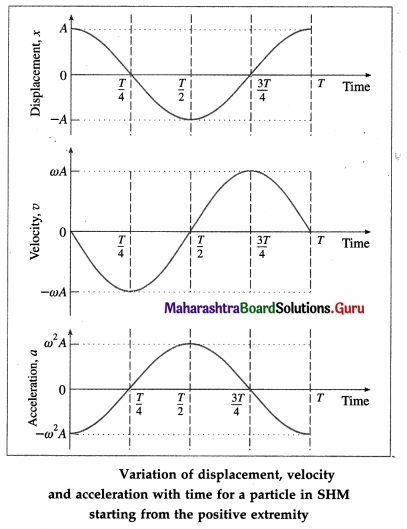
Conclusions :
- The displacement, velocity and acceleration of a particle performing linear SHM are periodic (harmonic) functions of time. For a particle starting from an extreme position, the x-t and a-t graphs are cosine curves; the v-t graph is a sine curve.
- There is a phase difference of \(\frac{\pi}{2}\) radians between x and v, and between v and a.
- There is a phase difference of n radians between x and a.
Explanations :
(1) v-t graph : It is a sine curve, i.e., the velocity is a periodic (harmonic) function of time which repeats after a phase of 2π rad. There is a phase difference of π/2 rad between a and v.
v is minimum (equal to zero) at the extreme positions (i.e., at x = ± A) and v is maximum ( = ± ωA) at the mean position (x = 0).
(2) a-t graph : It is a cosine curve, i.e., the acceleration is a periodic (harmonic) function of time which repeats after a phase of 2π rad. There is a phase difference of π rad between v and a. a is minimum (equal to zero) at the mean position (x = 0) and a is maximum ( = \(\mp\)ω2A) at the extreme positions (x = ±A).
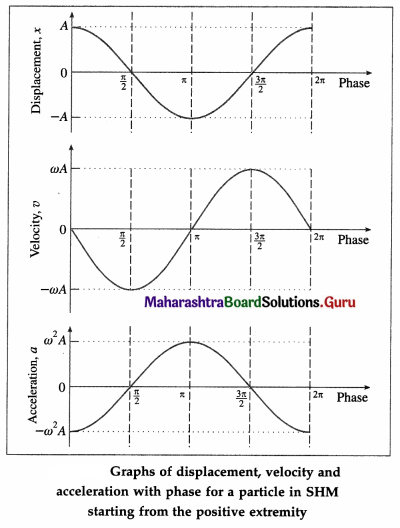
Question 6.
Deduce the expressions for the kinetic energy and potential energy of a particle executing S.H.M. Hence obtain the expression for total energy of a particle performing S.H.M and show that the total energy is conserved. State the factors on which total energy depends.
Answer:
Consider a particle of mass m performing linear SHM with amplitude A. The restoring force acting r on the particle is F = – kx, where k is the force constant and x is the displacement of the particle from its mean position.
(1) Kinetic energy : At distance x from the mean position, the velocity is
v = ω\(\sqrt{A^{2}-x^{2}}\)
where ω = \(\sqrt{k / m} .\) The kinetic energy (KE) of the particle is
KE = \(\frac{1}{2}\) mv2 = \(\frac{1}{2}\) mω2 (A2 – x2)
= \(\frac{1}{2}\)k(A2 – x2) … (1)
If the phase of the particle at an instant t is θ = ωt + α, where α is initial phase, its velocity at that instant is
v = ωA cos (ωt + α)
and its KE at that instant is
KE = \(\frac{1}{2}\)mv2 = \(\frac{1}{2}\)mω2A2 cos2(ωt + α) ….. (2)
Therefore, the KE varies with time as cos2 θ.
(2) Potential energy : The potential energy of a particle in linear SHM is defined as the work done by an external agent, against the restoring force, in taking the particle from its mean position to a given point in the path, keeping the particle in equilibirum.
Suppose the particle in below figure is displaced from P1 to P2, through an infinitesimal distance dx against the restoring force F as shown.
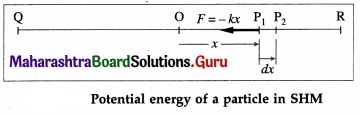
The corresponding work done by the external agent will be dW = ( – F)dx = kx dx. This work done is stored in the form of potential energy. The potential energy (PE) of the particle when its displacement from the mean position is x can be found by integrating the above expression from 0 to x.
∴ PE = \(\int\)dW = \(\int_{0}^{x}\) kx dx = \(\frac{1}{2}\) kx2 … (3)
The displacement of the particle at an instant t being
x = A sin (wt + α)
its PE at that instant is
PE = \(\frac{1}{2}\)kx2 = \(\frac{1}{2}\)kA2 sin2(ωt + α) … (4)
Therefore, the PE varies with time as sin2θ.
(3) Total energy : The total energy of the particle is equal to the sum of its potential energy and kinetic energy.
From Eqs. (1) and (2), total energy is E = PE + KE
= \(\frac{1}{2}\)kx2 + \(\frac{1}{2}\)k(A2 – x2)
= \(\frac{1}{2}\)kx2 + \(\frac{1}{2}\)kA2 – \(\frac{1}{2}\)kx2
∴ E = \(\frac{1}{2}\)kA2 = \(\frac{1}{2}\)mω2A2 … (5)
As m is constant, ω and A are constants of the motion, the total energy of the particle remains constant (or its conserved).
![]()
Question 7.
Deduce the expression for period of simple pendulum. Hence state the factors on which its period depends.
Answer:
An ideal simple pendulum is defined as a heavy point mass suspended from a rigid support by a weightless, inextensible and twistless string, and set oscillating under gravity through a small angle in a vertical plane.
In practice, a small but heavy sphere, called the bob, is used. The distance from the point of suspension to the centre of gravity of the bob is called the length of the pendulum.
Consider a simple pendulum of length L1 – suspended from a rigid support O. When displaced from its initial position of rest through a small angle θ in a vertical plane and released, it performs oscillations between two extremes, B and C, as shown in below figure. At B, the forces on the bob are its weight \(m \vec{g}\) and the tension \(\overrightarrow{F_{1}}\) in the string. Resolve \(m \vec{g}\) into two components : mg cos θ in the direction opposite to that of the tension and mg sin θ perpendicular to the string.

mg cos θ balanced by the tension in the string. mg sin θ restores the bob to the equilibrium position.
Restoring force, F = – mg sin θ
If θ is small and expressed in radian,
sin θ \(\approx\) θ = \(\frac{\text { arc }}{\text { radius }}\) = \(\frac{\mathrm{AB}}{\mathrm{OB}}\) = \(\frac{x}{L}\)
∴ F = – mgθ = -mg\(\frac{x}{L}\) …. (1)
Since m, g and L are constant,
F ∝ (-x) …. (2)
Thus, the net force on the bob is in the direction opposite to that of displacement x of the bob from its mean position as indicated by the minus sign, and the magnitude of the force is proportional to the magnitude of the displacement. Hence, it follows that the motion of a simple pendulum is linear SHM.
Acceleration, a = \(\frac{F}{m}\) = –\(\frac{g}{L}\)x … (3)
Therefore, acceleration per unit displacement
= |\(\frac{a}{x}\)| = \(\frac{g}{L}\) ….. (4)
Period of SHM,
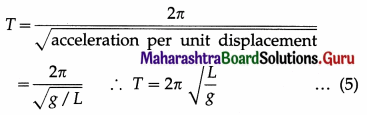
This gives the expression for the period of a simple pendulum.
The period of a simple pendulum at a given place is
T = 2π\(\sqrt{\frac{L}{g}}\)
where L is the length of the simple pendulum and g is the acceleration due to gravity at that place. From the above expression, the laws of simple pendulum are as follows :
(1) Law of length : The period of a simple pendulum at a given place (g constant) is directly proportional to the square root of its length.
∴ T ∝\(\sqrt{L}\)
(2) Law of acceleration due to gravity : The period of a simple pendulum of a given length (L constant) is inversely proportional to the square root of the acceleration due to gravity.
∴ T ∝ \(\frac{1}{\sqrt{g}}\)
Question 8.
At what distance from the mean position is the speed of a particle performing S.H.M. half its maximum speed. Given path length of S.H.M. = 10 cm. [Ans: 4.33 cm]
Answer:
Data : v = \(\frac{1}{2}\)vmax, 2A = 10 cm
∴ A = 5 cm
v = ω\(\sqrt{A^{2}-x^{2}}\) and vmax = ωA
Since v = \(\frac{1}{2}\)vmax,
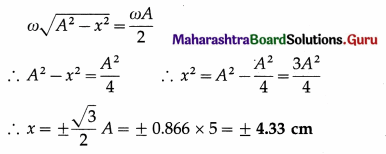
This gives the required displacement.
Question 9.
In SI units, the differential equation of an S.H.M. is \(\frac{d^{2} x}{d t^{2}}\) = -36x. Find its frequency and period. Find its frequency and period.
[Ans: 0.9548 Hz, 1.047 s]
Answer:
\(\frac{d^{2} x}{d t^{2}}\) = -36x
Comparing this equation with the general equation,
\(\frac{d^{2} x}{d t^{2}}\) = -ω2x
We get, ω2 = 36 ∴ ω = 6 rad/s
ω = 2πf
∴ The frequency, f = \(\frac{\omega}{2 \pi}\) = \(\frac{6}{2(3.142)}\) = \(\frac{6}{6.284}\) = 0.9548 Hz
and the period, T = \(\frac{1}{f}\) = \(\frac{1}{0.9548}\) = 1.047 s
Question 10.
A needle of a sewing machine moves along a path of amplitude 4 cm with frequency 5 Hz. Find its acceleration \(\frac{1}{30}\)s after it has crossed the mean position. [Ans: 34.2 m/s2]
Answer:
Data : A = 4 cm = 4 × 10-2 m, f = 5Hz, t = \(\frac{1}{30}\)s
ω = 2πf = 2π (5) = 10π rad/s
Therefore, the magnitude of the acceleration,
|a| = ω2x = ω2A sin ωt
= (10π)2 (4 × 102)
= 10π2 sin \(\frac{\pi}{3}\) = 10 (9.872)(0.866) = 34.20 m/s2
Question 11.
Potential energy of a particle performing linear S.H.M is 0.1 π2 x2 joule. If mass of the particle is 20 g, find the frequency of S.H.M. [Ans: 1.581 Hz]
Answer:
Data : PE = 0.1 π2 x2 J, m = 20 g = 2 × 10-2 kg
PE = \(\frac{1}{2}\)mω2x2 = \(\frac{1}{2}\)m (4π2f2)x2
∴ \(\frac{1}{2}\)m(4π2f2)x2 = 0.1 π2 x2
∴ 2mf2 = 0.1 ∴ f2 = \(\frac{1}{20\left(2 \times 10^{-2}\right)}\) = 2.5
∴ The frequency of SHM is f = \(\sqrt{2.5}\) = 1.581 Hz
Question 12.
The total energy of a body of mass 2 kg performing S.H.M. is 40 J. Find its speed while crossing the centre of the path. [Ans: 6.324 cm/s]
Answer:
Data : m = 2 kg, E = 40 J
The speed of the body while crossing the centre of the path (mean position) is vmax and the total energy is entirely kinetic energy.
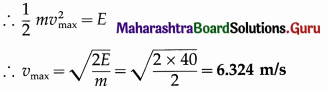
Question 13.
A simple pendulum performs S.H.M of period 4 seconds. How much time after crossing the mean position, will the displacement of the bob be one third of its amplitude. [Ans: 0.2163 s]
Answer:
Data : T = 4 s, x = A/3
The displacement of a particle starting into SHM from the mean position is x = A sin ωt = A sin \(\frac{2 \pi}{T}\) t
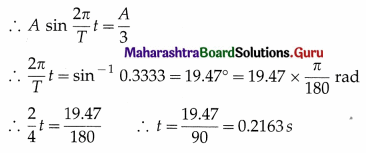
∴ the displacement of the bob will be one-third of its amplitude 0.2163 s after crossing the mean position.
Question 14.
A simple pendulum of length 100 cm performs S.H.M. Find the restoring force acting on its bob of mass 50 g when the displacement from the mean position is 3 cm. [Ans: 1.48 × 10-2 N]
Answer:
Data : L = 100 cm, m = 50 g = 5 × 10-2 kg, x = 3 cm, g = 9.8 m/s2
Restoring force, F = mg sin θ = mgθ
= (5 × 10-2)(9.8)\(\left(\frac{3}{100}\right)\)
= 1.47 × 10-2 N
Question 15.
Find the change in length of a second’s pendulum, if the acceleration due to gravity at the place changes from 9.75
m/s2 to 9.80 m/s2. [Ans: Decreases by 5.07 mm]
Answer:
Data : g1 = 9.75 m/s2, g2 = 9.8 m/s2
Length of a seconds pendulum, L = \(\frac{g}{\pi^{2}}\)

∴ The length of the seconds pendulum must be increased from 0.9876 m to 0.9927 m, i.e., by 0.0051 m.
![]()
Question 16.
At what distance from the mean position is the kinetic energy of a particle performing S.H.M. of amplitude 8 cm, three times its potential energy? [Ans: 4 cm]
Answer:
Data : A = 8 cm, KE = 3 PE
KE = \(\frac{1}{2}\) (A2 – x2) and PE = \(\frac{1}{2}\)kx2
Given, KE = 3PE.
∴ \(\frac{1}{2}\)k(A2 – x2) = 3\(\left(\frac{1}{2} k x^{2}\right)\)
∴ A2 – x2 = 3x2 ∴ 4x2 = A2
∴ the required displacement is
x = ±\(\frac{A}{2}\) = ±\(\frac{8}{2}\) = ± 4 cm
Question 17.
A particle performing linear S.H.M. of period 2π seconds about the mean position O is observed to have a speed of \(b \sqrt{3}\) m/s, when at a distance b (metre) from O. If the particle is moving away from O at that instant, find the
time required by the particle, to travel a further distance b. [Ans: π/3 s]
Answer:
Data : T = 2πs, v = b\(\sqrt{3}\) m/s at x = b
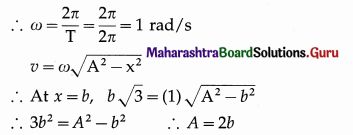
∴ Assuming the particle starts from the mean position, its displacement is given by
x = A sin ωt = 2b sin t
If the particle is at x = b at t = t1,
b = 2b sint1 ∴ t1 = sin-1 \(\frac{1}{2}\) = \(\frac{\pi}{6}\)s
Also, with period T = 2πs, on travelling a further distance b the particle will reach the positive extremity at time t2 = \(\frac{\pi}{2}\)s.
∴ The time taken to travel a further distance b from x = b is t2 – t1 = \(\frac{\pi}{2}\) – \(\frac{\pi}{6}\) = \(\frac{\pi}{3}\)s.
Question 18.
The period of oscillation of a body of mass m1 suspended from a light spring is T. When a body of mass m2 is tied to the first body and the system is made to oscillate, the period is 2T. Compare the masses m1 and m2 [Ans: 1/3]
Answer:
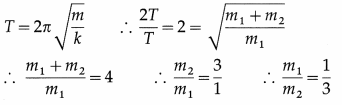
This gives the required ratio of the masses.
Question 19.
The displacement of an oscillating particle is given by x = asinωt + bcosωt where a, b and ω are constants. Prove that the particle performs a linear S.H.M. with amplitude A = \(\sqrt{a^{2}+b^{2}}\)
Answer:
x = asinωt + bcosωt
Let a = A cos φ and b = A sin φ, so that
A2 = a2 + b2 and tan φ = \(\frac{b}{a}\)
∴ x = A cos φ sin ωt + A sin φ cos ωt
∴ x = A sin (ωt + φ)
which is the equation of a linear SHM with amplitude A = \(\sqrt{a^{2}+b^{2}}\) and phase constant φ = tan-1 \(\frac{b}{a}\), as required.
Question 20.
Two parallel S.H.M.s represented by x1 = 5sin (4πt + \(\frac{\pi}{3}\)) cm and x2 = 3sin(4πt + π/4) cm are superposed on a particle. Determine the amplitude and epoch of the resultant S.H.M. [Ans: 7.936 cm, 54° 23′]
Answer:
Data: x1 = 5 sin (4πt + \(\frac{\pi}{3}\)) = A1 sin(ωt + α),
x2 = 3 sin (4πt + \(\frac{\pi}{4}\)) = A2 sin(ωt + β)
∴ A1 = 5 cm, A2 = 3 cm, α = \(\frac{\pi}{3}\) rad, β = \(\frac{\pi}{4}\) rad
(i) Resultant amplitude,

(ii) Epoch of the resultant SHM,
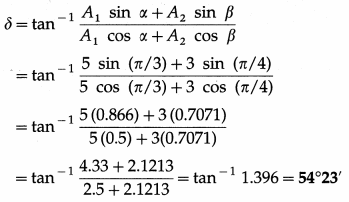
Question 21.
A 20 cm wide thin circular disc of mass 200 g is suspended to a rigid support from a thin metallic string. By holding the rim of the disc, the string is twisted through 60° and released. It now performs angular oscillations of period 1 second. Calculate the maximum restoring torque generated in the string under undamped conditions. (π3 ≈ 31)
[Ans: 0.04133 N m]
Answer:
Data: R = 10cm = 0.1 m, M = 0.2 kg, θm = 60° = \(\frac{\pi}{3}\) rad, T = 1 s, π3 ≈ 31
The Ml of the disc about the rotation axis (perperdicular through its centre) is
I = \(\frac{1}{2}\)MR2 = (0.2)(0.1)2 = 10-3 kg.m2
The period of torsional oscillation, T = 2π\(\sqrt{\frac{I}{c}}\)
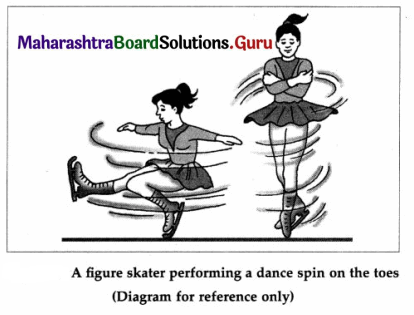
∴ The torsion constant, c = 4πr2\(\frac{I}{T^{2}}\)
The magnitude of the maximum restoring torque,
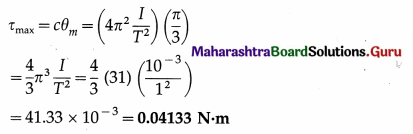
Question 22.
Find the number of oscillations performed per minute by a magnet is vibrating in the plane of a uniform field of 1.6 × 10-5 Wb/m2. The magnet has moment of inertia 3 × 10-6 kgm2 and magnetic moment 3 A m2. [Ans:38.19 osc/min.]
Answer:
Data : B = 1.6 × 10-5 T, I = 3 × 10-6kg/m2,
µ = 3 A.m2
The period of oscillation, T = 2π \(\sqrt{\frac{I}{\mu B_{\mathrm{h}}}}\)
∴ The frequency of oscillation is
f = \(\frac{1}{2 \pi}\)\(\sqrt{\frac{\mu B}{I}}\)
∴ The number of oscillations per minute
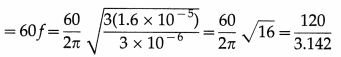
= 38.19 per minute
![]()
Question 23.
A wooden block of mass m is kept on a piston that can perform vertical vibrations of adjustable frequency and amplitude. During vibrations, we don’t want the block to leave the contact with the piston. How much maximum frequency is possible if the amplitude of vibrations is restricted to 25 cm? In this case, how much is the energy per unit mass of the block? (g ≈ π2 ≈ 10 m s-2)
[Ans: nmax = 1/s, E/m = 1.25 J/kg]
Answer:
Data : A = 0.25 m, g = π2 = 10 m/s2
During vertical oscillations, the acceleration is maximum at the turning points at the top and bottom. The block will just lose contact with the piston when its apparent weight is zero at the top, i. e., when its acceleration is amax = g, downwards.
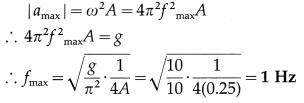
This gives the required frequency of the piston.
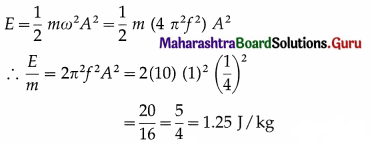
12th Physics Digest Chapter 5 Oscillations of Waves Intext Questions and Answers
Can you tell? (Textbook Page No. 112)
Question 1.
Why is the term angular frequency (ω) used here for a linear motion ?
Answer:
A linear SHM is the projection of a UCM on a diameter of the circle. The angular speed co of a particle moving along this reference circle is called the angular frequency of the particle executing linear SHM.
Can you tell? (Textbook Page No. 114)
Question 1.
State at which point during an oscillation the oscillator has zero velocity but positive acceleration ?
Answer:
At the left extreme, i.e., x = – A, so that a = – ω2x = – ω2(- A) = ω2A = amax
Question 2.
During which part of the simple harmonic motion velocity is positive but the displacement is negative, and vice versa ?
Answer:
Velocity v is positive (to the right) while displacement x is negative when the particle in SHM is moving from the left extreme towards the mean position. Velocity v is negative (to the left) while displacement x is positive when the particle in SHM is moving from the right extreme towards the mean position.
Can you tell? (Textbook page 76)
Question 1.
To start a pendulum swinging, usually you pull it slightly to one side and release. What kind of energy is transferred to the mass in doing this?
Answer:
On pulling the bob of a simple pendulum slightly to one side, it is raised to a slightly higher position. Thus, it gains gravitational potential energy.
Question 2.
Describe the energy changes that occur when the mass is released.
Answer:
When released, the bob oscillates in SHM in a vertical plane and the energy oscillates back and forth between kinetic and potential, going completely from one form of energy to the other as the pendulum oscillates. In the case of undamped SHM, the motion starts with all of the energy as gravitational potential energy. As the object starts to move, the gravitational potential energy is converted into kinetic energy, becoming entirely kinetic energy at the equilibrium position. The velocity becomes zero at the other extreme as the kinetic energy is completely converted back into gravitational potential energy,
and this cycle then repeats.
Question 3.
Is/are there any other way/ways to start the oscillations of a pendulum? Which energy is supplied in this case/cases?
Answer:
The bob can be given a kinetic energy at its equilibrium position or at any other position of its path. In the first case, the motion starts with all of the energy as kinetic energy. In the second case, the motion starts with partly gravitational potential energy and partly kinetic energy.
Can you tell? (Textbook Page No. 109)
Question 1.
Is the motion of a leaf of a tree blowing in the wind periodic ?
Answer:
The leaf of a tree blowing in the wind oscillates, but the motion is not periodic. Also, its displacement from the equilibrium position is not a regular function of time.
Maharashtra State Board 12th Std Physics Textbook Solutions
- Rotational Dynamics Class 12 Physics Textbook Solutions
- Mechanical Properties of Fluids Class 12 Physics Textbook Solutions
- Kinetic Theory of Gases and Radiation Class 12 Physics Textbook Solutions
- Thermodynamics Class 12 Physics Textbook Solutions
- Oscillations Class 12 Physics Textbook Solutions
- Superposition of Waves Class 12 Physics Textbook Solutions
- Wave Optics Class 12 Physics Textbook Solutions
- Electrostatics Class 12 Physics Textbook Solutions


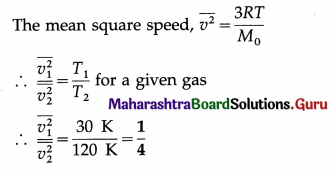



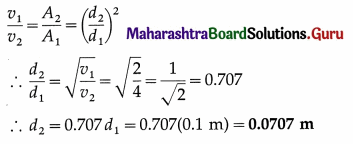
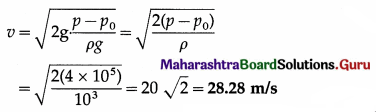
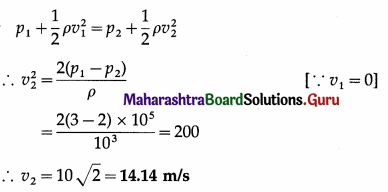
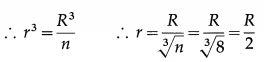

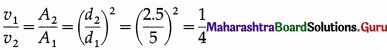
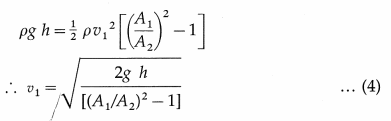
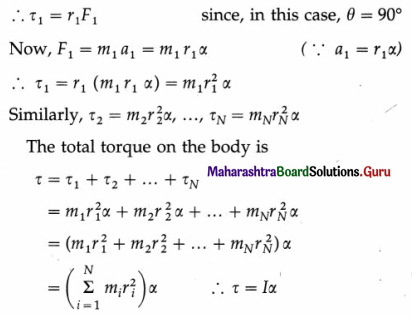






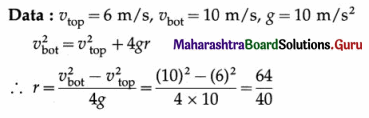
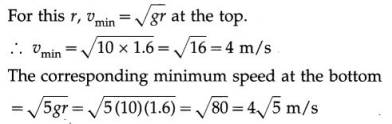


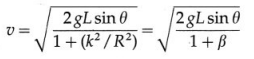
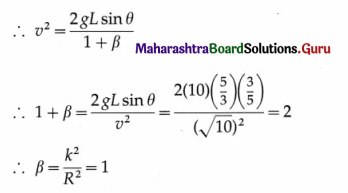



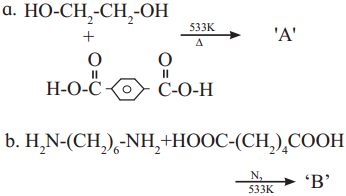
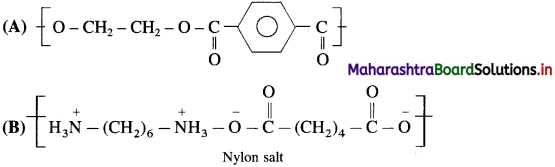
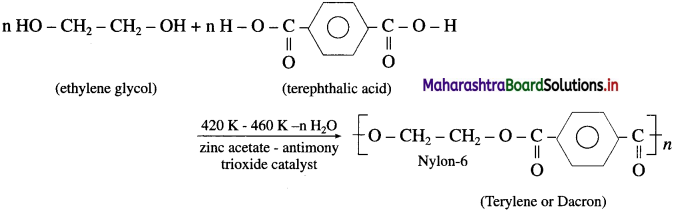
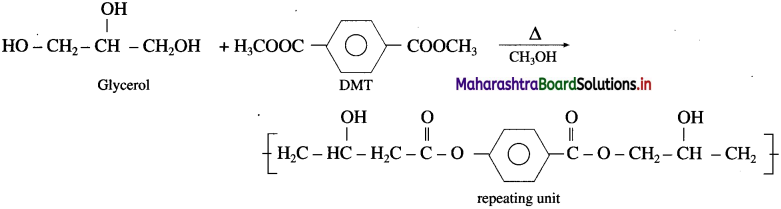
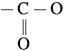 linkage is present in terylene or dacron polymer.
linkage is present in terylene or dacron polymer.
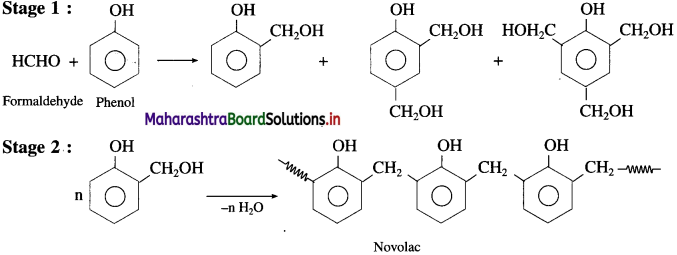
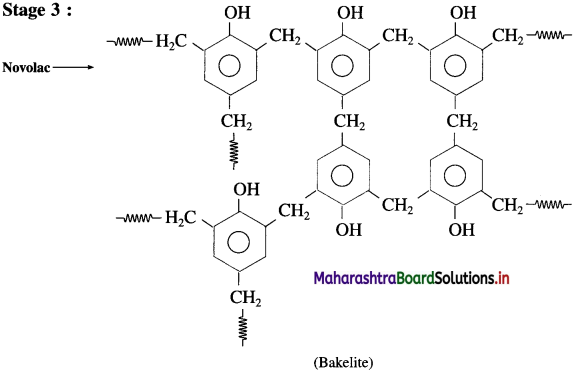
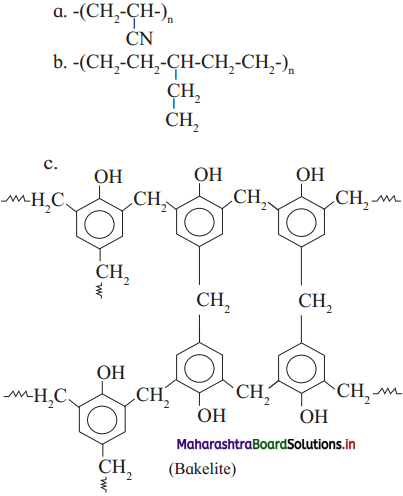
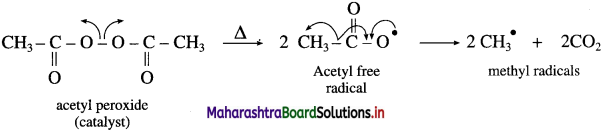
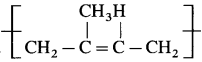 Repeating unit of natural rubber (Basic unit : isoprene)
Repeating unit of natural rubber (Basic unit : isoprene) and formaldehyde (HCHO)
and formaldehyde (HCHO)






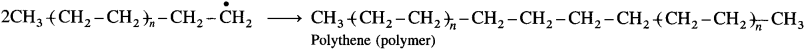


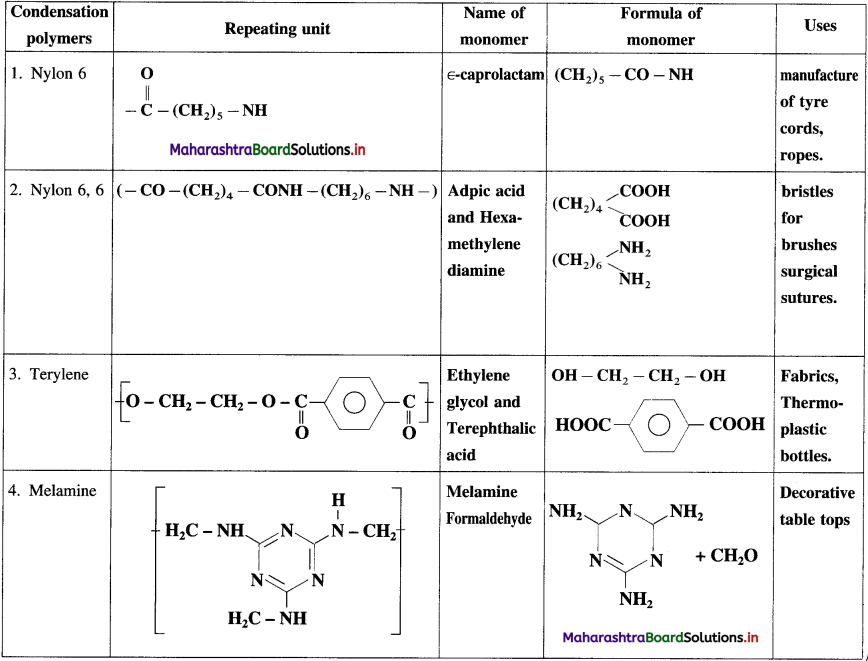
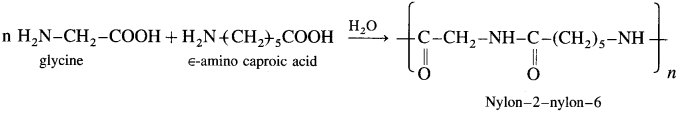

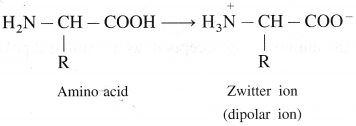



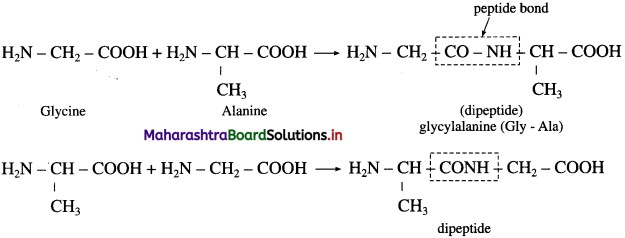




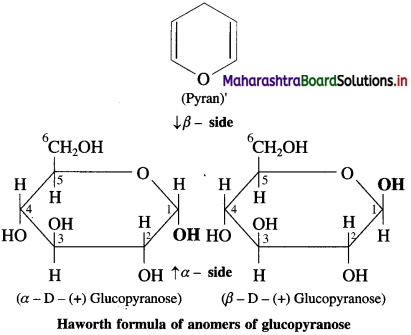
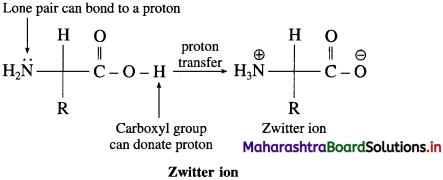
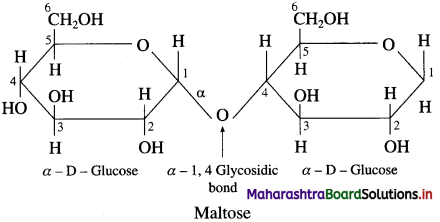











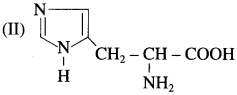



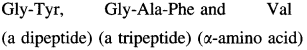




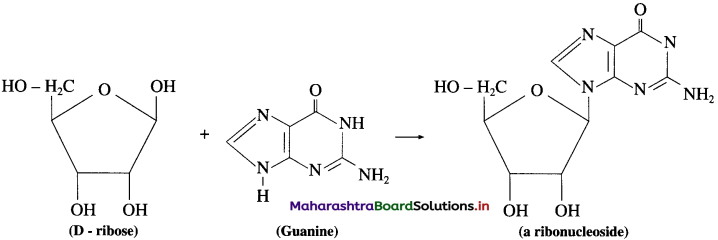






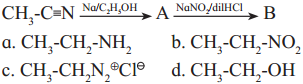



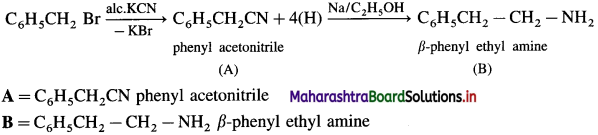
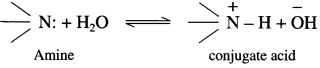


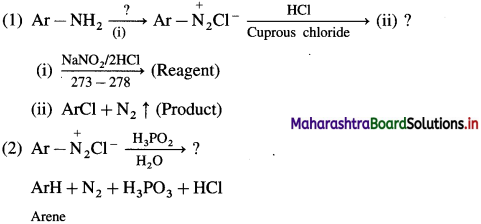
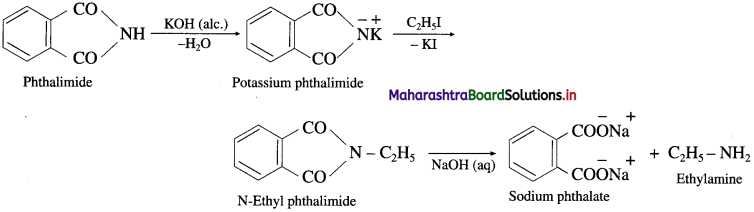
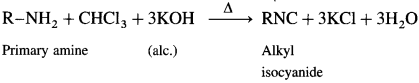

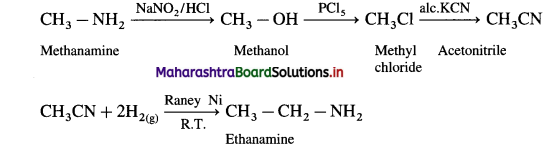
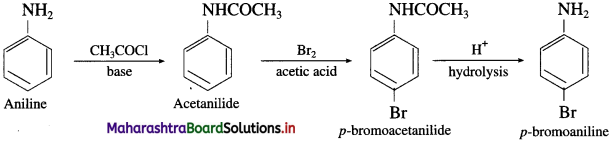
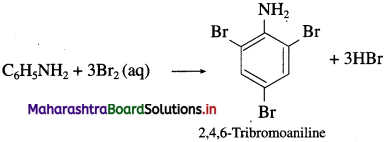
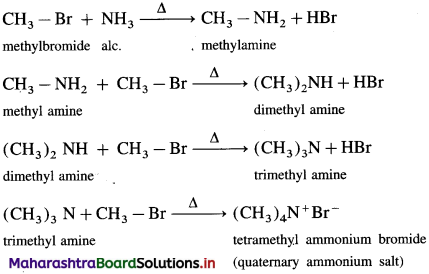



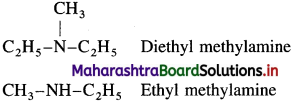
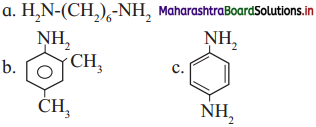

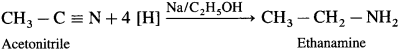
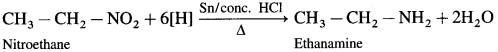

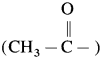 is called acetylation of amines.
is called acetylation of amines.



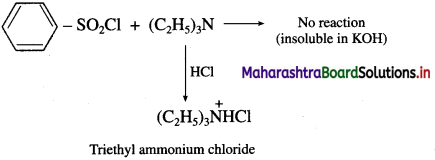
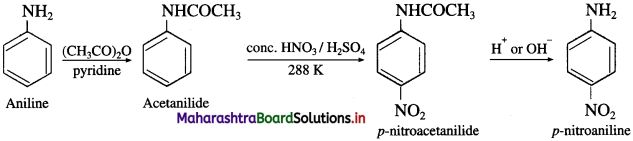
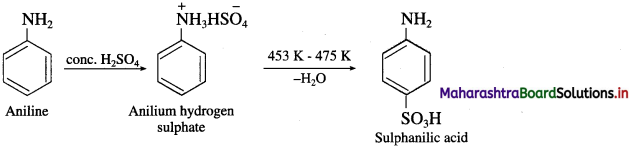


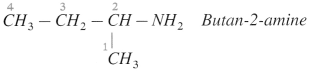




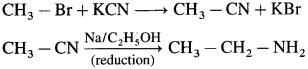
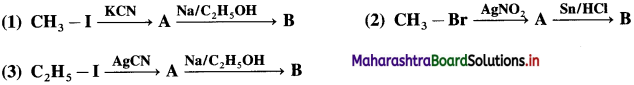

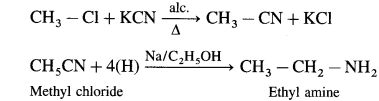


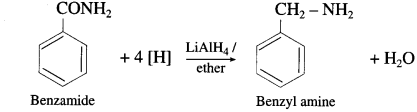

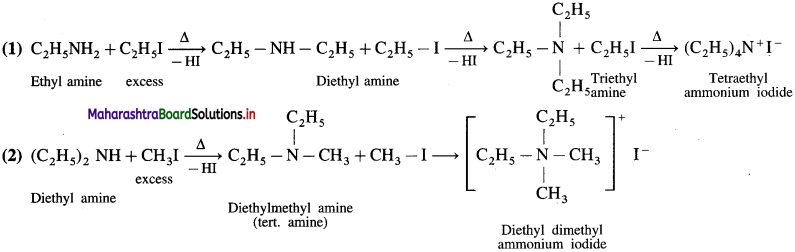






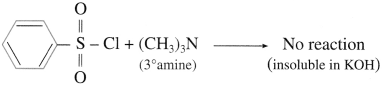
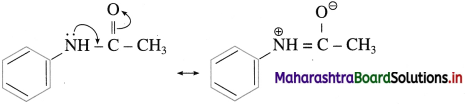

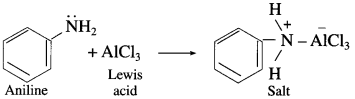
 do not have ‘H’ bonded to ‘N’.
do not have ‘H’ bonded to ‘N’.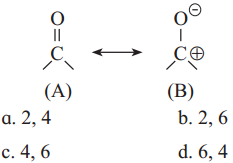
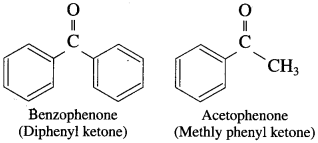
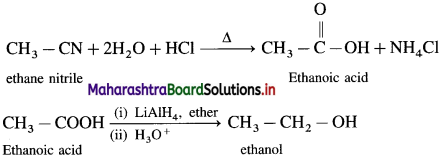

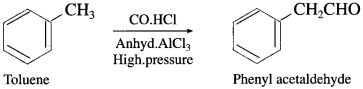

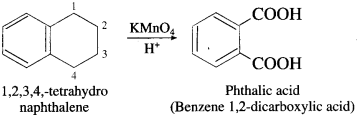



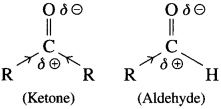
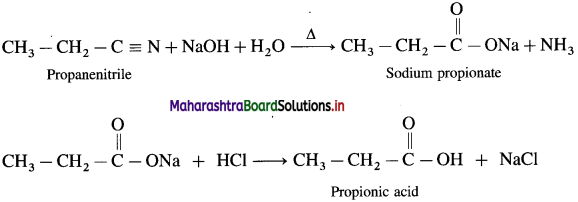

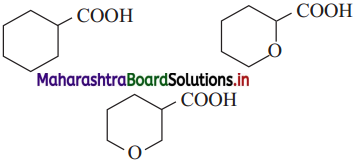
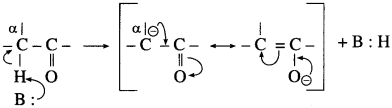
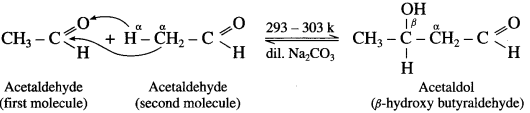
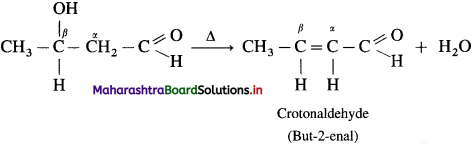
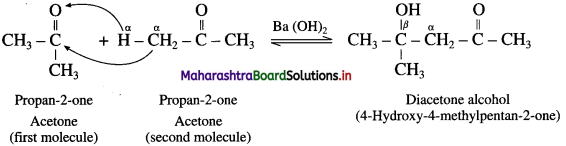

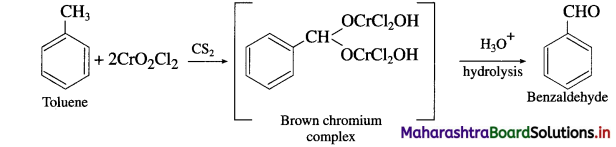


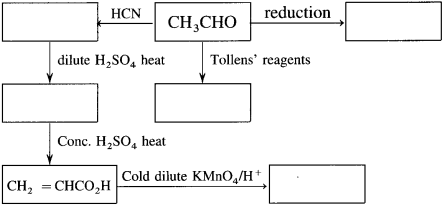
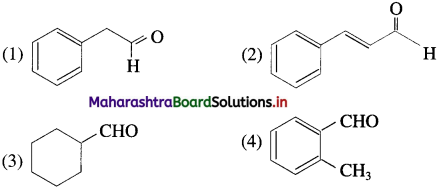




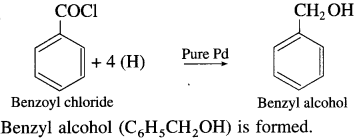
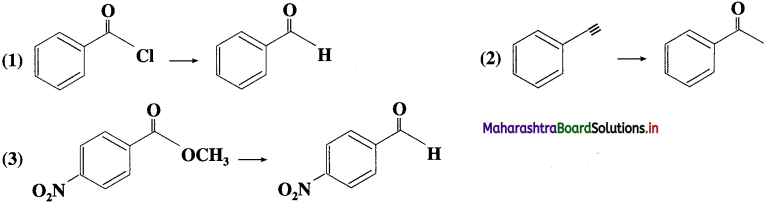
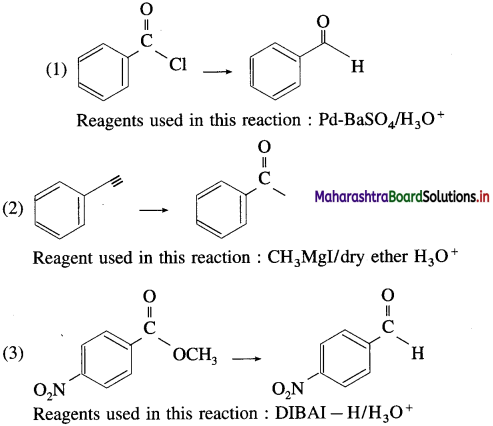

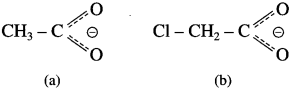
 The acetate ion formed gets destabilised due to electron releasing effect of methyl group
The acetate ion formed gets destabilised due to electron releasing effect of methyl group
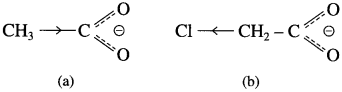
 The dichloroacetate ion formed gets stabilised due electron-withdrawing effect of two chlorine atoms. (- 1 effect)
The dichloroacetate ion formed gets stabilised due electron-withdrawing effect of two chlorine atoms. (- 1 effect)

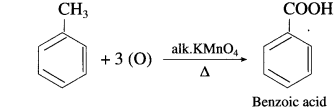
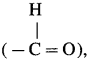 , an aldehyde is oxidised to carboxylic acid
, an aldehyde is oxidised to carboxylic acid  which is not possible in case of ethers, ketones, alcohols and hydrocarbons.
which is not possible in case of ethers, ketones, alcohols and hydrocarbons. can’t be broken easily.
can’t be broken easily.
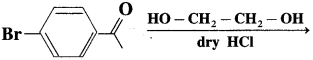
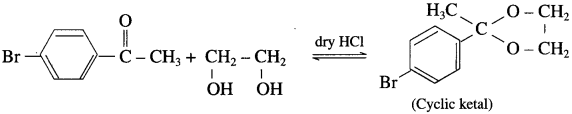


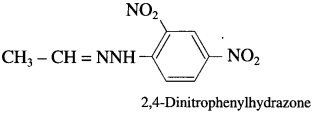

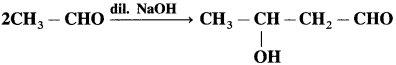
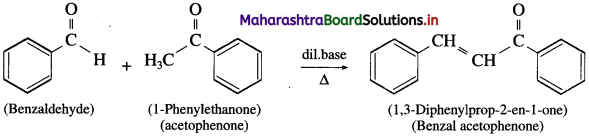
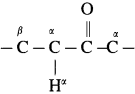
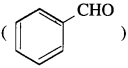 does not have a-hydrogen atom, it will not undergo self aldol condensation.
does not have a-hydrogen atom, it will not undergo self aldol condensation. contains a-carbon atom, it cannot undergo Cannizzaro reaction.
contains a-carbon atom, it cannot undergo Cannizzaro reaction.