Balbharti Maharashtra State Board Marathi Yuvakbharati 12th Digest व्याकरण वाक्यरूपांतर Notes, Textbook Exercise Important Questions and Answers.
Maharashtra State Board 12th Marathi Yuvakbharati Solutions व्याकरण वाक्यरूपांतर
12th Marathi Guide व्याकरण वाक्यरूपांतर Textbook Questions and Answers
कृती
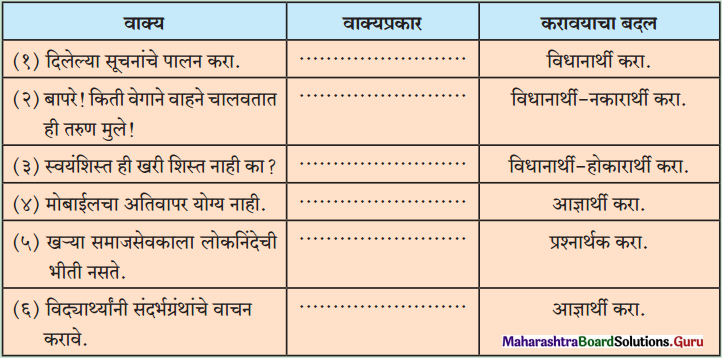
1. खालील तक्ता पूर्ण करा.
उत्तर :
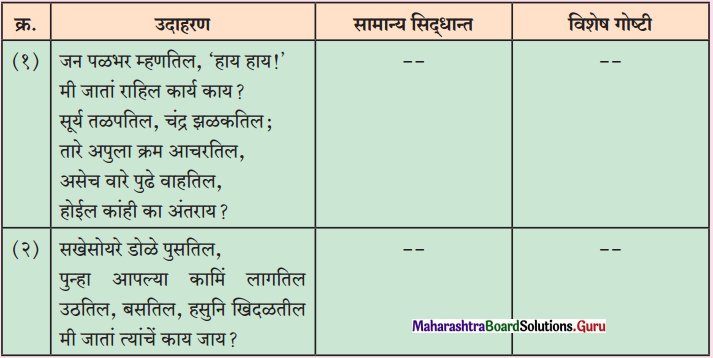
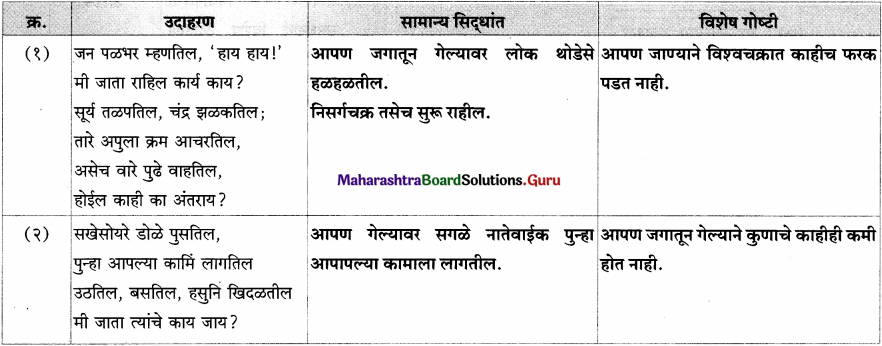
(१) दिलेल्या सूचनांचे पालन करा.
- वाक्यप्रकार → आज्ञार्थी वाक्य
- विधानार्थी वाक्य → दिलेल्या सूचनांचे पालन करणे आवश्यक आहे.
(२) बापरे! किती वेगाने वाहने चालवतात ही तरुण मुले!
- वाक्यप्रकार → उद्गारार्थी वाक्य
- विधानार्थी – नकारार्थी वाक्य → तरुण मुलांनी खूप वेगाने वाहने चालवू नयेत.
(३) स्वयंशिस्त ही खरी शिस्त नाही का?
- वाक्यप्रकार → प्रश्नार्थी वाक्य
- विधानार्थी – होकारार्थी वाक्य → स्वयंशिस्त ही खरी शिस्त आहे.
(४) मोबाइलचा अतिवापर योग्य नाही.
- वाक्यप्रकार → विधानार्थी – नकारार्थी वाक्य
- आज्ञार्थी वाक्य → मोबाइलचा अतिवापर टाळा.
(५) खऱ्या समाजसेवकाला लोकनिंदेची भीती नसते.
- वाक्यप्रकार → विधानार्थी – नकारार्थी वाक्य
- प्रश्नार्थी वाक्य → खऱ्या समाजसेवकाला लोकनिंदेची भीती असते का?
(६) विदयार्थ्यांनी संदर्भग्रंथांचे वाचन करावे.
- वाक्यप्रकार → विधानार्थी वाक्य
- आज्ञार्थी वाक्य → विदयार्थ्यांनो, संदर्भग्रंथांचे वाचन करा.
2. कंसातील सूचनेप्रमाणे वाक्यरूपांतर करा.
(a) सकाळी फिरणे आरोग्यास हितकारक आहे. (नकारार्थी करा.)
(b) तुम्ही काम अचूक करा. (विधानार्थी करा.)
(c) किती सुंदर आहे ही पाषाणमूर्ती! (विधानार्थी करा.)
(d) पांढरा रंग सर्वांना आवडतो. (प्रश्नार्थी करा.)
(e) चैनीच्या वस्तू महाग असतात. (नकारार्थी करा.)
(f) तुझ्या भेटीने खूप आनंद झाला. (उद्गारार्थी करा.)
(g) अबब! काय हा चमत्कार! (विधानार्थी करा.)
(h) तुम्ही कोणाशीच वाईट बोलू नका. (होकारार्थी करा.)
(i) निरोगी राहावे असे कोणाला वाटत नाही ? (विधानार्थी करा.)
(j) दवाखान्यात मोठ्या आवाजात बोलू नये. (होकारार्थी करा.)
उत्तर :
(a) सकाळी फिरणे आरोग्यास अपायकारक नाही.
(b) तुम्ही काम अचूक करणे आवश्यक आहे.
(c) ही पाषाणमूर्ती खूप सुंदर आहे.
(d) पांढरा रंग कुणाला आवडत नाही?
(e) चैनीच्या वस्तू स्वस्त नसतात.
(f) किती आनंद झाला तुझ्या भेटीने!
(g) हा अजब चमत्कार आहे.
(h) तुम्ही सगळ्यांशी चांगले बोला.
(i) निरोगी राहावे असे सर्वांना वाटते.
(j) दवाखान्यात हळू आवाजात बोलावे.
- लेखन करताना काही वेळा वाक्यरचनेत बदल करण्याची गरज भासते, अशा बदलाला ‘वाक्यरूपांतर किंवा वाक्यपरिवर्तन’ असे म्हणतात.
- वाक्यांचे रूपांतर करताना वाक्यरचनेत बदल होतो, पण वाक्यार्थाला बाध येत नाही.
विधानार्थी, प्रश्नार्थी, उद्गारार्थी, आज्ञार्थी या वाक्यांचे एकमेकांत रूपांतर होते.
उदाहरणार्थ,
पुढील वाक्ये नीट अभ्यासा :
- मुलांनी शिस्त पाळणे खूप आवश्यक आहे. (विधानार्थी वाक्य.)
- किती आवश्यक आहे मुलांनी शिस्त पाळणे! (उद्गारार्थी वाक्य.)
- मुलांनी शिस्त पाळणे आवश्यक नाही का? (प्रश्नार्थी वाक्य.)
- मुलांनो, शिस्त अवश्य पाळा. (आज्ञार्थी वाक्य.)
म्हणून :
| वाक्यार्थ्याला बाध न आणता वाक्याच्या रचनेत केलेला बदल म्हणजे वाक्यरूपांतर होय. |
होकारार्थी – नकारार्थी (वाक्यरूपांतर)
पुढील वाक्ये नीट अभ्यासा.
- क्रिकेट मालिकेत भारतीय संघ विजयी झाला. (होकारार्थी वाक्य.)
- क्रिकेट मालिकेत भारतीय संघ पराभूत झाला नाही. (नकारार्थी वाक्य.)
होकारार्थी वाक्याचे नकारार्थी वाक्यात रूपांतर करताना आपण काय केले?
- विजयी x पराभूत
- झाला x झाला नाही.
दोन विरुद्धार्थी शब्दबंध घेऊन वाक्य बदलले. पण वाक्याचा अर्थ बदलला नाही.
म्हणून,
| वाक्य रूपांतर करताना वाक्याच्या रचनेत बदल झाला, तरी वाक्याच्या अर्थात बदल होता कामा नये. |