Maharashtra Board 10th Class Maths Part 1 Practice Set 2.2 Solutions Chapter 2 Quadratic Equations

Balbharti Maharashtra State Board Class 10 Maths Solutions covers the Practice Set 2.2 Algebra 10th Class Maths Part 1 Answers Solutions Chapter 2 Quadratic Equations.

Practice Set 2.2 Algebra 10th Std Maths Part 1 Answers Chapter 2 Quadratic Equations

Question 1.
Solve the following quadratic equations by factorisation.
i. x² – 15x + 54 = 0
ii. x² + x – 20 = 0
iii. 2y² + 27y + 13 = 0
iv. 5m² = 22m + 15
v. 2x² – 2x + \(\frac { 1 }{ 2 } \) = 0
vi. 6x – \(\frac { 2 }{ x } \) = 1
vii. √2x² + 7x + 5√2 = 0 to solve this quadratic equation by factorisation complete the following activity
viii. 3x² – 2√6x + 2 = 0
ix. 2m(m – 24) = 50
x. 252 = 9
xi. 7m² = 21 m
xii. m² – 11 = 0
Solution:

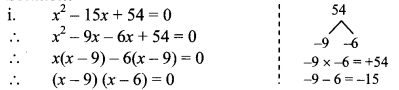
By using the property, if the product of two numbers is zero, then at least one of them is zero, we get
∴ x – 9 = 0 or x – 6 = 0
∴ x = 9 or x = 6
∴ The roots of the given quadratic equation are 9 and 6.

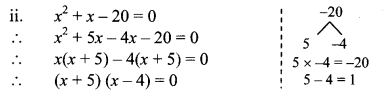
By using the property, if the product of two numbers is zero, then at least one of them is zero, we get
∴ x + 5 = 0 or x – 4 = 0
∴ x = -5 or x = 4
∴ The roots of the given quadratic equation are -5 and 4.

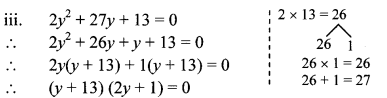
By using the property, if the product of two numbers is zero, then at least one of them is zero, we get
∴ y + 13 = 0 or 2y + 1 = 0
∴ y = – 13 or 2y = -1
∴ y = -13 or y = –\(\frac { 1 }{ 2 } \)
∴ The roots of the given quadratic equation are -13 and – \(\frac { 1 }{ 2 } \)

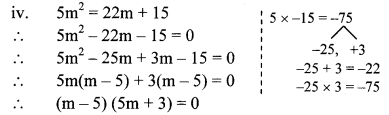
By using the property, if the product of two numbers is zero, then at least one of them is zero, we get
∴ m – 5 = 0 or 5m + 3 = 0
∴ m = 5 or 5m = -3
∴ m = 5 or m = \(\frac { -3 }{ 5 } \)
∴ The roots of the given quadratic equation are 5 and – \(\frac { 3 }{ 5 } \)

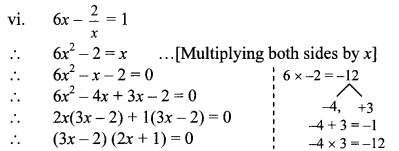
By using the property, if the product of two numbers is zero, then at least one of them is zero, we get
∴ 3x – 2 = 0 or 2x + 1 = 0
∴ 3x = 2 or 2x = -1
∴ x = \(\frac { 2 }{ 3 } \) or 2x = -1
∴ The roots of the given quadratic equation are \(\frac { 2 }{ 3 } \) and \(\frac { -1 }{ 2 } \).

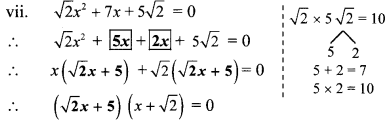
By using the property, if the product of two numbers is zero, then at least one of them is zero, we get

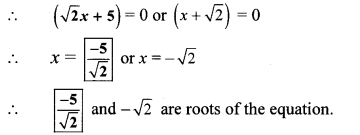
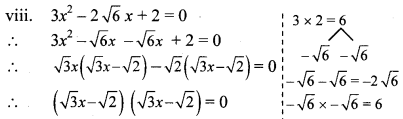
By using the property, if the product of two numbers is zero, then at least one of them is zero, we get

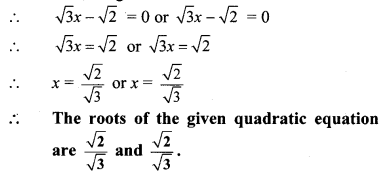
ix. 2m (m – 24) = 50
∴ 2m² – 48m = 50
∴ 2m² – 48m – 50 = 0
∴m² – 24m – 25 = 0 …[Dividing both sides by 2]

∴ m – 25 = 0 or m + 1 = 0
∴ m = 25 or m = -1
∴ The roots of thes given quadratic equation are 25 and -1.

x. 25m² = 9
∴ 25m² – 9 = 0
∴ (5m)² – (3)² = 0
∴ (5m + 3) (5m – 3) = 0
…. [∵a² – b² = (a + b) (a – b)]
By using the property, if the product of two numbers is zero, then at least one of them is zero, we get
∴ 5m + 3 = 0 or 5m – 3 = 0
∴ 5m = -3 or 5m = 3
∴ m = \(\frac { -3 }{ 5 } \) or m = \(\frac { 3 }{ 5 } \)
∴ The roots of the given quadratic equation are \(\frac { -3 }{ 5 } \) and \(\frac { 3 }{ 5 } \).

xi. 7m² = 21m
∴ 7m² – 21m = 0
∴ m² – 3m = 0 …[Dividing both sides by 7]
∴ m(m – 3) = 0
By using the property, if the product of two numbers is zero, then at least one of them is zero, we get
∴ m = 0 or m – 3 = 0
∴ m = 0 or m = 3
∴ The roots of the given quadratic equation are 0 and 3.

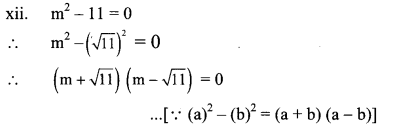
By using the property, if the product of two numbers is zero, then at least one of them is zero, we get
∴ m + √11 = 0 or m – √11 = 0
∴ m = -√11 or m = √11
∴ The roots of the given quadratic equation are – √11 and √11