Balbharti Maharashtra State Board Class 10 Maths Solutions covers the Practice Set 2.1 Geometry 10th Class Maths Part 2 Answers Solutions Chapter 2 Pythagoras Theorem.
Practice Set 2.1 Geometry 10th Std Maths Part 2 Answers Chapter 2 Pythagoras Theorem
Question 1.
Identify, with reason, which of the following are Pythagorean triplets.
i. (3,5,4)
ii. (4,9,12)
iii. (5,12,13)
iv. (24,70,74)
v. (10,24,27)
vi. (11,60,61)
Solution:
i. Here, 52 = 25
32 + 42 = 9 + 16 = 25
∴ 52 = 32 + 42
The square of the largest number is equal to the sum of the squares of the other two numbers.
∴ (3,5,4) is a Pythagorean triplet.
ii. Here, 122 = 144
42 + 92= 16 + 81 =97
∴ 122 ≠ 42 + 92
The square of the largest number is not equal to the sum of the squares of the other two numbers.
∴ (4,9,12) is not a Pythagorean triplet.
iii. Here, 132 = 169
52 + 122 = 25 + 144 = 169
∴ 132 = 52 + 122
The square of the largest number is equal to the sum of the squares of the other two numbers.
∴ (5,12,13) is a Pythagorean triplet.
iv. Here, 742 = 5476
242 + 702 = 576 + 4900 = 5476
∴ 742 = 242 + 702
The square of the largest number is equal to the sum of the squares of the other two numbers.
∴ (24, 70,74) is a Pythagorean triplet.
v. Here, 272 = 729
102 + 242 = 100 + 576 = 676
∴ 272 ≠ 102 + 242
The square of the largest number is not equal to the sum of the squares of the other two numbers.
∴ (10,24,27) is not a Pythagorean triplet.
vi. Here, 612 = 3721
112 + 602 = 121 + 3600 = 3721
∴ 612 = 112 + 602
The square of the largest number is equal to the sum of the squares of the other two numbers.
∴ (11,60,61) is a Pythagorean triplet.
Question 2.
In the adjoining figure, ∠MNP = 90°, seg NQ ⊥ seg MP,MQ = 9, QP = 4, find NQ.
Solution:
In ∆MNP, ∠MNP = 90° and [Given]
seg NQ ⊥ seg MP
NQ2 = MQ × QP [Theorem of geometric mean]
∴ NQ = \(\sqrt { MQ\times QP }\) [Taking square root of both sides]
= \(\sqrt { 9\times 4 } \)
= 3 × 2
∴NQ = 6 units
Question 3.
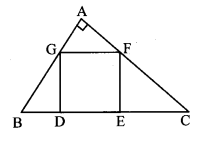
In the adjoining figure, ∠QPR = 90°, seg PM ⊥ seg QR and Q – M – R, PM = 10, QM = 8, find QR.
Solution:
In ∆PQR, ∠QPR = 90° and [Given]
seg PM ⊥ seg QR
∴ PM2 = OM × MR [Theorem of geometric mean]
∴ 102 = 8 × MR
∴ MR = \(\frac { 100 }{ 8 } \)
= 12.5
Now, QR = QM + MR [Q – M – R]
= 8 + 12.5
∴ QR = 20.5 units
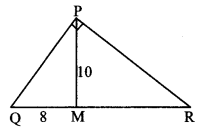
Question 4.
See adjoining figure. Find RP and PS using the information given in ∆PSR.
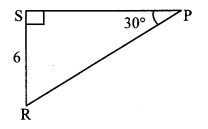
Solution:
In ∆PSR, ∠S = 90°, ∠P = 30° [Given]
∴ ∠R = 60° [Remaining angle of a triangle]
∴ ∆PSR is a 30° – 60° – 90° triangle.
RS = \(\frac { 1 }{ 2 } \) RP [Side opposite to 30°]
∴6 = \(\frac { 1 }{ 2 } \) RP
∴ RP = 6 × 2 = 12 units
Also, PS = \(\frac{\sqrt{3}}{2}\) RP [Side opposite to 60°]
= \(\frac{\sqrt{3}}{2}\) × 12
= \(6 \sqrt{3}\) units
∴ RP = 12 units, PS = 6 \(\sqrt { 3 }\) units
Question 5.
For finding AB and BC with the help of information given in the adjoining figure, complete the following activity.
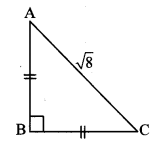
Solution:
AB = BC [Given]
∴ ∠BAC = ∠BCA [Isosceles triangle theorem]
Let ∠BAC = ∠BCA = x (i)
In ∆ABC, ∠A + ∠B + ∠C = 180° [Sum of the measures of the angles of a triangle is 180°]
∴ x + 90° + x = 180° [From (i)]
∴ 2x = 90°
∴ x = \(\frac { 90° }{ 2 } \) [From (i)]
∴ x = 45°
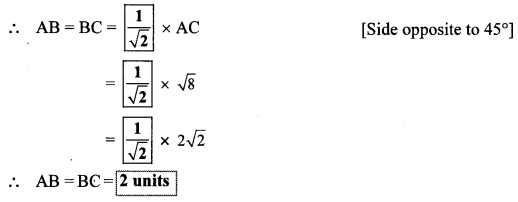
Question 6.
Find the side and perimeter of a square whose diagonal is 10 cm.
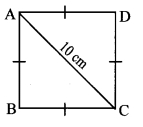
Solution:
Let ꠸ABCD be the given square.
l(diagonal AC) = 10 cm
Let the side of the square be ‘x’ cm.
In ∆ABC,
∠B = 90° [Angle of a square]
∴ AC2 = AB2 + BC2 [Pythagoras theorem]
∴ 102 = x2 + x2
∴ 100 = 2x2
∴ x2 = \(\frac { 100 }{ 2 } \)
∴x2 = 50
∴ x = \(\sqrt { 50 }\) [Taking square root of both sides]
= \(=\sqrt{25 \times 2}=5 \sqrt{2}\)
∴side of square is 5\(\sqrt { 2 }\) cm.
= 4 × 5 \(\sqrt { 2 }\)
∴ Perimeter of square = 20 \(\sqrt { 2 }\) cm
Question 7.
In the adjoining figure, ∠DFE = 90°, FG ⊥ ED. If GD = 8, FG = 12, find
i. EG
ii. FD, and
iii. EF
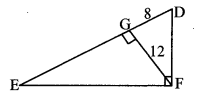
Solution:
i. In ∆DEF, ∠DFE = 90° and FG ⊥ ED [Given]
∴ FG2 = GD × EG [Theorem of geometric mean]
∴ 122 = 8 × EG .
∴ EG = \(\frac { 144 }{ 8 } \)
∴ EG = 18 units
ii. In ∆FGD, ∠FGD = 90° [Given]
∴ FD2 = FG2 + GD2 [Pythagoras theorem]
= 122 + 82 = 144 + 64
= 208
∴ FD = \(\sqrt { 208 }\) [Taking square root of both sides]
∴ FD = 4 \(\sqrt { 13 }\) units
iii. In ∆EGF, ∠EGF = 90° [Given]
∴ EF2 = EG2 + FG2 [Pythagoras theorem]
= 182 + 122 = 324 + 144
= 468
∴ EF = \(\sqrt { 468 }\) [Taking square root of both sides]
∴ EF = 6 \(\sqrt { 13 }\) units
Question 8.
Find the diagonal of a rectangle whose length is 35 cm and breadth is 12 cm.
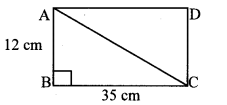
Solution:
Let ꠸ABCD be the given rectangle.
AB = 12 cm, BC 35 cm
In ∆ABC, ∠B = 90° [Angle of a rectangle]
∴ AC2 = AB2 + BC2 [Pythagoras theorem]
= 122 + 352
= 144 + 1225
= 1369
∴ AC = \(\sqrt { 1369 }\) [Taking square root of both sides]
= 37 cm
∴ The diagonal of the rectangle is 37 cm.
Question 9.
In the adjoining figure, M is the midpoint of QR. ∠PRQ = 90°.
Prove that, PQ2 = 4 PM2 – 3 PR2.
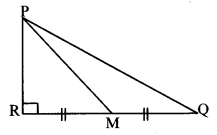
Solution:
Proof:
In ∆PQR, ∠PRQ = 90° [Given]
PQ2 = PR2 + QR2 (i) [Pythagoras theorem]
RM = \(\frac { 1 }{ 2 } \) QR [M is the midpoint of QR]
∴ 2RM = QR (ii)
∴ PQ2 = PR2 + (2RM)2 [From (i) and (ii)]
∴ PQ2 = PR2 + 4RM2 (iii)
Now, in ∆PRM, ∠PRM = 90° [Given]
∴ PM2 = PR2 + RM2 [Pythagoras theorem]
∴ RM2 = PM2 – PR2 (iv)
∴ PQ2 = PR2 + 4 (PM2 – PR2) [From (iii) and (iv)]
∴ PQ2 = PR2 + 4 PM2 – 4 PR2
∴ PQ2 = 4 PM2 – 3 PR2
Question 10.
Walls of two buildings on either side of a street are parallel to each other. A ladder 5.8 m long is placed on the street such that its top just reaches the window of a building at the height of 4 m. On turning the ladder over to the other side of the street, its top touches the window of the other building at a height 4.2 m. Find the width of the street.
Solution:
Let AC and CE represent the ladder of length 5.8 m, and A and E represent windows of the buildings on the opposite sides of the street. BD is the width of the street.
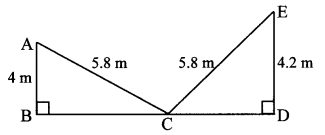
AB = 4 m and ED = 4.2 m
In ∆ABC, ∠B = 90° [Given]
AC2 = AB2 + BC2 [Pythagoras theorem]
∴ 5.82 = 42 + BC2
∴ 5.82 – 42 = BC2
∴ (5.8 – 4) (5.8 + 4) = BC2
∴ 1.8 × 9.8 = BC2

CE2 = CD2 + DE2 [Pythagoras theorem]
∴ 5.82 = CD2 + 4.22
∴ 5.82 – 4.22 = CD2
∴ (5.8 – 4.2) (5.8 + 4.2) = CD2
∴ 1.6 × 10 = CD2
∴ CD2 = 16
∴ CD = 4m (ii) [Taking square root of both sides]
Now, BD = BC + CD [B – C – D]
= 4.2 + 4 [From (i) and (ii)]
= 8.2 m
∴ The width of the street is 8.2 metres.
Question 1.
Verify that (3,4,5), (5,12,13), (8,15,17), (24,25,7) are Pythagorean triplets. (Textbook pg. no. 30)
Solution:
i. Here, 52 = 25
32 + 42 = 9 + 16 = 25
∴ 52 = 32 + 42
The square of the largest number is equal to the sum of the squares of the other two numbers.
∴ 3,4,5 is a Pythagorean triplet.
ii. Here, 132 = 169
52 + 122 = 25 + 144 = 169
∴ 132 = 52 + 122
The square of the largest number is equal to the sum of the squares of the other two numbers.
∴ 5,12,13 is a Pythagorean triplet.
iii. Here, 172 = 289
82 + 152 = 64 + 225 = 289
∴ 172 = 82 + 152
The square of the largest number is equal to the sum of the squares of the other two numbers.
∴ 8,15,17 is a Pythagorean triplet.
iv. Here, 252 = 625
72 + 242 = 49 + 576 = 625
∴ 252 = 72 + 242
The square of the largest number is equal to the sum of the squares of the other two numbers.
∴ 24,25, 7 is a Pythagorean triplet.
Question 2.
Assign different values to a and b and obtain 5 Pythagorean triplets. (Textbook pg. no. 31)
Solution:
i. Let a = 2, b = 1
a2 + b2 = 22 + 12 = 4 + 1 = 5
a2 – b2 = 22 – 12 = 4 – 1 = 3
2ab = 2 × 2 × 1 = 4
∴ (5, 3, 4) is a Pythagorean triplet.
ii. Let a = 4,b = 3
a2 + b2 = 42 + 32 = 16 + 9 = 25
a2 – b2 = 42 – 32 = 16 – 9 = 7
2ab = 2 × 4 × 3 = 24
∴ (25, 7, 24) is a Pythagorean triplet.
iii. Let a = 5, b = 2
a2 + b2 = 52 + 22 = 25 + 4 = 29
a2 – b2 = 52 – 22 = 25 – 4 = 21
2ab = 2 × 5 × 2 = 20
∴ (29, 21, 20) is a Pythagorean triplet.
iv. Let a = 4,b = 1
a2 + b2 = 42 + 12 = 16 + 1 = 17
a2 – b2 = 42 – 12 = 16 – 1 = 15
2ab = 2 × 4 × 1 = 8
∴ (17, 15, 8) is a Pythagorean triplet.
v. Let a = 9, b = 7
a2 + b2 = 92 + 72 = 81 + 49 = 130
a2 – b2 = 92 – 72 = 81 – 49 = 32
2ab = 2 × 9 × 7 = 126
∴ (130,32,126) is a Pythagorean triplet.
Note: Numbers in Pythagorean triplet can be written in any order.