Balbharti Maharashtra State Board Class 10 Maths Solutions covers the Practice Set 3.4 Geometry 10th Class Maths Part 2 Answers Solutions Chapter 3 Circle.
Practice Set 3.4 Geometry 10th Std Maths Part 2 Answers Chapter 3 Circle
Question 1.
In the adjoining figure, in a circle with centre O, length of chord AB is equal to the radius of the circle. Find measure of each of the following.
i. ∠AOB
ii. ∠ACB
iii. arc AB
iv. arc ACB.
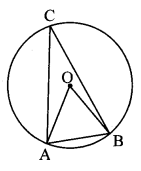
Solution:
i. seg OA = seg OB = radius…… (i) [Radii of the same circle]
seg AB = radius…… (ii) [Given]
∴ seg OA = seg OB = seg AB [From (i) and (ii)]
∴ ∆OAB is an equilateral triangle.
∴ m∠AOB = 60° [Angle of an equilateral triangle]
ii. m ∠ACB = \(\frac { 1 }{ 2 } \) m ∠AOB [Measure of an angle subtended by an arc at a point on the circle is half of the measure of the angle subtended by the arc at the centre]
= \(\frac { 1 }{ 2 } \) × 60°
∴ m ∠ACB = 30°
iii. m(arc AB) = m ∠AOB [Definition of measure of minor arc]
∴ m(arc AB) = 60°
iv. m(arc ACB) + m(arc AB) = 360° [Measure of a circle is 360°]
∴ m(arc ACB) = 360° – m(arc AB)
= 360° – 60°
∴ m(arc ACB) = 300°
Question 2.
In the adjoining figure, ꠸PQRS is cyclic, side PQ ≅ side RQ, ∠PSR = 110°. Find
i. measure of ∠PQR
ii. m (arc PQR)
iii. m (arc QR)
iv. measure of ∠PRQ
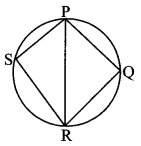
Solution:
i. ꠸PQRS is a cyclic quadrilateral. [Given]
∴ ∠PSR + ∠PQR = 180° [Opposite angles of a cyclic quadrilateral are supplementary]
∴ 110° + ∠PQR = 180°
∴ ∠PQR = 180° – 110°
∴ m ∠PQR = 70°
ii. ∠PSR= \(\frac { 1 }{ 2 } \) m (arcPQR) [Inscribed angle theorem]
110°= \(\frac { 1 }{ 2 } \) m (arcPQR)
∴ m(arc PQR) = 220°
iii. In ∆PQR,
side PQ ≅ side RQ [Given]
∴ ∠PRQ = ∠QPR [Isosceles triangle theorem]
Let ∠PRQ = ∠QPR = x
Now, ∠PQR + ∠QPR + ∠PRQ = 180° [Sum of the measures of angles of a triangle is 180°]
∴ ∠PQR + x + x= 180°
∴ 70° + 2x = 180°
∴ 2x = 180° – 70°
∴ 2x = 110°
∴ \(x=\frac{110^{\circ}}{2}=55^{\circ}\)
∴ ∠PRQ = ∠QPR = 55°….. (i)
But, ∠QPR = \(\frac { 1 }{ 2 } \) m(arc QR) [Inscribed angle theorem]
∴ 55° = \(\frac { 1 }{ 2 } \) m(arc QR)
∴ m(arc QR) = 110°
iv. ∠PRQ = ∠QPR =55° [From (i)]
∴ m ∠PRQ = 55°
Question 3.
□ MRPN is cyclic, ∠R = (5x -13)°, ∠N = (Ax + 4)°. Find measures of ∠R and ∠N.
Solution:
□ MRPN is a cyclic quadrilateral. [Given]
∴ ∠R + ∠N = 180° [Opposite angles of a cyclic quadrilateral are supplementary]
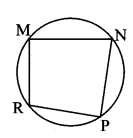
∴ 5x – 13 + 4x + 4 = 180
∴ 9x – 9 = 180
∴ 9x = 189
∴ x = \(\frac { 189 }{ 9 } \)
∴ x = 21
∴ ∠R = 5x – 13
= 5 × 21 – 13
= 105 – 13
= 92°
∠N = 4x + 4
= 4 × 21 +4
= 84 +4
= 88°
∴ m∠R = 92° and m ∠N = 88°
Question 4.
In the adjoining figure, seg RS is a diameter of the circle with centre O. Point T lies in the exterior of the circle. Prove that ∠RTS is an acute angle.
Given: O is the centre of the circle, seg RS is the diameter of the circle.
To prove: ∠RTS is an acute angle.
Construction: Let seg RT intersect the circle at point P. Join PS and PT.
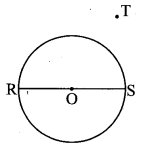
Proof:
seg RS is the diameter. [Given]
∴ ∠RPS = 90° [Angle inscribed in a semicircle]
Now, ∠RPS is the exterior angle of ∆PTS.
∴ ∠RPS > ∠PTS [Exterior angle is greater than the remote interior angles]
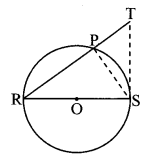
∴ 90° > ∠PTS
i.e. ∠PTS < 90°
i.e, ∠RTS < 90° [R – P -T]
∠RTS is an acute angle.
Question 5.
Prove that, any rectangle is a cyclic quadrilateral.
Given: ꠸ABCD is a rectangle.
To prove: ꠸ABCD is a cyclic quadrilateral.
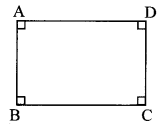
Proof:
꠸XBCD is a rectangle. [Given]
∴ ∠A = ∠B = ∠C = ∠D = 90° [Angles of a rectangle]
Now, ∠A + ∠C = 90° + 90°
∴ ∠A + ∠C = 180°
∴ ꠸ABCD is a cyclic quadrilateral. [Converse of cyclic quadrilateral theorem]
Question 6.
In the adjoining figure, altitudes YZ and XT of ∆WXY intersect at P. Prove that,
i. □ WZPT is cyclic.
ii. Points X, Z, T, Y are concyclic.
Given: seg YZ ⊥ side XW
seg XT ⊥ side WY
To prove: i. □WZPT is cyclic.
ii. Points X, Z, T, Y are concyclic.
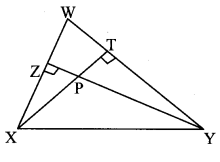
Proof:
i. segYZ ⊥ side XW [Given]
∴∠PZW = 90°…… (i)
seg XT I side WY [Given]
∴ ∠PTW = 90° ……(ii)
∠PZW + ∠PTW = 90° + 90° [Adding (i) and (ii)]
∴∠PZW + ∠PTW = 180°
∴□WZPT Ls a cyclic quadrilateral. [Converse of cyclic quadrilateral theorem]
ii. ∠XZY = ∠YTX = 90° [Given]
∴ Points X and Y on line XY subtend equal angles on the same side of line XY.
∴ Points X, Z, T and Y are concydic. [If two points on a given line subtend equal angles at two distinct points which lie on the same side of the line, then the four points are concyclic]
Question 7.
In the adjoining figure, m (arc NS) = 125°, m(arc EF) = 37°, find the measure of ∠NMS.
Solution:
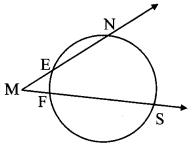
Chords EN and FS intersect externally at point M.
m∠NMS = \(\frac { 1 }{ 2 } \) [m (arc NS) – m(arc EF)]
= \(\frac { 1 }{ 2 } \) (125° – 37°) = \(\frac { 1 }{ 2 } \) × 88°
∴ m∠NMS = 44°
Question 8.
In the adjoining figure, chords AC and DE intersect at B. If ∠ABE = 108°, m(arc AE) = 95°, find m (arc DC).
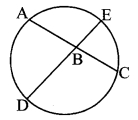
Solution:
Chords AC and DE intersect internally at point B.
∴ ∠ABE = \(\frac { 1 }{ 2 } \) [m(arc AE) + m(arc DC)]
∴ 108° = \(\frac { 1 }{ 2 } \) [95° + m(arc DC)]
∴ 108° × 2 = 95° + m(arc DC)
∴ 95° + m(arc DC) = 216°
∴ m(arc DC) = 216° – 95°
∴ m(arc DC) = 121°
Maharashtra Board Class 10 Maths Chapter 3 Circle Intext Questions and Activities
Question 1.
Draw a sufficiently large circle of any radius as shown in the figure below. Draw a chord AB and central ∠ACB. Take any point D on the major arc and point E on the minor arc.
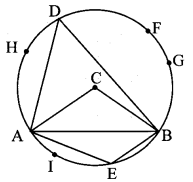
i. Measure ∠ADB and ∠ACB and compare the measures.
ii. Measure ∠ADB and ∠AEB. Add the measures.
iii. Take points F, G, H on the arc ADB. Measure ∠AFB, ∠AGB, ∠AHB. Compare these measures with each other as well as with measure of ∠ADB.
iv. Take any point I on the arc AEB. Measure ∠AIB and compare it with ∠AEB. (Textbook pg, no. 64)
Answer:
i. ∠ACB = 2 ∠ADB.
ii. ∠ADB + ∠AEB = 180°.
iii. ∠AHB = ∠ADB = ∠AFB = ∠AGB
iv. ∠AEB = ∠AIB
Question 2.
Draw a sufficiently large circle with centre C as shown in the figure. Draw any diameter PQ. Now take points R, S, T on both the semicircles. Measure ∠PRQ, ∠PSQ, ∠PTQ. What do you observe? (Textbook pg. no.65)
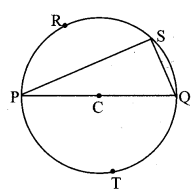
Answer:
∠PRQ = ∠PSQ = ∠PTQ = 90°
[Student should draw and verily the above answers.]
Question 3.
Prove that, if two lines containing chords of a circle intersect each other outside the circle, then the measure of angle between them is half the difference in measures of the arcs intercepted by the angle. (Textbook pg. no. 72)
Given: Chord AB and chord CD intersect at E in the exterior of the circle.
To prove: ∠AEC = \(\frac { 1 }{ 2 } \) [m(arc AC) – m(arc BD)]
Construction: Draw seg AD.
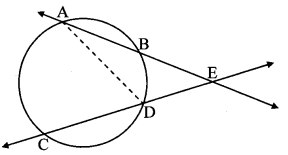
Proof:
∠ADC is the exterior angle of ∆ADE.
∴ ∠ADC = ∠DAE + ∠AED [Remote interior angle theorem]
∴ ∠ADC = ∠DAE + ∠AEC [C – D – E]
∴ ∠AEC = ∠ADC – ∠DAE ……(i)
∠ADC = \(\frac { 1 }{ 2 } \) m(arc AC) (ii) [Inscribed angle theorem]
∠DAE = \(\frac { 1 }{ 2 } \) m(arc BD) (iii) [A – B – E, Inscribed angle theorem]
∴ ∠AEC = \(\frac { 1 }{ 2 } \) m(arc AC) – \(\frac { 1 }{ 2 } \) m (arc BD) [From (i), (ii) and (iii)]
∴ ∠AEC = \(\frac { 1 }{ 2 } \) m(arc AC) – m (arc BD)
Question 4.
Angles inscribed in the same arc are congruent.
Write ‘given’ and ‘to prove’ with the help of the given figure.
Think of the answers of the following questions and write the proof.
i. Which arc is intercepted by ∠PQR ?
ii. Which arc is intercepted by ∠PSR ?
iii. What is the relation between an inscribed angle and the arc intercepted by it? (Textbook: pg. no. 68)
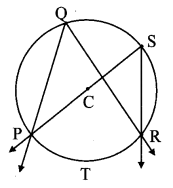
Given: C is the centre of circle. ∠PQR and ∠PSR are inscribed in same arc PTR.
To prove: ∠PQR ≅ ∠PSR
Proof:
i. arc PTR is intercepted by ∠PQR.
ii. arc PTR is intercepted by ∠PSR.
iii. ∠PQR = \(\frac { 1 }{ 2 } \) m(arc PTR), and (i) [inscribed angle theorem]
∠PSR = \(\frac { 1 }{ 2 } \) m(arcPTR) (ii) [Inscribed angle theorem]
∴ ∠PQR ≅ ∠PSR [From (i) and (ii)]
Question 5.
Angle inscribed in a semicircle is a right angle. With the help of given figure write ‘given’, ‘to prove’ and ‘the proof. (Textbook pg. no. 68)
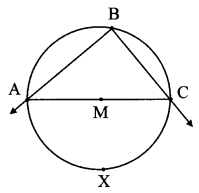
Given: M is the centre of circle. ∠ABC is inscribed in arc ABC.
Arcs ABC and AXC are semicircles.
To prove: ∠ABC = 90°
Proof:
∠ABC = \(\frac { 1 }{ 2 } \) m(arc AXC) (i) [Inscribed angle theorem]
arc AXC is a semicircle.
∴ m(arc AXC) = 180° (ii) [Measure of semicircular arc is 1800]
∴ ∠ABC = \(\frac { 1 }{ 2 } \) × 180°
∴ ∠ABC = 90° [From (i) and (ii)]
Question 6.
Theorem: Opposite angles of a cyclic quadrilateral are supplementry.
Fill in the blanks and complete the following proof. (Textbook pg. no. 68)
Given: □ ABCD is cyclic.
To prove: ∠B + ∠D = 180°
∠A + ∠C = 180°
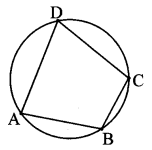
Proof:
arc ABC is intercepted by the inscribed angle ∠ADC.
∴ ∠ADC m(arcABC) (i) [Inscribed angle theorem]
Similarly, ∠ABC is an inscribed angle. It intercepts arc ADC.
∴ ABC = \(\frac { 1 }{ 2 } \) m(arc ADC) (ii) [Inscribed angle theorem]
∴ ∠ADC + ∠ABC
= \(\frac { 1 }{ 2 } \) m(arcABC) + \(\frac { 1 }{ 2 } \) m(arc ADC) [Adding (i) and (ii)]
∴ ∠D + ∠B = \(\frac { 1 }{ 2 } \) m(areABC) + m(arc ADC)]
∴ ∠B + ∠D = \(\frac { 1 }{ 2 } \) × 360° [arc ABC and arc ADC constitute a complete circle]
= 180°
∴ ∠B + ∠D = 180°
Similarly we can prove,
∠A + ∠C = 180°
Question 7.
In the above theorem, after proving ∠B + ∠D = 180°, can you use another way to prove ∠A + ∠C = 180°? (Textbook pg. no. 69)
Proof:
Yes, we can prove ∠A + ∠C = 180° by another way.
∠B + ∠D = 180°
In ꠸ABCD,
∠A + ∠B + ∠C + ∠D = 360° [Sum of the measures of all angles of a quadrilateral is 360°.]
∴ ∠A + ∠C + 180° = 360°
∴ ∠A + ∠C = 360° – 180°
∴ ∠A + ∠C = 180°
Question 8.
An exterior angle of a cyclic quadrilateral is congruent to the angle opposite to its adjacent interior angle. (Textbook pg. no. 69)
Given: ꠸ABCD is a cyclic quadrilateral.
∠BCE is the exterior angle of ꠸ABCD.
To prove: ∠BCE ≅ ∠BAD
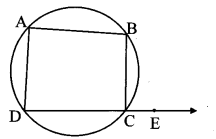
Proof:
∠BCE + ∠BCD = 180°…… (i) [Angles in a linear pair]
꠸ABCD is a cyclic quadrilateral. [Given]
∠BAD + ∠BCD = 180°………. (ii) [Opposite angles of a cyclic quadrilateral are supplementary]
∴ ∠BCE + ∠BCD = ∠BAD + ∠BCD [From (i) and (ii)]
∴ ∠BCE = ∠BAD
Question 9.
Theorem : If a pair of opposite angles of a quadrilateral is supplementary, then the quadrilateral is cyclic. (Textbook pg. no. 69)
Given: In ꠸ABCD, ∠A + ∠C = 180°
To prove: ꠸ABCD is a cyclic quadrilateral.
Proof:
(Indirect method)
Suppose ꠸ABCD is not a cyclic quadrilateral.
We can still draw a circle passing through three non collinear points A, B, D.
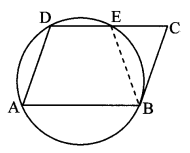
Case I: Point C lies outside the circle.
Then, take point E on the circle
such that D – E – C.
∴ ꠸ABED is a cyclic quadrilateral.
∠DAB + ∠DEB = 180° (i) [Opposite angles of a cyclic quadrilateral are supplementary]
∠DAB + ∠DCB = 180° (ii) [Given]
∴ ∠DAB + ∠DEB = ∠DAB + ∠DCB [From (i) and (ii)]
∴ ∠DEB = ∠DCB
But, ∠DEB ≠ ∠DCB as ∠DEB is the exterior angle of ∆BEC.
∴ Our supposition is wrong.
∴ ꠸ABCD is a cyclic quadrilateral.
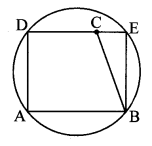
Case II: Point C lies inside the circle.
Then, take point E on the circle such that
D – C – E
∴ □ABED is a cyclic quadrilateral.
∠DAB + ∠DEB = 180° (iii) [Opposite angles of a cyclic quadrilateral are supplementary]
∠DAB + ∠DCB = 180° (iv) [Given]
∴ ∠DAB + ∠DEB = ∠DAB + ∠DCB [From (iii) and (iv)]
∴ ∠DEB = ∠DCB
But ∠DEB ≠ ∠DCB as ∠DCB is the exterior angle of ∆BCE.
∴ Our supposition is wrong.
∴ □ABCD is a cyclic quadrilateral.
Question 10.
Theorem: If two points on a given line subtend equal angles at two distinct points which lie on the same side of the line, then the four points are concyclic. (Textbook pg. no. 70)
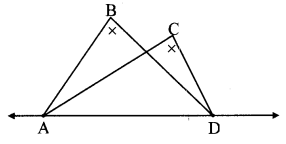
Given: Points B and C lie on the same side of the line AD.
∠ABD = ∠ACD
To prove: Points A, B, C, D are concyclic. i.e., □ABCD is a cyclic quadrilateral.
Proof:
Suppose points A, B, C, D are not concyclic points.
We can still draw a circle passing through three non collinear points A, B, D.
Case I: Point C lies outside the circle.
Then, take point E on the circle such that
A – E – C.
∠ABD ≅ ∠AED (i) [Angles inscribed in the same arc]
∠ABD ≅ ∠ACD (ii) [Given]
∴ ∠AED ≅ ∠ACD [From (i) and (ii)]
∴ ∠AED ≅ ∠ECD [A – E – C]
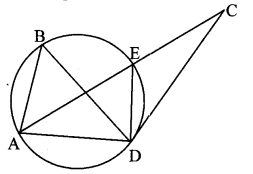
But, ∠AED ≅ ∠ECD as ∠AED is the exterior angle of ∆ECD.
∴ Our supposition is wrong.
∴ Points A, B, C, D are concyclic points.
Case II: Point C lies inside the circle. Then, take point E on the circle such that A – C – E.
∠ABD ≅ ∠AED (iii) [Angles inscribed in the same arc]
∠ABD ≅ ∠ACD (iv) [Given]
∴ ∠AED ≅ ∠ACD [From (iii) and (iv)]
∴ ∠CED ≅ ∠ACD [A – C – E]
But, ∠CED ≅ ∠ACD as ∠ACD is the exterior angle of ∆ECD.
∴ Our supposition is wrong.
∴ Points A, B, C, D are concyclic points.
Question 11.
The above theorem is converse of a certain theorem. State it. (Textbook pg. no. 70)
Answer:
If four points are concyclic, then the line joining any two points subtend equal angles at the other two points which are on the same side of that line.