Balbharti Maharashtra State Board Class 10 Maths Solutions covers the Problem Set 3 Geometry 10th Class Maths Part 2 Answers Solutions Chapter 3 Circle.
Problem Set 3 Geometry 10th Std Maths Part 2 Answers Chapter 3 Circle
Problem Set 3 Geometry Class 10 Question 1.
Four alternative answers for each of the following questions are given. Choose the correct alternative.
i. Two circles of radii 5.5 cm and 3.3 cm respectively touch each other. What is the distance between their centres?
(A) 4.4 cm
(B) 8.8 cm
(C) 2.2 cm
(D) 8.8 or 2.2 cm
Answer: (D)
Two circles can touch each other internally or externally.
∴ Distance between centres = 5.5 + 3.3 or 5.5 – 3.3 = 8.8 or 2.2
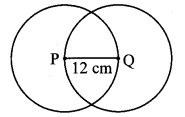
ii. Two circles intersect each other such that each circle passes through the centre of the other. If the distance between their centres is 12, what is the radius of each circle?
(A) 6 cm
(B) 12 cm
(C) 24 cm
(D) can’t say
Answer: (B)
PQ is the radius = 12 cm
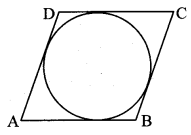
iii. A circle touches all sides of a parallelogram. So the parallelogram must be a __________.
(A) rectangle
(B) rhombus
(C) square
(D) trapezium
Answer: (B)
꠸ABCD is a rhombus.
Note: It cannot be square as the angles are not mentioned as 90°.
iv. Length of a tangent segment drawn from a point which is at a distance 12.5 cm from the centre of a circle is 12 cm, find the diameter of the circle.
(A) 25 cm
(B) 24 cm
(C) 7 cm
(D) 14 cm
Answer: (C)
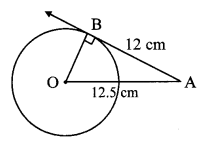
In ∆OAB, ∠B = 90° [Tangent theorem]
∴ OA2 = OB2 + AB2 [Pythagoras theorem]
∴ 12.52 = OB2 + 122
∴ OB2 = 156.25- 144
∴ OB = \(\sqrt { 12.25 }\) = 3.5 cm
∴ Diameter = 2 × OB = 2 × 3.5 = 7 cm
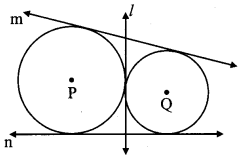
v. If two circles are touching externally, how many common tangents of them can be drawn?
(A) One
(B) Two
(C) Three
(D) Four
Answer: (C)
line l, line m and line n are the tangents.
vi. ∠ACB is inscribed in arc ACB of a circle with centre O. If ∠ACB = 65°, find m(arc ACB).
(A) 65°
(B) 130°
(C) 295°
(D) 230°
Answer: (D)
m∠ACB = \(\frac { 1 }{ 2 } \) m(arc AB) [Inscribed angle theorem]
∴ m(arc AB) = 2 m∠ACB =
= 2 × 65
= 130°
m(arc ACB) = 360° – m(arc AB) [Measure of a circle is 360°]
= 360° – 130°
= 230°
vii. Chords AB and CD of a circle intersect inside the circle at point E. If AE = 5.6, EB = 10, CE = 8, find ED.
(A) 7
(B) 8
(C) 11.2
(D) 9
Answer: (A)
Chords AB and CD intersect
internally at E.
AE × EB = CE × ED [Theorem of internal division of chords]
∴ 5.6 × 10 = 8 × ED
∴ ED = 7 units
viii. In a cyclic ꠸ABCD, twice the measure of ∠A is thrice the measure of ∠C. Find the measure of ∠C?
(A) 36°
(B) 72°
(C) 90°
(D) 108°
Answer: (B)
∠A + ∠C = 180° [Theorem of cyclic quadrilateral]
∴ 2∠A + 2∠C = 2 × 180° [Multiplying both sides by 2]
∴ 3∠C + 2∠C = 360° [∵ 2∠A = 3∠C]
∴ 5∠C = 360°
∴ ∠C = 72°
ix. Points A, B, C are on a circle, such that m(arc AB) = m(arc BC) = 120°. No point, except point B, is common to the arcs. Which is the type of ∆ABC?
(A) Equilateral triangle
(B) Scalene triangle
(C) Right angled triangle
(D) Isosceles triangle
Answer: (A)
m(arc AB) + m(arc BC) + m(arc AC) = 360° [Measure of a circle is 360°]
∴ 120° + 120° + m (arc AC) = 360°
∴ m(arc AC) = 120°
∴ arc AB = arc BC = arc AC
∴ seg AB ≅ seg BC ≅ seg AC [Corresponding chords of congruents arcs of a circle are congruent]
∴ ∆ABC is an equilateral triangle.
x. Seg XZ is a diameter of a circle. Point Y lies in its interior. How many of the following statements are true?
(i) It is not possible that ∠XYZ is an acute angle.
(ii) ∠XYZ can’t be a right angle.
(iii) ∠XYZ is an obtuse angle.
(iv) Can’t make a definite statement for measure of ∠XYZ.
(A) Only one
(B) Only two
(C) Only three
(D) All
Answer: (C)
x. seg XZ is the diameter.
∴ ∠XWZ is a right angle. [Angle inscribed in a semicircle]
Since, Y lies in the interior of ∆XWZ,
∴ ∠XYZ > 90°
i.e., ∠XYZ is an obtuse angle.
Problem Set 3 Question 2.
Line l touches a circle with centre O at point P. If radius of the circle is 9 cm, answer the following.
i. What is d(O, P) = ? Why?
ii. If d(O, Q) = 8 cm, where does the point Q lie?
iii. If d(O, R) = 15 cm, how many locations of point R are on line l ?
At what distance will each of them be from point P?
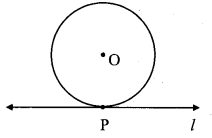
Solution:
i. seg OP is the radius of the circle.
∴ d(0, P) = 9 cm
ii. Here, 8 cm < 9 cm
∴ d(0, Q) < d(0, P)
∴ d(0, Q) < radius
Point Q lies in the interior of the circle.
iii. There can be two locations of point R on line l.
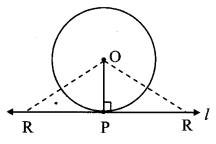
d(0, R) = 15 cm
Now, in ∆OPR, ∠OPR = 90° [Tangent theorem]
∴ OR2 = OP2 + PR2 [Pythagoras theorem]
∴ 152 = 92 + PR2
∴ 225 = 81 + PR2
∴ PR2 = 225 – 81 = 144 [Taking square root of both sides]
∴ PR = \(\sqrt { 144 }\)
= 12 cm
Standard 10th Geometry Problem Set 3 Question 3.
In the adjoining figure, M is the centre of the circle and seg KL is a tangent segment. If MK = 12, KL = 6\(\sqrt { 3 }\) ,then find
i. Radius of the circle.
ii. Measures of ∠K and ∠M.
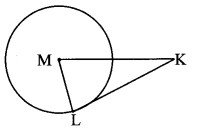
Solution:
i. Line KL is the tangent to the circle at point L and seg ML is the radius. [Given]
∴ ∠MLK = 90°…………. (i) [Tangent theorem]
In ∆MLK, ∠MLK = 90°
∴ MK2 = ML2 + KL2 [Pythagoras theorem]
∴ 122 = ML2 + (6\(\sqrt { 3 }\))2
∴ 144 = ML2 + 108
∴ ML2 = 144 – 108
∴ ML2 = 36
∴ ML = \(\sqrt { 36 }\) = 6 units. [Taking square root of both sides]
∴ Radius of the circle is 6 units.
ii. We know that,
ML = \(\frac { 1 }{ 2 } \) MK
∴ ∠K = 30° …………… (ii) [Converse of 30° – 60° – 90° theorem]
In ∆MLK ,
∠L = 90° [From (i)]
∠K = 30° [From (ii)]
∴ ∠M = 60° [Remaining angle of ∆MLK]
10th Class Geometry Problem Set 3 Question 4.
In the adjoining figure, O is the centre of the circle. Seg AB, seg AC are tangent segments. Radius of the circle is r and l(AB) = r. Prove that, □ABOC is a square.
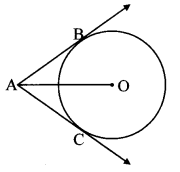
Given: O is the centre of circle.
seg AB and seg AC are the tangents, radius = r, /(AB) = r.
To prove: □ABOC is a square.
Construction: Draw seg OB and seg OC.
Proof:
seg AB and seg AC are the tangents to the circle. [Given]
∴ AB = AC [Tangent segment theorem]
But, AB = r [Given]
∴ AB = AC = r ……….. (i)
Also, OB = OC = r ……….. (ii) [Radii of the same circle]
∴ AB = AC = OB = OC [From (i) and (ii)]
∴ □ABOC is a rhombus.
∠OBA = 90° [Tangent theorem]
∴ □ABOC is a square [A rhombus is a square, if one of its angles is a right angle]
Question 5.
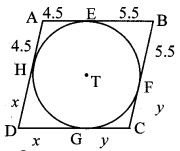
In the adjoining figure, ꠸ABCD is a parallelogram. It circumscribes the circle with centre T. Points E, F, G, H are touching points. If AE = 4.5, EB = 5.5, find AD.
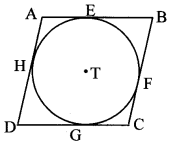
Solution:
Let the values of DH and CF be x and y respectively.
[ AE = AH = 4.5
BE = BF = 5.5
DH = DG = x
CF = CG = y ] [Tangent segment theorem]
□ABCD is a parallelogram. [Given]
∴ AB = CD [Opposite sides of a parallelogram]
∴ AE + BE = DG + CG [A – E – B, D – G – C]
∴ 4.5 + 5.5 = x + y
∴ x + y = 10 ……….. (i)
Also, AD = BC [Opposite sides of a parallelogram]
∴ AH + DH = BF + CF [A – H – D, B – F – C]
∴ 4.5 + x = 5.5 + y
∴ x – y = 1 ………… (ii)
Adding equations (i) and (ii), we get
2x = 11
∴ x = \(\frac { 11 }{ 2 } \) = 5.5
∴ AD = AH + DH [A – H – D]
= 4.5 + 5.5
∴ AD = 10 units
Question 6.
In the adjoining figure, circle with centre M touches the circle with centre N at point T. Radius RM touches the smaller circle at S. Radii of circles are 9 cm and 2.5 cm. Find the answers to the following questions, hence find the ratio MS : SR.
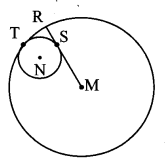
i. Find the length of segment MT.
ii. Find the length of seg MN.
iii. Find the measure of ∠NSM.
Solution:
i. MT = 9 cm [Radius of the bigger circle]
ii. MT = MN + NT [M – N – T]
∴ 9 = MN + 2.5
∴ MN = 9 – 2.5
∴ MN = 6.5 cm
iii. seg MR is a tangent to the smaller circle and NS is its radius.
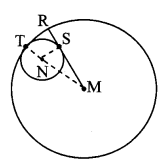
∴ ∠NSM = 90° [Tangent theorem]
iv. In ∆NSM, ∠NSM = 90°
∴ MN2 = NS2 + MS2 [Pythagoras theorem]
∴ 6.52 = 2.52 + MS2
∴ MS2 = 6.52 – 2.52
= (6.5 + 2.5) (6.5 – 2.5) [∵ a2 – b2 = (a + b)(a – b)]
= 9 × 4=36
∴ MS = \(\sqrt { 36 }\) [Taking square root of both sides]
= 6 cm
But, MR = MS + SR [M – S – R]
∴ 9 = 6 + SR
∴ SR = 9 – 6
∴ SR = 3cm
Now, \(\frac { MS }{ SR } \) = \(\frac { 6 }{ 3 } \) = \(\frac { 2 }{ 1 } \)
∴ \(\frac { MS }{ SR } \) = 2 : 1
10th Std Geometry Circle Problem Set Question 7.
In the adjoining figure, circles with centres X and Y touch each other at point Z. A secant passing through Z intersects the circles at points A and B respectively. Prove that, radius XA || radius YB. Fill in the blanks and complete the proof.
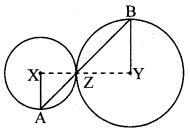
Given: X and Y are the centres of circle.
To prove: radius XA || radius YB
Construction: Draw segments XZ and YZ.
Proof:
By theorem of touching circles, points X, Z,
Y are collinear.
∴ ∠XZA ≅ ∠BZY [Vertically opposite angles]
Let ∠XZA = ∠BZY = a …………….. (i)
Now, seg XA seg XZ [Radii of the same circIe]
∴ ∠XAZ ≅∠XZA = a …………….. (ii) [Isosceles triangle theorem]
Similarly, seg YB ≅ seg YZ [Radii of the same circie]
∴ ∠BZY = ∠ZBY = a …………….. (iii) [Isosceles triangle theorem]
∴ ∠XAZ = ∠ZBY [From (i), (ii) and (iii)]
∴ radius XA || radius YB [Alternate angles test]
Circle Problem Set 3 Question 8.
In the adjoining figure, circles with centres X and Y touch internally at point Z. Seg BZ is a chord of bigger circle and it intersects smaller circle at point A. Prove that, seg AX || seg BY.
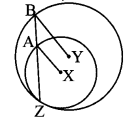
Given: X and Y are the centres of the circle.
To prove: seg AX || seg BY
Proof:
In ∆XAZ,
seg XA ≅ seg XZ [Radii of the same circle]
∴ ∠XZA ≅ ∠XAZ ………… (i) [Isosceles triangle theorem]
Also, in ∆YBZ,
seg YB ≅ seg YZ [Radii of the sanie circle]
∴ ∠YZB ≅∠YBZ [Isosceles triangle theorem]
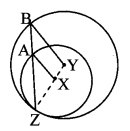
∴ ∠XZA ≅ ∠YBZ ………….. (ii) [Y – X – Z,B – A – Z]
∴ ∠XAZ ≅ ∠YBZ [From (i) and (ii)]
∴ seg AX || seg BY [Corresponding angles test]
Question 9.
In the adjoining figure, line l touches the circle with centre O at point P, Q is the midpoint of radius OP. RS is a chord through Q such that chords RS || line l. If RS = 12, find the radius of the circle.
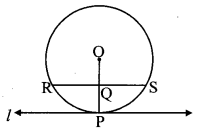
Solution:
Let the radius of the circle be r.
line l is the tangent to the circle and [Given]
seg OP is the radius.
∴ seg OP ⊥ line l [Tangent theorem]
chord RS || line l [Given]
∴ seg OP ⊥ chord RS
∴ QS = \(\frac { 1 }{ 2 } \) RS [Perpendicular drawn from the centre of the circle to the chord bisects the chord]
= \(\frac { 1 }{ 2 } \) × 12 = 6 cm
Also, OQ = \(\frac { 1 }{ 2 } \) OP [Q is the midpoint of OP]
= \(\frac { 1 }{ 2 } \) r
In ∆OQS, ∠OQS = 90° [seg OP ⊥ chord RS ]
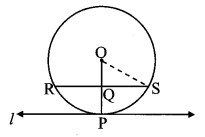
∴ OS2 = OQ2 + QS2 [Pythagoras theorem]
∴ r2 = (\(\frac { 1 }{ 2 } \)r)2 + 62
∴ r2 = \(\frac { 1 }{ 4 } \) r2 + 36
∴ r2 – \(\frac { 1 }{ 4 } \) r2 = 36
∴ \(\frac { 3 }{ 4 } \) r2 = 36
∴ r2 = \(\frac{36 \times 4}{3}\)
∴ r2 = 48
∴ r = \(\sqrt { 48 }\) [Taking square root of both sides]
= 4 \(\sqrt { 3 }\)
∴ The radius of the given circle is 4\(\sqrt { 3 }\) cm.
Question 10.
In the adjoining figure, seg AB is a diameter of a circle with centre C. Line PQ is a tangent, which touches the circle at point T. Seg AP ⊥ line PQ and seg BQ ⊥ line PQ. Prove that seg CP ≅ seg CQ.
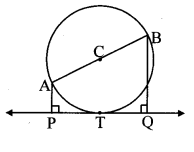
Given: C is the centre of circle.
seg AB is the diameter of circle.
line PQ is a tangent, seg AP ⊥ line PQ and seg BQ ⊥ line PQ.
To prove: seg CP ≅ seg CQ
Construction: Draw seg CT, seg CP and seg CQ.
Proof:
Line PQ is the tangent to the circle at point T. [Given]
∴ seg CT ⊥ line PQ (i) [Tangent theorem]
Also, seg AP ⊥ line PQ,
seg BQ ⊥ line PQ [Given]
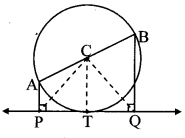
∴ seg AP || seg CT || seg BQ [Lines perpendicular to the same line are parallel to each other]
∴ \(\frac { AC }{ CB } \) = \(\frac { PT }{ TQ } \) [Property of intercepts made by three parallel lines and their transversals]
But, AC = CB [Radii of the same circle]
∴ \(\frac { AC }{ AC } \) = \(\frac { PT }{ TQ } \)
∴ \(\frac { PT }{ TQ } \) = 1
∴ PT = TQ ………… (ii)
∴ In ∆CTP and ∆CTQ,
seg PT ≅ seg QT [From (ii)]
∠CTP ≅ ∠CTQ [From (i), each angle is of measure 90° ]
seg CT ≅ seg CT [Common side]
∴ ∆CTP ≅ ∆CTQ [SAS test of congruence]
∴ seg CP ≅ seg CQ [c.s.c.t]
Question 11.
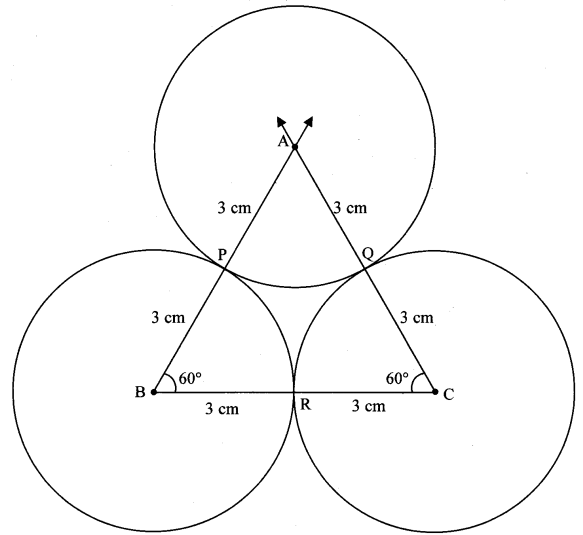
Draw circles with centres A, B and C each of radius 3 cm, such that each circle touches the other two circles.
Analysis:
Let the circles with centres A, B, C touch each other at points P, Q, R.
[∴ A – P – B
A – Q – C
B – R – C ] [Theorem of touching circles]
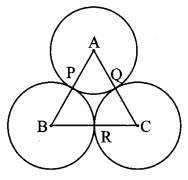
∴ AB = AP + BP [A – P – B]
∴ AB = 3 + 3 = 6 cm
Similarly, BC = 6 cm, AC = 6 cm
So, if we construct triangle ∆ABC of side 6 cm each, then with A, B, C as the centres and radius 3 cm, the touching circles can be drawn.
Question 12.
Prove that any three points on a circle cannot be collinear
Given: A circle with centre O.
Points A, B and C lie on the circle.
To prove: Points A, B and C are not collinear.
Proof:
OA = OB [Radii of the same circle]
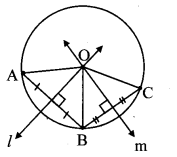
∴ Point O is equidistant from the endpoints A and B of seg AB.
∴ Point O lies on the perpendicular bisector of AB. [Perpendicular bisector theorem]
Similarly, we can prove that,
Point O lies on the perpendicular bisector of BC.
∴ Point O is the point of intersection of perpendicular bisectors of AB and BC (i.e., circumcentre of ∆ABC) ……… (i)
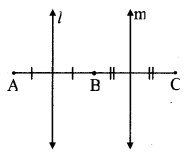
Now, suppose that the points A, B, C are collinear.
Then, the perpendicular bisector of AB and BC will be parallel. [Perpendiculars to the same line are parallel]
∴ The perpendicular bisector do not intersect at O.
This contradicts statement (i) that the perpendicular bisectors intersect each other at O.
∴ Our supposition that A, B, C are collinear is false.
∴ Points A, B and C are non collinear points.
Question 13.
In the adjoining figure, line PR touches the circle at point Q. Answer the following questions with the help of the figure.
i. What is the sum of ∠TAQ and ∠TSQ?
ii. Find the angles which are congruent to ∠AQP.
iii. Which angles are congruent to ∠QTS?
iv. ∠TAS = 65°, find the measures of ∠TQS and arc TS.
v. If ∠AQP = 42° and ∠SQR = 58° find measure of ∠ATS.
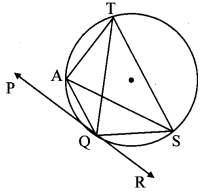
Solution:
i. ꠸AQST is a cyclic quadrilateral. [Given]
∴ ∠TAQ + ∠TSQ = 180° [Opposite angles of a cyclic quadrilateral are supplementary]
ii. line PR is the tangent and seg AQ is the secant. [Given]
∴∠AQP = \(\frac { 1 }{ 2 } \) m(arc AQ) [Theorem of angle between tangent and secant]
But,∠ASQ = \(\frac { 1 }{ 2 } \) m(arc AQ) [Inscribed angle theorem]
∴∠AQP ≅ ∠ZASQ
Similarly, we can prove that,
∠AQP ≅ ∠ATQ
iii. ∠QTS = \(\frac { 1 }{ 2 } \) m(arc QS) [Inscribed angle theorem]
But, ∠SQR = \(\frac { 1 }{ 2 } \) m(arc QS) [Theorem of angle between tangent and secant]
∴ ∠QTS ≅ ∠SQR
Also, ∠QTS = ∠QAS [Angles inscribed in the same arc]
iv. ∠TQS = ∠TAS [Angles inscribed in the same arc]
∴ ∠TQS = 65°
Now, ∠TQS = \(\frac { 1 }{ 2 } \) m(arc TS) [Inscribed angle theorem]
∴ 65°= \(\frac { 1 }{ 2 } \) m(arcTS)
∴ m(arc TS) = 65° × 2
∴ m(arc TS) = 130°
v. ∠AQP + ∠AQS + ∠SQR = 180° [Angles in a linear pair]
∴ 42° + ∠AQS + 58° = 180°
∴∠AQS + 100° = 180° ………… (i)
But, ꠸AQST is a cyclic quadrilateral.
∴ ∠AQS + ∠ATS = 180° ………… (ii) [Theorem of cyclic quadrilateral]
∴ ∠ATS = 100° [From (i) and (ii)]
Question 14.
In the adjoining figure, O is the centre of a circle, chord PQ ≅ chord RS.
If ∠POR = 70° and (arc RS) = 80°, find
i. m (arc PR)
ii. m (arc QS)
iii. m (arc QSR).
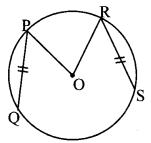
Solution:
i. m(arc PR) = m∠POR [Definition of measure of arc]
∴ m(arc PR) = 70°
ii. chord PQ chord RS [Given]
∴ m(arc PQ) = m(arc RS) = 80° [Corresponding arcs of congruents chords of a circle are congruent]
Now, m(arc QS) + m(arc PQ) + m(arc PR) + m(arcRS) = 360°
∴ m(arc QS) + 80° + 70° + 80° = 360° [Measure of a circle is 360°]
∴ m(arc QS) + 230° = 360°
∴ m(arc QS) = 130°
iii. m(arc QSR) = m(arc QS) + m(arc SR) [Arc addition property]
= 130° + 80°
∴ m(arc QSR) = 210°
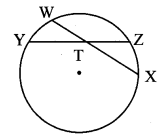
Question 15.
In the adjoining figure, m(arc WY) = 44°, m(arc ZX) = 68°, then
i. Find the measure of ∠ZTX.
ii. If WT = 4.8, TX = 8.0, YT = 6.4, find TZ.
iii. If WX = 25, YT = 8, YZ = 26, find WT.

Solution:
i. Chords WX and YZ intersect internally at point T.
∴ ∠ZTX = \(\frac { 1 }{ 2 } \) m(arc WY) + m(arc ZX)]
= \(\frac { 1 }{ 2 } \) (44° + 68°)
= \(\frac { 1 }{ 2 } \) × 112°
∴ m ∠ZTX = 56°
ii. WT × TX = YT × TZ [Theorem of internal division of chords]
∴ 4.8 × 8.0 = 6.4 × TZ
∴ TZ = \(\frac{4.8 \times 8.0}{6.4}\)
∴ l(TZ) = 6.0 units
iii. Let the value of WT be x. [W – T – X]
WT + TX = WX
∴ x + TX = 25
∴ TX = 25 – x
Also, YT + TZ = YZ [Y – T – Z]
∴ 8 + TZ = 26
∴ TZ = 26 – 8
= 18 units
But, WT × TX = YT × TZ [Theorem of internal division of chords]
∴ x × (25 – x) = 8 × 18
∴ 25x – x2 = 144
∴ x2 – 25x + 144 = 0
∴ (x – 16)(x – 9) = 0
∴ x = 16 or x = 9
∴ WT = 16 units or WT = 9units
Question 16.
In the adjoining figure,
i. Mn (arc CE) = 54°, m (arc BD) = 23°, find measure of ∠CAE.
ii. If AB = 4.2,BC = 5.4, AE = 12.0, find AD.
iii. If AB = 3.6, AC = 9.0, AD = 5.4, find AE.
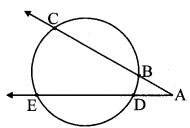
Solution:
i. Chords BC and ED intersect each other externally at point A.
∴ ∠CAE = \(\frac { 1 }{ 2 } \) [m(arc CE) – m(arc BD)]
= \(\frac { 1 }{ 2 } \) (54° – 23°)
= \(\frac { 1 }{ 2 } \) × 31°
∴ m∠CAE = 15.5°
ii. AC = AB + BC [A – B – C]
= 4.2 + 5.4
= 9.6 units
Now, AB × AC = AD × AE [Theorem of external division of chords]
∴ 4.2 × 9.6 = AD × 12.0
∴ AD = \(\frac{4.2 \times 9.6}{12.0}\)
∴ AD = 3.36 units
iii. AB × AC = AD × AE [Theorem of external division of chords]
∴ 3.6 × 9.0 = 5.4 × AE
∴ AE = \(\frac{3.6 \times 9.0}{5.4}\)
∴ AE = 6 units
Geometry Problem Set 3 Question 17.
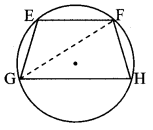
In the adjoining figure, chord EF || chord GH. Prove that, chord EG ≅ chord FH.
Fill in the blanks and write the proof.
Given: chord EF || chord GH
To prove: chord EG = chord FH
Construction: Draw seg GF.
Proof:
∠EFG = ∠FGH (i) Alternate angles
∠EFG = \(\frac { 1 }{ 2 } \) m (arcEG)] (ii) [Inscribed angle theorem]
∠FGH = \(\frac { 1 }{ 2 } \)m(arcFH) (iii) [Inscribed angle theorem]
∴ m(arcEG) = m (are FH) [From (i), (ii) and (iii)]
∴ chord EG ≅ chord FH The chords corresponding to congruent arcs of a circle are congruent
SSC Geometry Circle Chapter Solutions Pdf Question 18.
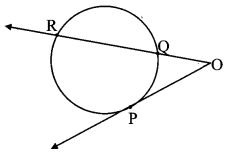
In the adjoining figure, P is the point of contact.
i. If m (arc PR) = 140°, L POR = 36°, find m (arc PQ)
ii. If OP = 7.2, OQ = 3.2, find OR and QR
iii. If OP = 7.2, OR = 16.2, find QR.
Solution:
i. ∠PQR m(arc PR) [Inscribed angle theorem]
= \(\frac { 1 }{ 2 } \) × 140° = 70°
∠PQR is the exterior angle of ∆POQ. [Remote interior angle theorem]
∴ ∠PQR = ∠POQ + ∠QPO [R – Q – O]
∴ 70° = ∠POR + ∠QPO
∴ 70 = 36° + ∠QPO
∴ ∠QPO = 70° – 36° = 340
Now, ray OP is tangent at point P and segment PQ is a secant.
∴ ∠QPO = \(\frac { 1 }{ 2 } \) m(arcPQ) [Theorem of angle between tangent and secant]
∴ 34° = \(\frac { 1 }{ 2 } \) m(arc PQ)
∴ m(arc PQ) = 68°
ii. Here, OP = 7.2, OQ = 3.2
Line OP is the tangent at point P [Given]
and seg OR is the secant.
∴ OP2 = OQ × OR [Tangent secant segments theorem]
∴ 7.22 = 3.2 × OR
∴ 51.84 = 3.2 × OR
∴ OR \(\frac { 51.84 }{ 3.2 } \)
∴ OR = 16.2 units
Now, OR = OQ + QR [O – Q – R]
∴ 16.2,= 3.2 + QR
∴ QR = 16.2 – 3.2
∴ QR = 13 units
iii. Here, OP = 7.2, OR = 16.2
OP2 = OQ × OR [Tangent secant segments theorem]
∴ 7.22 = OQ × 16.2
∴ OQ = \(\frac { 51.84 }{ 16.2 } \)
∴ OQ = 3.2 units
Now, OR = OQ + QR [O – Q – R]
∴ 16.2 = 3.2 + QR
∴ QR = 16.2 – 3.2
∴ QR = 13 units
Question 19.
In the adjoining figure, circles with centres C and D touch internally at point E. D lies on the inner circle. Chord EB of the outer circle intersects inner circle at point A. Prove that, seg EA ≅ seg AB.
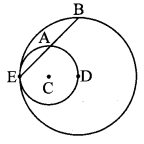
Given: Circles with centres C and D touch each other internally.
To prove: seg EA ≅ seg AB
Construction: Join seg ED and seg DA.
Proof:
E – C – D [Theorem of touching circles]
seg ED is the diameter of smaller circle.
∴∠EAD = 90° [Angle inscribed in a semicircle]
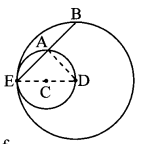
∴ seg AD ⊥ chord EB
∴ seg EA ≅ seg AB [Perpendicular drawn from the centre of the circle to the chord bisects the chord]
Question 20.
In the adjoining figure, seg AB is a diameter of a circle with centre O. The bisector of ∠ACB intersects the circle at point D. Prove that, seg AD ≅ seg BD. Complete the following proof by filling the blanks.
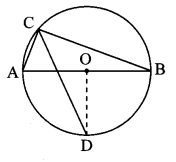
Given: seg AB is a diameter, seg CD bisects ∠ACB.
To prove: seg AD ≅ seg BD
Construction: Draw seg OD.
Proof:
∠ACB = 90° [Angle inscribed in a semicircle]
∠DCB = ∠DCA = 45° [CD is the bisector of ∠C]
m(arcDB) = 2∠DCA = 90° [Inscribed angle theorem]
∠DOB = m(arc DB) = 90° ………… (i) [Definition of measure of arc]
segOA ≅ segOB …………. (ii) [[Radii of the same circle]
∴ line OD is the perpendicular biscctor of [From (i) and (ii)]
seg AB.
∴ seg AD ≅ seg BD
10th Geometry Circle Question 21.
In the adjoining figure, seg MN is a chord of a circle with centre O. MN = 25, L is a point on chord MN such that ML = 9 and d(0, L) = 5. Find the radius of the circle.
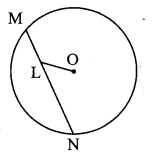
Construction: Draw seg OK ⊥ chord MN. Join OM.
Solution:
seg OK ⊥chord MN [Construction]
∴ MK = \(\frac { 1 }{ 2 } \) MN [Perpendicular drawn from the centre of the circle to the chord bisects the chord]
= \(\frac { 1 }{ 2 } \) × 25
= 12.5 units
MK = ML + LK [M – L – K]
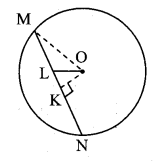
∴ 12.5 = 9 + LK
∴ LK= 12.5 – 9 = 3.5 units
In ∆OKL, ∠OKL = 90°
∴ OL2 = KL2 + OK2 [Pythagoras theorem]
∴ 52 = 3.52 + OK2
∴ OK2 = 25 – 12.25 = 12.75
Now, in ∆OKM, ∠OKM = 90°
∴ OM2 = OK2 + MK2
= 12.75 + 12.52
= 12.75 + 156.25
= 169
∴ OM = \(\sqrt { 169 }\)
= 13 units [Taking square root of both sides]
∴ The radius of the given circle is 13 units.
Question 22.
In the adjoining figure, two circles intersect each other at points S and R. Their common tangent PQ touches the circle at points P, Q.
Prove that, ∠PRQ + ∠PSQ = 180°.
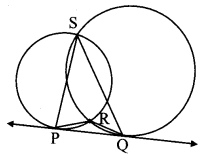
Given: Two circles intersect each other at points S and R.
line PQ is a common tangent.
To prove: ∠PRQ + ∠PSQ = 180°
Proof:
Line PQ is the tangent at point P and seg PR is a secant.
∴ [∠RPQ = ∠PSR …………. (i)
and ∠PQR = ∠QSR] ………… (ii) [Tangent secant theorem]
In ∆ PQR,
∠PQR + ∠PRQ + ∠RPQ = 180° [Sum of the measures of angles of a triangle is 180°]
∴ ∠QSR + ∠PRQ + ∠PSR = 180° [From (i) and (ii)]
∴ ∠PRQ + ∠QSR + ∠PSR = 180°
∴ ∠PRQ + ∠PSQ = 180° [Angle addition property]
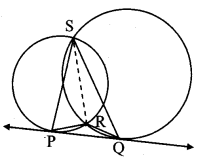
Question 23.
In the adjoining figure, two circles intersect at points M and N. Secants drawn through M and N intersect the circles at points R, S and P, Q respectively. Prove that: seg SQ || seg RP.
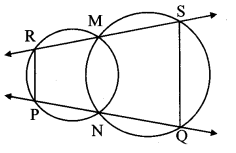
Given: Two circles intersect each other at points M and N.
To prove: seg SQ || seg RP
Construction: Join seg MN.
Proof:
□RMNP is a cyclic quadrilateral.
∴ ∠MRP = ∠MNQ …………. (i) [Corollary of cyclic quadrilateral theorem]
Also, □MNQS is a cyclic quadrilateral.
∴ ∠MNQ+ ∠MSQ = 180° [Theorem of cyclic quadrilateral]
∴ ∠MRP + ∠MSQ = 180° [From (i)]
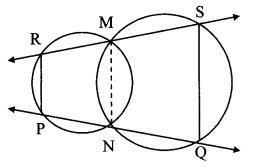
But, they are a pair of interior angles on the sarpe side of transversal RS on lines SQ and RP.
∴ seg SQ || seg RP [Interior angles test]
Question 24.
In the adjoining figure, two circles intersect each other at points A and E. Their common secant through E intersects the circles at points B and D. The tangents of the circles at points B and D intersect each other at point C. Prove that □ABCD is cyclic.
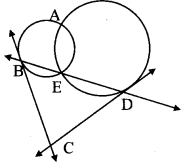
Given: Two circles intersect each other at A and E. seg BC and seg CD are the tangents to the circles.
To prove: □ABCD is cyclic.
Construction: Draw AB, AE and AD.
Proof:
[∠EBC = ∠BAE (i)
∠EDC = ∠DAE ] (ii) [Tangent secant theorem]
In ∆BCD,
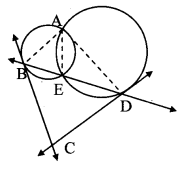
∠DBC + ∠BDC + ∠BCD = 180° [Sum of the measures of angles of a triangle is 180°]
∴ ∠EBC + ∠EDC + ∠BCD = 180° (iii) [B – E – D]
∴ ∠BAE + ∠DAE + ∠BCD = 180° [From (i), (ii) and (iii)]
∴ ∠BAD + ∠BCD = 180° [Angle addition property]
∴ □ABCD is cyclic. [Converse of cyclic quadrilateral theorem]
Question 25.
In the adjoining figure, seg AD ⊥ side BC, seg BE ⊥ side AC, seg CF ⊥ side AB. Point O is the orthocentre. Prove that, point O is the incentre of ∆DEF.
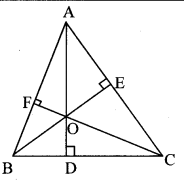
Given: seg AD ⊥ side BC,
seg BE ⊥ side AC,
seg CF ⊥ side AB.
To prove: Point O is the incentre of ∆DEF.
Construction: Draw DE, EF and DF.
Proof:
∠OFA = ∠OEA = 90° [Given]
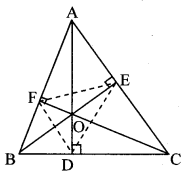
Now, ∠OFA + ∠OEA = 90° + 90°
∴ ∠OFA + ∠OEA = 180°
∴ □OFAE is a cyclic quadrilateral. [Converse of cyclic quadrilateral theorem]
∴ Points O, F, A, E are concyclic points.
∴ seg 0E subtends equal angles ∠OFE and ∠OAE on the same side of OE.
∴ ∠OFE = ∠OAE ……… (i)
∠OFB ∠ODB = 90° [Given]
Now, ∠OFB + ∠ODB = 90° + 90°
∴ ∠OFB + ∠ODB = 180°
∴ ꠸OFBD is a cyclic quadrilateral. [Converse of cyclic quadrilateral theorem]
∴ Points O, F, B, D are concyclic points.
∴ seg OD subtends equal angles ∠OFD and
∠OBD on the same side of OD.
∠OFD = ∠OBD ………….. (ii)
In ∆AEO and ∆BDO,
∠AEO = ∠BDO [Each angle is 90°]
∠AOE = ∠BOD [Vertically opposite angles]
∴ ∆AEO ~ ∆BDO [AA test of similarity]
∴ ∠OAE = ∠OBD …………….. (iii) [Corresponding angles of similar triangles]
∴ ∠OFE = ∠OFD [From (i), (ii) and (iii)]
∴ ray FO bisects ∠EFD.
Similarly, we can prove ray EO and ray DO bisects ∠FED and ∠FDE respectively.
∴ Point O is the intersection of angle bisectors of ∠D, ∠E and ∠F of ∆DEF.
∴ Point O is the incentre of ∆DEF.