Balbharati Maharashtra State Board 11th Commerce Maths Solution Book Pdf Chapter 1 Partition Values Miscellaneous Exercise 1 Questions and Answers.
Maharashtra State Board 11th Commerce Maths Solutions Chapter 1 Partition Values Miscellaneous Exercise 1
Question 1.
The data gives the number of accidents per day on a railway track. Compute Q2, P17, and D7.
4, 2, 3, 5, 6, 3, 4, 1, 2, 3, 2, 3, 4, 3, 2
Solution:
The given data can be arranged in ascending order as follows:
1, 2, 2, 2, 2, 3, 3, 3, 3, 3, 4, 4, 4, 5, 6
Here, n = 15
Q2 = value of 2\(\left(\frac{n+1}{4}\right)^{\text {th }}\) observation
= value of 2\(\left(\frac{15+1}{4}\right)^{\text {th }}\) observation
= value of (2 × 4)th observation
= value of 8th observation
∴ Q2 = 3
P17 = value of 17\(\left(\frac{n+1}{100}\right)^{\text {th }}\) observation
= value of 17\(\left(\frac{15+1}{100}\right)^{\text {th }}\) observation
= value of (17 × 0.16)th observation
= value of (2.72)th observation
= value of 2nd observation + 0.72 (value of 3rd observation – value of 2nd observation)
= 2 + 0.72 (2 – 2)
∴ P17 = 2
D7 = value of 7\(\left(\frac{n+1}{10}\right)^{\text {th }}\) observation
= value of 7\(\left(\frac{15+1}{10}\right)^{\text {th }}\) observation
= value of (7 × 1.6)th observation
= value of (11.2)th observation
= value of 11th observation + 0.2(value of 12th observation – value of 11th observation)
= 4 + 0. 2(4 – 4)
∴ D7 = 4
![]()
Question 2.
The distribution of daily sales of shoes (size-wise) for 100 days from a certain shop is as follows:
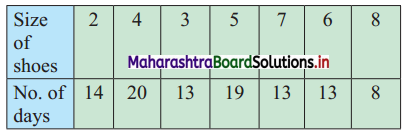
Compute Q1, D2, and P95.
Solution:
By arranging the given data in ascending order, we construct the less than cumulative frequency table as given below:

Here, n = 100
Q1 = value of \(\left(\frac{n+1}{4}\right)^{\text {th }}\) observation
= value of \(\left(\frac{100+1}{4}\right)^{\text {th }}\) observation
= value of (25.25)th observation
Cumulative frequency which is just greater than (or equal) to 25.25 is 27.
∴ Q1 = 3
D2 = value of 2\(\left(\frac{n+1}{10}\right)^{\text {th }}\) observation
= value of 2\(\left(\frac{100+1}{10}\right)^{\text {th }}\) observation
= value of (2 × 10.1)th observation
= value of (20.2)th observation
Cumulative frequency which is just greater than (or equal) to 20.2 is 27.
∴ D2 = 3
P95 = value of 95\(\left(\frac{n+1}{100}\right)^{\text {th }}\) observation
= value of 95\(\left(\frac{100+1}{100}\right)^{\text {th }}\) observation
= value of (95 × 1.01)th observation
= value of (95.95)th observation
The cumulative frequency which is just greater than (or equal) to 95.95 is 100.
∴ P95 = 8
Question 3.
Ten students appeared for a test in Mathematics and Statistics and they obtained the marks as follows:
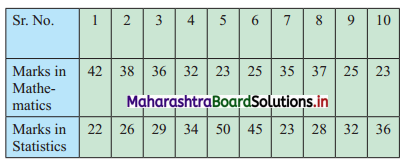
If the median will be the criteria, in which subject, the level of knowledge of the students is higher?
Solution:
Marks in Mathematics can be arranged in ascending order as follows:
23, 23, 25, 25, 32, 35, 36, 37, 38, 42
Here, n = 10
∴ Median = value of \(\left(\frac{n+1}{2}\right)^{\text {th }}\) observation
Median = value of \(\left(\frac{10+1}{2}\right)^{\text {th }}\) observation
= value of (5.5)th observation
= value of 5th observation + 0.5(value of 6th observation – value of 5th observation)
= 32 + 0.5 (35 – 32)
= 32 + 0.5(3)
= 32 + 1.5
= 33.5
Marks in Statistics can be arranged in ascending order as follows:
22, 23, 26, 28, 29, 32, 34, 36, 45, 50
Here, n = 10
∴ Median = value of \(\left(\frac{n+1}{2}\right)^{\text {th }}\) observation
= value of \(\left(\frac{10+1}{2}\right)^{\text {th }}\) observation
= value of (5.5)th observation
= value of 5th observation + 0.5(value of 6th observation – value of 5th observation)
= 29 + 0.5(32 – 29)
= 29 + 0.5(3)
= 29 + 1.5
= 30.5
∴ Median marks for Mathematics = 33.5 and
Median marks for Statistics = 30.5
∴ The level of knowledge in Mathematics is higher than that of Statistics.
![]()
Question 4.
In the frequency distribution of families given below, the number of families corresponding to expenditure group 2000 – 4000 is missing from the table. However, the value of the 25th percentile is 2880. Find the missing frequency.
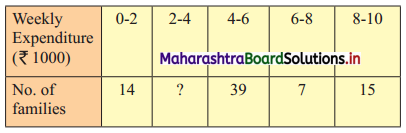
Solution:
Let x be the missing frequency of expenditure group 2000 – 4000.
We construct the less than cumulative frequency table as given below:
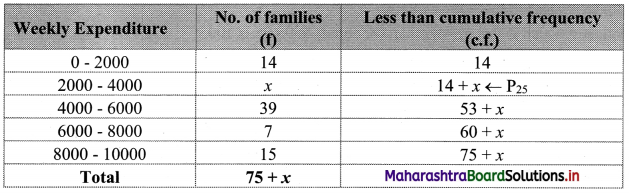
Here, N = 75 + x
Given, P25 = 2880
∴ P25 lies in the class 2000 – 4000.
∴ L = 2000, h = 2000, f = x, c.f. = 14
∴ P25 = L + \(\frac{h}{f}\left(\frac{25 \mathrm{~N}}{100}-\text { c.f. }\right)\)
∴ 2880 = 2000 + \(\frac{2000}{x}\left(\frac{75+x}{4}-14\right)\)
∴ 2880 – 2000 = \(\frac{2000}{x}\left(\frac{75+x-56}{4}\right)\)
∴ 880x = 500(x + 19)
∴ 880x = 500x + 9500
∴ 880x – 500x = 9500
∴ 380x = 9500
∴ x = 25
∴ 25 is the missing frequency of the expenditure group 2000 – 4000.
Question 5.
Calculate Q1, D6, and P15 for the following data:

Solution:
Since the difference between any two consecutive mid values is 50, the width of each class interval is 50.
∴ the class intervals will be 0 – 50, 50 – 100, etc.
We construct the less than cumulative frequency table as given below:

Here, N = 500
Q1 class = class containing \(\left(\frac{\mathrm{N}}{4}\right)^{\text {th }}\) observation
∴ \(\frac{\mathrm{N}}{4}=\frac{500}{4}\) = 125
Cumulative frequency which is just greater than (or equal) to 125 is 160.
Q1 lies in the class 100 – 150.
∴ L = 100, h = 50, f = 80, c.f. = 80
∴ Q1 = L + \(\left(\frac{\mathrm{N}}{4}-\text { c.f. }\right)\)
= 100 + \(\frac{50}{80}\)(125 – 80)
= 100 + \(\frac{5}{8}\)(45)
= 100 + 28.125
= 128.125
D6 class = class containing \(\left(\frac{6 \mathrm{~N}}{10}\right)^{\text {th }}\) observation
∴ \(\frac{6 \mathrm{~N}}{10}=\frac{6 \times 500}{10}\) = 300
Cumulative frequency which is just greater than (or equal) to 300 is 410.
∴ D6 lies in the class 200 – 250.
∴ L = 200, h = 50, f = 150, c.f. = 260
∴ D6 = L + \(\frac{\mathrm{h}}{\mathrm{f}}\left(\frac{6 \mathrm{~N}}{10}-\text { c.f. }\right)\)
= 200 + \(\frac{50}{150}\)(300 – 260)
= 200 + \(\frac{1}{3}\)(40)
= 200 + 13.33
= 213.33
P15 class = class containing \(\left(\frac{15 \mathrm{~N}}{100}\right)^{\text {th }}\) observation
∴ \(\frac{15 \mathrm{~N}}{100}=\frac{15 \times 500}{100}\) = 75
Cumulative frequency which is just greater than (or equal) to 75 is 80.
∴ P15 lies in the class 50 – 100.
∴ L = 50, h = 50, f = 70, c.f. = 10
∴ P15 = L + \(\frac{\mathrm{h}}{\mathrm{f}}\left(\frac{15 \mathrm{~N}}{100}-\text { c.f. }\right)\)
= 50 + \(\frac{50}{70}\) (75 – 10)
= 50 + \(\frac{5}{7}\) (65)
= 50 + \(\frac{325}{7}\)
= 50 + 46.4286
= 96.4286
∴ Q1 = 128.125, D6 = 213.33, P15 = 96.4286
![]()
Question 6.
Daily income for a group of 100 workers are given below:
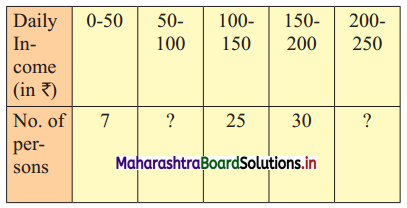
P30 for this group is ₹ 110. Calculate the missing frequencies.
Solution:
Let a and b be the missing frequencies of class 50 – 100 and class 200 – 250 respectively.
We construct the less than cumulative frequency table as given below:
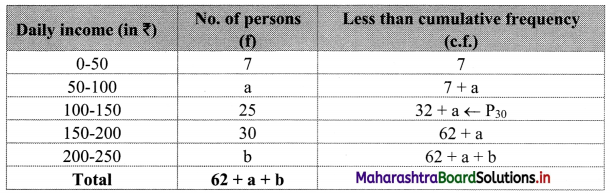
Here, N = 62 + a + b
Since, N = 100
∴ 62 + a + b = 100
∴ a + b = 38 ……(i)
Given, P30 = 110
∴ P30 lies in the class 100 – 150.
∴ L = 100, h = 50, f = 25, c.f. = 7 + a
\(\frac{30 \mathrm{~N}}{100}=\frac{30 \times 100}{100}\) = 30
∴ P30 = L + \(\frac{\mathrm{h}}{\mathrm{f}}\left(\frac{30 \mathrm{~N}}{100}-\text { c.f. }\right)\)
∴ 110 = 100 + \(\frac{50}{25}\) [30 – (7 + a)]
∴ 110 – 100 = 2(30 – 7 – a)
∴ 10 = 2(23 – a)
∴ 5 = 23 – a
∴ a = 23 – 5
∴ a = 18
Substituting the value of a in equation (i), we get
18 + b = 38
∴ b = 38 – 18
∴ b = 20
∴ 18 and 20 are the missing frequencies of the class 50 – 100 and class 200 – 250 respectively.
Question 7.
The distribution of a sample of students appearing for a C.A. examination is:
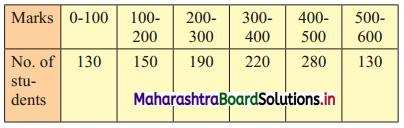
Help C.A. institute to decide cut-off marks for qualifying for an examination when 3% of students pass the examination.
Solution:
To decide cut-off marks for qualifying for an examination when 3% of students pass, we have to find P97.
We construct the less than cumulative frequency table as given below:

Here, N = 1100
P97 class = class containing \(\left(\frac{97 \mathrm{~N}}{100}\right)^{\text {th }}\) observation
∴ \(\frac{97 \mathrm{~N}}{100}=\frac{97 \times 1100}{100}\) = 1067
Cumulative frequency which is just greater than (or equal) to 1067 is 1100.
∴ P97 lies in the class 500 – 600.
∴ L = 500, h = 100, f = 130, c.f. = 970
∴ P97 = L + \(\frac{\mathrm{h}}{\mathrm{f}}\left(\frac{97 \mathrm{~N}}{100}-\text { c.f. }\right)\)
= 500 + \(\frac{100}{130}\)(1067 – 970)
= 500 + \(\frac{10}{13}\) (97)
= 500 + 74.62
= 574.62 ~ 575
∴ the cut off marks for qualifying an examination is 575.
![]()
Question 8.
Determine graphically the value of median, D3, and P35 for the data given below:
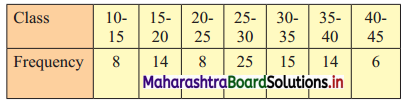
Solution:
To draw an ogive curve, we construct the less than cumulative frequency table as given below:
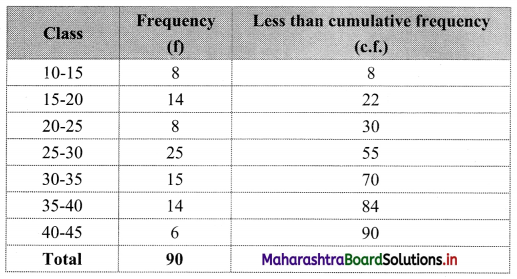
The points to be plotted for less than ogive are (15, 8), (20, 22), (25, 30), (30, 55), (35, 70), (40, 84), (45, 90).
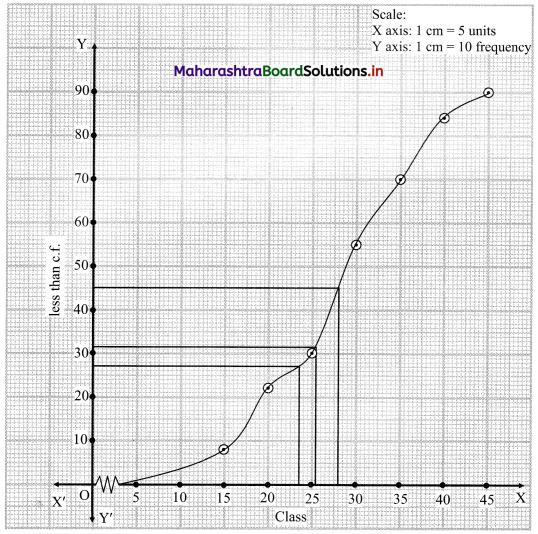
N = 90
For median, consider \(\frac{\mathrm{N}}{2}=\frac{90}{2}\) = 45
For D3, consider \(\frac{3 \mathrm{~N}}{10}=\frac{3 \times 90}{10}\) = 27
For P35, consider \(\frac{35 \mathrm{~N}}{100}=\frac{35 \times 90}{100}\) = 31.5
∴ We take the values 45, 27 and 31.5 on the Y-axis and draw lines from these points parallel to X-axis.
From the points where they intersect the less than ogive, we draw perpendicular on the X-axis.
Foot of the perpendicular represent the values of median, D3 and P35 respectively.
∴ Median ~ 29, D3 ~ 23.5, P35 ~ 26
Question 9.
The I.Q. test of 500 students of a college is as follows:
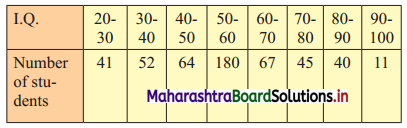
Find graphically the number of students whose I.Q. is more than 55 graphically.
Solution:
To draw an ogive curve, we construct the less than cumulative frequency table as given below:
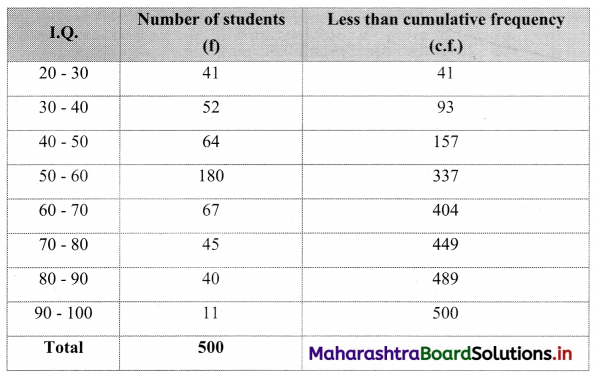
The points to be plotted for less than ogive are (30, 41), (40, 93), (50, 157), (60, 337), (70, 404), (80, 449), (90, 489), (100, 500)
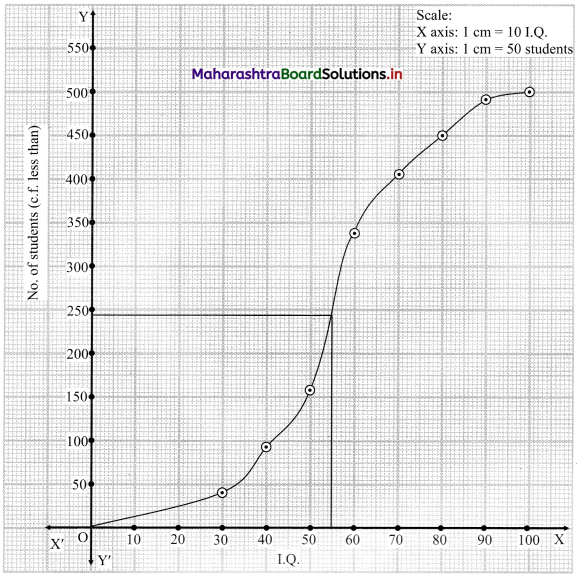
To find the number of students whose I.Q. is more than 55, we consider the value 55 on the X-axis.
From this point, we draw a line that is parallel to Y-axis.
From the point this line intersects the less than ogive, we draw a perpendicular on the Y-axis.
The foot of perpendicular gives the number of students whose I.Q. is less than 55.
∴ The foot of perpendicular ~ 244
∴ No. of students whose I.Q. is less than 55 ~ 244
∴ No. of Students whose I.Q. is more than 55 = 500 – 244 = 256
![]()
Question 10.
Draw an ogive for the following distribution. Determine the median graphically and verify your result by a mathematical formula.
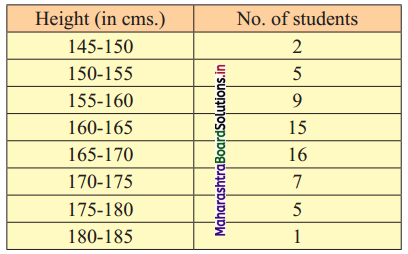
Solution:
To draw an ogive curve, we construct the less than cumulative frequency table as given below:
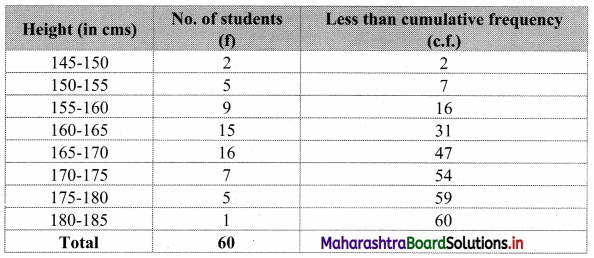
The points to be plotted for less than ogive are (150, 2), (155, 7), (160, 16), (165, 31), (170, 47), (175, 54), (180, 59) and (185, 60).
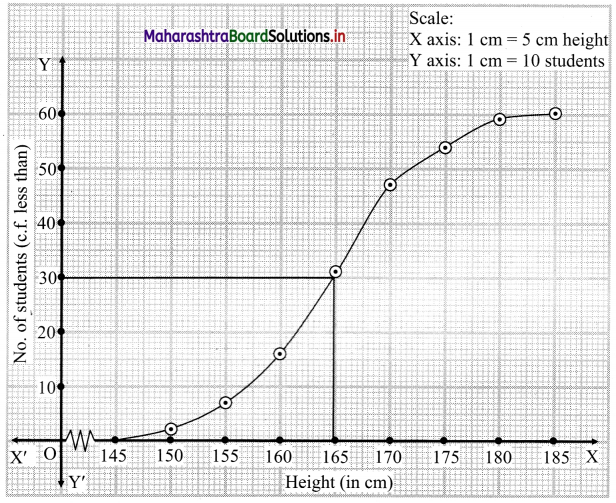
N = 60
∴ \(\frac{\mathrm{N}}{2}=\frac{60}{2}\) = 30
∴ We take the value 30 on the Y-axis and from this point, we draw a line parallel to X-axis.
From the point where this line intersects the less than ogive, we draw a perpendicular on X-axis.
The foot perpendicular gives the value of the median.
∴ Median ~ 164.67
Now, let us calculate the median from the mathematical formula.
∴ \(\frac{\mathrm{N}}{2}\) = 30
The median lies in the class interval 160 – 165.
∴ L = 160, h = 5, f = 15, c.f. = 16
Median = L + \(\frac{\mathrm{h}}{\mathrm{f}}\left(\frac{\mathrm{N}}{2}-\mathrm{c} . \mathrm{f} .\right)\)
= 160 + \(\frac{5}{15}\) (30 – 16)
= 160+ \(\frac{1}{3}\) × 14
= 160 + 4.67
= 164.67
Question 11.
In a group of 25 students, 7 students failed and 6 students got distinction and the marks of the remaining 12 students are 61, 36, 44, 59, 52, 56, 41, 37, 39, 38, 41, 64. Find the median marks of the whole group.
Solution:
n = 25
Median = \(\frac{\mathrm{n}+1}{2}=\frac{25+1}{2}\) = 13th observation
We have been stated that 7 students failed (assuming passing marks on 35) and 6 students got distinction (assuming distinction as 70+), and the marks of the remaining 12 students (who will be situated between the two groups mentioned above, if arranged in ascending order), we have,
F, F, F, F, F, F, F, 36, 37, 38, 39, 41, 41, 44, 52, 56, 59, 61, 64, D, D, D, D, D, D
∴ median = 13th observation = 41.
![]()
Question 12.
The median weight of a group of 79 students is found to be 55 kg. 6 more students are added to this group whose weights are 50, 51, 52, 59.5, 60, 61 kg. What will be the value of the median of the combined group if the lowest and the highest weights were 53 kg and 59 kg respectively?
Solution:
n = 79
Median = 55kg
Lowest observation = 53 kg
Flighest observation = 59 kg
6 new students are added to the group having weights in Kg as follows:
50, 51, 52, 59.5, 60, 61
From the above, we see that of the 6 new students, 3 have weights which are below the lowest weight of the earlier group and 3 have weights which are above the highest weight of the earlier group.
∴ the median remains the same
∴ median = 55 kg.
Question 13.
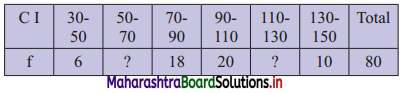
The median of the following incomplete table is 92. Find the missing frequencies:
Solution:
Let a and b be the missing frequencies of class 50 – 70 and class 110 – 130 respectively.
We construct the less than cumulative frequency table as given below:
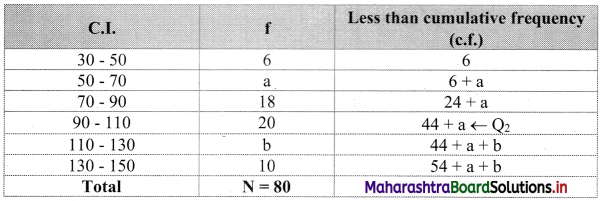
Here, N = 54 + a + b
Since, N = 80
∴ 54 + a + b = 80
∴ a + b = 26 …..(i)
Given, Median = Q2 = 92
∴ Q2 lies in the class 90 – 110.
∴ L = 90, h = 20, f = 20, c.f. = 24 + a
\(\frac{2 \mathrm{~N}}{4}=\frac{2 \times 80}{4}\) = 40
∴ Q2 = L + \(\frac{h}{f}\left(\frac{2 N}{4}-\text { c.f. }\right)\)
∴ 92 = 90 + \(\frac{20}{20}\) [40 – (24 + a)
∴ 92 – 90 = 40 – 24 – a
∴ 2 = 16 – a
∴ a = 14
Substituting the value of a in equation (i), we get
14 + b = 26
∴ b = 26 – 14 = 12
∴ 14 and 12 are the missing frequencies of the class 50 – 70 and class 110 – 130 respectively.
![]()
Question 14.
A company produces tables which are packed in batches of 100. An analysis of the defective tubes in different batches has received the following information:
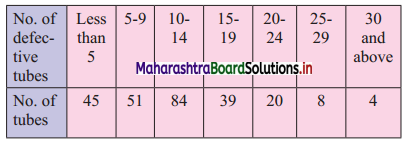
estimate the number of defective tubes in the central batch.
Solution:
To find the number of defective tubes in the central batch, we have to find Q2.
Since the given data is not continuous, we have to convert it into a continuous form by subtracting 0.5 from the lower limit and adding 0.5 to the upper limit of every class interval.
∴ the class intervals will be Less than 4.5, 4.5 – 9.5, etc.
We construct the less than cumulative frequency table as given below:
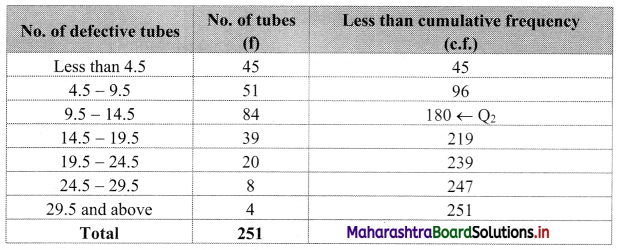
Here, N = 251
Q2 class = class containing \(\left(\frac{2 \mathrm{~N}}{4}\right)^{\mathrm{th}}\) observation
∴ \(\frac{2 \mathrm{~N}}{4}=\frac{2 \times 251}{4}\) = 125.5
Cumulative frequency which is just greater than (or equal to) 125.5 is 180.
∴ Q2 lies in the class 9.5 – 14.5.
∴ L = 9.5, h = 5, f = 84, c.f. = 96
∴ Q2 = L + \(\frac{\mathrm{h}}{\mathrm{f}}\left(\frac{2 \mathrm{~N}}{4}-\text { c.f. }\right)\)
= 9.5 + \(\frac{5}{84}\) (125.5 – 96)
= 9.5 + \(\frac{5}{84}\) × 29.5
= 9.5 + \(\frac{147.5}{84}\)
= 9.5 + 1.76
= 11.26
Question 15.
In a college, there are 500 students in junior college, 5% score less than 25 marks, 68 scores from 26 to 30 marks, 30% score from 31 to 35 marks, 70 scores from 36 to 40 marks, 20% score from 41 to 45 marks and the rest score 46 and above marks. What are the median marks?
Solution:
Given data can be written in tabulated form as follows:
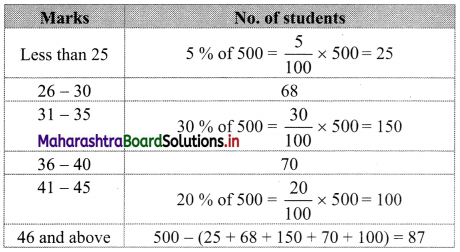
Since the given data is not continuous, we have to convert it into the continuous form by subtracting 0.5 from the lower limit and adding 0.5 to the upper limit of every class interval.
∴ the class intervals will be Less than 25.5, 25.5 – 30.5, etc.
We construct the less than cumulative frequency table as given below:
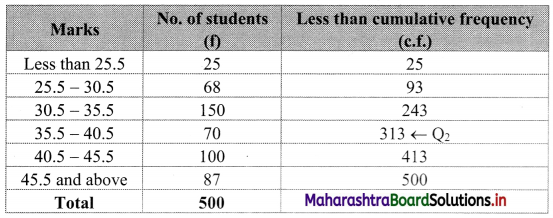
Here, N = 500
Q2 class = class containing \(\left(\frac{2 \mathrm{~N}}{4}\right)^{\text {th }}\) observation
∴ \(\frac{2 \mathrm{~N}}{4}=\frac{2 \times 500}{4}\) = 250
Cumulative frequency which is just greater than (or equal to) 250 is 313.
∴ Q2 lies in the class 35.5 – 40.5.
∴ L = 35.5, h = 5, f = 70, c.f. = 243
∴ Median = Q2 = L + \(\frac{\mathrm{h}}{\mathrm{f}}\left(\frac{2 \mathrm{~N}}{4}-\text { c.f. }\right)\)
= 35.5 + \(\frac{5}{70}\) (250 – 243)
= 35.5 + \(\frac{1}{14}\) (7)
= 35.5 + 0.5
= 36
![]()
Question 16.
Draw a cumulative frequency curve more than typical for the following data and hence locate Q1 and Q3. Also, find the number of workers with daily wages
(i) Between ₹ 170 and ₹ 260
(ii) less than ₹ 260
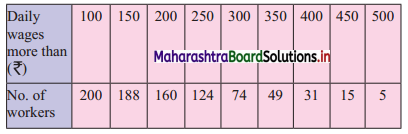
Solution:
For more than ogive points to be plotted are (100, 200), (150, 188), (200, 160), (250, 124), (300, 74), (350, 49), (400, 31), (450, 15), (500, 5)
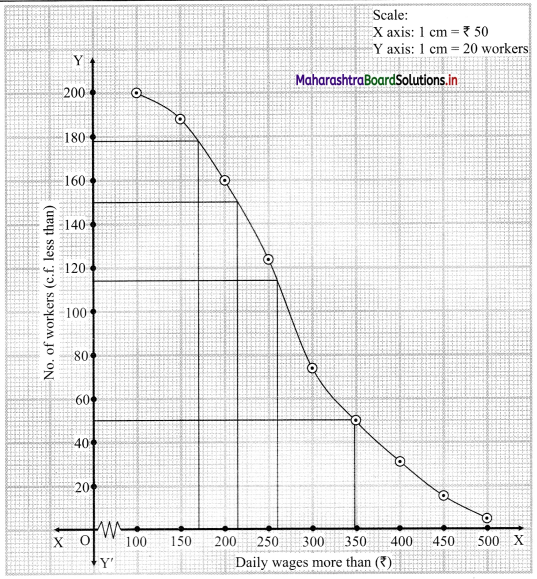
Here, N = 200
For Q1, \(\frac{\mathrm{N}}{4}=\frac{200}{4}\) = 4
For Q3, \(\frac{3 \mathrm{~N}}{4}=\frac{3 \times 200}{4}\) = 150
We take the points having Y co-ordinates 50 and 150 on Y-axis.
From these points, we draw lines which are parallel to X-axis.
From the points of intersection of these lines with the curve, we draw perpendicular on X-axis.
X-Co-ordinates of these points gives the values of Q1 and Q3.
Since X-axis has daily wages more than and not less than the given amounts.
∴ Q1 = Q3 and Q3 = Q1
∴ Q2 ~ 215 , Q3 ~ 348
(i) To find the number of workers with daily wages between ₹ 170 and ₹ 260,
Take the values 170 and 260 on X-axis. From these points, we draw lines parallel to Y-axis.
From the point where they intersect the more than ogive, we draw perpendiculars on Y-axis.
The points where they intersect the Y-axis gives the values 178 and 114.
∴ Number of workers having daily wages between ₹ 170 and ₹ 260 = 178 – 114 = 64
(ii) To find the number of workers having daily wages less than ₹ 260, we consider the value 260 on the X-axis.
From this point, we draw a line that is parallel to Y-axis.
From the point where the line intersects the more than ogive, we draw a perpendicular on the Y-axis.
The foot of perpendicular gives the number of workers having daily wages of more than 260.
The foot of perpendicular ~ 114
∴ No. of workers whose daily wages are more than ₹ 260 ~ 114
∴ No. of workers whose daily wages are less than ₹ 260 = 200 – 114 = 86
Question 17.
Draw ogive of both the types for the following frequency distribution and hence find the median.
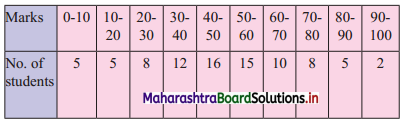
Solution:
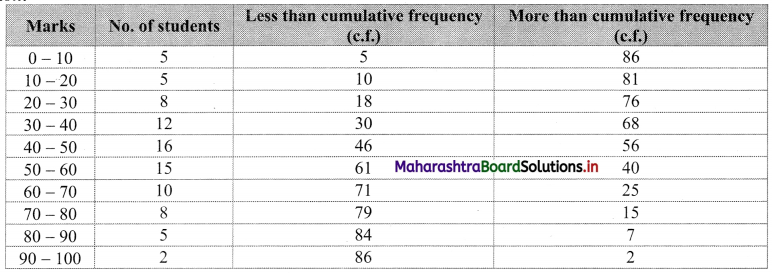
For less than given points to be plotted are (10, 5), (20, 10), (30, 18), (40, 30), (50, 46), (60, 61), (70, 71), (80, 79), (90, 84), (100, 86)
For more than given points to be plotted are (0, 86), (10, 81), (20, 76), (30, 68), (40, 56), (50, 40), (60, 25), (70, 15), (80, 7), (90, 2)
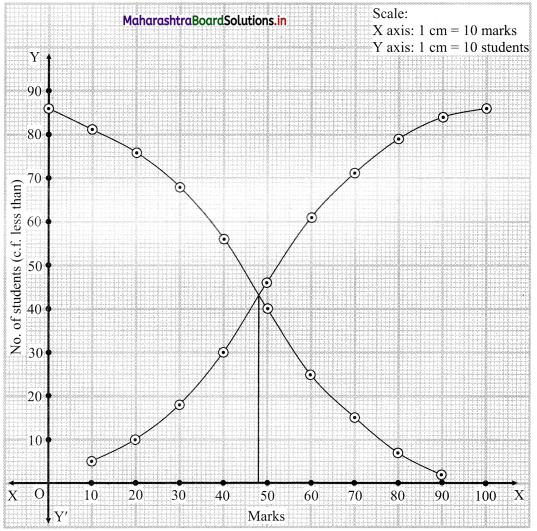
From the point of intersection of two ogives. We draw a perpendicular on X-axis.
The point where it meets the X-axis gives the value of the median.
![]()
Question 18.
Find Q1, D6 and P78 for the following data:
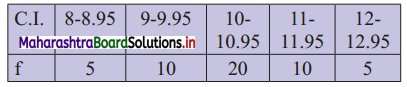
Solution:
Since the given data is not in the form of a continuous frequency distribution, we have to convert it into that form by subtracting 0.025 from the lower limit and adding 0.025 to the upper limit of each class interval.
∴ the class intervals will be 7.975 – 8.975, 8.975 – 9.975, etc.
We construct the less than cumulative frequency table as given below:

Here, N = 50
Q1 class = class containing \(\left(\frac{\mathrm{N}}{4}\right)^{\text {th }}\) observation
∴ \(\frac{N}{4}=\frac{50}{4}\) = 12.5
Cumulative frequency which is just greater than (or equal) to 12.5 is 15.
∴ Q1 lies in the class 8.975 – 9.975.
∴ L = 8.975, h = 1, f = 10, c.f. = 5
Q1 = L + \(\frac{\mathrm{h}}{\mathrm{f}}\left(\frac{\mathrm{N}}{4}-\mathrm{c} . \mathrm{f} .\right)\)
= 8.975 + \(\frac{1}{10}\) (12.5 – 5)
= 8.975 + 0.1(7.5)
= 8.975 + 0.75
= 9.725
D6 class = class containing \(\left(\frac{6 \mathrm{~N}}{10}\right)^{\text {th }}\) observation
∴ \(\frac{6 \mathrm{~N}}{10}=\frac{6 \times 50}{10}\) = 30
Cumulative frequency which is just greater than (or equal) to 30 is 35.
∴ D6 lies in the class 9.975 – 10.975.
∴ L = 9.975, h = 1, f = 20, c.f. = 15
D6 = L + \(\frac{h}{f}\left(\frac{6 N}{10}-\text { c.f. }\right)\)
= 9.975 + \(\frac{1}{20}\) (30 – 15)
= 9.975 + 0.05(15)
= 9.975 + 0.75
= 10.725
P78 class = class containing \(\left(\frac{78 \mathrm{~N}}{100}\right)^{\text {th }}\) observation
\(\frac{78 \mathrm{~N}}{100}=\frac{78 \times 50}{100}\) = 39
Cumulative frequency which is just greater than (or equal) to 39 is 45.
∴ P78 lies in the class 10.975 – 11.975.
∴ L = 10.975, h = 1, f = 10, c.f. = 35
∴ P78 = L + \(\frac{\mathrm{h}}{\mathrm{f}}\left(\frac{78 \mathrm{~N}}{100}-\text { c.f. }\right)\)
= 10.975 + \(\frac{1}{10}\) (39 – 35)
= 10.975 + 0.1(4)
= 10.975 + 0.4
= 11.375
Question 19.
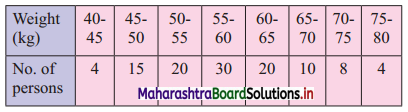
For the above data, find all quartiles and number of persons weighing between 57 kg and 72 kg.
Solution:
We construct the less than cumulative frequency table as given below:
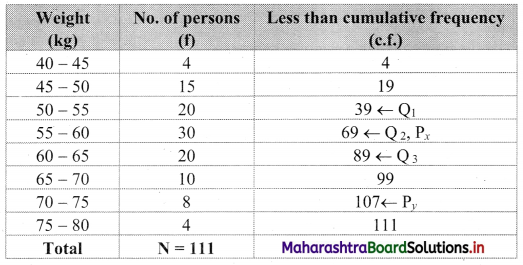
Here, N = 111
Q1 class = class containing \(\left(\frac{\mathrm{N}}{4}\right)^{\text {th }}\) observation
∴ \(\frac{N}{4}=\frac{111}{4}\) = 27.75
Cumulative frequency which is just greater than (or equal) to 27.75 is 39.
∴ Q1 lies in the class 50 – 55.
∴ Q1 = L + \(\frac{\mathrm{h}}{\mathrm{f}}\left(\frac{\mathrm{N}}{4}-\text { c.f. }\right)\)
= 50 + \(\frac{5}{20}\) (27.75 – 19)
= 50 + \(\frac{1}{4}\) × 8.75
= 50 + 2.1875
= 52.1875
Q2 class = class containing \(\left(\frac{2 \mathrm{~N}}{4}\right)^{\mathrm{th}}\) observation
∴ \(\frac{2 N}{4}=\frac{2 \times 111}{4}\) = 55.5
Cumulative frequency which is just greater than (or equal) to 55.5 is 69.
∴ Q2 lies in the class 55 – 60.
∴ L = 55, h = 5, f = 30, c.f. = 39
∴ Q2 = L + \(\frac{h}{f}\left(\frac{2 N}{4}-\text { c.f. }\right)\)
= 55 + \(\frac{5}{30}\) (55.5 – 39)
= 55 + \(\frac{1}{6}\) × 16.5
= 55 + 2.75
= 57.75
Q3 class = class containing \(\left(\frac{3 \mathrm{~N}}{4}\right)^{\mathrm{th}}\) observation
∴ \(\frac{3 \mathrm{~N}}{4}=\frac{3 \times 111}{4}\) = 83.25
Cumulative frequency which is just greater than (or equal) to 83.25 is 89.
∴ Q3 lies in the class 60 – 65.
∴ L = 60, h = 5, f = 20, c.f. = 69
∴ Q3 = L + \(\frac{h}{f}\left(\frac{3 N}{4}-c . f .\right)\)
= 60 + \(\frac{5}{20}\) (83.25 – 69)
= 60 + \(\frac{1}{4}\) × 14.25
= 60 + 3.5625
= 63.5625
In order to find the number of persons between 57 kg and 72 kg,
We need to find x in Px, where Px = 57 kg and y in Py, where Py = 72 kg
Then (y – x) would be the % of persons weighing between 57 kg and 72 kg
Px = 57
∴ L + \(\frac{\mathrm{h}}{\mathrm{f}}\left(\frac{x \times \mathrm{N}}{100}-\mathrm{c} . \mathrm{f} .\right)\) = 57
∴ 55 + \(\frac{5}{30}\) (1.11x – 39) = 57
∴ \(\frac{1}{6}\) (1.11x – 39) = 2
∴ 1.11x – 39 = 12
∴ 1.11x = 51
∴ x = 45.95
∴ Py = 72
∴ L + \(\frac{\mathrm{h}}{\mathrm{f}}\left(\frac{y \times \mathrm{N}}{100}-\mathrm{c} . \mathrm{f} .\right)\) = 72
∴ 70 + \(\frac{5}{8}\) (1.11y – 99) = 72
∴ 0.625(1.11y – 99) = 2
∴ 1.11y – 99 = 3.2
∴ 1.11y = 102.2
∴ y = 92.07
∴ % of people weighing between 57 kg and 72 kg = 92.07 – 45.95 = 46.12 %
∴ No. of people weighing between 57 kg and 72 kg = 111 × 46.12% = 51.1932 ~ 51
![]()
Question 20.
For the following data showing weights of 100 employees, find the maximum weight of the lightest 25% of employees.
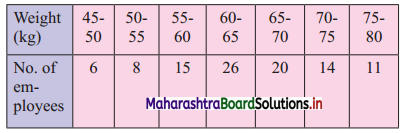
Solution:
We construct the less than cumulative frequency table as given below:

Here, N = 100
Q1 class = class containing \(\left(\frac{N}{4}\right)^{\text {th }}\) observation
∴ \(\frac{\mathrm{N}}{4}=\frac{100}{4}\) = 25
Cumulative frequency which is just greater than (or equal) to 25 is 29.
∴ Q1 lies in the class 55 – 60.
∴ L = 55, h = 5, f = 15, c.f. = 14
∴ Q1 = L + \(\frac{\mathrm{h}}{\mathrm{f}}\left(\frac{\mathrm{N}}{4}-\mathrm{c} . \mathrm{f} .\right)\)
= 55 + \(\frac{5}{15}\) (25 – 14)
= 55 + \(\frac{1}{3}\) × 11
= 55 + 3.67
= 58.67
∴ Maximum weight of the lightest 25% of employees is 58.67 kg.