Balbharati Maharashtra State Board 11th Commerce Maths Solution Book Pdf Chapter 5 Locus and Straight Line Miscellaneous Exercise 5 Questions and Answers.
Maharashtra State Board 11th Commerce Maths Solutions Chapter 5 Locus and Straight Line Miscellaneous Exercise 5
Question 1.
Find the slopes of the lines passing through the following points:
(i) (1, 2), (3, -5)
(ii) (1, 3), (5, 2)
(iii) (-1, 3), (3, -1)
(iv) (2, -5), (3, -1)
Solution:
(i) Let A = (1, 2) = (x1, y1) and B = (3, -5) = (x2, y2) say.
Slope of line AB = \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}=\frac{-5-2}{3-1}=\frac{-7}{2}\)
(ii) Let C = (1, 3) = (x1, y1) and D = (5, 2) = (x2, y2) say.
Slope of line CD = \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}=\frac{2-3}{5-1}=\frac{-1}{4}\)
(iii) Let E = (-1, 3) = (x1, y1) and F = (3, -1) = (x2, y2) say.
Slope of line EF = \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}=\frac{-1-3}{3-(-1)}=\frac{-4}{4}\) = -1
(iv) Let P = (2, -5) = (x1, y1) and Q = (3, -1) = (x2, y2) say.
Slope of line PQ = \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}=\frac{-1-(-5)}{3-2}\) = \(\frac{-1+5}{1}\) = 4
![]()
Question 2.
Find the slope of the line which
(i) makes an angle of 120° with the positive X-axis.
(ii) makes intercepts 3 and -4 on the axes.
(iii) passes through the points A(-2, 1) and the origin.
Solution:
(i) θ = 120°
Slope of the line = tan 120°
= tan (180° – 60°)
= -tan 60° …..[tan(180° – θ) = -tan θ]
= -√3
(ii) Given, x-intercept of line is 3 and y-intercept of line is -4
∴ The line intersects X-axis at (3, 0) and Y-axis at (0, -4).
∴ The line passes through (3, 0) = (x1, y1) and (0, -4) = (x2, y2) say.
∴ Slope of line = \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}=\frac{-4-0}{0-3}=\frac{-4}{-3}=\frac{4}{3}\)
(iii) Required line passes through O(0, 0) = (x1, y1) and A(-2, 1) = (x2, y2) say.
Slope of line OA = \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}=\frac{1-0}{-2-0}=\frac{1}{-2}\) = \(\frac{-1}{2}\)
Question 3.
Find the value of k:
(i) if the slope of the line passing through the points (3, 4), (5, k) is 9.
(ii) the points (1, 3), (4, 1), (3, k) are collinear.
(iii) the point P(1, k) lies on the line passing through the points A(2, 2) and B(3, 3).
Solution:
(i) Let P(3, 4), Q(5, k).
Slope of PQ = 9 …….[Given]
∴ \(\frac{\mathrm{k}-4}{5-3}\) = 9
∴ \(\frac{\mathrm{k}-4}{2}\) = 9
∴ k – 4 = 18
∴ k = 22
(ii) The points A(1, 3), B(4, 1) and C(3, k) are collinear.
∴ Slope of AB = Slope of BC
∴ \(\frac{1-3}{4-1}=\frac{k-1}{3-4}\)
∴ \(\frac{-2}{3}=\frac{\mathrm{k}-1}{-1}\)
∴ 2 = 3k – 3
∴ k = \(\frac{5}{3}\)
(iii) Given, point P(1, k) lies on the line joining A(2, 2) and B(3, 3).
∴ Slope of AB = Slope of BP
∴ \(\frac{3-2}{3-2}=\frac{3-k}{3-1}\)
∴ 1 = \(\frac{3-k}{2}\)
∴ 2 = 3 – k
∴ k = 1
![]()
Question 4.
Reduce the equation 6x + 3y + 8 = 0 into slope-intercept form. Hence, find its slope.
Solution:
Given equation is 6x + 3y + 8 = 0, which can be written as
3y = -6x – 8
∴ y = \(\frac{-6 x}{3}-\frac{8}{3}\)
∴ y = -2x – \(\frac{8}{3}\)
This is of the form y = mx + c with m = -2
∴ y = -2x – \(\frac{8}{3}\) is in slope-intercept form with slope = -2
Question 5.
Verify that A(2, 7) is not a point on the line x + 2y + 2 = 0.
Solution:
Given equation is x + 2y + 2 = 0.
Substituting x = 2 and y = 7 in L.H.S. of given equation, we get
L.H.S. = x + 2y + 2
= 2 + 2(7) + 2
= 2 + 14 + 2
= 18
≠ R.H.S.
∴ Point A does not lie on the given line.
Question 6.
Find the X-intercept of the line x + 2y – 1 = 0.
Solution:
Given equation of the line is x + 2y – 1 = 0
To find the x-intercept, put y = 0 in given equation of the line
∴ x + 2(0) – 1 = 0
∴ x + 0 – 1 = 0
∴ x = 1
∴ X-intercept of the given line is 1.
Alternate method:
Given equation of the line is x + 2y – 1 = 0
i.e. x + 2y = 1
∴ \(\frac{x}{1}+\frac{y}{\frac{1}{2}}=1\)
Comparing with \(\frac{x}{\mathrm{a}}+\frac{y}{\mathrm{~b}}=1\), we get a = 1
X-intercept of the line is 1.
![]()
Question 7.
Find the slope of the line y – x + 3 = 0.
Solution:
Equation of given line is y – x + 3 = 0
i.e. y = x – 3
Comparing with y = mx + c, we get
m = Slope = 1
Question 8.
Does point A(2, 3) lie on the line 3x + 2y – 6 = 0? Give reason.
Solution:
Given equation is 3x + 2y – 6 = 0.
Substituting x = 2 and y = 3 in L.H.S. of given equation, we get
L.H.S. = 3x + 2y – 6
= 3(2)+ 2(3) – 6
= 6
≠ R.H.S.
∴ Point A does not lie on the given line.
Question 9.
Which of the following lines passes through the origin?
(a) x = 2
(b) y = 3
(c) y = x + 2
(d) 2x – y = 0
Solution:
Any line passing through origin is of the form y = mx or ax + by = 0.
Here in the given option, 2x – y = 0 is in the form ax + by = 0.
Question 10.
Obtain the equation of the line which is:
(i) parallel to the X-axis and 3 units below it.
(ii) parallel to the Y-axis and 2 units to the left of it.
(iii) parallel to the X-axis and making an intercept of 5 on the Y-axis.
(iv) parallel to the Y-axis and making an intercept of 3 on the X-axis.
Solution:
(i) Equation of a line parallel to X-axis is y = k.
Since, the line is at a distance of 3 units below X-axis.
∴ k = -3
∴ the equation of the required line is y = -3
i.e., y + 3 = 0.
(ii) Equation of a line parallel to Y-axis is x = h.
Since, the line is at a distance of 2 units to the left of Y-axis.
∴ h = -2
∴ the equation of the required line is x = -2
i.e., x + 2 = 0.
(iii) Equation of a line parallel to X-axis with y-intercept ‘k’ is y = k.
Here, y-intercept = 5
∴ the equation of the required line is y = 5.
(iv) Equation of a line parallel to Y-axis with x-intercept ‘h’ is x = h.
Here, x-intercept = 3
∴ the equation of the required line is x = 3.
![]()
Question 11.
Obtain the equation of the line containing the point:
(i) (2, 3) and parallel to the X-axis.
(ii) (2, 4) and perpendicular to the Y-axis.
(iii) (2, 5) and perpendicular to the X-axis.
Solution:
(i) Equation of a line parallel to X-axis is of the form y = k.
Since, the line passes through (2, 3).
∴ k = 3
∴ the equation of the required line is y = 3.
(ii) Equation of a line perpendicular to Y-axis
i.e., parallel to X-axis, is of the form y = k.
Since, the line passes through (2, 4).
∴ k = 4
∴ the equation of the required line is y = 4.
(iii) Equation of a line perpendicular to X-axis
i.e., parallel to Y-axis, is of the form x = h.
Since, the line passes through (2, 5).
∴ h = 2
∴ the equation of the required line is x = 2.
Question 12.
Find the equation of the line:
(i) having slope 5 and containing point A(-1, 2).
(ii) containing the point (2, 1) and having slope 13.
(iii) containing the point T(7, 3) and having inclination 90°.
(iv) containing the origin and having inclination 90°.
(v) through the origin which bisects the portion of the line 3x + 2y = 2 intercepted between the co-ordinate axes.
Solution:
(i) Given, slope (m) = 5 and the line passes through A(-1, 2).
Equation of the line in slope point form is y – y1 = m(x – x1)
∴ the equation of the required line is y – 2 = 5(x + 1)
∴ y – 2 = 5x + 5
∴ 5x – y + 7 = 0
(ii) Given, slope (m) = 13 and the line passes through (2, 1).
Equation of the line in slope point form is y – y1 = m(x – x1)
∴ the equation of the required line is y – 1 = 13(x – 2)
∴ y – 1 = 13x – 26
∴ 13x – y = 25.
(iii) Given, Inclination of line = θ = 90°
∴ the required line is parallel to Y-axis (or lies on the Y-axis.)
Equation of a line parallel to Y-axis is of the form x = h.
Since, the line passes through (7, 3).
∴ h = 7
∴ the equation of the required line is x = 7.
(iv) Given, Inclination of line = θ = 90°
∴ the required line is parallel to Y-axis (or lies on the Y-axis.)
Equation of a line parallel to Y-axis is of the form x = h.
Since, the line passes through origin (0, 0).
∴ h = 0
∴ the equation of the required line is x = 0.
(v) Given equation of the line is 3x + 2y = 2.
∴ \(\frac{3 x}{2}+\frac{2 y}{2}=1\)
∴ \(\frac{x}{\frac{2}{3}}+\frac{y}{1}=1\)
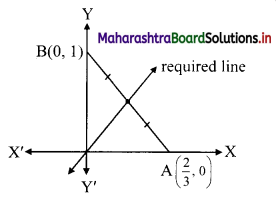
This equation is of the form \(\frac{x}{\mathrm{a}}+\frac{y}{\mathrm{~b}}=1\), with
a = \(\frac{2}{3}\), b = 1
∴ the line 3x + 2y = 2 intersects the X-axis at A(\(\frac{2}{3}\), 0) and Y-axis at B(0, 1).
Required line is passing through the midpoint of AB.
∴ Midpoint of AB = \(\left(\frac{\frac{2}{3}+0}{2}, \frac{0+1}{2}\right)=\left(\frac{1}{3}, \frac{1}{2}\right)\)
∴ Required line passes through (0, 0) and \(\left(\frac{1}{3}, \frac{1}{2}\right)\).
Equation of the line in two point form is
\(\frac{y-y_{1}}{y_{2}-y_{1}}=\frac{x-x_{1}}{x_{2}-x_{1}}\)
∴ the equation of the required line is
\(\frac{y-0}{\frac{1}{2}-0}=\frac{x-0}{\frac{1}{3}-0}\)
∴ 2y = 3x
∴ 3x – 2y = 0
Question 13.
Find the equation of the line passing through the points A(-3, 0) and B(0, 4).
Solution:
Since, the required line passes through the points A(-3, 0) and B(0, 4).
Equation of the line in two point form is
\(\frac{y-y_{1}}{y_{2}-y_{1}}=\frac{x-x_{1}}{x_{2}-x_{1}}\)
Here, (x1, y1) = (-3, 0) and (x2, y2) = (0, 4)
∴ the equation of the required line is
∴ \(\frac{y-0}{4-0}=\frac{x-(-3)}{0-(-3)}\)
∴ \(\frac{y}{4}=\frac{x+3}{3}\)
∴ 4x + 12 = 3y
∴ 4x – 3y + 12 = 0
![]()
Question 14.
Find the equation of the line:
(i) having slope 5 and making intercept 5 on the X-axis.
(ii) having an inclination 60° and making intercept 4 on the Y-axis.
Solution:
(i) Since, the x-intercept of the required line is 5.
∴ it passes through (5, 0).
Also, slope(m) of the line is 5
Equation of the line in slope point form is y – y1 = m(x – x1)
∴ the equation of the required line is y – 0 = 5(x – 5)
∴ y = 5x – 25
∴ 5x – y – 25 = 0
(ii) Given, Inclination of line = θ = 60°
∴ Slope of the line (m) = tan θ
= tan 60°
= √3
and the y-intercept of the required line is 4.
∴ it passes through (0, 4).
Equation of the line in slope point form is y – y1 = m(x – x1)
∴ the equation of the required line is y – 4 = √3(x – 0)
∴ y – 4 = √3x
∴ √3x – y + 4 = 0
Question 15.
The vertices of a triangle are A(1, 4), B(2, 3), and C(1, 6). Find equations of
(i) the sides
(ii) the medians
(iii) Perpendicular bisectors of sides
(iv) altitudes of ∆ABC
Solution:
Vertices of ∆ABC are A(1, 4), B(2, 3), and C(1, 6)
(i) Equation of the line in two-point form is

Since, both the points A and C have same x co-ordinates i.e. 1
∴ the points A and C lie on a line parallel to Y-axis.
∴ the equation of side AC is x = 1.
(ii) Let D, E, and F be the midpoints of sides BC, AC, and AB respectively of ∆ABC.
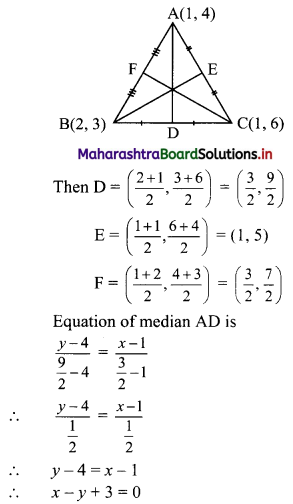

(iii) Slope of side BC = \(\left(\frac{6-3}{1-2}\right)=\left(\frac{3}{-1}\right)\) = -3
∴ Slope of perpendicular bisector of BC is \(\frac{1}{3}\) and the line passes through \(\left(\frac{3}{2}, \frac{9}{2}\right)\)
∴ Equation of the perpendicular bisector of side BC is \(\left(y-\frac{9}{2}\right)=\frac{1}{3}\left(x-\frac{3}{2}\right)\)
∴ \(\frac{2 y-9}{2}=\frac{1}{3}\left(\frac{2 x-3}{2}\right)\)
∴ 3(2y – 9) = (2x – 3)
∴ 2x – 6y + 24 = 0
∴ x – 3y + 12 = 0
Since, both the points A and C have the same x co-ordinates i.e. 1
∴ the points A and C lie on the line x = 1.
AC is parallel to Y-axis and therefore, the perpendicular bisector of side AC is parallel to X-axis.
Since, the perpendicular bisector of side AC passes through E(1, 5).
∴ the equation of the perpendicular bisector of side AC is y = 5.
Slope of side AB = \(\left(\frac{3-4}{2-1}\right)\) = -1
∴ Slope of perpendicular bisector of AB is 1 and the line passes through \(\left(\frac{3}{2}, \frac{7}{2}\right)\).
∴ Equation of the perpendicular bisector of side AB is \(\left(y-\frac{7}{2}\right)=1\left(x-\frac{3}{2}\right)\)
∴ \(\frac{2 y-7}{2}=\frac{2 x-3}{2}\)
∴ 2y – 7 = 2x – 3
∴ 2x – 2y + 4 = 0
∴ x – y + 2 = 0
![]()
(iv) Let AX, BY and CZ be the altitudes through the vertices A, B, and C respectively of ∆ABC.
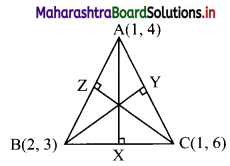
Slope of BC = -3
∴ Slope of AX = \(\frac{1}{3}\) …..[∵ AX ⊥ BC]
Since, altitude AX passes through (1, 4) and has slope \(\frac{1}{3}\)
∴ equation of altitude AX is y – 4 = \(\frac{1}{3}\)(x – 1)
∴ 3y – 12 = x – 1
∴ x – 3y + 11 = 0
Since, both the points A and C have the same x co-ordinates i.e. 1
∴ the points A and C lie on the line x = 1.
AC is parallel to Y-axis and therefore, altitude BY is parallel to X-axis.
Since, the altitude BY passes through B(2, 3).
∴ the equation of altitude BY is y = 3.
Also, slope of AB = -1
∴ Slope of CZ = 1 …..[∵ CZ ⊥ AB]
Since, altitude CZ passes through (1, 6) and has slope 1
∴ equation of altitude CZ is y – 6 = 1(x – 1)
∴ y – 6 = x – 1
∴ x – y + 5 = 0